Analyzing Vaccine Trials in Epidemics With Mild and Asymptomatic Infection

Abstract

Vaccine efficacy against susceptibility to infection (VE_S), regardless of symptoms, is an important endpoint of vaccine trials for pathogens with a high proportion of asymptomatic infection, because such infections may contribute to onward transmission and long-term sequelae, such as congenital Zika syndrome. However, estimating VE_S is resource-intensive. We aimed to identify approaches for accurately estimating VE_S when limited information is available and resources are constrained. We modeled an individually randomized vaccine trial by generating a network of individuals and simulating an epidemic. The disease natural history followed a “susceptible-exposed-infectious/symptomatic (or infectious/asymptomatic)-recovered” model. We then used 7 approaches to estimate VE_S, and we also estimated vaccine efficacy against progression to symptoms (VE_P). A corrected relative risk and an interval-censored Cox model accurately estimate VE_S and only require serological testing of participants once, while a Cox model using only symptomatic infections returns biased estimates. Only acquiring serological endpoints in a 10% sample and imputing the remaining infection statuses yields unbiased VE_S estimates across values of the basic reproduction number (R₀) and accurate estimates of VE_P for higher R₀ values. Identifying resource-preserving methods for accurately estimating VE_S and VE_P is important in designing trials for diseases with a high proportion of asymptomatic infection.

In 2015, the World Health Organization identified a list of priority pathogens with the potential to cause future public health emergencies of international concern (1). The Coalition for Epidemic Preparedness Innovations has committed 1 billion dollars to vaccine development efforts, starting with 3 of these pathogens: Middle East respiratory syndrome coronavirus, Lassa virus, and Nipah virus (2). These 3 pathogens, as well as others on the World Health Organization’s list, such as Zika virus, have high proportions of asymptomatic or mild infection (2–7). Vaccine efficacy (VE) against susceptibility to infection (VE_S) (8), regardless of symptom level, is an important endpoint of vaccine trials for these pathogens, because infection may contribute to onward transmission and to outcomes such as congenital Zika syndrome, even without primary symptoms (9–14). However, estimation of VE_S is resource-intensive, since it requires testing of all trial participants, either by periodically conducting assays for infection throughout the trial or by performing serological testing at the trial’s conclusion if natural and vaccine-derived immune responses can be distinguished. Testing of trial participants is also necessary for estimating vaccine efficacy against progression to symptoms (VE_P), another critical outcome measure (8). As Rodriguez-Barraquer et al. (15) noted in an analysis of dengue vaccine trial results, protection against symptomatic infection may differ from protection against infection (and, in the case of dengue, VE_P may be negative because of antibody-dependent enhancement) in general. It is therefore important to consider estimates of both VE_S and VE_P when analyzing trial results.

We aimed to identify a method for accurately estimating VE_S and VE_P when only a limited amount of information is available and resources—both time and money—are constrained. Throughout this paper, we use “asymptomatic” synonymously with “subclinical” to mean any infection episode which does not generate sufficient symptoms to prompt testing that would reveal the participant to be currently infected with the causative pathogen.

METHODS

We model a vaccine trial by first generating a model of a main population and a network of individuals grouped into communities, the structure of which has been described previously (see Web Table 1, available at https://academic.oup.com/aje, for parameters) (16). The model is compartmental, using deterministic (differential equation) dynamics for the main population and stochastic dynamics in the communities. We simulate an epidemic in the main population with a seasonal transmission rate that generates an epidemic curve with a shape similar to the epidemic curve of the 2015 Zika virus outbreak in Brazil (17). The disease is introduced into communities via infectious contact with the main population, and transmission occurs when infected persons transmit the virus to their susceptible contacts in the community. All susceptible persons have a daily probability of infection from each of their infectious contacts of 1 − e^−β, where β is the force of infection, as well as a daily external hazard of infection from the main population, which varies with the prevalence in the main population.

The disease natural history follows a “susceptible-exposed-infectious/symptomatic (or infectious/asymptomatic)-recovered” model, with estimated incubation and infectious periods of a Zika-like disease (Web Table 1). Vector transmission is not directly modeled, so the serial interval of the simulated disease is shorter than that of Zika virus disease. Symptomatic and asymptomatic infections are assumed to be equally infectious, and whether a person is infected by a symptomatic individual or an asymptomatic individual does not affect their probability of becoming symptomatic. The baseline parameters of the model assume that 20% of those infected in both the vaccine and control groups become symptomatic, based on the estimated proportion of Zika virus infections that are symptomatic (9). The epidemic and the vaccine trial are simulated in both a network of individuals grouped into 5 relatively disconnected communities and a network of individuals in 1 large community.

For the 150-day trial, 7.5% of people in the communities are enrolled and individually randomized to the vaccine group or the control group. All persons enrolled in the trial are assumed to be naive to the infection, which in practice might require serological testing of all individuals prior to enrollment. The vaccine is imperfect (“leaky”), meaning it reduces but does not eliminate the probability of infection upon each exposure to an infectious person. The daily probability of infection from vaccinees’ infectious contacts is 1 − e^{−β(1−VE)}, where VE is the assumed direct vaccine efficacy (8, 18).

VE_S is estimated by means of 7 different approaches, which are described in Table 1. Trial status (i.e., vaccine or control) is the explanatory variable for all Cox proportional hazards models, and persons who are never infected are censored at the end of the trial. Approach 1 assumes that the time of infection is known exactly (to the day), even for asymptomatic infections, and therefore would be strictly applicable only where very frequent testing was performed throughout the trial. Approach 2 assumes that infection is unobserved for asymptomatic infections, so only symptomatic infections are included in the Cox regression, and persons infected asymptomatically are assumed to survive without infection to the end of follow-up. Because this latter approach leads to bias in estimating VE_S (see Figure 1 and the Results section), we consider additional approaches (19).

Table 1.

Approaches for Estimating Vaccine Efficacy Against Susceptibility to Infection

Approach No.	Description of Approach	Symptomatic Infections	Asymptomatic Infections	Equation/Method	Testing Frequency in Asymptomatic Persons
1	Cox—“perfect knowledge”	Exact day of infection known	Exact day of infection known	$\mathrm{\lambda }\left(t|X_i\right)={\mathrm{\lambda }}_0\left(t\right)e^{\mathrm{\beta }{X}_i}$, where ${\mathrm{\lambda }}_0\left(t\right)$ is the unknown baseline hazard, β is the vector of coefficients for covariates (i.e., trial status, community if stratified), and t is the time of the event. t for nonevents is infinity.	Requires frequent monitoring for pathogen (polymerase chain reaction, oral or urine swabs, etc., depending on the pathogen) throughout trial
2	Cox—symptomatic onlya	Exact day of infection known	Treated as nonevents	$\mathrm{\lambda }\left(t|X_i\right)={\mathrm{\lambda }}_0\left(t\right)e^{\mathrm{\beta }{X}_i}$, where ${\mathrm{\lambda }}_0\left(t\right)$ is the unknown baseline hazard, β is the vector of coefficients for covariates (i.e., trial status, community if stratified), and t is the time of the event. t for nonevents or asymptomatic events is infinity.	N/A
3	Relative risk estimate	Ascertained prospectively and total counted at end of trial	Ascertained at end of trial	${\widehat{\mathrm{VE}}}_S=1-\frac{\mathrm{Attack}\mathrm{Rate}(\mathrm{Vaccinated})}{\mathrm{Attack}\mathrm{Rate}(\mathrm{Control})}$	Serological testing once at end of trial
4	Corrected relative risk estimate (25)	Ascertained prospectively and total counted at end of trial	Ascertained at end of trial	${\widehat{\mathrm{VE}}}_S=1-\frac{\ln \left(1-\mathrm{Attack}\mathrm{Rate}\left(\mathrm{Vaccinated}\right)\right)}{\ln \left(1-\mathrm{Attack}\mathrm{Rate}\left(\mathrm{Control}\right)\right)}$	Serological testing once at end of trial
5	Interval-censored Cox model (3 intervals)	Exact day of infection known	Interval for infection time known: 3 serological tests	$\mathrm{\lambda }\left(t|X_i\right)={\mathrm{\lambda }}_0\left(t\right)e^{\mathrm{\beta }{X}_i}$, where ${\mathrm{\lambda }}_0\left(t\right)$ is the unknown baseline hazard, β is the vector of coefficients for covariates (i.e., trial status, community if stratified), and t is the time of the event. t for nonevents is infinity; t for asymptomatic events is treated as an interval.	Serological testing 2 times throughout trial and once at end (i.e., day 50, day 100, and day 150)
6	Interval-censored Cox model (1 interval)	Exact day of infection known	Interval for infection time: length of trial		Serological testing once at end of trial
7	Imputation	Exact day of infection known	Interval for infection time: length of trial	Probability of infection (in 1-community analysis) or ratio of asymptomatic infections to symptomatic infections (in 5-community analysis) is estimated in a sample of 10% of the vaccinated and the control groups. Infectious status of the remaining asymptomatic individuals is imputed using multiple (10) imputation (28). Imputed data set is then analyzed using approach 6.	Serological testing once at end of trial for 10% sample

Abbreviations: N/A, not applicable; VE_S, vaccine efficacy against susceptibility to infection.

^a Assumes that the same proportions of vaccinated and control cases are symptomatic.

Figure 1.

Differential misclassification of at-risk person-time. Panel A shows reality—who is truly infected and who is truly still at risk. Panel B shows who we perceive to be infected and still at risk when considering only symptomatic individuals. When considering only symptomatic events, presumed person-time at risk increases for both the vaccine group and the control group, because all persons with asymptomatic infections are now perceived to be uninfected and at risk for the entire period of the trial. In the vaccine group, 11 people are perceived to still be at risk (panel B), when in reality only 7 remain at risk (panel A), since 4 people are asymptomatically infected. In the control group, 10 people are perceived to be at risk (panel B), when in reality only 2 remain at risk (panel A). Because there are more people infected and therefore more people incorrectly still perceived to be at risk in the control group than in the vaccine group, apparent incidence is underestimated in the controls more so than in the vaccine group, leading to bias towards the null. This bias is exacerbated as R₀ increases and more people in the control group become infected but are still perceived to be at risk. At time t postrandomization, person-time at risk in the controls will be overestimated by a factor of $e^{\mathrm{\Lambda }\left(t\right)\left(1-{\mathrm{\Theta }}_{P}p\right)(1-{\mathrm{\Theta }}_S)}$ relative to the vaccine group, where $\mathrm{\Lambda }(t)$ is the cumulative hazard up to time t, p is the symptomatic proportion in controls, and $\mathrm{1}-{\mathrm{\theta }}_S$ and $\mathrm{1}-{\mathrm{\theta }}_P$ are the efficacy of the vaccine against infection and the efficacy of the vaccine against disease given infection, respectively (29). This will be greater than 1 for nonnegative VE_P and positive VE_S. VE_P, vaccine efficacy against progression to symptoms; VE_S, vaccine efficacy against susceptibility to infection.

Approach 3 uses the risk ratio for infection (measured at the end of the trial), rather than the hazard ratio—an approach that is known to be biased when used with a leaky vaccine (18). Approach 4 corrects this relative risk estimate under the assumption that the VE can be recovered from the ratio of cumulative hazards. Approaches 5 and 6 use interval-censored models. Here, the exact day of infection for the symptomatic individuals is known (and in practice would be laboratory-confirmed). For the asymptomatically infected individuals, the interval for day of infection ranges from the day of the person’s last negative serological test to the day of their first positive serological test. Two different interval lengths are assessed to determine whether increased frequency of testing yields more precise results (20). As we mentioned above, this approach assumes the ability of the serological test to distinguish between vaccine-acquired immunity and naturally acquired immunity, which is currently possible for some but not all vaccines/pathogens (21–23). Finally, in approach 7, a sample of trial participants are tested, and the infection statuses of the asymptomatic individuals not in the sample are imputed. The interval-censored model from approach 6 is then used in the imputed data set.

The results from the network with 5 communities are analyzed first with the same 7 approaches, treating the 5 communities as if they were 1 large community. Alternatively, to account for the potential for heterogeneity in hazard rates between communities, the Cox models in approaches 1, 2, and 5–7 are stratified by community (16), and estimates from approaches 3 and 4 are calculated separately within each community and meta-analyzed using inverse-variance weighting.

Empirical coverage probabilities are calculated by the proportion of simulations with 95% confidence intervals that cover the true VE_S parameter of the model (60%). Statistical power is estimated by the proportion of simulations in which P is less than 0.05, using a 2-sided Wald test for the null hypothesis of VE_S = 0, and the estimated VE_S is greater than 0. The trial is also simulated with fewer participants to assess power in smaller trials.

Additionally, to evaluate the efficacy of the vaccine in preventing progression to symptoms, VE_P is estimated by

$$1-\frac{\frac{\mathrm{Symptomatic}\mathrm{infections}\mathrm{in}\mathrm{vaccinees}}{\mathrm{All}\mathrm{infections}\mathrm{in}\mathrm{vaccinees}}}{\frac{\mathrm{Symptomatic}\mathrm{infections}\mathrm{in}\mathrm{controls}}{\mathrm{All}\mathrm{infections}\mathrm{in}\mathrm{controls}}}.$$

Finally, to assess whether the results hold in other contexts, trial parameters such as trial length, VE_S, R₀, and the proportion of infected individuals in each arm of the trial who become symptomatic are varied.

R code (R Foundation for Statistical Computing, Vienna, Austria) for these analyses is available on GitHub (24).

RESULTS

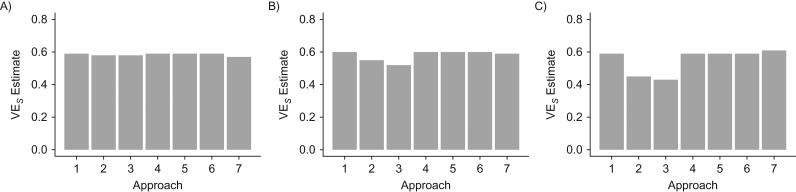
Figure 2 displays the results of the median of 500 simulations in the single-community network, showing VE_S estimates from the 7 approaches described above across 3 values of R₀, the basic reproduction number. As expected, approach 1 returns accurate VE_S estimates, while approach 2 returns estimates that are biased towards the null because there is differential overestimation of person-time at risk, with worse overestimates in the controls (Figure 1). This bias is exacerbated as R₀ increases. Approach 3 returns an estimate that is biased toward the null in comparison with the true value of VE_S, also as expected and also worsened at higher levels of R₀ (8). Approach 4 corrects this bias by converting the risk-based analysis into a rate-based analysis (18, 25).

Figure 2.

Estimates of vaccine efficacy against susceptibility to infection (VE_S) obtained using 7 different approaches for R₀ = 1 (A), R₀ = 1.25 (B), and R₀ = 1.5 (C) under the model’s baseline parameters in the 1-community network. The 7 approaches are: Cox—“perfect knowledge” (1), Cox—symptomatic only (2), relative risk estimate (3), corrected relative risk estimate (4), interval-censored Cox model (3 intervals) (5), interval-censored Cox model (1 interval) (6), and imputation (7).

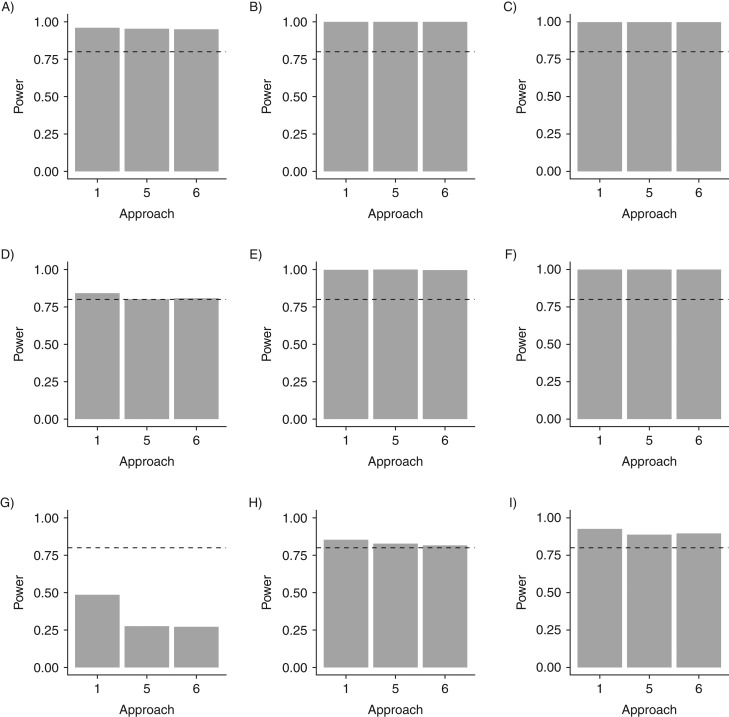
The interval-censored Cox proportional hazards models (approaches 5 and 6) return estimates approximately equal to the VE_S input into the model. These approaches require fewer resources than would be necessitated by the Cox model with perfect knowledge of infection time (approach 1) because they use only 3 serological tests or 1 serological test, respectively, rather than frequent monitoring for infection throughout the follow-up period. Approach 6, the interval-censored Cox model with testing only at the end of the trial, yields the same results as approach 5, testing 3 times, without substantial difference in coverage probability or power in the settings considered (Table 2 and Figure 3). Thus, both approach 4 and approach 6 yield accurate estimates, with testing only required once at the end of the trial.

Table 2.

Estimates of Vaccine Efficacy Against Susceptibility to Infection and Empirical Coverage Probabilities^a

Approach	R0 = 1.00				R0 = 1.25				R0 = 1.50
	1 Community		5 Communities		1 Community		5 Communities		1 Community		5 Communities
	${\widehat{\mathbf{VE}}}_{\mathbf{S}}$	Cov	${\widehat{\mathbf{VE}}}_{\mathbf{S}}$	Cov	${\widehat{\mathbf{VE}}}_{\mathbf{S}}$	Cov	${\widehat{\mathbf{VE}}}_{\mathbf{S}}$	Cov	${\widehat{\mathbf{VE}}}_{\mathbf{S}}$	Cov	${\widehat{\mathbf{VE}}}_{\mathbf{S}}$	Cov
1	0.59	0.96	0.59	0.95	0.60	0.95	0.59	0.94	0.59	0.93	0.59	0.94
2	0.58	0.96	0.58	0.94	0.55	0.90	0.52	0.85	0.45	0.49	0.46	0.52
3	0.58	0.95	0.58	0.95	0.52	0.51	0.51	0.49	0.43	0	0.44	0
4	0.59	0.96	0.59	0.94	0.60	0.95	0.59	0.95	0.59	0.94	0.59	0.94
5	0.59	0.96	0.59	0.95	0.60	0.94	0.59	0.94	0.59	0.94	0.59	0.93
6	0.59	0.95	0.59	0.95	0.60	0.94	0.59	0.93	0.59	0.93	0.59	0.92
7	0.57	0.88b	0.59	0.96	0.59	0.91	0.58	0.97	0.61	0.92	0.58	0.96

Abbreviations: Cov, coverage; VE_S, vaccine efficacy against susceptibility to infection.

^a Empirical coverage probabilities are calculated using the proportion of simulations with 95% confidence intervals that cover the true VE_S parameter of the model (0.60).

^b Imputation with a 20% sample results in VE_S = 0.61 with 96% empirical coverage probability, and imputation with a 30% sample results in VE_S = 0.58 with 99% empirical coverage probability.

Figure 3.

Statistical power of the Cox “perfect knowledge” approach (approach 1) and 2 interval-censored models (approaches 5 and 6) to estimate vaccine efficacy against susceptibility to infection in 1 community with 1,500 trial participants (baseline) and R₀ = 1 (A), R₀ = 1.25 (B), and R₀ = 1.5 (C) (first row); in 1 community with 250 trial participants and R₀ = 1 (D), R₀ = 1.25 (E), and R₀ = 1.5 (F) (second row); and in 1 community with 100 trial participants and R₀ = 1 (G), R₀ = 1.25 (H), and R₀ = 1.5 (I) (third row). The interval-censored models do not lead to a substantial loss of power, except in the trial with 100 participants enrolled when R₀ = 1. The dashed lines represent a power of 80%.

Even a single serological test could be resource-intensive. Approach 7, which only requires testing 10% of the trial participants at the end of the trial, results in accurate estimates of VE_S (Figure 2) for all values of R₀ considered and accurate estimates of VE_P (Table 3) for R₀ values of 1.25 or 1.50. Only testing 10% of the trial participants once at the end of the trial substantially reduces required resources. However, when the number of cases is very low (Web Table 2), a 10% sample does not accurately estimate VE_P, and this approach has larger variance than others under the baseline parameters (i.e., wider confidence intervals; see Web Table 3). A larger sample, such as a 20% or 30% sample, more accurately estimates a null VE_P (Table 3). A combination of approaches 5 and 7 performs similarly to approach 7, which is consistent with the similar performances of approaches 5 and 6.

Table 3.

Median Estimate of Vaccine Efficacy Against Progression to Symptoms (True VE_P = 0) in the Full Trial and in a 10% Sample From Approach 7

VEP	R0 = 1.00		R0 = 1.25		R0 = 1.50
	1 Community	5 Communities	1 Community	5 Communities	1 Community	5 Communities
Full trial	−0.020	0.003	0.020	−0.010	−0.010	−0.002
10% sample	0.500a	0.130	0.060	−0.010	0	−0.003

Abbreviation: VE_P, vaccine efficacy against progression to symptoms.

^a Imputation with a 20% sample results in VE_P = 0.17, and imputation with a 30% sample results in VE_P = 0.03.

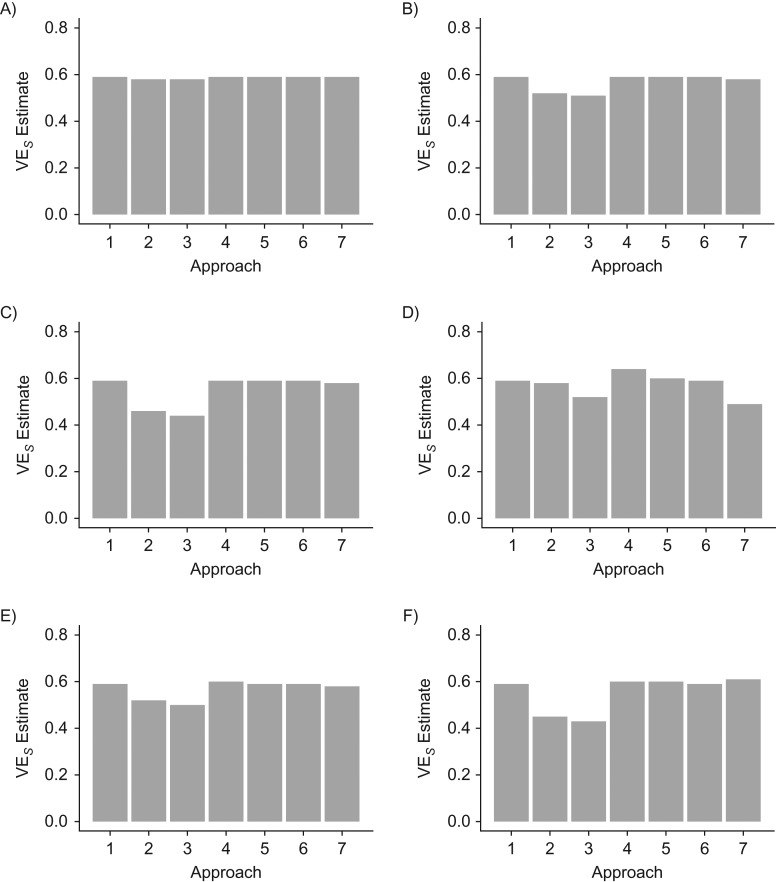
Similar results are obtained in the analyses of the 5 communities (Figure 4). However, when the number of cases is low (R₀ = 1), the meta-analyses of approaches 4 and 7 are imprecise. Results are essentially unchanged across simulations with a longer duration of the trial, with Ebola-like parameters (Web Table 1), with changes in VE, and with differing proportions of symptomatic persons among the vaccine and control groups (i.e., VE_P ≠ 0), as shown in Web Figures 1–3 and Web Tables 4 and 5. When the vaccine has an effect on both susceptibility to infection and progression to symptoms, serological testing helps differentiate between VE_S and VE_P except when the total number of cases is low. Similar results are also obtained from simulations with higher R₀ values (e.g., 2.5 and 5) (Web Table 5 and Web Figure 2). However, approach 7 is less precise (although it has >95% coverage) for R₀ = 5, because the number of people eligible for the trial (i.e., those who remain uninfected before the trial begins) is much lower due to the high rate of infection, decreasing the size of the sample used for imputation.

Figure 4.

Estimates of vaccine efficacy against susceptibility to infection (VE_S) obtained using 7 different approaches for a 5-community network analyzed as 1 large community for R₀ = 1 (A), R₀ = 1.25 (B), and R₀ = 1.5 (C) and with stratified and meta-analyses for R₀ = 1 (D), R₀ = 1.25 (E), and R₀ = 1.5 (F) under baseline parameters. The 7 approaches are: Cox—“perfect knowledge” (1), Cox—symptomatic only (2), relative risk estimate (3), corrected relative risk estimate (4), interval-censored Cox model (3 intervals) (5), interval-censored Cox model (1 interval) (6), and imputation (7).

DISCUSSION

For pathogens with a high proportion of mild or asymptomatic infection, understanding whether the vaccine prevents all infection, not solely symptomatic infection, as well as understanding the vaccine’s effect on progression to symptoms, is critical for determining the epidemiologic impact of the vaccine. However, costs and resources can pose major barriers to estimation of these important values. Here we have discussed different approaches and their varying levels of accuracy and resource requirements for estimating VE_S and VE_P. The corrected relative risk estimate (approach 4), the interval-censored Cox models (approaches 5 and 6), and the imputed interval-censored Cox model (approach 7) provide estimates close to the VE_S input into the model across values of R₀, which is of course also obtained under the assumption of perfect knowledge of the time of all asymptomatic infections (approach 1). A Cox model considering only symptomatic infections proves biased, especially at higher values of R₀. Approaches 1 and 4–7 return accurate estimates of VE_P, with the exception of approach 7 when R₀ is low due to the small number of cases overall and in the sample. In this case, or if higher coverage is desired, a larger sampling percentage can be used (Table 2). While these simulations are parameterized for a Zika-like pathogen given the high proportion of asymptomatic Zika infections, results from simulations with Ebola-like parameters show that these methods are applicable to pathogens other than Zika virus (Web Figure 2).

In practice, using a Cox proportional hazards model for the time of all infections would entail testing everyone frequently (perhaps weekly or even daily) for infection throughout the trial, requiring substantial expenditures of both money and time. Using a corrected relative risk estimate or an interval-censored Cox model, an accurate estimate of VE_S and VE_P can be obtained with serological testing only once at the end of the trial. Testing only 10% of the trial population and imputing the event status of the remaining asymptomatic trial participants substantially reduces the resources needed while still providing critical information about the vaccine.

These approaches work in both trials conducted in 1 large community and trials conducted in disconnected communities, such as the recent malaria trials (26). In trials with more communities or increased heterogeneity, the bias from heterogeneity in hazard rates will probably be more pronounced (16). Methods to account for this heterogeneity, such as stratification, meta-analyses, or incorporation of random effects, should therefore be used, although when the number of cases is very low, some of these approaches may be imprecise.

Many simplifying assumptions are made in the model, including complete ascertainment of infectious cases, perfect sensitivity and specificity of the diagnostic test, and comparability of the infected vaccinees and infected controls for the estimation of VE_P (8). While approaches 4–7 require substantially fewer resources for estimating VE_S and VE_P than approach 1 and are more accurate than approaches 2 and 3, all participants must be tested at the beginning of the trial to ensure that they are not exposed or immune. Including persons with preexisting immunity in the trial would reduce the total number of overall cases and thus the power, limiting the ability to draw a statistically significant conclusion about the vaccine’s effects. This challenge, however, is not limited to diseases with high proportions of mild or asymptomatic infection, since prior immunity would reduce the power of any trial. Additionally, distinguishing between natural and vaccine-derived immunity can be challenging, especially at the beginning of an outbreak of an emerging infectious disease about which not much is known and for which serological tests are likely in early stages of development (23, 27). Therefore, investments in diagnostic development will also be critical for ensuring accurate VE estimates.

We have identified methods that accurately estimate VE_S and VE_P and only require serological testing of trial participants once at the end of the trial. Only acquiring serological endpoints in a 10% sample yields unbiased VE_S estimates, substantially reducing required resources. While parameterized for a Zika-like disease, the approaches and exact parameters described above are not meant to represent a particular epidemic context but merely to serve as a guide when thinking through how to accurately estimate important endpoints of vaccine trials in different settings with limited resources and information. R code for this simple model can be readily modified to reflect disease-, vaccine-, and setting-specific parameters. Identifying resource-preserving methods is important in designing trials for diseases with a high proportion of asymptomatic or mild infection, especially when those cases are still infectious. Understanding the potential sources of bias from different approaches can allow for more accurate estimates in epidemic settings.

Abbreviations

VE

vaccine efficacy

VE_P

vaccine efficacy against progression to symptoms

VE_S

vaccine efficacy against susceptibility to infection