Abstract
Understanding how active dendrites are exploited for behaviorally relevant computations is a fundamental challenge in neuroscience. Grid cells in medial entorhinal cortex represent an attractive model system for addressing this question, as the computation they perform is clear: they convert synaptic inputs into spatially modulated, periodic firing. Whether active dendrites transform synaptic input into the dual temporal and rate codes characteristic of grid cell output is unknown. We show that dendrites of medial entorhinal cortex neurons are highly excitable and exhibit a supralinear input–output function in vitro, while in vivo recordings reveal membrane potential signatures consistent with recruitment of active conductances. By incorporating these nonlinear dynamics into grid cell models, we show that they can sharpen the precision of the temporal code and enhance the robustness of the rate code, thereby supporting a stable, accurate representation of space under varying environmental conditions. Our results suggest that active dendrites may therefore constitute a key cellular mechanism for ensuring reliable spatial navigation.
Active, voltage-dependent conductances in neuronal dendrites transform the relationship between synaptic input and neuronal output1,2. The resulting enrichment of the integration capabilities of single neurons has long been suggested as being exploited for computations relevant to behavior3,4. However, the details of how specific active-dendritic mechanisms are involved in behavioral computations have proved to be elusive. Recent work has provided evidence that the active properties of dendrites are engaged in somatosensory and visual cortical neurons during sensory processing5–8. Moreover, dendritic nonlinearities also appear to be activated during behavioral tasks involving spatial navigation9–11. While these studies have provided important correlative evidence that dendritic mechanisms are engaged under various circumstances, they do not provide a quantitative link for explaining how specific biophysical mechanisms can contribute to behavioral computations.
Grid cells in medial entorhinal cortex (MEC) represent a particularly attractive model system for linking cellular and circuit mechanisms to a behaviorally relevant computation. Grid cells exhibit a striking spatial code, with firing fields that span the environment of a navigating animal in a periodic hexagonal pattern, and have thus been proposed as representing a neural mechanism for path integration12. Moreover, there exist several well-developed single-cell and network models of grid cell generation13–19, providing a rigorous quantitative framework for understanding how particular biophysical mechanisms relate to the computation of spatial location. Layer 2 of MEC (MECII) contains the highest proportion of grid cells20,21, and stellate cells, which form most of the MECII principal cell population22, are likely grid cell candidates17,18,23,24. In stellate cells, the correlation between somatically recorded synaptic responses and the dorsoventral gradient in grid spacing in MECII25,26 has suggested that intrinsic voltage-gated conductances may be important for generating grid cell firing. However, very little is known about whether the dendrites of stellate cells are electrically excitable, and thus their contribution to grid cell firing is unclear.
Here we have combined in vitro two-photon glutamate uncaging and in vivo patch-clamp recording with modeling to assess the role of active dendrites in grid cell firing. We show that stellate cells have active dendrites that perform supralinear input–output transformations in vitro. We also identify electrophysiological signatures consistent with active dendritic integration in vivo, including membrane-potential-dependent boosting of excitatory postsynaptic potentials (EPSPs) and plateau potentials. We place our results in the context of single-cell and network models of grid cell firing and use modeling to show that active dendrites can promote the robustness of the grid cell rate code while sharpening the precision of the temporal phase precession code. Thus, dendrites of principal cells in MECII are highly excitable, and these active dendritic properties can enhance the accuracy and stability of the spatial map represented by grid cell firing.
Results
Supralinear integration in dendrites of MECII principal neurons
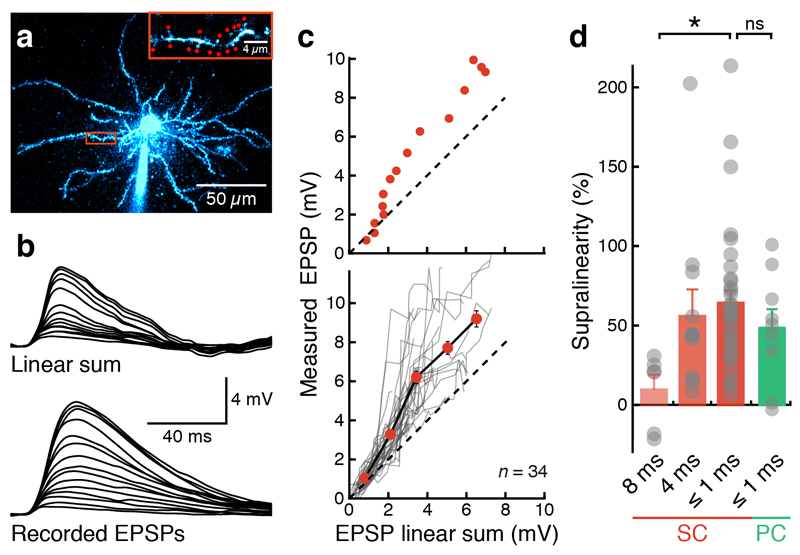
To assess how grid cells integrate synaptic inputs in single dendritic branches, we performed two-photon glutamate uncaging on dendritic spines of principal neurons in MECII (Fig. 1a). Activation of individual spines in MECII stellate cells produced glutamate uncaging-evoked EPSPs comparable to physiological synaptic responses (Fig. 1b and Supplementary Fig. 1). Activating increasing numbers of spines along a single dendrite or on two nearby dendrites evoked responses that were larger than the arithmetic sum of the corresponding individual responses (65 ± 7% supralinearity for intervals of ≤ 1 ms; n = 34 dendritic branches; Fig. 1b,c and Supplementary Fig. 2). Since recent data suggest that some MECII pyramidal cells may also display grid cell firing24,27, we also carried out experiments on MECII pyramidal cells and obtained similar results (Fig. 1d and Supplementary Fig. 3). The degree of supralinearity in stellate cells did not significantly scale with distance from the soma (Supplementary Fig. 4) but was reduced to 9 ± 9% (n = 6) when the intervals between spine activations were extended to 8 ms, demonstrating that it depends on millisecond timing of the inputs (Fig. 1d).
Figure 1. Supralinear synaptic integration in MEC principal neurons.
(a) Two-photon image of a MECII stellate cell filled with Alexa Fluor 594 via somatic patch-clamp recording. Inset shows the selected dendrite and the uncaging locations (red spots). (b) Somatic voltage responses to increasing number of stimulated synapses (indicated in the inset in a). Top traces show arithmetic sums expected from the individual responses; bottom traces show recorded responses (15 spines, 0.6-ms stimulation interval). (c) The amplitudes of somatically recorded glutamate uncaging-evoked EPSPs (gluEPSPs) were markedly larger than the arithmetic sum of the individual responses (dashed line indicates unity). Top, single experiment (as in a and b); bottom, summary of 34 experiments. Grey lines represent individual experiments; the black line connects binned averages across experiments (red). Error bars represent s.e.m.. (d) Nonlinearity depends on the interval between uncaging events (*P < 0.05). No significant difference in the degree of supralinearity was found between stellate cells (SC) and pyramidal cells (PC) of MECII (at ≤1-ms stimulation intervals). Nonlinearity in stellate cells at different stimulation intervals: 8 ms, 9 ± 9% (n = 6); 4 ms, 54 ± 16% (n = 11); ≤1 ms, 65 ± 7% (n = 34); one-way ANOVA for different stimulation intervals, P = 0.02, F = 4.22; nonlinearity in pyramidal cells at stimulation intervals; ≤1 ms: 48 ± 11% (n = 9; Mann-Whitney U test, P = 0.18 compared to stellate cells).
Dendritic spikes and supralinearity depend on Nav and NMDAR channels
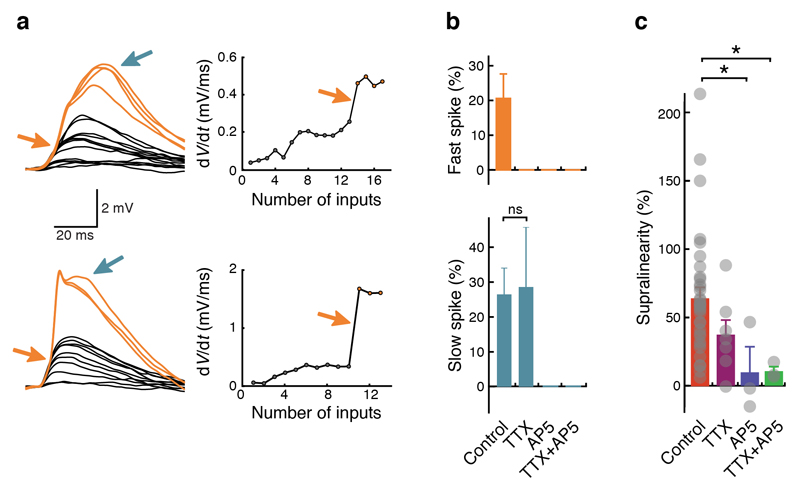
Activation of some dendritic branches produced clear signatures of dendritic spikes detected at the soma28,29. Dendritic spikes with fast and slow time-courses and distinct thresholds were observed (Fig. 2a), and application of pharmacological blockers revealed that these were generated by activation of voltage-gated sodium (Nav) channels and NMDA receptors (NMDARs), respectively (Fig. 2b and Supplementary Fig. 5). The NMDA receptor antagonist APV ((2R)-amino-5-phosphonovaleric acid) alone could also abolish fast spikes, indicating that NMDAR current was required to reach the threshold for Nav channel activation and that NMDARs and Nav channels thus acted cooperatively. This is also supported by the fact that a substantial fraction of fast spikes (43%) were followed by a slow spike, and many slow spikes (38%) were preceded by a fast spike. Both NMDAR channels, and to a lesser degree Nav channels, contributed to supralinearity (Fig. 2c).
Figure 2. Supralinear integration and dendritic spikes depend on voltage-gated sodium (Nav) and NMDA receptor channels.
(a) Left: examples of fast (orange arrows) and slow (blue arrows) dendritic spikes. Right: plots of dV/dt against number of uncaging locations. Fast dendritic spikes cause a step-like increase in dV/dt (arrows). (b) Top: fast dendritic spikes are present in 21 ± 7% (n = 34) of all recordings and abolished when Nav channels are blocked with tetrodotoxin (TTX) and/or when NMDARs are blocked with APV ((2R)-amino-5-phosphonovaleric acid). Bottom: slow dendritic spikes are present in 26 ± 7% (n = 34) of all recordings, still present in TTX (29 ± 17%; n = 7; Fisher’s exact test, P = 1.0) and abolished when NMDARs are blocked with APV. Uncaging interval ≤ 1 ms. Individual data points (not indicated in the figure) are either zeroes (no spikes were observed in a recording) or ones (spikes were observed in a recording). Bar graphs indicate the percentage of recordings containing spikes; error bars were calculated by Monte Carlo methods. (c) Application of TTX and APV reduces or abolishes supralinear dendritic integration. Grey dots represent individual recordings. Control: 65 ± 7% (n = 34); TTX: 36 ± 11% (n = 7; Mann-Whitney U test, P = 0.07 compared to control); APV: 11 ± 21% (n = 3; Mann-Whitney U test, P = 0.02 compared to control). TTX+APV: 11 ± 5% (n = 3; Mann-Whitney U test, P = 0.02 compared to control). One-way ANOVA, P = 0.03, F = 3.16.
Testing the contribution of nonlinear dendritic integration under in vivo conditions
To probe the contribution of dendritic nonlinearities in MECII stellate cells during more physiological in vivo-like conditions, we took advantage of the fact that the voltage profile underlying grid cell firing in vivo is represented by a ramp-like membrane potential depolarization17,18. We approximated this ramp-like depolarization in vitro by injecting a scaled current waveform that we had obtained from voltage-clamp recordings using the in vivo ramp as a voltage command (Online Methods). This allowed us to examine how in vivo-like membrane potential dynamics influenced dendritic integration of synaptic inputs. Both supralinear summation and dendritic spikes were more pronounced when uncaging was performed during the in vivo-like ramps (Supplementary Fig. 6), suggesting that these active events were likely to be engaged in vivo when an animal entered a grid firing field. Taken together, these results reveal that the dendrites of grid cells were highly excitable, exhibiting markedly nonlinear input–output functions in a manner that could transform the integration of synaptic inputs during navigational behavior.
Signatures of active dendrites in stellate cell recordings in vivo
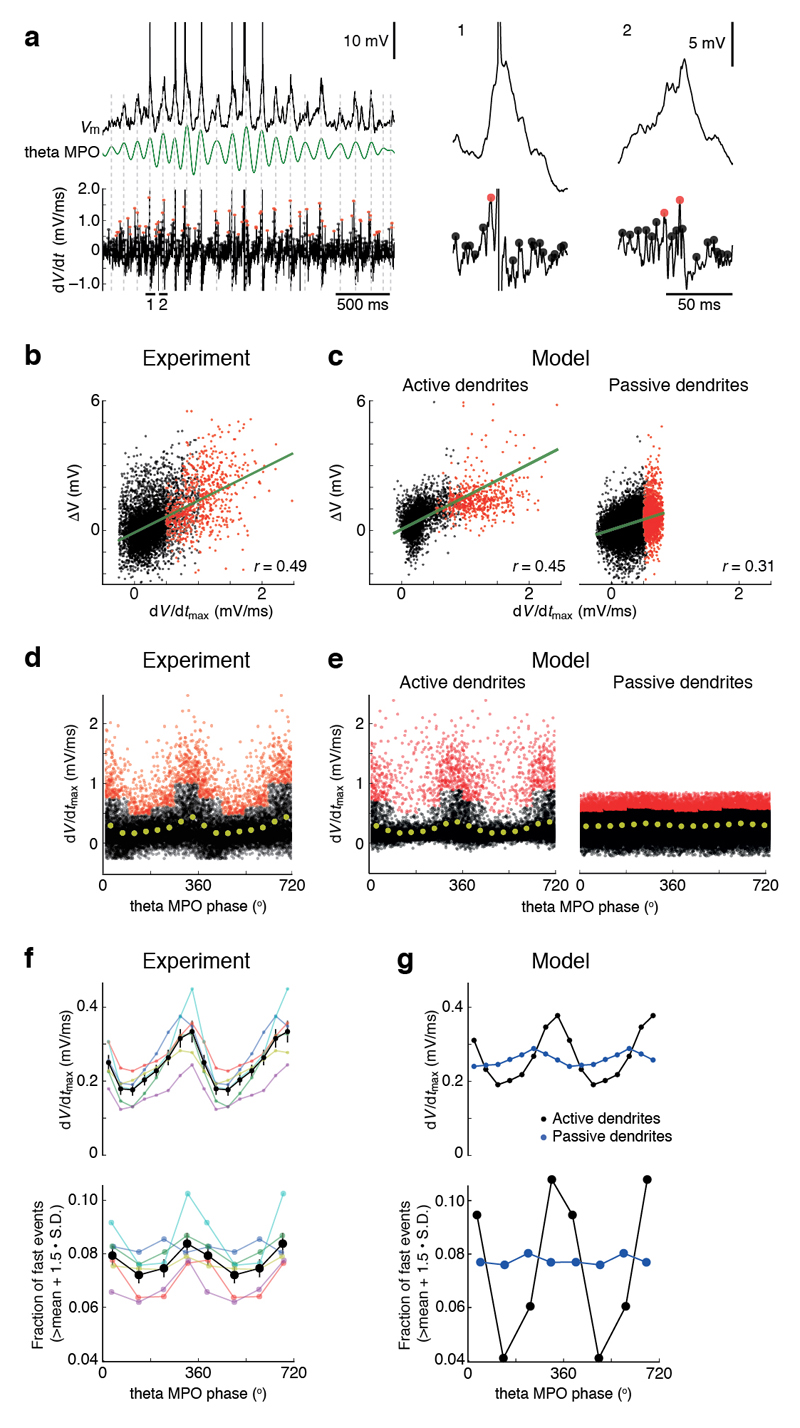
To determine whether active dendritic integration occurs in grid cells in vivo, we searched for the signatures of supralinear dendritic integration, as identified in our slice recordings, in patch-clamp recordings from MECII neurons of mice navigating in virtual reality18 (Fig. 3). By examining the differentiated membrane potential traces (dV/dt), we identified large peaks that were below the voltage threshold for action potentials and that were preferentially clustered around the peak of theta membrane potential oscillations (Fig. 3a), at a similar theta phase as action potentials during grid field crossings17,18. These dV/dt peaks in vivo were comparable in amplitude to dV/dt peaks of glutamate uncaging-evoked EPSPs exhibiting dendritic spikes in vitro (Fig. 2a and Supplementary Fig. 7). The in vivo dV/dt peaks were correlated with large depolarizations in Vm with amplitudes of up to ~6 mV (Fig. 3b), consistent with them being EPSPs that were boosted by activation of voltage-dependent conductances.
Figure 3. Engagement of active dendritic conductances in MECII principal neurons in vivo.
(a) Left: membrane potential (Vm; top), theta membrane potential oscillations (theta MPOs; middle, green trace) and differentiated membrane potential (dV/dt; bottom) during a firing field crossing in a MECII neuron (experimental data from Schmidt-Hieber and Häusser18). Grey dashed vertical lines indicate peaks (0° phase) of theta MPOs. Right: membrane potentials and differentiated membrane potentials at higher magnification for two episodes corresponding to the horizontal bars at the bottom of the traces on the left. Filled circles on dV/dt traces indicate peaks in dV/dt that are below (black) or above (red) the mean + 1.5 s.d. of all peaks within 90° bins of theta MPO phases. (b) Plot of peaks in membrane potential against corresponding peaks in dV/dt for the recording shown in a. Colors as in a. Green line represents a linear regression (r = 0.49; P < 10−5; n = 8,265 peaks). (c) As in b, for a detailed compartmental model of a MECII stellate cell with active (left; r = 0.45; P < 10−5; n = 14,411 peaks) or passive dendrites (right; r = 0.31; P < 10−5; n = 25,228 peaks). See Online Methods for model details. (d) Plot of peaks in dV/dt against the phase of theta MPOs for the recording shown in a. Colors as in a. Yellow filled circles represent binned averages. (e) As in d, for compartmental model data with active (left) or passive dendrites (right) as in c. (f) Analysis of n = 6 stellate cell recordings (data from Schmidt-Hieber & Häusser18). Peaks in dV/dt (top) and fraction of dV/dt peaks exceeding mean + 1.5 s.d. of all peaks within 90° bins of theta MPOs (bottom) are plotted against theta MPO phase. Black lines and symbols, average data. Error bars represent s.e.m. Colored lines and symbols show individual recordings. (g) As in f, for compartmental model data with active (black) or with passive dendrites (blue).
To probe the mechanisms underlying these dV/dt signatures in more detail, we used our experimental results to constrain a detailed compartmental model of MECII stellate cells that captures their measured passive, active and synaptic properties (Supplementary Fig. 8). Simulating grid cell firing in a model incorporating dendritic Nav and NMDAR channels reproduced the experimentally observed dV/dt signatures, including the correlation of dV/dt peak amplitudes with Vm (Fig. 3c). When dendritic Nav and NMDAR channels were removed from the model, these signatures were abolished (Fig. 3c). In our in vivo experimental data, the fastest-rising events occurred within the 90° phase-bin preceding the peak of theta membrane potential oscillations (MPOs; Fig. 3d,f). This phase-bin also contained a larger fraction of particularly fast events with maximal rates of rise resembling or exceeding the maximal rates of rise of fast dendritic spikes that we observed during our somatic in vitro recordings (Fig. 3f). These observations could also be faithfully reproduced by the model generating dendritic Na+ spikes in the presence of dendritic Nav channels but not in their absence (Fig. 3e,g).
To further quantify the contribution of nonlinear dendritic conductances to grid cell firing, we compared NMDAR activation and dendritic input currents in detailed compartmental models of stellate cells with active or passive dendrites (Supplementary Fig. 9). These simulations showed that during grid cell firing, with Vm trajectories representative of our in vivo recordings, NMDARs were substantially recruited (Supplementary Fig. 9a) and dendritic input currents were nonlinearly amplified by active, voltage-dependent conductances (Supplementary Fig. 9b). Furthermore, the membrane potential distributions in putative dendritic recordings in vivo covered the nonlinear range of the NMDAR open-probability curve, implying that NMDARs were nonlinearly engaged in vivo (Supplementary Fig. 10). In summary, we observed clear signatures of active dendritic integration in the membrane potential of MECII principal neurons during navigational behavior in vivo.
Plateau potentials during putative dendritic in vivo stellate cell recordings
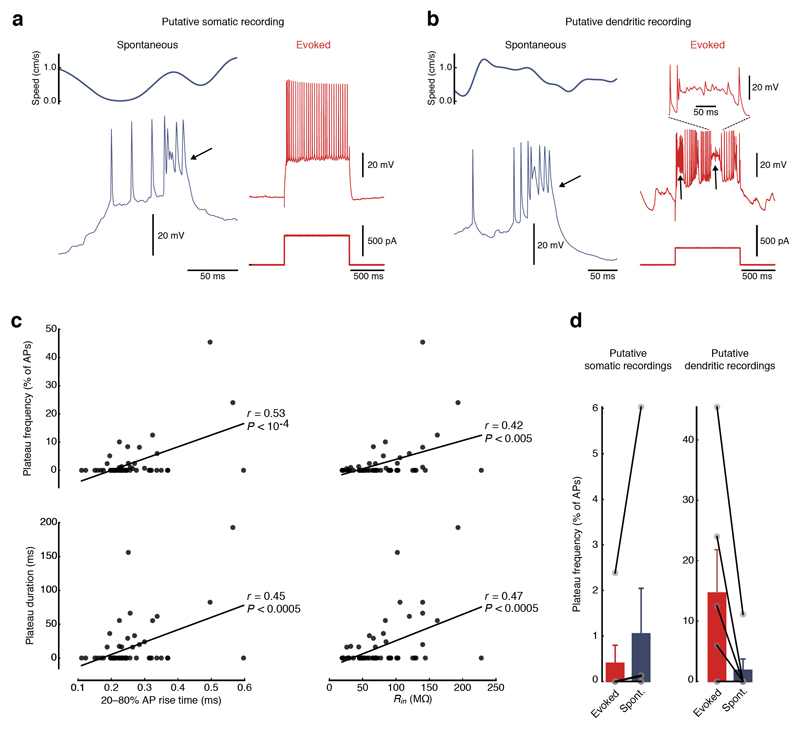
Next, we looked for direct evidence for activation of regenerative events in stellate cell dendrites in vivo. Excitable dendrites have been shown to produce long-lasting regenerative plateau potentials in several cell types, such as neocortical pyramidal cells30 and hippocampal CA1 pyramidal cells in vitro31 and in vivo11,32. We identified similar distinctive signatures of excitable dendrites in putative dendritic patch-clamp recordings from MEC neurons in vivo (Fig. 4 and Supplementary Fig. 11). Dendritic recordings were identified by a range of characteristic features6,33 such as slower action potential rise times and higher input resistances (Supplementary Fig. 12). Distinct, long-lasting plateau depolarizations could be observed following action potentials in both putative dendritic and somatic recordings (Fig. 4a,b). These plateau potentials occurred either spontaneously (Fig. 4a,b and Supplementary Fig. 13a) or could be evoked by current injection in putative dendritic recordings (Fig. 4b). We found that both the frequency (the percentage of action potentials followed by plateau potentials) and the duration of evoked plateau potentials were highly correlated with parameters that are also indicative of dendritic recordings (Fig. 4c), suggesting that they could be preferentially evoked in distal dendrites. While the frequency of evoked plateau potentials per action potential was more than an order of magnitude higher in putative dendritic than in somatic recordings from stellate cells in vivo (14.7 ± 7.2% of action potentials followed by plateau potentials in putative dendrites, n = 6, versus 0.4 ± 0.4% in soma, n = 6; P < 0.05), spontaneous plateaus occurred at comparable frequencies (1.9 ± 1.9% in putative dendrites, n = 6, versus 1.0 ± 1.0% in soma, n = 6; P = 0.22; Fig. 4d). Distinct plateau potentials could be evoked by current injections in 4 of 6 putative dendritic recordings but only in 1 of 6 putative somatic recordings (Fig. 4d). The results of these in vivo recordings indicate that plateau potentials could be evoked by strong, localized inputs to dendrites of grid cells and were readily detectable at their site of origin in the dendrite. However, plateau potentials were rarer and less prominent in somatic recordings and appeared to be substantially attenuated as they propagated to the soma from their origin in the dendritic tree. We further probed the biophysical mechanisms underlying dendritic plateau potentials using our active compartmental model of stellate cells. Strong, localized synaptic inputs to a dendrite of the stellate cell model could produce plateau potentials near the site of synaptic input that were similar to those observed in our putative dendritic recordings (Supplementary Fig. 14a). These dendritic plateau potentials were strongly attenuated as they propagated to other dendrites and to the soma, making them readily detectable only close to the dendritic location of the active synaptic inputs (Supplementary Fig. 14a). To produce a plateau potential detectable at the soma, a large number of simultaneously activated strong synaptic inputs had to be distributed across the dendritic tree (Supplementary Fig. 14b). The rare occurrence of strong, synchronous activation of many synapses, along with the pronounced attenuation of plateau potentials along the dendritic tree, can therefore explain why they were only rarely observed as spontaneously occurring events. Thus, despite their low rate, the presence of dendritic plateau potentials in vivo provides strong evidence that the active dendritic conductances underlying nonlinear integration in vitro can be recruited by synaptic input in vivo.
Figure 4. Plateau potentials suggest that active dendritic conductances are engaged in vivo.
(a) Example of a putative somatic recording from a MEC neuron in vivo. Plateau potentials (arrows) occur spontaneously (left, top trace shows animals speed, bottom trace shows membrane potential) but not during current injections (right, top traces show membrane potential, bottom traces show current injections). (b) Example of a putative dendritic recording from a MEC neuron in vivo. Plateau potentials (arrows) occur both spontaneously (left, top trace shows animals speed, bottom trace shows membrane potential) and upon current injections (right, top traces show membrane potential, bottom traces show current injections). Inset (top right) shows an enlarged view of an evoked plateau potential. (c) Frequency and duration of plateau potentials correlate with parameters that are characteristic of dendritic recordings. Plateau frequencies per action potential (top) and plateau durations (bottom) are significantly correlated with rise times of action potentials (left) and input resistance (right). Black lines represent linear regressions (n = 58 recordings). (d) Summary bar graphs of evoked and spontaneous plateau frequencies per action potential in (left) putative somatic (evoked, 0.4 ± 0.4%; spontaneous, 1.0 ± 1.0%, n = 6) and (right) dendritic recordings (evoked, 14.7 ± 7.2%; spontaneous, 1.9 ± 1.9%, n = 6). Filled gray circles represent individual recordings. Error bars represent s.e.m.
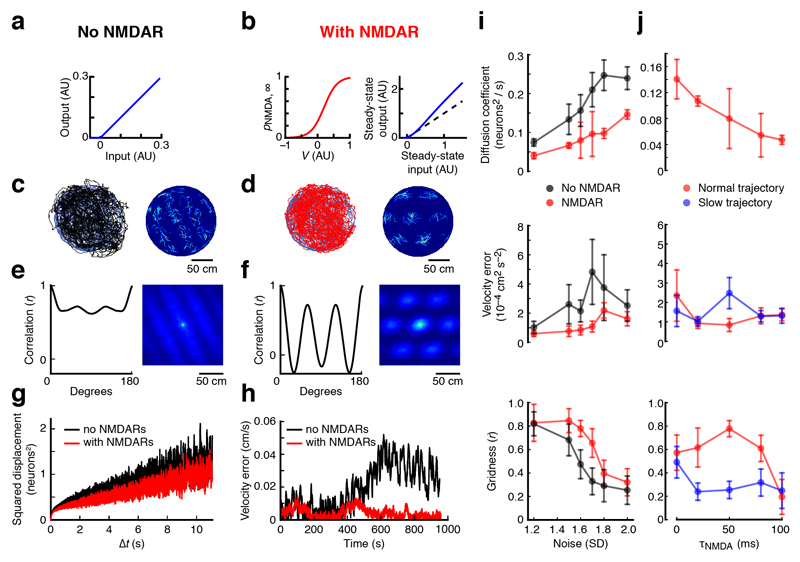
Slow supralinear integration promotes the robustness of the grid cell rate code
To provide a quantitative framework for understanding the contribution of active dendrites to generating the grid cell rate code, we used a rate-based continuous attractor network (CAN) model. Given that NMDAR activation underpins the various types of dendritic nonlinearities we discovered in grid cells, we implemented NMDARs as a slow, cooperative, supralinear integration mechanism in an existing CAN model of grid cell firing13, which allowed us to efficiently explore a large range of parameters and noise amplitudes (Fig. 5 and Supplementary Fig. 9). Adding NMDARs to the CAN model substantially enhanced grid cell firing in the presence of noise, measured by a range of metrics (Fig. 5a–h). Across a wide range of noise amplitudes, NMDARs reduced network drift and improved the network’s velocity response, resulting in higher gridness scores (Fig. 5i,j). Simulations in which we independently incorporated either supralinearity or a slow time-constant indicated that both mechanisms must act in concert to improve network performance (Supplementary Fig. 15). The robustness of these findings was confirmed by a spiking attractor network model consisting of integrate-and-fire neurons34, which also produces the best velocity response and the highest gridness scores when both mechanisms are engaged (Supplementary Fig. 16). Using actual animal trajectories to drive the rate-based model, we found that an NMDAR decay-time constant of ~50 ms produced a minimum in velocity error and a maximum in gridness (Fig. 5j). This optimum is remarkably consistent with the NMDAR decay-time constant we measured experimentally in stellate cells (46 ± 5 ms, n = 4; Supplementary Fig. 17). Simulations using an artificially slowed animal trajectory (Fig. 5j) indicate that the optimum depends on a realistic animal velocity driving the network response. Thus, NMDAR kinetics optimized for animal velocity can produce marked robustness to noise in a CAN model of grid cell firing.
Figure 5. Active dendrites in MECII neurons can enhance the robustness of the rate code of grid cell firing.
(a,b) CAN model simulations were performed either in the absence (a) or the presence (b) of a slow supralinear integration mechanism, as provided by NMDARs (τNMDA = 50 ms). (c,d) Left: animal trajectory (blue; data from Hafting et al.12) and CAN network prediction of animal position in the absence (c) (black) or in the presence (d) (red) of NMDARs are superimposed. Right: color-coded spatial rate maps for an example model neuron in the absence (c) or in the presence (d) of NMDARs. (e,f) Left: correlation between rotated autocorrelation maps plotted against the rotation angle. Simulations were performed in the absence (e) or in the presence (f) of NMDARs. Right: autocorrelation matrices of the spatial rate maps shown in c and d, respectively. (g) To quantify network drift, mean squared displacement is plotted as a function of simulation time interval in the absence of velocity inputs in the absence (black) or in the presence (red) of NMDARs. (h) Absolute difference between animal velocity and optimally scaled network velocity plotted against time in the absence (black) or in the presence (red) of NMDARs. (i) From top to bottom: network diffusion coefficient in the absence of velocity inputs, summed squared velocity error and gridness, each plotted against noise s.d. for CAN network simulations with (red symbols) or without (black symbols) NMDARs. (j) The same quantities as in i plotted against τNMDA. Simulations were performed using either the original animal trajectory (red symbols) or a version that was slowed by a factor of 2 (blue symbols). In the simulations in a–h, noise s.d. = 1.6, and error bars represent s.e.m. of 7 simulations, which were initialized with different pseudorandom number generator seeds.
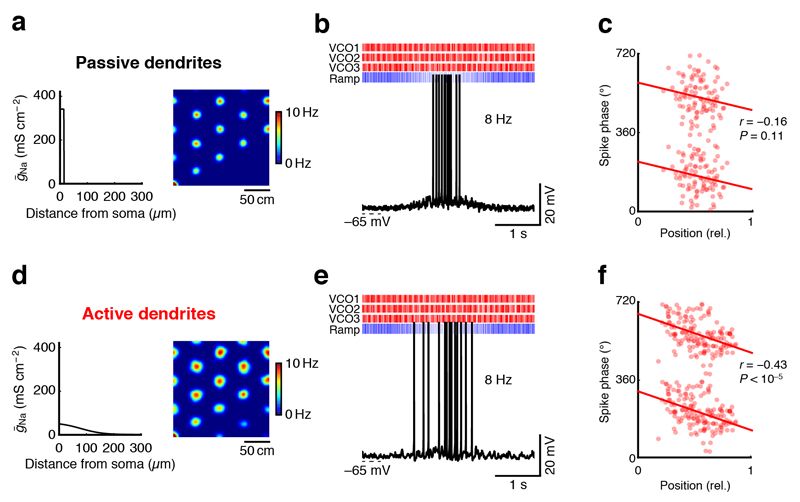
Supralinear integration sharpens the precision of phase precession
Finally, we investigated how the active dendritic conductances we revealed in stellate cells can contribute to the temporal phase precession code of grid cell firing35. To determine the precise spike timing produced by oscillatory synaptic inputs, we drove our detailed compartmental MECII stellate cell model (Supplementary Fig. 8) by realistic synaptic input patterns derived from a hybrid oscillatory-interference–CAN model based on in vivo recordings from grid cells18 (Fig. 6). While the model only produced weak phase precession in the absence of dendritic Nav channels (Fig. 6a–c), phase precession was strikingly precise when Nav channels were present in the dendrites (Fig. 6d–f). While the fast supralinearity provided by Nav channels was sufficient to sharpen phase precession even in the absence of distinct isolated regenerative events, the effect could further be enhanced if the model cell produced full-blown fast dendritic spikes (data not shown). Further analysis showed that dendritic Nav channels can sharpen phase precession by shortening the suprathreshold part of membrane potential oscillations, enabling precisely timed spikes across the full extent of a grid firing field (Supplementary Fig. 18). In agreement with this analysis, adjusting the width of grid fields by increasing excitatory drive in the model without dendritic Nav channels failed to improve phase precession, as more mistimed spikes were produced in the center of the grid field (Supplementary Fig. 19). Thus, our combined modeling results show that active dendritic conductances can both stabilize the rate code and sharpen the temporal code of grid cell firing.
Figure 6. Active dendrites in MECII neurons can promote the precision of the temporal code of grid cell firing.
(a,d) A detailed compartmental model of a MECII stellate cell was used to simulate grid cell firing in a hybrid CAN–oscillatory-interference model with passive (a) or active (d) dendrites (see Online Methods for details). Left: voltage-gated sodium conductance density plotted against dendritic distance from soma. Right: color-coded firing rate maps. (b,e) Example traces of simulated somatic membrane potential during a firing field crossing in the model with passive (b) and with active (e) dendrites. Raster plots at top show timings of excitatory velocity-controlled oscillators (VCOs, red) and inhibitory ramp inputs (blue). (c,f) While phase precession degraded in the model with (c) passive dendrites (n = 80 spikes), the model with (f) active dendrites (n = 153 spikes) produced clear phase precession of spikes with reference to the LFP. Red lines represent circular–linear regressions.
Discussion
We provide evidence that the dendrites of MECII principal cells are electrically excitable and exhibit a range of nonlinear dynamics. Our results reveal that the biophysical origins of dendritic nonlinearities in these cells—dendritic Nav and NMDAR channels—may underpin the two key aspects of the grid cell code. Dendritic Nav channels restrict the time window for action potential generation in an oscillatory-interference model of phase precession, thereby improving the precision of the temporal code. NMDARs in turn improve the robustness of the grid attractor in a rate-based model of grid cell firing. Together, our results provide strong evidence that active dendrites can make a critical contribution to a key behaviorally relevant computation in the mammalian brain. Our simulations also provide a general framework for understanding how active dendritic computations can stabilize attractor networks.
Active dendrites in MECII principal cells
Although principal cells in MECII, which form a large part of the grid cell population, have been shown to exhibit a rich variety of nonlinear excitability in somatic recordings19,25,36, there has been no direct information available about the contribution of dendritic excitability to the active properties of grid cells. Our in vitro experiments reveal that the dendrites of both types of principal neurons in MECII, stellate and pyramidal cells, exhibited nonlinear input–output functions and could trigger dendritic spikes mediated by both voltage-gated sodium channels and NMDA receptor channels. Moreover, they demonstrate that these nonlinearities could be further enhanced by in vivo-like membrane potential trajectories that underpin grid cell firing.
Our in vivo experiments strengthen and complement our in vitro results and provide multiple signatures of nonlinear dendritic integration in MEC neurons during spatial navigation. First, EPSPs were boosted at the peak of the MPOs when the neuron was depolarized, consistent with our in vitro experiments, as well as with predictions from a model with active dendrites (Fig. 3). Second, comparing a stellate cell model with nonlinear or linear dendritic conductances, we found that dendritic nonlinearities were robustly activated during simulations of grid cell firing (Supplementary Fig. 9). Third, we observed nonlinear plateau potentials in putative dendritic whole-cell recordings from MECII neurons. We found that plateau potentials frequently occurred with dendritic but not somatic current injections, whereas spontaneous plateaus occurred with similar probability in somatic and dendritic recordings, indicating that the plateaus were of dendritic origin. Plateau potentials have been observed as a signature of dendritic excitability in other cell types30, particularly in CA1 pyramidal cells11,32, where dendritic plateau potentials can positively modulate existing or induce new place fields11. Together, our modeling and experimental data suggest that the dendrites of grid cells are electrically highly excitable and that the resulting nonlinearities can be engaged in vivo during grid cell firing in mice performing a spatial navigation task.
How do active dendrites improve grid cell firing?
Our modeling results show that active dendrites can enhance both the rate and temporal code of grid cell firing. First, we show that incorporating a nonlinear NMDA conductance, with characteristics matching those underpinning the nonlinearities in our in vitro experiments, in a CAN model of grid cell firing can reduce network drift and improve the network’s velocity response, resulting in improved gridness. Our simulations show that this enhancement of gridness arises from a synergistic interaction between two cardinal features of the nonlinear NMDAR conductance. First, NMDAR activation depends nonlinearly on the amplitude of the synaptic inputs that a neuron receives, increasing the gain of the neural transfer function preferentially in active neurons receiving strong spatial inputs37. Second, the slow decay-time constant of NMDARs allows active neurons to average signals over a longer time (see also refs. 38–40), reducing the contribution of noise38 and stabilizing the attractor. Notably, the stabilizing effect of NMDARs depends on the noise amplitude (Fig. 5i). Thus, acute blockade of NMDARs in grid cells should most strongly disrupt grid firing in novel environments, where spatial inputs are expected to be imprecise41.
Our detailed compartmental model indicates that active dendrites also enhance phase precession, the signature of the temporal code of grid cell firing. Our simulations show that the mechanism underlying this effect operates by curtailing the suprathreshold part of the membrane potential trajectory during membrane potential oscillations. This ensures that spikes can occur only within a narrow time window, sharpening the precision of spike timing and thus the robustness of phase precession across the entire grid firing field. Notably, the effect of active dendrites on phase precession does not require the activation of full-blown dendritic spikes: even a model exhibiting subthreshold recruitment of nonlinearities demonstrates enhanced phase precession. Moreover, the model can reproduce the experimentally observed phase precession of both spikes and theta MPOs18,19. The simplicity and robustness of this mechanism suggests that it may generalize to other phase-precession models relying on coincidence of oscillations, such as those that have been proposed for CA1 pyramidal cells42–44.
Our findings suggest that dendritic nonlinearities are key elements in the creation of a stable grid code and are therefore critical for navigation. This complements recent work proposing that dendritic nonlinear events may contribute to behaviorally relevant computations in single neurons5–8. In hippocampal place cells, in vivo two-photon imaging has revealed dendritic Ca2+ transients that are correlated with their place field properties9, and intracellular recordings from place cells suggest that dendritic nonlinearities may contribute to defining the spatial tuning of a neuron10,11. Together with our in vivo results indicating that dendritic nonlinearities may also be engaged in MECII stellate cells during virtual navigation (Figs. 3 and 4), this suggests that active dendrites may provide a general mechanism for strengthening spatial representations at the single-cell level. Notably, the stabilizing role that we describe for active dendrites in a CAN may also generalize to other circuits that display attractor dynamics, both in the hippocampus45,46 and in other brain areas47.
Why use active dendrites to enhance circuit computations?
Active dendrites offer several key advantages over alternative mechanisms—such as tuning somatic and axonal excitability, or excitation–inhibition balance—for improving the signal-to-noise ratio during grid cell firing. The nonlinear voltage-dependence of NMDAR activation exhibits exquisite sensitivity, being engaged already by a small number of synapses due to the high dendritic-input impedance (Supplementary Fig. 20)48. At the same time, since dendritic synapses are electrotonically remote from the axonal site of action potential generation, nonlinear integration can proceed independently of somatic spiking49,50. Moreover, by regulating the density of dendritic Nav channels and NMDARs, the threshold for supralinear integration can be widely adjusted over a large range of synaptic input frequencies to maximize the signal-to-noise ratio for grid cell firing. In contrast, changes in somatic and axonal excitability have only small effects on the shape of the input–output transfer function of MECII principal neurons36. Furthermore, dendritic nonlinearities provide versatility, permitting a range of flexible transfer functions depending on the combination of dendritic branches that are activated (Supplementary Fig. 2). This allows grid cells to gate relevant inputs and suppress irrelevant inputs (similarly to what has been suggested for place cells10). Finally, active dendrites may also provide a mechanism for shaping circuit wiring during development: early in the assembly of the entorhinal circuit, synaptic inputs that contact a nonlinear dendritic branch may be strengthened by engaging these nonlinearities and in turn define the grid properties of a neuron.
Online Methods
Slice preparation
Acute horizontal brain slices were prepared from 26–30-d-old C57/BL6 male and female mice. Animals were briefly anesthetized with isoflurane before decapitation. All procedures were performed under license from the UK Home Office in accordance with the Animal (Scientific Procedures) Act 1986. Slicing was performed in ice-cold sucrose solution, containing (in mM): NaCl 87, sucrose 75, glucose 25, NaHCO3 25, MgCl2 7, KCl 2.5, NaH2PO4 1.25 and CaCl2 0.5. For a period of 30 min immediately after slicing, slices were stored in preheated (32 °C) artificial cerebrospinal fluid (ACSF) with low Ca2+ and high Mg2+ concentrations, containing (in mM): NaCl 125, glucose 25, NaHCO3 26, MgCl2 7, KCl 2.5, NaH2PO4 1.25 and CaCl2 0.5. Slices were subsequently stored at room temperature (20-25°C). Experiments were performed in ACSF, containing (in mM): NaCl 125, glucose 25, NaHCO3 26, MgCl2 1, KCl 2.5, NaH2PO4 1.25 and CaCl2 2 at a temperature of 32–34 °C. After some recordings (Supplementary Fig. 3), the slices were fixed in 4% paraformaldehyde and immunohistochemical staining was performed using rabbit anti-calbindin (ab11426, Abcam) as the primary antibody and donkey F(ab’)2 anti-rabbit IgG (Alexa Fluor 488, ab150069, Abcam) as the secondary antibody51,52.
Electrophysiology and pharmacology
Somatic whole-cell patch-clamp recordings were obtained from stellate and pyramidal cells in layer 2 of medial entorhinal cortex. Stellate and pyramidal cells were identified by their somatodendritic morphology and their characteristic electrophysiological properties19,25,26,36,53–56. Current-clamp recordings were acquired with a MultiClamp 700B amplifier at a 50-kHz sampling rate using custom software written in Matlab. Patch pipettes of 5-MΩ resistance were filled with internal solution containing (in mM): KMeSO4 140, HEPES 10, KCl 7.4, MgCl2 0.3, EGTA 0.1, NaGTP 0.3, Na2ATP 3 and sodium phosphocreatine 1. Alexa Fluor 594 (50 μM) was added to this solution to visualize cell morphology. Series resistance of the recordings was usually less than 30 MΩ. In some recordings, 50 μM of D-APV and 0.5 μM of TTX were added to the regular ACSF solution to block NMDA receptors and voltage-gated sodium channels, respectively. All extracellular solutions were equilibrated with carbogen (95% O2 / 5% CO2) and had a pH of 7.3. Miniature EPSPs (mEPSPs; Supplementary Fig. 1) were measured in the presence of 0.5 μM TTX in the recording solution. The detection threshold for mEPSPs was when dV/dt exceeded 1 mV/s.
To produce membrane potential ramps in vitro that mimicked membrane potential dynamics in vivo (Supplementary Fig. 6), we first applied the mean in vivo membrane potential waveform that we had previously recorded from stellate cells during firing field crossings18 as a voltage clamp command in n = 5 stellate cells in vitro. The resulting clamp-current waveform was then averaged across recordings and injected as a current-clamp command to produce an in vivo-like voltage ramp. For voltage-clamp recordings (Supplementary Fig. 17), pipettes were filled with internal solution containing (in mM): CsMeSO4 135, HEPES 10, EGTA 10, NaGTP 0.3, Na2ATP 2 and MgATP 2. Series resistance was less than 15 MΩ. EPSCs were evoked by extracellular stimulation in layer I of MEC while holding MECII stellate cells at a potential of +40 mV. NMDAR-mediated EPSCs were isolated by blocking GABAA receptors with SR95531 (20 μM) and AMPA receptors with NBQX (10 μM).
Two-photon imaging and uncaging
Simultaneous two-photon imaging and dendritic stimulation at single-synapse resolution by uncaging of MNI-caged-L-glutamate was performed with two Ti-sapphire lasers tuned to 810 nm and 720–730 nm for imaging and uncaging, respectively. To visualize dendrites and dendritic spines, cells were loaded with a fluorescent dye (50 μM Alexa Fluor 594) added to the pipette solution. Healthy dendrites close to the surface of the slice were selected for uncaging. MNI-caged-L-glutamate (24 mM, Tocris) was dissolved in a solution containing (in mM): NaCl 125, glucose 25, KCl 2.5, HEPES 10, CaCl2 2 and MgCl2 1 and applied locally via a glass pipette (tip diameter ~10 μm). Multiple spines were selected in a randomized manner within a maximal distance of ~50 μm on a single dendritic branch. gluEPSPs were first evoked by stimulating each spine individually at 300-ms intervals. We then stimulated an increasing number of synapses at short time intervals (0.6–8 ms, as indicated), with a 10-s pause between each trial. To estimate the expected linear summation of gluEPSPs, we first shifted individual membrane potential traces according to the corresponding experimental stimulation interval (0.6–8 ms for each trace) before computing the sum. Uncaging laser exposure time was 0.5 ms. The laser power was adjusted to produce gluEPSPs that were comparable to sEPSPs recorded in the same cell (Supplementary Fig. 1). Uncaging timing and location were controlled by custom software written in Matlab. Experiments were terminated if photodamage to the dendrite was observed (for example, swelling of the dendrite) or depolarization of the membrane potential was detected. Recordings from neurons with photodamaged dendrites were excluded from analysis. Recordings were also excluded if the slice exhibited physical drift due to slice swelling or inconsistency of perfusion. This was detected either by imaging or by sudden large changes (usually decreases) in EPSP amplitude.
Data analysis
Data analysis was performed with custom code written in Python57. Nonlinearity, D, of each experiment was quantified by
| (1) |
where Mi is the amplitude of the measured EPSP, Li is the amplitude of the EPSP constructed by linear summation of single synapse EPSPs, and n is the maximal number of synapses activated. Slow dendritic spikes were detected if the nonlinearity of the EPSP integral was 33% larger than the nonlinearity of the EPSP amplitude. A fast dendritic spike was defined as a step-like increase (>50%) in a plot of maximal dV/dt against the number of uncaging locations (Fig. 2 and Supplementary Fig. 3).
To examine whether signatures of active dendritic integration can be found in grid cells in vivo, we analyzed in vivo patch-clamp recordings from MECII neurons18. The full membrane potential (Vm) recording duration from n = 6 putative grid cells was used for this analysis. Peaks were identified in differentiated Vm traces (dV/dt) by detecting local maxima that exceeded 0.1 mV/ms within time windows of 200 μs. The analysis was restricted to subthreshold Vm by excluding parts of traces where dV/dt exceeded 5% of the maximal rate of rise of action potentials of each recording. Local Vm peaks corresponding to these dV/dt peaks were detected in high-pass-filtered Vm traces (fc = 10 Hz) within 5 ms following each dV/dt peak (Fig. 3b,c). dV/dt peaks were binned according to the phase of theta membrane potential oscillations (theta MPOs) during which they occurred. Theta MPOs were obtained by bandpass-filtering Vm between 5 and 10 Hz; 0° corresponds to the peak of theta MPOs. For each theta MPO bin with a width of 45° (as indicated), mean and s.d. of all dV/dt peaks were computed for each recording (Fig. 3d–g). Moreover, for each theta MPO bin with a width of 90° (as indicated), dV/dt peaks that exceeded the mean of all dV/dt peaks within a given bin by 1.5 s.d. were computed for each recording (Fig. 3f,g). These particularly fast peaks are indicated by red symbols in Figure 3. According to these criteria, the lowest threshold for these fast peaks was typically a maximal rate of rise of ~0.4 mV/ms (Fig. 3d). Thus, these fast in vivo events were characterized by maximal rates of rise resembling or exceeding the maximal rates of rise of fast dendritic spikes recorded in vitro (typically ~0.4 mV/ms; Fig. 2a).
We analyzed plateau potentials across both somatic18 and putative dendritic in vivo patch-clamp recordings from MECII neurons. Plateau potentials were defined as sustained depolarizations following action potentials with a full-width-at-half-maximal amplitude exceeding 15 ms. These criteria were chosen to identify plateau potentials that closely resembled published examples (for example, Bittner et al.11). Action potentials were detected when dV/dt exceeded 30 mV/ms. We did not observe any obvious isolated plateau potentials without a preceding action potential in our data set. We analyzed a total of n = 58 recordings that produced trains of action potentials in response to depolarizing 1-s current injections. Recordings were categorized into putative dendritic and putative somatic recordings according to input resistance (Rin) and 20–80% rise time of action potentials (t20–80)6 (putative somatic: t20–80 < 0.2 ms and Rin < 80 Ω putative dendritic: t20–80 > 0.3 ms and Rin > 120 MΩ). The frequency of plateau potentials did not depend on recording parameters such as resting membrane potential or seal resistance (Supplementary Fig. 11), indicating that recording quality did not affect their occurrence. To measure action potential kinetics (Fig. 4 and Supplementary Fig. 12), we used the first action potential that was evoked by the lowest suprathreshold sustained current injection.
Data are presented as mean ± s.e.m., unless stated otherwise. Error bars for dendritic spike proportions represent the s.d. of bootstrap analyses of the experimental data set (1,000 repeats). Statistical significance of continuous data was assessed using two-sided Mann-Whitney U tests and Wilcoxon signed-rank tests for unpaired and paired data, respectively. Statistical significance of dendritic spike proportions was assessed using Fisher’s exact test. Analyses of variance (ANOVA) were performed when more than two groups were tested. Differences were considered statistically significant when P < 0.05. No correction for multiple comparisons was applied58. No statistical methods were used to predetermine sample sizes, but our sample sizes are similar to those reported in previous publications11,17,18. Data collection and analysis were not performed blind to the conditions of the experiments.
Compartmental modeling
Studying phase precession required us to model the precise timing of action potentials produced by oscillatory synaptic inputs. To achieve realistic predictions of membrane potential trajectories, we therefore decided to use a detailed compartmental model implemented in NEURON59 (Figs. 3 and 6 and Supplementary Figs. 8 and 20). We used a reconstructed morphology of a mouse MEC stellate cell25 and HCN-channel gating kinetics based on experimental data from stellate cells60. Voltage-gated potassium (Kv) and sodium (Nav) channel kinetics were adopted from a CA1 pyramidal cell model61. Active conductance densities, axial resistivity (Ri), specific membrane resistance (Rm) and capacitance (Cm) were fitted to reproduce the experimentally determined mean f–I relationship, input resistance, sag ratio, sag time-constant, membrane time-constant, resting membrane potential and afterhyperpolarization amplitude using a genetic algorithm (NSGAII)62–64 (Supplementary Table 1).
Subthreshold synaptic input–output curves (Supplementary Fig. 8b) were produced by first finding all sites on the dendritic tree that were located 175 μm from the soma. We then performed simulations that closely followed our experimental protocol (Fig. 1): at each site, we distributed 20 synaptic conductances within 25 μm. We then activated individual synaptic conductance changes in isolation and computed the linear sums of the individual responses. Next, we stimulated an increasing number of synaptic conductance changes at 1-ms intervals and plotted the amplitudes of the measured responses against the amplitudes of the linear sums. This procedure was repeated for each site to yield a set of input–output curves. The analysis of simulated data was identical to that of experimental data.
To determine the effect of dendritic Nav channels on phase precession (Fig. 6 and Supplementary Fig. 19), we used a modeling and analysis strategy similar to one described previously18. In brief, we converted the synaptic inputs of rate-based neurons in a CAN model (see below) into discrete events driving synaptic conductance changes in our compartmental stellate cell model. Feedforward excitation was provided by six directional velocity-controlled oscillating (VCO) inputs that were only active when the current running direction matched the VCO’s preferred direction ± 90° (ref. 65).
Rate-based modeling (Fig. 5 and Supplementary Fig. 15)
Previous work has suggested that the mechanisms underlying the rate code of grid cell firing are best explained by a continuous attractor network (CAN) model17,18,66. We implemented a CAN model in a sheet of 128 × 128 neurons with periodic boundaries building on a previous implementation (courtesy of Y. Burak and I. Fiete13). This rate-based model allowed us to efficiently test the effect of a large range of parameters on network performance, which is essential for exploring the effects of a large range of noise amplitudes. The dynamics of rate-based neurons was defined by
| (2) |
| (3) |
| (4) |
where si represents the firing rate of neuron i, Vi represents the membrane potential of neuron i, τ = 10 ms is the integration time constant of the neural response, kNMDA = 0.4 (unless indicated otherwise) is the relative strength of NMDARs, pi is the fraction of open NMDARs in neuron i (equations (8) and (9)), Ii is inhibitory recurrent input to neuron i, Bi is excitatory feedforward input to neuron i, Wij is the synaptic weight from neuron j to neuron i, and ξi is colored synaptic noise (equations (10)–(12)). By subtracting 0.5 from pi, mean network firing rates were kept approximately constant across simulations. For a threshold-linear implementation of the model without NMDARs, we set kNMDA = 0. The gain of the neural transfer function, kV, was set to 0.88 (unless indicated otherwise), which minimized drift and velocity error for kNMDA = 0. This strategy was chosen to ensure that reductions of drift and velocity error by NMDARs could not be explained by a simple linear gain change. The implementation of NMDARs as a multiplicative term is consistent with predictions of NMDAR recruitment in a compartmental model (Supplementary Fig. 9). Bi was defined by
| (5) |
where êi is the unit vector pointing along neuron i's preferred direction i (one of W, N, S or E), v is the animal velocity vector in m s–1, and α was set to 0.0825. The recurrent weight matrix was purely inhibitory in our implementation:
| (6) |
| (7) |
where xi is neuron i’s location in the neural sheet and ranges from (−64, −64) to (64, 64). In our implementation, we used l = 2, γ = 1.02β, β = 3λ–2 and λ = 13. AB = 10 and AW = 10 are scaling factors that were chosen to compensate for the ‘notau’ option in the original implementation. As in Burak and Fiete13, we computed the animal velocity vector v from an experimentally determined rat trajectory12.
It is currently unknown how spatially modulated excitatory and inhibitory inputs are distributed on the dendritic tree of grid cells. To implement a model that applies to a large range of potential synaptic input configurations, we therefore used a generalized approach in which we subject the sum of all synaptic inputs to a single function, which can take a nonlinear form.
The dynamics of NMDAR open probability pi in neuron i was computed as follows:
| (8) |
| (9) |
where the steady-state open probability, p∞(V), was assumed to be a sigmoid function of membrane potential V with center cNMDA = 0.1 and slope mNMDA = 0.2, yielding a neural transfer function that qualitatively matched the experimentally determined dendritic input–output curves. Unless indicated otherwise, τNMDA was set to 50 ms, in agreement with our experimental data (Supplementary Fig. 17).
Synaptic noise, ξi, was implemented as an Ornstein-Uhlenbeck process using an exact update rule for an integration time step, h67, 68:
| (10) |
| (11) |
| (12) |
where ξi,exc and ξi,inh are excitatory and inhibitory synaptic noise, respectively; ξexc,0 and ξinh,0 are average synaptic noise; τexc and τinh are synaptic time constants; G1 and G2 are random numbers drawn from a normal distribution with zero mean; and unit s.d. Aexc and Ainh are amplitude coefficients given by
| (13) |
| (14) |
where Dexc and Dinh are noise diffusion coefficients. Excitatory and inhibitory noise were assumed to be symmetric in our simulations, with τexc = τinh = 2 ms. Noise diffusion coefficients and average synaptic noise were set as high as possible without disrupting the periodic activity bumps in the CAN when the original simulation parameters from Burak and Fiete13 were used (ξexc,0 = ξinh,0 = 1.2, Dexc = Dinh = 0.04, yielding a ratio similar to ξ0/D, as in Destexhe et al.67).
Integrate-and-fire neurons (Supplementary Fig. 16)
An implementation of a CAN model using integrate-and-fire neurons was adopted from Pastoll et al.34. Topology and connectivity of the model were adopted from the original implementation: the network consisted of 68 × 58 excitatory and 34 × 30 inhibitory neurons interconnected in an ‘E-surround’ configuration34. Constant excitatory input currents to the excitatory neurons in the original model (Iext_e_const and Iext_e_theta) were replaced by mixed AMPAR/NMDAR-type synapses driven by Poisson spike trains at 1 kHz. The dynamics of the synapses was defined by
| (15) |
| (16) |
| (17) |
where gAMPA and gNMDA are the AMPAR and NMDAR conductances, αNMDA = 0.5 defines NMDAR saturation, τNMDA,rise = 2 ms and τNMDA,decay = 100 ms are the rise and decay time constants of NMDAR, and x is the activation gating variable of NMDARs. For each presynaptic spike occurring at time t1, the synapse activity was updated from its previous state at time t0 according to the following equations:
| (18) |
| (19) |
where w = 1 is the synaptic weight and p∞(V) is the steady-state open probability of the NMDAR (equation (9)). Total synapse conductance was computed as gAMPA + kNMDA gNMDA. The maximal total conductance was set to 2.3 nS. A version of an AMPAR/NMDAR-type synapse without Mg2+ block was implemented by setting p∞(V) = 1 in equation (18).
Spatial rate maps of model neurons were discretized into 1-cm × 1-cm bins. No smoothing of the data was performed. To quantify spatial periodicity (‘gridness’), we first calculated the spatial autocorrelation for rate maps of each model neuron21. We then selected a centered ring-shaped region of interest from the autocorrelogram that included peaks closest to the center but excluded the central peak. We next rotated this ring in steps of 1° and at each step computed the correlation coefficient of the rotated with the original ring. We then determined maximal correlation values at 60° and 120° rotation (rmax,60 and rmax,120) and minimal correlation values at 30°, 90° and 150° rotation (rmin,30, rmin,90 and rmin,150). Gridness was then determined as min(rmax,60, rmax,120) – max(rmin,30, rmin,90, rmin,150)21. Mean gridness values were computed for ten randomly selected model neurons.
Supplementary Material
Editorial summary.
Combining electrophysiology and computational modeling, the authors show that the dendrites of entorhinal cortex stellate and pyramidal cells are electrically excitable and that this improves the robustness of grid cell firing. The results suggest that active dendrites are critical for spatial navigation, a fundamental computation in the brain.
Acknowledgments
We are grateful to P. Latham, A. Packer and S. Turaga for discussions and comments on the manuscript, and to S. Chun for assistance with histology. This work was supported by grants from the Wellcome Trust (M.H.), ERC (StG 678790 NEWRON to C.S.-H. and AdG 695709 DendriteCircuits to M.H.) and Gatsby Charitable Foundation (M.H.).
Footnotes
Code and data availability.
Data analysis and simulation code are available from a private repository on GitHub (https://github.com/neurodroid/SH2017, access available upon request). The data that support the findings of this study are available from the corresponding authors upon reasonable request.
Author Contributions
C.S.-H., A.R. and M.H. designed experiments and wrote the manuscript. C.S.-H. performed computational modeling, contributed to in vitro electrophysiology experiments and performed data analysis; G.T. performed in vitro experiments and data analysis. L.A. assisted with computational modeling. T.B. contributed to in vitro experiments. B.A.C. contributed to in vitro electrophysiology experiments and helped write the manuscript. M.H. supervised the project.
Competing Financial Interests
The authors declare no competing financial interests.
Reprints and permissions information is available online at http://www.nature.com/reprints/index.html. Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Magee JC. Dendritic integration of excitatory synaptic input. Nat Rev Neurosci. 2000;1:181–190. doi: 10.1038/35044552. [DOI] [PubMed] [Google Scholar]
- 2.Major G, Larkum ME, Schiller J. Active properties of neocortical pyramidal neuron dendrites. Annu Rev Neurosci. 2013;36:1–24. doi: 10.1146/annurev-neuro-062111-150343. [DOI] [PubMed] [Google Scholar]
- 3.London M, Häusser M. Dendritic computation. Annu Rev Neurosci. 2005;28:503–532. doi: 10.1146/annurev.neuro.28.061604.135703. [DOI] [PubMed] [Google Scholar]
- 4.Mel BW. Information processing in dendritic trees. Neural Comput. 1994;6:1031–1085. [Google Scholar]
- 5.Lavzin M, Rapoport S, Polsky A, Garion L, Schiller J. Nonlinear dendritic processing determines angular tuning of barrel cortex neurons in vivo. Nature. 2012;490:397–401. doi: 10.1038/nature11451. [DOI] [PubMed] [Google Scholar]
- 6.Smith SL, Smith IT, Branco T, Häusser M. Dendritic spikes enhance stimulus selectivity in cortical neurons in vivo. Nature. 2013;503:115–120. doi: 10.1038/nature12600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Xu NL, et al. Nonlinear dendritic integration of sensory and motor input during an active sensing task. Nature. 2012;492:247–251. doi: 10.1038/nature11601. [DOI] [PubMed] [Google Scholar]
- 8.Takahashi N, Oertner TG, Hegemann P, Larkum ME. Active cortical dendrites modulate perception. Science. 2016;354:1587–1590. doi: 10.1126/science.aah6066. [DOI] [PubMed] [Google Scholar]
- 9.Sheffield ME, Dombeck DA. Calcium transient prevalence across the dendritic arbour predicts place field properties. Nature. 2015;517:200–204. doi: 10.1038/nature13871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lee D, Lin BJ, Lee AK. Hippocampal place fields emerge upon single-cell manipulation of excitability during behavior. Science. 2012;337:849–853. doi: 10.1126/science.1221489. [DOI] [PubMed] [Google Scholar]
- 11.Bittner KC, et al. Conjunctive input processing drives feature selectivity in hippocampal CA1 neurons. Nat Neurosci. 2015;18:1133–1142. doi: 10.1038/nn.4062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hafting T, Fyhn M, Molden S, Moser MB, Moser EI. Microstructure of a spatial map in the entorhinal cortex. Nature. 2005;436:801–806. doi: 10.1038/nature03721. [DOI] [PubMed] [Google Scholar]
- 13.Burak Y, Fiete IR. Accurate path integration in continuous attractor network models of grid cells. PLOS Comput Biol. 2009;5:e1000291. doi: 10.1371/journal.pcbi.1000291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Burgess N, Barry C, O’Keefe J. An oscillatory interference model of grid cell firing. Hippocampus. 2007;17:801–812. doi: 10.1002/hipo.20327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Fuhs MC, Touretzky DS. A spin glass model of path integration in rat medial entorhinal cortex. J Neurosci. 2006;26:4266–4276. doi: 10.1523/JNEUROSCI.4353-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kropff E, Treves A. The emergence of grid cells: intelligent design or just adaptation? Hippocampus. 2008;18:1256–1269. doi: 10.1002/hipo.20520. [DOI] [PubMed] [Google Scholar]
- 17.Domnisoru C, Kinkhabwala AA, Tank DW. Membrane potential dynamics of grid cells. Nature. 2013;495:199–204. doi: 10.1038/nature11973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Schmidt-Hieber C, Häusser M. Cellular mechanisms of spatial navigation in the medial entorhinal cortex. Nat Neurosci. 2013;16:325–331. doi: 10.1038/nn.3340. [DOI] [PubMed] [Google Scholar]
- 19.Schmidt-Hieber C, Häusser M. How to build a grid cell. Phil Trans R Soc Lond B. 2013;369 doi: 10.1098/rstb.2012.0520. 20120520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Boccara CN, et al. Grid cells in pre- and parasubiculum. Nat Neurosci. 2010;13:987–994. doi: 10.1038/nn.2602. [DOI] [PubMed] [Google Scholar]
- 21.Sargolini F, et al. Conjunctive representation of position, direction, and velocity in entorhinal cortex. Science. 2006;312:758–762. doi: 10.1126/science.1125572. [DOI] [PubMed] [Google Scholar]
- 22.Gatome CW, Slomianka L, Lipp HP, Amrein I. Number estimates of neuronal phenotypes in layer II of the medial entorhinal cortex of rat and mouse. Neuroscience. 2010;170:156–165. doi: 10.1016/j.neuroscience.2010.06.048. [DOI] [PubMed] [Google Scholar]
- 23.Zhang SJ, et al. Optogenetic dissection of entorhinal-hippocampal functional connectivity. Science. 2013;340 doi: 10.1126/science.1232627. 1232627. [DOI] [PubMed] [Google Scholar]
- 24.Sun C, et al. Distinct speed dependence of entorhinal island and ocean cells, including respective grid cells. Proc Natl Acad Sci USA. 2015;112:9466–9471. doi: 10.1073/pnas.1511668112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Garden DL, Dodson PD, O’Donnell C, White MD, Nolan MF. Tuning of synaptic integration in the medial entorhinal cortex to the organization of grid cell firing fields. Neuron. 2008;60:875–889. doi: 10.1016/j.neuron.2008.10.044. [DOI] [PubMed] [Google Scholar]
- 26.Giocomo LM, Zilli EA, Fransén E, Hasselmo ME. Temporal frequency of subthreshold oscillations scales with entorhinal grid cell field spacing. Science. 2007;315:1719–1722. doi: 10.1126/science.1139207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Tang Q, et al. Pyramidal and stellate cell specificity of grid and border representations in layer 2 of medial entorhinal cortex. Neuron. 2014;84:1191–1197. doi: 10.1016/j.neuron.2014.11.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Golding NL, Staff NP, Spruston N. Dendritic spikes as a mechanism for cooperative long-term potentiation. Nature. 2002;418:326–331. doi: 10.1038/nature00854. [DOI] [PubMed] [Google Scholar]
- 29.Losonczy A, Magee JC. Integrative properties of radial oblique dendrites in hippocampal CA1 pyramidal neurons. Neuron. 2006;50:291–307. doi: 10.1016/j.neuron.2006.03.016. [DOI] [PubMed] [Google Scholar]
- 30.Schiller J, Major G, Koester HJ, Schiller Y. NMDA spikes in basal dendrites of cortical pyramidal neurons. Nature. 2000;404:285–289. doi: 10.1038/35005094. [DOI] [PubMed] [Google Scholar]
- 31.Takahashi H, Magee JC. Pathway interactions and synaptic plasticity in the dendritic tuft regions of CA1 pyramidal neurons. Neuron. 2009;62:102–111. doi: 10.1016/j.neuron.2009.03.007. [DOI] [PubMed] [Google Scholar]
- 32.Kamondi A, Acsády L, Buzsáki G. Dendritic spikes are enhanced by cooperative network activity in the intact hippocampus. J Neurosci. 1998;18:3919–3928. doi: 10.1523/JNEUROSCI.18-10-03919.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Larkum ME, Zhu JJ. Signaling of layer 1 and whisker-evoked Ca2+ and Na+ action potentials in distal and terminal dendrites of rat neocortical pyramidal neurons in vitro and in vivo. J Neurosci. 2002;22:6991–7005. doi: 10.1523/JNEUROSCI.22-16-06991.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Pastoll H, Solanka L, van Rossum MC, Nolan MF. Feedback inhibition enables θ-nested γ oscillations and grid firing fields. Neuron. 2013;77:141–154. doi: 10.1016/j.neuron.2012.11.032. [DOI] [PubMed] [Google Scholar]
- 35.Hafting T, Fyhn M, Bonnevie T, Moser MB, Moser EI. Hippocampus-independent phase precession in entorhinal grid cells. Nature. 2008;453:1248–1252. doi: 10.1038/nature06957. [DOI] [PubMed] [Google Scholar]
- 36.Fernandez FR, Malerba P, White JA. Non-linear membrane properties in entorhinal cortical stellate cells reduce modulation of input-output responses by voltage fluctuations. PLOS Comput Biol. 2015;11:e1004188. doi: 10.1371/journal.pcbi.1004188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Stringer SM, Trappenberg TP, Rolls ET, de Araujo IE. Self-organizing continuous attractor networks and path integration: one-dimensional models of head direction cells. Network. 2002;13:217–242. [PubMed] [Google Scholar]
- 38.Mongillo G, Barak O, Tsodyks M. Synaptic theory of working memory. Science. 2008;319:1543–1546. doi: 10.1126/science.1150769. [DOI] [PubMed] [Google Scholar]
- 39.Papoutsi A, Sidiropoulou K, Poirazi P. Dendritic nonlinearities reduce network size requirements and mediate ON and OFF states of persistent activity in a PFC microcircuit model. PLOS Comput Biol. 2014;10:e1003764. doi: 10.1371/journal.pcbi.1003764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Wang XJ. Synaptic basis of cortical persistent activity: the importance of NMDA receptors to working memory. J Neurosci. 1999;19:9587–9603. doi: 10.1523/JNEUROSCI.19-21-09587.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Barry C, Ginzberg LL, O’Keefe J, Burgess N. Grid cell firing patterns signal environmental novelty by expansion. Proc Natl Acad Sci USA. 2012;109:17687–17692. doi: 10.1073/pnas.1209918109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Kamondi A, Acsády L, Wang XJ, Buzsáki G. Theta oscillations in somata and dendrites of hippocampal pyramidal cells in vivo: activity-dependent phase-precession of action potentials. Hippocampus. 1998;8:244–261. doi: 10.1002/(SICI)1098-1063(1998)8:3<244::AID-HIPO7>3.0.CO;2-J. [DOI] [PubMed] [Google Scholar]
- 43.Losonczy A, Zemelman BV, Vaziri A, Magee JC. Network mechanisms of theta related neuronal activity in hippocampal CA1 pyramidal neurons. Nat Neurosci. 2010;13:967–972. doi: 10.1038/nn.2597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Magee JC. Dendritic mechanisms of phase precession in hippocampal CA1 pyramidal neurons. J Neurophysiol. 2001;86:528–532. doi: 10.1152/jn.2001.86.1.528. [DOI] [PubMed] [Google Scholar]
- 45.Samsonovich A, McNaughton BL. Path integration and cognitive mapping in a continuous attractor neural network model. J Neurosci. 1997;17:5900–5920. doi: 10.1523/JNEUROSCI.17-15-05900.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Zhang K. Representation of spatial orientation by the intrinsic dynamics of the head-direction cell ensemble: a theory. J Neurosci. 1996;16:2112–2126. doi: 10.1523/JNEUROSCI.16-06-02112.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Goldberg JA, Rokni U, Sompolinsky H. Patterns of ongoing activity and the functional architecture of the primary visual cortex. Neuron. 2004;42:489–500. doi: 10.1016/s0896-6273(04)00197-7. [DOI] [PubMed] [Google Scholar]
- 48.Branco T, Häusser M. Synaptic integration gradients in single cortical pyramidal cell dendrites. Neuron. 2011;69:885–892. doi: 10.1016/j.neuron.2011.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Behabadi BF, Mel BW. Mechanisms underlying subunit independence in pyramidal neuron dendrites. Proc Natl Acad Sci USA. 2014;111:498–503. doi: 10.1073/pnas.1217645111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Häusser M, Major G, Stuart GJ. Differential shunting of EPSPs by action potentials. Science. 2001;291:138–141. doi: 10.1126/science.291.5501.138. [DOI] [PubMed] [Google Scholar]
- 51.Kitamura T, et al. Island cells control temporal association memory. Science. 2014;343:896–901. doi: 10.1126/science.1244634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Ray S, et al. Grid-layout and theta-modulation of layer 2 pyramidal neurons in medial entorhinal cortex. Science. 2014;343:891–896. doi: 10.1126/science.1243028. [DOI] [PubMed] [Google Scholar]
- 53.Alonso A, Llinás RR. Subthreshold Na+-dependent theta-like rhythmicity in stellate cells of entorhinal cortex layer II. Nature. 1989;342:175–177. doi: 10.1038/342175a0. [DOI] [PubMed] [Google Scholar]
- 54.Dickson CT, et al. Properties and role of I(h) in the pacing of subthreshold oscillations in entorhinal cortex layer II neurons. J Neurophysiol. 2000;83:2562–2579. doi: 10.1152/jn.2000.83.5.2562. [DOI] [PubMed] [Google Scholar]
- 55.Erchova I, Kreck G, Heinemann U, Herz AV. Dynamics of rat entorhinal cortex layer II and III cells: characteristics of membrane potential resonance at rest predict oscillation properties near threshold. J Physiol (Lond.) 2004;560:89–110. doi: 10.1113/jphysiol.2004.069930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Pastoll H, Ramsden HL, Nolan MF. Intrinsic electrophysiological properties of entorhinal cortex stellate cells and their contribution to grid cell firing fields. Front Neural Circuits. 2012;6:17. doi: 10.3389/fncir.2012.00017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Guzman SJ, Schlögl A, Schmidt-Hieber C. Stimfit: quantifying electrophysiological data with Python. Front Neuroinform. 2014;8:16. doi: 10.3389/fninf.2014.00016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Saville DJ. Multiple comparison procedures: the practical solution. Am Stat. 1990;44:174–180. [Google Scholar]
- 59.Carnevale NT, Hines ML. The NEURON book. Cambridge University Press; 2006. [Google Scholar]
- 60.Fransén E, Alonso AA, Dickson CT, Magistretti J, Hasselmo ME. Ionic mechanisms in the generation of subthreshold oscillations and action potential clustering in entorhinal layer II stellate neurons. Hippocampus. 2004;14:368–384. doi: 10.1002/hipo.10198. [DOI] [PubMed] [Google Scholar]
- 61.Katz Y, et al. Synapse distribution suggests a two-stage model of dendritic integration in CA1 pyramidal neurons. Neuron. 2009;63:171–177. doi: 10.1016/j.neuron.2009.06.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Bahl A, Stemmler MB, Herz AV, Roth A. Automated optimization of a reduced layer 5 pyramidal cell model based on experimental data. J Neurosci Methods. 2012;210:22–34. doi: 10.1016/j.jneumeth.2012.04.006. [DOI] [PubMed] [Google Scholar]
- 63.Deb K. Multi-objective Optimization Using Evolutionary Algorithms. Wiley; 2001. [Google Scholar]
- 64.Schmidt-Hieber C, Bischofberger J. Fast sodium channel gating supports localized and efficient axonal action potential initiation. J Neurosci. 2010;30:10233–10242. doi: 10.1523/JNEUROSCI.6335-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Burgess N. Grid cells and theta as oscillatory interference: theory and predictions. Hippocampus. 2008;18:1157–1174. doi: 10.1002/hipo.20518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Yoon K, et al. Specific evidence of low-dimensional continuous attractor dynamics in grid cells. Nat Neurosci. 2013;16:1077–1084. doi: 10.1038/nn.3450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Destexhe A, Rudolph M, Fellous JM, Sejnowski TJ. Fluctuating synaptic conductances recreate in vivo-like activity in neocortical neurons. Neuroscience. 2001;107:13–24. doi: 10.1016/s0306-4522(01)00344-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Gillespie DT. Exact numerical simulation of the Ornstein-Uhlenbeck process and its integral. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics. 1996;54:2084–2091. doi: 10.1103/physreve.54.2084. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.