Significance
Natural phenomena are teeming with temporal complexity, but such dynamics, however fascinating, offer substantial obstacles to quantitative understanding. We introduce a general method based on the simple idea that even complicated time series are locally linear. Our analysis transforms dynamical data into a parameterized space of linear models, and we detail a hierarchical clustering of this space into dynamical categories. The linear models reveal fine-scaled, interpretable states in the posture behavior and global brain activity of the nematode Caenorhabditis elegans. Furthermore, we find that the population of stable and unstable oscillations suggests a near-critical dynamics across both brains and behavior. We expect our approach to be widely applicable.
Keywords: time-series segmentation, animal behavior, neural dynamics, clustering, dynamical criticality
Abstract
The dynamics of complex systems generally include high-dimensional, nonstationary, and nonlinear behavior, all of which pose fundamental challenges to quantitative understanding. To address these difficulties, we detail an approach based on local linear models within windows determined adaptively from data. While the dynamics within each window are simple, consisting of exponential decay, growth, and oscillations, the collection of local parameters across all windows provides a principled characterization of the full time series. To explore the resulting model space, we develop a likelihood-based hierarchical clustering, and we examine the eigenvalues of the linear dynamics. We demonstrate our analysis with the Lorenz system undergoing stable spiral dynamics and in the standard chaotic regime. Applied to the posture dynamics of the nematode Caenorhabditis elegans, our approach identifies fine-grained behavioral states and model dynamics which fluctuate about an instability boundary, and we detail a bifurcation in a transition from forward to backward crawling. We analyze whole-brain imaging in C. elegans and show that global brain dynamics is damped away from the instability boundary by a decrease in oxygen concentration. We provide additional evidence for such near-critical dynamics from the analysis of electrocorticography in monkey and the imaging of a neural population from mouse visual cortex at single-cell resolution.
Complex dynamics are ubiquitous in nature; their diversity in systems ranging from fluids and turbulence (1, 2) to collective motion (3) and brain dynamics (4) is unified by common challenges of analysis which include high dimensionality, nonlinearity, and nonstationarity. But how do we capture the quantitative details of the dynamics of complex systems with models simple enough to offer substantial interpretability?
Motivated by the remarkable increase in data quantity and quality as well as growing computational power, one approach is to fit a single global model to the dynamics with properties extracted from data. For example, deep neural networks and other machine-learning techniques (5, 6) often produce high-dimensional nonlinear models, which can precisely represent complex dynamics and yield accurate predictions. While powerful, however, these methods can create representations of the dynamics that are too intricate for simple conceptual understanding. Another approach uses sparse regression to find a system of differential equations governing a nonlinear dynamical system (7). Also, short-time brain oscillations were studied by using jPCA (8), a method that approximates the dynamics as a linear model with skew-symmetric couplings. Although promising, global methods are unable to handle nonstationarities, such as when a time series is composed of a set of distinct dynamics that change in time.
An alternative to global methods is to segment the dynamics into simpler components which change in time. For example, a low-dimensional representation of the spatiotemporal patterns found in the human brain was obtained through dynamic mode decomposition (9) in short temporal segments (10). Studies on self-regulated dynamical criticality in the human brain used vector autoregressive models locally in time (11). Behavioral motifs in Drosophila melanogaster were found by using local-time wavelet analysis (12). In these methods, however, the local windows are defined phenomenologically, which may conflate distinct dynamical behaviors.
Principled approaches for the segmentation of time series include those of change-point detection (13–20), which aim to identify structural changes in the time series but often focus on the location of change points or forecasting, instead of the underlying dynamics (15–20). Other techniques, such as hidden Markov models (21–23), assume that the global dynamics are composed of a set of underlying dynamical states which the system revisits, without providing a parameterization of the underlying dynamical patterns (23). More recently, switching linear dynamical systems (LDSs) and autoregressive hidden Markov models (24–26) were developed with the aim of providing such a parameterization, but they do so either by setting the number of breaks from the onset (27, 28) or by assuming that there is a set of underlying dynamical regimes and that the system switches between them (21, 22, 24–26, 29).
Here, we combine the simplicity of LDSs with a likelihood-based algorithm for identifying dynamical breaks to construct interpretable, data-driven models of complex dynamics, with minimal a priori assumptions about the breakpoints or the number of states. We approximate the full dynamics with first-order LDSs in short windows and use a likelihood-ratio test to estimate to what extent newly added observations fit the same linear model, thus adaptively determining the size of the local windows. The global dynamics is therefore parameterized as a set of linear couplings within windows of various lengths. We analyze the resulting model space using hierarchical clustering with a likelihood-based similarity measure and by examining the dynamical eigenvalue spectra in three illustrative systems: the Lorenz dynamical system and both posture and whole-brain dynamics of the nematode Caenorhabditis elegans. In addition, we extend our analysis to higher-dimensional dynamics: electrocorticography (ECoG) recordings in nonhuman primates and a population of hundreds of neurons in mouse visual cortex.
Locally Linear, Adaptive Segmentation Technique
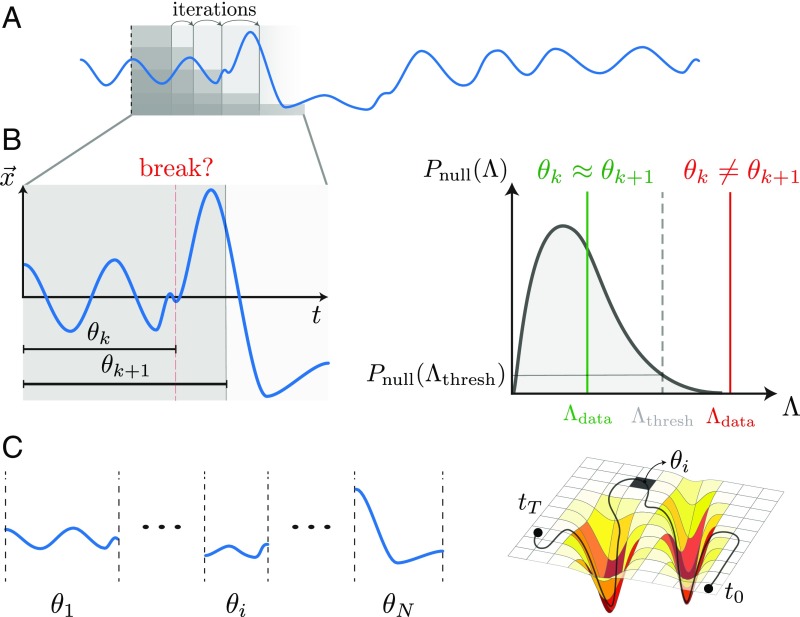
An overview of the segmentation technique is given in Fig. 1 and a detailed description as well as links to publicly available code are in Materials and Methods. Briefly, we iterate over pairs of consecutive windows (Fig. 1A) and estimate whether the linear model fit in the larger window is significantly more likely to model the observations in the larger window compared with the model found in the smaller window (Fig. 1B). We compare the two models by the log-likelihood ratio and assess the significance of by using Monte Carlo methods to construct a likelihood-ratio distribution under the null hypothesis of no model change. This null distribution is used to define according to a threshold probability or significance level . We identify a dynamical break when , in which case we save the model parameters and start a new modeling process from the break location. If , then no break is identified, and we move to the next window pair . Over the entire time series, our procedure yields a set of windows of varying sizes with their respective linear model parameters, (Fig. 1C) and is analogous to tiling a complex shaped manifold into local flat regions. We thus trade the complexity of the nonlinear time series for a space of simpler local linear models that captures important properties of the full dynamics.
Fig. 1.
Schematic of the adaptive, locally linear segmentation algorithm. (A) A -dimensional time series is depicted as a blue line. We iterate over pairs of subsequent windows and use a likelihood-ratio test to assess whether there is a dynamical break between windows. (B) We compare linear models and , found in the windows and , by the log-likelihood ratio (Eq. 3). To assess significance, we compute the distribution of log-likelihood ratios under the null hypothesis of no model change and identify a dynamical break when where . If no break is identified, we continue with the windows . (C) The result of the segmentation algorithm is a set of windows of varying lengths and model parameters . Our approach is similar to approximating a complex-shaped manifold by a set of locally flat patches and encodes a nonlinear time series through a trajectory within the space of local linear models.
Surveying the Space of Models
The application of locally linear, adaptive segmentation generally results in a large set of LDSs, and we explore this space both through the eigenvalues of the coupling matrices and by model clustering through a likelihood-based measure of similarity. Despite a typically large number of models, the dynamical eigenvalues offer a direct measure of local oscillations and stability. Complex conjugate eigenvalues represent oscillations, with frequency . A negative real part implies stable damped dynamics along that mode, while a positive real part implies unstable exponentially growing trajectories. As the least-stable eigenvalue approaches 0, the system becomes sensitive to external perturbations. At the bifurcation point, , the susceptibility diverges, and we enter a critical dynamical state (30–32). The full spectrum of eigenvalues across models thus provides not only information about oscillatory patterns but also stability and criticality.
To cluster the models, we note that simply using the Euclidean metric is inappropriate, since the space of linear models is invariant under the action of the GL() group* . Instead, we define dissimilarity as the loss in likelihood when two windows are modeled by a single linear model constructed fitting within the combination of windows. Given two windows, and , we define the dissimilarity as , where is the log-likelihood ratio and is the union of the windows . We note that this measure is symmetric , positive semidefinite , and does not require the windows to be the same size. If the dynamics in both windows are similar, then the combined model will still accurately fit each window. If not, then it will be far less likely to model the windows, resulting in a higher disparity between models. Once the dissimilarity is computed between all models, we perform hierarchical clustering by combining models according to Ward’s minimum variance criterion (33).
Lorenz System
As a demonstration of the locally linear approach, we analyze the time series generated from the Lorenz dynamical system (34):
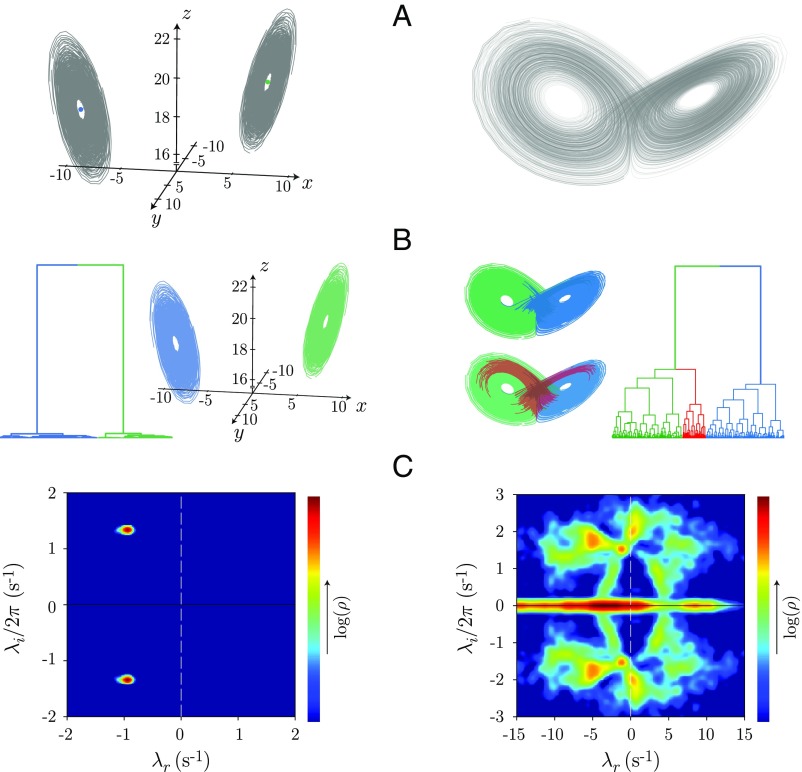
with and . We explore two dynamical regimes: transient chaos with late-time, stable spiral dynamics at and the standard chaotic attractor with . For spiral dynamics, we vary the initial conditions to sample the dynamics approaching the fixed point at the center of each lobe (Fig. 2A), which have the same period but vary in their phase space trajectories. We apply adaptive segmentation and show the result of model-space clustering in Fig. 2B. We find a single dominant split in the clustering dendrogram, which corresponds to approaching the two different fixed points. Inside each branch, the different linear models are all quite similar. In the chaotic regime, however, we find substantially more structure and large dissimilarities between models even at the lower branches of the tree. Notably, the first split occurs between the two lobes of the attractor, and, more generally, the linear model clustering provides a partition of the Lorenz phase space with different levels of description depending on the depth in the dendrogram.
Fig. 2.
Adaptive segmentation of the Lorenz dynamical system and likelihood-based clustering of the resulting model space. (A) Simulated Lorenz system for stable spiral dynamics (Left) and the standard chaotic regime (Right) . (B) Likelihood-based hierarchical model clustering. In the spiral dynamics, there is a large separation between models from each lobe, while the dynamics within lobe are very similar. In the chaotic regime, the model-space clustering first divides the two lobes of the attractor, and the full space is intricate and heterogeneous. (C) Dynamical eigenvalue spectrum for each regime, and , respectively represent the real and imaginary eigenvalues. The spiral dynamics (C, Left) exhibits a pair of stable, complex conjugate peaks, while in the chaotic regime (C, Right), we find a broad distribution of eigenvalues, often unstable, reflecting the complexity of the chaotic attractor.
Further insight into the dynamics is reflected in the distribution of the spectrum of eigenvalues across the local linear models (Fig. 2C). In the spiral dynamics, we find two peaks reflecting a dominant pair of complex conjugate eigenvalues, and these correspond to a decaying oscillation (). We note that while the local coupling matrix is constructed from finite temporal windows and is not the instantaneous Jacobian, the dynamical eigenvalues are close to those derived from linear stability of the fixed points (Materials and Methods). In contrast, the spectrum in the chaotic regime reflects a complexity of behaviors, with many models displaying unstable dynamics along the unstable manifold of the origin (SI Appendix, Fig. S1). In the locally linear perspective, the complexity of chaotic dynamics is associated with both substantial structure in the space of models as revealed through hierarchical clustering, as well as a wide range of dynamics, including eigenvalues that are broadly distributed across the instability boundary.
Posture Dynamics of C. elegans
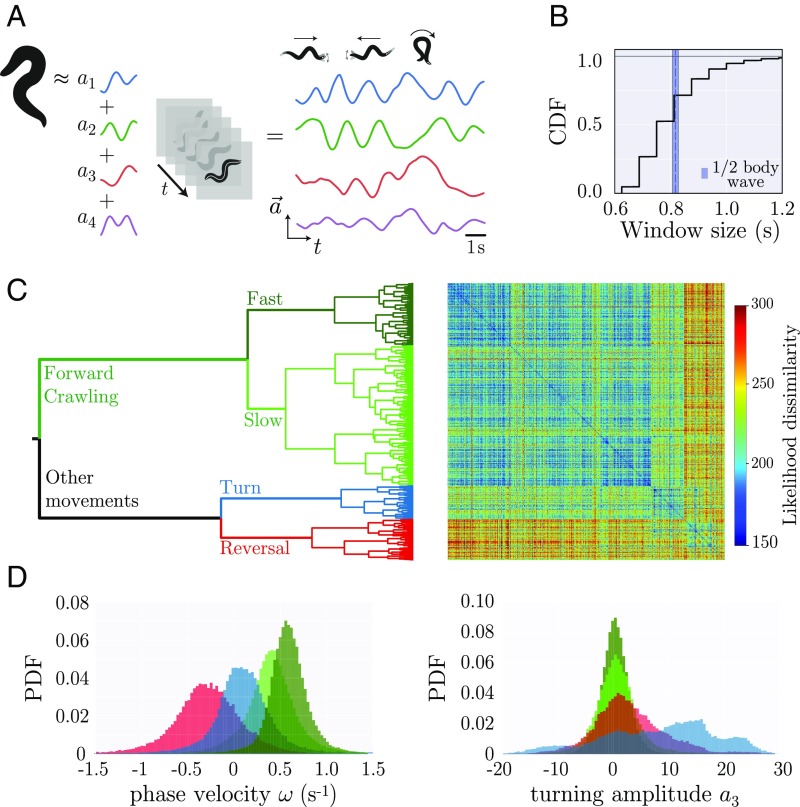
The posture dynamics of the nematode C. elegans is accurately represented by a low-dimensional time series of eigenworm projections (35) (Fig. 3A), although a quantitative understanding of the behaviors in these dynamics remains a topic of active research (36–39). More broadly, principled behavioral analysis is the focus of multiple recent advances in the video imaging of unconstrained movement across a variety of organisms (12, 24, 40–47). Here, we apply adaptive locally linear analysis to the eigenworm time series and find short model window lengths ranging from to (Fig. 3B). Notably, the median model window size is similar to the duration of half a worm’s body wave, suggesting that the body-wave dynamics provide an important timescale of movement control.
Fig. 3.
Locally linear analysis of C. elegans posture dynamics reveals a rich space of behavioral motifs. (A) We transform image sequences into a 4D posture dynamics using “eigenworm” projections (35), where the first two modes describe a body wave, with positive phase velocity for forward motion and negative when the worm reverses. High values of occur during deep turns, while captures head and tail movements. (B) The cumulative distribution function (CDF) of window sizes reveals rapid posture changes on the timescale of the locomotor wave (the average duration of a half body wave is shown for reference). (C) Likelihood-based hierarchical clustering of the space of linear posture dynamics. At the top of the tree, forward crawling models separate from other behaviors. At the next level, forward crawling splits into fast and slower body waves, while the other behaviors separate into turns and reversals. Hierarchical clustering results in a similarity matrix with weak block structure; while behavior can be organized into broad classes, large variability remains within clusters. (D) Cluster branches reveal interpretable worm behaviors. We show the probability distribution function (PDF) of body-wave phase velocities and turning amplitudes at the fourth-branch level of the tree. In the first forward state (dark green), worms move faster than in the second branch (light green). In the turn branch (blue), the phase velocity is centered around zero, and high values of indicate larger turning amplitudes. In the reversal branch (red), we find predominantly negative phase velocities.
Likelihood-based model clustering reveals that forward crawling separates from other worm behaviors at the top level of the hierarchy (Fig. 3C). At a finer scale, forward crawling breaks into faster and slower models, while turns and reversals emerge from the other branch. To clarify the structure of the model space, we leverage the interpretability of the eigenworm projections, where the first two modes ( and ) capture a primary body-wave oscillation with phase velocity , while a third projection captures broad body turns (35). In Fig. 3D, we show and for each cluster. We note that there are a few low-amplitude positive phase velocities in the reversal branch: The adaptive segmentation detects a dynamical break when the worm starts slowing down in preparation for a reversal, and those first frames are included in the reversal window. We note that changes in the activity of AIB, RIB, and AVB neurons also precede the reversal event (48). Further examination of the agreement between model clusters and behavioral states is provided in SI Appendix, Fig. S2. At a coarse level, the canonical behavioral states described since the earliest observations of the movements of C. elegans (49, 50) are identified here by using data-driven, quantitative methods.
The model parameters provide an additional opportunity for interpretation of the worm’s behavior, and in SI Appendix, Fig. S3, we show the coefficients for illustrative models at the clustering level consisting of four states. For models from the two forward states, the two pairs of complex conjugate eigenvalues have different imaginary values, corresponding to different frequencies of the locomotor wave oscillation. On the other hand, the turning model can be identified by the large mean turning amplitude. Finally, the reversal model exhibits an inversion in the sign of the coupling, which corresponds to a reversal in the direction of the body wave.
The full structure of the model dendrogram reveals that the behavioral repertoire of C. elegans is far more complicated than the canonical states of forward, reversal, and turning locomotion. For example, forward crawling behavior is rich and variable: Two forward crawling models can be almost as dissimilar as a turn is from a reversal. While the worm’s behavior is stereotyped at a coarse-grained level, there is significant variation within each of the broad behavioral classes. For example, at the 12-branch level of the tree, the reversal class splits into faster and slower reversals, as well as a new behavioral motif: a reversal-turn (SI Appendix, Fig. S4). Certainly, some of these “states” simply reflect the linear basis of the segmentation algorithm. However, longer nonlinear behavioral sequences can emerge from analysis of the resulting symbolic dynamics.
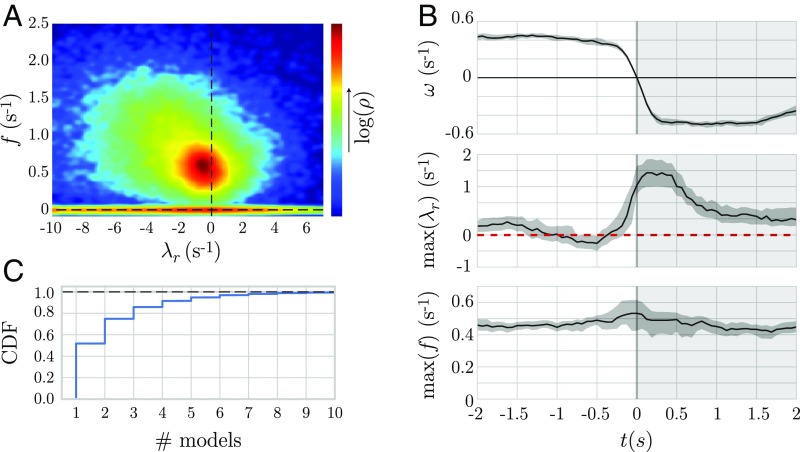
We analyze the spectrum of eigenvalues across the entire model space (Fig. 4A) and find that the worm’s dynamics includes both stable and unstable eigenvalues with a broad peak at , in agreement with the average forward undulatory frequency of the worm in these food-free conditions (35). Some of these unstable dynamics are explained by coarse behavioral transitions, and we align reversal trajectories by the moment when the body-wave phase velocity crosses zero from above to follow the median of the least-stable eigenvalues during this transition (Fig. 4B). We see that the reversal behavior is accompanied by an apparent Hopf bifurcation: A pair of complex conjugate eigenvalues crosses the instability boundary. More generally, we find that the dynamics rapidly switches stability (Fig. 4C). Indeed, the spectrum of eigenvalues shows that the worm’s dynamics is generically near the instability boundary, which is suggestive of a general feature of flexible movement control.
Fig. 4.
Linear posture dynamics in C. elegans is distributed across an instability boundary with spontaneous reversals evident as a bifurcation. (A) The eigenvalues of the segmented posture time series reveal a broad distribution of frequencies with a peak that spills into the unstable regime. (B) We align reversal events and plot the maximum real eigenvalue () and the corresponding oscillation frequency. As the reversal begins, the dynamics become unstable, indicating a Hopf-like bifurcation in which a pair of complex conjugate eigenvalues crosses the instability boundary. The shaded region corresponds to a bootstrapped 95% confidence interval. (C) Instabilities are both prevalent and short-lived. We show the cumulative distribution function (CDF) of the number of consecutive stable or unstable models, demonstrating that bifurcations also occur on short times between fine-scale behaviors.
Neural Dynamics of C. elegans
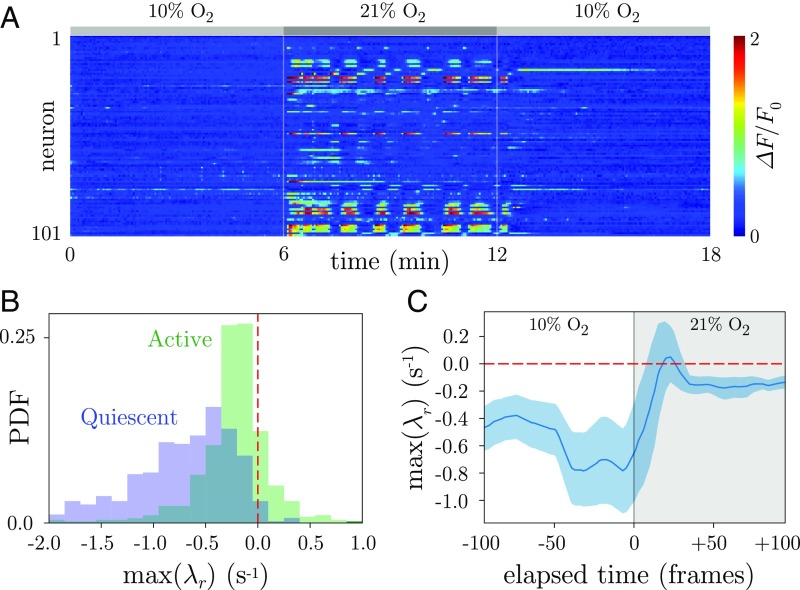
With recent progress in neural imaging, C. elegans also provides the opportunity to observe whole-brain dynamics at cellular resolution (48, 51–55), and we apply our techniques to analyze the differences between active and quiescent brain states driven by changes in oxygen () concentration (52). In these experiments, worms enter a “sleep”-like state when the levels are lowered to , and are aroused when the concentration is increased to . These conditions offer a probe of the neural dynamics of C. elegans and also suggest qualitative comparisons with sleep transitions measured through ECoG in human and nonhuman primates (11, 56, 57).
In Fig. 5A, we show an example trace of the recorded neural activity, and further details are available in Materials and Methods. We analyze the stability of the neural dynamics using “active” and “quiescent” global brain states identified previously (52), and we show the distribution of least-stable dynamical eigenvalues for each condition (Fig. 5B). To further characterize the transition between states, we align the maximum real dynamical eigenvalues by the time of increased concentration and show the mean of this distribution (Fig. 5C). As activity increases from the quiescent state, the dynamics move toward the instability boundary, eventually crossing and remaining nearly unstable in the aroused state. While the neural imaging occurs in paralyzed worms, the broad distribution of eigenvalues across the instability boundary in the active brain state is consistent with the complexity of the behavioral dynamics. Notably, the model space also contains clusters in approximate correspondence with previous state labels, both in these experiments (52) and in worms exhibiting more complex natural behaviors (48) (SI Appendix, Figs. S5 and S10).
Fig. 5.
Quiescence stabilizes global brain dynamics in C. elegans. (A) We analyze whole-brain dynamics from previous experiments in which worms were exposed to varying levels of concentration (52). We show the background-subtracted fluorescence signal from 101 neurons, while the concentration changed in 6-min periods: Low (10%) induces a quiescent state; high (21%) induces an active state. (B) We plot the distribution of maximum real eigenvalues () for the active and quiescent states. The active state is associated with substantial unstable dynamics, while the dynamics of the quiescent state is predominately stable, which is consistent with putative stable fixed-point dynamics. PDF, probability distribution function. (C) We plot the average maximum real eigenvalue as the concentration is changed. We align the time series from different worms to the first frame of increased concentration and show the accompanying increase in the maximum real eigenvalue, which crosses and remains near to the instability boundary. The shaded region corresponds to a bootstrapped 95% confidence interval, and curves were smoothed by using a five-frame running average.
Higher-Dimensional Systems
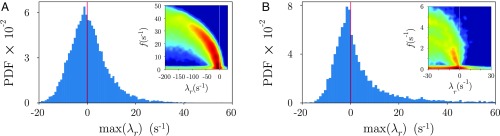
Beyond the previous examples, there are situations where high dimensionality and low sampling rate (relative to the signal correlation time) yield a minimum window size which is too large to capture important dynamics. This is as expected—more dimensions generally require more statistical samples—and our minimum window size is chosen conservatively to result in a good model fit without regularization and thus without bias. If the sampling rate is adequate, then we can easily apply our technique to higher-dimensional data, as we demonstrate in Fig. 6A and SI Appendix, Fig. S6, where we show the analysis of 40 components from ECoG recordings in nonhuman primates. For sparsely sampled systems, on the other hand, regularization is generally required to accurately compute the inverse of the data and error covariance matrices. We offer one straightforward procedure which is motivated by principal component regression (58) where we reduce the dimension locally, within each window. We detail this idea in Materials and Methods and provide a demonstration from recordings of hundreds of neurons in mouse visual cortex (Fig. 6B and SI Appendix, Fig. S7). In both of these high-dimensional systems, the local-linear analysis yields model dynamics that sit near the instability boundary, with a large fraction of unstable models (Fig. 6).
Fig. 6.
Higher-dimensional applications of the adaptive locally linear model technique: The dynamics exhibit a wide range of frequencies and near-critical behavior. (A) Distribution of the least-stable real eigenvalues from each window of the local-linear models obtained from the analysis of ECoG recordings in nonhuman primates. A, Inset shows the full distribution of eigenvalues—color code is the same as in Fig. 3. (B) Distribution of the least-stable real eigenvalues from each window of the local linear models obtained in recordings of 240 neurons in the visual cortex of Mus musculus. B, Inset shows the full distribution of eigenvalues—color code is the same as in Fig. 3. Here, due to the high-dimensionality, a regularization procedure was added to the original technique (Materials and Methods). PDF, probability distribution function.
Discussion
Simple linear models form the foundation for our analysis of complex time series based upon interpretable dynamics in short segments determined adaptively from data. The trajectories of a single model can only exponentially grow, decay, or oscillate. However, by tiling the global dynamics with many such models, we faithfully reproduce nonlinear, multidimensional, and nonstationary behavior and parameterize the full dynamics with the set of local couplings. To elucidate the resulting space of models, we construct hierarchical clusters with a new likelihood-based dissimilarity measure between local dynamics, and we examine the distribution and stability of the dynamical eigenvalues.
In the Lorenz system, chaos is distinguished by an increased model variety, including many with instabilities. In the chaotic attractor, the model hierarchy naturally splits across the two lobes with the clusters at deeper levels forming a progressively finer partition of the phase space. These partitions, as well as the recurrence structure in the space of models, can be used to estimate ergodic properties of the attractor, such as the Kolmogorov–Sinai entropy (59, 60). Adaptive locally linear analysis offers a new approach for thinking quantitatively about animal behavior, where recent advances have resulted in multiple efforts aimed at understanding movement at high resolution (12, 35, 36). In the posture dynamics of C. elegans, we find that interpretable behavioral motifs emerged naturally, with high-level clusters reflecting canonical behavioral states of forward, reversal, and turning locomotion (49) and finer-scale, novel states appearing deeper in the tree. An advantage of our clustering approach is that the level of behavioral description can be chosen appropriate to the nature of the analysis, and these states form a natural basis with which to apply techniques such as compression (36, 61) and to explore long-time behavioral dynamics like memory (12). The dissimilarity measure also enables the comparison of models across datasets, regardless of experimental details such as frame rate, as long as postures are projected into the same basis. This can be useful for developing a master repertoire of behaviors (36) as well as looking for differences between nematode species or studying perturbations to behavior (35, 38, 50, 61–64). We note that the success of the local linear basis in revealing interpretable worm behavior results in part from the ability to capture oscillations and the interactions between different posture modes, both common components of movement behavior.
The eigenvalues of the posture dynamics reflect variability and hint at the presence of flexible control. While the eigenvalue distribution is centered on the frequency of the locomotor wave, the peak is close to the instability boundary, and many models are unstable. Posture movements thus appear more complex than suggested by a model of stereotyped behaviors composed of a small collection of simple limit cycles (65).
The global neural activity of C. elegans also displays model dynamics which fluctuate across the instability boundary (Fig. 5B), suggesting a near-critical brain state (see ref. 66 for a similar, recent conclusion from a statistical perspective). Additionally, we obtain similar findings through local linear analysis of ECoG in monkey and single-cell recordings from a neural population in mouse visual cortex (Fig. 6). Such behavior is observed in whole brain activity (11, 56) and is consistent with the observation that the firing rate of neural populations exhibits subcritical dynamics (67). Dynamical criticality is advantageous for information processing in models of neural networks (68, 69) and can occur as a result of an anti-Hebbian balance of excitation and inhibition (32). Close to criticality, the dynamics is highly susceptible to external perturbations, and small changes to the stability can have a dramatic impact on the dynamical time scales (70). This susceptibility can change across brain regions (71), and we show that it can also be modulated with behavioral transitions and neural quiescence in C. elegans. Such modulation also occurs with the induction of anesthesia in ECoG (57) (SI Appendix, Fig. S6).
For simplicity and interpretability, we choose a basis of first-order linear models, although extensions to higher order are straightforward. Also, while we focus on the deterministic model properties, the error terms (Eq. 1, Materials and Methods) may also carry important information. For example, it has been recently shown that even deterministic chaotic systems can be accurately represented as linear dynamics with a heavy-tailed stochastic forcing, the magnitude of which can be used to identify bursting or lobe-switching events (72). In our analysis, we find that the error distribution exhibits heavy tails along the direction of the nonlinearities of the Lorenz system and that the magnitude increases with lobe switching in the Lorenz system or reversal events in C. elegans.
There have been multiple recent advances in applying linear models to the analysis of complex time series (24–26, 73, 74), and while our approach shares a linear basis, there are important differences. For example, both autoregressive hidden Markov models and switching LDSs assume that the dynamics is composed of a set of discrete coarse-grained dynamical modes, revisited by the system. The number of these modes is a hyperparameter of the model, chosen to balance model complexity and accuracy. In contrast, our analysis finds as many linear models as permitted by reliable estimation, and the depth of the hierarchical clustering can be chosen a posteriori, depending on the interpretation of the clusters. Our combination of adaptive segmentation and hierarchical clustering also enables the explicit examination of the variability of models within each cluster. The combination of the simplicity of linear models with the power of the statistical methods yields a compelling route for the deeper understanding of complex dynamics, and we expect our approach to be widely applicable.
Materials and Methods
Linear Dynamics and the Likelihood Function.
We approximate a given time series using first-order LDSs in short windows and use a likelihood-ratio test to estimate whether new observations can be modeled by the linear coefficients. Given a -dimensional discrete time series , we define the first-order vector autoregressive process,
| [1] |
where is an intercept vector, is a discrete time coupling matrix, and is a noise term with covariance , which we assume to be Gaussian and white. We estimate the linear parameters through least-squares regression. The continuous time linear couplings, , can be obtained by taking
| [2] |
where is a -dimensional identity matrix and is the inverse of the sampling rate.
Using windowed data , we construct the log-likelihood ratio between models with parameters and as
| [3] |
where the pseudo-log-likelihood function of model parameters from for a Gaussian process is given by
| [4] |
where is the error of modeling with .
Adaptive Locally Linear Segmentation Algorithm.
We first define a set of candidate windows in which to examine whether there are dynamical breaks. This is done iteratively: We set a minimum window size and then increment by which ensures that larger windows contain a proportionally larger number of observations. The candidate windows range between and some , which corresponds to the value at which the step size is larger or equal to . The specific value of depends on the dataset and the dimensionality , and we choose to be the smallest interval in which the data can be reliably fit. However, simply setting does not incorporate the possibility of multicollinearity, when two or more components are not linearly independent, which produces an ill-conditioned linear regression. This linear dependence results in a moment matrix that is not full rank or nearly singular, and therefore small perturbations result in large fluctuations in the estimated linear parameters. In addition, computing the log-likelihood function in Eq. 4 requires inverting the covariance matrix of the error . Thus, we require a minimum window size for which both and are well-conditioned. We compute the condition number of these matrices as a function of window size and choose as the smallest window for which the condition numbers are reasonably small. The results for each analyzed dataset are shown in SI Appendix, Fig. S8.
Given a set of candidate windows, we iterate over pairs of consecutive windows of size and , estimate the respective model parameters and , and locate a dynamical break if performs significantly better than in fitting the data from the window of size . We assess significance through a likelihood-ratio test and obtain from Eq. 3. We note that our models are nonnested, for which the likelihood ratio would be asymptotically distributed. Instead, we take as a null model for the observations in the window of size and use a Monte Carlo approach to generate n = 5,000 surrogate trials of size from to compute , the distribution of the log-likelihood ratio under the null hypothesis of having no model change. We identify a dynamical break if , where is defined by the larger solution of . A graphical representation of the technique is shown in Fig. 1, and the algorithm is detailed in SI Appendix. Finally, if the algorithm iterates to the maximum window size , we automatically assign a break, which we then assess through the following procedure: We start with and compare the models found in the intervals and as we increase until we span the entire set of candidate windows. If none of these tests suggest a break, then we simply remove it.
We choose the significance threshold empirically, and this choice reflects a tension between model complexity and accuracy; varying principally changes the number of breaks. While we have found to be reasonable across multiple datasets, we provide additional intuition through a toy segmentation problem illustrated in SI Appendix. The results reported in this work do not depend sensitively on the significance threshold.
Regularization for High-Dimensional Data.
Regularization can be incorporated straightforwardly into our method: At each iteration step, we project the windows of size and to a space of orthogonal vectors defined by the first eigenvectors of the covariance matrix of the window of size , estimate whether a break exists in this lower-dimensional space, and then project back the inferred model parameters to the original space through a simple linear transformation. The number of eigenvectors is chosen to keep the condition number of the covariance matrix of the data and the error below a certain threshold to ensure a well-conditioned model fit. We choose to use the condition number instead of the fraction of explained variance as a threshold, such that we could capture as much of the variance while being able to have a well-conditioned model fit. This results in projections that can capture more of the variance than that imposed by a variance threshold. We set the minimum window size at 10 frames, such that is at least 10% larger than (as in Algorithm 1 in SI Appendix). We demonstrate this regularization procedure on a dataset consisting of calcium imaging of hundreds of neurons in the mouse visual cortex (Fig. 6B and SI Appendix, Fig. S7). Other approaches such as lasso or ridge regression may also be incorporated, but at the cost of additional regularization parameters (75, 76).
Likelihood-Based Hierarchical Clustering.
The space of LDSs has a family of equivalent representations given by the transformation of the group of nonsingular matrices, and thus the Euclidean metric is not an appropriate dissimilarity measure. While previous solutions have been presented for measuring LDS distances (77, 78), the adaptation of these methods to our framework would be intricate and unnatural, and we instead define a likelihood dissimilarity measure, which is consistent with the adaptive segmentation method. In essence, two models are distant if the model found by combining the two corresponding windows is unlikely to fit either window. On the other hand, when the models are similar, then the model found by combining the two windows is very likely to fit both windows. Specifically, let and . We define the dissimilarity between models and as,
| [5] |
where , and is the result of fitting to Eq. 1. This measure is positive semidefinite since and ( is the maximum-likelihood estimate in ; ) and also symmetric; since we do not fit across windows, a first-order linear fit in yields the same linear couplings as in . After computing the dissimilarity between all linear models, we use Ward’s criterion (33) to perform hierarchical clustering by minimizing the within-cluster variance.
Lorenz Data.
We simulate the Lorenz system using the scipy.odeint package (79) with parameter choices , , and in the chaotic regime and for spirals. We use step size . In the chaotic regime, we integrate for a total of 1,000 s, waiting 200 s for the trajectories to fall onto the attractor. For the stable spirals in the late-time transient chaos regime, we choose initial conditions , where varies from −12 to −8 and 8 to 12 in steps of 0.2, yielding a total of 42 initial conditions. The trajectories are drawn to one of the stable fixed points , for which linear stability analysis yields a stable oscillation with and and a relaxation with . We wait for 10 s before sampling the spiraling trajectory on additional 10 s. To reduce multicollinearity, we add small-amplitude Gaussian white noise with a diagonal covariance matrix with variances to the simulated time series. The minimum window size frames is chosen by using SI Appendix, Fig. S8.
C. elegans Posture Data.
We analyze published data consisting of foraging behavioral conditions (35, 80) in which N2-strain C. elegans were imaged at with a video-tracking microscope. Coiled shapes are resolved, and the time series downsamples to (38). Worms are grown at under standard conditions (81). Before imaging, worms are removed from bacteria-strewn agar plates by using a platinum worm pick and rinsed from Escherichia coli by letting them swim for in nematode growth medium buffer. They are then transferred to an assay plate ( Petri dish) that contains a copper ring ( inner diameter) pressed into the agar surface, preventing the worm from reaching the side of the plate. Recording starts after the transfer and lasts for 2,100 s. In total, data from worms are recorded. Using SI Appendix, Fig. S8, we select a minimum window size of frames. Likelihood hierarchical clustering yield a dendrogram for which a cut at the four-branch level results in clusters with approximately 6,500 (fast forward), 14,400 (slow forward), 3,500 (turns), and 4,200 (reversals) models. In Fig. 4B, reversal events are identified when the phase velocity changes sign. Only segments for which there is a 2-s window of positive and negative phase velocity before and after the change of sign are considered.
C. elegans Neural Data.
We analyze whole-brain experiments from the Zimmer group in which transgenic C. elegans expressing a nuclear localized indicator are imaged in a microfluidic device where a reduction in concentration is observed to induce a sleep-like, quiescent state in npr-1 lethargus animals (52). A range of 99–126 neurons is imaged for worms, and each neural trace is normalized by subtracting the background and dividing by the mean signal. A linear component is also subtracted to correct for bleaching. We use principal components analysis to reduce each ensemble recording to an eight-dimensional time series capturing of the variance. Each of the experimental trials (one per worm) consists of three 6-min periods with alternating concentrations: starting with , increasing to , and returning to . We select a minimum window size frames using SI Appendix, Fig. S8. Likelihood hierarchical clustering yields a dendrogram for which a cut at the three-branch level results in one cluster with 24 models, another with 74 models, and a third outlier cluster containing just 1 model. Removing the outlier results in a dendrogram with a more even model distribution: one cluster with 24, another with 16, and a third with 55 models. We use this clustering to compare state labels with identified active and quiescent global brain states (52) (SI Appendix, Fig. S4). Data from unperturbed worms exhibiting more complex natural behaviors (48) are analyzed similarly.
ECoG in Monkey.
We analyze a publicly available dataset (neurotycho.org/) that has been described (4, 56, 82). The details of the experimental procedure can be found in ref. 83. The raw 128 electrode signals are preprocessed in the following way. First, the original signal is downsampled from 1 KHz to 500 Hz. Then, two channels are removed due to significant line noise contamination. The remaining 126 electrodes are filtered to remove the line noise at 50 Hz and subsequent harmonics. Multitaper filtering is performed by using the Chronux toolbox (84), available at chronux.org/, with a bandwidth of 5 Hz (nine tapers) in a moving window of 2 s with 0.5-s overlap. The overlap regions are smoothed by using a sigmoid function with smoothing parameter . Finally, the electrode signals are projected into 40 principal components that capture of the variance. We select a minimum window size frames using SI Appendix, Fig. S8.
Mus musculus Neural Data.
We analyze a publicly available dataset (observatory.brain-map.org/visualcoding/search/cell_list?experiment_container_id=511854338&sort_field=p_sg&sort_dir=asc) from the Allen Institute (85). The analyzed data constitute a total of 240 neurons from the anterolateral visual cortex of Mus musculus, at a depth of . Neural activity is sampled at for with a GCaMP6f calcium indicator, during exposure to a natural movie. The background subtracted bleach-corrected signals are accessed by using the Allen Software Development kit (86). The local linear analysis is performed with regularization by using a condition number threshold of .
Software.
Code for the adaptive locally linear segmentation and likelihood-based hierarchical clustering was written in Python (87) and is publicly available (https://github.com/AntonioCCosta/local-linear-segmentation.git).
Supplementary Material
Acknowledgments
We thank SURFsara (www.surfsara.nl) for computing resources through the Lisa system. This work was supported by the research program of the Foundation for Fundamental Research on Matter, which is part of the Netherlands Organization for Scientific Research; and also by The Okinawa Institute of Science and Technology Graduate University. G.J.S. acknowledges useful discussions at the Aspen Center for Physics, which is supported by National Science Foundation Grant PHY-1607611.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
Data deposition: Code for the adaptive locally linear segmentation and likelihood-based hierarchical clustering has been uploaded to GitHub (https://github.com/AntonioCCosta/local-linear-segmentation.git).
*The action of to the matrix of linear couplings results in new coupling matrix that is very different according to the Euclidean metric, while representing the same linear dynamics. Therefore, using the Euclidean distance is deeply misleading as two matrices that are distant in Euclidean metric can represent the same LDS.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1813476116/-/DCSupplemental.
References
- 1.Arratia PE, Voth GA, Gollub JP. Stretching and mixing of non-Newtonian fluids in time-periodic flows. Phys Fluids. 2005;17:1–10. [Google Scholar]
- 2.Majda AJ, Lee Y. Conceptual dynamical models for turbulence. Proc Natl Acad Sci USA. 2014;111:6548–6553. doi: 10.1073/pnas.1404914111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Alakent B, Doruker P, Çamurdan MC. Time series analysis of collective motions in proteins. J Chem Phys. 2004;120:1072–1088. doi: 10.1063/1.1630793. [DOI] [PubMed] [Google Scholar]
- 4.Yanagawa T, Chao ZC, Hasegawa N, Fujii N. Large-scale information flow in conscious and unconscious states: An ECoG study in monkeys. PLoS One. 2013;8:1–13. doi: 10.1371/journal.pone.0080845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Li K, Javer A, Keaveny EE, Brown AE. 2017. Recurrent neural networks with interpretable cells predict and classify worm behaviour. bioRxiv:10.1101/222208. Preprint, posted November 20, 2017.
- 6.Pathak J, Lu Z, Hunt BR, Girvan M, Ott E. Using machine learning to replicate chaotic attractors and calculate lyapunov exponents from data. Chaos. 2017;27:121102. doi: 10.1063/1.5010300. [DOI] [PubMed] [Google Scholar]
- 7.Brunton SL, Proctor JL, Kutz JN. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc Natl Acad Sci USA. 2016;113:3932–3937. doi: 10.1073/pnas.1517384113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Churchland MM, et al. Neural population dynamics during reaching. Nature. 2012;487:51–56. doi: 10.1038/nature11129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Schmid PJ. Dynamic mode decomposition of numerical and experimental data. J Fluid Mech. 2010;656:5–28. [Google Scholar]
- 10.Brunton BW, Johnson LA, Ojemann JG, Kutz JN. Extracting spatial-temporal coherent patterns in large-scale neural recordings using dynamic mode decomposition. J Neurosci Methods. 2016;258:1–15. doi: 10.1016/j.jneumeth.2015.10.010. [DOI] [PubMed] [Google Scholar]
- 11.Solovey G, Miller K, Ojemann J, Magnasco M, Cecchi G. Self-regulated dynamical criticality in human ECoG. Front Integr Neurosci. 2012;6:44. doi: 10.3389/fnint.2012.00044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Berman GJ, Choi DM, Bialek W, Shaevitz JW. Mapping the stereotyped behaviour of freely moving fruit flies. J Royal Soc Interface. 2014;11:1–21. doi: 10.1098/rsif.2014.0672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Guralnik V, Srivastava J. 1999. Event detection from time series data. Proceedings of the Fifth ACM SIGKKD International Conference on Knowledge Discovery and Data Mining (ACM, New York), 33–42.
- 14.Takeuchi JI, Yamanishi K. A unifying framework for detecting outliers and change points from time series. IEEE Trans Knowledge Data Engineering. 2006;18:482–492. [Google Scholar]
- 15.Wang Y, Sun G, Ji Z, Xing C, Liang Y. Weighted change-point method for detecting differential gene expression in breast cancer microarray data. PLoS One. 2012;7:e29860. doi: 10.1371/journal.pone.0029860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Liu S, Yamada M, Collier N, Sugiyama M. Change-point detection in time-series data by relative density-ratio estimation. Neural Networks. 2013;43:72–83. doi: 10.1016/j.neunet.2013.01.012. [DOI] [PubMed] [Google Scholar]
- 17.Chen Y, Li B, Niu L. A local vector autoregressive framework and its applications to multivariate time series monitoring and forecasting. Stat Interface. 2013;6:499–509. [Google Scholar]
- 18.Omranian N, Mueller-Roeber B, Nikoloski Z. Segmentation of biological multivariate time-series data. Sci Rep. 2015;5:8937. doi: 10.1038/srep08937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Preuss P, Puchstein R, Dette H. Detection of multiple structural breaks in multivariate time series. J Am Stat Assoc. 2014;110:654–668. [Google Scholar]
- 20.Kawahara Y, Yairi T, Machida K. Change-point detection in time-series data based on subspace identification. ICDM. 2007;2007:559–564. [Google Scholar]
- 21.Bryan JD, Levinson SE. Autoregressive hidden Markov model and the speech signal. Proced Comput Sci. 2015;61:328–333. [Google Scholar]
- 22.Stanculescu I, Williams CKI, Freer Y. Autoregressive hidden Markov models for the early detection of neonatal sepsis. IEEE J Biomed Health Inform. 2014;18:1560–1570. doi: 10.1109/JBHI.2013.2294692. [DOI] [PubMed] [Google Scholar]
- 23.Gallagher T, Bjorness T, Greene R, You YJ, Avery L. The geometry of locomotive behavioral states in C. elegans. PLoS One. 2013;8:e59865. doi: 10.1371/journal.pone.0059865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wiltschko AB, et al. Mapping sub-second structure in mouse behavior. Neuron. 2015;88:1121–1135. doi: 10.1016/j.neuron.2015.11.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Linderman S, et al. Bayesian learning and inference in recurrent switching linear dynamical systems. Proceedings of Machine Learning Research. 2017;54:914–922. [Google Scholar]
- 26.Markowitz JE, et al. The striatum organizes 3D behavior via moment-to-moment action selection. Cell. 2018;174:1–15. doi: 10.1016/j.cell.2018.04.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Guthery SB. Partition regression. J Am Stat Assoc. 1974;69:945–947. [Google Scholar]
- 28.Hawkins DM. Point estimation of the parameters of piecewise regression models. J R Stat Soc Ser C Appl Stat. 1976;25:51–57. [Google Scholar]
- 29.Chamroukhi F, Mohammed S, Trabelsi D, Oukhellou L, Amirat Y. Joint segmentation of multivariate time series with hidden process regression for human activity recognition. Neurocomputing. 2013;120:633–644. [Google Scholar]
- 30.Muñoz MA. Colloquium: Criticality and dynamical scaling in living systems. Rev Mod Phys. 2018;90:31001. [Google Scholar]
- 31.Magnasco MO, Piro O, Cecchi GA. Self-tuned critical anti-Hebbian networks. Phys Rev Lett. 2009;102:1–4. doi: 10.1103/PhysRevLett.102.258102. [DOI] [PubMed] [Google Scholar]
- 32.Magnasco MO, Piro O, Cecchi GA. Dynamical and statistical criticality in a model of neural tissue. Phys Rev Lett. 2009;102:1–5. [Google Scholar]
- 33.Ward JH. Hierarchical grouping to optimize an objective function. J Am Stat Assoc. 1963;58:236–244. [Google Scholar]
- 34.Lorenz EN. Deterministic nonperiodic flow. J Atmos Sci. 1963;20:130–141. [Google Scholar]
- 35.Stephens GJ, Johnson-Kerner B, Bialek W, Ryu WS. Dimensionality and dynamics in the behavior of C. elegans. PLoS Comput Biol. 2008;4:e1000028. doi: 10.1371/journal.pcbi.1000028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Brown AEX, Yemini EI, Grundy LJ, Jucikas T, Schafer WR. A dictionary of behavioral motifs reveals clusters of genes affecting Caenorhabditis elegans locomotion. Proc Natl Acad Sci USA. 2013;110:791–796. doi: 10.1073/pnas.1211447110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Yemini E, Jucikas T, Grundy LJ, Brown AE, Schafer WR. A database of Caenorhabditis elegans behavioral phenotypes. Nat Methods. 2013;10:877–879. doi: 10.1038/nmeth.2560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Broekmans OD, Rodgers JB, Ryu WS, Stephens GJ. Resolving coiled shapes reveals new reorientation behaviors in C. elegans. eLife. 2016;5:e17227. doi: 10.7554/eLife.17227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Liu M, Sharma AK, Shaevitz J, Leifer AM. Temporal processing and context dependency in C. elegans response to mechanosensation. eLife. 2018;7:e36419. doi: 10.7554/eLife.36419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Berman GJ, Bialek W, Shaevitz JW. Hierarchy and predictability in Drosophila behavior. Proc Natl Acad Sci USA. 2016;104:20167–20172. doi: 10.1073/pnas.1607601113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Berman GJ. Measuring behavior across scales. BMC Biol. 2018;16:23. doi: 10.1186/s12915-018-0494-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Klibaite U, Berman GJ, Cande J, Stern DL, Shaevitz JW. An unsupervised method for quantifying the behavior of paired animals. Phys Biol. 2017;14:015006. doi: 10.1088/1478-3975/aa5c50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Calhoun AJ, Murthy M. Quantifying behavior to solve sensorimotor transformations: Advances from worms and flies. Curr Opin Neurobiol. 2017;46:90–98. doi: 10.1016/j.conb.2017.08.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Han S, Taralova E, Dupre C, Yuste R. Comprehensive machine learning analysis of hydra behavior reveals a stable behavioral repertoire. eLife. 2018;7:e32605. doi: 10.7554/eLife.32605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Szigeti B, Deogade A, Webb B. Searching for motifs in the behaviour of larval Drosophila melanogaster and Caenorhabditis elegans reveals continuity between behavioural states. J Royal Soc Interface. 2015;12:20150899. doi: 10.1098/rsif.2015.0899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Todd JG, Kain JS, de Bivort BL. Systematic exploration of unsupervised methods for mapping behavior. Phys Biol. 2017;14:015002. doi: 10.1088/1478-3975/14/1/015002. [DOI] [PubMed] [Google Scholar]
- 47.Bruno AM, Frost WN, Humphries MD. A spiral attractor network drives rhythmic locomotion. eLife. 2017;6:e27342. doi: 10.7554/eLife.27342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Kato S, et al. Global brain dynamics embed the motor command sequence of Caenorhabditis elegans. Cell. 2015;163:1–14. doi: 10.1016/j.cell.2015.09.034. [DOI] [PubMed] [Google Scholar]
- 49.Croll NA. Behavioural analysis of nematode movement. Adv Parasitol. 1975;13:71–122. doi: 10.1016/s0065-308x(08)60319-x. [DOI] [PubMed] [Google Scholar]
- 50.Schwarz RF, Branicky R, Grundy LJ, Schafer WR, Brown AEX. Changes in postural syntax characterize sensory modulation and natural variation of C. elegans locomotion. PLoS Comput Biol. 2015;11:e1004322. doi: 10.1371/journal.pcbi.1004322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Nguyen JP, et al. Whole-brain calcium imaging with cellular resolution in freely behaving Caenorhabditis elegans. Proc Natl Acad Sci USA. 2016;113:E1074–E1081. doi: 10.1073/pnas.1507110112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Nichols ALA, Eichler T, Latham R, Zimmer M. A global brain state underlies C. elegans sleep behavior. Science. 2017;356:eaam6851. doi: 10.1126/science.aam6851. [DOI] [PubMed] [Google Scholar]
- 53.Schrödel T, Prevedel R, Aumayr K, Zimmer M, Vaziri A. Brain-wide 3D imaging of neuronal activity in Caenorhabditis elegans with sculpted light. Nat Methods. 2013;10:1013–1020. doi: 10.1038/nmeth.2637. [DOI] [PubMed] [Google Scholar]
- 54.Prevedel R, et al. Simultaneous whole-animal 3D imaging of neuronal activity using light-field microscopy. Nat Methods. 2014;11:727–730. doi: 10.1038/nmeth.2964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Venkatachalam V, et al. Pan-neuronal imaging in roaming Caenorhabditis elegans. Proc Natl Acad Sci USA. 2016;113:E1082–E1088. doi: 10.1073/pnas.1507109113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Solovey G, et al. Loss of consciousness is associated with stabilization of cortical activity. J Neurosci. 2015;35:10866–10877. doi: 10.1523/JNEUROSCI.4895-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Alonso LM, et al. Dynamical criticality during induction of anesthesia in human ECoG recordings. Front Neural Circuits. 2014;8:20. doi: 10.3389/fncir.2014.00020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Jolliffe IT. A note on the use of principal components in regression. J Royal Stat Soc Ser C Appl Stat. 1982;31:300–303. [Google Scholar]
- 59.Kolmogorov AN. On the entropy per unit time as a metric invariant of automorphisms. Doklady Russ Acad Sci. 1959;124:754–755. [Google Scholar]
- 60.Ott E. Chaos in Dynamical Systems. Cambridge Univ Press; Cambridge, UK: 2002. [Google Scholar]
- 61.Gomez-Marin A, Stephens GJ, Brown AEX. Hierarchical compression of Caenorhabditis elegans locomotion reveals phenotypic differences in the organization of behaviour. J Royal Soc Interface. 2016;13:20160466. doi: 10.1098/rsif.2016.0466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Vidal-Gadea A, et al. Caenorhabditis elegans selects distinct crawling and swimming gaits via dopamine and serotonin. Proc Natl Acad Sci USA. 2011;108:17504–17509. doi: 10.1073/pnas.1108673108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Gao S, et al. Excitatory motor neurons are local oscillators for backward locomotion. eLife. 2018;7:e29915. doi: 10.7554/eLife.29915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Fouad AD, et al. Distributed rhythm generators underlie Caenorhabditis elegans forward locomotion. eLife. 2018;7:e29913. doi: 10.7554/eLife.29913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Revzen S, Guckenheimer JM. Finding the dimension of slow dynamics in a rhythmic system. J Royal Soc Interface. 2012;9:957–971. doi: 10.1098/rsif.2011.0431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Chen X, Randi F, Leifer AM, Bialek W. 2018. Searching for collective behavior in a small brain. arXiv:1810.07623v1. Preprint, posted October 17, 2018.
- 67.Wilting J, Priesemann V. Inferring collective dynamical states from widely unobserved systems. Nat Commun. 2018;9:2325. doi: 10.1038/s41467-018-04725-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Toyoizumi T, Abbott LF. Beyond the edge of chaos: Amplification and temporal integration by recurrent networks in the chaotic regime. Phys Rev E. 2011;84:1–8. doi: 10.1103/PhysRevE.84.051908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Sussillo D, Abbott LF. Generating coherent patterns of activity from chaotic neural networks. Neuron. 2009;63:544–557. doi: 10.1016/j.neuron.2009.07.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Wilting J, et al. Dynamic Adaptive Computation: Tuning network states to task requirements. 2018 doi: 10.3389/fnsys.2018.00055. arXiv:1809.07550v1. Preprint, posted September 20, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Murray JD, et al. A hierarchy of intrinsic timescales across primate cortex. Nat Neurosci. 2014;17:1661–1663. doi: 10.1038/nn.3862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Brunton SL, Brunton BW, Proctor JL, Kaiser E, Nathan Kutz J. Chaos as an intermittently forced linear system. Nat Commun. 2017;8:1–8. doi: 10.1038/s41467-017-00030-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Oh SM, Rehg JM, Balch T, Dellaert F. Learning and inferring motion patterns using parametric segmental switching linear dynamic systems. Int J Comput Vis. 2008;77:103–124. [Google Scholar]
- 74.Fox E, Sudderth EB, Jordan MI, Willsky AS. Nonparametric bayesian learning of switching linear dynamical systems. In: Koller D, Schuurmans D, Bengio Y, Bottou L, editors. Advances in Neural Processing Systems 21. Neural Information Processings Systems 2008; Montréal: 2009. pp. 457–464. [Google Scholar]
- 75.Hoerl AE, Kennard RW. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics. 1970;12:55–67. [Google Scholar]
- 76.Santosa F, Symes WW. Linear inversion of band-limited reflection seismograms. SIAM J Sci Stat Comput. 1986;7:1307–1330. [Google Scholar]
- 77.Afsari B, Vidal R. 2013. The alignment distance on spaces of linear dynamical systems, Proceedings of the 52nd IEEE Conference on Decision and Control (IEEE, Piscataway, NJ), pp 1162–1167.
- 78.Ravichandran A, Chaudhry R, Vidal R. 2009. View-invariant dynamic texture recognition using a bag of dynamical systems. Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition (IEEE, Piscataway, NJ), pp 1651–1657.
- 79.Jones E, et al. SciPy: Open source scientific tools for Python. 2001 Available at www.scipy.org/
- 80.Stephens GJ, Bueno de Mesquita M, Ryu WS, Bialek W. Emergence of long timescales and stereotyped behaviors in Caenorhabditis elegans. Proc Natl Acad Sci USA. 2011;108:7286–7289. doi: 10.1073/pnas.1007868108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Sulston JE, Brenner S. The DNA of Caenorhabditis elegans. Genetics. 1974;77:95–104. doi: 10.1093/genetics/77.1.95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Tajima S, Yanagawa T, Fujii N, Toyoizumi T. Untangling brain-wide dynamics in consciousness by cross-embedding. PLoS Comput Biol. 2015;11:1–28. doi: 10.1371/journal.pcbi.1004537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Nagasaka Y, Shimoda K, Fujii N. Multidimensional recording (MDR) and data sharing: An ecological open research and educational platform for neuroscience. PLoS One. 2011;6:e22561. doi: 10.1371/journal.pone.0022561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Mitra P, Bokil H. Observed Brain Dynamics. Oxford Univ Press; New York: 2008. [Google Scholar]
- 85.Allen Institute for Brain Science Allen Brain Observatory. 2016 Available at observatory.brain-map.org/visualcoding/
- 86.Allen Institute for Brain Science Allen Brain Atlas Software Development Kit. 2015 Available at https://allensdk.readthedocs.io/en/latest/
- 87.Rossum G. Python Reference Manual. Python Software Foundation; Amsterdam: 1995. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.