Structure-based methods for binding mode and binding affinity prediction for peptide-MHC complexes

Abstract

Understanding the mechanisms involved in the activation of an immune response is essential to many fields in human health, including vaccine development and personalized cancer immunotherapy. A central step in the activation of the adaptive immune response is the recognition, by T-cell lymphocytes, of peptides displayed by a special type of receptor known as Major Histocompatibility Complex (MHC). Considering the key role of MHC receptors in T-cell activation, the computational prediction of peptide binding to MHC has been an important goal for many immunological applications. Sequence-based methods have become the gold standard for peptide-MHC binding affinity prediction, but structure-based methods are expected to provide more general predictions (i.e., predictions applicable to all types of MHC receptors). In addition, structural modeling of peptide-MHC complexes has the potential to uncover yet unknown drivers of T-cell activation, thus allowing for the development of better and safer therapies. In this review, we discuss the use of computational methods for the structural modeling of peptide-MHC complexes (i.e., binding mode prediction) and for the structure-based prediction of binding affinity.

INTRODUCTION

Although often imagined as a defense system waiting for an infection, our immune system is also constantly engaged in surveillance and maintenance of a complex microbiome (1, 2). While effective responses must be triggered against cancer cells and dangerous bacteria, harmful responses against healthy cells and gut bacteria must be avoided (3). Other potentially harmful impacts of immune responses that are undesirable include autoimmune reactions (4), as well as reactions to therapeutic products (5, 6) or tissue transplantation (7). For all these reasons, the ability to predict what triggers an immune response is of great biomedical interest.

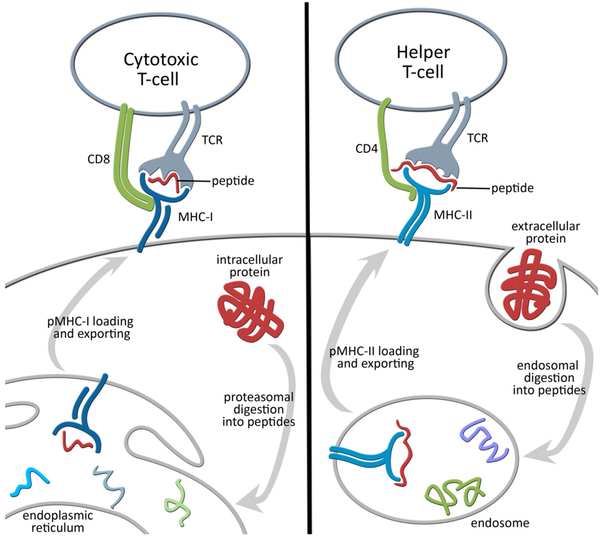
The ability of a given substance to trigger an immune response is referred to as immunogenicity (6, 8). In a broader sense, immunogenicity refers to the activation of both sides of adaptive immunity: cellular response (mediated by cytotoxic cells) and humoral response (mediated by antibodies). The activation of T-cells is a decisive step in both cases (8, 9), and it will also be referred to as immunogenicity here. T-cells are a special type of lymphocyte that undergo a complex maturation and selection process, which makes them capable of recognizing “non-self” peptides (10). Note that we are referring to T-cells in general; different subtypes of T-cells are involved on each side of adaptive immunity (Fig. 1).

Figure 1. Schematic view of the role of MHCs in T-cell activation.

Class I Major Histocompatibility Complexes (MHC-I) are present in almost every cell and involved in the surface presentation of peptides derived from intracellular proteins. On the other hand, class II MHCs are present only in “professional” antigen-presenting cells (phagocytes) and involved in the surface presentation of peptides derived from extracellular proteins. The recognition of displayed peptide-MHC complexes by the T-cell receptor (TCR) triggers T-cell activation, clonal expansion and immunological memory. While cytotoxic T-cells (CD8+) mediate cellular immunity, helper T-cells (CD4+) control the humoral response and have other regulatory roles. CD stands for cluster of differentiation.

T-cells only recognize peptides displayed by Major Histocompatibility Complex (MHC) receptors (8, 11). Specifically, the T-cell receptors (TCRs) of cytotoxic T-cells can only recognize peptides displayed by class I MHC receptors (MHC-I), while the TCRs of helper T-cells can only recognize peptides displayed by class II MHC receptors (MHC-II) (Fig. 1). Given their central role in both types of responses, MHC receptors have long been the focus of many studies in computational biology (12–16).

Binding to MHC receptors is a prerequisite for peptide immunogenicity (9, 17, 18). In turn, immunogenic peptides are needed for peptide-based vaccine design and cancer immunotherapy. Additional information on this topic can be found in reviews on epitope discovery (19, 20) and reverse vaccinology (21, 22). In this context, sequence motifs (14) and scoring matrices (23, 24) were among the first computational methods used to perform sequence-based binding affinity prediction. They were quickly overpowered by statistical learning algorithms (25–27), which remain the gold standard in the field (28–30).

Despite their unquestionable usefulness, sequence-based methods have known limitations. For instance, statistical learning methods require an experimental dataset for training, and predictions can be biased by the composition of this training dataset (22, 31). Therefore, predictions for MHC variants (i.e., allotypes) with larger datasets available for training tend to be more reliable than predictions for less studied allotypes. These gaps in the training data can be a limitation for some of the most interesting medical applications, such as personalized cancer immunotherapy. One of the goals in cancer immunotherapy is to find tumor-derived peptides that can bind to the MHC-I receptors of the patient, flagging cancer cells for destruction by the patient’s own immune system (32, 33). The MHC-I genes, however, are the most variable genes in the human genome. In humans, the three “classical” MHC-I genes are referred to as human leukocyte antigens (HLA-A, HLA-B and HLA-C), and combined together encode nearly 10,000 allotypes. Most of these MHC-I allotypes have very low prevalence in the population, and have limited or no experimental data available for training statistical learning methods. In spite of that, more recent sequence-based methods have aimed for generalizations based on available data (30).

An alternative approach, that is expected to be more general, is underpinned by structure-based methods (22). As discussed in pioneer studies in the 90’s (12, 34, 35), structure-based prediction relies on the biochemical properties of the amino acids involved in the peptide-MHC (pMHC) interaction, and do not require allotype-specific training datasets (22). In addition, access to structural information about pMHC complexes can be used to explore many other questions that cannot be addressed by sequence analysis alone. For instance, it can be used to analyze the impact of post-translational amino acid modifications, such as phosphorylation (36), citrullination (37), and glycosylation (38), which are known to affect both the binding affinity and immunogenicity of MHC-binding peptides. It can also be used to detail the structural basis of TCR/pMHC interactions, which can guide the production of alternative peptide ligands (39), allow for TCR-engineering (40), and even explain dangerous side-effects of T-cell-based immunotherapy (41, 42).

Three-dimensional structural data, however, is harder to obtain and process than sequential data. First, experimental methods for determining the structure of protein-ligand complexes are too expensive and time-consuming to be considered in the context of personalized medicine. Therefore, computational methods for structural prediction (or molecular modeling) are a prerequisite for conducting personalized structure-based analyses. However, the size and flexibility of the ligands involved make pMHC modeling and structure-based binding affinity prediction a challenging problem from a computational perspective (43).

To overcome these challenges and perform structural analyses in an efficient way, the solution has been to rely on adhoc constraints based on expert knowledge or available experimental data (12, 22, 43). Unfortunately, this has been done at the expense of the so-desired generality. In this review, we report previously proposed strategies for the efficient modeling of pMHC complexes (i.e., binding mode prediction) and for structure-based binding affinity prediction. We also discuss the main assumptions and trade-offs of the different approaches, and how the recent advances in high performance computing might finally allow for general and reliable methods.

SAMPLING, SCORING AND SCREENING

Molecular modeling has been an active field in computational chemistry since the 60’s (44), producing several approaches for structural prediction, analysis, and refinement (45, 46). A particular domain of molecular modeling relates to the prediction of the bound structure of protein-ligand complexes; a problem usually addressed with computational methods known as molecular docking tools (47–50). There are two main applications of molecular docking: binding mode prediction, also known as geometry optimization, and virtual screening (51, 52). The first application focuses on accurately predicting the 3D conformation of the ligand, upon binding to the target receptor. The second one focuses on checking a large number of potential ligands and selecting the ones that can bind to the target receptor.

Both applications share a central challenge: accounting for ligand flexibility. The greater the number of flexible bonds in a ligand, the greater the number of “shapes” (i.e., conformations) it can adopt. To determine the best possible binding mode, a docking method must consider these alternative conformations, in addition to the position and orientation of the ligand inside the receptor’s binding cleft. This search process is referred to as sampling (48).

As discussed in previous publications, sampling algorithms can be divided into three general categories: shape matching, systematic search and stochastic search (48, 53, 54). Briefly, matching algorithms perform geometric-based evaluations on how much the shape of the ligand fits the shape of the receptor’s binding cleft (47), often using a graph-based representation of the ligand’s structure (47, 55). These methods are usually applied to perform a fast exploration of the ligand’s rotational and translational degrees of freedom, without exploring its conformational flexibility (which is known as rigid docking) (55). On the other hand, systematic search algorithms explore all the degrees of freedom of the ligand (e.g., through exhaustive search, fragment-based search, or conformational ensemble search) (48, 53, 54). These methods are much more accurate than matching algorithms, but their computational cost prevents them from being used for larger ligands. Finally, stochastic search algorithms randomly explore the degrees of freedom of the ligand, using different heuristics to guide the exploration (e.g., Monte Carlo, genetic algorithms, tabu search or swarm optimization) (48, 53). As further discussed in the following sections, the size and flexibility of MHC-binding peptides represents a challenge that could not be efficiently handled even by stochastic algorithms, thus requiring additional strategies to make the sampling problem computationally tractable.

Regardless of the sampling method, some kind of ranking of the sampled conformations is needed to guide the sampling and select the best binding mode. This ranking is based on a “quality” assessment of the ligand conformations, which is referred to as scoring. Note that the scores used to rank conformations do not necessarily correspond to accurate binding affinity estimates. In fact, as the number of evaluated poses can be extremely large, scoring functions usually favor computational efficiency over accuracy (56). To achieve that, numerous scoring methods depart from explicitly calculating all relevant interactions between ligand and receptor at the atomic level.

Besides allowing for the assessment and comparison of different conformations of a given ligand to a given protein, a scoring method can also be used for screening (i.e., to assess how strongly different ligands might bind to a given protein). First, scoring methods can help distinguish between ligands that bind and ligands that do not bind the protein, in a purely qualitative manner. This requires performing a binary classification to separate so-called binders from non-binders, based on their respective scores. In this case, ligand scores do not have to correspond to actual binding affinities, as only relative differences between these scores are evaluated. Second, when using scoring methods that are biophysically accurate, one can quantitatively predict actual binding affinities. The capability of a scoring method to do that is usually assessed by evaluating the correlation between these predicted binding affinities and experimental binding affinities, and not by evaluating whether they match exactly. The differences between the qualitative and quantitative applications of scoring functions are clearly illustrated in Figure 3 of (57).

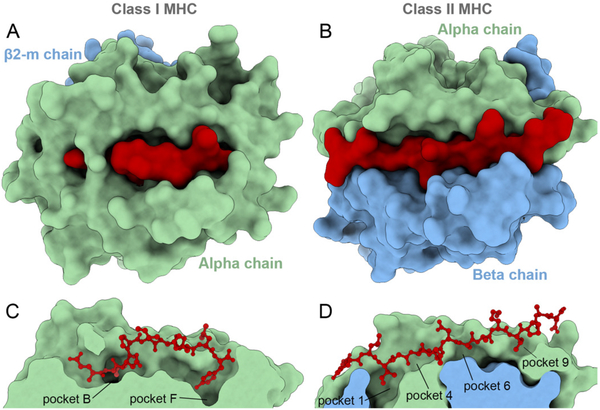
Figure 3. Molecular structures of class I and class II MHCs.

Molecular representation of a class I MHC (A, C) and a class II MHC (B, D). The upper panel shows a top view, while the bottom panel shows a cross section side-view of the binding clefts. Note that the binding cleft of a class I receptor is deeper, with “closed” extremities, while the class II cleft is shallower, with open extremities. The pockets involved in binding primary “anchor” residues are indicated. Together, structural differences in the shape of the cleft and the location of binding pockets have an impact on the overall conformation of bound ligands (e.g., peptides tend to adopt bulged conformations when bound to class I, and more linear conformations when bound to class II). Crystal structures of both complexes were downloaded from the PDB and superimposed to be in the same orientation. Class I complex: HLA-A*01:01 receptor presenting a tumor-derived 9-mer peptide (PDB code 5BRZ). Class II complex: HLA-DRB1*01:01 receptor presenting a 14-mer bacteria-derived peptide (PDB code 1KLU). Receptor chains α and β (or β2-microglobulin) are depicted in surface, while peptide ligands are depicted in surface (A, B) or ball-and-sticks (C, D). Graphics were obtained with UCSF ChimeraX (66).

Note that the main assumption underlying a docking-based binding affinity prediction is that the binding free energy of the complex can be approximated by the minimum internal energy of the system (58). In turn, the internal energy of the system is estimated by the scoring function, for each sampled conformation of the complex. Therefore, the accuracy of the binding affinity predicted by a molecular docking tool depends on the quality of both the sampling and the scoring. First, the sampling algorithm have to succeed in generating a conformation of the complex that presents the native set of stable interactions between ligand and receptor. Then, these key interactions must be identified by the scoring function, and properly summarized into an approximated binding affinity. In other words, insufficient sampling can hinder the docking prediction as much as an inaccurate scoring function. Insufficient sampling becomes an even greater issue in the case of highly-flexible ligands or flexible binding sites, since the search space becomes even larger and there is less confidence that the best values of the scoring function can be reached. It is also important to note that these components (i.e., sampling and scoring) and applications of structural prediction methods (i.e., geometry optimization and virtual screening) can be explored separately, or in a combined manner. In the context of docking-based virtual screening, for instance, a given scoring function can be used to (i) rank different conformations of each ligand to guide the sampling, (ii) rank different ligands to identify strong binders, and (iii) estimate the binding affinity of selected ligands. Here, we will discuss how each one of these components/applications was explored in the context of pMHC structural analysis.

COMPUTATIONAL METHODS FOR BINDING MODE PREDICTION

In this section we review publications focused on describing and validating methods for accurate binding mode prediction of pMHC complexes. Note that many additional publications report ad-hoc approaches to predict the structure of pMHC complexes as part of larger pipelines for epitope discovery or rational vaccine design (59–63), without focusing on accurate and reproducible binding mode prediction.

Evaluation of sampling methods

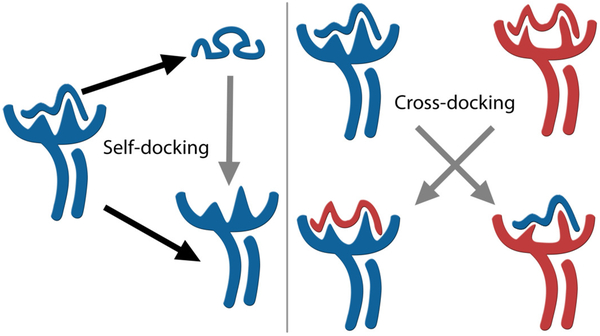
The two standard experiments for validating a docking method are self-docking and cross-docking (Fig. 2). Both methods rely on the use of experimentally-determined crystal structures of known complexes as controls. The accuracy of the method can be measured through the deviation (i.e., the “error”) between the predicted binding mode and the corresponding crystal structure. This error is usually assessed by calculating the Root Mean Square Deviation (RMSD) for the peptide only. An all-atom RMSD below 2Å is classically considered a successful reproduction of the native binding mode (64, 65).

Figure 2. Validation experiments for binding mode prediction.

Self-docking, also known as re-docking, focuses solely on sampling the ligand. For each target complex, the structures of the ligand and of the receptor are separated, the conformation of the ligand is randomized, and the method under evaluation is used to predict the best binding mode of the ligand to the receptor from the same (self) co-crystallization. On the other hand, cross-docking consists of predicting the binding mode of the ligand to a different conformation of the receptor (e.g., a model or a structure from a different co-crystallization). Therefore, cross-docking usually requires some type of relaxation or sampling of the receptor, in addition to that of the ligand.

Common strategies to make sampling tractable

Binding mode prediction for pMHC complexes is more challenging than most docking problems in drug discovery. Indeed, most drug-like ligands have less than 10 flexible bonds, while MHC-binding peptides usually have more than 30 flexible bonds (even more than 50 for MHC-II). Interestingly, data from the first crystal structures of pMHC-I complexes suggested the existence of conserved structural patterns (12, 17), which were imposed by structural constraints in the binding cleft (Fig. 3). Aiming at leveraging these structural constraints and limiting the computational cost of sampling, three strategies have been devised to predict the binding modes of pMHC complexes: constrained backbone prediction, constrained termini prediction, and incremental prediction (Table 1).

Table 1.

Key methods applied to pMHC binding mode prediction

Publication (Ref.)	Tool/Method	Strategy	Validation (size)	Dataset Composition	Best Results (RMSD)
Schueler-F. et al., 1998 (17)	rotamer libraries for side-chains with MOIL	constrained backbone	self-docking (23)	8-mers to 10-mers, 9 class I MHCs	Buried side-chains: 1.2 Å
Ota et al., 2001 (67)	MCSA-PCR (randomized crystal template)	constrained backbone	self-docking (1)	only one 8-mer peptide, 1 class I MHC	Backbone: 0.76 Å, All-atom: np
Todman et al., 2008 (68)	MHCSim (side chain mutations)	constrained backbone	self-docking (15), cross-docking (30)	only 9-mers, several human MHCs	np
Bordner et al., 2010 (69)	ICM + monte carlo + modeling	constrained backbone	self-docking (17), cross-doking (18)	11-mers to 15-mers, 17 class II MHCs	Backbone (core): 0.68 Å, All-atom (core): 1.37 Å
Antunes et al., 2010 (70)	D1-EM-D2 (AutoDock Vina + Gromacs)	constrained backbone	cross-docking (4)	8-mers and 9-mers, 4 class I MHCs	All-atom: 1.75 Å
Khan et al., 2010 (71)	pDOCK (modeling + ICM + monte carlo)	constrained backbone	self-docking (186)	8-mers to 10-mers, 12 class I MHCs and 9 class II MHCs	C-alpha (core): 0.32 Å, All-atom: np
Donsky et al., 2011 (72)	PepCrawler (RRT-based)	constrained backbone	self-docking (np)	np	Backbone: <= 1.2 Å, All-atom: np
Liu et al., 2014 (73)	PepFlexDock (Rosetta-based refinement protocol)	constrained backbone	self-docking (70)	only 9-mers, 4 class I MHCs and 1 non-classical MHC	C-alpha (top 5): 0.93 Å, All-atom (top 5): 1.8 Å
Rigo et al., 2015 (65)	DockTope (D1-EM-D2)	constrained backbone	cross-docking (135)	8-mers and 9-mers, only 4 class I MHCs	C-alpha: 0.88 Å, All-atom: 1.96 Å
Fagerberg et al., 2006 (74)	near native MD with simulated annealing steps	constrained backbone	self-docking (41), cross-docking (12)	8-mers to 10-mers, only 1 class I MHC	Backbone: 1 Å*, All-atom: 1.5 Å*
Rosenfield et al., 1993 (35)	multiple copy algorithm, loop closure, minimization	constrained termini	self-docking (1)	only 1 9-mer peptide, 1 class I MHC	Backbone: 2.7Å, All-atom: np
Sezerman et al., 1993 (34)	rigid-body grid search with EM	constrained termini	self-docking (1), cross-docking (4)	1 4-mer, 1 9-mer, 1 13-mer, 2 class I MHCs	Backbone: 0.83 Å, All-atom: np
Rognan et al., 1999 (75)	modeling, rotamer library, loop closure, EM, SA	constrained termini	self-docking (5)	8-mers and 9-mers, 11 class I MHCs	Backbone: 1.2 Å, All-atom: np
Tong et al., 2004 (76)	docking with ICM + loop closure	constrained termini	self-docking (40), cross-docking (15)	8-mers to 10-mers, 8 class I and 6 class II MHCs	C-alpha: 2.2 Å, All-atom: np
Bui et al., 2006 (77)	PePSSI (computed library of backbones)	constrained termini	self-docking (8)	only 9-mers, only 1 class I MHC	All-atom: 1.7 Å
Bordner et al., 2006 (78)	homology modeling + ICM + monte carlo	constrained termini	self-docking (3), cross-docking (23)	8-mers to 10-mers, 7 class I MHCs	Backbone: 0.93 Å, All-atom: np
Kyeong et al., 2018 (79)	GradDock (gradient-based method)	constrained termini	self-docking (107), cross-docking (70)	8-mers to 10-mers, 82 class I MHCs	Backbone: 1.2 Å**, All-atom: 2.5 Å**
Sezerman et al., 1996 (80)	fragment-based docking, rotamer (CONGEN)	incremental prediction	cross-docking (4)	only 4 9-mer peptides, 3 class I MHCs	All-atom: < 1.6 Å
Desmet et al., 1997 (81)	fragment-based docking, rotamer (BRUGEL)	incremental prediction	self-docking (1), cross-docking (1)	1 8-mer and 1 9-mer, 1 class I MHC	Backbone: 0.8 Å/1.3 Å, All-atom: np
Antes et al., 2006 (82)	DynaPred (near native exploration with MD)	incremental prediction	cross-docking (20)	only 9-mers, 1 class I MHC	Backbone: 1.53 Å, All-atom: np
Antunes et al., 2017 (43)	DINC (AutoDock4 + incremental method)	incremental prediction	self-docking (25)	8-mers to 10-mers, 10 class I MHCs	C-alpha: 0.99 Å, All-atom: 1.92 Å

RMSD, Root Mean Square Deviation. np, not provided.

^*Upper threshold for 92% of the dataset.

^**Reported averages vary depending on sample size, but are similar between self-docking and cross-docking

Constrained backbone prediction

The binding cleft of MHC-I receptors is “closed” at both ends (Fig. 3A and3C), with deeper “pockets” allowing for key interactions with the “anchor” residues of peptides. Analysis of the first pMHC-I crystal structures suggested a conserved conformation of the peptide’s backbone, despite the diversity of amino acid sequences (i.e., the diversity of side chains) (34, 70). These observations justified the use of a backbone template that is kept rigid or constrained during docking (Table 1). Although a backbone template simplifies the problem, the same template cannot be used for MHC-I and MHC-II (Fig. 3), or even for different MHC allotypes. The conformation of the peptide’s backbone is impacted by the composition of the different pockets inside the binding cleft, and the presence of alternative anchor residues. In addition, different templates are required for peptides of different lengths binding to a given MHC allotype (34, 70).

In this context, the work in (17) proposed using a library of crystallographic templates. They utilized the backbone of both the peptide and the MHC as a template, filling in the side-chains of the target sequence using rotamer libraries and the MOIL package (101). The method of utilizing a “clean” backbone to which desired side-chains are added is known as threading (102). Note that the term threading is also used to refer to another molecular modeling method, applied by tools such as ITASSER (103). Despite promising results on the prediction of the buried side chains of the peptide, they noticed that a general rotamer library from PDB-deposited structures did not include some side-chain conformations observed in pMHC crystal structures (17). Therefore, the generality and accuracy of their predictions was to some extent limited by the small dataset of available pMHC crystal structures.

The growing number of pMHC crystal structures continued to reveal additional backbone variation. To try and reduce biases introduced by the template, other methods added steps of backbone sampling or refinement to the docking process. For instance, the work in (71) proposed pDOCK. This method combines homology modeling of the MHC receptor, positioning of the peptide based on crystal structures, and refinement of the binding site residues using the Internal Coordinate Mechanics (ICM) docking algorithm (104) and a biased Monte Carlo procedure. pDOCK was validated in a self-docking experiment with 186 pMHC complexes (149 MHC-I and 37 MHC-II), reporting average backbone-atom RMSDs of only 0.32Å (computed for the 9-mer “core” residues). The accuracy of pDOCK in terms of all-atom RMSD was not reported.

Another method using a backbone template was proposed in (73). This approach was based on the Rosetta FlexPepDock refinement protocol (105) and validated through a series of cross-docking experiments using 30 selected crystal structures. Interestingly, the authors report good results even when the template is known to come from a peptide bound to a different MHC allotype (best all-atom RMSD of 1.8Å among the top 5 ranking conformations). However, the selected dataset was limited to 9-mers bound to MHC-I, and presented small backbone RMSD differences between template and target (the largest difference being 1.35 Å).

Most of these methods were not made available as software or webserver, which might have limited their use by other groups. The first webserver for the structural prediction of pMHC complexes was MHCSim (68). MHCSim relied on sequence alignment to find the closest template from a curated dataset of crystal structures, and side chains were mutated on both ligand and receptor. Rather than providing binding mode prediction, the goal of MHCSim is to generate initial pMHC structures for molecular dynamics (MD) simulations. More recently, the DockTope webserver was proposed in (65) (soon to be available at tools.iedb.org/docktope). DockTope relies on a template-based docking with AutoDock Vina (106), and a refinement loop involving energy minimization followed by a new round of docking (65, 70). DockTope was validated through the cross-docking of 135 non-redundant pMHC-I structures, reporting an average all-atom RMSD of only 1.96 Å. These results present DockTope as a valuable tool for the geometry optimization of pMHC-I complexes. Unfortunately, it only provides predictions for key allotypes for which conserved backbone conformations of the peptide have been observed.

Constrained termini prediction

An alternative assumption that is potentially more general, is that the locations of termini residues are more conserved than the conformation of the backbone (12). Depending on their implementation, “constrained termini” approaches can generalize across MHC-I allotypes because MHC-I binding clefts all have approximately the same length, and termini residues will be constrained by the same pockets. That was the rationale behind the pioneer studies in (34) and (35). The work in (35) proposed a modeling method involving a multiple-copy algorithm (107) to dock the termini residues, followed by a loop closure algorithm to fill the middle residues (108). This general strategy was further explored and perfected by others (69, 75–78).

The most recent implementation of the “constrained termini” strategy is GradDock (79). GradDock combines a fast peptide binding simulator with a Rosetta-based ranking function specifically designed for pMHC-I, and it is available for download (bel.kaist.ac.kr/research/GradDock). This method was tested through both self-docking (107 complexes) and cross-docking (70 complexes), providing impressive results (average all-atom RMSD around 2.5 Å). GradDock results suggest that fast virtual screening of pMHC complexes might be possible, and that the conserved termini assumption might be general enough to provide predictions across MHC-I allotypes. On the other hand, the greater all-atom RMSD observed in some cases suggest this might not be the best tool for geometry optimization.

The authors of GradDock also discuss the limitations imposed by the constrained termini strategy, having excluded from their analysis known cases of alternative binding modes. A notable example is that of a melanoma-derived 9-mer peptide bound to a highly prevalent human MHC (HLA-A*02:01), which uses an alternative anchor and has an unusual backbone conformation (PDB code 2GTW). Being an exception to observed patterns, this complex cannot be predicted by methods relying on constrained termini or constrained backbone strategies (65, 79). Since experimental data on alternative binding modes is still limited, especially considering the diversity of MHC allotypes, it is difficult to evaluate the actual impact of imposing such constraints.

Incremental prediction

As considering the entire conformational space of the peptide was impractical without constraints, another proposed strategy focused on incrementally exploring the flexibility of the ligand (e.g., one residue at a time). A fragment-based docking strategy was first proposed by (80) using the package CONGEN (109) and a similar approach was proposed by (81), using the BRUGEL package (110). This incremental strategy was later revisited with the publication of DynaPred (82). Instead of using a docking tool, DynaPred relies on a short MD simulation to sample each peptide residue inside the binding cleft. DynaPred uses a backbone template from crystal structures to help position amino acids in the binding cleft, but allows for the flexibility of this backbone during the simulation. Conformations from independent residues are then “stitched” together, and a minimization protocol is used to generate the final conformation.

More recently, the work in (43) proposed the use of an incremental meta-docking approach called DINC. DINC is not a traditional fragment-based docking tool (111), and does not explore the residues independently. Instead, DINC involves incrementally docking overlapping fragments with a growing number of atoms, while maintaining the number of flexible bonds constant during this incremental process (43, 111, 112). DINC handles the fragment expansion and the parallelization of the search, while relying on a regular docking tool, such as AutoDock4 (113), to perform the sampling. DINC was developed as a general tool for docking large ligands, and is available as a webserver (http://dinc.kavrakilab.org/). In the context of pMHC structural prediction, a customized version of DINC was tested through self-docking of a diverse set of known structures. Despite being a small dataset (25 structures), it included very different binding modes (e.g., 10 different human MHC-I allotypes and peptides of different lengths), and very challenging complexes (e.g., the unusual conformation under PDB code 2GTW). The reported average all-atom RMSD was 1.92 Å, and the results were presented as a proof-of-concept for a prediction method that could generalize across MHC-I allotypes. However, broader benchmarking of DINC is needed to evaluate its performance and accuracy across known MHC-I and MHC-II allotypes.

Additional challenges for modeling pMHC-II complexes

Although some of the aforementioned methods were applied to both classes of MHCs, MHC-II complexes represent a more challenging problem for computational modeling. MHC-I and MHC-II receptors have analogous functions and share general structural features, such as having a peptide-binding cleft limited by two parallel α-helices and a floor of β-sheets. A closer look, however, reveals key structural differences (Fig. 3). For instance, while the MHC-I cleft is “closed” at both ends and the peptides are forced to adopt a bulged conformation to fit in, the MHC-II cleft is shallower and allows longer peptides to go beyond both ends of the cleft (Fig. 3B and 3D). As a consequence, a given MHC-II allotype can bind to different portions of the same peptide (i.e., have different binding registers) (114). The portion of the peptide binding to the MHC-II is usually 9 amino acids long (84), but MHC-II receptors can bind peptides with up to 25 amino acids (76).

Longer peptides have a greater number of possible registers, but not all possible registers can bind. Similar to MHC-I receptors, there are key “pockets” that are primarily responsible for the binding of “anchor” peptide residues (Fig. 3D). In MHC-II receptors, pockets 1, 4, 6 and 9 appear to be the most crucial determinants for binding (115, 116). These pockets are hydrophobic cavities that favor hydrophobic side chains (116, 117). Nonetheless, the structural prediction of pMHCII complexes is a challenging task because it entails simultaneously predicting the binding register and the corresponding binding mode (69, 114).

Another peculiarity is that MHC-II receptors are heterodimers formed by two analogous chains (α and β), each one encoded by a different gene. Despite not having as many allotypes as MHC-I genes, the binding cleft of MHC-II receptors can be formed by the combination of α and β chains from different genes, which increases the diversity of MHC-II receptors at the cell surface, each one with slightly different peptide-binding requirements.

Despite these additional levels of diversity, the existence of termini anchor residues and the more linear conformation of the core 9-mer allowed for some of the aforementioned modeling methods to be applied to pMHC-II complexes. Most notably, the validation datasets used by (71) and (76) included MHCII allotypes. In both cases, the validation was focused on the accuracy of the backbone prediction for the binding core (Table 1). Finally, (69) has discussed the potential generality of a docking-based binding mode prediction method for pMHCII complexes, reporting very good results in both self-docking and cross-docking experiments (with 9-mer core mean all-atom RMSD of 0.73 Å and 1.37 Å, respectively).

COMPUTATIONAL METHODS FOR BINDING AFFINITY PREDICTION

In this section we review methods previously applied for structure-based binding affinity prediction for pMHC complexes. We discuss the differences between methods for qualitative ranking/classification, and methods for quantitative binding affinity prediction.

Qualitative ranking and ligand classification

Scoring methods used to guide sampling (i.e., rank conformations) are very general in nature: they are usually developed to score any protein-ligand complex. However, in order to improve accuracy, some scoring methods are intended for specific groups of ligands and receptors. For instance, a scoring method can be specific to peptides (as opposed to drug-like ligands), or designed specifically for pMHC complexes (Table 2).

Table 2.

Key methods applied to pMHC binding affinity prediction

Publication (Ref.)	Tool/Method	Validation (size)	Dataset Composition
Rognan et al., 1999 (75)	FRESNO scoring function	Correlation (84)	Class I: HLA-A*02:01, HLA-A*02:04, H-2K
Altuvia et al., 2004 (83)	PREDEP, residue-contact matrices	Classification and Correlation (>1000)	Class I: 2 HLA-A, 4 HLA-B, H-2D, H-2K, H-2L
Tong et al., 2006 (84)	calibrated scoring function	Classification (139)	Class II: HLA-DQ3.2β
Tong et al., 2006 (85)	calibrated scoring function	Classification and Correlation (84)	Class II: HLA-DRB1*0402, HLA-DQB1*0503
Liao et al., 2011 (86)	Modified version of FRESNO scoring function	Correlation (>100)	Class I and II: HLA-A2, HLA-DR15, HLA-DR1, and HLA-DR4
Knapp et al., 2011 (87)	PeptX, genetic algorithm	Classification (>1000)*	Class I: HLA-A*02:01
Yanover et al., 2011 (88)	Rosetta	Classification (>1000)*	Class I: 7 HLA-A, 12 HLA-B
Atanasova et al., 2011 (89)	EpiDOCK, generated quantitative matrices	Classification (4540)	Class II: 12 HLA-DRB1
Doytchinova et al., 2002 (90)	QSAR	Correlation (266)	Class I: HLA-A*02:01
Doytchinova et al., 2004 (91)	QSAR	Correlation (90)	Class I: HLA-A*02:01
Jojic et al., 2006 (92)	custom scoring function with calibrated weights	Classification and Correlation (>500)	Class I: 4 HLA-A, 5 HLA-B
Antes et al., 2006 (82)	DynaPred, SVM using quantitative matrices and MD-derived energy features	Classification (>1000)	Class I: HLA-A*02:01
Bordner et al., 2006 (78)	SVM using scoring function terms	Classification (331)	Class I: HLA-A*02:01, H-2Kb
Tian et al., 2009 (93)	QSAR	Correlation (152)	Class I: HLA-A*02:01
Bordner, 2010 (69)	random forest using scoring function terms	Classification (>1000)	Class II: various human and murine allotypes
Saethang et al., 2013 (94)	random forest using residue-residue contacts and topological descriptors	Classification (>1000)	Class I: HLA-A2
Mukherjee et al., 2016 (95)	learning statistical pair potentials to use as features for Gaussian process regression	Classification and Correlation (>10000)	Any Class I with experimental binding affinity data
Davies et al., 2003 (96)	simulated annealing, AMBER force field	Classification (>10)	Class II: 4 HLA-DR1
Zhang et al., 2010 (97)	position specific free energy contributions using MD and MM/PBSA	Correlation (3882)	Class II: HLA-DRB1*0101
Polydorides et al., 2016 (98)	Proteus, computational suite for the optimization of protein and ligand conformations	Correlation (1)**	Class II: HLA-DQ8
Wan et al., 2015 (99)	MD, MM/PB(GB)SA	Correlation (12)	Class I: HLA-A*02:01
Knapp et al., 2016 (100)	hierarchical natural move Monte Carlo simulations	Correlation (32)	Class I: HLA-A*02:01

Correlation: study reports computing affinity values that can be directly compared with experiment. Classification: study reports affinity predictions for the purpose of classifying peptides as binders or non-binders given an appropriate threshold.

^*These studies searched for strong binding peptides, instead of producing a score related to affinity. See text.

^**Only reported an example use case using their tool

Scoring functions for protein–peptide docking

Most protein–peptide docking tools involve energy-based scoring functions. These scoring functions have been previously classified into three main categories: Empirical, semi-empirical and knowledge-based (56).

Empirical scoring functions are inspired by the quantum mechanics / molecular mechanics (QM/MM) formalism, which allows calculating potential energies (118, 119). Such calculation relies on the definition of a force field as a sum of energy terms corresponding to both covalent and non-covalent interactions within and between molecules. Typical energy terms evaluate the bond stretching, angle bending and torsional angles of covalent interactions, as well as Van der Waals and electrostatic contributions of non-covalent interactions (120). Some studies have shown that the most important term is often the electro-static one (121). Empirical scoring functions have long been involved in popular docking tools, such as AutoDock, Glide and DOCK, as well as many others (122, 123). To achieve computational efficiency, energy terms assessing atomic interactions can be replaced by terms derived from coarse-grained potentials, such as the Go potential, that evaluate interactions between large pseudo-atoms representing entire amino acids (124). Also for the sake of computational efficiency, rather than considering explicit water molecules, one can implicitly evaluate solvent effects by using Poisson–Boltzmann surface area (PBSA) or generalized Born surface area (GBSA) energy terms (121). By adding an energy term evaluating entropic effects, for example using empirical conformational energy analysis (CFEA) (125) or normal mode analysis (NMA) (121), a force field allows calculating free energies. One can also directly calculate free energies by using free energy perturbation techniques (126).

Semi-empirical scoring functions differ from purely empirical scoring functions in that they do not attempt to include all physical interactions of protein–peptide poses or to recapitulate biophysically-relevant energies (56). Nonetheless, they include biophysically-plausible energy terms that correspond to physical properties describing the protein–peptide interface. The physical properties that are typically considered correspond to non-covalent interactions between peptides and proteins, such as hydrogen bonds, electrostatic and van der Waal interactions, hydrophobic interactions (127), as well as solvation (128, 129) and entropic effects. These energy terms are then added together with multiplicative weights assigned to them. These weights are usually tuned to optimize binding affinity predictions given a dataset of protein-ligand complexes with known structure (130). Classical examples of semi-empirical scoring functions are ChemScore and X-score, but others have been developed (122, 131).

Knowledge-based scoring functions calculate pseudo-energies that are not biophysically meaningful, but that reflect the likelihood for protein–peptide interface properties to be native or native-like (56). These functions are trained (i.e., calibrated) by performing a statistical analysis on available structural data contained in reported protein–peptide complexes (131). More precisely, an interaction potential is calculated by implicitly estimating the change in energy associated with a change in the distance between atoms of a specific type in a peptide and atoms of a specific type in a protein (123). Examples of popular knowledge-based scoring functions are DrugScore, PMF-score and SMoG (130). Note that this methodology can also be applied in a coarse-grained fashion, by considering distances between pairs of residues. Recently, going away from the classical linear regression approach, new scoring functions have been proposed, using a machine-learning approach based on nonlinear regression (132).

Instead of using scoring functions that are only based on energy calculations, attempts have been made to enhance them with additional information, such as co-evolutionary or muta-genesis data (133). Other approaches complement the energetic analyses with structural clustering or sequence-based predictions. In addition, it has often been observed that combining several scoring functions can improve their accuracy (134).

Ranking of pMHC binding modes

For sake of simplicity, we will treat the ranking of conformations during sampling as being merely qualitative, and we will discuss quantitative binding affinity prediction of pMHC complexes in a separate section. One of the early approaches used to guide sampling of pMHC complexes was based on empirically-derived residue-contact matrices (83, 127, 135–137). These matrices, also known as statistical-pair potentials, encode how favorable the interaction is between two given residues (138, 139). In (127), it was found that the so-called MJ matrix (138) only worked for MHC allotypes with hydrophobic binding pockets. Therefore, in follow-up studies (83, 127), the parameters of the newer BT matrix (139) were tuned to improve performance across all allotypes. Through a webserver (137), one can use these matrices or one’s own scoring potentials.

FRESNO (75, 140) was one of the first scoring functions specifically developed for pMHC complexes. This scoring function accounts for hydrogen bonding, lipophilic interactions, rotational entropy loss, buried polar-apolar contacts, and desolvation energies. FRESNO initially allowed making accurate predictions for the HLA-A*02:01 allotype. It was then re-implemented with open-source software (86), and its weights were re-calculated, using a more diverse training set including class II HLAs. This allowed making accurate predictions for the class II HLA-DR15 allotype.

Some studies have used statistical learning methods to optimize the weights of the scoring functions considering specific subsets of complexes (e.g., pMHC-II structures) (69, 78, 141, 142), or to predict the correct register of MHC-II-binders (69). For instance, the scoring function used in GradDock was optimized to guide the sampling of pMHC-I complexes (79). The authors improved a scoring function from the popular modeling library Rosetta, testing different combinations of terms and weight values while performing self-docking and cross-docking experiments.

Peptide classification (binders vs non-binders)

Structure-based methods have also been used to classify peptides into binders vs non-binders, considering specific MHC allotypes. For instance, the work in (84) reports high predictive power for HLA-DRB1*0402 and HLA-DQB1*0503, while the study in (85) reports an AUC of 0.9 for HLA-DQ3.2β. In another study, AUC values in the range 0.632–0.821 are reported for MHC-II receptors (69).

In (143), AutoDock4 was used to predict the binding of every possible peptide from a given protein sequence. Despite using several approximations, the authors reported that a known immunogenic peptide had good rank (i.e., high predicted affinity). The work in (89) used docking to derive qualitative matrices to predict binding across 12 HLA-DRB1 proteins. Docking scores were normalized to assess the contribution of each amino acid in each pocket. A server was built that enables predictions across several HLA class II allotypes (144).

In (88), a search was performed on the space of sequences as well as conformations of the peptide. Using the Rosetta scoring function (145), several thousand simulations were performed for a given allotype, and the final peptide sequences across all simulations were pooled into a single position-specific frequency matrix (PFMs). Their computed PFMs showed impressive similarity to experimentally-derived PFMs across seven different HLA-As and twelve HLA-Bs (88).

Another interesting way to predict MHC-binders involves a search for the peptide sequence minimizing affinity for a given scoring function. In (87), the PeptX framework is based on a genetic algorithm that explores the space of peptides for a sequence that binds the strongest to HLA-A*02:01. The fitness of a particular peptide sequence was evaluated using different scoring functions, including a variety of sequence-based methods and a structure-based scoring function, X-score (142). They found that different fitness definitions produced distinct preferences in the peptides predicted to bind, but common peptides were indeed found to bind experimentally (87).

Quantitative binding affinity prediction

Going beyond qualitative ranking of conformations and classification of binders vs non-binders, some methods aim at predicting realistic values of binding affinity. Two approaches for quantitative binding affinity prediction are discussed here (Table 2). First, we describe data-driven methods to derive binding affinity from a single pMHC conformation. Then, we describe simulation-based methods to derive binding affinity from an ensemble of conformations.

Data-driven predictions

Statistical learning methods mentioned in previous sections were applied to learn the weights of a given scoring function. In this section, statistical learning methods are used to predict binding affinities directly from structural features.

The two defining characteristics of data-driven methods are the representation of the dataset (through features or descriptors) and the type of statistical learning model. First, different types of structural features have been investigated: residue-residue contacts (91, 92, 94), general physical-chemical descriptors (90, 93, 146), energy terms from semi-empirical scoring functions (78), and features derived from molecular dynamics simulations (82). Second, several statistical learning models have been used: partial least squares (90, 91, 93), support vector machines (78, 82, 146), and random forests (94). All these methods report high prediction accuracies for their datasets which consist of one or several MHC allotypes.

A more recent structural data-driven approach is the method HLaffy (95). A statistical pair potential was constructed using the frequency of residue contacts present in the modeled structures of known binders. When the input is a sequence that was not explicitly modeled, a linear optimization problem allows maximizing the constructed statistical pair potential. Finally, a Gaussian process regression scheme is used to go from interaction profiles (encoded by the statistical pair potential) to predicted binding affinity values. HLaffy had an average prediction accuracy of 82.5% using 5-fold cross-validation.

Note that the limitations of statistical learning methods for sequence-based predictions, mentioned in section 1, also apply to structure-based data-driven predictions. In fact, biases are even greater given the small number of available pMHC structures. Despite the existence of nearly 10,000 MHC allotypes in humans, there are less than 650 pHLA structures in the PDB. In addition, more than one third of these structures relate to the same HLA allotype (HLA-A*02:01). Therefore, a scoring function using weights learned from all available pHLA structures would certainly overfit HLA-A*02:01, while lacking training on most other allotypes.

Simulation-based predictions

Other methods for binding affinity prediction are based on simulations, such as MD and Monte Carlo. MD simulations track the time evolution of a molecular system using a potential energy function, also known as a force field. MD-based methods hold a lot of promise in that they are completely model-based and do not require any experimental data for training. However, they are the most demanding computationally, and as such have most often been used to analyze important contacts in pMHC complexes with known affinity/immunogenicity (141, 147–154). We direct the interested reader to a dedicated review on the use of MD for pMHC systems (155). Here we highlight some recent work not covered in that review.

By far, the most extensive use of MD for computing pMHC binding affinities has been through the protocol named ESMACS: enhanced sampling of molecular dynamics with the approximation of continuum solvent (99). This technique relies on calculating free energy with the MM/PB(GB)SA method, which was mentioned in section 4.1.1 (156). The free energy of binding is computed as the free energy of the complex minus the free energies of the peptide and receptor (121). Typically, these free energies are derived from conformations sampled from a single MD simulation of the whole complex. This is in contrast with the so-called 3-trajectory variant, where the free energies are derived from three separate simulations: for the complex, the protein alone, and the peptide alone. Not performing the 3-trajectory variant means assuming that using the conformations sampled from the peptide bound to the receptor allow computing the free energy of the peptide alone, which neglects important changes in entropy between the bound and unbound states of the peptide.

Large variations in computed free energies have been observed when sampling from single, long MD trajectories, as opposed to ensembles of short simulations (156). Therefore, the study in (99) aimed to produce precise estimates of binding free energies by performing the 3-trajectory variant using ensembles of short MD simulations. For a given system (pMHC complex, MHC, or peptide), 50 replica MD simulations, 4 ns each, were ran using different initial velocities starting from a given crystal structure. For 12 diverse peptides bound to HLAA*02:01, computed binding affinities had a Pearson correlation coefficient of 0.80 with experimental binding (99).

Another interesting work features hierarchical natural move Monte Carlo simulations to explore pMHC detachment processes (100). The pMHC system is represented in a coarse-grained manner: each amino acid is modeled by its alpha carbon, its carbonyl oxygen, and the center of its side chain. The study involves 32 peptides bound to HLA-A*02:01; 100 independent simulations were performed for each peptide until detachment. The authors found that the average time it took for a simulation to completely sample the peptide detaching correlated with experimental binding affinity. Using these average simulation times and an appropriate cutoff, their method achieved an AUC of 0.85 when discriminating binders from non-binders.

Simulation-based predictions have also been applied to MHC-II systems. For instance, the work in (96) used simulated annealing of pMHC-II models and correlated the interaction terms from the AMBER force field with experimental affinity. The study in (97) compares three different ways of computing binding affinity for pMHC-IIs, including simulation, statistical pair potentials and contact analysis (97). However, the conclusion was that, while predictions made by these structure-based methods are significantly better than random, they are still not on par with the leading sequence-based methods. More recently, a computational suite for the optimization of protein and ligand conformations – Proteus – was proposed, featuring MM/PB(GB)SA calculations for pMHC-IIs and considering different pH values (98).

FUTURE CHALLENGES IN THE SEARCH FOR IMMUNOGENICITY

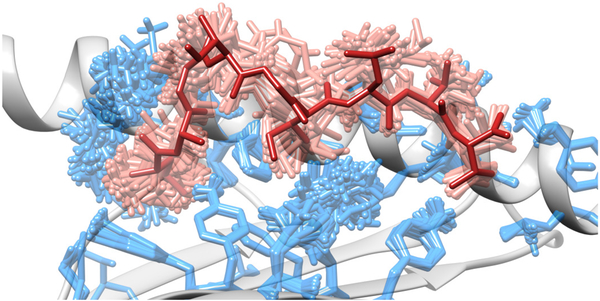
A recent study described the use of an ensemble refinement approach to reveal hidden dynamics in crystal structures of pMHC and TCR/pMHC complexes (157). By generating an ensemble of conformations (Fig. 4), all compatible with data from a given X-ray crystallography experiment, the authors illustrated how differing interpretations can be made using a single conformation as opposed to the whole ensemble. In fact, the ensemble derived from some pMHC crystal structures contained not only alternative peptide side chain configurations, but even alternative binding modes, with significantly different backbone conformations and coordination networks. These results are compatible with findings from molecular dynamics studies and highlight the need to consider the whole ensemble of peptide conformations, rather than a single binding mode. This suggests the need for a new paradigm in structural predictions. Instead of trying to find a single top scoring conformation that matches the corresponding binding mode observed in a crystal structure (e.g., cross-docking), a more reasonable goal would be to find an ensemble of peptide conformations that is “equivalent” to that of the crystal structure. This new goal would also require new metrics that could evaluate the accuracy of binding mode predictions in terms of the generated ensemble (157).

Figure 4. Side view of a pMHC complex after ensemble refinement.

Alternative conformations of selected MHC side chains are depicted in sticks, as well as alternative conformations of the ligand. All alternative conformations are compatible with the x-ray experimental data, and were obtained through a procedure of ensemble refinement (157). The single peptide conformation displayed in the crystal structure is represented in a darker shade of grey. Part of the conformational “frame” of the binding site can also be observed (i.e., a lateral alpha-helix and a floor of beta-sheets, both depicted in cartoon). Graphics were obtained with UCSF Chimera (158).

A paradigm shift from single binding modes to ensembles of conformations would also require new methods for ranking and binding affinity prediction, adding complexity to an already difficult problem. As discussed in previous sections, there is an inherent tradeoff between accuracy and scalability of binding prediction methods. Simulation-based affinity prediction tools can be more accurate and provide additional interpretability of molecular interactions, but cannot be used for peptide screening (97). On the other hand, docking-related scoring functions and data-driven approaches may be scalable, but their accuracy is not yet at the level of sequence-based methods. For instance, scoring functions notoriously suffer from a strong lack of accuracy, which is only partially explained by their focus on computational efficiency. Several evaluation studies of docking tools (some involving datasets containing pMHC complexes) have shown that existing scoring functions often fail to identify near-native poses (52, 53, 64, 159). Scoring functions also show limitations in distinguishing binders from non-binders, recapitulating known rankings, and reproducing experimental binding affinities (160, 161).

In a broader context, recent findings in drug discovery reveal that the binding kinetics is a decisive factor for drug efficacy and safety (162, 163). In this context, the dissociation rate constant (K_off) becomes a more important measure than binding affinity. However, this value is much harder to estimate computationally. It requires extensive sampling of transition states, derived from multiple paths from bound to unbound states (162). Considering that K_off is impacted by the residence time (i.e., the average time that the ligand stays in the binding site), and that the residence time is usually at the scale of minutes or hours, computing transition states becomes almost impossible with conventional MD simulations (with time scales of ns to μs). However, recent advances in the development of “optimized” MD sampling algorithms and the fast growing processing capacity of modern CPUs and GPUs are opening new avenues for K_off prediction (162, 163).

In the context of pMHC complexes, there is also evidence that pMHC stability is a better predictor of immunogenicity than pMHC binding affinity (164). As expected, predicting the K_off of peptides is a much harder problem as compared to drug-like ligands. Peptides are bigger and have a more complex network of interactions, which results in a much longer unbinding process (100). However, the advances in sampling methods discussed in this review could allow for the fast generation of a meaningful ensemble of bound peptide conformations, despite the use of imperfect scoring functions. In turn, these conformations could be used as seeds for “optimized” MD sampling algorithms, such as adaptive sampling (165–167), allowing for a more efficient prediction of K_off rates for pMHC complexes.

CONCLUSION

Over the past decades, different sampling methods have been applied to the structural prediction of pMHC complexes (Table 1). These methods are very diverse, relying on a variety of tools and procedures. In addition, research groups have used different datasets and metrics to report their results (e.g., α-carbon RMSD or all-atom RMSD). Therefore, a fair comparison of all these approaches would be difficult and beyond the scope of this review. Instead, we have focused on highlighting the main assumptions and trade-offs behind these approaches. We have proposed a classification of these methods into three general strategies: constrained backbone prediction, constrained termini prediction and incremental prediction. Note that each strategy solves a different formulation of the pMHC structural prediction problem. For instance, using a backbone template dramatically reduces the conformational space that must be explored, as compared to docking the entire ligand with full flexibility. On the other hand, relying on a template reduces the generality of the proposed method. This is particularly relevant for peptides with unusual binding modes and for MHC allotypes lacking experimental data.

Despite all the challenges, the latest publications show impressive results and suggest that sampling is not anymore a limitation for pMHC binding mode prediction. It is also worth noting that different methods might be better suited for different docking applications (51). For instance, the efficient sampling of GradDock (79) combined with a pMHC-specific scoring function makes this tool potentially useful for large-scale virtual screening, while the higher accuracy of DockTope (65) and DINC (43) make them more suitable for geometry optimization.

On the other hand, the development of fast and accurate scoring functions represent an unmet need for both pMHC binding mode prediction and structure-based binding affinity prediction. Similar to what was discussed for binding mode prediction, different approaches for binding affinity prediction make different assumptions and trade-offs. Fortunately, recent advances in high performance computing are allowing for computation intensive applications, which are expected to have a huge impact on both binding mode and binding affinity prediction. Although no single tool is yet capable of solving all these problems, we are finally getting closer to the point where different structure-based methods can be used to address specific problems in medicinal chemistry. Hopefully, structural methods will soon be combined with sequence-based methods, providing general and accurate predictions that will help researchers and physicians to tackle some of the most challenging health care problems of our time.