Ferrets as a model for higher-level visual motion processing

Summary

Ferrets are a major developmental animal model due to their early parturition. Here we show for the first time that ferrets could be used to study development of higher-level visual processes previously identified in primates. In primates, complex motion processing involves primary visual cortex (V1), which generates local motion signals, and higher-level visual area MT, which integrates these signals over more global spatial regions. Our data show similar transformations in motion signals between ferret V1 and higher-level visual area PSS, located in the posterior bank of the suprasylvian sulcus. We found that PSS neurons, like MT neurons, were tuned for stimulus motion and showed strong suppression between opposing direction inputs. Most strikingly, PSS, like MT, exhibited robust global motion signals when tested with coherent plaids – the classic test for motion integration across multiple moving elements. These PSS responses were described well by computational models developed for MT. Our findings establish the ferret as a strong animal model for development of higher-level visual processing.

eTOC blurb

Ferrets are a major animal model for development of early visual stages. Lempel and Nielsen establish signatures of complex motion processing in a higher visual area in the ferret, area PSS. This will allow developmental research in the ferret to expand into higher-level vision.

Introduction

Ferrets are paradigmatic for studying visual development because they are born at an early stage of brain development, and eye opening does not occur until about postnatal day 30 [1]. This provides a long window for investigation and manipulation of neural development, including of developmental stages that occur in utero in other higher mammals. The late date of eye opening additionally enables experimental access to changes in emerging brain functions due to the onset of visual experience. So far, research in the ferret has focused on the development of early visual stages, but not the higher-level visual functions commonly investigated in non-human primates. Here, we show that ferrets share important principles of complex visual motion processing with primates. This opens a new opportunity to examine the development of higher-level vision.

Motion perception is an extensively studied aspect of higher-level visual processing. In order to analyze the complex moving patterns present in nature, the visual system needs to integrate over local motion signals in a meaningful way. In primates, area MT implements a major integration stage of motion signals from V1 [2,3]. Because of their small receptive fields, direction-selective V1 neurons largely represent local motion signals. MT neurons then integrate these local motion signals into global signals. This change in motion processing is usually demonstrated using coherent plaids, which are generated by superimposing two gratings moving in different directions. Perceptually, plaids appear to move in a third, intermediate direction [4,5] computed by integrating the two component grating directions. Consistent with a transition from local to global motion processing, MT – but not V1 – contains a population of neurons sensitive to the integrated pattern direction [2,3].

In general, little is known about the functions of potential higher-level visual areas in the ferret. Yet, previous studies identified a visual area likely involved in motion processing, located in the posterior bank of the suprasylvian sulcus and referred to as PSS or PMLS (Figure 1A). PSS neurons are highly direction selective [6], receive input from V1 neurons that is biased towards motion processing [7], and PSS lesions impair motion perception [8]. Here, we use PSS responses to complex motion stimuli (including coherent plaids) to systematically assess the transformations in motion processing occurring between V1 and PSS, and to provide a detailed comparison with MT. Our data reveal signatures of motion integration in PSS that are not found in ferret V1. Changes in motion processing between V1 and PSS could be well explained by a computational model similar to those used to fit MT responses [9,10]. Our study therefore demonstrates a clear transformation in motion processing between V1 and higher-level visual cortex in the ferret, in a manner that is consistent with changes occurring in the primate motion pathway.

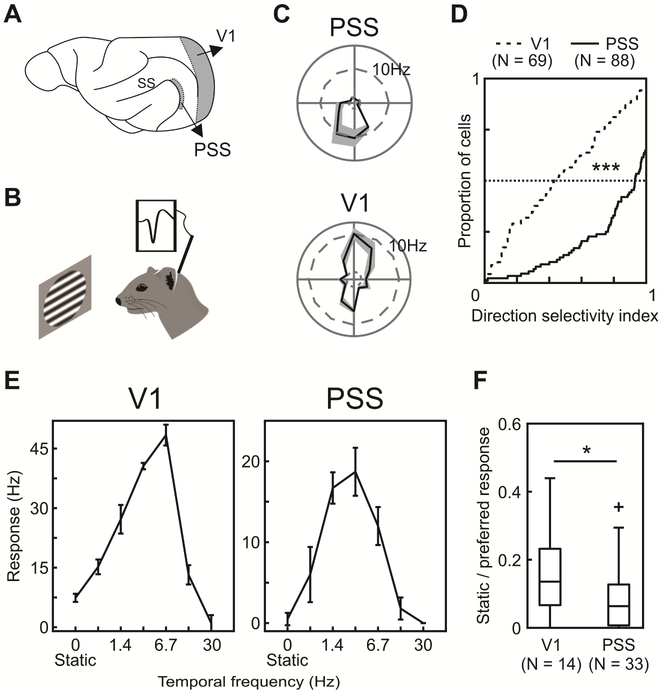
Figure 1: Basic PSS tuning properties indicate a role in motion processing.

(A) Sagittal view of the ferret brain indicating the location of PSS and V1 (ss: suprasylvian sulcus).

(B) Schematic of experimental setup. Neural responses to visual stimuli were recorded in anesthetized ferrets using tetrodes or multi-channel silicon probes.

(C) Direction tuning of an example PSS (top) and V1 neuron (bottom). The polar plot indicates mean firing rates to different directions (gray area: ± SEM).

(D) Cumulative DSI distributions for V1 and PSS.

(E) Temporal frequency tuning for a V1 neuron (left) and PSS neuron (right), measured using sinusoidal gratings drifting at different temporal frequencies (0 Hz indicates a static grating). Error bars represent ± SEM.

(F) Responses to static gratings relative to responses to preferred temporal frequencies. Boxplots indicate the spread of the observed response ratios in V1 and PSS. In this and all subsequent figures, the box indicates 25^th, 50^th and 75^th percentiles. Whiskers indicate range, and crosses indicate outliers.

* = p < 0.05; *** = p < 0.001.

Results:

Basic PSS tuning properties indicate role in motion processing:

To provide the foundation for assessing responses to more complex motion stimuli, we first measured a number of basic tuning properties in PSS – direction selectivity, responses to static versus moving stimuli, and speed tuning. In addition, we directly compared these tuning properties between PSS and V1. In all experiments, recordings in PSS and V1 were performed in anesthetized animals using single tetrodes and multi-channel silicon probes (Figure 1B).

Direction selectivity was assessed by measuring responses to sine-wave gratings drifting in 12 or 16 different directions (see Figure 1C for an example PSS direction tuning curve). We then quantified direction tuning strength by computing a direction selectivity index (DSI), which compares responses to the preferred and the null direction. DSI values close to 1 indicate strong direction selectivity, while values near 0 show lack of direction tuning. In general, PSS neurons were highly direction selective with a median DSI of 0.93 (Figure 1D). This is consistent with the results of a previous PSS study, which used stochastic random dot stimuli to determine direction responses [6]. The degree of direction selectivity observed in PSS differed significantly from that in V1 (Figure 1C & D), in which neurons generally were less direction selective (median DSI of 0.43; Kolmogorov-Smirnov test, p<0.001).

To further assess the processing of motion information in PSS and V1, we compared responses to static and moving stimuli. For this purpose, we systematically varied the temporal frequency of the drifting gratings. In both V1 and PSS, static gratings generally elicited weaker responses than moving gratings (Figure 1E & F). However, relative to responses to the optimal temporal frequency, static gratings evoked firing rates that were significantly lower in PSS than V1 (static/moving, PSS median: 0.06, V1 median: 0.14, Wilcoxon rank sum test, p = 0.03).

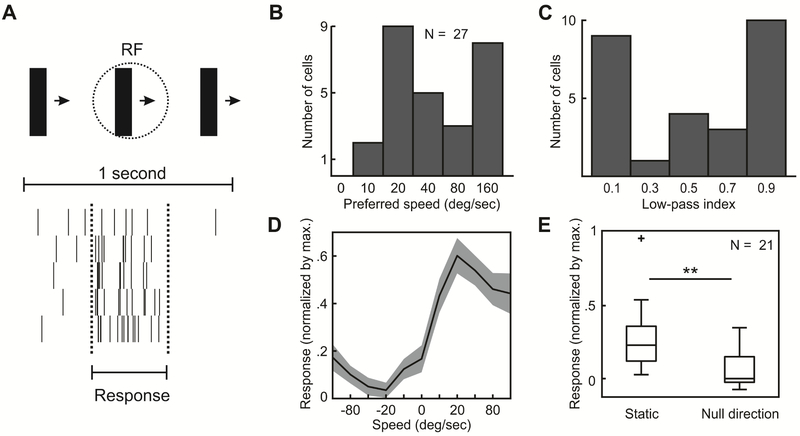
Lastly, we measured the speed tuning of PSS neurons using a drifting bar (Figure 2A). Bars could drift in 8 different directions at 5 different speeds, or remain static. PSS speed preferences were broadly distributed (Figure 2B): The median speed preference in PSS was 40 deg/s, but we encountered neurons with speed preference as high as 160 deg/s, the fastest speed sampled. Speed tuning of neurons was further assessed by computing a low-pass index as the ratio of responses to the fastest speed (160 deg/s) and the preferred speed. This analysis confirmed the broad tuning distribution (Figure 2C). Our PSS sample included both neurons that responded strongly to the fasted speed (low-pass index < 0.15, 9/27 cells), and neurons that did not respond to it (low-pass index > 0.85, 10/27 cells). Note that these conclusions are limited by the fact that speeds faster than 160 deg/s could not be sampled. None of the recorded neurons preferred static over moving stimuli (Figure 2D & E). Yet, on average responses to a static bar were greater than responses to motion in the null direction (median normalized response to static: 0.23, median response to null direction at 40 deg/s: 0; Wilcoxon signed-rank test, p = 0.001), suggesting that direction selectivity in PSS is partially driven by suppression of responses to the null direction. This is consistent with recent findings linking direction selectivity in layer 2/3 of ferret V1 to null-direction inhibition [11].

Figure 2: Speed tuning in PSS.

(A) Responses of an example PSS neuron to the drifting bar stimulus (illustrated on the top of the figure). Each row of the raster plot corresponds to one cycle of the bar drifting across the screen. The period during which the bar traverses the central 40 deg of the estimated receptive field is indicated by dashed lines. This time window was used to compute stimulus-evoked responses (see Methods).

(B) Distribution of preferred speeds.

(C) Distribution of low-pass indices for the same neurons as in (B).

(D) Average PSS speed tuning curve. To compute this curve, the response of each neuron was normalized by its maximum before averaging (same neurons as in (B)). Positive speeds indicate movement in the preferred direction, negative speeds movement in the null direction. 0 corresponds to a static bar. Note the decreased response to motion in the null direction relative to the static stimulus. Gray area: ± SEM.

(E) Comparison of responses to static bars and motion in the null direction at 40 deg/s. All responses were normalized by the maximum response per neuron.

** = p < 0.01.

In summary, the basic tuning properties of PSS neurons suggest a specialization for motion processing exceeding that of V1 (see Discussion for a comparison to the primate motion pathway).

PSS neurons show motion opponency:

In MT, responses to a stimulus drifting in the preferred direction can be strongly suppressed by superimposing a second stimulus drifting in the opposite direction (e.g. [12,13]). This phenomenon is termed motion opponency. Inhibition of opposing direction signals is believed to be a crucial aspect of how MT neurons combine local direction signals [14,15]. As a first assessment of PSS responses to more complex motion stimuli, we tested whether PSS neurons similarly exhibit motion opponency. To this end, we used a stimulus set previously used to measure MT motion opponency [13]. The main stimulus set (Figure 3A) consisted of three different random dot kinematograms (RDK). For two of these stimuli, all dots in the RDK moved in one direction, which was chosen to be either the preferred direction of the neuron under study (preferred stimulus) or the null direction (null stimulus). In the third stimulus, the preferred and null stimulus were superimposed to generate a RDK with opposing motion signals in the same region of space (motion-opponency stimulus). Note that the motion-opponency stimulus contained twice the number of dots than the other two RDKs, but maintained the same number of dots per direction. Perceptually, the motion-opponency stimulus appears as two surfaces sliding across each other [13,16].

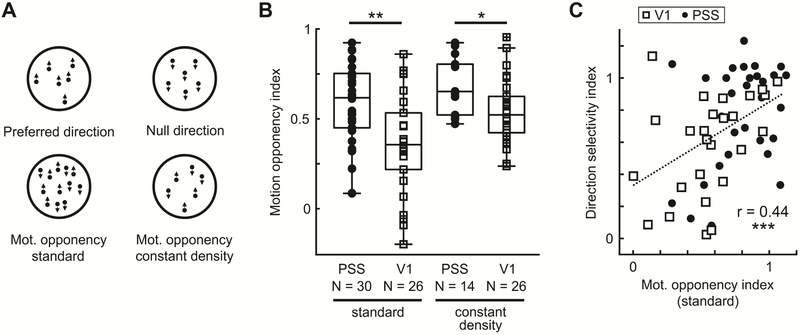
Figure 3: PSS neurons show motion opponency.

(A) Illustration of RDK used to investigate motion opponency in PSS and V1.

(B) MOI distributions for PSS and V1, using either the standard motion opponency stimulus (lower left in (A)) or the constant density version (lower right in (A)).

(C) DSI versus MOI for V1 and PSS neurons, calculated based on the standard motion opponency stimulus. Dotted line represents fit for both data sets combined.

* = p < 0.05; ** = p < 0.01; *** = p<0.001.

In general, PSS neurons responded vigorously to the preferred stimulus. Addition of the opposing direction signal in the motion-opponency stimulus reduced responses, demonstrating the presence of motion opponency. We quantified the strength of this effect by computing a motion opponency index (MOI) for each neuron. MOI values near 0 indicate equal responses to the preferred and motion-opponency stimulus, or a lack of motion opponency. MOI values near 1, on the other hand, indicate suppression of firing rates to baseline levels for the motion-opponency stimulus. The population data (Figure 3B) confirm strong motion opponency in PSS (median MOI: 0.62). In contrast, V1 neurons displayed a significantly lower degree of motion opponency (median MOI 0.36; Wilcoxon rank-sum test, p = 0.002).

To test whether this difference in motion opponency could be explained by the differences in direction selectivity in the two areas, we separately computed the MOI for direction-selective V1 cells only (DSI > 0.75). Indeed, the mean MOI for direction-selective V1 neurons was not significantly different from PSS cells (median MOI = 0.53, Wilcoxon rank-sum test, p = 0.53). In general, plotting motion opponency against direction selectivity (Figure 3C) revealed that motion opponency and direction selectivity were positively correlated in both areas, and that V1 and PSS data formed a continuum (correlation for the combined data set, r = 0.44, p<0.001). These results suggest that suppression of null direction responses may play a role in shaping direction selectivity across the ferret’s motion pathway. Furthermore, the observed levels of motion opponency, as well as the relationship to direction selectivity, replicate findings for the primate motion pathway (see Discussion).

One possible confound in this experiment is the increased dot density in the motion-opponency stimulus. To rule out effects of dot density, we generated a second motion-opponency stimulus that maintained the same dot density as the preferred stimulus by halving the number of dots per direction (Figure 3A, ‘constant density’ stimulus). We then compared responses between the constant density and the preferred stimulus for an additional group of PSS and V1 neurons (Figure 3B). For V1, using the constant density stimulus increased MOI levels (median MOI: 0.52, Wilcoxon rank sum test between the two motion opponency stimuli, p = 0.02). This change is likely due to the fact that the constant density stimulus contained fewer dots moving in the preferred direction than the original motion opponency stimulus, which would result in lower responses for the constant density stimulus and therefore stronger motion opponency (the preferred stimulus has the same number of dots in both experiments). At the same time, motion opponency remained stronger in PSS than V1 despite the changes in dot density (median MOI PSS: 0.65, Wilcoxon rank-sum test V1 versus PSS, p = 0.01).

A subset of PSS neurons encodes pattern motion:

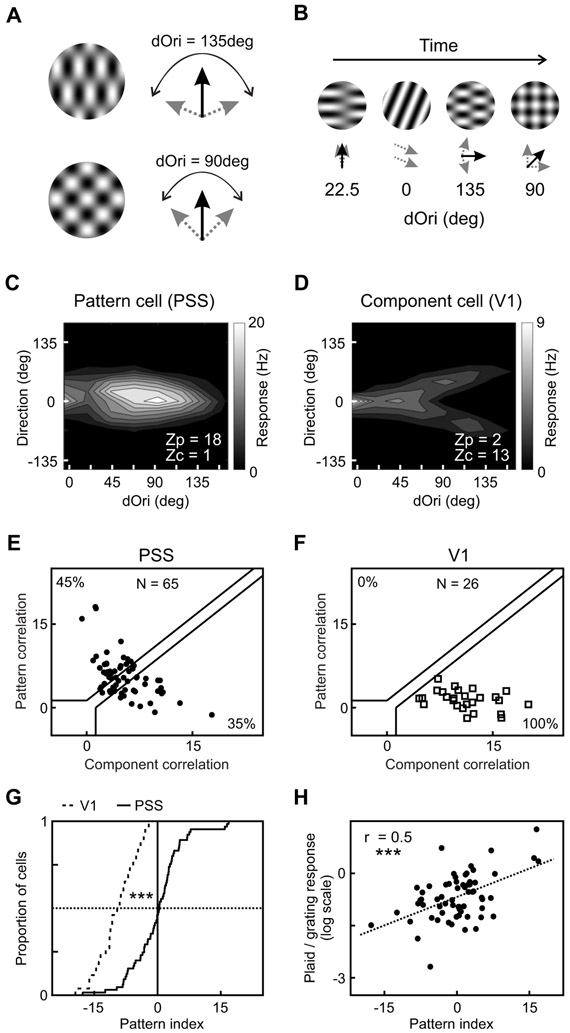
One of the hallmarks of information processing in primate higher order motion cortex is the computation of plaid pattern motion, which requires integration of local motion signals [4,17]. We therefore investigated whether PSS neurons similarly encode pattern motion. As in the initial MT experiments [17], we addressed this question by measuring neuronal responses to 50% contrast sine-wave gratings and coherent plaids. Plaids were generated by superimposing two 50% contrast sine-wave gratings with directions that were 135 deg apart (Figure 4A). Perceptually, plaids appear to move in a direction bisecting the angle between the component directions [5,18]. For both gratings and plaids, 16 motion directions were sampled. The degree of motion integration exhibited by a neuron was then determined from the tuning curves for plaids and gratings, using the same analysis commonly employed for MT [17,19]. It rests on the following assumptions: Neurons that are only sensitive to the integrated pattern motion (so called pattern neurons) should have plaid tuning curves with a single peak, corresponding to the plaid moving in their preferred direction (Figure 4B). On the other hand, neurons sensitive to the individual components (so called component neurons) should have a bi-lobed plaid tuning curve, with maximal responses when either one of the components moves in the preferred direction (Figure 4C). The degree of motion integration by a neuron can then be quantified by comparing its actual plaid tuning curve to these predictions.

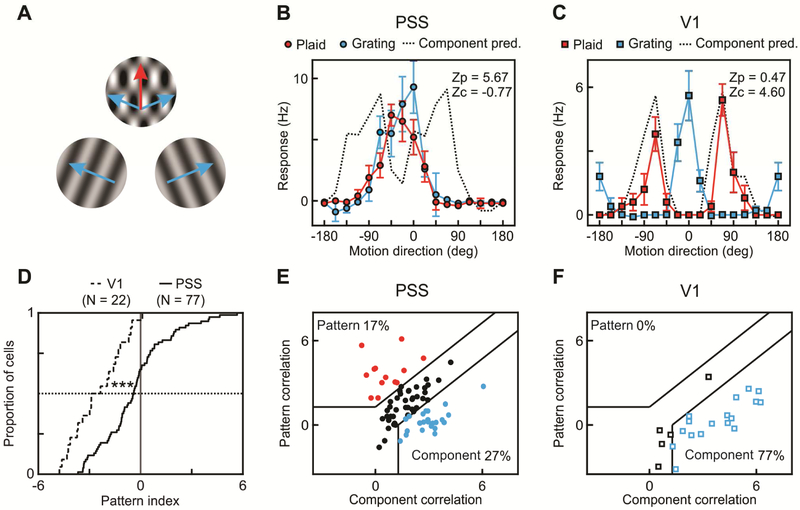
Figure 4: A subset of PSS neurons encodes pattern motion.

(A) Schematic representation of gratings and plaids used to investigate pattern motion responses in PSS and V1. Blue arrows indicate the directions of the component gratings, the red arrow the perceived plaid direction.

(B) Direction tuning curve of an example PSS pattern cell measured using plaids (red) and gratings (blue). Direction is relative to the neuron’s preferred direction for the grating. For plaids, direction indicates the perceived pattern direction (the components move at ±67.5 deg relative to this direction). For each neuron, the measured plaid tuning curve is compared to two predictions, one for idealized pattern responses (tuning curve identical to the grating tuning curve), one for idealized component responses (prediction indicated by dashed line). Z-transformed partial correlation indices Z_P and Z_C indicate how closely the measured plaid tuning curve resembles these predictions. Error bars: ± SEM.

(C) Plaid and grating direction tuning curves of an example V1 component cell. Same format as in (B).

(D) Cumulative pattern index distributions for V1 (dashed line) and PSS (solid line).

(E) Pattern versus component selectivity for PSS neurons. For each neuron, Z_P is plotted against Z_C. Black lines indicate the category boundaries used to classify cells into pattern, unclassified and component cells. Percentages indicate the portion of neurons falling into the different categories.

(F) Pattern versus component selectivity for V1, using the same format.

*** = p<0.001.

More precisely, we used each neuron’s grating tuning curve to generate two predictions for its plaid tuning curve. One prediction assumed pattern cell-like responses, and was identical to the grating tuning curve. The other prediction assumed component cell-like responses. It was computed as the sum of two copies of the grating tuning curve, shifted relative to each other to account for the direction difference between the two components. We then computed Z-corrected partial correlations between the measured plaid tuning curve and the two predictions. Z_P indicates the strength of pattern responses, and Z_C the strength of component responses. Cells were classified as pattern or component through comparisons of their Z_P and Z_C values. Neurons with significantly higher Z_P than Z_C (using p < 0.1 as in the primate studies [19]) were classified as pattern cells, while neurons that met the opposite criterion were classified as component cells (see Figure 4E & F for a depiction of the category boundaries; also see Methods). Using this analysis, 17% of PSS neurons (13/77) were classified as pattern cells, while 27% (21/77) were classified as component cells (Figure 4E). The rest of the cells remained unclassified. This result indicates that a substantial proportion of PSS neurons exhibits signatures of motion integration.

Given the existence of pattern cells in PSS, an important question is how much of this tuning is inherited from V1, i.e. whether V1 neurons can similarly extract pattern motion. To investigate this issue, we recorded responses to grating and plaid stimuli in V1. None of the recorded V1 neurons (0/22) was classified as a pattern cell, while 77% of V1 neurons (17/22) were classified as component cells (Figure 4F). Since comparisons based on the number of pattern and component cells depend on the criteria used to classify cells, we further compared PSS and V1 by computing a criterion-independent pattern index as Z_P-Z_C (Figure 4D). Across the population, pattern indices were significantly higher in PSS than in V1 (PSS median pattern index: −0.41, V1 median pattern index: −2.62; Kolmogorov-Smirnov test, p < 0.001). These data strongly suggest that pattern motion selectivity in PSS is not inherited from V1, just as pattern responses in primate MT are not inherited from V1.

Detailed characterization of PSS pattern selectivity

The above experiment assessed motion integration using plaids with one particular angle between the component directions (dOri). Yet, plaids can be constructed with a range of dOri values (as long as the extreme values of 0 and 180 deg are excluded). Importantly, while changing dOri impacts the overall appearance of the resulting plaid (Figure 5A), the perception of coherent pattern motion is maintained [4]. We therefore expanded our stimulus set by including more dOri values to probe PSS motion integration more finely. The expanded stimulus set consisted of 7 dOri values combined with 16 plaid directions. We also measured responses to individual gratings drifting in 16 directions, as well as a blank stimulus. To efficiently sample this large stimulus set, we modified the stimulus presentation paradigm. Instead of surrounding each stimulus presentation by blank periods as before, we adopted a streaming stimulus paradigm previously used for MT [9,19]. In this paradigm, each trial contained a 1 minute-long sequence of short stimulus presentations, with 3 to 6 stimuli presented per second (Figure 5B). Stimulus sequences were determined randomly from all conditions. The responses to individual stimuli embedded in these sequences were determined by computing firing rates during 150 ms-long windows time-locked to stimulus onset. To account for response latency, the temporal window used for firing rate calculations was shifted relative to stimulus onset by a delay optimized for each neuron individually (see Methods).

Figure 5: Detailed characterization of PSS pattern selectivity.

(A) Illustration of the stimulus set containing plaids generated from component gratings with different dOri values (left).

(B) Schematic representation of the streaming stimulus paradigm used to measure responses to the larger stimulus set.

(C) 2D contour plot showing responses of a PSS pattern cell as a function of dOri and direction (dOri = 0 deg corresponds to 100% contrast gratings). Direction is relative to the cell’s preferred grating direction, and indicates the perceived direction of the grating or plaid (i.e., the pattern direction). The response profile shows consistent responses to gratings and plaids moving in the preferred direction, independent of dOri, as would be expected for a pattern cell. The plot indicates Z_P and Z_C for the neuron, computed using the entire 2D response profile as described in the Methods.

(D) 2D contour plot for a V1 component cell (same format as (C)). The response profile shows the regular direction tuning curve for gratings at dOri = 0 deg. For plaids (dOri > 0 deg), direction tuning curves show two peaks with increasing distance for larger dOri values, which correspond to one of the two components moving in the neuron’s preferred direction.

(E) Pattern versus component selectivity for PSS neurons based on the large stimulus set. Plot format as in Figure 4E. See Figure S1 for examples of the predicted tuning curves underlying the computation of pattern and component selectivity.

(F) Pattern versus component selectivity for V1 neurons for the same stimulus set.

(G) Cumulative distribution of pattern indices for V1 and PSS based on the same data.

(H) Relationship between pattern index and the relative response to plaids versus gratings. Only responses to plaids with dOri = 90 deg were considered in this analysis. The response ratio compares the maximum response measured for all plaids with dOri = 90 deg to the maximum response measured for all 100% contrast gratings. The dotted line represents the linear fit for these data.

*** = p<0.001. See also Figure S1.

We first validated the effectiveness of this paradigm by analyzing only responses to plaids with a dOri value of 135 deg, the angle used in the first experiment. As before, we used each neuron’s plaid and grating tuning curves to compute Z_P and Z_C. Based on this analysis, 23% of PSS cells (9/40) were classified as pattern cells, and 35% (14/40) as component cells, in agreement with the first experiment. The pattern index distribution also did not differ significantly between experiments (Kolmogorov-Smirnov test, p = 0.4). We therefore concluded that the rapid succession of stimuli in the streaming paradigm did not interfere with the detectability of PSS pattern responses.

We then used the full stimulus set to provide a more general analysis of PSS motion integration. Each plaid in the stimulus set could be described by two parameters, pattern direction and dOri. dOri influences the plaid’s spatial parameters (such as spatial frequency) and apparent speed [4,20]. Since both parameters could be expected to impact neuronal responses, we chose to summarize the stimulus space as the 2D space spanned by them (see Figure 5C & D). We also assumed that direction and dOri tuning were separable, so that tuning curve predictions for the entire stimulus ensemble could be generated as the product of direction and dOri tuning curves.

Similar to the standard analysis, we quantified the amount of motion integration exhibited by a neuron by comparing its actual tuning curve to pattern and component predictions. Both predictions were generated by estimating a direction tuning curve and a dOri tuning curve and computing their product (see Figure S1 for examples). All tuning curves were estimated based on the entire data set (i.e., gratings and plaids) to increase their robustness. More precisely, the direction tuning curve for the pattern prediction was computed by averaging across all plaids moving in the same direction (independent of dOri) as well as the matching gratings. The dOri tuning curve was similarly computed by collapsing across all stimuli with the same dOri. For the component prediction, we first computed direction tuning as a function of component direction. This was achieved by averaging across all plaids based on component direction (i.e. each plaid contributed twice), again including the matching gratings. Since we chose to represent tuning curves in a 2D space spanned by plaid direction and dOri, we then transformed the direction tuning curve from a function of component direction to a function of plaid direction. For this transformation, we summed two copies of the component direction tuning curve at each dOri, shifted relative to each other according to the dOri value. The dOri tuning curve for the component prediction was identical to that of the pattern prediction. After generating both predictions, they were compared to the actual responses of each neuron by computing Z-corrected partial correlations.

In agreement with our previous results, we observed a range of motion integration behavior in PSS, including both pattern and component cells. 45% of cells (29/65) were classified as pattern cells, 35% (23/65) as component cells, and the rest remained unclassified (Figure 5E). In contrast, using the same stimulus set and analysis in V1 resulted in 100% component cells (26/26) and no pattern or unclassified cells (Figure 5F). The pattern index distributions were also significantly different between PSS and V1 (Figure 5G), with generally higher pattern indices in PSS than V1 (PSS median: 0.45, V1 median: −9.27; Kolmogorov-Smirnov test: p < 0.001).

In conclusion, the streaming stimulus experiment further confirms that signatures of motion integration can be found in PSS but not V1. It extends our other findings by demonstrating that PSS pattern cells extract pattern motion despite changes in dOri, in agreement with the perception of these stimuli. This is consistent with the behavior of pattern cells in MT [9]. In comparison with the previous data set, the analysis based on the larger stimulus set enhanced the differences between V1 and PSS. The large number of component cells detected in V1 rules out that the increased number of pattern cells in PSS is simply a product of the chosen analysis method. Rather, we suggest that the increased number of stimuli used for tuning curve computations, as well as the increased number of data points used for computing partial correlations, enhance the ability to differentiate the two cases.

This data set allowed a further comparison between PSS and MT: MT pattern cells tend to respond more strongly to plaids than gratings, reflected in a significant correlation between the pattern index and the ratio of firing rates for plaids versus gratings [21]. We similarly observed a significant correlation between pattern index and plaid/grating response ratio (expressed in logarithmic scale) in PSS (r = 0.5, p < 0.001; Figure 5H).

Motion representation in PSS can be explained by a multistage motion pathway model:

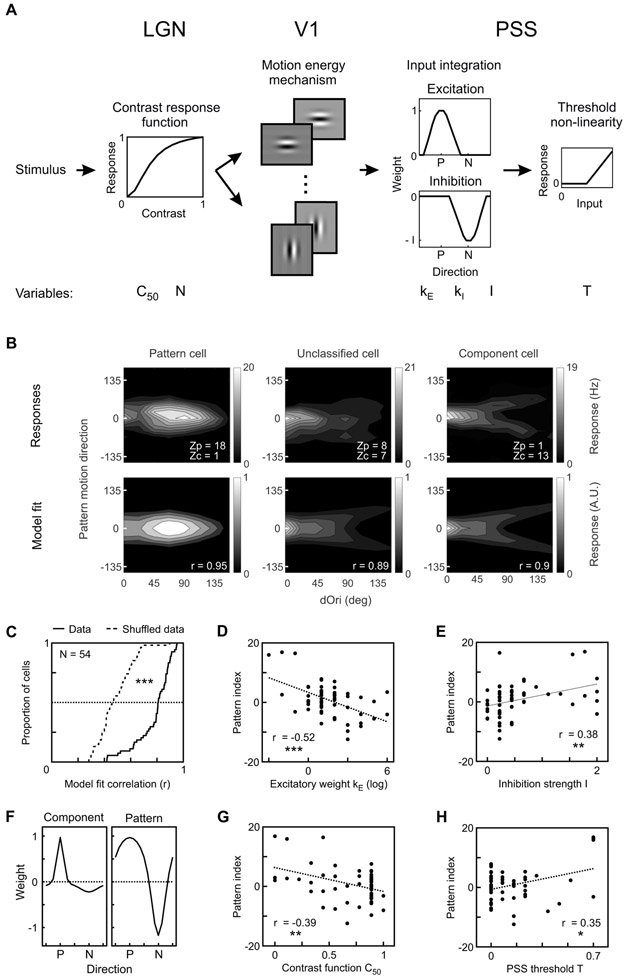
The results presented so far suggest strong similarities between PSS and MT. To further test this idea, we asked whether computational models developed for the primate motion pathway could be adapted to the ferret. To this end, we developed a multistage model of the ferret’s motion pathway based on recent V1-MT pathway models [9,10]. The model consisted of the following stages (Figure 6A):

Figure 6: Motion representation in PSS can be explained by a multistage motion pathway model.

(A) Diagram of model used to explain PSS plaid responses (see Methods for details). Stimuli first passed through LGN spatial filters, which also served to scale responses according to contrast. The next stage was composed of 16 V1 motion-energy filters. Responses from the V1 stage were integrated in PSS using a combination of an excitatory and an inhibitory weight function (P – preferred direction; N – null direction). Finally, an output non-linearity was applied to the PSS responses. The model had 6 variables, which are listed below the stage to which they belong. All other parameters were fixed.

(B) Top: Responses of 3 example PSS neurons to the large plaid set (format as in Figure 5C). Bottom: Model fits, chosen to minimize the mean square error for each of the 3 cells. For each cell, r denotes the correlation coefficient between modeled and measured responses.

(C) Cumulative distribution of the correlation coefficient between modeled and measured PSS responses (solid line) or between modeled and shuffled responses from the same neurons (dashed line).

(D, E, G, H) Relationship between different model parameters and the pattern index. Correlation coefficients and their significance are indicated for each parameter.

(F) PSS weight function for the component cell (left) and pattern cell (right) shown in (B). The weight functions show the shape and relative contribution of the excitatory and inhibitory components determined for these cells by the model. Component cells have a sharp excitatory weight function with little inhibition, while pattern cells have a broad excitatory function combined with strong inhibition. P – preferred direction; N – null direction. Note that the amplitude of the excitatory weight function was fixed at 1.

* = p < 0.05; ** = p < 0.01; *** = p<0.001.

(1) Contrast scaling: The first model stage implements the scaling of visual inputs resulting from contrast response functions in processing stages preceding V1. Contrast response functions were modeled using the Naka-Rushton equation [22], with the shape of the functions controlled by the parameters C₅₀ and N. We included this stage to allow future developmental studies to model the impact of maturing contrast response functions (e.g. [23–25]) on overall motion pathway behavior. Additionally, contrast scaling provides a mechanism for controlling the relative V1 response to gratings and plaids. This is necessary for generating pattern cells that respond more strongly to plaids than gratings, as observed in the data. For the same reason, recent V1-MT models included a so-called ‘tuned’ normalization stage in V1, which served to scale the responses of individual V1 direction channels. Here, contrast scaling was implemented as the first model stage to maintain contrast-invariant orientation tuning in V1 [26,27].

(2) Direction filters: The second stage represents a bank of 16 V1 direction filters. Direction selectivity was implemented using motion energy detectors [14] as in previous models [10,15,28]. All parameters determining the direction filters were fixed, and chosen based on existing values for carnivores (see Methods). Note that we chose not to include a divisive normalization stage in V1 as often found in V1-MT models [9,10,15,28]. The divisive normalization serves to scale overall responses across all direction channels. In V1-MT models using both this ‘untuned’ and the previously mentioned ‘tuned’ V1 normalization, the weight of the untuned normalization was generally low [9,10]. We therefore omitted the divisive normalization stage to reduce the number of model parameters.

(3) PSS integration: In the third stage, integration of V1 responses was modeled as a linear combination of the V1 direction channels. To account for motion opponency, we chose to include two weight functions in this stage, one for excitation and one for inhibition. The excitatory weight function was modeled as a von Mises function of concentration k_E, centered on the preferred direction. The amplitude of the excitatory weight function was fixed at 1. Inhibition was similarly modeled as a von Mises function of concentration k_I, and amplitude I, centered on the null direction. The complete weight function was then computed by subtracting the inhibitory weights from the excitatory weights.

(4) PSS non-linearity: In the last model stage, a threshold non-linearity with threshold T was applied to the PSS responses.

To test whether this model was capable of reproducing the range of plaid responses observed in PSS, we used it to fit a set of strongly direction selective (DSI>0.75) PSS neurons for which we had collected responses to the large plaid set. For each neuron, the fit procedure determined the best values for the six parameters listed above (C₅₀, N, k_E, k_I, I, T). The model was able to explain not only PSS component and pattern responses, but also the responses of unclassified, intermediate cells (Figure 6B). Generally, tuning profiles generated from the model fit agreed well with the actual data. Across neurons, the median correlation between model fit and actual data was 0.81, which is remarkable given that only six variables were used to fit 128 data points per tuning profile. As a control, we also fit the model to a shuffled data set, in which each neuron’s responses were shuffled across stimuli to destroy the tuning profile while preserving overall response rates. The model poorly explained the random structure of the shuffled data set (Figure 6C), resulting in significantly lower correlation values for the shuffled than the actual data (median correlation shuffle data 0.46; Kolmogorov-Smirnov test, p < 001).

In an effort to identify potential mechanisms responsible for generating pattern cells, we investigated how different model parameters contributed to the emergence of pattern responses. To this end, we tested how well individual parameters correlated with the pattern index. Amongst the six parameters, the concentration k_E of the excitatory PSS weight function (Figure 6D) correlated most strongly with the pattern index (r = −0.52, p < 0.001). In addition, the strength of inhibitory weights I (Figure 6E) was also significantly correlated with the pattern index (r = 0.38, p = 0.005). Together, these findings imply that pattern cells have an overall weight function with a broad excitatory peak and a strong inhibitory component (Figure 6F). Component cells, on the other hand, have a narrow excitatory peak with little inhibition (Figure 6F). Similar observations were made for MT [9]. The C₅₀ component of the contrast response function (Figure 6G) was also strongly correlated with pattern index (r = −0.39, p = 0.003) while the PSS threshold parameter T (Figure 6H) showed a weaker, but still significant correlation (r = 0.35, p = 0.01). The remaining parameters of the model (N and k_I) were not correlated with the pattern index (data not shown).

Discussion:

In this study, we investigated the properties of visual area PSS in ferrets. While previous studies pointed towards a general involvement in motion processing, our findings now identify PSS as a higher-level motion area. This conclusion is based on striking similarities between PSS and primate MT. Anatomically, PSS – like MT – is more heavily myelinated than the surrounding areas [6,29], and also receives direct input from V1 [2,7,30]. In terms of basic responses properties, PSS and MT exhibit a similarly high degree of direction selectivity. In our data, the mean DSI in PSS was 0.84; previous MT studies report a mean DSI of 0.8 – 1.05 depending on primate species and stimuli used [31–34]. For both PSS and MT, the degree of direction selectivity is significantly higher than that found in V1 (ferret mean V1 DSI: 0.48, macaque mean: 0.56 [31,34]), consistent with an increased specialization for motion processing in PSS/MT.

Similarities extend to more complex motion processing. PSS shows strong motion opponency, at comparable levels to MT (ferret median MOI: 0.62, mean: 0.59; primate median: 0.54 [13], mean: 0.36 [12]). In both species, these levels are higher than those observed in V1 (ferret median and mean: 0.36; primate median: 0.04 [13], mean 0.2 [12]). In addition, in ferrets and primates motion opponency correlates well with direction selectivity in V1 and PSS/MT [12,13], and the overall differences in motion opponency between areas can largely be explained by their different degrees of direction selectivity [12]. Thus, suppression of opposing direction signals may play an important role in generating direction selectivity across areas and species.

The most important similarity, however, is the existence of pattern cells in PSS, combined with the absence of these cells in V1. As for the primate, this allows us to conclude that lower visual stages like V1 are largely concerned with the extraction of local motion signals, while higher stages like PSS handle local motion integration. We observed 17% pattern cells in PSS for the most commonly used MT stimulus set. Enlarging the stimulus set so that more conditions could be included in the analysis increased this fraction to 45%, with the changes most likely due to an increase in discriminability of pattern and component predictions. In macaque MT, data pooled over many studies resulted in 23% pattern cells [21], while 19% pattern cells have been observed in the marmoset [35]. Note, however, that these studies usually only include highly direction-selective neurons in their analyses. If we similarly restrict our data set for the ‘classic’ stimulus set (criterion: DSI > 0.75), the proportion of pattern cells increases to 27% (13/49). Thus, the proportion of pattern cells in the ferret is comparable to that in the primate. This also holds for the fraction of component cells, which is 27% in PSS using the classic stimulus set, and 37% in the macaque [21].

Finally, PSS responses could be fit well with a computational model recapitulating main features of recent MT models, suggestive of similarities between areas on a more fundamental level. This is further supported by the observation that both PSS and MT modeling efforts point to the shape of the direction integration function in PSS/MT as an important determinant of pattern index. For both models, broader excitatory integration with stronger inhibition is linked with higher pattern indices [9]. Whether these predictions – which are based on the implementation of a particular motion pathway model – indeed accurately capture the mechanisms underlying motion integration in PSS and MT remains to be verified experimentally.

It should be noted that there are differences between PSS and MT, which so far largely seem to be related to the ferret’s overall lower visual acuity [36,37]. This includes the observation that PSS receptive fields are significantly larger than those in MT (Figure S2), and that preferred spatial frequencies are lower in PSS (PSS: 0.06 – 0.12 cycles/deg; MT: 0.1 – 4 cycles/deg [38]). For other processing aspects it is currently unknown how PSS compares with MT. For example, it remains to be determined whether PSS shares MT’s columnar organization for direction [39] and whether disparity is represented as strongly as in MT (e.g., [40]).

The evolution of motion processing from V1 to higher visual areas is well established in primates [2,3]. The findings presented here are the first demonstration of a very similar cortical motion processing cascade in the ferret, and more generally in a non-primate species. Complex motion processing in carnivores has previously been investigated in the cat. As in the ferret and primate, processing in cat V1 is restricted to local motion signals [17,41]. A number of higher-level visual areas were found to have strong direction tuning in the cat [42]. Motion integration was tested explicitly in one of these areas, PMLS, but failed to reveal pattern cells [17,41]. So far, pattern cells were only found in cat frontal cortex and pulvinar [43,44]. Our results strongly suggest the existence of a higher-level visual area with pattern cells in the cat, most likely one of the motion areas not tested so far. Motion processing has also been investigated in the mouse, in which local motion directions are already robustly represented at the level of retina and LGN [45,46]. Motion integration similarly appears to occur earlier. When probed with coherent plaids, the largest fraction of mouse V1 neurons consistently falls into the ‘unclassified’ category, in which neurons have intermediate levels of motion integration [47–49], unlike the strong predominance of component cells in primate and carnivore V1. Thus, motion processing in the mouse differs notably from that in ferrets and primates. It is possible that motion processing in other rodents proceeds differently: Visual areas ML and L of the squirrel have been shown to contain a large number of direction-selective neurons [50], but motion integration has not yet been studied in this species.

In summary, our data show striking similarities in complex motion processing in ferrets and primates. This presents opportunities for the investigation of higher-level visual processing: A transgenic ferret model of microcephaly was recently established [51], raising the prospect that transgenic ferrets might become increasingly more available. More important, however, are the advantages of ferrets as a developmental animal model. Previous research has already established the developmental timeline of direction selectivity in V1, as well as the impact of visual experience (e.g. [52–54]). Our results in adult ferrets lay the foundation to expand this research into development of complex motion processing in higher-level visual cortex, both under normal and abnormal conditions.

STAR Methods:

Contact for reagent and resource sharing:

Further information and requests for resources and reagents should be directed and will be fulfilled by the Lead Contact, Kristina J. Nielsen (Kristina.nielsen@jhu.edu).

Experimental model and subject details:

All procedures were approved by the Johns Hopkins Animal Care and Use Committee and adhered to the guidelines of the National Institute of Health. Experiments were performed in female sable ferrets (Mustela putoris furo, Marshall Farms) with normal immune status, with ages between 1.5 months and 1.8 years. Animals were housed in a 16h light/8h dark or a 12h light/12h dark cycle. Ferrets were not involved in previous studies.

Methods details:

Animal preparation and surgery

Ferrets were pretreated with atropine (0.05 mg/kg, IM) and anesthesia was induced with ketamine (40 mg/kg, IM). After induction, anesthesia was maintained with isoflurane (during surgery: 1.5 – 3%, during recording: 0.5 – 2%). A tracheostomy was performed and an IV catheter was inserted into the external jugular vein for delivery of 2.5% dextrose in lactated Ringer’s solution (4 mL/kg/hr). Body temperature was maintained at 37 – 39 deg C using a heat pad. A small metal plate was attached to the skull with dental acrylic (Dentsply or Lang Dental), which was then connected to a custom stereotaxic apparatus to rigidly hold the head. Two screws were implanted over frontal cortex to record the EEG. Throughout the procedure, heart rate, SpO2, EKG, EtCO2 and EEG were monitored continuously to maintain the animal in an adequate plane of anesthesia. Before the start of recording, animals were paralyzed with pancuronium bromide (0.15 mg/kg/hr). Respiration was maintained with a ventilator (Ugo Basile), adjusting breathing rate and volume to maintain the EtCO2 between 3.3 and 4.8%. Neosynephrine and atropine were applied to the eyes to retract the nictitating membrane and dilate the pupil, and animals were fitted with contact lenses. Before recordings, craniotomies were made above either V1 or the posterior bank of the suprasylvian sulcus to reach PSS. We targeted central visual field regions in V1, and central and more peripheral visual field regions in PSS. Small durotomies were made inside the craniotomies to allow recording probes to penetrate the brain. The brain was covered with 1.5 – 5% agarose (type III-A, Sigma-Aldrich) in artificial cerebrospinal fluid during recordings.

Electrophysiology

Neural signals were recorded using either custom-made tetrodes made from 12μm nichrome wire (California Fine Wire Company) or 64-channel silicon microprobes (Masmanides lab, UCLA). Tetrodes were plated using a gold solution (Sifco ASC) to reach final impedances of 150-500 kΩ; silicon probes were gold-plated to reach final impedances of 150-300 kΩ. Signals were amplified and recorded using a CerePlex Direct amplifier (Blackrock Microsystems) or a RHD2000 amplifier (intan Technologies). Raw data was acquired at 30 kHz and filtered between 250 Hz and 5 kHz. Spike detection threshold was set manually for each recording based on noise levels. Single unit isolation was performed off-line using MATLAB (MathWorks) custom-made software. Isolation was based on multiple waveform characteristics (e.g., spike amplitude peak, area under the waveform, repolarization phase slope) recorded on the four tetrode channels or on neighboring channels of the silicon probe. Quality of isolation was confirmed by inter-spike interval (ISI) analysis. Units that displayed ISIs below 1.2ms were not included in further analyses.

Visual stimuli and experiment design

Visual stimuli were generated using the Psychophysics Toolbox extensions for MATLAB [55,56] and displayed on a 24-inch LCD monitor with refresh rate of 120 Hz, placed 25 - 35 cm in front of the ferret. The monitor was gamma corrected using a SpectraScan 655 (PhotoResearch). For a subset of experiments, a 43-inch LCD monitor with a refresh rate of 60 Hz was used instead.

Classic stimulus presentations:

Experiments consisted of 5 repetitions of each stimulus condition (including a blank condition), presented in a pseudo-random sequence. This presentation mode was used with gratings, plaids, bars, and random dots. Stimulus parameters that varied across conditions are described for each experiment in the results section. Other stimulus parameters for the different experiments are listed below.

Gratings and plaids:

Stimulus sizes were optimized for each neuron. In most experiments, stimuli were shown in circular aperture with radius 8 – 30 deg (see Figure S2 for example receptive field sizes); in a few experiments, we instead used rectangular stimuli of 65 × 50 deg. All experiments used sine-wave gratings. Grating spatial frequency was set to the optimal value for each neuron (range 0.05 - 0.1 cycles/deg), as was temporal frequency (range 2 - 6 Hz) outside of the temporal frequency experiment. In plaid experiments, gratings were shown at 50% contrast; otherwise they were shown at 100% contrast. Plaids shown using the classic presentation mode were generated by superimposing two 50% contrast sine-wave gratings of optimal spatial and temporal frequency at an intersection angle of 135 deg. Plaids were always shown at full contrast. Stimuli were presented interspersed with presentation of a gray screen of equal mean luminance. Stimuli were presented for 1 s with inter-stimulus intervals of 2 – 5 s.

Drifting bar stimulus:

We presented either a white bar on a black background or a black bar on a white background, depending on the preferences of the neuron under study. Bar size was set to 10 × 5 deg. Bars moved perpendicular to their orientation, and their starting point was adjusted such that the bar reached the center of the neuron’s receptive field at half the stimulus presentation time. Static bars were positioned in the center of the neuron’s receptive field. Bar presentations were interspersed with presentation of a blank stimulus of background color. Stimuli were shown for 1 s, and inter-stimulus intervals ranged from 2 to 5 s.

Random dot kinematograms:

Random dot stimuli consisted of white dots on a black background. Dot size, density and speed were set manually to elicit the strongest neuronal responses. Dot radius ranged from 1 – 2 degrees, speed from 15 - 60 degrees/s, and dot density from 0.8 – 3.5 dots per 100 degree². This resulted in inter-dot distances of 3 - 7.5 deg, similar to a previous PSS study using random dot stimuli [6]. The overall size of the stimulus was also optimized for each neuron (either circular with radius of 15 – 30 deg, or 65 × 50 deg). To avoid contamination of responses by luminance changes, the presentation of dot motion was preceded by a static presentation of the first frame of the random dot stimulus, displayed for 2 – 3 s. The dots were then moved for 1 s. Any dot that left the stimulus aperture during this time period was replotted in a random position on the opposite side of the stimulus to preserve dot density. At the end of the stimulus, the last frame was shown static for another 1 – 2 s. Different random dot stimuli were separated by brief presentations of a black screen. In some of the motion opponency experiments (mostly using tetrodes), we first determined the preferred direction of each neuron manually, and then only presented the preferred, null and motion opponency stimuli. In the rest of the experiments, we instead sampled 8 or 12 directions for the single direction stimuli. We also generated motion opponency stimuli for each of these directions by superimposing the opposing direction.

Streaming stimulus presentation:

Each trial consisted of a 60 s long sequence of short stimulus presentations (3 - 6 stimuli/s). Each sequence was preceded and followed by a 2 s presentation of a gray screen of equal mean luminance. Stimulus sequence was determined randomly by picking from all stimulus conditions with replacement. The following stimulus conditions were used: blank (uniform gray screen), 100% contrast sine-wave gratings moving in 16 directions, and plaids with 7 different component intersection angles (dOri; 22.5, 45, 67.4, 90, 112.5, 135 and 157.5 deg) moving in 16 directions. In a subset of experiments we also included 50% contrast gratings moving in 16 directions. Spatial frequency (0.05 - 0.15 cycles/deg), temporal frequency (2 – 5 Hz) and stimulus size (circular aperture of radius 10 – 35 deg) were optimized per neuron. For each stimulus, the initial phase of each grating was chosen randomly from 4 possible values (0, 90, 180 and 270 deg). 30 or 45 trials were run for each experiment, which ensured that each stimulus was presented at least 10 times.

Data analysis and inclusion criteria

The number of animals and neurons per analysis are listed in Table 1. Note that data for multiple stimulus types could be collected in the same animal (i.e., animals may be used for multiple analyses).

Table 1: Number of animals and neurons for each analysis.

Experiment, analysis or metric (Figure and panel)	Group	Animals	Neurons
Direction selectivity index (Figure 1: D)	PSS	10	88
Direction selectivity index (Figure 1: D)	V1	9	69
Static vs moving stimulus response (Figure 1: F)	PSS	5	33
Static vs moving stimulus response (Figure 1: F)	V1	5	14
Speed tuning (Figure 2: B-D)	PSS	4	27
Static vs null motion response (Figure 2: E)	PSS	4	21
Motion opponency (Figure 3: B and C)	PSS standard	7	30
Motion opponency (Figure 3: B and C)	V1 standard	5	26
Motion opponency (Figure 3: B)	PSS constant density	4	14
Motion opponency (Figure 3: B)	V1 constant density	3	26
Pattern motion, classic stimulus set (Figure 4: D and E)	PSS	8	77
Pattern motion, classic stimulus set (Figure 4: D and F)	V1	4	22
Pattern motion, streaming stimulus (Figure 5: E, G and H)	PSS	12	65
Pattern motion, streaming stimulus (Figure 5: F and G)	V1	7	26
Motion pathway model (Figure 6: C-G)	PSS	12	54

Classic stimulus presentations:

For gratings, plaids and random dots, neuronal responses were calculated as the firing rate during stimulus presentation minus the firing rate during the last second of the prestimulus period. For bar stimuli, firing rates were measured during the time period in which the stimulus was within 20 deg of the center of the receptive field, corrected assuming a fixed response latency of 50 ms. All neurons were then screened for general stimulus responsiveness. For gratings, plaids and bars, we performed this test by using a one-way ANOVA to compare responses across all stimulus conditions (including the blank). Only cells that passed p<.01 for the ANOVA were included in further analyses. For random dot stimuli, we tested for responsiveness using a t-test between the best single direction stimulus and the blank, using a Bonferroni correction to adjust for multiple comparisons (either 2, 8 or 12, depending on how many directions were shown in an experiment). Cells that passed p<.05 were included in further analyses. In addition to these tests, neurons with a mean response lower than 2 Hz for the best stimulus condition were excluded. For all remaining neurons, tuning properties were then calculated from mean responses across stimulus repetitions.

Streaming stimulus presentation:

Computing stimulus-evoked responses from the streaming stimulus requires shifting spike times relative to stimulus onset to account for response latency. The analysis used to determine the optimal delay was based on the assumption that stimulus differences would be most pronounced for the real response latency, while other delay values would dilute these differences because of incorrect stimulus-response assignments [19]. First, we computed mean responses for all stimuli in stimulus-locked, 150 ms-long windows, offset from stimulus onset by 20 different delays ranging from 0 to 475 ms. When computing the mean, the initial phase of the gratings was ignored. For each delay, we then subtracted the mean blank response from all stimulus conditions (including the blank), and compared all conditions using a one-way ANOVA. The resulting p-values were Bonferroni corrected to account for the 20 comparisons. The delay resulting in the smallest p-value was then used in all further analyses for the neuron. At this point, neurons for which the smallest p-value was larger than 0.01 (after correction) were excluded. Two additional criteria were used to remove cells with limited responsiveness to gratings and/or plaids: For one, cells had to pass an ANOVA across all plaids with dOri = 90 deg and the blank with p<.01, using the optimal delay to compute responses. For the other, the responses to the best grating and the best plaid with dOri = 90 deg had to be larger than 2 Hz.

Tuning curve analyses

Direction selectivity was quantified using a direction index comparing responses between preferred and null direction, which was computed as

$$DSI=1-\frac{R(N)}{R(P)}$$

where R(P) is the response to the preferred direction, and R(N) is the response to the null direction. For drifting bar experiments we computed a low-pass index as

$$\text{Low}-\text{pass index}=1-\frac{R(S_{\text{max}})}{R(S_{\text{pref}})}$$

where S_max indicates the fasted speed sampled (160 deg/sec), and S_pref indicates the neuron’s preferred speed. The strength of motion opponency was determined by computing the following index:

$$MOI=1-\frac{R(MO)}{R(P)}$$

Here, R(MO) indicates the response to the motion opponency RDK and R(P) the response to the preferred RDK.

Analysis of plaid responses

Classic stimulus presentations:

We used standard methods to compute partial correlations between the measured responses to plaids and predictions for pattern and component responses [17]. Partial correlations were then Z-transformed to stabilize the variance and allow comparisons across conditions. The Z-transform was computed as [19]:

$$Z=\sqrt{N-3}\frac{1}{2}\ln \left(\frac{1+r}{1-r}\right)$$

where r is the partial correlation (either pattern or component), and N refers to the number of points in the correlation (here, 16). Cells were classified as pattern cells if they met Z_P – Z_c > 1.28 for Z_C ≥ 0, and Z_P > 1.28 otherwise. Component cells had to meet the opposite criterion. We also computed a pattern index as Z_P-Z_C. As in the cell classification, any negative values (Z_P or Z_C) were set to 0 when computing the index.

Streaming stimulus presentation:

Each neuron’s pattern and component predictions were computed for the larger plaid stimulus set in the following way: For the pattern prediction, we computed a direction tuning curve by averaging responses across all plaids with a shared pattern direction, as well as the gratings moving in the same direction. We also computed a dOri tuning curve, which was estimated by averaging across all stimuli with the same dOri. The complete pattern prediction was then computed as the product of the direction and dOri tuning curves.

For the component prediction, we first estimated a direction tuning curve as a function of component direction by averaging across all plaid stimuli with a shared component direction (i.e. each plaid contributed twice), as well as the gratings moving in the same direction. This tuning curve was then transformed into a function of plaid direction by summing two copies of the component direction curve at each dOri, shifted relative to each other according to the dOri value. The resulting direction tuning curve was multiplied with the dOri tuning curve (identical to the one used for the pattern prediction) to generate a complete component prediction. We then computed partial correlations of each neuron’s actual responses with the two predictions, and converted these values to Z-scores as before (with N set to 112 to account for the 7 plaid sets and 16 directions involved in the computation).

Image-computable motion pathway model

Stimulus:

We presented 1 s of each stimulus, divided into 50 frames, to the model. Stimuli were modeled to span 50 by 50 degrees of visual space, with a spatial resolution of 0.25 degree/pixel. Thus, each stimulus could be summarized by a 200 × 200 × 50 matrix. Stimuli consisted of gratings and plaids. Spatial frequency was fixed at 0.1 cycles/deg and temporal frequency at 1 cycles/s. Gratings and plaids could move in 16 different directions. Gratings were shown at 50% and 100% contrast, and plaids were constructed from 50% gratings using 7 different values of dOri. This stimulus set replicates the entire set of conditions used in the streaming stimulus experiments.

Thalamic layer:

LGN responses were calculated for each pixel in each frame of the stimulus matrix using a 2D LGN receptive field centered on each pixel. Receptive fields consisted of center and surround components modeled as 2D Gaussian functions with σ = 2 deg and 6 deg, respectively. Values were set to reflect the size of ferret LGN receptive field centers [57,58] and center-surround size ratios of cat LGN [59], similar to a previous image-computable LGN model [60]. Gaussian amplitudes were set so that the response to a homogeneous field with no contrast was 0 and the maximum response to a 100% contrast grating was 1.

Following the spatial filtering induced by the receptive field structure, we scaled responses at each pixel according to a contrast response function. This function was implemented as a hyperbolic function of the form

$$R=\frac{r^N}{r^N+C_{50}^N}$$

with r representing the value at each pixel derived after applying the spatial filters. C₅₀ and N are free model parameters. This kind of function has been widely used to model contrast-response functions, and fits well to experimental data [22,26,60,61].

V1 simple cell layer:

Responses of V1 simple cells were computed by applying space-time oriented Gabor filters to the output of the LGN layer, and then summing the output of each filter across all pixels and time. Following the standard motion energy model [14], we used two Gabor filters with a quadrature relationship per direction channel. In total, we used 16 direction channels, set to be 22.5 deg apart. We set the width of the V1 receptive fields (σ) to 5 deg, the spatial frequency to 0.1 cycles/deg, and the temporal frequency to 1 cycle/s. Receptive field size was chosen based on experimental estimations of LGN to V1 receptive field ratios in carnivores [62,63]. The ratio between V1 receptive field size and spatial frequency determines the orientation tuning of modeled V1 neurons. It was set so that V1 orientation tuning (quantified as the circular variance [64–66] of the model’s complex cells) was consistent with the high end of circular variance encountered in our own recordings from ferret V1 (circular variance of 0.81). All of our model V1 neurons were direction selective by design. This is consistent with MT motion pathway models, which usually assume a purely direction-selective V1 stage [9,10,15,28].

V1 complex cell layer:

Responses in the complex cell layer were computed by combining the output of the even and odd Gabor filter for each direction channel, following the standard motion energy model [10,14]:

$$c=\sqrt{s_{\text{even}}^2+s_{\text{odd}}^2}$$

where s represents the output of the V1 simple cell stage for one direction channel. We compute the square root of the simple cell responses to maintain the shape of the contrast response functions set in the LGN stage. For plaids, the phase difference between the two component gratings impacts the model’s response at the complex cell stage. To eliminate response contaminations caused by phase differences, responses to four plaids with different phase differences were computed, and the responses were averaged in the complex cell layer before being passed to the PSS layer.

PSS layer:

In the last stage of the model, the responses of the 16 V1 complex cells were combined linearly. We used two weight functions for this purpose, one representing excitatory interactions and one inhibitory. Weight functions were modeled as

$$W_E(\theta )=\frac{1}{\sqrt{2\pi B_0(k_E)}}\exp (-k_E\cos (\theta -{\theta }_P))$$

and

$$W_I(\theta )=\frac{1}{\sqrt{2\pi B_0(k_I)}}\exp (-k_I\cos (\theta -{\theta }_N))$$

Here, B₀(k) is a modified Bessel function of order 0, θ is one of the 16 directions represented in V1, θ_P is the direction preference of the PSS neuron, and θ_N is its null direction (i.e., θ_N = θ_P + 180 deg). k_E and k_I define the width of the weight functions and are free model parameters. The two weight functions are then combined into one final weight functions by computing

$$W(\theta )=W_E(\theta )-I*W_I(\theta )$$

I, which determines the relative amplitude of the inhibitory weights, is another free model parameter. The final stage of the model represented an output nonlinearity in PSS. We implemented this nonlinearity as a half-wave rectification by setting all responses below a threshold T to 0. T was the final free model parameter, and was expressed as a fraction of the maximum response of the modeled PSS neuron.

Model fitting:

One million instances of the model were computed using 10 possible values for each of the 6 variables described above. For each direction selective PSS cell (DSI > .75), we then picked the model instance with the lowest mean square error. To test for model over-fitting, a control data set was generated by shuffling the responses of each neuron across all conditions. We then fit the model to this control data set as described above for the real data.

Quantification and statistical analysis:

We used a one-way ANOVA or two-sided t-test to decide whether to include neurons in the data sets used for more detailed analysis (described in the previous section). Results of any test were Bonferroni-corrected where necessary. For statistical comparisons of two data sets, we used Wilcoxon rank-sum or Wilcoxon signed-rank tests as well as Kolmogorov-Smirnov tests. Center and spread values are reported as median or mean ± SEM, unless noted otherwise. Correlations were calculated as Pearson’s. Statistical tests and significance levels are reported in the Results section and Figure legends, and exact n values in Table 1. No tests were conducted to check for normality or homogeneity of variance. All statistical analyses were performed using MATLAB software.

Data and software availability:

Data are available from corresponding author upon reasonable request. The code for implementing the motion pathway model is available online (https://github.com/nielsenlabmbi/PSSModel2018).

Highlights.

• Visual area PSS is a higher-level motion area in ferrets

• PSS neurons show signatures of motion integration

• PSS responses can be fit by a motion pathway model similar to ones for the primate

• Complex motion processing in ferrets parallels that in primates