A de novo shape-motif discovery algorithm reveals preferences of transcription factors for DNA shape beyond sequence-motifs

Summary

DNA shape adds specificity to sequence-motifs but has not been explored systematically outside this context. We hypothesized that DNA binding proteins (DBPs) preferentially occupy DNA with specific structures (“shape-motifs”) regardless of whether or not these correspond to high information content sequence-motifs. We present ShapeMF, a Gibbs sampling algorithm that identifies de novo shape-motifs. Using binding data from hundreds of in vivo and in vitro experiments, we show that most DBPs have shape-motifs and can occupy these in the absence of sequence-motifs. This “shape-only binding” is common for many DBPs and in regions co-bound by multiple DBPs. When shape- and sequence-motifs co-occur, they can be overlapping, flanking, or separated by consistent spacing. Finally, DBPs within the same protein family have different shape-motifs, explaining their distinct genome-wide occupancy despite having similar sequence-motifs. These results suggest that shape-motifs not only complement sequence-motifs, but also facilitate recognition of DNA beyond conventionally defined sequence-motifs.

eTOC blurb

Building on the recent line of research that DNA shape encodes specificity signals for transcription factor (TF)-DNA binding, Samee et al. developed an algorithm to identify enriched patterns of DNA shape directly from DNA shape profiles of TF-bound regions. These patterns, or “shape-motifs”, correspond well with the conventional sequence-motifs, but often include additional nucleotides flanking the sequence-motifs. They also show that apparent mismatches to the sequence-motif can have similar shape to the shape-motif and are potential targets for TF binding. While the observations still need experimental validation, the work shows that motif-models that capture additional structural and biophysical aspects are necessary to understand the mechanism of TF-DNA binding.

Graphical Abstract

Introduction

Diverse cellular processes, including gene regulation, chromatin organization, provirus activity, and DNA replication, depend upon transcription factors (TFs) and other DNA-binding proteins (DBPs) being recruited to specific genome sites, either alone or in complexes with other molecules. DBP occupied regions can be identified in vivo via imaging and genomic techniques, such as chromatin immunoprecipitation followed by sequencing (ChIP-Seq). ChIP-Seq data may reflect factors beyond intrinsic affinities of DBPs for DNA, including chromatin accessibility, co-binding protein complexes, and promiscuously bound sequences (e.g., HOT regions (Boyle, Araya et al. 2014), zingers (Worsley Hunt and Wasserman 2014)). To quantify binding affinities, a variety of in vitro assays are deployed (Maerkl and Quake 2007, Le, Shimko et al. 2018). The specificity of DBP-DNA recognition is commonly modeled as sequence-motifs, i.e., a probabilistic description of nucleotide preference at each position of a binding site, often assuming independence between positions (Stormo and Zhao 2010).

We hypothesized that the binding sites of a DBP may be characterized by specific patterns of DNA shape features, e.g., helical twist, minor groove width, etc. Accordingly, shape-specific binding sites of a DBP may or may not correspond to its sequence-motif. Motivating this idea, sequence-motifs become more predictive of in vitro and in vivo binding when supplemented with DNA shape data (Zhou, Shen et al. 2015, Mathelier, Xin et al. 2016, Yang, Orenstein et al. 2017). Also, many bound sequences do not match sequence-motifs (von Hippel, Revzin et al. 1974, von Hippel and Berg 1986, Berg and von Hippel 1987, von Hippel 2007, Wang, Zhuang et al. 2012, Yip, Cheng et al. 2012, Afek, Schipper et al. 2014, Slattery, Zhou et al. 2014). Furthermore, sequence-motifs often fail to identify a subset of regions bound by DBPs, including validated and predicted regulatory elements and expression quantitative trait loci. Differential binding of proteins that have very similar sequence-motifs is another motivation. Finally, different nucleotide sequences can encode similar DNA structure, so shape features have the potential to be complementary to nucleotide features (Garvie and Wolberger 2001). Nonetheless, the role of DNA shape in DBP binding has not been investigated outside the context of sequence-motifs.

Since DNA shape is determined by the local sequence of nucleotides, shape-specific recognition of DNA binding sites is not independent of nucleotide sequence. But it is plausible that the nucleotide sequences encoding a DBP’s shape preference are not highly similar to one another (Parker, Hansen et al. 2009) and would be missed by the typical motif finding approaches that assume sequence similarity. If such shape preferences exist, detecting them from direct sequence analysis would require extending the concept of sequence-motif to consider higher order combinations of nucleotides, for example via a deep neural net. As an alternative approach, we propose to probe and learn shape preferences directly from DNA shape data. Specifically, we translate nucleotide sequences into DNA shape features. Then, we search for an enriched pattern of DNA shape, which we call a “shape-motif”. Thus, we can independently learn shape-motifs from the shape features of nucleotide sequences and compare such motifs and their genomic distributions to those of sequence-motifs to determine the extent to which shape-motifs complement or extend current understanding of DBP occupancy patterns. This is a different goal than improving affinity models by incorporating shape-features with sequence-motifs (Zhou, Shen et al. 2015, Mathelier, Xin et al. 2016) or quantifying the extent of shape-dependency within sequence-motifs (Yang, Orenstein et al. 2017, Rube, Rastogi et al. 2018); hence, new algorithmic approaches are needed to address our goal.

To implement this strategy, we introduced a Gibbs sampling algorithm to discover shape-motifs de novo without conditioning on the presence of a sequence-motif. Applying this method to more than 100 DBPs, several cell types, and both in vivo and in vitro data, we find that most DBPs recognize DNA shape beyond recognizing nucleotide sequence-motifs.

Results

An algorithm to discover variable-length shape-motifs de novo from unaligned genomic regions or oligonucleotides

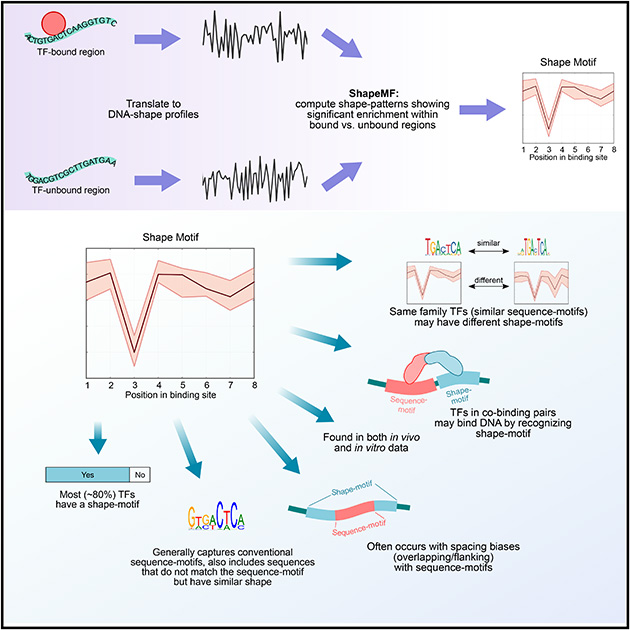
To explore DBP occupancy from the perspective of DNA shape, we first defined a parallel concept to a sequence-motif: a shape-motif is a significantly over-represented pattern in the profile of a DNA shape feature at regions bound by a DBP as compared to unbound regions. To learn shape-motifs de novo we developed the algorithm ShapeMF (Shape Motif Finder). We first translate DNA sequences of bound regions and matched unbound regions into vectors of shape-features. The shape-features in this study are helical twist (HelT), minor groove width (MGW), propeller twist (ProT), and roll (Roll), which were estimated from all-atom Monte Carlo simulations in (Chiu, Yang et al. 2015), ShapeMF can easily be extended to include additional structural features.

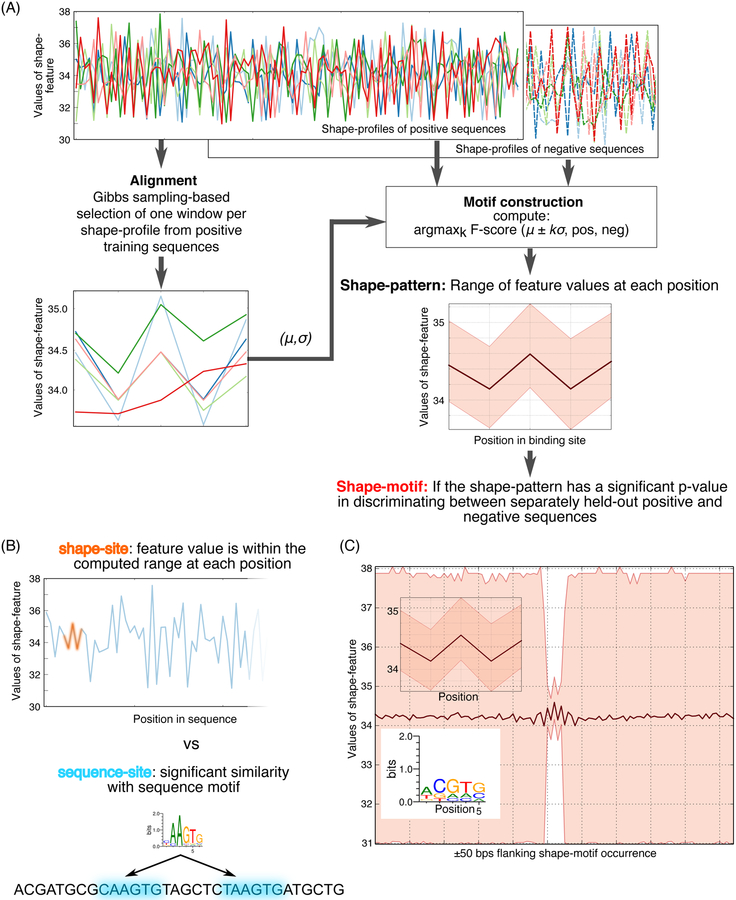
ShapeMF is a three-step algorithm. First, Gibbs sampling is used to compute local alignments of windows (one per region) from the shape-profiles of bound regions (Figure 1A; Methods), This alignment defines a shape-pattern by specifying a range of feature-values per position. A sequence has an occurrence of this pattern if the sequence’s shape-profile (in either forward or reverse orientation) has a window where the feature value at each position lies within a defined range of the average shape pattern (Figure 1B). The second step refines this pattern to optimize its ability (F-score) to distinguish bound from unbound regions. Different sets of unbound regions can be used to identify shape-motifs in different contexts. Finally, the optimized pattern is declared a shape-motif if it discriminates between a separately held-out set of bound and unbound regions with p-value stronger than a threshold. By repeating the search with different window sizes, ShapeMF identifies variable-length shape-motifs. The final output includes only the non-redundant motifs. A Python implementation of ShapeMF is available at: https://github.com/h-samee/shape-motif.

Figure 1.

Overview of ShapeMF. (A) Shape-motif discovery involves comparing DBP-bound regions (positives; solid lines) to non-bound regions (negatives; dashed lines). For each region (different colors) and each shape feature (e.g., MGW), ShapeMF takes the profile of feature values across the region. The Gibbs sampler then identifies a set of short windows from the positive profiles that have similar patterns of the shape feature. In the second step, this initial set of positive windows is refined so that the resulting windows share a shape pattern that has the maximum accuracy to discriminate between positives and negatives (according to F_1/3-score). Finally, this pattern is called a shape-motif if its enrichment in a separately held-out set of positive versus negative sequences is significant (Bonferroni-adjusted hypergeometric p-value < 10⁻⁵). The range of feature values at each position of the window defines the shape-motif. (B) A shape-motif occurs in a sequence if it contains a window whose feature values at every position fit within the ranges defined by the shape-motif. On the other hand, a sequence-motif occurs in a sequence if it contains a window that is significantly similar to the multinomial model defined by the sequence-motif. (C) We visualize sequence logos from the sequences underlying the occurrences of a shape-motif and the range of feature values in the 50-bp regions flanking up- and downstream its occurrences (both shown below the shape-motif), X-axis shows the positions along the shape-motif and its flanking regions; Y-axis shows the range of shape-feature values at each position.

Most DBPs have a shape-motif

We first used ShapeMF to discover shape-motifs in the ChIP-Seq peaks of 106 DBPs in the K562 (chronic myelogenous leukemia) and Gml2878 (lymphoblastoid) cell-lines (177 ENCODE datasets; Methods), This dataset included sequence-specific TFs and other non-specific DBPs, as defined in (Lambert, Jolma et al. 2018), therefore we have checked if our results hold for each set individually (see below). To avoid regions with high ChIP signal due to unknown artifacts of the assay or where DBPs were reported to cluster non-specifically, we filtered out peaks that overlap with high-occupancy target (HOT) regions (Boyle, Araya et al. 2014), From the filtered peaks, we took the strongest 2000 peaks and extracted 100 base-pair (bp) windows centered at the peak-summit to be the bound set of sequences. For unbound sequences, we randomly sampled 2000 sequences from the peaks of the other DBPs (Methods), This choice of negative sequences further assures that the discovered shape-motifs are specific to the DBP and not artifacts of ChIP-Seq. We also tried a second strategy of constructing negative sequences from non-peak regions flanking ChlP-peaks, and found similar results under both strategies (Methods, Figure S1, Figure S2A-D, and Text SI).

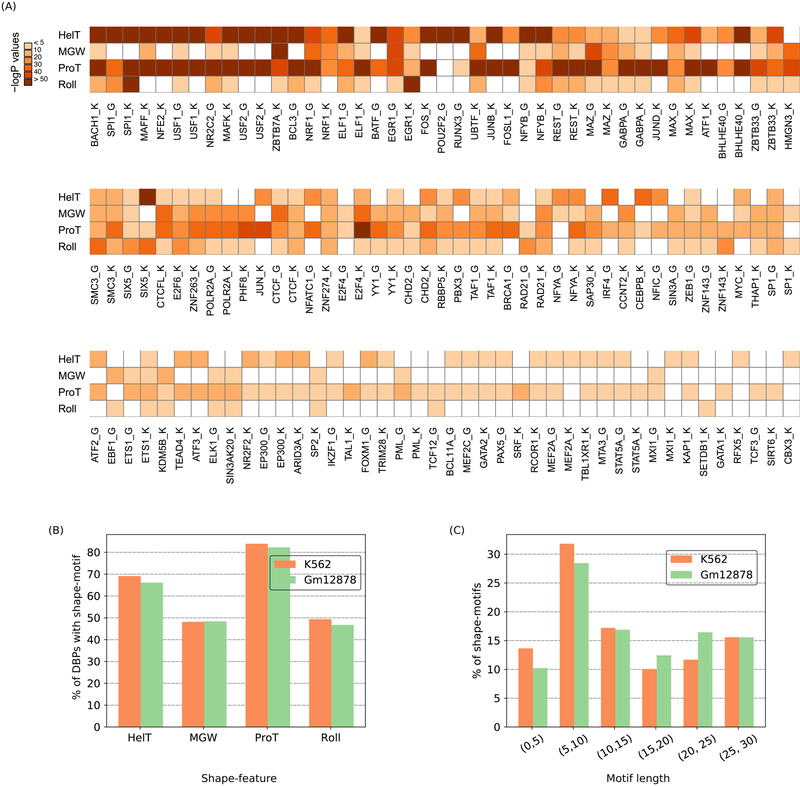
We found that most (>85%) of DBPs in each cell-line have a shape-motif (74/81 in K562, 54/62 in Gml2878; Bonferroni-adjusted p-value < 10⁻⁵; median false positive rate, F_1/3-score, recall, and odds ratio on separately held-out validation data: 0.13, 0.60, 0.36, and 2.9 respectively) (Figure 2A, Figure S3A,B). Few DBPs have shape-motifs for all features. However, most DBPs have a ProT-motif, with MGW- and Roll-motifs being less common (Figure 2B). We found shape-motifs up to 29 bps long, with an average length of 14.3 bps (Figure 2C), which is much longer than a typical sequence-motif (6–10 bps) (Stewart, Hannenhalli et al. 2012).

Figure 2.

Most DBPs have shape-motifs. (A) Heatmap of negative-log₁₀ transformed Bonferroni corrected p-values for each type of shape-motif of each DBP. White cells indicate no significant motif. ‘K’ or ‘G’ after a DBP’s name denotes K562 or Gml2878 cells, respectively. (B) Fraction (%) of DBPs with each type of shape-motif. (C) Length distribution of shape-motifs. Orange and green bars in B, C represent data from K562 and Gml2878 cell-lines, respectively.

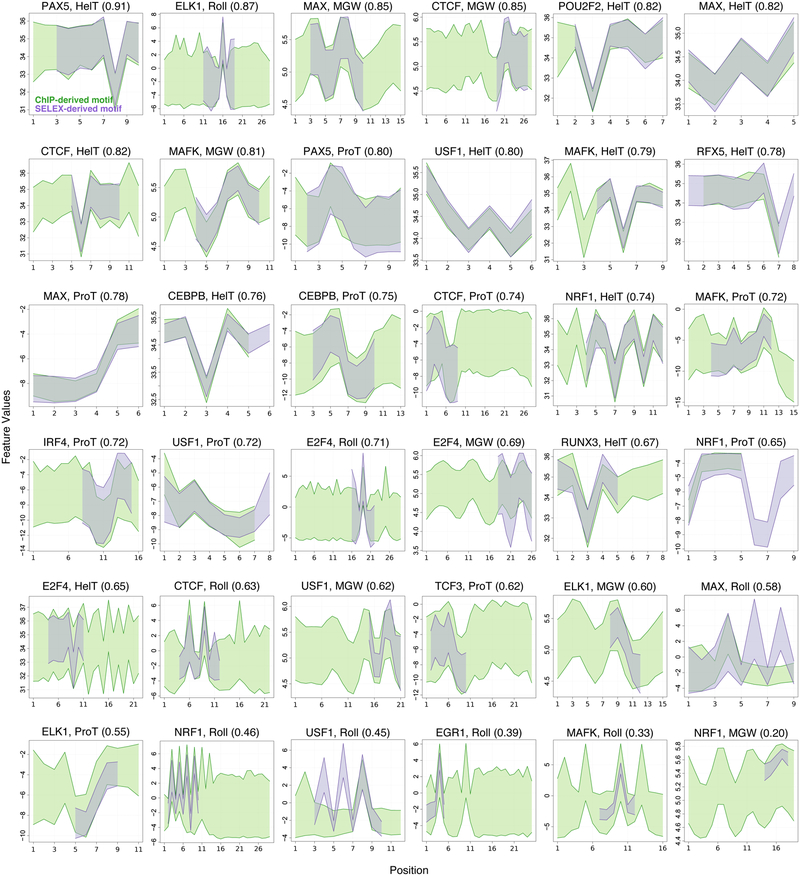
Applying ShapeMF to ChIP-Seq data identifies in vivo enriched shape patterns. However, chromatin accessibility, indirect binding, and other factors beyond the DBP’s intrinsic affinity may be affect ChIP-Seq read density. We therefore sought to test if DBPs show evidence of shape-motifs in vitro, including whether any learned shape-motifs are the same as those discovered in ChIP-Seq (Methods). We took HT-SELEX datasets from (Jolma, Yan et al. 2013, Yang, Orenstein et al. 2017) and repeated our analyses for the 30 DBPs that are common between ENCODE and HT-SELEX (40 HT-SELEX datasets). ShapeMF discovered de novo shape-motifs for 15 of the 30 DBPs. These HT-SELEX shape-motifs are in excellent agreement with the corresponding ChIP-Seq shape-motifs (Figure 3; mean Intersection over Union, IoU, score: 0.69 on a 0–1 scale, Methods and Figure S5). Also, sequence-motifs generated from the sequences underlying shape-motifs (e.g., Figure 1C) in the two data sources show strong similarity for 22/36 cases (Figure S5). Overall these results reveal a high concordance of shape-motifs learned in vitro and in vivo.

Figure 3.

Shape-motifs learned separately in vitro and in vivo are similar. Each panel shows the ShapeMF shape-motifs of one DBP for one shape feature. X-axis shows the positions along the shape-motif; Y-axis shows the range of shape-feature values at each position of the shape-motif. Shape-motifs derived from ChIP-Seq (purple) and HT-SELEX (green) are superimposed. The similarity score in parentheses is the mean intersection over union (IoU) optimized over the possible alignments between motifs from the two sources.

Shape-specific binding is prevalent in vivo

For each DBP with a shape-motif, we next identified all significant matches to the shape-motifs within its genome-wide ChIP-Seq peaks. We refer to shape-motif occurrences as shape-sites (Figure 1B). Since shape-motifs are a new concept and their occurrence beyond sequence-motifs would be novel, we were conservative by allowing at most one shape-motif per feature, thus using at most four shape-motifs per DBP (Methods). A shape-site is a shape-only site if it does not overlap with an occurrence of the DBP’s sequence-motif (as defined below). We identified thousands of shape-only sites across the human genome. A typical DBP has 0.87 shape-only sites per ChIP-Seq peak (Table S1), and DBPs have shape-only sites across a broad range of ChIP-Seq intensities (Methods, Text S2, Figure S6, Figure S7).

To put the genomic features and distributions of shape-motifs in context, we called sequence-motif occurrences within ChIP-Seq peaks of the same 106 DBPs. We were intentionally comprehensive in defining sequence-motifs and liberal in calling motif hits so as to have a high bar for identifying shape-motifs that do not directly correspond to sequence-motifs. We combined all motifs from TRANSFAC (2016 release) (Matys, Fricke et al. 2003), five gkmSVM motifs per DBP learned from its top 2000 ChlP-peaks (Ghandi, Lee et al. 2014), and an additional collection of sequence-motifs from major motif databases, in vitro studies, and de novo motif-discovery methods that was reported in (Kheradpour and Kellis 2014) (Kheradpour and Kellis reported six motifs on average for each DBP; range: 1–29). Hits to any of these motifs within the corresponding ChIP-Seq peaks were called using the tool FIMO with a p-value cutoff of 1e-4 (Methods). We refer to sequence-motif occurrences as sequence-sites. Although 1e-4 is a liberal significance threshold based on general practice (Maurano, Humbert et al. 2012, Thurman, Rynes et al. 2012, Hah, Murakami et al. 2013, Whyte, Orlando et al. 2013, Kheradpour and Kellis 2014), we cannot rule out the possibility that we might have missed some “weak” matches to sequence-motifs. We address this point of weak motif matches in the Discussion. A sequence-site is sequence-only if it does not overlap with a shape-site; otherwise it is an overlapping-site. The frequency of sequence-only sites and overlapping-sites in ChIP-Seq peaks are 1.75 and 1.81, respectively (Table S1). These higher rates compared to shape-sites could be driven in part by our being more conservative in calling shape-motifs than sequence-motifs.

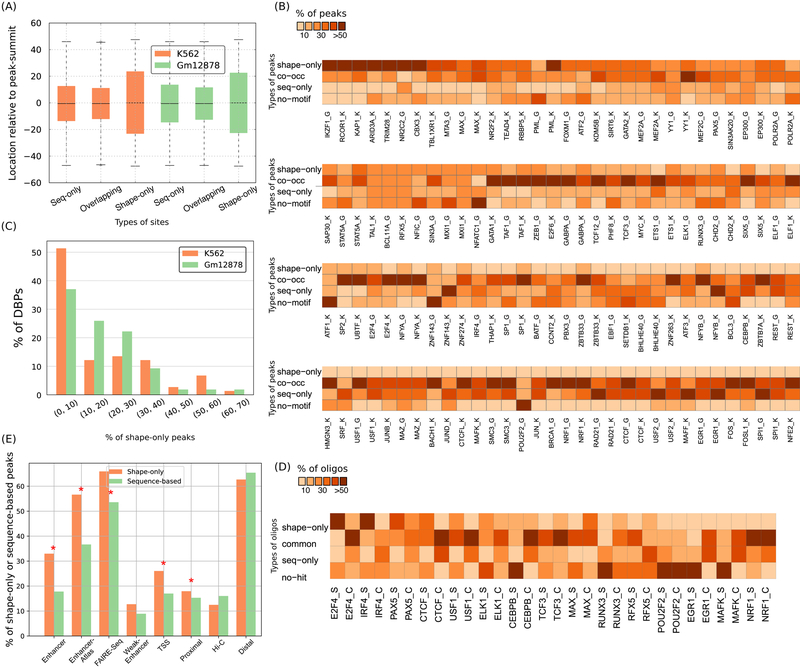
Shape-only sites share many features with sequence-only sites and overlapping-sites. The three types of sites generally occur within ±20 bps of peak-summits (Figure 4A). Their GC-contents are very similar (60%, 58%, and 61%, respectively) and is consistent with the previously reported GC-content of these ChIP-Seq peaks (Wang, Zhuang et al. 2012). So, shape-only sites resemble sequence-sites (i.e., sequence-only and overlapping-sites) in terms of genomic occurrence and sequence properties.

Figure 4.

Prevalence and genomic properties of shape- and sequence-motifs. (A) Sequence-only, shape-only, and overlapping-sites are located at similar distances relative to ChIP-Seq peak-summits. Each box extends from the lower to upper quartile values of the data, with a line at the median. The whiskers extend from the box to show the range of the data. Orange and green boxes represent data from K562 and Gml2878 cell-lines, respectively. (B) Heatmap showing the proportion of shape-only, common, and sequence-only peaks. ‘K’ or ‘G’ after a DBP’s name denotes K562 or Gml2878 cells, respectively. (C) Histogram showing fraction (%) of DBPs binned according to the fraction (%) of their shape-only peaks genome-wide. Orange and green bars represent data from K562 and Gml2878 cell-lines, respectively. (D) Fraction (%) of final-round HT-SELEX oligonucleotides and ChlP-Seq peaks that are shape-only, co-occurrence, and sequence-only. ‘S’ or ‘C’ after a DBP’s name denotes HT-SELEX or ChIP-Seq, respectively. (E) Barplots showing the faction (%) of shape-only peaks and sequence-based (sequence-only plus co-occurrence) peaks in different types of regulatory regions in the K562 cell-line. Shape-only peaks are more enriched in putative enhancer regions than are sequence-based peaks; significant enrichments are marked with stars.

Shape-motifs frequently occur without a consistent sequence-pattern

Next, we built sequence logos from shape-sites in the ChIP-peaks of each DBP (e.g., Figure 1C; Methods) and compared these to its sequence-motif logo. This revealed that shape-motifs generally occur with much lower sequence-specificity as compared to the corresponding sequence-motifs. Their average information content is about half that of sequence-motifs (8.10 bits versus 13.69 bits for TRANSFAC motifs; Methods). Similarly, mean information content per position (ICP) of a shape-motif is only 0.65 bits (Table S2), compared to 1.24 bits for TRANSFAC sequence-motifs and 1.20 bits for motifs derived from SELEX data (Ruan, Swamidass et al. 2017). Shape-motifs discovered above from HT-SELEX data for 15 DBPs have similarly low sequence specificity. The mean ICP of shape-motifs for these 15 DBPs derived from ChIP-Seq and HT-SELEX are 0.8 and 1.1 bits, respectively. The different shape features varied in their sequence specificity (Figure S4). Across shape features, DBPs differed in the information content per position of their shape-motifs by 2-fold. The DBPs whose shape-motifs had high sequence information content were largely the same as those with the highest number of overlapping-sites (Figure S3C). Thus, sequence-motifs can encode DNA shape, but shape-motifs frequently occur without a consistent DNA-sequence pattern.

DBPs occupy shape-sites in the absence of sequence-motifs in vivo and in vitro

Despite the overall high rate of sequence-sites, on average 25% of the top 2000 peaks for each DBP lack a sequence-site (i.e., sequence-only or overlapping-site) (range: 0–82%; Table S3). Many of these top peaks (range: 0–64%, 14% on average) have a shape-only site, suggesting a role for shape-motifs beyond high information content sequence-motifs. We therefore examined ChIP-Seq peaks genome-wide to determine if DBP binding at each genomic location is explained by shape-only sites, sequence-only sites, or a combination. Peaks fall into four categories: (i) sequence-only, (ii) co-occurrence, (iii) shape-only, and (iv) no motif occurrence (Figure 4B). On average, 17.2% of genome-wide peaks in a ChIP-Seq dataset are shape-only (range: 0–67.5%; Figure 4C), as compared to 23.8% sequence-only and 40.3% co-occurrence peaks. Notably, sequence-specific TFs and non-specific DBPs have similar proportions of shape-only peaks (Figure S8).

To more rigorously test whether DBPs occupy DNA with shape-motifs in the absence of sequence-motifs, we repeated shape-motif discovery on the set of peaks without any sequence-sites. For 56/74 and 36/54 DBPs in the K562 and Gm12878 cell-lines respectively, we found a shape-motif. Most (171/177) shape-motifs for peaks lacking sequence-motifs are also motifs for our initial dataset that included peaks with sequence-motifs. The cases where we could not discover a shape-motif from the peaks without sequence-motifs correspond to highly sequence-specific TFs, such as CTCF, ATF1, and JUND. It is also worth mentioning that, ~50% (186/354) of the motifs found from our initial dataset were not motifs for the set of peaks lacking sequence-sites. Thus, about half of our shape-motifs found from the initial dataset are strongly influenced by sequence-motifs.

We next explored the extent of shape-only binding in HT-SELEX data. Twelve of the DBPs with shape-motifs are among the 15 DBPs for which Yang et al. reported sequence-motifs in (Yang, Orenstein et al. 2017). To compare shape- and sequence-motif occurrences in HT-SELEX data for all 30 DBPs, we scanned the final round sequences with all sequence-motifs of the corresponding DBP collected from TRANSFAC and CIS-BP (Weirauch, Yang et al. 2014), and also the “M-words” (enriched k-mers) reported in (Yang, Orenstein et al. 2017). Co-occurrence binding is common in HT-SELEX final round sequences (mean = 34.4%), but shape-only (16.5%) and sequence-only (20.5%) binding are also prevalent (Figure 4D). Altogether, these analyses show that DBPs some times bind DNA with shape-only sites but no sequence-sites. They also suggest that shape-only binding may not always be similarly prevalent in ChIP-seq and SELEX, although several factors contribute to differences in the percentage of DBPs for which ShapeMF discovers a shape-motif from different types of data (Discussion).

Shape-motifs are enriched in putative enhancer elements

To explore the functional significance of shape-specific DBP occupancy, we checked how likely a shape-only ChIP-Seq peak is to occur in putative regulatory regions as compared to a sequence-based peak (i.e., sequence-only plus co-occurrence peaks). Shape-only peaks are significantly more enriched than sequence-based peaks within enhancers (as annotated by ChromHMM and Segway (Ernst and Kellis 2010, Ernst and Kellis 2012, Hoffman, Buske et al. 2012)), EnhancerAtlas regions (Gao, He et al. 2016), and ENCODE FAIRE-Seq regions (Consortium 2012) (Figure 4E, Figure S2F). For some other annotated regions, either the enrichment of shape-only peaks is slightly higher but not significant across both cell-lines (weak enhancers, transcription start sites, and promoter-proximal regions) or shape-only peaks are slightly less enriched than sequence-based peaks (Hi-C contacts (Rao, Huntley et al. 2014), and promoter-distal regions) (Methods).

Shape-sites and sequence-sites systematically co-occur

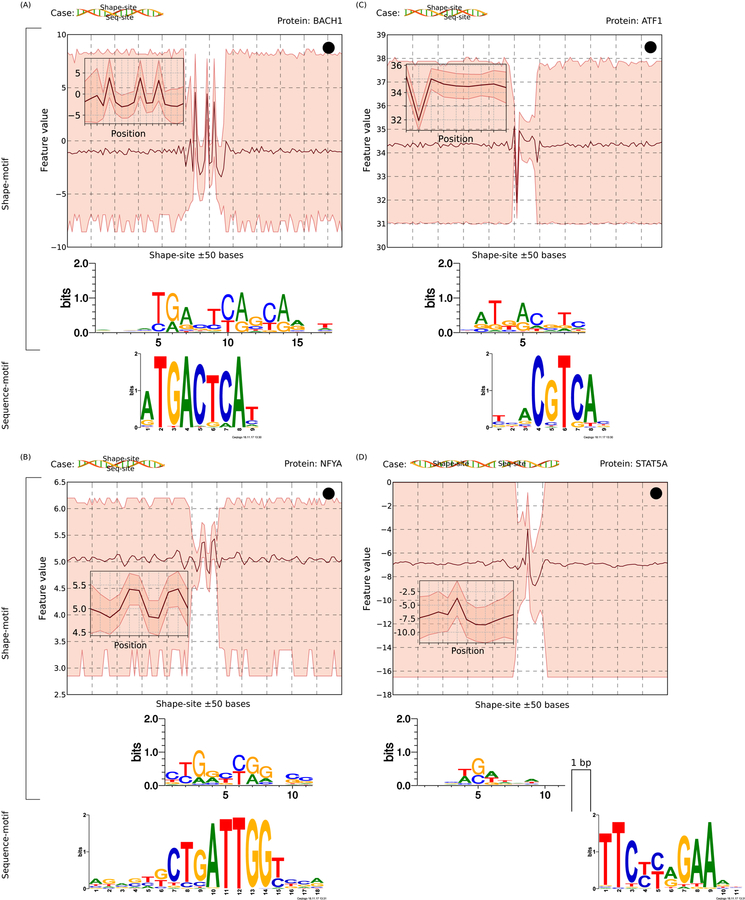
Because co-occurrence peaks are prevalent for most DBPs (mean odds ratio of a peak containing a shape-site given that it contains a sequence-site = 5.45, median = 2.95), we explored these sequences to understand the relationship between shape- and sequence-motifs. In particular, conditioning on the existence of ChIP-based binding signal, we wanted to understand whether and how shape-motifs confer specificity signal in context of sequence-motifs. Analyzing the spacing between pairs of shape- and sequence-motifs for consistent patterns between their sites (Methods), we found that for 25.5% pairs, shape-sites completely contain a sequence-site with shape information encoded by and on both sides of the sequence-motif instance (Figure 5A). Some DBPs representative of this trend are EFOS, ATF3, EGR1, ETS1, and ELF1. Thus, shape-motifs explain binding to low sequence information content positions flanking corresponding sequence-motifs (mean information content per position, ICP, within sequence-motif matches is 1.45 bits as compared to 0.626 bits within flanking sequences that are covered by shape-motif matches). On the other hand, shape-sites are completely contained within a sequence-site in 22.7% of motif-pairs (Figure 5B). Examples include motifs for ATF1, GATA2, MAX, NR2F2, and SPI1.

Figure 5.

Scenarios of shape- and sequence-motif co-occurrence. Each case is shown with a schematic and an example. A schematic uses a cartoon DNA double helix (from http://veleta.rosety.com) and two boxes representing sequence- and shape-sites. A shape-site can (A) flank a sequence-site from both ends, (B) be flanked by a sequence-site from both ends, (C) flank a sequence-site from one end, or (D) occur with an inter-site gap. For each case, the top panel shows shape-related information: the shape-motif pattern (in inset), the range of shape-feature values in the flanking 50-bp regions (up- and downstream) of occurrences of the shape-motif, and the sequence-logo created from sequences underlying the shape-motif. X-axis shows the positions along the genome (or the shape-motif occurrence); Y-axis shows shape-feature values. The bottom panel shows the known sequence-motif of the corresponding DBP.

We also observed many cases of side-by-side sequence-sites and shape-sites. Flanking shape-sites occur both upstream (41.5% of motif-pairs) and downstream (41.9%) of sequence-sites (Figure 5C), found to be up to 28 bps away with overlap up to 22 bps. For 1.9% of motif-pairs, sequence- and shape-motifs do not overlap yet occur with consistent inter-motif spacing (up to 19 bps) (Figure 5D). Examples of DBPs with consistent spacing include EGR1, CTCF, CTCFL, NRSF, NFYA, NFYB, and ZNF143. Overall, these analyses suggest that shape- and sequence-motifs collectively define a broad genomic context for DBP binding, corroborating a similar finding by Dror et al. (Dror, Golan et al. 2015). However, our findings are not directly comparable with this previous report. In particular, Dror et al. focused on ProT 300 bp upstream of and downstream from the core sequence-motifs, and identified the positions at which ProT was lower or higher in bound compared with unbound sequence-motifs. On the other hand, rather than focusing on significant variation of a shape-feature within and outside sequence-motif context, we followed a sequence-motif agnostic approach to discover shape-motifs de novo. Thus, we not only corroborate the finding of Dror et al., but also identify the specific information that a DBP recognizes. It is also worth mentioning that our observation of several DBPs having shape-sites that extend sequence-sites or flank them with consistent spacing shows that shape-associated binding cannot be fully captured by using shape profiles underlying sequence-motif hits.

DBPs in co-binding pairs commonly utilize shape-sites

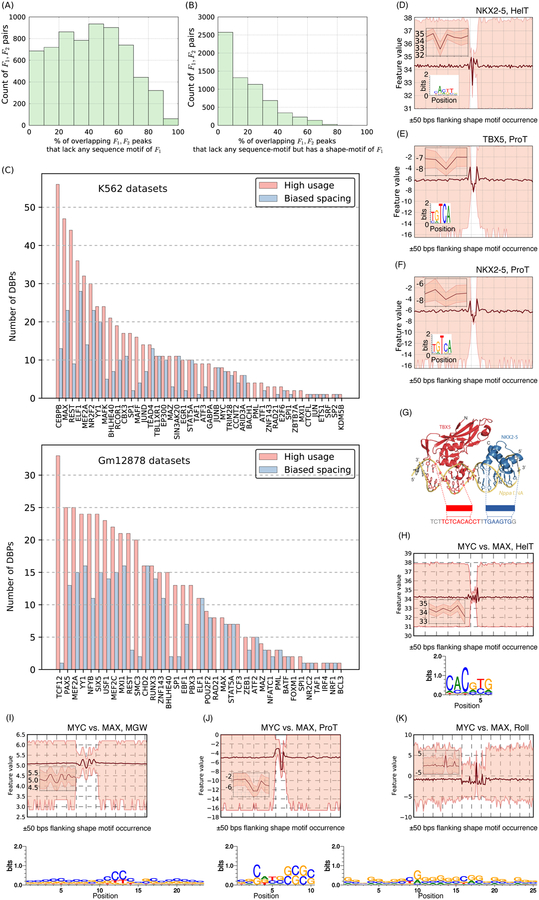
Co-binding of DBPs is common and critical for transcriptional regulation (Gerstein, Kundaje et al. 2012). Considering DBP-pairs that have more than 100 co-bound (overlapping) peaks, we found that on average 42% of a DBP’s co-bound peaks have no sequence-sites and nearly half of these (19% of co-bound peaks) are shape-only (Figure 6A,B, Figure S9A). To explore the nature of shape-specific co-binding, we tested whether a DBP’s co-bound peaks with a second DBP are enriched for being shape-only as compared to its co-bound peaks with other DBPs (Methods). This revealed that many DBPs preferentially use shape-specific co-binding with certain other partners (Figure 6C, pink bars) and there is wide variation in the choice of partnering DBPs. Notably, we also found that DBPs use shape-motifs and sequence-motifs differently when binding alone and with different partners (Figure S10). For example, many DBPs that have high proportions of sequence-only peaks genome-wide use mostly shape-only sites when co-binding with other DBPs.

Figure 6.

Co-binding DBP pairs often utilize shape-specific binding. For many DBP pairs F₁,F₂, (A) co-bound peaks lack a sequence-motif of F₁ and (B) these often have a shape-motif of F₁ (C) DBPs often show preferential utilization of shape-sites in the context of certain other DBPs (pink bars) and these shape-sites show specific spacing biases with the shape- and/or sequence-sites of the co-binding partner (blue bars), (D-K) Shape-motifs suggest models for genomic occupancy of dimer complexes where sequence-motifs are inadequate. (D-F) The shape-motifs for TBX5 and NKX2–5; note that the ProT-motif for NKX2–5 has the consensus sequence of TBX5 in its underlying sequences (also see Figure S9), (G) TBX5 and NKX2–5 shape-sites in a 22-bp DNA-sequence (from mouse Nppa promoter) where the two DBPs are known to bind. Crystal structure of the ternary complex comprising TBX5, NKX2–5, and DNA is from our previous study (Luna-Zurita, Stirnimann et al. 2016), (H-K) The shape-motifs enriched under MYC-peaks vs. MYC-unbound MAX-peaks; note that the HelT-motif has the E-box sequence in its underlying sequences, but the underlying sequences overall result in a motif with low specificity.

The prevalence of shape-sites in the context of co-binding also intrigued us to ask if there are shape-zingers: DBPs whose shape-motifs are enriched across ChIP-Seq peaks of many DBPs (similar to sequence-zingers (Worsley Hunt and Wasserman 2014)). Testing for enrichment of shape-sites of each DBP within the peaks of every other DBP (Methods), we found 22 shape-zingers, including previously reported sequence-zingers, such as CTCF, CTCFL, SMC3, GABPA, and THAP1. However, most shape-zingers are not sequence-zingers (Figure S9B). Arguably, shape-zingers may represent promiscuous binding, biases of ChIP-Seq, or proteins that are frequent co-factors of many other DBPs. However, some shape-zingers that were not reported previously (e.g., P300, PBX3, TCF12, MYC, REST) are known to act as regulators of large gene networks or across multiple cell types (Goodman and Smolik 2000, Lee, Chen et al. 2012, Rockowitz and Zheng 2015, Ramberg, Grytli et al. 2016). Consistent with the “loading station” model suggested by Hunt and Wasserman, all shape-zingers (except P300) show enrichment within peaks of CTCF, RAD21, and SMC3.

Co-bound DBPs may interact physically and form complexes. If DBPs in such complexes bind DNA shape-specifically, then it presents an alternative to the more common “tethering” mechanism whereby one or more DBPs of a complex recognize DNA sequence-specifically and the other DBPs do not contact DNA. To assess the extent of shape-specific co-binding versus tethering, we reasoned that motifs of the partnering DBPs in a complex should occur with some consistent inter-site spacing. We therefore evaluated motif spacing between shape-shape and shape-sequence motif pairs for all pairs of co-bound DBPs. We found that 74% (2388/3227) of DBP pairs have shape-shape or shape-sequence sites that occur with a bias for short (~3 bps) inter-site spacing (Figure 6C, S6). Indeed, 221 of these pairs have previously been reported to have physical interaction (Stark, Breitkreutz et al. 2006, Ravasi, Suzuki et al. 2010). Therefore, we find an interesting line of evidence that some DBPs in a DNA-binding complex may actually bind DNA shape-specifically, and it is possible that tethering is not the only explanation for binding of complexes in the absence of sequence-motifs.

Shape-motifs explain genomic occupancy of DBP-complexes where sequence-motif models are inadequate

We next examined whether DNA shape may explain the genomic occupancy of two well known DBP complexes, namely TBX5-NKX2.5 and MYC-MAX, several aspects of whose in vivo occupancies have remained unresolved in sequence-based analyses (Guo, Li et al. 2014, He, Johnston et al. 2015).

Analyzing ChIP-exo data of TBX5 and NKX2–5 occupancy from our previous study (Luna-Zurita, Stirnimann et al. 2016), we found that sequence-motifs of TBX5 and NKX2–5 co-occur in only 17% of their overlapping ChIP-exo peaks. ShapeMF discovered that both DBPs have shape-motifs for all four features and the HelT and ProT motifs in fact capture their sequence-motifs (Figure 6D,E, Figure S9D). Of note, the sequences underlying the ProT-motif of NKX2–5 contain a sequence-motif for TBX5 (Figure 6F), implying that in many NKX2–5 peaks, TBX5 may co-bind by recognizing the ProT pattern. Broadly supporting the hypothesis that NKX2–5 and TBX5 co-bind shape-specifically, 79% of co-bound regions have a shape-site for one DBP and a sequence-site for the other DBP, and 73% containing shape-sites of both DBPs. Furthermore, co-occurrences of their shape-shape and shape-sequence sites are enriched for 0–4 bps inter-site spacing, which is in the same range as the preferential distances between their sequence-motifs supported by crystal structure (Figure 6G) (Luna-Zurita, Stirnimann et al. 2016). TBX5-NKX2–5 co-binding clearly involves shape-sites that complement and extend their sequence-sites.

The bHLHZip protein MYC binds at E-box motifs (CACGTG) upon dimerization with MAX (Guo, Li et al. 2014). However, MAX binds the E-box motif in almost five-times as many locations as MYC, and it is not clear how the specificity of the MYC-MAX dimer is different from that of MAX in the other MAX-bound locations. We hypothesized that MYC-MAX has a differential shape-motif when compared to the other MAX-bound regions. A previous study found differences in MGW values within the E-box motif-matches for MAX and MYC-MAX in vitro (Yang, Zhou et al. 2014). We leveraged ShapeMF to perform a direct, differential shape-motif discovery from MYC-MAX ChIP-Seq peaks compared to MYC-unbound MAX regions. We found that MYC-MAX peaks have distinct shape-motifs (Figure 6H–K). It is known that crystallized structures of the MYC-MAX dimer and the MAX homodimer are different despite their apparent resemblances (Nair and Burley 2003). Combining this with our differential shape-motif analysis, we speculate that the structural differences between the MYC-MAX dimer and the MAX homodimer cause subtle differences in their preferences for different DNA structures.

DBPs within the same class recognize distinct shape-motifs

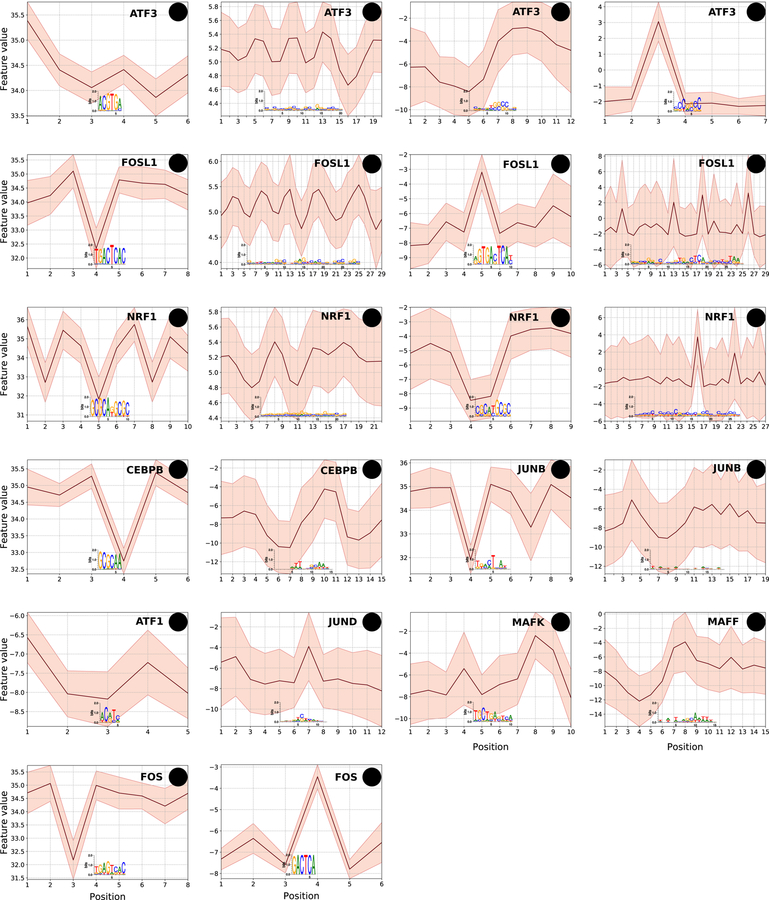
Sequence-motifs of DBPs within the same class of DNA-binding domain are often statistically indistinguishable, although the DBPs still bind different locations in the genome. It has been shown that sequence-based models of DBP-occupancy achieve improved performance for DBPs within the same class by using shape-features underlying sequence-motif hits (Mathelier, Xin et al. 2016, Yang, Orenstein et al. 2017). However, it is not clear if the predictive shape-features represent shape-motifs (i.e., are high information content in the shape domain versus more diffuse signals) or whether DBPs within a class show preferences for distinct shape-motifs outside the context of sequence-motifs. To explore these questions, we applied ShapeMF on ENCODE ChIP-Seq datasets of the bHLH and bZIP class DBPs (Methods). DBPs within each class have very similar sequence-motifs. We found that most bHLH (5/7) and bZIP (10/13) DBPs have shape-motifs, which are often for different combinations of shape features or represent different motifs for the same feature (Figure 7, Figure S11). This suggests that DBPs within the same class do utilize shape-sites to bind at distinct locations genome-wide.

Figure 7.

bZIP family DBPs utilize distinct shape-motifs and in different combinations. Shape-motifs for ten bZIP proteins; H, M, P, and R denote motifs for HelT, MGW, ProT, and Roll, respectively. X-axis shows the positions along the shape-motif; Y-axis shows the range of shape-feature at each position of the shape-motif. A feature is omitted for a DBP if the DBP does not have a shape-motif for that feature. DBPs have shape-motifs for different combinations of features. When two DBPs have a shape-motif for the same feature, they may be broadly similar (e.g., FOSL1 and CEBPB HelT) or quite distinct (e.g., FOS1 versus NRF1 ProT).

Discussion

Analyzing in vivo and in vitro binding data of hundreds of human DBPs with our algorithm that treats DNA as a structure rather than a string of nucleotides, we showed that DBPs frequently recognize specific patterns of DNA shape features. These shape-motifs occur beyond the conventional, PWM-based sequence-motifs, and a significant fraction of DBP-occupied regions (ChIP-peaks or oligonucleotides) can be explained by shape-but not sequence-motifs. Shape-motifs also shed light on DBP occupancy at weak matches to sequence-motifs, and our results suggest that sites that are weakly specific using current PWM-based sequence-motifs may actually have strong specificity from the perspective of DNA shape. Overall, in addition to confirming the importance of DNA shape in the context of sequence-motifs as shown in several recent models (Abe, Dror et al. 2015, Zhou, Shen et al. 2015, Mathelier, Xin et al. 2016, Yang, Orenstein et al. 2017) and proposed previously (Aggarwal, Rodgers et al. 1988, Zheng, Fraenkel et al. 1999, Liu, Blackwell et al. 2001, Rohs, West et al. 2009, Jolma, Yan et al. 2013), our results suggest that the role of DNA shape extends beyond sequence-motifs.

Importantly, since shape is determined by sequence, ours is not an attempt to represent shape- and sequence-recognition as orthogonal mechanisms. In our presentation, shape-specificity is agnostic of sequence-specificity only from an algorithmic, but not mechanistic, perspective. Our notions of shape-only sites and shape-only peaks reflect lack of statistical signal that the conventional motif models could capture, but not a mechanism that is independent of the underlying sequence. Since DNA sequence contains complete information about shape, our study rather highlights the need to refine the notion of sequence specificity, where the current standard is based on PWMs that assume independence between nucleotides. The refinement should capture specificity signals coming from higher-order interactions between nucleotides. Such an extended alphabet of DNA sequence would, in principle, be able to capture any biophysical property of DBP binding sites, and would be able to identify if a “weak-scoring” site under current convention has a significant specificity signal due to any other biophysical property. However, interpretation is key to any model and if a model incorporates such extended alphabets in a mechanism agnostic manner, the model may lack interpretability. This is where an approach of de novo shape-motif discovery like ours should be useful. Shape-specific binding discovered in our analysis is directly interpretable as a mechanism where DBPs recognize such higher-order nucleotide interactions that encode specific patterns of DNA shape features. On the other hand, although the gkmSVM model can assign positive scores to about half of the shape-only sites (even though the scores are low compared to sequence-only and overlapping sites; see Figure S3D), the model cannot elicit the source of binding specificity at those sites.

Our analyses revealed important functional and mechanistic consequences of shape-specific binding. DBPs within the same family bind distinct instances of a shared sequence-motif that are distinguished by DBP-specific shape-motifs. Similarly, DBPs (e.g., MAX) that bind different instances of a sequence-motif as homodimers or heterodimers appear to utilize shape-sites to distinguish these contexts. These examples suggest that DNA shape may be a general mechanism to increase the information content of binding sites beyond that encoded by sequence-motifs, which is insufficient for eukaryotic DBPs to uniquely recognize specific sites in genomic DNA (Wunderlich and Mirny 2009). We also find that co-binding DBP pairs frequently utilize shape-based binding, providing a mechanism beyond tethering to explain co-binding in regions that lack one or both sequence-motifs. With relation to co-binding of DBPs, it is worth mentioning that shape-only sites discovered in our study are generally not explained by sequence-sites of other TFs, although that would be expected under the tethering model (the median percentage of shape-only sites that have at least 50% overlap with sequence sites of any other DBP is 25.4%; see Figure S3E). Finally, DBP’s in crystal structures generally contact nucleotide bases at sequence-specific binding sites and the DNA backbone at non-sequence-specific sites (Aishima and Wolberger 2003, von Hippel 2004, Romanuka, Folkers et al. 2009). Our results suggest that shape-specific sites contain preferential “pockets” - defined by shape-motifs - where a DBP can stabilize and interact with the DNA backbone. It is also plausible that such stabilization is facilitated by enhanced electrostatic potential at the location of shape-motif occurrences (Rohs, Jin et al. 2010). Importantly, these insights would have been missed if we had only searched for shape patterns within the context of sequence-motifs.

An important methodological contribution of our manuscript is ShapeMF, a de novo shape-motif discovery algorithm. ShapeMF enabled us to pursue the hypothesis that some DBPs have intrinsic preferences for shape-motifs and such preferences can be discovered without taking sequence information into account. It is challenging to design such an algorithm since it requires discovering variable-length shape-patterns de novo from unaligned shape-profiles with the criterion that the discovered shape-motifs are comparable to sequence-motifs in terms of discriminating bound from unbound regions. The recent alignment-free algorithm (Ma, Yang et al. 2017) does not require aligning sequences based on sequence-motif hits, but assumes that shape- and sequence-specific signals coincide and span the same length. We found that the shape-motifs of many DBPs go beyond these assumptions. For the same reason, ShapeMF’s outputs cannot be learned from shape-profiles of sequence-motif hits. Our solution was to implement Gibbs sampling with a notion of similarity between the shapes of two DNA sequences that is appropriate for quantitative features, replacing the four-letter nucleotide alphabet used for sequence-motif discovery. Alternatively, we might have discretized shape features and then directly applied de novo sequence-motif algorithms, as in (Greenbaum, Parker et al. 2007, Pal, Hoinka et al. 2018). However, it was not clear how to bin and/or smooth shape features in a biophysically appropriate manner, or how to characterize the background distribution for these features. Time series “shapelet” discovery algorithms are also relevant to our problem (Ye and Keogh 2009, Grabocka, Schilling et al. 2014, Hou, Kwok et al. 2016). But their efficacy has been shown for datasets where discriminative shapelets appear very frequently (so that sampling a very small subset of the data would suffice to yield shape-motifs) or where the constituent time series are aligned, which does not hold for DBP occupancy data. Hence, a computationally intensive brute-force method would likely be needed to apply shapelet algorithms. In contrast, ShapeMF does not (a) discretize data, (b) use any empirical background distribution of shape features, (c) assume that bound regions are aligned, nor (d) assume that shape-specific and sequence-specific recognition signal have the same length.

Several future directions are suggested from our results. Since our current findings are computational and largely from in vivo data, our obvious next goal is to perform in vitro DNA-binding assays with libraries designed to test the full spectrum of shape-and sequence-motifs for a DBP. We observed some differences in prevalence of shape-only binding in HT-SELEX versus ChIP-Seq. There may be technical reasons for such differences, e.g., biased oligo generation in HT-SELEX (Orenstein and Shamir 2014). Furthermore, some oligonucleotide libraries may not have sufficient coverage to include the larger pool of in vivo sequences that correspond to the same shape-motif. Improved in vitro assays built upon longer and specifically designed oligonucleotides could be used to construct models of DBP-DNA binding affinity in the sequence and shape domains. Resulting shape-motifs could then be added to DBP affinity models (Stormo and Zhao 2010) to potentially improve accuracy and reveal binding mechanisms. Another future goal is to quantify the amount of information that each DBP utilizes from the shape domain in different contexts, including determining the extent to which shape-based binding is an alternative explanation to tethering. In terms of methodology, our current work is limited to the four common shape-features, but we need to study overrepresented patterns of other shape- and biophysical features (e.g., electrostatic potential) as well. We could also analyze shape-features jointly rather than individually. Multivariate regularized analysis of shape-features would require careful algorithm design since a DBP may not have a motif for every feature and the motifs may differ in length and relative location. We also need to formulate shape-specificity as a continuous function and define appropriate continuous functions representing genome-wide background distributions of shape-features. These improvements will make the notion of enrichment for shape-motifs comparable to that for sequence-motifs. However, straightforward approaches will likely not be sufficient for these formulations. For example, a random sample of windows from one of the training datasets (the starting windows for our Gibbs sampler) shows a nearly identical distribution (characterized by wide range, and nearly identical mean and variance) across positions, which is uninformative for the purpose of computing enrichments (Figure S2E). Modeling frameworks for capturing continuous motion, e.g., those based on Kalman Filters, could be suitable for these purposes. Finally, the notion that shape-motifs could be conserved without sequence conservation opens the door to a complimentary view of regulatory evolution and the opportunity to develop shape aware measures of DNA change to shed light on gene regulatory evolution and the role of abnormal DBP function in disease.

STAR Methods

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Katherine S. Pollard rkatherine.pollard@gladstone.ucsf.edul

METHOD DETAILS

The ShapeMF tool

The ShapeMF algoritm searches a set of positive regions bound by a given DBP for one window of fixed length per region such that the resulting set of windows has a narrow distribution of values for a particular DNA shape feature at each position in the window. Specifically, we find the set of windows that minimizes the sum or pairwise Euclidean distances between the vectors of shape feature values for windows from different regions. The algorithm then derives a shape-motif from the resulting windows as the mean feature value per position across the windows plus or minus a constant times the standard deviation of feature values per position, where the constant is selected to optimize discrimination between the positive regions and set of negative, un-bound regions. This motif is considered significant if it is enriched in an independent set of positive versus negative regions. This algorithm is similar to approaches commonly used to discover de novo sequence motifs, modified to work with continuous shape features rather than an alphabet of four nucleotides and tuned to be relatively conservative about calling shape-motifs.

Definitions and notation.

Let $S={\left\{s_i\right\}}_{i=1}^N$ denote a set of peaks (or HT-SELEX enriched oligonucleotides, or any other bound regions) of a DBP. $\psi ={\left\{{\psi }_i\right\}}_{i=1}^N$ denote the corresponding shape-data for a feature F (roll, helical twist, propeller twist, or minor groove width from GBshape), Thus each ψ_i is a sequence of real numbers ψ_i,j denoting the value of feature F at position j in peaks s_i A shape pattern of length l is a l-length sequence $P={\left(\left(m_k,d_k\right)\right)}_{k=1}^l$ of 2-tuples of real numbers. We say that P occurs in peak s_i if there is a l-length sequence window $W_i={\left({\psi }_{i,j}\right)}_{j=t_i}^{t_i+l-1}$ starting at position t_i in the shape-data ψ_i such that either $m_{j-t_i+1}-d_{j-t_i+1}\le {\psi }_{i,j}\le m_{j-t_i+1}+d_{j-t_i+1}$, or $m_{t_i+l-j}-d_{t_i+l-j}\le {\psi }_{i,j}\le m_{t_i+l-j}+d_{t_i+l-j}$ for all j, t_i ≤ j ≤ t_i + l − 1. In other words, the shape-values of W_i at each position j are within a range defined by m_j and d_j. We estimate the values of m_j and d_j in the second step of ShapeMF, as described below.

Algorithm.

ShapeMF uses a two-step approach to first compute a shape pattern P from the shape-data of positive peaks in a training dataset of matched positive and negative control peaks and then modify the pattern to one that maximizes F-score between the positive and control peaks in the training data. In a third step, the modified pattern is called a motif if its Bonferroni-corrected hypergeometric p-value, computed on a separate validation dataset of matched positive and negative peaks is significant. In the Discussion section, we have explained the reasons for making these methodological choices and compared our overall approach against state of the art approaches that are apparently applicable to this problem setting.

Step 1.

From the shape-data ψ of positive peaks in the training data, we first compute a set of windows W (one window W_i in each ψ_i J such that the sum of pairwise Euclidean distances between the windows, i.e., D = Σ_x≠y Euclidean (W_x, W_y), is minimized. We use Gibbs sampling to compute such a set of windows. Gibbs sampling is a Markov Chain Monte Carlo technique for generating samples from a desired distribution. A Gibbs sampler sweeps through each variable to sample from its conditional distribution with the remaining variables fixed to their current values, and repeats this process until some convergence criterion is met. In our case, the desired distribution is over all possible sets of windows (where a window is a vector of shape-feature values of a given length and a set of windows comprises one window from every sequence in the dataset, located anywhere in the sequence and in either strand) and assigns high probability to sets where the windows are highly similar to each other. We assume that the probability of a set follows the Boltzmann distribution where the energy term is the sum of pairwise Euclidean distances between windows in that set. In particular, we start by selecting W_i’s randomly. To select a new window from ψ_i to replace W_i, we consider two windows per position in ψ_i (to consider forward and reverse directions). In particular, let $V_{i,k,+}={\left({\psi }_{i,j}\right)}_{j=k}^{k+l-1}$ and $V_{i,k,-}={\left({\psi }_{i,j}\right)}_{j=k+l-1}^k$ denote the two l-length windows associated with position k in ψ_i. That is, V_{i,k +} starts at position k and includes all shape-values forward up to position k + l − 1, and V_i,k − starts at position k + l − l and includes all shape-values backward up to position k. Let D_U = Σ_x≠y≠i Euclidean (W_x,W_y) + Σ._j≠i Euclidean(W_j, U) denote the new value of D if a window U replaces W_i in the current set of windows. We then sample a window U from ψ_i with probability $\raisebox{1ex}{$\text{exp}\left(-D_U\right)$}\!\left/ \!\raisebox{-1ex}{${\sum }_V\text{exp}\left(-D_V\right)$}\right.$ and update W_i with the sampled U. We iterate through the ψ_i’s in the order they appear in ψ, and for each ψ_i, we update the window W_i following the above steps. We continue to repeat this iterative updating until convergence in the value of D. In our implementation, we decide that the value of D has converged if it does not change in two successive iterations, or if the improvement in the value of D is negligible for ten consecutive iterations. We assume that the improvement is negligible when the current and the previous values of D satisfies:

D_prev (1‒ ϵ) < D_current < D_prev, where ϵ =10⁻⁵.

Step 2.

We next compute a pattern $P={\left(\left(m_k,d_k\right)\right)}_{k=1}^l$ from the set W of windows computed above. By way of construction in Step 1, the windows in the set W are already aligned. At each position in these aligned windows, we first compute the mean and the variance of shape-feature values. As noted above, the pattern P is formulated as a range of shape-feature values [m_k − d_k,m_k + d_k] at each position k (1 ≤ k ≤ l). We compute the terms m_k and d_k at position k as the mean and a multiple of the standard deviation of shape-feature values at that position, respectively. More formally, let W_i denote the window selected from ψ_i. We then take $m_k=\text{mean}\left({\left\{W_{i,k}\right\}}_{i=1}^N\right)$ and d_k = α × standard_deviation $\left({\left\{W_{i,k}\right\}}_{i=1}^N\right)$, where α is a constant whose optimum value is computed as follows. We try each value of α in the range [0.1,2], in increments of 0.1, and compute the corresponding pattern P_α from W. We quantify the goodness of each P_α as a discriminator between the positive and control peaks of the training data by its F_1/3-score. Note that the F_1/3-score here is a more conservative objective than used typically in classification settings, yet we wanted to weigh precision much higher than recall so that the number of false positives remains low. We then choose P to be the pattern argmax_α (F_1/3(P_α)).

Step 3.

Motif identification. Using an independent validation set of positive and control peaks, patterns are tested for enrichment in positive peaks, as is done in other discriminative motif finding tools (Bailey 2011), Let $n_P^{+}$ and $n_P^{-}$ denote the number of validation positive and control peaks, respectively, where pattern P has an occurrence. We say that P is a motif of feature F (or a ‘F-motif’) for DBP if a hypergeometric test parameterized by $n_P^{+}+n_P^{-}$, and $n_P^{+}$ yields a significant p-value after Bonferroni correction. We use a Bonferroni corrected p-value threshold of 10⁻⁵. Shape-motifs P that meet this criterion are retained for further analysis, and others are discarded.

It is worth clarifying why we chose a combination of F_1/3-score in step 2 and hypergeometric test in step 3. We note that the first step in our algorithm selects one window from each sequence. However, every sequence may not have an occurrence of a shape-motif; hence the selected pool of windows in the first step may have some outliers. The F_1/3-score is optimized in step 2 to remove such outliers. We could call this F_1/3-score optimized shape pattern a shape-motif, but we also wanted to provide a statistical significance as is commonly done for sequence-motifs. Therefore, we did not call every F_1/3-score optimized shape-pattern a motif, rather we call a pattern a shape-motif only if it is significantly enriched in bound versus unbound regions based on a hypergeometric test with p-value comparable to those of sequence motifs in the literature.

Finding variable-length motifs.

The above steps 1 and 2 compute a motif for a given length l. In our analysis we have considered all values of l between 5 and 30. For computational efficiency, we first compute motifs for values of l that are multiples of 5. For all other values of l, we take the starting positions t_i’s of the motifs computed for length $\lfloor \raisebox{1ex}{$l$}\!\left/ \!\raisebox{-1ex}{$5$}\right.\rfloor$ as our initial guess for starting positions and search for motifs within the positions t_i ‒ l and t_i + l.

Calling redundant motifs.

In a last post-processing step, we eliminate redundant motifs. We first partition all motifs according to their lengths: two motifs of lengths l₁ and l₂ are put in the same partition if $\lfloor \raisebox{1ex}{$l_1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.\rfloor =\lfloor \raisebox{1ex}{$l_2$}\!\left/ \!\raisebox{-1ex}{$5$}\right.\rfloor$. For two motifs P₁ and P₂, if P₁ has lower false positive rate than P₂ on validation data and the occurrences of P₁ “cover” at least 75% of the occurrences of P₂, then we assume that P₂ is redundant and discard P₂. An occurrence of P₁ covers an occurrence of P₂ if the occurrence of Pi overlaps with at least 75% length of the occurrence of P₂. This strategy to remove redundant motifs is akin to the one utilized in (Beer and Tavazoie 2004).

Data Processing

We downloaded uniformly processed ChIP-Seq datasets (narrowPeak format) from the ENCODE Downloads section at UCSC (http://genome.ucsc.edu/ENCODE/downloads.html: “Last Modified” date: 12-Apr-2013) and genome-wide shape-data (bigwig format) from the FTP interface of the GBshape database (http://rohsdb.cmb.usc.edu/GBshape/), We used only the ChIP-Seq datasets with quality=good and treatment=None. We also discarded the histone deacetylase (HDAC) datasets from consideration, since our focus here was on DBPs. We also labeled DBPs as sequence-specific or non-specific, as defined in (Lambert, Jolma et al. 2018), to check if our major findings are different for these two groups of DBPs. From each dataset, we filtered out the ChIP regions that overlap with HOT (high-occupancy target) regions (as determined at significance threshold 0.01 in (Boyle, Araya et al. 2014)).

We used the following strategy to create training and validation data comprising positive and control peaks for each ChIP-Seq dataset. For positive peaks, we took 100 base pair (bp) windows centered at the peak summits. We used the top 2000 positive peaks (ranked by the signalValue field after discarding peaks overlapping HOT regions) or all positive peaks if less than 2000 remain. For negative control peaks, we took an equal sized sample of 100-bp HOT-filtered ChIP-Seq peaks of all other DBPs. We then randomly shuffled the positive peaks and split them into equal halves, and likewise for negative peaks, to obtain our training data (for learning motifs, algorithm steps 1 and 2) and validation data (for assessing statistical enrichment of motifs, algorithm step 3), This training-validation split was not maintained in 4/177 datasets where the total number of positive peaks was less than 1000; in these cases we trained and validated on the same dataset.

Sequence-motifs from shape-motif hits

We took all sequences underlying a shape-motif and repeated the following process ten times, every time starting from a randomly selected seed sequence. We build the initial sequence motif from the seed sequence and taking a pseudo-count of 0.001 for each nucleotide. For each remaining sequence s, we update the sequence motif by including s or the reverse complement of s - whichever gives a motif with higher information content, assuming background GC-content = 41% (Merchant, Prochnik et al. 2007).

We report the highest information content motif out of the ten motifs computed in these ten runs.

Promoter-proximal and distal regions

We followed the strategy of Setty and Leslie (Setty and Leslie 2015) to identify promoter-proximal and -distal regions. From UCSC table browser (https://genome.ucsc.edu/cgi-bin/hgTables), we collected the coordinates (hg19) of RefSeq genes (group=genes and gene predictions, track=refseq genes, table=refgene, region=genome). We then select promoter-proximal regions as the 2-kilobase (kb) regions flanking each gene, and the distal regions as the windows spanning 10-kb to 1-megbase regions flanking each gene.

Similarity score (loll) for shape-motifs

For two given shape-motifs, we slide the shorter motif (and the motif created by considering its values in reverse order) along the longer motif, and at each position, we computed the mean IoU (Intersection over Union, defined below) score between the two motifs starting at that position. We report the maximum of the mean IoU scores computed in this scan and plot the two motifs superimposed at this maximal alignment. The IoU score at a given position is the ratio between: (i) the range of feature values at that position common between the two motifs (i.e., intersection) and (ii) the range of feature values at that position when the two motifs are considered together (i.e., union).

Co-binding regions for a given pair of DBPs

For two DBPs F₁ and F₂, we first identify the peaks S₁ of F₁ that intersects with a peak of F₂, and likewise the peaks S₂ of F₂ that intersects with a peak of F₁. We then merge the genomic regions denoted by S₁ and S₂ to obtain the regions where F₁ and F₂ co-bind. These co-bound peaks are labeled as shape-only or not for F₁ We perform a Binomial test of the null hypothesis that the proportion of shape-only co-bound peaks for F₁ and F₂ is equal to the proportion for F₁ with any other DBP. The resulting p-value is Bonferroni corrected, and F₁ is considered enriched for shape-only co-binding with F₂ if the adjusted p-value < 10⁻⁴.

Calling shape-zingers

A shape-motif P₁ of a DBP F₁ is also a motif for a DBP F₂ if P₁ can discriminate the positive peaks (top 2000 or all if there are less than 2000 positive peaks) of F₂ from control peaks with a Bonferroni-corrected hypergeometric p-value < 10⁻⁵. A DBPFi is a shape-zinger if one or more of its shape-motifs are shape-motifs for at least 30% DBPs with a shape-motif in the same cell-line. We chose the fraction 30% following Hunt and Wasserman (Worsley Hunt and Wasserman 2014) who reported sequence-zingers to be enriched in 30–60% datasets.

Shape-motif analysis for DBP families

We took the classification of DBPs into families according to their DNA-binding domains from TFClass (Wingender, Schoeps et al. 2013), For each DBP in a family, we first selected the sets of peaks that do not overlap with the peaks of any other DBP in the same family. We then used ShapeMF on the remaining sets of peaks to identify the shape motifs of each DBP.

QUANTIFICATION AND STATISTICAL ANALYSIS

Sequence motif analysis

We applied the tool gkm-SVM (Ghandi, Lee et al. 2014) to compute the sequence motifs that could discriminate between the positive and the control peaks in each training dataset. We note that gkm-SVM outputs the scores of all 10-mers as predicted by a support vector machine (svm) trained to discriminate between the positive and the control peaks. Thus, gkm-SVM does not directly provide a description of a DBP’s specificity. To overcome this issue, the gkm-SVM package includes an algorithm that iteratively learns a specified number of sequence motifs from the svm scores. We used this algorithm to learn five motifs for each ChIP-Seq dataset. Note that, in the original work featuring gkm-SVM (Ghandi, Lee et al. 2014), the authors used three motifs to describe specificity of DBPs. By utilizing five motifs, we in fact allowed redundancy and presumably weak (low information content) motifs to be included in our analysis in order to ensure that we have a broad sequence-based definition of DBP binding sites.

As a second source of sequence-motifs, we took all the motifs for each DBP from a recent (2016) release of TRANSFAC (Matys, Fricke et al. 2003), As a final source of sequence-motif hits, we took the genome-wide annotations for occurrences of sequence-motifs curated by Kheradpour and Kellis (Kheradpour and Kellis 2014), In their curated collection, Kheradpour and Kellis used all motifs from available motif libraries and also motifs from several de novo motif finders.

For analyzing HT-SELEX data, we did not learn gkmsvm motifs; instead, we took all the M-words (over-represented k-mers) as reported in (Yang, Orenstein et al. 2017) and all the CIS-BP motifs (Weirauch, Yang et al. 2014) for each DBP. We chose CIS-BP as the additional source since the core-motifs in (Yang, Orenstein et al. 2017) were obtained from CIS-BP motifs. We did not trim any sequence-motif.

We used the tool fimo (Grant, Bailey et al. 2011) to identify all occurrences of the gkmsvm-derived and TRANSFAC motifs in the ChIP-peaks, and the CIS-BP motifs in HT-SELEX sequences. We used the default p-value cutoff of 10⁻⁴ in fimo for calling a motif hit. This is a less stringent threshold than is commonly utilized in the literature (Maurano, Humbert et al. 2012, Thurman, Rynes et al. 2012, Hah, Murakami et al. 2013, Whyte, Orlando et al. 2013).

Enrichment of peaks in genomic categories

For each DBP, we permuted the labels of its peaks (shape-only or sequence-based) and constructed new sets of shape-only and sequence-based peaks by redrawing the same number of peaks as before. We then recomputed the percentages of each type of peaks within each functional category. We repeated this 1000 times and took the quantile of the observed difference in percentages in this permutation distribution as an empirical p-value. All reported significant enrichments have p-value < 1e-3.

ShapeMF analysis of HT-SELEX data

We asked whether final round HT-SELEX sequences have shape-motifs. For computational feasibility, we used random samples of final round sequences, which should still be enriched for bound sequences. From the final round of each HT-SELEX dataset, we took up to 100 random samples where each sample had 2500 unique sequences. To apply ShapeMF, we treated each random sample as a positive set and paired it with a negative set (shape-profiles generated from scrambled sequences of the positive set) of the same size. We also held-out a separate, size-matched validation set of positive and negative sequences. A pattern discovered from the training set is a shape-motif if it discriminates bound from unbound sequences in the validation data with a Bonferroni-corrected hypergeometric p-value < 10⁻⁵. A resulting shape-motif was included in our analysis if it was able to discriminate the positive and negative sets of every other random sample with the same threshold of Bonferroni-corrected p-value < 10⁻⁵. Given that HT-SELEX oligos are typically ~20 bps long, we searched for shape-motifs of length between 5 and 10.

Statistical significance of loll scores

For reporting significance of the IoU score between two shape-motifs M₁and M₂, we computed one million IoU scores for two random motifs generated from M₁and M₂ as follows. First, for each position in M₁ we randomly generate a value within the range of feature values at that position in M₁. This gives us a random motif RM₁. Similarly, we generate a random motif RM₂ from motif M₂. We then compute the IoU score between RM₁ and RM₂. We repeat the process one million times and report the p-value of our observed IoU between M₁ and M₂.

Peak distribution across ChIP-Seq intensity

We followed the example of (Isakova, Groux et al. 2017) to use ChIP signal intensity as a proxy for the affinity of the corresponding DBP for those peaks. For each ChIP-Seq dataset, we partitioned the peaks into deciles according to ChIP signal intensity, and computed the fraction of sequence-only, overlapping, and shape-only peaks within every decile.

Spacing bias between motif pairs

We followed the strategy of Ng et al. (Ng, Schutte et al. 2014) for analysis of biased spacing between a given pair of motifs. For the given motif pairs, we first compute the distances between their non-overlapping neighboring (adjacent) occurrences. We arbitrarily decide one motif as primary and the other as secondary. A distance between the primary-secondary motif pair is positive if the primary-motif occurs upstream of the secondary-motif, zero if they occur at the same location, and it is negative otherwise. We test each distance between −25 to +25 bps, and call a distance to be significant if the binomial Bonferroni-corrected p-value is < 10⁻⁴.

Using flanking non-ChIP regions as background

Motif calling of any type depends on an appropriate background model. Different background models (based on different non-bound sequences) could skew the resulting discovered motifs towards particular properties, like different GC-contents or dinucleotides. In our primary analysis, for every DBP, we had taken ChIP-peaks of other DBPs as our control sequences. This choice was motivated to ensure that our results are not artifacts of the ChIP-Seq assay itself.

Here, we repeated our entire analysis using flanking non-ChIP regions as negative controls, which is also common in the literature. We adopted the specifics of constructing negative controls from Arvey et al. and Setty and Leslie (Arvey, Agius et al. 2012, Setty and Leslie 2015). Following their approach, we took the strongest 2000 peaks and extracted 100 base-pair (bp) windows centered at the peak-summit (i.e., the location of maximum ChIP intensity) as positive peaks. For negative control peaks, we took 100-bp non-peak windows located 100 bp upstream of the positive peaks. Negative control peaks that intersect with positive peaks were discarded along with the corresponding downstream positive peak.

Our results are summarized in Figure S1 and Figure S2. We noted that the GC-contents for all four types of datasets, i.e., positive and negative data in training and validation sets, were highly similar under the two strategies (Figure S1; Pearson correlation coefficients are between 0.96 and 0.98). Also, our results and conclusions remained unchanged under this new background distribution, despite the fact that ChIP peaks do differ in their sequence properties from flanking regions, as shown in Figure S2.

Other highlighting points of our analysis are given below.

1. We found that motifs discovered under the two settings are highly concordant. For a given TF, the IoU based similarity score for its two most concordant shape-motifs Ml and M2 (where Ml is derived using flanking non-ChIP regions as control and M2 is derived using ChIP peaks of other TFs as control) is 0.89 on average (range: 0.41 – 0.98, median: 0.91). Such IoU scores are highly significant (p-values < le-5).

2. The 2 × 2 contingency table also shows high concordance between the two approaches (Chi-squared statistics = 79.3, p-value < 2.2e-16):

   		ChIP-peak as control
   		Found motif	Not found motif
   Flanking non-ChIP regions as control	Found motif	261	50
   	Not found motif	93	108

3. The above table also shows that taking control sequences from ChIP-peaks of other TFs slightly more conservative than taking control sequences from flanking non-ChIP regions (probability of finding a motif = 0.60 vs 0.69).

For the cases where we did not find motifs with both choices of negative controls, we noted that those motifs are the ones with weaker p-values. Our threshold for the negative logarithm of Bonferroni corrected p-value was 5. For the cases where one choice of negative control could find a motif but the other could not, the median of the negative logarithm of Bonferroni corrected p-value was 7.28 (range: 5.02—118.49). This is conceivable since with changes in background sets, the p-values associated with motifs may change and we may lose some motifs that fall just below the (multiple testing corrected) threshold with one background model and fall just above the threshold with the other model.

Affinity of DBPs for different types of sites

It is important to check how the affinities of DNA binding proteins for shape-only sites compare to their affinities for sequence-only and overlapping sites. Unfortunately, we could not find any such assay that quantifies affinity over the entire spectrum of binding sites sequences. Still, we did the following analyses to understand this interesting point.

First, we took the MITOMI data (Maerkl and Quake 2007) that has one TF, MAX, in common with our analyzed dataset. The MITOMI study attempted to quantify the affinity landscape for MAX binding. However, the library covered the canonical MAX binding site (E-box motif, CACGTG) and its minor variants, and ultimately reported the affinity of 256 (= 4⁴) 7-mer sequences where the first four nucleotides were varied to generate the 256 possible combinations and the last three nucleotides were fixed at GTG.

In our analysis, we assumed that the affinity of MAX for a given site (sequence-only, overlapping, or shape-only) could be approximated by the affinity of the highest-affinity 7-mer that appears in the site (or, if the site is smaller than seven bases, then the affinity of the site could be approximated by the highest-affinity 7-mer within which the site appears). For a given site, we therefore assigned it the rank of the highest-affinity 7-mer that appears within the site (or the rank of the highest-affinity 7-mer within which the site appears). However, since the MITOMI dataset is biased toward sequences that strongly match the E-box motifs, we were able to estimate the affinity of only 15% shape-only sites, whereas we could estimate the affinity of 72% sequence-only and 70% overlapping sites.

We found that the sequence-only and overlapping sites are enriched within the highest-affinity bins (Figure S12), For shape-only sites, the ProT sites show enrichment within the highest-affinity bins, while HelT and Roll sites are enriched within medium-affinity bins. MGW sites, on the other hand, span the entire range of affinity. This analysis, albeit on a partially characterized dataset, thus shows that shape-only sites can possess high affinity, and can also occur across a much broader range of affinity that current motif models (PWMs) may not effectively capture. This also agrees with the observation by Maerkl and Quake that MAX possibly has a “rugged” affinity landscape, i.e., MAX may have high affinity for sequences much different from the canonical site.

In a second analysis, we followed the SMiLE-Seq paper’s approach (Isakova, Groux et al. 2017) and binned ChIP-Seq peaks into deciles of ChIP intensity. For each decile, we then plotted the fraction of peaks that are sequence-only, co-occurrence, and shape-only (Figure S6 and Figure S7), This gave us a means to estimate the probability that a peak, given its affinity bin, belongs to one of the three classes.

For 47/128 datasets, at least 10% peaks in the highest affinity bin are shape-only. For 18 datasets, at least 25% peaks in the highest affinity bin are shape-only. These observations suggest that shape-only sites may have affinity comparable to those of highest affinity sequence-only and overlapping sites.

There is also a trend in Figure S6 and Figure S7 that the fraction of shape-only peaks increases as we consider weaker affinity bins. However, we cannot conclude that weaker affinity binding is generally mediated by shape-specific binding since for any given affinity bin, the largest fraction of peaks are generally the co-occurrence peaks (where sequence and shape sites co-occur), as shown in Table S4.

Overall, the above two analyses suggested two important points. First, shape-only binding may occur even at the highest affinity sites (or bins) and does not necessarily imply weaker-affinity binding. Secondly, joint modeling of shape and sequence is necessary to capture the entire affinity landscape for DBPs.

DATA AND SOFTWARE AVAILABILITY

We downloaded uniformly processed ChIP-Seq datasets (narrowPeak format) from the ENCODE Downloads section at UCSC (http://genome.ucsc.edu/ENCODE/downloads.html; “Last Modified” date: 12-Apr-2013) and genome-wide shape-data (bigwig format) from the FTP interface of the GBshape database (http://rohsdb.cmb.usc.edu/GBshape/).

We used bwtool (Pohl and Beato 2014) to extract shape profiles of the positive and control peaks from the bigwig files.

The HT-SELEX datasets were downloaded from https://www.ebi.ac.uk/ena; study identifiers: PRJEB14744 (this study did not have CTCF data) and PRJEB3289 (for CTCF). M-words were taken from (Yang, Orenstein et al. 2017).

For DBP-DBP interaction, we used the version 3.4.153 (most recent as of October 2017) of protein interaction data from BioGRID (Stark, Breitkreutz et al. 2006).

The ShapeMF tool is available at: https://github.com/h-samee/shape-motif

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and Algorithms
ShapeMF	https://github.com/h-samee/shape-motif	N/A
bwtool	https://github.com/CRG-Barcelona/bwtool/wiki	N/A
Original source of public datasets
GBShape	http://rohsdb.cmb.usc.edu/GBshape/	N/A
ENCODE	http://genome.ucsc.edu/ENCODE/downloads.html	N/A
HT-SELEX	https://www.ebi.ac.uk/ena	PRJEB14744, PRJEB3289
BioGRID	https://thebiogrid.org/	N/A
MITOMI data	http://lbnc.epfl.ch/data.html	N/A

Highlights.

1. The ShapeMF algorithm works on DNA shape data, extending de novo motif discovery

2. ShapeMF identifies shape-motifs enriched in regions bound by transcription factors

3. Many transcription factors have shape-motifs in both in vivo and in vitro data

4. Shape-motifs may encode specificity that goes beyond the sequence-motifs of a TF