Significance
The ordering of chemical units within DNA, RNA, and proteins carries information about how living cells operate, and copying these sequences accurately is vital. We have a limited understanding of the fundamental physical underpinnings of these processes, since important mechanistic constraints due to the need to separate daughter sequences from their templates have never been investigated in detail. By considering the simplest models that incorporate these constraints, we highlight their profound consequences in terms of the effort that must be expended to make accurate copies. These insights will help us to understand not only life today but also how early replicators may have functioned in the past, and how we might develop synthetic copiers in the future.
Keywords: biophysics, stochastic processes, thermodynamics, information transmission
Abstract
Living systems produce “persistent” copies of information-carrying polymers, in which template and copy sequences remain correlated after physically decoupling. We identify a general measure of the thermodynamic efficiency with which these nonequilibrium states are created and analyze the accuracy and efficiency of a family of dynamical models that produce persistent copies. For the weakest chemical driving, when polymer growth occurs in equilibrium, both the copy accuracy and, more surprisingly, the efficiency vanish. At higher driving strengths, accuracy and efficiency both increase, with efficiency showing one or more peaks at moderate driving. Correlations generated within the copy sequence, as well as between template and copy, store additional free energy in the copied polymer and limit the single-site accuracy for a given chemical work input. Our results provide insight into the design of natural self-replicating systems and can aid the design of synthetic replicators.
The copying of information from a template into a substrate is fundamental to life. The most powerful copying mechanisms are persistent, autonomous, and generic. A persistent copy retains the copied data after physically decoupling from its template (1, 2). An autonomous copy process does not require systematically time-varying external conditions (2), making it more versatile. Finally, a generic copy process is able to copy arbitrary data. DNA replication and both steps of gene expression necessarily exhibit all three characteristics.
Unlike natural systems, synthetic polymer copying mechanisms developed hitherto have not incorporated all three features. Early work focused on using template polymers to synthesize specific daughter polymers, but failed to adequately demonstrate subsequent separation of copy and template (3, 4). We describe such a process as templated self-assembly (TSA), by analogy with molecular systems that assemble into a well-defined structure determined by highly specific interactions that are retained in the final state.
Due to cooperativity, the tendency of such copies to remain bound to templates grows with template length (5–7). Consequently, generic copying of long polymers [as opposed to dimers and trimers (5, 8, 9)] has proved challenging. One tactic is to consider environments in which the system experiences cyclically varying conditions, with assembly of the copy favored in one set of conditions and detachment from the template favored in another (10–12). A more subtle approach is to use a spatially nonuniform environment, so that individual molecules undergo cyclic variation in conditions (13). While these experiments may indeed reflect early life (14, 15), they do not demonstrate copying in a truly autonomous context.
We also contrast the copying of a generic polymer sequence with the approach in refs. 7 and 16. Here, the information is propagated between successive units of a single self-assembling polymer, rather than between a template and a daughter polymer, limiting information transmission. Externally induced mechanical stress on long length scales severs the polymers, leading to exponential growth of the number of polymers.
These challenges suggest that a full understanding of the basic biophysics of copying is lacking. Recently, we outlined fundamental thermodynamic constraints imposed by persistence (1), but did not propose a dynamical mechanism for autonomous copying. Previous dynamical models fall into two major categories: those that remain agnostic about the distinction between TSA and copying by considering thermodynamically self-consistent models for only part of the polymerization process (17) and those that explicitly address TSA (18–25).
In this work, we analyze a family of model systems that generate persistent copies in an autonomous and generic way. We introduce a metric for the thermodynamic efficiency of copying, and investigate the accuracy and efficiency of our models. We highlight the profound consequences of requiring persistence, namely, that correlations between copy and template can only be generated by pushing the system out of equilibrium. Previous work has considered self-assembly (26–28) or TSA (18–25, 28) in nonequilibrium contexts; in these cases, however, the nonequilibrium driving merely modulates a nonzero equilibrium specificity. Alongside the effect on copy–template interactions, we find that intra–copy-sequence correlations arise naturally. These correlations store additional free energy in the copied polymer, which does not contribute toward the accuracy of copying.
Models and Methods
Model Definition.
We consider a copy polymer , made up of a series of subunits or monomers , growing with respect to a template (). Inspired by transcription and translation, we consider a copy that detaches from the template as it grows; Fig. 1B shows the simplest model of this type. We consider whole steps in which a single monomer is added or removed, encompassing many individual chemical substeps (21, 24). After each step, there is only a single interpolymer bond at position , between and . As a new monomer joins the copy at position , the bond position is broken, contrasting with previous models of TSA (20–25) (Fig. 1A). Importantly, as explained in the next paragraphs of this section, each step therefore depends on both of the two leading monomers, generating extra correlations within the copy sequence.
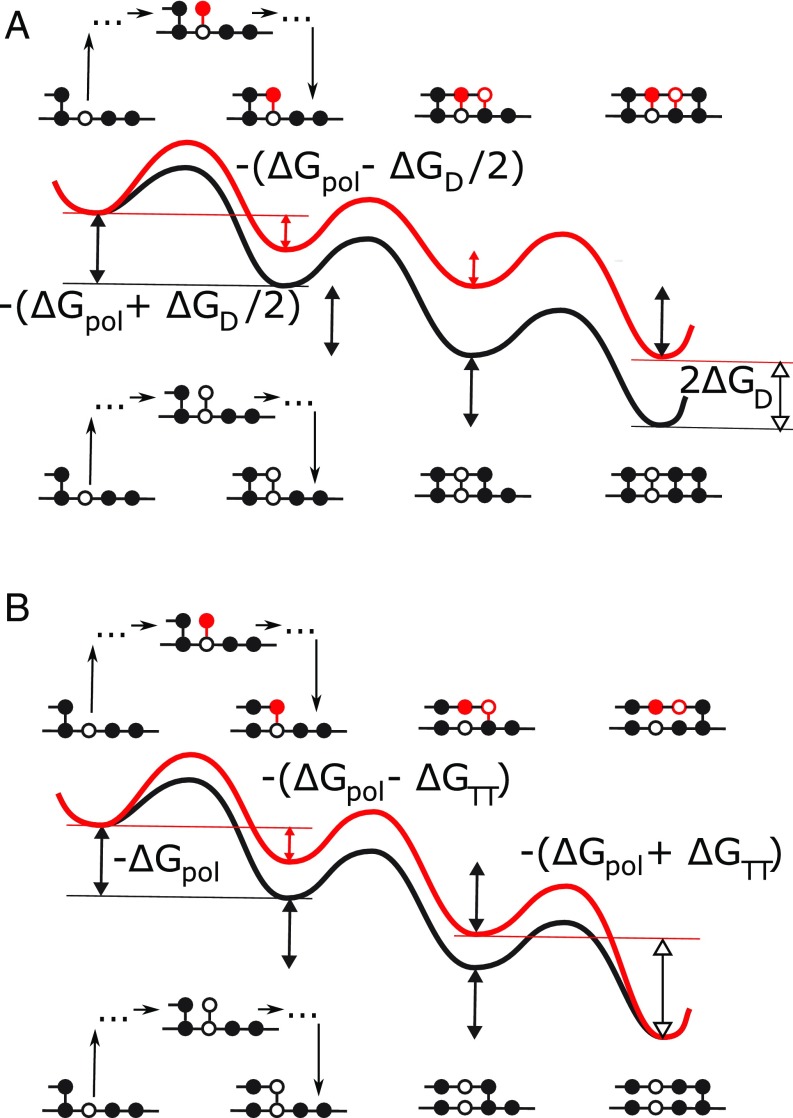
Fig. 1.
Free-energy landscapes for simple examples of (A) TSA, in which the monomers remain bound to the template during the copy process and (B) persistent copying, in which the monomers detach from the template after they have been incorporated into the polymer. Both diagrams show the addition of three monomers to a growing polymer, driven by a chemical free energy of backbone polymerization . In each subfigure, two scenarios are considered: the addition of two incorrect monomers, followed by a correct one (Top), and the addition of three correct monomers (Bottom). Local minima in the landscape represent macrostates following complete incorporation of monomers; intermediate configurations, illustrated schematically for the first transition, are part of the effective barriers. In TSA, the chemical free-energy cost of previously incorporated mismatches is retained as the daughter grows (20–25). Thus, in A, each mismatch in the daughter increases the chemical free energy by relative to the perfect match. In persistent copying (in B), the chemical free-energy penalty for incorporating wrong monomers is only temporary; it arises when the incorrect monomer is added to the growing polymer, but is lost when that monomer subsequently detaches from the template. As a result, the overall chemical free-energy change of creating an incorrect polymer is the same as that for a correct one. Analyzing the consequences of this constraint, which is a generic feature of copying but does not arise in TSA, is the essence of this work. The figure also shows that, in our specific model, incorporating a wrong monomer after a correct one tends to reduce the chemical free-energy drop to , and incorporating a correct monomer after an incorrect one tends to increase it to ; however, adding a wrong monomer to a wrong one, and adding a correct monomer to a correct one, does not change the free-energy drop .
Following earlier work, we assume that both polymers are copolymers, and that the two monomer types are symmetric (20–25). Thus, the relevant question is whether monomers and match; we ignore the specific sequence of and describe simply as right or wrong. Thus, , with example chain . An excess of indicates a correlation between template and copy sequences. Breaking this symmetry would favor specific template sequences over others, disfavoring the accurate copying of other templates and compromising the generality of the process.
Given the model’s state space, we now consider state free energies (which must be time-invariant for autonomy). We treat the environment as a bath of monomers at constant chemical potential (20–25). By symmetry, extending the polymer while leaving the copy–template interaction unchanged involves a fixed polymerization free energy. We thus define as the chemical free-energy change for the transition between any specific sequence and any specific sequence , ignoring any contribution from interactions with the template. We then define as the effect of the free-energy difference between and interactions with template. This bias can be describes as “temporary thermodynamic” (TT), since it only lasts until that contact is broken.
Overall, each forward step makes and breaks one copy–template bond. There are four possibilities: either adding or at position to a template with or adding or in position to a template with . The first and last of these options make and break the same kind of template bond, so the total free-energy change is . For the second case, there is a bond broken and a bond added, implying a free-energy change of . Conversely, for the third case, there is a bond broken and a bond added, giving a free-energy change of . These constraints are highlighted in Fig. 1B; the contribution of this work is to study the consequences of these constraints. Models of TSA (Fig. 1A) of equivalent complexity can be constructed, but they are not bound by these constraints, and hence the underlying results and biophysical interpretation are distinct.
Having specified model thermodynamics, we now parameterize kinetics. We assume that there are no “futile cycles,” such as appear in kinetic proofreading (17). Reactions are thus tightly coupled: Each step requires a well-defined input of free energy determined by and (29), and no free-energy release occurs without a step.
A full kinetic treatment would be a continuous time Markov process incorporating the intermediate states shown schematically in Fig. 1B. To identify sequence output, however, we need only consider the state space in Fig. 1B and the relative probabilities for transitions between these explicitly modeled states, ignoring the complexity of nonexponential transition waiting times (21). We define propensity as the rate per unit time in which a system in state starts the process of becoming and, propensity as the equivalent quantity in the reverse direction ( is an unspecified polymer sequence). Our system has eight of these propensities (, , , and ); the simplest TSA models require four (20, 21, 23–25).
Prior literature on TSA (23) has differentiated between purely “kinetic” discrimination, in which and have an equal template-binding free energy but different binding rates, and purely thermodynamic discrimination in which and bind at the same rate, but is stabilized in equilibrium by stronger binding interactions. Eventually, all discrimination is kinetic for persistent copying, since there is no lasting equilibrium bias (Fig. 1B). However, by analogy with TSA, we do consider two distinct mechanisms for discrimination: a kinetic one, in which is added faster than to the growing tip, and one based on the TT bias toward correct matches at the tip of the growing polymer due to short-lived favorable interactions with the template, quantified by (Fig. 1B). The kinetic mechanism should not be conflated with fuel-consuming “kinetic proofreading” cycles that are not considered.
We parameterize the propensities as follows. Assuming, for simplicity, that the propensity for adding or is independent of the previous monomer, we have and , also defining the overall timescale. Kinetic discrimination is then quantified by . Forward propensities are thus differentiated solely by ; backward propensities are set by fixing the ratios according to the free-energy change of the reaction, which follows from and (Fig. 1B). Thus, setting ,
| [1] |
| [2] |
| [3] |
| [4] |
For a given , , and , Eqs. 1–4 describe a set of models with distinct intermediate states that yield the same copy sequence distribution. We can thus analyze the simplest model in each set, which is Markovian at the level of the explicitly modeled states, and has as rate constants.
Model Analysis.
We use Gaspard’s method to solve the system (28); we note that the underlying kinetic equations can also be mapped to models of distinct physical systems that have different constraints on the parameters (26). In this approach, the tip monomer identity probabilities , the joint tip and penultimate monomer identity probabilities , and the conditional probabilities become stationary for a long polymer and can be calculated. One must first calculate the partial velocities, and . The quantity is the net rate at which monomers are added after an ,
| [5] |
Following ref. 28, these velocities can be solved in terms of the propensities. In turn, the velocities and propensities determine tip and conditional probabilities and (28). Further details are provided in SI Appendix.
Gaspard’s method describes the chain while it is still growing through the stochastic variables and , with the index being the current length of the polymer. We, however, are interested in the identity of the monomer at position when . We label this “final” state of the monomer at position as . As discussed in SI Appendix, is distinct from near the tip. is described by the error probability and the conditional error probabilities and , defined as the probability that given that or , respectively. In SI Appendix, we show that , and are sufficient to describe the final state, by proving that the is a Markov chain of and monomers (this requirement is distinct from the Markovian growth dynamics). We note that as a direct result of the dependence of the transition propensities on the current and previous tip monomers, which in turn arises from detachment.
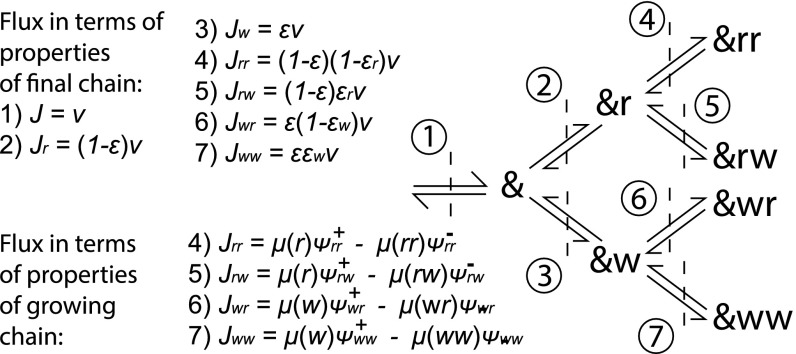
To calculate , , and , we define currents that are related to , and to , , and , separately. The current is the net rate per unit time at which transitions occur: . By considering the transitions in our system as a tree, as in Fig. 2, we can relate the current through a branch to the overall rate at which errors are permanently incorporated into a polymer growing at total velocity ,
| [6] |
| [7] |
| [8] |
| [9] |
Eliminating from the simultaneous Eqs. 6–9 yields and in terms of known quantities. To find , note that the final sequence itself is a Markov chain with a transition matrix parameterized by and , with the overall error given by its dominant eigenvector. As detailed in SI Appendix, we obtain . From , , and , we calculate copy properties in terms of and thus the free energies. We corroborate the results with simulation (see SI Appendix).
Fig. 2.
Transitions of an arbitrary polymer . To relate the final chain to the growing chain, it is useful to consider fluxes through interfaces in this transition diagram. Using the tip and combined probabilities, along with relative propensities, it is possible to describe the fluxes through interfaces 4 to 7 in terms of properties of the growing chain. Equally, by considering errors and conditional errors and taking fractions of the overall growth velocity, it is possible to find the fluxes through interfaces 4 to 7 in terms of properties of the final chain and growth velocity.
Results
General Thermodynamic Bounds.
The free energy of the combined bath and polymer system decreases over time. There are two contributions to the free-energy change per added monomer: the chemical free energy and a contribution from the uncertainty of the final polymer sequence (1). The latter is quantified by the entropy rate (30, 31),
| [10] |
which, in our case, is given by (31)
| [11] |
The overall free-energy change per added monomer is then , which must be negative for growth: . Since copy–template interactions are not extensive in the copy length, they do not contribute. Given that , growth is possible in the region where , corresponding to the “entropically driven” regime (20, 25).
The entropy rate is bounded by the single-site entropy . quantifies the desired correlations between copy and template. For previous models of TSA with uncorrelated monomer incorporation, (20–25, 28). In our model, the necessary complexity of generates correlations within the copy, as well as between copy and template. A stronger constraint on the single site entropy, and hence accuracy, then follows: .
Fundamentally, a persistent copy is a high free-energy state, as the entropic cost of copy–template correlations cannot be counteracted by stabilizing copy–template interactions. Thus, the process moves a system between two high free-energy states, converting chemical work into correlations. In general, only a fraction of the chemical work done by the monomer bath is retained in the final state, implying dissipation, and so it is natural to introduce an efficiency. The overall free energy stored in the polymer has contributions both from the creation of an equilibrium (uncorrelated) polymer and from correlations within the copy and with the template. We are interested only in the contributions above equilibrium. The efficiency is then the proportion of the additional free energy expended in making a copy above the minimum required to grow a random equilibrium polymer that is successfully converted into the nonequilibrium free energy of the copy sequence rather than being dissipated. In our simple case,
| [12] |
Here, is the extra chemical work done by the buffer above that required to grow an equilibrium polymer, . The free energy stored in the copy sequence, above that stored in an equilibrium system, is ; follows from . Similarly, since , we can define a single-site efficiency,
| [13] |
Unlike , the single-site efficiency discounts the free energy stored in “useless” correlations within the copy.
Behavior of Specific Systems.
We consider three representative models consistent with Eqs. 1–4. First, we consider the purely kinetic mechanism obtained by setting and in Eqs. 1–4. Originally proposed by Bennett (20) for TSA, it is coincidentally a limiting case of persistent copying, since there is no equilibrium bias. We also consider two other mechanisms: pure “TT discrimination,” with and , and a “combined discrimination mechanism,” in which both template binding strengths and rates of addition favor monomers: .
All three mechanisms have two free parameters, the overall driving strength and the discrimination parameter . We plot error probability against for various in Fig. 3. Also shown is the thermodynamic lower bound on implied by . All three cases have no accuracy () in equilibrium (), since an accurate persistent copy is necessarily out of equilibrium (1). By contrast, TSA allows for accuracy in equilibrium (19, 23, 24).
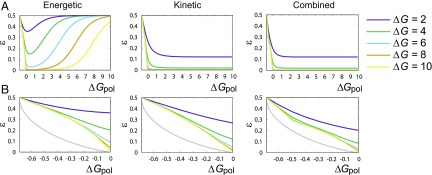
Fig. 3.
Error probability as a function of for all three mechanisms: (A) over a wide range of and (B) within the entropy-driven region . The TT mechanism is always the least accurate, and the combined mechanism is the most accurate. All mechanisms have no accuracy in the limit of , and are far from the fundamental bound on single-site accuracy imposed by , except at .
The TT mechanism is always the least effective. It has no accuracy for high , as the difference between and is only manifest when stepping backward, and, for high , back steps are rare (23, 24). More interestingly, TT discrimination is also inaccurate as , when the system takes so many back steps that it fully equilibrates. Low only occurs when is sufficient to inhibit the detachment of monomers, but not the detachment of monomers. This trade-off region grows with . By contrast, both the combined case and the kinetic case have accuracy in the limit of , since they allow to bind faster than . Considering closely (Fig. 3B) shows the combined case to be superior.
Intriguingly, all three mechanisms are far from the fundamental bound on implied by as , and there is an apparent cusp in at as in the combined case. The performance relative to the bound is quantified by (Fig. 4). Surprisingly, we observe, in Fig. 4A, that not only does go to zero as , but so does in all cases. For small nonequilibrium driving, none of the extra chemical work input is stored in correlations with the template. Mathematically, this inefficiency arises because as (as observed in Fig. 3), and for , by definition. Thus, from Eq. 13, as . That this result only depends on error probability decreasing proportionally with for small driving suggests that a vanishing in equilibrium may be quite general.
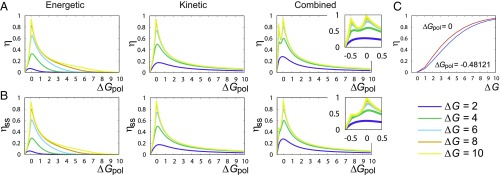
Fig. 4.
Efficiencies (A) and (B) plotted against show sharp peaks at as in all three cases. In the combined case, we see a second peak in , and a shoulder in at . (C) Both of these peaks in tend to unity at .
In all cases, the single-site efficiency increases from 0 at to a peak near , with as . Beyond this peak, drops as the stored free energy is bounded by per monomer. To understand the peak, note that, for every , there is a hypothetical highest accuracy copy with fixed by that is marginally thermodynamically permitted. However, this copy is not usually kinetically accessible. At , the marginal copy has 100% accuracy, and, unusually, all three mechanisms can approach it kinetically, causing a peak. The efficiency approaches its limit of unity even for moderate values of . We note that, as , growth is slow for : The total number of steps taken diverges.
A related argument explains the apparent cusp in the error for the combined mechanism at and high . On the plot of (Fig. 4 A), this cusp manifests as a shoulder. The full efficiency (Fig. 4 B) has a prominent second peak. Uniquely, the combined mechanism’s kinetics strongly disfavor chains of consecutive s for high . A final copy with no consecutive s has but . Maximizing the entropy rate of such a Markov chain over gives ; matches the location of our peak/cusp. Thus, the combined mechanism initially eliminates consecutive s, and, at , a state with is thermodynamically permitted for the first time. For large , this polymer is kinetically accessible and grows with thermodynamic efficiency approaching unity (Fig. 4 C). In this limit, the overall entropy generation is zero.
The above behavior is a striking example of correlations being generated within the copy sequence, as well as with the template. Notably, while approaches unity at this point, does not (Fig. 4). Correlations within the copy sequence limit the chemical work that can be devoted to improving the single-site accuracy of the copy polymer, since they prevent the bound from being saturated.
Conclusion
The thermodynamic constraint on copying that underlies this work is deceptively simple: Unlike TSA, the overall chemical contribution to the free energy of a copy must be independent of the match between template and copy sequences. By studying the simplest mechanisms satisfying this constraint, however, we can draw important conclusions for copying mechanisms and thermodynamics more generally.
For copying, the most immediate contrast with previous work on TSA (20–25, 28) is that accuracy is necessarily zero when the copy assembles in equilibrium, since equilibrium correlations between physically separated polymers are impossible (1). Consequently, unlike self-assembly, no autonomous copying system can rely on relaxation to near-equilibrium; fundamentally different paradigms are required.
A direct result of the temporary nature of thermodynamic discrimination in persistent copying is that relying solely on the strong binding of correct copies is ineffective in ensuring accuracy. At , comparable to the cost of a mismatched base pair (32), the TT discrimination model never improves upon , which is more than 10 times the equilibrium error probability based on energetic discrimination obtainable in TSA, . This performance would degrade further if many competing monomers were present. Mechanisms for copying must therefore be more carefully optimized than those for TSA. Either some degree of direct kinetic discrimination (with correct monomers incorporated more quickly), or, as an alternative, fuel-consuming proofreading cycles, appear necessary. It is well established that proofreading cycles can enhance discrimination above equilibrium in TSA (18, 20, 24), and the challenges in achieving direct kinetic discrimination in diffusion-influenced reactions via the details of the microscopic substeps may explain the ubiquity of such cycles in true copying systems.
Correlations within the copy, as well as between copy and template, arise naturally in persistent mechanisms. Indeed, in one case, pairs of mistakes are eliminated well before individual mistakes. These correlations contribute to the nonequilibrium free energy of the final state, reducing the single-site copy accuracy achievable for a given chemical work input. Biologically, however, it is arguably the accuracy of whole sequences, rather than individual monomers, that matters. In this case, positive correlations could advantageously increase the number of 100% correct copies for a given average error rate. It remains to be seen whether positive correlations, which may arise in real systems (33), can feasibly be used in this way. Regardless, we predict that within-copy correlations may be significant, particularly in simple systems with low accuracy. These correlations may change significantly if the requirement to remain bound exactly one bond, and exploiting correlations to extend functionality beyond simple copying is an intriguing prospect.
Relaxing this requirement also raises the possibility of early copy detachment. This risk is likely to be worse for genome replication than for transcription and translation, which may explain why the latter proceed by mechanisms analogous to our model, while DNA replication does not: Here, the copy of a single DNA strand from the double helix is first completely assembled on the template, and separated only much later at the next round of cell division.
Thermodynamically, a persistent copying mechanism converts the high free energy of the input molecules into a high free-energy copy state; we have defined a general efficiency of this free-energy transduction for copying. In typical physical systems with tight coupling of reactions, high efficiency occurs when the load is closely matched to the driving, either in autonomous systems operating near the stall force or in quasistatically manipulated systems. For the polymer copying mechanisms studied here, however, we find that the thermodynamic efficiency of information transfer, and not just the accuracy, approaches zero as polymer growth stalls. We predict that this result is general, since the alternative would require a sublinear convergence of the error rate on 50% as thermodynamic driving tends toward the stall point.
Fundamentally, the copy process transduces free energy into a complex system with many degrees of freedom (the sequence), and not just the polymer length. To be accurate, the sequence must be prevented from equilibrating. Thus, while weak driving leads to polymer growth with little overall entropy generation, it does a poor job of pushing the polymer sequence out of equilibrium. We predict that similar behavior will arise whenever an output must have a subset of its degrees of freedom out of equilibrium.
Away from the equilibrium limit, the efficiency shows one or more peaks as the polymerization free energy is varied. At these peaks, the system transitions between two nonequilibrium states with remarkably little dissipation. These particular values of are sufficient to stabilize nonequilibrium distributions that happen to be especially kinetically accessible, rendering the true equilibrium particularly inaccessible. This alignment of kinetic and thermodynamic factors is most evident in the combined mechanism that efficiently produces a state with few adjacent mismatches at . These results slightly qualify the prediction of ref. 1 that accurate copying is necessarily entropy-generating, since entropy generation can be made arbitrarily small, while retaining finite copy accuracy, by taking at these specific values of .
The behavior of the efficiency in these models emphasizes the importance, in both natural and synthetic copying systems, of kinetically preventing equilibration. Our work emphasizes that this paradigm should be applied not only to highly evolved systems with kinetic proofreading mechanisms (17) but also the most basic mechanisms imaginable.
Extending our analysis to consider fuel-consuming proofreading cycles would be natural. However, these cycles will not change the fundamental result that the entropy of the copy sequence is thermodynamically constrained, in this case by , where the final term is the additional free energy expended per step to drive the system around proofreading cycles. We predict that nonequilibrium proofreading cycles, by their very nature, are unlikely to approach efficiencies of unity.
Supplementary Material
Acknowledgments
We thank Charles Bennett for instructive conversations. T.E.O. is supported by the Royal Society, and P.R.t.W. is supported by the Netherlands Organization for Scientific Research.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission. D.J.S. is a guest editor invited by the Editorial Board.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1808775116/-/DCSupplemental.
References
- 1.Ouldrige TE, ten Wolde PR. Fundamental costs in the production and destruction of persistent polymer copies. Phys Rev Lett. 2017;118:158103. doi: 10.1103/PhysRevLett.118.158103. [DOI] [PubMed] [Google Scholar]
- 2.Ouldridge TE, Govern CC, ten Wolde PR. Thermodynamics of computational copying in biochemical systems. Phys Rev X. 2017;7:021004. [Google Scholar]
- 3.Tjivikua T, Ballester P, Rebek J., Jr Self-replicating system. J Am Phys Soc. 1990;112:1249–1250. [Google Scholar]
- 4.Feng Q, Park TK, Rebek J. Crossover reactions between synthetic replicators yield active and inactive recombinants. Science. 1992;256:1179–1180. doi: 10.1126/science.256.5060.1179. [DOI] [PubMed] [Google Scholar]
- 5.Vidonne A, Douglas P. Making molecules make themselves–The chemistry of artificial replicators. Eur J Org Chem. 2009;2009:593–610. [Google Scholar]
- 6.Orgel LE. Molecular replication. Nature. 1992;358:203–209. doi: 10.1038/358203a0. [DOI] [PubMed] [Google Scholar]
- 7.Colomb-Delsuc M, Mattia E, Sadownik JW, Otto S. Exponential self-replication enabled through a fibre elongation/breakage mechanism. Nat Commun. 2015;6:7427. doi: 10.1038/ncomms8427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sievers D, Von Kiedrowski G. Self-replication of complementary nucleotide-based oligomers. Nature. 1994;369:221–224. doi: 10.1038/369221a0. [DOI] [PubMed] [Google Scholar]
- 9.Lincoln TA, Joyce GF. Self-sustained replication of an RNA enzyme. Science. 2009;323:1229–1232. doi: 10.1126/science.1167856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wu N, Willner I. ph-stimulated reconfiguration and structural isomerization of origami dimer and trimer systems. Nano Lett. 2016;16:6650–6655. doi: 10.1021/acs.nanolett.6b03418. [DOI] [PubMed] [Google Scholar]
- 11.Wang T, et al. Self-replication of information-bearing nanoscale patterns. Nature. 2011;478:225–228. doi: 10.1038/nature10500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Li T, Nicolaou KC. Chemical self-replication of palindromic duplex DNA. Nature. 1994;369:218–221. doi: 10.1038/369218a0. [DOI] [PubMed] [Google Scholar]
- 13.Mast CB, Braun D. Thermal trap for DNA replication. Phys Rev Lett. 2010;104:188102. doi: 10.1103/PhysRevLett.104.188102. [DOI] [PubMed] [Google Scholar]
- 14.Orgel LE. The origin of life—A review of facts and speculations. Trends Biochem Sci. 1998;23:491–495. doi: 10.1016/s0968-0004(98)01300-0. [DOI] [PubMed] [Google Scholar]
- 15.Martin W, Baross J, Kelley D, Russell MJ. Hydrothermal vents and the origin of life. Nat Rev Microbiol. 2008;6:805–814. doi: 10.1038/nrmicro1991. [DOI] [PubMed] [Google Scholar]
- 16.Schulman R, Bernard Y, Winfree E. Robust self-replication of combinatorial information via crystal growth and scission. Proc Natl Acad Sci USA. 2012;109:6405–6410. doi: 10.1073/pnas.1117813109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hopfield JJ. Kinetic proofreading: A new mechanism for reducing errors in biosynthetic processes requiring high specificity. Proc Natl Acad Sci USA. 1974;71:4135–4139. doi: 10.1073/pnas.71.10.4135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ehrenberg M, Blomberg C. Thermodynamic constraints on kinetic proofreading in biosynthetic pathways. Biophys J. 1980;31:333–358. doi: 10.1016/S0006-3495(80)85063-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Johansson M, Lovmar M, Ehrenberg M. Rate and accuracy of bacterial protein synthesis revisited. Curr Opin Microbiol. 2008;11:141–147. doi: 10.1016/j.mib.2008.02.015. [DOI] [PubMed] [Google Scholar]
- 20.Bennett CH. Dissipation-error tradeoff in proofreading. Biosystems. 1979;11:85–91. doi: 10.1016/0303-2647(79)90003-0. [DOI] [PubMed] [Google Scholar]
- 21.Cady F, Qian H. Open-system thermodynamic analysis of DNA polymerase fidelity. Phys Biol. 2009;6:036011. doi: 10.1088/1478-3975/6/3/036011. [DOI] [PubMed] [Google Scholar]
- 22.Andrieux D, Gaspard P. Nonequilibrium generation of information in copolymerization processes. Proc Natl Acad Sci USA. 2008;105:9516–9521. doi: 10.1073/pnas.0802049105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Sartori P, Pigolotti S. Kinetic versus energetic discrimination in biological copying. Phys Rev Lett. 2013;110:188101. doi: 10.1103/PhysRevLett.110.188101. [DOI] [PubMed] [Google Scholar]
- 24.Sartori P, Pigolotti S. Thermodynamics of error correction. Phys Rev X. 2015;5:041039. [Google Scholar]
- 25.Esposito M, Lindenberg K, Van den Broeck C. Extracting chemical energy by growing disorder: Efficiency at maximum power. J Stat Mech Theory Exp. 2010;2010:P01008. [Google Scholar]
- 26.Whitelam S, Schulman R, Hedges L. Self-assembly of multicomponent structures in and out of equilibrium. Phys Rev Lett. Dec 2012;109:265506. doi: 10.1103/PhysRevLett.109.265506. [DOI] [PubMed] [Google Scholar]
- 27.Nguyen M, Vaikuntanathan S. Design principles for nonequilibrium self-assembly. Proc Nat Acad Sci. 2016;113:14231–14236. doi: 10.1073/pnas.1609983113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Gaspard P, Andrieux D. Kinetics and thermodynamics of first-order Markov chain copolymerization. J Chem Phys. 2014;141:044908. doi: 10.1063/1.4890821. [DOI] [PubMed] [Google Scholar]
- 29.Wachtel A, Rao R, Esposito M. Thermodynamically consistent coarse graining of biocatalysts beyond Michaelis–Menten. New J Phys. 2018;20:042002. [Google Scholar]
- 30.Boyd AB, Mandal D, Crutchfield JP. Identifying functional thermodynamics in autonomous Maxwellian ratchets. New J Phys. 2016;18:023049. [Google Scholar]
- 31.Cover TM, Thomas JA. Elements of Information Theory. John Wiley; New York: 2012. [Google Scholar]
- 32.SantaLucia J, Jr, Hicks D. The thermodynamics of DNA structural motifs. Annu Rev Biophys Biomol Struct. 2004;33:415–440. doi: 10.1146/annurev.biophys.32.110601.141800. [DOI] [PubMed] [Google Scholar]
- 33.Rao R, Peliti L. Thermodynamics of accuracy in kinetic proofreading: Dissipation and efficiency trade-offs. J Stat Mech Theor Exp. 2015;2015:P06001. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.