Theoretical Study on Gold-Nanorod-Enhanced Near-Infrared Neural Stimulation

Abstract

Over the past decade, optical methods have emerged for modulating brain functions as an alternative to electrical stimulation. Among various optical techniques, infrared neural stimulation has been effective via a thermal mechanism enabling focused and noninvasive stimulation without any genetic manipulation, but it results in bulk heating of neural tissue. Recently, it has been shown that neural cells can be activated more efficiently by pulsed near-infrared (NIR) light delivered to gold nanorods (GNRs) near the neural cells. Despite its potential, however, the biophysical mechanism underlying this GNR-enhanced NIR stimulation has not been clearly explained yet. Here, we propose an integrative and quantitative model to elucidate the mechanism by modeling heat generated from interaction between NIR light and GNRs, the temperature-dependent ion channels (transient receptor potential vanilloid 1; TRPV1) in the neuronal membrane, and a heat-induced capacitive current through the membrane. Our results show that NIR pulses induce abrupt temperature elevation near the neuronal membrane and lead to both the TRPV1-channel and capacitive currents. Both current sources synergistically increase the membrane potential and elicit an action potential, and which mechanism is dominant depends on conditions such as the laser pulse duration and TRPV1 channel density. Although the TRPV1 mechanism dominates in most cases we tested, the capacitive current makes a larger contribution when a very short laser pulse is illuminated on neural cells with relatively low TRPV1 channel densities.

Introduction

Optical techniques to modulate the activity of nervous systems have gained increasing attention in neuroscience researches and clinical fields (1, 2, 3, 4, 5, 6). Compared to traditional electrical means, the optical approaches are relatively free from invasiveness-oriented issues and spatial dispersion of the electric current. Among the optical methods, infrared neural stimulation (INS) employs transient and localized heating mechanisms without any genetic manipulation (3, 6). Recently, combination of INS with plasmonic gold nanoparticles has been shown to more efficiently modulate the neuronal membrane potential to initiate an action potential in neuron or to evoke cortically controlled motor behaviors (7, 8, 9, 10, 11, 12, 13). Contrary to previous INS that uses no nanomaterials, the plasmonic nanoparticle-mediated neural stimulation approach significantly reduced the radiant exposure required for neural activation and allowed us to substitute near-infrared light for infrared light that is mainly absorbed by water, minimizing a chance of possible tissue damage caused by bulk tissue heating (7, 8, 9).

Since the INS method was introduced approximately a decade ago (3, 6, 14), growing evidence has shown that tissue temperature elevation is critical for triggering the neural activation (11, 15, 16, 17, 18). Specifically, it was found that pulsed infrared light rapidly increases the temperature adjacent to the neuronal membrane and elevates the membrane capacitance, thus inducing a capacitive current through the membrane without any specific ion channels being involved (16, 17, 18). Shapiro et al. theoretically and experimentally proved that the electrical capacitance elevation in the neuronal membrane could evoke an action potential by depolarizing the target cell in a reversible way (16). Another hypothesis has been proposed based on the activation of temperature-sensitive ion channels. Pharmacological studies have shown that transient receptor potential vanilloid 4 (TRPV4) and TRPV1 channels are responsible for the laser-evoked response in sensory neurons and primary cultured neurons, respectively (11, 19).

Despite those studies regarding the biophysical mechanism underlying INS (9, 11), no quantitative analysis has been carried out to investigate the effects of the capacitive current and TRPV1 channels at the same time, especially for the recently tested, more efficient, gold-nanoparticle-enhanced near-infrared neural stimulation (NINS) (7, 8, 9, 10). In this work, we theoretically investigate the two primary mechanisms in an integrative and quantitative manner. From laser exposure to a change in the membrane potential, a mathematical model is developed to simulate how heat generation by plasmonic nanoparticles initiates neural depolarization. In-depth understanding of synergetic effects of the two mechanisms on neural activation will be essential for advancing the emerging plasmonic NINS technology into robust clinical techniques and neuroscience research tools.

Materials and Methods

Theoretical overview

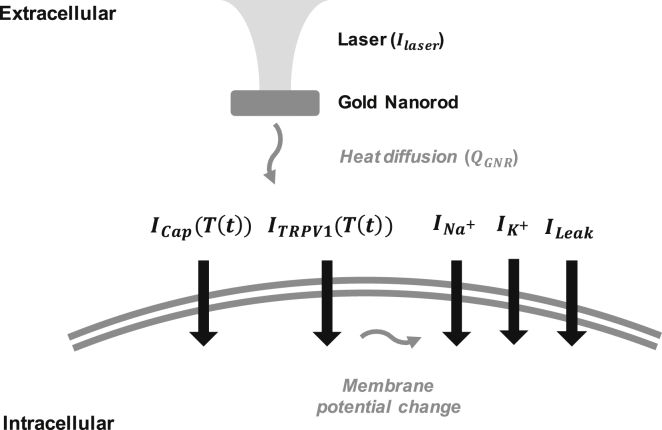
Based on the previously but separately studied hypotheses (9, 11, 16), we modeled both the capacitive and TRPV1 currents flowing through a neuronal cell membrane induced by interaction between gold nanorods (GNRs) and near-infrared (NIR) light illumination, as illustrated in Fig. 1. When an NIR light wave is incident to GNRs, its energy is greatly absorbed to GNRs via localized surface plasmon resonance (LSPR). The absorbed energy is converted into a thermal heat, and the heat diffuses to the neuronal membrane. A rapid elevation in the membrane temperature (T(t)) causes ion displacement near the membrane, which leads to an equivalent electric current called capacitive current (I_cap(T(t))), as well as cation influx through the TRPV1 channel (I_TRPV1(T(t))) (all the currents in this manuscript are in units of ampere per unit area). Both factors affect the membrane potential and the voltage-gated ion channels, finally generating an action potential. We intend to use this model to simulate how local heating obtained from GNRs evokes a neural activation and to understand how individual current sources play a role in a synergistic way.

Figure 1.

Illustration of the GNR-enhanced NINS model. Localized thermal heat generated by GNRs diffuses to the neuronal membrane. A transient temperature increase elicits both inward capacitive current and inward TRPV1 channel current and changes the membrane potential, finally triggering an action potential.

Heat generation by NIR illumination on GNRs

First, we modeled laser-induced heat generation in a GNR and its subsequent diffusion to the membrane. When an electromagnetic wave is incident to a GNR with the frequency that matches the resonance frequency of the plasmonic field, the GNR absorbs the electromagnetic fields within the absorptive cross-sectional area (20). The cross-sectional area was calculated using the Gans theory (21, 22) (see Supporting Materials and Methods for details). The Gans theory extends Mie’s theory to spheroidal nanoparticles (21) and models longitudinal surface plasmon resonance of a GNR by assuming the cylindrical GNR as a spheroid (22). The absorbed electromagnetic fields are then converted into thermal heat (Q_GNR, in the energy per unit time per unit volume, Eq. 1) (23):

$$Q_{GNR}=\frac{C_{abs}{I}_{laser}}{v_p},$$ (1)

where C_abs is the absorptive cross-sectional area of a GNR (m²), I_laser is the laser intensity (W ⋅ m^–2), and v_p is the volume of a GNR (m^–3) (23).

For simplicity, we assumed a monolayer of GNRs parallel to the neuronal membrane with a constant distance (see Table 2 for specific values used in numerical calculation) so that the heat generated from GNRs can be considered to diffuse one-dimensionally. Then, the temperature profile at the neuronal membrane can be computed by using a one-dimensional heat diffusion equation:

$$\frac{1}{\alpha }\frac{\partial T}{\partial t}=\frac{{\partial }^{2}T}{\partial x^2}+\frac{c{Q}_{GNR}}{k},$$ (2)

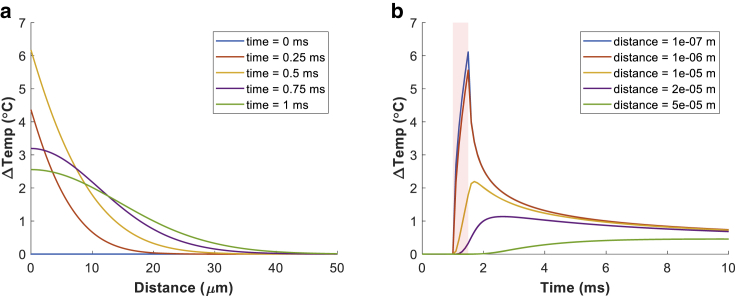
where α is the thermal diffusivity of cerebrospinal fluid (1.48 × 10⁻⁷ (m² ⋅ s⁻¹)); k is the thermal conductivity of cerebrospinal fluid (0.57 (W ⋅ m⁻¹ ⋅ K⁻¹)), the external heat source of Q_GNR; x is the distance from the GNR monolayer (m); t is the time (s); T(x, t) is the temperature (K); and c is the “coverage” of GNRs in the monolayer (unitless) (see Supporting Materials and Methods). We will denote the temperature at the membrane, T(x = (the distance), t), simply by T(t) in the following sections. We used the analytic solution (9) to calculate temperature changes, ΔT(t). To validate our modeling at every step, we tested whether the analytic solution properly provides heat diffusion profiles. As shown in the example of Fig. 2, the temperature decays as the distance increases, implying that the heat generated from the GNR sheet flows toward the neuronal membrane.

Table 2.

Numerical Values of the Parameters Tested in This Study

Parameters	Values
GNR dimensiona	15.3 nm in diameter
	80.4 nm in length
Distance between GNRs and the neuronal membraneb	100∗ and 1000 nm
GNR coveragec	0.031∗ and 0.31
TRPV1 channel density (represented by the conductance)d	1.05, 2.1∗, and 4.2 S ⋅ m–2
Laser duratione	0.005, 0.05, 0.5∗, and 5 ms

Asterisks indicate the default values.

^aThis dimension is widely used in NINS experiments and associated with the surface plasmon resonance wavelength of 980 nm, combinedly resulting in C_abs = 1.67 × 10⁻¹⁵ m² for Eq. 1 (see Supporting Materials and Methods for detailed derivation). We used the fixed GNR dimension because it will not make a significant impact on simulation results as far as its corresponding resonant wavelength is used.

^bThe default 100 nm was chosen from the transmission electron microscopy imaging of GNRs vicinity to the sciatic nerve (7).

^cThe default 0.031 was chosen from temperature data and its corresponding laser intensity (8) (see Supporting Materials and Methods).

^dThe default 2.1 S ⋅ m^–2 was chosen from the I-V response measured under the voltage-clamped condition of human embryonic kidney 293 cells expressing TRPV1 (28) (see Supporting Materials and Methods). The higher and lower densities were tested to consider the variety in the channel density across cell types (e.g., higher density in hippocampus and cortex; lower density in corpus callosum) (26).

^eThis range of laser duration was selected based on the previous theoretical and experimental NINS studies (7, 8, 9, 38), including the recent report that microsecond-scale short flashes effectively induce capacitive currents to trigger action potentials (38).

Figure 2.

Examples of the temperature profile (a) as a function of the distance for various time points and (b) as a function of the time for various distances. For this example, we used a laser pulse duration of 0.5 ms and intensity of 519 W ⋅ cm^–2. To see this figure in color, go online.

TRPV1 channel current

Thermosensation is commonly achieved by the thermotransient receptor potentials, a subset of ion channels activated by temperature. Among them, the heat-sensitive TRPV1 channel is gated (half of the maximal channel current occurs) when the temperature exceeds 43°C (24) and allows cations to pass through the channel. Because this channel exhibits high divalent selectivity, its gating produces a significant flux of Ca²⁺ ions. The TRPV1 channel is generally expressed in peripheral nerve endings, dorsal root ganglions (DRG), the spinal cord, and the central nervous system (25, 26). It has been reported that local heat artificially generated by neuronal-membrane-targeted GNRs triggers the activation of TRPV1 channel in the DRG cell and evokes high Ca²⁺ influx (11). Hence, it is reasonable to assume that the GNR-enhanced NINS is attributed, at least partially, to the TRPV1-channel-oriented current flow through the membrane.

According to the previous research (27), the TRPV1 channel current can be depicted as a function of the linear conductance multiplied by the Boltzmann activation term:

$$I_{TRPV1}\left(T\left(t\right)\right)=G_{TRPV1}\left(V_m\left(t\right)-E_{TRPV1}\right)\times \frac{1}{1+\exp \left(\frac{-\left(V_{1/2}-V_m\left(t\right)\right)}{\frac{RT\left(t\right)}{zF}}\right)},$$ (3)

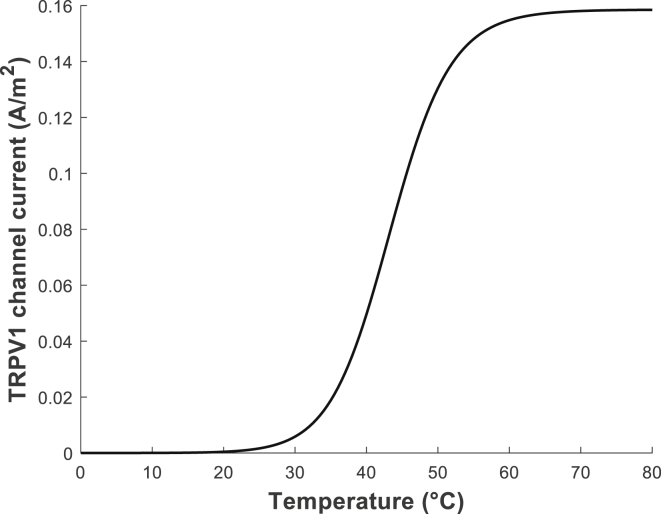
where G_TRPV1 is the conductance of TRPV1 channel per unit area (S ⋅ m^–2), E_TRPV1 is the reversal potential of TRPV1 channel (V), V_1/2 is the potential for half maximal activation (V), z is the effective gating charge, R is the gas constant (J ⋅ mol⁻¹ ⋅ K⁻¹), and F is the Faraday constant (C ⋅ mol⁻¹). We determined the value of G_TRPV1 and the equation of V_1/2 from the data presented in the previous publication and used the z-value as determined in the study (28). The reversal (or equilibrium) potential of nonselective cation TRPV1 channel (E_TRPV1 was calculated using the Goldman equation (see the Supporting Materials and Methods). As an in-step validation, we checked whether our implemented model provided the well-known characteristics of TRPV1 channels. As can be seen in the example of Fig. 3, the TRPV1 channel current at the membrane potential of −65 mV shows the temperature-dependent characteristic, at which it reaches half of its maximal current value (maximum: ∼0.16 A ⋅ m^–2), when the temperature is increased to ∼43°C (29).

Figure 3.

Temperature dependence of the TRPV1 channel current at the membrane potential of −65 mV.

Capacitive current

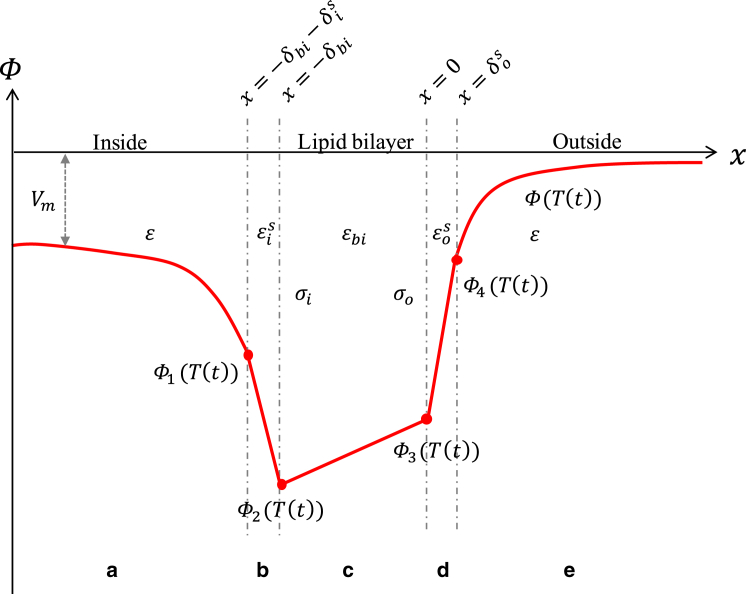
It was found that localized heat near the neuronal membrane alters the ion concentration profiles asymmetrically (17). Because of the asymmetrical charge movements in the intracellular and extracellular media, a net ion displacement occurs near the lipid bilayer. This is called capacitive current. A membrane potential change due to this capacitive current may also play an important role in GNR-enhanced NINS (9). The capacitive current (I_cap(T(t))) across the lipid bilayer can be expressed by the time derivative of the lipid bilayer charge. The charge can be obtained from the electric potentials at the outer and inner surfaces of the lipid bilayer (Φ₃(T(t)) and Φ₂(T(t)), respectively) and the lipid bilayer capacitance (C_bi(T)) (Fig. 4).

$$\begin{array}{l}{I}_{Cap}\left(T\left(t\right)\right)=\frac{d\left[\left({\mathit{\Phi }}_3\left(T\left(t\right)\right)-{\mathit{\Phi }}_2\left(T\left(t\right)\right)\right)\times C_{bi}\left(T\left(t\right)\right)\right]}{dt}=C_{bi}\left(T\left(t\right)\right)\frac{d\left({\mathit{\Phi }}_3\left(T\left(t\right)\right)-{\mathit{\Phi }}_2\left(T\left(t\right)\right)\right)}{dt}\\ +\left({\mathit{\Phi }}_3\left(T\left(t\right)\right)-{\mathit{\Phi }}_2\left(T\left(t\right)\right)\right)\frac{d{C}_{bi}\left(T\left(t\right)\right)}{dT}\frac{dT\left(t\right)}{dt}\end{array}$$ (4)

Figure 4.

A model illustrating the potential (Φ) across the cell membrane. The intra- and the extracellular media are separated by the lipid bilayer (region c) having the thickness δ_bi, the permittivity ε_bi, the inner intrinsic surface membrane charge σ_i, and the outer intrinsic surface membrane charge σ_o. The inner (region b) and the outer (region d) Stern layers that reside next to the membrane have the thickness ${\mathit{\delta }}_{\mathit{i}/\mathit{o}}^{\mathit{s}}$ and the permittivity ${\mathit{\epsilon }}_{\mathit{i}/\mathit{o}}^{\mathit{s}}$ (i and o represent inner and outer). The inner (region a) and outer (region e) diffuse layers are located next to the Stern layer. To see this figure in color, go online.

To obtain Φ₃(T(t)) and Φ₂(T(t)), we used the Gouy-Chapman-Stern (GCS) theory, elucidating the ion distribution along the electrical double layer, to model the cell membrane as illustrated in Fig. 4 (16, 30, 31). Electrostatic forces exerted between ions in the electrolyte and the intrinsic surface membrane charges (σ_i, σ_o) distribute the ions at the medium, creating diffuse layers (regions (b, d)) and Stern layers (regions (a, e)) in the intra- and extracellular matrix. In the diffuse layers, ions are distributed by the electrical forces originating from the charged surface and the random thermal motion (regions a and e), whereas in the Stern layers, ions reside at the innermost layer to the charged surface (regions b and d). Such electrical double layers will be created on both sides of the cell membrane (32). Coupled equations of the surface potentials at the outer and inner surfaces of the lipid bilayers were derived as follows (16).

Upon presence of the negatively charged lipid bilayer, ions are distributed in the diffuse layers by the Boltzmann’s distribution (regions (a, e)):

$$\frac{c_i^j\left(x_a\right)}{c_i^j\left(x_b\right)}=\exp \left(-\frac{z_i^{j}F\left[\mathit{\Phi }\left(x_a\right)-\mathit{\Phi }\left(x_b\right)\right]}{RT}\right),\left(x_{a/b}<-{\delta }_{bi}\right)$$

$$\frac{c_o^j\left(x_a\right)}{c_o^j\left(x_b\right)}=\exp \left(-\frac{z_o^{j}F\left[\mathit{\Phi }\left(x_a\right)-\mathit{\Phi }\left(x_b\right)\right]}{RT}\right),\left(x_{a/b}>0\right)$$

where, $c_{\text{i}/\text{o}}^j\left(x\right)$ is the j-th ion concentration at the inner/outer region x, $z_{\text{i}/\text{o}}^j$ is the valence of the j-th ion at the inner/outer region, F is the faraday constant, R is the gas constant, and T represents the temperature. We included Na⁺, K⁺, Cl⁻, and Ca²⁺ ions (i.e., j = 1, 2,...n = 4) and applied Gauss’s law for regions (a) and (e).

Region (e):

$$\frac{d^2\mathit{\Phi }\left(x\right)}{d{x}^2}=-\frac{{\rho }_o\left(x\right)}{\epsilon },where{\rho }_o\left(x\right)=\sum _j^n{c}_o^j\left(x\right)z_o^{j}F$$

$$c_o^j\left(x\right)=c_o^j\left(\mathit{\infty }\right)\exp \left(-\frac{z_o^{j}F\left[\mathit{\Phi }\left(x\right)-0\right]}{RT}\right),where\underset{x\to \infty }{\lim }\mathit{\Phi }\left(x\right)=0$$

$$\frac{d^2\mathit{\Phi }\left(x\right)}{d{x}^2}=-\frac{F}{\epsilon }\sum _{j=1}^n{z}_o^j{c}_o^j\left(\mathit{\infty }\right)\exp \left(-\frac{z_o^{j}F\mathit{\Phi }\left(x\right)}{RT}\right)$$ (5)

Region (a):

$$\frac{d^2\mathit{\Phi }\left(x\right)}{d{x}^2}=-\frac{{\rho }_i\left(x\right)}{\epsilon },where{\rho }_i\left(x\right)=\sum _j^n{c}_i^j\left(x\right)z_i^{j}F$$

$$c_i^j\left(x\right)=c_i^j\left(-\mathit{\infty }\right)\exp \left(-\frac{z_i^{j}F\left[\mathit{\Phi }\left(x\right)-V_m\right]}{RT}\right),where\underset{x\to -\infty }{\lim }\mathit{\Phi }\left(x\right)=V_m$$

$$\frac{d^2\mathit{\Phi }\left(x\right)}{d{x}^2}=-\frac{F}{\epsilon }\sum _{j=1}^n{z}_i^j{c}_i^j\left(-\mathrm{\infty }\right)\exp \left(-\frac{z_i^{j}F\left[\mathit{\Phi }\left(x\right)-V_m\right]}{RT}\right)$$ (6)

Using a formula $\left(d^2\mathit{\Phi }\left(x\right)/d{x}^2\right)=\left(1/2\right)\left(d/d\mathit{\Phi }\left(x\right)\right){\left(d\mathit{\Phi }\left(x\right)/dx\right)}^2$ and integrating Eqs. 5 and 6 with respect to $\mathit{\Phi }\left(x\right)$ led to Eqs. 7 and 8.

$${\left(\frac{d\mathit{\Phi }\left(x\right)}{dx}\right)}^2=\frac{2RT}{\epsilon }\sum _{j=1}^n{c}_o^j\left(\infty \right)\left(\exp \left(-\frac{z_o^{j}F\mathit{\Phi }\left(x\right)}{RT}\right)-1\right),\left(x>0\right)$$ (7)

$${\left(\frac{d\mathit{\Phi }\left(x\right)}{dx}\right)}^2=\frac{2RT}{\epsilon }\sum _{j=1}^n{c}_i^j\left(-\infty \right)\left(\exp \left(-\frac{z_i^{j}F\left[\mathit{\Phi }\left(x\right)-V_m\right]}{RT}\right)-1\right),\left(x<-{\delta }_{bi}\right)$$ (8)

The electric fields at x = 0 and −δ_bi must satisfy the boundary conditions below.

$$x=0$$

$$-{\epsilon }_o^s\frac{d\mathit{\Phi }\left(0{|}^{+}\right)}{dx}-\left(-{\epsilon }_{bi}\frac{d\mathit{\Phi }\left(0{|}^{-}\right)}{dx}\right)={\sigma }_o$$ (9)

$$x=-{\delta }_{bi}$$

$$-{\epsilon }_{bi}\frac{d\mathit{\Phi }\left(-{\delta }_{bi}{|}^{+}\right)}{dx}-\left(-{\epsilon }_i^s\frac{d\mathit{\Phi }\left(-{\delta }_{bi}{|}^{-}\right)}{dx}\right)={\sigma }_i$$ (10)

The electric flux density (D = εE) is constant within a medium with no free charge. Because there is no free charge in the outer Stern layer and the lipid bilayer, we obtained

$${\epsilon }_o^s\frac{d\mathit{\Phi }\left(0{|}^{+}\right)}{dx}={\epsilon }_o^s\frac{d\mathit{\Phi }\left({\delta }_o^s{|}^{-}\right)}{dx}$$

$${\epsilon }_{bi}\frac{d\mathit{\Phi }\left(0{|}^{-}\right)}{dx}={\epsilon }_{bi}\frac{d\mathit{\Phi }\left(-{\delta }_{bi}{|}^{+}\right)}{dx}={\epsilon }_{bi}\frac{\mathit{\Phi }\left(0\right)-\mathit{\Phi }\left(-{\delta }_{bi}\right)}{0-\left(-{\delta }_{bi}\right)}.$$

Also, the electric flux density is constant across a boundary with no free surface charges. Because there is no free charge at the boundary between the outer Stern layer and the outer electrolyte, we obtained

$${\epsilon }_o^s\frac{d\mathit{\Phi }\left({\delta }_o^s{|}^{-}\right)}{dx}=\epsilon \frac{d\mathit{\Phi }\left({\delta }_o^s{|}^{+}\right)}{dx}$$

by plugging the above three equations into Eq. 9:

$$\frac{d\mathit{\Phi }\left(0{|}^{+}\right)}{dx}=-\frac{1}{{\epsilon }_o^s}\left({\sigma }_o-{\epsilon }_{bi}\frac{d\mathit{\Phi }\left(0{|}^{-}\right)}{dx}\right)$$

$$\frac{d\mathit{\Phi }\left(0{|}^{+}\right)}{dx}=\frac{d\mathit{\Phi }\left({\delta }_o^s{|}^{-}\right)}{dx}=-\frac{1}{{\epsilon }_o^s}\left({\sigma }_o-{\epsilon }_{bi}\frac{d\mathit{\Phi }\left(0{|}^{-}\right)}{dx}\right)=\frac{\epsilon }{{\epsilon }_o^s}\frac{d\mathit{\Phi }\left({\delta }_o^s{|}^{+}\right)}{dx}$$

$$\frac{d\mathit{\Phi }\left({\delta }_o^s{|}^{+}\right)}{dx}=-\frac{1}{\epsilon }\left({\sigma }_o-{\epsilon }_{bi}\frac{d\mathit{\Phi }\left(0{|}^{-}\right)}{dx}\right)$$

$$\therefore \frac{d\mathit{\Phi }\left({\delta }_o^s{|}^{+}\right)}{dx}=-\frac{1}{\epsilon }\left({\sigma }_o+{\epsilon }_{bi}\frac{\mathit{\Phi }\left(-{\delta }_{bi}\right)-\mathit{\Phi }\left(0\right)}{{\delta }_{bi}}\right).$$ (11)

Similarly, the inner Stern layer has no free charge:

$${\epsilon }_i^s\frac{d\mathit{\Phi }\left(-{\delta }_{bi}-{\delta }_i^s{|}^{+}\right)}{dx}={\epsilon }_i^s\frac{d\mathit{\Phi }\left(-{\delta }_{bi}{|}^{-}\right)}{dx}.$$

And there is no free surface charge at the boundary between the inner Stern layer and the inner electrolyte:

$${\epsilon }_i^s\frac{d\mathit{\Phi }\left(-{\delta }_{bi}-{\delta }_i^s{|}^{+}\right)}{dx}=\epsilon \frac{d\mathit{\Phi }\left(-{\delta }_{bi}-{\delta }_i^s{|}^{-}\right)}{dx}.$$

By plugging the above two equations into Eq. 10, we obtained

$$\frac{d\mathit{\Phi }\left(-{\delta }_{bi}{|}^{-}\right)}{dx}=\frac{1}{{\epsilon }_i^s}\left({\sigma }_i+{\epsilon }_{bi}\frac{d\mathit{\Phi }\left(-{\delta }_{bi}{|}^{+}\right)}{dx}\right)$$

$$\frac{d{\mathit{\Phi }}_i^s\left(-{\delta }_{bi}{|}^{-}\right)}{dx}=\frac{d\mathit{\Phi }\left(-{\delta }_{bi}-{\delta }_i^s{|}^{+}\right)}{dx}=\frac{1}{{\epsilon }_i^s}\left({\sigma }_i+{\epsilon }_{bi}\frac{d\mathit{\Phi }\left(-{\delta }_{bi}{|}^{+}\right)}{dx}\right)=\frac{\epsilon }{{\epsilon }_i^s}\frac{d\mathit{\Phi }\left(-{\delta }_{bi}-{\delta }_i^s{|}^{-}\right)}{dx}$$

$$\frac{d\mathit{\Phi }\left(-{\delta }_{bi}-{\delta }_i^s{|}^{-}\right)}{dx}=\frac{1}{\epsilon }\left({\sigma }_i+{\epsilon }_{bi}\frac{d\mathit{\Phi }\left(-{\delta }_{bi}{|}^{+}\right)}{dx}\right)$$

$$\therefore \frac{d\mathit{\Phi }\left(-{\delta }_{bi}-{\delta }_i^s{|}^{-}\right)}{dx}=\frac{1}{\epsilon }\left({\sigma }_i-{\epsilon }_{bi}\frac{\mathit{\Phi }\left(-{\delta }_{bi}\right)-\mathit{\Phi }\left(0\right)}{{\delta }_{bi}}\right).$$ (12)

Introducing Eqs. 11 and 12 into Eqs. 7 and 8, respectively, leads to Eqs. 13 and 14.

$${\left({\sigma }_o+\frac{{\epsilon }_{bi}}{{\delta }_{bi}}\left(\mathit{\Phi }\left(-{\delta }_{bi}\right)-\mathit{\Phi }\left(0\right)\right)\right)}^2=2\epsilon RT\sum _j^n{c}_o^j\left(\infty \right)\left(\exp \left(-\frac{z_o^{j}F\mathit{\Phi }\left({\delta }_o^s\right)}{RT}\right)-1\right)$$ (13)

$${\left({\sigma }_i-\frac{{\epsilon }_{bi}}{{\delta }_{bi}}\left(\text{Φ}\left(-{\delta }_{bi}\right)-\mathit{\Phi }\left(0\right)\right)\right)}^2=2\epsilon RT\sum _j^n{c}_i^j\left(-\infty \right)\left(\exp \left(-\frac{z_i^{j}F\left[\mathit{\Phi }\left(-{\delta }_{bi}-{\delta }_i^s\right)-V_m\right]}{RT}\right)-1\right)$$ (14)

The potential drop at the outer and inner Stern layers can be simply expressed as Eqs. 15 and 16.

$$\mathit{\Phi }\left(0\right)-\mathit{\Phi }\left({\delta }_o^s\right)=-{\frac{d{\mathit{\Phi }}_o^s\left(x\right)}{dx}|}_{x=0{|}^{+}or{\delta }_o^s{|}^{-}}\times {\delta }_o^s$$

$$=\frac{{\delta }_o^s}{{\epsilon }_o^s}\left({\sigma }_o-{\epsilon }_{bi}\frac{d{\mathit{\Phi }}_{bi}\left(0{|}^{-}\right)}{dx}\right)=\frac{{\delta }_o^s}{{\epsilon }_o^s}\left({\sigma }_o+\frac{{\epsilon }_{bi}}{{\delta }_{bi}}\left(\mathit{\Phi }\left(-{\delta }_{bi}\right)-\mathit{\Phi }\left(0\right)\right)\right)$$

$$\mathit{\Phi }\left(0\right)-\mathit{\Phi }\left({\delta }_o^s\right)=\frac{{\delta }_o^s}{{\epsilon }_o^s}\left({\sigma }_o+\frac{{\epsilon }_{bi}}{{\delta }_{bi}}\left(\mathit{\Phi }\left(-{\delta }_{bi}\right)-\mathit{\Phi }\left(0\right)\right)\right)$$ (15)

$$\mathit{\Phi }\left(-{\delta }_{bi}\right)-\mathit{\Phi }\left(-{\delta }_{bi}-{\delta }_i^s\right)={\frac{d\mathit{\Phi }\left(x\right)}{dx}|}_{x=-{\delta }_{bi}-{\delta }_i^s{|}^{+}or-{\delta }_{bi}{|}^{-}}\times {\delta }_i^s$$

$$=\frac{1}{{\epsilon }_i^s}\left({\sigma }_i+{\epsilon }_{bi}\frac{d\mathit{\Phi }\left(-\delta {|}^{+}\right)}{dx}\right)=\frac{{\delta }_i^s}{{\epsilon }_i^s}\left({\sigma }_i-\frac{{\epsilon }_{bi}}{{\delta }_{bi}}\left(\mathit{\Phi }\left(-{\delta }_{bi}\right)-\mathit{\Phi }\left(0\right)\right)\right)$$

$$\mathit{\Phi }\left(-{\delta }_{bi}\right)-\mathit{\Phi }\left(-{\delta }_{bi}-{\delta }_i^s\right)=\frac{{\delta }_i^s}{{\epsilon }_i^s}\left({\sigma }_i-\frac{{\epsilon }_{bi}}{{\delta }_{bi}}\left(\mathit{\Phi }\left(-{\delta }_{bi}\right)-\mathit{\Phi }\left(0\right)\right)\right)$$ (16)

The thickness of Stern layers $\left({\delta }_o^s,{\delta }_i^s\right)$ were derived as Eqs. 17 and 18.

$${\delta }_o^s={\delta }_o^{lipid}+\frac{{\sum }_{j=1}^n{r}_o^j\left[c_o^j\left(\infty \right)\exp \left(-\frac{z_o^{j}F}{RT}\left(\mathit{\Phi }\left({\delta }_o^s\right)\right)\right)\right]}{{\sum }_{j=1}^n{c}_o^j\left(\infty \right)\exp \left(-\frac{z_o^{j}F}{RT}\left(\mathit{\Phi }\left({\delta }_o^s\right)\right)\right)}$$ (17)

$${\delta }_i^s={\delta }_i^{lipid}+\frac{{\sum }_{j=1}^n{r}_i^j\left[c_i^j\left(-\infty \right)\exp \left(-\frac{z_i^{j}F}{RT}\left(\mathit{\Phi }\left(-{\delta }_{bi}-{\delta }_i^s\right)-V_m\right)\right)\right]}{{\sum }_{j=1}^n{c}_i^j\left(-\infty \right)\exp \left(-\frac{z_i^{j}F}{RT}\left(\mathit{\Phi }\left(-{\delta }_{bi}-{\delta }_i^s\right)-V_m\right)\right)}$$ (18)

In consequence, we obtained four coupled equations (Eqs. 13, 14, 15, and 16) for four unknowns ($\mathit{\Phi }\left(-{\delta }_{bi}-{\delta }_i^s\right)={\mathit{\Phi }}_1$, Φ(−δ_bi) = Φ₂, Φ(0) = Φ₃, and $\mathit{\Phi }\left({\delta }_o^s\right)={\mathit{\Phi }}_4$), so we can find the unknowns by numerically solving the coupled equations. By plugging a time course of the temperature obtained by Eq. 2 into these coupled equations, time-course changes in Φ₁, Φ₂, Φ₃, and Φ₄ were found. Then, they were plugged into Eq. 4 to obtain a time course of the capacitive current.

It was reported that a transient temperature change may affect the morphology of the lipid bilayer as it undergoes axial shrinkage and lateral expansion. Because of this structural change, the capacitance of the lipid bilayer can change, leading to an additional capacitive current (33). For this reason, we empirically deduced the temperature dependence of our lipid bilayer capacitance from Shapiro et al.’s experimental data, which had described a temperature transient and its corresponding current response (16) (see the Supporting Materials and Methods for details). Overall, we simulated the capacitive current by taking all the potentials at the outer and inner surfaces of the lipid bilayer, the temperature-dependent lipid bilayer capacitance, and the time course of temperature into consideration.

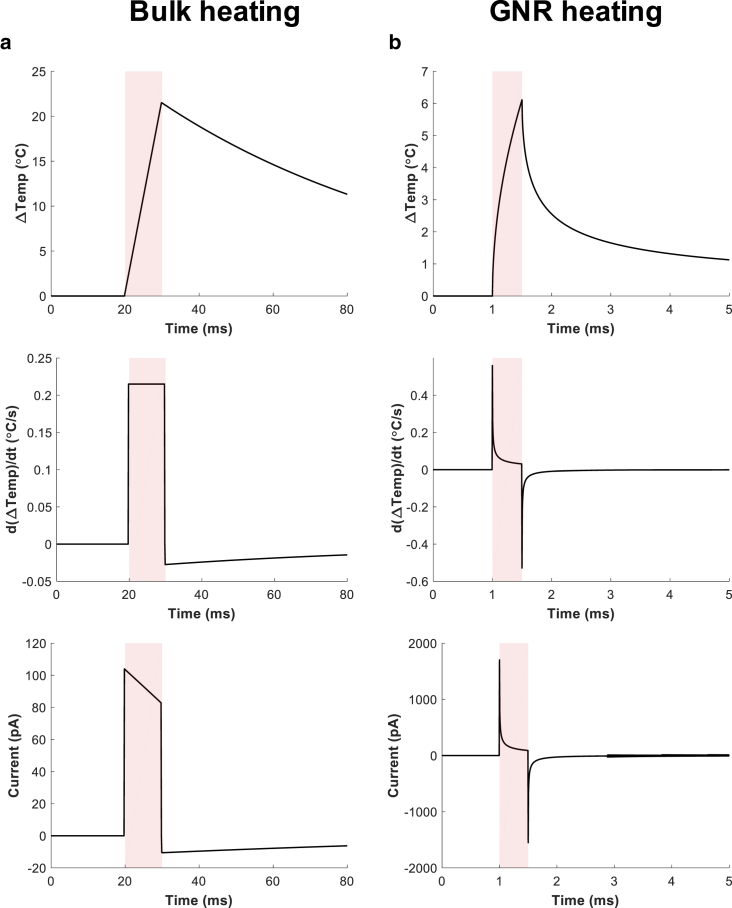
To confirm our implemented model for the capacitive current, we checked what the current looks like under a simulated voltage clamp condition with both Shapiro’s experimental temperature data (bulk IR heating) (16) and our numerical temperature data (local NIR GNR heating). The examples presented in Fig. 5 show that our simulated capacitive currents approximately follow $dT/dt$, and especially the one simulated from the Shapiro’s experimental data is very close to their experimentally measured capacitive current (Fig. S2), combinedly supporting the validity of our implemented code.

Figure 5.

Examples of temperature changes, its time derivatives, and the resulting capacitive current. The capacitive currents were simulated under the voltage-clamp condition at the holding potential of 0.2 (V) with the temperature data previously reported by Shapiro et al. (16) (a), or with temperature data obtained by our model for GNR heating (b) (laser intensity: 519 W ⋅ cm⁻²; laser duration: 0.5 ms; GNR coverage: 0.031; GNR distance: 100 nm; TRPV1 channel conductance: 2.1 S ⋅ m⁻²; see Table 2 for details of parameters). To see this figure in color, go online.

Neuronal membrane modeling

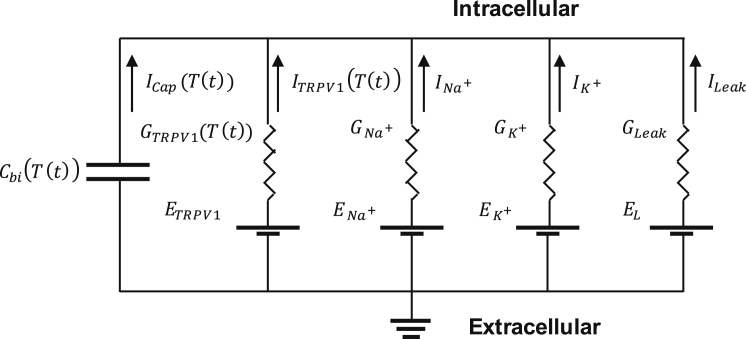
Our neuronal membrane was modeled based on the classical Hodgkin-Huxley (HH) model (34). The HH model describes the neuronal membrane by an electric circuit involving a lipid bilayer, voltage-dependent sodium and potassium channels, and a leakage pathway to show how the membrane potential behaves to generate an action potential. In this study, the classical HH model was modified by adding the TRPV1 channel current and capacitive current to include the temperature dependence of the neuronal membrane.

As in Fig. 6, the TRPV1 channel was added to the classical HH model by connecting the conductance (G_TRPV1(T(t))) and the voltage source (E_TRPV1) to the original circuit in parallel. The current direction was defined as being positive when it flows from the exterior to the interior of the membrane. In addition, the capacitive current reflecting the temperature change-induced ion displacement was introduced as a displacement current through the capacitor. When the TRPV1 channel current and the capacitive current are combined to the classical HH model, it leads to a set of coupled equations:

$$I_{Cap}\left(T\left(t\right)\right)+I_{TRPV1}\left(T\left(t\right)\right)+I_{N{a}^{+}}+I_{K^{+}}+I_{Leak}=0,$$

$$I_{N{a}^{+}}=G_{N{a}^{+}}\left(0+E_{N{a}^{+}}-V_m\right)=-G_{N{a}^{+}}\left(V_m\left(t\right)-E_{N{a}^{+}}\right),$$

$$I_{K^{+}}=G_{K^{+}}\left(0+E_{K^{+}}-V_m\right)=-G_{K^{+}}\left(V_m\left(t\right)-E_{K^{+}}\right),$$

$$I_{leak}=G_{leak}\left(0+E_{leak}-V_m\right)=-G_{leak}\left(V_m\left(t\right)-E_{leak}\right),$$

and

$$-I_{Cap}\left(T\left(t\right)\right)+I_{TRPV1}\left(T\left(t\right)\right)+G_{N{a}^{+}}\left(V_m\left(t\right)-E_{N{a}^{+}}\right)+G_{K^{+}}\left(V_m\left(t\right)-E_{K^{+}}\right)+G_{leak}\left(V_m\left(t\right)-E_{leak}\right)=0,$$ (19)

where $E_{N{a}^{+}}$ is the reversal potential for Na⁺ channels (61.4 mV), $E_{K^{+}}$ is the reversal potential for K⁺ channels (−79.9 mV), E_Leak is the reversal potential for the leak current pathway (−54.4 mV) (35), $G_{N{a}^{+}}$ is the conductance for Na⁺ channels (S ⋅ m⁻²), $G_{K^{+}}$ is the conductance for K⁺ channels (S ⋅ m⁻²), and G_Leak is the conductance for the leak current pathway (S ⋅ m⁻²). The reversal potentials for Na⁺ and K⁺ channels were calculated by using the Nernst equation. The values used in our modified HH model and the equations for Na⁺ and K⁺ conductances can be found in the Supporting Materials and Methods.

Figure 6.

Electrical circuit model representing the neuronal membrane. Both the temperature-dependent TRPV1 channel current (I_TRPV1(T(t))) and capacitive current (I_cap(T(t))) are added into the classical HH model.

Simulation strategy

In summary, we used the GCS theory to model an electrical double layer of the biological membrane based on the previous publications of Shapiro et al. and Genet et al. (16, 32). We also employed an idea of Plaksin et al. (33) that the capacitance of the lipid bilayer changes when the temperature changes and to model the capacitance of the lipid bilayer. Capacitive current was calculated using the potentials obtained by GCS theory and the capacitance of the lipid bilayer, and TRPV1 channel current was adopted from the previous publication by Voet et al. (28). We integrated the capacitive current and the TRPV1 channel current into the Hodgkin-Huxley model to find the membrane potential (34). Based on our model, we solved two sets of equations, the first set to determine T(t) and then the other set to find eight variables: V_m(t), n(t), m(t), h(t), Φ₁(t), Φ₂(t), Φ₃(t), and Φ₄(t) based on the determined T(t), where n(t), m(t), and h(t) are gating probabilities of the subunit of the potassium (n(t)) and the sodium (m(t) and h(t)) channels. The first set of equations were presented in Eqs. 1 and 2. The second set of equations for the eight variables are summarized as Eqs. 20, 21, 22, 23, 24, 25, 26, and 27, and the definitions and values of variables are listed in Tables 1 and S1, respectively:

$$\begin{array}{l}{G}_{TRPV1}\left(V_m\left(t\right)-E_{TRPV1}\right)\times \frac{1}{1+exp\left(-\frac{\left(V_{1/2}-V_m\left(t\right)\right)}{\frac{RT\left(t\right)}{zF}}\right)}+\overline{G_{K^{+}}}{n}^4\left(V_m\left(t\right)-E_{K^{+}}\right)\\ +\overline{G_{N{a}^{+}}}m{\left(t\right)}^{3}h\left(t\right)\left(V_m\left(t\right)-E_{N{a}^{+}}\right)+\overline{G_{Leak}}\left(V_m\left(t\right)-E_{leak}\right)\\ -\frac{d\left[\left({\text{Φ}}_3\left(T\left(t\right)\right)-{\text{Φ}}_2\left(T\left(t\right)\right)\right)\times C_{bi}\left(T\left(t\right)\right)\right]}{dt}=0,\end{array}$$ (20)

$$\frac{dn\left(t\right)}{dt}=\frac{-100\left(100V_m\left(t\right)+6\right)}{e^{\left(-100V_m\left(t\right)-6\right)}-1}\times 3^{\frac{T\left(t\right)-279.3}{10}}\left(1-n\left(t\right)\right)-125e^{\left(-12.5\left(V_m\left(t\right)+0.07\right)\right)}\times 3^{\frac{T\left(t\right)-279.3}{10}}n\left(t\right),$$ (21)

$$\frac{dm\left(t\right)}{dt}=\frac{-100\left(1000V_m\left(t\right)+45\right)}{e^{\left(-100V_m\left(t\right)-4.5\right)}-1}\times 3^{\frac{T\left(t\right)-279.3}{10}}\left(1-m\left(t\right)\right)-4000e^{\left(\frac{-1000\left(V_m\left(t\right)+0.07\right)}{18}\right)}\times 3^{\frac{T\left(t\right)-279.3}{10}}m\left(t\right),$$ (22)

$$\frac{dh\left(t\right)}{dt}=70e^{\left(50V_m\left(t\right)+3.5\right)}\times 3^{\frac{T\left(t\right)-279.3}{10}}\left(1-h\left(t\right)\right)-\frac{1000}{e^{\left(-100V_m\left(t\right)-4\right)}+1}\times 3^{\frac{T\left(t\right)-279.3}{10}}h\left(t\right),$$ (23)

$${\mathit{\Phi }}_2\left(T\left(t\right)\right)-{\mathit{\Phi }}_1\left(T\left(t\right)\right)+\frac{{\epsilon }_{bi}}{{\delta }_{bi}}\left({\mathit{\Phi }}_2\left(T\left(t\right)\right)-{\mathit{\Phi }}_3\left(T\left(t\right)\right)\right)=\frac{{\sigma }_i{\delta }_i^s}{{\epsilon }_i^s},$$ (24)

$${\mathit{\Phi }}_3\left(T\left(t\right)\right)-{\mathit{\Phi }}_4\left(T\left(t\right)\right)-\frac{{\epsilon }_{bi}}{{\delta }_{bi}}\left({\mathit{\Phi }}_2\left(T\left(t\right)\right)-{\mathit{\Phi }}_3\left(T\left(t\right)\right)\right)=\frac{{\sigma }_o{\delta }_o^s}{{\epsilon }_o^s},$$ (25)

$${\left({\sigma }_i-\frac{{\epsilon }_{bi}}{{\delta }_{bi}}\left({\mathit{\Phi }}_2\left(T\left(t\right)\right)-{\mathit{\Phi }}_3\left(T\left(t\right)\right)\right)\right)}^2-2\epsilon \left(T\left(t\right)\right)RT\sum _j^n{c}_i^j\left(-\infty \right)\left(\exp \left(-\frac{z_i^{j}F\left[{\mathit{\Phi }}_1\left(T\left(t\right)\right)-V_m\left(t\right)\right]}{RT}\right)-1\right)=0,$$ (26)

and

$${\left({\sigma }_o+\frac{{\epsilon }_{bi}}{{\delta }_{bi}}\left({\mathit{\Phi }}_2\left(T\left(t\right)\right)-{\mathit{\Phi }}_3\left(T\left(t\right)\right)\right)\right)}^2-2\epsilon \left(T\left(t\right)\right)RT\sum _j^n{c}_o^j\left(\infty \right)\left(\exp \left(-\frac{z_o^{j}F{\mathit{\Phi }}_4\left(T\left(t\right)\right)}{RT}\right)-1\right)=0,$$ (27)

where j represents the four (= n) ions in the electrolyte (Na⁺, K⁺, Cl⁻, Ca²⁺).

Table 1.

Definition of Variables Used in Our Model

Variable	Definition
Vm(t)	membrane potential/potential difference between outer- and inner bulk medium
Φ1(T(t))	potential at the interface between the inner Stern layer and the inner diffuse layer
Φ2(T(t))	surface potential at the inner lipid bilayer
Φ3(T(t))	surface potential at the outer lipid bilayer
Φ4(T(t))	potential at the interface between the outer Stern layer and the outer diffuse layer
σi	intrinsic charge density of the inner side of the lipid bilayer
σo	intrinsic charge density of the outer side of the lipid bilayer
${\mathit{\sigma }}_{\mathit{i}}^{\mathit{s}}$	intrinsic charge density at the interface between the inner Stern layer and the inner diffuse layer
${\mathit{\sigma }}_{\mathit{o}}^{\mathit{s}}$	intrinsic charge density at the interface between the outer Stern layer and the outer diffuse layer
εbi	permittivity of the lipid bilayer
δbi	thickness of the lipid bilayer
ε(T(t))	permittivity of electrolyte medium
δis	thickness of inner Stern layer
δos	thickness of outer Stern layer
δilipid	hydrated size of inner polar lipid head groups
δolipid	hydrated size of outer polar lipid head groups
εis	permittivity of inner Stern layer
εos	permittivity of outer Stern layer
cij(−∞)	concentration of j-th ionic species in the inner bulk medium
coj(∞)	concentration of j-th ionic species in the outer bulk medium
${\mathit{z}}_{\mathit{i}}^{\mathit{j}}$	valence of j-th ionic species in the inner electrolyte
${\mathit{z}}_{\mathit{o}}^{\mathit{j}}$	valence of j-th ionic species in the outer electrolyte
rij	hydrated ionic radius of j-th ionic species in inner electrolyte
roj	hydrated ionic radius of j-th ionic species in outer electrolyte
$\overline{{\mathit{G}}_{{\mathit{K}}^{+}}}$	maximal conductance of the potassium channel
$\overline{{\mathit{G}}_{\mathit{N}{\mathit{a}}^{+}}}$	maximal conductance of the sodium channel
$\overline{{\mathit{G}}_{\mathit{Leak}}}$	maximal conductance of the leak current

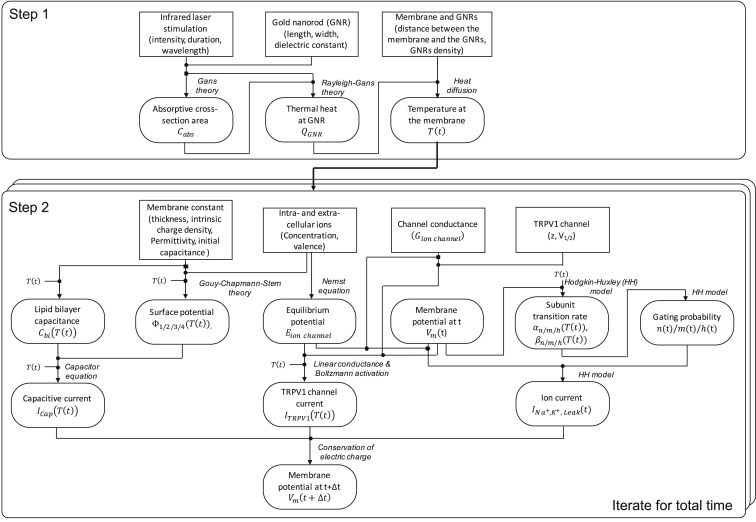
In consequence, we have built an integrative model as outlined in Fig. 7 that employs a number of fundamental biophysical principles ranging from the Gans theory and heat diffusion to the HH model and the GCS theory. We numerically solved this model in two steps: 1) we determined the temperature at the membrane as a function of time, and then 2) we solved the coupled nonlinear differential equations for the determined temperature profile to get the membrane potential over time. In detail, the numerical process began with the calculation of the thermal profile at the neuronal membrane for given laser parameters (e.g., intensity and duration) using Eqs. 1 and 2. For each time point, the corresponding temperature value was plugged into Eq. 3 to obtain the TRPV1 channel current, for which we used the membrane potential of the previous time point (the baseline potential was used for the initial time point). On the other hand, the capacitive current was found from Eq. 4 after calculating the surface potentials of Φ₂(T(t)) and Φ₃(T(t)) using Eqs. 24, 25, 26, and 27. Both the TRPV1 channel current and capacitive current were then applied to the modified HH model in Eqs. 20, 21, 22, and 23 to compute the new membrane potential value. This process was repeated for every time point, resulting in the TRPV1 channel current, capacitive current, and the membrane potential as functions of time, which are mainly used to present and discuss our results in this work. All the simulations were implemented using MATLAB, and our scripts have been uploaded to Brown Digital Repository (DOI: 10.7301/Z0K64GKB) for public access (36).

Figure 7.

A block diagram of GNR-enhanced NINS model, which consists of two steps: 1) determining the temperature as a function of time and 2) determining a time course of the membrane potential based on the temperature time course. The second step was solved in the iterative manner. The rectangle indicates the input constant, whereas the rectangle with rounded corners show variables that were numerically calculated at given input(s). The filled circle indicates the addition of incoming constants and/or variables, and the filled rectangle illustrates the outgoing of the constant or variable into multiple paths.

As outlined so far, we expect that the time-varying change in the temperature, induced by the heat generated from GNRs, results in the ion displacements (capacitive current) and the gating of TRPV1 channels and thus leads to a notable increase in membrane potential, eventually triggering an action potential. In the following sections, we investigate how two mechanisms are responsible for producing an action potential. In particular, individual contributions of the TRPV1 channel current and capacitive current in generating action potentials are quantified and compared. For this quantitative comparison, we designed three types of the modified HH models: 1) HH model #1 involving both the TRPV1 channel current and capacitive current, 2) HH model #2 involving only the TRPV1 channel current, and 3) HH model #3 involving only the capacitive current (i.e., simulating TRPV1-channel-blocked neurons).

Finally, we investigate how a variety of cellular, physical, and optical parameters affect the relative roles of two mechanisms and stimulation efficacy. For this purpose, we repeated the above simulation 96 times to test all combinations of three TRPV1 channel densities, two different GNR coverages (along with the coverage, the orientation of the GNRs are discussed in the Supporting Materials and Methods), two different distances between the GNR and neuronal membrane, four laser durations, and two mechanisms (HH models #2 and #3). Specific values we tested are listed in Table 2.

Results

Photothermal effects of GNRs trigger an action potential

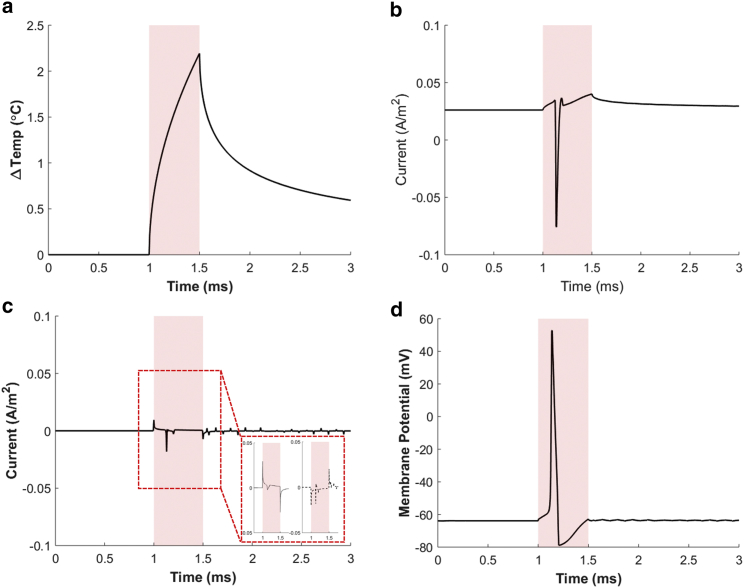
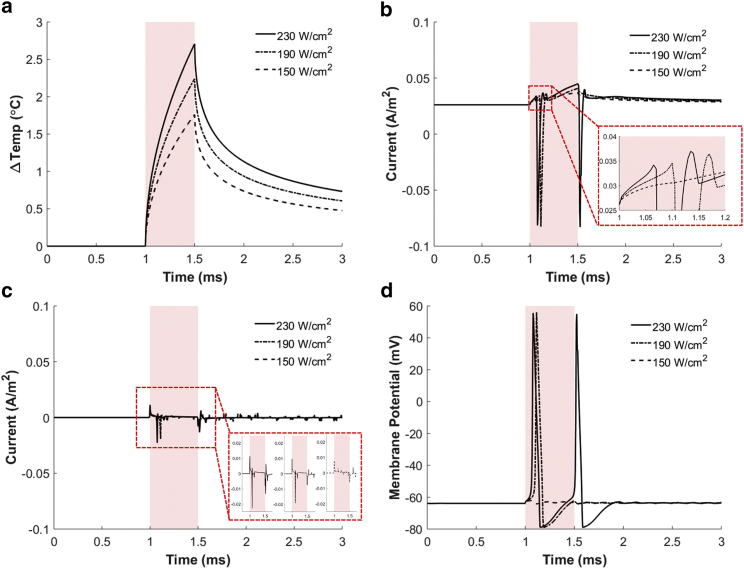
In the case of HH model #1 (including both the TRPV1 channel and capacitive currents) and with our parameters, a single pulse of NIR laser (0.5 ms pulse duration) triggers an action potential when its intensity reaches 186 W ⋅ cm^–2. Fig. 8 presents the results at this stimulation threshold. Fig. 8 a displays the GNR heat-induced thermal profile at the neuronal membrane as a temperature change with respect to the body temperature (36.5°C). The temperature increases abruptly at the onset of laser irradiation, with a maximal change of 2.2°C under our stimulation parameters, and then returns to body temperature with a time constant of ∼0.71 ms after switching off optical illumination. The corresponding TRPV1 channel current and capacitive current in response to the temperature change are displayed in Fig. 8, b and c, respectively. Through the TRPV1 channel, a small inward current occurs first after the onset of laser illumination and is followed by an outward current with an amplitude ∼13 times larger. The initial inward current corresponds to the opening of the TRPV1 channel in response to the initial temperature increase, whereas the following outward current may be due to the increased membrane potential (i.e., elicited action potential) (see Discussion for further interpretation of this and following results). On the other hand, as for the capacitive current, an abrupt inward current is monitored at the onset of laser stimulation and followed by an abrupt outward current at the end of laser illumination. Both the inward and outward current peaks are highly synchronized with the start and end time points of the laser illumination. In addition, a larger outward capacitive current appears between these time points, which is close to the moment of the outward TRPV1-channel-current peak. The membrane potential in Fig. 8 d shows that an action potential is elicited at this stimulation threshold. From the membrane potential waveform and two current profiles, we believe that both the initial inward TRPV1 and capacitive currents are responsible for triggering the action potential.

Figure 8.

Simulation results of GNR-enhanced NINS in the case of HH model #1 (considering both the TRPV1 and capacitive currents) and at the stimulation threshold. (a) The time course of the membrane temperature changes relative to body temperature (36.5°C) when illuminating NIR light onto the GNRs. (b) The TRPV1 channel current exhibits an initial inward current followed by a larger outward current. (c) The capacitive current plot shows that inward and outward currents are generated exactly when switching on and off the laser, respectively. The capacitive current consists of two components: the one associated with the time derivative of the capacitance (dotted line in the inset) and the other one associated with the time derivative of the potential difference (dashed line in the inset). We intentionally used the same current scale as (b) for comparison with the TRPV1 current. (d) The membrane potential shows that the action potential is evoked at this threshold (186 W ⋅ cm⁻²). The red shaded boxes indicate the NIR pulse illumination (0.5 ms duration). To see this figure in color, go online.

To confirm the threshold behavior, we present one subthreshold (150 W ⋅ cm^–2) and two suprathreshold (190 and 230 W ⋅ cm^–2) results in Fig. 9. The maximal temperature changes at the neuronal membrane were 1.7, 2.5, and 3.3°C for the laser intensities of 150, 190, and 230 W ⋅ cm^–2, respectively (Fig. 9 a). After laser illumination was turned off, the temperature returned to body temperature, with the same time constant of ∼0.71 ms for all cases. Regarding the TRPV1 channel currents (Fig. 9 b), the larger intensity results in a larger peak and steeper slope of the initial inward current, which resembles the initial part of the temperature change profiles. Interestingly, the following outward current only appears by the suprathreshold stimulation, which supports the above interpretation regarding Fig. 9 b. Meanwhile, both the inward and outward capacitive current peaks appear regardless of the laser intensity at the start and end time of the illumination, although their magnitudes were larger for higher laser intensities, as displayed in the inset of Fig. 9 c. Even though both the intensities of 190 and 230 W ⋅ cm^–2 are suprathreshold and thus trigger action potentials, the higher intensity triggers the faster initial action potential and produces the stronger inward TRPV1 channel current after the action potential, resulting in the generation of another action potential (Fig. 9 d). This result suggests that larger laser intensities may allow for a higher firing rate.

Figure 9.

Simulation results of GNR-enhanced NINS for varying stimulation laser intensities in the case of HH model #1. (a) Membrane temperature changes relative to the body temperature (36.5°C) for three different laser intensities are shown. (b) TRPV1 channel currents are shown. (c) Capacitive currents are shown. The inset shows the currents for three stimulation intensities separately for clear comparison. (d) The membrane potentials upon laser irradiation are shown. Solid, dashed, and dash-dot lines indicate the results obtained upon optical stimulation intensities of 230, 190, and 150 W ⋅ cm^–2, respectively. The red shaded boxes indicate the NIR pulse illumination (0.5 ms duration). To see this figure in color, go online.

Individual contributions of TRPV1 channel current and capacitive current to neural activation

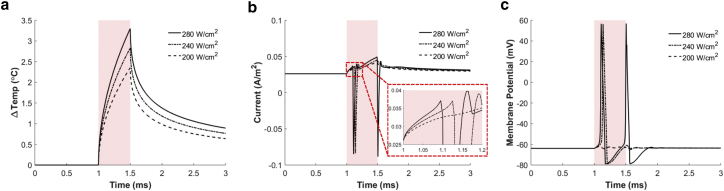
HH models #2 (only TRPV1 channels) and #3 (only capacitive current) were used to investigate each contribution separately. Results from HH model #2 (Fig. 10) show that membrane depolarization by the TRPV1 channel current can elicit action potentials at the stimulation threshold of 234 W ⋅ cm^–2, which is 1.3 times greater than the threshold of HH model #1. The temperature at the membrane was increased by 2.8°C at this threshold laser intensity. Similar to HH model #1, the TRPV1 channel creates an initial gentle inward current when the laser illumination starts, followed by a larger outward current occurring when the action potential appears. Also, in HH model #2, stronger laser illumination creates the first action potentials faster and makes the following inward current stronger, triggering an additional action potential.

Figure 10.

Simulation results of GNR-enhanced NINS in the case of HH model #2. (a) Changes in the membrane temperature in response to a laser pulse with different laser intensities are shown. (b) The TRPV1 channel current in response to a laser pulse is shown. (c) The membrane potential in response to a laser pulse is shown. Solid, dash-dot, and dashed lines indicate the results for NIR stimulation with the laser intensities of 280, 240, and 200 W ⋅ cm^–2, respectively. The red shaded boxes indicate the NIR pulse illumination (0.5 ms duration). To see this figure in color, go online.

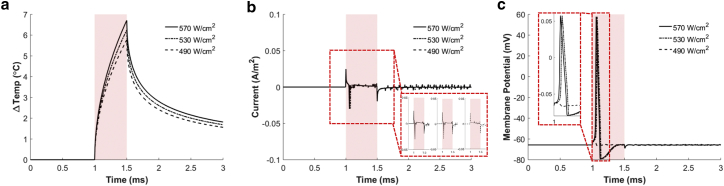
Fig. 11 presents the result from HH model #3 involving the capacitive current only. Like in the other models, optical stimulation fails to fire an action potential when stimulation is below the threshold, but the threshold becomes 519 W ⋅ cm^–2, which is 2.8 and 2.2 times bigger than those of HH models #1 and #2, respectively. This increment in the stimulation threshold is associated with a higher temperature elevation (6.1°C) required for triggering an action potential. This model exhibits highly synchronized inward and outward current spikes at the onset and end of laser illumination, respectively. Interestingly, the time courses of the initial inward current are very similar to those of the time derivative of the temperature changes until the action potentials appear. As shown in the inset of Fig. 11 c, the abrupt membrane depolarization starts immediately after the inward current, suggesting that the inward current at the onset of laser illumination is responsible for the neural activation. Different from the other models, in this model #3 in which there is no TRPV1 channel, the depolarization induced by laser stimulation occurs only once at the onset of the laser, and thus the action potential would not be elicited more than once by a single pulse even with a very large laser stimulation. More importantly, the magnitude of the inward current spikes of the capacitive current are 22.6 and 9.47 mA ⋅ m^–2 for models #3 and #1, respectively, indicating that ∼2.39 times stronger capacitive current is required to initiate an action potential without the aid of TRPV1 channel current.

Figure 11.

Simulation results of GNR-enhanced NINS in the case of HH model #3 (capacitive current only). (a) The membrane temperature in response to a laser pulse with different laser intensities is shown. (b) The capacitive current in response to a laser pulse is shown. (c) The membrane potential in response to a laser pulse is shown. Solid, dash-dot, and dashed lines indicate the results for NIR stimulation with laser intensities of 570, 530, and 490 W ⋅ cm^–2, respectively. The red shaded boxes indicate an NIR pulse illumination of 0.5 ms duration. To see this figure in color, go online.

Comparisons between contributions of TRPV1 channel current and capacitive current to neural activation

The results summarized in Table 3 suggest that both the TRPV1 channel current and capacitive current contribute to the generation of action potential but to different degrees. To compare the degree of contribution from each mechanism, the stimulation threshold was compared between HH models #2 and #3. The result that a higher NIR stimulation is demanded to evoke an action potential in HH model #3 (capacitive current only) than in model #2 (TRPV1 current only) strongly suggests that the TRPV1 channel current contributes to the generation of action potential more significantly than the capacitive current. In addition, at the condition of stimulation threshold, the maximal initial inward capacitive current in HH model #3 is ∼2.4 times higher than that of HH model #1 (both mechanisms), whereas the maximal initial inward TRPV1 current in HH model #2 is only ∼1.1 times higher than that of HH model #1. These results imply that although synergistic contribution of the TRPV1 channel current and capacitive current exists in normal neurons during GNR-enhanced NINS, the TRPV1 channel current plays a more important role in triggering action potentials and the contribution of the capacitive current is limited. Furthermore, according to this theoretical result, the capacitive current alone cannot explain the experimental observation that more than one action potential was elicited by a single pulse (19).

Table 3.

Thresholds, Membrane Currents, Timing, and Action Potentials in Three Models

		Tested Subthresholda	Threshold	Tested Suprathreshold 1	Tested Suprathreshold 2
HH #1	laser intensity [W ⋅ cm–2]	150	186	190	230
	action potential peak time (ms)	N/A	0.14	0.12	0.080 (1st)b
					0.53 (2nd)
	inward TRPV1 current peak time (ms)	N/A	0.12	0.11	0.065 (1st)b
					0.50 (2nd)b
	inward capacitive current peak time (ms)	0.0	0.0	0.0	0.075 (1st)b
					0.52 (2nd)b
	maximal initial inward TRPV1 current (A ⋅ m–2)	N/Ac	0.035	0.035	0.034 (1st)b
					0.045 (2nd)b
	maximal initial inward capacitive current (A ⋅ m–2)	0.0079	0.0095	0.0096	0.011
HH #2	laser intensity (W ⋅ cm–2)	200	234	240	280
	action potential peak time (ms)	N/A	0.17	0.14	0.11 (1st)b
					0.51 (2nd)b
	inward TRPV1 current peak time (ms)	N/A	0.165	0.13	0.095 (1st)b
					0.49 (2nd)b
	maximal initial inward TRPV1 current (A ⋅ m–2)	N/Ac	0.038	0.037	0.037 (1st)b
					0.050 (2nd)b
HH #3	laser intensity (W ⋅ cm–2)	490	519	530	570
	action potential peak time (ms)	N/A	0.11	0.075	0.060
	inward capacitive current peak time (ms)	0.0	0.0	0.0	0.055
	maximal initial inward capacitive current (A ⋅ m–2)	0.021	0.023	0.023	0.025

^aThe peak time in this table represents the time from the onset of laser stimulation.^bIn the case of multiple action potentials, their corresponding timings and currents are listed as first and second in chronological order.

^cWe defined the maximal initial inward TRPV1 current as the maximal value in the time range between the stimulation onset and the action potential, so it is not applicable to the subthreshold cases, although the TRPV1 current continuously increased during the stimulation period.

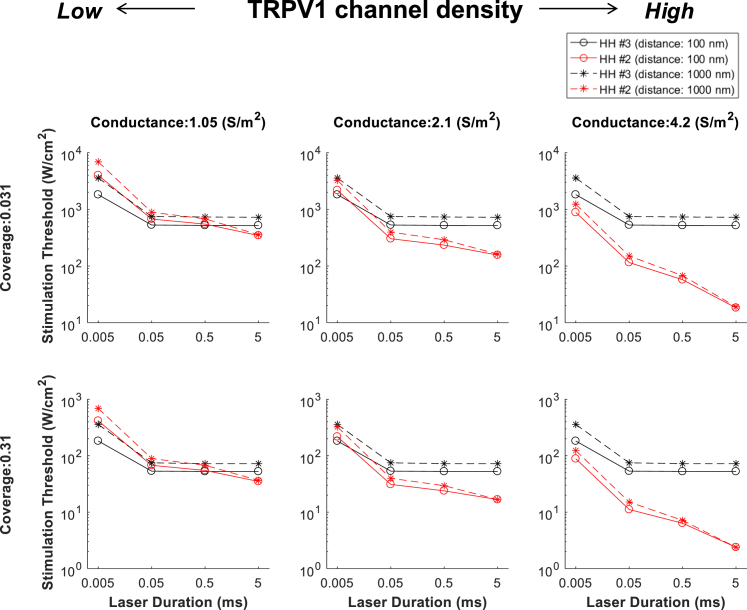
Under the default values (Table 2), the TRPV1 channel current has a bigger impact on the neural activation compared to the capacitive current, but to further investigate the relative roles of the two mechanisms in a wide range of conditions, we tested 48 combinations of the parameters as listed in Table 2. Fig. 12 shows the stimulation thresholds of HH model #2 and HH model #3 for the 48 different conditions. This result confirms the important hypothesis on the effect of laser duration, for the first time to our knowledge in a quantitative way, that as the pulse duration decreases, the relative contribution of capacitive current increases within the tested variety of TRPV1 density, GNR coverage, and GNR distance. Although the TRPV1 current has a larger contribution than the capacitive current in most cases, the capacitive current becomes a significantly larger contributor when the laser duration is as short as 5 μs and the TRPV1 channel density is relatively lower (with the associated conductance around 1 S ⋅ m^–2). It is obvious that the TRPV1 channel conductance (i.e., channel density) only influences the TRPV1 channel current (the black lines in Fig. 12 are identical across different densities), and thus the relative contribution of capacitive current mechanism becomes larger as the TRPV1 channel conductance decreases.

Figure 12.

Comparisons of stimulation threshold of HH #2 (TRPV1 channel current; red) and HH #3 (capacitive current; black) model. Four laser durations (0.005, 0.05, 0.5, and 5 ms) were simulated along with three TRPV1 conductances (1.05, 2.1, and 4.2 S ⋅ m^–2), two GNR coverages (0.031, 0.31), and two distances (100 nm filled line and 1000 nm dotted line), and the resulting 48 combinations are simulated. To see this figure in color, go online.

We found that as the GNR distance decreases, the relative contribution of capacitive current mechanism increases. However, this effect does not change which mechanism makes a major contribution within the realistic distance range we tested (Table 4). Also, the GNR coverage has few effects on the relative roles but only scales the threshold value as we anticipated above. The coverage just influences on the amount of heat generated from the GNRs, not on the profile of the temperature.

Table 4.

The Major Contributors between Two Mechanisms

	Low TRPV1 Density				Typical TRPV1 Densitya				High TRPV1 Density
Laser duration (ms)	0.005	0.05	0.5	5	0.005	0.05	0.5	5	0.005	0.05	0.5	5
Short distance	C	$\cong$	$\cong$	T	$\cong$	T	T	T	T	T	T	T
Long distance	C	$\cong$	$\cong$	T	$\cong$	T	T	T	T	T	T	T

“C” is the capacitive current, “T” is the TRPV1 channel current, and “≅” represents both mechanisms having a similar degree of contribution. The GNR coverage does not change the major contributors but only scales the threshold values.

^aThe typical TRPV1 channel density represents the one in human embryonic kidney 293 cell.

Discussion

In this work, we demonstrate the integrated model for GNR-enhanced NINS by incorporating both the TRPV1 channel current and the capacitive current for the first time, to our knowledge. Using this integrated model, we quantitatively compared the contribution from each mechanism under the wide range of different cellular, physical, and optical conditions to photothermal neural activation.

TRPV1 channel current and capacitive current

First, ion movements by the TRPV1 channel current are discussed. As we noted in the result section (Fig. 10 b), the TRPV1 channel current increases after the laser illumination starts. Because the channel is more permeable to calcium ions than other cations (e.g., sodium and potassium ions) and the extracellular free calcium concentration is higher than the intracellular region (24, 37), mainly calcium ions enter into the cell when the channel is open, thereby depolarizing the membrane. The rise of the inward current is sustained during the optical stimulation, except when the large outward current occurs when an action potential fires; therefore, multiple action potentials can be generated during the single-pulse stimulation as far as the laser intensity is strong enough. The direction of current flow is reversed (to the outward current) once the neuron fires an action potential. This outward current is a result of the abrupt increase in membrane potential, as we can expect from Eq. 3 that the direction of the current should become opposite when the membrane potential exceeds the reversal potential of the TRPV1 channel. This outward TRPV1 channel current involves calcium ions as well as potassium ions because the potassium ions dominate the other ions, including calcium, in the intracellular space. The outward TRPV1 channel current, however, has negligible influence on the membrane potential during and after the action potential fires because its amplitude is ∼100 times smaller than the current flowing through the sodium and potassium channels during the period.

When we modeled the TRPV1 channel current with respect to the temperature change, we adopted the relation of Eq. 3 reported by Nilius et al. (27). They obtained the equation based on their patch-clamp experiments, in which they measured the channel current while applying the voltage step. In this patch-clamp experiment, they obtained the nearly steady-state current-voltage relationship and fitted it with a function that combines a linear conductance and a Boltzmann activation term (Eq. 3). In this work, however, our dynamic model simulates transient changes in both the membrane potential and channel currents (along with the other variables as in Eq. 7) for the given temperature time course but uses the quasistatic current-voltage relationship. This can be one of the limitations in our current model, but we do not expect that it might significantly affect the trends found from our final simulation results. Because the membrane potential stays near the resting potential without any large voltage step before the action potential fires, the effect of this steady-to-transient application would be minimal during the initial period of triggering an action potential. Therefore, the relative relations between the threshold values, one of the key findings from this study, will not significantly differ from the true relations. It is noteworthy that the effect can become non-negligible after the initiation of the action potential such that the time course and the absolute threshold value presented in this work might be slightly different from experimental results.

Second, the capacitive current is discussed in more detail. From Eq. 4, the capacitive current can be divided into two components: the one associated with the time-varying capacitance and the other associated with the time-varying potential difference across the lipid bilayer. As shown in Fig. 9 c inset, the capacitance-oriented component (dash-dot) shows inward current at the onset of laser illumination followed by the outward current at the cessation of laser, whereas the potential-oriented component (dashed line) exhibits the opposite directions. However, the magnitude of current peaks of the capacitance-oriented component is greater than that of the potential-oriented component, resulting in a brief inward net current at the beginning and a short outward net current at the end of laser stimulation. This inward net capacitive current occurs only once during a single laser pulse (at its onset), so the capacitive current contributes to the elevation of the membrane potential only once at the onset of the laser irradiation.

Effects of the laser duration, GNR distance, and TRPV1 channel density

First, we discuss the effect of GNR distance in more detail. If the GNRs move away from the membrane, the maximal temperature at the membrane decreases, and more importantly, the slope, which is a critical factor in capacitive mechanism, becomes more gradual because of the characteristic of heat diffusion (Fig. 2). Because of this trend and the fact that the capacitive current depends on the first-order derivative (i.e., slope) of temperature (Fig. 5), the relative contribution of capacitive mechanism decreases as the distance increases. This effect can be seen in our simulation result. In Fig. 12, the data at the laser duration of 0.005 ms and the conductance of 2.1 S ⋅ m^–2 show that the capacitive current makes a slightly larger contribution than the TRPV1 channel (lower threshold) when the distance is 100 nm, but the contribution is slightly smaller than the TRPV1 channel when the distance is 1000 nm. However, differences are very small, and overall, the effect of GNR distance does not have a significant impact on which mechanism makes a major contribution compared to the laser duration and TRPV1 channel density (Table 3).

Second, the effect of laser duration is discussed. Because the capacitive current is highly related to the temperature change (its first-order derivative), capacitive current has a sharp peak right after the onset of the laser pulse, and it falls quickly during the laser stimulation. Therefore, the contribution of the capacitive current mechanism does not change even when the laser duration changes (50 μs ∼ 5 ms) because the initial current peak is responsible for the action potential generation. Interestingly, the contribution of capacitive mechanism decreases (i.e., stimulation threshold increases) when the laser pulse decreases to 5 μs. Because the initial peak of the capacitive current has a finite width, extremely short laser duration on the order of a microsecond would not produce sufficient current to elicit an action potential, and thus stronger laser intensity is required. Moreover, the negative capacitive current occurring at the end of the pulse is so close (in time) to the initial positive current that it might have negatively impacted the initial depolarization, which in turn would make it require higher laser intensity to generate an action potential. On the other hands, TRPV1 channel current is related to the absolute temperature, which results in the steady increase of the current during the laser pulse but just before the action potential fires. Because of the persistent inward current, contribution of the TRPV1 channel increases as the laser duration increases.

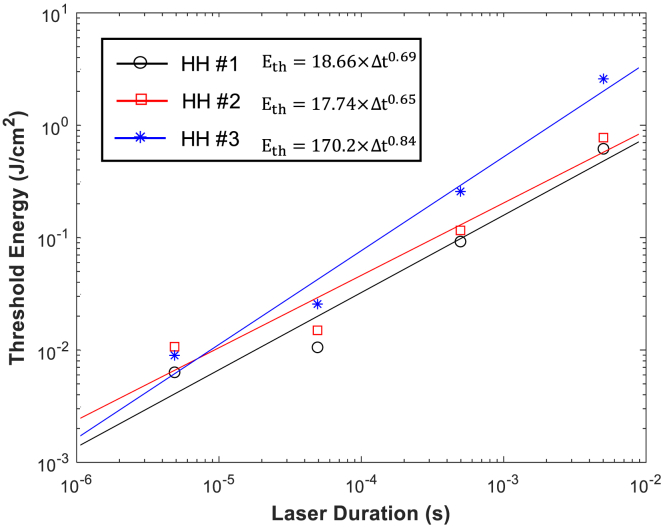
Thus far, the stimulation threshold has been presented in the light intensity (power per unit area) unless otherwise noted. Here, we have plotted the stimulation threshold energy (energy per unit area, E_th) as a function of the duration (Δt) in log-log coordinates at a selected condition for an example (coverage: 0.031, TRPV1 channel density: 2.1 S ⋅ m^–2, and distance: 100 nm), and then fitted the E_th-Δt relation to find the power-law dependency, E_th = a(Δt)^b, as shown in Fig. 13. Meanwhile, Carvalho-de-Souza et al. (38) experimentally determined the power-law exponent (b) in DRG cells to be b = 0.6–0.79 (Figs. 2 E and 3 of the (38)). Because DRG cells have abundant TRPV1 channels (24, 25, 39), it is reasonable to compare the experimental value to our theoretically obtained exponent in the combined mechanism (HH #1) in which TRPV1 channel and capacitive current are both considered (b = 0.69). Although the heat-source materials and the wavelengths of light used in the experimental work are different from those used in our simulation, the theoretical value is in a good agreement with the experimental values.

Figure 13.

Stimulation thresholds in energy per unit area for various laser durations for the capacitive current (blue), the TRPV1 channel current (red), and both (black) considered models. To see this figure in color, go online.

Third, because of the synergetic effect of the TRPV1 channel current and the capacitive current, the power-law exponent of the combined mechanism should be between two values of the individual mechanisms and intriguingly may provide a means to indirectly estimate the TRPV1 channel density, at least in a relative manner. In the above example, the exponent is 0.69, closer to that of the TRPV1-only mechanism. A neural sample with a lower TRPV1 channel density would lead to a higher exponent of the power law. For example, the combined-model exponent determined by our simulation in a lower-density case (1.05 S ⋅ m^–2) becomes high, up to 0.98.

Baseline temperature

We assumed body temperature (36.5°C) as the baseline because we aimed to better understand the GNR-NINS mechanisms in vivo, as we believed that most of the GNR-NINS techniques currently being developed will have in vivo applications as a goal. However, if a GNR-NINS experiment is conducted in vitro under room temperature (25°C), which is lower than body temperature, the TRPV1 channel might not be a robust contributor because its activation temperature is known to be >43°C (28). For this case, other channels (e.g., TRPV4 and TRPV3, with activation temperatures of >25 and 31°C, respectively) will become more important players than the TRPV1 channel (28). Therefore, for accurate numerical simulation of such in vitro experiments, one will need to additionally model the TRPV4 and/or TRPV3 channel. As an additional note, the temperature increment from the body temperature required for action potential generation varies with the conditions such as the laser duration and TRPV1 density but generally ranges between 39 and 43°C.

Comparison of experimental and theoretical results

The simulation results are compared with previously reported experimental data. Our finding that the stimulation threshold (in power per unit area) decreases when the laser duration increases (Fig. 12) agrees with the experiment report in the DRG neuron under GNR-NINS (38) and the gerbil cochlea under INS stimulation (40). The stimulation threshold of HH model #3 (186 W ⋅ cm^–2) obtained at the default parameters shows a good agreement with that experimentally obtained (75.3 W ⋅ cm^–2) in cultured hippocampal neuron samples (8). Another study using a 532 nm wavelength reported a much higher threshold (9), the trend of which agrees with our finding in Fig. S3. Remarkably, the multiple firing per pulse observed in the literature can only be explained by the activation of the temperature-sensitive ion channels (19). When we involved the capacitive current only, it could not explain this observation. To narrow the gap between the theory and practice, complex photothermal heat effect of GNRs such as inhomogeneous distribution of GNRs (e.g., aggregated GNRs) and three-dimensional heat diffusion should be considered. These will also help us to understand the effects of the density of GNRs and their distance from the membrane on GNR-enhanced NINS. For our simulation, because we are focusing on a small region where it is reasonable to assume the GNR sheet and the membrane as infinite planes separated by a small distance, the long distance becomes unrealistic to solve using the one-dimensional heat diffusion equation. We think that for long distances, the actual temperature should be smaller than the calculated temperature. It is worth noting that the TRPV1 channel current varies upon types of tissue because the level of TRPV1 channel expression varies, and thus the TRPV1 conductance should be appropriately selected based on the target simulation tissue.

In conclusion, the theoretical studies presented in this work show that both capacitive and TRPV1 currents, produced by the transient temperature elevation due to LSPR of GNRs, contribute to generation of an action potential. The contribution of TRPV1 channel current increases when the TRPV1 channel conductance increases and/or the distance decreases and/or the duration increases, whereas the orientation and the density of GNRs have no influence on it. We also found that the initial inward capacitive current appears instantly at the onset of laser pulse but the initial inward TRPV1 current increases relatively slowly. When the laser illumination continues after an action potential is triggered, it allows persistent elevation of the TRPV1 current, which can result in another action potential within the single-pulse period, whereas almost no capacitive current is induced until the end of the laser pulse. Thus, multiple action potentials within a single laser pulse can be only explained with the TRPV1 current. This interesting finding could be experimentally tested with TRPV1 channel knockout tissue. This work sheds a new light on our understanding about how NIR-induced GNR LSPR heat evokes an action potential in diverse conditions and in different excitable neural tissue types and thus will facilitate advancing the recently experimented, promising GNR-enhanced NINS strategy for clinical and basic research applications.

Author Contributions

K.E., S.J.K., and J.L. designed research. K.E. performed experiments. K.E., K.M.B., S.J.K., and J.L. analyzed data. K.E., K.M.B., S.B.J., S.J.K., and J.L. wrote the manuscript.

Editor: Vivek Shenoy.