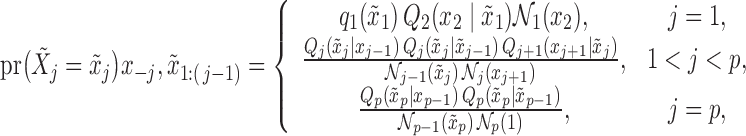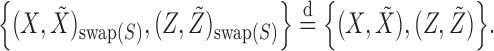SUMMARY
Modern scientific studies often require the identification of a subset of explanatory variables. Several statistical methods have been developed to automate this task, and the framework of knockoffs has been proposed as a general solution for variable selection under rigorous Type I error control, without relying on strong modelling assumptions. In this paper, we extend the methodology of knockoffs to problems where the distribution of the covariates can be described by a hidden Markov model. We develop an exact and efficient algorithm to sample knockoff variables in this setting and then argue that, combined with the existing selective framework, this provides a natural and powerful tool for inference in genome-wide association studies with guaranteed false discovery rate control. We apply our method to datasets on Crohn’s disease and some continuous phenotypes.
Keywords: False discovery rate, Genome-wide association study, Knockoff, Variable selection
1. Introduction
1.1. The need for controlled variable selection
Automatic variable selection is a fundamental challenge in statistics, the urgency of which is induced by the growing reliance of many fields of science on the analysis of large amounts of data. As researchers strive to understand increasingly complex phenomena, the technology of high-throughput experiments allows them to measure and simultaneously examine millions of covariates. However, despite the abundance of variables available, often only a fraction of these are expected to be relevant to the question of interest. By discovering which variables are important, scientists can design a more targeted follow-up investigation and hope to understand how certain factors influence an outcome. A compelling example is offered by genome-wide association studies, whose goal is to identify which markers of genetic variation influence the risk of a particular disease or a trait, choosing from up to millions of single-nucleotide polymorphisms. A good selection algorithm should be able to detect as many relevant variables as possible using only a small number of samples, since these tend to be expensive to acquire. It should also ensure that the findings are replicable. Several statistical techniques have been proposed in an effort to address and balance these conflicting needs. The standard approach in genome-wide association studies is to separately compute a 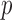 -value for the null hypothesis of no association between the outcome of interest and each polymorphism, using a generalized linear model with one fixed effect and possibly random effects capturing the contribution of all other variables. To identify significant associations, the
-value for the null hypothesis of no association between the outcome of interest and each polymorphism, using a generalized linear model with one fixed effect and possibly random effects capturing the contribution of all other variables. To identify significant associations, the 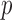 -values may be compared to a threshold that guarantees approximate control of the familywise error rate at the 0
-values may be compared to a threshold that guarantees approximate control of the familywise error rate at the 0 05 level, i.e., the probability of committing at least one Type I error, across all tests. This approach is very conservative and the selected variables, while apparently reproducibly associated with the response, can typically only explain a small portion of the genetic variance in the phenotype of interest (Manolio et al., 2009).
05 level, i.e., the probability of committing at least one Type I error, across all tests. This approach is very conservative and the selected variables, while apparently reproducibly associated with the response, can typically only explain a small portion of the genetic variance in the phenotype of interest (Manolio et al., 2009).
An alternative criterion for evaluating significance is the false discovery rate (Benjamini & Hochberg, 1995). This is attractive when one expects a multiplicity of true discoveries and it has been adopted in studies involving gene expression and many other genomic measurements (Storey & Tibshirani, 2003), including the study of expression quantitative trait loci. A broader adoption of the false discovery rate has been advocated as a natural strategy for improving the power of association studies for complex traits (Sabatti et al., 2003; Storey & Tibshirani, 2003; Brzyski et al., 2017).
Controlled variable selection is inherently difficult in high dimensions, but genome-wide association studies present at least two specific challenges. First, many phenotypes depend on the genetic variants through mechanisms that are mostly unknown (Zuk et al., 2012) and may involve interactions (Carlborg & Haley, 2004). Unfortunately, methods based on marginal testing are ill-equipped to detect interactions and the few current approaches that simultaneously analyse the role of multiple variants rely on linearity assumptions. The second prominent obstacle arises from the presence of correlations between the explanatory variables, as polymorphisms that occupy nearby positions in the genome are tightly linked. This results from the process by which the DNA is transmitted in humans and, as a fundamental characteristic of association studies, it cannot be neglected by methods aiming for valid inference.
These issues motivate the need for methods that can identify important variables for complex phenomena, while providing rigorous guarantees of Type I error control under milder and well-justified assumptions. In the following, we will present our solution and its detailed application to a few studies, after a brief summary of related previous work. Since a few technical terms from genetics appear in this paper, a glossary is included in the Supplementary Material.
1.2. Model-X knockoffs
Knockoffs (Candès et al., 2018) partially address the aforementioned issues by taking a radically different path from the traditional literature on high-dimensional variable selection. They provide a powerful and versatile method that rigorously controls the false discovery rate, under no modelling assumptions on the conditional distribution 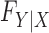 of the response
of the response 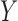 given the covariates
given the covariates 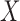 . In fact,
. In fact, 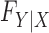 may remain completely unspecified. This result is achieved by considering a setting in which the distribution
may remain completely unspecified. This result is achieved by considering a setting in which the distribution 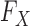 of the covariates is presumed to be known. When this is the case, the latter can be used to generate a new set of artificial variables, the knockoff copies, that serves as a negative control for the original variables. It thus becomes possible to estimate and control the false discovery rate. Since this procedure takes the somewhat unusual path of modelling the covariates instead of the response, we sometimes refer to it as model-X knockoffs. In many circumstances, the premise of model-X knockoffs is arguably more principled than those of its traditional counterparts. In general, it is reasonable to shift the central burden of assumptions from
of the covariates is presumed to be known. When this is the case, the latter can be used to generate a new set of artificial variables, the knockoff copies, that serves as a negative control for the original variables. It thus becomes possible to estimate and control the false discovery rate. Since this procedure takes the somewhat unusual path of modelling the covariates instead of the response, we sometimes refer to it as model-X knockoffs. In many circumstances, the premise of model-X knockoffs is arguably more principled than those of its traditional counterparts. In general, it is reasonable to shift the central burden of assumptions from 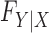 to
to 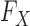 , since the former is the object of inference. In a genome-wide association study, an agnostic approach to the conditional distribution of the response is especially valuable, due to the possibly complex nature of the relations between genetic variants and phenotypes. Moreover, the presumption of knowing
, since the former is the object of inference. In a genome-wide association study, an agnostic approach to the conditional distribution of the response is especially valuable, due to the possibly complex nature of the relations between genetic variants and phenotypes. Moreover, the presumption of knowing 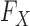 is well-grounded, since geneticists have at their disposal a rich set of models for how DNA variants arise and spread across human populations over time. Genetic variation has been assessed in large collections of individuals: the UK Biobank (Sudlow et al., 2015) contains the genotypes of 500 000 subjects, while hundreds of thousands of additional samples are available from the National Center for Biotechnology Information (Mailman et al., 2007). This combination of theoretical knowledge and data gives us a good understanding of
is well-grounded, since geneticists have at their disposal a rich set of models for how DNA variants arise and spread across human populations over time. Genetic variation has been assessed in large collections of individuals: the UK Biobank (Sudlow et al., 2015) contains the genotypes of 500 000 subjects, while hundreds of thousands of additional samples are available from the National Center for Biotechnology Information (Mailman et al., 2007). This combination of theoretical knowledge and data gives us a good understanding of 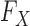 .
.
Since knockoffs require knowledge of the underlying distribution 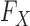 of the original variables, which may not be accessible exactly, in practice some approximation is needed. However, even if the true
of the original variables, which may not be accessible exactly, in practice some approximation is needed. However, even if the true 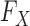 is known, creating the knockoff copies is in general very difficult. To this date, the only special case for which an algorithm has been developed is that of multivariate Gaussian covariates (Candès et al., 2018). In this sense, knockoffs have not yet fully resolved the second crucial difficulty of association studies mentioned earlier, because a multivariate Gaussian approximation cannot fully take advantage of our prior information on the sequential structure of DNA (Wall & Pritchard, 2003). It thus seems important to develop new techniques that can benefit from advances in the study of population genetics and exploit more accurate parametric models for
is known, creating the knockoff copies is in general very difficult. To this date, the only special case for which an algorithm has been developed is that of multivariate Gaussian covariates (Candès et al., 2018). In this sense, knockoffs have not yet fully resolved the second crucial difficulty of association studies mentioned earlier, because a multivariate Gaussian approximation cannot fully take advantage of our prior information on the sequential structure of DNA (Wall & Pritchard, 2003). It thus seems important to develop new techniques that can benefit from advances in the study of population genetics and exploit more accurate parametric models for 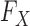 .
.
1.3. Our contributions
In this paper, we introduce a new algorithm to sample knockoff copies of variables distributed as a hidden Markov model. To the best of our knowledge, this result is the first extension of model-X knockoffs beyond the special case of a Gaussian design, and it involves a class of covariate distributions that is of great practical interest. In fact, hidden Markov models are widely employed to describe sequential data with complex correlations.
While many applications of hidden Markov models are found in the context of speech processing (Juang & Rabiner, 1991) and video segmentation (Boreczky & Wilcox, 1998), their presence has also become nearly ubiquitous in the statistical analysis of biological sequences. Important instances include protein modelling (Krogh et al., 1994), sequence alignment (Hughey & Krogh, 1996), gene prediction (Krogh, 1997), copy number reconstruction (Wang et al., 2007), segmentation of the genome into diverse functional elements (Ernst & Kellis, 2012) and identification of ancestral DNA segments (Falush et al., 2003; Tang et al., 2006; Li & Durbin, 2011). Of special interest to us, following the empirical observation that variation along the human genome could be described by blocks of limited diversity (Patil et al., 2001), hidden Markov models have been broadly adopted to describe haplotypes, i.e., the sequence of alleles at a series of markers along one chromosome. The literature is too extensive to recapitulate: starting from some initial formulations (Stephens et al., 2001; Zhang et al., 2002; Qin et al., 2002; Li & Stephens, 2003), a vast set of models and algorithms is used routinely and effectively to reconstruct haplotypes and to impute missing genotype values. Software implementations include fastPHASE (Scheet & Stephens, 2006), Impute (Marchini et al., 2007; Marchini & Howie, 2010), Beagle (Browning & Browning, 2007; Browning & Browning, 2011), Bimbam (Guan & Stephens, 2008) and MaCH (Li et al., 2010). The success of these algorithms in reconstructing partially observed genotypes can be tested empirically, and their realized accuracy is a testament to the fact that hidden Markov models offer a good phenomenological description of the dependence between the explanatory variables in genome-wide association studies.
By developing a suitable construction for the knockoffs, we incorporate the prior knowledge on patterns of genetic variation and obtain a new variable selection method that addresses all the critical issues of association studies discussed in §1.1.
1.4. Related work
This paper is most closely related to Candès et al. (2018), which introduced the framework of model-X knockoffs and considered the special case of multivariate Gaussian variables. Earlier work (Barber & Candès, 2015) developed a closely related methodology specific to linear regression with a fixed design matrix, i.e., fixed-X knockoffs. In the interest of simplicity, in the rest of this paper we will refer to model-X knockoffs simply as knockoffs.
Traditional multivariate variable selection techniques have been applied in genome-wide association studies on numerous occasions. Some works have employed penalized regression, but they either lack Type I error control (Hoggart et al., 2008; Wu et al., 2009) or require very restrictive modelling assumptions (Brzyski et al., 2017). Similarly, their Bayesian alternatives (Li et al., 2011; Guan & Stephens, 2011) do not provide finite-sample guarantees. Some have tried to control the Type I errors of standard penalized regression methods through stability selection (Alexander & Lange, 2011), but the resulting procedure does not correctly account for variable correlations and is less powerful than marginal testing. Others have employed machine learning tools (Bureau et al., 2005) that can produce variable importance measures but no valid inference. In theory, some inferential guarantees have been obtained for the lasso (Zhao & Yu, 2006; Candès & Plan, 2009), generalized linear models (van de Geer et al., 2014) and even random forests (Wager & Athey, 2018), but they only hold under rather stringent sparsity assumptions.
Hidden Markov models have appeared before as part of a variable selection procedure for association studies, in order to combine marginal tests of association from correlated polymorphisms (Sun & Cai, 2009; Wei et al., 2009). However, this approach is fundamentally different from ours, since it is not multivariate and makes very different modelling assumptions.
2. Controlled variable selection via knockoffs
2.1. Problem statement
The controlled variable selection problem can be stated in formal terms by adopting the general setting of Candès et al. (2018). Suppose that we can observe a response 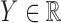 and a vector of covariates
and a vector of covariates 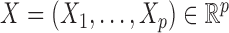 . Given
. Given 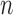 such samples
such samples 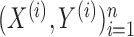 drawn from a population, we would like to know which variables are associated with the response. This can be made more precise by assuming that the observations are sampled independently from
drawn from a population, we would like to know which variables are associated with the response. This can be made more precise by assuming that the observations are sampled independently from
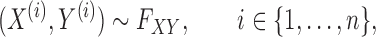 |
for some joint distribution 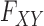 . The concept of a relevant variable can be understood by first defining its opposite. We say that
. The concept of a relevant variable can be understood by first defining its opposite. We say that 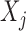 is null if and only if
is null if and only if 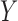 is independent of
is independent of 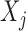 , conditionally on all other variables
, conditionally on all other variables 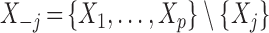 . This uniquely defines the set of null covariates
. This uniquely defines the set of null covariates 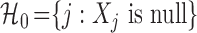 and the complement
and the complement 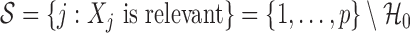 . Our goal is to obtain an estimate
. Our goal is to obtain an estimate 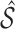 of
of 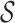 while controlling the false discovery rate, the expected value of the false discovery proportion,
while controlling the false discovery rate, the expected value of the false discovery proportion,
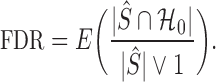 |
We emphasize the logic of this definition: a variable is null if it has no predictive power once we take into account all the other variables, i.e., it does not influence the response in any way. To relate this to traditional inference, in a generalized linear model, being null is equivalent to having a vanishing regression coefficient, under an extremely mild condition (Candès et al., 2018).
2.2. The limitations of marginal testing
Although by far the most common data analysis strategy in genome-wide association studies, marginal inference is not necessarily a principled choice, but rather one of convenience. Indeed, the scientific goal is to uncover the genetic basis of complex traits, those that are expected to be influenced by a large number of possibly interacting genetic variants. In this framework, the most natural model for relating a trait to genetic polymorphisms includes many such DNA variations. Adopting the simplifying additive assumption that is pervasive in genetics, one might be interested in estimating a generalized linear model that relates the trait value to a linear combination of the allele counts at many polymorphisms. Indeed, the statistical genetics literature documents many contributions in this direction, both in the Bayesian (Hoggart et al., 2008; Guan & Stephens, 2011) and in the frequentist (Wu et al., 2009) setting, as more comprehensively reviewed in Sabatti (2013). Yet, approaches that study the effects of many variants jointly, and try to identify the contribution of each one conditional on the rest, have not become part of the standard analysis pipeline for genome-wide data, even if they are the prevalent approach for variants prioritization and follow-up studies (Hormozdiari et al., 2014). This is due to difficulties encountered in articulating an effective genome-wide search for variants that influence the phenotype given every other polymorphism. These range from considerations of computational and data manipulation convenience, e.g., handling of missing data, to the challenge of distinguishing the contribution of highly correlated neighbouring variants, to the fact that, until recently, high-dimensional model selection strategies lacked finite-sample guarantees on the quality of the selected set. The contribution of this paper stems from the observation that this latest impasse can now in principle be overcome by deploying the knockoffs framework (Candès et al., 2018). We will describe how we handle the other difficulties in §6.1 and §7. For an up-to-date discussion of the advantages of investigating the effects of a variant in the context of all other recorded polymorphisms, see Brzyski et al. (2017).
2.3. The method of knockoffs
The main idea in Candès et al. (2018) is to generate a set of artificial covariates that have the same structure as the original ones but are known to be null. These are called the knockoff copies of 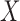 and they can be used as negative controls to estimate the false discovery rate with almost any existing variable selection algorithm. In this paper, we develop new methods for sampling the knockoff copies, but we do not alter other aspects of the variable selection procedure of Candès et al. (2018). Therefore, we only present a short summary below, leaving a more detailed description for the Supplementary Material.
and they can be used as negative controls to estimate the false discovery rate with almost any existing variable selection algorithm. In this paper, we develop new methods for sampling the knockoff copies, but we do not alter other aspects of the variable selection procedure of Candès et al. (2018). Therefore, we only present a short summary below, leaving a more detailed description for the Supplementary Material.
For each variable 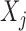 , we need to construct a knockoff copy
, we need to construct a knockoff copy 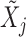 in such a way that
in such a way that 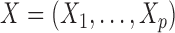 and
and 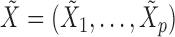 satisfy the following conditions:
satisfy the following conditions:
 |
(1) |
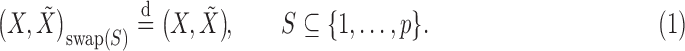 |
(2) |
Above, the symbol 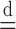 indicates equality in distribution, while
indicates equality in distribution, while 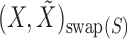 denotes the vector obtained by swapping the entries
denotes the vector obtained by swapping the entries 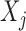 and
and 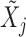 for each
for each 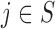 . The pairwise exchangeability condition (2) requires the distribution of
. The pairwise exchangeability condition (2) requires the distribution of 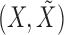 to be invariant under this transformation. As we discuss later, (2) is essential and it is not always easy to produce a nontrivial, i.e., different from
to be invariant under this transformation. As we discuss later, (2) is essential and it is not always easy to produce a nontrivial, i.e., different from 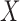 itself, vector
itself, vector 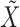 that satisfies it. We refer to (1) as the nullity condition, since it implies that all knockoff copies are null variables in the augmented model that includes both
that satisfies it. We refer to (1) as the nullity condition, since it implies that all knockoff copies are null variables in the augmented model that includes both 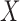 and
and 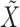 . This clearly holds whenever
. This clearly holds whenever 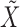 is constructed without looking at
is constructed without looking at 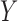 .
.
Once we have the knockoff copies 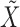 , we can perform controlled variable selection in two steps. First, we compute feature importance statistics
, we can perform controlled variable selection in two steps. First, we compute feature importance statistics 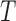 and
and 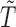 , such that
, such that 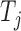 and
and 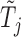 measure the importance of
measure the importance of 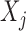 and
and 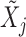 in predicting
in predicting 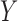 , for each
, for each 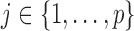 . For example, we can think of
. For example, we can think of 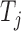 and
and 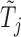 as the magnitudes of the lasso coefficients for
as the magnitudes of the lasso coefficients for 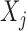 and
and 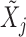 , obtained by regressing
, obtained by regressing 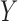 on
on 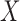 and
and 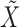 jointly, although many other options are available. Then, we combine them into a vector
jointly, although many other options are available. Then, we combine them into a vector 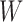 with
with 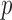 entries defined as
entries defined as 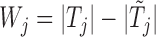 . Intuitively, a positive and large value of
. Intuitively, a positive and large value of 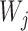 indicates that the
indicates that the  th variable is truly important. More precisely, the knockoff filter of Barber & Candès (2015) is used to compute a data-dependent significance threshold
th variable is truly important. More precisely, the knockoff filter of Barber & Candès (2015) is used to compute a data-dependent significance threshold 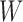 in such a way as to select important variables with provable control of the false dicovery rate. In summary, knockoffs can be seen as a versatile wrapper that makes it possible to extend rigorous statistical guarantees, under very mild assumptions, to powerful practical methods that would otherwise be too complex for a direct theoretical analysis.
in such a way as to select important variables with provable control of the false dicovery rate. In summary, knockoffs can be seen as a versatile wrapper that makes it possible to extend rigorous statistical guarantees, under very mild assumptions, to powerful practical methods that would otherwise be too complex for a direct theoretical analysis.
2.4. Constructing knockoffs
In §2.3 we have said that the knockoff variables need to satisfy the nullity and pairwise exchangeability properties, (1) and (2). We now develop exact and computationally efficient procedures for the case in which 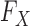 corresponds to a Markov chain or a hidden Markov model, inspired by following result.
corresponds to a Markov chain or a hidden Markov model, inspired by following result.
Proposition 1 (Appendix B in Candès et al., 2018).
Let
be a vector of
covariates with some known distribution
. Suppose that, with a single iteration over
, we sequentially sample
from
, independently of the observed value of
. Then, the vector
that we obtain is a knockoff copy of
.
The conditional distribution above of 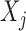 given all the other variables
given all the other variables 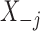 and
and 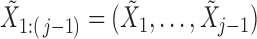 depends on the knockoff copies generated during the previous iterations, and it can be very difficult to compute in general, even though the distribution of
depends on the knockoff copies generated during the previous iterations, and it can be very difficult to compute in general, even though the distribution of 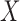 is known. Therefore, Proposition 1 suggests a general recipe, but obtaining a practical algorithm is not always straightforward.
is known. Therefore, Proposition 1 suggests a general recipe, but obtaining a practical algorithm is not always straightforward.
3. Knockoffs for Markov chains
We begin by focusing our attention on discrete Markov chains. Formally, we say that a vector of random variables 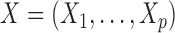 , each taking values in a finite state space
, each taking values in a finite state space 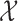 , is distributed as a discrete Markov chain if its joint probability mass function can be written as
, is distributed as a discrete Markov chain if its joint probability mass function can be written as
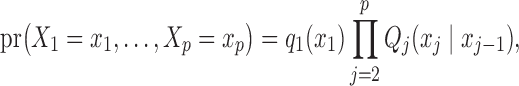 |
(3) |
where 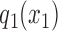 denotes the marginal distribution of the first element of the chain and the transition matrices between consecutive variables are
denotes the marginal distribution of the first element of the chain and the transition matrices between consecutive variables are 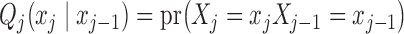 .
.
Our first result, whose proof can be found in the Supplementary Material, provides a way of sampling exact knockoff copies of a discrete Markov chain.
Proposition 2.
Suppose that
is distributed as the Markov chain in (3), with known parameters
. Then, a knockoff copy
can be obtained by sequentially sampling, with a single iteration over
, the
th knockoff variable
from
(4) with the normalization functions
defined recursively as
(5) Therefore, Algorithm 1 is an exact procedure for sampling knockoff copies of a Markov chain.
Algorithm 1.
Knockoff copies of a discrete Markov chain.
For
to
:
For
in
:
Compute
according to (5).
Sample
according to (4).
At each step  of Algorithm 1, the evaluation of the normalization function
of Algorithm 1, the evaluation of the normalization function 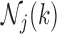 involves a sum over all elements of the finite state space
involves a sum over all elements of the finite state space  and depends only on the previous
and depends only on the previous 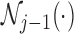 . Since this operation must be repeated for all values of
. Since this operation must be repeated for all values of 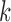 , sampling the
, sampling the 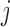 th knockoff variable requires
th knockoff variable requires 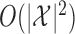 time, where
time, where 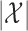 is the number of possible states of the Markov chain. This procedure is sequential, generating one knockoff variable at a time. Therefore, the total computation time is
is the number of possible states of the Markov chain. This procedure is sequential, generating one knockoff variable at a time. Therefore, the total computation time is 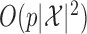 , while the required memory is
, while the required memory is 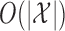 . It is also trivially parallelizable if one wishes to construct a knockoff copy for each of
. It is also trivially parallelizable if one wishes to construct a knockoff copy for each of 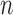 independent Markov chains. These features make Algorithm 1 efficient and suitable for high-dimensional applications.
independent Markov chains. These features make Algorithm 1 efficient and suitable for high-dimensional applications.
4. Knockoffs for hidden Markov models
4.1. Hidden Markov models
A hidden Markov model assumes the presence of a latent Markov chain, whose states are not directly visible but conditional on which the observations are independently sampled. Formally, we say that 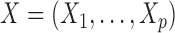 , taking values in a finite state space
, taking values in a finite state space 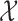 , is distributed as a hidden Markov model with
, is distributed as a hidden Markov model with 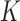 hidden states if there exists a vector
hidden states if there exists a vector 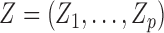 such that
such that
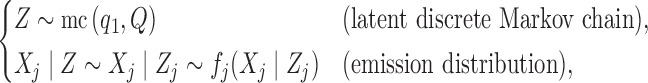 |
(6) |
where 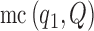 indicates the law of a discrete Markov chain as in (3), with each element
indicates the law of a discrete Markov chain as in (3), with each element 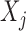 taking values in
taking values in 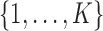 . Conditional on
. Conditional on 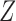 , each
, each 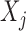 is sampled independently from the emission distribution
is sampled independently from the emission distribution 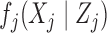 . We emphasize that we are restricting our attention to these discrete distributions solely for simplicity. At the price of slightly more involved notation, the knockoff construction can easily be extended to continuous emission distributions.
. We emphasize that we are restricting our attention to these discrete distributions solely for simplicity. At the price of slightly more involved notation, the knockoff construction can easily be extended to continuous emission distributions.
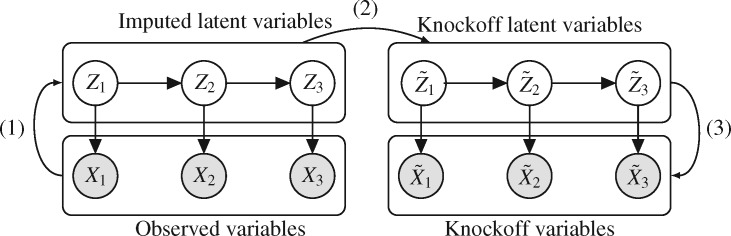
4.2. Generating knockoffs for hidden Markov models
The observed variables 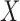 in the hidden Markov model (6) do not satisfy the Markov property. In fact, computing the conditional distributions
in the hidden Markov model (6) do not satisfy the Markov property. In fact, computing the conditional distributions 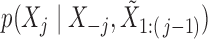 from Proposition 1 would involve a sum over all possible configurations of
from Proposition 1 would involve a sum over all possible configurations of 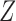 . The complexity of this operation is exponential in
. The complexity of this operation is exponential in 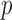 , thus making the naïve approach unfeasible even for moderately large datasets. Our solution is inspired by the traditional forward-backward methods for hidden Markov models. Having observed
, thus making the naïve approach unfeasible even for moderately large datasets. Our solution is inspired by the traditional forward-backward methods for hidden Markov models. Having observed 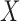 , we propose to construct a knockoff copy
, we propose to construct a knockoff copy 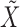 according to Algorithm 2.
according to Algorithm 2.
Algorithm 2.
Knockoff copies of a hidden Markov model.
Sample
from
using Algorithm 3.
Sample a knockoff copy
of
using Algorithm 1.
Sample
from
, which is easy by conditional independence.
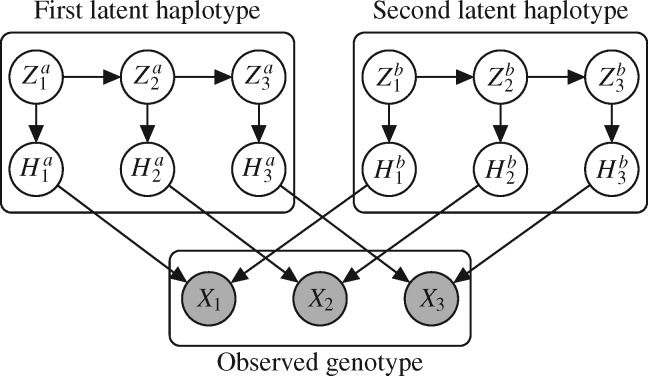
A graphical representation of Algorithm 2 is shown in Fig. 1. In the first stage, the latent Markov chain is imputed by sampling from the conditional distribution of 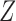 given
given 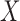 . This is done efficiently with Algorithm 3, a forward-backward iteration discussed in the Supplementary Material and similar to the Viterbi algorithm. Once
. This is done efficiently with Algorithm 3, a forward-backward iteration discussed in the Supplementary Material and similar to the Viterbi algorithm. Once 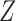 has been sampled, a knockoff copy
has been sampled, a knockoff copy 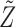 can be obtained with Algorithm 1. Finally, we sample
can be obtained with Algorithm 1. Finally, we sample 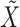 from
from 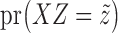 , which is easy because of the conditional independence between the emission distributions in the hidden Markov model.
, which is easy because of the conditional independence between the emission distributions in the hidden Markov model.
Fig. 1.
Sketch of Algorithm 2 for knockoff copies of a hidden Markov model, in the case 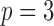 .
.
Algorithm 3.
Forward-backward sampling for a hidden Markov model.
Initialize
,
and
for all
.
For
to
(forward pass):
For
to
:
.
For
to
(backward pass):
Sample
according to
.
Return
.
The computation time required by Algorithms 1 and 3 is 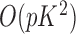 , while the complexity of the final stage is simply
, while the complexity of the final stage is simply 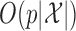 because the emission distributions are independent conditional on the latent Markov chain. Therefore, Algorithm 2 runs in
because the emission distributions are independent conditional on the latent Markov chain. Therefore, Algorithm 2 runs in 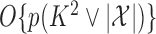 time. The following two results establish the correctness of this approach.
time. The following two results establish the correctness of this approach.
Proposition 3.
Suppose that
is observed from the hidden Markov model in (6), with known parameters
. Then, Algorithm 3 produces an exact sample from the conditional distribution of its latent Markov chain
given
.
Theorem 1.
Suppose that
is observed from the hidden Markov model in (6), with known parameters
. Then
generated by Algorithm 2 is a knockoff copy of
. That is, for any subset
,
(7) In particular, this implies that
is a knockoff copy of
.
Proof.
It suffices to prove (7), since marginalizing over
implies that
has the same distribution as
. Conditioning on the values of the latent variables, one can write
The first equality above follows from line 1 of Algorithm 2 and Proposition 3, whose proof can be found in the Supplementary Material. The second equality follows from the conditional independence of the emission distributions in a hidden Markov model. The third equality follows from
being a knockoff copy of
, as established in Proposition 2. □
5. Hidden Markov models in genome-wide association studies
5.1. Modelling single-nucleotide polymorphisms
In a genome-wide association study, the response 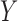 is the status of a disease or a quantitative trait of interest, while each sample of
is the status of a disease or a quantitative trait of interest, while each sample of 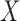 consists of the genotype for a set of single-nucleotide polymorphisms. In particular, we consider the case in which
consists of the genotype for a set of single-nucleotide polymorphisms. In particular, we consider the case in which 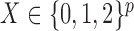 collects unphased genotypes. For simplicity, in this section we restrict our attention to a single chromosome, since distinct ones are typically assumed to be independent. Different hidden Markov models have been proposed to describe the block-like patterns observed in the distribution of the alleles at adjacent markers, but in this paper we adopt the model implemented in fastPHASE (Scheet & Stephens, 2006) and outlined below. We opt for this model because we find that it has both an intuitive interpretation and remarkable computational efficiency. However, our knockoff construction from §4 can easily be implemented with other parameterizations.
collects unphased genotypes. For simplicity, in this section we restrict our attention to a single chromosome, since distinct ones are typically assumed to be independent. Different hidden Markov models have been proposed to describe the block-like patterns observed in the distribution of the alleles at adjacent markers, but in this paper we adopt the model implemented in fastPHASE (Scheet & Stephens, 2006) and outlined below. We opt for this model because we find that it has both an intuitive interpretation and remarkable computational efficiency. However, our knockoff construction from §4 can easily be implemented with other parameterizations.
The unphased genotype of an individual can be seen as the componentwise sum of two unobserved sequences, called haplotypes 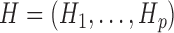 , where
, where  is a binary variable representing the allele on the
is a binary variable representing the allele on the 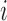 th marker. The main modelling assumption is that the two haplotypes are independent and identically distributed as hidden Markov models. This idea is sketched in Fig. 2 for
th marker. The main modelling assumption is that the two haplotypes are independent and identically distributed as hidden Markov models. This idea is sketched in Fig. 2 for 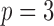 . In order to precisely describe this model, we begin by focusing on a single sequence
. In order to precisely describe this model, we begin by focusing on a single sequence 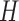 . Its distribution is in the same form as the model defined earlier in (6),
. Its distribution is in the same form as the model defined earlier in (6),
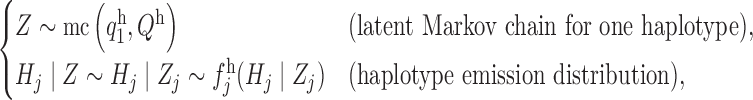 |
with a latent Markov chain 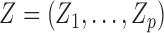 whose elements indicate membership in one of
whose elements indicate membership in one of 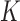 groups of closely related haplotypes. These groups are characterized by specific allele frequencies at the various markers, so that one can see
groups of closely related haplotypes. These groups are characterized by specific allele frequencies at the various markers, so that one can see 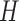 as a mosaic of segments, each originating from one of
as a mosaic of segments, each originating from one of 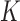 distinct motifs that can be loosely taken as representing the genome of the population founders. This model provides a good description of the local patterns of correlation, but it is phenomenological in nature and should not be interpreted as an accurate representation of the real sequence of mutations and recombinations that originate the population haplotypes.
distinct motifs that can be loosely taken as representing the genome of the population founders. This model provides a good description of the local patterns of correlation, but it is phenomenological in nature and should not be interpreted as an accurate representation of the real sequence of mutations and recombinations that originate the population haplotypes.
Fig. 2.
Sequence of 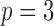 genotype polymorphisms (shaded) as the componentwise sum of two hidden Markov model haplotypes (white).
genotype polymorphisms (shaded) as the componentwise sum of two hidden Markov model haplotypes (white).
The marginal distribution of the first element of the hidden Markov chain 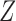 is
is
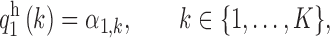 |
while the transition matrices are
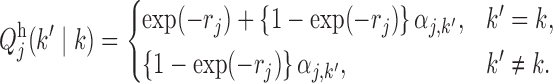 |
The parameters 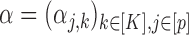 describe the propensity of different motifs to succeed each other. The occurrence of a transition is regulated by the values of
describe the propensity of different motifs to succeed each other. The occurrence of a transition is regulated by the values of 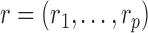 , which are intuitively related to the genetic recombination rates. Once a sequence of ancestral segments is fixed, the allele
, which are intuitively related to the genetic recombination rates. Once a sequence of ancestral segments is fixed, the allele 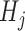 in position
in position 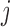 is sampled from the emission distribution
is sampled from the emission distribution
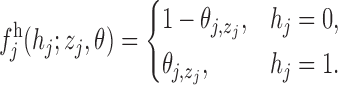 |
The parameters 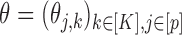 represent the probabilities of the alleles being equal to 1, for each of the
represent the probabilities of the alleles being equal to 1, for each of the 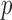 polymorphisms and the
polymorphisms and the 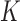 ancestral haplotype motifs. These can be estimated along with
ancestral haplotype motifs. These can be estimated along with 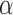 and
and 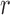 .
.
Having defined the distribution of 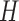 , we return our attention to the observed genotype vector. By definition, the genotype
, we return our attention to the observed genotype vector. By definition, the genotype 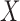 of an individual is obtained by pairing, marker by marker, the alleles on each haplotype and discarding information on the haplotype of origin, i.e., the phase. Then, under standard assumptions such as the Hardy–Weinberg equilibrium, the population from which the genotype vector of a subject is randomly sampled can be described as the elementwise sum of two independent and identical haplotype distributions described by the above model. Consequently, its distribution is also a hidden Markov model. The latent Markov chain has bivariate states, corresponding to unordered pairs of haplotype latent states. It is easy to verify that these can take
of an individual is obtained by pairing, marker by marker, the alleles on each haplotype and discarding information on the haplotype of origin, i.e., the phase. Then, under standard assumptions such as the Hardy–Weinberg equilibrium, the population from which the genotype vector of a subject is randomly sampled can be described as the elementwise sum of two independent and identical haplotype distributions described by the above model. Consequently, its distribution is also a hidden Markov model. The latent Markov chain has bivariate states, corresponding to unordered pairs of haplotype latent states. It is easy to verify that these can take 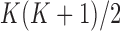 possible values. By this construction, it follows that the initial-state probabilities for the genotype model are
possible values. By this construction, it follows that the initial-state probabilities for the genotype model are
 |
(8) |
and the transition matrices are
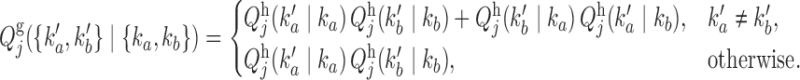 |
(9) |
Similarly, the emission probabilities for 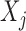 are
are
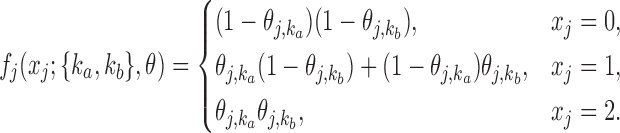 |
(10) |
5.2. Parameter estimation
The construction of knockoff copies requires knowing the distribution of the covariates, as discussed in §2.3. However, exact knowledge is unrealistic in practical applications and some degree of approximation is ultimately unavoidable. Since we have argued that the model in (8)– (10) offers a sensible and tractable description of real genotypes, it makes sense to estimate the 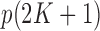 parameters in
parameters in 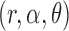 from the data. In the usual setting for genome-wide association studies, one has available
from the data. In the usual setting for genome-wide association studies, one has available 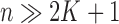 observations for each of the
observations for each of the 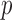 sites, so this task is not unreasonable. Moreover, the validity of this approach is empirically verified in our simulations with real genetic covariates, as discussed in the next section. Alternatively, if additional unsupervised observations, i.e., including only the covariates, from the same population are available, one could include them to improve the estimation.
sites, so this task is not unreasonable. Moreover, the validity of this approach is empirically verified in our simulations with real genetic covariates, as discussed in the next section. Alternatively, if additional unsupervised observations, i.e., including only the covariates, from the same population are available, one could include them to improve the estimation.
All parameters can be efficiently estimated with a standard expectation-maximization technique in 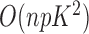 time, as already implemented in the freely available imputation software fastPHASE. This fits the model described above, for the original purpose of recovering missing observations, and it conveniently provides the estimates
time, as already implemented in the freely available imputation software fastPHASE. This fits the model described above, for the original purpose of recovering missing observations, and it conveniently provides the estimates 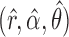 . An important advantage of the hidden Markov model is that the number of parameters only grows linearly in
. An important advantage of the hidden Markov model is that the number of parameters only grows linearly in 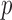 , thus greatly reducing the risk of overfitting compared to a multivariate Gaussian approximation. The complexity of this model is controlled by the number
, thus greatly reducing the risk of overfitting compared to a multivariate Gaussian approximation. The complexity of this model is controlled by the number 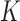 of haplotype motifs, whose typical recommended values are in the range of 10 (Scheet & Stephens, 2006) and can be fine-tuned with crossvalidation. Even though the theoretical guarantee of false discovery rate control with knockoffs requires
of haplotype motifs, whose typical recommended values are in the range of 10 (Scheet & Stephens, 2006) and can be fine-tuned with crossvalidation. Even though the theoretical guarantee of false discovery rate control with knockoffs requires 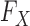 to be known, we have observed that our procedure is robust with respect to estimation, by performing several numerical experiments discussed in the next section and in the Supplementary Material.
to be known, we have observed that our procedure is robust with respect to estimation, by performing several numerical experiments discussed in the next section and in the Supplementary Material.
6. Numerical simulations
6.1. Numerical simulation with real genetic covariates
We now verify the power and robustness of our procedure with real covariates obtained from a genome-wide association study. We consider 29 258 polymorphisms on chromosome 1, genotyped in 14 708 individuals from WTCCC (2007). Following Candès et al. (2018), we simulate the response from a conditional logistic regression model of 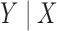 with
with 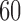 nonzero coefficients, as described in the Supplementary Material.
nonzero coefficients, as described in the Supplementary Material.
Before applying our procedure, we reduce the number of covariates by pruning. This is desirable due to the presence of extremely high correlations between neighbouring sites, which makes it fundamentally impossible to distinguish nearly identical variables with a limited amount of data. Our solution uses hierarchical clustering to identify groups of sites in such a way that no two polymorphisms in different clusters have correlation greater than 0 5. Then, within each group we identify a single representative that is most strongly associated with the phenotype in a hold-out set of 1000 observations, described in more detail in the Supplementary Material. At this point, we will use knockoffs to perform variable selection on the cluster representatives, thus effectively interpreting these groups as the basic units of inference among which we search for important variables. Far from removing all correlations and making variable selection trivial, by pruning we acknowledge that a limited amount of data only allows limited resolution. Had we more data, we would prune less. This approach is also consistent with the common practice in genome-wide association studies of interpreting findings as identifying regions in the genome rather than as individual polymorphisms.
5. Then, within each group we identify a single representative that is most strongly associated with the phenotype in a hold-out set of 1000 observations, described in more detail in the Supplementary Material. At this point, we will use knockoffs to perform variable selection on the cluster representatives, thus effectively interpreting these groups as the basic units of inference among which we search for important variables. Far from removing all correlations and making variable selection trivial, by pruning we acknowledge that a limited amount of data only allows limited resolution. Had we more data, we would prune less. This approach is also consistent with the common practice in genome-wide association studies of interpreting findings as identifying regions in the genome rather than as individual polymorphisms.
Having reduced the number of variables to 5260 by pruning, we split the samples, i.e., the rows of 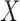 , into 10 subsets and separately fit the model of §5.1 with fastPHASE, using the default settings and assuming the presence of
, into 10 subsets and separately fit the model of §5.1 with fastPHASE, using the default settings and assuming the presence of 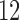 latent haplotype clusters. Once the parameters are estimated, we construct the knockoff copies using Algorithm 2. With our implementation, this takes approximatively 0
latent haplotype clusters. Once the parameters are estimated, we construct the knockoff copies using Algorithm 2. With our implementation, this takes approximatively 0 1 seconds on a single core of a 2
1 seconds on a single core of a 2 60 GHz Intel Xeon CPU for each individual. We run the knockoffs procedure on each split, adopting as variable importance measures the magnitudes of the logistic regression coefficients fitted with a
60 GHz Intel Xeon CPU for each individual. We run the knockoffs procedure on each split, adopting as variable importance measures the magnitudes of the logistic regression coefficients fitted with a 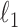 -norm penalty tuned by crossvalidation. The knockoff filter is then applied at level
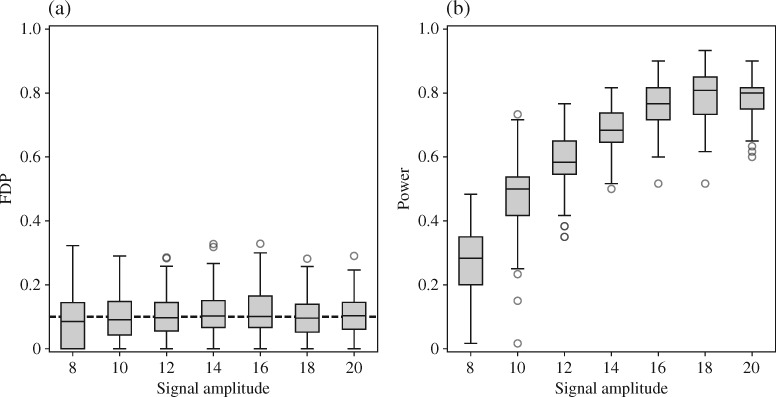
-norm penalty tuned by crossvalidation. The knockoff filter is then applied at level 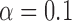 and with offset equal to 0. The power and proportion of false discoveries are estimated by comparing our selections to the true logistic model, counting a finding as true if and only if any of the polymorphisms in the selected cluster has a nonzero coefficient. The entire experiment is repeated 10 times, starting with the choice of the logistic model. This yields 100 point estimates for the power and false discovery rate, whose empirical distribution is shown in Fig. 3 and Table 1, for different values of the signal amplitude. We have also applied the knockoff filter with offset, i.e., its slightly more conservative version, as explained in the Supplementary Material. As shown in Table 1, the value of the offset is of little practical consequence, except when very few discoveries are made, i.e., for a weak signal.
and with offset equal to 0. The power and proportion of false discoveries are estimated by comparing our selections to the true logistic model, counting a finding as true if and only if any of the polymorphisms in the selected cluster has a nonzero coefficient. The entire experiment is repeated 10 times, starting with the choice of the logistic model. This yields 100 point estimates for the power and false discovery rate, whose empirical distribution is shown in Fig. 3 and Table 1, for different values of the signal amplitude. We have also applied the knockoff filter with offset, i.e., its slightly more conservative version, as explained in the Supplementary Material. As shown in Table 1, the value of the offset is of little practical consequence, except when very few discoveries are made, i.e., for a weak signal.
Fig. 3.
(a) False discovery proportion, FDP, and (b) power of our procedure with real genetic variables. A box represents 100 experiments. The dashed black line in (a) indicates the target level 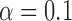 . The offset of the knockoff filter is set equal to 1.
. The offset of the knockoff filter is set equal to 1.
Table 1.
False discovery rate and power, in percentage, for the experiment of Fig. 3 with 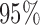 normal confidence intervals, i.e., standard errors multiplied by
normal confidence intervals, i.e., standard errors multiplied by 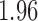 , with and without offset
, with and without offset
| Signal amplitude | FDR (95% c.i.) | Power (95% c.i.) | ||
|---|---|---|---|---|
| Offset 0 | Offset 1 | Offset 0 | Offset 1 | |
| 8 | 9 3 3 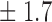
|
4 7 7 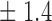
|
27 9 9 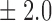
|
17 3 3 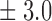
|
| 10 | 10 3 3 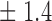
|
7 6 6 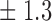
|
47 9 9 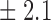
|
42 2 2 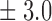
|
| 12 | 10 6 6 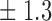
|
8 2 2 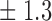
|
59 1 1 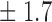
|
55 8 8 
|
| 14 | 11 1 1 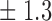
|
9 1 1 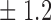
|
68 4 4 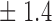
|
66 7 7 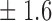
|
| 16 | 11 8 8 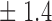
|
9 7 7 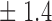
|
76 0 0 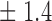
|
74 3 3 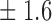
|
| 18 | 10 1 1 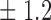
|
8 0 0 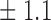
|
79 1 1 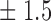
|
77 9 9 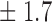
|
| 20 | 10 5 5 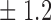
|
8 7 7 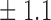
|
78 3 3 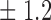
|
77 6 6 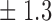
|
c.i., confidence interval.
The results show that the false discovery rate is controlled and suggest that one can safely apply our method to a genome-wide association study. Our confidence derives from the fact that our procedure enjoys the rigorous robustness of knockoffs for any conditional distribution of the phenotype. As far as Type I error control is concerned, it does not seem consequential that in this experiment we have chosen to simulate the response from a generalized linear model. In fact, the false discovery rate is provably controlled for any 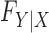 , provided that
, provided that 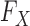 is well-specified. Since we have not artificially simulated the covariates but used real genotypes, we can see no reason why our procedure should not similarly enjoy the same control on a real association study.
is well-specified. Since we have not artificially simulated the covariates but used real genotypes, we can see no reason why our procedure should not similarly enjoy the same control on a real association study.
7. Applications to genome-wide association studies
7.1. Analysis of genome-wide association data
We apply our procedure to data from two association studies: the Northern Finland 1966 Birth Cohort study of metabolic syndrome (Sabatti et al., 2009), accession number phs000276.v2.p1, and the Wellcome Trust Case Control Consortium study of Crohn’s disease (WTCCC, 2007).
The metabolic syndrome study comprises observations on 5402 individuals from northern Finland, including genotypes for approximately 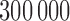 polymorphisms and nine phenotypes. We focus on measurements of cholesterol, triglyceride levels and height, as there is a rich literature on their genetic bases that we can rely upon for comparison. Since not all outcome measurements are available for every subject, the effective values of
polymorphisms and nine phenotypes. We focus on measurements of cholesterol, triglyceride levels and height, as there is a rich literature on their genetic bases that we can rely upon for comparison. Since not all outcome measurements are available for every subject, the effective values of 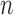 are different for each phenotype and a little lower than 5402. From the Crohn’s disease study, we analyse 2996 control and
are different for each phenotype and a little lower than 5402. From the Crohn’s disease study, we analyse 2996 control and 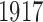 disease samples typed at
disease samples typed at 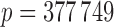 polymorphisms.
polymorphisms.
We pre-process the data as described in the Supplementary Material and reduce the number of variables by pruning with the same method used in the numerical simulation of §6.1. Then, we perform variable selection using our knockoff procedure. Before applying Algorithm 2 to construct the knockoff copies, we estimate the parameters 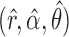 of the hidden Markov model from §5.1 using fastPHASE, separately for each of the first 22 chromosomes. Since the estimation of the covariate distribution does not make use of the response, we compute a single set of estimates for all phenotypes in the metabolic syndrome study, and a separate one for the Crohn’s disease study. In both cases, we run fastPHASE with a prespecified number of latent haplotype clusters
of the hidden Markov model from §5.1 using fastPHASE, separately for each of the first 22 chromosomes. Since the estimation of the covariate distribution does not make use of the response, we compute a single set of estimates for all phenotypes in the metabolic syndrome study, and a separate one for the Crohn’s disease study. In both cases, we run fastPHASE with a prespecified number of latent haplotype clusters 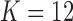 . With its default settings, the imputation software estimates
. With its default settings, the imputation software estimates 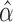 with the additional constraint that
with the additional constraint that 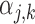 can only depend on the first index
can only depend on the first index 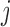 . For simplicity, we do not modify this setting.
. For simplicity, we do not modify this setting.
Having sampled the knockoff copies, we assess variable importance as in §6.1, by performing a lasso regression of 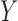 on the standardized knockoff-augmented matrix of covariates
on the standardized knockoff-augmented matrix of covariates 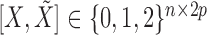 , with a regularization parameter
, with a regularization parameter 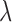 chosen through ten-fold crossvalidation. For the Crohn’s disease study the response is binary and we use logistic regression with an
chosen through ten-fold crossvalidation. For the Crohn’s disease study the response is binary and we use logistic regression with an 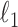 -norm penalty instead of the lasso. Relevant polymorphisms are then selected by applying the knockoff filter with target level
-norm penalty instead of the lasso. Relevant polymorphisms are then selected by applying the knockoff filter with target level 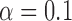 and offset equal to
and offset equal to 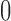 .
.
7.2. Results
We performed the analysis described above on the four datasets. Since our method is not deterministic, in each case the selections depend on the realization of 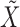 . Repeating the procedure multiple times and cherry-picking the results would obviously violate the control of the false discovery rate, so we instead display all findings that are selected at least 10 times over 100 independent repeats of the knockoffs procedure. This is only supposed to provide the reader with an impression of the variability of our method, since in principle control of the false discovery rate does not necessarily hold if one aggregates selections obtained with different realizations of
. Repeating the procedure multiple times and cherry-picking the results would obviously violate the control of the false discovery rate, so we instead display all findings that are selected at least 10 times over 100 independent repeats of the knockoffs procedure. This is only supposed to provide the reader with an impression of the variability of our method, since in principle control of the false discovery rate does not necessarily hold if one aggregates selections obtained with different realizations of 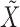 . Finding a good way of combining these selections remains an open research problem.
. Finding a good way of combining these selections remains an open research problem.
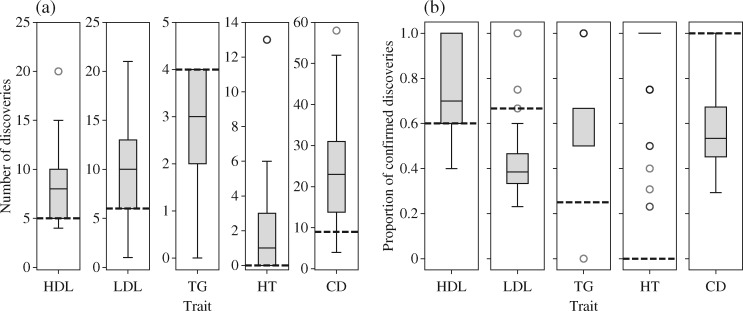
While we do not have sufficient experimental evidence to assess which of our discoveries are true, we can compare our results to those of studies carried out on much larger samples and consider these as the only available approximation of the truth. For lipids we rely on Global Lipids Genetics Consortium (2013), for height on Wood et al. (2014) and Marouli et al. (2017), and for Crohn’s disease on Franke et al. (2010). Since different studies include slightly different sets of polymorphisms and our analysis involves a pruning phase, some care has to be taken in deciding when findings match. Each of our clusters spans a genomic locus that can be described by the positions of the first and last polymorphisms. We consider one of our findings to be replicated if the larger study reports as significant a variable whose position is within the region spanned by the cluster we discover.
Our procedure identifies a larger number of potentially significant loci than traditional methods based on marginal testing, except in the case of triglycerides, for which very few findings are obtained with either approach. In Fig. 4(a), the distribution of the number of discoveries over 100 independent realizations of our knockoff variables is compared to the corresponding fixed quantity from the standard genomic analysis on the same dataset, as performed in the earlier works cited above. We can thus verify that, while our procedure is not deterministic, we consistently select more variables. In Fig. 4(b), we show the proportion of our discoveries that is confirmed by the corresponding meta-analyses, separately for each dataset. If we tried to naïvely estimate the false discovery rate from these plots, we would obtain a value much larger than the target level 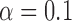 , but this would not be very meaningful because none of the meta-analyses is believed to have correctly identified all relevant associations. Instead, some perspective can be gained by comparing our proportion of confirmed discoveries to that obtained with marginal testing on the same data. In the case of one type of cholesterol and triglycerides, our confirmed proportion is appreciably higher, even though one may have intuitively expected a better agreement between studies relying on the same testing framework.
, but this would not be very meaningful because none of the meta-analyses is believed to have correctly identified all relevant associations. Instead, some perspective can be gained by comparing our proportion of confirmed discoveries to that obtained with marginal testing on the same data. In the case of one type of cholesterol and triglycerides, our confirmed proportion is appreciably higher, even though one may have intuitively expected a better agreement between studies relying on the same testing framework.
Fig. 4.
Discoveries made on different datasets: (a) Total number of discoveries; (b) proportion of the discoveries that are confirmed by the meta-analysis. The boxplots refer to our method, while the dashed black lines represent the standard genomic analysis with the same data. The phenotypes are cholesterol, HDL, LDL; triglycerides, TG; height, HT, and Crohn’s disease, CT.
It should not be surprising that our results are at least partially consistent with those of previous studies. In spite of the fact that our method relies on fundamentally different principles, we have selected relevant variables after computing importance measures based on sparse generalized linear regression. The robustness of our Type I error control is completely unaffected by the validity of such a model, but a bias towards the discovery of additive linear effects naturally arises. In future studies, one may discover additional associations by easily deploying our procedure with more complex nonlinear measures of feature importance.
8. Discussion
Conditionally on 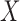 and
and 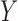 , the selections depend on the specific realization of the knockoffs
, the selections depend on the specific realization of the knockoffs 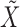 . Different repetitions of our procedure provide reasonably consistent answers on the same data, but at this point it is not clear how to best aggregate the different results.
. Different repetitions of our procedure provide reasonably consistent answers on the same data, but at this point it is not clear how to best aggregate the different results.
In our analysis of genetic data, we have pruned the variables during the pre-processing phase and restricted the inference to the representatives for each group. Alternatively, one could try to adapt the idea of group knockoffs in Dai & Barber (2016) to our method.
Different parameterizations of the hidden Markov model have been developed within the genotype imputation community and they can be easily exploited by our procedure. For example, if a collection of known haplotypes is available, it is possible to include them in the description of 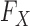 used to generate the knockoff copies. It would be interesting to investigate from an applied perspective the relative advantages of one choice over another.
used to generate the knockoff copies. It would be interesting to investigate from an applied perspective the relative advantages of one choice over another.
Since we have computed variable importance measures based on generalized linear models, even though our false discovery rate control does not rely on any assumptions of linearity, the power may be negatively affected if the true likelihood is far from linear. In order to fully exploit the flexibility and robustness of knockoffs, it would be interesting to explore the use of alternative statistics that can better capture interactions and nonlinearities, e.g., trees.
At this point we know how to perform controlled variable selection with knockoffs in the special cases where the variables can be described by either a hidden Markov model or a multivariate normal distribution. It would be interesting to extend this to other classes of covariates, such as more general graphical models.
Supplementary Material
Acknowledgement
Candès was partially supported by the U.S. Office of Naval Research and by a Math+X Award from the Simons Foundation. Sesia was partially supported by the U.S. National Institutes of Health and the Simons Foundation. We thank Lucas Janson for inspiring discussions and for sharing his computer code.
Supplementary material
Supplementary material available at Biometrika online includes proofs of the theoretical results, a summary of existing knockoff methodology, further methodological details related to the numerical simulation and the data analysis, and a glossary of relevant technical terms from genetics.
References
- Alexander, D. H. & Lange, K. (2011). Stability selection for genome-wide association. Genet. Epidemiol. 35, 722–8. [DOI] [PubMed] [Google Scholar]
- Barber, R. F. & Candès, E. J. (2015). Controlling the false discovery rate via knockoffs. Ann. Statist. 43, 2055–85. [Google Scholar]
- Benjamini, Y. & Hochberg, Y. (1995). Controlling the false discovery rate: A practical and powerful approach to multiple testing. J. R. Statist. Soc. B 57, 289–300. [Google Scholar]
- Boreczky, J. S. & Wilcox, L. D. (1998). A hidden Markov model framework for video segmentation using audio and image features. In Proc. 1998 IEEE Int. Conf. Acoust. Speech Sig. Proces., vol. 6 IEEE. [Google Scholar]
- Browning, S. & Browning, B. (2007). Rapid and accurate haplotype phasing and missing-data inference for whole-genome association studies by use of localized haplotype clustering. Am. J. Hum. Genet. 81, 1084–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Browning, S. R. & Browning, B. L. (2011). Haplotype phasing: Existing methods and new developments. Nature Rev. Genet. 12, 703–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brzyski, D., Peterson, C. B., Sobczyk, P., Candès, E. J., Bogdan, M. & Sabatti, C. (2017). Controlling the rate of GWAS false discoveries. Genetics 205, 61–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bureau, A., Dupuis, J., Falls, K., Lunetta, K. L., Hayward, B., Keith, T. P. & Van Eerdewegh, P. (2005). Identifying SNPs predictive of phenotype using random forests. Genet. Epidemiol. 28, 171–82. [DOI] [PubMed] [Google Scholar]
- Candès, E. J., Fan, Y., Janson, L. & Lv, J. (2018). Panning for gold: ‘model-X’ knockoffs for high dimensional controlled variable selection. J. R. Statist. Soc. B 80, 551–77. [Google Scholar]
-
Candès, E. J. & Plan, Y. (2009). Near-ideal model selection by
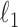 minimization. Ann. Statist. 37, 2145–77. [Google Scholar]
minimization. Ann. Statist. 37, 2145–77. [Google Scholar] - Carlborg, O. & Haley, C. S. (2004). Epistasis: Too often neglected in complex trait studies? Nature Rev. Genet. 5, 618–25. [DOI] [PubMed] [Google Scholar]
- Dai, R. & Barber, R. (2016). The knockoff filter for FDR control in group-sparse and multitask regression. In Proc. 33rd Int. Conf. Mach. Learn., Balcan M. F. & Weinberger K. Q., eds., vol. 48 of Proceedings of Machine Learning Research. New York: Association for Computing Machinery. [Google Scholar]
- Ernst, J. & Kellis, M. (2012). ChromHMM: Automating chromatin-state discovery and characterization. Nature Meth. 9, 215–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Falush, D., Stephens, M. & Pritchard, J. K. (2003). Inference of population structure using multilocus genotype data: Linked loci and correlated allele frequencies. Genetics 164, 1567–87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franke, A., McGovern, D. P. B., Barrett, J. C., Wang, K., Radford-Smith, G. L., Ahmad, T., Lees, C. W., Balschun, T., Lee, J., Roberts, R. et al. (2010). Genome-wide meta-analysis increases to 71 the number of confirmed Crohn’s disease susceptibility loci. Nature Genet. 42, 1118–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Global Lipids Genetics Consortium (2013). Discovery and refinement of loci associated with lipid levels. Nature Genet. 45, 1274–83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guan, Y. & Stephens, M. (2008). Practical issues in imputation-based association mapping. PLOS Genet. 4, 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guan, Y. & Stephens, M. (2011). Bayesian variable selection regression for genome-wide association studies and other large-scale problems. Ann. Appl. Statist. 5, 1780–815. [Google Scholar]
- Hoggart, C. J., Whittaker, J. C., De Iorio, M. & Balding, D. J. (2008). Simultaneous analysis of all SNPs in genome-wide and re-sequencing association studies. PLOS Genet. 4, 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hormozdiari, F., Kostem, E., Kang, E. Y., Pasaniuc, B. & Eskin, E. (2014). Identifying causal variants at loci with multiple signals of association. Genetics 198, 497–508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hughey, R. & Krogh, A. (1996). Hidden Markov models for sequence analysis: Extension and analysis of the basic method. Bioinformatics 12, 95–107. [DOI] [PubMed] [Google Scholar]
- Juang, B. H. & Rabiner, L. R. (1991). Hidden Markov models for speech recognition. Technometrics 33, 251–72. [Google Scholar]
- Krogh, A. (1997). Two methods for improving performance of a HMM and their application for gene finding. In Proc. 5th Int. Conf. on Intelligent Systems for Molecular Biology, Gaasterland, T. Karp, P. Karplus, K. Ouzounis, G. Sander C. & Valencia, A. eds. Menlo Park, California: AAAI Press, pp. 179–86. [PubMed] [Google Scholar]
- Krogh, A., Brown, M., Mian, I., Sjӧlander, K. & Haussler, D. (1994). Hidden Markov models in computational biology. J. Molec. Biol. 235, 1501–31. [DOI] [PubMed] [Google Scholar]
- Li, H. & Durbin, R. (2011). Inference of human population history from individual whole-genome sequences. Nature 475, 493–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li, J., Das, K., Fu, G., Li, R. & Wu, R. (2011). The Bayesian lasso for genome-wide association studies. Bioinformatics 27, 516–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li, N. & Stephens, M. (2003). Modeling linkage disequilibrium and identifying recombination hotspots using single-nucleotide polymorphism data. Genetics 165, 2213–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li, Y., Willer, C. J., Ding, J., Scheet, P. & Abecasis, G. R. (2010). MaCH: Using sequence and genotype data to estimate haplotypes and unobserved genotypes. Genet. Epidemiol. 34, 816–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mailman, M. D., Feolo, M., Jin, Y., Kimura, M., Tryka, K., Bagoutdinov, R., Hao, L., Kiang, A., Paschall, J., Phan, L.. et al. (2007). The NCBI dbGaP database of genotypes and phenotypes. Nature Genet. 39, 1181–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manolio, T. A., Collins, F.S., Cox, N.J., Goldstein, D.B., Hindorff, L.A., Hunter, D.J., McCarthy, M.I., Ramos, E.M., Cardon, L.R., Chakravarti, A.. et al. (2009). Finding the missing heritability of complex diseases. Nature 461, 747–53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marchini, J. & Howie, B. (2010). Genotype imputation for genome-wide association studies. Nature Rev. Genet. 11, 499–511. [DOI] [PubMed] [Google Scholar]
- Marchini, J., Howie, B., Myers, S., McVean, G. & Donnelly, P. (2007). A new multipoint method for genome-wide association studies by imputation of genotypes. Nature Genet. 39, 906–13. [DOI] [PubMed] [Google Scholar]
- Marouli, E., Graff, M., Medina-Gomez, C., Lo, K.S., Wood, A.R., Kjaer, T.R., Fine, R.S., Lu, Y., Schurmann, C., Highland, H.M.. et al. (2017). Rare and low-frequency coding variants alter human adult height. Nature 542, 186–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patil, N., Berno, A.J., Hinds, D.A., Barrett, W.A., Doshi, J.M., Hacker, C.R., Kautzer, C.R., Lee, D.H., Marjoribanks, C., McDonough, D.P.. et al. (2001). Blocks of limited haplotype diversity revealed by high-resolution scanning of human chromosome 21. Science 294, 1719–23. [DOI] [PubMed] [Google Scholar]
- Qin, Z. S., Niu, T. & Liu, J. S. (2002). Partition-ligation-expectation-maximization algorithm for haplotype inference with single-nucleotide polymorphisms. Am. J. Hum. Genet. 71, 1242–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sabatti, C. (2013). Multivariate linear models for GWAS In Advances in Statistical Bioinformatics, Do, K.-A. Qin Z. & Vannucci, M. eds. Cambridge: Cambridge University Press, pp. 188–207. [Google Scholar]
- Sabatti, C., Hartikainen, A.-L., Pouta, A., Ripatti, S., Brodsky, J., Jones, C.G., Zaitlen, N.A., Varilo, T., Kaakinen, M., Sovio, U.. et al. (2009). Genome-wide association analysis of metabolic traits in a birth cohort from a founder population. Nature Genet. 41, 35–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sabatti, C., Service, S. & Freimer, N. (2003). False discovery rate in linkage and association genome screens for complex disorders. Genetics 164, 829–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheet, P. & Stephens, M. (2006). A fast and flexible statistical model for large-scale population genotype data: Applications to inferring missing genotypes and haplotypic phase. Am. J. Hum. Genet. 78, 629–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stephens, M., Smith, N. J. & Donnelly, P. (2001). A new statistical method for haplotype reconstruction from population data. Am. J. Hum. Genet. 68, 978–89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storey, J. D. & Tibshirani, R. J. (2003). Statistical significance for genomewide studies. Proc. Nat. Acad. Sci. 100, 9440–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sudlow, C., Gallacher, J., Allen, N., Beral, V., Burton, P., Danesh, J., Downey, P., Elliott, P., Green, J., Landray, M.. et al. (2015). UK Biobank: An open access resource for identifying the causes of a wide range of complex diseases of middle and old age. PLoS Med. 12, e1001779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun, W. & Cai, T. T. (2009). Large-scale multiple testing under dependence. J. R. Statist. Soc. B 71, 393–424. [Google Scholar]
- Tang, H., Coram, M., Wang, P., Zhu, X. & Risch, N. (2006). Reconstructing genetic ancestry blocks in admixed individuals. Am. J. Hum. Genet. 79, 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van de Geer, S., Buhlmann, P., Ritov, Y. & Dezeure, R. (2014). On asymptotically optimal confidence regions and tests for high-dimensional models. Ann. Statist. 42, 1166–202. [Google Scholar]
- Wager, S. & Athey, S. (2018). Estimation and inference of heterogeneous treatment effects using random forests. J. Am. Statist. Assoc. DOI: 10.1080/01621459.2017.1319839. [DOI] [Google Scholar]
- Wall, J. D. & Pritchard, J. K. (2003). Haplotype blocks and linkage disequilibrium in the human genome. Nature Rev. Genet. 4, 587–97. [DOI] [PubMed] [Google Scholar]
- Wang, K., Li, M., Hadley, D., Liu, R., Glessner, J., Grant, S. F., Hakonarson, H. & Bucan, M. (2007). PennCNV: An integrated hidden Markov model designed for high-resolution copy number variation detection in whole-genome SNP genotyping data. Genome Res. 17, 1665–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei, Z., Sun, W., Wang, K. & Hakonarson, H. (2009). Multiple testing in genome-wide association studies via hidden Markov models. Bioinformatics 25, 2802–8. [DOI] [PubMed] [Google Scholar]
- Wood, A. R., Esko, T., Yang, J., Vedantam, S., Pers, T.H., Gustafsson, S., Chu, A.Y., Estrada, K., Luan, J., Kutalik, Z.. et al. (2014). Defining the role of common variation in the genomic and biological architecture of adult human height. Nature Genet. 46, 1173–86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- WTCCC (2007). Genome-wide association study of 14,000 cases of seven common diseases and 3,000 shared controls. Nature 447, 661–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu, T. T., Chen, Y. F., Hastie, T. J., Sobel, E. & Lange, K. (2009). Genome-wide association analysis by lasso penalized logistic regression. Bioinformatics 25, 714–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, K., Deng, M., Chen, T., Waterman, M. S. & Sun, F. (2002). A dynamic programming algorithm for haplotype block partitioning. Proc. Nat. Acad. Sci. 99, 7335–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao, P. & Yu, B. (2006). On model selection consistency of lasso. J. Mach. Learn. Res. 7, 2541–63. [Google Scholar]
- Zuk, O., Hechter, E., Sunyaev, S. R. & Lander, E. S. (2012). The mystery of missing heritability: Genetic interactions create phantom heritability. Proc. Nat. Acad. Sci. 109, 1193–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.