Abstract
Exploration of brain dynamics patterns has attracted increasing attention due to its fundamental significance in understanding the working mechanism of the brain. However, due to the lack of effective modeling methods, how the simultaneously recorded LFP can inform us about the brain dynamics remains a general challenge. In this paper, we propose a novel sparse coding based method to investigate brain dynamics of freely-behaving mice from the perspective of functional connectivity, using super-long local field potential (LFP) recordings from thirteen distinct regions of the mouse brain. Compared with surrogate datasets, six and four reproducible common functional connectivities (CFCs) were discovered to represent the space of brain dynamics in the frequency bands of alpha and theta respectively. Modeled by a finite state machine (FSM), temporal transition framework of functional connectivities was inferred for each frequency band, and evident preference was discovered. Our results offer a novel perspective for analyzing neural recording data at such high temporal resolution and recording length, as common functional connectivities and their transition framework discovered in this work reveal the nature of the brain dynamics in freely behaving mice.
Keywords: local field potential (LFP), brain dynamics, sparse coding, freely behaving, volume conduction
1. Introduction
Studying functional connectivity of the brain has recently received increasing interest due to its significant importance in basic and clinical neuroscience (Koenig et al. 2002; Friston et al. 2003; Biswal et al. 2010; Williams 2010; Mueller et al. 2013). In early studies, functional connectivity has been widely assumed to be temporally stationary (Wang et al. 2006; Lynall et al. 2010; Liu 2011; Ou et al. 2015) , where the data during the whole scan were used for estimating functional connectivity. However, there are accumulating evidences (Fox and Raichle 2007; Gilbert and Sigman 2007; Smith et al. 2012) indicating that brain activities are under dramatic temporal changes at various time scales. For instance, it has been found that each cortical brain area runs different ‘‘programs’’ according to the cognitive context and to the current perceptual requirements, where intrinsic cortical circuits mediate the moment-by-moment functional state changes in the brain (Gilbert and Sigman 2007). Inspired by the important observations on the brain dynamics from prior studies, there have been many studies aiming to quantitatively characterize the temporal dynamics and transition patterns of functional brain connectivity (Khan et al. 2013; Li et al. 2013; Ou et al. 2014; Tomescu et al. 2014; Lopour et al. 2016; Allen et al. 2017).
Functional neuroimaging has been a major tool for neuroscience research and clinical applications, whose capability far determines our knowledge. Recently, functional neuroimaging techniques such as fMRI (Koshino et al. 2005; Di et al. 2008; Ryali et al. 2012), EEG (Koenig et al. 1999; Stam et al. 2007; Van Mierlo et al. 2014), and LFP (Adrian and Moruzzi 1939; Hubel and Wiesel 1962; Hamill et al. 1981; Pinault 1996) have been widely used for such functional connectivity data acquisition and modeling. However, there are key methodological and technical limitations in fMRI/EEG-based brain connectivity dynamics studies. Specifically, fMRI-based brain connectivity dynamics is limited by its temporal resolution and the lack of time series data with sufficient length (Fox and Raichle 2007). The EEG-based studies have much better temporal resolution and much longer scan length. However, as EEG only measures the scalp electric potential field, it lacks the spatial accuracy for more precise neuroscience studies (Lee et al. 2009; Da Silva 2013). Recently, the local field potential (LFP), as recorded with high-impedance (small contact size) microelectrodes, is thought to reflect synaptic activity in the vicinity of the microelectrode (Katzner et al. 2009; Khawaja et al. 2009). Highlighted in high temporal resolution, precise spatial accuracy and sufficiently-long recording length on cellular-level neural activities, the direct measurement of local field potentials (LFPs) at all depths throughout the brain in a freely behaving animal provides us a new way to explore the dynamic interactions between individual neurons and local networks (Lin et al. 2005; Klausberger and Somogyi 2008; Uhlhaas et al. 2010; Donner and Siegel 2011). Recently, many studies used LFP recordings from animals, such as mice (Nauhaus et al. 2009), monkeys (Ray and Maunsell 2011; Hu and Liang 2013), ferrets (Stitt et al. 2017), cats (Katzner et al. 2009) etc., to investigate functional brain connectivity and its dynamics. In terms of functional segregation and coordination, LFP recordings with high spatio-temporal resolution would greatly benefit better understanding the mechanisms of perception, attention, learning, etc.
In order to investigate the functional brain connectivity and its dynamics via simultaneously recorded LFP, we selected thirteen distinct regions from the mouse brain, which have close relationship with the processing of stimulus recognition and fear-conditioning memory. Specifically, the hippocampal CA1 (CA1) (Gigg et al. 2000; Chen et al. 2009; Zhang et al. 2013), dentate gyrus (DG) (Xavier and Costa 2009; Nakashiba et al. 2012), subiculum (S) (O’Mara 2005; O Mara 2015; Fröhlich 2016; Eichenbaum 2017), retrosplenial cortices (RSG & RSA) (Pothuizen et al. 2009; Czajkowski et al. 2014), are crucial for associative fear memories, and subregions of the anterior cingulate cortices (Cg1 & Cg2) (Pardo et al. 1990; Bush et al. 2000), prelimbic cortex (PrL) (Vidalgonzalez et al. 2006; Ye et al. 2017) encode emotionally fearful experiences. Besides, somatosensory cortices (S2Tr & S1HL), secondary auditory cortex (AuV) encode inputs of stimulus. Lateral entorhinal cortex (LEnt) (Gigg et al. 2000; Wilson et al. 2013; Kuruvilla and Ainge 2017) plays a role in encoding space, particularly the current and previous locations of objects within the local environment. The perirhinal cortex (PRh) (Murray et al. 2007; Kinnavane et al. 2016) is involved in both visual perception and memory, and it facilitates the recognition and identification of environmental stimulus These regions constitute the main network of fearful memory processing, which benefit us to investigate the brain activities in freely behaving condition.
To explore brain dynamics of freely-behaving mice, such as what constitutes the transition space of brain dynamics, and how functional connectivities temporally transit across such a space, in this paper, we propose a novel sparse coding based method. We used a state-of-the-art 512-channel tetrode recording system (Xie et al. 2016) to record super-long LFP data (about 2 million time points) for each freely behaving mouse. To circumvent the problem of volume conduction artefact (Buchthal et al. 1957; van den Broek et al. 1998; Kajikawa and Schroeder 2011), the imaginary part of coherency (iCoh) (i.e., excluding the zero-phase lag part) was applied to robustly measure brain functional connectivity (Nolte et al. 2004; Garcia et al. 2013; Sanchez Bornot et al. 2018). As functional connectivity changed systematically across brain states with largest changes occurring in the phase synchronization of theta and alpha oscillations (He et al. 2011; Stitt et al. 2017), in this paper, we focused on the dynamics of functional connectivity in frequency bands of alpha and theta. Inspired by the superior performances of sparse coding in numerous signal processing and neuroimaging analysis (Olshausen and Field 1996; Donoho and Elad 2003; Olshausen and Field 2004; Smith and Lewicki 2006; Wright et al. 2009), we employed an efficient sparse coding method of stochastic coordinate coding (SCC) (Lin et al. 2014) to discover underlying functional connectivities, which sparsely encode the brain dynamics. By hierarchically clustering, we discovered six common functional connectivities (CFCs) for alpha band and four for theta. Further investigation with finite state machine (FSM) revealed a dominant CFC and evident preference in the temporal transitions among CFCs. In general, the proposed method and the results can add new insights into the neuroscience researches for better understanding the brain dynamics through a data-driven approach supported by advanced recording techniques.
2. Materials and Methods
2.1. Overview
In order to explore the dynamics of functional brain connectivity hidden in LFP, we simultaneously recorded LFP signals of thirteen distinct brain regions from three mice via 512-channel tetrode system, with sampling rate 1,000 Hz and recording lengths of 2,045,004, 1,863,283 and 2,268,864 time points for each mouse respectively. Then, functional brain connectivity based on thirteen brain regions was represented via the imaginary part of coherency (iCoh) measurement. By efficient sparse coding of stochastic coordinate coding (SCC) algorithm, an over-complete dictionary was obtained, from which CFCs were derived by Bayesian Information Criterion (BIC). Furthermore, a transition framework modeled by finite state machine (FSM) was established to estimate the transition of CFCs. Details will be described in the following sections.
2.2. Data Acquisition and Processing
Animal Subjects
Three adult male mice were used for experiments, and detailed information of each mouse on surgery day is shown in Table 1. All mice were maintained by the trained Animal Facility staff and an experienced veterinarian who conducted routine daily health surveillance. All animal handling and tissue preparation were performed in accordance with NIH guideline and the protocols approved by IAUCC committee at Augusta University.
Table 1.
Information of mice subjects
| Mouse #1 | Mouse #2 | Mouse #3 | |
|---|---|---|---|
| Age (days) | 81 | 83 | 86 |
| Weight (g) | 28.6 | 29.5 | 33.3 |
512-Channel Tetrode System
The names, abbreviations, region index, stereotaxic coordinates, and tetrode numbers of thirteen carefully selected brain regions are shown in Table 2. The electrode positions are pre-calibrated according to these brain-region coordinates provided by the Mouse Brain Atlas (Franklin and Paxinos 2001).
Table 2.
Configurations of thirteen brain regions.
| Name | Abbreviations | Region Index |
Stereotaxic Coordinates |
Tetrodes (Channels) |
|---|---|---|---|---|
| Hippocampal CA1 | CA1 | 1 | −3.8 mm AP, ± 3.0 mm ML |
16 (64) |
| Dentate Gyrus | DG | 2 | −3.75 mm AP, ± 2.0 mm ML |
16 (64) |
| S1 Trunk Region of the Somatosensory Cortex | S1Tr | 3 | −1.6 mm AP, ± 1.75 mm ML |
8 (32) |
| S1 Hind Limb of the Somatosensory Cortex | S1HL | 4 | −1.1 mm AP, ± 1.5 mm ML |
8 (32) |
| Granular Cortex of the Retrosplenial Cortex | RSG | 5 | −2.3 mm AP, ± 0.3 mm ML |
8 (32) |
| Agranular Cortex of the Retrosplenial Cortex | RSA | 6 | −2.3 mm AP, ± 0.6 mm ML |
8 (32) |
| Subiculum | S | 7 | −3.08 mm AP, ± 1.5 mm ML |
8 (32) |
| Perirhinal Cortex | PRh | 8 | −3.80 mm AP |
8 (32) |
| Lateral Entorhinal Cortex | LEnt | 9 | −3.80 mm AP |
16 (64) |
| Secondary Auditory Cortex Ventral Portion | AuV | 10 | −1.94 mm AP, ± 4.75 mm ML |
8 (32) |
| Cg1 of Anterior Cingulate Cortices | Cg1 | 11 | +0.50 mm AP, ± 0.3 mm ML |
8 (32) |
| Cg2 of Anterior Cingulate Cortices | Cg2 | 12 | +0.50 mm AP, ± 0.6 mm ML |
8 (32) |
| Prelimbic Cortex | PrL | 13 | +1.70 mm AP, ± 0.5 mm ML |
8 (32) |
All positions were measured with respect to the bregma point. “AP” and “ML” are short for anteroposterior and mediolateral.
The recording tetrodes were made up of four wires, which were twisted together using a manual turning device and soldered with a low-intensity heat source. The impedances of tetrodes were typically between 0.7 and 1 MΩ. Importantly, the recording ends of the tetrodes were cut differentially so that multiple recording sites, located at different depths, could be reached. In order to minimize tissue damage, only tetrodes, but not the surrounding polyimide tubes, were inserted into the brain tissue. Thirteen modular bundles of tetrodes targeting these thirteen brain regions were used to record the neuronal electrical activity simultaneously as shown in Fig.2. More details about configurations of 512-channel tetrode system are described in Supplementary Materials.
Fig. 2.
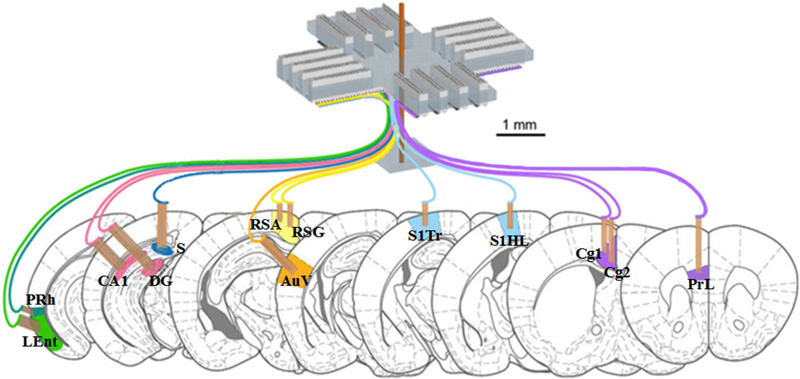
The design of the 512-channel tetrode system for recording in a total of thirteen different brain regions in mice. Bundles in same color are grouped in a single module. The scale is marked by black bar.
The surgery could be completed in about five hours for each mouse, and for chronic recordings, the mice were allowed to recover for 3 ∼ 5 days before the experiment began. Helium balloons were applied to balance the system’s weight, so that the mouse with the implanted part and cables could move around freely enough. LFPs were recorded once the 512-channel cables were connected to the 512-channel Plexon multiplex-recording system (Lin et al. 2006; Kuang et al. 2010). Since the recordings were almost the same among the 4 channels in a single tetrode, we selected the highest amplitude channel without cut-offs from each tetrode for the recording. The stability of the ensemble recordings was verified by comparing waveforms at the beginning, during, and after the experiments, and the analysis showed that the units recorded could maintain good separation and stability over days or even week(s).
2.3. Functional Brain Connectivity Representation
LFP signals of 128 tetrodes from thirteen brain regions are obtained by 512-channel tetrode system. To eliminate the ill effects of few tetrodes of signals, as well as to avoid the potential collinearity problem, we further select only one tetrode LFP signal for each brain region by correlation strength, which is described in supplementary material in detail.
Compared with other commonly used functional connectivity measures, such as Pearson correlation coefficient, mutual information, and magnitude squared coherence, the imaginary part of coherency is the most robust to VC artifact theoretically and practically (Khadem and Hossein-Zadeh 2013). Coherency is a measure of the linear relationship at a specific frequency between two signals. Given two time series xi(t) and xj(t)of signal i and j, their complex Fourier transforms are xi(f) and xj(f) respectively. Coherency is now defined as below:
| (1) |
| (2) |
where Sij(f) is the cross-spectrum, * means complex conjugation, and ⟨ ⟩ means expectation value. The expectation value can be estimated as an average over a sufficiently large number of epochs in practice.
In the case of brain dynamics, we are interested in the alteration of brain states along time. Therefore, in order to acquire the dependence of coherency as a function of the time, we applied a sliding window with length T of 500 msec (typically between 250 msec and 1 s) (Nolte et al. 2004; Sander et al. 2010; Garcia et al. 2013; Sanchez Bornot et al. 2018), which is small enough for the desired time-resolution, given by T (500 msec) itself, and large enough for the desired frequency resolution, given by 1/T (2Hz). According to recent studies (Van De Ville et al. 2010; He et al. 2011; Keilholz 2014), which suggested that continuous resting states could be classified into a limited number of micro states for a time on the order of 100 msec, the window skipping step was determined as 100 msec. Coherency then becomes a function of both frequency and time:
| (3) |
where t indicates the time of the center of the window. Then, the summation of coherency was calculated according to the frequency range (alpha: 8~12 Hz, theta: 4~8 Hz) as the coherency of a certain frequency band.
| (4) |
where B indicates the frequency band.
We represent brain connectivity by the imaginary part of coherency (iCoh), which captures true source interactions at a given time-lag. The imaginary part of coherency cannot be generated by artefact of volume conduction (Nolte et al. 2004), which cannot cause a time-lag. Therefore, the functional brain connectivity composed by 13 brain regions can be represented as below:
| (5) |
As FC is a skew-symmetric matrix, to reduce dimension, the upper triangular elements of FC are picked up and reshaped to a vector with 78 (13×12/2) features, and indicates the functional connectivity vector (FCV) at time point t.
2.4. Common Functional Connectivity Estimation
Functional brain connectivity represented by the imaginary part of the coherency is a linear combination of a few independent atomic common functional connectivities (derivation process is presented in supplementary material in detail). Therefore, investigating brain functional connectivity represented by iCoh can be transformed into solving a sparse coding problem. Considering the big data of super-long LFP recordings, a highly effective sparse coding method, stochastic coordinate coding (SCC), was applied in this paper.
Given the FCV time series X = (x1,…, xn), each FCV is a p dimensional vector, xi ∈ ℝp (i = 1,…,n). Here is a set D containing m items dj ∈ ℝp, (j = 1,…,m). Then, each FCV can then be represented as Therefore, each p dimensional image patch xi is represented by a m-dimensional vector Zi(Zi,1,…, Zi,m)T. The learned feature vector Zi is a sparse vector. Given a FCV xi, one can formularize the above idea as the following optimization problem:
| (6) |
where λ is the regularization parameter, ‖·‖ is the standard Euclidean norm and Each zi is often called the sparse code, in which only a few entries are non-zero, and we call these non-zero entries as supports. Here D = (d1, …, dm) ∈ ℝm × p is called the dictionary. To prevent an arbitrary scaling of the sparse code, each column of D is restricted to be in a unit ball, i.e., ‖dj‖≤ 1.
It is a non-convex problem with respect to joint parameters in the dictionary D and the sparse codes Z = (z1, … ,zn). Therefore, it is often difficult to find a global optimum. However, it is a convex problem when either D or Z is fixed. One often uses an alternating optimization approach to solve sparse coding problems. When the sparse codes are fixed, it is a simple quadratic problem, when the dictionary D is fixed, solving each sparse code zi is the well-known lasso problem. Since FCV time series are tremendous datasets and dictionaries are also very large, thus, solving a lasso problem is very time consuming.
To deal with large-data sparse coding problem, stochastic coordinate coding (SCC) algorithm is applied, which aims to dramatically reduce the computational cost of the sparse coding while keeping comparable performance. It is known that updating the sparse code is the most time consuming part, and coordinate descent is one of state-of-the-art methods for solving this lasso problem. Coordinate descent initializes and then updates the sparse code many times via matrix-vector multiplication and thresholding. Empirically, the iteration may take thousands steps to converge. However, it is observed that the support locations of zi are very accurate after only less than ten steps. Note that the support of the sparse code is usually more important than the exact value of the sparse code. Moreover, since the original sparse coding is a non-convex problem and it involves an alternating updating, it is unnecessary to run the coordinate descent to final convergence. Therefore, the sparse code zi is updated by running a few steps of coordinate descent, and stable supports are obtained. When updating the dictionary, only the supports of the dictionary but not all dictionary items need to be focused on. The algorithmic pipeline of SCC is shown as Fig. 3.
Fig. 3.
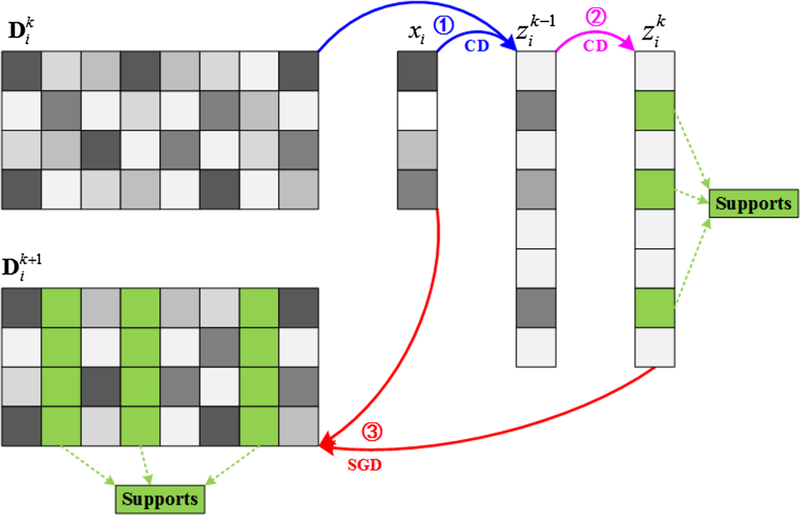
Pipeline of stochastic coordinate coding algorithm. In k-th iteration, given one FCV xi, ① a few steps of coordinate descent (CD) are performed to find the support of the sparse code. ② A few more steps of coordinate descent (CD) are implemented on the supports to obtain a new sparse code ③ The supports of the dictionary are updated by second order stochastic gradient descent (SGD).
After sparse coding process, the super long FCV time series is represented by an over-complete dictionary D, where the number of items m is usually much smaller than the length of time series n but larger than the dimension of the item p. According to some previous studies (Li et al. 2014; Ou et al. 2014; Ou et al. 2015), functional connectivities can be divided into a few clusters based on the combination of activated nodes and connections. Therefore, in this paper, we applied clustering method to derive a few common functional connectivities (CFCs) from the over-complete dictionary items. The optimal number of CFCs is identified by Bayesian Information Criterion (BIC) (Schwarz 1978), which is defined as:
| (7) |
where is the estimation for error variance, which is defined as the summed variance of each dictionary item within its corresponding class in this paper. m is the total number of dictionary items, and k is the number of classes. The trade-off between class number and error variance is balanced by the BIC value, and the optimized number of cluster is determined by finding k to minimize BIC value. After clustering items into a few classes, common functional connectivity (CFC) is defined as the weighted average of items in a cluster.
2.5. Temporal Transition Modeling
Sparse code vector zi indicates how the dictionary items represent i-th FCV xi. After CFC estimation, a CFC-based sparse code series ZCFC can be obtained. Since each sparse code may contain more than one non-zero entries, there may be a few CFCs activated in brain simultaneously. We assume that the brain state is determined by the dominant CFC whose occurrence is the highest. Therefore, brain state at each time point can be labelled with a CFC, and the transition of CFCs can be reflected by the transition of brain states. Because the length of skipping step has a great influence on the accuracy of CFC duration, we only focus on the transitions between two different CFCs, rather than self-transitions.
In order to establish a finite state machine (FSM), all transitions between CFCs should be counted, and transition probability for each CFC can be calculated. As CFC with higher occurrence is certain to own higher transition probability, thus, the value of transition probability is not convincible enough to character CFC transitions. Therefore, transition preference, which can eliminate the effect of CFC occurrence, is defined as below:
| (8) |
| (9) |
| (10) |
where Nk is the overall occurrence of k-th CFC during whole duration, denotes the occurrence of transition from CFCi to CFCk. Thus, is the overall occurrence probability of CFCk excluding CFCi, and represents the probability to transit from CFCk to CFCi. Here, because self-transition is not in consideration. Therefore, is the ratio of transition probability over overall occurrence probability. When evidently, it means there is a preference that CFCi are more likely to transit to CFCk than any other CFCs. As such, the preference of mutual transitions among CFCs can be discovered and a FSM can be established.
3. Results
3.1. CFCs Inferred from Mouse Brain LFP Data
In our work, based on the optimal dictionary size and sparseness determined beforehand, we implemented a total of 160 trials of SCC sparse coding for each mouse. According to BIC, the optimal clustering number of functional connectivity was explored, and the statistics results for each mouse are shown in Fig. 4. In Fig. 4(a), it is easy to appreciate that six clusters are the most clustered for alpha band, and it is consistent in all three mice. The same exploration was also applied to theta band, and four clusters occur the most, as shown in Fig. 4(b). Therefore, the CFC numbers of frequency band alpha and theta are determined as six and four. Six CFCs of alpha band are shown in Fig. 5.
Fig. 4.
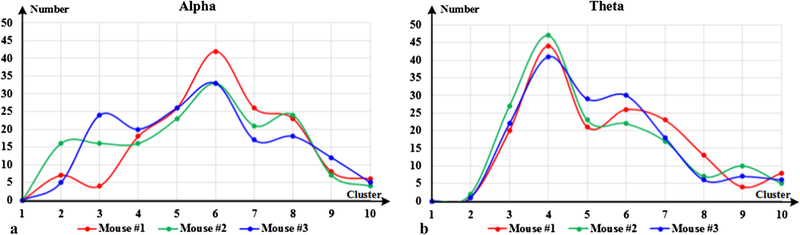
Optimal clustering number for each mouse dataset.
Fig. 5.
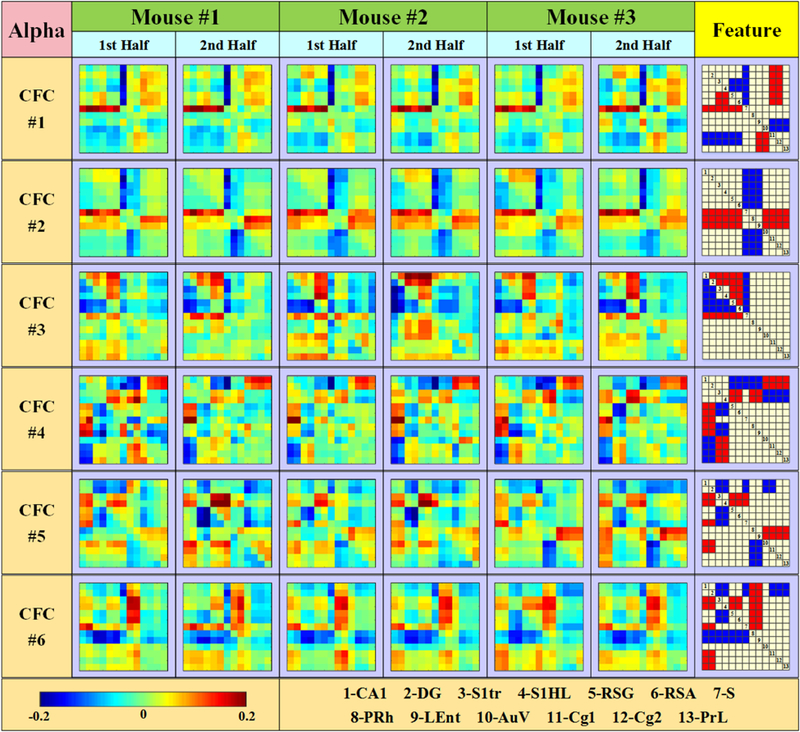
Six CFCs inferred from alpha frequency band.
For the purpose of reproducibility validation, each mouse dataset was divided into two parts. Then, six CFCs were obtained from each subdataset. Comparing six groups of CFCs obtained from 3 mice, it is easy to identify and match each CFC. This result demonstrates that six CFCs are stable along time and general among subjects. To make intuitive visualization, common features are extracted for each CFC and shown in the right column of Fig. 5. Since iCoh indicates phase differences of two signals, therefore, in each CFC, positive value (red block) means that signal of column region leads that of row region, whereas negative value (blue block) means lagging behind. The bigger the magnitude is, the bigger phase difference to lead or lag.
In addition, it is easy to observe that each CFC pattern shows obvious block format, which indicates that some brain regions have similar interactions. We identify these regions and separate those from the others. Therefore, thirteen brain regions can be separated into seven groups: CA1 & DG, S1Tr & S1HL, RSG & RSA, S, PRh & LEnt, AuV, and Cg1& Cg2 & PrL. It is interesting to observe that these seven brain region groups from CFCs by data-driven method are closely related with their spatial locations in brain. As expected, from the perspective of brain structure, the interactions between regions within the same brain structure are quite stable, such as Cg1 & Cg2 (Anterior Cingulate Cortices), S1HL & S1Tr (Somatosensory Cortex), and RSA & RSG (Retrosplenial Cortex). Also, the regions adjacent to each other (with direct connections) tends to cooperate coherently, such as CA1 & DG, PRh & LEnt and PrL & Cg1 & Cg2.
For the four CFCs obtained from frequency band theta (as shown in Fig. 6), similar block characteristics also can be easily observed. Besides, it is interesting to observe that three CFCs in alpha band also can be found in theta band. Specifically, CFC#1, CFC#3 and CFC#6 in alpha band match CFC#1, CFC#2 and CFC#3 in theta band, which indicates that CFCs are stable among frequency bands. In general, despite sharing the same structural basis, different bands have their own rhythm of fluctuation, and run respective “program”. This finding demonstrates that some brain activities may lead fluctuation in a broad range of frequency, which may cover a few frequency bands. Three pairs of identical CFCs in alpha and theta bands maybe correspond to three distinct brain activities.
Fig. 6.
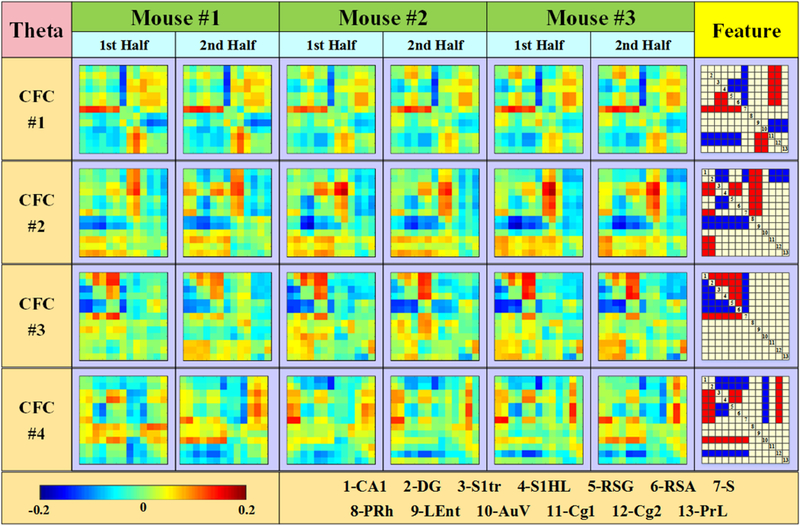
Six CFCs inferred from theta frequency band.
Because CFCs are extracted from LFP signals of freely behaving mice, observing and exploratory behaviors might occur during recording. Therefore, it is difficult to identify the function of a certain CFC without other references, such as synchronous videos or manually annotations. Even though, CFCs discovered in this paper still can provide us a new method to understand brain functional connectivity.
3.2. Occurrences and Transitions of CFCs.
Through sparse coding with SCC and CFC estimation, a CFC-based sparse code series ZCFC is obtained for each subdataset, by which we can investigate the occurrence of each CFC. As each mouse LFP recordings are divided into two parts, CFCs’ occurrences in six subdatasets are shown in Fig. 7.
Fig. 7.
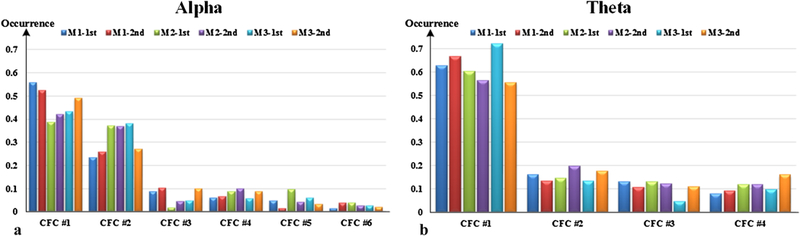
Occurrences of CFCs of alpha and theta frequency band. “M1–1st” denotes the first half of mouse #1 dataset.
In Fig. 7(a), six CFCs of alpha band are quite different in occurrence. CFC#1 has the most occurrence of over 40 percent, then followed by CFC#2, whose occurrence is about 30 percent, on average. In contrast, CFC#3 ~ CFC#6 have small occurrences of less than 10 percent, respectively. For each CFC, the occurrence varies among different subdatasets, which can be observed within a single subject or between subjects. For instance, in mouse #3, CFC#2 occurs about 10 percent less in second half than in the first. Besides, the occurrence differences of CFC#1 between mouse#1 and mouse #2 can be over 10 percent. However, these differences of CFC’s occurrence are thought to be reasonable, due to individual specificity and free behaviors. In Fig. 7(b), four CFCs of theta band also have different occurrences. CFC#1 has a dominant occurrence of 60 percent, on average, whereas the other three CFCs have only about 10 percent occurrences, respectively. These results reveal that three pairs of identical CFCs in alpha and theta bands also show high similarities in occurrence. From the perspective of occurrence, as well as connectivity pattern, it can be inferred that a CFC maybe reflect a distinct brain activity, which may cause rhythmic fluctuation across different frequency bands.
Based on the assumption that brain state can be labelled with a certain CFC and the transition of CFCs can be reflected by the transition of brain states, we built a FSM with CFC series (brain state series where each state is labelled by only one CFC). Among all directional transitions, we discovered that six transitions in alpha band and three transitions in theta have evident preference by significance test (t-test), and these transitions are shown in Table 3a and 3b. It is easy to appreciate that all these transitions are related to CFC#1. In frequency band of alpha, five of six transitions with evident preference are the transitions towards CFC#1, and the rest one is from CFC#1 to CFC#2, which may interpret to some extents why CFC#2 has the second highest occurrence. In theta band, all three special transitions are all towards CFC#1. The transition patterns of frequency bands of alpha and theta with preference are shown in Fig. 8. This special preference of transition demonstrates that CFC#1, in both alpha and theta bands, corresponds to a sort of default brain activity or brain state, and plays a role as an “intermediate center”.
Table 3a.
CFC transitions with evident preference in alpha frequency band.
| Transition | C#2→C#1 | C#3→C#1 | C#4→C#1 | C#5→C#1 | C#6→C#1 | C#1→C#2 |
|---|---|---|---|---|---|---|
| Preference | 1.3195 | 1.2655 | 1.2793 | 1.2056 | 1.1885 | 1.1511 |
| Confidence | P < 0.0001 | P < 0.005 | P < 0.05 | P < 0.05 | P < 0.05 | P < 0.0001 |
Table 3b.
CFC transitions with evident preference in theta frequency band.
| Transition | C#2→C#1 | C#3→C#1 | C#4→C#1 |
|---|---|---|---|
| Preference | 1.2714 | 1.2761 | 1.2038 |
| Confidence | P < 0.0001 | P < 0.0001 | P < 0.0001 |
Fig. 8.
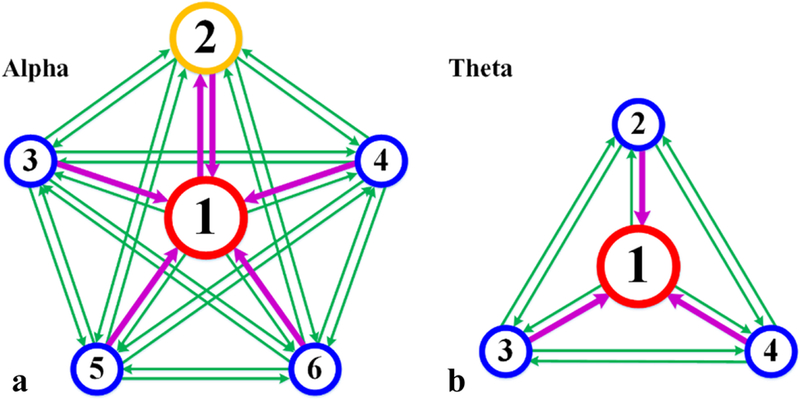
CFCs’ transitions in alpha and theta frequency bands. Magenta arrows represent transitions with evident preference. Green arrows represent common transitions.
3.3. Validation of Effectiveness
Because of small body size and thin skull, the vast majority of electrodes used in freely behaving mice is still largely limited to 32 or fewer channels, and to only one or two brain structures. Therefore, it is difficult to make a straight comparison between our work and recent studies, especially based on thirteen distinct brain regions. In order to validate the effectiveness of the proposed method, we tested our method on surrogate datasets, which were generated by randomizing the LFP recordings of each mouse in time. Therefore, in surrogate datasets, temporal dependency was destroyed, and phase-lags caused by real brain activity were removed. Specially, we generated surrogate datasets for each mouse, and repeated our method 80 times for each dataset. Based on BIC, the optimal clustering number for each mouse was investigated, and it was interesting to find that 4 clusters were the best for both alpha and theta bands. The statistics results of mouse #1 are shown in Fig. 9.
Fig. 9.
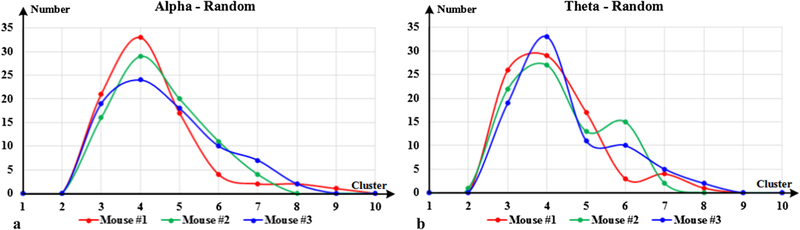
Optimal clustering number for each mouse surrogate dataset.
For intuitive comparison, the CFCs inferred from surrogate datasets are shown in Fig. 10. In Fig.10, it is easy to observe that there are great differences among CFCs, and no CFC group could totally match with others. Compared with the results shown in Fig.5 and Fig. 6, it is quite difficult to observe any similarities or consistencies of CFCs, neither in alpha band nor in theta band. As the LFP recordings were shuffled in time, there were no stable temporal dependences hidden within a single surrogate dataset, or among surrogate datasets. These results demonstrate that our proposed method have good sensitivity to temporal dependency and can reveal functionally relevant CFCs caused by real brain activities.
Fig. 10.
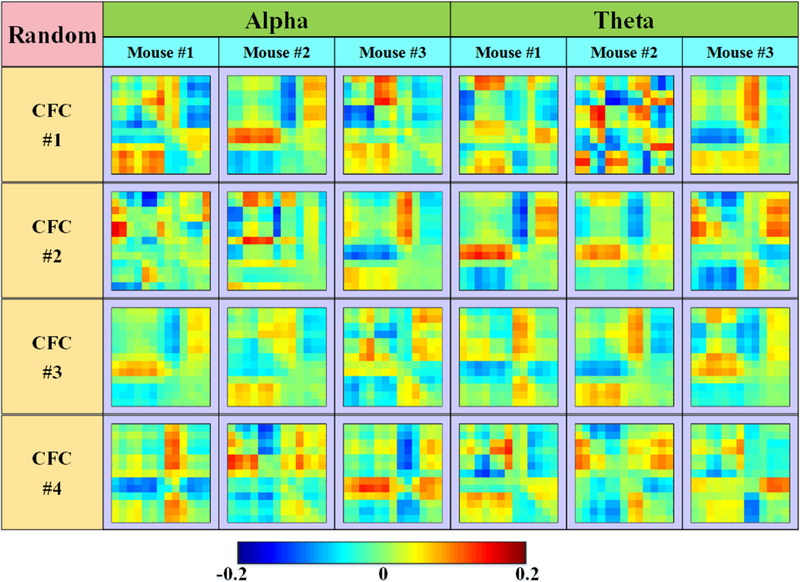
Surrogate dataset CFCs of two frequency bands from three mice.
3.4. Effects of Free Parameters in SCC
As introduced in section 2.4, SCC is a highly effective method to deal with sparse coding problems of big data. Before running a task, hyper parameters, especially dictionary size and sparseness, which have great influences on the performance of sparse coding, should be carefully explored and determined.
The size of dictionary reflects the representing capability of sparse coding. Generally, larger dictionary size leads better diversity and more accurate representation. However, an over large dictionary may also cause unnecessary segmentation and redundancy, which decreases coding efficiency. To determine the size of dictionary, we tried it in a range from 50 to 400, with an interval of 50, on the whole FCV time series of Mouse #1, and the results are shown in Fig. 11. In Fig. 11(a), it is easy to appreciate that all curves gather closely. They have similar changing trend in residual with the change of sparseness. To make a clear comparison, we select an area and zoom in as shown in Fig. 11(b). It is easy to observe that larger dictionary size corresponds to lower residual, and residual difference decreases as the increase of dictionary size, for instance, the residual difference between size 150 and 400 is almost the same as that between 50 and 150. Similar curves and traits are also obtained in theta frequency band, as shown in Fig. 11(c) ~ 11(d). As residual difference becomes small enough after 150, which means that a dictionary with 150 items has sufficient capability to represent FCV time series, therefore, we determine the size of dictionary as 150 finally.
Fig. 11.
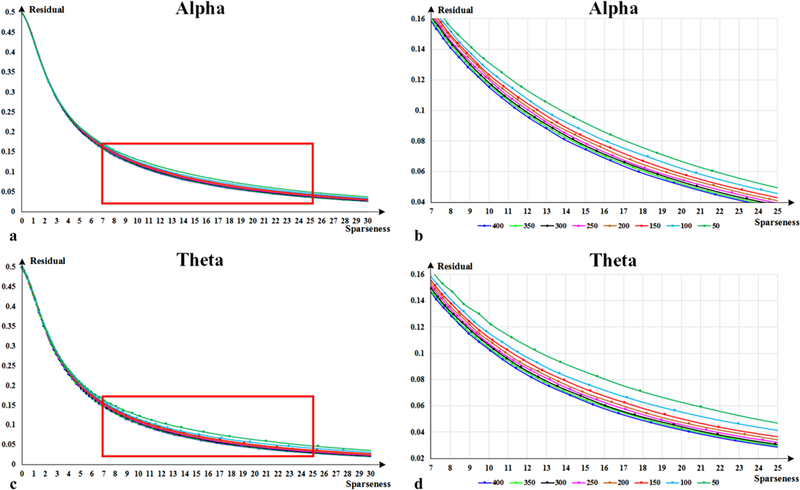
Residual curves of dictionary size exploration. (b) is the zoom in view of red box area in (a), as well as (d) and (c).
Sparseness is a measurement indicating how many dictionary items are used to represent a single FCV. Generally, higher sparseness contributes to more accurate representation. In this paper, we only focus on the functional connetivities which are relatively common and stable in brain activity, however, over high sparseness may bring trivial or insignificant components, such as impulse and noise. Therefore, finding an optimal sparseness is of vital importance to our work. Based on the residual curve of dictionary size 150 (as shown in Fig. 11), we calculated the residual difference based on different sparseness, and the results are shown in Fig. 12.
Fig. 12.
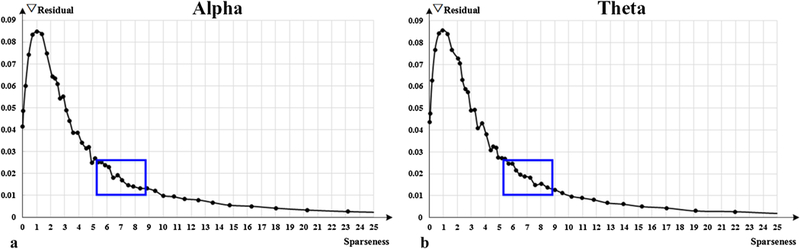
Residual difference curves of sparseness. Optimal sparseness locations are marked with blue box.
In Fig. 12, it is easy to observe that along with the decrease of sparseness, the residual difference increases very slowly at the beginning, then bursts rapidly. The critical changing point is thought to be the optimal sparseness, where the FCV series can be represented at the most optimal cost. Meanwhile, the part represented by the dictionary items at optimal sparseness is considered as the core component of FCV. Similar curve is also obtained from frequency band theta, as shown in Fig. 12(b). In SCC, the sparseness is controlled by sparse parameter λ. Because the residual difference curve is relatively smooth, it is difficult to identify an abrupt changing point. Therefore, we selected a small range of sparseness (labeled with blue box) for main experiments.
4. Discussion
Functional connectivity has been recently shown to be powerful in studying the network topology of the brain, revealing important information on the interactions between brain regions, no matter in humans and experimental animal models. Recent studies indicate that dynamic analysis of functional connectivity can better capture the brain region interactions, providing additional insights into the macroscale organization and dynamics of neural activity (Calhoun et al. 2014; Keilholz 2014b). In the majority of the studies published to date, the functional connectivity and its dynamics in mice are investigated via fMRI recording data (Mechling et al. 2014; Liska et al. 2015; Grandjean et al. 2017; Belloy et al. 2018). Compared to electrophysiological measurements, these studies of dynamic functional connectivity with fMRI are inherently limited to the coarse time-scale due to the low-pass filtering effect of the hemodynamic response. Furthermore, a few LFP-based studies of functional connectivity recorded only a few (no more than 32) channels of signals from only one or two brain structures, even in rat (Wei et al. 2015; Qi et al. 2017) and pigeon (Chen et al. 2018), whose brain sizes are much bigger than that of mouse. In contrast, our work is based on super-long LFP signals recorded from thirteen distinct brain regions, with outstanding temporal resolution over fMRI-based studies and finer spatial scale compared with other LFP-based studies. Until recently, Grandjean et al. applied sliding-window approach and dictionary learning method to identify several reproducible dynamic functional states in mice based on fMRI (Grandjean et al. 2017). In spite that their work used a few similar steps as ours, we applied iCoh and SCC methods to deal with volume conduction artefacts and exploding computations, which are quite common only in electrophysiological brain studies. Therefore, our work investigated dynamic properties of functional brain connectivity in freely behaving mice via such higher temporal resolution and super-long length LFP recordings for the first time, as far as we know.
Though our proposed method has achieved remarkable performances in mouse brain dynamics investigation via LFP recordings, it still can be improved in a few aspects. First, CFCs were derived from the whole dictionary items, and their numbers were determined by Bayesian information criterion in this paper. Although sparse coding has extracted more critical components of functional connectivity, we still cannot guarantee that all dictionary items are significant. Therefore, better clustering methods or criterions should be explored to achieve more accurate establishment of CFCs, and some dictionary items could be excluded if necessary. Second, CFC is not an accurate enough measure. Because of magnitude normalization during sparse coding, the CFC only illustrates the general information, such as leading or lagging phase trait and how distinct regions coordinate with each other, rather precise quantitative information, like how much time a region leads or lags another region. If some additional benchmarks or criterions could be developed to indicate the phase-lags, the results would be more accurate and meaningful. Third, in our work, only LFP recordings were applied to derive CFCs, and the CFCs are sort of data-driven results. In the future, if other references, such as synchronous videos or manually annotations could be available, it would be of great help to identify the function of a certain CFC. In addition, in spite that the imaginary part of coherency is the most robust to VC artifact theoretically and practically (Khadem and Hossein-Zadeh 2013), compared with Pearson Correlation Coefficient, Mutual Information, and magnitude squared Coherence, it lacks the detection of zero-lag connectivity which are thought to be preserved in the real part (Sanchez Bornot et al. 2018). Therefore, if more advanced brain connectivity method could be developed and applied, the results of CFCs would be more comprehensive.
In summary, as large-scale, multi-site in vivo recording techniques have offered a new avenue to gain the critical insights into functional connectivity and brain dynamics in the freely behaving animals, we proposed a novel sparse coding based method, by which we uncovered a set of characteristic functional brain connectivities that are associated with the brain dynamics in freely behaving mice. We believe that our method can be potentially applied to reveal intrinsic functional brain connectivity in both unconditioned and conditioned tasks (i.e. contextual, cued, or trace fear conditioning) (Chen et al. 2009; Zhang et al. 2013), in addition to the task-free condition as in this work, and reach beyond the current brain regions and animal model. Further, we envision that the scheme proposed in this work utilizing super long recording and data-driven approach can contribute to transforming the research in brain science into data science, which entails advanced and more effective analytics strategies, providing a new perspective for the neuroscience field.
Supplementary Material
Fig. 1.
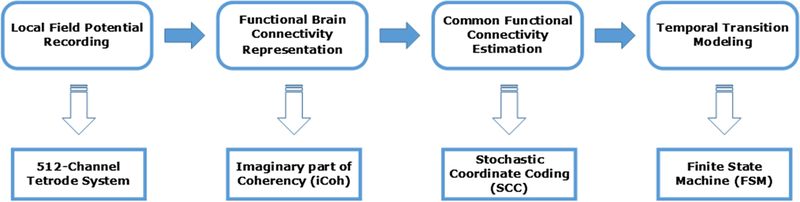
Pipeline of the proposed method.
Acknowledgments
H Wang was supported by the Fundamental Research Funds for the Central Universities, the National Natural Science Foundation of China (Grant No. 31627802). T. Liu is supported by NIH R01 DA-033393, NIH R01 AG-042599, NSF CAREER Award IIS-1149260, NSF BME-1302089, NSF BCS-1439051 and NSF DBI-1564736.
References
- Adrian ED, Moruzzi G (1939) Impulses in the pyramidal tract. J Physiol 97: 153–199 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allen EA, Damaraju E, Eichele T, Wu L, Calhoun VD (2017) EEG Signatures of Dynamic Functional Network Connectivity States. Brain Topography: 1–16 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Belloy ME, Naeyaert M, Abbas A, Shah D, Vanreusel V, van Audekerke J, Keilholz SD, Keliris GA, Van der Linden A, Verhoye M (2018) Dynamic resting state fMRI analysis in mice reveals a set of Quasi-Periodic Patterns and illustrates their relationship with the global signal. NeuroImage 180: 463–484 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biswal BB, Mennes M, Zuo XN, Gohel S, Kelly C, Smith SM, Beckmann CF, Adelstein JS, Buckner RL, Colcombe S, Dogonowski AM, Ernst M, Fair D, Hampson M, Hoptman MJ, Hyde JS, Kiviniemi VJ, Kotter R, Li SJ, Lin CP, Lowe MJ, Mackay C, Madden DJ, Madsen KH, Margulies DS, Mayberg HS, McMahon K, Monk CS, Mostofsky SH, Nagel BJ, Pekar JJ, Peltier SJ, Petersen SE, Riedl V, Rombouts SARB, Rypma B, Schlaggar BL, Schmidt S, Seidler RD, Siegle GJ, Sorg C, Teng GJ, Veijola J, Villringer A, Walter M, Wang L, Weng XC, Whitfield-Gabrieli S, Williamson P, Windischberger C, Zang YF, Zhang HY, Castellanos FX, Milham MP (2010) Toward discovery science of human brain function. Proceedings of the National Academy of Sciences 107: 4734–4739 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buchthal F, Guld C, Rosenfalck P (1957) Volume conduction of the spike of the motor unit potential investigated with a new type of multielectrode. Acta Physiol Scand 38: 331–354 [DOI] [PubMed] [Google Scholar]
- Bush G, Luu P, Posner AMI (2000) Cognitive and emotional influences in anterior cingulate cortex. Trends in Cognitive Sciences 4: 215. [DOI] [PubMed] [Google Scholar]
- Calhoun VD, Miller R, Pearlson G, Adalı T (2014) The Chronnectome: Time-Varying Connectivity Networks as the Next Frontier in fMRI Data Discovery. Neuron 84: 262–274 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen G, Wang LP, Tsien JZ (2009) Neural population-level memory traces in the mouse hippocampus. Plos One 4: e8256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y, Liu X, Li S, Wan H (2018) Decoding Pigeon Behavior Outcomes Using Functional Connections among Local Field Potentials. Computational Intelligence and Neuroscience 2018: 1–13 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Czajkowski R, Jayaprakash B, Wiltgen B, Rogerson T, Guzmankarlsson MC, Barth AL, Trachtenberg JT, Silva AJ (2014) Encoding and storage of spatial information in the retrosplenial cortex. Proceedings of the National Academy of Sciences 111: 8661–8666 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Da Silva FL (2013) EEG and MEG: Relevance to Neuroscience. Neuron 80: 1112–1128 [DOI] [PubMed] [Google Scholar]
- Di MA, Scheres A, Margulies DS, Kelly AM, Uddin LQ, Shehzad Z, Biswal B, Walters JR, Castellanos FX, Milham MP (2008) Functional connectivity of human striatum: a resting state FMRI study. Cerebral Cortex 18: 2735–2747 [DOI] [PubMed] [Google Scholar]
- Donner TH, Siegel M (2011) A framework for local cortical oscillation patterns. Trends in Cognitive Sciences 15: 191–199 [DOI] [PubMed] [Google Scholar]
- Donoho DL, Elad M (2003) Optimally sparse representation in general (nonorthogonal) dictionaries via l(1) minimization. Proceedings of the National Academy of Sciences 100: 2197–2202 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eichenbaum H (2017) Memory Systems. In: Learning and Memory: A Comprehensive Reference, vol 3 Academic Press [Google Scholar]
- Fox MD, Raichle ME (2007a) Spontaneous fluctuations in brain activity observed with functional magnetic resonance imaging. Nature Reviews Neuroscience 8: 700–711 [DOI] [PubMed] [Google Scholar]
- Franklin KBJ, Paxinos G (2001) The Mouse Brain: In Stereotaxic Coordinates Academic Press [Google Scholar]
- Friston KJ, Harrison L, Penny WD (2003) Dynamic causal modeling. Neuroimage 19: 1273–1302 [DOI] [PubMed] [Google Scholar]
- Fröhlich F (2016) Network Neuroscience Academic Press [Google Scholar]
- Garcia DL, Stieben J, Perez VJ, Shanker S (2013) The imaginary part of coherency in autism: differences in cortical functional connectivity in preschool children. PLoS One 8: e75941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gigg J, Finch DM, O Mara SM (2000) Responses of rat subicular neurons to convergent stimulation of lateral entorhinal cortex and CA1 in vivo. Brain Research 884: 35–50 [DOI] [PubMed] [Google Scholar]
- Gilbert CD, Sigman AM (2007a) Brain States: Top-Down Influences in Sensory Processing. Neuron 54: 677–696 [DOI] [PubMed] [Google Scholar]
- Grandjean J, Preti MG, Bolton TAW, Buerge M, Seifritz E, Pryce CR, Van De Ville D, Rudin M(2017) Dynamic reorganization of intrinsic functional networks in the mouse brain. NeuroImage 152: 497–508 [DOI] [PubMed] [Google Scholar]
- Hamill OP, Marty A, Neher E, Sakmann B, Sigworth FJ (1981) Improved patch-clamp techniques for high-resolution current recording from cells and cell-free membrane patches. Pflügers Archiv -European Journal of Physiology 391: 85–100 [DOI] [PubMed] [Google Scholar]
- He B, Yang L, Wilke C, Yuan H (2011) Electrophysiological imaging of brain activity and connectivity-challenges and opportunities. IEEE Transactions on Biomedical Engineering 58: 1918–1931 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu M, Liang H (2013) Perceptual suppression revealed by adaptive multi-scale entropy analysis of local field potential in monkey visual cortex. International Journal of Neural Systems 23: 1350005. [DOI] [PubMed] [Google Scholar]
- Hubel DH, Wiesel TN (1962) Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. Journal of Physiology 160: 106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kajikawa Y, Schroeder CE (2011) How Local Is the Local Field Potential? Neuron 72: 847–858 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katzner S, Nauhaus I, Benucci A, Bonin V, Ringach DL, Carandini M (2009) Local Origin of Field Potentials in Visual Cortex. Neuron 61: 35–41 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keilholz SD (2014a) The Neural Basis of Time-Varying Resting-State Functional Connectivity. Brain Connectivity 4: 769–779 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keilholz SD (2014b) The Neural Basis of Time-Varying Resting-State Functional Connectivity. Brain Connectivity 4: 769–779 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khadem A, Hossein-Zadeh GA (2013) Comparing the robustness of brain connectivity measures to Volume Conduction artifact. Biomedical Engineering: 209–214 [Google Scholar]
- Khan S, Gramfort A, Shetty NR, Kitzbichler MG, Ganesan S, Moran JM, Lee SM, Gabrieli JD, Tager-Flusberg HB, Joseph RM, Herbert MR, Hamalainen MS, Kenet T (2013) Local and long-range functional connectivity is reduced in concert in autism spectrum disorders. Proceedings of the National Academy of Sciences 110: 3107–3112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khawaja FA, Tsui JMG, Pack CC (2009) Pattern Motion Selectivity of Spiking Outputs and Local Field Potentials in Macaque Visual Cortex. Journal of Neuroscience 29: 13702–13709 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kinnavane L, Amin E, Olartesánchez CM, Aggleton JP (2016) Detecting and discriminating novel objects: The impact of perirhinal cortex disconnection on hippocampal activity patterns. Hippocampus 26: 1393–1413 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klausberger T, Somogyi P (2008) Neuronal diversity and temporal dynamics: The unity of hippocampal circuit operations. Science 321: 53–57 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koenig T, Lehmann D, Merlo MC, Kochi K, Hell D, Koukkou M (1999) A deviant EEG brain microstate in acute, neuroleptic-naive schizophrenics at rest. European Archives of Psychiatry and Clinical Neuroscience 249: 205–211 [DOI] [PubMed] [Google Scholar]
- Koenig T, Prichep L, Lehmann D, Sosa PV, Braeker E, Kleinlogel H, Isenhart R, John ER (2002) Millisecond by Millisecond, Year by Year: Normative EEG Microstates and Developmental Stages. NeuroImage 16: 41–48 [DOI] [PubMed] [Google Scholar]
- Koshino H, Carpenter PA, Minshew NJ, Cherkassky VL, Keller TA, Just MA (2005) Functional connectivity in an fMRI working memory task in high-functioning autism. Neuroimage 24: 810–821 [DOI] [PubMed] [Google Scholar]
- Kuang H, Lin L, Tsien JZ (2010) Temporal Dynamics of Distinct CA1 Cell Populations during Unconscious State Induced by Ketamine. Plos One 5: e15209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuruvilla MV, Ainge JA (2017) Lateral Entorhinal Cortex Lesions Impair Local Spatial Frameworks. Frontiers in Systems Neuroscience 11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee M, Shin HS, Choi JH (2009) Simultaneous recording of brain activity and functional connectivity in the mouse brain. IEEE Engineering in Medicine and Biology Society: 2934–2936 [DOI] [PubMed] [Google Scholar]
- Li X, Lim C, Li K, Guo L, Liu T (2013) Detecting Brain State Changes via Fiber-Centered Functional Connectivity Analysis. Neuroinformatics 11: 193–210 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X, Zhu D, Jiang X, Jin C, Zhang X, Guo L, Zhang J, Hu X, Li L, Liu T (2014) Dynamic functional connectomics signatures for characterization and differentiation of PTSD patients. Human Brain Mapping 35: 1761–1778 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin B, Li Q, Sun Q, Lai MJ, Davidson I, Fan W, Ye J (2014) Stochastic Coordinate Coding and Its Application for Drosophila Gene Expression Pattern Annotation. Computer Science [Google Scholar]
- Lin L, Chen G, Xie K, Zaia KA, Zhang S, Tsien JZ (2006) Large-scale neural ensemble recording in the brains of freely behaving mice. Journal of Neuroscience Methods 155: 28–38 [DOI] [PubMed] [Google Scholar]
- Lin L, Osan R, Shoham S, Jin W, Zuo W, Tsien JZ (2005) Identification of network-level coding units for real-time representation of episodic experiences in the hippocampus. Proceedings of the National Academy of Sciences 102: 6125–6130 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liska A, Galbusera A, Schwarz AJ, Gozzi A (2015) Functional connectivity hubs of the mouse brain. NeuroImage 115: 281–291 [DOI] [PubMed] [Google Scholar]
- Liu T (2011) A few thoughts on brain ROIs. Brain Imaging and Behavior 5: 189–202 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopour BA, Staba RJ, Stern JM, Fried I, Ringach DL (2016) Characterization of long-range functional connectivity in epileptic networks by neuronal spike-triggered local field potentials. Journal of Neural Engineering 13: 26031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynall ME, Bassett DS, Kerwin R, McKenna PJ, Kitzbichler M, Muller U, Bullmore E (2010) Functional Connectivity and Brain Networks in Schizophrenia. Journal of Neuroscience 30: 9477–9487 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mechling AE, Hübner NS, Lee H, Hennig J, von Elverfeldt D, Harsan L (2014) Fine-grained mapping of mouse brain functional connectivity with resting-state fMRI. NeuroImage 96: 203–215 [DOI] [PubMed] [Google Scholar]
- Mueller S, Wang D, Fox M, Yeo BTT, Sepulcre J, Sabuncu M, Shafee R, Lu J, Liu H (2013) Individual Variability in Functional Connectivity Architecture of the Human Brain. Neuron 77: 586–595 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray EA, Bussey TJ, Saksida LM (2007) Visual perception and memory: a new view of medial temporal lobe function in primates and rodents. Annual Review of Neuroscience 30: 99. [DOI] [PubMed] [Google Scholar]
- Nakashiba T, Cushman JD, Pelkey KA, Renaudineau S, Buhl DL, Mchugh TJ, Rodriguez BV, Chittajallu R, Iwamoto KS, Mcbain CJ (2012) Young dentate granule cells mediate pattern separation, whereas old granule cells facilitate pattern completion. Cell 149: 188–201 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nauhaus I, Busse L, Carandini M, Ringach DL (2009) Stimulus contrast modulates functional connectivity in visual cortex. Nature Neuroscience 12: 70–76 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nolte G, Bai O, Wheaton L, Mari Z, Vorbach S, Hallett M (2004) Identifying true brain interaction from EEG data using the imaginary part of coherency. Clinical Neurophysiology 115: 2292–2307 [DOI] [PubMed] [Google Scholar]
- O Mara S (2015) The Connected Hippocampus. In: Progress in Brain Research, vol 219 Elsevier; [DOI] [PubMed] [Google Scholar]
- Olshausen BA, Field DJ (1996) Emergence of simple-cell receptive field properties by learning a sparse code for natural images. Nature 381: 607–609 [DOI] [PubMed] [Google Scholar]
- Olshausen BA, Field DJ (2004) Sparse coding of sensory inputs. Current Opinion in Neurobiology 14: 481–487 [DOI] [PubMed] [Google Scholar]
- O’Mara S (2005) The subiculum: what it does, what it might do, and what neuroanatomy has yet to tell us. Journal of Anatomy 207: 271–282 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ou J, Lian Z, Xie L, Li X, Wang P, Hao Y, Zhu D, Jiang R, Wang Y, Chen Y, Zhang J, Liu T (2014) Atomic dynamic functional interaction patterns for characterization of ADHD. Human Brain Mapping 35: 5262–5278 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ou J, Xie L, Jin C, Li X, Zhu D, Jiang R, Chen Y, Zhang J, Li L, Liu T (2015) Characterizing and Differentiating Brain State Dynamics via Hidden Markov Models. Brain Topography 28: 666–679 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ou J, Xie L, Li X, Zhu D, Terry DP, Puente AN, Jiang R, Chen Y, Wang L, Shen D, Zhang J, Miller LS, Liu T (2015) Atomic connectomics signatures for characterization and differentiation of mild cognitive impairment. Brain Imaging and Behavior 9: 663–677 [DOI] [PubMed] [Google Scholar]
- Pardo JV, Pardo PJ, Janer KW, Raichle ME (1990) The anterior cingulate cortex mediates processing selection in the Stroop attentional conflict paradigm. Proceedings of the National Academy of Sciences 87: 256–259 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pinault D (1996) A novel single-cell staining procedure performed in vivo under electrophysiological control: morpho-functional features of juxtacellularly labeled thalamic cells and other central neurons with biocytin or Neurobiotin. Journal of Neuroscience Methods 65: 113–136 [DOI] [PubMed] [Google Scholar]
- Pothuizen HH, Davies M, Albasser MM, Aggleton JP, Vann SD (2009) Granular and dysgranular retrosplenial cortices provide qualitatively different contributions to spatial working memory: evidence from immediate-early gene imaging in rats. European Journal of Neuroscience 30: 877–888 [DOI] [PubMed] [Google Scholar]
- Qi D, Xiao Z, Liu S, Jiao Y (2017) Functional Connectivity Analysis from Theta Band of Multi Local Field Potentials on Prefrontal Cortex of Rat during Working Memory Task. In: International Conference on Intelligent Human-Machine Systems and Cybernetics, pp 30–34 [Google Scholar]
- Ray S, Maunsell JHR (2011) Network Rhythms Influence the Relationship between Spike-Triggered Local Field Potential and Functional Connectivity. Journal of Neuroscience 31: 12674–12682 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ryali S, Chen T, Supekar K, Menon V (2012) Estimation of functional connectivity in fMRI data using stability selection-based sparse partial correlation with elastic net penalty. Neuroimage 59: 3852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanchez Bornot JM, Wong-Lin K, Ahmad AL, Prasad G (2018) Robust EEG/MEG Based Functional Connectivity with the Envelope of the Imaginary Coherence: Sensor Space Analysis. Brain Topography [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sander TH, Bock A, Leistner S, Ku Hn A, Trahms L (2010) Coherence and imaginary part of coherency identifies cortico-muscular and cortico-thalamic coupling. IEEE Engineering in Medicine and Biology Society: 1714–1717 [DOI] [PubMed] [Google Scholar]
- Schwarz G (1978) Estimating the Dimension of a Model. Annals of Statistics 6: 15–18 [Google Scholar]
- Smith EC, Lewicki MS (2006) Efficient auditory coding. Nature 439: 978–982 [DOI] [PubMed] [Google Scholar]
- Smith SM, Miller KL, Moeller S, Xu J, Auerbach EJ, Woolrich MW, Beckmann CF, Jenkinson M, Andersson J, Glasser MF, Van Essen DC, Feinberg DA, Yacoub ES, Ugurbil K (2012a) Temporally-independent functional modes of spontaneous brain activity. Proceedings of the National Academy of Sciences 109: 3131–3136 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stam CJ, Nolte G, Daffertshofer A (2007) Phase lag index: Assessment of functional connectivity from multi channel EEG and MEG with diminished bias from common sources. Human Brain Mapping 28: 1178–1193 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stitt I, Hollensteiner KJ, Galindo-Leon E, Pieper F, Fiedler E, Stieglitz T, Engler G, Nolte G, Engel AK (2017) Dynamic reconfiguration of cortical functional connectivity across brain states. Scientific Reports 7: 8797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tomescu MI, Rihs TA, Robert B, Juliane B, Anna C, Frédéric G, Maude S, Martin D, Stephan E, Michel CM (2014) Deviant dynamics of EEG resting state pattern in 22q11.2 deletion syndrome adolescents: A vulnerability marker of schizophrenia? Schizophrenia Research 157: 175. [DOI] [PubMed] [Google Scholar]
- Uhlhaas PJ, Roux F, Rodriguez E, Rotarska-Jagiela A, Singer W (2010) Neural synchrony and the development of cortical networks. Trends in Cognitive Sciences 14: 72–80 [DOI] [PubMed] [Google Scholar]
- Van De Ville D, Britz J, Michel CM (2010) EEG microstate sequences in healthy humans at rest reveal scale-free dynamics. Proceedings of the National Academy of Sciences 107: 18179–18184 [DOI] [PMC free article] [PubMed] [Google Scholar]
- van den Broek SP, Reinders F, Donderwinkel M, Peters MJ (1998) Volume conduction effects in EEG and MEG. Electroencephalography and Clinical Neurophysiology 106: 522–534 [DOI] [PubMed] [Google Scholar]
- Van Mierlo P, Papadopoulou M, Carrette E, Boon P, Vandenberghe S, Vonck K, Marinazzo D (2014) Functional brain connectivity from EEG in epilepsy: Seizure prediction and epileptogenic focus localization. Progress in Neurobiology 121: 19–35 [DOI] [PubMed] [Google Scholar]
- Vidalgonzalez I, Vidalgonzalez B, Rauch SL, Quirk GJ (2006) Microstimulation reveals opposing influences of prelimbic and infralimbic cortex on the expression of conditioned fear. Learning & Memory 13: 728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Zang Y, He Y, Liang M, Zhang X, Tian L, Wu T, Jiang T, Li K (2006) Changes in hippocampal connectivity in the early stages of Alzheimer’s disease: Evidence from resting state fMRI. NeuroImage 31: 496–504 [DOI] [PubMed] [Google Scholar]
- Wei J, Bai W, Liu T, Tian X (2015) Functional connectivity changes during a working memory task in rat via NMF analysis. Frontiers in Behavioral Neuroscience 9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams R (2010) The human connectome: just another ‘ome? The Lancet Neurology 9: 238–239 [DOI] [PubMed] [Google Scholar]
- Wilson DIG, Langston RF, Schlesiger MI, Wagner M, Watanabe S, Ainge JA (2013) Lateral entorhinal cortex is critical for novel object-context recognition. Hippocampus 23: 352–366 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright J, Yang AY, Ganesh A, Sastry SS, Ma Y (2009) Robust Face Recognition via Sparse Representation. IEEE Transactions on Pattern Analysis and Machine Intelligence 31: 210–227 [DOI] [PubMed] [Google Scholar]
- Xavier GF, Costa VC (2009) Dentate gyrus and spatial behaviour. Progress in Neuro-Psychopharmacology and Biological Psychiatry 33: 762–773 [DOI] [PubMed] [Google Scholar]
- Xie K, Fox GE, Liu J, Tsien JZ (2016) 512-Channel and 13-Region Simultaneous Recordings Coupled with Optogenetic Manipulation in Freely Behaving Mice. Frontiers in Systems Neuroscience 10 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ye X, Kapeller-Libermann D, Travaglia A, Inda MC, Alberini CM (2017) Direct dorsal hippocampal-prelimbic cortex connections strengthen fear memories. Nature Neuroscience 20: 52–61 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang H, Chen G, Kuang H, Tsien JZ (2013) Mapping and deciphering neural codes of NMDA receptor-dependent fear memory engrams in the hippocampus. Plos One 8: e79454. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


