Applying Machine Learning Algorithms to Segment High-Cost Patient Populations

Abstract

Background

Efforts to improve the value of care for high-cost patients may benefit from care management strategies targeted at clinically distinct subgroups of patients.

Objective

To evaluate the performance of three different machine learning algorithms for identifying subgroups of high-cost patients.

Design

We applied three different clustering algorithms—connectivity-based clustering using agglomerative hierarchical clustering, centroid-based clustering with the k-medoids algorithm, and density-based clustering with the OPTICS algorithm—to a clinical and administrative dataset. We then examined the extent to which each algorithm identified subgroups of patients that were (1) clinically distinct and (2) associated with meaningful differences in relevant utilization metrics.

Participants

Patients enrolled in a national Medicare Advantage plan, categorized in the top decile of spending (n = 6154).

Main Measures

Post hoc discriminative models comparing the importance of variables for distinguishing observations in one cluster from the rest. Variance in utilization and spending measures.

Key Results

Connectivity-based, centroid-based, and density-based clustering identified eight, five, and ten subgroups of high-cost patients, respectively. Post hoc discriminative models indicated that density-based clustering subgroups were the most clinically distinct. The variance of utilization and spending measures was the greatest among the subgroups identified through density-based clustering.

Conclusions

Machine learning algorithms can be used to segment a high-cost patient population into subgroups of patients that are clinically distinct and associated with meaningful differences in utilization and spending measures. For these purposes, density-based clustering with the OPTICS algorithm outperformed connectivity-based and centroid-based clustering algorithms.

Electronic supplementary material

The online version of this article (10.1007/s11606-018-4760-8) contains supplementary material, which is available to authorized users.

INTRODUCTION

Efforts to improve the value of care for high-cost patients may benefit from care management strategies targeted at clinically distinct subgroups of patients ^1–4. Existing frameworks for segmenting high-cost patients are derived from expert opinion and are based predominately on patterns of comorbidity and functional status ^1,3,5,6. There may be an opportunity to supplement these approaches using machine learning methods.

Clustering is an unsupervised machine learning technique that groups observations (e.g., patients) according to similarities among measured characteristics. There are a variety of approaches to clustering. Three of the most commonly used are connectivity-based clustering (also known as hierarchical clustering), centroid-based clustering, and density-based clustering ^7,8. Connectivity-based clustering algorithms sequentially combine, or split, groups of observations based on a metric reflecting the similarity among observations. Centroid-based clustering algorithms begin with a pre-specified number of subgroups and then assign observations to the subgroup with the closest centroid based on a distance metric. Common centroid-based clustering algorithms include k-means and k-medoids. Density-based clustering algorithms identify areas of varied density within a dataset and group together observations that make up areas of high density. One popular density-based clustering algorithm is ordering points to identify the clustering structure (OPTICS), which is an extension of the earlier density-based spatial clustering of applications with noise (DBSCAN) algorithm. Table 1 provides a broad overview of these three clustering approaches and summarizes selected advantages and disadvantages of each.

Table 1.

Overview of Common Clustering Methods Used in This Study

Method	Algorithm	Computational approach	Advantages	Disadvantages
Connectivity-based	Agglomerative hierarchical clustering with Ward’s criterion	Clusters are sequentially merged according to a chosen distance metric to form a hierarchy.	• Does not require a priori specification of the number of clusters. • Works with a variety of distance metrics and linkage methods to merge clusters. • Standard methods exist to be able to visualize the entire cluster hierarchy.	• High computational cost with high-dimensional data such that obtaining a clustering solution may be infeasible. • Requires specifying what level to split the hierarchy to extract a final clustering. • Does not allow for outlier observations (i.e., forces every observation into a cluster)
Centroid-based	K-medoids	Assigns subjects to the nearest medoid, defined as the most central observation within a cluster.	• Simple, fast. • Works with a variety of distance metrics. • More robust to outliers than other centroid-based approaches, such as k-means.	• More memory intensive than other centroid-based approaches, such as k-means. • Must specify the number of clusters a priori or evaluate a large number of different clustering solutions to choose the number of clusters. • Does not allow for outlier observations (i.e., forces every observation into a cluster)
Density-based	Ordering points to identify the clustering structure (OPTICS)	Orders observations based on information about their nearest neighbors and defines clusters as areas with a high density of data points.	• Robust to outliers, with the ability to label them as noise points. • Can return clusters of arbitrary shapes and unequal sizes. • Does not require a priori specification of the number of clusters.	• Requires specification of multiple tuning parameters that are not intuitive. • Produces noise points (can also be considered an advantage). • May fail to converge in some cases if there is large variance in the density of clusters.

Clustering has been used to identify novel disease subgroups across various conditions, including asthma ^9,10, COPD ^11,12, CHF ^13,14, and neurologic disorders ^15,16. However, the application of clustering to health care delivery remains nascent ^17,18. In this study, we aimed to evaluate the performance of connectivity-based, centroid-based, and density-based clustering for identifying subgroups of high-cost patients using a clinical and administrative dataset.

METHODS

Study Population and Data

The study population consisted of patients enrolled in a national Medicare Advantage plan who were in the top decile of total per-patient spending in 2014 (n = 6154). See an accompanying article for a full description of the study population ¹⁹. We extracted demographic and clinical data directly from the health plan’s electronic data warehouse (EDW). Data were obtained for the years 2013–2015. We grouped 377 unique variables into several major categories: demographics, chronic conditions, active diagnoses, procedures, laboratory, and pharmacy. A full list and description of the study variables is provided in Appendix 1.

Data Pre-processing

An important first step in analyzing datasets with large numbers of variables is to remove redundancies and correlations that limit the ability to extract meaningful information. Since we aimed to identify clinically distinct subgroups of patients, we sought to remove variables that would not provide meaningful differentiation among patients. First, we removed variables with extremely low variance based on two criteria: (1) the ratio of the second most common value to the most common value was ≥ 0.99 and (2) the percentage of unique values (the number of unique values divided by the number of observations) was ≤ 1%. A total of 214 (of 377) variables were removed based on these criteria. Next, we removed non-binary variables that were highly correlated with others. We defined high correlation as a Pearson correlation coefficient greater than 0.85. A total of 2 (of 163) variables were removed based on this criterion. A complete list of the remaining 161 variables and a description of a standard method used for imputing missing values are provided in Appendices 2 and 3, respectively.

Dimension Reduction

When clustering datasets with large numbers of variables (i.e., dimensions), a common task is to reduce the number of variables in the dataset while retaining as much of the original information and structure as possible, a task known as dimension reduction. Dimension reduction not only reduces computational burden but also mitigates the “curse of dimensionality”—the fact that data become increasingly sparse as the number of variables increases ^20,21. The curse of dimensionality makes it conceptually and computationally difficult to converge on a reasonable clustering solution.

We utilized a validated, non-linear dimension reduction algorithm called t-distributed stochastic neighbor embedding (t-SNE) ²². The t-SNE method takes as input a high-dimensional data set and maps each observation to a lower-dimensional space. We ran a specific implementation of t-SNE known as the Barnes-Hut algorithm and mapped to a two-dimensional space in order to facilitate visualization ^22,23. Full details on t-SNE implementation are provided in Appendix 4.

Model Tuning

For each of the algorithms described below, we followed a standardized approach for tuning model parameters. First, we a priori restricted algorithm solutions to those that yielded between five and ten clusters. This helped to ensure that the resultant subgroups of patients would not be so small as to be operationally insignificant. Next, we calculated the average silhouette width for each solution. Average silhouette width, which we calculated using Euclidean distance, reflects how similar an observation is to those in its own cluster as compared to observations in other clusters ²⁴. Finally, we selected the solution that maximized average silhouette width. Additional information on model tuning is provided in Appendix 5.

Connectivity-Based Clustering

For connectivity-based clustering, we used agglomerative hierarchical clustering with Ward’s criterion ²⁵. This algorithm places each observation in its own cluster and then sequentially merges the two most similar clusters until there is only one large group. The decision of which clusters to merge at each step is made by selecting the combination that minimizes the squared Euclidean distance (e.g., the “ordinary” straight-line distance) between observations within each cluster. The result is a hierarchy, or dendrogram, that classifies each observation as a member of progressively larger clusters. Cutting the hierarchy at different levels, therefore, generates a different number of final clusters. We cut the hierarchy at six different levels to produce solutions with five to ten clusters. We then computed the average silhouette width for all observations and selected the clustering with the highest value.

Centroid-Based Clustering

For centroid-based clustering, we used the k-medoids algorithm ²⁶. K-medoids requires pre-specification of the number of clusters (k) within which to group observations. The algorithm begins with a random selection of k observations to serve as the center, or medoid, of each cluster. Observations are then assigned to the cluster with the closest medoid, as defined by a chosen distance metric (e.g., Euclidean). Next, the algorithm re-selects the most central observation for each cluster and conducts a re-assignment of observations until it converges to a final, stable assignment. We ran several iterations of the k-medoids algorithm using Euclidean distance and varying k between 5 and 10. We calculated the average silhouette width for each solution and selected the k that yielded the solution with the highest average silhouette width.

Density-Based Clustering

For density-based clustering, we used the OPTICS algorithm ^27,28. OPTICS requires a specified minimum number of nearest neighbors (MinPts) within a specified radius around the observation (ε). Points located in relatively low-density regions have few “neighbors” and may be classified as outliers. We set MinPts at 1% of the study population, or 62 patients (observations), to help ensure that clusters would not be so small as to be operationally insignificant. Given a specified ε, OPTICS returns any cluster solution corresponding to a radius less than ε. We varied ε such that we extracted all of the clustering solutions that produced between five and ten clusters. Then, we then calculated the average silhouette width for each solution and selected the solution with the highest average silhouette width.

Evaluating Algorithm Performance

First, we performed a visual examination of the cluster assignments using the two-dimensional representation of the data set generated by the t-SNE algorithm. We created colored hull plots to visualize the clusters generated by each algorithm.

Second, we employed a set of ridge regression ²⁹ models to better understand the relationship between cluster assignment and clinical variables. A separate set of models was implemented for each cluster. The dependent variable in each model was a dichotomous indicator of assignment to a given cluster, and the original 161 variables were independent variables. The magnitudes of the resulting model coefficient estimates represent the relative contribution of each independent variable to discriminating patients in one cluster from other high-cost patients. Details of model fitting are provided in Appendix 6, including technical details about how we averaged across models and how we chose penalization terms to ensure comparability across clusters and methods. Following model fitting, we computed the range of the estimated coefficients (maximum value minus minimum value) across clusters for each independent variable. This metric is a measure of variable importance, where a large value suggests that the variable is useful for distinguishing observations in one cluster from the rest. In order to visualize these results, we plotted the values of the variables with the largest 20 ranges for each of the clustering methods.

Finally, we examined the extent to which cluster assignments were associated with differences in utilization and spending. As noted above, these variables were not used for clustering. First, we calculated intra-cluster averages for the following utilization and spending variables: inpatient hospital (IP) admissions; total number of IP days; emergency department (ED) visits; total spending; the percentage of spending attributable to inpatient care, medications, and other sources; and the percentage of persistently high-cost patients (those who remained in the top decile of spending the subsequent year). Next, we calculated inter-cluster variance in these utilization and spending averages for each clustering method.

Implementation Details

Data preparation was done in SAS version 9.4 (SAS Institute, Cary, NC). R version 3.2.5 was used for all other analyses. The Rtsne package version 0.13 was used for dimension reduction and the dbscan package version 1.1–1 was used for OPTICS density-based clustering analysis. The cluster package version 2.0.7–1 was used for agglomerative hierarchical clustering with Ward’s criterion and k-medoids clustering.

RESULTS

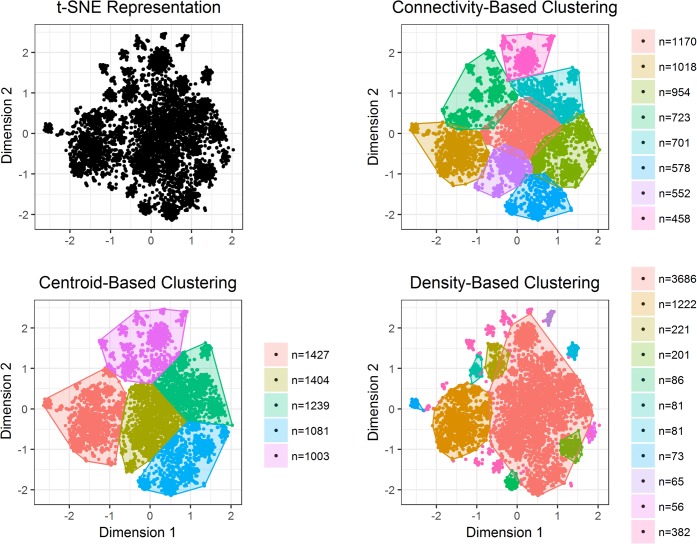
Figure 1 summarizes the results of each clustering algorithm. Connectivity-based clustering identified eight subgroups of high-cost patients, ranging in size from 458 to 1170 patients. Centroid-based clustering identified five subgroups, ranging in size from 1003 to 1427 patients. Density-based clustering identified ten subgroups, ranging in size from 56 to 3686 patients, with 382 not assigned to any subgroup.

Figure 1.

Visual representation of patient subgroups, by clustering method. The figures represent two-dimensional projection of our dataset generated by the t-SNE dimension reduction algorithm (t-SNE projection). Each point is a patient in the study population, and the distance between two points approximates their similarity in high-dimensional space. The top left plot represents the t-SNE projection in insolation. The remaining plots overlay colored convex cluster outlines to the t-SNE projection for each of the three clustering methods. The number of patients in each cluster is provided next to the plots.

Figure 1 also graphically depicts the clustering results in the two-dimensional projection of our dataset generated by the t-SNE dimension reduction algorithm. Each point is a patient in the study population, and the distance between two points approximates their similarity in high-dimensional space. Colored hull plots are used to depict the subgroups of patients identified by each clustering method. Connectivity- and centroid-based clustering identified subgroups of roughly similar sizes and shapes. Density-based clustering, on the other hand, yielded subgroups of markedly varied sizes and shapes. Figure 1 also highlights the difference between the three clustering methods with respect to the treatment of outliers. The density-based clustering algorithm permitted outliers, whereas the connectivity- and centroid-based algorithms did not. By forcing all points into clusters, most of the subgroups identified by the connectivity- and centroid-based algorithms appear more heterogeneous.

Results from the ridge regression analysis are summarized in Figure 2, which depicts the estimated coefficient ranges for the 20 variables with the ranges among each clustering method. This range roughly corresponds to the extent to which the variable contributes to differentiation among subgroups. Centroid-based clustering had the largest range for the top ranked variable. Density-based clustering resulted in a larger range for the next 11 highest ranked variables, after which the three methods converged. The estimated coefficient ranges for each variable, as well as a list of the variables depicted in Figure 2, are provided in Appendix 8.

Figure 2.

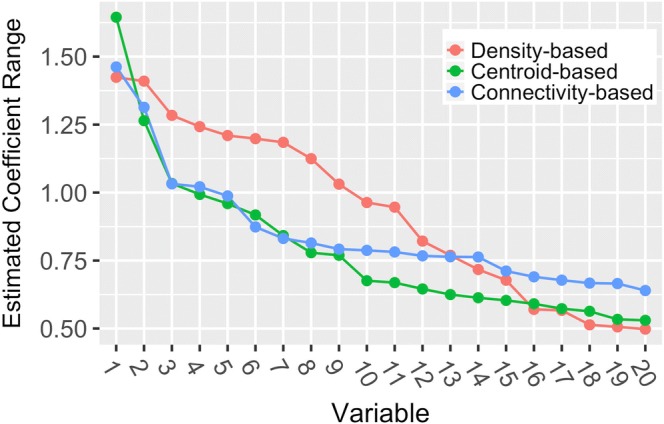
Summary of the results of the ridge regression analysis. The ridge regression estimated coefficient range represents the range of estimated coefficients (maximum value minus minimum value) for a given variable, across all subgroups. These ranges correspond to the extent to which a variable drives differentiation among the subgroups of patients identified by that method—a large value suggests that the variable is useful for distinguishing observations in one subgroup from the rest. For each clustering method, the 20 variables with the largest coefficient ranges are included. A list of the variables depicted along the x-axis for each method is provided in Appendix 8.

Variance of utilization and spending measures across subgroups is summarized in Table 2. Higher variance corresponds to more differentiation across subgroups. Density-based clustering resulted in subgroups with the greatest variance across all utilization and spending variables, with the exception of ED visits. The difference was most pronounced among IP admissions, IP days, total spending, and the percent of spending attributable to medications. The mean values from which variances were calculated are provided in Appendix 9.

Table 2.

Variance of Utilization and Spending Variables Across Subgroups, by Clustering Method

	Connectivity-based clustering	Centroid-based clustering	Density-based clustering
Inpatient admissions	0.55	0.51	0.77
Inpatient days	5.23	5.17	7.17
ED visits	0.86	0.88	0.78
Total spending, $	11,887	12,441	14,621
Inpatient, %	12%	12%	18%
Medication, %	5%	5%	22%
Other, %	14%	16%	23%
Persistently high-cost, %	20%	23%	25%

Persistently high-cost was defined as remaining in the highest decile of spending in the subsequent year. The mean values from which variances were calculated are provided in Appendix 9

ED emergency department

DISCUSSION

We evaluated the performance of three different clustering methods for identifying subgroups of high-cost patients using a multi-dimensional clinical and administrative data set. Specifically, we compared connectivity-based clustering using agglomerative hierarchical clustering, centroid-based clustering with the k-medoids algorithm, and density-based clustering with the OPTICS algorithm.

We performed several analyses to assess the performance of the three clustering algorithms. Our intention was to evaluate the capability of each algorithm to identify subgroups of patients that were (1) clinically distinct and (2) associated with meaningful differences in relevant utilization metrics. To answer the first question, we fit a set of post hoc ridge regression models to the subgroups in order to learn about how patients in one subgroup were different from the rest of the population. We then compared the estimated model coefficients for each variable across subgroups. This allowed us to determine the extent to which specific variables (i.e., clinical characteristics) created differentiation across subgroups. In general, we found that the estimated coefficient ranges for the density-based algorithm were greater than those for the connectivity- and centroid-based algorithms, suggesting that the subgroups identified by the density-based algorithm were the most clinically distinct.

To answer the second question, we examined the variance of selected utilization and spending measures across subgroups. The level of variance across subgroups identified by the density-based clustering algorithm exceeded that of the connectivity- and centroid-based algorithms for nearly all measures. High variance across utilization and spending measures has important operational implications. For example, a subgroup with high rates of inpatient admissions will benefit from different care management interventions than those necessary for a subgroup with high rates of spending attributable to medications.

Since utilization and spending variables were not used for clustering, this analysis also functioned as a test of external validity. For all three clustering methods, we found significant variance in utilization and spending variables across subgroups. This suggests that clustering patients on clinical variables can effectively identify unique subgroups of patients with distinct patterns of utilization and spending.

Taken together, our results suggest that density-based clustering with the OPTICS algorithm performs best for identifying clinically distinct and operationally significant subgroups of high-cost patients in our data, and may be a promising and feasible approach for subgroup analysis in health plan or health system data. An accompanying article provides an in-depth description of the clinical composition, utilization patterns, and spending trajectories of the subgroups identified by the OPTICS algorithm ¹⁹.

Differences in the algorithmic approach of density-based clustering with OPTICS may explain why it outperformed connectivity- and centroid-based algorithms in this study. First, OPTICS allows for “noise” points (i.e., observations not assigned to any cluster), whereas connectivity- and centroid-based clustering algorithms force all observations into clusters. By forcing outlier observations into subgroups, the resultant subgroups become more heterogeneous. Since outliers are frequent in medical data, this may limit clinical utility. We found that including outliers (as defined by OPTICS) led to subgroups that were less clinically distinct and, therefore, less operationally significant. Second, the OPTICS algorithm is able to identify subgroups of uneven sizes, as demonstrated in Figure 1. In care management settings, programs are often designed for various patient groups, and the size of sub-populations to which the programs apply may vary drastically. Lastly, OPTICS does not require one to specify the number of clusters a priori, an attractive property in clinical settings where the underlying data structure may not be well understood. However, the process of tuning models to maximize discrimination and select the optimal number of clusters may mitigate this advantage.

Using unsupervised machine learning algorithms to identify subgroups of high-cost patients is a departure from existing efforts to segment high-cost populations that rely predominately on expert-opinion derived taxonomies ^1,3,5,6,30. We do not expect, nor advocate, that clustering and other machine learning methods replace existing, expert-opinion derived taxonomies. Rather, these methods could serve as an important complement through two major channels. First, for payers and large delivery organizations, there likely exists sufficient in-house technical expertise to use clustering to derive high-cost patient subgroups directly from internal data sets. This approach, which utilizes free, publicly available algorithms and software packages, contrasts with the recent proliferation of proprietary, “black box” commercial risk-prediction and population segmentation algorithms. Second, researchers and policy analysts may be able to use clustering to identify common subgroups across populations that could be added to existing taxonomies.

This study has several limitations. First, by pre-specifying a small number of subgroups (five to ten), we may have failed to identify a more quantitatively optimal segmentation of the data set that included several small, homogeneous subgroups. However, we selected this range based on prior literature ^1,3,5 and to avoid identifying subgroups so small that they would be operationally insignificant. Second, our comparison of different clustering methods used illustrative algorithms from each class of methods and was limited to three classes of methods. This should not be construed to be a comprehensive, or definitive, assessment of clustering approaches. We chose to focus on three of the most common clustering methods that can be implemented with standard packages in open source software. Finally, we limited our study to a single approach to dimensional reduction, t-SNE. Although t-SNE has been shown to produce well-separated clusters in a variety of biomedical settings ^31–34, it is a stochastic method that relies on a number of user-specified inputs. Future work should include comparisons of t-SNE to other projection techniques, such as principal component analysis (PCA).

Funding Information

This study was supported by a grant from the Anthem Public Policy Institute and, in part, under a grant with the Pennsylvania Department of Health.

Compliance with Ethical Standards

This study was approved by the Institutional Review Board of the University of Pennsylvania.

Conflict of Interest

Dr. Navathe reports that he has received grant support from Hawaii Medical Service Association, Anthem Public Policy Institute, and Oscar Health; personal fees from Navvis and Co, Navigant Inc., Lynx Medical, Indegene Inc., Agathos, Inc, and Sutherland Global Services; personal fees and equity from NavaHealth; serves on the board without compensation for Integrated Services, Inc., speaking fees from the Cleveland Clinic, and honoraria from Elsevier Press. Dr. Linn reports that she has received grant support from Hawaii Medical Service Association. Dr. Jain reports employment by Anthem, Inc.; stock ownership in Anthem, Inc., and honoraria from Elsevier Press. Ms. Kowalski reports employment by Anthem, Inc. and stock ownership in Anthem, Inc. and Amazon. Dr. Powers reports employment by Anthem, Inc. All other authors declare no conflicts of interest.

Disclaimer

The Pennsylvania Department of Health specifically disclaims responsibility for any analyses, interpretations, or conclusions.