Cognitive Assessment Prediction in Alzheimer’s Disease by Multi-Layer Multi-Target Regression

Abstract

Accurate and automatic prediction of cognitive assessment from multiple neuroimaging biomarkers is crucial for early detection of Alzheimer’s disease. The major challenges arise from the nonlinear relationship between biomarkers and assessment scores and the inter-correlation among them, which have not yet been well addressed. In this paper, we propose multi-layer multi-target regression (MMR) which enables simultaneously modeling intrinsic inter-target correlations and nonlinear input-output relationships in a general compositional framework. Specifically, by kernelized dictionary learning, the MMR can effectively handle highly nonlinear relationship between biomarkers and assessment scores; by robust low-rank linear learning via matrix elastic nets, the MMR can explicitly encode inter-correlations among multiple assessment scores; moreover, the MMR is flexibly and allows to work with non-smooth l_2,1-norm loss function, which enables calibration of multiple targets with disparate noise levels for more robust parameter estimation. The MMR can be efficiently solved by an alternating optimization algorithm via gradient descent with guaranteed convergence. The MMR has been evaluated by extensive experiments on the ADNI database with MRI data, and produced high accuracy surpassing previous regression models, which demonstrates its great effectiveness as a new multi-target regression model for clinical multivariate prediction.

Introduction

Alzheimer’s disease (AD) is the most common cause of dementia and is characterized by progressive loss of memory. AD severely impacts human thinking and behavior. The influence of AD is both extensive and complex, making it difficulties to prevent or diagnose this disease (Association et al. 2016). Neuroimaging techniques provide a powerful tool for the early diagnosis and response monitoring of Alzheimer’s such that the diagnostic capabilities can be improved. The Alzheimer’s Disease Neuroimaging Initiative (ADNI) study (Jack et al. 2008; Mueller et al. 2005) collects neuroimaging and cognitive measurement of normal aging, mild cognitive impairment as well as AD samples, which provides a wealth of resources for the study of Alzheimer’s diagnosis, treatment and prevention.

According to the statistics in Association et al. (2016), by 2016 Alzheimer’s affects a total of 5.4 million American people. This disease is incurable and there is no accurate way to diagnose AD. Thus, the current consensus emphasizes the need to diagnose and explore cognitive performance of brain function. Several cognitive tests have been presented to assess individual’s cognitive level, such as Mini-Mental State Examination (MMSE) (Folstein et al. 1975) and Rey Auditory Verbal Learning Test (RAVLT) (Schmidt and et al. 1996). In recent AD research, a wide range of work has employed regression models to uncover the relationship between neuroimaging data and cognitive test scores (Seshadri et al. 2007; Moradi et al. 2016). The major challenges arise from the jointly modeling nonlinear relationship between biomarkers and assessment scores and the intrinsic correlation among assessment scores.

Since the biomarkers are features extracted from imaging data and therefore contain relatively low-level information, while the assessment scores are high-level measurement of disease progress, the relationship between biomarkers and scores tends be complex and highly nonlinear. However, most previous methods use linear regression models to predict the relationship between imaging biomarkers and cognitive assessment (Ferrarini et al. 2008; Moradi et al. 2016), which is not appropriate to illustrate the complex influence of brain structure impairment.

Since different cognitive assessment scores provide the measurement related to the same disease progress, these scores as regression targets are correlated. Finding out such inter-target relations can be beneficial to analyzing the influence of neuroimaging biomarkers on memory assesment performance. In this paper, we address cognition assessment by formulating it as a multi-task learning problem with a newly proposed multi-target regression (a.k.a., multi-output regression) model. Although multi-target regression has been extensively explored, existing models have some shortcomings and would not achieve satisfactory performance on our specific application.

To explore inter-target correlations, existing multi-target regression models were focused mainly on linear regression models (Rothman et al. 2010; Sohn and Kim 2012; Rai et al. 2012; Gong et al. 2014; Liu et al. 2014; Pan et al. 2015; Zhu et al. 2017) or specifically developed under particular assumptions with prior knowledge (Argyriou et al. 2008; Agarwal et al. 2010; Zhang and Yeung 2013; Kumar and Daume 2012; Ciliberto et al. 2015), which facilitates the correlation modeling. By building upon linear regression models, sparsity or low rank is simply imposed on the regression matrix to capture inter-target correlations (Kolar et al. 2011; Liu et al. 2014; Molstad and Rothman 2015); however, these linear models suffer from the limited ability to handle nonlinear relationships between high-dimensional inputs and multiple targets (Hara and Chellappa 2014), and moreover it is non-trivial to extend these linear models for nonlinear regression due to the non-convexity of sparsity constraints or loss functions (Liu et al. 2014; Dinuzzo and Schölkopf 2012). By making some specific assumptions, e.g., regression task parameters share a common prior (Yu et al. 2005; Lee et al. 2007; Daume´ III 2009), or lie in on a low-dimensional manifold (Agarwal et al. 2010) or share a linear subspace (Kumar and Daume 2012), particular inter-target correlations were explored in previous work (Yu et al. 2005; Lee et al. 2007; Daume´ III 2009; Agarwal et al. 2010; Kumar and Daume 2012); however, these assumptions can be too restrictive and would not necessarily hold or be shared by different applications in practice (Zhang and Yeung 2014), which makes them lack of generality.

To handle the complex nonlinear input-output relationships, kernel methods (Evgeniou et al. 2005; Alvarez et al. 2012; Li et al. 2015) were extended from single task learning to multi-task learning. In Evgeniou et al. (2005), the regression matrix of multiple tasks is simply reshaped into a vector to explore inter-target correlations, which however does not distinguish between inter and intra tasks and tends to be less effective to encode the correlations. Moreover, the method assumes that the task similarity between tasks is given and the regularization term is based on the similarity which however is mostly unknown and varies dramatically with different applications. In addition, since the similarity is nonnegative, the model can only model positive relationships between multiple tasks.

To achieve this goal, in this paper we propose a novel model, Multi-layer Multi-target Regression (MMR). Our model enables simultaneously modeling intrinsic inter-target correlations and complex input-output relationships in one single general framework. The MMR accomplishes a multi-layer learning architecture which is composed of the input, hidden and target (output) layers as illustrated in Fig. 1.

Fig. 1.

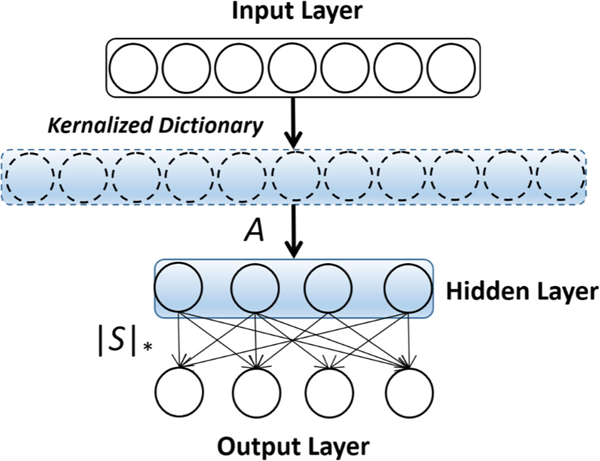
The learning architecture of the multi-layer multi-target regression (MMR) model

The proposed MMR leverages the strength of kernel methods for nonlinear feature learning and the structural advantage of multi-layer architectures to capture inter-target correlations, which could explicitly encode the correlations among different cognitive learning tasks. More importantly, it provides a new multi-layer learning paradigm that is endowed with high generality, flexibility and expressive ability for multi-target clinical data prediction.

The contributions of this work are summarized as follows:

• –We formulate cognitive assessment as a multi-task learning problem, which is fulfilled by a newly proposed multi-layer multi-target regression (MMR) model.
• –We introduce the compositional learning framework which enables jointly modeling nonlinear input-output relationship and intrinsic inter-target correlations.
• –We introduce the l_2,1-norm loss function to achieve automatic calibration of multiple targets with disparate noise levels, which enables more robust parameter estimation.

Related Work

In this section, we briefly review related work in terms of both multi-target regression and the Alzheimer’s disease application.

Since AD is a chronic neuro-degenerative disease, it is important to reveal the correlation between changes in brain structure and cognitive dysfunction. Recent studies have employed different machine learning models to analyze the association between imaging markers and cognitive performance. In Ferrarini et al. (2008), the authors employed linear regression models to evaluate the correlation between structural brain atrophy and MMSE cognitive score, where well-defined periventricular structures like left temporal horn, left corona radiata, and the right caudate nuclei were found to have distinct impact on the performance in MMSE cognitive test.

Moradi et al. (2016) applied elastic net linear regression in the prediction of RAVLT test score via MRI data. They identified several neuroimaging features for the estimation of RAVLT, including medial temporal lobe structures angular gyrus, hippocampus and amygdala, which shed insights on understanding the influence of these important brain regions for episodic memory.

Falahati et al. (2016) conducted a longitudinal investigation among an non-demented and stroke-free people from the Rotterdam study. By means of linear and Cox regression models, the authors revealed the correlation between hippocampal subiculum and the onset of dementia, which indicated an important marker for dementia prediction.

Zhu et al. (2015) combined support vector regression (SVR) and support vector machine (SVM) to jointly predict the clinical scores as well as the disease status. They formulated the joint learning process in a multi-task learning framework such that different tasks will strengthen each other in AD diagnosis.

The successful applications of machine learning approaches in the prediction of cognitive impairment strengthened the study of underlying pathology in Alzheimer’s. In a cognitive assessment, there are usually several different tests involved. The output from different tests can be correlated. Rothman et al. (2010) put forward an approach to explore the output structure. They proposed a multivariate regression model with covariance estimation (MRCE), in which a procedure is developed for constructing a sparse estimator of a multivariate regression coefficient matrix that accounts for correlation of the response variables. However, the MRCE does not leverage the learned output structure to share similar input variables among related outputs (Sohn and Kim 2012). Moreover, it is a linear regression model with limited ability to handle nonlinear regression tasks.

Moreover, if we treat the estimation of each cognitive test score as one task, we can naturally formulate the situation of multiple cognitive test estimation as a multi-task learning problem. Previous machine learning models provided different approaches on how to automatically capture the structure among tasks. In Zhang and Yeung (2014), Zhang and Yeung proposed a convex formulation for multi-task relationship learning (MTRL), which models the relationships between tasks in a nonparametric manner based on the assumption that all tasks are close to each other by measuring the Frobenius norms of their differences. The MTRL is developed based on prior assumptions of multivariate normal distributions on both multiple targets and regression parameters. However, those assumptions do not necessarily hold in practice or be shared by different applications.

The MTRL is further generalized in Rai et al. (2012) where multi-target regression with output and task structures (MROTS) is proposed to jointly explore the covariance structure of latent model parameters and the conditional covariance structure of multiple targets. MROTS outperforms both MTRL and MRCE, which however similar to the MRCE (Rothman et al. 2010) does not admit trivial extensions to nonlinear regression. Sohn and Kim (2012) introduce a matrix l₁ norm based inverse-covariance regularization for joint estimation of structured sparsity and output structure for multi-target regression, where the output structure of multiple targets is represented as a graph.

Inter-target correlation has also been investigated in kernel scenarios. the output kernel learning (OKL) was developed for vector-valued functions to explore inter-target correlations for multiple task learning (Alvarez et al. 2012; Dinuzzo et al. 2011; Dinuzzo 2013). Nevertheless, the OKL does not fully capture inter-target correlations since it simply learns a semi-definite similarity matrix of multiple targets.

Multi-target regression has also been studied under the framework of ensemble learning. A fitted rule ensembles (FIRE) algorithm is introduced in Aho et al. (2012) to improve multi-target regression by adding simple linear functions to the ensemble. Based on ensemble learning, Tsoumakas et al. (2014) construct new target variables by random linear combination (RLC) of existing targets, which is heuristically derived from multi-label classification. However, those methods fail to take into account the correlation of multiple targets.

Recently, Zhou and Zhao (2016) propose flexible clustered multi-task (FCMTL) which is an improved version of clustered multi-task learning (CMTL). In order to explore inter-target correlation, also based on the cluster assumption, the cluster structure is learned in FCMTL by identifying representative tasks. However, the assumption of the existence of representative tasks would be too strong and not necessarily shared by different applications due to the diversity.

Multi-Layer Multi-Target Regression

Multi-Target regression is to learn a holistic mapping function h from the input space X ∈ ℝ^d to the multivariate target (output) space y ∈ ℝQ, where d is the dimensionality of the input space and Q is the number of targets. We will find a function h that is able to simultaneously handle the aforementioned multiple challenges within one single framework by a general compact formulation of compositional learning.

A General Compositional Learning Framework

Given a training set of training data X = {x₁,…, x_i,…, x_N } associated with targets Y = {y₁,…, y_i,…, y_N }, the MMR seeks a mapping function h: X → Y, which takes a generic formula as follows

$$\mathbf{\text{y}}\hspace{0.17em}=\hspace{0.17em}h\hspace{0.17em}\left(\mathbf{\text{x}}\right)\hspace{0.17em}=\hspace{0.17em}f\hspace{0.17em}\left(g\left(\mathbf{\text{x}}\right)\right)\hspace{0.17em}=\hspace{0.17em}\left(f\hspace{0.17em}o\hspace{0.17em}g\right)\hspace{0.17em}\left(\mathbf{\text{x}}\right)$$ (1)

where g and f are two functions that are jointly learned to establish the overall mapping h from input image representations to target shapes. g serves to extract high-level features, i.e., the latent variables, z that span the latent space, where z ∈ ℝ^Q,

$$\mathbf{\text{z}}\hspace{0.17em}=\hspace{0.17em}g\left(\mathbf{\text{x}}\right)$$ (2)

From the latent space, we propose explicitly encoding the inter-target correlations via f by:

$$\mathbf{\text{y}}\hspace{0.17em}=\hspace{0.17em}f\left(\mathbf{\text{z}}\right)$$ (3)

Both g and f can be customized according to diverse applications and regulated by different constraints to favor specific properties, which ensures the generality of the MMR. It establishes a multi-layer learning architecture which is endowed with high generality, great flexibility and strong expressive ability to jointly handle highly complex input-output relationships and intrinsic correlations of multiple targets in one single framework.

The functions f and g can be found by the following general regularized learning framework:

$$\underset{f,g\in \mathcal{H}K}{\min }\frac{1}{\mathcal{N}}\sum _i^{\mathcal{N}}\mathcal{L}\left(f,g,{\mathbf{\text{x}}}_i,{\mathbf{\text{y}}}_i\right)\hspace{0.17em}+\hspace{0.17em}\lambda \mathrm{\Omega }\left(g\right)\hspace{0.17em}+\beta \mathrm{\Omega }\left(f\right)$$ (4)

where ℒ is the general loss function which could be the least square error or the hinge loss; λ and β are the regularization parameters; Ω(g) is the regularization term g to control its complexity to prevent overfitting; Ω(f) is the regularization term on S to encode intrinsic inter-target correlations. The latent variables can be viewed as higher-level features that facilitate jointly modeling input-output relationships and inter-target correlation. In the following, we specify functions f and g to achieve the multi-layer multi-target regression (MMR).

Nonlinear Learning via Kernelized Dictionary

We propose building the nonlinear function g via Kernelized dictionary rather than based on the kernel extension of a linear regression model (Zhen et al. 2017). Specifically, the function g takes the following forms:

$$\mathbf{\text{z}}\hspace{0.17em}=\hspace{0.17em}\sum _{i=\hspace{0.17em}1}^N\alpha iK\hspace{0.17em}\left({\mathbf{\text{x}}}_i,\mathbf{\text{x}}\right)\hspace{0.17em}=\hspace{0.17em}A{K}_{\mathbf{\text{x}}}$$ (5)

Where $K{\left({\mathbf{\text{x}}}_i,\hspace{0.17em}\hspace{0.17em}\cdot \right)}_{i\hspace{0.17em}=1}^N$ is the Kernelized dictionary, k_x = [… ;k(xi, x); …] ∈ ℝ^N; α ∈ ℝ^Q is the coefficients associated with each atom in the dictionary and A ∈ ℝ^Q×N = [α1, …, αi, …, α_N]. To achieve nonlinear learning, we usually employ the radius basis function as the kernel function, i.e., k(xi, xj ) = exp(||xi − xj ||²/σ ²), where σ is the band width.

It is notable that (5) is the multivariate extension of the conventional kernel dictionary (Feng et al. 2016), which has recently drawn great attention. The advantages of using kernelized dictionary for nonlinear learning rather than kernel extension (Zhen et al. 2017) lie in two major aspects. On one hand, the kernel k is not necessarily the Mercer kernel, which makes learning more applicable because the Mercer condition on the kernel may be difficult to satisfy. On the other hand, it allows to more flexibly design loss functions, not necessarily restricted to strictly smooth functions. This benefit will be shown in the calibration of multiple targets (Section 3).

If we choose the Frobenius norm loss, the objective function (4) turns out to be the form as follows

$$\underset{f,A}{\min }\frac{1}{\mathcal{N}}{\Vert Y\hspace{0.17em}-\hspace{0.17em}AK\Vert }_F^2+\hspace{0.17em}\lambda {\Vert A\Vert }_F^2\hspace{0.17em}+\hspace{0.17em}\beta \mathrm{\Omega }\left(f\right)$$ (6)

The multi-target regression model in (6) is decoupled into several single-target problems, which does not take into account inter-target correlations, resulting in suboptimal multi-target regression with inferior performance. In what follows, we introduce our MMR, which is a multi-layer learning architecture to explicitly model the correlations by a robust low-rank learning with matrix elastic nets (MEN).

Robust Low-Rank Learning via Matrix Elastic Nets

Rather than directly imposing sparsity regression coefficients in existing methods, we propose incorporating a structure matrix S to explicitly encode inter-target correlations via a rank minimization.

$$\underset{W,S}{\min }\frac{1}{\mathcal{N}}{\Vert Y\hspace{0.17em}-\hspace{0.17em}SZ\Vert }_F^2+\hspace{0.17em}\lambda {\Vert A\Vert }_F^2+\hspace{0.17em}\beta Rank\left(S\right)+\hspace{0.17em}\gamma {\Vert S\Vert }_F^2,$$ (7)

where Z = [z₁,…, z_i,…, z^N ] ∈ ℝ^Q×N, z_i = Ak_xi ∈ ℝ_Q contains the latent variables in the latent space, S ∈ ℝ^Q×Q is the structure matrix that serves to explicitly model inter-target correlations, β is the regularization parameter to control the rank of S, that is, a larger β induces lower rank, and the Frobenius norm control the shrinkage of S with the associated parameter γ. The rank minimization of the structure matrix S explores the low-rank structure existing between tasks to capture the intrinsic inter-target correlation. S is learned automatically from data without relying on any specific assumptions, which allows to adaptively cater different applications.

However, the objective function in (7) is NP-hard due to the noncontinuous and non-convex nature of the rank function. The nuclear norm ||S||_* is commonly used and has been proven to be the convex envelop of the rank function over the domain ||S||₂ ≤ 1, which provides the tightest lower bound among all convex lower bounds of the rank function Rank(S).

As a consequence, the combination of the nuclear norm with the Frobenius norm on S gives rise to the matrix elastic net (MEN) (Li et al. 2012) as a regularizer of (7):

$$\underset{W,S}{\min }\frac{1}{\mathcal{N}}{\Vert Y\hspace{0.17em}-\hspace{0.17em}SZ\Vert }_F^2+\hspace{0.17em}\lambda {\Vert A\Vert }_F^2+\hspace{0.17em}\beta {\Vert S\Vert }_{*}\hspace{0.17em}+\hspace{0.17em}\gamma {\Vert S\Vert }_F^2,$$ (8)

where the nuclear norm ||S||_* is also known as the trace norm.

The MEN is an analog to the elastic-net regularization (Zou and Hastie 2005) from compressive sensing and sparse representation (Zou and Hastie 2005). It has been shown that the elastic net often outperforms the lasso (Zou and Hastie 2005). In the MEN, the nuclear-norm constraint enforces the low-rank property of the solution S to encode inter-target correlations, and the Frobenius-norm constraint induces a linear shrinkage on the matrix entries leading to stable solutions (Li et al. 2012). The MEN regularization generalizes the matrix lasso and provides improved performance than lasso (Tibshirani 1996). To the best of our knowledge, this is the first work that introduces the MEN to multi-target regression for robust low-rank learning, which offers a general framework to encode inter-target correlations.

Calibration of Multiple Targets

Multivariate targets (outputs) exhibit distinct noise levels which are usually unknown a priori in practice (Rakitsch et al. 2013; Gillberg et al. 2016). It is theoretically shown that regularization parameters should be chosen in proportion to the maximum standard deviations of the noise for each target to achieve optimal parameter estimation error bound (Lounici et al. 2011). It is crucial to take into account the disparate noise levels of multivariate targets to achieve robust parameter estimation for improved prediction performance.

We replace the Frobenius norm in (8) with the l_2,1-norm as the loss function to calibrate multivariate targets (Liu et al. 2014), which accomplishes the final objective function as follows:

$$\underset{A,S}{\min }\frac{1}{\mathcal{N}}{\Vert Y\hspace{0.17em}-\hspace{0.17em}SAK\Vert }_{2,1}+\hspace{0.17em}\lambda tr\left(A^{\top }A\right)+\hspace{0.17em}\beta tr(\sqrt{S^{\top }S)}+\hspace{0.17em}\gamma tr\left(S^{\top }S\right).$$ (9)

In (9), the induced latent variables Z = Ak can extract high-level representations for multiple semantic targets, which allows to disentangle the nonlinear relationship between low-level inputs and semantic-level targets. The latent variables are represented by notes of hidden layers in Fig 1. The latent space with high-level features will also facilitate the efficient linear low-rank learning of S to model inter-target correlations to achieve more accurate multi-target prediction. The MMR in (9) leverages the strength of kernel methods for nonlinear feature extraction and the structural advantage of multi-layer architectures for inter-target correlation modeling. In contrast to existing multi-target regression models, the obtained MMR in (9) accomplishes a new multi-layer learning architecture, which 2 min is endowed with great generality, flexibility and expressive ability for diverse challenging tasks. We derive a new alternating optimization algorithm to efficiently solve the objective in (9), which associated with the convergence proof is attached in the supplementary material due to the space limit.

Alternating Optimization

The obtained objective function (9) is non-trivial to solve simultaneously for A and S due to the non-convexity of the objective function. We derive a new alternating optimization algorithm to efficiently solve the objective function. Denote J (A, S) as the objective function in (9), and we seek A and S alternately by solving J (A, S) for one with the other fixed.

Fix S to Optimize A

We calculate the gradients of the objective function with respect to A as follows:

$$\frac{\partial J}{\partial A}=-\frac{1}{\mathcal{N}}{S}^{\top }G\left(\Delta \right)K+\lambda A.$$ (10)

Where

$${\left(G\right)}_{ii}=\frac{1}{2{\Vert \Delta \Vert }_2}$$ (11)

and ∆ = Y − SAk. Denote $\mathcal{G}\left(A\right)\frac{\partial J}{\partial A}.$ A is updated by gradient descent as

$$A^{t+1\hspace{0.17em}}=\hspace{0.17em}{A}^t-{\eta }_t\mathcal{G}\left(A^t\right).$$ (12)

where η_t is the learning rate which can adaptively chosen by line search algorithms (Armijo 1966).

Fix A to Optimize S

We propose a gradient based alterative optimization to solve for S, before which we provide the following proposition to calculate the derivative of J w.r.t. S.

Proposition 1 Assume that the singular value decomposition (SVD) of S is

$$S=U\sum V^{\top },$$ (13)

where U and V are unitary matrices and Σ is the diagonal matrix with real numbers on the diagonal. Then the derivative of ||S||_* w.r.t. S takes the form as follows:

$$\frac{\partial {\Vert S\Vert }_{*}}{\partial S}=U{V}^{\top }$$ (14)

The proof is provided in the Appendix section.

Proposition 1 associated with the rigorous proof provides a theoretical foundation, which can be directly used to solve a large while important family of optimization problems with trace norm minimization.

Based on the Proposition 1, we have the derivative of J w.r.t S as follows:

$$\frac{\partial J}{\partial S}=-\hspace{0.17em}2\frac{1}{\mathcal{N}}\left(Y\hspace{0.17em}-\hspace{0.17em}SAK\right){\left(AK\right)}^{\top }+\beta U{V}^{\top }+2\gamma S$$ (15)

where U and V are obtained by the SVD in (13).

Denote G(S) as the gradient w.r.t. S in (15). Therefore, S can be solved by an iterative optimization based on gradient descent.

$$S^{t+1}\hspace{0.17em}=\hspace{0.17em}{S}^t\hspace{0.17em}-\hspace{0.17em}{\eta }_t\mathcal{G}\left(S^t\right)$$ (16)

where η_t is the learning rate, which can be adaptively chosen by line search algorithms (Armijo 1966). In each iteration, S^t+1 is calculated with the current S^t associated with U, Σ and V. Since the objective function J (A, S) is convex with respect to S, it is guaranteed to find a global minimum of S.

Note that the size of S depends only on the number 2 of targets, which is usually much smaller than the dimensionality d of inputs. Therefore, the complexity of the singular value decomposition (SVD) of the structure matrix S involved in the calculation of the derivative of the nuclear norm is O (Q³). This guarantees the efficiency of both the iterative algorithm to update S and the alternating optimization algorithm (Algorithm 1).

$$\begin{array}{l}\underset{\_}{\overline{\mathbf{\text{Algorithm}} \mathbf{1}\hspace{0.17em}\text{Alternating}\hspace{0.17em}\mathrm{Optimization}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}}}\\ \begin{array}{l}\begin{array}{l}\mathbf{\text{Require}}:\text{Data matrices}\hspace{0.17em}X\hspace{0.17em}\text{associated with corresponding}\\ \hspace{1em}\hspace{0.17em}\text{targets}\hspace{0.17em}Y, \text{regularization parameters} \lambda , \mathrm{\beta and and} \gamma .\end{array}\hfill \\ \begin{array}{l}\mathbf{\text{Ensure}}:\text{The regression coefficient matrix}\hspace{0.17em}A\hspace{0.17em}\text{and the} \\ \hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{structure matrix}\hspace{0.17em}S.\end{array}\hfill \end{array}\\ 1:\text{Randomly initialize}\hspace{0.17em}\hspace{0.17em}S\in {ℝ}^{\mathcal{Q}\times \mathcal{Q}}\text{and set}\hspace{0.17em}i = 1;\\ 2:\mathbf{\text{repeat}}\\ 3:\text{Update A}\hspace{0.17em}\text{using }\left(12\right);\\ 4:\text{Update S}\hspace{0.17em}\text{using }\left(16\right);\\ 5:i\leftarrow i+ 1;\\ \underset{\_}{6:\mathbf{\text{until}}\hspace{0.17em}\text{Convergence}.\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}}\hspace{1em}\end{array}$$

Convergence Analysis

The efficiency of the proposed MMR is ensured by the guaranteed convergence of the newly-derived alternating optimization algorithm. The objective function J (A, S) in Section 3 is bounded from below and monotonically decreases with each optimization step for A and S, and therefore it converges. We give the brief sketch of the convergence analysis.

Since J (A, S) is the summation of norms, we have J (A, S) ≥ 0 for any A and S. Then J (A, S) is bounded from below. Denote A^(t) and S^(t) as the A and S in the t -th iteration, respectively. For the t -th step, A^(t) is computed by A^(t) ← arg min_A J (A, S^(t−1)). And we also have J (A^(t), S^(t−1)) ≥ J (A^(t), S^(t)). In this way, we obtain the following inequality:

$$\cdot \cdot \cdot \ge J(A^{\left(t-1\right)},S^{\left(t-1\right)})\ge J(A^{\left(t\right)},S^{\left(t-1\right)})\ge J(A^{\left(t\right)},S^{\left(t\right)})\ge \cdot \cdot \cdot \hspace{0.17em}\hspace{0.17em}.$$

Therefore, J (A^(t), S^(t)) is monotonically decreasing as t → +∞, which indicates that the objective function J (A, S) converges according to the monotone convergence theorem.

Experiments and Results

In this section, we conduct extensive experiments to test the performance of the proposed multi-layer multi-target regression (MMR) model in predicting cognitive scores on public ADNI data. We provide comprehensive comparison with representative multi-output regression models to show the advantages of the MMR. The experimental results have demonstrated the effectiveness of the MMR for cognitive assessment of AD.

Data Description

The data used in this article comes from the ADNI database (adni.loni.usc.edu). Firstly, for each MRI T1-weighted image, we corrected the anterior commissure (AC) posterior commissure (PC) via MIPAV2; corrected the intensity inhomogeneity using N3 algorithm (Sled et al. 1998); stripped the skull (Wang et al. 2011) with manual editing, and removed the cerebellum (Wang et al. 2014). Afterwards, we divided the image into gray matter (GM), white matter (WM), as well as cerebrospinal fluid (CSF) by means of FAST (Zhang et al. 2001) in the FSL package3, and then used HAMMER (Shen and Davatzikos 2002) to register the images to a common space. The GM volumes that were obtained from 93 ROIs defined in Kabani (1998), normalized by the total intra-cranial volume, were characterized as features. We downloaded the cognitive scores from three independent cognitive assessments, including Fluency Test, Rey’s Auditory Verbal Learning Test (RAVLT) and Trail making test (TRAILS). We suggest interested readers to find the details of these cognitive assessments in the ADNI procedure manuals. All participants with no missing baseline MRI measurements and cognitive measures were included in this study. A total of 804 sample subjects were considered, of which we have 225 health control (HC) samples, 393 MCI samples and 186 AD samples. This study involved seven cognitive scores, which are: 1) RAVLT TOTAL, RAVLT TOT6 and RAVLT RECOG scores from RAVLT cognitive assessment; 2) FLU ANIM and FLU VEG scores from Fluency cognitive assessment; 3) Trails A and Trails B scores from Trail making test.

Experimental Settings

To evaluate the performance of our model, MMR (multi-layer multi-target regression), we compare with several representative regression models as used in Wang et al. (2012), which includes least square regression (LSR), multi-target ridge regression (MRR) and multi-target low-rank regression model with trace norm regularization (MR-Trace).

To make contrast to our multi-layer multi-target regression (MMR), we give the formulation of the baseline methods. The LSR takes the following form of objective,

$$\underset{W}{\min }\hspace{0.17em}\frac{1}{\mathcal{N}}\hspace{0.17em}\sum _{i=1}^{\mathcal{N}}{\Vert {\mathbf{\text{y}}}_i\hspace{0.17em}-\hspace{0.17em}W{\mathbf{\text{x}}}_i\Vert }^2,$$ (17)

where W ∈ ℝ^Q×d is the weight matrix;

MMR is the baseline kernel method which takes the following form

$$\underset{W}{\min }\hspace{0.17em}\frac{1}{\mathcal{N}}\hspace{0.17em}\sum _{i=1}^{\mathcal{N}}{\Vert {\mathbf{\text{y}}}_i\hspace{0.17em}-\hspace{0.17em}W{\mathbf{\text{x}}}_i\Vert }^2\hspace{0.17em}+\hspace{0.17em}\lambda {\Vert W\Vert }_F^2,$$ (18)

where ${\Vert W\Vert }_F^2,$ is the regularization term to avoid overfitting and λ is the hyper-parameter for the regularization term;

The MR-Trace is a single-layer learning model with a trace norm regularization:

$$\underset{W}{\min }\hspace{0.17em}\frac{1}{\mathcal{N}}\hspace{0.17em}\sum _{i=1}^{\mathcal{N}}{\Vert {\mathbf{\text{y}}}_i\hspace{0.17em}-\hspace{0.17em}W{\mathbf{\text{x}}}_i\Vert }^2\hspace{0.17em}+\hspace{0.17em}\lambda {\Vert W\Vert }_{*},$$ (19)

where the trace norm ||W||_* is the trace norm regularization term to impose sparsity constraint.

The major methodological differences between the baseline and the proposed method is our multi-layer learning architecture. Specifically, our MMR incorporates a hidden layer of latent variables rather than directly projecting the input data to the multiple outputs as in the baseline methods. This actually enables us to simultaneously handle nonlinear input-output relationship (thorough the kernelized dictionary) and the interdependency of multiple outputs (by low-rank learning). The major methodological differences indeed explains the improvement of our method over baseline methods.

In the experiment, we use the root mean square error (RMSE) and the correlation coefficient (CorCoe) between the predicted value and ground truth as the evaluation measurements. We normalize the RMSE value with the Frobenius norm of the ground truth. To illustrate the stability of the comparing methods, we adopt 5-fold cross validation and report average performance in these 5 trials.

For MMR model, we choose the regularization parameters by cross validation. We tune other hyper-parameters, i.e., parameter for the regularization term in MMR, MR-Trace as well as λ of MMR, in the range of {10⁻⁵, 10⁻⁴, …, 10⁵} and report the best result w.r.t. each method. We tune the hyper-parameters via 5-fold cross validation and report the best parameter w.r.t. RMSE for each method.

Comparison on Memory Impairment Prediction

We summarize the comparison results of cognitive score prediction in Tables 1 and 2, where we mark the best results in bold. In Table 1, we perform the t-test to compare the MMR result in each data with other methods to show if the advantage is significant w.r.t. the p-value. We set the significance level as 0.10. In each data, we mark the methods with significant difference with the “_*” sign.

Table 1.

RMSE results of cognitive score prediction using MRI biomarkers. The “*” sign indicates statistically significant difference between MMR result and other methods. The significance level is 0.10

Methods	Fluency	RAVLT	TRAILS
LSR	0.3395 ± 0.0159	0.3304 ± 0.0182	0.5284± 0.0273
MRR	0.3261 ± 0.0165(*)	0.3192 ± 0.0170(*)	0.5007± 0.0242
MR-Trace	0.3251 ± 0.0158	0.3191 ± 0.0165(*)	0.5008± 0.0303
MMR	0.3235± 0.0163	0.3172 ± 0.0153	0.5113± 0.0153

Table 2.

CorCoe results of cognitive score prediction using MRI biomarkers

Methods	Fluency	RAVLT	TRAILS
LSR	0.5202 ± 0.0243	0.8776± 0.0129	0.5658±0.0556
MRR	0.5451 ± 0.0207	0.8851± 0.0115	0.6030±0.0425
MR-Trace	0.5485 ± 0.0185	0.8852± 0.0112	0.6045±0.0542
MMR	0.5427 ± 0.0153	0.8865± 0.0101	0.5796±0.0311

From these results we can notice that MMR performs equal or better than all the comparing methods, which indicates the advantage of adopting nonlinear regression in our model. We can find that in Fluency and RAVLT, MMR outperforms other methods with statistically significant advantage. In the TRAILS data, even though MMR gets slight higher RMSE value than MR-Trace, the difference is not statistically significant. It confirms that MMR is more suitable to describe the complicated relationship between imaging features and cognitive scores. In addition, the prediction results of MMR show the effectiveness of finding low-rank structure among multiple learning tasks. Since the number of tasks in the data is small (two tasks in Fluency while three tasks in RAVLT and TRAILS), the advantage of MMR may not be shown significantly. We can notice that MMR performs the best in the RAVLT data, as the MMR model is able to explore and utilize the interrelations among multiple learning tasks and improve the overall performance. In addition, we find that the range of the target variable in TRAILS data is much larger (the range in TRAILS data is 300 while the range for the other two data is smaller than 100). Since our model could better fit the task relationship among the training data, a larger testing data range may introduce higher testing error if the training data is slightly overfitted. The experimental results have validated the effectiveness of the MMR for simultaneously handling nonlinear relationship between neuroimaging biomarkers and cognitive scores and the correlation among the scores. The high performance of the proposed MMR and its huge advantages over previous representative regression models indicate its great potential to conduct even more challenging multivariate prediction tasks in clinical practice.

Stability of the MMR Method

In this subsection, we show the stability of the MMR method when we set the number of nodes in the hidden layer as different values. From the results in Fig. 2 we can find that the MMR results are quite stable w.r.t. different number of nodes. This is important in real applications since MMR does not require much effort in tuning the hyper-parameters.

Fig. 2.

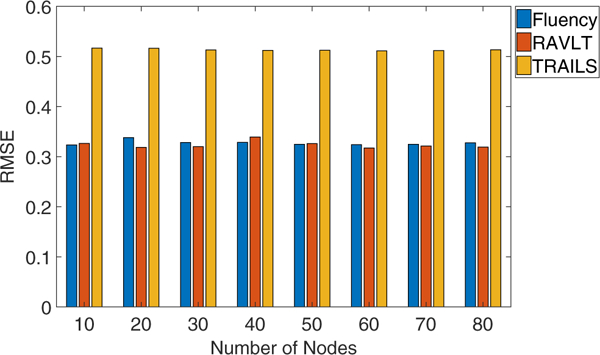
RMSE results with different number of hidden nodes in the MMR model

Conclusion

In this paper, we have presented a new multi-target regression model, called multi-layer multi-target regression (MMR), for cognitive assessment of Alzheimer’s disease. The MMR is able to simultaneously handle the nonlinear relationship between neuraoimaging biomarkers and cognitive assessment scores and the inter-correlation among the scores, which can largely improve the prediction performance. The MMR has been evaluated by extensive experiments on the public ADNI database, and produced high prediction performance surpassing most of the previous representative regression models. The results have shown the great effectiveness of the MMR in cognitive assessment prediction, which indicates its great potential for multi-target prediction in clinical prediction.

Information Sharing Statement

The data used in this paper can be obtained from the ADNI database (RRID:SCR 003007, adni.loni.usc.edu). An executable program of our model is available upon request.

Appendix

Proof By the definition of the nuclear norm, we can re-write it in terms of traces as follows

$$\begin{gathered} {\Vert S\Vert }_{*}\hspace{0.17em}=\hspace{0.17em}tr(\sqrt{S^{\top }S)}\hspace{0.17em}=\hspace{0.17em}tr(\sqrt{{\left(U\sum V^{\top }\right)}^{\top }\hspace{0.17em}\left(U\sum V^{\top }\right)}) \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\hspace{0.17em}tr(\sqrt{V{\sum }^{\top }{U}^{\top }U\sum V^{\top }}\hspace{0.17em}=\hspace{0.17em}tr\hspace{0.17em}(\sqrt{V{\sum }^{\top }\sum V^{\top })} \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=tr(\sqrt{V{\sum }^{\top }\sum V^{\top })} \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=tr(\sqrt{V\sum V^{\top }V\sum V^{\top }} \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=tr(V\sum V^{\top }) \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=tr(\sum ) \end{gathered}$$ (20)

Therefore, the nuclear norm of S can be also defined as the sum of the singular value decomposition of S. From (13), we have

$$\partial S=\partial U\sum V^{\top }\hspace{0.17em}+\hspace{0.17em}\hspace{0.17em}U\partial \sum V^{\top }\hspace{0.17em}+\hspace{0.17em}\hspace{0.17em}U\sum \partial V^{\top },$$ (21)

which gives rise to

$$U\partial \sum V^{\top }\hspace{0.17em}=\hspace{0.17em}\partial S\hspace{0.17em}-\hspace{0.17em}\partial U\sum V^{\top }\hspace{0.17em}-\hspace{0.17em}U\sum \partial V^{\top }.\hspace{0.17em}$$ (22)

Multiplying U^⊤ on both sides of (22), we have

$$U^{\top }U\partial \sum V^{\top }V\hspace{0.17em}=\hspace{0.17em}{U}^{\top }\partial SV\hspace{0.17em}-U^{\top }\partial U\sum V^{\top }V\hspace{0.17em}-U^{\top }U\sum \partial V^{\top }V$$ (23)

Since U is also an orthogonal matrix, we achieve

$$\partial \sum \hspace{0.17em}=\hspace{0.17em}{U}^{\top \hspace{0.17em}}\partial SV\hspace{0.17em}-\hspace{0.17em}{U}^{\top \hspace{0.17em}}\partial U\sum \hspace{0.17em}-\hspace{0.17em}\sum \partial V^{\top }V.$$ (24)

Note that we have the fact that

$$0\hspace{0.17em}=\hspace{0.17em}\partial I\hspace{0.17em}=\hspace{0.17em}\partial \left(U^{\top }\hspace{0.17em}U\right)\hspace{0.17em}=\hspace{0.17em}\partial U^{\top }\hspace{0.17em}U\hspace{0.17em}+\hspace{0.17em}{U}^{\top }\hspace{0.17em}\partial U,$$ (25)

where I is an identity matrix, and therefore U^⊤∂U is an antisymmetric matrix. We have

$$\begin{gathered} tr\left(U^{\top }\hspace{0.17em}\partial U\sum \right)\hspace{0.17em}=\hspace{0.17em}\hspace{0.17em}tr\left({\left(U^{\top \hspace{0.17em}}\partial U\sum \right)}^{\top }\right)\hspace{0.17em}=\hspace{0.17em}tr\left({\sum }^{\top }\hspace{0.17em}\partial U^{\top }\hspace{0.17em}U\right) \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\hspace{0.17em}-tr\left(\sum U^{\top }\hspace{0.17em}\partial U\right)\hspace{0.17em}=\hspace{0.17em}-tr\left(U^{\top }\partial U\sum \right) \end{gathered}$$ (26)

which indicates that tr(U^⊤∂UΣ) = 0. Similarly, we also have tr(Σ∂V^⊤V) = 0. Therefore, we achieve

$$tr\left(\partial \sum \right)\hspace{0.17em}=\hspace{0.17em}tr\left(U^{\top }\hspace{0.17em}\partial SV\right)$$ (27)

By taking the derivative of ||S||_* w.r.t. S, we obtain

$$\frac{\partial {\Vert S\Vert }_{*}}{\partial S}\hspace{0.17em}=\hspace{0.17em}\frac{tr\left(\partial \sum \right)}{\partial S}\hspace{0.17em}=\hspace{0.17em}\frac{tr\hspace{0.17em}\left(U^{\top }\hspace{0.17em}\partial SV\right)}{\partial S}\hspace{0.17em}U{V}^{\top }$$ (28)

which closes the proof.