Fluid-attenuated inversion recovery MRI synthesis from multisequence MRI using three-dimensional fully convolutional networks for multiple sclerosis

Abstract.

Multiple sclerosis (MS) is a white matter (WM) disease characterized by the formation of WM lesions, which can be visualized by magnetic resonance imaging (MRI). The fluid-attenuated inversion recovery (FLAIR) MRI pulse sequence is used clinically and in research for the detection of WM lesions. However, in clinical settings, some MRI pulse sequences could be missed because of various constraints. The use of the three-dimensional fully convolutional neural networks is proposed to predict FLAIR pulse sequences from other MRI pulse sequences. In addition, the contribution of each input pulse sequence is evaluated with a pulse sequence-specific saliency map. This approach is tested on a real MS image dataset and evaluated by comparing this approach with other methods and by assessing the lesion contrast in the synthetic FLAIR pulse sequence. Both the qualitative and quantitative results show that this method is competitive for FLAIR synthesis.

1. Introduction

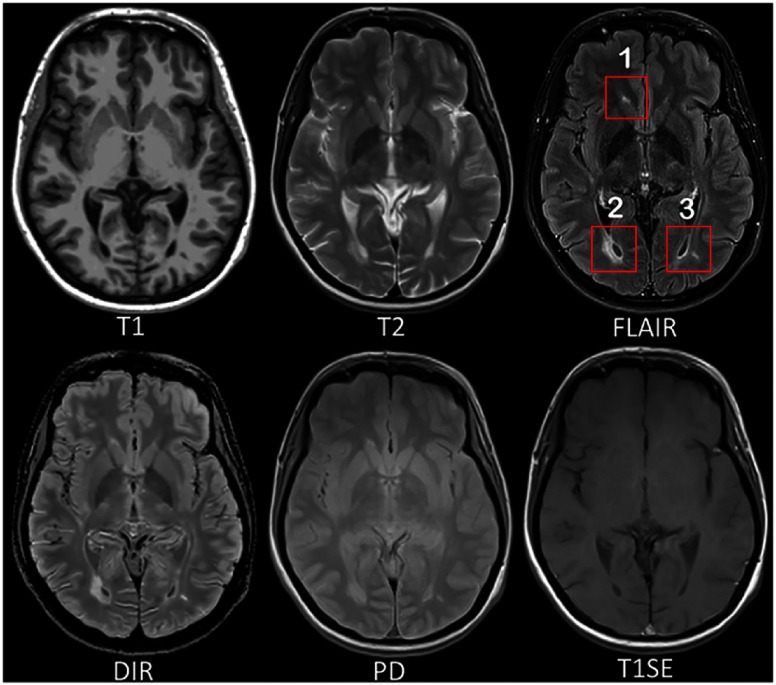
Multiple sclerosis (MS) is a demyelinating and inflammatory disease of the central nervous system and a major cause of disability in young adults.¹ MS has been characterized as a white matter (WM) disease with the formation of WM lesions, which can be visualized by magnetic resonance imaging (MRI).^2,3 The fluid-attenuated inversion recovery (FLAIR) MRI pulse sequence is commonly used clinically and in research for the detection of WM lesions which appear hyperintense compared to the normal-appearing WM (NAWM) tissue. Moreover, the suppression of the ventricular signal, characteristic of the FLAIR images, allows an improved visualization of the periventricular MS lesions⁴ and can also suppress any artifacts created by cerebrospinal fluid (CSF). In addition, the decrease of the dynamic range of the image can make the subtle changes easier to view. Typical MRI pulse sequences used in a clinical setting are shown in Fig. 1. WM lesions (red rectangles) characteristic of MS are clearly best seen on FLAIR pulse sequences. However, in a clinical setting, some MRI pulse sequences could be missed because of the limited scanning time or patients’ interruptions in case of anxiety, confusion, or severe pain. Hence, there is a need for predicting the missing FLAIR when it has not been acquired during patients’ visits. FLAIR may also be absent in some legacy research datasets, which are still of major interest due to their number of subjects and long follow-up periods, such as ADNI.⁵ Furthermore, the automatically synthesized MR images may also improve the brain tissue classification and segmentation results as suggested in Refs. ⁶ and ⁷, which are additional motivations for this work.

Fig. 1.

MRI pulse sequences usually used in a clinical setting. T1-w provides an anatomical reference and T2-w is used for WM lesions visualization. However, on the T2-w, periventricular lesions are often indistinguishable from the adjacent CSF, which is also of high signal. WM lesions (red rectangles) characteristic of MS are best seen on the FLAIR pulse sequence because of the suppression of the ventricular signal. DIR has direct application in MS for evaluating cortical pathology. PD and T1SE are also used clinically. (Note: for interpretation of the references to color in this figure legend, the reader is referred to the online version of this article.)

In Ref. 8, the authors proposed an atlas-based patch-matching method to predict the FLAIR from T1-w and T2-w. In this approach, given a set of atlas images $(I_{\mathrm{T}1},I_{\mathrm{T}2},I_{\mathrm{FLAIR}})$ and a subject $S$ with $(S_{\mathrm{T}1},S_{\mathrm{T}2})$, the corresponding FLAIR ${\widehat{S}}_{\mathrm{FLAIR}}$ is formed patch by patch. A pair of patches in $(S_{\mathrm{T}1},S_{\mathrm{T}2})$ is extracted and used to find the most similar one in the set of patches extracted from the atlas $(I_{\mathrm{T}1},I_{\mathrm{T}2})$. Then, the corresponding patch in $I_{\mathrm{FLAIR}}$ is picked and used to form ${\widehat{S}}_{\mathrm{FLAIR}}$.

In Ref. 9, random forests (RFs) are used to predict the FLAIR from T1-w, T2-w, and proton density (PD). In this approach, a patch at position $i$ is extracted from each of these three input pulse sequences. All these three patches are then rearranged and concatenated to form a column vector $X_i$. The vector $X_i$ and the corresponding intensity $y_i$ in FLAIR at the position of $i$ are used to train the RFs. There are also some other close research fields doing subject-specific image synthesis of a target modality from another modality. For example, in Refs. ¹⁰ and ¹¹, computed tomography (CT) imaging is predicted from MRI pulse sequences.

Recently, deep learning has achieved many state-of-the-art results in several computer vision domains, such as image classification,¹² object detection,¹³ segmentation,¹⁴ and also in the fields of medical image analysis.¹⁵ Various methods of image enhancement and reconstruction using a deep architecture have been proposed, for instance, reconstruction of 7T-like images from 3T MRI,¹⁶ reconstruction of CT images from MRI,¹⁷ and prediction of positron emission tomography (PET) images with MRI.¹⁸ The research work most similar to ours is Ref. 19. In this method, FLAIR is generated from T1-w MRI by a five-layer two-dimensional (2-D) deep neural network, which treats the input image slice by slice.

However, these FLAIR synthesis methods have their own shortcomings. The method in Ref. 8 breaks the input images into patches. During inference process, the extracted patch is then used to find the most similar patch in the atlas. But this process is often computationally expensive. Moreover, the result heavily depends on the similarity between the source image and the images in the atlas. This makes the method fail in the presence of abnormal tissue anatomy, as the images in the atlas do not have the same pathology. The learning-based methods in Refs. ⁹ and ¹⁹ are less computationally intensive, because they store only the mapping function. However, they do not take into account the spatial nature of three-dimensional (3-D) images and can cause discontinuous predictions between adjacent slices. Moreover, many works used multiple MRI pulse sequences as the inputs,^8,9 but none of them evaluated how each pulse sequence influences the prediction results.

To overcome the disadvantages mentioned above, we propose 3-D fully convolutional neural networks (3-D FCNs) to predict the FLAIR. The proposed method can learn an end-to-end and voxel-to-voxel mapping between other MRI pulse sequences and the corresponding FLAIR. Our networks have three convolutional layers and the performance is evaluated qualitatively and quantitatively. Moreover, we propose a pulse sequence-specific saliency map (P3S map) to visually measure the impact of each input pulse sequence on the prediction result.

2. Method

Standard convolutional neural networks (CNNs) are defined, for instance, in Refs. ²⁰ and ²¹. Their architectures basically contain three components: convolutional layers, pooling layers, and fully connected layers. A convolutional layer is used for feature learning. A feature at some locations in the image can be calculated by convolving the learned feature detector and the patches at those locations. A pooling layer is used to progressively reduce the spatial size of the feature maps to reduce the computational cost and the number of parameters. However, the use of a pooling layer can cause the loss of spatial information, which is important for image prediction, especially the lesion regions. Moreover, a fully connected layer has all the hidden units connected to all the previous units, so it contains a majority of the total parameters and an additional fully connected layer makes it easy to reach the hardware limits both in memory and in computation power. Therefore, we propose FCNs composed of only three convolutional layers.

2.1. Three-Dimensional Fully Convolutional Neural Networks

Our goal is to predict the FLAIR pulse sequences by finding a nonlinear function $s$, which maps the multipulse-sequence source images $I_{\text{source}}=(I_{\mathrm{T}1},I_{\mathrm{T}2},I_{\mathrm{PD}},I_{\mathrm{T}1\mathrm{SE}},I_{\mathrm{DIR}})$ to the corresponding target pulse sequence $I_{\text{target}}$. Given a set of source images $I_{\text{source}}$, and the corresponding target pulse sequence $I_{\text{target}}$, our method finds the nonlinear function by solving the following optimization problem:

$$\widehat{s}=\arg \underset{s\in S}{\min }\frac{\sum _{i=1}^N{\Vert (I_{\text{target}}^i),s(I_{\text{source}}^i)\Vert }_2}{N},$$ (1)

where $S$ denotes a group of potential mapping functions, $N$ is the number of subjects, and mean squared error (MSE) is used as our loss function, which calculates a discrepancy between the predicted images and the ground truth.

To learn the nonlinear function, we propose the architecture of our 3-D FCNs shown in Fig. 2. The input layer is composed of the multipulse-sequence source images, $I_{\text{source}}$, which are arranged as channels and then sent altogether to the network. Our network architecture consists of three convolutional layers ($L=3$) followed by rectified linear functions [$\mathrm{relu}(x)=\max (x,0)$]. If we denote the $m$’th feature map at a given layer as $h^m$, whose filters are determined by the weights $k^m$ and bias ${\mathbf{b}}^m$, then the feature map $h^m$ is obtained as follows:

$$h^m=\max (k^{m}x+{\mathbf{b}}^m,0),$$ (2)

where the size of input $x$ is $H\times W\times D\times M$. Here, $H$, $W$, $D$ indicate the height, width, and depth of each pulse sequence or feature map, and $M$ is the number of the pulse sequences or feature maps. To form a richer representation of the data, each layer is composed of multiple feature maps $\{h^m:1,\dots ,F\}$, also referred as channels. Note that the kernel $k$ has a dimension $H_k\times W_k\times D_k\times M\times F$, where $H_k$, $W_k$, $D_k$ are the height, width, and depth of the kernel, respectively. The kernel $k$ operates on $x$ with $M$ channels, generating $h$ with $F$ channels. The parameters $k$, $\mathbf{b}$ in our model can be efficiently learned by minimizing the function 1 using stochastic gradient descent (SGD).

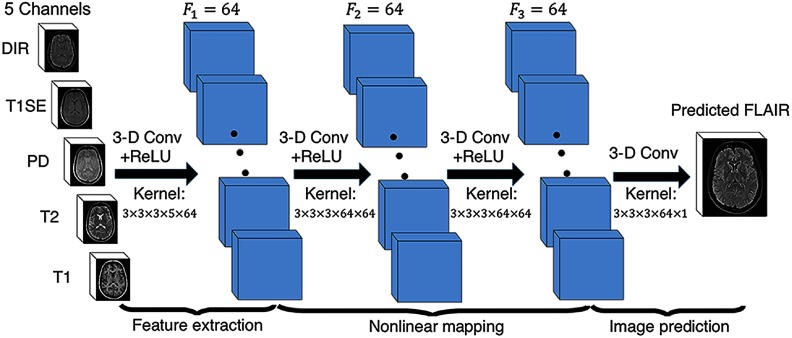
Fig. 2.

The proposed 3-D FCNs. Our network architecture consists of three convolutional layers. The input layer is composed of five pulse sequences arranged as channels. The first layer extracts a 64-dimensional feature from input images through convolution process with a $3\times 3\times 3\times 5\times 64$ kernel. The second and third layers apply the same convolution process to find a nonlinear mapping for image prediction.

2.2. Pulse Sequence-Specific Saliency Map

Multiple MRI pulse sequences are used as inputs to predict the FLAIR. Given a set of input pulse sequences and a target pulse sequence, we would like to assess the contribution of each pulse sequence on the prediction result. One method is class saliency visualization proposed in Ref. 22, which is used for image classification to see which pixels most influence the class score. Such pixels can be used to locate the object in the image. We call the method presented in this paper P3S map to visually measure the impact of each pulse sequence on the prediction result. Our P3S map is the absolute partial derivative of the difference between the predicted image and the ground truth with respect to the input pulse sequence of subject $i$. It is calculated by standard backpropagation:

$$M_i=\left|\frac{\partial {\Vert I_{\text{target}}^i-{\widehat{I}}_{\text{target}}^i\Vert }_2}{\partial I_{\text{source}}^i}\right|,$$ (3)

where $i$ denotes the subject, and $I_{\text{target}}$ and ${\widehat{I}}_{\text{target}}$ are the ground truth and the predicted image, respectively.

2.3. Materials and Implementation Details

Our dataset contains 24 subjects including 20 MS patients [eight women, mean age 35.1, standard deviation (SD) 7.7] and four age- and gender-matched healthy volunteers (two women, mean age 33, SD 5.6). Each subject underwent the following pulse sequences:

• a.T1-w ($1\times 1\times 1.1{\mathrm{mm}}^3$)
• b.T2-w and PD ($0.9\times 0.9\times 3{\mathrm{mm}}^3$)
• c.FLAIR ($0.9\times 0.9\times 3{\mathrm{mm}}^3$)
• d.T1 spin-echo (T1SE, $1\times 1\times 3{\mathrm{mm}}^3$)
• e.Double inversion recovery (DIR, $1\times 1\times 1{\mathrm{mm}}^3$)

A written informed consent form has been signed by all subjects to participate in a clinical imaging protocol approved by the local ethics committee. The preprocessing steps include intensity inhomogeneity correction²³ and intrasubject affine registration²⁴ onto FLAIR space. Finally, each preprocessed image has a size of $208\times 256\times 40$ and a resolution of $0.9\times 0.9\times 3{\mathrm{mm}}^3$.

Our networks have three convolutional layers ($L=3$). The filter size is $3\times 3\times 3$ and for every layer the number of the filters is 64, which is designed with empirical knowledge from the widely used FCN architectures, such as ResNet.¹² We used Theano²⁵ and Keras²⁶ libraries for both training and testing. The whole data are first normalized by using $\overline{x}=(x-\text{mean})/\mathrm{std}$, where mean and std are calculated over all the voxels of all the images in each sequence. We do not use any data augmentation. Our networks were then trained using standard SGD optimizer with 0.0005 as the learning rate and 1 as the batch size. The stopping criteria used in our work is early stopping. We stopped the training when the generalization error increased in $p$ successive $q$-length strips:

• •${\mathrm{STOP}}_p$: stop after epoch $t$ iff ${\mathrm{STOP}}_{p-1}$ stops after epoch $t-q$ and $E_{ge}(t)>E_{ge}(t-q)$,
• •$STO{P}_1$: stop after first end-of-strip epoch $t$ and $E_{ge}(t)>E_{ge}(t-q)$. where $q=5$, $p=3$, and $E_{ge}(t)$ are the generalization error at epoch $t$. It takes 1.5 days for training and $<2\mathrm{s}$ for predicting one image on a NVIDIA GeForce GTX TITA X.

Our method is validated through a fivefold cross validation in which the dataset is partitioned into fivefolds (fourfolds have five subjects with one healthy subject in each fold and the last fold has four subjects). Subsequently, five iterations of training and validation are performed such that within each iteration one different fold is held out for validation and remaining four folds are used for training. The validation error is used as an estimate of the generalization error. And we then compared it qualitatively and quantitatively with four state-of-the-art approaches: modality propagation;²⁷ RFs with 60 trees;⁹ U-Net;²⁸ and voxel-wise multilayer perceptron (MLP), which consists of two hidden layers and 100 hidden neurons for each layer, trained to minimize the MSE. The patch size used in the modality propagation and the RF is $3\times 3\times 3$, as suggested in their works.^9,27 The U-Net architecture is classified into three parts: downsampling, bottleneck, and upsampling. The downsampling path contains two blocks. Each block is composed of two $3\times 3\times 3$ convolution layers and a max-pooling layer. Note that the number of feature maps doubles at each pooling, starting with 16 feature maps for the first block. The bottleneck is built from simply two 64-width convolutional layers. And the upsampling path also contains two blocks. Each block includes a deconvolution layer with stride 2, a skip connection from the downsampling path and two $3\times 3\times 3$ convolution layers. Last, we use our P3S map to visually measure the contribution of each input pulse sequence.

3. Experiments and Results

3.1. Model Parameters and Performance Trade-offs

3.1.1. Number of filters

Generally, when the network is wider, more features can be learned so that better performance can be obtained. Based on this, in addition to our default setting ($F_1=F_2=F_3=64$), we also did two experiments for comparison: (1) a wider architecture ($F_1=F_2=F_3=96$) and (2) a thinner architecture ($F_1=F_2=F_3=32$). The training process is the same as described in the Sec. 2.3. The results are shown in Table 1. We can observe that increasing the width of network from 32 to 64 leads to a clear improvement. However, increasing the filter numbers from 64 to 96 only slightly improved the performance. However, if less computational cost is needed, a thinner network which can also achieve a good performance is more suitable.

Table 1.

Comparison of different number of filters.

	MSE (SD)	Number of parameters	Inference time (s)
$F_1=F_2=F_3=32$	1094.52 (49.46)	60.6 K	0.72
$F_1=F_2=F_3=64$	918.07 (41.70)	213.7 K	1.34
$F_1=F_2=F_3=96$	909.84 (38.68)	513.5 K	2.58

3.1.2. Number of layers

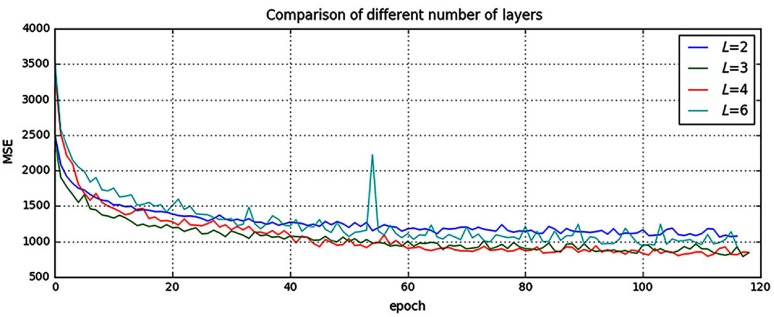
It is indicated in Ref. 12 that neural networks could benefit from increasing the depth of the networks. We, thus, tested two different number of layers by adding or removing a 64-width layer based on our default setting ($L=3$), i.e., (1) $L=2$ and (2) $L=4$. The comparison result is shown in Fig. 3. It can be found that when $L=2$, the result is worse than our default setting ($L=3$). However, when we increased the number of layers to $L=4$, it converges slower and finally to the same level as the three-layer network. In addition, we also designed a much deeper network ($L=6$) by adding three more 64-width layers to our default setting ($L=3$). It is shown in Fig. 3 that the performance even dropped and failed to surpass the three-layer network. The cause for this drop could be that the complexity increases while the networks go deeper. During the training process, it is, thus, more difficult to converge or it falls into a bad minimum.

Fig. 3.

Comparison of different number of layers. Shown are learning curves for different number of layers ($L=\mathrm{2,3},\mathrm{4,6}$). As the network goes deeper, the result can be increased. However, deeper structure cannot always lead to better results, sometimes even worse. (Note: for interpretation of the references to color in this figure legend, the reader is referred to the online version of this article.)

3.2. Evaluation of Predicted Images

Image quality is evaluated by MSE and structural similarity (SSIM). Table 2 shows the result of MSE and SSIM on a fivefold cross validation. Our method is statistically significantly better than the rest of the methods ($p<0.05$) except for U-Net, which got the best result on two folds for MSE and three folds for SSIM. However, the difference with our method is very small and we outperformed at the average level. Furthermore, the number of parameters in U-Net is 375.6 K, which is much more than ours (213.7 K). If less computational cost is needed, our method is preferred. To further evaluate the quality of our method, in particular on the MS lesions detection, we have chosen to evaluate the MS lesion contrast with the NAWM tissue (Ratio 1) and the surrounding NAWM tissue (ratio 2), defined by a dilatation of five voxels around the lesions. Given the mean intensity of each region $I_i(R)$ of subject $i$, ratio 1, and ratio 2 are defined as

$$\text{Ratio}1=\frac{1}{N}\sum _{i=1}^N\frac{I_i(\text{Lesions})}{I_i(\mathrm{NAWM})},\text{Ratio}1=\frac{1}{N}\sum _{i=1}^N\frac{I_i(\text{Lesions})}{I_i(\mathrm{SNAWM})}.$$ (4)

Table 2.

Quantitative comparison between our method and other methods.

	Random forest 60	Modality propagation	Multilayer perceptron	U-Net	Our method
(a) MSE (SD)
Fold 1	993.68 (67.21)	2194.79 (118.73)	1532.89 (135.82)	921.69 (38.51)	905.05 (26.06)
Fold 2	1056.76 (125.51)	2037.69 (151.23)	1236.53 (100.95)	912.03 (38.58)	913.34 (39.95)
Fold 3	945.38 (59.42)	1987.32 (156.11)	1169.78 (142.43)	916.16 (38.97)	898.76 (46.90)
Fold 4	932.67 (74.48)	2273.58 (217.85)	1023.35 (97.93)	938.34 (52.54)	945.33 (63.80)
Fold 5	987.63 (78.34)	1934.25 (140.06)	1403.57 (146.35)	908.11 (36.13)	927.88 (31.80)
Average	983.22 (80.99)	2085.53 (156.80)	1273.22 (124.70)	919.26 (40.95)	918.07 (41.70)
(b) SSIM (SD)
Fold 1	0.814 (0.044)	0.727 (0.044)	0.770 (0.052)	0.847 (0.038)	0.868 (0.036)
Fold 2	0.822 (0.038)	0.718 (0.045)	0.773 (0.045)	0.856(0.025)	0.854 (0.028)
Fold 3	0.832 (0.040)	0.713 (0.047)	0.790 (0.044)	0.854 (0.036)	0.880 (0.031)
Fold 4	0.850 (0.032)	0.708 (0.049)	0.786 (0.044)	0.853 (0.031)	0.846 (0.035)
Fold 5	0.830 (0.041)	0.723 (0.039)	0.781 (0.047)	0.861 (0.034)	0.850 (0.027)
Average	0.830 (0.039)	0.718 (0.045)	0.780 (0.046)	0.854 (0.033)	0.860 (0.031)

The best results are indicated in boldface.

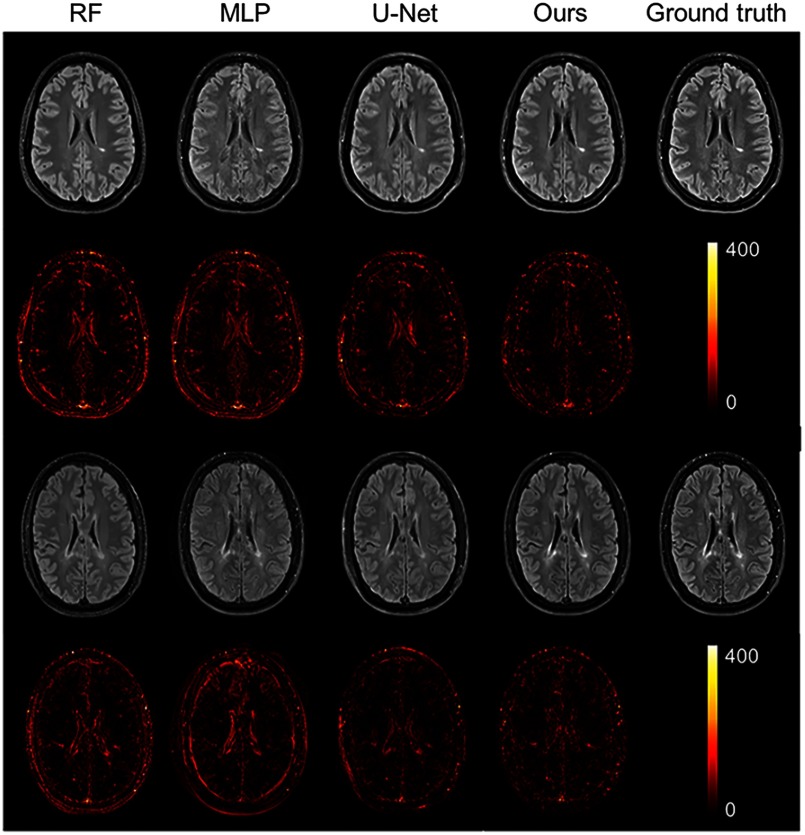
As shown from Table 3, our method achieves statistically significantly better performances ($p<0.01$) than other methods on both ratio 1 and ratio 2, which reflects a better contrast for MS lesions. The evaluation results can be visualized in Fig. 4 with the absolute difference maps on the second and fourth rows. It can be observed that RFs and U-Net can generate good global anatomical information but the MS lesion contrast is poor. This can be truly reflected by a good MSE and SSIM value (see in Table 2), but a low ratio $1/2$ (see in Table 3). On the contrary, our method can well keep the anatomical information and also yield the best contrast for WM lesions.

Table 3.

Evaluation of MS lesion contrast (SD).

	Random forest 60	Modality propagation	Multilayer perceptron	U-Net	Our method	Ground truth
Ratio 1	1.33 (0.07)	1.31 (0.06)	1.39 (0.11)	1.34 (0.09)	1.47 (0.13)	1.66 (0.12)
Ratio 2	1.15 (0.04)	1.13 (0.04)	1.20 (0.05)	1.17 (0.04)	1.22 (0.07)	1.33 (0.09)

The best results are indicated in boldface.

Fig. 4.

Qualitative comparison of the methods to predict the FLAIR sequence. Shown are synthetic FLAIR obtained by RFs with 60 trees, MLP, U-Net, and our method followed by the true FLAIR. The second and fourth rows show the absolute difference maps between each synthetic FLAIR and the ground truth. (Note: for interpretation of the references to color in this figure legend, the reader is referred to the online version of this article.)

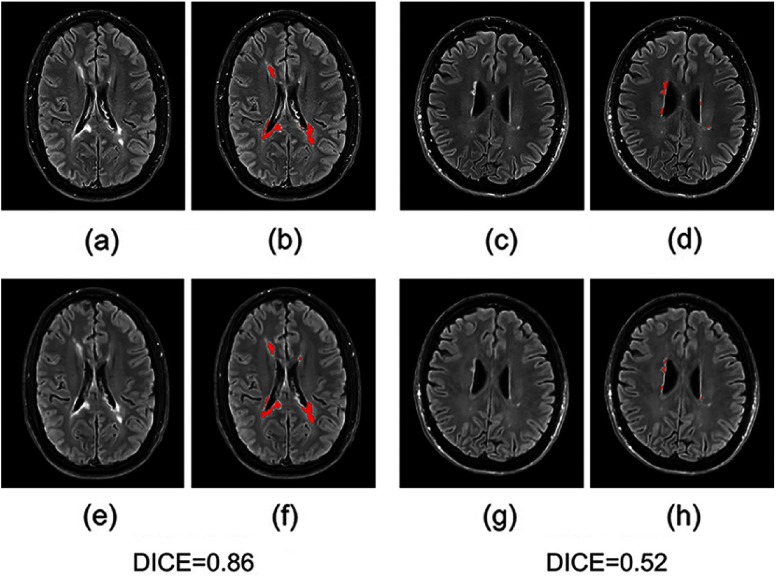
Moreover, we input the synthetic FLAIR and the ground truth to a brain segmentation pipeline²⁹ to generate automatic segmentations of WM lesions. A similar segmentation should be obtained if the FLAIR synthesis is good enough and the DICE score is used to compare the overlap of the segmentations previously obtained from both the synthetic FLAIR and the ground truth. We got a very good WM lesion segmentation agreement with a mean (SD) DICE of 0.73(0.12). Some examples are shown in Fig. 5.

Fig. 5.

Examples of WM lesion segmentation for a high and a low DICE. The WM lesions are very small and diffuse, so even a slight difference in the overlap can cause a big decrease in the DICE score; (a) and (c) true FLAIR; (e) and (g) predicted FLAIR; (b) and (d) segmentation of WM lesions (red) using true FLAIR; and (f) and (h) segmentation of WM lesions using predicted FLAIR. (Note: for interpretation of the references to color in this figure legend, the reader is referred to the online version of this article.)

3.3. Pulse Sequence-Specific Saliency Map

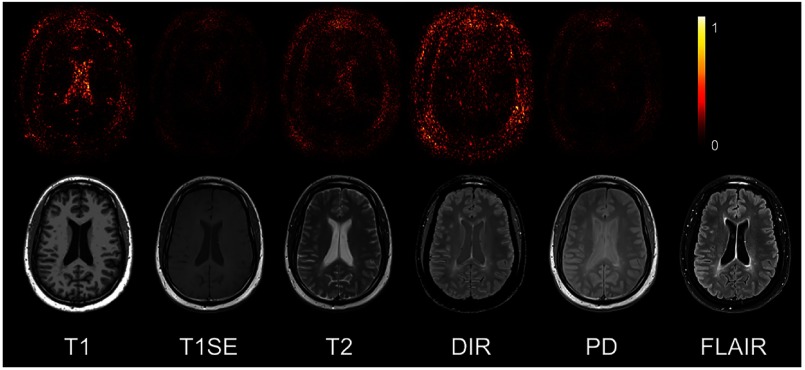
It can often happen that not all the subjects have the five complete protocols (T1-w, T2-w, T1SE, PD, and DIR). Therefore, it might be useful to measure the impact of each input pulse sequence. Our proposed P3S map is to visually measure the contribution of each input pulse sequence. It can be observed in Fig. 6 that T1-w, DIR, and T2-w contribute more for FLAIR MRI prediction than PD or T1SE. In the P3S map, the intensity reflects the contribution of each input pulse sequence. In particular, from the P3S map we can easily find which sequence affects more the generation of which specific regions of interest. For example, as shown in the first row of Fig. 6, even though generally DIR is the most important sequence [see Table 4(a)], T1-w contributes more for the synthesis of the ventricle, which can be proved by the high degree of resemblance of ventricle between T1-w and FLAIR (see second row of Fig. 6).

Fig. 6.

The P3S maps for input pulse sequences. The first row is the saliency maps for T1, T1SE, T2, PD, and DIR, respectively. And the second row is the corresponding multisequence MRIs. It can be found that T1-w, DIR, and T2-w contribute more to the FLAIR MRI prediction than PD or T1SE. (Note: for interpretation of the references to color in this figure legend, the reader is referred to the online version of this article.)

Table 4.

FLAIR prediction results by using different input pulse sequences.

(a) MSE (SD)
	Removed pulse sequence
	T1	T1SE	T2	PD	DIR
Fold 1	959.75 (60.58)	926.89 (73.25)	981.15 (83.45)	945.79 (67.23)	1097.99 (93.27)
Fold 2	987.13 (91.47)	940.00 (86.34)	994.47 (78.47)	919.09 (69.82)	1097.00 (98.57)
Fold 3	942.76 (59.22)	938.98 (64.27)	940.92 (69.44)	924.59 (61.39)	1065.08 (101.95)
Fold 4	999.64 (100.57)	940.56 (72.98)	939.60 (76.22)	932.46 (59.49)	1151.93 (113.21)
Fold 5	986.55 (71.25)	936.89 (63.23)	953.35 (70.12)	933.12 (65.23)	1068.72 (98.56)
Average	975.16 (76.62)	936.67 (72.00)	961.90 (75.54)	931.01 (64.63)	1096.14 (101.11)
(b) Performance comparison by removing DIR (SD)
	Random forest 60	Multilayer perceptron	U-Net	Our method
Fold 1	1035.17 (102.37)	1589.62 (131.32)	1068.59 (100.28)	1097.99 (93.27)
Fold 2	1167.52 (127.67)	1375.28 (121.12)	998.66 (106.79)	1097.00 (98.57)
Fold 3	1170.36 (105.37)	1316.53 (128.46)	1135.24 (128.15)	1065.08 (101.95)
Fold 4	1218.38 (129.01)	1235.26 (117.26)	1175.68 (107.33)	1151.93 (113.21)
Fold 5	1189.64 (108.28)	1537.61 (135.78)	1003.54 (95.18)	1068.72 (98.56)
Average	1156.21 (114.54)	1410.86 (126.79)	1076.34 (107.55)	1096.14 (101.11)
(c) MSE (SD)
	Input pulse sequences
	T1 + DIR	T2 + DIR	T1 + T2	T1 + T2 + DIR	T1 + T2 + PD
Fold 1	966.67 (70.12)	993.25 (99.35)	1375.83 (123.68)	926.88 (83.68)	1281.06 (112.57)
Fold 2	953.87 (68.57)	974.88 (86.32)	1562.46 (132.68)	944.39 (79.23)	1324.17 (121.37)
Fold 3	998.71 (84.90)	1007.69 (103.87)	1158.65 (112.29)	961.19 (71.68)	1261.68 (128.91)
Fold 4	973.24 (77.79)	998.56 (98.23)	1078.67 (103.89)	931.47 (69.31)	1143.58 (98.95)
Fold 5	968.55 (71.59)	986.57 (91.33)	1212.59 (126.79)	958.28 (73.45)	1156.79 (102.67)
Average	972.21 (74.60)	992.19 (95.82)	1277.64 (119.87)	944.44 (75.47)	1233.46 (112.89)

The best results are indicated in boldface.

To test our P3S map, five experiments were designed. In each one, we removed one of the five pulse sequences (T1-w, T2-w, T1SE, PD, and DIR) from the input images. Table 4(a) shows the testing result on the fivefold cross validation by using MSE as the error metric. As shown in the table, these results are consistent with the observation revealed by our P3S map. The DIR, T1-w, and T2-w contribute more than T1SE and PD. In particular, DIR is the most relevant pulse sequences for the FLAIR prediction. However, DIR is not commonly used in clinical settings. We, thus, show a performance comparison among other methods in Table 4(b). It can be observed that when DIR is missing, the performance decreases in all the methods, thereby suggesting a high similarity between DIR and FLAIR. In addition, even though DIR is not much common, we still got an acceptable result for FLAIR prediction without DIR.

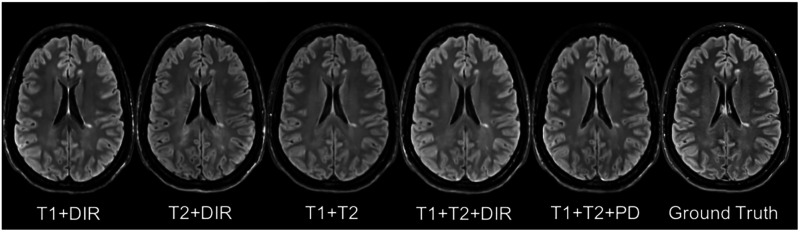
In addition to, some legacy research datasets do not have T1SE or PD, and we, thus, predicted the FLAIR from different combinations of T1, T2, DIR, and PD [see in Table 4(c) and Fig. 7]. It indicates that our method can be used to get an acceptable predicted FLAIR from the datasets that contain only some sequences. From Table 4(c) we can also infer that adding a pulse sequence improves the prediction result.

Fig. 7.

Different combinations of T1, T2, DIR, and PD as input sequences. Shown are synthesized FLAIR with different MRI pulse sequences as inputs from T1 + DIR to T1 + T2 + PD. A better performance can be achieved when both DIR and T1 exist.

4. Discussion and Conclusion

We introduced 3-D FCNs for the FLAIR prediction from multiple MRI pulse sequences and a sequence-specific saliency map for investigating each pulse sequence contribution. Even though the architecture of our method is simple, the nonlinear relationship between the source images and the FLAIR can be well captured by our network. Both the qualitative and quantitative results have shown its competitive performance for the FLAIR prediction. Compared to previous methods, representative patches selection is not required so that this speeds up the training process. In addition, 2-D CNNs have become popular in computer vision; however, they are not suitable to directly use for volumetric medical image data. Unlike Refs. ⁹ and ¹⁹, our method can better keep the spatial information between slices. Moreover, the generated FLAIR has a good contrast for MS lesions. In practice, in some datasets, not all the subjects have all the pulse sequences. Our proposed P3S map can be used to reflect the impact of each input pulse sequence on the prediction result so that the pulse sequences that contribute very little can be removed. Furthermore, DIR is often used for the detection of MS cortical gray matter lesions, and if we have DIR, we can use it to generate the FLAIR so that the acquisition time for FLAIR can be saved. Also, our P3S map can be generated by any kinds of neural networks trained by standard backpropagation.

Our 3-D FCNs have some limitations. The synthetic images appear slightly more blurred and smoother than the ground truth. This may be because we use a more traditional loss L2 distance as our objective function. As mentioned in Ref. 30, the use of L1 distance can encourage less blurring and generate sharper image. In addition, the proposed P3S map is generated after the data normalization which may affect the gradient. However, the network changes as the normalization strategy changes. And the saliency map is based on the network. Moreover, the dataset should be ideally partitioned into training–validation–test sets. However, our dataset has only 24 subjects, which is quite small to split into training–validation–test set. Instead, we divided it into training–testing set and the testing error is used as an estimate of the generalization error.

In future it would be interesting to also assess the utility of the method in the context of other WM lesions (e.g., age-related WM hyperintensities). Specifically, FLAIR is the pulse sequence of choice for studying different types of WM lesions,³¹ including leukoaraiosis (due to small vessel disease), which is commonly found in elderly subjects, and which is associated with cognitive decline and is a common co-pathology in neurodegenerative dementias.

Biographies

Wen Wei received his MSc degree from the University of Paris XI and is a PhD student in ARAMIS Laboratory and EPIONE project team at Inria. His current research interests include deep learning for medical image analysis and medical image synthesis, in particular for multiple sclerosis.

Emilie Poirion received her MSc degree from the UPMC Paris VI and is a PhD student in the team Pr. Stankoff at the Brain and Spine Institute (ICM, Paris, France). Her research interests include PET, and medical image analysis applied to neurological disease, in particular multiple sclerosis.

Benedetta Bodini is a MD and PhD graduate and is an associate professor of neurology at Sorbonne-Université in Paris. She is part of the research team “Repair in Multiple Sclerosis, from basic science to clinical translation,” at the Brain and Spinal Cord Institute (ICM) in Paris, where she studies the mechanisms underlying the pathogenesis of MS using MRI and molecular imaging.

Stanley Durrleman is a PhD graduate and is the cohead of joint Inria/ICM ARAMIS Laboratory at the Brain and Spine Institute (ICM) in Paris. He is also the coordinator of the ICM Center of Neuroinformatics and is scientific director of the ICM platform of biostatistics and bioinformatics. His team focuses on the development of new statistical and computational approaches for the analysis of image data and image-derived geometric data, such as surface meshes.

Olivier Colliot is a PhD graduate and is a research director at CNRS and the head of the ARAMIS Laboratory, a joint laboratory between CNRS, Inria, Inserm, and Sorbonne University within the Brain and Spine Institute (ICM) in Paris, France. He received his PhD in signal processing from Telecom ParisTech in 2003 and his Habilitation degree from the University Paris-Sud in 2011. His research interests include machine learning, medical image analysis, and their applications to neurological disorders.

Bruno Stankoff is a MD and PhD graduate and is a professor of neurology at Sorbonne-Université in Paris. He leads the MS center of Saint Antoine Hospital (AP-HP) and coleads the research team entitled “Repair in Multiple Sclerosis, from basic science to clinical translation,” at the Brain and Spinal Cord Institute (ICM). He is a member of the ECTRIMS executive committee, MAGNIMS network, OFSEP steering committee, ARSEP medico-scientific committee, and French MS Society (SFSEP).

Nicholas Ayache is a PhD graduate and is a member of the French Academy of Sciences and a Research Director at Inria (French Research Institute for Computer Science and Applied Mathematics), Sophia-Antipolis, France, where he leads the EPIONE project team dedicated to e-Patients for e-Medicine. His current research interests are in biomedical image analysis and simulation. He graduated from Ecole des Mines de Saint-Etienne and holds a PhD and a thèse d’état from University of Paris-Sud (Orsay).

Disclosures

Authors have no conflict of interest regarding this article.