Minimal NMR distance information for rigidity of protein graphs

Abstract

Nuclear Magnetic Resonance (NMR) experiments provide distances between nearby atoms of a protein molecule. The corresponding structure determination problem is to determine the 3D protein structure by exploiting such distances. We present a new order on the atoms of the protein, based on information from the chemistry of proteins and NMR experiments, which allows us to formulate the problem as a combinatorial search. Additionally, this order tells us what kind of NMR distance information is crucial to understand the cardinality of the solution set of the problem and its computational complexity.

1. Introduction: distance geometry

1.1. Protein structure

The 3D protein structure determination problem is of fundamental importance for studying protein function [19]. Indeed, biochemical reactions taking place in protein structure are the basic operations hidden behind all biological processes, including cell division, protein translation, host–pathogen interactions, and cell–cell communication. As a consequence, protein structure determination effectively builds a bridge between the description of biological cellular processes and the world of physical chemistry.

X-ray crystallography was the first method to enable the determination of protein structures. Crystallized proteins were perceived as rigid objects, displaying mostly a unique conformation, with some harmonic vibrations around this conformation. Beginning in the nineties, the development of Nuclear Magnetic Resonance (NMR) permitted the study of protein structures in solution. Further developments in NMR relaxation methods exposed the rich internal dynamics of proteins, painting a more realistic picture of protein structure [27]. Protein internal flexibility was then recognized as playing a critical role in many biological processes. For example, many proteins are thought to be functionally important, despite the fact that they lack a precisely defined 3D structure.

NMR structure determination is mainly based on the measurement of inter-atomic distances, determined through the observation of the Nuclear Overhauser Effect (NOE). This is induced by the transfer of magnetization through dipolar coupling between the observed hydrogens. The obtained distance values contain both systematic and random errors, due to the numerous paths of magnetization transfer and to internal molecular dynamics [66]. Nevertheless, NOE-derived NMR experiments may be used to determine some (short) Euclidean distances between hydrogen atoms in a protein. Given this partial set of inexact distances, we are left with the problem of determining the 3D structure of the protein.

We use a weighted simple undirected graph G = (V, E, d) to model this problem, where V represents the set of atoms and E represents the set of atom pairs for which a distance is available, given by the function d : E ↦ [0, ∞) (the fact that we allow distances to be zero will be explained in Section 3).

The representation of a molecule as a set of atomic symbols linked by segments was originally described in [18] and, in fact, the origin of the word graph is due to this representation of molecules [64]. This relationship between molecules and graphs is probably the deepest one existing between chemistry and discrete mathematics. In effect, the graph G = (V, E, d) is a mathematical abstraction to represent the problem data. The problem itself is to find a function x : V ↦ ℝ³ that associates each element of V with a point in ℝ³ in such a way that the Euclidean distances between the points correspond to the values given by d. This is a Distance Geometry Problem (DGP) in ℝ³, formally described as follows.

Definition 1

Given an integer K > 0 and a simple undirected graph G = (V, E, d) whose edges are weighted by a function d : E ↦ [0, ∞), find a function x : V ↦ ℝ^K such that

$$\forall \{u,v\}\in E,\Vert x_u-x_v\Vert =d_{uv},$$ (1)

where x_u = x(u), x_v = x(v), d_uv = d({u, v}), and ||x_u − x_v|| is the Euclidean distance between x_u and x_v.

For the remainder of this work, we will fix K = 3, since we are interested in the application of the DGP to protein conformation [17]. Recent surveys on Distance Geometry (DG) are given in [7,48], an edited book with different applications can be found in [54], two very recent books are given in [38,45], and some historical notes on DG are presented in [44].

In 1983, the first DG-based method for molecular conformation was proposed [28] and in 1984, the first protein structure was determined in its native solution state from NMR data [29].

The simplest approach to the problem is to directly attempt to solve the set of Eqs. (1). However, there is evidence that a closed-form solution is not possible [5]. Since the equations are also difficult to solve numerically, a common approach is to formulate the DGP as a nonlinear global minimization problem,

$$\underset{x_1,\dots ,x_n\in {ℝ}^3}{min}\sum _{\{u,v\}\in E}{({\Vert x_u-x_v\Vert }^2-d_{uv}^2)}^2,$$

where |V| = n. However, solving such a problem is hard from a computational complexity point of view, as well as from a practical one [48,62,63]. In [39], some global optimization algorithms were tested, but none of them scale well to medium or large instances. A survey of different methods to the DGP is given in [49].

Assuming the input data are correct and precise (see Section 3 for other cases), the set X of solutions of a DGP will yield all the 3D structures of the protein that are compatible with the given distances. Any x ∈ X can be translated and rotated in ℝ³, implying that the solution set is not only infinite, but uncountable. However, if we do not consider the effect of translations and rotations, the cardinality of X depends generically on the structure of the associated graph G = (V, E, d). If the set of edges E contains all possible pairs from V, there is only one solution which can be found in linear time [20]. In general, the problem is NP-hard [59].

Using algebraic geometry, it is possible to prove that there are just two possibilities regarding the cardinality of the solution set X: it is either finite or uncountable, supposing that X ≠ Ø [6]. This result is strongly related to graph rigidity [26]. For example, if the graph is rigid, the solution set is finite (up to translations and rotations). In this case, a combinatorial search is better suited than a continuous one, because in addition to the accuracy and efficiency of combinatorial methods, graph rigidity allows us to obtain more information about the cardinality and the structure of the solution set X [41,50] (in Section 3, we will see that these results change when distance values are not precise).

The original contribution of this paper is theoretical. We present a new order on the vertices V of the protein graph G that uses information from the chemistry of proteins and NMR experiments (an order on V is a sequence r : ℕ ↦ V ∪ {0}, for which r(i) = 0 for all i > |r|, where |r| ∈ ℕ is the length of r). This order guarantees the rigidity of G and most importantly, “organizes the search space” in such a way that it can be searched efficiently for all solutions to the problem. Also, it tells us what kind of information from the NMR experiments is crucial to understanding the cardinality of the solution set and the computational complexity of the problem.

To explain the properties of the proposed order, important connections between NMR protein structure, distance geometry, graph rigidity, and graph vertex orders are established. This is done without excessive formalism, although all important concepts and results are presented.

In the following subsection, we give the necessary results from graph rigidity. Section 1.3 shows the importance of vertex orders in DGP graphs. Section 2 presents the discrete version of the DGP. In Section 3, the new order is defined along with its most important properties. Finally, we end with conclusions and some new research directions in Section 4.

1.2. Graph rigidity

Given a graph G = (V, E, d) of a DGP, a function x : V ↦ ℝ³ is called a realization of the graph in ℝ³. If x satisfies all Eqs. (1), it is a valid realization. A pair (G, x) where G is a graph and x is a realization is called a framework.

In order to use frameworks to model protein structures and to have a precise notion of framework rigidity [32], we must define two relations: isometry and congruence.

Two frameworks (G, x) and (G, y) are isometric, denoted as (G, x) ~ (G, y), if

$$\forall \{u,v\}\in E,\Vert x_u-x_v\Vert =\Vert y_u-y_v\Vert ,$$

and congruent, denoted as (G, x) ≡ (G, y), if

$$\forall u\ne v\in V,\Vert x_u-x_v\Vert =\Vert y_u-y_v\Vert .$$

Thus, two frameworks are congruent only if all pairs of vertices from V have the same related distances, not only the pairs in E. Trivially, congruency implies isometry, but the converse is not true in general. We remark that any congruence is a composition of translations, rotations, and reflections [8].

(G, x) is a rigid framework if for any other realization y of G

$$(G,x)~(G,y)\Rightarrow (G,x)\equiv (G,y).$$

Geometrically, this means that a framework is rigid if it has no continuous deformations aside from composition of translations, rotations and reflections. That is, the only way to continuously move a point in a rigid framework is moving all points such that all pairwise distances are preserved, and not only those given by the edges. Using the concept of infinitesimal rigidity of a framework [65], we can define graph rigidity.

Let (G, x) be a framework in ℝ³, where |V| = n and |E| = m. Consider the linear system Rλ = 0, where λ ∈ ℝ³ⁿ and R is the m × 3n matrix each {u, v}th row of which has exactly 6 nonzero entries given by

$$x_i(u)-x_i(v)\text{and}{x}_i(v)-x_i(u),\{u,v\}\in E\text{and}i=1,2,3,$$

where x₁(u), x₂(u), x₃(u) are the Cartesian coordinates of x_u in ℝ³.

The framework is infinitesimally rigid if the only solutions of Rλ = 0 are translations or rotations. Infinitesimal rigidity implies rigidity [23], and if a graph has a single infinitesimally rigid framework, then almost all its frameworks are rigid [30].

Consequently, it makes sense to define a rigid graph as a graph having an infinitesimally rigid framework. There is also a notion of a graph being rigid independently of the framework assigned to it, known as generic rigidity [14], which will not be used here.

A characterization of all rigid graphs in ℝ² was described by Laman [35], but no such complete characterization is known in ℝ³. A heuristic method was introduced in [61] and current conjectures can be found in [33].

If a DGP graph has a unique valid realization, up to congruences, it is called globally rigid. In [14], necessary and sufficient conditions for global rigidity in ℝ² were presented. Hendrickson [30] conjectured that the same conditions would be sufficient for ℝ³, but this was disproved by Connelly [14]. Some graph properties ensuring global rigidity in ℝ² and ℝ³ are given in [4].

1.3. Vertex orders

The idea of exploiting vertex orders to investigate graph rigidity first appeared in [31]. In fact, vertex orders are important for solving many problems modeled by graphs [9,55].

If there is a trilateration order in a DGP graph (every vertex beyond the first four is adjacent to at least four predecessors) and the first four vertices induce a clique, the graph is globally rigid in ℝ³. Such an order makes it possible to uniquely triangulate the position of each subsequent vertex in the order. This implies the existence of a linear time algorithm to find the unique solution [21].

Adjacent predecessors in a vertex order are critical: any fewer than three, and the number of DGP solutions might be uncountable; any more, and the corresponding DGP can be solved uniquely in linear time [48]. So, the number of adjacent predecessors in a given order is related to the cardinality of the DGP solution set and also to the required computational effort to find a solution.

In general, we do not have trilateration orders in protein graphs G = (V, E, d) [40], but using the information provided by NMR experiments and chemistry of proteins, we can try to find vertex orders v₁, …, v_n ∈ V such that:

• The first three vertices form a clique:

  $$\{v_1,v_2\},\{v_1,v_3\},\{v_2,v_3\}\in E.$$
• Each vertex with rank greater than 3 is adjacent to at least 3 predecessors:

  $$\forall i>3,\exists j,k,l\text{with}j<i,k<i,l<i:\{v_j,v_i\},\{v_k,v_i\},\{v_l,v_i\}\in E.$$

The class of DGP instances possessing these orders, where the initial clique has a valid realization and the strict triangular inequalities relating the adjacent predecessors v_j, v_k, v_l to v_i, i > 3, are satisfied (i.e. d_vjvk + d_vkvl > d_vjvl), is called the Discretizable Distance Geometry Problem (DDGP), and the orders themselves DDGP orders [24,52].

The initial clique guarantees that the solution set X will contain just incongruent solutions (aside from a single reflection) and the strictness of the triangular inequality prevents an uncountable number of solutions [52]. In the same paper, it was proved that the graph of any DDGP instance is rigid. An exact solution method, called Branch-and-Prune (BP), was presented for finding all incongruent solutions. The BP algorithm can be exponential in the worst case, which is consistent with the fact that the DDGP is an NP-hard problem [10,47,52].

In a DDGP order, the fourth vertex v₄ can be realized by solving the following quadratic system (to simplify the notation, we will use x_i instead of x_vi and d_i,j instead of d_vivj)

$$\begin{gathered} {\Vert x_4-x_1\Vert }^2=d_{1,4}^2 \\ {\Vert x_4-x_2\Vert }^2=d_{2,4}^2 \\ {\Vert x_4-x_3\Vert }^2=d_{3,4}^2, \end{gathered}$$

which can result in up to two possible positions for v₄ [40]. Using the same strategy, for each position already determined for v₄, we obtain other two positions for v₅, and so on. Because of the rigidity of the DDGP graph, the search space is finite and has 2ⁿ⁻³ possible solutions.

If we have any “extra” distance information, {v_r, v_i} ∈ E with r < i, we can add more one equation to the system related to v_i, i > 3, resulting in

$$\begin{gathered} \Vert x_i-x_j\Vert =d_{j,i} \\ \Vert x_i-x_k\Vert =d_{k,i} \\ \Vert x_i-x_l\Vert =d_{l,i} \\ \Vert x_i-x_r\Vert =d_{r,i}. \end{gathered}$$

Squaring both sides of these equations, we obtain ( $x_i^{\top }$ denotes the transpose of x_i):

$$\begin{gathered} {\Vert x_i\Vert }^2-2(x_i^{\top }{x}_j)+{\Vert x_j\Vert }^2=d_{j,i}^2 \\ {\Vert x_i\Vert }^2-2(x_i^{\top }{x}_k)+{\Vert x_k\Vert }^2=d_{k,i}^2 \\ {\Vert x_i\Vert }^2-2(x_i^{\top }{x}_l)+{\Vert x_l\Vert }^2=d_{l,i}^2 \\ {\Vert x_i\Vert }^2-2(x_i^{\top }{x}_r)+{\Vert x_r\Vert }^2=d_{r,i}^2. \end{gathered}$$

Now, subtracting one of these equations from the others, we eliminate the term ||x_i||² and obtain a linear system in the variable x_i. If the points x_j, x_k, x_l, x_r are not in the same plane, we have a unique solution $x_i^{\ast }$ for v_i, supposing $\Vert x_i^{\ast }-x_r\Vert =d_{r,i}$. When there are other adjacent predecessors of v_i besides v_j, v_k, v_l, one or both possible positions for v_i may be infeasible with respect to those additional distances. If both are infeasible, it is necessary to backtrack and try a different position for previous vertices [52].

The DDGP order organizes the search space in a binary tree and the additional distance information can be used to reduce the search space by pruning infeasible positions in the tree.

The tree begins with the three fixed positions for the initial clique, x₁, x₂, x₃. At level i > 3, the tree contains all (2ⁱ⁻³) possible positions for vertex v_i, if no pruning occurs. The search ends when a path from the root (i = 1) of the tree to a leaf node (i = n) is found by the BP algorithm: the positions relative to vertices in the path satisfy the DGP equations (1), and thus encode a valid realization of G. Considering precise input data, the BP performance is impressive from the points of view of both efficiency and reliability [39,40]. Although the DDGP is NP-hard, a DDGP order can be found in polynomial time [37].

In the definition of the DDGP, the only requirement on the adjacent predecessors v_j, v_k, v_l to v_i (for i > 3) is that the associated strict triangular inequality must be satisfied. However, depending on the instance, if the distances d_j,i, d_k,i, d_l,i are not well scaled, the influence of numerical floating point error in solving the related quadratic system is increased. In some cases, this prevents the BP from finding solutions [52].

Protein graphs provided by NMR experiments have enough information to allow definition of vertex orders involving immediately contiguous adjacent predecessors that can avoid those kinds of problems in DDGP instances.

2. The discretizable molecular distance geometry problem (DMDGP)

The class of DGP instances that replaces a DDGP order by one with contiguous adjacent predecessors is called the Discretizable Molecular Distance Geometry Problem (DMDGP) and the order itself is a DMDGP order [40]. Formally, the DMDGP is defined as follows:

Definition 2

Given a DGP graph G = (V, E, d) and a vertex order v₁, …, v_n such that

• there exists a valid realization for v₁, v₂, v₃ and

• i > 3, the set {v_i−3, v_i−2, v_i−1, v_i} is a clique with d_i−3,i−2 + d_i−2,i−1 > d_i−3,i−1,

find a function x : V ↦ ℝ³ such that

$$\forall \{u,v\}\in E,\Vert x_u-x_v\Vert =d_{uv}.$$

We remark that the DMDGP is a subclass of instances of the DDGP. However, the structural properties and hardness of the DMDGP and DDGP are very different, which justifies Defn. 2.

The distance information in the clique {v_i−3, v_i−2, v_i−1, v_i} allows us to get the following values:

• d_1,2, …, d_n−1,n (distances associated to consecutive vertices),

• θ_1,3, …, θ_n−2,n (angles in (0, π) defined by three consecutive vertices),

• cos(ω_1,4), …, cos(ω_n−3,n) (cosines of torsion angles in [0, 2π] defined by four consecutive vertices), given by [36]:

  $$cos({\omega }_{i-3,i})=\frac{2d_{i-2,i-1}^2(d_{i-3,i-2}^2+d_{i-2,i}^2-d_{i-3,i}^2)-(d_{i-3,i-2,i-1})(d_{i-2,i-1,i})}{\sqrt{4d_{i-3,i-2}^2{d}_{i-2,i-1}^2-(d_{i-3,i-2,i-1}^2)}\sqrt{4d_{i-2,i-1}^2{d}_{i-2,i}^2-(d_{i-2,i-1,i}^2)}},$$ (2)

where

• $d_{i-3,i-2,i-1}=d_{i-3,i-2}^2+d_{i-2,i-1}^2-d_{i-3,i-1}^2$

• $d_{i-2,i-1,i}=d_{i-2,i-1}^2+d_{i-2,i}^2-d_{i-1,i}^2$.

Using cos(ω_i−3,i), for i = 4, …, n, we obtain two possible values for each torsion angle, implying that we do no longer need to solve quadratic systems. Computational results presented in [40] show that avoiding resolution of quadratic systems guarantees more stability in the branching phase of BP.

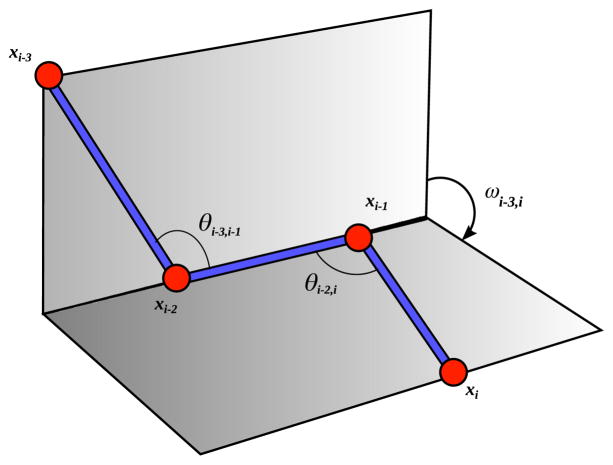
Considering that the vertex order v₁, …, v_n represents bonded atoms of a molecule, the values d_i−1,i, θ_i−2,i, ω_i−3,i are exactly the internal coordinates of the molecule that can also be used to describe its 3D structure [40] (Fig. 1).

Fig. 1.

Cartesian and internal coordinates.

Another advantage of the DMDGP order is that it is enough to apply the BP (or other algorithm) to find only one solution, since all the others can be easily obtained using symmetry properties defined in the BP tree [50,53]. These properties are also related to the cardinality of the DMDGP solution set, which can be computed based on the DMDGP graph [46], prior to actually finding realizations. In [50], possible extensions of this result when distances are not precise are also discussed.

There is a price to pay for all these results: in contrast to DDGP orders, finding a DMDGP order is an NP-complete problem [12], even considering cases when the initial clique is given. However, exploiting the chemistry of proteins and NMR data, it is possible to design a “hand-crafted” DMDGP order for any protein graph. We will see that this order can also be used to solve DMDGP instances that incorporate uncertainties from NMR data [15].

3. A new DMDGP order for protein graphs

In order to reduce the number of variables and also the computational effort required to solve problems related to protein structure, it is common to assume that all bond lengths and bond angles are fixed at their equilibrium values, which is known as the rigid geometry hypothesis [22]. This means that, in terms of internal coordinates, all the values d_i−1,i, for i = 2, …, n, and θ_i−2,i, for i = 3, …, n, are given a priori, and that the 3D protein structure can be determined by the values ω_i−3,i, for i = 4, …, n. Because of the properties of DMDGP orders, we can also know a priori all the values cos(ω_i−3,i), for i = 4, …, n, implying that the protein structure is defined by choosing + or − from $sin({\omega }_{i-3,i})=\pm \sqrt{1-{cos}^2({\omega }_{i-3,i})}$, for i = 4, …, n. These signs (+ or −) are related to the branches of the BP tree.

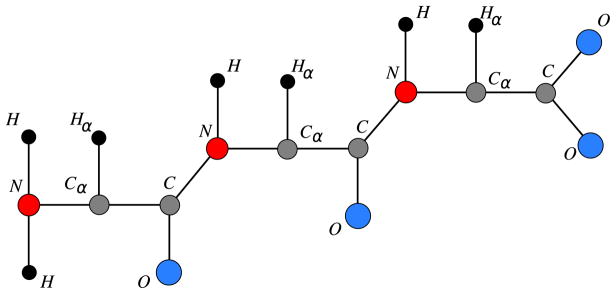
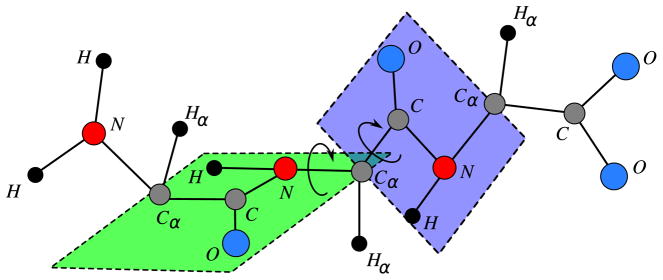
We will consider protein graphs related to the backbone of a protein, the “skeleton” of the molecule, from which its general 3D structure is determined. The protein backbone is a chain of smaller molecules, called amino acids, which are chemically bound to each other. The backbone is defined by a sequence of three atoms, N, C_α, C, where each C_α is bound to another group of atoms (the side chains of the protein) that distinguishes one amino acid from another. The atoms attached to N, C_α, C, respectively H, H_α, O, will be very important to establishing our results (Fig. 2 presents a backbone with three amino acids). More details about protein graphs including side chains are given in [16,57,58].

Fig. 2.

Protein backbone.

3.1. Repetition orders

Since we are interested in determining the 3D structure of the backbone of a protein, the sequence of atoms Nⁱ, $C_{\alpha }^i$, Cⁱ, for i = 1, …, p (where p is the number of amino acids), would be the first candidate for defining the DMDGP order we are looking for. However, for this kind of order, we do not have all the distances d_i−3,i necessary to define a DMDGP instance. On the other hand, NMR experiments, in general, provide distances between hydrogen atoms that are close enough (less than 5 Åapart). An order involving only hydrogens was defined in [43]; unfortunately, this order has some limitations, mainly because of uncertainty in NMR data [43]. These limitations have been partially addressed by simultaneously using hydrogen atoms bonded to the backbone and the backbone itself [42].

As in [42], we allow the repetition of some vertices in the order, so that at least three adjacent predecessors can always be chosen to be contiguous. Such orders are called repetition orders (or re-orders), defined below. First, the set of edges E of the protein graph G = (V, E, d) is partitioned into E = E′ ∪ E″, where {u, v} ∈ E′ if d_uv ∈ (0, ∞), and {u, v} ∈ E″ if d_uv = [d_uv, d̄_uv], with 0 < d_uv < d̄_uv. Note that the function d is now more general: the interval values represent the uncertainties in NMR data. As we will see, E′ represents pairs of atoms separated by one and two covalent bonds and E″ represents pairs of hydrogen atoms whose distances are provided by NMR.

Definition 3

A re-order is a sequence r : ℕ ↦ V ∪ {0}, with length |r| ∈ ℕ (for which r_i = r(i) = 0 for all i > |r|), such that

1. {r₁, r₂}, {r₁, r₃}, {r₂, r₃} ∈ E′;

2. ∀i ∈ {4, …, |r|}, {r_i−1, r_i}, {r_i−2, r_i} ∈ E′;

3. ∀i ∈ {4, …, |r|}, {r_i−3, r_i} ∈ E′ ∪ E″ or r_i−3 = r_i.

The first property says that d_r1r2, d_r1r3, d_r2r3 ∈ (0, ∞) and the second one says that d_ri−1ri, d_ri−2ri ∈ (0, ∞), for i = 4, …, |r|. That is, all of them must be precise distances and greater than zero.

From the third property, there are three possibilities for d_ri−3ri, i = 4, …, |r|:

• d_ri−3ri = 0, meaning that there is a vertex repetition (r_i−3 = r_i);

• d_ri−3ri ∈ (0, ∞), when r_i−3, r_i are related to atoms separated by one or two covalent bonds;

• d_ri−3ri = [d_ri−3ri, d̄_ri−3ri], with 0 < d_ri−3ri < d̄_ri−3ri (these distances are called interval distances).

If r_i = r_j for some i ≠ j (r_i−3 = r_i is a specific case), then d_rirj = 0. However, if vertex repetition is used inappropriately, we might end up with a triangle with a side of zero length, which might in turn imply an infinity of possible positions for the next atom (we emphasize the importance of strict triangular inequalities in the definition of the DMDGP). Thus, to preserve discretization, vertex repetition can occur only between pairs {r_i, r_j} with |i − j| ≥ 3. In this case, there is no branching at level max(i, j).

A repetition of a vertex only increases the length of the sequence without affecting the search, since its position in ℝ³ is already known. However, it can be recomputed in order to control possible numerical instabilities and to check if there are any inconsistencies in the distance information.

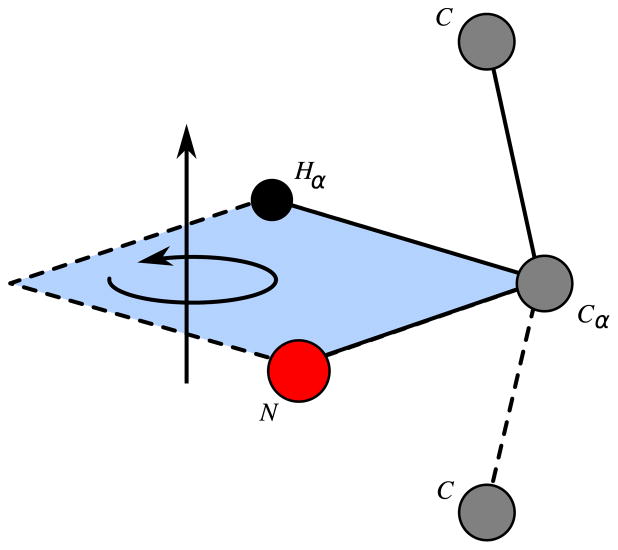
To understand what happens when {r_i−3, r_i} ∈ E″, let us rewrite expression (2) as

$$cos({\omega }_{i-3,i})=\frac{a+b{d}_{i-3,i}^2}{c},$$

where a, b, c ∈ ℝ and d_i−3,i ∈ [d_ri−3ri, d̄_ri−3ri]. The fact that a, b, c are precise numbers is a consequence of the second condition above, i.e. {r_i−1, r_i}, {r_i−2, r_i} ∈ E′.

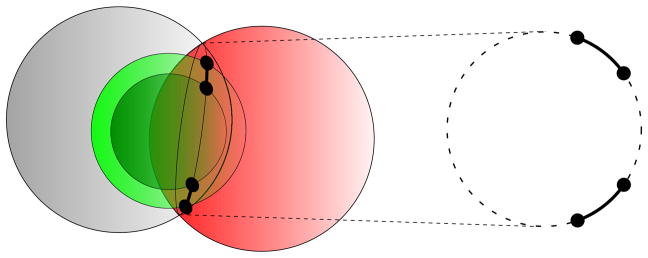
Considering the cases ω_i−3,i = 0 and ω_i−3,i = 2π, we get the minimum value for d_ri−3ri, denoted by $d_{r_{i-3}{r}_i}^{min}$, and the maximum value for d̄_ri−3ri, denoted by $d_{r_{i-3}{r}_i}^{max}$, respectively. Thus, $[{\underset{\_}{d}}_{r_{i-3}{r}_i},{\overline{d}}_{r_{i-3}{r}_i}]\subset [d_{r_{i-3}{r}_i}^{min},d_{r_{i-3}{r}_i}^{max}]$. When d_i−3,i is a precise number (d_i−3,i ∈ ℝ), with $d_{r_{i-3}{r}_i}^{min}<d_{i-3,i}<d_{r_{i-3}{r}_i}^{max}$, we obtain two possible values for ω_i−3,i, associated to two positions in ℝ³ for r_i. However, when d_i−3,i = [d_ri−3ri, d̄_ri−3ri], with $d_{r_{i-3}{r}_i}^{min}<{\underset{\_}{d}}_{r_{i-3}{r}_i}<{\overline{d}}_{r_{i-3}{r}_i}<d_{r_{i-3}{r}_i}^{max}$, we have two possible intervals for ω_i−3,i, associated to two arcs in ℝ³ for r_i. In Fig. 3, we illustrate these two arcs given as the intersection of two spheres (centered at x_i−1, x_i−2 with radii d_i−1,i, d_i−2,i, respectively) and a spherical shell, defined by two other spheres with the same center x_i−3 but with radii given by d_ri−3ri and d̄_ri−3ri [51]. This is the geometrical interpretation of the branching phase of BP.

Fig. 3.

Geometric interpretation of branching in BP.

Thus, any re-order corresponds to a DMDGP order, where some of the pairs {r_i, r_j}, with |i − j| ≥ 3, may not correspond to precise distances, but rather to intervals.

The concept of a re-order was an important step to apply all the properties of the DMDGP as a mathematical model for problems related to 3D protein structure determination using NMR data. In the same paper that introduced re-orders [42], an extension of the BP algorithm, called iBP, was developed. The basic idea to deal with interval distances is to sample values from the intervals [d_ri−3ri, d̄_ri−3ri], implying that the search space will no longer be a binary tree. Computational results presented in [11,25] reveal the main difficulty of iBP: even for large samples, there is no guarantee that a solution will be found.

Essentially, there are two reasons for this difficulty:

• The re-orders presented in [25,42] have some pairs of vertices {r_i−3, r_i} whose interval distances may not be associated to NMR data, i.e.

  $$[{\underset{\_}{d}}_{r_{i-3}{r}_i},{\overline{d}}_{r_{i-3}{r}_i}]=[d_{r_{i-3}{r}_i}^{min},d_{r_{i-3}{r}_i}^{max}],$$ (3)

  implying that sample values will be taken from a circle instead of two arcs;

• The sampling process “transforms” the iBP into a heuristic: we can no longer guarantee that a solution may be found.

Very recent results [2,3] using Clifford algebra propose an alternative that avoids the sampling process in the branching phase of iBP. However, in order to apply these results to protein structure calculations, a new re-order must be defined that avoids the situation (3). The most important property of the re-order we will describe now is that it allows branches (in the iBP search) only at hydrogen atoms that are bonded to the protein backbone. Previous re-orders [25,42] do not have this property.

3.2. The hand-crafted vertex order

Let us define a protein graph G = (V, E, d) associated to the backbone of a protein ({N^k, $C_{\alpha }^k$, C^k}, for k = 1,…, p), including oxygen atoms O^k, bonded to C^k, and hydrogen atoms H^k and $H_{\alpha }^k$, bonded to N^k and $C_{\alpha }^k$, respectively (see Fig. 2, for p = 3).

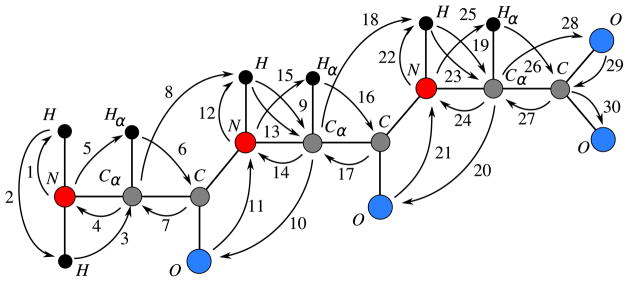
The hand-crafted vertex order (hc order) we propose is the following:

$$hc=\{N^1,H^1,H^{1^{\prime }},C_{\alpha }^1,N^1,H_{\alpha }^1,C^1,C_{\alpha }^1,\dots ,H^i,C_{\alpha }^i,O^{i-1},N^i,H^i,C_{\alpha }^i,N^i,H_{\alpha }^i,C^i,C_{\alpha }^i,\dots ,H^p,C_{\alpha }^p,O^{p-1},N^p,H^p,C_{\alpha }^p,N^p,H_{\alpha }^p,C^p,C_{\alpha }^p,O^p,C^p,O^{p^{\prime }}\},$$ (4)

where i = 2,…, p−1, H^1′ is the second hydrogen bonded to N¹ and O^p′ is the second oxygen bonded to C^p (Fig. 4 illustrates this order for p = 3).

Fig. 4.

The hc order.

We will now prove that hc is a re-order. We have assigned the following order to the atoms of the first amino acid of a protein:

$$\left\{N^1,H^1,H^{1^{\prime }},C_{\alpha }^1,N^1,H_{\alpha }^1,C^1,C_{\alpha }^1\right\}.$$ (5)

Since we are assuming that all bond lengths and bond angles are fixed at their equilibrium values (the rigid geometry hypothesis mentioned in the beginning of Section 3), the first and the second requirements of a re-order are satisfied. The third requirement is also satisfied, with the following distances for {r_i−3, r_i} (we will denote by I(Hⁱ, H^j) the interval distance related to the pair of hydrogens {Hⁱ, H^j}):

• $d(N^1,C_{\alpha }^1)\in (0,\infty )$,

• d(H¹, N¹) ∈ (0, ∞),

• $d(H^{1^{\prime }},H_{\alpha }^1)=\mathbf{I}(H^{1^{\prime }},H_{\alpha }^1)$,

• $d(C_{\alpha }^1,C^1)\in (0,\infty )$,

• $d(N^1,C_{\alpha }^1)\in (0,\infty )$.

The nitrogen N¹ and the carbon $C_{\alpha }^1$ appear twice in the sequence, but they are related to the pairs {r₁, r₅} and {r₄, r₈}.

To prove that hc is a re-order, we have to check the connection between the order (5) and the order for the second amino acid, given by the last three atoms of (5) and the first six atoms of the second amino acid:

$$\left\{H_{\alpha }^1,C^1,C_{\alpha }^1,H^2,C_{\alpha }^2,O^1,N^2,H^2,C_{\alpha }^2\right\}.$$ (6)

Here, in addition to the rigid geometry hypothesis, we also have to use the properties of the so-called peptide plane [19], which states that the atoms { $C_{\alpha }^1$, C¹, O¹, N², H², $C_{\alpha }^2$} are in the same plane (Fig. 5). This implies that $d(C_{\alpha }^1,H^2)$ (related to the pair {r₈, r₉}), $d(C_{\alpha }^1,C_{\alpha }^2)$ (related to the pair {r₈, r₁₀}), d(H², O¹) (related to the pair {r₉, r₁₁}), $d(C_{\alpha }^2,O^1)$ (related to the pair {r₁₀, r₁₁}), and d(O¹, H²) (related to the pair {r₁₁, r₁₃}) are all precise distances, satisfying the second requirement for a re-order. The third requirement is also satisfied, with the following distances for {r_i−3, r_i}:

Fig. 5.

Peptide plane.

• $d(H_{\alpha }^1,H^2)=\mathbf{I}(H_{\alpha }^1,H^2)$,

• $d(C^1,C_{\alpha }^2)\in (0,\infty )$,

• $d(C_{\alpha }^1,O^1)\in (0,\infty )$,

• d(H², N²) ∈ (0, ∞),

• $d(C_{\alpha }^2,H^2)\in (0,\infty )$,

• $d(O^1,C_{\alpha }^2)\in (0,\infty )$.

The atoms H² and $C_{\alpha }^2$ are repeated, but they are related to the pairs {r₉, r₁₃} and {r₁₀, r₁₄}, respectively.

We have assigned the following order to the atoms of a generic amino acid of a protein:

$$\left\{H^i,C_{\alpha }^i,O^{i-1},N^i,H^i,C_{\alpha }^i,N^i,H_{\alpha }^i,C^i,C_{\alpha }^i\right\}.$$ (7)

By the same arguments used for the orders (5) and (6), the second and the third re-order requirements are satisfied, with the following distances for {r_i−3, r_i}:

• d(Hⁱ, Nⁱ) ∈ (0, ∞),

• $d(C_{\alpha }^i,H^i)\in (0,\infty )$,

• $d(O^{i-1},C_{\alpha }^i)\in (0,\infty )$,

• d(Nⁱ, Nⁱ) = 0,

• $d(H^i,H_{\alpha }^i)=\mathbf{I}(H^i,H_{\alpha }^i)$,

• $d(C_{\alpha }^i,C^i)\in (0,\infty )$,

• $d(N^i,C_{\alpha }^i)\in (0,\infty )$.

In the order (7), Hⁱ, $C_{\alpha }^i$, Nⁱ are repeated, where Hⁱ and $C_{\alpha }^i$ are related to pairs {r_i, r_j}, with i − 3 < j, and Nⁱ is related to a pair {r_i−3, r_i}, which explains d(Nⁱ, Nⁱ) = 0 above.

The connection between two generic amino acids, given by

$$\left\{H_{\alpha }^i,C^i,C_{\alpha }^i,H^{i+1},C_{\alpha }^{i+1},O^i,N^{i+1},H^{i+1},C_{\alpha }^{i+1}\right\},$$

and the one between a generic amino acid and the last one, given by

$$\left\{H_{\alpha }^{p-1},C^{p-1},C_{\alpha }^{p-1},H^p,C_{\alpha }^p,O^{p-1},N^p,H^p,C_{\alpha }^p\right\},$$

both have the same order given in (6).

The result above implies the following distances for {r_i−3, r_i}, related to the connection between two generic amino acids,

• $d(H_{\alpha }^i,H^{i+1})=\mathbf{I}(H_{\alpha }^i,H^{i+1})$,

• $d(C^i,C_{\alpha }^{i+1})\in (0,\infty )$,

• $d(C_{\alpha }^i,O^i)\in (0,\infty )$,

• d(Hⁱ⁺¹, Nⁱ⁺¹) ∈ (0, ∞),

• $d(C_{\alpha }^{i+1},H^{i+1})\in (0,\infty )$,

• $d(O^i,C_{\alpha }^{i+1})\in (0,\infty )$,

and related to the connection between a generic amino acid and the last:

• $d(H_{\alpha }^{p-1},H^p)=\mathbf{I}(H_{\alpha }^{p-1},H^p)$,

• $d(C^{p-1},C_{\alpha }^p)\in (0,\infty )$,

• $d(C_{\alpha }^{p-1},O^{p-1})\in (0,\infty )$,

• d(H^p, N^p) ∈ (0, ∞),

• $d(C_{\alpha }^p,H^p)\in (0,\infty )$,

• $d(O^{p-1},C_{\alpha }^p)\in (0,\infty )$.

Finally, we have assigned the following order to the atoms of the last amino acid of a protein:

$$\left\{H^p,C_{\alpha }^p,O^{p-1},N^p,H^p,C_{\alpha }^p,N^p,H_{\alpha }^p,C^p,C_{\alpha }^p,O^p,C^p,O^{p^{\prime }}\right\}.$$ (8)

Using once more the rigid geometry hypothesis and the peptide plane properties, the second and the third requirements of a re-order are satisfied, with the following distances related to {r_i−3, r_i}:

• d(H^p, N^p) ∈ (0, ∞),

• $d(C_{\alpha }^p,H^p)\in (0,\infty )$,

• $d(O^{p-1},C_{\alpha }^p)\in (0,\infty )$,

• d(N^p, N^p) = 0,

• $d(H^p,H_{\alpha }^p)=\mathbf{I}(H_{\alpha }^p,H^p)$,

• $d(C_{\alpha }^p,C^p)\in (0,\infty )$,

• $d(N^p,C_{\alpha }^p)\in (0,\infty )$,

• $d(H_{\alpha }^p,O^p)=\mathbf{I}(H_{\alpha }^p,O^p)$,

• d(C^p, C^p) = 0,

• $d(C_{\alpha }^p,O^p)\in (0,\infty )$.

The distance $d(H_{\alpha }^p,O^p)$ is an interval, but the last level of the search tree can be related to the position of C^p, already determined using $d(C_{\alpha }^p,C^p)$.

The presented analysis can be summarized in the following theorem:

Theorem 4

The hc order is a re-order.

3.3. Minimal NMR distance information

In NMR experiments, the protein is placed within a magnetic field, inducing an alignment of the magnetic moments of the observed nuclei. The through-space transmission of this magnetization between nuclei is called the Nuclear Overhauser Effect (NOE), which is approximately proportional to d⁻⁶, where d is the distance between the nuclei of two different atoms [13]. In general, if two nuclei are more than 5 Å apart, the NOE signal is too weak to be measured for estimating distances.

The measured signal recorded during NOE experiments may be distorted, due to dynamics of the protein under study, experimental noise, and the influence of neighboring atoms [56]. NOE measurements are often converted into upper distance bounds, where the corresponding lower bounds are given by the sum of the van der Waals radii of the involved atoms [34]. Therefore, interval distances may be defined for hydrogen pairs that are close enough, implying the following result.

Theorem 5

Using the hc order, the rigid geometry hypothesis, and the properties of peptide planes, the set of distances between the pairs of hydrogen atoms

$$\{H^{1^{\prime }},H_{\alpha }^1\},\dots ,\{H_{\alpha }^{i-1},H^i\},\{H^i,H_{\alpha }^i\},\{H_{\alpha }^i,H^{i+1}\},\dots ,\{H^p,[H_{\alpha }^p]\},$$ (9)

where i = 2,…, p − 1 and p is the number of amino acids of a protein, are sufficient conditions to represent the solution space of the associated DGP as a search tree.

Let us consider this search tree more carefully. Since the hc order is a re-order, all distances d_i−1,i and d_i−2,i are precise values, greater than zero. Thus, concerning the size of the search space, we have to analyze all distances d_i−3,i (recall that the branching of the search tree is the result of intersecting two spheres with precise radii d_i−1,i, d_i−2,i with a third one of radius d_i−3,i, possibly given by an interval distance (Fig. 3)).

In addition to the rigid geometry hypothesis and the peptide plane properties, we also need the chirality property [19], which defines the orientation of the tetrahedra formed by {N¹, H¹, H^1′, $C_{\alpha }^1$} and { $C_{\alpha }^i$, Nⁱ, $H_{\alpha }^i$, Cⁱ}, implying only one possible position for $C_{\alpha }^1$ and Cⁱ, i = 1,…, p (Fig. 6).

Fig. 6.

Chirality property.

Considering the first amino acid and the links to the second one, we have:

• $d(N^1,C_{\alpha }^1)>0\Rightarrow 2$ possible positions in ℝ³ for $C_{\alpha }^1$, but we can fix one of them because of chirality defined on {N¹, H¹, H^1′, $C_{\alpha }^1$}.

• d(H¹, N¹) > 0 ⇒ 2 possible positions in ℝ³ for N¹, but we can fix one of them, since N¹ is repeated.

• $d(H^{1^{\prime }},H_{\alpha }^1)=\mathbf{I}(H^{1^{\prime }},H_{\alpha }^1)\Rightarrow 2$possible arcs in ℝ³ for $H_{\alpha }^1$.

• $d(C_{\alpha }^1,C^1)>0\Rightarrow 2$ possible positions in ℝ³ for C¹, but we can fix one of them because of chirality defined on { $C_{\alpha }^1$, N¹, $H_{\alpha }^1$, C¹}.

• $d(N^1,C_{\alpha }^1)>0\Rightarrow 2$ possible positions in ℝ³ for $C_{\alpha }^1$, but we can fix one of them, since $C_{\alpha }^1$ is repeated.

• $d(H_{\alpha }^1,H^2)=\mathbf{I}(H_{\alpha }^1,H^2)\Rightarrow 2$ possible arcs in ℝ³ for H².

• $d(C^1,C_{\alpha }^2)>0\Rightarrow 2$ possible positions in ℝ³ for $C_{\alpha }^2$, but we can fix one of them because of the plane already defined by {C¹, $C_{\alpha }^1,H_{\alpha }^2$}.

• $d(C_{\alpha }^1,O^1)>0\Rightarrow 2$ possible positions in ℝ³ for O¹, but we can fix one of them because of the plane already defined by {C¹, $C_{\alpha }^1,H_{\alpha }^2$}.

These are the distances d_i−3,i in the generic amino acid (with the links to the next one):

• d(Hⁱ, Nⁱ) > 0 ⇒ 2 possible positions in ℝ³ for Nⁱ, but we can fix one of them because of the plane already defined by {Cⁱ⁻¹, $C_{\alpha }^{i-1}$, Hⁱ}.

• $d(C_{\alpha }^i,H^i)>0\Rightarrow 2$ possible positions in ℝ³ for Hⁱ, but we can fix one of them, since Hⁱ is repeated.

• $d(O^{i-1},C_{\alpha }^i)>0\Rightarrow 2$ possible positions in ℝ³ for $C_{\alpha }^i$, but we can fix one of them, since $C_{\alpha }^i$ is repeated.

• d(Nⁱ, Nⁱ) = 0 ⇒ 1 possible position in ℝ³ for Nⁱ (the related torsion angle is 0).

• $d(H^i,H_{\alpha }^i)=\mathbf{I}(H^i,H_{\alpha }^i)\Rightarrow 2$ possible arcs in ℝ³ for $H_{\alpha }^i$.

• $d(C_{\alpha }^i,C^i)>0\Rightarrow 2$ possible positions in ℝ³ for Cⁱ, but we can fix one of them because of chirality defined on { $C_{\alpha }^i$, Nⁱ, $H_{\alpha }^i$, Cⁱ}.

• $d(N^i,C_{\alpha }^i)>0\Rightarrow 2$ possible positions in ℝ³ for $C_{\alpha }^i$, but we can fix one of them, since $C_{\alpha }^i$ is repeated.

• $d(H_{\alpha }^i,H^{i+1})=\mathbf{I}(H_{\alpha }^i,H^{i+1})\Rightarrow 2$ possible arcs in ℝ³ for Hⁱ⁺¹.

• $d(C^i,C_{\alpha }^{i+1})>0\Rightarrow 2$ possible positions in ℝ³ for $C_{\alpha }^{i+1}$, but we can fix one of them because of the plane already defined by {Cⁱ, $C_{\alpha }^i,H_{\alpha }^{i+1}$}.

• $d(C_{\alpha }^i,O^i)>0\Rightarrow 2$ possible positions in ℝ³ for Oⁱ, but we can fix one of them because of the plane already defined by {Cⁱ, $C_{\alpha }^i,H_{\alpha }^{i+1}$}.

Now, let us analyze the distances d_i−3,i in the last amino acid (as we already mentioned, we are considering that the last level of the search tree is being related to the position of C^p):

• d(H^p, N^p) > 0 ⇒ 2 possible positions in ℝ³ for N^p, but we can fix one of them because of the plane already defined by {C^p−1, $C_{\alpha }^{p-1}$, H^p}.

• $d(C_{\alpha }^p,H^p)>0\Rightarrow 2$ possible positions in ℝ³ for H^p, but we can fix one of them, since H^p is repeated.

• $d(O^{p-1},C_{\alpha }^p)>0\Rightarrow 2$ possible positions in ℝ³ for $C_{\alpha }^p$, but we can fix one of them, since $C_{\alpha }^p$ is repeated.

• d(N^p, N^p) = 0 ⇒ 1 possible position in ℝ³ for N^p (the related torsion angle is 0).

• $d(H^p,H_{\alpha }^p)=\mathbf{I}(H^p,H_{\alpha }^p)\Rightarrow 2$ possible arcs in ℝ³ for $H_{\alpha }^p$.

• $d(C_{\alpha }^p,C^p)>0\Rightarrow 2$ possible positions in ℝ³ for C^p, but we can fix one of them because of chirality defined on { $C_{\alpha }^p$, N^p, $H_{\alpha }^p$, C^p}.

The discussion above implies the following result.

Theorem 6

Using the hc order, the rigid geometry hypothesis, the peptide plane properties, the chirality property, and the set of distances between the pairs of hydrogen atoms

$$\{H^{1^{\prime }},H_{\alpha }^1\},\dots ,\{H_{\alpha }^{i-1},H^i\},\{H^i,H_{\alpha }^i\},\{H_{\alpha }^i,H^{i+1}\},\dots ,\{H^p,H_{\alpha }^p\},$$ (10)

where i = 2,…, p − 1 and p is the number of amino acids of a protein, the branches in the search tree occur only at hydrogen atoms given by

$$\{H_{\alpha }^1,\dots ,H^i,H_{\alpha }^i,\dots ,H^p,H_{\alpha }^p\}.$$ (11)

There are two main consequences of this theorem:

1. If the distances related to the pairs (10) are precise values, the search space of the associated DGP is finite, represented as a binary tree;

2. If the distances related to the pairs (10) are precise values and there is at least one additional distance (from NMR data) for each hydrogen in the list (11) to previous hydrogens, there is only one DGP solution that can be found in linear time.

Although precise and additional distances are very strong hypotheses, this kind of information emphasizes the relationship of the cardinality of the DGP solution set with the computational complexity of the problem.

From the definition of the hc order (4) and from Theorem 6, we can note that the position of atom Nⁱ depends on the position of atom Hⁱ and that the position of atom Cⁱ depends on the position of atom $H_{\alpha }^i$. Since the protein backbone is determined by the torsion angles defined by {Nⁱ⁻¹, $C_{\alpha }^{i-1}$, Cⁱ⁻¹, Nⁱ} and {Cⁱ⁻¹, Nⁱ⁻¹, $C_{\alpha }^{i-1}$, Cⁱ} (the so-called (ϕ,ψ) angles [19]), the term minimal NMR distance information is justified by the fact that we require only NMR distances related to $d(H^i,H_{\alpha }^i)$ and $d(H_{\alpha }^{i-1},H^i)$.

Since atoms Hⁱ, $H_{\alpha }^i$ are in the same amino acid, the associated distance $d(H^i,H_{\alpha }^i)$ is likely to be detected by NMR. Although atoms $H_{\alpha }^{i-1}$, Hⁱ are in consecutive amino acids, there is just one torsion angle (the one defined by {Nⁱ⁻¹, $C_{\alpha }^{i-1}$, Cⁱ⁻¹, Nⁱ}) related to the position of Hⁱ, because the peptide plane “constrains” the torsion angle defined by { $C_{\alpha }^{i-1}$, Cⁱ⁻¹, Nⁱ⁻¹, $C_{\alpha }^i$} to be π radians. In the worst case, supposing that the distance $d(H_{\alpha }^{i-1},H^i)$ is not available, we can use “implicit” information associated with the fact that the distance was not detected [1] or some estimations given in [67].

4. Conclusion and future directions

The contribution of this paper is related to how to combine information from protein geometry (rigid geometry hypothesis, peptide plane, and chirality) and NMR experiments in order to model the problem of 3D protein calculation using NMR data as a DMDGP that also considers interval distances. From the results of this work, we select four new research directions:

1. Exploit the hc order for the purpose of designing new pruning devices for the iBP;

2. Apply the hc order and the corresponding pruning devices to the Clifford algebra approach recently proposed in the literature;

3. Investigate the possibility of designing new NMR experiments that focus on the accuracy of distances between hydrogen atoms used in the hc order;

4. Develop robust algorithms that can integrate all of the above items.

Regarding item 1, we can do the following: (a) exploit information on lower and upper bounds to the backbone torsion angles provided by NMR chemical shifts [60]; (b) and exploit information on hydrogen bonds defined between a hydrogen (bound to N) of one amino acid and the oxygen (bound to C) of another one. More precisely:

• Since the position of atom Oⁱ⁻¹ is determined by the position of atom Hⁱ, hydrogen bond distances can be used to prune infeasible positions of Hⁱ;

• Since the position of atom Nⁱ is also determined by the position of atom Hⁱ, NMR chemical shift information on the torsion angle defined by {Nⁱ⁻¹, $C_{\alpha }^{i-1}$, Cⁱ⁻¹, Nⁱ} can be used to prune infeasible positions of Hⁱ;

• Since the position of atom Cⁱ is determined by the position of atom $H_{\alpha }^i$, NMR chemical shift information on the torsion angle defined by {Cⁱ⁻¹, Nⁱ⁻¹, $C_{\alpha }^{i-1}$, Cⁱ} can be used to prune infeasible positions of $H_{\alpha }^i$.

Of course, all the information related to the NMR distances

$$d(H^j,H^i),d(H_{\alpha }^{j-1},H^i)\text{and}d(H^{j-1},H_{\alpha }^i),d(H_{\alpha }^j,H_{\alpha }^i),$$

where j < i, can also be used to prune infeasible positions of Hⁱ and $H_{\alpha }^i$.