Abstract
The aim of this study is to develop a fully automated convolutional neural network (CNN) method for quantification of breast MRI fibroglandular tissue (FGT) and background parenchymal enhancement (BPE). An institutional review board-approved retrospective study evaluated 1114 breast volumes in 137 patients using T1 precontrast, T1 postcontrast, and T1 subtraction images. First, using our previously published method of quantification, we manually segmented and calculated the amount of FGT and BPE to establish ground truth parameters. Then, a novel 3D CNN modified from the standard 2D U-Net architecture was developed and implemented for voxel-wise prediction whole breast and FGT margins. In the collapsing arm of the network, a series of 3D convolutional filters of size 3 × 3 × 3 are applied for standard CNN hierarchical feature extraction. To reduce feature map dimensionality, a 3 × 3 × 3 convolutional filter with stride 2 in all directions is applied; a total of 4 such operations are used. In the expanding arm of the network, a series of convolutional transpose filters of size 3 × 3 × 3 are used to up-sample each intermediate layer. To synthesize features at multiple resolutions, connections are introduced between the collapsing and expanding arms of the network. L2 regularization was implemented to prevent over-fitting. Cases were separated into training (80%) and test sets (20%). Fivefold cross-validation was performed. Software code was written in Python using the TensorFlow module on a Linux workstation with NVIDIA GTX Titan X GPU. In the test set, the fully automated CNN method for quantifying the amount of FGT yielded accuracy of 0.813 (cross-validation Dice score coefficient) and Pearson correlation of 0.975. For quantifying the amount of BPE, the CNN method yielded accuracy of 0.829 and Pearson correlation of 0.955. Our CNN network was able to quantify FGT and BPE within an average of 0.42 s per MRI case. A fully automated CNN method can be utilized to quantify MRI FGT and BPE. Larger dataset will likely improve our model.
Keywords: Convolutional neural network, Breast cancer, MRI
Introduction
According to the American Cancer Society, breast cancer is the second leading cause of death in women, with 40,610 breast cancer deaths expected to occur among US women in 2017 [1]. As such, prevention and early detection are important in minimizing breast cancer mortality. Family history, genetic mutations such as BRCA 1 and 2, and hormonal risk factors are some of the established risk factors that increase breast cancer risk [2–4]. It is established that high mammographic breast density correlates with breast cancer risk [5–7].
The breast is composed of fat and fibroglandular tissue (FGT), which includes epithelial and stromal elements. Mammographic breast density correlates to the amount of FGT on breast MRI. Depending on the amount of FGT, the breast is classified into four different categories determined by the Breast Imaging Reporting and Data System (BI-RADS) lexicon, which include almost entirely fatty, scattered fibroglandular tissue, heterogeneous fibroglandular tissue, and extreme fibroglandular tissue on breast MRI [8], which correspond to almost entirely fatty, scattered areas of fibroglandular density, heterogeneously dense, and extremely dense categorizations on mammography. Patients with heterogeneously dense or extremely dense breasts have a fourfold increased risk of developing breast cancer compared to patients with fatty breasts [5–7].
Breast MRI BPE refers to the volume and intensity of normal FGT enhancement after intravenous contrast administration on breast MRI. Similar to FGT categorization, the amount of BPE can be qualitatively assessed by the interpreting radiologist based on the BI-RADS lexicon as minimal, mild, moderate, or marked [8]. It has been recently shown that the amount of breast MRI parenchymal enhancement (BPE) is a significant risk factor for breast cancer, independent of the amount of FGT [9, 10]. Similar to mammographic density, there is an association between a high degree of BPE and breast cancer [10, 11].
Currently, both FGT and BPE are qualitatively assessed by the interpreting radiologist. Such assessment can be prone to inter- and intra-observer variability due to the inherent subjectivity of the interpretation [11]. Quantitative three-dimensional assessments of FGT and BPE using semi-automated computerized methods have been published [12–16]. While quantitative methods provide a more accurate measurement of FGT and BPE [12–16], they are time-consuming and require initial selection of the region of interest by the operator, which introduces potential subjectivity bias.
Recently, a subset of machine learning through artificial neural network such as convolutional neural network (CNN) has shown significant promise in visual tasks and is currently being applied in the medical field for clinical applications [17]. The U-Net is convolutional network architecture shown to be fast and precise in segmenting biomedical images [18, 19]. In this study, we propose utilization of a U-Net architecture for fully automated segmentation and quantification of breast FGT and BPE.
Materials and Methods
Subjects
After institutional review board approval, an institutional PACS database was queried for breast MRIs obtained between 2013 and 2015 and randomly selected 137 patients for analysis. In patients with a breast tumor, only the contralateral normal breast was included for evaluation.
MRI Acquisition
MRI was performed on a 1.5 or 3.0-T commercially available system (Signa Excite, GE Healthcare) using an eight-channel breast array coil. The imaging sequence included a triplane localizing sequence followed by a sagittal fat-suppressed T2-weighted sequence (TR/TE, 4000–7000/85; section thickness, 3 mm; matrix, 256 × 192; FOV, 18–22 cm; no gap). A bilateral sagittal T1-weighted fat-suppressed fast spoiled gradient-echo sequence (17/2.4, flip angle, 35°, bandwidth, 31–25 Hz) was then performed before and three times after a rapid bolus injection (gadobenate dimeglumine/Multihance; Bracco Imaging; 0.1 mmol/kg) delivered through an IV catheter. Image acquisition started after contrast material injection and was obtained consecutively up to four times with each acquisition time of 120 s. Section thickness was 2–3 mm using a matrix of 256 × 192 and a field of view of 18–22 cm. Frequency was in the antero-posterior direction. After the examination, postprocessing was performed including subtraction of the unenhanced images from the first contrast-enhanced images on a pixel-by-pixel basis and reformation of sagittal images to axial images.
Ground Truth Segmentation and Quantification
Ground truth segmentation and quantification was performed based on our previously published work [12–14]. Briefly for each breast, the outer margins of the entire breast as well as margins for fibroglandular tissue were manually segmented using custom semi-automated software developed in MATLAB (R2015a, The MathWorks, Inc., Natick, MA, USA). The software is based on an active contour algorithm that is iteratively refined after manually initiated segmentations. All segmentation masks were visually inspected by a board-certified subspecialized breast radiologist with 8 years of experience. FGT calculation was based on [FGT volume / whole breast volume]. BPE calculation was based on [BPE volume / FGT volume] as described in our previously published studies [12–14].
Convolutional Neural Network
Image Preprocessing
Each breast MRI was split into two separate volumes, one containing each breast. These volumes were then resized to an input matrix of 64 × 128 × 128 using bicubic interpolation, yielding an approximately isotropic volume. Subsequently, each volume was independently normalized using z score values, such that the mean and standard deviation voxel value for each volume are 0 and 1, respectively. For whole breast segmentation, all available sequences were used for training. For subsequent FGT segmentation, only T1 precontrast volumes were used.
Convolutional Neural Network Algorithm
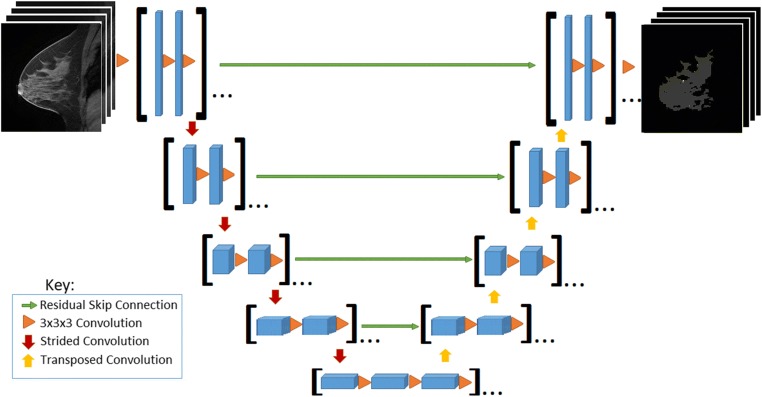
Two serial fully convolutional 3D CNNs were implemented for voxel-wise prediction whole breast and FGT margins (Fig. 1). The serial architecture is designed such that the predicted whole breast margins are used to mask the original MRI volume so that FGT can only be predicted in areas identified as breast parenchyma. The foundation for each serial 3D CNN arises from the standard 2D U-Net architecture originally described in [18] for segmentation of pathology slides.
Fig. 1.
Convolutional neural network architecture. [Feature map sizes: 128-64-32-16-8-8-16-32-64-128; depth: 8-16-32-64-96-96-64-32-16-8; orange triangle: Conv3D-BatchNorm-ReLU; padding: valid]
In the collapsing arm of the network, a series of 3D convolutional filters of size 3 × 3 × 3 are applied for standard CNN hierarchical feature extraction. To reduce feature map dimensionality, a 3 × 3 × 3 convolutional filter with stride 2 in all directions is applied; a total of 4 such operations are used. In the expanding arm of the network, a series of convolutional transpose filters of size 3 × 3 × 3 are used to up-sample each intermediate layer. To synthesize features at multiple resolutions, connections are introduced between the collapsing and expanding arms of the network. These are implemented through residual connections (addition operations) [20] instead of concatenations originally described by [21] given the overall increased stability and speed of algorithm convergence of residual architectures.
No pooling is used at any stage in line with observations by [21] to preserve flow of gradients during back-propagation. Furthermore, the scheme above allows for efficient and flexible prediction during deployment such that outputs at every voxel location can be obtained in just a single forward pass regardless of the number of input slices in the volume.
Implementation Details
The network was trained from random weights initialized using the heuristic described by He et al. [22]. The final loss function included a term for L2 regularization to prevent over-fitting of data by limiting the squared magnitude of the convolutional weights. Gradients for back-propagation were estimated using the Adam optimizer, an algorithm for first-order gradient-based optimization of stochastic objective functions based on adaptive estimates of lower order moments [23]. The default Adam optimizer parameters were used. This included beta-1 = 0.9, beta-2 = 0.999, epsilon = 1e−8. An initial learning rate of 0.001 was used and annealed (along with an increase in mini-batch size) whenever a plateau in training loss was observed.
Software code for this study was written in Python 3.5 using the open-source TensorFlow r1.2 library (Apache 2.0 license). Training was performed on a GPU-optimized workstation with four NVIDIA GeForce GTX Titan X cards (12GB, Maxwell architecture). Validation statistics including time for model prediction were benchmarked on a GPU-optimized workstation with just a single NVIDIA GeForce GTX Titan X (12 GB, Maxwell architecture).
Statistical Analysis
Overall algorithm accuracy in mask generation used for FGT and BPE quantification was determined using two different metrics. First, predicted whole breast, FGT, and BPE volumes were compared to gold-standard manual segmentations using a Dice score coefficient:
The Dice score estimates the amount of spatial overlap (e.g., union) between two binary masks, with a score of 0 indicating no overlap and a score of 1 indicating perfect overlap. Second, predicted whole breast, FGT, and BPE volumes (cm3) were compared to gold-standard annotated volumes using a Pearson correlation coefficient (r).
Results
A total of 1114 breast volumes of 169 single breasts from 137 patients were included for evaluation. When available, T1 precontrast, T1 postcontrast (up to three phases), and T1 subtraction (up to three phases) acquisitions were used for each breast, yielding a total of 1114 single breast volumes. A fivefold cross-validation scheme was used for analysis. In this experimental paradigm, 80% of the data was randomly assigned into the training cohort while the remaining 20% was used for validation. This process was then repeated five times until each study in the entire dataset was used for validation once. During randomization, all breast volumes arising from the same patient were kept in the same validation fold. Final results below are reported for the cumulative validation set statistics across the entire dataset, with ranges indicating minimum and maximum values observed in any single validation fold.
Whole Breast, FGT, and BPE Segmentation and Quantification
Automated CNN-generated masks of whole breast volume demonstrated high accuracy, with cross-validation Dice score coefficient of 0.947 and Pearson correlation of 0.998 in comparison to manual annotations (Fig. 2). Visually, the 3D CNN network generated smooth mask boundaries (red) in each dimension, as opposed to the “stair-step” artifact (blue) that is typically encountered when estimating margins on a 2D slice-by-slice basis. Similarly automated CNN generated masks of FGT and quantified BPE with high accuracy in matching the ground truth quantification results (Dice score coefficient of 0.813 and Pearson correlation of 0.975 for FGT and Dice score coefficient of 0.829 and Pearson correlation of 0.955 for BPE). Examples of FGT segmentation and BPE images are show in Figs. 3 and 4.
Fig. 2.

Whole breast segmentation. Selected T1 sagittal image showing the outlines of CNN-based segmentation which is color coded in red with almost complete overlap with manual ground truth segmentation which is color coded in blue
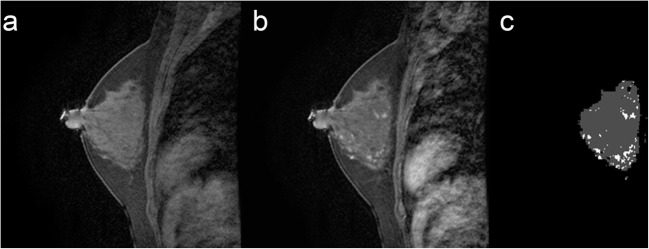
Fig. 3.
FGT and BPE segmentation. a Selected T1 sagittal precontrast image. b Corresponding T1 sagittal post contrast image. c Segmented FGT and BPE. Example of mild BPE with 16.6% enhancement
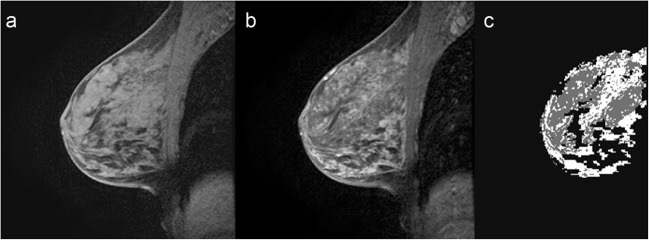
Fig. 4.
FGT and BPE segmentation. a Selected T1 sagittal precontrast image. b Corresponding T1 sagittal post contrast image. c Segmented FGT and BPE. Example of marked BPE with 62.7% enhancement
Network Statistics
Each network for a corresponding validation fold trained for approximately 80,000 iterations before convergence. Subsequently, a trained network was able to determine whole breast and FGT margins, as well as estimates of BPE on a new test case within an average of 0.42 s.
Discussion
The purpose of this study was to apply a U-Net architecture for fully automated segmentation and quantification of breast FGT and BPE, which are important imaging biomarkers of breast cancer risk. Our results show high degree of accuracy in quantifying FGT and BPE and indicate feasibility of utilizing CNN algorithm to accurately and objectively predict these important measures.
Up to date, many published FGT and BPE qualitative and quantitative assessment studies have been performed [12–16]. Qualitative FGT and BPE assessment can be prone to inter- and intra-observer variability due to the inherent subjectivity of the interpretation [11]. In addition, categorizing the amount of FGT and BPE into only four qualitative groups limits statistical analysis assessing for small but potentially significant differences. Quantitative 3D assessment studies have also been published, showing a more accurate assessment of FGT and BPE volume. One such study uses custom semi-automated software, which is based on an active contour algorithm that is iteratively refined after manually initiated segmentations [12–14]. Others have used techniques such as fuzzy c-means (FCM) data clustering technique [15] and principal component analysis (PCA) [16]. While there are significant advantages in 3D assessment of FGT and BPE including robust segmentation with easy initialization and efficient modification, such segmentation softwares are time-consuming. Furthermore, they often rely on segmentation masks being visually inspected by a subspecialized breast radiologist for accuracy, which introduces inter- and intra-observer variability. More fully automated whole breast and FGT segmentation by Gubern-Mérida et al. [24] has been described. They used a multistep process including the identification of landmarks such as a sternum and used the expectation–maximization algorithm to estimate the image intensity distributions of breast tissue and automatically discriminate between fatty and fibroglandular tissue. A dataset of 50 cases with manual segmentations was used for evaluation yielding reasonable results. However, the multistep process was time-consuming taking approximately 8 min. In contrast, our algorithm is much faster even accounting for the differences in the hardware capacity with result output in a fraction of a second. In addition, the performance of their study was based on overlap of the manual segmentation. It was not clear if the manual segmentation has clinical validation with a known standardized value such as qualitative BI-RADS assessment. Our ground truth segmentation was based on our previously published validation with BI-RADS assessments [12–14].
In our study, we applied a 3D U-Net, which is a convolutional network architecture for fast and precise segmentation of images. More recently published studies [18, 19] show a network and training strategy that relies on the strong use of data augmentation to use the available annotated samples more efficiently. The architecture consists of a contracting path to capture context and a symmetric expanding path that enables precise localization allowing for segmentation with less number of training cases. We showed high degree of accuracy in quantifying FGT and BPE utilizing a 3D U-Net architecture to predict these important measures.
There is strong evidence that breast density is an independent risk factor for breast cancer, reportedly associated with fourfold increase in the risk for breast cancer [5, 6]. Breast density correlates with the amount of FGT on breast MRI. More recent studies have showed that BPE is also associated with breast cancer risk. King et al. was the first study to propose the relationship between BPE and breast cancer risk showing that similar to mammographic density, there is an association between a high degree of BPE and breast cancer [9]. A paper by Donichos et al. again demonstrated that BPE is associated with a higher probability of developing breast cancer in women with high risk for cancer [10]. However, the exact increase in risk remains unclear partly due to variable classification systems used for assessing FGT and BPE including the BI-RADS classification, the percentage classification, and the Wolfe classification [16]. The studies mentioned above utilize qualitative assessment of FGT and BPE with the aforementioned limitations. Additional studies using CNN quantitative method such as ours will be important in order to validate these types of studies as well as to better define the true risk of breast cancer.
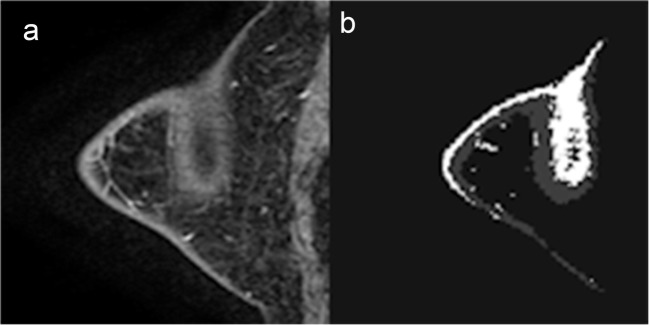
To our knowledge, this is the first study of a FGT and BPE quantitative technique utilizing a U-Net architecture for fully automated segmentation and quantification of breast FGT and BPE. Our algorithm predicted FGT and BPE volume with high accuracy using a gold-standard semi-automated segmentation MRI dataset. However, minor errors in segmentation were most commonly seen on MR acquisitions with relatively poor fat saturation along the subcutaneous skin margins. These segmentation discrepancies were most evident when incomplete fat saturation was combined with volume averaging in the out-of-plane direction resulting in apparent high signal intensity centrally within the breast tissue (Fig. 5). These errors may in part be related to the down-sampling needed to accommodate GPU memory limitations for otherwise high-resolution 3D volumes, which could result in increased slice gap and thus inability of the algorithm to smoothly trace the central signal abnormality to the periphery of the skin. In future studies, larger datasets, improved hardware, and newer algorithmic designs including hybrid 3D/2D techniques that maximize the in-plane and adjacent slice resolution may be able to help overcome this limitation.
Fig. 5.
FGT and BPE segmentation. a Selected T1 sagittal postcontrast image. b Segmented FGT and BPE. MR acquisitions with relatively poor fat saturation along the subcutaneous skin margins. Incomplete fat saturation was combined with volume averaging in the out-of-plane direction resulting in apparent high signal intensity centrally within the breast tissue
Major limitation of our study is that it is a small, feasibility study in a single institution. The performance of CNN has been shown to increase logarithmically with larger datasets [17], and larger MRI datasets are likely to significantly improve FGT/BPE quantification method. In addition, CNN algorithms are susceptible to over-fitting. To address this, the final loss function included a term for L2 regularization to prevent over-fitting of data by limiting the squared magnitude of the convolutional weights. We ran our algorithm using a fivefold cross-validation scheme. This could provide an unbiased predictor, but running our model on a separate and independent testing dataset may produce a more objective evaluation. In the future, we plan to test on additional datasets from multiple sites. For our data before normalization, no bias field correction was applied. Bias field correction is the correction of the image contrast variations due to magnetic field inhomogeneity. The most commonly adopted approach is N4 bias field correction [25]. Future work would incorporate bias field correction preprocessing followed by denoising algorithm before data normalization for feeding into our algorithm. In addition, there are several parameters that need to be carefully tuned in our network such as L2 regularizer, optimizer, and learning rate. Currently, all the parameters were determined empirically. In the future, random search or Bayesian search method would be incorporated to choose the best hyperparameters.
In conclusion, a CNN-based fully automated MRI FGT and BPE quantification method was developed yielding a high degree of accuracy. Larger dataset will likely further improve our model and may ultimately lead to clinical use for prognosticating patients’ likelihood of breast cancer.
Compliance with Ethical Standards
Conflict of Interest
The authors declare that they have no conflict of interest.
References
- 1.DeSantis C, Ma J, Sauer AG, et al. Breast cancer statistics, 2017, racial disparity in mortality by state. CA Cancer J Clin. 2017;67(6):439–448. doi: 10.3322/caac.21412. [DOI] [PubMed] [Google Scholar]
- 2.Pal T, Permuth-Wey J, Betts JA, Krischer JP, Fiorica J, Arango H, LaPolla J, Hoffman M, Martino MA, Wakeley K, Wilbanks G, Nicosia S, Cantor A, Sutphen R. BRCA1 and BRCA2 mutations account for a large proportion of ovarian carcinoma cases. Cancer. 2005;104(12):2807–2816. doi: 10.1002/cncr.21536. [DOI] [PubMed] [Google Scholar]
- 3.Burke W, Daly M, Garber J, Botkin J, Kahn MJ, Lynch P, McTiernan A, Offit K, Perlman J, Petersen G, Thomson E, Varricchio C. Recommendations for follow-up care of individuals with an inherited predisposition to cancer. II. BRCA1 and BRCA2. Cancer genetics studies consortium. JAMA. 1997;277(12):997–1003. doi: 10.1001/jama.1997.03540360065034. [DOI] [PubMed] [Google Scholar]
- 4.Schairer C, Lubin J, Troisi R, Sturgeon S, Brinton L, Hoover R. Menopausal estrogen and estrogen-progestin replacement therapy and breast cancer risk. JAMA. 2000;283(4):485–491. doi: 10.1001/jama.283.4.485. [DOI] [PubMed] [Google Scholar]
- 5.Byrne C, Schairer C, Brinton LA, Wolfe J, Parekh N, Salane M, Carter C, Hoover R. Effects of mammographic density and benign breast disease on breast cancer risk (United States) Cancer Causes Control. 2001;12(2):103–110. doi: 10.1023/A:1008935821885. [DOI] [PubMed] [Google Scholar]
- 6.McCormack VA, dos Santos SI. Breast density and parenchymal patterns as markers of breast cancer risk: a meta-analysis. Cancer Epidemiol Biomark Prev. 2006;15(6):1159–1169. doi: 10.1158/1055-9965.EPI-06-0034. [DOI] [PubMed] [Google Scholar]
- 7.Boyd N, Martin L, Gunasekara A, Melnichouk O, Maudsley G, Peressotti C, Yaffe M, Minkin S. Mammographic density and breast cancer risk: evaluation of a novel method of measuring breast tissue volumes. Cancer Epidemiol Biomarkers Prev. 2009;18(6):1754–1762. doi: 10.1158/1055-9965.EPI-09-0107. [DOI] [PubMed] [Google Scholar]
- 8.American College of Radiology . Breast imaging reporting and data system (BI-RADS) 5. Reston: American College of Radiology; 2013. [Google Scholar]
- 9.King V, Brooks JD, Bernstein JL, Reiner AS, Pike MC, Morris EA. Background parenchymal enhancement at breast MR imaging and breast cancer risk. Radiology. 2011;260(1):50–60. doi: 10.1148/radiol.11102156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Dontchos BN, Rahbar H, Partridge SC, Korde LA, Lam DL, Scheel JR, Peacock S, Lehman CD. Are qualitative assessments of background parenchymal enhancement, amount of fibroglandular tissue on MR images, and mammographic density associated with breast cancer risk? Radiology. 2015;276(2):371–380. doi: 10.1148/radiol.2015142304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Melsaether A, McDermott M, Gupta D, Pysarenko K, Shaylor SD, Moy L. Inter- and intrareader agreement for categorization of background parenchymal enhancement at baseline and after training. AJR Am J Roentgenol. 2014;203(1):209–215. doi: 10.2214/AJR.13.10952. [DOI] [PubMed] [Google Scholar]
- 12.Ha R, Mema E, Guo X, Mango V, Desperito E, Ha J, Wynn R, Zhao B. Quantitative 3D breast magnetic resonance imaging fibroglandular tissue analysis and correlation with qualitative assessments: a feasibility study. Quant Imaging Med Surg. 2016;6(2):144–150. doi: 10.21037/qims.2016.03.03. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ha R, Mema E, Guo X, Mango V, Desperito E, Ha J, Wynn R, Zhao B. Three-dimensional quantitative validation of breast magnetic resonance imaging background parenchymal enhancement assessments. Curr Probl Diagn Radiol. 2016;45(5):297–303. doi: 10.1067/j.cpradiol.2016.02.003. [DOI] [PubMed] [Google Scholar]
- 14.Mema E, Mango V, Guo X, et al. Does breast MRI background parenchymal enhancement indicate metabolic activity? Qualitative and 3D quantitative computer imaging analysis. J Magn Reson Imaging. 2018;47(3):753–759. doi: 10.1002/jmri.25798. [DOI] [PubMed] [Google Scholar]
- 15.Clendenen TV, Zeleniuch-Jacquotte A, Moy L, Pike MC, Rusinek H, Kim S. Comparison of 3-point Dixon imaging and fuzzy C-means clustering methods for breast density measurement. J Magn Reson Imaging. 2013;38(2):474–481. doi: 10.1002/jmri.24002. [DOI] [PubMed] [Google Scholar]
- 16.Eyal E, Badikhi D, Furman-Haran E, Kelcz F, Kirshenbaum KJ, Degani H. Principal component analysis of breast DCE-MRI adjustedwith a model-based method. J Magn Reson Imaging. 2009;30(5):989–998. doi: 10.1002/jmri.21950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.LeChun Y, Bengio T, Hinton G. Deep learning. Nature. 2015;521:436–444. doi: 10.1038/nature14539. [DOI] [PubMed] [Google Scholar]
- 18.Ronneberger O, Fischer P, Brox T. U-Net: convolutional networks for biomedical image segmentation. Medical image computing and computer-assisted intervention (MICCAI), springer. LNCS. 2015;9351:234–241. [Google Scholar]
- 19.Çiçek O, Abdulkadir A, Lienkamp S, et al. 3D U-Net: learning dense volumetric segmentation from sparse annotation. Medical image computing and computer-assisted intervention (MICCAI), springer. LNCS. 2016;9901:424–432. [Google Scholar]
- 20.He K, Zhang X, Ren S et al.: Deep residual learning for image recognition. ArxivOrg [Internet]. 7(3):171–180, 2015. 10.1007/978-3-319-10590-1_53%5Cnhttp://arxiv.org/abs/1311.2901%5Cnpapers3://publication/uuid/44feb4b1-873a-4443-8baa-1730ecd16291
- 21.Springenberg JT, Dosovitskiy A, Brox T, et al. Striving for simplicity: the all convolutional net. 2014 Dec 21 [cited 2017 Jul 21]; Available from: http://arxiv.org/abs/1412.6806
- 22.He K, Zhang X, Ren S, et al. “Delving deep into rectifiers: surpassing human-level performance on ImageNet classification,” arXiv:1502.01852, (2015).
- 23.Kingma DP, Ba J, Adam: A method for stochastic optimization. arXiv:1412.6980 [cs.LG], December 2014.
- 24.Gubern-Mérida A, Kallenberg M, Mann RM, et al. Breast segmentation and density estimation in breast MRI: a fully automatic framework. IEEE J Biomed Health Inform. 2015;19(1):349–357. doi: 10.1109/JBHI.2014.2311163. [DOI] [PubMed] [Google Scholar]
- 25.Tustison NJ, Avants BB, Cook PA, Yuanjie Zheng, Egan A, Yushkevich PA, Gee JC. N4ITK: improved N3 bias correction. IEEE Trans Med Imaging. 2010;29(6):1310–1320. doi: 10.1109/TMI.2010.2046908. [DOI] [PMC free article] [PubMed] [Google Scholar]