Significance
Structural hierarchy is ubiquitous in nature and an emerging trend in engineered materials. Despite their many virtues, hierarchical materials also add complexity and dramatically increase the opportunities for random errors in assembly. Nonetheless, highly hierarchical tissues have evolved many times in diverse lineages; this prevalence suggests a common source of mechanical robustness. In this work, we introduce a tractable, model hierarchical lattice with controllable attributes on each length scale. We find, contrary to intuition, that adding additional levels of structure actually reduces the relative variation in mechanical properties, despite an increase in assembly errors. This finding informs our understanding of the emergence of hierarchically structured biological materials, while also offering a practical heuristic in materials design.
Keywords: network mechanics, evolution of biomaterials, structural hierarchy, biophysics, soft matter
Abstract
Structural hierarchy, in which materials possess distinct features on multiple length scales, is ubiquitous in nature. Diverse biological materials, such as bone, cellulose, and muscle, have as many as 10 hierarchical levels. Structural hierarchy confers many mechanical advantages, including improved toughness and economy of material. However, it also presents a problem: Each hierarchical level adds a new source of assembly errors and substantially increases the information required for proper assembly. This seems to conflict with the prevalence of naturally occurring hierarchical structures, suggesting that a common mechanical source of hierarchical robustness may exist. However, our ability to identify such a unifying phenomenon is limited by the lack of a general mechanical framework for structures exhibiting organization on disparate length scales. Here, we use simulations to substantiate a generalized model for the tensile stiffness of hierarchical filamentous networks with a nested, dilute triangular lattice structure. Following seminal work by Maxwell and others on criteria for stiff frames, we extend the concept of connectivity in network mechanics and find a similar dependence of material stiffness upon each hierarchical level. Using this model, we find that stiffness becomes less sensitive to errors in assembly with additional levels of hierarchy; although surprising, we show that this result is analytically predictable from first principles and thus potentially model independent. More broadly, this work helps account for the success of hierarchical, filamentous materials in biology and materials design and offers a heuristic for ensuring that desired material properties are achieved within the required tolerance.
Living systems organize across many distinct levels, spanning from molecular to macroscopic scales. Such hierarchical arrangements endow organisms with many beneficial material properties; they may have high strength-to-weight ratios, exhibit strain stiffening, or be robust against fracture (1–5). A seeming drawback of this approach, however, is the enormous amount of information needed to specify the structure of highly hierarchical tissues and the increased number of opportunities for stochastic errors. Even for a self-assembled material, each hierarchical level likely increases the number of local minima in the free energy landscape, increasing the opportunity for kinetic errors in assembly (6, 7). While one may reasonably fear that this cascade of errors will undermine the reliable realization of self-assembled hierarchical materials, structural hierarchy is used effectively by organisms belonging to many diverse evolutionary lineages (2, 8, 9). Such widespread success suggests the presence of an underlying mechanism responsible for this emergent robustness. However, the number of elements necessary to describe a hierarchical structure grows geometrically with the number of hierarchical levels; thus, a 10-level structure is currently computationally inaccessible. While identification of the underlying principles responsible for hierarchical robustness would greatly aid in explaining the ubiquity of natural hierarchical structures, this objective first requires developing a mechanistic understanding of how each scale contributes to a material’s overall properties.
To gain a foothold in the study of hierarchical materials mechanics, we focus on a highly tractable model system: a triangular lattice of nodes connected by harmonic springs. Frames made of slender, elastic beams have long been of interest in technical mechanics (10–18) and the physics of living tissue (1–3, 9, 19–23), and recent work has demonstrated that fibers can generically emerge from diverse building blocks (24). Further, the mechanics of elastic networks are easily interpretable through the Maxwell counting heuristic; briefly, to constrain every degree of freedom in the network, there must be bonds per node, where is the dimensionality of the system (12, 25). While much work has been done to characterize elastic networks constructed with a single important length scale (10, 13–15, 26, 27), we lack a general characterization of elastic networks constructed with multiple disparate length scales; a priori, it is unclear how Maxwell counting applies to hierarchical structures. Are there distinct degrees of freedom associated with “large” nodes, just as there are with “small” nodes? How do constraints on large and small length scales compare? Identification of underlying mechanisms that make hierarchical structures robust first requires developing a comprehensible hierarchical model.
Here, we introduce a model system with a nested, dilute triangular lattice structure, in which distinct network connectivities can be defined on multiple scales. We examine the dependence of tensile stiffness on each of these connectivities and capture this relationship with a simple model. Using this model, we then assess the resilience of a hierarchical material’s mechanical properties in the presence of random errors in assembly.
Geometrical Characteristics of the Model System
We consider an extension of the well-studied dilute, triangular lattice in 2D. Nodes arranged in a triangular Bravais lattice are connected to nearest neighbors, and bonds are then removed at random such that some fraction, referred to as the bond portion, , remains. The infinite triangular lattice has a connectivity of six bonds per node when , while in 2D Maxwell counting dictates a minimum connectivity of four bonds per node; thus, the infinite, dilute triangular lattice should lose stiffness when falls below . Lattices of finite size would require a slightly higher bond portion, due to the presence of underconstrained nodes at the boundary. This prediction has been thoroughly confirmed for ball-and-spring networks, via simulation and mean-field theoretic approaches (10, 13–15).
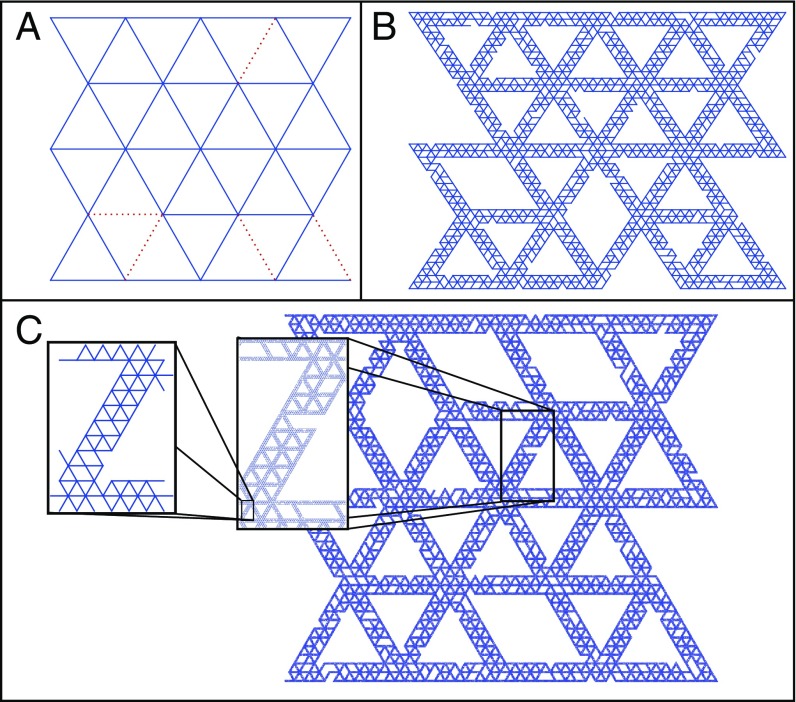
We create hierarchical triangular lattices through an iterative process, in which the bonds of the lattice at one length scale are in turn crafted from smaller-scale triangular lattices. In principle, this process can be iterated ad infinitum; in practice, if the number of large bonds is held constant, the total number of nodes grows geometrically with the number of hierarchical levels. This places a practical limit on the number of levels that can be considered in simulations. We have numerically constructed and simulated lattices with one, two, and three levels of structural hierarchy (Fig. 1); bond portion is independently set on each hierarchical level.
Fig. 1.
(A) A dilute triangular lattice with one level of structure. Missing bonds are indicated with dashed lines. (B) A two-level triangular lattice, with each bond replaced by a smaller-scale, dilute triangular lattice. (C) An extension to three levels of structural hierarchy.
Hierarchical Model of Stiffness
We propose to model the stiffness of our networks by generalizing the scaling law proposed by Garboczi and Thorpe (10), for a single-scale, diluted triangular lattice. Garboczi and Thorpe (10) found that, for the ball-and-spring case, components of the elastic constant tensor should have the form
| [1] |
where is the minimum bond portion necessary for marginal stiffness, and is the value of the modulus when the network is fully connected. We propose to describe large-scale bonds using an effective stiffness with the form of Eq. 1 and introduce and , the portion of bonds retained on the large and small scales. Because of the finite width of large-scale bonds, we do not assume that the minimum small- or large-scale bond portions needed for marginal stiffness are . The stiffness of a large-scale bond will be inherited from its small-scale structure, such that the overall stiffness scales as
| [2] |
where is tensile stiffness and is the stiffness for a network fully connected on all scales. Now consider a general network with distinct length scales. The stiffness of bonds at scale will be inherited from the structure at scale , so that
| [3] |
The overall stiffness for some general number levels of structural hierarchy will then be
| [4] |
Simulation Procedure
Networks were simulated in 2D, with ball-and-spring interactions between pairs of connected nodes. To measure stiffness, nodes along the tops of networks were uniformly displaced along the vertical direction, after which the y coordinates of the top and bottom nodes were fixed. Next, the x coordinates of top and bottom nodes, as well as both coordinates of all other points, were relaxed using the fast inertial relaxation engine algorithm (28). Each bond is modeled as a fiber that resists stretching with a 1D stretching modulus, . Let each bond be a parametric curve , where ranges from 0 to the length of the bond, and let be a field describing the displacement of a point on the bond in the strained state. The energy for a bond of length is described by the functional
| [5] |
A uniform, 1D stretching modulus of unity was assigned to each bond, and nodes were relaxed until the rms residual force in the network was less than in units of stretching modulus in the case of the one- and two-level networks and in units of stretching modulus for three-level networks. We extract the tensile stiffness by fitting plots of elastic energy vs. strain to parabolas.
Simulation Results
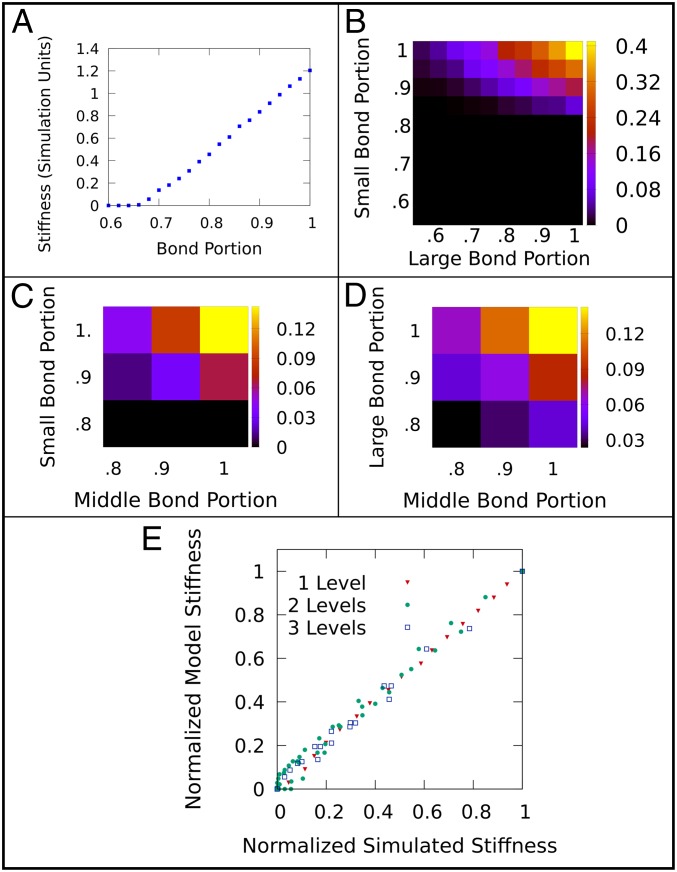
We simulated one-, two-, and three-level lattices with a wide range of bond portions and measured their stiffness (Fig. 2). Large-scale bonds are 10 small-scale bonds long and contain three rows of small-scale bonds. Before comparing to our model, we must identify each critical bond portion for one-, two-, and three-level lattices.
Fig. 2.
(A) Simulated stiffness plotted vs. bond portion for one length scale. (B) Heat map of simulated stiffness as a function of small and large bond portion for a two-level network. Stiffness is plotted in simulation units, as indicated in the key. (C) Heat map of simulated stiffness for a slice in bond portion space for three-level networks with full connectivity on the largest scale. Stiffness is plotted in simulation units, as indicated in the key. (D) Heat map of simulated stiffness for a slice in bond portion space for three-level networks with full connectivity on the smallest scale. Stiffness is plotted in simulation units, as indicated in the key. (E) Stiffness normalized by maximum stiffness for networks with one, two, and three levels of structure.
For the one-level lattice, we recover the expected linear relationship between stiffness and bond portion (Fig. 2A). We find the critical bond portion to be 0.670 (SI Appendix).
For the two-level lattice, we find that stiffness increases as either the small or the large bond portion is increased (Fig. 2B). To determine the threshold bond portion for the large (small) scale, we find those points in bond portion space for which the small (large) bond portion is equal to 1. We then fit a plot of large (small) bond portion vs. stiffness and fit these data to an equation of the form Eq. 1. We find that the critical bond portions are 0.83 and 0.58 for the small and large scales, respectively (SI Appendix). Initially, it may be surprising to find that the critical bond portion on the large scale is less than 0.67. However, as large-scale bonds are endowed with a finer-scale structure, they acquire an effective bending stiffness, rather than being governed strictly by harmonic, central force interactions. Notably, networks with bonds possessing bending stiffness have been demonstrated to be rigid even below the classic isostatic point (14, 15). Thus, it is crucial that be directly measured and not assumed from Maxwell counting.
For the three-level lattice, we find that stiffness increases as any bond portion is increased (Fig. 2 C and D and SI Appendix). Following an approach similar to that used for the two-level lattice, we find the critical bond portions are 0.83, 0.72, and 0.62 for the small, medium, and large scales, respectively.
To test our model, we compare the stiffness obtained from simulations to the stiffness predicted by our model. In Fig. 2E, we plot stiffness values from our model against stiffness values from simulations for one, two, and three levels. For ease of comparison, stiffness values for an -level network are normalized to the maximum attainable stiffness for an -level network. Each point in the plot compares a simulation result with its model prediction counterpart. There are no free parameters in our model; we normalize stiffnesses by the maximum values for one-, two-, or three-level lattices and use the identified critical bond portions. We find remarkable agreement; linear fits between simulated and predicted quantities have values and slopes, respectively, of 0.983 and 1.003 for one level, 0.989 and 1.01 for two levels, 0.988 and 0.98 for three levels, and 0.993 and 1 for all data combined.
Experimental Prospects
While the attempt to manipulate actual tissues as we have manipulated our networks may prove elusive, we envision, as an accessible proof-of-principle experiment, cutting networks described in this work from elastic sheets. Such sheets would ideally have an out-of-plane thickness that is large in comparison with the in-plane width of bonds, to frustrate buckling, as described in ref. 29. Existing work has also established tapering of bonds at junctions as a useful technique for controlling the ratio of bending to stretching stiffness (30).
Model Applicability
We next performed a series of tests and analyses to determine how broadly our model can be applied. As a first step, we varied the size and aspect ratio of large-scale bonds. Up to this point we have shown results for networks in which large-scale bonds are 10 small-scale bonds long and contain three rows of small-scale bonds; however, we have also considered two-level networks whose large-scale bonds are 20 small-scale bonds long and contain five rows of small-scale bonds. In both cases, we find similarly strong agreement. More details are provided in SI Appendix.
While these two systems captured the same phenomena, we cannot test all possible configurations and must instead carefully consider the circumstances under which our model is applicable. Large-scale bonds can be too wide or too narrow. If the width of large-scale bonds is too great in comparison with their length, then the resulting structure will effectively be a single-scale lattice with a regular array of small perforations. If large-scale bonds contain two or fewer rows of small-scale bonds, the coordination number of the network with all bonds present will be four, making the network susceptible to immediate loss of stiffness upon dilution of bonds. Moreover, stretching of networks will lead to transverse contraction, producing a lateral load on horizontal bonds. If large-scale bonds buckle, our picture of a primarily stretching-stabilized network will be invalid. We here propose methods to identify the range of aspect ratios for which our model should be expected to apply.
We performed tensile simulations to determine the change in the displacement field of a single-scale lattice under tension due to the presence of a hole of width . Note that a two-scale lattice with bonds of length and width , in units of small-scale bond length, may be viewed as a single-scale network with a periodic array of equilateral triangular holes with side length . We argue that our model, with a separation of scales, is appropriate when the change to the displacement field is of the order of the applied strain times the small-scale bond length over a length equal to or greater than the separation between neighboring holes. This analysis, explained in detail in SI Appendix, yields
| [6] |
Large-scale bonds may also be too narrow and thus buckle. Using the theory of slender rods as discussed in ref. 31, we find buckling will become a concern when the ratio of length to width is of the order of the square root of the applied strain (); thus, to avoid buckling, the ratio of length to width must satisfy
| [7] |
In our case, large-scale bonds have length 10 and width , in units of small-scale bond length, for an aspect ratio of 5.77. This is above the limit separating hierarchical networks from perforated sheets (3.73). Further, as strains used in simulations do not exceed , this aspect ratio is below the limit at which buckling may be expected to occur (14.1). This places us comfortably within the constraints on the applicability of our model discussed above.
Thus, our proposed formulation for stiffness of a hierarchical lattice is expected to apply to a wide range of networks. Crucially, we observe that it accurately describes 1-, 2-, and 3-level lattices (Fig. 2E), suggesting that the smallest length scale can always be replaced by a network of even smaller bonds, and the stiffness will remain the product of all excess bond portions. This general formulation facilitates investigation of highly hierarchical (e.g., 10-level) lattices.
Structural Error Tolerance
Now that we have obtained a general relationship for the stiffness of a hierarchical structure, we are primed to consider the possibility of random errors in assembly, a likely complication in any real assembly process. We focus in particular on how stochastic deviation from a targeted set of connectivities (on all relevant length scales) results in a deviation in network stiffness. We consider two distinct regimes. In the first case, we consider a target point near the isosurface along which stiffness vanishes. In the second one, we consider a target point in bond portion space far from both the limiting case of full connectivity on any length scale and the contour of vanishing stiffness.
We first consider target points in bond portion space corresponding to marginally stiff structures. Such points are of interest, as highly compliant materials have critical biological roles (1) and are attracting increasing attention for applications (11). Such materials typically must not be susceptible to critical transitions in their elastic moduli as a result of small fluctuations in their fine-scale structure.
We use a numerical technique to estimate the distribution of stiffness arising from random errors. First, we choose a nominal point in bond portion space, such that a certain target stiffness is achieved, and the excess bond portion is the same for each length scale. We next add Gaussian random noise to the bond portion on each length scale. The stiffness of the resulting “noisy” point is then estimated by means of an interpolated function computed from simulation data for one- and two-level lattices and a fitted model for three-level lattices (Fig. 2); for lattices with more than three levels, we use Eq. 4. This process is carried out for 50,000 trials.
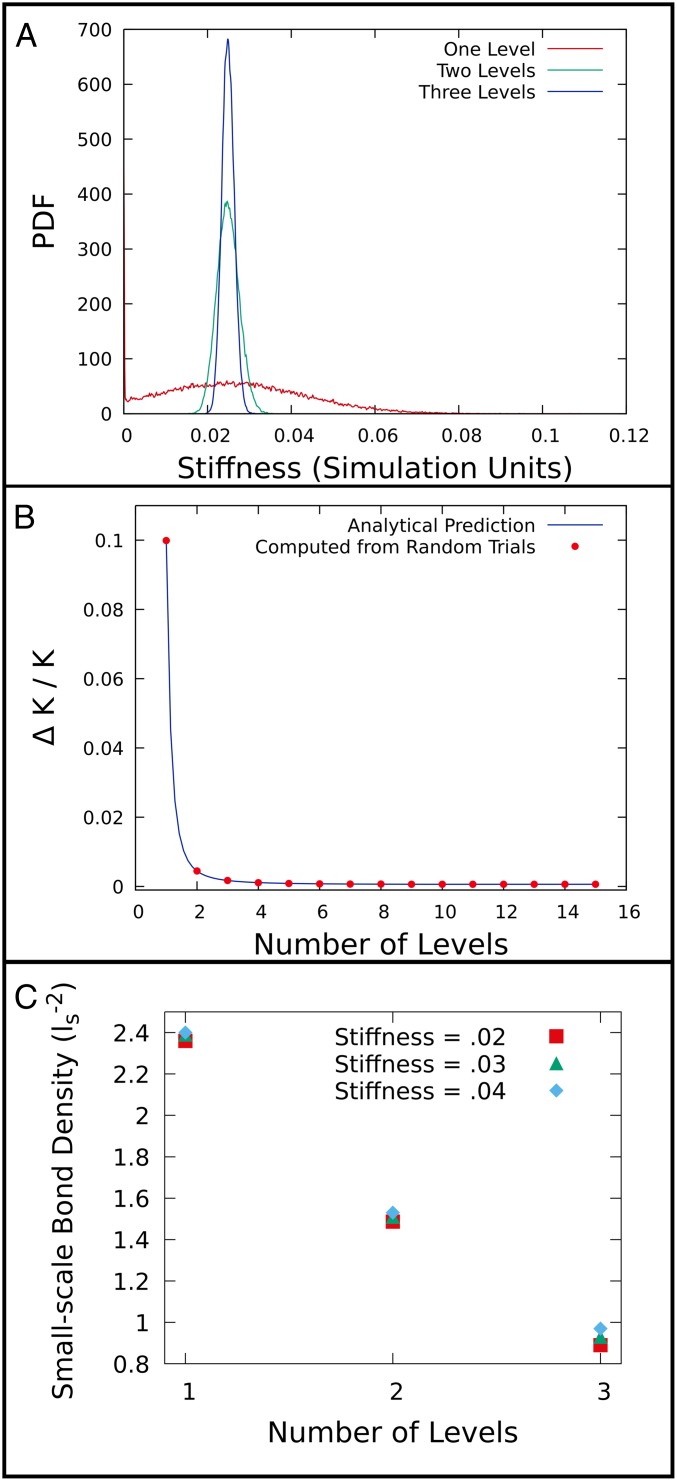
Strikingly, the variance in stiffness is greatly reduced with each additional level of hierarchical structure (Fig. 3A). Further, the stiffness distribution for the single-level network exhibits a large peak at zero, which is absent in the stiffness distribution of the two- and three-level networks. Thus, despite having opportunities for errors at three separate stages of assembly, the three-level network is more reliably constructed than the one-level network and can more reliably avoid stochastically generating a floppy network.
Fig. 3.
(A) Stiffness probability distribution functions (PDFs) estimated from histogram data for networks with one, two, and three levels of structural hierarchy. Points in 1D, 2D, and 3D bond portion with the same minute nominal stiffness were chosen, and Gaussian random variables were added to each bond portion. Note the spike in the PDF for the one-level network at zero stiffness. In this case, we consider a nominal stiffness of 0.025 and Gaussian random noise for each bond portion with zero mean and a SD of 0.005. Other cases are addressed in SI Appendix. (B) Relative error in stiffness vs. levels of hierarchy is plotted for , . As additional levels of structural hierarchy are added, the relative error in the tensile stiffness decreases precipitously at first, and the effect saturates at a certain number of levels. Provided the assumptions leading to Eq. 9 hold, our analytical theory and numerical approach are in close agreement (). Here, the product of excess bond portions is 0.001, and the noise has amplitude 0.0001 on each scale. (C) The number of all small-scale bonds in a network, divided by the area enclosed by the outer perimeter of the network, is shown vs. number of hierarchical levels for stiffness values of 0.02, 0.03, and 0.04, in units of stretching modulus over small-scale bond length. Networks were chosen to have the same bond portion on all three levels. In each case, increasing hierarchy leads to markedly lower density of small-scale bonds, attesting to the ability of hierarchy to confer both robustness and efficiency.
Next, we seek a general understanding of target points far from any boundary in bond portion space (see SI Appendix for detailed derivation). For levels, there is a nominal excess bond portion, , for each level; we consider identically and independently distributed deviations from the nominal bond portions according to a normal distribution with zero mean and standard deviation (SD) . Referring to Eq. 4, we define the reduced stiffness:
| [8] |
With this definition we find the expected deviation in the stiffness of a network with hierarchical levels to be
| [9] |
where the approximation holds when . For a target , this functional form predicts the optimal number of levels to be
| [10] |
where “” denotes the floor.
To test our analytical result, we again use the above numerical approach to calculate SD in stiffness for networks with 1–15 hierarchical levels. For lattices with more than 3 levels, we use Eq. 4 to estimate the stiffness of the resulting noisy point. We find very good agreement between the numerically generated data and our analytical prediction ( for the case shown in Fig. 3B).
The above derivations were performed assuming identically and independently distributed random errors in bond portion; however, the results presented above do not strictly require such stringent conditions. Similar robustness against fluctuation in stiffness can occur for error rates that vary on different scales and for distributions of random errors in which errors in bond portion on different length scales are correlated (see SI Appendix for an in-depth treatment).
Interestingly, investigating networks with different error rate distributions allows us to identify a useful heuristic. Consider a two-level network with the same error rate in its large-scale bond portion as a one-level network. The two-level network will have a smaller variance in its stiffness than the one-level network as long as its small bond portion error rate is less than three times larger than its large bond portion error rate (note that this argument also works if the roles of the small and large scales are swapped; see SI Appendix for details).
These observations do not simply arise from the generic properties of random variables. Although a relation of the form Eq. 9 with would hold for a general product of random numbers, the dependence upon of the divisor indicates a scaling of the relative fluctuation specific to a stiffness with the functional form of Eq. 4. To produce a supple solid of a particular stiffness, the portion of bonds that must be retained on each scale to achieve this stiffness increases with increasing hierarchy. This can ensure that the connectivity of the network on each scale exceeds the threshold connectivity by an amount large in comparison with the the typical fluctuations in connectivity.
We further find that hierarchical structures offer superior economy of material, in keeping with previous studies (16). To quantify this benefit, we define the number density, , of small-scale bonds as follows: Let be the length of a single small-scale bond, denote the total number of small-scale bonds, and denote the area enclosed by the perimeter of the network. Then, is given by
| [11] |
and has units of . We regard small-scale bonds as the fundamental structural units of a network, such that provides a measure of the number of connections per unit area needed to achieve a target set of mechanical properties. To compare one-, two-, and three-level networks, we chose target stiffness values and identified the points in bond portion space with equal bond portions on each level corresponding to these stiffness values. We then estimated accompanying values of for networks with these bond portions by interpolation. For each stiffness chosen, there was a sharp decline in the number of bonds per unit area needed with increasing numbers of hierarchical levels. This result emphasizes that hierarchical materials’ greater error tolerance is a benefit inherent to their geometry, rather than deriving from redundancy. A nested, modular assembly process thus enables the creation of a structure that is both more reliable and more frugal.
Discussion and Conclusion
Contrary to expectation, the elastic moduli of hierarchical materials are more reliably controlled than the elastic moduli of materials with one relevant length scale. Thus, with respect to random errors, it is easier to make hierarchical structures than to make single–length-scale structures. This finding may have wide-ranging implications for evolutionary biology and materials design.
It may seem that evolving progressively larger, more complex bodies is accompanied, and impeded, by a growing assortment of mechanical challenges. To the contrary, this work provides evidence that adding hierarchical complexity can actually reduce stochastic variation in material properties. This effect decreases the need for coevolving error-correcting mechanisms, thus facilitating the evolution of new traits that are “good enough” for an organism to survive.
Upon successful assembly, structural hierarchy is known to endow materials with a host of desirable properties that are unattainable with single–length-scale structures. Our finding that hierarchy also reduces susceptibility to stochastic errors suggests that bottom–up production processes for synthetic hierarchical materials may produce finished products which perform as intended despite modest, but discernible errors.
While we have explicitly addressed 2D, lattice-based networks in this study, we anticipate that our findings will have broader applicability. Feng et al. (13) have demonstrated that an analogous model to Eq. 1 describes the dependence of the elastic moduli of a dilute face-centered cubic lattice in 3D on the portion of bonds retained. Moreover, connectivity has been established as a useful control parameter for predicting the mechanical properties of many disordered solids, such as jammed packings of hard (32, 33) and soft (34) particles and semiflexible biopolymer networks (21).
More generally, we have broadened the scope of Maxwell’s visionary means of characterizing frames to account for structural hierarchy, facilitating the understanding of cases in which it has proved difficult to relate materials’ emergent properties to their fine-scale structure. While recent computational advancements have enabled study of biological macromolecules over experimentally relevant time scales (35), comprehensive understanding at the level of an organism demands a coarse-graining procedure for which our model may offer a useful road map. A generalized counting heuristic may also offer a means of expediting feasible, yet cumbersome calculations in materials design. Hierarchical materials necessarily have many design attributes, but our accessible model may considerably narrow the search of parameter space needed to reach a goal.
Materials and Methods
Network Creation.
First, a large-scale lattice is created and diluted. Dilution begins with the shuffling of all bonds, after which a random minimum spanning tree is created using Kruskal’s algorithm. Bonds are then drawn at random from those bonds not used to create the spanning tree and added to the network until the desired bond portion is reached. Next, a small-scale lattice is overlaid such that the large-scale bond length is an integer multiple of the small-scale bond length, and the position of each large-scale node coincides with the position of a small-scale node. Each small-scale bond lying within a large-scale bond is retained, after which small-scale bonds are diluted to the desired bond portion. Small-scale bond dilution is carried out in such a way that a system-spanning contact network remains, no large-scale bond is severed, and all adjacent large-scale bonds remain connected. In each successive iteration, a smaller scale may then be introduced, with the previously smallest scale taking the role of the large scale. This process is described schematically in Fig. 1.
Finding the Critical Bond Portions.
Critical bond portions for a network with levels are computed from simulation data for each level by choosing all points in bond portion space for which the network is fully connected on the other levels, and the stiffness is nonzero. For each level, we then fit a plot of stiffness vs. the bond portion of interest to an equation of the form Eq. 1. For three-level networks, data for stiffness vs. bond portion for three-level networks were fitted to a line of the form
| [12] |
and the x intercept of this line was taken to be the critical bond portion. For more details, please see SI Appendix.
Supplementary Material
Acknowledgments
The authors thank Alberto Fernandez-Nieves and Zeb Rocklin for helpful comments. The authors acknowledge funding from Georgia Institute of Technology’s Soft Matter Incubator and the NSF through Grant IOS-1656549.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1813801116/-/DCSupplemental.
References
- 1.Fratzl P, Weinkamer R. Nature’s hierarchical materials. Prog Mater Sci. 2007;52:1263–1334. [Google Scholar]
- 2.Meyers MA, McKittrick J, Chen P. Structural biological materials: Critical mechanics-materials connections. Science. 2013;339:773–780. doi: 10.1126/science.1220854. [DOI] [PubMed] [Google Scholar]
- 3.Launey ME, Buehler M, Ritchie RO. On the mechanistic origins of toughness in bone. Annu Rev Mater Res. 2010;40:25–53. [Google Scholar]
- 4.Yao H, Gao H. Multi-scale cohesive laws in hierarchical materials. Int J Solids Struct. 2007;44:8177–8193. [Google Scholar]
- 5.Sen D, Buehler MJ. Structural hierarchies define toughness and defect-tolerance despite simple and mechanically inferior brittle building blocks. Sci Rep. 2011;1:35. doi: 10.1038/srep00035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hormoz S, Brenner MP. Design principles for self-assembly with short-range interactions. Proc Natl Acad Sci USA. 2011;108:5193–5198. doi: 10.1073/pnas.1014094108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Zeravcic Z, Manoharan VN, Brenner MP. Size limits of self-assembled colloidal structures made using specific interactions. Proc Natl Acad Sci USA. 2014;111:15918–15923. doi: 10.1073/pnas.1411765111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Harris J, Böhm C, Wolf S. Universal structure motifs in biominerals: A lesson from nature for the efficient design of bioinspired functional materials. Interface Focus. 2017;7:20160120. doi: 10.1098/rsfs.2016.0120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Dunlop JWC, Fratzl P. Biological composites. Annu Rev Mater Res. 2010;40:1–24. [Google Scholar]
- 10.Garboczi EJ, Thorpe MF. Effective-medium theory of percolation on central force elastic networks. II. Further results. Phys Rev B. 1985;31:7276–7281. doi: 10.1103/physrevb.31.7276. [DOI] [PubMed] [Google Scholar]
- 11.Wegst U, Bai H, Saiz E, Tomsia A, Ritchie R. Bioinspired structural materials. Nat Mater. 2015;14:23–26. doi: 10.1038/nmat4089. [DOI] [PubMed] [Google Scholar]
- 12.Maxwell JC. On the calculation of the equilibrium and stiffness of frames. Philos Mag. 1864;27:294–299. [Google Scholar]
- 13.Feng S, Thorpe MF, Garboczi E. Effective-medium theory of percolation on central-froce elastic networks. Phys Rev B. 1985;31:276–280. doi: 10.1103/physrevb.31.276. [DOI] [PubMed] [Google Scholar]
- 14.Das M, MacKintosh FC, Levine AJ. Effective medium theory of semiflexible filamentous networks. Phys Rev Lett. 2007;99:038101. doi: 10.1103/PhysRevLett.99.038101. [DOI] [PubMed] [Google Scholar]
- 15.Mao X, Stenull O, Lubensky TC. Effective-medium theory of a filamentous triangular lattice. Phys Rev E. 2013;87:042601. doi: 10.1103/PhysRevE.87.042601. [DOI] [PubMed] [Google Scholar]
- 16.Lakes R. Materials with structural hierarchy. Nature. 1993;361:511–515. [Google Scholar]
- 17.Wilhelm J, Frey E. Elasticity of stiff polymer networks. Phys Rev Lett. 2003;91:108103. doi: 10.1103/PhysRevLett.91.108103. [DOI] [PubMed] [Google Scholar]
- 18.Feng J, Levine H, Mao X, Sander L. Nonlinear elasticity of disordered fiber networks. Soft Matter. 2016;12:1419–1424. doi: 10.1039/c5sm01856k. [DOI] [PubMed] [Google Scholar]
- 19.Head DA, Levine AJ, MacKintosh FC. Distinct regimes of elastic response and deformation modes of cross-linked cytoskeletal and semiflexible polymer networks. Phys Rev E. 2003;68:061907. doi: 10.1103/PhysRevE.68.061907. [DOI] [PubMed] [Google Scholar]
- 20.Lindstrom SB, Vader DA, Kulachenko A, Weitz DA. Biopolymer network geometries: Characterization, regeneration, and elastic properties. Phys Rev E. 2010;82:051905. doi: 10.1103/PhysRevE.82.051905. [DOI] [PubMed] [Google Scholar]
- 21.Broedersz CP, MacKintosh FC. Modeling semiflexible polymer networks. Rev Mod Phys. 2014;86:995–1036. [Google Scholar]
- 22.Amuasi HE, Heussingler C, Vink RLC, Zippelius A. Nonlinear and heterogeneous elasticity of multiply crosslinked biopolymer networks. New J Phys. 2015;17:083035. [Google Scholar]
- 23.Licup AJ, et al. Stress controls the mechanics of collagen networks. Proc Natl Acad Sci USA. 2015;112:9573–9578. doi: 10.1073/pnas.1504258112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lenz M, Witten TA. Geometrical frustration yields fibre formation in self-assembly. Nat Phys. 2017;13:1100–1105. doi: 10.1038/nphys4184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Broedersz CP, Mao X, Lubensky TC, MacKintosh FC. Criticality and isostaticity in fibre networks. Nat Phys. 2011;7:983–985. [Google Scholar]
- 26.Zhang T, Schwarz JM, Das M. Mechanics of anisotropic spring networks. Phys Rev E. 2014;90:062139. doi: 10.1103/PhysRevE.90.062139. [DOI] [PubMed] [Google Scholar]
- 27.Lubensky TC, Kane CL, Mao X, Souslov A, Sun K. Phonons and elasticity in critically coordinated lattices. Rep Prog Phys. 2015;78:073901. doi: 10.1088/0034-4885/78/7/073901. [DOI] [PubMed] [Google Scholar]
- 28.Bitzek E, Koskinen P, Gaehler F, Moseler M, Gumbsch P. Structural relaxation made simple. Phys Rev Lett. 2006;97:170201. doi: 10.1103/PhysRevLett.97.170201. [DOI] [PubMed] [Google Scholar]
- 29.Coulais C, Sabbadini A, Vink F, van Hecke M. Multi-step self-guided pathways for shape-changing metamaterials. Nature. 2018;561:512–515. doi: 10.1038/s41586-018-0541-0. [DOI] [PubMed] [Google Scholar]
- 30.Rocks JW, et al. Designing allostery-inspired response in mechanical networks. Proc Natl Acad Sci USA. 2017;114:2520–2525. doi: 10.1073/pnas.1612139114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Landau LD, Lifshitz EM. Theory of Elasticity. 2nd Ed. Pergamon Press; Oxford: 2012. pp. 97–98. [Google Scholar]
- 32.Liu A, Nagel S. The jamming transition and the marginally jammed solid. Annu Rev Condens Matter Phys. 2010;1:347–369. [Google Scholar]
- 33.O’Hern C, Liu A, Nagel S. Jamming at zero temperature and zero applied stress: The epitome of disorder. Phys Rev E Stat Nonlin Soft Matter Phys. 2003;68:011306. doi: 10.1103/PhysRevE.68.011306. [DOI] [PubMed] [Google Scholar]
- 34.van Hecke M. Jamming of soft particles: Geometry, mechanics, scaling and isostaticity. J Phys Condens Matter. 2010;22:033101. doi: 10.1088/0953-8984/22/3/033101. [DOI] [PubMed] [Google Scholar]
- 35.Phillips JC, et al. Scalable molecular dynamics with NAMD. J Comput Chem. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.