A stochastic analysis of first-order reaction networks

Abstract

A stochastic model for a general system of first-order reactions in which each reaction may be either a conversion reaction or a catalytic reaction is derived. The governing master equation is formulated in a manner that explicitly separates the effects of network topology from other aspects, and the evolution equations for the first two moments are derived. We find the surprising, and apparently unknown, result that the time evolution of the second moments can be represented explicitly in terms of the eigenvalues and projections of the matrix that governs the evolution of the means. The model is used to analyze the effects of network topology and the reaction type on the moments of the probability distribution. In particular, it is shown that for an open system of first-order conversion reactions, the distribution of all the system components is a Poisson distribution at steady state. Two different measures of the noise have been used previously, and it is shown that different qualitative and quantitative conclusions can result, depending on which measure is used. The effect of catalytic reactions on the variance of the system components is also analyzed, and the master equation for a coupled system of first-order reactions and diffusion is derived.

1. Introduction

Understanding the time-dependent behavior of a system of interacting species is necessary for analyzing numerous problems, including the dynamics of chemical reactions, gene expression profiles, signal transduction, and other biochemical processes. Many of these systems are characterized by low numbers of interacting species: for example, gene transcription involves interactions between 1–3 promoter elements, 10–20 polymerase holoenzyme units, 10–20 molecules of repressor proteins, 3000 RNA polymerase molecules, and ca. 1000 ribosomes (Kuthan, 2001). Since interactions at the molecular level are inherently stochastic there is an inherent “irreproducibility” in these dynamics, which has been demonstrated experimentally for single cell gene expression events (Ozbudak et al., 2002; Spudich and Koshland, 1976; Levsky and Singer, 2003). A major unsolved problem is to understand how the interplay between the nature of the individual steps and the connectivity or topology of the entire network affects the dynamics of the system, irrespective of whether a deterministic or a stochastic description is the most appropriate. In this paper we formulate and analyze the master equation that governs the time evolution of the number density of species that participate in a network of first-order reactions. The network may comprise both conversion reactions of the form A → B, in which one component is converted to another, and catalytic reactions of the form $\varphi \stackrel{B}{\to }A$, in which the rate of formation of a particular component depends on the concentration of the other (the catalyst), but the concentration of the catalyst is unchanged by the reaction. This is the first step in the analysis of higher-order reaction networks.

There are numerous examples of first-order reaction networks that involve a small number of molecules, for which this analysis is directly applicable. Transcription and translation have been modeled as first-order catalytic reactions (Thattai and van Oudenaarden, 2001). The evolution of the surface morphology during epitaxial growth involves the nucleation and growth of atomic islands, and these processes may be described by first-order adsorption and desorption reactions coupled with diffusion along the surface. Proteins exist in various conformational states, and the reversible transitions between states may be described as a first-order conversion processes (Mayor et al., 2003). Fluctuating protein conformations are important in the movement of small molecules through proteins such as myoglobin; hence it is important to understand the distribution of these states (Iorio et al., 1991; Austin et al., 1975). RNA also exists in several conformations, and the transitions between various folding states follow first-order kinetics (Bokinsky et al., 2003).

One of the earliest investigations of stochastic effects in reactions is by Delbruck (1940), who studied the distribution of the number of molecules for a single reacting species in an auto-catalytic one-component system, and derived an expression for the variance as a function of the mean and initial values of the mean and variance. Siegert (1949) derived the probability distribution for the momentum of a gas as a function of time, and formulated the first stochastic model of a system of first-order conversion reactions, using a matrix formulation to derive the master equation for first and second-order reaction networks. He also outlined the generating function approach for characterizing the distribution of the network components. The system he studied is equivalent to a closed system (i.e., the total mass is conserved) of conversion reactions. He proved that one eigenvalue of the matrix of reaction rate constants is zero and the rest are real and negative. Unfortunately, this important work was largely overlooked in the field of stochastic chemical reaction kinetics for more than a decade, until Krieger and Gans (1960) re-derived these results formulating the problem as a chemical reaction network problem.

Klein (1956) used Siegert’s results to analyze the Ehrenfest Urn problem, in which balls are transferred between two urns with given probabilities. Klein treated the number of balls in an urn as a measure of the occupancy of an energy state, and calculated the probability of the number of balls in an urn as a function of the transition probability and the initial distribution. This can be interpreted as a closed system with one first-order reversible reaction, with the urns characterizing the reactant and product of the reversible reaction. He showed that the stationary distribution is independent of the initial distribution, but assumed that transitions occur at fixed intervals of time. Kendall (1948) formulated a master equation for a birth–death process starting with one ancestor and computed the extinction time of the population. He also discussed the case of time-dependent rate constants. Birth processes may be modeled as auto-catalytic production reactions and death as a first-order degradation reaction. Bartholomay (1958) was apparently the first to derive the master equation for a unimolecular reaction allowing steps at random times, and he used the generating function approach to calculate the mean and standard deviation of the number of reactant molecules. He also showed that the stochastic process is “consistent in the mean” with the deterministic description, and later showed how to calculate the observed first-order rate constant (Bartholomay, 1959).

At about the same time Montroll and Shuler (1958) modeled chemical decomposition as a random walk between reflecting and absorbing barriers, and Kim (1958) computed mean first passage times for general first-order stochastic processes. Shuler (1960) analyzed the relaxation kinetics of a multi-state system, which is equivalent to a closed first-order system of reversible conversion reactions, and pointed out that there was no single characteristic “relaxation time”. He re-derived the property that such a system cannot exhibit any form of periodic behavior, and showed that the relaxation of any one of the moments of the distribution does not convey any information about the relaxation of the distribution.

A systematic analysis of a closed system of first-order conversion reactions was done by Krieger and Gans (1960), who showed that a multinomial distribution characterizes the temporal evolution of the system. This generalized results of Montroll and Shuler, who had proved that the end states were characterized by a multinomial distribution. Gans extended this and previous analyses of closed systems to an open system of first-order conversion reactions (Gans, 1960). Following Krieger and Gans (1960), he derived a condition for the eigenvalues associated with the evolution of the mean to be negative (α_ii ≤ ∑_j α_ij), but did not analyze the evolution of the higher moments or their relation to the mean. McQuarrie (1963) derived solutions for the mean and variance of closed systems with reactions of the type as A → B, A ⇌ B, and A → B, A → C. He also discussed the use of a cumulant generating function as a method of generating lower-order moments. Gani (1965) formulated a birth–death model for bacteriophage kinetics that was similar to an open system model for one species. Fredrickson (1966) computed the stochastic mean and variance for the concentrations in a closed cyclic ternary system, and again showed that these moments do not oscillate in time. Darvey and Staff (1966) presented the first derivation for the time-dependent mean and variance of all the species present in a closed system with first-order conversion reactions. They derived an expression for the moment generating function for a case when only one species is present initially, and showed that the first moment is the same as the solution of the corresponding deterministic system, but did not analyze the evolution of the variance.

Other processes such as the waiting times in a queue have also been analyzed, and some of these results can be applied to reaction networks. Kelly (1979) considered reversible queuing processes in which “customers” enter a queue either with a defined distribution from a source or defined transition probabilities from other queues. Every queue has a finite number of “servers”, with a characteristic waiting time associated with the service. The entry into a queue from another queue can be regarded as a conversion process, entry from the source is equivalent to production from the source, and service can be thought of as a degradation process that removes customers from the queue. A pure conversion process can be considered as an infinite server queue (see Appendix), but catalytic reactions have no apparent analog in queuing theory. Kelly considered several aspects of the process, such as whether it was open or closed, and the nature of the connections between the queues (linear vs. looped), and derived the important result that the equilibrium distribution for a closed system tends to the equilibrium distribution for an open system when the number of individuals is large. We show later that this result is also true for open and closed systems where all the reactions are first-order conversion reactions. For a particular class of open migration processes in which the transition probabilities between queues (or colonies) is proportional to the number of individuals in the colony, Kelly proved that the number of individuals in each queue has a Poisson distribution, assuming that the inflow of individuals to queues (or colonies) from outside the system (source) are Poisson processes. If one considers each colony to be a distinct species, the open migration process is equivalent to an open conversion reaction system, and the proof for the stationary distribution of the number of individuals in each colony stated by Kelly (1979) may be considered as another proof for the distribution of the number of each species in an open conversion network that we derive later. Branching Markov processes also give rise to problems with a similar mathematical structure to that in kinetics (Harris, 1963; Athreya and Ney, 1972). Athreya and Ney (1972) considered continuous-time, multi-type branching processes initiated by one particle of each type and derived first and second moments of the distribution of the number of particles of each type. Catalytic reactions can be interpreted as the death of a particle with two offspring, one identical to the original and the other possibly different, but a systematic analysis of the effect of catalytic reactions on the resulting probability distribution has not been reported earlier to our knowledge.

Thattai and van Oudenaarden (2001) presented the first analysis of a system of first-order catalytic reactions. They formulated a procedure for deriving the master equation for such systems, similar to the general procedure given in Gardiner (1983). They incorporated a negative feedback regulation of some reactions (production from source), and derived the steady-state means and covariances for a system of catalytic transformations with one source term, and first-order degradation of all the species. Recently, Brown (2003) derived the probability of the number of forward and reverse steps in a reversible first-order conversion reaction in which the transition probabilities are time-dependent.

A major objective of many of the analyses treating biological systems is prediction of the stochastic variations or noise of the concentrations. Two measures of the noise have been used in the past. Until recently the standard measure was the coefficient of variation (CV), defined as the standard deviation divided by the mean (Delbruck, 1940; Singer, 1953; Kepler and Elston, 2001), or its square. The CV is used as a measure of noise in McQuarrie et al. (1964), Darvey et al. (1966), Laurenzi (2000), Elowitz et al. (2002) and Swain et al. (2002), while the Fano factor $\mathcal{F}$, defined as the variance divided by the mean, was introduced by Thattai and van Oudenaarden (2001), and used in Blake et al. (2003) and Ozbudak et al. (2002). It has been shown that the use of different measures of noise may lead to different conclusions concerning the importance of noise in the underlying process (Swain et al., 2002).

Our objectives here are (i) to introduce a derivation of the master equation that clarifies the separate roles of reaction rates and network topology in the master equation, (ii) to develop a unified treatment of first-order networks, including the evolution of both the mean and the variance of any species and (iii) to understand the effect of network topology on the stochastic fluctuations in specified components. We compare the noise in the amount of a species as measured by the Fano factor or the coefficient of variation for both conversion and catalytic reactions, as well as for species in open and closed systems. We also demonstrate through simple examples the utility of this framework in the analysis of the effect of reaction network topology on the variation of the number of molecules of each network component. All of the preceding analyses can be treated as special cases of the general framework that we develop here. No previous analysis of first-order reaction systems has to our knowledge considered a system consisting of both catalytic and conversion reactions, nor has a systematic comparison of the stochastic behavior of conversion and catalytic systems been made.

2. Formulation of the master equation

We first derive the master equation for a general system of reactions to provide a framework for the analysis of reactions of arbitrary order. We then focus on first-order reactions and specialize the general result for a very large class of first-order processes.

2.1. The master equation for a general system of reactions

We begin with some background on a general deterministic description of reacting systems, and then derive the master equation for an arbitrary network of reacting species. The abstract formulation is presented in brief here and follows that given elsewhere (Othmer, 1979, 1981).

Suppose that the reacting mixture contains the set $\mathcal{M}$ of s chemical species ${\mathcal{M}}_i$ that participate in a total of r reactions. Let v_ij be the stoichiometric coefficient of the ith species in the jth reaction. The v_ij are non-negative integers that represent the normalized molar proportions of the species in a reaction. Each reaction is written in the form

$$\sum _i^{reac.}{v}_{ij}^{reac}{\mathcal{M}}_i=\sum _i^{prod}{v}_{ij}^{prod}{\mathcal{M}}_{i}j=1,\dots ,r,$$ (1)

where the sums are over reactants and products, respectively in the jth reaction. In this formulation, the forward and reverse reaction of a reversible pair are considered separately as two irreversible reactions.

For each reaction, once the reactants and products are specified, the significant entities so far as the network topology is concerned are not the species themselves, but rather the linear combinations of species that appear as reactants or products in the various elementary steps. Following Horn and Jackson (1972), these linear combinations of species will be called complexes. A species may also be a complex (as is the case for first-order reactions). We assume that changes in temperature, pressure and volume V of the mixture during reaction are negligible. Thus the state of the system is specified by the concentration vector c = (c₁, … , c_s)^T, where c_i is the non-negative concentration of species ${\mathcal{M}}_i$ measured in moles/liter.

Let $\widehat{\mathcal{M}}$ be the set of linear combinations with integral coefficients of the species, and let $\mathcal{C}=\{C(1),\dots ,C(p)\}$ be a set of complexes. A reaction network consists of the triple $\{\mathcal{M},\widehat{\mathcal{M}},\mathcal{C}\}$, together with a stoichiometric function $\widehat{v}:\widehat{\mathcal{M}}\to \mathcal{C}$ and a binary relation $R\subset \mathcal{C}\times \mathcal{C}$. The function $\widehat{v}$, which identifies a linear combination of species as a complex is onto, and the relation R has the properties (i) (C(i), C(j)) ∈ R if and only if there exists one and only one reaction of the form C(i) → C(j), (ii) for every i there is a j ≠ i such that (C(i), C(j)) ∈ R, (iii) (C(i), C(i)) ∉ R. Thus every complex is related to at least one other complex and the trivial reaction C(i) → C(i) that produces no change is not admitted. Therefore R is never reflexive and in general it is neither symmetric nor transitive.

The relation on $\mathcal{C}$ gives rise is to a directed graph $\mathcal{G}$ in the following way. Each complex identified with a vertex V_k in $\mathcal{G}$ and a directed edge E_ℓ is introduced into $\mathcal{G}$ for each reaction. Each edge carries a non-negative weight ${\widehat{\mathcal{R}}}_{\mathcal{l}}(c)$ given by the intrinsic rate of the corresponding reaction. $\mathcal{G}$ provides a concise representation of the reaction network.

The topology of $\mathcal{G}$ is in turn represented in its vertex–edge incidence matrix $\mathcal{E}$, which is defined as follows.

$${\mathcal{E}}_{i\mathcal{l}}=\{\begin{array}{ll}+1\hfill & \text{ if }{E}_{\mathcal{l}}\text{ is incident at }{V}_i\text{ and is directed toward it }\hfill \\ -1\hfill & \text{ if }{E}_{\mathcal{l}}\text{ is incident at }{V}_i\text{ and is directed away from it }\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}$$ (2)

If there are r reactions on $\mathcal{C}$, then $\mathcal{E}$ has p rows and r columns and every column has exactly one +1 and one −1. The rate ${\widehat{\mathcal{R}}}_{\mathcal{l}}(C)$ of an elementary reaction C(j) → C(k) is generally not a function of C(j), but of the concentration or activity of the individual species in the complex. Once the complexes and reactions are fixed, the stoichiometry of the complexes is specified unambiguously, and we let ν denote the s × p matrix whose jth column encodes the stoichiometric amounts of the species in the jth complex. Then the temporal evolution of the composition of a reacting mixture is governed by

$$\frac{\text{d}c}{\text{d}t}=v\mathcal{E}\widehat{\mathcal{R}}(c),$$ (3)

where the columns of ν are given by the columns of ν^reac and ν^prod, and the initial condition is c(0) = c₀. It follows from (2) that the columns of the product $v\mathcal{E}$ are the stoichiometric vectors of reactions written according to the standard convention. When the reactions are first-order this deterministic equation also governs the evolution of the mean in the Markov process description discussed later.

A special but important class of rate functions is that in which the rate of the ℓth reaction can be written as

$${\widehat{\mathcal{R}}}_{\mathcal{l}}(c)=k_{\mathcal{l}}{R}_j(c)$$ (4)

for every reaction that involves the jth complex as the reactant. This includes ideal mass action rate laws, in which the rate is proportional to the product of the concentrations of the species in the reactant complex, each concentration raised to a power equal to the stoichiometric coefficient of the corresponding species in the complex. In that case

$$R_j=\prod _{i=1}^s{\left(c_i\right)}^{v_{ij}}.$$ (5)

For mass-action kinetics (4) implies that

$$\widehat{\mathcal{R}}(c)=KR(c)$$ (6)

where K is an r × p matrix with $k_{{\mathcal{l}}_j}>0$ if and only if the ℓth edge leaves the jth vertex, and $k_{{\mathcal{l}}_j}=0$ otherwise. The topology of the underlying graph $\mathcal{G}$ enters into K as follows. Define the exit matrix ${\mathcal{E}}_o$ of $\mathcal{G}$ by replacing all 1’s in $\mathcal{E}$ by zeros, and changing the sign of the resulting matrix. Let $\widehat{K}$ be the r × r diagonal matrix with the kℓ’s, ℓ = 1, … , r, along the diagonal. Then it is easy to see that $K=\widehat{K}{\mathcal{E}}_0^T$ and therefore

$$\frac{\text{d}c}{\text{d}t}=v\mathcal{E}KR(c)=v\mathcal{E}\widehat{K}{\mathcal{E}}_o^{T}R(c).$$ (7)

It follows from the definitions that (i) the (p, q)th entry, p ≠ q, of $\mathcal{E}\widehat{K}{\mathcal{E}}_0^T$ is nonzero (and positive) if and only if there is a directed edge $(q,p)\in \mathcal{G}$, (ii) each diagonal entry of $\mathcal{E}\widehat{K}{\mathcal{E}}_0^T$ is minus the sum of the k’s for all edges that leave the jth vertex, and (iii) the columns of $\mathcal{E}{\widehat{K}}_0^T$ all sum to zero, and so the rank of $\mathcal{E}\widehat{K}{\mathcal{E}}_0^T$ is ≤ p − 1. When all complexes are species and all reactions are first-order, ν = I for a closed system and ν = [I | 0] for an open system, where I is the s × s identity matrix and 0 is the zero vector, and the right-hand side reduces to the usual form Kc for a suitably-defined matrix K. In the following section we will treat the stochastic analysis of first-order systems in detail.

As it stands, (5) includes all reacting species, but those whose concentration is constant on the time scale of interest can be deleted from each of the complexes in which it appears and its concentration or mole fraction can be absorbed into the rate constant of that reaction in which it participates as reactant.³ As a result of these deletions, it will appear that reactions which involve constant species do not necessarily conserve mass. Furthermore, some complexes may not comprise any time-dependent species; these will be called zero or null complexes. Each null complex gives rise to a column of zeros in ν and the rate of any reaction in which the reactant complex is a null complex is usually constant. For instance, any transport reaction of the form ${\mathcal{M}}^0\to {\mathcal{M}}_i$ introduces a null complex and the corresponding flux of ${\mathcal{M}}_i$ represents a constant input to the reaction network, provided that rate of the transport step does not depend on the concentration of a time-dependent species. Of course, a constant species that appears in a complex which also contains a variable species likewise represents an input to the network, and to distinguish these from inputs due to null complexes, the former are called implicit inputs and the latter are called explicit inputs.

An alternate description of the deterministic dynamics is obtained by introducing an extent for each reaction and expressing composition changes in terms of extents. It follows from (3) that the composition changes due to reaction lie in a coset by c₀ of the range of $v\mathcal{E}$, and this coset is called the reaction simplex (Othmer, 1979, 1981). Therefore, by choosing coordinates in the simplex, the composition changes can be expressed in terms of an extent for each reaction as follows

$$c=c_0+v\mathcal{E}\xi .$$ (8)

If the reactions are all independent, i.e. if the rank of $v\mathcal{E}$ is r, it follows from (3) and (8) that

$$\frac{\text{d}\xi }{\text{d}t}=\widehat{\mathcal{R}}\left(c_0+v\mathcal{E}\xi \right),$$ (9)

but in general we can only conclude that

$$\frac{\text{d}\xi }{\text{d}t}=\widehat{\mathcal{R}}\left(c_0+v\mathcal{E}\xi \right)+\sum _k{\gamma }_k{\mathcal{N}}_k,$$ (10)

where $\left\{{\mathcal{N}}_k\right\}$ is a basis for the null space of $v\mathcal{E}$. The γ_k can be chosen so as to remove all dependent steps, in particular, those that arise from cycles in the graph.

We can also describe the evolution in terms of the number of molecules present for each species. Let n = (n₁, n₂, … , n_s) denote the discrete composition vector whose ith component n_i is the number of molecules of species ${\mathcal{M}}_i$ present in the volume V. This is the discrete version of the composition vector c, and they are related by $n={\mathcal{N}}_{A}Vc$, where ${\mathcal{N}}_A$ is Avogadro’s number. From (3) we obtain the deterministic evolution for n as

$$\frac{\text{d}n}{\text{d}t}=v\mathcal{E}\tilde{\mathcal{R}}(n)$$ (11)

where $\tilde{\mathcal{R}}(n)\equiv {\mathcal{N}}_{A}V\widehat{\mathcal{R}}\left(n/{\mathcal{N}}_{A}V\right)$. In particular, for mass-action kinetics

$$\begin{gathered} {\tilde{\mathcal{R}}}_{\mathcal{l}}(n)={\mathcal{N}}_{A}V{k}_{\mathcal{l}}{\mathcal{R}}_j\left(n/{\mathcal{N}}_{A}V\right)={\mathcal{N}}_{A}V{k}_{\mathcal{l}}\prod _{i=1}^s{\left(\frac{n_i}{{\mathcal{N}}_{A}V}\right)}^{v_{ij}} \\ =\frac{k_{\mathcal{l}}}{{\left({\mathcal{N}}_{A}V\right)}^{\sum _i{v}_{ij}-1}}\prod _{i=1}^s{\left(n_i\right)}^{v_{i\mathcal{l}}}={\widehat{k}}_{\mathcal{l}}\prod _{i=1}^s{\left(n_i\right)}^{v_{ij}}. \end{gathered}$$ (12)

The number of molecules can be expressed in terms of the integer extents of each reaction as

$$n=n_0+v\mathcal{E}\eta ,$$ (13)

and it follows from (11) that

$$\frac{\text{d}\eta }{\text{d}t}=\tilde{\mathcal{R}}\left(n_0+v\mathcal{E}\eta \right)+\sum _k{\gamma }_k{\mathcal{N}}_k.$$ (14)

The description in terms of the number of molecules present assumes that there are sufficient numbers present so that we can assume they vary continuously in time, but the same assumption is needed for (4).

2.2. The stochastic description

The first level of stochastic description is to consider an ensemble of deterministic systems that differ in the initial condition. Let P(c, t) be the probability that the state of the system is c; then the evolution of P is governed by

$$\frac{\partial P}{\partial t}+\sum _{i=1}^s\frac{\partial }{\partial c_i}\left({(v\mathcal{E}\widehat{R}(c))}_{i}P\right)=0$$ (15)

subject to the initial condition P(c, 0) = P₀. The characteristic equations for this hyperbolic equation are precisely the evolution equations given at (3).

At the next level of description the numbers of the individual components are followed in time and the reactions are modeled as a continuous-time Markov jump process. Let N_i(t) be a random variable that represents the number of molecules of species ${\mathcal{M}}_i$ at time t, and let N denote the vector of N_i s. Further, let P(n, t) be the joint probability that N(t) = n, i.e., N₁ = n₁, N₂ = n₂, …,N_s = n_s. Clearly the state of the system at any time is now a point in ${\mathcal{Z}}_0^s$, where ${\mathcal{Z}}_0$ is the set of non-negative integers. Formally the master equation that governs the evolution of P is

$$\frac{\text{d}}{\text{d}t}P(n,t)=\sum _{m\in \mathcal{S}(n)}\mathcal{R}(m,n)\cdot P(m,t)-\sum _{m\in \mathcal{T}(n)}R(n,m)\cdot P(n,t)$$ (16)

where $\mathcal{R}(m,n)$ is the probability per unit time of a transition from state m to state n, $\mathcal{R}(n,m)$ is the probability per unit time of a transition from state n to state m, $\mathcal{S}(n)$ is the set of all states that can terminate at n after one reaction step, and $\mathcal{T}(n)$ is the set of all states reachable from n in one step of the feasible reactions. The notation is meant to suggest the ‘source’ and ‘target’ states at n; one could also call $\mathcal{S}(n)$ the predecessors of state n and $\mathcal{T}(n)$ the successors of state n. The predecessor states must be non-negative for production reactions and positive for conversion, degradation and catalytic reactions. Similar bounds on the target states are naturally enforced by zero rates of reaction when the reactants are absent.

The sets $\mathcal{S}(n)$ and $\mathcal{T}(n)$ are easily determined using the underlying graph structure. It follows from the definition of ν and $\mathcal{E}$ that the ℓth reaction C(j) → C(k) induces a change $\mathrm{\Delta }{n}^{(\mathcal{l})}=v{\mathcal{E}}_{(\mathcal{l})}$ in the number of molecules of all species after one step of the reaction, where subscript ℓ denotes the ℓth column. Therefore the state $m=n-\nu {\mathcal{E}}_{(\mathcal{l})}$ is a source or predecessor to n under one step of the ℓth reaction. Similarly, states of the form $m=n+\nu {\mathcal{E}}_{(\mathcal{l})}$ are reachable from n in one step of the ℓth reaction.⁴ Once the graph of the network and the stoichiometry are fixed, we can sum over reactions rather than sources and targets, and consequently the master equation takes the form

$$\frac{\text{d}}{\text{d}t}P(n,t)=\sum _{\mathcal{l}}{\mathcal{R}}_{\mathcal{l}}\left(n-v{\mathcal{E}}_{(\mathcal{l})}\right)\cdot P\left(n-v{\mathcal{E}}_{(\mathcal{l})},t\right)-\sum _{\mathcal{l}}{\mathcal{R}}_{\mathcal{l}}(n)\cdot P(n,t).$$ (17)

However, the transition probabilities ${\mathcal{R}}_{\mathcal{l}}(n)$ are not simply the macroscopic rates $\widehat{\mathcal{P}}$ if the reactions are second-order (or higher), because as Gillespie (1976) and others have noted, combinatorial effects may play a significant role when the number of molecules is small. Hereafter we restrict attention to mass-action kinetics, and we suppose that the ℓth reaction involves conversion of the jth to the kth complex: C(j) → C(k). Then using the notation of Gillespie (1976), we can write,

$${\mathcal{R}}_{\mathcal{l}}=c_{\mathcal{l}}{h}_{j(\mathcal{l})}(n)$$ (18)

where c_ℓ is the probability per unit time that the molecular species in the jth complex react, j(ℓ) denotes the reactant complex for the ℓth reaction, and h_j(ℓ)(n) is the number of independent combinations of the molecular components in this complex. Thus

$$c_{\mathcal{l}}=\frac{k_{\mathcal{l}}}{{\left({\mathcal{N}}_{A}V\right)}^{\sum _i{v}_{ij(\mathcal{l})}-1}}={\widehat{k}}_{\mathcal{l}}$$ (19)

and

$$h_{j(\mathcal{l})}=\prod _i\left(\begin{array}{c}{n}_i\\ v_{ij(\mathcal{l})}\end{array}\right).$$ (20)

In the definition of h we use the standard convention that $\left(\begin{array}{l}n\hfill \\ 0\hfill \end{array}\right)=1$.

We can write the master equation in terms of integer extents in the form

$$\begin{gathered} \frac{\text{d}}{\text{d}t}\tilde{\mathcal{P}}(\eta ,t)=\sum _{\mathcal{l}}{\mathcal{R}}_{\mathcal{l}}\left(n_0+v\mathcal{E}\eta -v{\mathcal{E}}_{(\mathcal{l})}\right)\cdot P\left(n_0+v\mathcal{E}\eta -v{\mathcal{E}}_{(\mathcal{l})},t\right)-\sum _{\mathcal{l}}{\mathcal{R}}_{\mathcal{l}}\left(n_0+v\mathcal{E}\eta \right)\cdot P\left(n_0+v\mathcal{E}\eta ,t\right) \\ =\sum _{\mathcal{l}}{\tilde{\mathcal{R}}}_{\mathcal{l}}\left(\eta -v{\mathcal{E}}_{(\mathcal{l})}\right)\cdot \tilde{P}\left(\eta -v{\mathcal{E}}_{(\mathcal{l})},t\right)-\sum _{\mathcal{l}}{\tilde{\mathcal{R}}}_{\mathcal{l}}(\eta )\cdot \tilde{P}(\eta ,t). \end{gathered}$$ (21)

Moments of this equation or of (16) can be used to obtain the evolution equations for average extents and from this, the equations for the average change in the numbers. Only in the linear case is the right-hand side of the equation for the first moment the deterministic rate, as is shown in the following subsection. Others have derived a similar master equation for reacting systems, without the explicit inclusion of the underlying graph-theoretic structure (Gardiner, 1983; Rao and Arkin, 2003).

2.3. The master equation for general system of first-order reactions

The stochastic analysis of first-order reaction networks can be done in essentially complete generality, and in this section we analyze all cases in which every reactant and product complex is a species. We thereby exclude only those first-order splitting reactions of the type ${\mathcal{M}}_i\to {\mathcal{M}}_j+{\mathcal{M}}_k$. Our aim is to separate the effects of various types of reactions (catalytic, conversion) on the distribution of the chemical species, and to this end we divide the set of all reactions, represented by the directed edges E_ℓ, ℓ = 1, 2, …,r into four subsets corresponding to the following reactions: production from a constant source (which in fact is a zero-order step), degradation, conversion to another species, and production catalyzed by another species. These four types are summarized in Table 1. The first type represents an explicit input to the system, whereas the last type represents an implicit input.

Table 1.

The four classes of first-order reactions considered in the stochastic model

Label	Type of reaction	Reaction	Rate
I	Production from a source	$\varphi \to {\mathcal{M}}_i$	$k_i^S$
II	Degradation	${\mathcal{M}}_i\to \varphi$	$k_i^d{n}_i$
III	Conversion	${\mathcal{M}}_j\to {\mathcal{M}}_i$	$k_{ij}^{con}{n}_j$
IV	Catalytic production from source	$\varphi \stackrel{{\mathcal{M}}_j}{\to }{\mathcal{M}}_i$	$k_{ij}^{cat}{n}_j$

Every species ${\mathcal{M}}_i$ can be produced from a source at a specific rate $k_i^s$, and every species can be removed by degradation at a rate proportional to its concentration, with rate constant given by $k_i^d$. Each species may participate in two other types of first-order reactions: conversion reactions, in which species ${\mathcal{M}}_i$ is converted to species ${\mathcal{M}}_j$ at a rate proportional to its concentration, and catalytic reactions, in which species ${\mathcal{M}}_i$ catalyzes the formation of species ${\mathcal{M}}_j$ from a source, but is itself unchanged during the process. The first-order rate constant for the conversion reaction of species ${\mathcal{M}}_i$ to species ${\mathcal{M}}_j$ is denoted by $k_{ji}^{con}$, and the first-order rate constant for the catalytic production of species ${\mathcal{M}}_j$, with species ${\mathcal{M}}_i$ catalyzing the reaction, is denoted by $k_{ji}^{cat}$. Thus there are s uncatalyzed source reactions, s first-order decay reactions, s(s − 1) conversion and s² catalytic reactions, for a total of up to 2s² + s reactions.

Since all reactant and product complexes are species, the stoichiometric matrix is

$$v=\left[\text{I}|\mathbf{0}\right]$$

if at least one reaction of type I, II, or IV is present, and

$$v=[\text{I}]$$

if the system is closed. The corresponding incidence matrices for the different types are equally simple, and if we order the types as in Table 1, then $\mathcal{E}$ can be written as follows.

$$\mathcal{E}=\left[\frac{\text{I}}{-{\mathbf{1}}^T}\left|\frac{-\text{I}}{{\mathbf{1}}^T}\right|{\mathcal{E}}^{con}|\frac{\text{I}}{-{\mathbf{1}}^T}\right]$$ (22)

where 1^T = (1, 1, …,1), I is the identity matrix of the appropriate dimension, and ${\mathcal{E}}^{con}$ is the incidence matrix for the conversion network. Thus the stoichiometry of the reactions and the topology of the network are easily encoded in ν and $\mathcal{E}$, respectively.

It follows easily that the deterministic equations for the first-order reaction network can be written as

$$\frac{\text{d}c}{\text{d}t}=K^s\mathbf{1}-K^{d}c+K^{cat}c+K^{con}c$$ (23)

where $K^s=diag\left\{k_i^s\right\}$, $K^d=diag\left\{k_i^d\right\}$, $K_{ij}^{cat}=k_{ij}^{cat}$ and K^con is defined as follows.

$$K_{ij}^{con}=\{\begin{array}{ll}{k}_{ij}^{con}\hfill & \text{ if }i\ne j\hfill \\ -\sum _k^{\prime }{k}_{kj}^{con}\hfill & \text{ if }i=j.\hfill \end{array}$$

It is clear that type I and IV reactions induce an increase of 1 in the number of species i without other changes, type IV induces a decrease of one in i alone, and type III induces a decrease of one in j and an increase of 1 in i. Therefore, for reactions of type I the predecessor state to state n is ${\mathcal{S}}_i^{-1}n\equiv \left(n_1,n_2,\dots ,n_i-1,\dots ,n_s\right)$, and the successor state is ${\mathcal{S}}_i^{+1}n\equiv \left(n_1,n_2,\dots ,n_i+1,\dots ,n_s\right)$, where ${\mathcal{S}}_i^k$ is the shift operator that increases the ith component of n by an integer amount k. For degradation of ${\mathcal{M}}_i$, the predecessor state is ${\mathcal{S}}_i^{+1}n$ and the successor state is ${\mathcal{S}}_i^{-1}n$. In type III reactions the predecessor state is ${\mathcal{S}}_i^{-1}{\mathcal{S}}_j^{+1}n$ and the successor state is ${\mathcal{S}}_i^{+1}{\mathcal{S}}_j^{-1}n$. Finally, for the catalytic reaction the predecessor and successor states are ${\mathcal{S}}_i^{-1}n$ and ${\mathcal{S}}_i^{+1}n$, respectively. Using these, the master equation for the first-order reaction network can be written as follows (here and hereafter we drop the explicit time dependence in P(., .)).

$$\frac{\text{d}P\left(n\right)}{\text{d}t}=\sum _{i=1}^s\left[K_{ii}^s\left({\mathcal{S}}_i^{-1}-1\right)P\left(n\right)+\sum _{j=1}^s(K_{ij}^{con}\left({\mathcal{S}}_i^{-1}{\mathcal{S}}_j^{+1}\right)+K_{ij}^{cat}\left({\mathcal{S}}_i^{-1}-1\right)-K_{ij}^d\left({\mathcal{S}}_i^{+1}-1\right))\left(n_{j}P\left(n\right)\right)\right]$$ (24)

where $S_i^k\left(n_{i}P(n)\right)=S_i^k{n}_i\cdot P\left(S_i^{k}n\right)$.

3. Evolution equations for the mean and variance

The master equation derived in the previous section cannot be solved analytically except for a small number of specific simple systems. Usually the objective of a stochastic analysis is to calculate the moments of the distribution of the number of reactant molecules. There are several ways in which evolution equations for the moments of the distribution function can be obtained. One is to multiply both sides of the master equation by n_i, n_i n_j, n_i n_j n_k etc and sum over all possible values of n. Alternatively, one can use the moment generating function (MGF) approach, which is what we use here to calculate the mean and variance for all the reactants in an arbitrary network. The advantage of the MGF approach is that it allows us to get an analytical solution for the MGF of purely conversion systems, thus enabling the calculation of the probability distribution function for the distribution of each reactant in such systems.

Let z ≡ (z₁, … , z_s) where z_i ∈ [0, 1]; then the MGF is defined as

$$G(z,t)=\sum _{n_i=0}^{\infty }{z}_1^{n_1}\cdots z_s^{n_s}P(n).$$

It follows that G(z, t)|_{z = 1} = 1. The first and second moments can be obtained through successive derivatives of the MGF evaluated after setting all z_i to one.

$$M_k(t)=\frac{\partial G(z,t)}{\partial z_k}{|}_{z=1}\equiv G_k(z,t){|}_{z=1}=E\left[N_k\right]$$

$$V_{lk}(t)=G_{lk}(z,t){|}_{z=1}=\{\begin{array}{ll}E\left[N_l{N}_k\right]\hfill & \text{ if }l\ne k\hfill \\ \left(E\left[N_k^2\right]-E\left[N_k\right]\right)\hfill & \text{ if }l=k\hfill \end{array}$$

where E[ ] denotes the expectation of the quantity in the square brackets, and for any combination of indices we define

$$G_{ijk\dots ,t}=\frac{\partial }{\partial z_i}\frac{\partial }{\partial z_j}\frac{\partial }{\partial z_k}\cdots \frac{\partial }{\partial t}G.$$

The probability distribution of the number of molecules of the ith species (N_i) at steady state can be derived from the MGF. Differentiating the MGF k times w.r.t. z_i, we get

$$\frac{{\partial }^{k}G(z,t)}{\partial z_i^k}=\sum _{n_i=k}^{\infty }\frac{n_i!}{\left(n_i-k\right)!}{z}_i^{n_i-k}\sum _{n_j=0,j\ne i}^{\infty }{z}_1^{n_1}\cdots z_{i-1}^{n_{i-1}}{z}_{i+1}^{n_{i+1}}\cdots z_s^{n_s}P(n,t),$$

and therefore

$$\frac{{\partial }^{k}G(z,t)}{\partial z_i^k}{|}_{z_i=0,z_j=1,j\ne i}=k!\sum _{n_j,j\ne i}{P}_{n_1,\dots ,n_{i-1},k,n_{i+1},\dots ,n_s}(t)=k!P_{N_i}(k,t),$$

where $P_{N_i}(k,t)$ represents the marginal probability density function of N_i. Therefore

$$P_{N_i}(k,t)=\frac{1}{k!}\frac{{\partial }^{k}G(z,t)}{\partial z_i^k}{|}_{z_i=0,z_j=1,j\ne i}.$$

These relationships are valid for the MGF corresponding to any reaction network. In the case of a system of reactions with first-order kinetics we obtain the partial differential equation for the MGF as

$$G_t=\sum _{i=1}^s\left(z_i-1\right)\left(K_{ii}^{s}G+\sum _{j=1}^s\left(K_{ij}^{con}+K_{ij}^{cat}{z}_j-K_{ij}^d\right)G_j\right).$$ (25)

Alternatively, and somewhat more directly, one can use a backward equation to obtain Eq. (25) (see the Appendix).

For simple network topologies with a small number of nodes, (25) can be solved analytically to get the complete characterization of the evolution of the probability distribution function P(n). We shall later derive such expressions for systems where only conversion reactions occur. However, this is not feasible for an arbitrary network structure, and therefore we first outline the procedure for obtaining the evolution equation for the moments, and then we focus on the first two moments. Differentiating Eq. (25) with respect to z_k, we obtain

$$G_{k,t}=\sum _{i=1}^s\left(z_i-1\right)\left(K_{ii}^s{G}_k+\sum _{j=1}^s\left(K_{ij}^{con}+K_{ij}^{cat}{z}_j-K_{ij}^d\right)G_{jk}+K_{ik}^{cat}{G}_k\right)+\left(K_{kk}^{s}G+\sum _{j=1}^s\left(K_{kj}^{con}+K_{kj}^{cat}{z}_j-K_{kj}^d\right)G_j\right).$$ (26)

Therefore the evolution equation for the mean of the kth component is

$$E{\left[N_k\right]}^{\prime }=\sum _{j=1}^S\left(K_{kj}^{con}+K_{kj}^{cat}-K_{kj}^d\right)E\left[N_j\right]+K_{kk}^s$$

or in matrix form

$$M(t{)}^{\prime }=\left(K^{con}+K^{cat}-K^d\right)M(t)+K^s\mathbf{1}$$ (27)

$$=\mathcal{K}M(t)+K^s\mathbf{1},$$ (28)

where M(t) = [E[N₁(t)], …,E[N_s(t)]]^T and $\mathcal{K}$ is defined by the second equality. From this one sees that the explicit inputs contained in the last term serve as a nonhomogeneous forcing term for the evolution of the mean. This equation is identical to Eq. (23) given earlier for the evolution of the deterministic first-order system. Therefore a general stochastic system of first-order interactions is “consistent in the mean” with the corresponding system for systems comprised of catalytic and conversion reactions, as is well known (Darvey and Staff, 1966).

Higher moments of the distribution are obtained by successive differentiation of (25). For the second moment we obtain

$$G_{lk,t}=\sum _{i=1}^s\left(z_i-1\right)\left(K_{ii}^s{G}_{kl}+\sum _{j=1}^S\left(K_{ij}^{con}+K_{ij}^{cat}{z}_j-K_{ij}^d\right)G_{jkl}+K_{ik}^{cat}{G}_{kl}+K_{il}^{cat}{G}_{lk}\right)+\left(K_{ll}^s{G}_k+\sum _{j=1}^s\left(K_{lj}^{con}+K_{lj}^{cat}{z}_j-K_{lj}^d\right)G_{jk}+K_{lk}^{cat}{G}_k\right)+\left(K_{kk}^s{G}_l+\sum _{j=1}^s\left(K_{kj}^{con}+K_{kj}^{cat}{z}_j-K_{kj}^d\right)G_{jl}+K_{kl}^{cat}{G}_l\right).$$

Thus the matrix containing the second-order moments can be written as

$$V(t{)}^{\prime }=\mathcal{K}V(t)+{(\mathcal{K}V(t))}^T+\Gamma (t)+{\Gamma }^T(t)$$ (29)

where

$${\Gamma }_{ij}(t)\equiv \left(K_{ij}^{cat}+K_{ii}^s\right)M_j(t).$$

It is noteworthy that in this equation both the implicit and explicit inputs, as well as the mean, appear in the forcing term for the evolution of the second moments. In the equation for the mean the forcing is time-independent, but here the forcing is time-dependent via the appearance of the mean in this term. Later we will see how this time-dependence is filtered via the action of the kinetic matrix. The somewhat unusual structure on the right-hand side arises from the fact that V is a symmetric matrix, and thus the evolution equation for it must be symmetric as well.

The equations for the mean and the second moments can be integrated to get the first two moments of the distribution. Thus we now have an algorithm to compute both the steady-state and time-dependent behavior of the mean and variance of every species in a general first-order network. Next we analyze this behavior in detail.

3.1. The steady-state and time-dependent solution for the mean

The steady-state solution M^s for the mean is the solution of

$$\mathcal{K}{M}^s=-K^s\mathbf{1}=-k^s$$ (30)

where $k^s=\left(k_1^s,\dots ,k_s^s\right)$. The nature of the reaction types and rates, as reflected in the spectral structure of $\mathcal{K}$, dictates the steady-state mean. In general, if $\mathcal{K}$ is singular then K^s1 must lie in the range of $\mathcal{K}$, and in particular, if there are no explicit inputs (K^s = 0) then $M_1^s$ is given by an eigenvector corresponding to a zero eigenvalue of $\mathcal{K}$. On the other hand, if degradation reactions are the only type present, and all species react, then $\mathcal{K}$ is nonsingular and $M_1^s=0$ is the only solution. This case is of little interest and will be excluded in what follows. Results concerning the localization of the spectrum of $\mathcal{K}$ are summarized in the following theorem.

Theorem 1. The eigenvalues of $\mathcal{K}$ have non-positive real parts if either of the following conditions hold.

1. The sum of the specific rates of formation for each species ${\mathcal{M}}_i$ by conversion and catalytic reactions does not exceed the sum of the specific rates of loss of ${\mathcal{M}}_i$ by conversion reactions and degradation (this implies that the column sums of $\mathcal{K}$ are non-positive).

2. The sum of the specific rates of formation catalyzed by each species ${\mathcal{M}}_i$ is less than or equal to the sum of the specific rates of degradation of that species.

Proof. The statement in (a) can be translated into the inequality

$$\sum _{j\ne i}{K}_{ij}^{con}+\sum _j{K}_{ij}^{cat}\le \sum _{j\ne i}{K}_{ji}^{con}+K_{ii}^d.$$ (31)

Since all the terms are non-negative, each of the terms on the left-hand side of the inequality is less than the right-hand side. In particular,

$$K_{ii}^{cat}\le \sum _{j\ne i}{K}_{ji}^{con}+K_{ii}^d,$$ (32)

and therefore

$${\mathcal{K}}_{ii}=K_{ii}^{con}+K_{ii}^{cat}-K_{ii}^d$$ (33)

$$=-\sum _{j\ne i}{K}_{ji}^{con}+K_{ii}^{cat}-K_{ii}^d$$ (34)

$$\le 0.$$ (35)

Using the definition of $K_{ii}^{con}$ and ${\mathcal{K}}_{ii}$, we can rewrite (31)

$$\sum _{j\ne i}\left[K_{ij}^{con}+K_{ij}^{cat}\right]\le -\left[K_{ii}^{con}+K_{ii}^{cat}-K_{ii}^d\right]$$ (36)

$$\sum _{j\ne i}{\mathcal{K}}_{ij}\le -{\mathcal{K}}_{ii}.$$ (37)

Now, bounds on the eigenvalues of $\mathcal{K}$ are given by the Levy–Hadamard theorem (Bodewig, 1959), which states that for every eigenvalue λ of $\mathcal{K}$,

$$\left|\mathrm{\lambda }-{\mathcal{K}}_{ii}\right|\le \sum _{j\ne i}\left|{\mathcal{K}}_{ij}\right|.$$

Since the off-diagonal elements of $\mathcal{K}$ are non-negative, this can be written as

$$\left|\mathrm{\lambda }-{\mathcal{K}}_{ii}\right|\le \sum _{j\ne i}{\mathcal{K}}_{ij}\le -{\mathcal{K}}_{ii}$$ (38)

where the second inequality follows from (37). Since ${\mathcal{K}}_{ii}<0$, it follows that Re(λ) ≤ 0, which proves (a).

To prove (b) we do a similar analysis, using the Levy–Hadamard theorem expressed in terms of a sum over the columns of $\mathcal{K}$. The constraint (b) can be written as

$$\sum _j{K}_{ji}^{cat}\le K_{ii}^d.$$

By reasoning similar to that used in the proof of (a), this constraint leads to the relations

$${\mathcal{K}}_{ii}\le 0$$

$$\sum _{j\ne i}{\mathcal{K}}_{ji}\le -{\mathcal{K}}_{ii}.$$

The Levy–Hadamard theorem applied to the columns of $\mathcal{K}$ states that

$$\left|\mathrm{\lambda }-{\mathcal{K}}_{ii}\right|\le \sum _{j\ne i}{\mathcal{K}}_{ji},$$

and the proof of (b) now follows as before. □

Remark 2. (i) A special case of (a) shows that in a closed system the eigenvalues have non-negative real parts, for in that case $K_{ii}^d=0$, $K_{ii}^{cat}=0$ and $K_{jj}^{con}=-{\sum }_{i\ne j}{K}_{ij}^{con}$. In fact in that case it is known that the eigenvalues are all real as well if the system satisfies detailed balance (Gans, 1960; Wei and Prater, 1962). If the underlying graph is strongly connected, then there is exactly one zero eigenvalue (Othmer, 1979).

The theorem gives conditions for the stability of an arbitrary first-order system of reactions in terms of the specific rates of the reactions. The first sufficient condition for stability is easily understood, as it is expected that for stability of a system the specific rates of production for all species should be less than the specific rates of degradation for every component of the system. The second criterion, which requires that the rate at which any component catalyzes the formation of other species is less than its degradation rate, is less immediately obvious. This is however an important relationship that can be used to guarantee stability of the mean of artificial transcriptional networks. In particular, once the inequality between the catalytic and degradation rates is satisfied, the system will be stable irrespective of the conversion reactions in the system, and may be used in the design of such networks. In the theory of branching processes condition b is equivalent to the assumption that the offspring distribution has mean less than or equal to 1.

Further information about the structure of the solution can be gotten from a spectral representation of $\mathcal{K}$. Hereafter we assume that $\mathcal{K}$ is semisimple (i.e., it has a complete set of eigenvectors), which is the generic case, and then it has the spectral representation

$$\mathcal{K}=\sum _i{\mathrm{\lambda }}_i{P}_i$$ (39)

where λ_i is the ith eigenvalue of $\mathcal{K}$ and P_i is the associated projection onto the span of the eigenvectors associated with λ_i. Since $\mathcal{K}$ is assumed to be semisimple, they have the property that ∑_i P_i = I.

The projections have the representation

$$P_i=\sum _{p=1}^{m_i}{\varphi }_p*\overline{{\varphi }_p^{*}}$$ (40)

where m_i is the algebraic multiplicity of the ith eigenvalue, ‘*’ represents the dyad product, and the ϕ’s and ϕ*’s are the corresponding eigenvectors and adjoint eigenvectors, defined via

$$\mathcal{K}{\varphi }_p={\mathrm{\lambda }}_i{\varphi }_p\text{for }p=1,m_i$$ (41)

$${\mathcal{K}}^T{\varphi }_p^{*}=\overline{{\mathrm{\lambda }}_i}{\varphi }_p^{*}\text{for }p=1,m_i.$$ (42)

They can be chosen to satisfy the orthogonality relations

$$\langle {\varphi }_p^{*},{\varphi }_q\rangle =\sum _{i=1}^{m_i}{\left(\overline{{\varphi }_p^{*}}\right)}_i{\left({\varphi }_q\right)}_i={\delta }_{pq}$$

and the projection of any vector is defined as

$$P_{i}u\equiv \left(\sum _{p=1}^{m_i}{\varphi }_p*\overline{{\varphi }_p^{*}}\right)u=\sum _{p=1}^{m_i}\langle {\varphi }_p^{*},u\rangle {\varphi }_p.$$

When $\mathcal{K}$ is invertible the steady-state mean can be written as

$$M_1^s=-\left(\sum _i\frac{P_i}{{\mathrm{\lambda }}_i}\right)k^s=-\sum _i\sum _{p=1}^{m_i}\frac{\langle {\varphi }_p^{*},k^s\rangle }{{\mathrm{\lambda }}_i}{\varphi }_p.$$ (43)

Thus in the nonsingular case the steady-state mean is the weighted sum of projections onto the ith eigenspace of $\mathcal{K}$, weighted by the corresponding eigenvalue. In particular, projections corresponding to eigenvalues of large modulus contribute less to the sum than those of small modulus. If $\mathcal{K}$ has a d-dimensional null space there are vectors {η₁, η₂, …,η_d} with the property that the functionals 〈η, M〉 are time-invariant, and this restricts the dynamics and steady-state solution to a lower-dimensional set. We leave the details of this case to the reader.

The transient solution of (28) is given by

$$\begin{gathered} M(t)={\text{e}}^{\mathcal{K}t}M(0)+\left({\int }_0^t{\text{e}}^{\mathcal{K}(t-\tau )}\text{d}\tau \right)K^s\mathbf{1} \\ =\left(\sum _i{\text{e}}^{{\mathrm{\lambda }}_{i}t}{P}_i\right)M(0)+\left({\int }_0^t\sum _i{\text{e}}^{{\mathrm{\lambda }}_i(t-\tau )}{P}_i\text{d}\tau \right)K^s\mathbf{1} \\ =\left(\sum _i{\text{e}}^{{\mathrm{\lambda }}_{i}t}{P}_i\right)M(0)-\sum _i\left(1-{\text{e}}^{{\mathrm{\lambda }}_{i}t}\right)\frac{P_i}{{\mathrm{\lambda }}_i}{K}^s\mathbf{1}. \end{gathered}$$ (44)

Since ${\text{e}}^{\mathcal{K}t}$ is non-negative, i.e. all its entries are non-negative, the solution remains nonnegative if M(0) is non-negative. Therefore if there are no eigenvalues with a positive real part the solution converges to a non-negative steady state. If the real part of all eigenvalues is negative, the solution is globally asymptotically stable. However these conditions do not guarantee that the solution has strictly positive components, i.e. that it does lie on the boundary of the positive ‘orthant’ of R^s. Under stronger hypotheses one can guarantee that the solution lies in the interior of the orthant, as shown in the following theorem.

Theorem 3. Suppose that the graph $\mathcal{G}$ associated with the reactions is strongly connected, and that the eigenvalues of $\mathcal{K}$ have negative real parts. Then ${\mathcal{K}}^{-1}<0$ and if there is at least one species produced by a source then the solution (30) is component-wise positive.

Proof. Notice that $\mathcal{K}$ is irreducible since the graph $\mathcal{G}$ is strongly connected. Write $\mathcal{K}={\mathcal{K}}^{+}-\kappa I$, where ${\mathcal{K}}^{+}\ge 0$ and κ > 0. Observe that ${\mathcal{K}}^{+}$ is also irreducible. Let

$$Q=-\mathcal{K}=\kappa I-{\mathcal{K}}^{+}.$$ (45)

Since the eigenvalues of $\mathcal{K}$ have negative real parts by hypothesis, the eigenvalues λ(Q) of Q have positive real parts and

$$\mathrm{\lambda }(Q)=\kappa -\mathrm{\lambda }\left({\mathcal{K}}^{+}\right).$$

Let $\rho \left({\mathcal{K}}^{+}\right)$ be the spectral radius of ${\mathcal{K}}^{+}$; then by Perron–Frobenius theorem $\rho \left({\mathcal{K}}^{+}\right)$ is a simple positive real eigenvalue of ${\mathcal{K}}^{+}$ and $\kappa -\rho \left({\mathcal{K}}^{+}\right)$ is an eigenvalue of Q. Thus $\kappa -\rho \left({\mathcal{K}}^{+}\right)>0$, i.e., $\rho \left({\mathcal{K}}^{+}\right)/\kappa <1$. Since $\rho \left({\mathcal{K}}^{+}\right)/\kappa <1$, the series

$$I+\frac{{\mathcal{K}}^{+}}{\kappa }+{\left(\frac{{\mathcal{K}}^{+}}{\kappa }\right)}^2+\cdots$$

converges, and so

$${\left(I-\frac{{\mathcal{K}}^{+}}{\kappa }\right)}^{-1}=\sum _{n=0}^{\infty }{\left(\frac{{\mathcal{K}}^{+}}{\kappa }\right)}^n.$$

Since $\left(I+\frac{{\mathcal{K}}^{+}}{\kappa }\right)$ is an s × s irreducible non-negative matrix with positive diagonal elements, it can be obtained that

$${\left(I+\frac{{\mathcal{K}}^{+}}{\kappa }\right)}^{s-1}>0,$$

which implies that

$$I+\frac{{\mathcal{K}}^{+}}{\kappa }+{\left(\frac{{\mathcal{K}}^{+}}{\kappa }\right)}^2+\cdots +{\left(\frac{{\mathcal{K}}^{+}}{\kappa }\right)}^{s-1}>0.$$

Therefore

$$\begin{gathered} Q^{-1}={\kappa }^{-1}{\left(I-\frac{{\mathcal{K}}^{+}}{\kappa }\right)}^{-1} \\ =\frac{1}{\kappa }\left(I+\frac{{\mathcal{K}}^{+}}{\kappa }+{\left(\frac{{\mathcal{K}}^{+}}{\kappa }\right)}^2+\cdots \right) \\ \text{> 0}. \end{gathered}$$

Thus Q⁻¹ > 0, so ${\mathcal{K}}^{-1}<0$ and finally, if there is at least one species produced by a source, i.e., $k_i^s>0$ for at least one i, then

$$M^s=-{\mathcal{K}}^{-1}{k}^s>0.$$

Next we analyze the evolution of the second moment, and find that the conditions (a) and (b) in Theorem 1 will also guarantee the stability of the second moments.

3.2. Evolution of the second moment

One can show (cf. Appendix) that the evolution equation for the second moment (29) can be written in the form⁵

$$\frac{\text{d}v}{\text{d}t}=\mathcal{V}v+\gamma$$ (46)

where

$$v(t)=col(V(t))\mathcal{V}=\left(\mathcal{K}\otimes I_n+I_n\otimes \mathcal{K}\right)\text{and}\gamma (t)=col\left(\Gamma (t)+\Gamma {(t)}^T\right).$$

Here the notation col(A) denotes a vector of length s² whose elements are the columns of A stacked in order (cf. Appendix). By the definition of the tensor product

$$\begin{gathered} \mathcal{V}\left({\varphi }_i\otimes {\varphi }_j\right)=\left(\mathcal{K}\otimes I_n+I_n\otimes \mathcal{K}\right)\left({\varphi }_i\otimes {\varphi }_j\right)=\mathcal{K}{\varphi }_i\otimes I_n{\varphi }_j+I_n{\varphi }_i\otimes \mathcal{K}{\varphi }_j \\ =\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)\left({\varphi }_i\otimes {\varphi }_j\right), \end{gathered}$$ (47)

and therefore ϕ_i ⊗ ϕ_j are the eigenvectors of $\mathcal{K}\otimes I_n+I_n\otimes \mathcal{K}$ corresponding to λ_i + λj. It follows that if P_i and P_j are the projections associated with the ith and jth eigenvalues, respectively, then

$$P_{ij}\equiv P_i\otimes P_j=\left(\sum _{p=1}^{m_i}{\varphi }_p*\overline{{\varphi }_p^{*}}\right)\otimes \left(\sum _{p=1}^{m_j}{\varphi }_p*\overline{{\varphi }_p^{*}}\right)$$ (48)

is the projection associated with λ_i + λ_j. Consequently

$$\mathcal{V}=\sum _{i,j}\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)P_{ij}.$$

After some simplification one finds (cf. Appendix) that the solution for the second moment is

$$\begin{gathered} v={\text{e}}^{\mathcal{V}t}v\left(0\right)+{\int }_0^t{\text{e}}^{\mathcal{V}(t-\tau )}\gamma \left(\tau \right)\text{d}\tau \\ =\sum _{i,j}{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}{P}_{ij}v\left(0\right)+\sum _{i,j}{\int }_0^t{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)(t-\tau )}{P}_{ij}\gamma \left(\tau \right)\text{d}\tau \\ =\sum _{i,j}{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}{P}_{ij}v\left(0\right)+\sum _{i,j}(\frac{{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-{\text{e}}^{{\mathrm{\lambda }}_{i}t}}{{\mathrm{\lambda }}_j}\left(P_i{M}_0\otimes P_j\right)+\left(\frac{1}{{\mathrm{\lambda }}_i{\mathrm{\lambda }}_j}\left({\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-{\text{e}}^{{\mathrm{\lambda }}_{i}t}\right)-\frac{1}{{\mathrm{\lambda }}_i\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)}\left({\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-1\right)\right)\left(P_{i}S\otimes P_j\right)+\frac{{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-{\text{e}}^{{\mathrm{\lambda }}_{j}t}}{{\mathrm{\lambda }}_i}\left(P_i\otimes P_j{M}_0\right)+(\frac{1}{{\mathrm{\lambda }}_i{\mathrm{\lambda }}_j}\left({\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-{\text{e}}^{{\mathrm{\lambda }}_{j}t}\right)-\frac{1}{{\mathrm{\lambda }}_j\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)}\left({\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-1\right)\left)\left(P_i\otimes P_{j}S\right)\right)col{K}^s+\sum _{i,j}{\int }_0^t{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)(t-\tau )}\left(P_i{K}^{cat}\otimes P_j+P_i\otimes P_j{K}^{cat}\right)col{M}_d\text{d}\tau , \end{gathered}$$ (49)

where M₀ = [M(0)|M(0)|⋯|M(0)], S = [k^s|k^s|⋯|k^s] and M_d = diag{M₁ (t), M₂ (t)⋯M_n(t)}. From (49) and (47) it is clear that the time-dependent behavior of the covariance is governed by the set of eigenvalues ${\mathrm{\lambda }}_i^{\mathcal{K}}+{\mathrm{\lambda }}_j^{\mathcal{K}}$, and if the eigenvalues of $\mathcal{K}$ have negative real parts, so do the eigenvalues of $\mathcal{V}$. Thus the sufficient conditions for the stability of the mean derived in the preceding section also guarantee the stability of the second moment. For a closed system, one of the eigenvalues is zero and hence the longest characteristic time for the evolution of M and V will be identical. For an open system, the characteristic time for the evolution of the second moment will be twice as large as that for the evolution of M. Note however that V_ii = (E [N_i (t)²] – E [N_i (t)]), and therefore this should not be interpreted to imply that the variance of the number of molecules of a particular species evolves twice as rapidly as the mean.

From the expression for v, one obtains the variance of the lth species (cf. Appendix) explicitly as

$${\sigma }_l^2(t)=-\sum _{i,j}{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}{\left(P_i\odot P_{j}M(0)\right)}_l+\sum _i{\text{e}}^{{\mathrm{\lambda }}_{i}t}\left[{\left(P_{i}M(0)\right)}_l+\frac{\left(P_i{k}^s\right)l}{{\mathrm{\lambda }}_i}\right]-\sum _i\frac{1}{{\mathrm{\lambda }}_i}{\left(P_i{k}^s\right)}_l+\sum _{i,j}\sum _{k}D(l,k,j)[\sum _r\left({\left(P_{r}M(0)\right)}_k+\frac{{\left(P_r{k}^s\right)}_k}{{\mathrm{\lambda }}_r}\right)f_{r,i,j}(t)-\frac{{\left(P_r{k}^S\right)}_k}{{\mathrm{\lambda }}_r\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)}\left({\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-1\right)],$$

where

$$D(l,k,j)=\left({\left(P_j\right)}_{lk}C(l,k,i)+{\left(P_i\right)}_{lk}C(l,k,j)\right),$$

$$C(l,k,i)=\sum _{m=1}^n{\left(P_i\right)}_{lm}{K}_{mk}^{cat}$$

$$f_{r,i,j}(t)=\{\begin{array}{ll}\frac{1}{{\mathrm{\lambda }}_r-{\mathrm{\lambda }}_i-{\mathrm{\lambda }}_j}\left({\text{e}}^{{\mathrm{\lambda }}_{r}t}-{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}\right)\hfill & \text{ if }{\mathrm{\lambda }}_r\ne {\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\hfill \\ t{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}\hfill & \text{ if }{\mathrm{\lambda }}_r={\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\hfill \end{array}$$

and ⊙ denotes element-wise multiplication. Using the expression for the mean of the lth reactant given in (44), we obtain the relationship between the mean and variance of every species in the reaction network.

$${\sigma }_l^2(t)=-\sum _{i,j}{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}{\left(P_i\odot P_{j}M(0)\right)}_l+M_l(t)+\sum _{i,j}\sum _{k}D(l,k,j)[\sum _r\left({\left(P_{r}M(0)\right)}_k+\frac{{\left(P_r{k}^S\right)}_k}{{\mathrm{\lambda }}_r}\right)f_{r,i,j}(t)-\frac{{\left(P_r{k}^s\right)}_k}{{\mathrm{\lambda }}_r\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)}\left({\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-1\right)].$$ (50)

From this expression one can calculate the evolution of the Fano factor $\mathcal{F}={\sigma }_l^2/M_l$ and CV = σ_l/M_l for every species, and thus determine the effect of various network structures and reaction types on the noise. We study several examples in the following section.

4. The effect of network structure on the dynamics

The master equation for a system of first-order chemical reactions reflects three major characteristics of the system, (i) whether it is open or closed, (ii) the topology of the network of the chemical interactions, and (iii) whether or not the reacting mixture is spatially uniform, i.e., whether or not diffusive or other transport mechanisms play an important role. The effect of each of these factors on the distribution of species undergoing first-order catalytic and conversion reactions can be studied using the general results of the preceding section.

4.1. Open and closed conversion systems

In the context of first-order reaction dynamics, catalytic systems are necessarily open because they involve production from a source catalyzed by a time-dependent species (cf. Table 1). Thus the comparison of open and closed systems can only be made for those in which there are no catalytic reactions. Therefore we compare open conversion networks in which there is at least one Type I reaction and one Type II reaction, with closed networks in which all reactions are type III and thus the total mass is constant.

The equation for the MGF for a system of stochastic conversion reactions can be solved analytically (Gans, 1960; Darvey and Staff, 1966), and for closed conversion networks it has been shown that the distribution is multinomial when the eigenvalues are distinct (Darvey and Staff, 1966). We derive the general result via a backward equation. For open systems we prove that the distribution is Poisson, and we demonstrate how the choice of the noise measure leads to differing conclusions about the noise in open and closed conversion networks.

4.1.1. Closed conversion systems

In a closed system of linear reactions the molecules independently execute a random walk through the states, where the state of a molecule is the property of being a molecule of type i; i = 1, s, where s is the number of species or states. We let X (t) be the random process whose value at t is the state of a given molecule. Let P_ij be Pr{X(t) = j | X(0) = i}; then the matrix P of transition probabilities satisfies the backward Kolmogorov differential equation

$$\frac{\text{d}P(t)}{\text{d}t}=K^{T}P(t),$$ (51)

where K = K^con. Since P(0) = I, this has the solution

$$P(t)={\text{e}}^{K^{T}t}.$$

If we denote by pi(t) the probability that the molecule is of type i at time t, then p(t) = (p₁(t), … , p_s(t))^T is the solution of

$$\frac{\text{d}p}{\text{d}t}=Kp$$

and therefore

$$p(t)=P{(t)}^{T}p(0)={\text{e}}^{Kt}p(0).$$ (52)

Assume that the graph of the underlying network is strongly-connected; then K has exactly one zero eigenvalue and the equilibrium probability distribution is given by

$${\pi }_i=\frac{{\varphi }_{1,i}}{\sum _j{\varphi }_{1,j}}$$ (53)

where ϕ₁ is the unique positive eigenvector of K corresponding to the zero eigenvalue.

Now if there are a total of N molecules in the system, the joint equilibrium distribution is the multinomial distribution

$$\pi \left(n_1,n_2,\dots ,n_s\right)=\frac{N!}{n_1!n_2!\cdots n_S!}\prod _{i=1}^S{\pi }_i^{n_i},$$ (54)

since there are s classes to put the N molecules into, and the probability of the ith class is π_i. In particular, the number of individuals of the ith species is binomially distributed according to

$$\pi \left(n_i\right)=\left(\begin{array}{c}N\\ n_i\end{array}\right){\pi }_i^{n_i}{\left(1-{\pi }_i\right)}^{N-n_i}.$$ (55)

If in addition the joint distribution of molecular numbers of two species is multinomial initially, then the joint distribution at any time t is also multinomial. First suppose there are only two molecular species and N molecules initially. Then for 0 ≤ m ≤ N, one can show that (see the Appendix for details)

$$\begin{gathered} Pr\left(N_1\left(t\right)=m,N_2\left(t\right)=N-m\right) \\ =\sum _{i=0}^{N}Pr\left(N_1\left(t\right)=m,N_2\left(t\right)=N-m\left|N_1\right(0)=i,N_2(0)=N-i\right)\cdot Pr\left(N_1\left(0\right)=i,N_2\left(0\right)=N-i\right) \\ =\sum _{k=0}^m\sum _{i=k}^{N-m+k}\left(\begin{array}{l}i\hfill \\ k\hfill \end{array}\right)\left(p_t^k(1,1)p_t^{i-k}(1,2)\right)\left(\begin{array}{c}N-i\\ m-k\end{array}\right)\times \left(p_t^{m-k}(2,1)p_t^{N-i-m+k}(2,2)\right)\left(\begin{array}{c}N\\ i\end{array}\right)p_1{\left(0\right)}^i{p}_2{\left(0\right)}^{N-i} \\ =\left(\begin{array}{c}N\\ m\end{array}\right){\left(p_1\left(t\right)\right)}^m{\left(p_2\left(t\right)\right)}^{N-m} \end{gathered}$$

where the last step follows from (52). Thus {N₁(t), N₂(t)} has a binomial distribution if initially it has a binomial distribution. By induction, it follows that the joint distribution of {N₁(t), N₂(t), …,N_s(t)} is multinomial if the initial distribution is multinomial. That is to say, if the initial joint distribution of molecular numbers of species is multinomial, i.e.,

$$P(n,0)\equiv Pr\left(N_1(0)=n_1,\dots ,N_s(0)=n_s\right)=\frac{N!}{n_1!\cdots n_s!}{\left(p_1(0)\right)}^{n_1}\cdots {\left(p_s(0)\right)}^{n_s},$$

then the joint distribution at any time t is also multinomial and the density function is given by

$$P\left(N_1(t)=n_1,\dots ,N_s(t)=n_s\right)=\frac{N!}{n_1!\cdots n_s!}{\left(p_1(t)\right)}^{n_1}\cdots {\left(p_s(t)\right)}^{n_s},$$

where the probabilities p_i(t), 1 ≤ i ≤ s are given by (52).

It follows from (55) that the mean and variance for the mth species at the steady state are given by

$$\begin{gathered} M_m=N{\pi }_m=E\left[N_m\right] \\ {\sigma }^2\left(N_m\right)=N{\pi }_m\left(1-{\pi }_m\right)=E\left[N_m\right]\left(1-\frac{E\left[N_m\right]}{N}\right). \end{gathered}$$ (56)

Notice that π_m is the steady-state fraction of the mth molecular species in a deterministic description, and since this is fixed by the reaction rates, the variance σ²(N_m) does not approach the mean even as N → ∞. Thus the distribution is never Poisson in a closed conversion network. The maximum variance is attained for that species for which π_m is closest to 1/2. The Fano factor ${\mathcal{F}}_m=1-{\pi }_m$ is always less than 1 for all m, it is independent of N, and it is fixed entirely by the network topology and reaction rates. Thus it is an inappropriate measure of stochastic fluctuations in these networks.

In contrast,

$$C{V}_m=\frac{1}{\sqrt{N}}\sqrt{\frac{1-{\pi }_m}{{\pi }_m}}=\frac{\sqrt{1-{\pi }_m}}{\sqrt{M_m}}$$ (57)

varies as $1/\sqrt{N}$, while for fixed N it is monotone decreasing with π_m. In both cases the measures are smallest for the most-abundant species in the system.

4.1.2. Open conversion systems

Next we derive the steady-state distribution of species in an open conversion network. Here $\mathcal{K}=K^{con}-K^d$, and (25) can be written as

$$\frac{\partial G}{\partial t}-\sum _{j=1}^s\sum _{i=1}^s{\mathcal{K}}_{ij}\left(z_i-1\right)\frac{\partial G}{\partial z_j}=\sum _{i=1}^s{K}_i^s\left(z_i-1\right)G.$$

We find the solution of this PDE using the method of characteristics, analogous to the procedure outlined by Gans (1960). The result is that

$$G=\text{exp}\left(\frac{1}{\text{det }\Phi }\sum _i^s{K}_i^s\sum _k^s\frac{1}{{\mathrm{\lambda }}_k}{\Phi }^{ki}\left({\text{e}}^{{\mathrm{\lambda }}_{k}t}-1\right)\sum _j^s{\varphi }_{kj}\left(z_j-1\right)\right)\cdot \prod _i{\left(1+\frac{1}{\text{det }\Phi }\sum _k{\Phi }^{ki}\sum _j{\varphi }_{kj}\left(z_j-1\right){\text{e}}^{{\mathrm{\lambda }}_{k}t}\right)}^{m_i},$$

where Φ is the matrix whose rows are the eigenvectors ϕ_k, Φ^kj is the cofactor of ϕ_kj, and m_i is the number of molecules of species i present initially. Therefore at steady state

$$G(z,\infty )=\text{exp }\left(-\frac{1}{\text{det }\Phi }\sum _i{K}_i^s\sum _k\frac{1}{{\mathrm{\lambda }}_k}{\Phi }^{ki}\sum _j{\varphi }_{kj}\left(z_j-1\right)\right),$$

and the steady-state value of the mean is given by

$$M_m=E\left(N_m\right)=\frac{\partial G(z,\infty )}{\partial z_m}=-\frac{1}{\text{det }\Phi }\sum _i^s{K}_i^s\sum _k\frac{1}{{\mathrm{\lambda }}_k}{\Phi }^{ki}{\varphi }_{ki}.$$

To obtain the probability distribution, we differentiate k times to get

$$\frac{{\partial }^{k}G(z,\infty )}{\partial z_m^k}={\left(-\frac{1}{\text{det }\Phi }\sum _i{K}_i^s\sum _k\frac{1}{{\mathrm{\lambda }}_k}{\Phi }^{ki}{\varphi }_{km}\right)}^k\times \text{exp }\left(-\frac{1}{\text{det }\Phi }\sum _i{K}_i^s\sum _k\frac{1}{{\mathrm{\lambda }}_k}{\Phi }^{ki}\sum _j{\varphi }_{kj}\left(z_j-1\right)\right)$$

and then

$$P_{N_m}(k,\infty )=\frac{1}{k!}{\frac{{\partial }^{k}G(z,\infty )}{\partial z_m^k}|}_{z_m=0,z_j=1,j\ne m}=\frac{1}{k!}{M}_m^k{\text{e}}^{-M_m}.$$

This defines the density for a Poisson distribution, and as in any Poisson distribution, the variance is equal to the mean. This shows that the steady-state distribution of any species in an open first-order conversion network is a Poisson distribution, but this does not extend to the transient dynamics unless one assumes that the initial distribution of molecules is a Poisson distribution, rather than the Dirac distribution generally used.⁶

4.1.3. The noise during transients in conversion systems

The time-dependent variance in an open conversion system is given by (50) wherein K^cat = 0. In that case C(l, k, i) = 0 and (50) reduces to

$${\sigma }_m^2(t)=-\sum _{i,j}{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}{\left(P_i\odot P_{j}M(0)\right)}_m+M_m(t).$$

Evidently ${\text{lim}}_{t\to \infty }{\sigma }_m^2(t)={\text{lim}}_{t\to \infty }{M}_m(t)$ and if M(0) = 0, then ${\sigma }_m^2(t)=M_m(t)$. Thus ${\mathcal{F}}_m$ will always be 1 for open conversion systems when no species is present initially (M(0) = 0, which is by definition a Poisson initial distribution), and for more general initial conditions, ${\mathcal{F}}_m=1$ for all species at the steady state. On the other hand, it is easy to see that the CV_m is always inversely proportional to the square root of the mean for all these situations where ${\mathcal{F}}_m$ is a constant. There is thus a clear difference in the qualitative estimation of the noise predicted by the two factors during transients as well as at steady state.

For closed systems, ${\mathcal{F}}_m=1-p_m$ at steady state, while CV_m is given by (57). When M_m ~ N for some m, p_m ~ 1 and ${\mathcal{F}}_m$ and CV_m are both small. However when N ≫ M_n, ${\mathcal{F}}_m\to 1$, while CV_m is inversely proportional to $\sqrt{M_m}$. We illustrate this and the transient behavior of the noise measures with an example of a closed three-component system shown in the following figure, where arrows indicate conversion reactions, and the symbols on the arrows indicate the specific rate constant associated with that reaction.

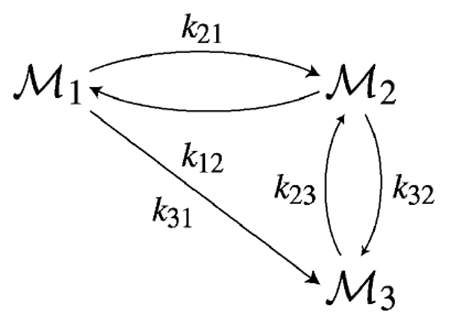
Using the procedure given earlier, one can find the means and covariances by solving

$$M(t{)}^{\prime }=\mathcal{K}M(t)$$ (58)

$$V(t{)}^{\prime }=\mathcal{K}V(t)+{(\mathcal{K}V(t))}^T,$$ (59)

where

$$\mathcal{K}=\left[\begin{array}{ccc}-k_{21}-k_{31}& k_{12}& 0\\ k_{21}& -k_{12}-k_{32}& k_{23}\\ k_{31}& k_{32}& -k_{23}\end{array}\right].$$

The eigenvalues of $\mathcal{K}$ are given by

$$\begin{gathered} {\mathrm{\lambda }}_1=0 \\ {\mathrm{\lambda }}_{2,3}=\frac{1}{2}\left[-k_{12}-k_{21}-k_{23}-k_{31}-k_{32}\pm \sqrt{{\left(k_{12}+k_{21}+k_{23}+k_{31}+k_{32}\right)}^2-4\left(k_{12}{k}_{23}+k_{21}{k}_{23}+k_{12}{k}_{31}+k_{23}{k}_{31}+k_{21}{k}_{32}+k_{31}{k}_{32}\right)}\right] \end{gathered}$$

and because

$${\left(k_{12}+k_{21}+k_{23}+k_{31}+k_{32}\right)}^2-4\left(k_{12}{k}_{23}+k_{21}{k}_{23}+k_{12}{k}_{31}+k_{23}{k}_{31}+k_{21}{k}_{32}+k_{31}{k}_{32}\right)>0,$$

the eigenvalues are distinct and $\mathcal{K}$ is semisimple. Thus,

$$\begin{gathered} M(t)={\text{e}}^{\mathcal{K}t}M(0) \\ =\sum _{i=1}^3{\text{e}}^{{\mathrm{\lambda }}_{i}t}{\left(P_{i}M(0)\right)}_k \end{gathered}$$

and furthermore

$${\sigma }_k^2(t)=\sum _{i,j}{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}{\left(-P_i\odot P_{j}M(0)\right)}_k+\sum _{i=1}^3{\text{e}}^{{\mathrm{\lambda }}_{i}t}{\left(P_{i}M(0)\right)}_k.$$

Assuming that only one species ${\mathcal{M}}_l$ for l ∈ {1, 2, 3} is present initially with N molecules, we find that for k = 1, 2, 3,

$$M_k(t)=N\sum _{i=1}^3{\text{e}}^{{\mathrm{\lambda }}_{i}t}{\left(P_i\right)}_{kl}$$

and so

$$\begin{gathered} {\sigma }_k^2\left(t\right)=\sum _{i,j=1}^3{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}{\left(-P_i\odot P_{j}M\left(0\right)\right)}_k+M_k\left(t\right) \\ =M_k\left(t\right)-\sum _{i,j=1}^3{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}{\left(P_i\right)}_{kl}{\left(P_j\right)}_{kl}N \\ =M_k\left(t\right)\left(1-\frac{M_k\left(t\right)}{N}\right). \end{gathered}$$

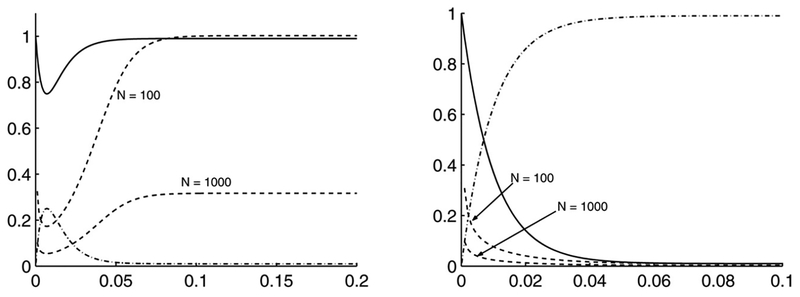
Fig. 1 shows the evolution of the Fano factor and CV for two components of the network. Since the sum of the number of molecules of all components at any instant is equal to the sum of the initial number, the mean and variance of the first component can be calculated from the mean and variance of the other two. It is clear that for these values of the rate parameters, which produce a steady state in which most of the total molecules exist as Species 3 and the steady-state value of the mean for Species 2 is a small fraction of the total number of molecules, the Fano factor for species 2 is close to one at steady state, and does not change as the total number of molecules is increased 10-fold. For Species 3 the steady-state value of the mean is almost equal to the total number of molecules, and both the Fano factor and the CV predict that the steady-state noise will not change appreciably when the total number of molecules in the system is changed.

Fig. 1.

Time-evolution (x-axis) of the mean scaled to the total number of molecules (-.-.-.), Fano factor (solid line) and CV (dashed line) for Species 2 (left) and Species 3 (right) for two values of N = 100 and N = 1000. Profiles for the fraction in each state and the Fano factor are independent of N. These plots illustrate the fact that use of the Fano factor leads to the conclusion that the noise of both species does not change on increasing N, whereas use of the CV predicts that increasing N reduces the noise in Species 2, whereas the noise in Species 3 remains essentially unchanged at steady state. The values of the rate constants are (in units of time⁻¹) k₂₁ = 100, k₃₁ = 100, k₁₂ = 1, k₂₃ = 1, k₃₂ = 100 and all N molecules exist as ${\mathcal{M}}_1$ initially.

4.2. The effect of network topology on stochastic reaction networks

The structure of the graph of interactions among the network components influences the transient stochastic evolution of the network through its effect on the eigenvalues and eigenvectors of $\mathcal{K}$. However, we have shown that the steady-state distribution is always multinomial for a closed conversion system and Poisson for an open conversion system, and these conclusions are independent of the topology of the network. In both cases the distribution is completely characterized by the mean, and the effect of topology on the mean of the various species can be derived from an analysis of the structure of the vertex–edge incidence matrix $\mathcal{E}$ (Othmer, 1979). We illustrate the effects of a change in network topology on the steady-state distribution of a simple catalytic network, and on the evolution of the distribution to the steady state for general conversion or catalytic networks through a simple example.

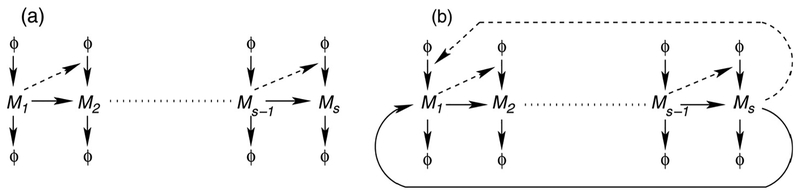
We consider reaction networks that either form closed “loops” (Fig. 2(b)), with either a feedforward or feedback interaction, and compare the results with the evolution of the distribution in linear reaction networks of the form shown in Fig. 2(a). In general, for a conversion chain the ith species is formed from the (i − 1)st species and is converted to the (i + 1)st species; and in a catalytic chain the ith species is formed from the source with the reaction being catalyzed by the (i − 1)st species, and catalyzes the formation of the (i + 1)st species. All species undergo first-order degradation. The conversion chain is an example of an open conversion system, and we have shown that the distribution of the number of molecules of all components is a Poisson distribution. The analysis of the dynamics of the mean for feedback networks has been carried out earlier (Tyson and Othmer, 1978).

Fig. 2.

Linear (a) and looped (b) reaction networks. The arrows represent the dependence of one species on the rate of formation of the species at the head of the arrow: the reactions may be conversion (solid lines) or catalytic (dashed lines).

Consider an example of a feedback loop with s = 2, where only ${\mathcal{M}}_1$ has a non-negative rate of production from the source. Table 2 gives the steady-state mean of both species for conversion and catalytic reactions, and the steady-state variance for a network of catalytic reactions (the variance is equal to the mean in the conversion case).

Table 2.

Mean and variance for a 2-component feedback network with either conversion or catalytic reactions

Species	Meanconversion	Meancatalytic	Vanancecataiytic
${\mathcal{M}}_1$	$\frac{pt{k}_1^S\left(k_{12}^{con}+k_2^d\right)}{\left(k_{12}^{con}+k_2^d\right)\left(k_{21}^{con}+k_1^d\right)-k_{21}^{con}{k}_{12}^{con}}$	$\frac{pt{k}_1^S{k}_2^d}{k_1^d{k}_2^d-k_{21}^{cat}{k}_{12}^{cat}}$	$\frac{pt{k}_1^d{k}_2^d\left(k_1^d+k_2^d\right)-k_{21}^{cat}{k}_{12}^{cat}\left(k_1^d-k_{12}^{cat}\right)}{\left(k_1^d{k}_2^d-k_{21}^{cat}{k}_{12}^{cat}\right)\left(k_1^d+k_2^d\right)}\times M_1$
${\mathcal{M}}_2$	$\frac{pt{k}_1^S{k}_{21}^{con}}{\left(k_{12}^{con}+k_2^d\right)\left(k_{21}^{con}+k_1^d\right)-k_{21}^{con}{k}_{12}^{con}}$	$\frac{pt{k}_1^S{k}_{21}^{cat}}{k_1^d{k}_2^d-k_{21}^{cat}{k}_{12}^{cat}}$	$\frac{pt{k}_1^d{k}_2^d\left(k_1^d+k_2^d\right)+k_{21}^{cat}{k}_2^d\left(k_1^d-k_{12}^{cat}\right)}{\left(k_1^d{k}_2^d-k_{21}^{cat}{k}_{12}^{cat}\right)\left(k_1^d+k_2^d\right)}\times M_2$

It is clear that the presence or absence $\left(k_{12}^{con}=0\right)$ of a feedback loop in a conversion network changes the mean value of both ${\mathcal{M}}_1$ and ${\mathcal{M}}_2$, but the variance is always equal to the mean and the Fano factor is always equal to one. In contrast, for a catalytic network the presence of a feedback loop changes not only the mean, but also the steady-state fluctuations, as is most clear from the change in the Fano factor for ${\mathcal{M}}_1$ from a value of one in the absence of a feedback $\left(k_{12}^{cat}=0\right)$, to the value indicated in Table 2 for a network with feedback. We will further explore the differences in the variance of conversion and catalytic networks in the following subsection.

We can also compare the change in the evolution rates for these networks. For the reaction networks in Fig. 2, the matrix of reaction rates takes the form

$$\mathcal{K}=\left[\begin{array}{ccccc}{\mathcal{K}}_{11}& 0& 0& \dots & {\mathcal{K}}_{1s}\\ {\mathcal{K}}_{21}& {\mathcal{K}}_{22}& 0& \dots & 0\\ 0& {\mathcal{K}}_{32}& {\mathcal{K}}_{33}& \dots & 0\\ ⋮& \ddots & \ddots & \ddots & ⋮\\ 0& 0& \dots & {\mathcal{K}}_{ss-1}& {\mathcal{K}}_{ss}\end{array}\right].$$

For the linear network, the value of ${\mathcal{K}}_{1s}$ is zero and ${\mathcal{K}}_{ii}$ are its eigenvalues.

The characteristic equation f (λ) of $\mathcal{K}$ is given by

$$\begin{gathered} f(\mathrm{\lambda })=\left[\left({\mathcal{K}}_{11}-\mathrm{\lambda }\right)\left({\mathcal{K}}_{22}-\mathrm{\lambda }\right)\cdots \left({\mathcal{K}}_{ss}-\mathrm{\lambda }\right)\right]+{\left(-1\right)}^{s+1}{\mathcal{K}}_{1s}{\mathcal{K}}_{21}\cdots {\mathcal{K}}_{ss-1} \\ ={\left(-1\right)}^s\left[\prod _{i=1}^S\left(\mathrm{\lambda }-{\mathcal{K}}_{ii}\right)-{\mathcal{K}}_{1s}{\mathcal{K}}_{21}\cdots {\mathcal{K}}_{ss-1}\right]\equiv {\left(-1\right)}^{s}g(\mathrm{\lambda }). \end{gathered}$$

Consider a looped network that conforms to the stability condition (1) that the specific rate of production of each species is less than the specific rate of degradation. This requires that

$${\mathcal{K}}_{21}<-{\mathcal{K}}_{11},{\mathcal{K}}_{32}<-{\mathcal{K}}_{22},\dots ,{\mathcal{K}}_{ss-1}<-{\mathcal{K}}_{s-1s-1},{\mathcal{K}}_{1s}<-{\mathcal{K}}_{SS}$$

and this implies that

$${\mathcal{K}}_{1s}{\mathcal{K}}_{21}{\mathcal{K}}_{32}\cdots {\mathcal{K}}_{ss-1}<\prod _{i=1}^s\left(-{\mathcal{K}}_{ii}\right).$$

Hence, for all ${\mathcal{K}}_{kk},1\le k\le s$ we have

$$g\left({\mathcal{K}}_{kk}\right)=-{\mathcal{K}}_{1s}{\mathcal{K}}_{21}\cdots {\mathcal{K}}_{ss-1}<0$$

and

$$g(0)=\prod _{i=1}^S\left(-{\mathcal{K}}_{ii}\right)-{\mathcal{K}}_{1n}{\mathcal{K}}_{21}{\mathcal{K}}_{32}\cdots {\mathcal{K}}_{SS-1}>0.$$

Therefore there is a real root λ_r of g(λ) = 0 such that max_i ${\mathcal{K}}_{ii}<{\mathrm{\lambda }}_r<0$, which implies that in the loops there exists at least one real negative eigenvalue λ_r of $\mathcal{K}$ which is bigger than max_i ${\mathcal{K}}_{ii}$.

Thus the presence of a loop leads to a slowing down of the evolution of the moments to the steady-state values. Notice that for a feed-forward looped network (i.e. Fig. 2(b) with the the arrow from ${\mathcal{M}}_1$ to ${\mathcal{M}}_s$ reversed), the corresponding reaction rate k_s1 is still in the lower triangular part of $\mathcal{K}$ and the eigenvalues will be identical to those of the corresponding linear system.

4.3. Effect of the nature of the chemical reaction

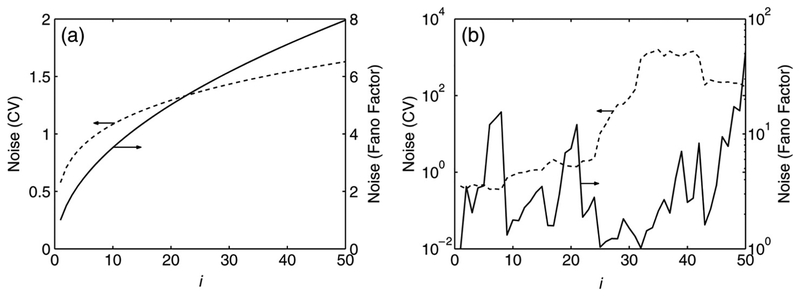
Previous analyses of stochastic first-order reaction systems have been restricted to either all-conversion or all-catalytic systems, but they have not been compared directly. Let us consider reactions of the form shown in Fig. 2(a) in which the first component is produced from a source, and then is either converted to the second species (conversion chain), or catalyzes the formation of the second species (catalysis chain). As we know, the distribution of the number of molecules is a Poisson distribution for an open conversion chain, the Fano factor is one for all species at steady state, and the CV is inversely proportional to the square root of the mean. The results are quite different for a catalytic chain. In Fig. 3 we show the Fano factor and CV for a catalytic chain with rate parameters such that the means are identical 3(a) and different 3(b). It is clear that for a catalytic chain with identical means $\left(k_{i(i-1)}^{cat}=k_i^d\forall i\ge 2\right)$, the variance reaches a limiting value as the chain length is increased. This agrees with the results of Thattai and van Oudenaarden (2001), who studied catalytic chains with hyperbolic activation functions. However, it is important to note that variance may not saturate when the means are different, which is almost always the case in biological systems. When the means are the same, the Fano factor and CV give estimations of the noise that are qualitatively consistent, but when the means are different the use of the two measures of noise give different predictions of the effect of increasing the number of species in a catalytic chain on the level of fluctuations.

Fig. 3.

Fano factor (solid line) and CV (dashed line) at steady state for the ith species in a catalytic chain with equal (a) and unequal (b) means. In (a) all species have a steady-state mean value of 3, resulting from setting all catalysis and degradation rate constants to 2 and the production rate for ${\mathcal{M}}_1$ to 2, random parameters for rate constants lead to mean values between 10⁻⁴ and 120 for species in (b). In both simulations, one molecule of each species was assumed to be present initially: but the results do not depend on the choice of the initial condition.

5. The effect of diffusion on stochastic reaction networks

Heretofore we have ignored the possible effects of spatial nonuniformity in the distribution of species, but when transport is solely by diffusion we can analyze a suitably-discretized spatial model within the preceding framework, because diffusion is a linear process. As the reader will appreciate after the development of the equations, the same analysis applies to compartmental models in which transport between compartments is linear in the concentration of the species. Here we restrict the discussion to a closed system containing an isotropic medium having no diffusive coupling between species, but the general formulation of the corresponding deterministic linear equations allows for bi-directional exchange with a reservoir, diffusive coupling, anisotropy in the transport (Othmer and Scriven, 1971).

For simplicity of exposition we begin with a symmetric domain that is subdivided into identical cubical compartments, and denote the number of molecules of species ${\mathcal{M}}_i$ present in the jth compartment as N_ji. Diffusive transport from compartment j to compartment k can be represented as the reaction (N_j,i, N_k,i) → (N_j,i, − 1, N_k,i, + 1) at a rate given by D_i/δ², where δ is the length scale of each compartment and D_i is the diffusion constant for species i (Nicolis and Prigogine, 1977; Stundzia and Lumsden, 1996).

Suppose that there are N_c cells and s reacting species. As before, $\mathcal{K}$ is the s × s reaction rate constant matrix = K^cat + K^con + K^d defined for reactions without diffusion. Let Δ be the N_c × N_c structural matrix of the network of cells, whose elements Δ_jk for j ≠ k are 1 or 0, resp., if cell k is connected to cell j, or not, resp., and −Δ_jj is the number of cells connected to cell j. Δ encodes the connectivity of the network, and in the simple case treated here simply reflects the discretization of the Laplace operator on the domain in question. We define $\mathcal{D}$ as the s ×s diagonal matrix of diffusion rates D_i/δ² for the species.

The deterministic evolution of the system is governed by

$$\frac{\text{d}\mathbf{c}}{\text{d}t}=\Omega \mathbf{c},$$

where c is the composition vector for all cells and the n_s · N_c × n_s · N_c matrix $\Omega \equiv I_{N_c}\otimes K+\Delta \otimes D$. It follows immediately that the equations for the means and second moments are

$$M(t{)}^{\prime }=\Omega M(t)+K^s\mathbf{·}\mathbf{1}$$

$$V(t{)}^{\prime }=\Omega V(t)+{[\Omega V(t)]}^T+C+C^T.$$

Here the matrix of means is defined as

$$M(t)=diag[M_{11}(t),M_{12}(t),\dots M_{1s}(t),M_{21}(t),\dots M_{2s}(t),\dots M_{N_{c}1}(t),\dots M_{N_{c}s}(t)]$$

and K^s is a matrix containing the rate constants for production of each of the N_c × s species, given by

$$K^s=diag\left[k_{11}^s,k_{12}^s,\dots k_{1s}^s,k_{21}^s,\dots k_{2s}^s,\dots k_{N_{c}s}^s\right],$$

where $k_{ij}^S$ is the rate of inflow of species j from sources.

The covariance matrix V(t) has matrix-valued elements V_ij defined as

$$V_{ij}(k,m)=\{\begin{array}{ll}E\left[N_{ik}{(t)}^2\right]-E\left[N_{ik}(t)\right]\hfill & \text{if }i=j\text{ and }k=m\hfill \\ E\left[N_{ik}(t)N_{jm}(t)\right]\hfill & \text{otherwise}.\hfill \end{array}$$

Finally, C = W + K^s1 · M(t)^T where W is a block-diagonal matrix, with each block defined as $W_{kk}(i,j)=K_{ij}^{cat}E\left[N_{kj}(t)\right]$.

It is clear from earlier sections that the evolution of the first and second moments are formally known once the eigenvalues and eigenvectors of Ω are known, and these are known from earlier work. Let α_k be an eigenvalue of the symmetric matrix Δ; then the eigenvalues λ_kj of Ω are solutions of the family of N_c sth-order determinantal equations

$$\left|\mathcal{K}+{\alpha }_k\mathcal{D}-{\mathrm{\lambda }}_k{\mathbf{I}}_s\right|=0$$ (60)

(Othmer and Scriven, 1971). It is known that whenever $\mathcal{K}$ is not diagonal there may be counter-intuitive effects of diffusion on the eigenvalues determined by (60), and this lies at the heart of Turing’s mechanism of pattern formation (Turing, 1952; Othmer, 1969).

The foregoing has been formulated for a regular discretization of a domain, but it holds whatever the topology of the connections between the compartments, as long as transport depends only on the concentration difference between compartments. The advantage of the present formulation is that the effects of network structure in the reaction dynamics can be separated to the maximal extent possible from the topology of the compartmental connections, and effects due to spatial variations arise from the effect of the α_k’s for different spatial modes. It should be noted here that in our treatment of reaction–diffusion systems there is an assumption that individual compartments are well-mixed, and for this to be valid, the size of each compartment should be related to the diffusion coefficient (and ultimately to the mean free path) of the diffusing species. However, the basis for the choice of compartment size is not clear for a system containing species with very different diffusion coefficients. On the one hand, if the size is based on the faster-diffusing species the well-mixed assumption may not be true for species that diffuse slowly, but if the size is computed using the slower-diffusing species, any solution algorithm will become computationally inefficient. More generally, the problem of how to treat wide disparities in time scales in the full master equation remains to be solved.

6. Discussion and conclusion

We have analyzed a general system of first-order reactions amongst s species that can be produced from sources, converted to other species or degraded, and catalyze the formation of other species. All previous stochastic analyses of systems of first-order reactions can be formulated as special cases of the general model studied here. We have derived explicit evolution equations for the mean and variance of the number of molecules of each reactant, and have solved them explicitly in a number of cases when the rate matrix $\mathcal{K}$ is semisimple. We find that the evolution of the second moments is completely determined by the spectral properties of $\mathcal{K}$ and the mean itself. To our knowledge this is the first report of a method to analytically compute the first two moments for an arbitrary first-order network comprising both conversion and catalytic reactions.

We have used the general framework to explore the effect of changes in the network topology on the distribution of the number of reactant molecules, and the difference between conversion and catalytic networks with the same topology. We prove that for an open system of first-order conversion reactions, the distribution of the number of molecules of every species is always a Poisson distribution. This is not the case for closed conversion systems, since the total number of molecules is constant. This result can be directly applied to the interpretation of experimental results on protein conformational-state transitions. The folding of a protein from its unfolded state to the fully folded (“native”) state occurs through a series of intermediates. The first-order rate constants governing the reversible transitions from the unfolded state to the native state are calculated experimentally (Mayor et al., 2003). The above theory suggests the distributions that the experimental data may be fitted to in order to derive accurate estimates of the first-order transition rates. If ingress and egress through flow is allowed for the measurement device, each of the protein folding states will exhibit a Poisson distribution. If the system is closed, each state will be characterized by a multinomial distribution with a mean that is lower than the variance. A protein molecule undergoing conformational-state transitions is but one example of a set of chemical reactions that may be carried out in a closed or batch process, where there is no inflow or outflow of the chemical species, or in an open or continuous process, where one or more chemicals are introduced at a constant rate, or removed from the system. The inflows may be modeled as production reactions of the form $\varphi \to {\mathcal{M}}_i$ where species ${\mathcal{M}}_i$ is produced at a constant rate from a source. The outflows are modeled as degradation reactions that result in a depletion of species at a rate proportional to their concentration, with the specific rate constant corresponding to the dilution rate for the reactor. These equations exactly describe the addition and removal of species in microfluidic devices which may be modeled as continuous stirred-tank reactors. Our analysis of open and closed systems may be used to distinguish between the effects of batch-mode operations and continuous operations on the stochastic behavior of the chemical species undergoing the same set of chemical conversion reactions.

Two measures are used to estimate the stochastic fluctuations of reactant concentrations: the Fano factor and the coefficient of variance. We have shown that the equilibrium distribution of all components is a Poisson distribution for open conversion networks, in which case use of the Fano factor as the measure of noise leads to the prediction that the fluctuations of all components in an open conversion reaction system are identical. Thus a species that has a mean of 10 molecules will exhibit the same amount of noise as a species that has a mean concentration of 1M. This is clearly not correct, and the use of the CV as the measure of the noise will correctly predict that the noise is inversely proportional to the square root of the mean value. The only instance when the use of the Fano factor has a distinct advantage is when noise is defined as a deviation from the Poisson distribution. Our work is the first instance where the two measures have been compared theoretically, and we conclude that the only instance where either measure can be used to compare the noise of two species is when the mean values are identical. We have also shown that the use of the two measures leads to contradictory conclusions about the noise when the means are not identical.

We use the example of a linear reaction chain with and without feedback to demonstrate the effect of changes in the species interconnectivity on the dynamics of the evolution of the moments of the distribution. For the same interconnectivity, the nature of the distribution changes depending on whether the reactions are conversion reactions or catalytic reactions. It has been shown for a catalytic chain whose mean values are equal at steady state that the variance of the last species in the chain increases as the number of species in the chain increases (Thattai and van Oudenaarden, 2001), but ultimately saturates for long chains. We show with a counterexample that the ratio of the variance to the mean does not show this saturation behavior when the steady-state mean values of all the components are different.

The mathematical formulation that leads to a direct solution of the moment equations for a well-stirred system can be extended to arbitrary networks of well-mixed compartments that are coupled by diffusion. We demonstrate that the eigenvalues that govern the evolution in such distributed systems are solutions of a one-parameter family of modified kinetic matrices and thus one can formally display the solution for the first two moments in this case as well. However much remains to be done for this case to develop computationally-efficient algorithms.

We anticipate that the analytical framework presented here will be extended to the stochastic analysis of nonlinear reaction networks, and our analysis of first-order reaction network will lead to insights into the local linear behavior of such networks.

Appendix

An alternate approach to the evolution equation for the MGF⁷

To obtain the generating function for the first-order network, one may use the Kolmogorov backward equation instead of the master equation (24), which is generally used in the field of chemical reaction networks.

The Kolmogorov backward equation is given by

$$\frac{\text{d}}{\text{d}t}E[f(N(t))]=E[\mathcal{A}f(N(t))],$$

where

$$\mathcal{A}f(n)=\sum _i{k}_i^s\left({\mathcal{S}}_i^{+1}f(n)-f(n)\right)+\sum _{i,j}{k}_{ij}^{con}{n}_j\left({\mathcal{S}}_i^{+1}{\mathcal{S}}_j^{-1}f(n)-f(n)\right)+\sum _{i,j}{k}_{ij}^{cat}{n}_j\left({\mathcal{S}}_i^{+1}f(n)-f(n)\right)+\sum _i{k}_i^d{n}_i\left({\mathcal{S}}_i^{-1}f(n)-f(n)\right).$$

Notice that $G(z,t)=E\left[\prod z_i^{N_i(t)}\right]$, and therefore, taking $f(N(t))=\prod z_i^{N_i(t)}$,

$$\frac{\text{d}}{\text{d}t}G(z,t)=\frac{\text{d}}{\text{d}t}E\left[\prod z_i^{N_i(t)}\right]=\sum _i{k}_i^s\left(z_i-1\right)E\left[\prod z_i^{N_i(t)}\right]+\sum _{i,j}{k}_{ij}^{con}\left(\frac{z_i}{z_j}-1\right)E\left[N_j(t)\prod z_i^{N_i(t)}\right]+\sum _{i,j}{k}_{ij}^{cat}\left(z_i-1\right)E\left[N_j(t)\prod z_i^{N_i(t)}\right]+\sum _i{k}_i^d\left(\frac{1}{z_i}-1\right)E\left[N_i(t)\prod z_i^{N_i(t)}\right].$$

Using the fact that

$$E\left[N_j(t)\prod z_i^{N_i(t)}\right]=z_j\frac{\partial }{\partial z_j}E\left[\prod z_i^{N_i(t)}\right],$$

we obtain Eq. (24).

Tensor products and the column operation

Here we record a few basic facts about tensor products and the col operation that are used throughout.

Let x = (x₁, x₂, … , x_n)^T and y = (y₁, y₂, … , y_m)^T. Then we define the tensor product of x and y as (cf. Othmer and Scriven (1971) and references therein)

$$\begin{gathered} x\otimes y=\left(x_{1}y,x_{1}y,\cdot ,x_{1}y\right) \\ ={\left(x_1{y}_1,x_1{y}_2,\dots ,x_1{y}_n,x_2{y}_1,x_2,y_2,\dots ,x_2{y}_n,\dots ,x_n{y}_m\right)}^T. \end{gathered}$$

For any n × n matrix B = [b_ij] and an m × m matrix C, we define

$$(\mathbf{B}\otimes \mathbf{C})=\left[\begin{array}{cccc}{b}_{11}C& b_{12}C& \dots & b_{1n}C\\ b_{21}C& b_{22}C& \dots & b_{2n}C\\ ⋮& ⋮& \ddots & ⋮\\ b_{n1}C& b_{n2}C& \dots & b_{nn}C\end{array}\right].$$

Let B(i) be the ith column of a n × n matrix B. Then define the column operation as

$$colB=\left(\begin{array}{c}B(1)\\ B(2)\\ ⋮\\ B(n)\end{array}\right).$$

Then we have

$$col(BC)=\left(\begin{array}{c}BC(1)\\ BC(2)\\ ⋮\\ BC(n)\end{array}\right)=\left[\begin{array}{cccc}B& & & \\ & B& & \\ & & \ddots & \\ & & & B\end{array}\right]\left(\begin{array}{c}C(1)\\ C(2)\\ ⋮\\ C(n)\end{array}\right)=\left(I_n\otimes B\right)colC.$$

Similarly

$$col(CB)=\left(B^T\otimes I_n\right)colC.$$

We can use these results to rewrite (29) as follows. We have

$$V(t{)}^{\prime }=\mathcal{K}V(t)+{(\mathcal{K}V(t))}^T+\Gamma (t)+{\Gamma }^T(t)$$

and therefore

$$col\left(V{(t)}^{\prime }\right)=col(\mathcal{K}V(t))+col\left({(\mathcal{K}V(t))}^T\right)+col\left(\Gamma (t)+{\Gamma }^T(t)\right).$$

We apply the above to the first term on the right-hand side by setting $B=\mathcal{K}$ and C = V, and to the second term by setting $B={\mathcal{K}}^T$ and C = V, and noting that V is symmetric. This leads to (46).

Evolution of the moments

We consider the differential equation for the second moment

$$\frac{\text{d}v}{\text{d}t}=\mathcal{V}v+\gamma$$

where

$$v(t)=col(V(t))\mathcal{V}=\left(\mathcal{K}\otimes I_n+I_n\otimes \mathcal{K}\right)\text{and}\gamma (t)=col\left(\Gamma (t)+\Gamma {(t)}^T\right).$$

Since

$${[\Gamma (t)]}_{ij}=K_{ij}^{cat}E\left[N_j(t)\right]+k_i^{s}E\left[N_j\right]$$

and K^s and M_d are diagonal matrices,

$$\begin{gathered} \gamma (t)=col\left(\Gamma (t)+\Gamma {(t)}^T\right) \\ =col\left(K^{cat}{M}_d(t)+{\left(K^{cat}{M}_d(t)\right)}^T\right)+col\left(K^{s}L(t)+{\left(K^{s}L(t)\right)}^T\right) \\ =\left(K^{cat}\otimes I_n+I_n\otimes K^{cat}\right)col{M}_d+\left(L^T\otimes I_n+I_n\otimes L^T\right)col{K}^s. \end{gathered}$$

Thus

$$\begin{gathered} P_{ij}\gamma (t)=P_{ij}col\left(K^{cat}{M}_d+{\left(K^{cat}{M}_d\right)}^T+K^{s}L+{\left(K^{s}L\right)}^T\right) \\ =\left(P_i\otimes P_j\right)\left(K^{cat}\otimes I_n+I_n\otimes K^{cat}\right)col{M}_d+P_{ij}\left(L^T\otimes I_n+I_n\otimes L^T\right)col{K}^s \\ =\left(P_i{K}^{cat}\otimes P_j+P_i\otimes P_j{K}^{cat}\right)col{M}_d+\left(P_i{L}^T\otimes P_j+P_i\otimes P_j{L}^T\right)col{K}^s. \end{gathered}$$

We have that

$$\begin{gathered} P_{i}M(t)=P_i\left(\left(\sum _i{\text{e}}^{{\mathrm{\lambda }}_{i}t}{P}_i\right)M(0)-\sum _i\frac{\left(1-{\text{e}}^{{\mathrm{\lambda }}_{i}t}\right)}{{\mathrm{\lambda }}_i}{P}_i{k}^s\right) \\ ={\text{e}}^{{\mathrm{\lambda }}_{i}t}{P}_{i}M(0)-\frac{\left(1-{\text{e}}^{{\mathrm{\lambda }}_{i}t}\right)}{{\mathrm{\lambda }}_i}{P}_i{k}^S \end{gathered}$$

and

$$\begin{gathered} P_i{L}^T=P_i[M(t)|\cdots |M(t)] \\ =\left[P_{i}M(t)|\cdots |P_{i}M(t)\right] \\ ={\text{e}}^{{\mathrm{\lambda }}_{i}t}{P}_i{M}_0-\frac{\left(1-{\text{e}}^{{\mathrm{\lambda }}_{i}t}\right)}{{\mathrm{\lambda }}_i}{P}_{i}S, \end{gathered}$$

where M₀ = [M(0)|M(0)|⋯|M(0)], and S = [k^s|k^s|⋯|k^s]. Thus

$$P_{ij}\gamma \left(t\right)=\left(P_i{K}^{cat}\otimes P_j+P_i\otimes P_j{K}^{cat}\right)col{M}_d+[{\text{e}}^{{\mathrm{\lambda }}_{i}t}\left(P_i{M}_0\otimes P_j\right)-\frac{1-{\text{e}}^{{\mathrm{\lambda }}_{i}t}}{{\mathrm{\lambda }}_i}\left(P_{i}S\otimes P_j\right)+{\text{e}}^{{\mathrm{\lambda }}_{j}t}\left(P_i\otimes P_j{M}_0\right)-\frac{1-{\text{e}}^{{\mathrm{\lambda }}_{j}t}}{{\mathrm{\lambda }}_j}\left(P_i\otimes P_{j}S\right)]col{K}^s$$

and therefore

$$\begin{gathered} v={\text{e}}^{\mathcal{V}t}v\left(0\right)+{\int }_0^t{\text{e}}^{\mathcal{V}(t-\tau )}\gamma \left(\tau \right)\text{d}\tau \\ =\sum _{i,j}{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}{P}_{ij}v\left(0\right)+{\int }_0^t\sum _{i,j}{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)(t-\tau )}{P}_{ij}\gamma \left(\tau \right)\text{d}\tau \\ =\sum _{i,j}{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}{P}_{ij}v\left(0\right)+\sum _{i,j}(\frac{{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-{\text{e}}^{{\mathrm{\lambda }}_{i}t}}{{\mathrm{\lambda }}_j}\left(P_i{M}_0\otimes P_j\right)+\left(\frac{1}{{\mathrm{\lambda }}_i{\mathrm{\lambda }}_j}\left({\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-{\text{e}}^{{\mathrm{\lambda }}_{i}t}\right)-\frac{1}{{\mathrm{\lambda }}_i\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)}\left({\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-1\right)\right)\left(P_i{K}^S\otimes P_j\right)+\frac{{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-{\text{e}}^{{\mathrm{\lambda }}_{j}t}}{{\mathrm{\lambda }}_i}\left(P_i\otimes P_j{M}_0\right)+(\frac{1}{{\mathrm{\lambda }}_i{\mathrm{\lambda }}_j}\left({\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-{\text{e}}^{{\mathrm{\lambda }}_{j}t}\right)-\frac{1}{{\mathrm{\lambda }}_j\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)}\left({\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-1\right)\left)\left(P_i\otimes P_j{K}^s\right)\right)col{K}^s+\sum _{i,j}{\int }_0^t{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)(t-\tau )}\left(P_i{K}^{cat}\otimes P_j+P_i\otimes P_j{K}^{cat}\right)col{M}_d\text{d}\tau . \end{gathered}$$

Using the fact that col(ABC) = (C^T ⊗ A)col B, we obtain

$$V\left(t\right)=\sum _{i,j}{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}\left[P_{j}V\left(0\right)P_i^T\right]+\sum _{i,j}[\left(\frac{{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-{\text{e}}^{{\mathrm{\lambda }}_{i}t}}{{\mathrm{\lambda }}_j}\right)\left[P_j{K}^s{\left(P_i{M}_0\right)}^T\right]+\left(\frac{{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-{\text{e}}^{{\mathrm{\lambda }}_{i}t}}{{\mathrm{\lambda }}_i{\mathrm{\lambda }}_j}-\frac{{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-1}{{\mathrm{\lambda }}_i\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)}\right)\left[P_j{K}^s{\left(P_{i}S\right)}^T\right]+\frac{{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-{\text{e}}^{{\mathrm{\lambda }}_{j}t}}{{\mathrm{\lambda }}_i}\left[P_j{M}_0{K}^s{P}_i^T\right]+\left(\frac{{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-{\text{e}}^{{\mathrm{\lambda }}_{j}t}}{{\mathrm{\lambda }}_i{\mathrm{\lambda }}_j}-\frac{{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-1}{{\mathrm{\lambda }}_i\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)}\right)\left[P_{j}S{K}^s{P}_i^T\right]]+\sum _{i,j}{\int }_0^t{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)(t-\tau )}\left(P_j{M}_d{\left(P_i{K}^{cat}\right)}^T+P_j{K}^{cat}{M}_d{P}_i^T\right)\text{d}\tau .$$

Thus

$$V_{ll}\left(t\right)=\sum _{i,j}{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}\left[P_{j}V\left(0\right)P_i^T\right]ll+\sum _{i,j}[\left(\frac{{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-{\text{e}}^{{\mathrm{\lambda }}_{i}t}}{{\mathrm{\lambda }}_j}\right){\left[P_j{K}^s{\left(P_i{M}_0\right)}^T\right]}_{ll}+\left(\frac{{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-{\text{e}}^{{\mathrm{\lambda }}_{i}t}}{{\mathrm{\lambda }}_i{\mathrm{\lambda }}_j}-\frac{{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-1}{{\mathrm{\lambda }}_i\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)}\right){\left[P_j{K}^s{\left(P_{i}S\right)}^T\right]}_{ll}+\frac{{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-{\text{e}}^{{\mathrm{\lambda }}_{j}t}}{{\mathrm{\lambda }}_i}{\left[P_j{M}_0{K}^s{P}_i^T\right]}_{ll}+\left(\frac{{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-{\text{e}}^{{\mathrm{\lambda }}_{j}t}}{{\mathrm{\lambda }}_i{\mathrm{\lambda }}_j}-\frac{{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-1}{{\mathrm{\lambda }}_i\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)}\right){\left[P_{j}S{K}^s{P}_i^T\right]}_{ll}]+\sum _{i,j}{\int }_0^t{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)(t-\tau )}{\left(P_j{M}_d{\left(P_i{K}^{cat}\right)}^T+P_j{K}^{cat}{M}_d{P}_i^T\right)}_{ll}\text{d}\tau .$$

We have

$$\begin{gathered} P_j{M}_d=\left[\begin{array}{cccc}{P}_{j11}{M}_1& P_{j12}{M}_2& \cdots & P_{j1n}{M}_n\\ P_{j21}{M}_1& P_{j22}{M}_2& \cdots & P_{j2n}{M}_n\\ ⋮& \ddots & \ddots & ⋮\\ P_{jn1}{M}_1& P_{jn2}{M}_2& \cdots & P_{jnn}{M}_n\end{array}\right] \\ {\left(P_i{K}^{cat}\right)}^T=\left[\begin{array}{cccc}\sum _j{P}_{i1j}{K}_{j1}^{cat}& \sum _j{P}_{i2j}{K}_{j1}^{cat}& \cdots & \sum _j{P}_{inj}{K}_{j1}^{cat}\\ \sum _j{P}_{i1j}{K}_{j2}^{cat}& \sum _j{P}_{i2j}{K}_{j2}^{cat}& \cdots & \sum _j{P}_{inj}{K}_{j2}^{cat}\\ ⋮& \ddots & \ddots & ⋮\\ \sum _j{P}_{i1j}{K}_{jn}^{cat}& \sum _j{P}_{i2j}{K}_{jn}^{cat}& \cdots & \sum _j{P}_{inj}{K}_{jn}^{cat}\end{array}\right]. \end{gathered}$$

Thus

$$\begin{gathered} {\left[P_j{M}_d{\left(P_i{K}^{cat}\right)}^T\right]}_{ll}=P_{jl1}{M}_1\left(\sum _j{P}_{ilj}{K}_{j1}^{cat}\right)+P_{jl2}{M}_2\left(\sum _j{P}_{ilj}{K}_{j2}^{cat}\right)+\cdots +P_{iln}{M}_n\left(\sum _j{P}_{ilj}{K}_{jn}^{cat}\right) \\ =\sum _k{P}_{jlk}{M}_{k}C(i,k,l) \end{gathered}$$

where

$$C(i,k,l)=\sum _j{P}_{ilj}{K}_{jk}^{cat}.$$

Similarly

$${\left[P_j{K}^{cat}{M}_d{P}_i^T\right]}_{ll}=\sum _m{P}_{ilm}{M}_{m}C(j,k,l).$$

Thus

$$\begin{gathered} {\int }_0^t{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)(t-\tau )}{\left(P_j{M}_d{\left(P_i{K}^{cat}\right)}^T+P_j{K}^{cat}{M}_d{P}_i^T\right)}_{ll}\text{d}\tau \\ ={\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}{\int }_0^t{\text{e}}^{-\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)\tau }\left(\sum _k{\left(P_j\right)}_{lk}{M}_{k}C(i,k,l)+\sum _k{\left(P_i\right)}_{lk}{M}_{k}C(j,k,l)\right)\text{d}\tau \\ ={\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}{\int }_0^t{\text{e}}^{-\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)\tau }[\sum _k{\left(P_j\right)}_{lk}(\sum _r{\text{e}}^{{\mathrm{\lambda }}_r\tau }{\left(P_{r}M\left(0\right)\right)}_k-\sum _r\frac{1-{\text{e}}^{{\mathrm{\lambda }}_r\tau }}{{\mathrm{\lambda }}_r}{\left(P_r{k}^s\right)}_k\left)C\right(i,k,l)+\sum _k{\left(P_i\right)}_{lk}\left(\sum _r{\text{e}}^{{\mathrm{\lambda }}_r\tau }{\left(P_{r}M\left(0\right)\right)}_k-\sum _r\frac{1-{\text{e}}^{{\mathrm{\lambda }}_r\tau }}{{\mathrm{\lambda }}_r}{\left(P_r{k}^S\right)}_k\right)C(j,k,l\left)\right)]\text{d}\tau \\ ={\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}\sum _k{\left(P_j\right)}_{lk}\sum _{r}C(i,k,l)[{\left(P_{r}M\left(0\right)\right)}_k{\int }_0^t{\text{e}}^{\left({\mathrm{\lambda }}_r-{\mathrm{\lambda }}_i-{\mathrm{\lambda }}_j\right)\tau }\text{d}\tau -\frac{{\left(P_r{k}^s\right)}_k}{{\mathrm{\lambda }}_r}\times \left({\int }_0^t{\text{e}}^{-\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)\tau }\text{d}\tau -{\int }_0^t{\text{e}}^{\left({\mathrm{\lambda }}_r-{\mathrm{\lambda }}_i-{\mathrm{\lambda }}_j\right)\tau }\text{d}\tau \right)]+{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}\sum _k{\left(P_i\right)}_{lk}\sum _{r}C(j,k,l)[{\left(P_{r}M\left(0\right)\right)}_k{\int }_0^t{\text{e}}^{\left({\mathrm{\lambda }}_r-{\mathrm{\lambda }}_i-{\mathrm{\lambda }}_j\right)\tau }\text{d}\tau -\frac{{\left(P_r{k}^S\right)}_k}{{\mathrm{\lambda }}_r}\left({\int }_0^t{\text{e}}^{-\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)\tau }\text{d}\tau -{\int }_0^t{\text{e}}^{\left({\mathrm{\lambda }}_r-{\mathrm{\lambda }}_i-{\mathrm{\lambda }}_j\right)\tau }\text{d}\tau \right)] \\ =\sum _k\left({\left(P_j\right)}_{lk}C(i,k,l)+{\left(P_i\right)}_{lk}C(j,k,l)\right)\times [\sum _{r,{\mathrm{\lambda }}_r\ne {\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j}{\left(P_{r}M\left(0\right)\right)}_k\frac{1}{{\mathrm{\lambda }}_r-{\mathrm{\lambda }}_i-{\mathrm{\lambda }}_j}\left({\text{e}}^{{\mathrm{\lambda }}_{r}t}-{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}\right)-\frac{{\left(P_r{k}^S\right)}_k}{{\mathrm{\lambda }}_r}\left(\frac{1}{{\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j}\left({\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-1\right)-\frac{1}{{\mathrm{\lambda }}_r-{\mathrm{\lambda }}_i-{\mathrm{\lambda }}_j}\left({\text{e}}^{{\mathrm{\lambda }}_{r}t}-{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}\right)\right)+\sum _{r,{\mathrm{\lambda }}_r={\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j}{\left(P_{r}M\left(0\right)\right)}_{k}t{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-\frac{{\left(P_r{k}^S\right)}_k}{{\mathrm{\lambda }}_r}\left(\frac{1}{{\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j}\left({\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-1\right)-t{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}\right)], \end{gathered}$$

where

$$C(i,k,l)=\sum _{m=1}^n{P}_{ilm}{K}_{mk}^{cat}.$$

Thus the (l, l) component of V is

$$V_{ll}\left(t\right)=\sum _{i,j}{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}{\left[P_{j}V\left(0\right)P_i^T\right]}_{ll}+\sum _{i,j}[\left(\frac{{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-{\text{e}}^{{\mathrm{\lambda }}_{i}t}}{{\mathrm{\lambda }}_j}\right){\left[P_j{K}^s{\left(P_i{M}_0\right)}^T\right]}_{ll}+\left(\frac{{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-{\text{e}}^{{\mathrm{\lambda }}_{i}t}}{{\mathrm{\lambda }}_i{\mathrm{\lambda }}_j}-\frac{{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-1}{{\mathrm{\lambda }}_i\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)}\right){\left[P_j{K}^s{\left(P_{i}S\right)}^T\right]}_{ll}+\frac{{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-{\text{e}}^{{\mathrm{\lambda }}_{j}t}}{{\mathrm{\lambda }}_i}{\left[P_j{M}_0{K}^s{P}_i^T\right]}_{ll}+\left(\frac{{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-{\text{e}}^{{\mathrm{\lambda }}_{j}t}}{{\mathrm{\lambda }}_i{\mathrm{\lambda }}_j}-\frac{{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-1}{{\mathrm{\lambda }}_i\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)}\right){\left[P_{j}S{K}^s{P}_i^T\right]}_{ll}]+\sum _{i,j}\sum _k\left({\left(P_j\right)}_{lk}C(i,k,l)+{\left(P_i\right)}_{lk}C(j,k,l)\right)\times [\sum _{r,{\mathrm{\lambda }}_r\ne {\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j}{\left(P_{r}M\left(0\right)\right)}_k\frac{1}{{\mathrm{\lambda }}_r-{\mathrm{\lambda }}_i-{\mathrm{\lambda }}_j}\left({\text{e}}^{{\mathrm{\lambda }}_{r}t}-{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}\right)-\frac{{\left(P_r{k}^S\right)}_k}{{\mathrm{\lambda }}_r}\left(\frac{1}{{\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j}\left({\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-1\right)-\frac{1}{{\mathrm{\lambda }}_r-{\mathrm{\lambda }}_i-{\mathrm{\lambda }}_j}\left({\text{e}}^{{\mathrm{\lambda }}_{r}t}-{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}\right)\right)+\sum _{r,{\mathrm{\lambda }}_r={\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j}{\left(P_{r}M\left(0\right)\right)}_{k}t{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-\frac{{\left(P_r{k}^S\right)}_k}{{\mathrm{\lambda }}_r}\left(\frac{1}{{\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j}\left({\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-1\right)-t{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}\right)].$$

Note that

$$E\left[N_l(t)\right]={[M(t)]}_l=\sum _i{\text{e}}^{{\mathrm{\lambda }}_{i}t}{\left(P_{i}M(0)\right)}_l-\sum _i\frac{1-{\text{e}}^{{\mathrm{\lambda }}_{i}t}}{{\mathrm{\lambda }}_i}{\left(P_i{k}^S\right)}_l$$

and that

$$E{\left[N_l\left(t\right)\right]}^2={\left({\left[M\right(t\left)\right]}_l\right)}^2=\sum _{i,j}{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}{\left(P_{i}M\left(0\right)\right)}_l{\left(P_{j}M\left(0\right)\right)}_l+\sum _{i,j}\frac{\left(1-{\text{e}}^{{\mathrm{\lambda }}_{i}t}\right)\left(1-{\text{e}}^{{\mathrm{\lambda }}_{j}t}\right)}{{\mathrm{\lambda }}_i{\mathrm{\lambda }}_j}{\left(P_i{k}^s\right)}_l{\left(P_j{k}^s\right)}_l-2\sum _{i,j}\frac{{\text{e}}^{{\mathrm{\lambda }}_{i}t}\left(1-{\text{e}}^{{\mathrm{\lambda }}_{j}t}\right)}{{\mathrm{\lambda }}_j}{\left(P_{i}M\left(0\right)\right)}_l{\left(P_j{k}^s\right)}_l.$$

Therefore we have the variance of lth species

$$\begin{gathered} {\sigma }_l^2\left(t\right)=V_{ll}\left(t\right)+{\left[M\left(t\right)\right]}_l-{\left({\left[M\left(t\right)\right]}_l\right)}^2 \\ =\sum _{i,j}{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}\left(P_{j}V\left(0\right)P_i^T\right)n+\sum _{i,j}[\left(\frac{{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-{\text{e}}^{{\mathrm{\lambda }}_{i}t}}{{\mathrm{\lambda }}_j}\right){\left[P_j{K}^s{\left(P_i{M}_0\right)}^T\right]}_{ll}+\left(\frac{{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-{\text{e}}^{{\mathrm{\lambda }}_{i}t}}{{\mathrm{\lambda }}_i{\mathrm{\lambda }}_j}-\frac{{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-1}{{\mathrm{\lambda }}_i\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)}\right){\left[P_j{K}^s{\left(P_{i}S\right)}^T\right]}_{ll}+\frac{{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-{\text{e}}^{{\mathrm{\lambda }}_{j}t}}{{\mathrm{\lambda }}_i}\left[P_j{M}_0{K}^s{P}_i^T\right]n+\frac{{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-{\text{e}}^{{\mathrm{\lambda }}_{j}t}}{{\mathrm{\lambda }}_i{\mathrm{\lambda }}_j}-\frac{{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-1}{{\mathrm{\lambda }}_j\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)}{\left[P_{j}S{K}^s{P}_i^T\right]}_{ll}]+\sum _{i,j}\sum _k\left({\left(P_j\right)}_{lk}C\left(i,k,l\right)+{\left(P_i\right)}_{lk}C\left(j,k,l\right)\right)\times [\sum _{r,{\mathrm{\lambda }}_r\ne {\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j}{\left(P_{r}M\left(0\right)\right)}_k\frac{1}{{\mathrm{\lambda }}_r-{\mathrm{\lambda }}_i-{\mathrm{\lambda }}_j}\left({\text{e}}^{{\mathrm{\lambda }}_{r}t}-{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}\right)-\frac{\left(P_r{k}^S\right)k}{{\mathrm{\lambda }}_r}\left(\frac{1}{{\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j}\left({\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-1\right)-\frac{1}{{\mathrm{\lambda }}_r-{\mathrm{\lambda }}_i-{\mathrm{\lambda }}_j}\left({\text{e}}^{{\mathrm{\lambda }}_{r}t}-{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}\right)\right)+\sum _{r,{\mathrm{\lambda }}_r={\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j}{\left(P_{r}M\left(0\right)\right)}_{k}t{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-\frac{{\left(P_r{k}^S\right)}_k}{{\mathrm{\lambda }}_r}\times \left(\frac{1}{{\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j}\left({\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-1\right)-t{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}\right)]-\sum _{i,j}{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}{\left(P_{i}M\left(0\right)\right)}_l{\left(P_{j}M\left(0\right)\right)}_l-\sum _{i,j}\frac{\left(1-{\text{e}}^{{\mathrm{\lambda }}_{i}t}\right)\left(1-{\text{e}}^{{\mathrm{\lambda }}_{j}t}\right)}{{\mathrm{\lambda }}_i{\mathrm{\lambda }}_j}{\left(P_i{k}^s\right)}_l{\left(P_j{k}^s\right)}_l+2\sum _{i,j}\frac{{\text{e}}^{{\mathrm{\lambda }}_{i}t}\left(1-{\text{e}}^{{\mathrm{\lambda }}_{j}t}\right)}{{\mathrm{\lambda }}_j}{\left(P_{i}M\left(0\right)\right)}_l{\left(P_j{k}^s\right)}_l. \end{gathered}$$

After some computation we get

$${\sigma }_l^2\left(t\right)=-\sum _{i,j}{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}{\left(P_i\odot P_{j}M\left(0\right)\right)}_l+\sum _i{\text{e}}^{{\mathrm{\lambda }}_{i}t}\left[{\left(P_{i}M\left(0\right)\right)}_l+\frac{{\left(P_i{k}^S\right)}_l}{{\mathrm{\lambda }}_i}\right]-\sum _i\frac{1}{{\mathrm{\lambda }}_i}{\left(P_i{k}^S\right)}_l+\sum _{i,j}\sum _{k}D(i,j,k,l)[\sum _r\left({\left(P_{r}M\left(0\right)\right)}_k+\frac{{\left(P_r{k}^s\right)}_k}{{\mathrm{\lambda }}_r}\right)f_{r,i,j}\left(t\right)-\frac{{\left(P_r{k}^S\right)}_k}{{\mathrm{\lambda }}_r\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)}\left({\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}-1\right)],$$

where

$$\begin{gathered} C(i,k,l)=\sum _{m=1}^n{\left(P_i\right)}_{lm}{K}_{mk}^{cat}, \\ D(i,j,k,l)=\left({\left(P_j\right)}_{lk}C(i,k,l)+{\left(P_i\right)}_{lk}C(j,k,l)\right), \\ {f}_{r,i,j}(t)=\{\begin{array}{ll}\frac{1}{{\mathrm{\lambda }}_r-{\mathrm{\lambda }}_i-{\mathrm{\lambda }}_j}\left({\text{e}}^{{\mathrm{\lambda }}_{r}t}-{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}\right)\hfill & \text{ if }{\mathrm{\lambda }}_r\ne {\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\hfill \\ t{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}\hfill & \text{ if }{\mathrm{\lambda }}_r={\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j,\hfill \end{array} \end{gathered}$$

and ‘⊙’ is componentwise matrix multiplication.

If there is no catalysis in the system, then

$$D\left(i,j,k,l\right)=0$$

and we have

$${\sigma }_l^2\left(t\right)=-\sum _{i,j}{\text{e}}^{\left({\mathrm{\lambda }}_i+{\mathrm{\lambda }}_j\right)t}{\left(P_i\odot P_{j}M\left(0\right)\right)}_l+\sum _i{\text{e}}^{{\mathrm{\lambda }}_{i}t}\left[{\left(P_{i}M\left(0\right)\right)}_l+\frac{{\left(P_i{k}^S\right)}_l}{{\mathrm{\lambda }}_i}\right]-\sum _i\frac{1}{{\mathrm{\lambda }}_i}{\left(P_i{k}^s\right)}_l.$$

Details for the proof of the binomial distribution

$$\begin{gathered} P\left(N_1\left(t\right)=m,N_2\left(t\right)=N-m\right) \\ =\sum _{i=0}^{N}P(N_1\left(t\right)=m,N_2\left(t\right)=N-m|N_1\left(0\right)=i,N_2\left(0\right)=N-i)\cdot P\left(N_1\left(0\right)=i,N_2\left(0\right)=N-i\right) \\ =\sum _{k=0}^m\sum _{i=k}^{N-m+k}\left(\begin{array}{l}i\hfill \\ k\hfill \end{array}\right)\left(p_t^k\left(1,1\right)p_t^{i-k}\left(1,2\right)\right)\left(\begin{array}{c}N-i\\ m-k\end{array}\right)\left(p_t^{m-k}(2,1)p_t^{N-i-m+k}(2,2)\right)\left(\begin{array}{c}N\\ i\end{array}\right)p_1{\left(0\right)}^i{p}_2{\left(0\right)}^{N-i} \\ =\sum _{k=0}^m\sum _{i=k}^{N-m+k}\left(\begin{array}{l}i\hfill \\ k\hfill \end{array}\right)\left(\begin{array}{c}N-i\\ m-k\end{array}\right)\left(\begin{array}{c}N\\ i\end{array}\right)\cdot {\left(p_1\left(0\right)p_t(1,1)\right)}^k{\left(p_1\left(0\right)p_t(1,2)\right)}^{i-k}{\left(p_2\left(0\right)p_t(2,1)\right)}^{m-k}\times {\left(p_2\left(0\right)p_t(2,2)\right)}^{N-i-m+k} \\ =\sum _{k=0}^m\sum _{l=0}^{N-m}\left(\begin{array}{c}k+l\\ k\end{array}\right)\left(\begin{array}{c}N-(k+l)\\ m-k\end{array}\right)\left(\begin{array}{c}N\\ k+l\end{array}\right)\cdot {\left(p_1\left(0\right)p_t(1,1)\right)}^k{\left(p_1\left(0\right)p_t(1,2)\right)}^l{\left(p_2\left(0\right)p_t(2,1)\right)}^{m-k}\times {\left(p_2\left(0\right)p_t(2,2)\right)}^{N-m-l},\text{ by letting }l=i-k \\ =\sum _{k=0}^m\sum _{l=0}^{N-m}\left(\begin{array}{c}N\\ m\end{array}\right)\left(\begin{array}{c}m\\ k\end{array}\right)\left(\begin{array}{c}N-m\\ l\end{array}\right){\left(p_1\left(0\right)p_t(1,1)\right)}^k{\left(p_1\left(0\right)p_t(1,2)\right)}^l\times {\left(p_2\left(0\right)p_t(2,1)\right)}^{m-k}{\left(p_2\left(0\right)p_t(2,2)\right)}^{N-m-1} \\ =\left(\begin{array}{c}N\\ m\end{array}\right)\left(\sum _{k=0}^m\left(\begin{array}{l}m\hfill \\ k\hfill \end{array}\right){\left(p_1\left(0\right)p_t(1,1)\right)}^k{\left(p_2\left(0\right)p_t(2,1)\right)}^{m-k}\right)\cdot \left(\sum _{l=0}^{N-m}\left(\begin{array}{c}N-m\\ l\end{array}\right){\left(p_1\left(0\right)p_t(1,2)\right)}^l{\left(p_2\left(0\right)p_t(2,2)\right)}^{N-m-l}\right) \\ =\left(\begin{array}{c}N\\ m\end{array}\right){\left(p_1\left(0\right)p_t(1,1)+p_2\left(0\right)p_t(2,1)\right)}^m\times {\left(p_1\left(0\right)p_t(1,2)+p_2\left(0\right)p_t(2,2)\right)}^{N-m} \\ =\left(\begin{array}{c}N\\ m\end{array}\right){\left(p_1\left(t\right)\right)}^m{\left(p_2\left(t\right)\right)}^{N-m},\text{ by }(52) \end{gathered}$$

where we used the fact that

$$\begin{gathered} \left(\begin{array}{c}k+l\\ k\end{array}\right)\left(\begin{array}{c}N-(k+l)\\ m-k\end{array}\right)\left(\begin{array}{c}N\\ k+l\end{array}\right) \\ =\frac{(k+l)!}{k!l!}\frac{(N-(k+l\left)\right)!}{(m-k)!(N-l-m)!}\frac{N!}{(k+l)!(N-(k+l\left)\right)!} \\ =\frac{N!}{m!(N-m)!}\frac{m!}{(m-k)!k!}\frac{(N-m)!}{l!(N-m-l)!} \\ =\left(\begin{array}{c}N\\ m\end{array}\right)\left(\begin{array}{l}m\hfill \\ k\hfill \end{array}\right)\left(\begin{array}{c}N-m\\ l\end{array}\right). \end{gathered}$$

Queuing theory and chemical reaction networks

There are formal similarities between chemical reaction networks and queuing networks (Arazi et al., 2004) that can be used to translate results between the two contexts. For example, the following shows that an open conversion network is equivalent to an M/M/∞ queuing network.

Consider an irreducible or strongly connected network consisting of M/M/∞ queues with s stations. The notation M/M/∞ means Poisson arrivals, exponential service time and an infinite number of servers. The scheme of this queuing network is as follows:

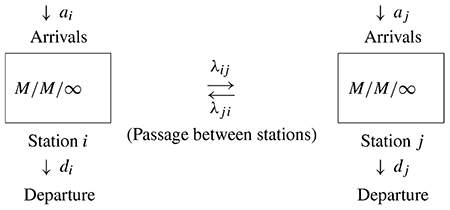
• Each station has M/M/∞ queuing scheme.

• a_i = rate of arrivals from outside the network into station i.

• When station i has n occupants, then individuals may depart the system at rate d_in.

• A customer leaving station i goes to station j with probability λ_ij, for i ≠ j.

The connection between the network of M/M/∞ queue and the open conversion network is as follows.

Network of M/M/∞ queues	Open conversion network
Station	Species
Customer	Molecule
Number of customers in station	Number of molecules of species
Arrival of a customer from outside the system	Production of a molecule from source
Departure out of system	Degradation
Transition from ith to jth station	Conversion from ith species to jth species

From this table we can see that N_i (t), the number of customers in the ith station at time t, corresponds to the number of molecules of the ith species at time t, and the rate a_i can be considered as $k_i^s$, d_i as $k_i^d$ and λ_ij as $K_{ji}^{con}$.

It can be shown that in a network of M/M/∞ queues the stationary distribution is Poisson. Furthermore, the distributions of N₁(t), …,N_s(t) for each time t are independent Poisson if the system is empty initially (Durrett, 1999).