Enzyme activation through the utilization of intrinsic dianion binding energy

Abstract

We consider ‘the proposition that the intrinsic binding energy that results from the noncovalent interaction of a specific substrate with the active site of the enzyme is considerably larger than is generally believed. An important part of this binding energy may be utilized to provide the driving force for catalysis, so that the observed binding energy represents only what is left over after this utilization’ [Jencks,W.P. (1975) Adv. Enzymol. Relat. Areas. Mol. Biol., 43, 219–410]. The large ~12 kcal/mol intrinsic substrate phosphodianion binding energy for reactions catalyzed by triosephosphate isomerase (TIM), orotidine 5′-monophosphate decarboxylase and glycerol-3-phosphate dehydrogenase is divided into 4–6 kcal/mol binding energy that is expressed on the formation of the Michaelis complex in anchoring substrates to the respective enzyme, and 6–8 kcal/mol binding energy that is specifically expressed at the transition state in activating the respective enzymes for catalysis. A structure-based mechanism is described where the dianion binding energy drives a conformational change that activates these enzymes for catalysis. Phosphite dianion plays the active role of holding TIM in a high-energy closed active form, but acts as passive spectator in showing no effect on transition-state structure. The result of studies on mutant enzymes is presented, which support the proposal that the dianion-driven enzyme conformational change plays a role in enhancing the basicity of side chain of E167, the catalytic base, by clamping the base between a pair of hydrophobic side chains. The insight these results provide into the architecture of enzyme active sites and the development of strategies for the de novo design of protein catalysts is discussed.

Introduction

There is a strong correlation between the rate acceleration for enzymatic reactions and enzyme affinity for the reaction transition state, but little or no correlation between rate acceleration and enzyme affinity for the substrate (Wolfenden and Snider, 2001). In 1975, William P. Jencks published a paper entitled ‘Binding Energy, Specificity and Enzymic Catalysis’ (Jencks, 1975), which contemplated possible explanations for the high specificity shown by enzymes in binding their transition states. This review focused on ‘the proposition that the intrinsic binding energy that results from the noncovalent interaction of a specific substrate with the active site of the enzyme is considerably larger than is generally believed. An important part of this binding energy may be utilized to provide the driving force for catalysis, so that the observed binding energy represents only what is left over after this utilization’ (Jencks, 1975). The review considered possible differences in the process for the binding of substrate from solution to form the Michaelis complex, and for conversion of this complex to the reaction transition state, and provided lucid explanations for complex experimental results. This classic paper provides a broad umbrella that presents several mechanisms for the utilization of intrinsic substrate binding energy in enzymatic catalysis. It has engendered the controversy expected for an article that expands the frontiers of Science (Kazemi et al., 2016).

We were fascinated by the results in Table I, highlighted in this review (Jencks, 1975), from William Ray's comprehensive study of phosphoryl transfer from the phosphoenzyme intermediate (E-P_i) to hydroxylic acceptors ROH (Scheme 1) catalyzed by β-phosphoglucomutase (β-PGM) (Ray and Long, 1976). The binding of phosphite dianion to β-PGM is shown in this table to result in a 580-increase in the reactivity of E-P_i for transfer of the phosphoryl group to water, and a (3 × 10⁴)-fold increase in the reactivity for transfer to oxygen-1 of xylose. What is most interesting is that the rate of the phosphite dianion activated reaction approaches that for the physiological reaction of substrate β-glucose 1-phosphate.

Table I.

Relative rate constants for phosphoryl transfer from the phosphoenzyme intermediate of β-PGM to acceptors ROH (Scheme 1)^a

ROH	Activator	(kcat)rel
HOH	None	1b
HOH	HPO32−	580
c	None	7 × 104
c	HPO32−	2 × 109
d	None	3 × 1010

^aThese data are abstracted from Table I of Jencks (1975), and were later reported in Ray and Long (1976).

^bThe value of (k_cat)_rel = 3.2 × 10⁻⁸ s⁻¹ was determined for phosphoryl transfer from β-PGM to water. The other values of (k_cat)_rel are reported for reactions at saturating concentrations of ROH and activator.

^cFor transfer of the phosphoryl group to O-1 of xylose.

^dFor transfer of the phosphoryl group to O-6 of β-glucose 6-phosphate.

Scheme 1.

Transfer of a phosphoryl group from a serine side chain of β-phosphoglucomutase to an alcohol acceptor. The activator is phosphite dianion (Table I).

The conclusion from these experiments is that the binding energy of exogenous phosphite dianion, and presumably the substrate phosphodianion, is utilized to activate β-PGM for catalysis of transfer of the phosphoryl group from the serine hydroxyl to oxygen-1 of xylose. This observation of a large enzyme activation by binding of the small phosphite dianion was largely ignored on entering the new millennium, when we considered the possibility that the result might be generalized to other enzymes.

Dianion binding energy and catalysis

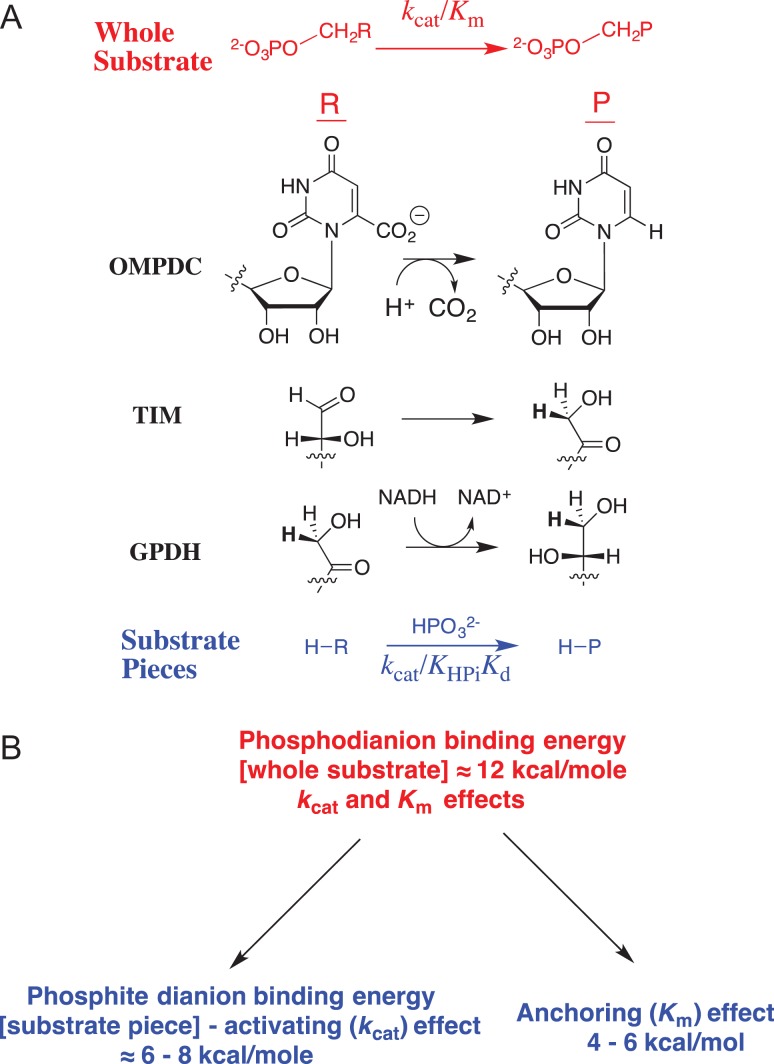
J.P.R. read this review in 1976 and viewed it as a starting point for launching a career in mechanistic enzymology, but then waited 25 years to act on this insight. Stimulated by the results summarized in Table I, we developed the following protocol (Fig. 1A) to separate the contribution of phosphodianion binding energy to catalysis by triosephosphate isomerase (TIM), orotidine 5′-monophosphate decarboxylase (OMPDC) and glycerol-3-phosphate dehydrogenase (GPDH) into binding interactions expressed at the Michaelis complex, and interactions that are expressed specifically at the transition state (Morrow et al., 2008). This three-step protocol compares (i) the total phosphodianion binding energy observed for the enzyme-catalyzed reaction of the whole phosphorylated substrate, where the binding interactions may utilize both to anchor the substrate to the enzyme and activate the enzyme for catalysis with; (ii) the binding energy expressed in enzyme-catalyzed reactions of the substrate pieces (see Table I), where the covalent anchor is eliminated, and only enzyme activation by interactions with the dianion is possible. This comparison then provides an estimate of the advantage provided by covalent attachment of the substrate pieces.

1. The total transition-state stabilization from interactions between these enzymes and their substrate phosphodianion – the intrinsic phosphodianion binding energy of 11–13 kcal/mol – is determined from the ratio of the second-order rate constants for enzyme catalysis of reactions of the whole and phosphodianion-truncated substrates (Amyes et al., 2001, 2005; Tsang et al., 2008).

2. The part of the total transition-state stabilization observed in the absence of a covalent connection between the dianion and the substrate – the intrinsic phosphite dianion binding energy of 6–8 kcal/mol – is determined by an analysis of the activation of phosphodianion-truncated substrates for enzyme catalysis by phosphite dianion (Amyes et al., 2005; Amyes and Richard, 2007; Tsang et al., 2008; Go et al., 2009). Dianion binding to form a Michaelis complex is scarcely detectable, and the binding energy is ≤2 kcal/mol. Most of the phosphite dianion binding energy is expressed specifically at the transition state for the catalyzed reaction.

3. The binding energy that is utilized to anchor the whole substrate to the enzyme (4–6 kcal/mol) is calculated as the difference in the intrinsic phosphodianion and phosphite dianion binding energy.

Fig. 1.

(A) Reactions of whole substrates RCH₂OPO₃²⁻ (k_cat/K_m), and substrate pieces RH + HPO₃²⁻ (k_cat/K_HPiK_d) catalyzed by OMPDC, TIM and GPDH. (B) Partitioning of the total 12 kcal/mol binding energy into the parts used for ground-state and transition-state stabilization

Figure 1B summarizes what we have learned about the partitioning of the intrinsic phosphodianion binding energy between ground-state (anchoring) and transition-state (activating) interactions, and the advantage obtained from covalent attachment of substrate pieces. Similar results were reported from studies to characterize the utilization of substrate binding energy by 1-deoxy-d-xylulose-5-phosphate reductoisomerase (Kholodar et al., 2015). The five enzymes for which dianion activation has been observed represent a limited sample size. However, it is probably significant that we have not encountered an example of an enzyme, which utilizes phosphodianion binding energy for the sole purpose of anchoring its substrate to the protein.

Mechanism for enzyme activation

The results from our studies on the utilization of phosphodianion binding energy in enzyme catalysis confirmed Bill Jencks's proposition ‘that the intrinsic binding energy that results from the noncovalent interaction of a specific substrate with the active site of the enzyme is considerably larger than is generally believed’. The observation that the phosphodianion binding energy is utilized for enzyme activation presents exciting opportunities for obtaining new insight into enzyme mechanisms through classical kinetic and product studies, while highlighting the limitations of X-ray crystallographic structural analyses that failed to identify bound substrate dianions as activators of TIM, OMPDC or GPDH.

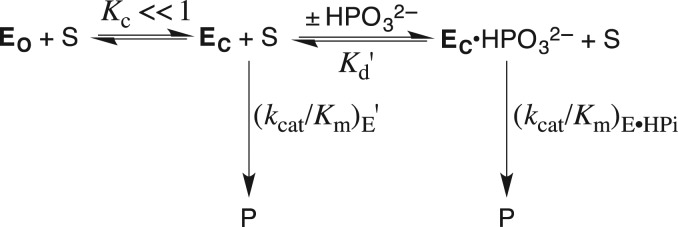
X-ray crystal structures provide a starting point for the development of a structure-based explanation for the observation of dianion activation (Go et al., 2009; Amyes and Richard, 2013). These structures show that each of TIM, OMPDC and GPDH has a flexible loop that is open at the unliganded enzyme (E_O), and which closes over the phosphodianion (E_C) of bound substrate to sequester the ligand from interaction with bulk solvent in a protein cage (Lolis and Petsko, 1990; Miller et al., 2000; Ou et al., 2006). Scheme 2 shows our model for enzyme activation. This model requires the following properties for the open (E_O) and closed (E_C) forms of these enzymes, in order to rationalize enzyme activation by phosphite dianion. The first two properties are documented by X-ray crystallographic data, and the third is easily justified.

1. There is a large difference in the reactivity of the open enzyme E_O (inactive) and the closed enzyme E_C (catalytic) for catalysis of the reaction of the truncated substrate. This is consistent with the large difference in the structures of unliganded open enzyme and the liganded closed form, where the catalytic side chains appear to be positioned to carry out the chemistry of the catalyzed reaction.

2. Loop closure is driven by interactions with phosphite dianion, which stabilize E_C relative to E_O. This suggests a role for the dianion gripper loops at TIM and OMPDC (Lolis and Petsko, 1990; Miller et al., 2000). These loops are open at the unliganded enzyme, and fold over the substrate phosphodianion to trap the ligand in a protein cage where it is sequestered from interaction with bulk solvent. The situation is more complicated for GPDH, where the loop that folds over, but does not interact directly with the dianion (Ou et al., 2006).

3. The unliganded enzyme shows a low activity towards catalysis of the reaction of the truncated substrate, because only a small fraction of the enzyme exists in the active closed form (K_C « 1, Scheme 2). The observed 4–6 kcal/mol stabilization of the transition state for the unactivated reaction of the truncated substrate by the binding of phosphite dianion requires a 4–6 kcal/mol barrier to quantitative conversion of E_O to E_C (Amyes and Richard, 2013). We have proposed that this represents the sum of the barriers to extrusion of protein bound waters to bulk solvent (Malabanan et al., 2010), and to the freezing motions at protein loops and catalytic side chains at the tightened structure for the protein-substrate cage (Malabanan et al., 2010, Richard et al., 2014a).

Scheme 2.

A model for enzyme activation, where the binding energy of phosphite dianion is used to drive the activating and thermodynamically unfavorable conversion of open enzyme E_O to E_C.

The model in Scheme 2 shows the utilization of the intrinsic substrate binding energy to drive an activating change in enzyme conformation. This is consistent with the notion that ‘An important part of [the substrate] binding energy may be utilized to provide the driving force for catalysis …’; but, does not illustrate the Circe Effect, which refers to ‘the utilization of strong attractive forces to lure a substrate into a site in which it undergoes an extraordinary transformation of form and structure’ (Jencks, 1975). The question of whether the intrinsic substrate binding energy might be utilized to induce strain into the substrate, which is relieved at the transition state, is beyond the scope of this review.

Enzyme architecture

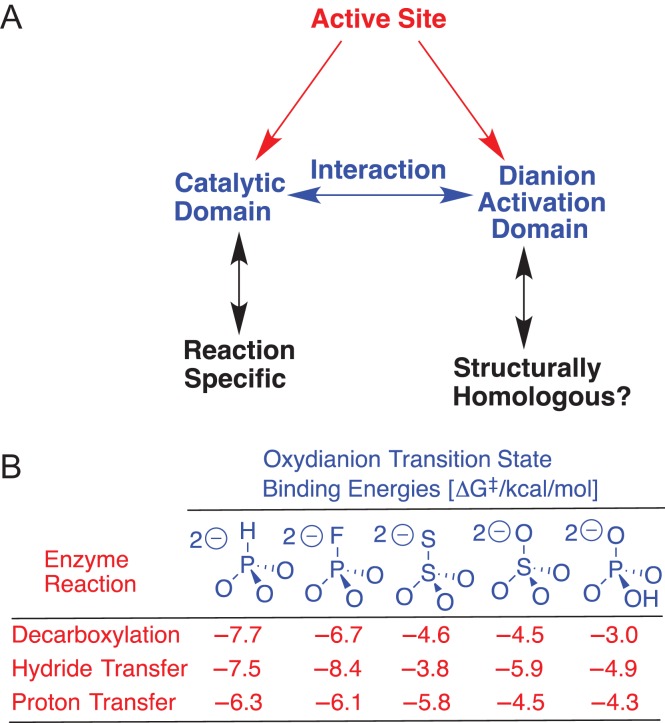
We proposed that whole active site for TIM, and by analogy other enzymes for which dianion activation has been observed, is divided into two domains (Fig. 2A) (Zhai et al., 2013). (i) A catalytic domain that carries out chemistry at the enzyme-bound substrate. This domain has typically been the focus of mechanistic studies on these enzymes. (ii) A dianion activation domain, which interacts with the catalytic domain and activates this site for chemical catalysis. This division facilitates a critical analysis of X-ray crystal structures of TIM, OMPDC and GPDH, which is required to move beyond the now simplistic notion that interactions between these enzymes and their dianion substrate fragments serve the exclusive function of anchoring the whole substrate to the protei. .

Fig. 2.

(A) A schematic for the now documented division of enzyme active site into interacting catalytic and dianion activation domains. (B) The stabilization of the transition states for OMPDC, GPDH and TIM-catalyzed reactions of phosphodianion-truncated substrates by interactions with dianion activators

We are working to examine the hypothesis that similar arrays of protein–dianion interactions have evolved to activate TIM, OMPDC and GPDH for catalysis of a chemically diverse set of reactions (Scheme 1A), and note the following similarities between their dianion activation sites.

1. The different dianion activation sites show similar interactions with a series of dianions XYO₃⁻², which are utilized in stabilization of the respective reaction transition states (Fig. 2B) (Spong et al., 2013; Zhai et al., 2015).

2. Each of TIM, OMPDC and GPDH has a cationic side chain, which interacts with the substrate phosphodianion to provide a large stabilization of the transition state for the catalyzed reaction: K12 for TIM, 7.8 kcal/mol (Go et al., 2010); R235 for OMPDC, 5.6 kcal/mol (Barnett et al., 2010); and R269 for GPDH, 9.1 kcal/mol (Reyes et al., 2015a).

3. Each of these side chain cations sits on the protein surface and forms an ion pair with the buried phosphodianion (Reyes et al., 2015a,b). The placement of the side chain on the surface favors efficient rescue (Peracchi, 2008) of catalytic activity, which is lost when the side chain is truncated by mutation, by interactions with small molecule analogs for the truncated side chain. The transition-state stabilization provided by 1.0 M exogenous cation is similar for these different mutant enzymes: K12G from TIM, 3.4 kcal/mol by 1.0 M EtNH₃⁺ (Go et al., 2010a,b); R235A from OMPDC, 3.0 kcal/mol by 1.0 M guanidine cation (Barnett et al., 2010); and R269A from GPDH, 6.7 kcal/mol by 1.0 M guanidine cation (Reyes et al., 2015a).

TIM (Go et al. 2010a) and GPDH (Reyes et al., 2015a) show 7.8 and 9.1 kcal/mol transition-state stabilization, respectively, from interactions with their respective cationic side chains, which is larger than the 5.6 kcal/mol transition-state stabilization observed for OMPDC (Barnett et al., 2010). The stronger interactions are observed for the former enzymes, because their side chain cations interact with both the negatively charged phosphodianion and the partly negatively charged carbonyl oxygen at the respective transition states. By contrast, the side chain cation of R235 for OMPDC lies 10 Å distant from the site of decarboxylation at the orotate ring, and interacts nearly exclusively with the phosphodianion of OMP (Amyes et al., 2012). The large 7.8 and 9.1 kcal/mol transition-state stabilization for TIM and GPDH, respectively, from interactions with cationic amino acid side chains illustrates the power of the precise organization of enzyme active sites in providing large stabilizing electrostatic interactions (Warshel, 1998). We suggest that these experimental results are an attractive target for modeling in computational studies.

Mutagenesis studies

A rigorous proof of the model shown in Scheme 2 requires that a direct connection be established between the magnitude of the barrier to the putative enzyme conformational change (K_C) and the enzyme activation by phosphite dianion. However, we do not know of a good protocol to determine the value for K_C. We have adopted an alternative approach of determining the effect of site-directed mutations of enzyme structure on the kinetic parameters for the enzyme-catalyzed reactions of the whole substrate and substrate pieces. These kinetic data have been rationalized by Scheme 2, and in fitting these data to Scheme 2 we obtain additional insight into the mechanism for enzyme activation.

Orotidine 5′-monophosphate decarboxylase

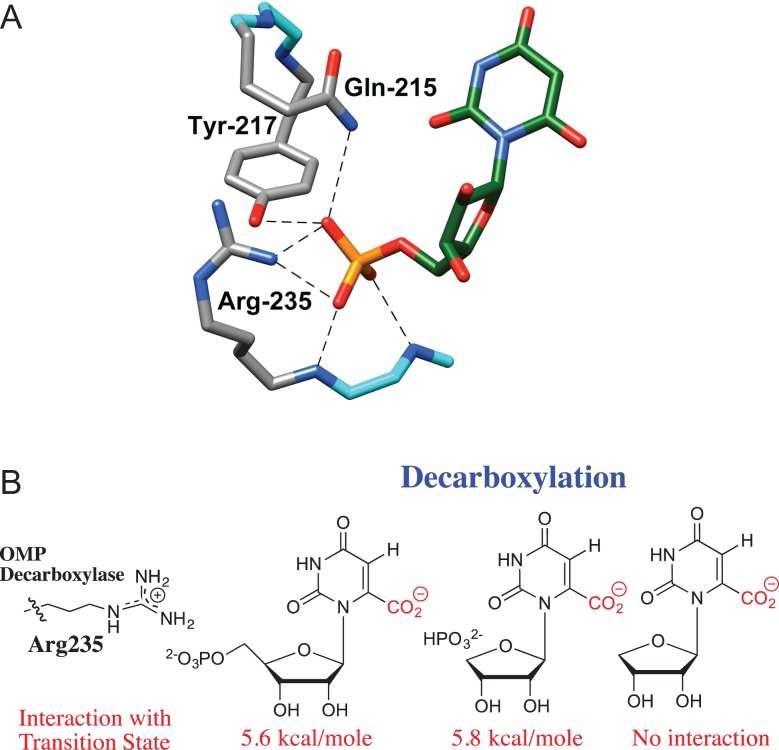
The dianion activation site of OMPDC consists of Q215, Y217 and R235, which lie ~10 Å distant from the site of decarboxylation of OMP (Fig. 3A) (Miller et al., 2000). This healthy separation between the catalytic and dianion activation sites is consistent with the notion that activation site may be treated as allosteric (Monod et al., 1965) in discussions of the mechanism of phosphite dianion activation of the OMPDC-catalyzed reaction of the truncated substrate 1-(β-d-erythrofuranosyl)orotic acid (EO). The following experimental observations show that there is little or no interaction between side chains at the dianion activation site and the substrate at the catalytic site.

1. The R235A mutation results in a 5.6-kcal/mol destabilization of the transition state for decarboxylation of the whole substrate OMP, a 5.8-kcal/mol destabilization of the transition state for decarboxylation of a complex between phosphite dianion and the truncated substrate 1-(β-d-erythrofuranosyl)orotic acid (EO), but the mutation has no effect on the stability of the transition state for decarboxylation of EO alone (Fig. 3B) (Goldman et al., 2014). If there is no interaction between the guanidine cation side chain and the orotate ring at the rate determining transition state for decarboxylation of EO, then no interaction is expected at the transition states for decarboxylation of the whole substrate OMP. These results are easily rationalized by a model where the binding energy is utilized for the sole purpose of driving an energetically unfavorable enzyme conformational change (Scheme 2).

2. Results similar to those described above were obtained for the Q215A, Y217F, Q215A/Y217F, Q215A/R235A, Y217F/R235A and Q215A/Y217F/R235A mutants of OMPDC. These mutations do not cause a large change in the activation barrier to decarboxylation of EO, but result in similar increases in the activation barriers to OMPDC-catalyzed decarboxylation of the whole substrate OMP and to decarboxylation of the complex between the substrate pieces EO and phosphite dianion (Goldman et al., 2014).

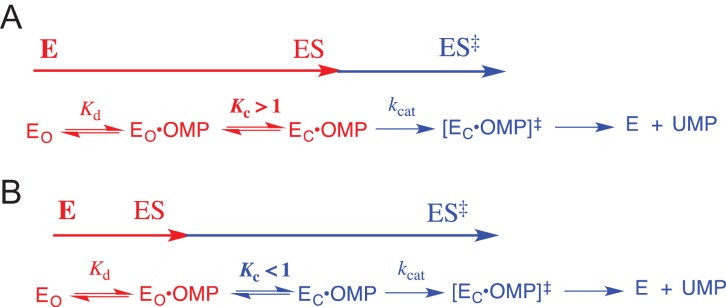
3. The effect of a single Q215A, Y217F and R235A mutation on the kinetic parameters for wildtype OMPDC is mainly on the kinetic parameter K_m, but the effect of the same mutation on OMPDC previously mutated at one of the remaining two positions is mainly on the kinetic parameter k_cat (Goldman et al., 2014). This is consistent with: (i) a value of K_C >> 1 for the Michaelis complex between OMP and wildtype OMPDC, which shows optimal stabilization by interactions with the phosphodianion, so that changes in the stability of E_C•OMP are expressed as changes in K_m (Scheme 3A), (ii) a large decrease to K_C < 1 for mutant enzymes with weakened enzyme–phosphodianion interactions. Now the enzyme conformational change is a step on the pathway for conversion of the dominant Michaelis complex E_O•OMP to the decarboxylation transition state [E_C•OMP]^†, and the effect of mutations that results in additional decreases in K_C is expressed as decreases in k_cat (Scheme 3B).

Fig. 3.

(A) A representation of the catalytic side chains that interact with OMP bound to OMPDC. Reprinted with permission from Goryanova et al. (2013) Copyright 2012 American Chemical Society. (B) Interaction of the respective transition states for OMPDC-catalyzed decarboxylation with the guanidine side chain of R235, determined from the effect of R235A mutations on enzyme activity (Goryanova et al., 2013)

Scheme 3.

A model for OMPDC-catalyzed decarboxylation of OMP, which includes the step for loop closure over enzyme-bound OMP. (A) The limiting case where there is a large driving force for loop closure (K_C > 1), so that changes in K_C are expressed as changes in the kinetic parameter K_m for decarboxylation of OMP. (B) The limiting case where loop closure is unfavorable (K_C < 1), so that changes in K_C are expressed as changes in the kinetic parameter k_cat for decarboxylation of OMP.

The above results show that dianion activation of OMPDC does not involve direct interactions between the enzyme-bound dianion and the orotate ring. This leaves the alternative explanation that activation is due to an indirect interaction between the catalytic and dianion activation domains (Fig. 2A). This interaction, which has not yet been characterized, is a proposed consequence of the dianion-driven enzyme conformational change shown in Scheme 2.

OMPDC from Methanothermobacter thermoautotrophicum was proposed to use phosphodianion binding energy to induce destabilizing electrostatic stress from interactions between substrate and enzyme [D70] carboxylates, which is then relieved at the transition state for decarboxylation to form CO₂ (Wu et al., 2000). This relief of destabilizing ground-state interactions at the decarboxylation transition state would result in an increase in k_cat for decarboxylation. The proposal is a potential example of the Circe effect, where ‘utilization of strong attractive forces to lure a substrate into a site in which it undergoes an extraordinary transformation of form and structure’ (Jencks, 1975).

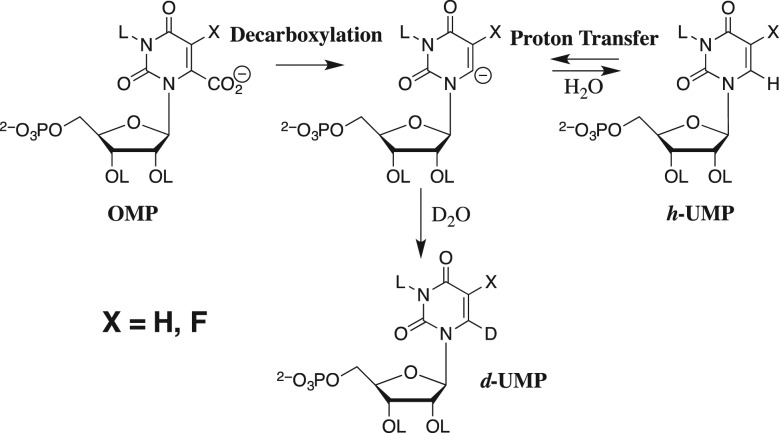
There is good evidence that OMPDC introduces no more than modest electrostatic stress into the bound substrate (Wu et al., 2000). OMPDC also catalyzes the exchange of deuterium between solvent D₂O and the C-6 position of OMP or 5-fluorouridine 5′-monophosphate (Scheme 4), where the enzyme-catalyzed decarboxylation and deuterium exchange reactions proceed through similar transition states that resemble their common C-6 carbanion intermediates (Amyes et al., 2008; Tsang et al., 2012). Only the ground state for the decarboxylation reaction might by destabilized by electrostatic stress from interactions between substrate and enzyme [D40] carboxylates. We have reported for OMPDC from Saccharomyces cerevisiae that the binding energy of phosphite dianion is utilized to provide similar activation of the enzyme-catalyzed decarboxylation and deuterium exchange reactions (Goryanova et al., 2011), and that the R235A mutation results in similar destabilization of the two reaction transition states (Goryanova et al., 2013). These results provide evidence that the OMPDC utilizes dianion binding energy mainly in the stabilization of the carbanion reaction intermediate common to the decarboxylation and deuterium exchange reactions. By contrast, results of studies on the effect of a D70N mutation of OMPDC from M. thermoautotrophicum on the kinetic parameters for enzyme-catalyzed decarboxylation and deuterium exchange reactions are consistent with modest substrate destabilization by interactions between substrate and enzyme [D70] carboxylates (Chan et al., 2009).

Scheme 4.

The decarboxylation of OMP and the deuterium exchange reaction of UMP in D₂O through a common vinyl carbanion reaction intermediate.

We have few experimental results that are relevant to the mechanism by which the dianion-driven conformational change of OMPDC (Scheme 2) activates this enzyme for the formation of an enzyme-bound vinyl carbanion intermediate. Our general model for such activation has been discussed in recent reviews (Amyes and Richard, 2013; Malabanan et al., 2014a,b).

Triosephosphate isomerase

In the case of OMPDC, the 10 Å separation between the substrate phosphodianion and orotate ring favors evolution of a dianion binding site whose side chains interact weakly with reactive substrate fragment at the catalytic site. By contrast, the phosphodianion bound at the activation site of TIM is close to the catalytic site for carbon deprotonation, so that side chains may interact directly with both the phosphodianion and the carbon acid. For example, K12 is commonly regarded as part of the catalytic assembly (Joseph-McCarthy et al., 1994; Lodi et al., 1994), and this side chain ammonium cation interacts with both the negatively charged phosphodianion and the partly negatively charged carbonyl oxygen at the transition states for deprotonation of enzyme-bound substrate (Go et al. 2010b).

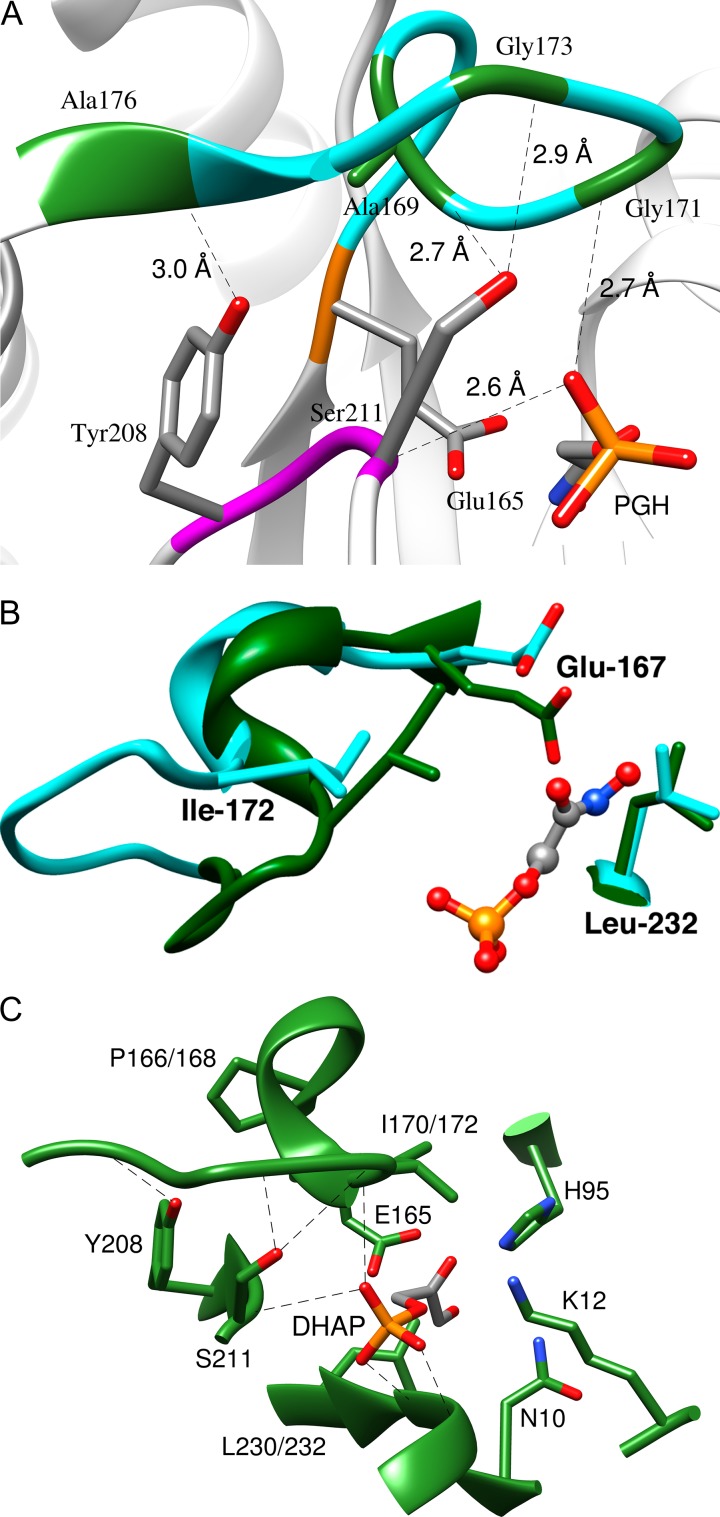
Figure 4A shows the complex between TIM and the enediolate analog phosphoglycolohydroxamate (PGH). The closed enzyme E_C is stabilized relative to E_O by the formation of the following H-bonds between flexible loop 6 [166-PVWAIGTGKTA] and loop 7 [208-YGGS] (Zhang et al., 1994): (i) the backbone amide NH of G173 and the γ-O of S211; (ii) the backbone amide NH of A176 and the phenol oxygen of Y208; (iii) the carbonyl oxygen of A169 and the γ-OH of S211. The important phosphodianion interactions at the activation site are hydrogen bonds between the phosphodianion backbone amide NH groups of G171 (loop 6), S211 (loop 7), G232 and G233 (loop 8).

Fig. 4.

(A) The closed form of TIM from chicken muscle (cTIM) in a complex with the intermediate analog PGH (PDB entry 1TPH) (Zhang et al., 1994), which shows hydrogen bonds between loops 6 and 7; and hydrogen bonds with the ligand phosphodianion. Reprinted with permission from Zhai et al. (2015). Copyright 2015 American Chemical Society. (B) Representations of the active sites of unliganded open (cyan, PDB entry 5TIM) and the PGH liganded closed (green, PDB entry 1TRD) forms of TbbTIM. Reprinted with permission from Malabanan et al. (2012). Copyright 2012 American Chemical Society. (C) A model, from an X-ray crystal structure, of the complex between yTIM and DHAP (PDB entry 1NEY). The side chains of H95, K12 and N10 play key roles in catalysis of the isomerization reaction. Reprinted with permission from Zhai et al. (2014). Copyright 2014 American Chemical Society

One mechanism for activation of TIM by dianion binding is suggested by the dianion-driven changes in the structure at the catalytic site shown in Fig. 4B. (i) There is movement of the active site base E167 into a position to deprotonate the bound substrate, and towards the hydrophobic side chain of L232. (ii) There is movement of the hydrophobic side chain from I172 towards the carboxylate side chain of E167. The clamping of the carboxylate side chain of E167 by the hydrophobic side chains of I172 and L232 was proposed to promote deprotonation of the carbon acid substrate by enhancing the basicity of this active site side chain. This proposal is supported by the observation that the I172A mutation of TIM results in a 100-fold falloff in k_cat/K_m for TIM-catalyzed isomerization (Malabanan et al., 2012) and in a ~2 unit decrease in the pK_a of the carboxylate side chain of E167 hydrogen-bonded to intermediate analog phosphoglycolate (PGA), from pK_a ≈ 10 for active, basic wildtype enzyme to 7.7 for the crippled I172A mutant (Malabanan et al., 2013). A more complicated explanation has been proposed to rationalize the effects of the L232A mutation on enzyme activity (Malabanan et al., 2011, 2012).

The X-ray crystal structures of complexes of PGA to I172A, L232A and I172A/L232A mutant TIMs are essentially superimposable on the structure of the PGA complex to wildtype TIM, except that the excised hydrophobic side chains are replaced by water molecules that lie ~3–4 Å distant from the active site base (Richard et al., 2016). The substitution of water for these hydrophobic side chains provides a rationalization for the decreased catalytic activity and basicity observed for the I172A mutant, but cannot rationalize the complex effects of L232A mutation.

Linear free energy relationships

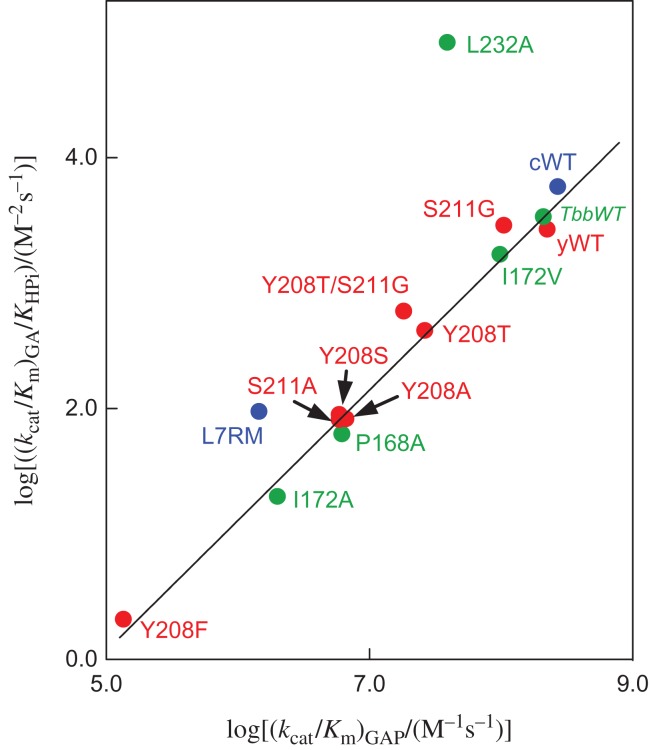
We proposed a model where phosphite dianion plays the active role of holding TIM in a high-energy closed active form (E_C, Scheme 2), but acts as a passive spectator in showing no effect on transition-state structure (Zhai et al., 2014). This model is strongly supported by the linear correlation, with slope 1.04 ± 0.03, between the second-order rate constant log (k_cat/K_m)_GAP for wildtype and mutant (Fig. 4C) TIM-catalyzed isomerization of GAP and the corresponding third-order rate constant log (k_cat/K_HPiK_GA) for the TIM-catalyzed reactions of the GA and HP_i (Fig. 5) (Zhai et al., 2014, 2015). The observation that mutations of TIM result in the same change in ΔG^† for the formation of the transition state for reactions of the whole substrate and the substrate in pieces (Scheme 5) is compelling evidence that these transition states show the same interactions with the mutated amino acid side chains, and that the transition states differ by only the covalent connection between the pieces at the whole substrate.

Fig. 5.

Logarithmic linear free energy relationship, with slope 1.04 ± 0.03, between rate constants (k_cat/K_m)_GAP (M⁻¹ s⁻¹) and (k_cat/K_HPiK_GA) (M⁻² s⁻¹) for wildtype and mutant TIM-catalyzed reactions of the whole substrate GAP and the pieces GA and HP_i, respectively (Scheme 5). The position of the amino acid side chains is shown in Fig. 4C: L7RM refers to a loop 7 replacement mutant (Zhai et al., 2013). Key: green symbols, mutants of TIM from Trypanosoma brucei (TbbTIM); blue symbols, mutants of TIM from chicken muscle (cTIM); red symbols, mutants of TIM from yeast (yTIM). Reprinted with permission from Zhai et al. (2015). Copyright 2015 American Chemical Society

Scheme 5.

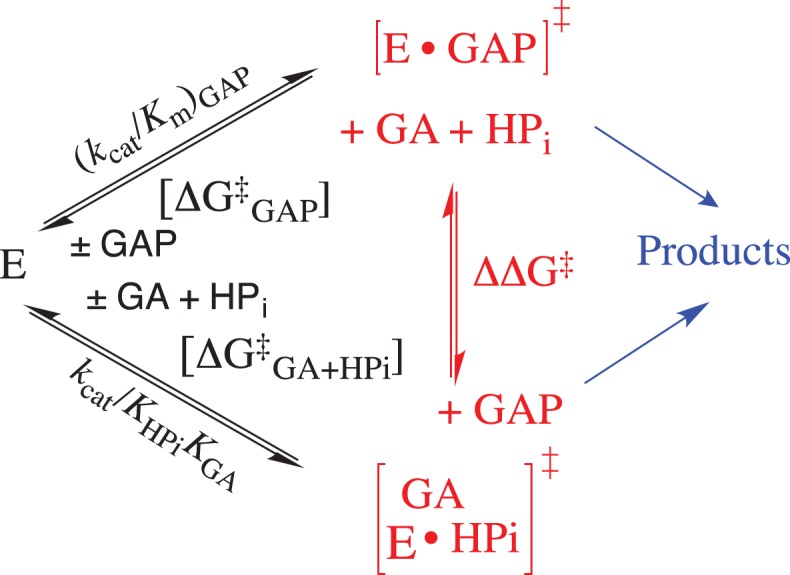
The TIM catalyzed reactions of the whole substrate GAP and the substrate pieces GA + HPO32-, where the relative activation barriers are shown as DDG^† for exchange of the respective enzyme-bound transition states at the enzyme active site.

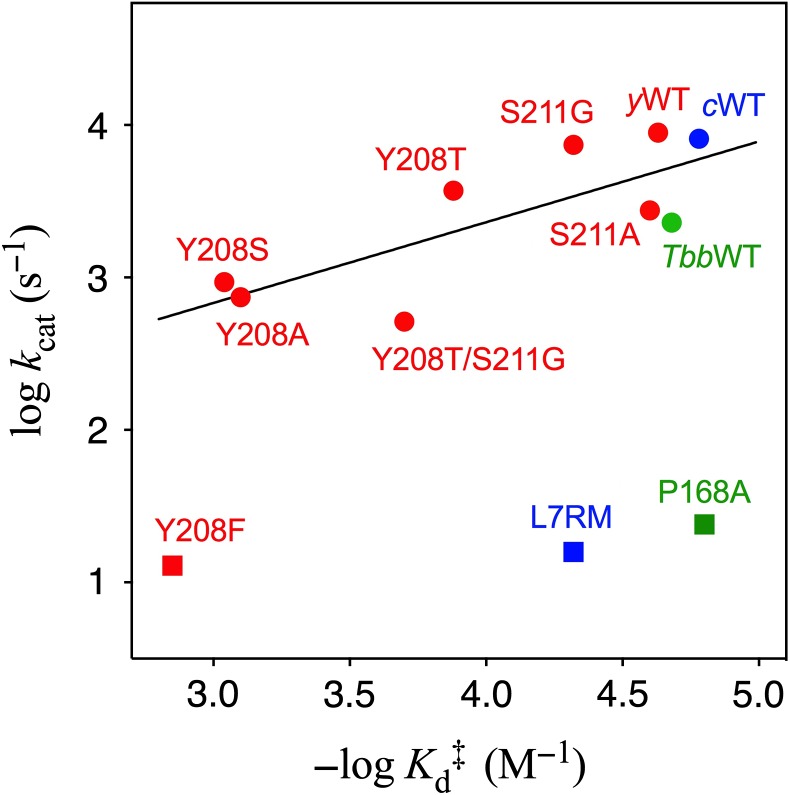
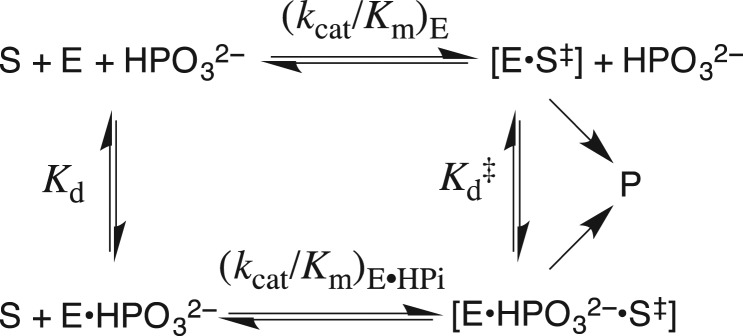
The data shown in Fig. 6 distinguish between mutations that affect the functioning of the dianion activation domain from mutations that directly affect the functioning of catalytic domain. Figure 6 shows the logarithmic plot of K_d^‡ against k_cat for mutations of TIM from yeast, where K_d^‡ is the affinity of phosphite dianion for the transition state, calculated from Equation (1) derived for Scheme 6, and k_cat is the kinetic parameter for TIM-catalyzed isomerization of GAP (Zhai et al., 2015). Most of these data for mutations of Y208 and S211 at the dianion activation site are correlated by a slope of 0.53 ± 0.16. This slope shows that ~50% of the change in the total intrinsic phosphite dianion binding energy (ΔG^‡ = –RTln($K_{\mathrm{d}}^{‡}$)) is expressed as decreases in activating phosphodianion binding energy for mutant TIM-catalyzed isomerization of GAP and result in reductions in k_cat (Richard et al., 2014a). There are several decreases in k_cat that cannot be attributed to a decrease in the total in dianion binding energy, but reflect the effect of the mutation on chemistry at the catalytic domain. For example, the catalytic base of E167 lies at an unreactive ‘swung-out’ position for the P168A mutant (Casteleijn et al., 2006). The position of the carboxylate of E167 changes from swung-in to swung-out for the P168A mutant (Casteleijn et al., 2006). This results in decreases in the values of k_cat and (k_cat/K_m)_E for reaction of the whole and truncated substrates, respectively, but in little change in K_d^‡ for binding of phosphite at the dianion activation domain (Zhai et al., 2013). These results are consistent with a decrease in the substrate reactivity at the catalytic domain. The kinetic parameters for most mutations of Y208, a side chain at the dianion activation domain (Sampson and Knowles, 1992), lie on the upper linear correlation from Fig. 6. The large negative deviation observed for Y208F shows that the effect of this mutation extends from the dianion activation domain to cause a decrease in the reactivity of substrate bound at the catalytic domain.

$$K_d^{\text{‡}}\text{=}\left[\frac{{K_d\left(k_{\text{cat}}\text{/}{K}_m\right)}_E}{{\left(k_{\text{cat}}\text{/}{K}_m\right)}_{\mathit{E•HPi}}}\right]$$ (1)

Fig. 6.

The logarithmic correlation between values of k_cat for TIM-catalyzed isomerization of GAP and $K_d^{\text{‡}}$ for phosphite dianion activation of wildtype and mutant TIM-catalyzed reactions of GA (Scheme 6). Key: green symbols, mutants of TIM from Trypanosoma brucei (TbbTIM); blue symbols, mutants of TIM from chicken muscle (cTIM); red symbols, mutants of yTIM. Reprinted with permission from Zhai et al. (2015). Copyright 2015 American Chemical Society

Scheme 6.

A thermodynamic cycle, which compares the binding of phosphite dianion to TIM (K_d) with the binding to the transition state for TIM-catalyzed deprotonation of GA (K_d^‡).

Broader issues

The satisfaction obtained from bringing order to the complex kinetic data described above is substantial and real, and yet pales in comparison to that which might be obtained from successfully drawing broader conclusions from these experimental results. Our results provide support for the model illustrated by Scheme 2, and insight into the imperatives for evolution of protein catalysts. This model suggests: (i) Non-reacting appendages at substrates, such as the phosphodianion, coenzyme A (Fraser et al., 2010) or ADP ribose (Plapp et al., 2016), have evolved to provide the binding energy to drive large protein conformational changes. (ii) Enzymes have evolved to undergo large conformational changes during turnover, because of the requirement that their active sites be accessible to solvent, and because of the advantages to catalysis at cage structures that maximize protein–ligand interactions (Wolfenden, 1974; Richard et al., 2014a). (iii) Flexible loops have evolved (in part) to confer floppy structures to proteins (Malabanan et al., 2010), which favor fast, kinetically competent conformational changes with rate constants ≥k_cat for turnover, and as large as ≥7300 s⁻¹ for the reaction catalyzed by TIM from yeast.

The problems experienced in developing protocol for the de novo design of active protein catalysts reflect, in part, the difficulties in defining the properties desired for the starting catalytic scaffold. Our results from studies on the mechanism for enzyme activation by dianions suggest that consideration should be given to the engineering scaffolds with the following properties.

1. Scaffolds, such as the TIM barrel, which contain flexible loops attached to rigid α-helices or β-sheets. Catalysis of reactions at protein cages is generally preferred to catalysis at a protein cleft (Richard et al., 2014a), because active site cages provide for optimal interactions with the bound substrate (Wolfenden, 1974). Rapid cage formation may be preferred for catalytic scaffolds such at the TIM barrel that contains flexible protein loops with the potential to rapidly fold into a protein cage (Richard et al., 2014a,b). The alternative is substrate binding at a deep active site cavity that is connected to the protein surface by a long tunnel, as is observed for a designed HG3.17 Kemp eliminase (Blomberg et al., 2013).

2. Scaffolds, such as the TIM barrel, where the side chains are restricted to flexible loops. There may be an advantage to placing catalytic side chains at flexible loops, because this will allow sampling of many energetically similar side chain conformations and selection of the conformation that provides optimal transition-state stabilization. This should reduce the difficulties associated with obtaining an optimal arrangement of a complex array side chains at a rigid protein when there are large penalties for small misalignments of these side chains (Blomberg et al., 2013).

3. Scaffolds engineered by the connections of dianion activation and catalytic domains. The former domain might be modeled by using a known phosphate gripper loop (Arsenieva and Jeffery, 2002; Chan et al., 2008) or phosphate cups (Denesyuk et al., 2003) as the dianion activation domain. This could then be connected to a designed catalytic domain.

Funding

The work from the authors laboratory described in this review was supported by following grants from the US National Institutes of Health: [GM116921 and GM039754 to J.P.R.]