Abstract
Archetypal analysis and non-negative matrix factorization (NMF) are staples in a statisticians toolbox for dimension reduction and exploratory data analysis. We describe a geometric approach to both NMF and archetypal analysis by interpreting both problems as finding extreme points of the data cloud. We also develop and analyze an efficient approach to finding extreme points in high dimensions. For modern massive datasets that are too large to fit on a single machine and must be stored in a distributed setting, our approach makes only a small number of passes over the data. In fact, it is possible to obtain the NMF or perform archetypal analysis with just two passes over the data.
Keywords: convex hull, random projections, group lasso
1 Introduction
Archetypal analysis (by Cutler and Breiman (1994)) and non-negative matrix factorization (NMF) (by Lee and Seung (1999)) are staple approaches to finding low-dimensional structure in high-dimensional data. At a high level, the goal of both tasks boils down to approximating a data matrix X ∈ Rn×p with factors W ∈ Rn×k and H ∈ Rk×p :
| (1.1) |
In archetypal analysis, the rows of H are archetypes, and the rows of W are convex combinations that (approximately) represent the data points. The archetypes are forced to be convex combinations of the data points:
| (1.2) |
By requiring the data points to be convex combinations of the rows of H, archetypal analysis forces the archetypes to lie on the convex hull of the data cloud. Thus the archetypes are interpretable as “pure” data points. Given (1.1) and (1.2), a natural approach to archetype analysis is to solve the optimization problem
| (1.3) |
The problem is solved by alternating minimization over W and B. The overall problem is non-convex, so the algorithm converges to a stationary point of the problem.
In NMF, the entries of X and H are also required to be non-negative. NMF is usually motivated as an alternative to principal components analysis (PCA), in which the data and components are assumed to be non-negative. In some scientific applications, requiring the components to be non-negative makes the factorization consistent with physical reality, and gives more interpretable results versus more classical tools. Given its many applications NMF has been studied extensively, and many clever heuristics were proposed over the years to find NMFs. Lee and Seung (2001) proposes a multiplicative update algorithm that solves the optimization problem
| (1.4) |
The solution to (1.4) is the maximum likelihood estimator for a model in which xij is Poisson distributed with mean (WH)ij. An alternative approach is to minimize the residual sum-of-squares by alternating minimization over W and H. Although these heuristics often perform admirably, none are sure to return the correct factorization.1 However, a recent line of work started by Arora et al. (2012) showed that the problem admits an efficient solution when the matrix is separable. In this work, we also focus on factorizing separable matrices.
Although the goal of both archetypal analysis and NMF boils down to the same matrix nearness problem, the two approachs are usually applied in different settings and have somewhat different goals. In NMF, we require k ≤ p. Otherwise, we may obtain a trival exact NMF by setting W = I and H = X. In archtypal analysis, we require k ≤ n, but allow k ≥ p. The archetype constraint (1.2) implies the archetypal approximation will not be perfect even if we allow k ≥ p.
1.1 Separable archetypal analysis and NMF
The notion of a separable NMF was introduced by Donoho and Stodden (2003) in the context of image segmentation.
Assumption 1.1
A non-negative matrix X ∈ Rn×p is separable if and only if there exists a permutation matrix P ∈ Rn×n such that
where W2 ∈ R(n−k)×k and H ∈ Rk×p are non-negative.
The notion of separability has a geometric interpretation. It asserts that the conical hull of a small subset of the data points (the points that form H) contain the rest of the data points, i.e. the rows of X are contained in the cone generated by the rows in H:
The rows of H are the extreme rays of the cone. If x1, …, xn are normalized to lie on some (affine) hyperplane A, then the separability assumption implies x1, …, xn are contained in a polytope P ⊂ A and h1, …, hk are the extreme points of P.
The separable assumption is justified in many applications of NMF; we give two common examples.
In hyperspectral imaging, a common post-processing step is unmixing: detecting the materials in the image and estimating their relative abundances. Unmixing is equivalent to computing a NMF of the hyperspectral image. The separability assumption asserts for each material in the image, there exists at least one pixel containing only that material. The assumption is so common that it has a name: the pure-pixel assumption. We refer to Gillis and Vavasis (2014) for further details.
In document modeling, documents are usually modeled as additive mixtures of topics. Given a collection of documents, the NMF of the document-term matrix reveals the topics in the collection. The separability assumption is akin to assuming for each topic, there is a word that only appears in documents concerning that topic. Arora et al. (2012) call such special words are called anchor words.
Given the geometric interpretation of separability, it is straightfoward to generalize the notion to archetypal analysis. In archetypal analysis, the archetypes hk, …, hk are usually convex combinations of the data points. If we force the archetypes to be data points, i.e. enforce
where the rows of E ∈ Rk×n are a subset of the rows of the identity matrix, then we are forcing the archetypes to be extreme points of the data cloud. The analogous optimization problem for separable archetype analysis is
| (1.5) |
where E is constrained to consist of a subset of the rows of the identity. It seems (1.5) is harder than (1.3) because minimizing over E is a combinatorial problem. However, as we shall see, separability allows us to reduce archetypal analysis and NMF to an extreme point finding problem that admits an efficient solution.
1.2 Related work on separable NMF
To place our algorithm in the correct context, we review the recently proposed algorithms for computing a NMF when X is separable. All these algorithms exploit the geometric interpretation of a separability and find the extreme points/rays of the smallest polytope/cone that contains the rows of X.
Arora et al. (2012) describe a method which checks whether each column of X is an extreme point by solving a linear program (LP). Although this is the first polynomial time algorithm for separable NMF, solving a LP per data point is not practical when the number of data points is large.
- Bittorf et al. (2012) make the observation that X has the form
for some C ∈ Rn×n. To find C, they solve a LP with n2 variables. To handle large problems, they use a first-order method to solve the LP. Gillis (2013) later developed a post-processing procedure to make the approach in Bittorf et al. (2012) more robust to noise. Esser et al. (2012) formulate the column subset selection problem as a dictionary learning problem and use ℓ1,∞ norm regularization to promote sparse dictionaries. Although convex, the dictionary learning problem may not find the sparsest dictionary.
Gillis and Vavasis (2014) describe a family of recursive algorithms that maximize strongly convex functions over the cloud of points to find extreme points. Their algorithms are based on the intuition that the maximum of a strongly convex function over a polytope is attained at an extreme point.
Kumar et al. (2013) describe an algorithm called Xray for finding the extreme rays by “expanding” a cone one extreme ray at a time until all the columns of X are contained in this cone.
Algorithms 1, 2, and 3 require the solution of convex optimization problems and are not suited to factorizing large matrices (e.g. document-term matrices where n ~ 109). Algorithms 1, 2, and 5 also require the non-negative rank k to be known a priori, but k is usually not known in practice. Algorithms 1 and 2 also depend heavily on separability, while our approach gives interpretable results even when the matrix is not separable. Finally, algorithm 4 requires U to be full rank, but this may not be the case in practice.
The idea of finding the extreme points of a point cloud by repeatedly maximizing and minimizing linear functions is not new. An older algorithm for unmixing hyperspectral images is pure-pixel indexing (PPI) by Boardman (1994). PPI is a popular technique for unmixing due to its simplicity and availability in many image analysis packages. The geometric intuition behind PPI is the same as the intuition behind our algorithm, but there are few results concerning the performance of this simple algorithm. Since its introduction, many extensions and modifications of the core algorithm have been proposed; e.g. Nascimento and Bioucas Dias (2005); Chang and Plaza (2006).
Recently, Ding et al. (2013) propose algorithms for topic modeling based on similar ideas. However, their sample complexity results are suboptimal. Their results imply O(k2 log k) random projections are necessary to recover all k extreme points with high probability. Our results show that the sample complexity is in fact O(k log k). In follow-up work, Ding et al. (2015) improve their results to match our result. More recently, Zhou et al. (2014) derive a divide-and-conquer scheme for finding the extreme points of a point cloud that divides the original problem into O(k log k) subproblem. We remark that their geometric intuition and proof technique is similar to ours. However, they do not relate the solid angle of normal cones at extreme points to the notion of α-simplicial.
2 Archetype pursuit
Given a cloud of points in the form of a data matrix X ∈ Rn×p, we focus on finding the extreme points of the cloud. We propose a randomized approach that finds all k extreme points in O(npk log k) floating point operations (flops) with high probability. In archetypal analysis, the extreme points are the candidate archetypes. Thus we refer to our approach as archetype pursuit. After finding the extreme points, we solve for the weights by nonnegative least squares (NNLS):
| (2.1) |
The geometric intuition behind archetype pursuit is simple: the extrema of linear functions over a convex polytope is attained at extreme points of the polytope. By repeatedly maximizing and minimizing linear functions over the point cloud, we find the extreme points. As we shall see, by choosing random linear functions, the number of optimizations required to find all the extreme points with high probability depends only on the number of extreme points (and not the total number of points).
Another consequence of the geometric interpretation is the observation that projecting the point cloud onto a random subspace of dimension at least k + 1 preserves all of the extreme points with probability one. Such a random projection could be used as a precursor to existing NMF algorithms as it effectively reduces the dimension of the problem. However, given the nature of the algorithm we discuss here a random projection of this form would yield no additional benefits.
2.1 A prototype algorithm
We first describe and analyze a proto-algorithm for finding the extreme points of a point cloud. This algorithm closely resembles the original PPI algorithm as described in Boardman (1994).
Algorithm 1.
Proto-algorithm
| Require: X ∈ Rn×p |
| 1: Generate an p × m random matrix G with independent standard normal entries. |
| 2: Form the product XG. |
| 3: Find the indices of the max Imax and min Imin in each column of XG. |
| 4: Return H = XImax∪Imin. |
The proto-algorithm finds points attaining the maximum and minimum of random linear functions on the point cloud. Each column of the random matrix G is a random linear function, hence forming XG evaluates m linear functions at the n points in the cloud. A natural question to ask is how many optimizations of random linear functions are required to find all the extreme points with high probability?
2.1.1 Relevant notions from convex geometry
Before delving into the analysis of the proto-algorithm, we review some concepts from convex geometry that appear in our analysis. A convex cone K ⊂ Rp is a convex set that is positively homogeneous, i.e. K = λK for any λ ≥ 0. Two examples are subspaces and the non-negative orthant . A cone is pointed if it does not contain a subspace. A subspace is not a pointed cone, but the non-negative orthant is. The polar cone K◦ of a cone K is the set
The notion of polarity is a generalization of the notion of orthogonality. In particular, the polar cone of a subspace is its orthogonal complement. Given a convex cone K ⊂ Rp, any point x ∈ Rp has an orthogonal decomposition into its projections2 onto K and K◦. Further, the components PK(x) and PK◦ (x) are orthogonal. This implies a conic Pythagorean theorem, i.e.
| (2.2) |
Two cones that arise in our analysis deserve special mention: normal and circular cones. The normal cone of a convex set C at a point x ∈ C is the cone
It is so called because it comprises the (outward) normals of the supporting hyperplanes at x.
A circular cone or ice cream cone is a cone of the form
In other words, a circular cone is a set of points making an angle smaller than arccos(t) with the axis a (arccos(t) is called the angle of the cone). The polar cone of a circular cone (with axis a ∈ Rp and aperture arccos(t)) is another circular cone (with axis −a and angle − arccos(t))
A solid angle is a generalization of the angles in the (Cartesian) plane to higher dimensions (see, e.g., Ball (1997) for details). Given a (convex) cone K ⊂ Rp, the solid angle ω(K) is the proportion of space that the cone K occupies; i.e. if we pick a random directionx ∈ Rp, the probability that x ∈ K is the solid angle at the apex of K. Mathematically, the solid angle of a cone K is given by
where the integral is taken over span(K). By integrating over the linear hull of K, we ensure ω(K) is an intrinsic measure of the size of K. When K is full-dimensional (i.e. span(K) = Rp), the solid angle is equivalent to (after a change of variables)
| (2.3) |
| (2.4) |
For a convex polytope P ⊂ Rp (the convex hull of finitely many points), the solid angles of the normal cones at its extreme points also form a probability distribution over the extreme points, i.e.
Furthermore, . Calculating the solid angle of all but the simplest cone in Rp, p > 3 is excruciating. Fortunately, we know bounds on solid angles for some cones.
For a point θ ∈ Sp−1, the set
is called a spherical cap of height t. Since the solid angle of a (convex) cone K ⊂ Rp is the proportion of Sp−1 occupied by K, the solid angle of a circular cone with angle arccos(t) is given by the normalized area of the spherical cap Cap(θ, t) for any θ ∈ Sp−1:
where σp−1 is the rotation-invariant measure on Sp−1 of total mass 1.
To state estimates for the area of spherical caps, it is sometimes convenient to measure the size of a cap in terms of its chordal radius. The spherical cap of radius r around a point θ ∈ Sp−1 is
Two well-known estimates for the area of spherical caps are given in Ball (1997). The lower bound is exactly (Ball, 1997, Lemma 2.3), and the upper bound is a sharper form of (Ball, 1997, Lemma 2.2).
Lemma 2.1 (Lower bound on the area of spherical caps)
The spherical cap of radius r has (normalized) area at least .
Lemma 2.2 (Upper bounds on the area of spherical caps)
The spherical cap of height t has (normalized) area at most
We are now ready to analyze the proto-algorithm. Our analysis focuses on the solid angles of normal cones at the extreme points hi of a convex polytope P ⊂ Rp. To simplify notation, we shall say ωi in lieu of ω(NP(hi)) when the polytope P and extreme point hi are clear from context. The main result shows we need O(k log k) optimizations to find all the extreme points with high probability.
Theorem 2.3
If , then the proto-algorithm finds all k extreme points with probability at least 1 − δ.
Sketch of proof
The basic methodology behind the proof is similar to that of the so-called coupon collector problem. Each time a random linear function is drawn, maximizing it over the polytope corresponds to finding a single extreme point with probability one. Furthermore, the probability that a random linear function will be maximized at a given extreme point is proportional to the size of that points normal cone. Therefore, we can think of the problem as having k extreme points to find and drawing with replacement from a discrete distribution over the points. All that remains is to work out how many samples are needed to ensure that we see each extreme point with probability 1 − δ.
Proof
Let hi, i = 1, …, k be the extreme points. By a union bound,
| (2.5) |
By the optimality conditions for optimizing a linear function, denoted gj, over a convex polytope, the event {miss xi} is equivalent to
Since the (random) linear functions gj, j = 1, …, m are i.i.d. 𝒩(0, I), we have
We substitute this expression into (2.5) to obtain
If we desire the probability of missing an extreme point to be smaller than δ, then we must optimize at least
linear functions.
The constant is smallest when . Thus, κ is at least , which is approximately when k is large. Since κ grows linearly with k, we restate Theorem 2.3 in terms of the normalized constant
Corollary 2.4
If , then the proto-algorithm finds all k extreme points with probability at least 1 − δ.
2.2 Simplicial constants and solid angles
The constant κ is a condition number for the problem. κ is large when the smallest normal cone at an extreme point is small. If ωi is small, then
is close to one. Intuitively, this means the polytope has extreme points that protrude subtly. The simplicial constant makes this notion precise. For any extreme point hi, the simplicial constant is
| (2.6) |
The simplicial constant is simply the distance of the extreme point hi to the convex hull formed by the other extreme points. To simplify notation, we shall say αi in lieu of αP (hi) when the polytope P and extreme point hi are clear from context. The following pair of lemmas serve to justify our intuition that an extreme point with a small normal cone protrudes subtly and vice versa. They also serve to connect the normal cones used in our analysis with the simplicial constants used elsewhere.
Lemma 2.5
Let P ⊂ Rk be a (convex) polytope and hi ∈ ext(P). If the solid angle of NP(hi) is ωi, then the simplicial constant
where and Rmax is a constant independent of hi.
Remark 2.6
Though we present Lemma 2.5 with a constant, Rmax, dependent on the geometry of the polytope, we observe that this constant is bounded by a quantity that is independent of hi and depends only on its “base.” Such geometric dependence is necessary because ω is scale invariant while αi is not. In fact, αi and diam(BP(hi)) depends on scale in the same manner as αi does, and thus implicitly adds the appropriate scaling to our bound.
Lemma 2.7
Let P ⊂ Rk be a (convex) polytope and hi ∈ ext(P). If the simplicial constant is αP(hi) = αi, then
when
and where rmin is a constant that depends on geometric properties of the polytope.
Remark 2.8
Similar to the situation for Rmax, rmin depends on geometric properties of the polytope.
To our knowledge, Lemmas 2.5 and 2.7 are new and the proofs may be found in the supplementary material. The constants Rmax in Lemma 2.5 and rmin in 2.7 are non-optimal but their dependence on P is unavoidable since normal cones are scale invariant, but simplicial constants are not. Although sharper bounds on the area of spherical caps are known,3 we state our results in the aforementioned form for the sake of clarity.
In the literature on NMF, a common assumption is the simplical constant of any extreme point is at least some α > 0. By Lemma 2.5, the simplicial constant being at least α implies
The relationship between solid angles and simplicial constants is often obscure, and in the rest of the paper, we state results in terms of solid angles ω1, …, ωk.
Before we move on to develop variants of the proto-algorithm, we comment on its computational cost in a distributed setting. On distributed computing platforms, communication between the nodes is the major computational cost. Algorithms that make few passes over the data may be substantially faster in practice, even if they require more flops. As we shall see, it is possible to perform NMF or archetypal analysis with just two passes over the data.
Consider a typical distributed setting: the data consists of n data points distributed across D nodes of a large cluster. Let Id ⊂ [n] be the indicies of the data points stored on the d-th node. To perform NMF or archetypal analysis, each node evaluates (random) linear functions on the data points stored locally and returns (i) the indices of the data points that maximize and minimize the linear functions Id,max, Id,min ⊂ Id and (ii) the optimal values. Each node evaluates the same set of linear functions on its local data points, so the optimal values are comparable. A node collects the optimal values and finds the maximum and minimum values to find the extreme points. We summarize the distributed protoalgorithm in algorithm 2. While we present the algorithm here under the assumption that each node contains a subset of the data points, it is equally amenable to parallelization in the situation where each node contains a subset of the features for all of the data point.
Algorithm 2.
Proto-algorithm (distributed)
| 1: | Choose a random seed and distribute it to all nodes. |
| 2: | for d = 1, …, D do in parallel |
| 3: | Generate a p × m random matrix G with independent 𝒩(0, 1) entries. |
| 4: | Form the product XIdG. |
| 5: | for i = 1, …, p do |
| 6: | Let (Vi,d,max, Ii,d,max) and (Vi,d,min, Ii,d,min) denote pairs of the max and min values in column i of XIdG and the corresponding index. |
| 7: | end for |
| 8: | end for |
| 9: | for i = 1, …, p do |
| 10: | Let and denote the indices of the max and min values in the sets and , respectively. |
| 11: | Set . |
| 12: | end for |
| 13: | Return H = XImax∪Imin. |
The algorithm makes a single pass over the data: each node makes a single pass over its (local) data points to evaluate the linear functions. The subsequent operations are performed on the indices Id,min, Id,max and optimal values and do not require accessing the data points. The communication costs are also minimal. As long as the nodes are set to produce the same stream of random numbers, the linear functions don’t need to be communicated. The only information that must be centrally collected are the pairs of values and indices for the maximum and minimum values in each column of the distributed matrix product.
The proto-algorithm finds the extreme points of the point cloud. We obtain the coefficients W ∈ Rn×k that expresses the data points in terms of the extreme points by solving (2.1). The NNLS problem (2.1) is separable across the rows of W. Thus it suffices to solve D small NNLS problems: each node solves a NNLS problem on the data points stored locally to obtain the coefficients that represent its (local) data point in terms of the extreme points. Solving the NNLS problem requires a second pass over the data. Thus it is possible to perform archeypal analysis or NMF with two passes over the data.
2.3 Three practical algorithms
The proto-algorithm requires the non-negative rank k and the condition number κ to be known a priori (to set m correctly). In this section, we describe three practical algorithms: one for noiseless X and two for noisy X. When X is noiseless, we seek to recover all the extreme points, no matter how subtly a point protrudes from the point cloud.
Algorithm 3.
Noiseless algorithm
| Require: X ∈ Rn×p | |
| 1: | Set Imax = Imin = ∅. |
| 2: | repeat |
| 3: | Generate a p × m random matrix G with independent 𝒩(0, 1) entries. |
| 4: | Form the product XG. |
| 5: | Find the indices of the max and min in each column of XG. |
| 6: | Set . |
| 7: | until adds nothing to . |
| 8: | Return H = XImax∪Imin. |
The noiseless algorithm stops when m optimization find no missed extreme points (m failures). This stopping rule admits an a posteriori estimate of the size of the normal cone at any missed extreme point. Consider each optimization as a Bernoulli trial with p = 2Σi∈Imiss ωi (success is finding a missed extreme point). The noiseless algorithm stops when we observe m failures. A 1 − α confidence interval for p is
Lemma 2.9
The noiseless algorithm finds all extreme points with with probability at least 1 − δ.
In the presence of noise, we seek to select “true” extreme points and discard spurious extreme points created by noise. Since optimizing linear functions over the point cloud gives both true and spurious extreme points, we propose two approaches to selecting extreme points.
The first approach is based on the assumption that spurious extreme points protrude subtly from the point cloud. Thus the normal cones at spurious extreme points are small, and these points are less likely to be found by optimizing linear functions over the point cloud. This suggests a simple approach to select extreme points: keep the points that are found most often.
The second approach is to select extreme points by sparse regression. Given a set of extreme points (rows of H), we solve a group lasso problem (each group corresponds to an extreme point) to select a subset of the points:
| (2.7) |
where λ is a regularization parameter that trades-off goodness-of-fit and group sparsity. The group lasso was proposed by Yuan and Lin (2006) to select groups of variables in (univariate) regression and extended to multivariate regression by Obozinski et al. (2011). Recently, Kim et al. (2012) and Elhamifar et al. (2012) propose similar approaches to NMF.
We enforce a non-negativity constraint to keep W non-negative. Although seemingly innocuous, most first-order solvers cannot handle the nonsmooth regularization term and the non-negativity constraint together. Fortunately, a simple reformulation allows us to use off-the-shelf first-order solvers to compute the regularization path of (2.7) efficiently. The reformulation hinges on a key observation.
Lemma 2.10
The projection of a point x ∈ Rp onto the intersection of the second-order cone and the non-negative orthant is given by
Although we cannot find Lemma 2.10 in the literature, this result is likely known to experts. For completeness, we provide a proof in the Supplementary material. We formulate (2.7) as a second-order cone program (SOCP) (with a quadratic objective function):
Since ti, i = 1, …, k are non-negative, the problem is equivalent to
| (2.8) |
Since the we know how to projection onto the feasible efficiently, most off-the-shelf first-order solvers (with warm-starting) are suited to computing the regularization path of (2.8).
In practice, the non-negative rank k is often unknown. Fortunately, both approaches to selecting extreme points also give estimates for the (non-negative) rank. In the greedy approach, an “elbow” on the scree plot of how often each extreme point is found indicates how many extreme points should be selected. In the group lasso approach, persistence of groups on the regularization path indicates which groups correspond to “important” extreme points; i.e. extreme points that are selected by the group lasso on large portions of the regularization path should be selected. These observations are borne out in our computational experiments.
3 Simulations
We conduct simulations to
validate our results on exact recovery by archetype pursuit.
evaluate the sensitivity of archetype pursuit to noise.
3.1 Noiseless
To validate our results on exact recovery, we form matrices that we know admit a separable NMF and use our algorithm to try and find the matrix H. We construct one example to be what we consider a well conditioned matrix, i.e. all of the normal cones are large, and we construct another example where the matrix is ill conditioned, i.e. some of the normal cones may be small.
In order to construct matrices to test the randomized algorithm we use the following procedure. First, we construct a k×p matrix H and a n×k matrix W such that X = W H has a separable NMF. The matrix W contains the identity matrix as its top k × k block and the remainder of its entries are drawn from uniform random variables on [0, 1] and then each row is normalized to sum to one. This means that given the matrix X we know that the first k rows of X are the rows we wish to recover using our algorithm.
In Section 2 we discussed the expected number of random linear functions that have to be used in order to find the desired rows of the matrix X with high probability. To demonstrate these results we use Algorithm 3 with various choices of m and see if the algorithm yields the first k rows of X.
To generate the plots shown here we vary k and for each k we vary the number of random projections used, m. For each pair of k and m we construct matrices W and H 500 times, run the algorithm on the resulting X and report the percentage of time that the algorithm correctly found the first k rows of X to be the necessary columns to form a separable NMF. For all of the experiments here we use n = 500 and p = 1000.
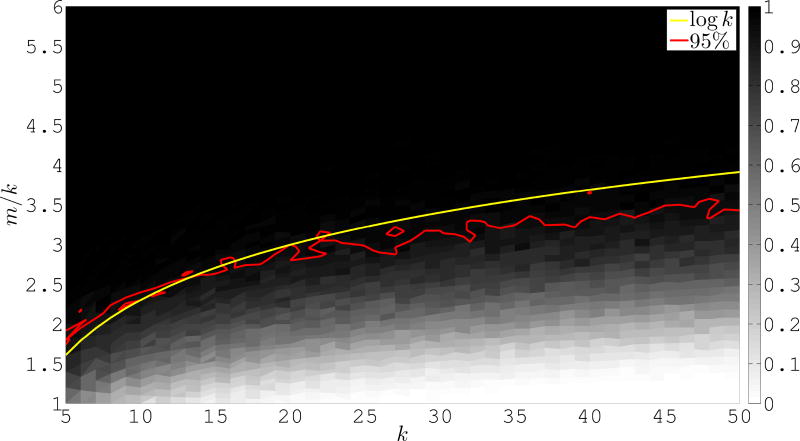
To demonstrate the algorithm on a well conditioned example we construct the matrix H to have independent entries each of which are uniform on [0, 1]. We expect the convex hull of the point cloud formed by H to have reasonably sized normal cones. Figure 1 shows the recovery percentages for this experiment as we vary m and k. We measure the number of random linear functions used as a factor times k. To show the scaling that we expect, up to the aforementioned constant, we also plot the line m/k = log k. Finally, we plot the 95% isocline. We observe that the isoclines behave like m = k log k and in fact appear to grow slightly slower. Furthermore, in this case the constant factor in the bounds appears to be very small.
Figure 1.
Percentage of experiments in which the algorithm correctly identified the first k rows of X as the rows of H in a separable NMF. Here H is a matrix with independent entries each of which is uniform on [0, 1].
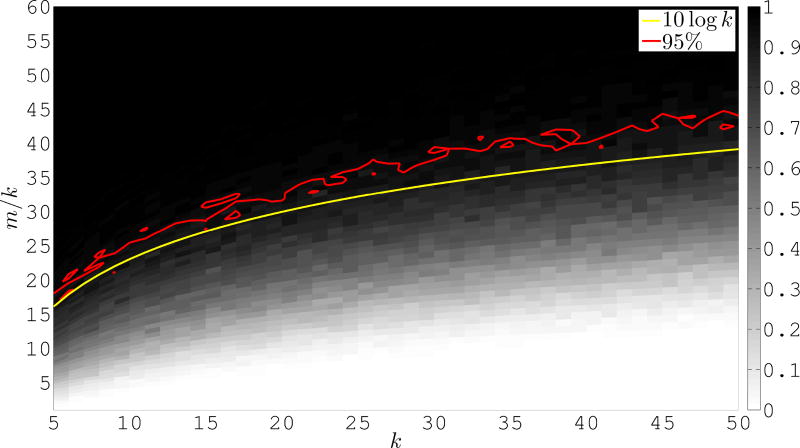
For our poorly conditioned example we take the matrix H to be the first k rows of the p × p Hilbert matrix, whose i, j entry is given by . This matrix is notoriously ill conditioned in the classical sense, e.g. for a 1000 × 1000 Hilbert matrix the computed condition number of a matrix constructed from the first 50 rows is on the order of 1017 and may in fact be considerably larger. Because even a reasonably small subset of the leading rows of the Hilbert matrix are very close to linearly dependent we expect that the convex polytope defined by there points is very flat and thus some of the extreme points have very small normal cones. Figure 2 shows the recovery percentages for this experiment as we vary m and k. Similar to before we measure the number of random linear functions used as a factor times k. Once again, to demonstrate the scaling that we expect, up to the aforementioned constant, we also plot the line m/k = log k. As before, we also plot the 95% isocline.
Figure 2.
Percentage of experiments in which the algorithm correctly identified the first k rows of X as the rows of H in a separable NMF. Here H is the first k rows of a p × p Hilbert matrix.
We observe that once again the isoclines behave like m = k log k, though in this case the constant factor is considerably larger than it was before. Given the interpretation of this experiment as trying to find the NMF of a very ill conditioned matrix we expected to observe a larger constant for complete recovery. Though, the algorithm does not require an unreasonable number of projections to recover the desired columns. In fact here we see that in order to recover the correct columns close to 95% of the time we require m to be slightly larger than 10k log k.
3.2 Noisy
We now demonstrate the performance of the algorithm when rather than being given the matrix X = W H, we instead have a matrix of the form X̃ = W H +N, where N represents additive noise.
For the first example, similar to before, we construct H to be a 20 × 1000 matrix. However, now, similar to the experiments in Gillis and Vavasis (2014) we let WT = [I W2] where W2 is a matrix whose columns are all the possible combinations of placing a 1/2 in two distinct rows and 0 in the remaining rows. Finally, the matrix N is constructed with independent ε𝒩(0, 1) entries.
To demonstrate the performance of the algorithm on this noisy example we ran the algorithm using the majority voting scheme on matrices with varying levels of noise. We fixed the nonnegative rank to be 20 and took various values of m and ε. For each value of m and ε we constructed the matrices W, H, and N as previously described. After forming the matrix XN we ran the algorithm 50 times on the matrix. Each time the 20 most frequently found rows are collected into the rows of a matrix denoted H̃ and the rows of W̃ are computed using nonnegative least squares to try and satisfy X = W̃ H̃.
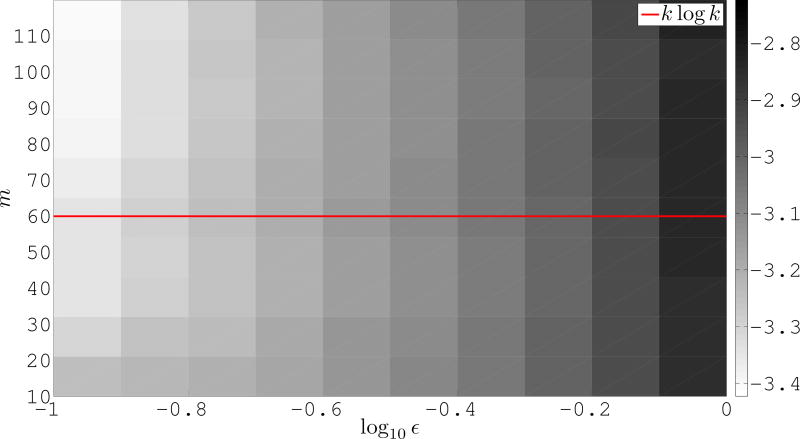
Figure 3 shows the error computed as
for various values of m and ε on a log10 scale. Each pixel represents the average error over 50 trials. We observe that as expected the overall error increases with ε, but that after an appropriate number of random projections the error does not significantly decay.
Figure 3.
‖X − W̃ H̃‖F/n on a log10 scale for various ε and m when using a majority vote scheme to select H̃.
To complement the plot of the residual error, we demonstrate the behavior of the random voting scheme itself in the presence of noise. To do this, we construct 100 matrices XN for 10 distinct ε and use m = 20k log k. Figure 4 shows a sorted version of the number of times each row is found, as a fraction of the maximum number of votes a singe row received. Each row of the image represents an experiment, and each block of 100 rows corresponds to a fixed noise level. As expected we see that there is a significant drop off in votes between the 20 significant rows and the remaining columns as long as the noise is small. Once the noise becomes larger, we see that more points are becoming relevant extreme points and thus there is no longer a sharp transition at 20. One interesting note is that, because each row receives at least one vote, adding the noise has perturbed the convex polytope in a way such that all points are now extreme points.
Figure 4.
Number of votes received for each row, sorted and normalized by the largest number of votes received. Each row of the image represents a distinct instance of the experiment, and each block of 100 rows corresponds to a given noise level, ε.
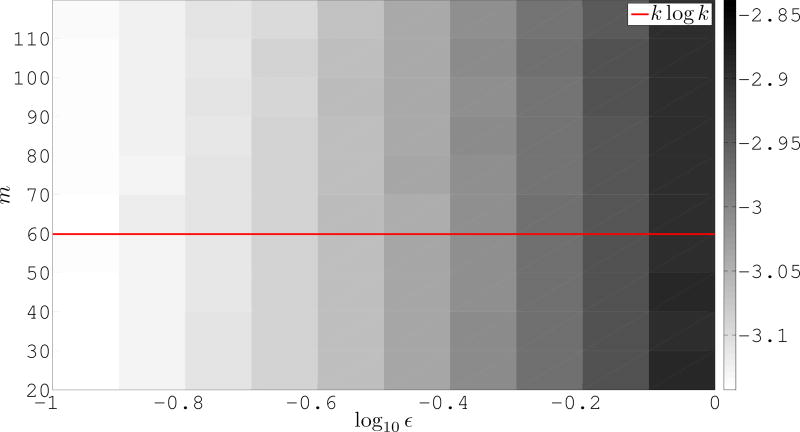
Finally, we demonstrate the behavior of the algorithm when coupled with the group LASSO approach for picking rows we ran the algorithm using the same setup as for the random voting example. This means that we fixed the rank at 20 and used the group LASSO path to pick which 20 columns, of those found via the prototype algorithm, should form H̃. The rows of W̃ are then computed using nonnegative least squares to try and satisfy X = W̃ H̃.
Figure 5 shows the error computed as before for various values of m and ε on a log10 scale. Each pixel represents the average error over 50 trials. We observe, once again, that as expected the overall error increases with ε, but that the algorithm is not sensitive to the number of random linear functions used. Even a small number of random linear functions is sufficient to identity the key columns.
Figure 5.
‖X − W̃ H̃‖F/n on a log10 scale for various ε and m when using the group LASSO to select the rows of H̃.
3.3 Comparison with the successive projection algorithm (SPA)
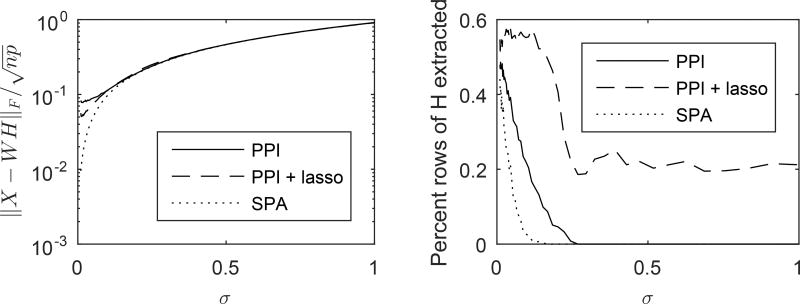
It is known that PPI performs poorly when there are near-duplicate extreme points. However, our theoretical analysis suggests that there is more to the story: the extreme points that PPI tends to miss are those with small normal cones, and, as the theoretical results in Section 2.2 show, point with small normal cones protrude subtly from the convex hull. Thus missing such extreme points are unlikely to degrade the approximation properties of the selected extreme points. That is, missing such points does not cause
to increase significantly. In this section, we present the results of simulations that support the preceding thesis.
We adopt the setup of Gillis and Vavasis (2014). For completeness, we describe it here. The entries of H are i.i.d. unif(0, 1) random variables. The weights W are given by
where the rows of H3 are i.i.d. Dirichlet random vectors whose parameters are chosen uniformly at random in [0, 1]. We form M = W H and add i.i.d. 𝒩(0, σ2) noise to each entry of M, where σ2 is allowed to vary. We point out that the implementation of PPI is different from that of Gillis and Vavasis (2014). The implementation of Gillis and Vavasis (2014) fixes the number of random projections at 1000, while we vary the number of random projections according to Algorithm 3.
The results of our simulations are shown in Figures 6. We find that although PPI and PPI + lasso both miss a significant fraction of the extreme points, the approximation error remains comparable to that of SPA, an approach that is known to be robust to noise. In terms of extreme point recovery, our simulation results agree with those of Gillis and Vavasis (2014). In particular, Figure 6 shows that the k extreme points most often found by PPI are usually not the true extreme points. However, PPI + lasso consistently recovers a higher fraction of extreme points than SPA. From a statistical perspective, this is unsurprising. SPA is essentially a greedy matching pursuit type algorithm while PPI + lasso is a regularized M-estimator. Over the past decade, there has been a flurry of results, both theoretical and computational, that regularized M-estimators outperform their greedy counterparts.
Figure 6.
The performance of PPI and PPI + lasso versus that of SPA in terms of approximation error and recovery of true extreme points.
To complement the simulations presented here, we provide two experiments using real world data sets in the supplementary material. The first example is based on the origins of PPI and seeks to find the important pixels, interpreted as a pure version of each class of object in the image, in a hyper-spectral image of the National Mall in Washington, DC. The second example seeks to discover “metagenes” from gene expression data via NMF.
4 Conclusion and discussion
Archetype pursuit is a unified approach to archetypal analysis and non-negative matrix factorization. The approach is motivated by a common geometric interpretation of archetypal analysis and separable NMF. Two key benefits of the approach are
scalability: The main computational bottleneck is forming the product XG, and matrix-vector multiplication is readily parallelizable.
simplicity: The proto-algorithm is easy to implement and diagnose (when it gives unexpected results).
Furthermore, our simulation results show the approach is robust to noise.
In the context of NMF, an additional benefit is that our approach gives interpretable results even when the matrix is not separable. When the matrix is not separable, the approach no longer gives the (smallest non-negative rank) NMF. However, the geometric interpretation remains valid. Thus, instead of the (minimum non-negative rank) NMF, our approach gives two non-negative factors W and H such that X ≈ W H, where the rows of H are the extreme rays of a polyhedral cone that contains most of the rows of X. An alternative approach in the non separable case is to utilize semidefinite preconditioning techniques proposed by Gillis and Vavasis (2013).
Supplementary Material
Footnotes
The authors gratefully acknowledge Trevor Hastie, Jason Lee, Philip Pauerstein, Michael Saunders, Jonathan Taylor, Jennifer Tsai and Lexing Ying for their insightful comments. Trevor Hastie suggested the group-lasso approach to selecting extreme points. A. Damle was supported by a NSF Graduate Research Fellowship DGE-1147470. Y. Sun was partially support by the NIH, grant U01GM102098.
Vavasis (2009) showed computing the NMF is, in general, NP-hard.
In fact, exact expressions in terms of the hypergeometric function or the regularized incomplete beta function are known. We refer to Li (2011) for the details.
Contributor Information
Anil Damle, Institute for Computational and Mathematical Engineering, Stanford University.
Yuekai Sun, Department of Statistics, University of Michigan.
References
- Arora S, Ge R, Kannan R, Moitra A. Computing a nonnegative matrix factorization – provably; Proceedings of the 44th symposium on Theory of Computing; 2012. pp. 145–162. [Google Scholar]
- Ball K. An elementary introduction to modern convex geometry. Flavors of geometry. 1997;31:1–58. [Google Scholar]
- Bittorf V, Recht B, Re C, Tropp J. Factoring nonnegative matrices with linear programs. Advances in Neural Information Processing Systems. 2012;25:1223–1231. [Google Scholar]
- Boardman J. Geometric mixture analysis of imaging spectrometry data. Geoscience and Remote Sensing Symposium (IGARSS) ’94. 1994;4:2369–2371. vol.4. [Google Scholar]
- Chang C-I, Plaza A. A fast iterative algorithm for implementation of pixel purity index. Geoscience and Remote Sensing Letters, IEEE. 2006;3:63–67. [Google Scholar]
- Cutler A, Breiman L. Archetypal analysis. Technometrics. 1994;36:338–347. [Google Scholar]
- Ding W, Hossein Rohban M, Ishwar P, Saligrama V. Topic Discovery through Data Dependent and Random Projections; Proceedings of The 30th International Conference on Machine Learning; 2013. pp. 1202–1210. [Google Scholar]
- Ding W, Ishwar P, Saligrama V. Necessary and Sufficient Conditions and a Provably Efficient Algorithm for Separable Topic Discovery. arXiv preprint arXiv:1508.05565 2015 [Google Scholar]
- Donoho D, Stodden V. When does non-negative matrix factorization give a correct decomposition into parts? Advances in neural information processing systems 2003 [Google Scholar]
- Elhamifar E, Sapiro G, Vidal R. Computer Vision and Pattern Recognition (CVPR), 2012 IEEE Conference on. IEEE; 2012. See all by looking at a few: Sparse modeling for finding representative objects; pp. 1600–1607. [Google Scholar]
- Esser E, Moller M, Osher S, Sapiro G, Xin J. A convex model for nonnegative matrix factorization and dimensionality reduction on physical space. Image Processing, IEEE Transactions on. 2012;21:3239–3252. doi: 10.1109/TIP.2012.2190081. [DOI] [PubMed] [Google Scholar]
- Gillis N. Robustness analysis of Hottopixx, a linear programming model for factoring nonnegative matrices. SIAM Journal on Matrix Analysis and Applications. 2013;34:1189–1212. [Google Scholar]
- Gillis N, Vavasis SA. Semidefinite Programming Based Preconditioning for More Robust Near-Separable Nonnegative Matrix Factorization. ArXiv e-prints 2013 [Google Scholar]
- Gillis N, Vavasis SA. Fast and robust recursive algorithms for separable nonnegative matrix factorization. Pattern Analysis and Machine Intelligence, IEEE Transactions on. 2014;36:698–714. doi: 10.1109/TPAMI.2013.226. [DOI] [PubMed] [Google Scholar]
- Kim J, Monteiro R, Park H. SDM. SIAM; 2012. Group Sparsity in Nonnegative Matrix Factorization; pp. 851–862. [Google Scholar]
- Kumar A, Sindhwani V, Kambadur P. Fast conical hull algorithms for near-separable non-negative matrix factorization; Proceedings of the 30th International Conference on Machine Learning.2013. [Google Scholar]
- Lee D, Seung H. Learning the parts of objects by non-negative matrix factorization. Nature. 1999;401:788–791. doi: 10.1038/44565. [DOI] [PubMed] [Google Scholar]
- Lee DD, Seung HS. Algorithms for non-negative matrix factorization. Advances in neural information processing systems. 2001:556–562. [Google Scholar]
- Li S. Concise formulas for the area and volume of a hyperspherical cap. Asian Journal of Mathematics and Statistics. 2011;4:66–70. [Google Scholar]
- Nascimento J, Bioucas Dias J. Vertex component analysis: a fast algorithm to unmix hyperspectral data. Geoscience and Remote Sensing, IEEE Transactions on. 2005;43:898–910. [Google Scholar]
- Obozinski G, Wainwright MJ, Jordan MI, et al. Support union recovery in high-dimensional multivariate regression. The Annals of Statistics. 2011;39:1–47. [Google Scholar]
- Vavasis S. On the complexity of nonnegative matrix factorization. SIAM Journal on Optimization. 2009;20:1364–1377. [Google Scholar]
- Yuan M, Lin Y. Model selection and estimation in regression with grouped variables. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2006;68:49–67. [Google Scholar]
- Zhou T, Bilmes JA, Guestrin C. Divide-and-Conquer Learning by Anchoring a Conical Hull. Advances in Neural Information Processing Systems. 2014:1242–1250. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.