Abstract
Motivation
Kinetic models contain unknown parameters that are estimated by optimizing the fit to experimental data. This task can be computationally challenging due to the presence of local optima and ill-conditioning. While a variety of optimization methods have been suggested to surmount these issues, it is difficult to choose the best one for a given problem a priori. A systematic comparison of parameter estimation methods for problems with tens to hundreds of optimization variables is currently missing, and smaller studies provided contradictory findings.
Results
We use a collection of benchmarks to evaluate the performance of two families of optimization methods: (i) multi-starts of deterministic local searches and (ii) stochastic global optimization metaheuristics; the latter may be combined with deterministic local searches, leading to hybrid methods. A fair comparison is ensured through a collaborative evaluation and a consideration of multiple performance metrics. We discuss possible evaluation criteria to assess the trade-off between computational efficiency and robustness. Our results show that, thanks to recent advances in the calculation of parametric sensitivities, a multi-start of gradient-based local methods is often a successful strategy, but a better performance can be obtained with a hybrid metaheuristic. The best performer combines a global scatter search metaheuristic with an interior point local method, provided with gradients estimated with adjoint-based sensitivities. We provide an implementation of this method to render it available to the scientific community.
Availability and implementation
The code to reproduce the results is provided as Supplementary Material and is available at Zenodo https://doi.org/10.5281/zenodo.1304034.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Mechanistic kinetic models provide a basis to answering biological questions via mathematical analysis. Dynamical systems theory can be used to interrogate these kinetic models, enabling a more systematic analysis, explanation and understanding of complex biochemical pathways. Ultimately, the goal is the model-based prediction of cellular functions under new experimental conditions (Almquist et al., 2014; Kyriakopoulos et al., 2018; Link et al., 2014; van Riel, 2006). During the last decade, many efforts have been devoted to developing increasingly detailed and, therefore, larger systems biology models (Karr et al., 2012; Smallbone and Mendes, 2013; Srinivasan et al., 2015). Such models are often formulated as nonlinear ordinary differential equations (ODEs) with unknown parameters. As it is impossible to measure all parameters directly, parameter estimation (i.e. model calibration) is crucial for the development of quantitative models. The unknown parameters are typically estimated by solving a mathematical optimization problem which minimizes the mismatch between model predictions and measured data (Ashyraliyev et al., 2009; Banga and Balsa-Canto, 2008; Jaqaman and Danuser, 2006; Raue et al., 2013).
Parameter estimation for dynamical systems is an inverse problem (Villaverde and Banga, 2013) that exhibits many possible challenges and pitfalls, mostly associated with ill-conditioning and non-convexity (Schittkowski, 2013). These properties, which are in general only known a posteriori, influence the performance of optimization methods. Even if we restrict our attention to a specific class of problems within the same field (e.g. parameter estimation in systems biology), there are often large differences in performance between different applications (Kreutz, 2016). Hence, methods need to be benchmarked for a representative collection of problems of interest in order to reach meaningful conclusions. In this study, we consider the class of medium to large scale kinetic models. These models pose several challenges, such as computational complexity, and an assessment of the performance of optimization methods is particularly important (Babtie and Stumpf, 2017; Degasperi et al., 2017; Villaverde et al., 2015).
The calibration of large-scale kinetic models usually requires the optimization of a multi-modal objective function (Chen et al., 2010; Ljung and Chen, 2013; Moles et al., 2003), i.e. there will be several local optima. Local optimization methods, such as Levenberg-Marquardt or Gauss-Newton (Schittkowski, 2013), which converge to local optima, will only find a global optimum for appropriate starting points. Convergence to a suboptimal solution is an estimation artifact that can lead to wrong conclusions: we might think that the mechanism considered is not suitable to explain the data, while the real reason might be that the method failed to locate the global optimum (Chachuat et al., 2006). In order to avoid suboptimal solutions, many studies have recommended the use of global optimization techniques (Ashyraliyev et al., 2009; Banga and Balsa-Canto, 2008; Chen et al., 2010; Mendes and Kell, 1998). One of the earliest and simplest global optimization methods is the multi-start, which consists of launching many local searches from different initial points in parameter space, assuming that one of them will be inside the basin of attraction of the global solution. It has been shown that multi-starts of local optimization methods can be sufficient for successful parameter estimation in kinetic models (Fröhlich et al., 2017b; Raue et al., 2013), although the use of other approaches, such as metaheuristics, has also been advocated (Gábor and Banga, 2015; Villaverde et al., 2015).
The comparison of global optimization methods was the topic of several research papers. Interestingly, the evaluation results led to apparently contradictory conclusions, advocating the use of either multi-start local optimization (Hross and Hasenauer, 2016; Raue et al., 2013), or global optimization metaheuristics (Egea et al., 2009a, 2010; Gábor and Banga, 2015; Moles et al., 2003). These contradictions cannot be explained by the no-free lunch theorems for optimization (Wolpert and Macready, 1997), since (i) the problems analyzed possessed relatively similar characteristics (i.e. the comparisons did not consider every possible class of problems); and (ii) they were formulated in continuous search domains, where these theorems do not hold (Auger and Teytaud, 2010). Hence, we suggest two alternative explanations: (i) the comparisons were carried out by researchers who had substantially more experience with (the tuning of) one type of the considered methods, and (ii) the performance metrics differed and might even have been biased towards particular approaches. To circumvent these issues, we established an intensive collaboration between experienced users of multi-start local optimization (the HZM group) and metaheuristics (the CSIC group). Through a joint development of performance metrics and evaluation procedures we attempted to ensure a fair comparison of different approaches.
In this study, we present the results of this collaboration: the development of a performance metric suited for the comparison of different methods, and the evaluation of the state-of-the-art in parameter estimation methodologies. Based on these results we provide guidelines for their application to large kinetic models in systems biology. To this end, we use seven previously published estimation problems to benchmark a number of optimization methods. The selected problems are representative of the medium and large scale kinetic models used in systems biology, with sizes ranging from dozens to hundreds of state variables and parameters (see Table 2 for details). To the best of our knowledge, this is the first time that a systematic evaluation of parameter estimation methods is conducted on a set of problems of this size and characteristics. We compare several variants of state-of-the-art optimization methods which have been recently reported as competitive options for large problems, including multi-start (Raue et al., 2013) and hybrid metaheuristics (Villaverde et al., 2015). We perform systematic comparisons between these different approaches using metrics capturing the performance/robustness trade-off. Finally, we discuss the implications of our results and provide guidelines for the successful application of optimization methods in computational systems biology.
Table 2.
Main features of the benchmarks.The model IDs follow the nomenclature in Villaverde et al. (2015) and Fröhlich et al. (2017a)
| ID | B2 | B3 | B4 | B5 | BM1 | BM3 | TSP |
|---|---|---|---|---|---|---|---|
| Original ref. | Chassagnole et al. (2002) | Kotte et al. (2010) | Villaverde et al. (2014) | MacNamara et al. (2012) | Smith and Shanley (2013) | Chen et al. (2009) | Moles et al. (2003) |
| Organism | Escherichia coli | Escherichia coli | Chinese hamster | Generic | Mouse | Human | Generic |
| Description | Metabolic | Metabolic | Metabolic | Signaling | Signaling | Signaling | Metabolic |
| level | & transcription | ||||||
| Parameters | 116 | 178 | 117 | 86 | 383 | 219 | 36 |
| Upper bounds | varying | ||||||
| Lower bounds | varying | ||||||
| Dynamic states | 18 | 47 | 34 | 26 | 104 | 500 | 8 |
| Observed states | 9 | 47 | 13 | 6 | 12 | 5 | 8 |
| Experiments | 1 | 1 | 1 | 10 | 1 | 4 | 16 |
| Data points | 110 | 7567 | 169 | 960 | 120 | 105 | 2688 |
| Data type | Measured | Simulated | Simulated | Simulated | Measured | Measured | Simulated |
| Noise level | Reala | No noise | Variableb | Uniformc | Reala | Reala |
Noise levels are unknown as real measurement data are used.
Noise levels differ for readouts.
Noise level is constant (); the data values generated by this model are between 0 and 1 by construction.
Noise levels are proportional to the signal intensity.
2 Methods and benchmark problems
2.1 Problem definition: parameter optimization for ODE models describing biological processes
We consider deterministic dynamic systems described by nonlinear ODEs of the following form:
| (1) |
in which x(t) is the vector of state variables at time t, x0 is the vector of initial conditions, f is the vector field of the ODE, g is the observation function and p is the vector of unknown constant parameters with lower and upper bounds .
Parameter optimization for dynamical systems is a nonlinear dynamic optimization problem that aims to find the vector of parameter values p that minimizes the distance between model simulation and measured data subject to the dynamics of the system and (potentially) other possible constraints. The distance is measured by a scalar objective function (or cost function), which can be of several forms. One common choice is the weighted least squares objective function given by:
| (2) |
in which is the number of experiments, is the number of observables per experiment, is the number of samples per observable per experiment, is the measured data, is the corresponding simulated output, and are constants that weight the observables in the objective function according to their magnitudes and/or the confidence in the measurements.
Another common choice for the objective function is the log-likelihood. Assuming independent, normally distributed additive measurement noise with standard deviation , the likelihood of observing the data D given the parameters p is:
| (3) |
Maximizing (3) is equivalent to minimizing the negative log-likelihood function:
| (4) |
If the standard deviations are known, and possess the same optimal parameters. Furthermore, for , the log-likelihood and least squares functions are related by
| (5) |
We remark that a good agreement of model output and data does not imply that the parameter estimates are correct or reliable. Practical and structural non-identifiabilities can prevent a parameter from being precisely determined (DiStefano Iii, 2015). Still, an accurate fit—and hence optimization—is the starting point for many uncertainty analysis methods. State-of-the-art identifiability analysis methods have been recently evaluated elsewhere (Chiş et al., 2011; Ligon et al., 2017; Raue et al., 2014; Miao et al., 2011; Villaverde and Barreiro, 2016).
2.2 Overview of optimization methods
The ideal optimization method for the above class of problems would be able to find the global optimum with guarantees and in a short computation time. Furthermore, it should scale well with problem size and be able to handle arbitrary non-linearities. Currently, no such method exists.
Local gradient-based methods (Schittkowski, 2013) can be efficient but will converge to the local optimum in the basin of attraction where they are initialized. Local gradient-free (also called zero-order) methods, such as pattern search (Wright, 1996), are less efficient than gradient-based methods but more robust with respect to situations where the gradient is unavailable or unreliable (Conn et al., 2009).
Global methods aim to locate the global solution by means of either deterministic (Esposito and Floudas, 2000) or stochastic (Zhigljavsky and Zilinskas, 2007) strategies. Deterministic methods include so-called complete and rigorous approaches, both of which can ensure convergence to the global solution under certain circumstances. In contrast, stochastic (also known as probabilistic) methods can only guarantee global optimality asymptotically in the best case (Neumaier, 2004), but can solve many problems that cannot be handled using available deterministic methods. Both deterministic and stochastic global optimization methods have been used to solve parameter estimation problems in systems biology. The results show that deterministic methods suffer from lack of scalability (Miró et al., 2012). The computational cost of purely stochastic methods (such as simulated annealing, particle swarm optimization, or genetic algorithms) usually scales up better, but the computation times can still be excessive for problems of realistic size (Mendes and Kell, 1998; Moles et al., 2003).
Hybrid global-local methods attempt to exploit the benefits of global and local methods. By combining diversification phases (global search) and intensification phases (local search), hybrid methods facilitate reliable global exploration and fast local convergence. As a result, hybrid methods can potentially outperform the efficiency (convergence rate) of purely stochastic methods while keeping their success rate. One such hybrid method is the so called multi-start (MS) strategy (Zhigljavsky and Zilinskas, 2007), which solves the problem repeatedly with local methods initialized from different (e.g. random) initial points. Thus, MS can be regarded as one of the earliest hybrid strategies, and there are different extensions available (Hendrix and Tóth, 2010; Zhigljavsky and Zilinskas, 2007). An alternative family of hybrid methods are metaheuristics (i.e. guided heuristics). An example is the enhanced scatter search (eSS) method (Egea et al., 2009b), an improvement of the method designed by Glover et al. (2000). The eSS method combines a global stochastic search phase with local searches launched at selected times during the optimization, in order to accelerate convergence to local optima. Further accelerations can be achieved by parallelization (Penas et al., 2017; Villaverde et al., 2012).
In all hybrid methods the efficiency of local methods plays a major role. The most efficient local methods are gradient-based, so their performance depends crucially on the accuracy of the gradient calculations (Nocedal and Wright, 1999). The simplest way of approximating the gradient is by finite differences. However, more accurate gradients are provided by forward sensitivity analysis (Raue et al., 2015) and adjoint sensitivity analysis (Fröhlich et al., 2017b). While the former provides information on individual residuals which can be used in least squares algorithms, the latter is more scalable.
2.3 Choice of optimization methods for benchmarking
In this study, we consider several competitive hybrid methods based on the recent results reported by Fröhlich et al. (2017b) and Villaverde et al. (2015). These methods are summarized in Table 1 and combine two global strategies:
Table 1.
Classification of the hybrid optimization methods considered in the benchmarking
| Global strategy | Local method & gradient calculation |
Parameter scaling | |||
|---|---|---|---|---|---|
| FMINCON-ADJ | NL2SOL-FWD | DHC | None | ||
| MS | MS-FMINCON-ADJ-LOG | MS-NL2SOL-FWD-LOG | MS-DHC-LOG | – | LOG |
| MS-FMINCON-ADJ-LIN | MS-NL2SOL-FWD-LIN | MS-DHC-LIN | – | LIN | |
| eSS | eSS-FMINCON-ADJ-LOG | eSS-NL2SOL-FWD-LOG | eSS-DHC-LOG | eSS-NOLOC-LOG | LOG |
| eSS-FMINCON-ADJ-LIN | eSS-NL2SOL-FWD-LIN | eSS-DHC-LIN | eSS-NOLOC-LIN | LIN | |
Notes: These methods result from the combination of two global strategies with three local methods and two types of scaling for the search space. Additionally, we tested a global metaheuristics optimization method, Particle Swarm Optimization (PSO) both in logarithmic and linear scale (PSO-LOG, PSO-LIN). The abbreviations are defined in Sections 2.3 and 2.4.
MS: multi-start local optimization.
eSS: enhanced scatter search metaheuristic
with three different local methods:
NL2SOL-FWD: the nonlinear least-squares algorithm NL2SOL, using forward sensitivity analysis for evaluating the gradients of the residuals. The use of NL2SOL (Dennis Jr et al., 1981) has recently been advocated for parameter estimation by Gábor and Banga (2015). Additionally, Raue et al. (2013) showed that least-squares algorithms with residual sensitivities computed using forward sensitivity analysis outperform many alternative approaches.
FMINCON-ADJ: the interior point algorithm included in FMINCON (MATLAB and Optimization Toolbox Release 2015a, The MathWorks, Inc., Natick, Massachusetts, United States), using adjoint sensitivities for evaluating the gradient of the objective function. This method has been shown to outperform the least-squares method using forward sensitivities for large-scale models (Fröhlich et al., 2017a,b), due to the accelerated gradient evaluation.
DHC: a gradient-free dynamic hill climbing algorithm. This algorithm has been proposed by De La Maza and Yuret (1994) and outperformed several alternative approaches in a recent study (Villaverde et al., 2015). In our experience, this method is competitive when the gradient is numerically difficult to evaluate, e.g. if objective function values are corrupted by numerical integration errors.
Furthermore, we consider eSS without any local method (eSS-NOLOC), and particle swarm optimization (PSO) (Kennedy and Eberhart, 1995). The considered global strategies and local methods are a representative subset that covers distinct approaches, which have been shown in the past to exhibit competitive performances on a number of problems (Egea et al., 2007; Fröhlich et al., 2017b; Gábor and Banga, 2015; Penas et al., 2017; Raue et al., 2013; Rodriguez-Fernandez et al., 2006; Villaverde et al., 2012, 2015). The local methods are applicable to time-resolved and steady-state data [see Raue et al. (2013), Rosenblatt et al. (2016), Fröhlich et al. (2017a) and references therein].
2.4 Choice of scaling for the optimization variables
In addition to the optimization methods, we consider two different choices for the scaling of the optimization variables:
LIN: linear scale
LOG: logarithmic scale
While it is possible to consider the model parameters, p, directly as optimization variables, several studies suggest that using the logarithms of the model parameters, , improves the performance of local optimization methods (Kreutz, 2016; Raue et al., 2013). This is implemented as the LOG option, which performs all parameter searches (both in the global and local phases) in logarithmic space, . Before every evaluation of the objective function the variables are back-transformed to , thus simulating the original equations.
2.5 Comparison of optimization methods
The performance of optimization methods can be compared using several evaluation criteria. Ideally, a criterion should be:
single, interpretable quantity
comparable across models and methods (to enable an integrated analysis)
account for computation time and objective function value
A number of evaluation criteria have been used in the literature to compare the performance of optimization methods, e.g. dispersion plots of objective function value versus computation time and waterfall plots showing the ordered objective function values found by the different searches. These and other plots are reported in the Supplementary Figures S1–S14. Alternative criteria are performance profiles (Dolan and Moré, 2002) which report for a given set of optimization problems how often one algorithm was faster than all others. The required assumption that all algorithms converge is relaxed in data profiles (Moré and Wild, 2009) by considering the decrease in objective function value and reporting the fraction of solved problems as a function of the budget per variable. While all these plots are useful tools, they do not provide a single, interpretable quantity and fail in other ways.
Upon consideration of a variety of different evaluation criteria, we decided to adopt a workflow consisting of several steps, which lead to a newly proposed metric that is a distillation of the information obtained in previous steps. The workflow considers the following criteria:
Convergence curves
Fixed-budget scenario and fixed-target scenario
Dispersion plots of the success rate versus average computation time
Overall efficiency (OE)
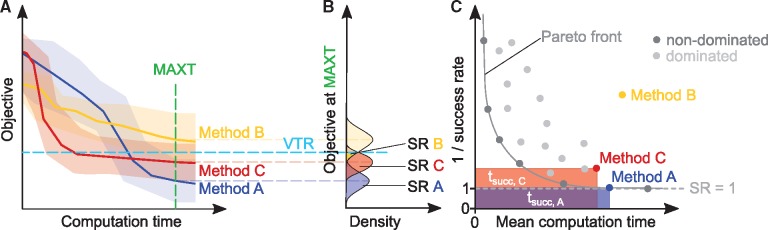
The first step is to evaluate convergence curves, which show the objective function value as a function of computation time (Fig. 1A). For eSS and PSO, the convergence curves are constructed from single searches as they reach the predefined maximum CPU time. For MS optimization, each convergence curve corresponds to a sequence of local searches and continues until the predefined maximum CPU time was reached.
Fig. 1.
Illustration of performance criteria. (A) Convergence curves for three different methods. Shaded areas show the range of all runs, while solid lines represent their median. The dashed horizontal line is the value to reach (VTR), that is the maximum objective function value that can be considered a successful result. The dashed vertical line is the maximum time allowed (MAXT). (B) Dispersion plot of objective value after the maximum time allowed and the derived success rates (SR). The SR is the area under the curve where objective VTR. (C) Success rate and computation time. Points indicate individual methods. The Pareto front is the set of non-dominated methods. Methods to the right or above the Pareto front are dominated by other methods with either shorter computation time or higher success rate. Filled areas show the average computation time required to obtain a successful run for the respective method. For algorithms with a success rate of zero, meaning that no optimization run reached the VTR, 1/success rate is set to infinity
The information encoded in the convergence curves is in the second step summarized by considering a fixed-budget scenario and a fixed-target scenario, as proposed by Hansen et al. (2016). In the fixed-budget scenario, the distribution of the objective function for a given computation time is considered, meaning that a vertical line is drawn. In the fixed-target scenario the distribution of time points is considered at which a desired objective function value or value to reach (VTR) is reached, meaning that a horizontal line is drawn. Once an optimization has reached the desired VTR (horizontal view), it is considered successful. The success rate (SR) of an algorithm is the fraction of searches that reached the VTR within this maximum computation time, MAXT (Fig. 1B). Complementary, we evaluate the average computation time required by an algorithm, , which is the minimum of the time required to reach VTR and MAXT. In the third step, we consider dispersion plots of the success rate versus average computation time to study the relation of the two quantities (Fig. 1C). Note that this dispersion plot may reveal in some cases a Pareto set structure, consisting of algorithms which provide an optimal trade-off between conflicting goals (in this case, high success rate and low computation time): it is not possible to improve one of its objectives without worsening the other. We are interested in methods that are located towards the bottom (i.e. high success rate) and left (i.e. low computation time) of this plot. Therefore, in the fourth step, we quantify the trade-off between success rate and average computation time using a novel metric called overall efficiency (OE). The OE for method i on a given problem is defined as:
| (6) |
where is the average computation time we need to run method i to obtain one successful run. It is calculated as , where and are the average computation time and the success rate of method i for that problem. The computation time is directly related to the area in the dispersion plot (Fig. 1C); accordingly, the OE is the ratio of the minimal area and the area for a given algorithm. The inverse of the overall efficiency, , quantifies how much longer one has to run method i—compared to the best method—in order to find a good solution. The OE ranges between 0 and 1; for each particular problem the best performing method achieves the maximum score, . To evaluate methods on a set of optimization problems, we compute a method’s cumulative overall efficiency as the sum of its OEs for the individual problems. The method with highest cumulative OE will be the one exhibiting the best trade-off between success rate and computation time for the set of problems.
In summary, our workflow considers multiple metrics and summarizes the trade-off between computational complexity and success with the novel performance metric OE. As the OE is interpretable, comparable between models and methods and accounts for computation time and final objective function values, it fulfils all the afore-defined criteria.
2.6 Benchmark problems
In this study, we consider seven benchmark problems based on previously published kinetic models (Chassagnole et al., 2002; Chen et al., 2009; Kotte et al., 2010; MacNamara et al., 2012; Moles et al., 2003; Smith and Shanley, 2013; Villaverde et al., 2014) which describe metabolic and signalling pathways of different organisms (from bacteria to human). These problems possess 36 to 383 parameters and 8 to 104 state variables. The data points are collected under up to 16 experimental conditions, corresponding to the number of required numerical simulations. The features of all problems are summarized in Table 2. The benchmarks B2–B5 had been previously included in the BioPreDyn-bench collection (Villaverde et al., 2015), and BM1 & BM3 were used in (Fröhlich et al., 2017a).
2.7 Implementation
The benchmark problems have been implemented in MATLAB (MathWorks, Natick, MA, USA) using the AMICI toolbox (Fröhlich et al., 2017b), a free MATLAB interface for SUNDIALS solvers (Hindmarsh et al., 2005). The optimization methods have been implemented as MATLAB scripts calling solvers from the MATLAB Optimization Toolbox, the MATLAB Global Optimization Toolbox and the MEIGO toolbox (Egea et al., 2014), and making use of the efficient gradient computation provided by the AMICI toolbox. The code necessary for reproducing the results reported here is provided as Supplementary Material and is also available at Zenodo https://doi.org/10.5281/zenodo.1304034.
3 Results and discussion
3.1 Comprehensive evaluation of the considered optimization methods on the benchmark problems
To assess the performance of the different optimization methods, we solved the 7 benchmark problems using the 16 optimization methods listed in Table 1. For each problem, multi-start local optimization (MS) used 100 starting points, while enhanced scatter search (eSS) and particle swarm optimization (PSO) were run 10 times, each time until the predefined, maximum problem-specific CPU time (Supplementary Table S1) was reached. The overall computational effort was CPU days (Intel Xeon E5-2600 2.50GHz processor).
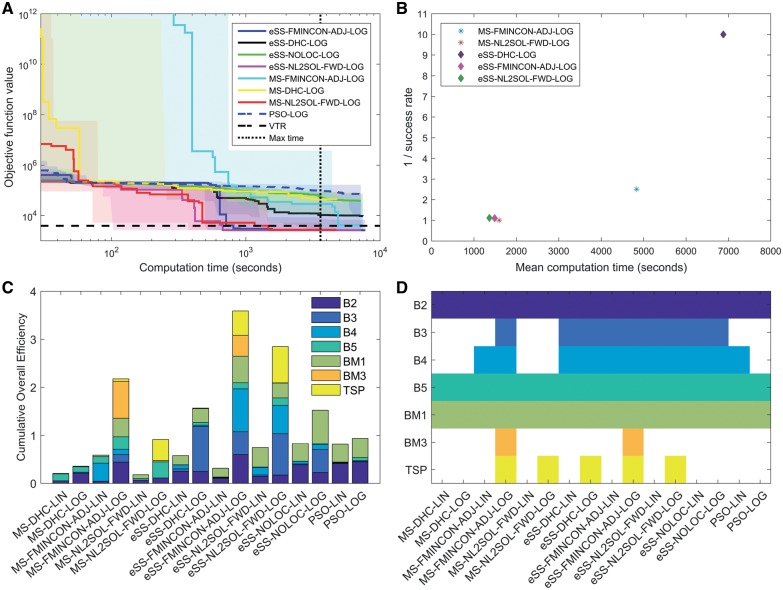
The convergence curves for all optimization methods on all problems were evaluated (see Fig. 2A for a representative example and Supplementary Figs S15–S28 for the complete set). Convergence curves for MS were plotted by mimicking the scenario in which eSS and PSO were used: we emulate 10 virtual processors, each of which performs local searches sequentially for the same time allowed to the eSS/PSO runs. The local searches in these emulated sequential optimizations are sampled without replacement from the pool of 100 searches launched in each MS. Thus, the success ratio (SR) reported for MS methods is the fraction of the 10 virtual processors that find a solution whose objective function value falls below the VTR. Note that this SR is not the same as the fraction of successful searches of the 100 launched in the MS. Numerical values of the horizontal and vertical views of said curves are provided in the Supplementary Tables S3–S20, and graphically in Supplementary Figures S65–S82.
Fig. 2.
Results of performance evaluation. (A) Convergence curves of the different methods for benchmark TSP. Results for the remaining benchmarks are reported in the Supplementary Material. (B) Average computation time of each method versus the inverse of its success rate for benchmark TSP. Methods with zero success rate are not shown. Results for the remaining benchmarks are reported in the Supplementary Material. (C) Cumulative overall efficiency: Each method is represented by a stack of the OEs observed for the individual benchmark problems. The maximum possible score is the same as the number of benchmarks, i.e. seven. (D) Successful methods for each benchmark are shown in color; methods which never succeeded for a given problem are shown in white. A, B and D use the thresholds VTR C and MAXT A as defined in the Supplementary Table S1. Panel C shows the average OE across all considered VTRs and MAXTs
As expected, the optimization results indicate that the performance of the optimization methods varies substantially among the benchmark problems. This is in agreement with previous studies (Kreutz, 2016; Villaverde et al., 2015).
For the quantitative evaluation we performed the analyses for two MAXTs and nine VTRs per benchmark (see Supplementary Table S1). We found that the ranking of the methods with respect to the OE depends only weakly on the MAXTs and the VTRs (Supplementary Figs S47–S64). For visualization in Figure 2A, B and D, we use a high MAXT (MAXT A) and a moderate VTR (VTR C) which ensures a good agreement of model simulation and data. Results for other choices of VTR including larger and smaller values are shown in the Supplementary Figures S29–S82 and Tables S3–S21.
In the following, we present the key findings of our analysis and address, amongst others, the question of which is the most efficient method for performing parameter optimization. The detailed evaluation results are presented in the Supplementary Material. In particular, quantitative values for the performance improvements mentioned in Sections 3.2–3.4 can be found in Supplementary Table S21.
3.2 Gradient-based local searches outperform gradient-free local searches
Our comprehensive evaluation clearly shows that high-quality sensitivity calculation methods provide a competitive advantage to local methods that exploit them. Optimization using adjoint and forward sensitivity analysis (FMINCON-ADJ and NL2SOL-FWD) usually outperform the gradient-free alternative (DHC). This is reflected in the dispersion plots (see, e.g. Fig. 2B) and in a higher cumulative OE (Fig. 2C) and holds for MS and eSS settings. The combinations of eSS with gradient-based methods, eSS-FMINCON-ADJ and eSS-NL2SOL-FWD, clearly outperform the gradient-free alternatives, eSS-DHC and eSS-NOLOC, as well as the also gradient-free PSO. Notably, successful optimization of BM3 for the given computational budget required adjoint sensitivity analysis in combination with optimization in the log-scale (Fig. 2D).
3.3 Enhanced scatter search outperforms multi-start local optimization
Our results show that MS is usually sufficient to find a good solution, given the same computation time as eSS (Fig. 2D). For strict VTRs (i.e. VTR E and VTR F), MS and eSS perform equally well. However, eSS were generally more efficient than MS (Fig. 2C). On average a 2-fold improvement of the OE is observed, almost independent of the local method. The reasons for the efficiency improvement is probably that eSS starts the local searches from promising points found through advanced exploration and recombination strategies. In this regard, it can be considered as an ‘advanced multi-start’ (Ugray et al., 2007).
3.4 Optimization in logarithmic scale outperforms optimization in linear scale
Previous studies reported that the transformation of the optimization variable to log-scale improves the reliability and computational efficiency of local methods (Kreutz, 2016; Raue et al., 2013). Our findings corroborate these results and show for the first time that also global optimization methods are more efficient when using log-scale (LOG) than linear-scale (LIN). Overall, we observe an average improvement of the cumulative OE at least by a factor of 2 (Fig. 2C). Indeed, for some problems (BM3, TSP), reasonable fits could only be obtained using the log-transformed parameters (Fig. 2D).
3.5 Best performing method
The comparison of all methods reveals that eSS-FMINCON-ADJ-LOG possesses the best overall efficiency on the considered benchmark problems and settings, followed by eSS-NL2SOL-FWD-LOG (Fig. 2C). The difference in performance between both methods is small; indeed, for certain VTRs, eSS-NL2SOL-FWD-LOG is the best performer (VTR C, see Supplementary Figs S51 and S52). However, eSS-FMINCON-ADJ-LOG is the only method that successfully solves all problems (Fig. 2D), while eSS-NL2SOL-FWD-LOG fails for BM3, possibly due to the very large number of states and parameters of this problem. In summary, our performance evaluation hence suggests the use of eSS-FMINCON-ADJ-LOG.
Interestingly, our study of the dispersion plots revealed that eSS-FMINCON-ADJ-LOG often maximizes success rate and minimizes mean computation time. Accordingly, in these cases there is—in contrast to what we expected—no trade-off, but we have a clear winner.
4 Conclusion
In this paper we have presented a comparative evaluation of state-of-the-art optimization methods for parameter estimation in systems biology. We have applied these methods to benchmark problems of different sizes (medium to large) and complexities. To compare the different methodologies in detail, we have used a multi-criteria workflow, exploring several possible ways of assessing the performance of optimization methods for this task. We have reported results using a number of selected indicators and evaluation tools. Furthermore, we have introduced the concept of overall efficiency (OE), which quantifies the trade-off between success rate and computation time, providing a numerical indication of the most efficient method. We have found that this metric is a convenient summary of the comparative performance of a method on a set of problems.
A central goal of our work was to re-examine past results regarding the performance of multi-start and metaheuristics (i.e. enhanced scatter search). Firstly, we have confirmed that multi-start local optimization is a powerful approach (Hross and Hasenauer, 2016; Raue et al., 2013) as it solved most considered benchmark problems in a reasonable time. The only exception is B3, a problem for which numerical simulation fails for many parameter points. Secondly, we verified that the enhanced scatter search metaheuristic often possesses higher success rates and efficiency compared to plain multi-start optimization methods (Gábor and Banga, 2015). However, the difference of a factor of two was smaller than suggested by several previous studies and will likely depend on the set of benchmark problems. Furthermore, the average improvement by a factor of two is smaller than the variability across benchmarks, implying that for many problems the use of multi-start methods is still beneficial (e.g. BM3). Thirdly, our results confirm that purely global optimization strategies (i.e. not combined with a local method), such as PSO and eSS-NOLOC, are less efficient than hybrid ones. Finally, we have assessed the influence of parameter transformations, concluding that optimizations in logarithmic scale clearly outperform those in linear scale. This parameterization can always be easily adopted, irrespective of the optimization method used.
We considered two sophisticated gradient-based methods, FMINCON with adjoint sensitivities and NL2SOL with forward sensitivities, whose use was mostly beneficial. A gradient-free local method, DHC, was found to be less precise than the gradient-based counterparts, although its use may still be advantageous in problems with numerical issues that limit the efficacy of gradient-based techniques.
In this study, we assessed the average performance of optimization methods for the benchmark problems. Complementary, it would be interesting to see how the performance of each method depends on problem characteristics, e.g. problem size. The assessment of this would however require a large number of problems with different characteristics. Since this is currently not available, we refrain from attempting a systematic evaluation of this feature.
Overall, the best performing method in our tests was eSS-FMINCON-ADJ-LOG, that is, a hybrid approach combining the global metaheuristic eSS with the local method FMINCON, provided with gradients estimated with adjoint-based sensitivities. This was the only method that succeeded in calibrating all the benchmarks and it also achieved the highest overall efficiency for the set of thresholds adopted in this study. To facilitate the application of this and other methods, we provide their implementations in the Supplementary Material. In the case of the best performing method, our solver is—to the best of our knowledge—the first publicly available implementation. Accordingly, our study provides access to a novel optimizer applicable to a broad range of application problems in systems biology.
Funding
This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 686282 (‘CANPATHPRO’), from the Spanish MINECO/FEDER projects SYNBIOFACTORY (DPI2014-55276-C5-2-R) and SYNBIOCONTROL (DPI2017-82896-C2-2-R), and from the German Research Foundation (DFG) through the Graduate School of Quantitative Biosciences Munich (QBM; F.F.).
Conflict of Interest: none declared.
Supplementary Material
References
- Almquist J. et al. (2014) Kinetic models in industrial biotechnology – improving cell factory performance. Metab. Eng., 24, 38–60. [DOI] [PubMed] [Google Scholar]
- Ashyraliyev M. et al. (2009) Systems biology: parameter estimation for biochemical models. FEBS J., 276, 886–902. [DOI] [PubMed] [Google Scholar]
- Auger A., Teytaud O. (2010) Continuous lunches are free plus the design of optimal optimization algorithms. Algorithmica, 57, 121–146. [Google Scholar]
- Babtie A.C., Stumpf M.P. (2017) How to deal with parameters for whole-cell modelling. J. R. Soc. Interface, 14, 20170237.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Banga J.R., Balsa-Canto E. (2008) Parameter estimation and optimal experimental design. Essays Biochem., 45, 195–210. [DOI] [PubMed] [Google Scholar]
- Chachuat B. et al. (2006) Global methods for dynamic optimization and mixed-integer dynamic optimization. Ind. Eng. Chem. Res., 45, 8373–8392. [Google Scholar]
- Chassagnole C. et al. (2002) Dynamic modeling of the central carbon metabolism of Escherichia coli. Biotechnol. Bioeng., 79, 53–73. [DOI] [PubMed] [Google Scholar]
- Chen W. et al. (2009) Input output behavior of erbb signaling pathways as revealed by a mass action model trained against dynamic data. Mol. Syst. Biol., 5, 239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen W.W. et al. (2010) Classic and contemporary approaches to modeling biochemical reactions. Genes Dev., 24, 1861–1875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chiş O.-T. et al. (2011) Structural identifiability of systems biology models: a critical comparison of methods. PLoS One, 6, e27755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conn A.R. et al. (2009) Introduction to Derivative-Free Optimization. SIAM, Philadelphia. [Google Scholar]
- Degasperi A. et al. (2017) Performance of objective functions and optimisation procedures for parameter estimation in system biology models. NPJ Syst. Biol. Appl., 3, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dennis J.E., Jr et al. (1981) An adaptive nonlinear least-squares algorithm. ACM Trans. Math. Softw. (TOMS), 7, 348–368. [Google Scholar]
- DiStefano III J. (2015) Dynamic Systems Biology Modeling and Simulation. Academic Press, London, UK. [Google Scholar]
- Dolan E.D., Moré J.J. (2002) Benchmarking optimization software with performance profiles. Math. Program., Ser. A, 91, 201–213. [Google Scholar]
- Egea J. et al. (2014) MEIGO: an open-source software suite based on metaheuristics for global optimization in systems biology and bioinformatics. BMC Bioinformatics, 15, 136.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Egea J.A. et al. (2007) Scatter search for chemical and bio-process optimization. J. Global Optim., 37, 481–503. [Google Scholar]
- Egea J.A. et al. (2009) Dynamic optimization of nonlinear processes with an enhanced scatter search method. Ind. Eng. Chem. Res., 48, 4388–4401. [Google Scholar]
- Egea J.A. et al. (2010) An evolutionary method for complex-process optimization. Comput. Oper. Res., 37, 315–324. [Google Scholar]
- Esposito W.R., Floudas C. (2000) Global optimization for the parameter estimation of differential-algebraic systems. Ind. Eng. Chem. Res., 39, 1291–1310. [Google Scholar]
- Fröhlich F. et al. (2017a) Efficient parameterization of large-scale mechanistic models enables drug response prediction for cancer cell lines. bioRxiv, 174094. [Google Scholar]
- Fröhlich F. et al. (2017b) Scalable parameter estimation for genome-scale biochemical reaction networks. PLoS Comput. Biol., 13, e1005331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gábor A., Banga J.R. (2015) Robust and efficient parameter estimation in dynamic models of biological systems. BMC Syst. Biol., 9, 74.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glover F. et al. (2000) Fundamentals of scatter search and path relinking. Control Cybern., 39, 653–684. [Google Scholar]
- Hansen N. et al. (2016) COCO: performance assessment arXiv preprint arXiv: 1605.03560. [Google Scholar]
- Hendrix E., Tóth B. (2010) Introduction to Nonlinear and Global Optimization. Springer Verlag, New York. [Google Scholar]
- Hindmarsh A.C. et al. (2005) Sundials: suite of nonlinear and differential/algebraic equation solvers. ACM Trans. Math. Softw. (TOMS), 31, 363–396. [Google Scholar]
- Hross S., Hasenauer J. (2016) Analysis of CFSE time-series data using division-, age- and label-structured population models. Bioinformatics, 32, 2321–2329. [DOI] [PubMed] [Google Scholar]
- Jaqaman K., Danuser G. (2006) Linking data to models: data regression. Nat. Rev. Mol. Cell Biol., 7, 813–819. [DOI] [PubMed] [Google Scholar]
- Karr J.R. et al. (2012) A whole-cell computational model predicts phenotype from genotype. Cell, 150, 389–401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kennedy J., Eberhart R. (1995) Particle swarm optimization In: Proceedings of the IEEE International Conference on Neural Networks, pp. 1942–1945. [Google Scholar]
- Kotte O. et al. (2010) Bacterial adaptation through distributed sensing of metabolic fluxes. Mol. Syst. Biol., 6, 355.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kreutz C. (2016) New concepts for evaluating the performance of computational methods. IFAC-PapersOnLine, 49, 63–70. [Google Scholar]
- Kyriakopoulos S. et al. (2018) Kinetic modeling of mammalian cell culture bioprocessing: the quest to advance biomanufacturing. Biotechnol. J., 13, 1700229.. [DOI] [PubMed] [Google Scholar]
- Ligon T.S. et al. (2017) Genssi 2.0: multi-experiment structural identifiability analysis of sbml models. Bioinformatics, 34, 1421–1423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Link H. et al. (2014) Advancing metabolic models with kinetic information. Curr. Opin. Biotechnol., 29, 8–14. [DOI] [PubMed] [Google Scholar]
- Ljung L., Chen T. (2013) Convexity issues in system identification In: 2013 10th IEEE International Conference on Control and Automation (ICCA). IEEE, pp. 1–9. [Google Scholar]
- MacNamara A. et al. (2012) State–time spectrum of signal transduction logic models. Phys. Biol., 9, 045003.. [DOI] [PubMed] [Google Scholar]
- Maza M.D.L., Yuret D. (1994) Dynamic hill climbing. AI Expert, 9, 26–26. [Google Scholar]
- Mendes P., Kell D. (1998) Non-linear optimization of biochemical pathways: applications to metabolic engineering and parameter estimation. Bioinformatics, 14, 869–883. [DOI] [PubMed] [Google Scholar]
- Miao H. et al. (2011) On identifiability of nonlinear ode models and applications in viral dynamics. SIAM Rev. Soc. Ind. Appl. Math., 53, 3–39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miró A. et al. (2012) Deterministic global optimization algorithm based on outer approximation for the parameter estimation of nonlinear dynamic biological systems. BMC Bioinformatics, 13, 90.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moles C. et al. (2003) Parameter estimation in biochemical pathways: a comparison of global optimization methods. Genome Res., 13, 2467–2474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moré J.J., Wild S.M. (2009) Benchmarking derivative-free optimization algorithms. SIAM J. Optim., 20, 172–191. [Google Scholar]
- Neumaier A. (2004) Complete search in continuous global optimization and constraint satisfaction. Acta Numerica, 13, 271–369. [Google Scholar]
- Nocedal J., Wright S. (1999) Numerical Optimization. Springer, New York, USA. [Google Scholar]
- Penas D.R. et al. (2017) Parameter estimation in large-scale systems biology models: a parallel and self-adaptive cooperative strategy. BMC Bioinformatics, 18, 52.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raue A. et al. (2013) Lessons learned from quantitative dynamical modeling in systems biology. PLoS One, 8, e74335.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raue A. et al. (2014) Comparison of approaches for parameter identifiability analysis of biological systems. Bioinformatics, 30, 1440–1448. [DOI] [PubMed] [Google Scholar]
- Raue A. et al. (2015) Data2dynamics: a modeling environment tailored to parameter estimation in dynamical systems. Bioinformatics, 31, 3558–3560. [DOI] [PubMed] [Google Scholar]
- Rodriguez-Fernandez M. et al. (2006) Novel metaheuristic for parameter estimation in nonlinear dynamic biological systems. BMC Bioinformatics, 7, 483.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenblatt M. et al. (2016) Customized steady-state constraints for parameter estimation in non-linear ordinary differential equation models. Front, 4, 41.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schittkowski K. (2013) Numerical Data Fitting in Dynamical Systems: A Practical Introduction with Applications and Software, vol. 77 Springer Science & Business Media, Dordrecht, The Netherlands. [Google Scholar]
- Smallbone K., Mendes P. (2013) Large-scale metabolic models: from reconstruction to differential equations. Ind. Biotechnol., 9, 179–184. [Google Scholar]
- Smith G.R., Shanley D.P. (2013) Computational modelling of the regulation of insulin signalling by oxidative stress. BMC Syst. Biol., 7, 41.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Srinivasan S. et al. (2015) Constructing kinetic models of metabolism at genome-scales: a review. Biotechnol. J., 10, 1345–1359. [DOI] [PubMed] [Google Scholar]
- Ugray Z. et al. (2007) Scatter search and local nlp solvers: a multistart framework for global optimization. INFORMS J. Comput., 19, 328–340. [Google Scholar]
- van Riel N. (2006) Dynamic modelling and analysis of biochemical networks: mechanism-based models and model-based experiments. Brief. Bioinform., 7, 364–374. [DOI] [PubMed] [Google Scholar]
- Villaverde A.F., Banga J.R. (2013) Reverse engineering and identification in systems biology: strategies, perspectives and challenges. J. R. Soc. Interface, 11, 20130505.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Villaverde A.F., Barreiro A. (2016) Identifiability of large nonlinear biochemical networks. MATCH Commun. Math. Comput. Chem., 76, 259–296. [Google Scholar]
- Villaverde A.F. et al. (2012) A cooperative strategy for parameter estimation in large scale systems biology models. BMC Syst. Biol., 6, 75.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Villaverde A.F. et al. (2014) High-confidence predictions in systems biology dynamic models. Adv. Intell. Soft-Comput., 294, 161–171. [Google Scholar]
- Villaverde A.F. et al. (2015) Biopredyn-bench: a suite of benchmark problems for dynamic modelling in systems biology. BMC Syst. Biol., 9, 8.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolpert D.H., Macready W.G. (1997) No free lunch theorems for optimization. IEEE Trans. Evol. Comput., 1, 67–82. [Google Scholar]
- Wright M.H. (1996) Direct search methods: once scorned, now respectable. Pitman Res. Notes Math. Ser., 344, 191–208. [Google Scholar]
- Zhigljavsky A., Zilinskas A. (2007) Stochastic Global Optimization, vol. 9 Springer Science & Business Media, New York, USA. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.