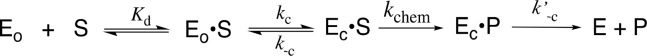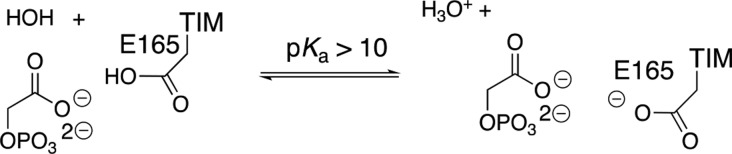Protein Flexibility and Stiffness Enable Efficient Enzymatic Catalysis

Abstract

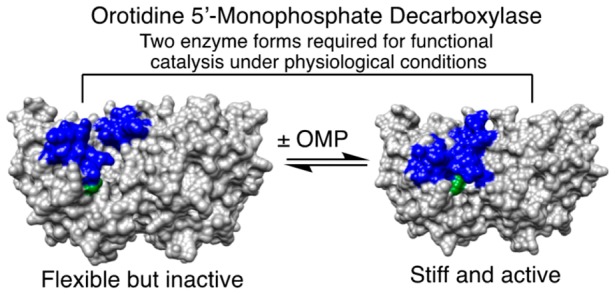
The enormous rate accelerations observed for many enzyme catalysts are due to strong stabilizing interactions between the protein and reaction transition state. The defining property of these catalysts is their specificity for binding the transition state with a much higher affinity than substrate. Experimental results are presented which show that the phosphodianion-binding energy of phosphate monoester substrates is used to drive conversion of their protein catalysts from flexible and entropically rich ground states to stiff and catalytically active Michaelis complexes. These results are generalized to other enzyme-catalyzed reactions. The existence of many enzymes in flexible, entropically rich, and inactive ground states provides a mechanism for utilization of ligand-binding energy to mold these catalysts into stiff and active forms. This reduces the substrate-binding energy expressed at the Michaelis complex, while enabling the full and specific expression of large transition-state binding energies. Evidence is presented that the complexity of enzyme conformational changes increases with increases in the enzymatic rate acceleration. The requirement that a large fraction of the total substrate-binding energy be utilized to drive conformational changes of floppy enzymes is proposed to favor the selection and evolution of protein folds with multiple flexible unstructured loops, such as the TIM-barrel fold. The effect of protein motions on the kinetic parameters for enzymes that undergo ligand-driven conformational changes is considered. The results of computational studies to model the complex ligand-driven conformational change in catalysis by triosephosphate isomerase are presented.

Introduction

Bioorganic chemists have understood for more than 50 years that the first step toward determining the mechanism for enzymatic catalysis of polar reactions, such as proton transfer and nucleophilic substitution at carbon, is to determine the mechanisms for catalysis of these reactions by molecules that model the active-site amino acid side chains.^1,2 The results from studies on catalysis by these models generally show that enzymes follow one of the reaction mechanisms observed in solution.^3,4 However, the synthetic enzyme models fail to capture the large rate accelerations observed for enzyme catalysts.

Why do rate accelerations for catalysis by synthetic enzyme models fall short of those by enzymes? Answers can be found through a consideration of what has been selected for during enzyme evolution. The high conservation of the structure of glycolytic enzymes,⁵ present in all forms of life, over the past several billion years provides strong evidence that evolution has eliminated non-essential elements of enzyme structure. This suggests that regions distant from the active sites of glycolytic enzymes are essential for efficient function because of interactions between the active site and remote protein side chains. These are not through-space electrostatic interactions, which fall off rapidly with increasing separation from the active site.⁶ Rather, the interactions are thought to be associated with protein motions that extend from the active site to other parts of the catalyst—hence, the intense interest in establishing links between enzyme catalytic function, enzyme conformational changes, and the dynamics of these conformational changes.⁷⁻¹²

Lock-and-Key or Induced Fit?

The lock-and-key analogy postulated in 1894 by Emil Fischer compares the substrate to a key that must be the correct size and shape to fit into the stiff enzyme and undergo the catalyzed reaction.¹³ This analogy is supported by the rigid structures of enzyme–ligand complexes from X-ray crystallographic analyses. These structures are routinely used in high-level calculations of activation barriers for formation of enzyme-bound transition states that are in good agreement with the experimental activation barriers.¹⁴⁻¹⁹ This suggests that the rigid structures capture the full catalytic power of many enzymes.

By contrast, the induced-fit model postulated by Daniel Koshland in 1958²⁰ asserts that binding interactions between flexible enzymes and their substrates are utilized to mold enzyme active sites into structures that are complementary to the reaction transition state. There are abundant examples of such ligand-driven conformational changes,^9,21,22 several of which will be discussed in this Perspective. The coexistence of lock-and-key and induced-fit models represents two assessments of enzyme catalysis. In fact, stiffness and flexibility are complementary protein properties that are required to obtain the extraordinary catalytic efficiency of many enzymes. This Perspective presents evidence that the catalytic events for the turnover of enzyme-bound substrate to product occur at stiff protein active sites, and it describes the imperatives for the evolution of enzymes with flexible structures in their unliganded form that undergo large ligand-driven protein conformational changes to an active stiff form.

Reactive Michaelis Complexes Are Stiff

Many results are consistent with the conclusion that the structures for reactive Michaelis complexes of enzyme catalysts are stiff and allow for minimal protein motions away from highly organized forms. As noted above, enzyme-ligand complexes from X-ray crystallographic analyses serve as good starting points for calculations that model the experimental activation barrier for turnover at enzyme active sites,^14,15 so that the stiffness of reactive enzyme–substrate complexes is similar to that for crystalline enzymes. The empirical valence bond (EVB) computational methods developed by Arieh Warshel strongly emphasize the modeling of electrostatic interactions.^17,23,24 The success of these methods at reproducing the activation barriers for enzymatic reactions is consistent with the primacy of electrostatic interactions in transition-state stabilization and with Warshel’s strongly held conviction that optimal electrostatic stabilization is achieved by preorganization of active-site side chains into a stiff catalytic conformation.²⁵⁻²⁹ The results of a recent study on the directed evolution of a designed Kemp eliminase provide evidence for the requirement for the precision in placement of catalytic side chains in order to obtain robust catalysis.³⁰ These models and proposals are modern reformulations of Fisher’s lock-and-key model.

Antibodies are also stiff and show affinities for ligands comparable to that of some less proficient enzymes for their transition states. Antibodies have been produced that catalyze chemical reactions, but with smaller rate accelerations than for the most proficient enzymes.³¹⁻³³ This suggests that protein stiffness alone will not produce the largest enzymatic rate accelerations, but must be combined with protein flexibility to obtain well-rounded and efficient catalysts.

Specificity in Transition-State Binding

The failure to capture the full catalytic rate accelerations of enzymes in synthetic models,^34,35 catalytic antibodies,³¹⁻³³ or in designed protein catalysts³⁶ has driven studies to eliminate gaps in our understanding of enzymatic catalysis.³⁷⁻⁴² Watching events as an outsider engaged in studies on organic reaction mechanisms in aqueous solution, I became infected with the ambition to expand our understanding of enzyme catalysis. I was intrigued by William P. Jencks’s proposal that the most important difference between catalysis by enzymes and that by small molecules is that only enzymes have evolved mechanisms for the utilization of substrate-binding energy in the specific stabilization of the transition states for catalyzed reactions.⁴³ These mechanisms remained poorly characterized 30 years after Jencks’s classic 1975 review.⁴³

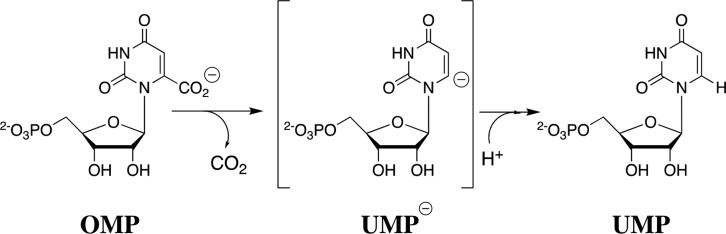
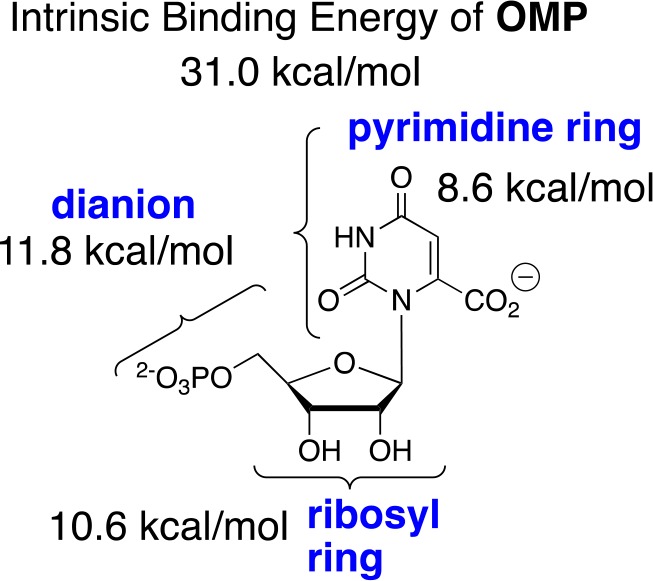
The difficulty in rationalizing the specificity shown by enzymes in binding their transition states with a higher affinity than substrate is highlighted by the difference between the modest 8 kcal/mol stabilization of the ground-state complex (K_d = 10^–6 M) to orotidine 5′-monophosphate (OMP) and the large 31 kcal/mol stabilization of the transition state (K_d^⧧ = 10^–23 M) for OMP decarboxylase-catalyzed (OMPDC) decarboxylation to form uridine monophosphate (UMP) through a UMP carbanion reaction intermediate (Schemes 1 and 2).^44,45 It is as though a switch is turned on at OMPDC as the transition state is approached, which releases the full substrate-binding energy from interactions with both the reacting portions of the substrate and the non-reacting portions such as the phosphodianion and ribosyl hydroxyls.^46,47 When there is no such switch, such as for the binding of biotin to avidin with a binding energy of −20 kcal/mol,⁴⁸ binding is effectively irreversible, and the biotin–avidin complex has a lifetime of 200 days.^49,50

Scheme 1. OMPDC-Catalyzed Decarboxylation of OMP through a UMP Carbanion Reaction Intermediate.

Scheme 2. OMPDC-Catalyzed Decarboxylation, with an 8 kcal/mol Stabilization of the Ground-State Complex (K_d = 10^–6 M) and a 31 kcal/mol Stabilization of the Rate-Determining Transition State (K_d^⧧ = 10^–23 M)^44,45.

In taking up the challenge to characterize these protein/ligand switches, I hoped to add one missing link to our understanding of enzyme catalysis, while connecting or discarding disparate proposals about how enzymes work. Our studies on the specificity of enzymes for binding their transition states with a higher affinity than substrate have had the unforeseen consequence of identifying a strong imperative for the evolution of enzymes that are flexible in their unliganded form and undergo ligand-driven conformational changes to stiff and active catalysts.

Utilization of Dianion-Binding Energy for Enzyme Activation

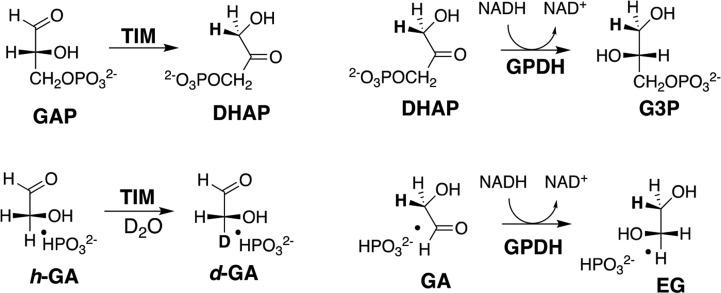
Five enzymes which catalyze reactions of substrates that contain a non-reacting phosphate monoester handle have been shown to utilize binding interactions with the phosphite dianion substrate piece to specifically stabilize the transition state for enzyme-catalyzed reactions of phosphodianion-truncated substrates.⁵¹⁻⁵³ In a representative case phosphite dianion shows a ca. 2 kcal/mol binding affinity for free enzyme and provides an 8 kcal/mol stabilization of the transition state for OMPDC-catalyzed decarboxylation of the truncated substrate 1-β-d-erythrofuranosyl-5-fluoroorotate (EO). This gives rise to an 80 000-fold larger second-order rate constant for decarboxylation of EO by the binary E·HP_i complex (HP_i = phosphite dianion) compared with decarboxylation by E alone (Scheme 3).⁴⁶ We also reported HP_i activation of triosephosphate isomerase (TIM)⁵⁴ and of glycerol phosphate dehydrogenase (GPDH)⁵⁵ for catalysis of proton-transfer and hydride-transfer reactions, respectively, of the small phosphodianion-truncated substrate glycolaldehyde (GA, Figure 1). A similar HP_i activation of truncated substrate was observed in studies on phosphoglucomutase⁵³ and on 1-deoxy-d-xylulose-5-phosphate reductoisomerase.^52,56 Our studies on dianion activation of OMPDC, TIM, and GPDH have been described in several reviews⁵⁷⁻⁶¹ that focus on the mechanism for dianion activation of enzyme-catalyzed decarboxylation, proton-transfer, and hydride-transfer reactions. I look outwardly in this Perspective and consider whether the architectural elements that enable enzyme activation by dianions are propagated widely in enzymes that catalyze polar reactions in water.

Scheme 3. Phosphite Dianion-Activated, OMPDC-Catalyzed Decarboxylation of a Phosphodianion-Truncated Substrate through a Carbanion Reaction Intermediate.

Figure 1.

Dianion-activated proton- and hydride-transfer reactions catalyzed by TIM (reactions on the left) and by GPDH (reactions on the right). TIM catalyzes isomerization of the whole substrate glyceraldehyde 3-phosphate (GAP) to form dihydroxyacetone phosphate (DHAP)⁶² and exchange between deuterium in D₂O and the α-carbonyl hydrogen of the substrate piece glycolaldehyde (GA) that is activated by the second piece of phosphite dianion (HP_i = HPO₃^2–).^54,63 GPDH catalyzes reduction of the whole substrate DHAP by NADH to form l-glycerol 3-phosphate (G3P) and reduction of GA by NADH to form ethylene glycol (EG) that is activated by HP_i.⁵⁵ In each case phosphite dianion binds weakly to free enzyme, while the transition state for the reactions of the whole substrate is stabilized by 11–12 kcal/mol by interactions with the substrate phosphodianion, and the transition state for reaction of the truncated substrate is stabilized by 6–8 kcal/mol by interactions with the phosphite dianion.⁵¹

A Role for Protein Conformational Changes in Enzyme Catalysis

Our rationale for parallel studies on TIM, OMPDC, and GPDH follows from studies by Jeremy Knowles on TIM,^64,65 which show that this enzyme meets two criteria for perfection in achieving efficient catalysis of a reaction in glycolysis.⁶⁶ The catalytic strategies first realized by TIM more 3 billion years ago^5,67 may extend beyond the chemistry of the catalyzed proton-transfer reactions and include perfection of the mechanism for enzyme activation by dianions. This prompted the hypothesis that the proliferation of the TIM barrel protein fold to 10% of all proteins (including OMPDC)⁶⁸⁻⁷¹ was favored by structural elements that enable dianion and other types of enzyme activation.

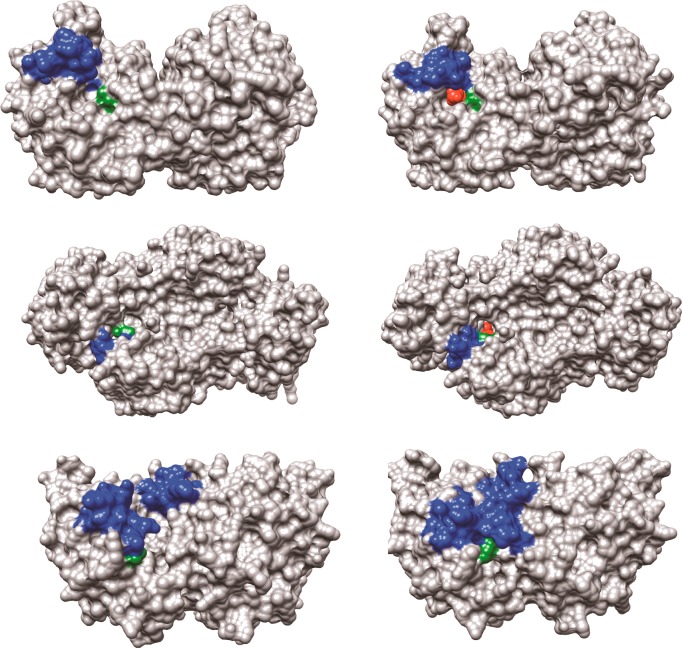
The structures for unliganded and liganded forms of OMPDC, TIM, and GPDH are shown in Figure 2, with the phosphodianion gripper loops shaded blue and a side-chain cation shaded green. Each enzyme undergoes a large conformational change upon substrate binding that is driven by interactions between the protein and substrate phosphodianion (shaded red) or the phosphite dianion piece. Each enzyme is inactive in the open form because of the poor positioning of catalytic side chains at the enzyme active site. In each case, the ligand-driven enzyme conformational change to form the active closed enzyme is the switch that turns on the expression of the full transition-state binding energy.

Figure 2.

Surface structures for TIM (top), GPDH (middle), and OMPDC (bottom). The binding energy of the ligand phosphodianion is utilized to immobilize these loops, in driving the conformational changes to the stiff and catalytically active closed structures shown on the right. The ligand phosphodianion at the closed enzymes is shaded red, and the side-chain cations, which interact with the phosphodianion, are shaded green. Key: Top structures; TIM from Trypanosoma brucei brucei (open form, PDB entry 3TIM; closed form with 3-phosphoglycerate bound, PDB entry 1IIH). The phosphodianion gripper loop (residues 165–177) is shaded blue, and the side chain from K12 is shaded green. Not shown is loop 7 (residues 208–216), whose side chains Y208 and S211 move as the planes defined by the peptide bonds from G209 and G210 undergo 90° and 180° rotations, respectively.⁷⁴ Middle structures; GPDH from human liver (open form, PDB entry 1X0V; closed form with NAD and DHAP bound, PDB entry 1WPQ). The phosphodianion gripper loop (residues 292–297) is shaded blue, and the side chain from R269 is shaded green. The side chain of Q295 interacts with the substrate phosphodianion through the intervening side chain of R269.⁷⁵ Bottom structures; OMPDC from Saccharomyces cerevisiae (open form, PDB entry 1DQW; closed form with 6-hydroxyuridine 5′-monophosphate bound, PDB entry 1DQX). The phosphodianion gripper loop (residues 202–220) is shaded blue, and the side chain from R235 is shaded green. The pyrimidine umbrella loop (residues 151–165) is also shaded blue. The blue loops interact at the closed form of OMPDC through a hydrogen bond between the side chains of S154 and Q215.^76,77

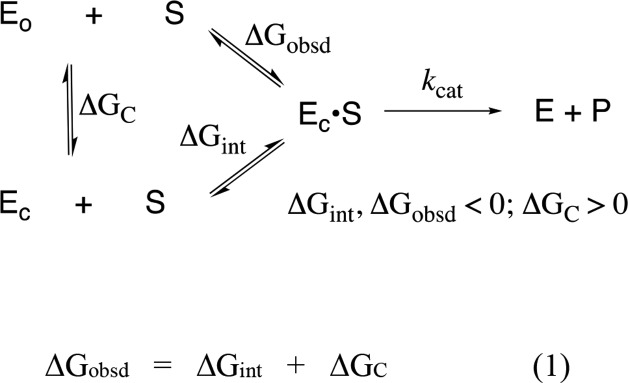
Figure 2 shows that the dianion-binding energy for OMPDC, TIM, and GPDH is utilized to drive protein conformational changes, which activate these enzymes for catalysis of decarboxylation, proton transfer, and hydride transfer, respectively. This activation is described by the model in Scheme 4.^43,61Scheme 4 holds for enzymes that exist mainly in an inactive open form (E_O) that is in equilibrium with an active but conformationally unstable (ΔG_C > 0) closed form (E_C), which shows a much higher affinity than E_O for binding to the phosphodianion of whole substrate or to the phosphite dianion piece. Equation 1 in Scheme 4 shows that the observed substrate-binding energy ΔG_obsd is then equal to the sum of the intrinsic substrate-binding energy ΔG_int plus ΔG_C.^43,61 The absolute value of ΔG_int is greater than ΔG_obsd, because of the binding energy ΔG_C required to drive the enzyme conformational change from E_O to E_C. This binding energy is used, partly or entirely, to drive desolvation of active-site side chains at E_O and to hold the flexible unliganded protein catalyst in the stiff conformation that is required for the observation of high enzymatic activity.^72,73

Scheme 4. Relationship between the Observed and Intrinsic Substrate-Binding Energy, When Binding Drives a Conformational Change from E_O to E_C.

Connections

The existence of unliganded enzymes in inactive, flexible, and entropically rich open forms provide a mechanism for the utilization of large intrinsic dianion-binding energies to drive conformational changes to stiff, closed, and entropically depleted active enzymes. There are many connections between the common mechanisms for dianion activation of OMPDC, TIM, and GPDH that are relevant to more general observations on enzyme-catalyzed reactions.

(1) The imperatives for the existence of unliganded enzymes in stable open forms deserves scrutiny.^43,78 Why do not these enzymes exist in the stiff and catalytically active closed form, thereby eliminating expenditure of substrate-binding energy to create a stiff enzyme? There is a two-part answer to this question. First, Wolfenden noted that the existence of enzymes in an open form with the active site accessible to solvent is required when the substrate is ultimately bound at a protein cage E_C that would occlude ligand (Figure 2).^73,79 Second, efficient catalysis is facilitated by a sizable difference in the stability of E_O and E_C whenever the substrate-binding energy required to obtain the total transition-state stabilization is large, because part of this binding energy must then be expended during ligand binding to avoid effectively irreversible ligand association.^43,61

(2) The conformational change from E_O to E_C (Scheme 4) is not limited to the closure of flexible loops over substrate (Figure 2). Others examples include the “oyster-like” clamping motion of protein domains over diaminopimelate (DAP) bound to DAP epimerase,⁸⁰ the closure of the capping lid domains over substrate observed for members of the enolase^81,82 and haloalkane dehalogenase superfamilies,^83,84 and the changes in the shape of flexible binding pockets observed upon ligand binding.⁹ The common feature of these ligand-driven protein enzyme conformational changes is that each activates the enzyme for catalysis, as shown in Scheme 4.

(3) The phosphodianion is one of several non-reacting substrate fragments whose binding energy is utilized to drive enzyme-activating protein conformational changes. Others include the coenzyme A fragment of acetyl CoA,^85,86 the ADP-ribose fragment of NAD/NADH,⁸⁷ the pyrophosphate and tripolyphosphate fragments of ADP and ATP, respectively,⁴² and fragments that interact with the capping domains of members of the enolase^81,82 and haloalkane dehalogenase superfamilies.^83,84

(4) TIM barrel proteins undergo rapid conformational changes from movement of 16 enzyme loops. These loops provide a flexible unliganded enzyme and their interactions with bound substrates are used to mold TIM into a stiff and active Michaelis complex. The rapid exploration of many different ground-state conformations during loop movement at TIM-barrel proteins provides access to a large suite of protein conformations, in comparison to the single conformation for a stiff unliganded protein. Each of these conformations is a potential starting point for the evolution of a new enzyme activity. Natural selection of the active conformations has given rise to proteins with a large number of enzymatic activities.^88,89

(5) There is evidence for a correlation between the increasing complexity of ligand-driven enzyme conformational changes and increasing total transition-state stabilization. This reflects the increasing number of side-chain interactions that must develop in creating a caged substrate complex with the necessary large transition-state stabilization. For example, the very large 31 kcal/mol total binding energy of OMPDC for the decarboxylation transition state is partitioned between interactions with the phosphodianion, ribosyl, and substrate fragments (Scheme 5).^47,90 The interactions of the protein that develop with both the phosphodianion and ribosyl hydroxyls are utilized to drive a complex conformational change that activates OMPDC for catalysis at the pyrimidine ring (Figure 1).^47,91

Scheme 5. Partitioning of the Total 31 kcal/mol Intrinsic Binding for OMPDC-Catalyzed Decarboxylation into the Binding Energy for Three Substrate Fragments⁴⁷.

(6) At the other extreme small enzymatic rate accelerations are associated with small or the absence of ligand-driven conformational changes. Non-enzymatic hydration of CO₂ occurs over a period of minutes in water. The rate of the carbonic anhydrase-catalyzed hydration of CO₂ is limited by a fast proton-transfer reaction between solvent and enzyme.⁹² The rate-determining step is thought to involve rapid rotation of the side chain of His-64, which shuttles protons between solvent and the enzyme active site.⁹³ The enzyme 3-oxo-Δ⁵-steroid isomerase (KSI) catalyzes double-bond migration at a relatively strong carbon acid substrate (pK_a = 13, Scheme 6).⁹⁴ The rate enhancement for KSI is small⁹⁵ compared to the flexible enzymes triosephosphate isomerase⁹⁶ and diaminopimelate racemase, which catalyze deprotonation of much more weakly acidic carbon acid substrates.^3,80 It is achieved at an active site situated in a shallow cleft on the protein surface,⁷³ which interacts with only a single face of the steroid substrate whose binding induces only a small protein conformational change.⁹⁷⁻⁹⁹ Additional work is needed to extend these observations, which suggest a correlation between enzymatic rate accelerations⁴⁴ and the magnitude of the substrate-driven conformational change.

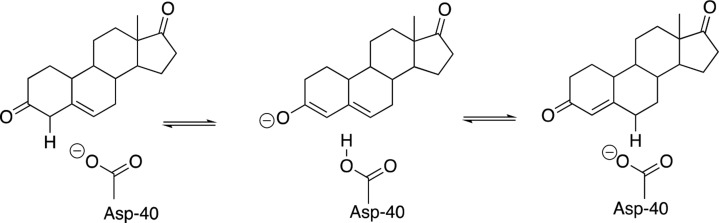
Scheme 6. Isomerization Reaction Catalyzed by 3-Oxo-Δ⁵-Steroid Isomerase (KSI).

(7) The binding pockets of OMPDC, TIM, and GPDH are divided into dianion activation and catalytic sites. The dianion-binding interactions at the activation site trigger protein conformational changes that prime the enzyme for catalysis at the catalytic site.⁵¹ Similar principals should govern the operation of these dianion activation sites and traditional allosteric regulation sites, which regulate enzyme activity by binding an effector molecule at a site different from the active site.^21,100 It is not known which type of effector site appeared first during evolution. For example, pressure might have been applied first toward the evolution of effector-type sites that optimized the total activity of primordial forms of TIM, OMPDC, and GPDH, through the utilization of the substrate phosphodianion-binding energy. These are cryptic dianion activation sites that also utilize the binding energy of phosphite, sulfate, thiosulfate, and related dianions for activation of the enzyme-catalyzed reactions phosphodianion-truncated substrates.⁵¹ They are potential starting points for the evolution of allosteric regulation sites.

(8) OMPDC, TIM, and GPDH use protein–dianion interactions to drive large enzyme conformational changes, which lock their substrates into active protein cages that provide strong stabilization of the transition state for the respective catalyzed reactions.^73,101 Another model has been proposed for enzyme-catalyzed hydride-transfer reactions where the substrate-binding energy is used to stabilize a tunneling-ready state that promotes quantum-mechanical (QM) tunneling of the transferred hydron through the energy barrier.^38,102,103 The small values for primary deuterium isotope effects (k_H/k_D = 2.4–3.1) that we have determined for numerous wild-type and mutant GPDH-catalyzed hydride-transfer reactions from NADH/NADD to DHAP or GA (Figure 1) show that there can be only incidental QM tunneling of the transferred hydride through the energy barrier^104,105 and no more than a small reduction in the effective barrier height from tunneling.^18,106 If this analysis is correct, then there is no imperative for GPDH to utilize the dianion-binding energy for stabilization of a tunneling-ready state.^104,105,107

(9) The model from Scheme 4 provides a mechanism for phosphite dianion activation of several enzymes that catalyze polar reactions in water. The model may be generalized to enzymes that catalyze the formation of unstable radical intermediates, for which slow ligand-driven conformational changes to form protein radical cages of defined structure are observed.^108,109 Radical cage formation provides for selectivity in the binding of non-reacting substrate fragments at the transition state for enzyme-catalyzed radical formation, while the structured protein cage directs the reaction of reactive and non-selective radical intermediates toward the physiological product(s).

Effect of Protein Motions on Enzyme Turnover

The time scales for protein motions range from femtoseconds for bond vibrations to milliseconds for the large protein conformational changes illustrated by Figure 2.¹¹⁰ It may be difficult for researchers engaged in studies that probe for links between enzymatic rate accelerations and protein dynamics to conclude that there are few important links. However, this possibility should be considered when there are no clear imperatives for coupling protein motions to formation of an enzymatic transition state. For example, if stabilization of the enzymatic transition state by static protein–ligand interactions is sufficient to account for the entire enzymatic rate acceleration, then there may be no requirement for assistance from coupled protein motions.

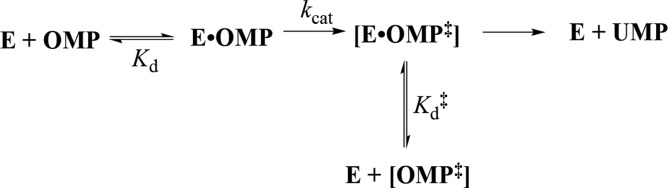
In many cases loop and side-chain protein motions at entropically rich unliganded enzymes (E_O, Scheme 7) exist so that binding energy will be expended for their elimination, thereby providing for specificity in transition-state binding. In these cases the results of biophysical studies on protein dynamics may not be relevant to the explanation for the enzymatic rate acceleration.¹¹¹ Now the only protein motions clearly relevant to the rate acceleration are those associated with the creation and breakdown of E_C·S during the steps for k_c, k_–c, and k′_–c in Scheme 7. These motions may affect the reaction rate, if they occur together with conversion of enzyme-bound substrate to product in a single reaction stage. However, there are no imperatives for such a coupled-concerted reaction mechanism¹¹² and little or no experimental evidence to support this coupling for catalysis by TIM or OMPDC.

Scheme 7. Stepwise Substrate Binding (K_d) Followed by a Protein Conformational Change (k_c).

When the protein conformational change is uncoupled from the active-site chemistry (k_chem, Scheme 7) the protein motions that control the rate constant k_c for this conformational change will only limit the value of the kinetic parameter k_cat/K_m, when k_c is rate determining for turnover at low substrate concentrations (k_–c < k_chem, Scheme 7).^113,114 These motions will only limit the value of k_cat when they are rate-determining for reactions at saturating [S] (k′_–c < k_chem).^113,114 The open and closed forms of TIM have been distinguished in solid-state NMR,^41,115,116 solution NMR,¹¹⁷ and laser-induced temperature jump fluorescence spectroscopy studies.⁴⁰ The results from studies on the conversion of E_O·S to E_C·S provide evidence that closure of flexible loop 6 over the substrate GAP is partly rate determining for k_cat/K_m and that opening of this loop to release product DHAP is partly rate determining for k_cat for TIM-catalyzed isomerization of GAP (Figure 1).^40,41,116

The rate of binding of OMP to OMPDC to form E_C·S partly limits the value of k_cat/K_m = 1.1 × 10⁷ M^–1 s^–1, and the rate of release of product from E_C·P partly limits the value of k_cat = 16 s^–1 for yeast OMPDC-catalyzed decarboxylation of (S = OMP, Scheme 7).¹¹⁸ 5-Fluororotidine 5′-monophosphate (S = FOMP, Scheme 7) is ca. 500-fold more reactive toward OMPDC-catalyzed decarboxylation than OMP.¹¹³ This large difference in the reactivity of OMP and FOMP is not strongly expressed at the transition states for wild-type OMPDC-catalyzed decarboxylation at low [FOMP] (k_cat/K_m = 1.2 × 10⁷ M^–1 s^–1) or at high [FOMP] (k_cat = 95 s^–1), so that chemistry is not rate-determining for this OMPDC-catalyzed decarboxylation. The values of k_cat/K_m for wild-type OMPDC-catalyzed decarboxylation of FOMP do not show the linear dependence on solvent viscosity expected for a cleanly diffusion-controlled reaction.^119−121 This provides strong evidence that k_cat/K_m for OMPDC-catalyzed decarboxylation of FOMP is limited by the values of k_c for the enzyme conformational change (Scheme 7).^113,114 There is good evidence that the rate constant k_cat for decarboxylation of FOMP catalyzed by wild-type and several mutant enzymes is limited by k′_–c for the enzyme conformational change.¹¹³

Lessons from Computational Studies

The difference in the calculated activation barriers ΔG^⧧ to k_cat and to k_cat/K_m for an enzymatic reaction provides the substrate-binding energy expressed at the Michaelis complex. This difference may then be compared with the calculated total transition-state binding energy to obtain an estimate for the enzyme specificity in transition-state binding. However, current computational methods are directed toward obtaining the activation barriers to k_cat and do not provide the barriers to k_cat/K_m, presumably because this barrier cannot be accurately modeled by existing computational methods. I am not aware of computational methods that routinely model the substrate-binding energy as the difference between the energy of (E + S) in solution and at the Michaelis complex (ES) for enzymes that undergo large ligand-driven conformational changes. For example, molecular docking methods serve as tools for identifying ligand-binding sites by gauging the strength of protein–ligand interactions,^122−125 but do not model the barriers to protein conformational changes. Finally, there have been few computational studies to evaluate proposals that ligand binding is accompanied by the induction of strain into the ligand, which is then relieved at the transition state for the enzymatic reaction.^{19,43,126−129}

One consequence of the lack of computational methods that provide reliable substrate-binding energies is that it is not possible to examine enzyme specificity in binding the reaction transition state by comparing calculated ground-state and transition-state binding energies. The difficulties in interpreting the results of computational studies relevant to this issue are illustrated by calculations on the Michaelis complex between OMP and OMPDC from Methanothermobacter thermautotrophicus. These calculations were concluded to support the conclusion that “the enzyme conformation is more distorted in the reactant state than in the transition state”.¹²⁹ This distortion energy was proposed to be released by protein conformational relaxation at the transition state, providing a significant contribution to the enzymatic rate acceleration.^129,130 However, this analysis failed to note that enzyme or substrate strain, which is induced by formation of the Michaelis complex and then relieved at the reaction transition state, cannot contribute to a reduction in the activation barrier to k_cat/K_m for OMPDC or for any other enzyme,⁴³ because the Gibbs free energy added to the system in forming the “strained” substrate complex must then be subtracted on formation of the “unstrained” product complex. In other words, binding energy used to induce strain into the substrate or enzyme is not related to the mechanism for transition-state stabilization, but rather ensures specificity in transition-state binding.⁶¹

Triosephosphate Isomerase

The results of computational studies on TIM to model the barriers to k_cat for reactions of whole substrate and the substrate pieces catalyzed by wild-type and mutant enzymes have been combined with experimental results to provide insight into the role of the dianion-driven conformational change in catalysis.^14,15 These studies represent a first step toward modeling the activation of TIM by the dianion-driven conformational change.

TIM-Catalyzed Reaction of the Substrate Pieces

Experimental studies on wild-type and mutant TIM-catalyzed reactions of the whole substrate GAP and the substrate pieces [GA + HP_i] show that the two reaction transition states are stabilized by essentially the same interactions with several side chains of the protein catalyst.^131,132 This provides strong evidence that these protein–dianion interactions for whole substrate and for substrate pieces are utilized to hold the protein in the active closed conformation. The result predicts that the “stiff” closed conformation of TIM determined by X-ray crystallographic analyses will show the same activation barrier for deprotonation of the whole substrate GAP, of the substrate pieces GA·HP_i′, and of GA alone (Scheme 8).

Scheme 8. Proton Transfer from TIM-Bound Carbon Acids to the Carboxylate Side Chain of E165.

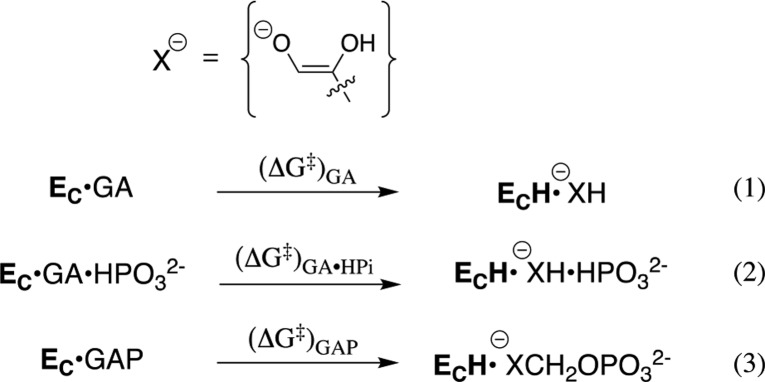
This prediction from experiments was confirmed by the results of empirical valence bond (EVB) calculations,¹⁴ which give similar activation barriers (Scheme 8) for the TIM-catalyzed deprotonation of GAP [(ΔG^⧧)_GAP = 12.9 ± 0.8 kcal/mol], for deprotonation of the substrate piece GA [(ΔG^⧧)_GA = 15.0 ± 2.4 kcal/mol], and for deprotonation of the pieces GA·HP_i [(ΔG^⧧)_GA·HPi = 15.5 ± 3.5 kcal/mol].¹⁴ We concluded that the closed form of TIM created by protein–dianion binding interactions is competent to carry out fast deprotonation of the carbon acid whole substrate or the substrate piece GA. The effect of the enzyme-bound dianion on ΔG^⧧ for reaction of the active closed enzyme is small (≤2.6 kcal/mol), in comparison to the larger 12 and 5.8 kcal/mol intrinsic phosphodianion and phosphite dianion-binding energy that is utilized in stabilization of the transition states for TIM-catalyzed deprotonation of GAP and GA·HP_i, respectively. This analysis provides support for the conclusion that once dianion-binding energy has been used to hold TIM in the active closed conformation, the dianion behaves as a spectator during the proton-transfer reaction.¹³²

I170A and L230A Mutations

The activating conformational change of TIM positions the highly conserved hydrophobic side chains from I170 and L230 [numbering for yeast enzyme] over the carboxylate side chain of the active-site base E165.¹³³ We proposed that this conformational change activates TIM for carbon deprotonation by increasing the basicity of the E165 side chain toward deprotonation of carbon, and then we examined this proposal in studies on I172A, L232A, and I172A/L232A mutants of TIM from Trypanosoma brucei brucei (TbbTIM, numbering displaced two units from the yeast enzyme).^134−136 The X-ray crystal structures of complexes for wild-type and the three mutant TIMs with the enediolate analogue 2-phosphoglycolate (PGA) are essentially superimposable, except that the space(s) created by truncation of the hydrophobic side chain(s) at the mutant enzymes are occupied by water molecules that lie ca. 3.5 Å distant from the carboxylate side chain of Glu165.¹³⁴ This occlusion of water from the active site by these hydrophobic side chains is consistent with an enhancement of the ground-state basicity of E165 at the Michaelis complex to wild-type TIM.¹³⁷

We were unable to fully rationalize the complex effects of mutations at I170 and L230 on the kinetic parameters for TIM-catalyzed deprotonation of GAP and DHAP.^134−136 The interpretation of our experimental results was clarified by EVB calculations, which accurately model the effect of I170A and L230A mutations on the barriers to deprotonation of GAP and DHAP bound to TIM.¹⁵Figure 3 shows the reaction free energy profiles for deprotonation of DHAP by TIM to form enediolate reaction intermediates.^15,62,138 The computed activation barriers for conversion of the Michaelis complexes to the respective transition states are in good agreement with the activation barriers from experiment. The computed effects of mutations on the thermodynamic barrier to substrate deprotonation to form the enediolate intermediate (ΔΔG^o_calc, Figure 3) were combined with their effects on the stability of the Michaelis complex (ΔΔlog K_m ≈ ΔΔlog K_d) from experiment to give the effect of the mutations on the stability of the complexes to the enediolate reaction intermediates relative to free enyzme.^15,134−136 This analysis (Figure 3) focused on the complex interplay of ground- and transition-state effects in catalysis by TIM.

Figure 3.

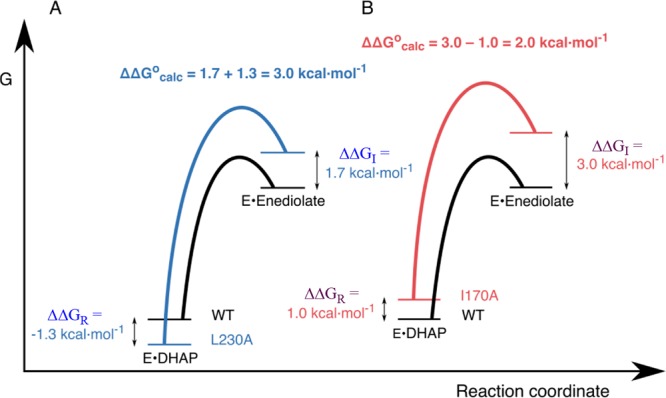
Free energy profiles for deprotonation of enzyme-bound DHAP catalyzed by wild-type and mutant TIMs, which combine results from experimental and computational studies. The diagrams show the effect of these mutations on the stability of the Michaelis complex (ΔΔG_R) relative to free TIM determined by experiment, and on the stability of the enediolate intermediate relative to the Michaelis complex (ΔΔG^o_calc) determined by EVB calculations.¹⁵ The effect of these mutations on the stability of the enediolate intermediate relative to free TIM (ΔΔG_I) is equal to [(ΔΔG^o_calc + ΔΔG_R]. (A) Profiles for wild-type TIM and the L230A mutant. (B) Profiles for wild-type TIM and the I170A mutant. Reprinted with permission from ref (15). Copyright 2017 American Chemical Society.

The L230A mutation results in a 9-fold decrease in K_m ≈ K_d for DHAP, which corresponds to ΔΔG_R = −1.3 kcal/mol for Figure 3. This is consistent with the utilization of the binding energy of DHAP to drive desolvation of E165 at wild-type TIM, and with a stabilizing interaction between the side-chain carboxylate and the water molecule that moves into the space created by L230A mutation. A water molecule also enters the space created by the I170A mutation, but this is associated with an increase in K_m (destabilization of the Michaelis complex, Figure 3) instead of the decrease in K_m observed for the L230A mutation. This effect on ground-state stability cannot be modeled by EVB calculations and is still not understood. However, the EVB calculations do reproduce the effects of the mutations on the activation barriers ΔG^⧧ determined be experiment.

The computational results define a linear free energy relationship (LFER, slope = 0.8) between the kinetic (ΔG^⧧) and thermodynamic (ΔG°) reaction barriers to formation of the enediolate intermediates of wild-type and mutant TIM-catalyzed deprotonation of DHAP.¹⁵ This LFER provides strong support for the conclusions that the I170 and L230 side chains act to minimize the thermodynamic barrier to substrate deprotonation, and that 80% of this effect on reaction driving force is expressed at the transition state for substrate deprotonation.¹⁵

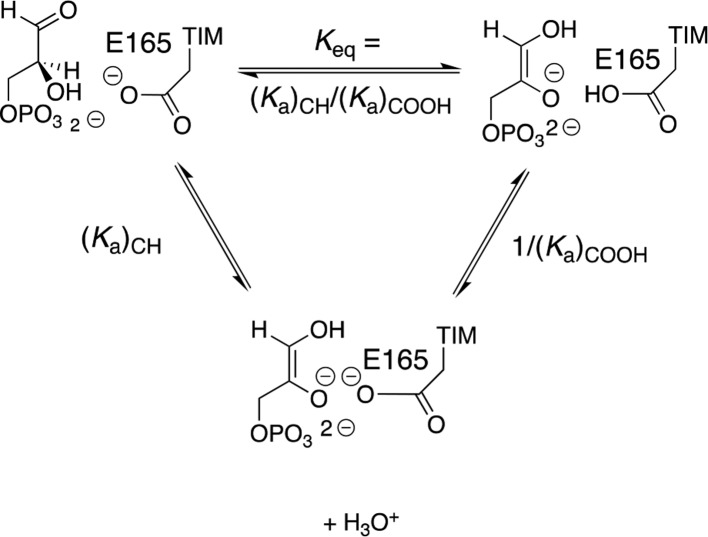
The prime imperative for efficient catalysis by TIM is to reduce the large thermodynamic barrier for deprotonation of the carbon acid substrate (pK_a = 18 in water)⁹⁶ to form the enediolate intermediate.⁵⁸ The value of log K_eq for substrate deprotonation at TIM (Scheme 9) is equal to the difference between p(K_a)_CH and p(K_a)_COOH, where the p(K_a)_COOH is similar to the highly perturbed pK_a > 10 determined for deprotonation of the carboxylic acid side chain at the complex to the enediolate analogue phosphoglycolate (PGA, Scheme 10).¹³⁹ There is a good correlation for wild-type and several mutants of TIM between the decrease in log k_cat/K_m for TIM-catalyzed isomerization of GAP and the decrease in the pK_a for deprotonation of the complex between TIM and PGA (Scheme 10). This correlation provides direct evidence that the decrease in the strong side-chain basicity at wild-type TIM is directly linked to the reduction in the catalytic activity of these mutant enzymes.¹³⁹

Scheme 9. Deprotonation of TIM-Bound Substrate (K_eq) and Competing Pathways for Proton Transfer through Solvent Water [(K_a)_CH/(K_a)_COOH].

Scheme 10. Proton Transfer from the Hydrogen-Bonded TIM·PGA Complex to Water.

Summary and Speculation

Efficient enzymatic catalysis requires a strong stabilization of the enzyme-bound transition state by the protein catalyst, and a switch to activate the expression of this transition-state binding energy following the weak and reversible binding of substrate. These protein switches are often associated with the expenditure of substrate-binding energy to drive a change in enzyme conformation from the stable, flexible, and inactive open enzyme E_O (Scheme 4) featured in Koshland’s induced-fit model to the stiff, closed, and active enzyme E_C featured in Fisher’s lock-and-key model. The evolution of enzymes that exist in both a flexible unliganded form that shows a weak affinity for the substrate and a stiff liganded form that shows a strong affinity for the transition state has occurred in order to avoid the tight and irreversible binding of substrate. These coexisting flexible and stiff forms for single enzymes favor efficient catalysis at physiological reaction conditions. They comprise two halves that together complete the whole catalyst in enabling the extraordinary operational proficiency of many enzymes.

Experimental and computational protocols for obtaining proteins with enzyme-like activity have focused on optimizing transition-state stabilization from catalysis by stiff proteins.^140−143 If these designed proteins were to mimic the very tight transition-state binding observed for some enzymes, then they might suffer the defect of tight and irreversible binding of the substrate and/or product. To the best of my knowledge there have been no efforts to engineer enzyme-activating ligand-driven conformational changes of the type discussed in this Perspective. This may be a requirement to obtain the impressive catalytic efficiency observed for enzymes such as TIM, OMPDC, glycerol 3-phosphate dehydrogenase, and phosphoglucomutase.

The author declares no competing financial interest.