Accurate molecular polarizabilities with coupled cluster theory and machine learning

Significance

The dipole polarizability of molecules and materials is central to several physical phenomena, modeling techniques, and the interpretation of many experiments. Its accurate evaluation from first principles requires quantum chemistry methods that are often too demanding for routine use. The highly accurate calculations reported herein provide a much-needed benchmark of the accuracy of hybrid density functional theory (DFT) as well as training data for a machine-learning model that can predict the polarizability tensor with an error that is about $50\%$ smaller than DFT. This framework provides an accurate, inexpensive, and transferable strategy for estimating the polarizabilities of molecules containing dozens of atoms, and therefore removes a considerable obstacle to accurate and reliable atomistic-based modeling of matter.

Abstract

The molecular dipole polarizability describes the tendency of a molecule to change its dipole moment in response to an applied electric field. This quantity governs key intra- and intermolecular interactions, such as induction and dispersion; plays a vital role in determining the spectroscopic signatures of molecules; and is an essential ingredient in polarizable force fields. Compared with other ground-state properties, an accurate prediction of the molecular polarizability is considerably more difficult, as this response quantity is quite sensitive to the underlying electronic structure description. In this work, we present highly accurate quantum mechanical calculations of the static dipole polarizability tensors of 7,211 small organic molecules computed using linear response coupled cluster singles and doubles theory (LR-CCSD). Using a symmetry-adapted machine-learning approach, we demonstrate that it is possible to predict the LR-CCSD molecular polarizabilities of these small molecules with an error that is an order of magnitude smaller than that of hybrid density functional theory (DFT) at a negligible computational cost. The resultant model is robust and transferable, yielding molecular polarizabilities for a diverse set of 52 larger molecules (including challenging conjugated systems, carbohydrates, small drugs, amino acids, nucleobases, and hydrocarbon isomers) at an accuracy that exceeds that of hybrid DFT. The atom-centered decomposition implicit in our machine-learning approach offers some insight into the shortcomings of DFT in the prediction of this fundamental quantity of interest.

The last decade has seen great progress in the first principles evaluation of the structures, stabilities, and properties of molecules and materials. Kohn–Sham density functional theory (DFT) has played a pivotal role in this endeavor by providing ground-state properties with an accuracy that is sufficient for many useful applications at a manageable computational cost (1–3). However, DFT is not equally accurate for every property of interest. For instance, an accurate and reliable description of the molecular dipole polarizability $\mathit{\alpha }$, a tensor that describes how the molecular dipole changes in the presence of an applied electric field $\mathbf{E}$, can be quite difficult to obtain (4). This is primarily due to the fact that $\mathit{\alpha }$ is a response property that is particularly sensitive to the quantum mechanical description of the underlying electronic structure. As such, nontrivial electron correlation effects and basis set incompleteness error must be simultaneously accounted for when determining $\mathit{\alpha }$. For these reasons and in light of the fact that $\mathit{\alpha }$ is a fundamental quantity of interest that underlies induction and dispersion interactions (5–7) and Raman and sum frequency generation spectroscopy (8–11), and represents a key ingredient in the development of next generation polarizable force fields (12–16), it is important to provide benchmark values for $\mathit{\alpha }$ beyond the accuracy of DFT. In this regard, linear response coupled cluster singles and doubles theory (LR-CCSD) (17–19) has been shown to provide considerably more accurate and reliable predictions for $\mathit{\alpha }$ when used in conjunction with a sufficiently large (diffuse) one-particle basis set (20–23). However, such a prediction is accompanied by a substantially larger computational cost (scaling with the sixth power of the system size), which can become quite prohibitive even when treating molecules with as few as $10-15$ atoms.

In the last few years, machine learning (ML) has gained traction as an alternative approach to the prediction of molecular properties, substituting or complementing electronic structure methods (24–26). In particular, it has been shown that accuracy on par with (or even better than) DFT can be achieved in the prediction of many molecular properties (27, 28) and that DFT (29) or coupled cluster (30) accuracy can be reached more easily when using a less accurate but more computationally efficient electronic structure method as a stepping stone. The polarizability, however, poses an additional challenge to ML. Due to its tensorial nature, the predicted $\mathit{\alpha }$ must transform according to the symmetries of the $SO\left(3\right)$ rotation group. For rigid molecules, this is easily achieved by learning the components of the tensor written in the reference frame of the molecule (31, 32). However, to obtain a transferable model that would also be suitable for flexible molecules—as well as different compounds—this line of thought would require a cumbersome and inelegant fragment decomposition. To avoid these complications, a symmetry-adapted Gaussian process regression (SA-GPR) scheme has recently been derived to naturally incorporate this $SO\left(3\right)$ covariance into an ML scheme that is suitable to predict tensorial quantities of arbitrary order (33). In this paper, we present comprehensive coupled cluster-level benchmarks for the polarizabilities of the $\sim \mathrm{7,000}$ small organic molecules contained in the QM7b database (34). We use these reference calculations to assess the accuracy of different hybrid DFT schemes and train an SA-GPR–based ML scheme (AlphaML) that can accurately predict the polarizability tensor with nominal computational cost. We then test the extrapolative prediction capabilities of AlphaML on a showcase dataset composed of 52 larger molecules and demonstrate that this approach provides a viable alternative to state-of-the-art and computationally prohibitive electronic structure methods for predicting molecular polarizabilities.

Results

Electronic Structure Calculations.

The QM7b database (26, 34, 35) includes N = 7,211 molecules containing up to seven “heavy” atoms (i.e., C, N, O, S, Cl) with varying levels of H saturation. This dataset is based on a systematic enumeration of small organic compounds (35) and contains a rich diversity of chemical groups, making it a challenging test of the accuracy associated with DFT and quantum chemical methodologies. DFT-based molecular polarizabilities were obtained by (numerical) differentiation of the molecular dipole moment, $\mathit{\mu }$, with respect to an external electric field $\mathbf{E}$ using the hybrid B3LYP (36, 37) and SCAN0 (38) functionals. Reference molecular polarizabilities were obtained using LR-CCSD. To account for basis set incompleteness error, which can be even more important than higher-order electron correlation effects in an accurate and reliable determination of $\mathit{\alpha }$ (21–23, 39), we used the d-aug-cc-pVDZ basis set (39) for all calculations herein. Although this double-$\zeta$ basis set has only a moderate number of polarization functions, augmentation with an additional set of diffuse functions almost always increases the convergence of $\mathit{\alpha }$ with respect to aug-cc-pVDZ (21, 22, 39–41). The alternative choice of retaining a single set of diffuse functions and simply increasing the angular momentum by using the slightly larger aug-cc-pVTZ basis set yields $\mathit{\alpha }$ values of comparable quality to d-aug-cc-pVDZ (SI Appendix) (21, 22, 39–41), albeit with a significant increase in the computational effort required to treat the entire QM7b dataset. A more detailed description of the electronic structure calculations performed in this work is in Materials and Methods.

To enable comparisons between molecules of different sizes, all error estimates (explicit expressions for which are given in Materials and Methods) are computed based on molecular polarizabilities divided by the number of atoms, $n_i$, contained within a given molecule. On the QM7b database, the popular B3LYP hybrid DFT functional predicts $\mathit{\alpha }$ with a mean signed error (MSE) of 0.259 a.u., a mean absolute error (MAE) of 0.302 a.u., and a root mean square error (RMSE) of 0.404 a.u. with respect to the reference LR-CCSD values. These errors, which include both scalar and anisotropic contributions, are quite substantial and correspond to $18.3\%$ of the intrinsic variability within the QM7b database, defined as ${\sigma }_{\text{CCSD}}={\left[\frac{1}{N}{\sum }_i{\Vert {\mathit{\alpha }}_i^{\left(\text{CCSD}\right)}-⟨{\mathit{\alpha }}^{\left(\text{CCSD}\right)}〉\Vert }_F^2/n_i^2\right]}^{1/2}$. The large MSE value obtained with B3LYP indicates a systematic overestimation of $\mathit{\alpha }$ by this functional (4, 42); results from the SCAN0 hybrid functional show a substantially reduced MSE of 0.059 a.u. Despite the smaller systematic overestimation of $\mathit{\alpha }$ in comparison with B3LYP, the statistical errors obtained with SCAN0 are still quite large, with computed MAE (RMSE) values of 0.217 (0.316) a.u. From the ML point of view, the AlphaML model presented herein performs almost equally well for B3LYP and SCAN0. For this reason, we focus our discussion on the B3LYP and LR-CCSD results, which will be referred to as DFT and coupled cluster singles and doubles theory (CCSD), respectively, throughout the remainder of the manuscript.

Improved SA-GPR.

The formalism underlying the SA-GPR scheme in general and the $\lambda$-SOAP (smooth overlap of atomic positions) descriptors on which our model is based have been introduced elsewhere (33) and are summarized in Materials and Methods. In this work, we include several substantial improvements that increase the accuracy and speed of the SA-GPR model, and these are worth a separate discussion. For one, evaluation of the $\lambda$-SOAP representation is greatly accelerated by choosing the most significant few hundred spherical harmonic components (of several tens of thousands) using farthest point sampling (FPS) (43). The calculation of the kernel in Eq. 1 can be carried out with essentially the same result as if all components were retained but with a much lower computational cost. A second improvement is the generalization of the $\lambda$-SOAP kernels beyond the linear kernels used in ref. 33. It has been shown that, in many cases, taking an integer power of the scalar SOAP kernel improves the performance of the associated ML model. This can be understood in terms of the order (two body, three body,…) of the interatomic correlations that are described by different kernels (44, 45). In the tensorial case, one should be careful, as the linear nature of the kernel is essential to ensure the correct covariant behavior. To include nonlinearity and increase the order of the model without affecting the symmetry properties, we multiplied the $\lambda >0$ kernels by the scalar $\lambda =0$ kernel raised to the power of $\zeta -1$ as in Eq. 2. Finally, we combined multiple kernels computed with different environment radii, $r_{\text{c}}$, which have been shown to be beneficial in the scalar case (30). Together, these improvements halve the error on QM7b as discussed in detail in SI Appendix.

Learning on the QM7b Database.

These highly accurate reference CCSD calculations and the SA-GPR scheme lay the foundation for a transferable model to predict molecular polarizabilities. In this first incarnation of the AlphaML model, we use the reference DFT and CCSD calculations on the QM7b set for training (34). As a first verification of its performance, we computed learning curves for the DFT and CCSD polarizabilities of the QM7b dataset. We used up to 5,400 structures for training with subsequent assessment of the accuracy and reliability of the AlphaML model in the prediction of $\mathit{\alpha }$ for the 1,811 structures that were not included in the training set. The structures were added to the training set according to their FPS order (43) (i.e., starting from the most diverse configurations). This procedure is representative of an efficient learning strategy that aims to obtain uniform accuracy with the minimum number of reference calculations (30). Using the best kernel hyperparameters (as described in SI Appendix), we trained a model to learn the CCSD polarizabilities. We report ML errors in terms of the percentage of the intrinsic variability of the CCSD dataset (${\sigma }_{\text{CCSD}}=2.216$ a.u. per atom) so as to provide a direct measure of the learning performance. As illustrated by the learning curves in Fig. 1, using up to $75\%$ of the QM7b database for training yields a 2.5% RMSE with respect to ${\sigma }_{\text{CCSD}}$ in predicting CCSD polarizabilities.

Fig. 1.

Learning curves for the per atom polarizabilities of the molecules in the QM7b database calculated using either CCSD or DFT as well as for the difference ($\mathrm{\Delta }$) between the two. The testing set consists of 1,811 molecules, and the right-hand axis shows the RMSE as a fraction of the intrinsic variability of the CCSD polarizability, ${\sigma }_{\text{CCSD}}$.

To get a clearer idea of the accuracy associated with these ML-based predictions, one can compare these values against hybrid DFT. Using the same metric, the intrinsic error of DFT is $18\%$ of ${\sigma }_{\text{CCSD}}$ in the prediction of CCSD polarizabilities. This demonstrates that an ML model based on SA-GPR can yield polarizabilities with an accuracy that is approximately one order of magnitude greater than DFT. At the same time, the corresponding DFT polarizabilities can be learned with an error of $3.2\%$ of ${\sigma }_{\text{CCSD}}$. As seen in other cases (29, 30), highly accurate quantum chemistry calculations are smoother and slightly easier to learn than more approximate methods, like DFT.

The AlphaML model can also be trained to evaluate the correction between different levels of theory, a correction commonly referred to as $\mathrm{\Delta }$ learning that is often found to result in much smaller error than learning the raw quantity itself (29, 30). For instance, the use of DFT as a baseline to learn CCSD polarizabilities reduces the error by an additional factor of $\sim \hspace{0.17em}2\times$ relative to the direct learning of ${\mathit{\alpha }}_{\text{CCSD}}$ (Fig. 1). $\mathrm{\Delta }$ learning therefore provides a way to further reduce the prediction error at the cost of performing a baseline DFT calculation. In SI Appendix, we demonstrate that the performance of AlphaML is rather insensitive to the details of the target electronic structure method, showing similar accuracy for SCAN0 as that observed for B3LYP.

Extrapolation to Larger Molecules.

Our definition of the kernel between two molecules as an average of environmental kernels means that the polarizabilities predicted by AlphaML are given as a sum of predicted polarizabilities for each environment (30). This feature allows one to predict $\mathit{\alpha }$ for larger molecules. To test the behavior of AlphaML in this extrapolative regime, we trained this model on the entire QM7b database and then predicted the polarizabilities in a showcase dataset of 52 large molecules, which includes amino acids, nucleobases, drug molecules, carbohydrates, and 23 isomers of ${\mathrm{C}}_8{\mathrm{H}}_n$ (the molecule key is in SI Appendix). As discussed in SI Appendix, many of these molecules are at the periphery of the portion of chemical compound space spanned by the QM7b dataset and therefore constitute a challenging test for AlphaML.

In Table 1, we show the RMSE errors in predicting $\mathit{\alpha }$ for the showcase molecules using AlphaML as well as the error made when using DFT to approximate CCSD. Table 1 also breaks down the error into the $\lambda =0$ and $\lambda =2$ components of $\mathit{\alpha }$; with an error in the anisotropic response comparable with that in the trace, this demonstrates that AlphaML learns both components with similar efficiency. As seen in the previous section, we again note that using the AlphaML model to predict CCSD polarizabilities is more accurate than simply using DFT. However, the use of DFT as the baseline in the $\mathrm{\Delta }$-learning sense leads to an additional reduction of $\sim 20-30\%$ in the error. In SI Appendix, we further discuss the behavior of the model when using the SCAN0 functional, which is similar to that observed here for B3LYP. While AlphaML predicts CCSD polarizabilities of the showcase molecules with better than DFT accuracy, we observe a substantial decrease in accuracy, which is to be expected when the model is extrapolated to the larger molecules in the showcase dataset.

Table 1.

RMSE in the prediction of the per atom polarizabilities of 52 showcase molecules

Method	RMSE	RMSE ($\lambda =0$)	RMSE ($\lambda =2$)
CCSD/DFT	0.573	0.348	0.456
CCSD/ML	0.244	0.120	0.212
DFT/ML	0.302	0.143	0.266
$\mathrm{\Delta }$(CCSD-DFT)/ML	0.181	0.083	0.161

CCSD/DFT denotes the discrepancy between CCSD and DFT values, while CCSD/ML and DFT/ML give the errors in predicting CCSD and DFT polarizabilities using AlphaML. $\mathrm{\Delta }$(CCSD-DFT)/ML gives the error in predicting the differences between the CCSD and DFT polarizabilities. All ML predictions are based on training on the full QM7b database. The total RMSE is expressed in atomic units (a.u.) per atom and broken down into the errors associated with the scalar ($\lambda =0$) and tensorial ($\lambda =2$) components of $\mathit{\alpha }$.

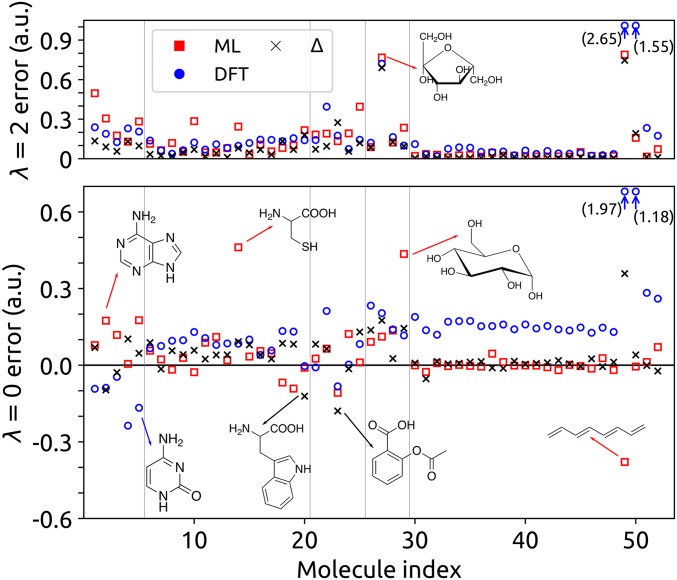
We can investigate the performance of AlphaML in more detail by analyzing the errors of individual molecules in the showcase dataset. Fig. 2 shows that the errors are actually very small for most molecules. Large errors occur predominantly for highly polarizable compounds, particularly those that show a large degree of conjugation, such as long-chain alkenes and the purine nucleobases. For these systems, the underlying electronic structure is characterized by a high degree of delocalization, which requires larger cutoffs and more complex reference molecules to ensure accurate predictions. The ML predictions for the tensorial component of the polarizability, ${\mathit{\alpha }}^{\left(2\right)}$, tend to be slightly less accurate than the DFT reference except for the highly polarizable alkenes, for which AlphaML dramatically outperforms DFT. Sulfur-containing structures, which are poorly represented in QM7b, also exhibit comparatively large errors.

Fig. 2.

RMSE made in approximating the $\lambda =0$ (Lower) and $\lambda =2$ (Upper) components of the per atom polarizability in the showcase dataset. The x axis corresponds to the numerical indices provided in the showcase molecule key in SI Appendix, and the vertical lines show the partitioning of the dataset into the different groups outlined in the same figure. Red squares show the ML error, blue circles show the error made in using DFT to approximate CCSD, and black crosses show the error made when $\mathrm{\Delta }$ learning the CCSD correction with respect to DFT.

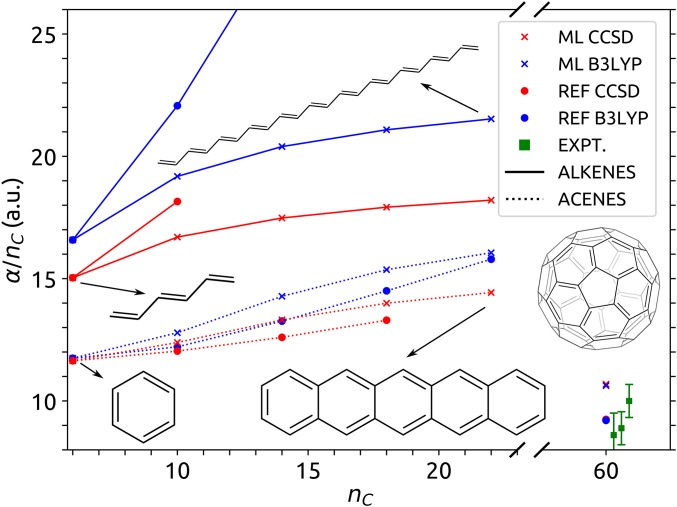
The large discrepancy between DFT, CCSD, and AlphaML observed for alkenes (like octatetraene) reflects the nonlocal and collective nature of the underlying physics in these systems as well as the inherent structure of the AlphaML model. For DFT and CCSD, the narrowing HOMO-LUMO (highest occupied molecular orbital-lowest unoccupied molecular orbital) gaps in conjugated hydrocarbons lead to near-metallic states, which are known to exhibit strong multireference character (46). As such, these systems represent a significant challenge for electronic structure methods (like DFT and CCSD) that are not explicitly based on a multireference wavefunction. In practice, this leads to divergent polarizabilities (47, 48), and methods like CCSD are no longer reliable as the source of reference quantum chemical data for ML. An ML framework like AlphaML, which relies on local atomic environments to represent structures, tacitly disregards any collective (nonlocal) behavior that extends beyond the range of the local domains and the size of the molecules included in the training set. As shown in Fig. 3, the per carbon polarizabilities predicted by AlphaML therefore saturate to a constant value for the s-trans alkenes and acenes that are larger than those included in the QM7b dataset (i.e., hexatriene and benzene, respectively). Although this is a limitation when trying to learn collective and nonlocal physics, the local structure of AlphaML is also instrumental for obtaining the accurate and transferable predictions that we demonstrated on the showcase dataset.

Fig. 3.

Polarizability per C atom for the series of s-trans alkenes (from C₆H₈ to C₂₂H₂₄) and acenes (from benzene to pentacene) as well as fullerene (C₆₀). The reference CCSD results for anthracene and tetracene were taken from ref. 49, and the reference CCSD result for C₆₀ was taken from ref. 50. The green squares (and error bars) indicate the experimental measurements for C₆₀ (51). Results are provided from DFT and CCSD calculations as well as the corresponding AlphaML models.

Even when it comes to challenging conjugated systems with a vanishing HOMO-LUMO gap, the predictions of AlphaML are stable and completely avoid the unphysical and divergent predictions of costlier (but far from reference) quantum mechanical methods, like DFT and CCSD. For molecules with a sizable gap (like C₆₀), the nonlocality is less pathological, and AlphaML performs remarkably well. For this prototypical nanotechnological system, ML predictions are within 10% of DFT and CCSD results and within the range of experimental values, despite the extrapolation to a system size that is one order of magnitude larger than the molecules in the training set.

Atom-Centered Environmental Polarizabilities.

The atom-centered structure of AlphaML provides a natural additive decomposition of $\mathit{\alpha }$ into a sum of local terms, ${\sum }_i{\mathit{\alpha }}_i$, which can be used to better understand how different functional groups contribute to the molecular polarizability. Unlike other methods for decomposing the polarizability, such as an atoms-in-molecules scheme (52) or a self-consistent decomposition (53), the approach used in this section does not require any additional calculations on top of the molecular polarizability, as the atom-centered polarizabilities are obtained as a by-product of the local nature of the SA-GPR scheme. When interpreting the ${\mathit{\alpha }}_i$, one should keep in mind that each term corresponds to the contribution from the entire atom-centered environment, and the way that the polarizability is split between neighboring atoms is entirely inductive, reflecting the interplay between data, structure (as represented by the kernels), and regression rather than explicit physicochemical considerations. For instance, a few atoms within the showcase dataset (in particular, several H environments) have ${\mathit{\alpha }}_i$ with negative eigenvalues, which reflects the fact that they reduce the dielectric response of the functional group to which they belong.

With this in mind, one can recognize physically meaningful features in the magnitude and anisotropy of the ${\mathit{\alpha }}_i$. Fig. 4 depicts eight representative examples. Comparing saturated and unsaturated hydrocarbons (e.g., 2,2-dimethylhexane, cis-4-octene, and octatetraene), one sees that AlphaML predicts the contribution from the unsaturated carbon atoms to be large and very anisotropic, which is consistent with the higher degree of electron delocalization along conjugated molecules. Similarly large and anisotropic contributions are associated with aromatic systems as seen, for example, in guanine and the indole ring of tryptophan. Oxygen atoms are associated with a very anisotropic ${\mathit{\alpha }}_i$; a large fraction of the polarizability of −OH and −COOH groups is assigned to the environments centered around nearby H and C atoms, but O atoms systematically contribute another anisotropic term oriented perpendicularly to the highly polarizable lone pairs (e.g., fructose as well as the carboxyl group in the amino acids). The sulfur-centered environments in cysteine and methionine have the largest contribution to the total polarizability in the showcase set and exhibit a strongly anisotropic response. All of these examples suggest that AlphaML can use relatively local structural information to determine an atom-centered decomposition of $\mathit{\alpha }$ that encodes nontrivial quantum mechanical contributions from each functional group (or moiety) contained within a given molecule. It is this ability to predict such an environment-dependent decomposition of $\mathit{\alpha }$ that underlies the observed better than DFT performance of AlphaML when faced with the often insurmountable challenge of transferability to a sector of chemical compound space that contains molecules that are quite distinct and notably larger than those included in the training set. A similar atom-centered decomposition can also be performed in the context of $\mathrm{\Delta }$ learning, revealing the molecular features that are associated with the most substantial errors of the approximate methods. As shown in SI Appendix, this approach reveals how the large discrepancy between DFT and CCSD for alkenes is associated primarily with the extended conjugate system.

Fig. 4.

Predicted atomic contributions to the total CCSD polarizability tensor for a selection of showcase molecules. The ellipsoids are aligned along the principal axes of ${\mathit{\alpha }}_i$, and their extent is proportional to the square root of the corresponding eigenvalue. The principal axes are shown, and they are colored based on whether the corresponding eigenvalues are positive (black) or negative (red). The figure key (which is not drawn to scale) has additional details.

Discussion

Polarizability calculations with traditional quantum chemical methods have always implied a tradeoff between accuracy and computational cost. While CCSD calculations give more accurate predictions for the polarizabilities of molecules (especially large molecules) than DFT with various functionals (4, 21), the associated computational cost can be prohibitive. In our case, the CCSD calculations for the largest molecules in the showcase dataset required thousands of central processing unit (CPU) hours and approximately 500 GB of RAM. In this paper, we have demonstrated that the AlphaML framework, which combines SA-GPR with $\lambda$-SOAP kernels and CCSD reference calculations on small molecules, allows us to sidestep these expensive calculations and obtain results with an accuracy that almost always exceeds DFT but at a fraction of the computational cost. Although this model was trained on a database of small organic molecules, it can be used to predict larger compounds with an accuracy that rivals DFT and can be systematically improved by extending the training set. The atom-centered decomposition of the ML predictions of $\mathit{\alpha }$ can be interpreted in terms of physicochemical considerations, revealing for instance the large and anisotropic contributions that originate from delocalized $\pi$ systems. In doing so, however, one should keep in mind that these contributions correspond to chemical environments rather than an atoms-in-molecules decomposition scheme.

Having shown the promise of the AlphaML framework by learning polarizabilities of small molecules, future work will focus on extensions of the training set to include larger molecules and oligomers, improvements in the accuracy of the underlying reference calculations, incorporation of methods to estimate the uncertainty in the predictions, as well as more efforts to include collective and nonlocal physics into the model. The need for these fundamental developments is underscored by an analysis of the behavior of the challenging series of conjugated alkenes, which are predicted by DFT and CCSD to have divergent polarizabilities due to vanishing HOMO-LUMO gaps. These improvements will make it possible to predict the polarizability for increasingly complex molecular systems and eventually, condensed phases. The availability of inexpensive atom-centered estimates of the fully anisotropic $\mathit{\alpha }$ will be useful to design more accurate polarizable force fields for atomistic simulations as well as to computationally evaluate Raman and sum frequency generation spectroscopies, thereby improving the predictive power of simulations and increasing the insight that can be obtained from experiments.

Materials and Methods

First Principles Calculations.

In this work, DFT calculations with the B3LYP functional (36, 37) and all LR-CCSD calculations were performed with Psi4 v1.1 (54), while DFT calculations with the SCAN0 functional (38) were performed with Q-Chem v5.0 (55). All of the molecular geometries used for ML were taken from the QM7b database (34, 35). All 52 showcase molecules (as well as the alkene series, acene series, and fullerene molecule in Fig. 3) were relaxed following the protocol used for QM7b (34). All DFT polarizabilities were computed with the finite-field method using a central difference formula with a step size of $\delta \mathit{E}=1.8897261250\times 10^{-5}\hspace{0.17em}$ a.u. All CCSD polarizabilities were calculated using LR-CCSD, except for those of the eight largest molecules in the showcase dataset (which include molecules 18, 19, 20, 21, 23, 25, 26, and 28 as listed in SI Appendix). CCSD polarizabilities for these molecules were obtained using the (orbital unrelaxed) finite-field method due to the prohibitively large computational resources (memory and disk) needed by LR-CCSD. The frozen core approximation and direct scf_type were used during all CCSD calculations. In the cases where the finite-field method was used, CCSD polarizabilities were obtained as $\mathit{\alpha }={\partial }^{2}U/\partial {\mathit{E}}^2$. Additional details of the calculations are given in SI Appendix. The polarizability data generated can be found in Yang et al. (56).

Error Assessment.

We use the Frobenius norm, defined as ${∥\mathit{\alpha }∥}_F^2={\sum }_{i,j\in \left\{x,y,z\right\}}{\alpha }_{ij}^2$, to assess the accuracy of a polarizability estimate $\mathit{\alpha }$ in a way that is rotationally invariant and includes both scalar and anisotropic components. Given two sets of polarizabilities, ${\mathit{\alpha }}_i$ and ${\mathit{\alpha }}_i^{\prime }$, for $N$ structures (each containing $n_i$ atoms), we define the following quantities: $\text{MSE}\equiv \frac{1}{N}{\sum }_i\left({∥{\mathit{\alpha }}_i∥}_F-{∥{\mathit{\alpha }}_i^{\prime }∥}_F\right)/n_i$; $\text{MAE}\equiv \frac{1}{N}{\sum }_i{∥{\mathit{\alpha }}_i-{\mathit{\alpha }}_i^{\prime }∥}_F/n_i$; and $\text{RMSE}\equiv {\left[\frac{1}{N}{\sum }_i{∥{\mathit{\alpha }}_i-{\mathit{\alpha }}_i^{\prime }∥}_F^2/n_i^2\right]}^{1/2}$. Errors are defined on a per atom basis to simplify the comparison between molecules of different sizes.

SA-GPR.

The SA-GPR framework used herein to build an ML model for the polarizability is based on the following steps. (i) Each polarizability tensor, $\mathit{\alpha }$, is decomposed into its irreducible (real spherical) components: the scalar ${\alpha }^{\left(0\right)}=\left({\alpha }_{xx}+{\alpha }_{yy}+{\alpha }_{zz}\right)/\sqrt{3}$ and the five-vector ${\mathit{\alpha }}^{\left(2\right)}=\sqrt{2}\left[{\alpha }_{xy},{\alpha }_{yz},{\alpha }_{xz},\frac{2{\alpha }_{zz}-{\alpha }_{xx}-{\alpha }_{yy}}{2\sqrt{3}},\frac{{\alpha }_{xx}-{\alpha }_{yy}}{2}\right]$. One can compute the RMSE separately on these two components, since ${∥\mathit{\alpha }∥}_F^2={\left|{\alpha }^{\left(0\right)}\right|}_F^2+{\left|{\mathit{\alpha }}^{\left(2\right)}\right|}_F^2$. (ii) $\lambda$-SOAP vector components $⟨\alpha nl\alpha \prime n\prime l\prime |{\mathcal{X}}_{j,\lambda \mu }^{\left(2\right)}〉$ are computed for each environment ${\mathcal{X}}_j$ and describe interatomic correlations within a prescribed cutoff radius, $r_{\mathrm{c}}$, of the central atom $j$. The definition of these components is given in ref. 33. (iii) The base kernel between two environments, suitable to learn tensor components of order $\lambda$, is then defined as

$$k_{\mu j,\mu \prime k}^{\lambda }\equiv k_{\mu \mu \prime }^{\lambda }\left({\mathcal{X}}_j,{\mathcal{X}}_k\right)=\sum _{\left\{J\right\}}⟨{\mathcal{X}}_{j,\lambda \mu }|J〉{⟨J|{\mathcal{X}}_{k,\lambda \mu \prime }〉}^{\star },$$ [1]

where we use the shorthand $\left\{J\right\}$ to indicate a subset of the possible spherical harmonic components of the descriptors, $\left|\alpha nl\alpha \prime n\prime l\prime \right.$, that are automatically selected with a farthest-point sampling procedure (43). (iv) The linear SOAP kernel can describe atomic correlations up to three-body terms. Many-body correlations can be introduced by normalizing it and then raising it to an integer power. To preserve the linear nature of the $\lambda$-SOAP kernels, which is crucial to enforce the correct symmetry properties, we use

$$\begin{array}{cc}\hfill k_{\mu \mu \prime }^{\lambda ,\zeta }\left({\mathcal{X}}_j,{\mathcal{X}}_k\right)& \leftarrow k_{\mu \mu \prime }^{\lambda }\left({\mathcal{X}}_j,{\mathcal{X}}_k\right)\hspace{0.17em}{k}_{00}^0{\left({\mathcal{X}}_j,{\mathcal{X}}_k\right)}^{\zeta -1};\hfill \\ \hfill {\mathbf{k}}_{j,k}^{\lambda }& \leftarrow {\mathbf{k}}_{j,k}^{\lambda }/\sqrt{{∥{\mathbf{k}}_{j,j}^{\lambda }∥}_F{∥{\mathbf{k}}_{k,k}^{\lambda }∥}_F}.\hfill \end{array}$$ [2]

(v) For each component of $\mathit{\alpha }$, we build a kernel ridge regression model with weights $w_{k\mu }$ that are determined by optimizing the loss

$${\ell }^2=\sum _{\mu ,\mathcal{A}\in N}{|{\alpha }_{\mu }^{\left(\lambda \right)}\left(\mathcal{A}\right)-\sum _{\begin{array}{c}k\in M\\ j\in \mathcal{A}\end{array}}{\mathit{\text{w}}}_{k\mu \prime }{\left({\mathbf{k}}_{j,k}^{\lambda }\right)}_{\mu \mu \prime }|}^2+{\sigma }^2{\mathbf{w}}^T{\mathbf{K}}_{MM}\mathbf{w},$$ [3]

in which $N$ is the training set, $M$ is a (possibly sparse) set of representative environments used as the basis, and ${\mathbf{K}}_{MM}$ is the matrix of kernels between representative environments. An online prediction tool for $\mathit{\alpha }$, based on the AlphaML framework, is also available at http://alphaml.org.