A Bayesian design for phase I cancer therapeutic vaccine trials

Abstract

Phase I clinical trials are the first step in drug development to test a new drug or drug combination on humans. Typical designs of Phase I trials use toxicity as the primary endpoint and aim to find the maximum tolerable dosage. However, these designs are poorly applicable for the development of cancer therapeutic vaccines because the expected safety concerns for these vaccines are not as much as cytotoxic agents. The primary objectives of a cancer therapeutic vaccine phase I trial thus often include determining whether the vaccine shows biologic activity and the minimum dose necessary to achieve a full immune or even clinical response. In this paper, we propose a new Bayesian phase I trial design that allows simultaneous evaluation of safety and immunogenicity outcomes. We demonstrate the proposed clinical trial design by both a numeric study and a therapeutic human papillomavirus vaccine trial.

1. INTRODUCTION

Cancer vaccines are vaccines that stimulate or restore the immune system’s ability to prevent development of a cancer in healthy people or treat existing cancer. Vaccines that treat existing precancer or cancer are known as cancer therapeutic vaccines. Cancer cells produce mutant or abnormally expressed proteins, many of which are important for their functions, survival, and growth. These tumor associated antigens (TAAs) are potentially suitable targets for cancer therapeutic vaccines. These TAA may be combined with nonspecific immuno-stimulants, termed adjuvants, for immunization. There is consensus that cancer therapeutic vaccines are likely to produce clinical benefit.^1–3 In fact, the FDA already approved the first cancer therapeutic vaccine, ie, sipuleucel-T, for use in patients with metastatic prostate cancer in April 2010.⁴ Through a pilot project, the National Cancer Institute identified 75 cancer vaccine target antigens, 20 of which have shown hints of clinical efficacy in human clinical trials.⁵

Phase I clinical trials for a new cancer therapeutic vaccine are normally conducted as the first step in humans. At the phase I stage, safety of the vaccine is evaluated and a safe dosage range is determined. However, typical phase I clinical trial designs for cytotoxic drugs are generally inapplicable for the development of cancer therapeutic vaccines.^6,7 This is because cytotoxic drug phase I clinical trial designs assume that, as the dose increases, both the toxicity and efficacy increase monotonically. Consequently, these designs use toxicity as the primary endpoint. By gradually increasing the dose of the study drug or drugs, they aim to find the maximum tolerable dosage (MTD) based on the occurrence of dose-limiting toxicities (DLTs). DLTs are drug side effects that are serious enough to prevent a dose increase of the drug. For example, the standard 3+3 design treats patients in cohorts of three based on rules. If none of the three patients experience a DLT, then another cohort of three patients will be treated at the next higher dose level. On the other hand, if there is one patient with a DLT observed, an additional three patients will be treated at the same dose level. When there are two or more patients who experience DLT among a cohort of three or six patients, the dose escalation stops and the next lower dose level is determined as MTD. Similar algorithms include the accelerated titration design, the rolling six design, and the “A+B” design.^8–10

Alternatively, algorithms may make model assumptions about the dose-toxicity curve and rely on the estimated dose-toxicity relationship for determining dose level for the current patient cohort. For example, the continual reassessment method (CRM)¹¹ adopts the Bayesian method to estimate the probability of having DLT at different dose levels after each cohort of patients are treated. The next cohort of patients are subsequently treated at an estimated dose level that corresponds to the targeted DLT risk. The trial is stopped when a desirable precision of the estimation is achieved or a prespecified stopping condition is met. Similar model-based algorithms include CRM with its various modifications, modified toxicity probability interval design,¹² escalation with overdose control design,¹³ etc. See the work of Le Tourneau et al¹⁴ for a thorough review of these dose escalation algorithms.

Cancer vaccines, however, are generally much safer than cytotoxic agents in terms of their adverse event occurrence risk and the severity of such adverse events. As a result, the dose-toxicity curve of cancer vaccines may be so flat that the highest dose that one can administer is still not the MTD but a manufacturing limit. Additionally, the efficacy, which is often measured by immune response, may not always increase as the dose increases.^15,16 Thus, the selection of vaccine dose levels for future studies should not depend entirely on the evaluation of the vaccine safety profile or the MTD. Instead, the primary objectives of a vaccine phase I trial should include determining whether the vaccine shows clinical efficacy or immunogenicity.^17–23 The FDA guidance for industry on cancer therapeutic vaccines²⁴ also specifically suggests that alternative designs other than the standard 3+3 design be considered and the optimization of outcomes such as immune responses be taken into account. This point has been reflected in the recent early phase (cancer) vaccine clinical trial design literature. For example, randomized phase I study designs have been proposed for optimizing the dose level or the schedule of therapeutic cancer vaccines.^25–27 In a nonrandomized setting, Zohar et al proposed a Bayesian “up-and-down” phase I design for a cancer vaccine that makes dose level escalation decisions after each patient.²⁸

There are numerous descriptions in the literature of dose escalation algorithms that simultaneously take into account safety and efficacy. Common approaches include introducing univariate “composite” endpoints (eg, a success defined as achieving immune response with no toxicity) to simplify the decision making process,^29,30 explicitly characterizing the efficacy and toxicity trade-off by a family of contours,^31,32 or applying a target function³³ or utility function^34–38 as a one-dimensional numerical summary of the bivariate outcome for decision making. Yuan et al³⁹ provided a thorough discussion on this approach.

We argue that these algorithms need further modifications to be fully suitable for cancer therapeutic vaccines. This is mostly because the objective when designing cancer vaccine trials is to find an optimal dose level in respect to the immune (or clinical) response while ensuring the safety of the participants.²⁴ On the contrary, most algorithms in the trade-off design arena aim to find dose levels that correspond to a target toxicity rate, which may be adjusted for efficacy, as fast as possible. As a consequence, it is desirable for these algorithms to treat as few as possible patients at lower dose levels. This more is better strategy, however, is not necessarily advantageous for cancer therapeutic vaccines since higher dose levels do not imply better immune response outcomes.

Human papillomaviruses (HPV) infection is the primary etiologic agent of cervical cancer. The importance of cell-mediated immune responses in controlling both HPV infections and HPV-associated neoplasms has long been realized.⁴⁰ The recent development of several therapeutic HPV vaccine candidates has considerably promised to improve control of HPV-associated precursor lesions and invasive cervical cancer. Motivated by the burgeoning development of such promising candidate therapeutic HPV vaccines, we propose a new Bayesian phase I clinical study design specifically for cancer therapeutic vaccines. The proposal uses lower dose levels as the reference for determining if the current dose level is optimal in terms of immune response. It also ensures subject safety by capping the toxicity rate with a given upper bound. These two criteria are simultaneously evaluated using an intuitive decision region that avoids complicated safety and immunogenicity trade-off elicitation from physicians. We propose several probability models that can fit in the proposed Bayesian design and evaluate their performances under multiple scenarios via a simulation study.

The paper is organized as follows. In Section 2, we introduce the overall study design scheme, its dose escalation algorithm, and options for the probability models. Numerical studies are conducted in Section 3 to evaluate the performance of the proposed study design in different scenarios. As an example, a cervical cancer therapeutic vaccine phase I trial design is described in Section 4. Finally, Section 5 is devoted to discussions.

2. METHOD

2.1. Notation

For subject s, let D_s = l (l = 1, …, L) denote the received dose level, T_s = 1 if any DLT event is observed from the subject and 0 otherwise, R_s = 1 if immune response is achieved for the subject and 0 otherwise.

Let ${\theta }_{ij}^{(l)}=P(T=i,R=j|D=l)$ for i, j = 0, 1, ${\mathit{\theta }}^{(l)}=\left\{{\theta }_{ij}^{(l)}:i,j=0,1\right\}$ and Θ = {θ^(l) ∶ l = 1, …, L}. Furthermore, for dose level l, let $p^{(l)}=P(T=1|D=l)={\theta }_{10}^{(l)}+{\theta }_{11}^{(l)}$ be the DLT risk, $q^{(l)}=P(R=1|D=l)={\theta }_{01}^{(l)}+{\theta }_{11}^{(l)}$ be the immune response probability, and $r^{(l)}={\theta }_{00}^{(l)}{\theta }_{11}^{(l)}/{\theta }_{01}^{(l)}{\theta }_{10}^{(l)}$ be the odds ratio. Let $n_{ij}^{(l)}$ be the observed number of subjects with T = i and R = j at dose level l, ${\mathit{n}}^{(l)}=\{n_{ij}^{(l)}:i,j=0,1\}$ and H denote all the data observed by the time the current analysis is conducted.

Let L(Θ|H) denote the likelihood derived from some sampling distribution F(H|Θ). Different model specifications of F will be discussed in later sections. Let π(Θ) denote the prior distribution of Θ. Then, the posterior distribution of Θ at the current analysis is

$$\pi (\text{Θ}|H)\propto L(\text{Θ}|H)\pi (\text{Θ}).$$ (1)

By taking proper integration, the marginal posterior distributions π(θ^(l)|H) and π(p^(l), q^(l)|H) can be readily derived for all l from (1).

2.2. Dose escalation algorithm

The dose escalation algorithm is based on both the toxicity and efficacy risks of the current dose level. There are several considerations that are clinically necessary for developing the algorithm. First, we assume that there is a nondecreasing relationship that exists between toxicity and dosage, ie, the toxicity risk does not decrease as dose level increases. Second, the immune response rate may reach a plateau or even start to decline as the dose level increases.

With these considerations in mind, we propose a dose escalation algorithm that is based on the joint toxicity and efficacy risks via a decision region approach. The details are described in this section.

2.2.1. Decision regions

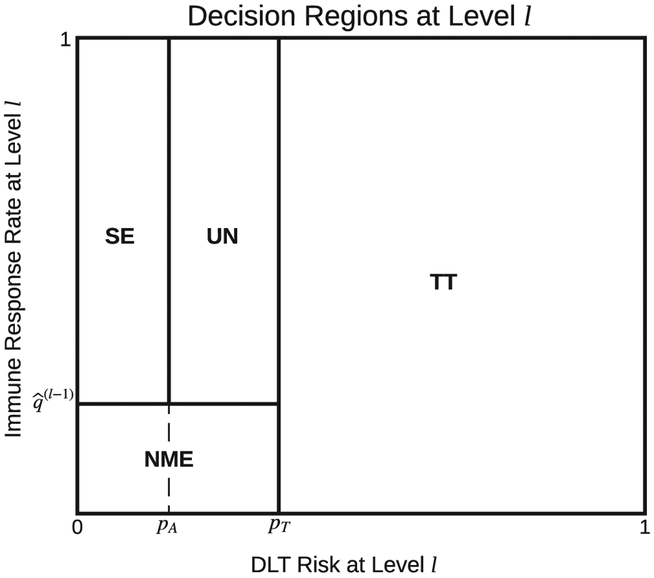
Let p_A denote the lower boundary of DLT risk below that the dose is considered absolutely safe and p_T denote the upper boundary of DLT risk above that the dose is considered toxic. The choice of (p_A, p_T) should be prespecified and reflect the clinical safety concerns of the vaccine under investigation. Let ${\widehat{q}}^{(l-1)}=E\left(q^{(l-1)}|H\right)$ denote the expected posterior immune response probability of dose level l − 1 with ${\widehat{q}}^{(l-1)}=0$ for l = 1.

At each interim analysis, given our best understanding about the safety and efficacy risks of the current dose level l based on π(p^(l), q^(l)|H), we propose to first conceptually categorize dose level l into the following four categories to take the corresponding dose escalation actions to stop the trial or to continue the trial with higher or the same dose level.

• Too Toxic (TT): DLT risk p^(l) exceeds boundary p_T(ie, p^(l) > p_T) and the current dose level is (and all higher dose levels are) considered too toxic.

• No More Effective (NME) than dose level l − 1 : DLT risk p_l is below boundary p_T(ie, p^(l) ≤ p_T); thus, not too toxic. On the other hand, immune response probability q^(l) is below ${\widehat{q}}^{(l-1)}$. That is, the current dose level is no more effective than dose level l − 1.

• Safe and Effective (SE): DLT risk p^(l) is below boundary p_A and the immune response probability q^(l) exceeds ${\widehat{q}}^{(l-1)}$ (ie, $p^{(l)}\le p_A,q^{(l)}>{\widehat{q}}^{(l-1)}$). The current dose level has no safety concern and is more effective than its lower dose levels; it is therefore considered safe and effective.

• Uncertain (UN): DLT risk p^(l) is below boundary p_T but exceeds boundary p_A (ie, p_A < p^(l) ≤ p_T). The immune response probability q^(l) exceeds boundary ${\widehat{q}}^{(l-1)}$. The dose is considered more effective than its lower dose levels and not too toxic. However, uncertainty about safety still exists. The status of the current dose level is thus uncertain.

As a straightforward illustration of the four categories, we split the joint parameter space of (p^(l), q^(l)), [0, 1]², into four regions that correspond to the four categories (Figure 1), termed as decision regions.

FIGURE 1.

Dose escalation decision regions based on the posterior distribution π(p^(l), q^(l)|H). The entire space is split into Regions TT: too toxic, NME: no more effective than its lower dose levels, SE: safe and effective, and UN: uncertain

2.2.2. Decision region determination

The actual determination of the category, or equivalently the decision region, of the current dose level is based on the probability distribution π(p^(l), q^(l)|H). Specifically, we propose a sequential identification approach based on conditional probabilities derived from π(p^(l), q^(l)|H).

Let ${\mathcal{C}}_1$, ${\mathcal{C}}_2$, and ${\mathcal{C}}_3$ be fixed cut-off values in (0, 1). The steps are as follows.

• Step 1: If $Pr\left(p^{(l)}>p_T|H\right)>{\mathcal{C}}_1$, then the current dose level is considered to be in Region TT, ie, too toxic. Go to Step 5.

• Step 2: If $Pr\left(q^{(l)}\le {\widehat{q}}^{(l-1)}|p^{(l)}\le p_T,H\right)>{\mathcal{C}}_2$, then the current dose level is considered to be in Region NME, ie, nomore effective than its lower dose levels. Go to Step 5.

• Step 3: If $Pr\left(p^{(l)}\le p_A|p^{(l)}\le p_T,q^{(l)}>{\widehat{q}}^{(l-1)},H\right)>{\mathcal{C}}_3$, then the current dose level is considered to be in Region SE, ie, safe and effective. Go to Step 5.

• Step 4: The current dose level is considered to be in Region UN, ie, uncertain.

• Step 5: Category determination finishes.

The values of ${\mathcal{C}}_1$, ${\mathcal{C}}_2$, and ${\mathcal{C}}_3$ should be chosen prior to study initiation and reflect the considerations of the investigators and patients. These thresholds’ values should also give reasonable overall study operating characteristics.

2.2.3. Actions

Now that the current dose level l has been identified as belonging to one of the four regions, the following actions can be taken.

• Region TT: The current dose level is considered as too toxic. The trial should be stopped and the next lower dose level should be reported as the recommended dose.

• Region NME: The current dose level is no more effective than its lower dose level. Its next lower dose level is considered to be safe and have already achieved the maximum immune response probability. The trial should stop and report the next lower dose level as the recommended dose.

• Region SE: The current dose level is considered to be both safe and more effective than its lower dose levels. The trial will escalate to dose level l + 1. If dose level l is already the highest dose level, the trial will stop and report dose level l as the recommended dose.

• Region UN: There exists concern about the safety of the current dose level l. The trial should continue to treat more patients at dose level l unless the maximum number of patients has been reached for the current dose level. If the maximum number of patients have been treated at this dose level, depending on the choice of (p_A, p_T) and the clinical considerations of the investigational vaccine, one may choose to continue the trial with dose escalation because there is no evidence that the current dose is too toxic.

2.3. Probability models

In this section, we propose several options for the probability models F that can be considered for Bayesian inference. We note that the proposed dose escalation algorithm is flexible in regard to F. In fact, the dose-toxicity model in Section 2.3.2 is based on the typical dose-toxicity single-parameter power model for phase I studies. We do emphasize, though, that a desirable F should be nondecreasing with respect to the dose-toxicity relationship and avoid monotonic assumptions for the dose-immune response curve.

2.3.1. Nonparametric model

As one of the simplest models, we posit no assumptions on the dose-toxicity or dose-immune response relationships. That is, θ^(l) ⫫ θ^(l′) for all l ≠ l^′a priori. Furthermore, at each dose level, we assume that the observed data n^(l) follow a multinomial distribution with parameters θ^(l) and assign Jeffreys’ prior (ie, Dirichlet prior with parameters $\frac{1}{2}$) to θ^(l).

The likelihood function is given by

$$L\left({\mathit{\theta }}^{(l)};{\mathit{n}}^{(l)}\right)\propto \prod _{i=0}^1\prod _{j=0}^1{\left\{{\theta }_{ij}^{(l)}\right\}}^{n_{ij}^{(l)}}$$

and the posterior distribution of θ^(l) is still Dirichlet

$$\pi \left({\theta }_{00}^{(l)},{\theta }_{01}^{(l)},{\theta }_{10}^{(l)},{\theta }_{11}^{(l)}|H\right)=\text{Dirichlet}\left(n_{00}^{(l)}+\frac{1}{2},n_{01}^{(l)}+\frac{1}{2},n_{10}^{(l)}+\frac{1}{2},n_{11}^{(l)}+\frac{1}{2}\right).$$ (2)

We refer to (2) as the nonparametric model.

We may further simplify the model by assuming that the odds ratio r^(l) = 1, ie, DLT risk is independent of immune response probability a priori. The likelihood can be computed as

$$L\left(p^{(l)},q^{(l)};{\mathit{n}}^{(l)}\right)\propto {\left\{p^{(l)}\right\}}^{n_{10}^{(l)}+n_{11}^{(l)}}{\left\{1-p^{(l)}\right\}}^{n_{00}^{(l)}+n_{01}^{(l)}}{\left\{q^{(l)}\right\}}^{n_{01}^{(l)}+n_{11}^{(l)}}{\left\{1-q^{(l)}\right\}}^{n_{00}^{(l)}+n_{10}^{(l)}}.$$

By assigning a Jeffreys’ prior Beta($\frac{1}{2},\frac{1}{2}$) to p^(l) and q^(l), the posterior distribution will be

$$\pi \left(p^{(l)},q^{(l)}|H\right)=\text{Beta}\left(p^{(l)};n_{10}^{(l)}+n_{11}^{(l)}+\frac{1}{2},n_{00}^{(l)}+n_{01}^{(l)}+\frac{1}{2}\right)\text{Beta}\left(q^{(l)};n_{01}^{(l)}+n_{11}^{(l)}+\frac{1}{2},n_{00}^{(l)}+n_{10}^{(l)}+\frac{1}{2}\right).$$ (3)

We refer to (3) as the nonparametric+ model.

Admittedly, both models (2) and (3) are likely misspecified in the sense that they ignore the correlations among Θ across dose levels. However, they may still be suitable for phase I studies with vaccines since the primary objective is not to understand the dose-toxicity and dose-efficacy relationships. Moreover, data from phase I studies are often limited, which necessitates parsimonious statistical models. In the simulation studies, we examine the robustness of these models in detail.

2.3.2. Partially parametric model

Compared to nonparametric models, a parametric specification of F may allow the incorporation of dose-toxicity, dose-efficacy, and toxicity-efficacy relationships in dose escalation. The parametric specification also allows information sharing among different dose levels and, thus, is potentially more efficient. In the context of evaluating cancer vaccines, however, it is difficult to posit assumptions on the dose-efficacy relationship since the immune response rate may even decrease as the dose level increases. On the other hand, it remains reasonable to assume that the dose-toxicity curve is nondecreasing. Therefore, we propose a partially parametric model that only makes assumptions about dose-toxicities but leaves the dose-immune response relationship unspecified.

Specifically, we construct the dose-toxicity model similar to the one considered by Yin and Yuan⁴¹

$$\text{log}{p}^{(l)}=e^{\alpha }\text{log}{\tau }^{(l)}.$$ (4)

The τ^(l)s are deterministic design parameters reflecting the expectation of the DLT risk at dose level l with τ^(l) > τ^(l′) for l > l′. The dose-toxicity model is thus indexed by the single parameter α. For the immune response and the odds ratio, we assume q^(l) and r^(l) at different dose levels are independent a priori.

The priors are specified as follows:

$$\begin{gathered} \alpha ~N\left(0,{\sigma }_{\alpha }^2\right) \\ {q}^{(l)}~Beta\left(\frac{1}{2},\frac{1}{2}\right) \\ \text{log}{r}^{(l)}~N\left(0,{\sigma }_r^2\right). \end{gathered}$$

Let β^(l)-= {α, q^(l), r^(l)} or equivalently β^(l) = {p^(l), q^(l), r^(l)}. Given β^(l), it is reasonable to guess the prior means of ${\theta }_{ij}^{(l)}$ by a function g_ij(β^(l)) that is defined as, for r^(l) = 1, g_ij(β^(l)) = (p^(l))ⁱ(1 − p^(l))¹⁻ⁱ(q^(l))^j(1 − q^(l))^1−j, and for r^(l) ≠ 1,

$$g_{11}\left({\mathit{\beta }}^{(l)}\right)=\frac{b+\sqrt{b^2-4\left(r^{(l)}-1\right)p^{(l)}{q}^{(l)}{r}^{(l)}}}{2\left(1-r^{(l)}\right)},$$

where b = (p^(l) + q^(l))(1 − r^(l)) − 1, g₁₀(β^(l)) = p^(l) −g₁₁(β^(l)), g₀₁(β^(l)) = q^(l) −g₁₁(β^(l)), and g₀₀(β^(l)) = 1−p^(l) −q^(l) +g₁₁(β^(l)). This induces a mixture of Dirichlet distributions prior⁴² for Θ by

$$\pi (\text{Θ})\propto \underset{r^{(1)},\dots ,r^{(L)}}{\int }\underset{q^{(1)},\dots ,q^{(L)}}{\int }\underset{\alpha }{\int }\{\prod _{l=1}^L\left(\prod _{i=1}^1\prod _{j=0}^1{\left\{{\theta }_{ij}^{(l)}\right\}}^{g_{ij}\left({\beta }_l\right)}\right)\pi \left(q^{(l)}\right)\pi \left(r^{(l)}\right)\pi (\alpha )\}d\alpha d{q}^{(1)}\dots d{q}^{(L)}d{r}^{(1)}\dots d{r}^{(L)}$$

and the posterior distribution of Θ give H at dose level l is given by

$$\pi (\text{Θ}|H)\propto \pi (\text{Θ})\prod _{l^{\prime }=1}^l\prod _{i=0}^1\prod _{j=0}^1{\left\{{\theta }_{ij}^{\left(l^{\prime }\right)}\right\}}^{n_{ij}^{(l^{\prime })}}.$$ (5)

We refer to model (5) as the parametric model. Similar to the nonparametric case, we may simplify the model by assuming that r^(l) = 1. Then, the posterior distribution π(p^(l), q^(l)|H) can be obtained by

$$\pi \left(p^{(l)},q^{(l)}|H\right)\propto \prod _{l^{\prime }=1}^l{\left\{p^{\left(l^{\prime }\right)}\right\}}^{n_{10}^{(l^{\prime })}+n_{11}^{\left(l^{\prime }\right)}}{\left\{1-p^{\left(l^{\prime }\right)}\right\}}^{n_{00}^{\left(l^{\prime }\right)}+n_{01}^{\left(l^{\prime }\right)}}\pi \left(p^{(l)}\right)\times \text{Beta}\left(q^{(l)};n_{01}^{(l)}+n_{11}^{(l)}+\frac{1}{2},n_{00}^{(l)}+n_{10}^{(l)}+\frac{1}{2}\right),$$ (6)

where log p^(l′) = log p^(l)(log τ^(l′) − log τ^(l)), and $\pi \left(p^{(l)}\right)=-\frac{\pi (\alpha )}{p^{(l)}\text{log}{p}^{(l)}}$ is the prior on p^(l) induced by π(α). We refer to (6) as the parametric+ model.

2.4. Large sample property

Large sample properties in general do not apply in phase I settings when the sample size is small or medium at most. However, we still consider a theoretical large sample property proof necessary to better understand the proposed sequential decision region determination approach. We report these properties in this section.

For compactness, we suppress the superscript (l) in this section unless necessary. Let p* and q* denote the true DLT risk and immune-response probability for the current dose level. Denote ω* ∈ {TT, NME, SE, UN} the true region in which (p*, q*) is located in reference to the decision region definitions given in Section 2.2.1 and ω the region identified following the steps in Section 2.2.2 given π(p, q H).

Theorem 1. Under the conditions that region ω* is in the support of the prior distributions π(p)π(q) and the likelihood is a continuous function of p and q, if (p*, q*) is in the interior of ω*, then Pr(ω = ω*|H) → 1 as ∑_i,jn_ij → ∞ (ie, ω → ω* almost surely) for all ${\mathcal{C}}_1$, ${\mathcal{C}}_2$, and ${\mathcal{C}}_3$ in (0, 1).

Corollary 1. If (p*, q*) is in the interior of ω*, the nonparametric and partially-parametric models specified in Section 2.3 all guarantee ω → ω* almost surely.

The proofs are provided in the Appendix.

2.5. Summary

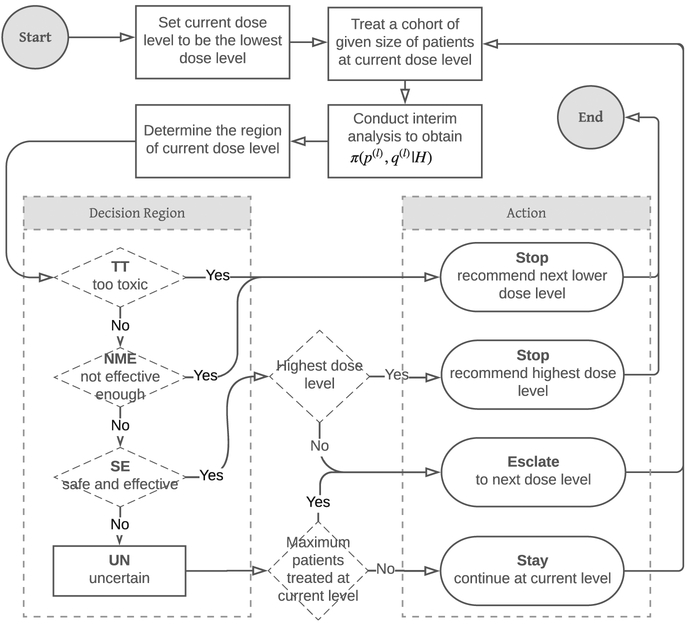
Figure 2 summarizes the overall study design. The study will start from the lowest dose level and treat patients in a cohort of prespecified size. After treating the cohort, when their toxicity and immune response data are available, a statistical analysis will update the toxicity and efficacy risks for the current dose level. The analysis is based upon an appropriate probability model and all the data observed from the study so far. The study will then determine the region in which the current dose level belongs and takes the actions either to stop the trial or to treat the next cohort of patients at the current or the next higher dose level.

FIGURE 2.

Flow chart of the overall study design

3. SIMULATION STUDY

3.1. Settings

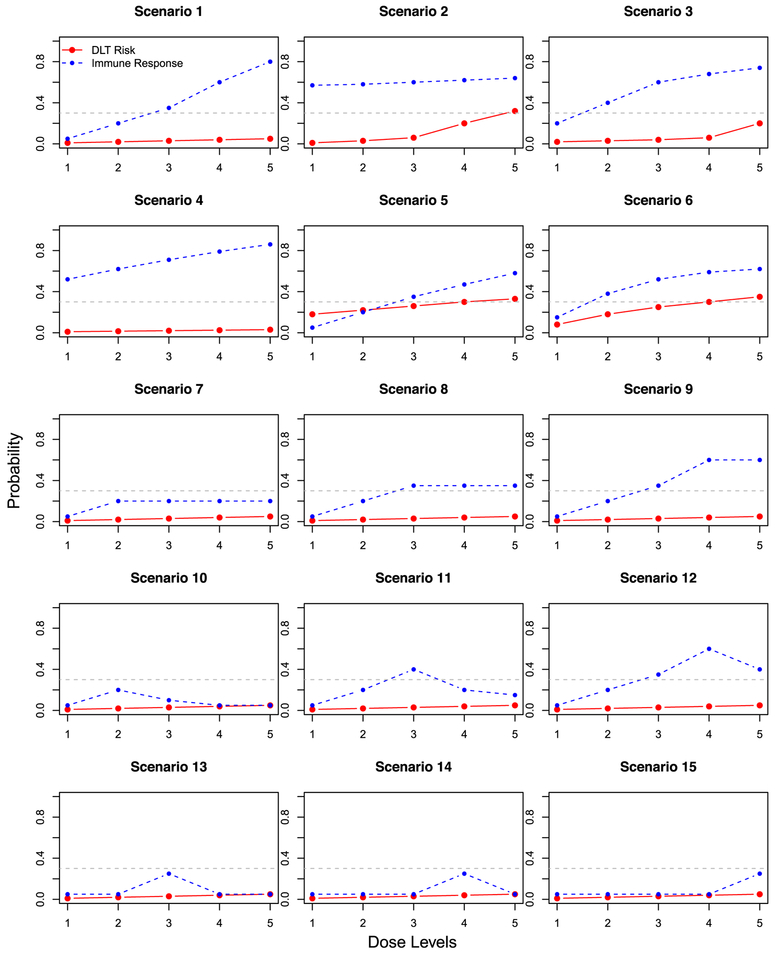
We consider 15 scenarios in the simulation study (Figure 3) to thoroughly evaluate the proposed method. Scenarios 1 to 6 are from the work of Thall and Cook³¹ and represent the typical toxicity and efficacy risks for cytotoxic drugs. We consider these scenarios to evaluate how the proposed design works for typical phase I scenarios. Scenarios 7 to 15 are modified from Scenario 1, where the toxicity risks are low. In order to represent the cases for cancer therapeutic vaccines, scenarios 7 to 9 consider that the immune response probabilities have a plateau; 10 to 12 consider when the immune response probabilities are unimodal; and 13 to 15 consider when the immune response probabilities are unimodal but are not increasing at the beginning dose levels. For all the scenarios, we assume the odds ratio r^(l) = 10 for all l. Plots of θ^(l) for all the 15 scenarios are included in the Web Supplement document.

FIGURE 3.

Scenarios for the simulation study. The solid red line is DLT risk p^(l); the dashed blue line is the immune response probability q^(l); the gray dashed line is at p_T = 0.3

We consider a cohort size of 7 and a maximum of 14 patients for each dose level. There are several reasons for these cohort size choices. First, since toxicity is not the most serious concern and most toxicities are not life-threatening for cancer therapeutic vaccines, it is feasible to consider a larger cohort size than the typical number 3. Second, when measuring immune responses in practice, samples are placed on assay plates with control calibrators. The study investigators thus prefer having fewer interim analyses and more samples for each assay plate to batch the assays to reduce interassay variability and cost. We thus propose to have one interim analysis at each dose level. Lastly, for decision region determination, we choose p_A = 0.1, p_T = 0.3, ${\mathcal{C}}_1={\mathcal{C}}_2=0.8$, and ${\mathcal{C}}_3=0.5$.

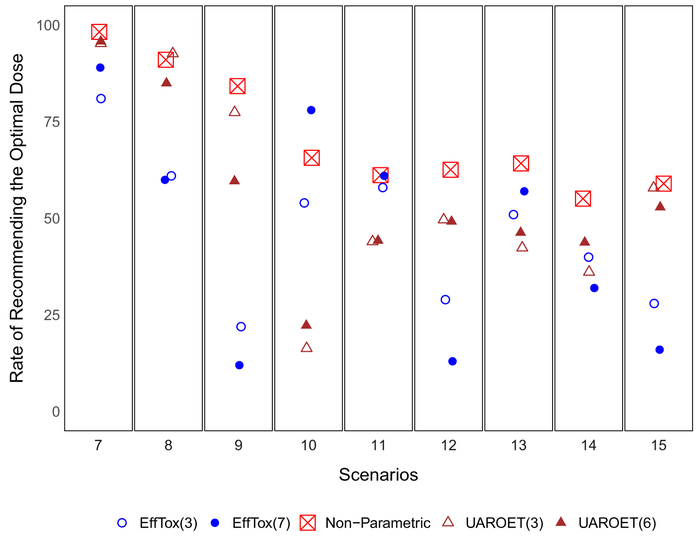
Scenarios 7 to 15 represent cases relevant to cancer therapeutic vaccines. We compare the performance of the proposed design to two alternative designs, ie, the EffTox design³¹ that is based on safety and efficacy trade-off contours, and the UAROET design³⁵ that is based on safety and efficacy utility functions. We chose the two alternative designs for two reasons. First, the two designs are representative of major phase I designs in the literature that simultaneously take into account safety and efficacy. Second, software implementing the two designs is readily available. For the alternative designs, we consider a maximum sample size of 42 to be comparable to the proposed design. Furthermore, in addition to a cohort size of 7 (6 for UAROET because of its software restriction), we also consider cohorts of 3 subjects, the default cohort size in the software for the two alternative designs, to allow more frequent interim analysis. Other details about the software and the settings (eg, trade-off contours and utility function) for the two alternative designs are presented in the Web Supplement document.

3.2. Results

For evaluating the performance of the proposed design, based on 1000 replications, we report for each dose level the average number of patients treated, the chance for the dose level to be recommended and, the average number of DLTs and immune responses observed. We also report the average total number of patients treated and the average total number of DLTs and responses observed on the study.

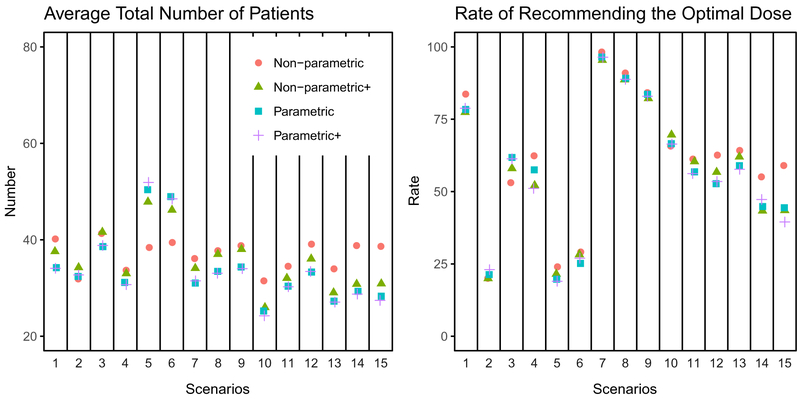
We first compare the four modeling approaches, ie, nonparametric (2), nonparametric+ (3), parametric (5), and parametric+ (6). For parametric and parametric+ models, we set the skeleton τ^(l)(4) to be the true DLT risk. Figure 4 presents the average total number of patients treated on the study and the average rate of reporting the correct dose level(s) (ie, dose level(s) with p^(l) < p_T and largest q^(l)) for all the scenarios. For most of the scenarios, the four models perform similarly in terms of the total number of patients and the rate of recommending the correct dose level(s). Thus, we report the detailed performance metrics for the nonparametric model approach in this section. Complete simulation results of all the models and scenarios are reported in the Web Supplement document.

FIGURE 4.

Average total number of patients and rate of reporting the optimal dose level(s) for scenarios 1 to 15

Features of the simulation results for scenarios 1 to 6 are as follows (Table 1). For Scenario 1, the DLT risk is well below p_A = 0.1 for all dose levels, and the immune response rate increases monotonically and significantly. There is 83.7% chance that dose level 5 is recommended. Scenario 2 is difficult for the proposed design because the increasing trend of the immune response probabilities is very shallow. As a result, there is a similar chance for dose levels 1 to 4 to be recommended with dose level 3 being slightly more favorable. Scenarios 3 and 4 both have monotonically increasing immune response probabilities. The trend is not as strong as Scenario 1 but stronger than Scenario 2. There is 53% and 62% chance to recommend dose level 5. Note that, for Scenario 3, dose level 5 has a DLT risk 0.2, which leads to a larger number of DLTs and a higher recommendation rate for dose level 4, as compared to Scenario 4. Scenarios 5 and 6 both have dose level 5 that is overly toxic compared to p_T = 0.3. We notice that there is less than 10% chance for dose level 5 to be recommended. Furthermore, the proposed design did not distinguish dose levels 2 and 3, where dose level 3 has a higher immune response probability but also a DLT risk rate close to p_T. For scenarios 5 and 6, we observe that the nonparametric approach requires fewer total subjects, on average, compared to the other modeling approaches (Figure 4). The explanation is that scenarios 5 and 6 have high DLT risk that are close to the threshold (30%). The different model choices affect the chances that dose level 3 is recognized as too toxic. With the nonparametric modeling approach, the study is more likely to stop at dose level 3, which reduces the total number of patients treated on the study.

TABLE 1.

Simulation results using the nonparametric model for scenarios 1 to 6 from Thall and Cook.³¹(p, q): DLT risk and immune response probability. Dose levels that are safe (p ≤ p_T) and have the highest immune response probability are in bold. %: rate of reporting a dose level. N: average number of patients treated. (D, R): average number of DLTs and immune responses. Note that the total rate of reporting any dose level is less than 100% when the chance that dose level 1 is considered too toxic is larger than 0 (eg, in scenarios 5 and 6)

Scenario	Dose Level
		1	2	3	4	5	Total
1	(p, q)	(0.01,0.05)	(0.02,0.2)	(0.03,0.35)	(0.04,0.6)	(0.05,0.8)
	%	2.1	6.2	3.7	4.3	83.7	100
	N	7.47	8.48	8.16	8.05	8.01	40.17
	(D,R)	(0.08,0.38)	(0.14,1.65)	(0.24,2.89)	(0.34,4.81)	(0.43,6.39)	(1.23,16.12)
2	(p, q)	(0.01,0.57)	(0.03,0.58)	(0.06,0.6)	(0.2,0.62)	(0.32,0.64)
	%	21.7	20.3	27.7	20	10.3	100
	N	7.5	8.3	7.16	5.98	2.93	31.88
	(D,R)	(0.08,4.3)	(0.28,4.84)	(0.46,4.34)	(1.23,3.66)	(0.99,1.92)	(3.04,19.06)
3	(p, q)	(0.02,0.2)	(0.03,0.4)	(0.04,0.6)	(0.06,0.68)	(0.2,0.74)
	%	4.1	5	12.9	24.9	53.1	100
	N	7.86	8.34	8.3	8.36	8.46	41.32
	(D,R)	(0.14,1.55)	(0.24,3.29)	(0.32,5.03)	(0.49,5.67)	(1.71,6.27)	(2.91,21.81)
4	(p, q)	(0.01,0.52)	(0.01,0.62)	(0.02,0.71)	(0.03,0.79)	(0.03,0.86)
	%	12.4	10.9	7.9	6.4	62.4	100
	N	7.46	7.58	6.96	6.1	5.59	33.68
	(D,R)	(0.07,3.85)	(0.11,4.68)	(0.16,4.9)	(0.14,4.87)	(0.16,4.8)	(0.63,23.09)
5	(p, q)	(0.18,0.05)	(0.22,0.2)	(0.26,0.35)	(0.3,0.47)	(0.33,0.58)
	%	15.6	24.1	24	15.6	9.9	89.2
	N	11.65	10.57	8.35	5.26	2.58	38.4
	(D,R)	(2.09,0.6)	(2.22,2.03)	(2.2,3.04)	(1.6,2.5)	(0.89,1.53)	(9,9.7)
6	(p, q)	(0.08,0.15)	(0.18,0.38)	(0.25,0.52)	(0.3,0.59)	(0.35,0.62)
	%	14.9	26.7	29.1	19.7	8.2	98.6
	N	10	11.32	9.5	6	2.62	39.44
	(D,R)	(0.8,1.49)	(2.03,4.25)	(2.39,4.91)	(1.82,3.5)	(0.96,1.71)	(7.99,15.85)

For scenarios 7 to 15, the scenarios are in general more suitable for cancer therapeutic vaccines, Table 2 reports the average rate of recommending the optimal dose and the average number of patients treated on each dose level. For scenarios 7 to 9, where there is plateau in immune response probabilities, the proposed design recognizes the dose levels that have immune response probabilities below the plateau. For dose levels corresponding to the plateau (ie, optimal), the proposed design does not distinguish them and allows dose escalation to continue. For instance, the optimal dose levels 4 and 5 are selected with 84.2% chance in Scenario 9 (19.4% for level 4 and 64.8% for level 5). For scenarios 10 to 12 where the immune response probabilities are unimodal, there is more than 60% chance that the proposed design correctly identifies the optimal dose level that corresponds to the mode of the immune response probabilities. For scenarios 13 to 15, where the immune response probabilities are also unimodal but the beginning dose levels are equally lacking in efficacy, the proposed design allows the study to continue until it finds the optimal dose level. The rate to recommend the optimal dose levels are from 55% to 64%.

TABLE 2.

Selected percentage followed by the average number of patients treated in parenthesis. Dose levels with bold (p, q) are the optimal dose level(s) in each scenario. The numbers in the parenthesis following the design are batch sizes

Scenario	Dose Level
		1	2	3	4	5	Total
7	(p, q)	(0.01,0.05)	(0.02,0.25)	(0.03,0.25)	(0.04,0.25)	(0.05,0.25)
	Nonparametric(7)	1.8(7.4)	20(8.4)	20(8.4)	15.4(6.6)	42.8(5.3)	100(36.1)
	EffTox(7)	5(9.1)	52(18.2)	32(11.1)	4(1.2)	1(0.2)	94(39.8)
	EffTox(3)	4(5.6)	40(15.2)	26(10.9)	10(3.4)	5(1.1)	85(36.2)
	UAROET(6)	0.5(7.5)	16.2(12)	29.7(11.1)	34.4(7)	15.5(3.5)	96.3(41.1)
	UAROET(3)	0.2(4.5)	11(8.8)	25(10)	28.8(9.2)	30.5(8.1)	95.5(40.7)
8	(p, q)	(0.01,0.05)	(0.02,0.25)	(0.03,0.4)	(0.04,0.4)	(0.05,0.4)
	Nonparametric(7)	1.5(7.5)	7.5(8.2)	21.5(8.1)	17.6(7.7)	51.9(6.2)	100(37.7)
	EffTox(7)	4(8.8)	31(14.8)	52(15)	7(1.4)	1(0.2)	95(40.2)
	EffTox(3)	4(5.5)	27(11.9)	48(16.9)	11(3.2)	2(0.8)	92(38.3)
	UAROET(6)	0.3(7.2)	12.5(11.1)	33.8(12.5)	34.7(7.2)	16.5(3.3)	97.8(41.3)
	UAROET(3)	0.1(4.4)	4.9(8.4)	28.2(11.1)	34.1(9.5)	30.3(7.8)	97.6(41.2)
9	(p, q)	(0.01,0.05)	(0.02,0.25)	(0.03,0.4)	(0.04,0.6)	(0.05,0.6)
	Nonparametric(7)	1.4(7.5)	7.3(8.1)	7.1(8.2)	19.4(7.8)	64.8(7.2)	100(38.8)
	EffTox(7)	3(8.6)	32(14.8)	47(14.3)	9(1.7)	3(0.2)	94(39.6)
	EffTox(3)	5(5.7)	22(10.9)	39(14.7)	18(4.8)	4(0.9)	88(37)
	UAROET(6)	0.6(7.4)	9.1(11)	28.2(11.9)	40.3(7.8)	19.3(3.1)	97.5(41.3)
	UAROET(3)	0(4.3)	3.7(7.7)	16.4(9.9)	40.4(10.9)	37(8.4)	97.5(41.2)
10	(p, q)	(0.01,0.05)	(0.02,0.25)	(0.03,0.05)	(0.04,0.05)	(0.05,0.05)
	Nonparametric(7)	1.2(7.6)	65.7(8.3)	10.3(9.2)	5.2(3.8)	17.6(2.6)	100(31.5)
	EffTox(7)	5(9.4)	78(22.6)	4(6.2)	2(0.7)	1(0.3)	90(39.2)
	EffTox(3)	5(5.7)	54(19.7)	6(4.2)	5(1.8)	3(1.2)	73(32.6)
	UAROET(6)	0.5(7.4)	22.3(12.2)	17.9(8.2)	21.7(5.9)	8.5(3.8)	70.9(37.5)
	UAROET(3)	0.6(4.4)	16.3(10)	18.7(8)	17.9(7.1)	10.3(6.1)	63.8(35.7)
11	(p, q)	(0.01,0.05)	(0.02,0.2)	(0.03,0.4)	(0.04,0.15)	(0.05,0.15)
	Nonparametric(7)	2.3(7.5)	4.7(8.4)	61.2(8.2)	10.7(7.3)	21.1(3)	100(34.5)
	EffTox(7)	5(9.5)	23(12.2)	61(15.9)	3(1.5)	0(0)	92(39.1)
	EffTox(3)	4(5.7)	19(9.5)	58(19.1)	5(2.1)	3(0.7)	89(37.1)
	UAROET(6)	0.3(7.3)	11.3(11)	44.2(12.6)	29.8(6.7)	9.8(3.3)	95.4(40.8)
	UAROET(3)	0.3(4.6)	6.5(7.8)	44(12.7)	26.9(8.6)	16.5(6.8)	94.2(40.5)
12	(p, q)	(0.01,0.05)	(0.02,0.2)	(0.03,0.3)	(0.04,0.6)	(0.05,0.3)
	Nonparametric(7)	1.7(7.5)	8.3(8.4)	2.2(8.4)	62.6(7.9)	25.2(6.9)	100(39.1)
	EffTox(7)	6(9.2)	32(14)	39(13.5)	13(2.2)	2(0.3)	92(39.2)
	EffTox(3)	4(5.7)	25(11.1)	28(11.3)	29(8)	2(0.8)	88(36.9)
	UAROET(6)	0.2(7.5)	10(10.7)	24.1(10.9)	49.2(8.7)	13.4(3.3)	96.9(41.1)
	UAROET(3)	0.1(4.4)	6(8)	13.8(10)	49.6(11.3)	27.2(7.3)	96.7(41)
13	(p, q)	(0.01,0.05)	(0.02,0.05)	(0.03,0.3)	(0.04,0.05)	(0.05,0.05)
	Nonparametric(7)	15.1(7.4)	0.8(9.5)	64.2(7.3)	6.2(7.3)	13.7(2.4)	100(34)
	EffTox(7)	15(12.6)	8(8.8)	57(14.4)	6(2.5)	2(0.2)	88(38.5)
	EffTox(3)	6(6.7)	6(4.9)	51(16.6)	5(2.7)	3(1.1)	71(32)
	UAROET(6)	0.6(7.4)	2.1(6.7)	46.3(13.8)	20.5(6.6)	9(3.3)	78.5(38)
	UAROET(3)	0.2(4.4)	1.9(5.5)	42.4(13.1)	15.5(7.3)	11.7(5.6)	71.7(35.9)
14	(p, q)	(0.01,0.05)	(0.02,0.05)	(0.03,0.05)	(0.04,0.3)	(0.05,0.05)
	Nonparametric(7)	13.3(7.5)	14.8(9.5)	0.6(8.9)	55.1(6.7)	16.2(6.2)	100(38.8)
	EffTox(7)	20(13.9)	18(10.9)	7(6.2)	32(4.9)	4(1.3)	81(37.2)
	EffTox(3)	8(6.8)	8(6)	8(4.5)	40(11)	4(2.1)	68(30.4)
	UAROET(6)	0.6(7.3)	3.3(6.6)	7.3(6.5)	43.8(11.2)	22.9(6.3)	77.9(37.9)
	UAROET(3)	0.5(4.3)	0.8(5.1)	6.2(6)	36.1(11.2)	29.1(9.6)	72.7(36.2)
15	(p, q)	(0.01,0.05)	(0.02,0.05)	(0.03,0.05)	(0.04,0.05)	(0.05,0.3)
	Nonparametric(7)	15(7.5)	13.2(9.5)	11.9(8.6)	0.9(7.7)	59(5.4)	100(38.6)
	EffTox(7)	20(13.7)	18(10.6)	13(7.2)	9(3.2)	16(1.8)	76(36.5)
	EffTox(3)	10(7.3)	8(5.7)	9(5.1)	8(3.2)	28(7.1)	63(28.4)
	UAROET(6)	0.5(7.4)	4.3(6.6)	6.6(6.5)	13.4(6.4)	52.9(10.9)	77.7(37.8)
	UAROET(3)	0.1(4.4)	1.8(5.3)	4.8(5.8)	9.2(6.5)	57.9(14)	73.8(36)

Results with the alternative EffTox and UAROET designs are also reported in Table 2. Figure 5 compares the proposed design to the alternative designs in their relative frequencies of recommending the optimal dose. We observe that the average total number of patients in the proposed design is smaller than in the alternative designs in all scenarios except 14 and 15, in which the average total number of patients in the proposed design is slightly larger than the alternative designs. With respect to the average proportion recommending the optimal dose, the proposed design performs almost always better than the alternative designs, even when the alternative designs use cohort size 3 (ie, conduct more interim analysis). The only exception is in Scenario 10, where the Efftox design with batch size 7 results in 78% chance of selecting the optimal dose level 2 compared to 65.7% by the proposed design. The largest benefit is observed in Scenario 9, where the immune response probability reaches its plateau at dose level 4. The EffTox design with cohort size 7 recommends the optimal dose 12% of the time (9% for level 4 and 3% for level 5), compared to the proposed design, which recommends the optimal dose 84.2% of the time (19.4% for level 5 and 64.8% for level 5).

FIGURE 5.

Average rate of reporting the optimal dose level(s) for scenarios 7 to 15. The numbers in the parenthesis following the design are batch sizes

3.3. Robustness analysis

We consider four additional settings to evaluate the robustness of the proposed design to cohort size; the odds ratio r^(l); misspecification of the skeleton τ^(l); and the cut-off thresholds ${\mathcal{C}}_1$, ${\mathcal{C}}_2$, and ${\mathcal{C}}_3$. The complete results are reported in the Web Supplement.

In the first additional setting, we evaluate the performance of the design when the cohort size is enlarged to 10 and the maximum size for each dose level is increased to 20. We notice that there is a rise of about 20 patients in the average total number of patients treated on the study. In return, the rates of recommending the optimal dose level increase as much as 14% for scenarios 7 to 15. As for scenarios 1 to 6, the increase in sample size does not seem to significantly improve the rate of recommending the optimal dose except for Scenario 1, where the rate for recommending dose level 5 increases from 83.7% to 87.3%.

In the second additional setting, we evaluate the performance of the design when the odds ratio r = 1. We are not able to find any noticeable difference in the results.

In the third additional setting, we evaluate the performance of the design when the skeleton τ^(l)s (Equation (4)) are misspecified and optimistically expected to be half of the true DLT risk. Table 3 reports the simulation results for scenarios 5 and 6 based on the parametric model. The impact of having τ^(l) misspecified when the true DLT risk is close to the threshold p_T is clearly observed: there is an increase of about 13% and 9% chance in scenarios 5 and 6, respectively, for recommending dose level 5. This suggests that, when taking the parametric and parametric+ modeling approaches, the choice of τ’s should be carefully discussed with clinicians, especially when previous knowledge of the toxicity profile of the vaccine is limited.

TABLE 3.

Simulation results based on the parametric model approach for scenarios 5 and 6. Correct τ^(l) are chosen to be the true p^(l); misspecified τ^(l) are chosen to be half of the true p^(l)

Scenario	Dose Level
	τ(l)		1	2	3	4	5	Total
5	Correct	(p, q)	(0.18,0.05)	(0.22,0.2)	(0.26,0.35)	(0.3,0.47)	(0.33,0.58)
		%	9.3	12.6	19.7	19.1	33.7	94.4
		N	12.11	11.73	11.06	9.11	6.38	50.39
		(D,R)	(2.24,0.65)	(2.59,2.28)	(2.88,3.89)	(2.89,4.39)	(2.08,3.65)	(12.69,14.86)
	Misspecified	%	8.3	11.2	15.5	14.9	46.6	96.5
		N	12.25	12.22	11.57	9.93	7.83	53.8
		(D,R)	(2.23,0.59)	(2.66,2.36)	(3.02,4.1)	(2.94,4.65)	(2.57,4.54)	(13.41,16.24)
6	Correct	(p, q)	(0.08,0.15)	(0.18,0.38)	(0.25,0.52)	(0.3,0.59)	(0.35,0.62)
		%	4.8	15.6	25.2	31	23.3	99.9
		N	9.99	11.45	11.97	9.71	5.85	48.97
		(D,R)	(0.76,1.5)	(2.1,4.43)	(3.06,6.17)	(2.9,5.73)	(2.02,3.6)	(10.84,21.43)
	Misspecified	%	4.6	11.5	21.9	29.3	32.5	99.8
		N	10.03	11.19	12.26	10.46	7.1	51.04
		(D,R)	(0.8,1.5)	(2.05,4.24)	(3.14,6.43)	(3.25,6.22)	(2.53,4.39)	(11.77,22.78)

In the last additional setting, we evaluate the robustness of the design with respect to the cut-off thresholds. Specifically, we consider settings with $\left\{{\mathcal{C}}_1=0.75,{\mathcal{C}}_2=0.8,{\mathcal{C}}_3=0.5\right\}$, $\left\{{\mathcal{C}}_1=0.8,{\mathcal{C}}_2=0.75,{\mathcal{C}}_3=0.5\right\}$, and $\{{\mathcal{C}}_1={\mathcal{C}}_2=0.8,{\mathcal{C}}_3=0.55\}$ for evaluating the sensitivity of ${\mathcal{C}}_1$, ${\mathcal{C}}_2$, and ${\mathcal{C}}_3$, respectively. For ${\mathcal{C}}_1$, we notice that the average total number of patients is reduced to 34.98 from 47.87 in Scenario 5, and to 36.12 from 46.18 in Scenario 6, when taking the nonparametric+ modeling approach. This implies that the proposed design may be sensitive to the ${\mathcal{C}}_1$ when the true DLT risk is close to the upper boundary of DLT risk. For ${\mathcal{C}}_2$, the rate of recommending the optimal dose is reduced to 44.2% from 55.1% in Scenario 14 and to 36.6% from 59% in Scenario 15, when taking the nonparametric modeling approach. The explanation is that the proposed design may be sensitive to the ${\mathcal{C}}_2$ when the immune response probabilities are not increasing at the initial dose levels. For ${\mathcal{C}}_3$, no obvious difference is observed, which implies the design is robust when changing ${\mathcal{C}}_3$ from 0.5 to 0.55.

4. APPLICATION

Human papillomaviruses (HPV) are small, nonenveloped DNA viruses that induce self-limited epithelial lesions of the skin or mucosa. HPV type 16 (HPV16) is the most prevalent HPV type detected in cervical cancers, which appears in approximately 50% to 60% cases of cervical cancer. TA-CIN is a single fusion protein comprising HPV16 E6, E7, and L2 proteins linked in tandem. Vaccination with TA-CIN of HPV16-infected advanced cervical cancer patients is believed to be able to trigger therapeutic immunity targeting the E6, E7, and L2 of HPV16.⁴³ Thus, the investigators wish to run a phase I dose-finding study of the TA-CIN vaccine as an adjuvant therapy for patients with a history of HPV16-associated cervical cancer. In this section, we demonstrate the proposed Bayesian design by applying it to this clinical study.

The study will investigate three dose levels of TA-CIN: Level I: 0.25 mL (injection volume) of 31.25 μg TA-CIN; Level II: 0.5 mL of 62.5 μg TA-CIN, and Level III: 1 mL of 125 μg TA-CIN. The vaccines will be administered three times via intramuscular needle injection on day one of weeks 1, 5, and 9. The dose limiting toxicities considered by the study include death, events that are life threatening or require inpatient hospitalization, and events that result in persistent or significant disability. When T cells are exposed to their cognate antigen, they respond by proliferating; therefore, one measure of the presence of antigen-specific T cells is to measure their proliferation in the presence versus absence of their antigen and the ratio of this response is termed the proliferation index. Thus, the proliferation index based on blood samples taken before and after the administration of TA-CIN is measured and used to determine the induction of an immune response on this study. The cut-off for immune-response based on the proliferation index is prespecified in the protocol. Both DLT and immune-response are defined based on follow-up measurements by week 11–13 (the fourth follow-up).

With the same rationale considered for the simulation studies, we restrict the design to have a single interim analysis for each dose level and choose a cohort size of 10 for better evaluation of the immune response probabilities. Furthermore, we limit the maximum size for each dose level to be 15. The expected DLT risk rate is 0.02, 0.06, and 0.08 for the three levels, respectively. The expected immune response probabilities are 0.05, 0.15, and 0.25 for the three levels, respectively. The thresholds of toxicity are (p_A, p_T) = (0.10, 0.20). The cut-off thresholds are chosen to be ${\mathcal{C}}_1={\mathcal{C}}_2=0.7$ and ${\mathcal{C}}_3=0.5$. We consider the nonparametric model for the design and analysis.

A total of five scenarios, including the expected Scenario 1 and robustness analysis scenarios 2 to 5, are evaluated for study operating characteristics (Figure 6). For each scenario, we considered cases when r = 10 and r = 100 (ie, toxicity and efficacy are positively correlated). Based on 1000 replications, the results are reported in Table 4.

FIGURE 6.

Scenarios under which the study operating characteristics are evaluated for the TA-CIN phase I study

TABLE 4.

Study operating characteristics for the TA-CIN phase I study

Scenario	Dose Level
	r		1	2	3	Total
1		(p, q)	(0.02,0.05)	(0.06,0.1)	(0.08,0.25)
	10	%	20.5	12.3	67.2	100
		N	10.9	11.94	9.86	32.69
		(D,R)	(0.21,0.57)	(0.76,1.23)	(0.78,2.48)	(1.76,4.28)
	100	%	17.9	13.7	68.1	99.7
		N	10.92	12.14	10.25	33.3
		(D,R)	(0.23,0.55)	(0.76,1.26)	(0.86,2.55)	(1.85,4.36)
2		(p, q)	(0.02,0.05)	(0.06,0.15)	(0.08,0.15)
	10	%	11.3	38.1	50.5	99.9
		N	10.84	12.16	10.48	33.48
		(D,R)	(0.2,0.51)	(0.73,1.8)	(0.83,1.57)	(1.76,3.87)
	100	%	12.6	39	48.2	99.8
		N	10.93	12.21	10.43	33.56
		(D,R)	(0.22,0.56)	(0.75,1.86)	(0.86,1.61)	(1.83,4.03)
3		(p, q)	(0.02,0.05)	(0.06,0.25)	(0.08,0.1)
	10	%	5.6	74.8	19.5	99.9
		N	11.02	12.13	10.12	33.27
		(D,R)	(0.24,0.57)	(0.68,3.08)	(0.78,1.01)	(1.71,4.66)
	100	%	4.3	80	15.5	99.8
		N	10.88	12.14	10.32	33.34
		(D,R)	(0.22,0.55)	(0.72,3.08)	(0.84,1.04)	(1.78,4.66)
4		(p, q)	(0.02,0.05)	(0.06,0.05)	(0.08,0.25)
	10	%	25.6	6	68.4	100
		N	10.93	11.7	9.5	32.13
		(D,R)	(0.22,0.51)	(0.69,0.59)	(0.8,2.34)	(1.71,3.44)
	100	%	28.1	5.8	65.9	99.8
		N	10.94	11.86	9.09	31.88
		(D,R)	(0.23,0.57)	(0.7,0.58)	(0.74,2.23)	(1.68,3.38)
5		(p, q)	(0.02,0.05)	(0.08,0.2)	(0.3,0.35)
	10	%	10.8	73	16.1	99.9
		N	10.96	12.55	10.16	33.67
		(D,R)	(0.23,0.58)	(1.03,2.52)	(3.02,3.57)	(4.28,6.68)
	100	%	11.6	74.7	13.6	99.9
		N	10.82	12.54	9.88	33.24
		(D,R)	(0.2,0.54)	(1.02,2.53)	(2.95,3.46)	(4.17,6.54)

We note that the results are not sensitive to the choices of r as expected from the robustness analysis (see Section 3.3). Under the expected Scenario 1, there is about 67% chance of recommending the ideal dose level 3. The average number of patients required for the study is about 33. An average of 1.8 patients will experience DLT and an average of 4.3 patients will achieve immune response on the study. In Scenario 2, where the immune response rate reaches its plateau at dose level 2, there is about 88.6% chance of recommending dose level 2 (38.1%) or 3 (50.5%). In Scenario 3, where the immune response rate reaches its mode at dose level 2, there is more than 75% chance of recommending dose level 2 as the optimal dose. In Scenario 4, where immune response probabilities only increase after dose level 2, there is about 68% chance of identifying dose level 3 as the optimal dose. In Scenario 5, where dose level 3 is too toxic albeit effective, there is about 16% chance to treat patients on this dose level and about 73% chance to recommend dose level 2. The average number of patients required for scenarios 2 to 4 is similar to Scenario 1.

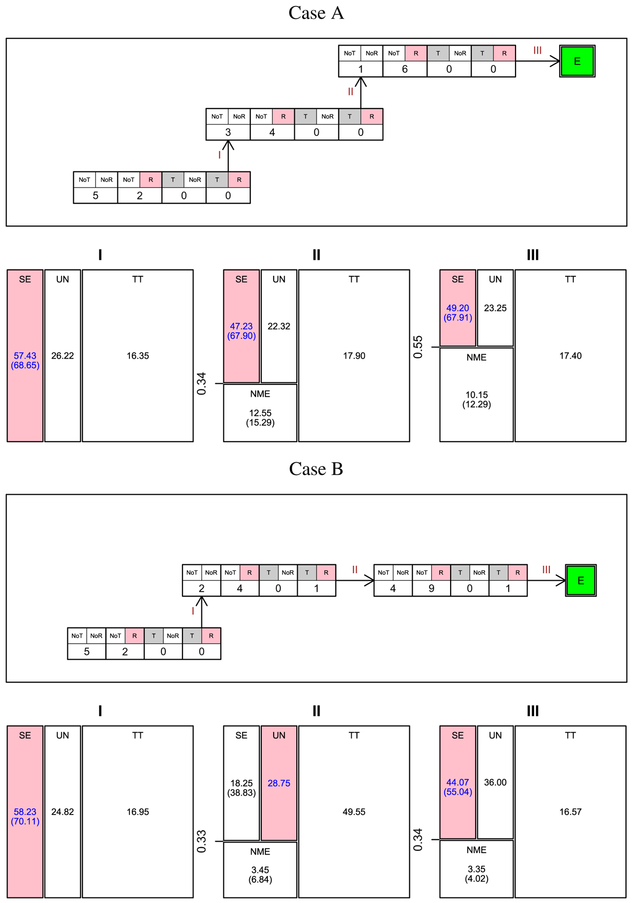
Figure 7 presents a cohort-by-cohort illustration of dose escalation with the proposed design for two cases. In both cases, Jeffreys’ prior (see Equation 2), the prior probabilities corresponding to regions TT, SE, and UN are 80%, 9.5%, and10.5%, respectively. In Case A, interim analysis I is conducted after the first cohort of seven patients were treated at dose level 1. Of the seven patients, five had no DLT or immune response, and two had no DLT but had an immune response. Decision map I presents the results of interim analysis I. The posterior probabilities corresponding to regions TT, SE, and UN are 16.35%, 57.43%, and 26.22%, respectively. The probability of SE, conditioning on not being too toxic, is 68.65%. By comparing to the thresholds ${\mathcal{C}}_1={\mathcal{C}}_2=0.7$ and ${\mathcal{C}}_3=0.5$, following the proposed algorithm, SE is determined to be the region. Consequently, the dose level is escalated for the next cohort of seven patients. After three cohorts, the dose escalation is finished and dose level 3 is reported as the recommended dose level. In Case B, at the second interim analysis, decision map II shows that the probability of NME conditioning on not being too toxic is 6.84%. The probability of SE conditioning on not being too toxic or no more effective than dose level 1 is 38.83%. Following the proposed algorithm, dose level 2 is determined to be in region UN, and the next cohort of patients are still treated at dose level 2. At interim analysis III, however, the region is determined to be SE. Thus, the next cohort of patients will be treated at the escalated dose level 3.

FIGURE 7.

Cohort-by-cohort dose escalation illustration. NoT(T): Without(With) DLT; NoR(R): Without(With) immune response. E: Escalate to the next higher dose level when applicable. In the decision maps I-III that correspond to interim analyses I-III, respectively, the region filled with color corresponds to the region identified by the proposed algorithm. The numbers in each region are the posterior probabilities (%) and the numbers in parenthesis are the conditional probabilities (%)

Based on these study operating characteristics, the proposed design is accepted by the study’s principle investigators.

5. DISCUSSION

Cancer therapeutic vaccines have huge potential for producing promising clinical benefits in cancer patients. Candidate cancer therapeutic vaccines must be investigated in phase I clinical studies to determine the dose level considered safe and immunogenic for later phase efficacy studies. Many of the existing dose-finding designs, however, are not suitable or need to be modified for such cancer therapeutic vaccine dose-finding studies. The FDA guidance for the industry on cancer therapeutic vaccines²⁴ urges use of nonstandard study designs of cancer therapeutic vaccine phase I trials.

In this paper, we propose a new phase I Bayesian design for cancer therapeutic vaccines. The proposal simultaneously evaluates safety and immunogenicity in the dose escalation algorithm. In an adaptive manner, the proposed algorithm sets the benchmark of immune response based on the observed immune response data. It then uses this benchmark to determine whether a dose-escalation is warranted. Through a sequential decision approach, the proposed algorithm evaluates the safety of the vaccine on top of the efficacy evaluation.

The proposed algorithm allows flexibility in specifying the probability models for toxicity and efficacy. As examples, four different models are suggested in this paper. It should be noted that the probability models need to take into consideration the restriction that the dose-efficacy curve may not be monotonically increasing for cancer therapeutic vaccines. That is, the models should allow the dose-efficacy curve to be unimodal or to reach a plateau. On the other hand, it remains reasonable to assume that the dose-toxicity relationship is monotonic; that is, the DLT risk increases as dosage of the vaccine increases.

We consider the proposed design to be largely rule based in the sense that subjects do not receive the dose level considered optimal at the time they enroll. Unlike typical model-based designs such as CRM, which intend to update model parameters as frequently as possible, this rule-based design allows evaluation of as many immune samples as possible in a batch to reduce interassay variability (a frequent issue with complex cell-based immunology assays). This approach potentially reduces the cost of running the study and limits the likelihood of exhausting precious clinical specimens during testing. As a result of these considerations, only one interim analysis at each dose level is considered in the example TA-CIN phase I study. In general, the choices of cohort size and number of interim analyses should be carefully evaluated at the design stage with simulation studies accounting for practical considerations.

Note that it is straightforward to apply the proposed design to a typical phase I study that only aims to find the MTD. In the typical setting, we may simplify the decision region by setting ${\widehat{q}}^{(l-1)}=0$ to exclude Region NME, where the current dose level is less effective for immunogenicity than the previous lower dose level.

The proposed design assumes that the immune response criteria are well established. This is an acceptable assumption because a vaccine is very unlikely to enter a clinical trial without an understanding of its potential immunologic mechanism, and the regulatory agencies specifically examine and typically require monitoring of a suitable biomarker of response. For example, in the case of candidate therapeutic HPV vaccines, there is a massive body of literature supporting the central role of HPV-specific T cell responses in immune clearance of virally infected cells. In the example study, the investigators, therefore, assess the immune response in the peripheral blood of patients by measuring the fold increase in antigen-specific T cell number after vaccination. On the other hand, there exist situations when the correlates of protection (ie, surrogate markers) are unknown a priori or are based on several markers. As a possible solution, one may consider defining a composite endpoint for the immunological response and applying the proposed design. Alternatively, it is also plausible to extend the proposed design by incorporating a joint model for several immunological markers and make dose escalation decisions accordingly. In cases when the investigators do not know the appropriate response threshold or cut-off for declaring response based on the immunologic assay measurements, the proposed design needs to be extended to allow recalibrating the cut-off threshold. For example, if all, or nearly all patients exhibit a positive response, the researchers may increase the assay’s cut-off threshold such that only 50% are above the new threshold. It is also important to consider simulation scenarios at the design stage to evaluate the impact of changing the response threshold (eg, ±20% of the threshold).

One more possible extension to the proposed design is to allow the probability models to account for any intercohort batch effect should one exist. We have assumed that the data already incorporate a standard batch correction. However, it remains unclear how severe the impact of the batch effect is and whether the batch effect can be well assessed in the context of phase I studies when the sample size is small.

We are developing web-based software with an interactive and friendly user-interface to aid clinicians to implement the proposed design.

APPENDIX

LARGE SAMPLE PROPERTY

Lemma 1. If Pr(X_n ∈ [x₀, x₁]) → 1 and Pr(Y_n ∈ [y₀, y₁]) → 1 as n → ∞, then Pr((X_n, Y_n) ∈ [x₀, x₁] × [y₀, y₁]) → 1.

Proof. Obviously, lim {Pr((X_n, Y_n) ∈ [x₀, x₁] × [y₀, y₁])} ≤ 1.

Since

$$\begin{gathered} \text{Pr}\left(\left(X_n,Y_n\right)\in \left[x_0,x_1\right]\times \left[y_0,y_1\right]\right)=\text{Pr}\left(X_n\in \left[x_0,x_1\right]\right)+\text{Pr}\left(Y_n\in \left[y_0,y_1\right]\right)-\text{Pr}\left(X_n\in \left[x_0,x_1\right]\cup Y_n\in \left[y_0,y_1\right]\right) \\ \ge \text{Pr}\left(X_n\in \left[x_0,x_1\right]\right)+\text{Pr}\left(Y_n\in \left[y_0,y_1\right]\right)-1, \end{gathered}$$

we can also show that

$$\text{lim}\left\{\text{Pr}\left(\left(X_n,Y_n\right)\in \left[x_0,x_1\right]\times \left[y_0,y_1\right]\right)\right\}\ge \text{lim}\text{Pr}\left(X_n\in \left[x_0,x_1\right]\right)+\text{lim}\text{Pr}\left(Y_n\in \left[y_0,y_1\right]\right)-1=1.$$

Therefore, it is proved that lim {Pr((X_n, Y_n) ∈ [x₀, x₁] × [y₀, y₁])} = 1. □

The proof of Theorem 1 is as follows.

Proof. Since (p*, q*) is in the interior of w*, there exists ϵ > 0 such that [p* − ϵ, p* + ϵ] × [q* − ϵ, q* + ϵ] ∈ w*.

Following the convergence theorem of the posterior distribution,⁴⁵ Pr(p ∈ [p* − ϵ, p* + ϵ]|H) → 1 and Pr(q ∈ [q* − ϵ, q* + ϵ]|H) → 1.

Following Lemma 1, we then have

$$Pr\left((p,q)\in \left[p^{*}-ϵ,p^{*}+ϵ\right]\times \left[q^{*}-ϵ,q^{*}+ϵ\right]|H\right)\to 1.$$

Since Pr((p, q) ∈ ω*|H) ≥ Pr ((p, q) ∈ [p* − ϵ, p* + ϵ] × [q* − ϵ, q* + ϵ]|H), we also have

$$Pr\left((p,q)\in {\omega }^{*}|H\right)\to 1.$$

It is also true that

$$Pr\left((p,q)\in {\omega }^{\prime }|H\right)\to 0,$$

where ω^′ is any union of the sets in {TT, NME, SE, UN} − ω*.

If ω* = TT, then we have

$$Pr\left(p>p_T|H\right)=Pr((p,q)\in TT|H)\to 1.$$

Thus,

$$Pr\left(\omega ={\omega }^{*}|H\right)=Pr\left\{Pr\left(p>p_T|H\right)>{\mathcal{C}}_1\right\}\to Pr\left(1>{\mathcal{C}}_1\right)=1.$$

If ω* = NME, then we have

$$\begin{gathered} Pr\left(p>p_T|H\right)=Pr((p,q)\in TT|H)\to 0 \\ Pr(q\le {\widehat{q}}^{(l-1)}|p\le p_T,H)=\frac{Pr((p,q)\in NME|H)}{1-Pr((p,q)\in TT|H)}\to 1. \end{gathered}$$

Thus,

$$\begin{gathered} Pr\left(\omega ={\omega }^{*}|H\right)=Pr\left\{Pr\left(p>p_T|H\right)\le {\mathcal{C}}_1\cap Pr\left(q\le {\widehat{q}}^{(l-1)}|p\le p_T,H\right)>{\mathcal{C}}_2\right\} \\ \to Pr\left(0\le {\mathcal{C}}_1\cap 1>{\mathcal{C}}_2\right)=1. \end{gathered}$$

If ω* = SE, then we have

$$\begin{gathered} Pr\left(p>p_T|H\right)=Pr((p,q)\in TT|H)\to 0 \\ Pr\left(q\le {\widehat{q}}^{(l-1)}|p\le p_T,H\right)=\frac{Pr((p,q)\in NME|H)}{1-Pr((p,q)\in TT|H)}\to 0 \\ Pr\left(p\le p_A|p\le p_T,q>{\widehat{q}}^{(l-1)},H\right)=\frac{Pr((p,q)\in SE|H)}{Pr((p,q)\in SE|H)+Pr((p,q)\in UN|H)}\to 1. \end{gathered}$$

Thus,

$$\begin{gathered} Pr\left(\omega ={\omega }^{*}|H\right)=Pr\{Pr(p>p_T|H)\le {\mathcal{C}}_1\cap Pr(q\le {\widehat{q}}^{(l-1)}|p<p_T,H)\le {\mathcal{C}}_2\cap Pr(p\le p_A|p\le p_T,q>{\widehat{q}}^{(l-1)},H)>{\mathcal{C}}_3\} \\ \to Pr(0\le {\mathcal{C}}_1\cap 0\le {\mathcal{C}}_2\cap 1>{\mathcal{C}}_3)=1. \end{gathered}$$

If ω* = UN, then we have

$$\begin{gathered} Pr\left(p>p_T|H\right)=Pr((p,q)\in TT|H)\to 0 \\ Pr\left(q\le {\widehat{q}}^{(l-1)}|p\le p_T,H\right)=\frac{Pr((p,q)\in NME|H)}{1-Pr((p,q)\in TT|H)}\to 0 \\ Pr\left(p\le p_A|p\le p_T,q>{\widehat{q}}^{(l-1)},H\right)=\frac{Pr((p,q)\in SE|H)}{Pr((p,q)\in SE|H)+Pr((p,q)\in UN|H)}\to 0. \end{gathered}$$

□

Thus,

$$\begin{gathered} \text{Pr}(\omega ={\omega }^{*}|H)=\text{Pr}\{\text{Pr}(p>p_T|H)\le {\mathcal{C}}_1\cap \text{Pr}(q\le {\widehat{q}}^{(l-1)}|p<p_T,H)\le {\mathcal{C}}_2\cap \text{Pr}(p\le p_A|p\le p_T,q>{\widehat{q}}^{(l-1)},H)\le {\mathcal{C}}_3\} \\ \to \text{Pr}(0\le {\mathcal{C}}_1\cap 0\le {\mathcal{C}}_2\cap 0\le {\mathcal{C}}_3)=1. \end{gathered}$$

The proof of Corollary 1 is as follows.

Proof. The proof is trivial since, for all the models, the likelihood is a continuous function of p and q. Moreover, the prior distributions, possibly induced by π(θ), all have support [0, 1] × [0, 1]. □