The tarantula toxin GxTx detains K⁺ channel gating charges in their resting conformation

Guangxitoxin-1E (GxTx) is a peptide from tarantula venom that binds to Kv2.1 voltage sensors and inhibits channel activity. Tilley et al. investigate the allosteric mechanism of GxTx and show that it stabilizes the resting state of voltage sensors and limits opportunities for the pore to open.

Abstract

Allosteric ligands modulate protein activity by altering the energy landscape of conformational space in ligand–protein complexes. Here we investigate how ligand binding to a K⁺ channel’s voltage sensor allosterically modulates opening of its K⁺-conductive pore. The tarantula venom peptide guangxitoxin-1E (GxTx) binds to the voltage sensors of the rat voltage-gated K⁺ (Kv) channel Kv2.1 and acts as a partial inverse agonist. When bound to GxTx, Kv2.1 activates more slowly, deactivates more rapidly, and requires more positive voltage to reach the same K⁺-conductance as the unbound channel. Further, activation kinetics are more sigmoidal, indicating that multiple conformational changes coupled to opening are modulated. Single-channel current amplitudes reveal that each channel opens to full conductance when GxTx is bound. Inhibition of Kv2.1 channels by GxTx results from decreased open probability due to increased occurrence of long-lived closed states; the time constant of the final pore opening step itself is not impacted by GxTx. When intracellular potential is less than 0 mV, GxTx traps the gating charges on Kv2.1’s voltage sensors in their most intracellular position. Gating charges translocate at positive voltages, however, indicating that GxTx stabilizes the most intracellular conformation of the voltage sensors (their resting conformation). Kinetic modeling suggests a modulatory mechanism: GxTx reduces the probability of voltage sensors activating, giving the pore opening step less frequent opportunities to occur. This mechanism results in K⁺-conductance activation kinetics that are voltage-dependent, even if pore opening (the rate-limiting step) has no inherent voltage dependence. We conclude that GxTx stabilizes voltage sensors in a resting conformation, and inhibits K⁺ currents by limiting opportunities for the channel pore to open, but has little, if any, direct effect on the microscopic kinetics of pore opening. The impact of GxTx on channel gating suggests that Kv2.1’s pore opening step does not involve movement of its voltage sensors.

Introduction

Voltage-gated ion channels are proteins critical for physiological electrical signaling. Each voltage-gated ion channel type responds differently to voltage waveforms, and the kinetics of their responses shape downstream electrical responses. Venomous creatures make peptides that hijack ion channel gating to suit their predatory needs. Understanding the mechanism by which a venom toxin acts can reveal mechanisms by which the channels operate. Study of powerful gating-modifier toxins by patch clamp electrophysiology offers an opportunity to precisely investigate the coupling between ligand binding, voltage gating, and protein conformational change. Here, we investigate the mechanism by which a gating-modifier toxin from tarantula venom inhibits opening of a voltage-gated K⁺ (Kv) channel.

Found in eukaryotes and prokaryotes, Kv channel proteins possess a conserved tetrameric architecture with each monomer consisting of six transmembrane helical segments, S1–S6. The S1–S4 segment forms a voltage sensor domain, and the central pore domain spans S5 and S6 (see Long et al., 2007). While maintaining a tightly conserved structure, Kv channels exhibit widely varying voltage-gating responses. A key determinant of voltage response is how voltage sensor conformational change is coupled to pore opening. Kv2.1 voltage sensors translocate a similar amount of gating charge as the voltage sensors of their Kv1 channel relatives, and a component of gating charge moves over a similar time course, yet Kv2.1 requires more positive potentials to achieve the same open probability and has markedly slower activation kinetics (Islas and Sigworth, 1999; Scholle et al., 2004; Jara-Oseguera et al., 2011). The coupling that produces this striking difference in channel gating has yet to be fully elucidated.

Voltage sensor targeting toxins from spider venoms have been found that target voltage-gated Na⁺, Ca²⁺, and K⁺ channels. Structurally, all share the “inhibitory cystine knot” fold. In each case where the site of action has been studied in depth, studies have concluded that the toxins act by binding the outer S3 region of the voltage sensor domain (Swartz and MacKinnon, 1997b; Winterfield and Swartz, 2000; Ruta and MacKinnon, 2004; Bosmans et al., 2008; Milescu et al., 2009). This class of spider toxins acts by modulating voltage sensor conformations to stabilize closed, open, or inactivated states of channels (Swartz, 2007).

The first spider-venom toxin targeting Kv2 channels to be discovered was hanatoxin (HaTx; Swartz and MacKinnon, 1995). Since its discovery, additional spider toxins have been identified that inhibit Kv2 channels by allosteric modulation (Escoubas et al., 2002; Lee et al., 2004; Herrington et al., 2006; Yuan et al., 2007). Within the family of Kv2 channel peptide toxins, guangxitoxin-1E (GxTx), from the Chinese fawn tarantula Chilobrachys guangxiensis, is notable for its channel selectivity and use as a research tool. GxTx is a potent Kv2 inhibitor that acts at low nanomolar concentrations (Herrington et al., 2006). GxTx is the most selective inhibitor of Kv2 channels known and is used to selectively inhibit and isolate endogenous Kv2 currents (Li et al., 2013; Liu and Bean, 2014; Kimm et al., 2015; Pathak et al., 2016; Hönigsperger et al., 2017; Palacio et al., 2017). GxTx partitions into the lipid bilayer to bind Kv2 channels and reveals functional interactions between lipids and the channels themselves (Milescu et al., 2009; Gupta et al., 2015). GxTx also forms the scaffold for fluorescent probes of Kv2 channel localization and function (Tilley et al., 2014; Cobb et al., 2015; Kirmiz et al., 2018). Understanding the mechanism of GxTx interaction with Kv2 channels is critical to the interpretation of experiments involving GxTx. Here we report a detailed investigation of the mechanism by which GxTx impacts the conformational changes underlying gating of Kv2.1 currents.

In this study, we determine how the conformational transitions of Kv2.1 voltage sensors are impacted by GxTx and how voltage sensor modulation is coupled to opening of the K⁺-conductive channel pore.

Materials and methods

Peptides

GxTx used in whole-cell experiments was an oxidation-resistant variant of GxTx with methionine at position 35 replaced by norleucine, synthesized in house as described previously (Tilley et al., 2014). Single-channel experiments used commercially purchased wild-type GxTx (PGX-4433-s; Peptides International).

Cell culture

A tetracycline-inducible Chinese Hamster Ovary (CHO)–K1 cell line expressing the rat Kv2.1 channel (Trapani and Korn, 2003) was cultured as described previously (Tilley et al., 2014). The cell line was found negative for mycoplasma contamination by biochemical tests (LT07; MycoAlert; Lonza). A dose of 1 µg/ml tetracycline was added to the cellular media for indicated durations to induce channel expression for electrophysiological recordings. For voltage-clamp recording, cells were harvested by manual scraping in divalent-free PBS with 1 mM EDTA, pelleted at 1,000 g for 2 min, suspended in media (CHO-SFMII; 12052-114; Life Technologies) supplemented with 25 mM HEPES (pH 7.3), and slowly rotated in polypropylene tubes at room temperature until use. Aliquots of cell suspension were added to a recording chamber containing external solution, allowed to settle, and rinsed with external solution before recording.

Electrophysiology

Patch clamp experiments were performed at room temperature (22–24°C). Voltage clamp was achieved with an Axopatch 200B amplifier (Axon Instruments) run by Patchmaster software (HEKA).

Whole-cell ionic current measurements

The external bath solution contained (in mM) 155 NaCl, 50 HEPES, 20 KOH, 2 CaCl₂, 2 MgCl₂, and 0.1 EDTA, adjusted to pH 7.3 with HCl. The higher than physiological external [K⁺] was chosen to minimize ion accumulation artifacts and the occurrence of multiple conductance states (Trapani et al., 2006). The internal pipette solution contained (in mM) 50 KF, 70 KCl, 35 KOH, 5 EGTA, and 50 HEPES, adjusted to pH 7.3 with HCl. A calculated liquid-junction potential of 6 mV between the bath and pipette solution was corrected. Recording pipettes were pulled from thin-walled borosilicate glass (1.5 mm outer diameter, 1.1 mm inner diameter, with filament; Sutter Instrument), on a horizontal micropipette puller (Flaming/Brown Model P-87; Sutter Instrument) using five or more cyclical heating cycles to achieve a taper to the tip over minimal length. Pipettes were coated with a silicone elastomer (Sylgard 184; Dow Corning) and heat-cured, and tips were then heat-polished with a microforge. Pipette-tip resistances with the above solutions were 1.8–2.9 MΩ. As the ionic conductance from Kv2.1 channels heterologously expressed in mammalian cell lines can be large, the calculated cell voltage error due to series resistance between the pipette and cell membrane was a concern. To minimize voltage errors at the cell membrane due to series resistance, several measures were taken. Channel expression was induced with tetracycline incubation for a minimal time (1–2 h) to limit Kv2.1 conductance magnitude. Detached and settled CHO cells (see Cell culture) with a round shape and smooth surface were whole-cell voltage clamped, and then lifted up into the bath solution. Improved solution exposure of the lifted cells is expected to minimize extracellular K⁺ accumulation artifacts. The approximately spherical shape of the dissociated cells is expected to minimize series resistances within the cell, and hence space clamp errors. Series resistances of 3–8 MΩ (before compensation) were estimated from the value arrived at during whole-cell capacitive transient subtraction by manual adjustment of the whole-cell parameters circuit of the amplifier. Series-resistance compensation lag was set to 10 µs. To constrain voltage error, the series resistance compensation correction circuit was set to ≥85%. The product of current amplitude and estimated series resistance remaining after compensation indicated that voltage error at the cell membrane due to series resistance was <3 mV during the largest currents in this dataset, 3–8 nA during steps to +120 mV pulses in the BSA-containing vehicle control solutions. Cell capacitances were 4–7 pF, resulting in cell membrane charging time constants of <50 µs before compensation, at least an order of magnitude faster than time constants fitted to ionic currents. The series resistance compensation prediction (supercharging) circuit was not used. Low-pass filtering at 10 kHz and digitization at 100 kHz were used during recordings. Holding potential was −100 mV. Remaining capacitance and Ohmic leak were subtracted offline using traces recorded during P/5 voltage protocols from holding potential. In sequences of voltage steps, at least 2 s elapsed between the start times of each recording.

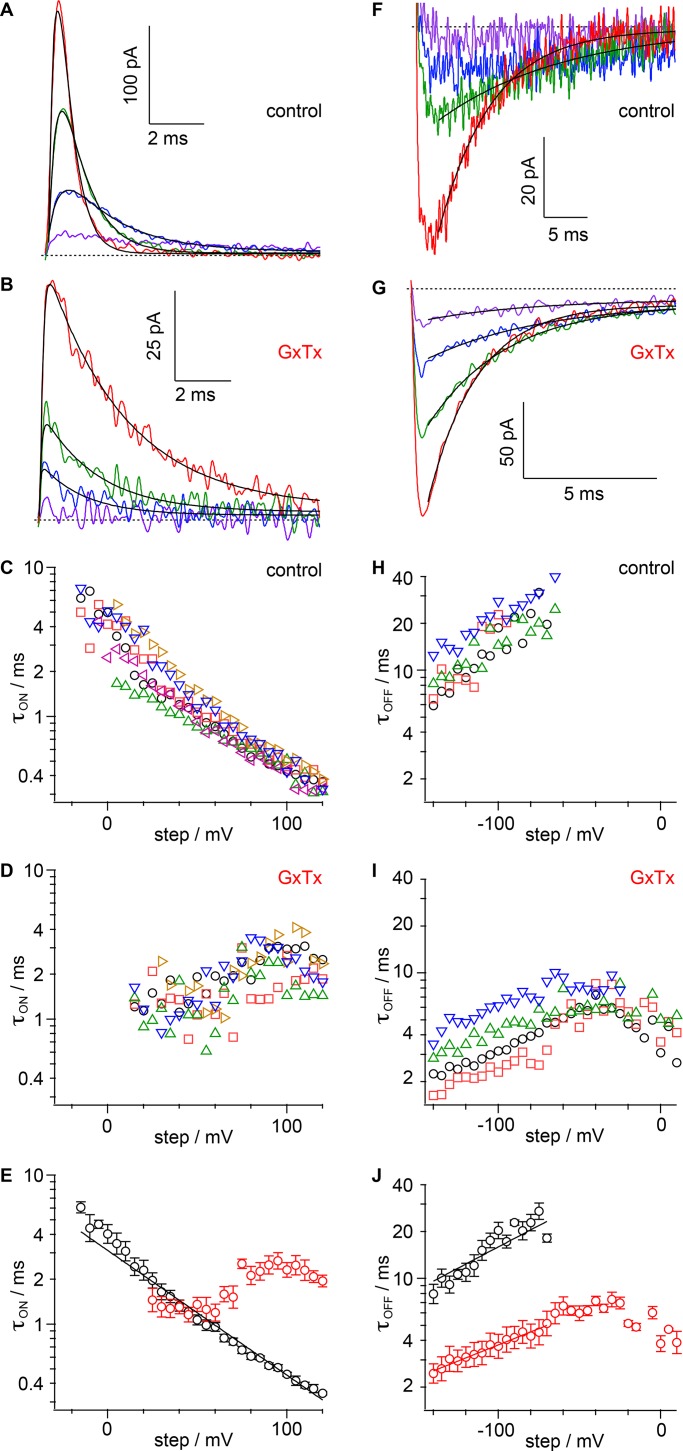
Solution was exchanged by flushing a volume of at least 100 µl through a <100-µl recording chamber (Warner R-24N). To reduce GxTx depletion by adsorption to surfaces, GxTx solutions contained 0.1% BSA (Fraction V, protease-free; 03117332001; Roche). After whole-cell configuration was established, bath solution was replaced by a vehicle control solution with 0.1% BSA added. GxTx was applied to patched cells after recording in vehicle and in order of increasing concentration. An unknown mechanism causes the voltage-dependent response of Kv2.1 channels to drift toward more negative potentials after whole-cell break-in. This can result in a slight acceleration of activation, slowing of deactivation, and shift of steady-state properties a few millivolts more negative. The vector of these drifts was opposite the effects of GxTx, and this instability was tolerated. In some instances (e.g., Fig. 2), 100 nM GxTx appears to be slightly more efficacious than 1 µM; this is likely to be an artifact of this time-dependent drift.

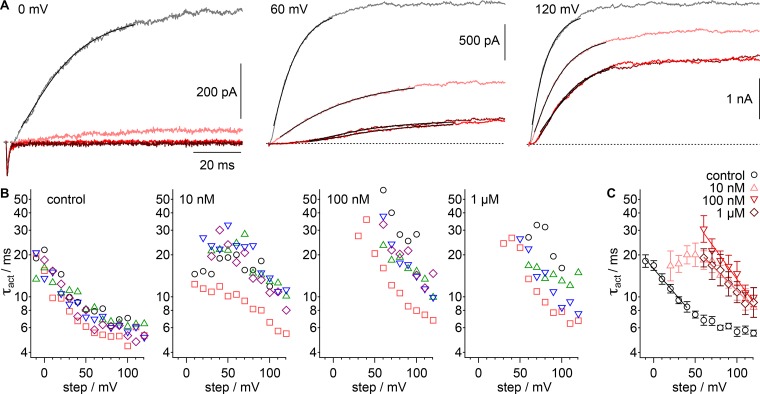
Figure 2.

GxTx slows Kv2.1 activation kinetics in whole-cell recordings. (A) Example current from a voltage clamped cell in response to indicated voltage steps. Gray, vehicle; pink, 10 nM GxTx; red, 100 nM GxTx; dark red, 1 µM GxTx. Inward current at 0 mV is endogenous sodium current. Dotted lines, zero current level. Lines, fit of Eq. 3 (0 mV vehicle: A = 454.7 ± 0.5 pA, τ_act = 16.29 ± 0.06 ms, σ =1.915 ± 0.008; 60 mV vehicle: A = 1,841 ± 1 pA, τ_act = 8.34 ± 0.03 ms, σ = 1.373 ± 0.004; 60 mV 10 nM GxTx: A = 868 ± 1 pA, τ_act = 25.1 ± 0.1 ms, σ = 1.299 ± 0.004; 60 mV 100 nM GxTx: A = 293 ± 1 pA, τ_act = 21.4 ± 0.1 ms, σ = 3.89 ± 0.03; 60 mV 1 µM GxTx: A = 319 ± 1 pA, τ_act = 18.7 ± 0.1 ms, σ = 4.03 ± 0.05; 120 mV vehicle: A = 3,216 ± 4 pA, τ_act = 6.61 ± 0.04 ms, σ = 1.127 ± 0.006; 120 mV 10 nM GxTx: A = 2,640 ± 2 pA, τ_act = 10.23 ± 0.03 ms, σ = 1.367 ± 0.003; 120 mV 100 nM GxTx: A = 1,971 ± 2 pA, τ_act = 10.06 ± 0.04 ms, σ = 2.203 ± 0.009; 120 mV 1 µM GxTx: A = 2,256 ±4 pA, τ_act = 15.79 ± 0.08 ms, σ = 1.489 ± 0.006). (B) Values of τ_act from fitting of Eq. 3. Symbols denote individual cells. (C) Geometric mean of τ_act from cells in B. Black circles, control; pink triangles, 10 nM GxTx; red inverted triangles, 100 nM; dark red diamonds, 1 µM. Lines, fit of Eq. 8 (vehicle: τ_0mV = 15.9 ± 0.3 ms, z = 0.41 ± 0.03 e₀; 10 nM τ_0mV = 43 ± 11 ms, z = 0.35 ± 0.07 e₀; 100 nM τ_0mV = 91 ± 14 ms, z = 0.49 ± 0.05 e₀; 1 µM τ_0mV = 44 ± 3 ms, z = 0.35 ± 0.02 e₀).

Gating-current recordings

The following modifications from the whole-cell protocol were applied during gating-current recordings. Channel expression was maximized by continuous incubation with tetracycline during culture. The external solution contained (in mM) 140 NMDG, 50 HEPES, 2 CaCl₂, 2 MgCl₂, 0.1 EDTA, and 0.01 CsCl, adjusted to pH 7.3 with methanesulfonic acid. The internal (pipette) solution contained (in mM) 140 NMDG, 1 NMDG-Cl, 50 HF, 5 EGTA, and 50 HEPES, adjusted to pH 7.3 with methanesulfonic acid. A calculated liquid-junction potential of −3.9 mV between the bath and pipette solution was corrected. Recording pipettes were pulled from thick-walled borosilicate glass (1.5 mm outer diameter, 0.86 mm inner diameter, with filament; Sutter Instrument) and Sylgard-coated, and tips were fire polished. Pipette-tip resistances with gating current solutions were 5.4–10 MΩ. Series resistances were 8–29 MΩ (before compensation). Cell capacitances were 5–12 pF. The series resistance compensation correction circuit was set to 80–85% when series resistance exceeded 10 MΩ. This resulted in effective cell membrane charging time constants of <100 µs in all cells, at least three times faster than the fastest time constants fitted to gating current decays. The kinetics of rising phases of gating currents were expected to be impacted by the membrane charging times and were not analyzed. In pilot experiments, gating-current amplitudes diminished over time, presumably due to Kv2.1 channels adopting a defunct conformation in the absence of ions in the selectivity filter (Melishchuk et al., 1998; Ambriz-Rivas et al., 2005). To prevent channels from becoming defunct, the blocker Cs⁺ (10 µM) was added to the external solution. The slow-rising phase of OFF gating currents, saturation of inward charge movement, and lack of inward charge movement at voltages where channels remain open suggest inward Cs⁺ current negligibly impacted current levels.

Single-channel recordings

The following modifications from the whole-cell protocol were applied during single-channel recordings. Optimal channel expression for single channels was induced by incubation with tetracycline for 1–2 h. Single-channel recordings were made from on-cell patches, to avoid Kv2.1 current rundown that occurs after patch excision (Lopatin and Nichols, 1994). Cells were bathed in a high [K⁺] variant of the external solution used for whole-cell recording (in mM): 155 KCl, 50 HEPES, 20 NaOH, 2 CaCl₂, 2 MgCl₂, and 0.1 MgEDTA, adjusted to pH 7.3 with HCl. A calculated liquid-junction potential of −3.3 mV between the bath and pipette solution was corrected. Recording pipettes were pulled from thick-walled borosilicate glass (1.5 mm outer diameter, 0.86 mm inner diameter, with filament; Sutter Instrument), Sylgard-coated, and fire-polished. Pipette-tip resistances with these solutions were >10 MΩ. Single Kv2.1 channel amplitudes were consistent with a resting potential of 0 mV in this solution. As BSA can prevent peptide adsorption to glass surfaces, yet interferes with the patch clamp seal, a pipette-filling technique similar to that used for perforated-patch recording (Horn and Marty, 1988) was used to apply GxTx to on-cell patches. Immediately before patching, the pipette tip was filled with the 20 mM K⁺ external solution used for whole-cell ionic currents (no BSA), via the glass filament capillary action. The pipette was then backfilled with the same solution with 0.1% BSA ± 1 µM GxTx. Most recordings also included 5 µM tetrodotoxin in the pipette solution, to block endogenous sodium channels observed in a subset of patches. This procedure allowed formation of tight, typically 10–500 GΩ on-cell seals, before BSA and GxTx diffused to the pipette tip. An increase in traces consistent with GxTx binding (see Single-channel analysis) was seen at times >10 min after pipette filling, indicating GxTx diffusion into the pipette tip to reach Kv2.1 channels. Recordings were low-pass filtered at 1 kHz and digitized at 10 kHz.

Analysis

Electrophysiology analysis, curve fitting, and plotting were performed with IgorPro (Wavemetrics) or Matlab (MathWorks). For presentation, macroscopic and gating current traces were Gaussian-filtered at 2 kHz. Nonlinear least-squares curve fitting used a Levenberg-Marquardt algorithm. Uncertainties reported with fit parameters are SDs. Arithmetic means and errors are reported for conductance and charge measurements. Geometric means and errors are reported for time constants, rates, and sigmoidicity measurements. In all figures, error bars indicate standard errors.

Macroscopic ionic-current analysis

Conductance values were determined from current level at the end of 100-ms steps to the indicated voltage, divided by the driving force for K⁺ relative to the calculated Nernst potential of −53 mV. Conductance levels were normalized to the mean conductance from 80 to 100 mV in the presence of vehicle. G–V relations were fit with Boltzmann functions:

$$G_K=A{\left(1+e^{\frac{-\left(V-V_{1/2}\right)zF}{RT}}\right)}^{-x}.$$ (1)

G is conductance, A is maximum amplitude, V_1/2 is the activation midpoint for the independent transition in units of millivolts, z is valence in units of elementary charge (e₀), F is the Faraday constant, R is the ideal gas constant, T is absolute temperature, and x represents the number of independent identical transitions required to open a channel. G–V relations were also fit by the product of two Boltzmann functions when Eq. 1 was insufficient:

$$G_K=A{\left(1+e^{\frac{-\left(V-V_{independent}\right)z_{independent}F}{RT}}\right)}^{-4}{\left(1+e^{\frac{-\left(V-V_{concerted}\right)z_{concerted}F}{RT}}\right)}^{-1}.$$ (2)

In Eq. 2, channel opening is the product of two classes of voltage sensitive transitions: an independent transition in each of four subunits and a concerted transition.

Macroscopic ionic activation kinetics were fit from 10–90% of current rise with the power of an exponential function (Sack and Aldrich, 2006):

$$I_K=A{\left(1-e^{\raisebox{1ex}{$-t$}\!\left/ \!\raisebox{-1ex}{${\tau }_{act}$}\right.}\right)}^{\sigma }.$$ (3)

Eq. 3 was fit such that (time) t = 0 is the beginning of a voltage step from the holding potential of 100 mV. The t = 0 mark was adjusted to 100 µs after voltage step start to correct for filter delay and cell charging. Eq. 3 yields a curve that originates at I_K = 0 and asymptotically approaches its maximum amplitude, A, in units of picoamperes, with a time course determined by time constant τ_act, in units of milliseconds, and sigmoidicity σ, which is unitless. The use of Eq. 3 improves goodness of fit at early activation time points. When σ = 1, Eq. 3 describes a monoexponential rise, as would be expected from an activation process involving one transition from a closed state to the open state. As σ increases, the delay before the I_K rise increases and I_K becomes sigmoid in shape. In a model where channel opening is preceded by a number of independent and identical activation transitions, the value of σ is equal to the number of transitions required to produce such a sigmoidicity. Sigmoidicity has also been previously quantified as time to half-maximal rise or the delay of a monoexponential function (Zagotta et al., 1994b; Schoppa and Sigworth, 1998a). Deactivation kinetics were fit by a single exponential:

$$I_K=A{e}^{\raisebox{1ex}{$-t$}\!\left/ \!\raisebox{-1ex}{${\tau }_{deact}$}\right.}+B.$$ (4)

B is the residual baseline current, in units of picoamperes, and all other variables have the same meaning as Eq. 3.

Gating-current analysis

Charge movement was quantified by integrating gating currents from the end of any obvious fast capacitive artifact to the time indicated (see Results). Currents were baseline-subtracted to a period after current decay had ceased. Q_OFF measurements at −140 mV were determined by integrating currents until roughly 10× τ_OFF after stimulus: 60 ms under control conditions and 20 ms in GxTx. Q_fast measurements from ON gating currents were calculated by integrating the initial 10 ms after stimulus. Cells were observed to develop outward leak currents when held at strong positive voltages for extended times. We suspect these leak currents were Cl⁻ based, as they were more pronounced when solutions containing more Cl⁻ were used in pilot studies. Q_fast/Q_OFF values were normalized to individual cells. Charge movement–voltage data were fit with a Boltzmann distribution function:

$$Q=A{\left(1+e^{\frac{-\left(V-V_{1/2}\right)zF}{RT}}\right)}^{-1}.$$ (5)

Q is the charge moved, and all other variables are as in Eq. 1.

Time constants were extracted from I_{g ON} with fits of a double-exponential function,

$$I_{gON}=A{e}^{\raisebox{1ex}{$-t$}\!\left/ \!\raisebox{-1ex}{${\tau }_{ON}$}\right.}+B-A_{rise}{e}^{\raisebox{1ex}{$-t$}\!\left/ \!\raisebox{-1ex}{${\tau }_{rise}$}\right.},$$ (6)

where current decays from maximum amplitude, A, to baseline, B, with a time constant, τ_ON. The rising phase of I_{g ON} was accounted for by A_rise and τ_rise. The rising phase was predicted to be affected by the rate of cell charging and was not used in analyses. The rising phase of I_{g OFF} was not well fit by Eq. 6. A monoexponential, Eq. 4, was fit to the decaying phase of inward gating currents to determine τ_OFF.

Single-channel analysis

We established a specific voltage-pulse protocol for individual traces to assess whether an individual Kv2.1 channel was either bound by GxTx or free. This protocol was developed using the response characteristics of the Kv2.1 conductance in whole-cell mode. Kv2.1 has significant conductance at both 0 mV and +75 mV. When inhibited by GxTx, Kv2.1 has very low conductance at 0 mV, but substantial conductance at +75 mV (see Fig. 1). The pulse protocol shown in Fig. 2 (inspired by Phillips et al., 2005) was used to classify whether GxTx was inhibiting the channel: if channel openings were observed during the +75 mV pulse as well as the pulses to 0 mV, then the channel behavior was consistent with an uninhibited Kv2.1 channel opening (and classified as “free”); if channel openings were observed during the +75 mV pulse without openings at 0 mV, the channel behavior was consistent with inhibition by GxTx (and classified as “bound”). Every individual single-channel trace was inspected and classified according to this criterion. Traces that were not classified as “free” or “bound” were not analyzed; these were traces where GxTx apparently bound or dissociated during a trace, or were compromised by a change in resistance or an electrical artifact. After 10 min or more following backfilling the patch pipette with 1 µM GxTx, “bound” traces were commonly observed. In each patch, we quantified this occurrence by calculating the fraction of analyzed current traces scored as bound with the following relationship (see Fig. 5 C):

$$fractio{n}_{bound}=\frac{{\#}_{bound}}{{\#}_{bound}+{\#}_{free}}.$$ (7)

fraction_bound is the probability that the toxin is bound, #_bound is the number of traces classified as “bound,” and #_free is the number of traces classified as “free” with 1 µM GxTx present in the pipette solution. Under control conditions, traces that were classified as “bound” were rare (see Fig. 5 C). Notably, “free” traces occurred throughout experiments with 1 µM GxTx. The K_d of GxTx for Kv2.1 is ∼1 µM when held at 0 mV and predicted to be weaker than 1 µM during positive-voltage stimuli (Tilley et al., 2014). The single-channel pulse protocol was repeated at a rate of 1 Hz, leading the membrane to be held at +75 mV for 50% of the time during stimulus trains. This is distinct from the voltage protocols for whole-cell or gating currents, where the cell membrane was depolarized less than 5% of the time, and 1 µM GxTx had a saturating effect on the Kv2.1 conductance (see Fig. 1).

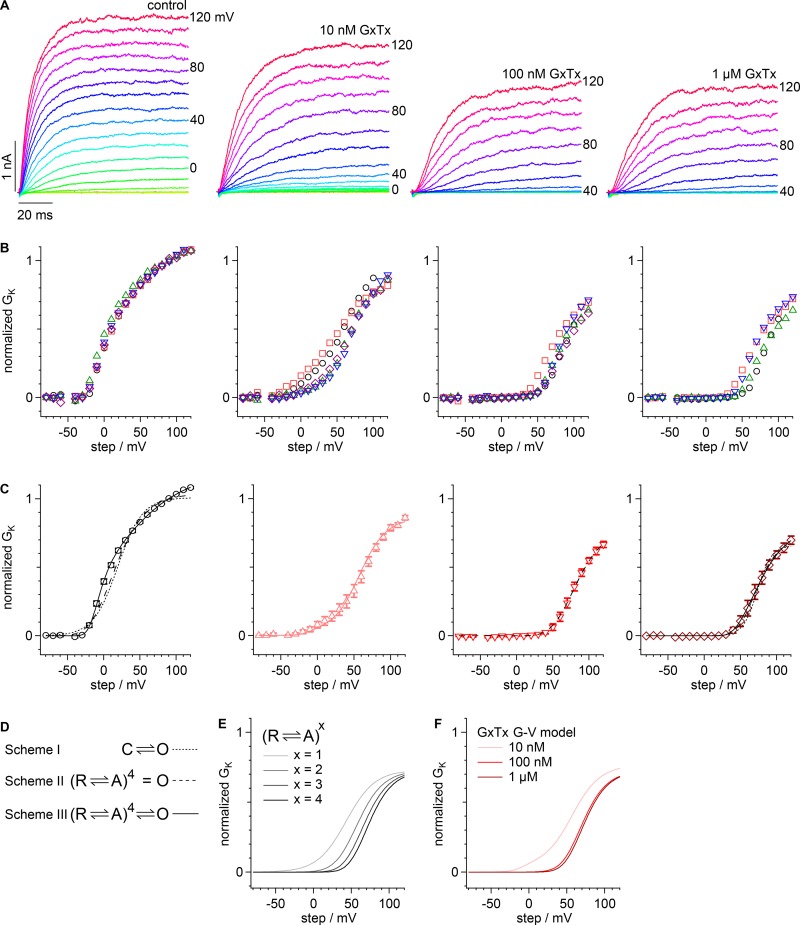
Figure 1.

GxTx modulation of Kv2.1 conductance in whole-cell recordings. (A) Kv2.1 current response to 10-mV increment voltage steps ranging from −80 to +120 mV. The holding potential was −100 mV. Traces were recorded in vehicle (left) or the indicated concentration of GxTx. Voltage stimuli colored identically in all panels. (B) Conductance calculated from the mean current of the last 20 ms of each voltage step. GxTx concentrations are the same as in A. Symbols denote individual cells (n = 4–5). (C) Mean conductance from cells in B. Black circles, control; pink triangles, 10 nM GxTx; red inverted triangles, 100 nM GxTx; dark red diamonds, 1 µM GxTx. Dotted lines, fit of Eq. 1 with x = 1 (vehicle: V_1/2 = 19.4 ± 0.4 mV, z = 1.50 ± 0.02 e₀, A =1.008 ± 0.002; 1 µM GxTx: V_1/2 = 73 ± 2 mV, z = 2.6 ± 0.2 e₀, A = 0.66 ± 0.02); dashed lines, fit of Eq. 1 with x = 4 (vehicle: V_1/2 = −23.6 ± 0.6 mV, z =1.02 ± 0.02 e₀, A = 1.041 ± 0.003; 100 nM GxTx: V_1/2 = 44.5 ± 1.5 mV, z = 1.06 ± 0.06 e₀, A = 0.79 ± 0.04; 1 µM GxTx: V_1/2 = 43 ± 2 mV, z = 1.3 ± 0.1 e₀, A = 0.73 ± 0.04); black lines, fit of Eq. 2 (vehicle: V_independent = −26 ± 6 mV, z_independent = 2.6 ± 0.2 e₀, V_concerted = 12 ± 2 mV, z_concerted = 0.54 ± 0.04 e₀, A = 1.19 ± 0.02; 1 µM GxTx: V_independent = 27 ± 14 mV, z_independent = 2.0 ± 1.4 e₀, V_concerted = 74 ± 13 mV, z_concerted = 1.1 ± 0.1 e₀, A = 0.79 ± 0.18); pink line, fit of sum of fits of Eq. 2 to vehicle and 1 µM GxTx (10 nM GxTx: A_vehicle = 24 ± 2%). (D) Gating schemes underlying fitting from C. C = closed channel, O = open channel, R = resting voltage sensor, A = active voltage sensor. (E) Calculated conductance of channels with varying GxTx stoichiometry. Each voltage sensor has a V_1/2 = 43 mV and z = 1.3 e₀ as in the fit of Eq. 1 to 1 µM in C. (F) Calculated conductance of channels in varying concentrations of GxTx. GxTx stoichiometry from binomial distribution with K_d = 12.7 nM. Channels with zero voltage sensors bound are represented by fit of Eq. 2 to vehicle from C. Channels with GxTx as in E.

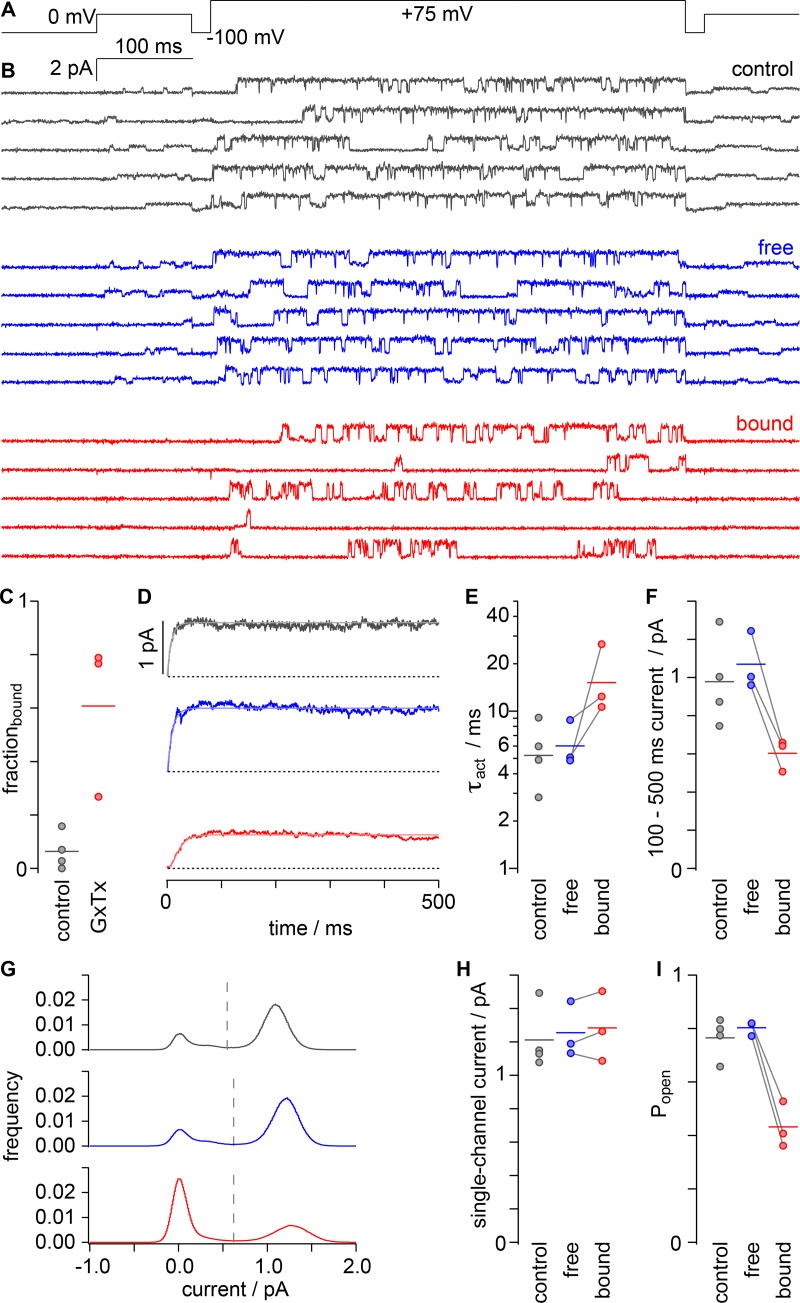
Figure 5.

Kv2.1 open probability is decreased by GxTx in single-channel recordings. (A) Voltage protocol used to classify single-channel traces. Currents recorded with 1 µM GxTx in the pipette solution were classified as “free” or “bound” based on the presence or lack of openings at 0 mV, respectively. (B) Single-channel current responses to protocol shown in A after subtraction of leak currents and capacitive transients. On-cell patches. Gray, “control”; blue, “free”; red, “bound.” (C) Fraction of trials classified as “bound” in the absence (gray) or presence (red) of 1 µM GxTx. Circles, individual patches. Horizontal bars, arithmetic means. (D) Average single-channel currents during the +75-mV segment. Dotted lines, zero current level. Smooth lines, fits of Eq. 3 (control: A = 0.97 ± 0.23 pA, τ_act = 5.2 ± 2.6 ms, σ = 1.05 ± 0.21; free: A = 1.06 ± 0.16 pA, τ_act = 6.0 ± 2.2 ms, σ = 1.39 ± 0.29; bound: A = 0.60 ± 0.09 pA, τ_act = 15.5 ± 8.8 ms, σ = 2.10 ± 0.82). (E) τ_act from average single-channel currents as in D. Circles, individual patches; gray lines connect measurements from the same patch. Horizontal lines, geometric means. (F) Mean single-channel current between 100 and 500 ms after stimulation to +75 mV. Horizontal lines, arithmetic means. (G) Current histograms at +75 mV from patches in B. Dotted lines, single-channel current half amplitude from Gaussian fits to histogram peaks. (H) Mean single-channel current amplitude from Gaussian histogram fits to individual patches. Horizontal lines, arithmetic means. (I) Open probability determined from integral of current histograms above half-amplitude threshold. Horizontal lines, arithmetic means.

To isolate single-channel currents from leak current and uncompensated capacitive transients, multiple traces without openings were averaged and subtracted from each trace with single-channel openings. Drifts in capacitance were corrected for by subtracting the first 25 ms after each voltage pulse from an average of the immediately previous and subsequent traces without openings. Each trace was inspected to ensure that this subtraction procedure did not add or remove openings or closings. The activation kinetics of average single-channel currents were characterized by fitting them with Eq. 3.

Single-channel current histograms were obtained from corrected traces at +75 mV that were clearly bimodal, and each peak was fitted (to its half maximum) with a Gaussian function. The single-channel current amplitude was defined as the difference between the peaks of the fits (see Fig. 5 H), and a half-amplitude threshold at the midpoint between them. Sub-conductance levels of Kv2.1 have been well documented (Benndorf et al., 1994; Chapman et al., 1997; Trapani et al., 2006) and were apparent in these single-channel traces. Occurrences of K⁺-sensitive sub-conductance levels were minimized by the 20 mM K⁺ extracellular solution in the pipette (Trapani et al., 2006). The remaining sub-conductance occurrences were predominantly to a current level ∼20% of the open state, and these occurred <10% as often as openings to the full conductance level. Larger sub-conductance states occurred even less frequently. Visual inspection of traces did not reveal an obvious impact of GxTx binding on the occurrence of sub-conductance current levels. Due to the small size and infrequent occurrence of these sub-conductance levels, we did not treat them explicitly during analysis. All traces reported were idealized to include only a single fully open conductance level. Idealization of traces resulted in channel event artifacts occurring when variant sub-conductance currents crossed the half-amplitude threshold. This resulted in overrepresentation of fast, flickery openings and closings. Hence, no conclusions were made concerning the kinetics of fast, flickery states, and conclusions were drawn only from states with longer-lived dwell time constants.

Open probability was calculated as the fraction of the integral of the amplitude histogram above the half-amplitude threshold. The half-amplitude threshold of idealized traces was also used to determine the latencies to first opening after the step to +75 mV and the open and closed dwell times. The kinetics of activation were characterized by fitting the cumulative probability of latencies to first opening with Eq. 3; one control patch was excluded from this particular fitting because the data were sparse. The distributions of dwell times were analyzed, fitted, and displayed by quantifying the square-root of the number of events in logarithmic bins (Sigworth and Sine, 1987). Open dwell times were well described by a single exponential component. Closed dwell times required multiple exponential components (see “Results”).

Channel-gating simulations

Markov-Chain models were constructed using R version 3.3.2 (R Foundation for Statistical Computing; https://www.R-project.org/). For numerical simulations, a Runge-Kutta Order Four integrator was used with a time step of 0.1 ms. In cases when the cumulated error exceeded a probability greater than the threshold value of ±0.01, the time step was halved until the error was maintained below threshold. The kinetics of simulated open probabilities were fit with Eq. 3 between 10% and 90% of the rising phase. To generate Model F, cubic splines were used for interpolation to calculate rates corresponding to experimental values in Fig. 9, B and C. For Models FR and FRT, rates were manually adjusted and simulations run and fitted as above, recursively, until τ_act and σ values approached mean values from experiments (Fig. S1). To plot overlays, fitted time constants, τ, were compared with the reciprocal of microscopic rates $k^{-1}$. Rates from models that best matched experiments were fitted to obtain rates at neutral voltage, $k_{0mV},$ and a voltage dependence in units of elementary charge, z, with an exponential as a function of voltage:

$$k^{-1}=k_{0mV}{}^{-1}{e}^{\raisebox{1ex}{$-VzF$}\!\left/ \!\raisebox{-1ex}{$RT$}\right.} .$$ (8)

All other values have the same meaning as stated in Eq. 1. In the kinetic models in which the final concerted opening step was constrained to a voltage-independent rate, the experimental macroscopic activation time constants were fit by the function

$${\tau }_{act}=\frac{1}{\left(k_{open}+k_{close}\right){\left(1+\frac{{\beta }_{0mV}}{{\alpha }_{0mV}}{e}^{\raisebox{1ex}{$-VzF$}\!\left/ \!\raisebox{-1ex}{$RT$}\right.}\right)}^{-4}},$$ (9)

where the values k_open and k_close are the voltage independent rates of the concerted step and ${\beta }_{0mV}/{\alpha }_{0mV}$ is the ratio of the reverse and forward rates of the independent movement of each of the four subunits at 0 mV. All other values have the same meaning as stated in Eq. 1.

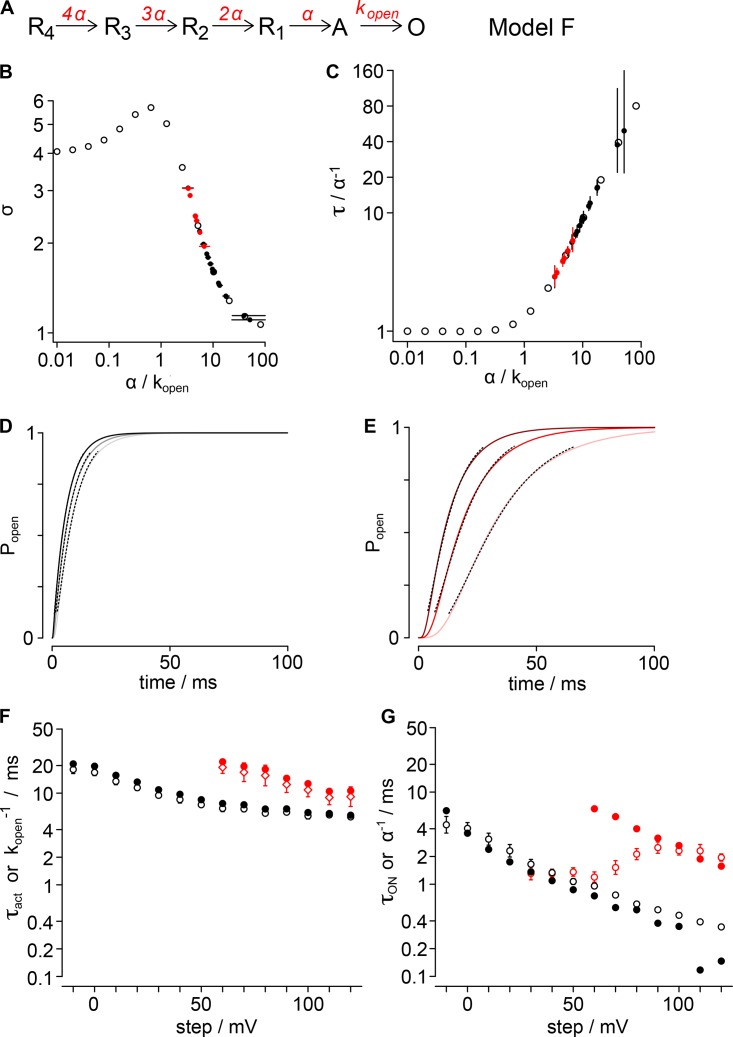
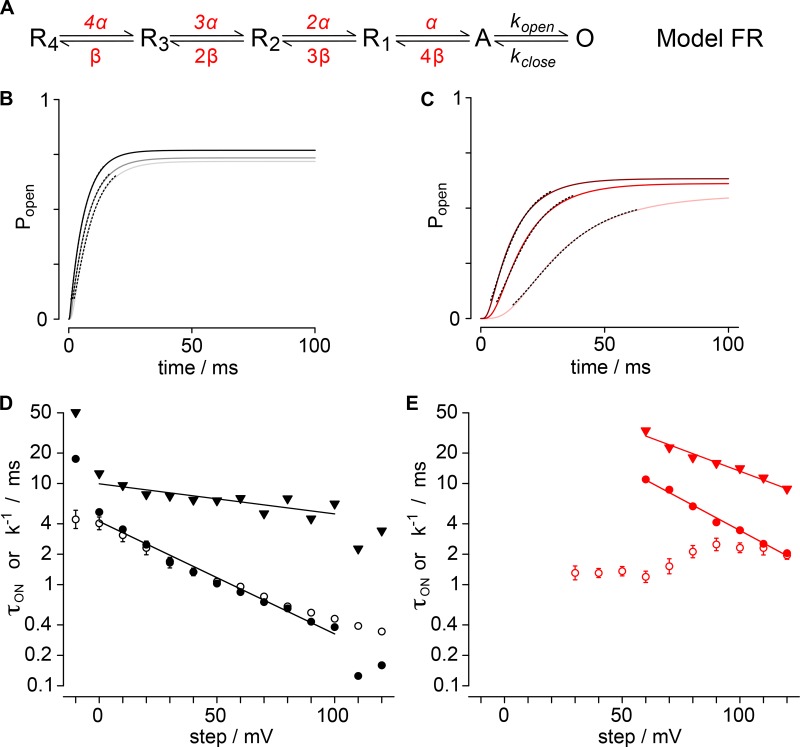
Figure 9.

Forward activation model (Model F). (A) Gating scheme for Model F activation. Four identical resting voltage sensors independently activate with rate α. Pore opening is modeled as a concerted event with rate k_open. Rates susceptible to GxTx are red. (B) Activation sigmoidicity, σ, is plotted for varying α/k_open ratios. Hollow black circles, σ from fit of Eq. 3 to simulations; filled circles, σ values of Kv2.1 experiments from Fig. 3 B, assigned to α/k_open ratios; black, vehicle; red, 1 µM GxTx. (C) The relation of τ_act to the reciprocal of α is plotted for varying α/k_open ratios. Hollow black circles, τ_act from fit of Eq. 3 to simulations; filled circles, τ_act values from Fig. 2 C, assigned to α/k_open ratios by σ in panel B; black, control; red, 1 µM GxTx. (D) Simulated P_open from Model F under control conditions. Light gray, 60 mV; dark gray, 90 mV; black, 120 mV. Dotted lines show fits of Eq. 3. τ_60mV = 6.81 ± 0.01 ms, σ_60mV =1.596 ± 0.003; τ_90mV = 6.196 ± 0.008 ms, σ_90mV = 1.326 ± 0.002; τ_120mV = 5.502 ± 0.004 ms, σ_120mV = 1.141 ± 0.001. (E) Simulated P_open from Model F with GxTx. Light pink, 60 mV; red, 90 mV; dark red, 120 mV. Dotted lines show fits of Eq. 3. τ_60mV = 19.03 ± 0.01 ms, σ_60mV = 3.036 ± 0.003; τ_90mV = 12.35 ± 0.01 ms, σ_90mV = 2.466 ± 0.004; τ_120mV = 9.11 ± 0.01 ms, σ_120mV = 1.958 ± 0.004. (F) Comparison of the reciprocal of k_open from Model F to τ_act from Kv2.1 experiments. Hollow circles or diamonds, mean τ_act from Fig. 2 C; filled circles, k_open⁻¹ from model; black, control; red, 1 µM GxTx. (G) Comparison of the reciprocal of α from Model F to τ_ON from Kv2.1 gating currents. Hollow circles, mean τ_ON from Fig. 8 E; filled circles, α⁻¹ from model; black, vehicle; red, 1 µM GxTx.

Online supplemental material

Fig. S1 provides comparisons of kinetic models to fitted data parameters.

Results

Kv2.1 requires more voltage to activate with GxTx bound

To begin characterizing the impact of GxTx on Kv2.1 gating, we examined the voltage sensitivity of the Kv2.1 conductance. A stably transfected CHO-K1 cell line was induced to express the rat Kv2.1 channel and voltage clamped in the whole-cell configuration. In a previous study, we found that the voltage dependence of GxTx dissociation is accelerated when the voltage sensors activate, with dissociation time constants of 340 s at −100 mV and 45 s at 0 mV (Tilley et al., 2014). To ensure GxTx did not appreciably dissociate during voltage steps in this study, we applied brief 100-ms voltage steps from a holding potential of −100 mV. Delayed-rectifier currents were observed when voltage was stepped more positive than −30 mV (Fig. 1, A and B). Exposure to GxTx (10 nM, 100 nM, and 1 µM) decreased the amplitude of Kv2.1 currents in a dose-dependent manner. When 100 nM or 1 µM GxTx was present in the external bath solution, positive voltages exceeding +50 mV were required to activate the Kv2.1 conductance, similar to previous reports (Herrington et al., 2006; Tilley et al., 2014).

To assess the voltage dependence of gating-charge movement underlying channel opening, the G–V relation was fit with a series of Boltzmann functions that correspond to distinct channel-gating models (Fig. 1 C). We found that the G–V relation was fit poorly by a single Boltzmann function (Eq. 1 with x = 1; Fig. 1 C, dotted line), which corresponds to a gating model with one closed state and one open state (Scheme I in Fig. 1 D). The G–V fit with a fourth power Boltzmann (Eq. 1 with x = 4; Fig. 1 C, dashed line), corresponding to a Hodgkin–Huxley–style model involving four independent and identical gates, was also inadequate (Scheme II in Fig. 1 D). We found that the relationship was fit best by Eq. 2 (Fig. 1 C, solid line), the product of a first- and fourth-degree Boltzmann function, which represents a gating process with an independent step in each of four subunits coupled to a single step concerted among subunits (Scheme III in Fig. 1 D). The fit of Eq. 2 suggests that the G–V relation results from two types of gating-charge movements, which must both occur before channel opening. In this fit, the gating process representing independent subunit activation translocated more charge (2.6 ± 0.2 e₀) than the concerted transition (0.50 ± 0.04 e₀), which had its V_1/2 ∼36 mV more positive. G–V relations with GxTx did not saturate by +120 mV, but higher voltages resulted in variable outward currents unrelated to Kv2.1 opening occurring much more frequently. The 1 µM GxTx G–V was better fit by Scheme II than Scheme I, and fitting with Scheme III was poorly constrained (Fig. 1 C). The insufficiency of Scheme I indicated that more than one gating transition limits channel conductance with GxTx, consistent with findings with HaTx and other related spider toxins that inhibit the movement of four independent voltage sensors (Swartz and MacKinnon, 1997a; Lee et al., 2003; Wang et al., 2004; Phillips et al., 2005).

These fitting procedures give a means of quantifying the inhibition by GxTx. The fit of Eq. 1 with x = 4 to the G–V with either 100 nM or 1 µM GxTx was indistinguishable, indicating that channel modulation is effectively saturated by 100 nM (Fig. 1 C). We have previously calculated the K_d for each subunit to be 12.7 ± 0.9 nM under these conditions (Tilley et al., 2014), by assuming independent binding of GxTx to each of four channel subunits, and that channels with one or more toxins bound do not conduct at the test potential of 0 mV (Swartz and MacKinnon, 1997a). For a K_d of 12.7 nM, the binomial distribution predicts that in 1 µM GxTx, 95% of channels will have four toxins per channel, whereas in 100 nM GxTx, only 62% of channels will have four toxins per channel, 31% with three, 6% with two, 0.5% with one, and 0.01% with zero. If our K_d measurement and assumption of independent subunit binding are valid, they indicate that the G–V relation must be similar when three or four toxins are bound; otherwise, the G–V would not appear saturated at 100 nM.

To determine what a Scheme II mechanism might predict with fewer than four toxins bound, we constructed a simple model. According to the fits in Fig. 1, the four voltage sensors of Kv2.1 have V_1/2 = −26 mV under control conditions, and +43 mV with GxTx. If we assume all subunits not bound by GxTx are active at the positive voltages where GxTx-bound subunits activate, then the G–V relation will be determined by Eq. 1, with x equal to the number of subunits bound. When the parameters from the fit of Eq. 1 (x = 4) to 1 µM GxTx is plotted with x = 1, 2, and 3, the result is a prediction of how Kv2.1 channels will gate with one to four subunits bound (Fig. 1 E). The voltage midpoint of the x = 2, 3, and 4 G–Vs are all within 15 mV of each other, smaller than the cell-to-cell variation seen experimentally (Fig. 1 B). This suggests that the slight conductance differences between channels bound by two, three, or four toxins would be difficult to empirically detect.

By assuming a binomial distribution of toxins per channel, we predicted G–Vs in different concentrations of GxTx (Fig. 1 F). These predictions are based only on a 12.7 nM K_d, and the G–V fits to control and saturating (1 µM) GxTx, yet recapitulate the G–Vs in 10 and 100 nM GxTx quite well. The 100-nM voltage midpoint was within 2 mV of the 1-µM midpoint, consistent to within the error of experimental data, and this supports the hypothesis that the channels are functionally saturated before all subunits are bound. An additional test of this model is to determine how well it predicts the G–V at 10 nM where the x = 0, 1, 2, 3, and 4 are predicted to coexist at 10, 31, 36, 19, and 4%, respectively. For the sake of simplicity, the model assumes the maximal conductance of channels with one, two, or three GxTx bound to be the same as x = 4. The 10-nM model matched the experimental G–V reasonably well (Fig. 1 C, 10-nM panel, pink line), consistent with the assumption that GxTx binds to each voltage sensor independently, and shifts bound voltage sensor activation to more positive voltages.

Overall, the analysis of the Kv2.1 G–V reveals key aspects of how this channel is activated by voltage and how activation is modified by GxTx. First, Kv2.1 undergoes multiple voltage-dependent conformational changes, and these conformational changes have very different voltage dependencies. Second, when GxTx is bound, the G–Vs suggest that the toxin inhibits a single voltage-dependent change that occurs independently in each subunit. Third, when GxTx binds only one, two, or three subunits, the activation of that channel is limited by the bound subunits.

GxTx slows activation of K⁺-conductance

The modulation of the Kv2.1 G–V relation suggests that GxTx inhibits the movement of independent voltage sensors, and we sought to test whether this phenomenon was also evident in channel-activation kinetics. To quantitate the impact of GxTx on activation kinetics, current rise after voltage steps was fit with the power of an exponential function (Eq. 3). When fit to 10–90% current rise, residuals were minimal, and values reasonably consistent from cell to cell (Fig. 2, A and B). While Eq. 3 does not fit current rise perfectly, it is tightly constrained, with only three free parameters: A, the final amplitude, σ, the sigmoidicity or delay before current rise, and τ_act, which reports the slowest process in the activation path.

We found that at all voltages, GxTx increased τ_act. Similar to the G–V relation, GxTx modulatory effects on τ_act saturated at 100 nM and higher concentrations (Fig. 2, B and C). Under saturating conditions, GxTx shifted the τ_act values ∼80 mV more positive compared with control conditions (Fig. 2 C). Remarkably, τ_act was similar in 10 nM, 100 nM, or 1 µM when the voltage step was more positive than +60 mV (Fig. 2 C). This result is expected if subunits bound by GxTx each activate independently, yet more slowly, such that channels with one, two, three, or four GxTx bound activate at similar rates. This is consistent with Scheme III, where GxTx slows an independent voltage sensor transition in each subunit it binds.

We assessed the voltage dependence of τ_act by fitting Eq. 8 over voltage ranges where τ_act was linear and steep on a semi-logarithmic plot. τ_act had a similar valence, 0.3–0.5 e₀, under all conditions (Fig. 2 C). This similar voltage dependence would be predicted by a Scheme III activation model in which GxTx inhibits the independent movement of voltage sensors.

GxTx increases the sigmoidicity of K⁺-conductance activation kinetics

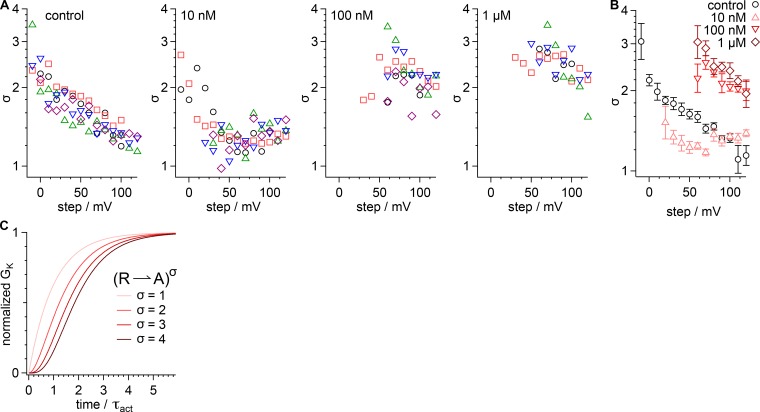
The activation sigmoidicity is a quantitation of the delay in ionic current after membrane depolarization, before the current can be well approximated by an exponential function. Sigmoidal activation can be used to infer the minimum number of conformational changes preceding opening of the channel pore (Zagotta et al., 1994b). We characterized degree of sigmoidicity in Kv2.1 activation by the power of the exponential (σ, Eq. 3) that best fits the current rise in response to a depolarizing step (Sack and Aldrich, 2006). The value of σ is equivalent to the number of conformational transitions with an identical time constant that must occur before pore current is observed; as σ increases, a delay before current rise and sigmoid shape becomes apparent (Fig. 3 C).

Figure 3.

Saturating GxTx increases Kv2.1 activation sigmoidicity in whole-cell recordings. (A) Values of σ from fits of Eq. 3 and in Fig. 2 A. Symbols denote individual cells. (B) Geometric mean of σ from cells in A. Black circles, control; pink triangles, 10 nM GxTx; red inverted triangles, 100 nM; dark red diamonds, 1 µM. (C) Activation curves calculated from Eq. 3 when σ is varied.

For Kv2.1 in vehicle, σ declines from ∼3 toward a value of 1 as voltage increases (Fig. 3, A and B), indicating that a single conformational change limits the kinetics of activation at the most positive voltages tested. The voltage dependence of τ_act indicates that this rate-limiting conformational change at high voltages has a time constant of ∼6 ms and little voltage dependence (Fig. 2, B and C). In 10 nM GxTx, sigmoidicity decreased to between σ = 1 and σ = 2 at most voltages. In 10 nM GxTx, the majority of channels are predicted to have one or two GxTx (see above). The σ values between one and two are consistent with activation being rate-limited by one to two slow subunits in each channel. In both 100 nM and 1 µM GxTx, σ increases (Fig. 3, A and B), consistent with GxTx binding to more voltage sensors, leading to more delay before opening. This supports a mechanism in which GxTx binds to each of the four voltage sensors to impact the kinetics of channel activation.

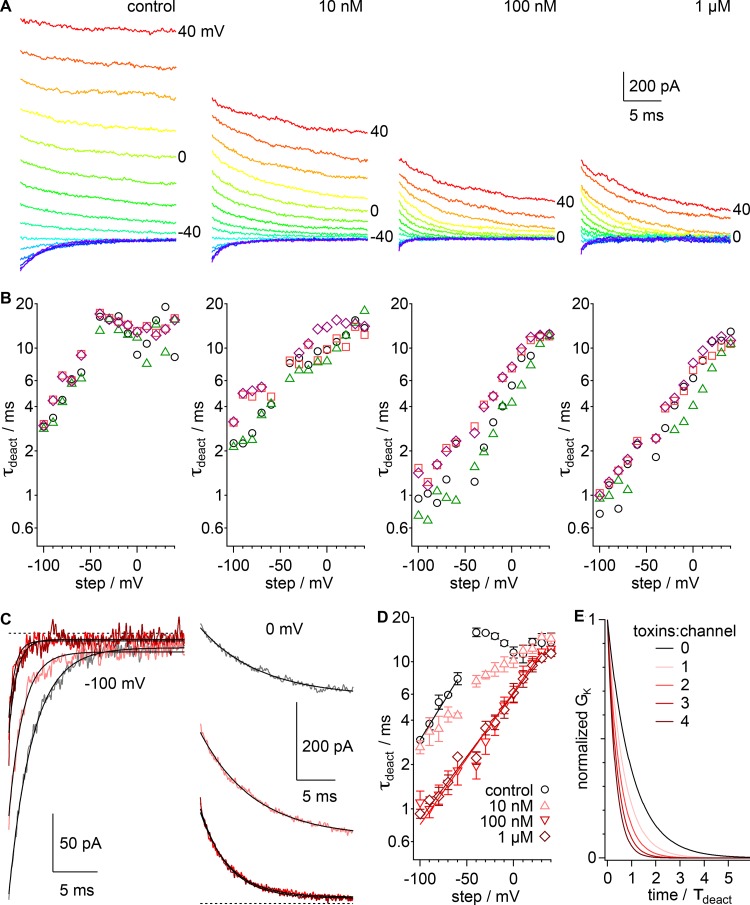
GxTx accelerates K⁺-conductance deactivation

To further understand GxTx modulation of Kv2.1, we measured deactivation kinetics. To compare Kv2.1 deactivation with and without GxTx, we activated channels with 50-ms pulses to +80 mV and examined currents during voltage steps down to +40 through −100 mV (Fig. 4 A). Traces were fit with a mono-exponential (Eq. 4). In vehicle, Kv2.1 deactivation time constants (τ_deact) had a pronounced multiphasic voltage dependence. τ_deact was steeply voltage-dependent below −50 mV and nearly voltage-independent above −50 mV, where it ranged from 10 to 20 ms (Fig. 4 B).

Figure 4.

GxTx accelerates Kv2.1 deactivation kinetics in whole-cell recordings. (A) Current in response to a series of voltage steps from +40 mV down to −100 mV in −10-mV increments following a 50-ms prepulse to +80 mV. Current recorded in indicated concentration of GxTx. Voltage stimuli colored identically in all panels. (B) Values of τ_deact from fits of Eq. 4. Symbols denote individual cells. (C) Deactivation current response to voltage steps from −80 mV down to −100 or 0 mV. Gray, vehicle; pink, 10 nM GxTx; red, 100 nM; dark red, 1 µM. Dotted lines, zero current level. Lines, fit of Eq. 4 (−100 mV vehicle: A = −210.8 ± 0.4 pA, B = −12.3 ± 0.1 pA, τ_deact = 2.67 ± 0.01 ms; −100 mV 10 nM: A = −140.4 ± 0.7 pA, B = −15.6 ± 0.1 pA, τ_deact = 1.60 ± 0.01 ms; −100 mV 100 nM: A = −66 ± 1 pA, B = −6.4 ± 0.1 pA, τ_deact = 0.69 ± 0.02 ms; −100 mV 1 µM: A = −80 ± 1 pA, B = −5.1 ± 0.1 pA, τ_deact = 0.91 ± 0.02 ms; 0 mV vehicle: A = 176.1 ± 0.5 pA, B = 531.3 ± 0.6 pA, τ_deact = 7.75 ± 0.07 ms; 0 mV 10 nM: A = 267.6 ± 0.5 pA, B = 171.4 ± 0.5 pA, τ_deact = 6.96 ± 0.04 ms; 0 mV 100 nM: A = 217.6 ± 0.5 pA, B = 16.5 ± 0.2 pA, τ_deact = 3.72 ± 0.02 ms; 0 mV 1 µM: A = 229.1 ± 0.5 pA, B = 13.8 ± 0.2 pA, τ_deact = 3.55 ± 0.02 ms). (D) Geometric mean of τ_deact from cells in B. Black circles, control; pink triangles, 10 nM GxTx; red inverted triangles, 100 nM; dark red diamonds, 1 µM. Lines, fit of Eq. 8 (vehicle: τ_0mV = 31 ± 2 ms, z = −0.60 ± 0.02 e₀; 100 nM: τ_0mV = 6.2 ± 0.2 ms, z = −0.53 ± 0.02 e₀; 1 µM τ_0mV = 6.1 ± 0.1 ms, z = −0.50 ± 0.02 e₀). (E) Deactivation curves calculated from Eq. 4 when τ_deact is varied. Calculation for four independent deactivation gates closing with rate k_gate where τ_deact = (k_gate1 + k_gate2 + k_gate3 + k_gate4). Toxin binding accelerates k_gate fourfold.

Consistent with its effects as an allosteric inhibitor, GxTx accelerated deactivation of Kv2.1 currents (Fig. 4). The effects of GxTx on τ_deact appeared to saturate by 100 nM. The voltage-dependent regimen of τ_deact in vehicle had a similar charge valence, z = −0.6 to −0.5 e₀, in 0, 100 nM, or 1 µM GxTx (Fig. 4 D). The similarity of valence suggests that at voltages where τ_deact is strongly voltage-dependent, the same conformational change limits the rate of deactivation with or without GxTx. This conformational change appears to be accelerated three- to fourfold by GxTx. Interestingly, at voltages >+10 mV, measurements of τ_deact in 100 nM or 1 µM GxTx converge to 10–20 ms, the same range as of τ_deact in control conditions. This suggests a GxTx-insensitive, voltage-independent deactivation process with a time constant of 10–20 ms determines deactivation kinetics at more positive voltages. The similar valence of the voltage-dependent phase of τ_deact, and the convergence of τ_deact with or without GxTx at more positive voltages, suggest that GxTx accelerates return of voltage sensors to rest, but does not affect a voltage-independent conformational change that determines deactivation kinetics at more positive voltages.

The kinetics of τ_deact in the subsaturating 10-nM concentration fall between control and saturating values. As with the effects of 10 nM on activation, the effect on deactivation can be explained by independent binding to the channel’s four voltage sensors. If the deactivation rate of each voltage sensor is accelerated by a fixed amount when toxin binds, and the rate of channel closing is determined by how quickly any one voltage sensor deactivates, then the rate of deactivation of a channel with four GxTx would be four times faster than a channel with only one GxTx (Fig. 4 E). Channels with zero, one, or two GxTx would constitute >70% of channels at 10 nM. In this case, sub-saturating toxin concentrations are expected to accelerate τ_deact in a graded fashion by progressive binding of GxTx to independent voltage sensors, even though channels with one GxTx bound activate with similar kinetics as saturated channels.

Overall, the effects of GxTx on Kv2.1 kinetics and steady-state conductance levels are consistent with a model where GxTx binds independently to each of four channel subunits and biases their gating equilibria toward a resting conformation. Notably, the effects of a saturating 1-µM dose of GxTx on the G–V, τ_act, σ, and τ_deact can be overcome by ∼80 mV of voltage (Fig. 1 C, Fig. 2 C, Fig. 3 B, and Fig. 4 D). This uniform shift in voltage dependence is consistent with GxTx uniformly biasing the equilibrium of voltage-dependent conformational changes, without affecting the rates of conformational changes that have little or no voltage dependence.

Single-channel K⁺-conductance amplitude is unaltered by GxTx

Our mechanistic interpretations of macroscopic currents thus far have assumed that Kv2.1 conductance changes are due to changes in open probability (P_open), where a single open state of a static unitary conductance occurs. However, the effects of voltage sensor toxins on unitary K⁺-channel currents have yet to be reported. To test the hypothesis that GxTx inhibits I_K by changing P_open, we measured currents from single Kv2.1 channels.

On-cell patches were made with pipettes backfilled with 1 µM GxTx. Long positive voltage steps were required to acquire meaningful single-channel currents in GxTx, but these promoted GxTx dissociation, so we developed a means to assess whether GxTx remained bound to a single channel throughout any given trace. On-cell patches containing single Kv2.1 channels were stimulated with a 500-ms “test” step to +75 mV, flanked by steps to 0 mV, and interleaved with short excursions to −100 mV to cause channel closing between the test and the flanking steps (Fig. 5 A). As Kv2.1 channels are prevented from opening at 0 mV when GxTx is bound, the flanking steps were used to assess whether GxTx was likely to be bound throughout each trace. Traces were classified as “free” (channel is likely not bound by GxTx) if channel openings were observed during the +75-mV segment and in both flanking 0-mV segments. We classified traces as “bound” by GxTx if the +75-mV segment contained channel openings, but channel openings were not observed in either of the flanking 0-mV segments (Fig. 5 B). Under control conditions (no GxTx in pipette), free traces were commonly observed while bound traces were rare (Fig. 5 C). In contrast, bound traces were commonly observed when the pipette contained 1 µM GxTx (Fig. 5 C). The activation kinetics and average amplitude of currents responding to +75-mV test segments were similar in GxTx-free traces and control conditions with GxTx absent (Fig. 5, D–F). However, in GxTx-bound traces, the channels activated more slowly, and the average amplitude of currents decreased (Fig. 5, D–F), mimicking the impact of GxTx on macroscopic Kv2.1 conductance (compare to Fig. 2 A). While we cannot determine the toxin-channel stoichiometry in bound traces, this classification criterion appeared to distinguish bound from free channels with reasonable fidelity. Control, free, and bound traces all contained single-channel openings to a similar current level (Fig. 5, B, G, and H), indicating that GxTx does not inhibit channels by reducing Kv2.1 unitary conductance. When the current density was integrated above and below the half amplitude of unitary current, a measure of open probability was derived that was similar between control and free traces, yet decreased markedly in bound traces (Fig. 5 I), indicating that GxTx stabilizes closed states.

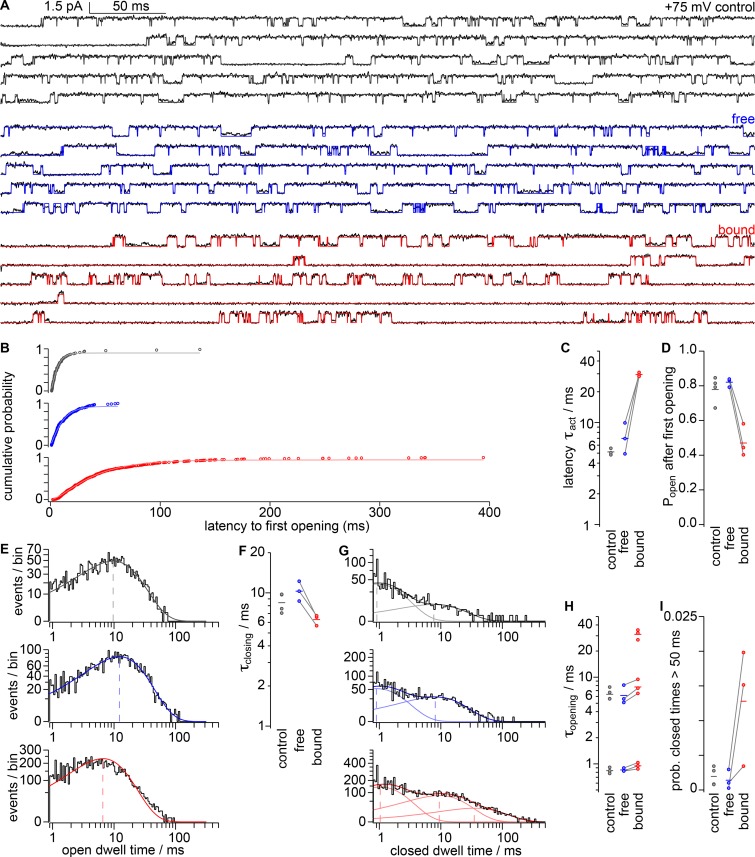
GxTx detains channels in long-lived closed states

We analyzed the gating of single channels to elucidate kinetic details of how GxTx reduces the Kv2.1 open probability. To determine the distributions of open and closed dwell times, currents were idealized by classifying sampled time points as either open or closed using a half-amplitude threshold criterion (Fig. 6 A). This simple method of assigning open and closed conformations is imperfect, as Kv2.1 channels enter subconductance states that result from heteromeric pore conformations (Chapman and VanDongen, 2005). However, subconductance states occurred rarely, and we tolerated the artifactual short dwell times they introduced, as GxTx did not appear to affect the relative occurrence of subconductances, and no conclusions were drawn from the kinetics of fast flickers. The idealized traces revealed that the latencies to the first opening measured in GxTx-bound traces were longer than control or free traces (Fig. 6, B and C), consistent with GxTx slowing activation of macroscopic currents (Fig. 2). Following the first opening, we observed that GxTx reduced P_open (Fig. 6 D), consistent with analyses of single-channel amplitude histograms (Fig. 5 I). The open dwell times were fit reasonably well with a single-exponential distribution with a time constant of ∼10 ms (Fig. 6 E), indicating that Kv2.1 current is dominated by a single open state under these conditions. The time constant of closing determined from open dwell times was slightly faster in GxTx-bound traces compared with free or control traces (Fig. 6 F).

Figure 6.

GxTx stabilizes long-lived closed states of Kv2.1. (A) Gray, blue, and red lines: idealized single-channel traces during the +75 mV segment of the voltage protocol in Fig. 5 A. Gray, control; blue, “free” with 1 µM GxTx; red, “bound” with 1 µM GxTx. (B) Cumulative probability of latencies to the first opening. Smooth lines, fits of Eq. 3 (control A = 0.934 ± 0.038 pA, τ_act = 5.14 ± 0.39 ms, σ = 1.95 ± 0.61; free A = 0.98 ± 0.03 pA, τ_act = 7.0 ± 2.5 ms, σ = 1.45 ± 0.24; bound A = 0.934 ± 0.006 pA, τ_act = 29.5 ± 1.3 ms, σ = 1.40 ± 0.29). (C) τ_act from first latencies to first opening as in B. Circles, individual patches; gray lines connect measurements from the same patch. Horizontal lines, geometric means. (D) Open probability after the first opening derived from idealized traces. Horizontal lines, arithmetic means. (E) Log-binned open dwell-time distributions and single exponential fits. y axis is square root scaling. Dashed lines indicate microscopic time constant of closing. (F) Microscopic time constant of closing from individual patches. Horizontal lines, geometric means. (G) Log-binned closed dwell-time distribution and multi-exponential fit from representative patches. Two exponential components for control and free traces, three exponential components for bound traces. Dashed lines indicate time constant of channel opening. (H) Time constants of channel opening from individual patches. Horizontal lines, geometric means. (I) Probability (prob.) of channel-closing events that are longer than 50 ms. Horizontal lines, arithmetic means.

To investigate the possibility that closed states of Kv2.1 are modulated by GxTx, the dwell times of idealized closed channels were determined by fits with multicomponent exponential functions. Free and control closed dwell times were reasonably fit by double exponential distributions (Fig. 6 G). In bound traces, Kv2.1 had marked increases in long-lived closed events that extended beyond 100 ms (Fig. 6, A and H). It was evident that GxTx induced sojourns to a long-lived closed state that was not regularly observed in free channels. We found the mean dwell times of the two underlying closed dwells in control and free channels reemerged when fitting bound distributions with three, rather than two, exponential components, and that a long-lived closed dwell time appeared (Fig. 6, G and H). This finding indicates that GxTx does not substantially affect the transitions most adjacent to the open state but increases the probability of long-lived closed states occurring (Fig. 6 I).

Our single-channel data suggest that GxTx modulates Kv2.1 in an allosteric fashion and does not affect channel conductance. The single-channel currents support the conclusion that GxTx can remain bound to open channels. The inhibitory effect is achieved by biasing a gating equilibrium toward closed conformations, consistent with our hypothesis, based on macroscopic K⁺ currents, that GxTx stabilizes independent voltage sensors in a resting conformation. If it can be assumed that the Kv2.1 gating is approximated with Scheme III in Fig. 1 D, single-channel currents suggest the concerted opening transition is represented by the closed dwell time constant of ∼6 ms. Neither this opening transition, nor the fast flickery closings were affected by GxTx. The single-channel data were gathered at a voltage where bound and control channels are likely to be activated. The long-lived closed dwells in the GxTx-bound state had a characteristic time constant between 20 and 40 ms (Fig. 6 H), as did the first latencies (Fig. 6 C). This range is similar to τ_act at +70 mV in GxTx, which ranged between 10 and 40 ms (Fig. 2 B). This similarity between timing of the initial channel opening after holding at a negative potential, and the long-lived closings that are responsible for channel inhibition, suggests that GxTX inhibits channels by returning their voltage sensors to a resting conformation.

GxTx inhibits outward movement of all gating charge

To better understand the effects of GxTx on voltage sensor gating transitions, we measured the modulatory effects on gating currents. Voltage gating is governed by a series of charge movements through the membrane electric field that drive conformational changes within the ion channel protein and lead to opening of the pore. The single-channel results indicate GxTx inhibits I_K by modulating P_open, but yield little information about how GxTx affects transitions before the final opening step.

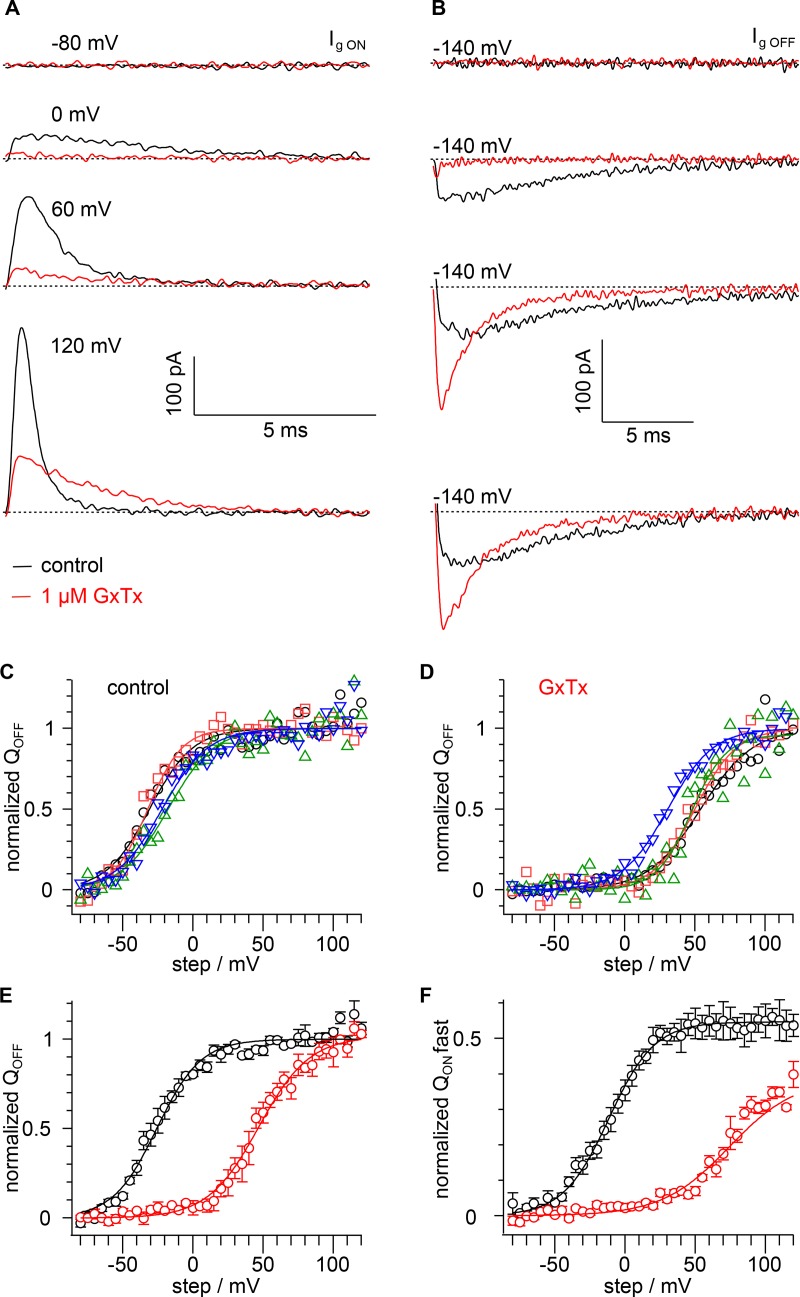
To test how GxTx affects these earlier transitions, gating currents (I_g; Armstrong and Bezanilla, 1973) of Kv2.1 channels were measured in the absence of K⁺. When channels were expressed at high density, nonlinear capacitive transients were apparent in response to 100-ms activating voltage steps (I_{g ON}), and inward transients were observable upon a returning voltage step to negative potential (I_{g OFF}; Fig. 7, A and B), similar to prior reports of Kv2.1 I_g from CHO-K1 cells (Consiglio and Korn, 2004; Scholle et al., 2004). GxTx was then applied at a concentration of 1 µM and essentially eliminated activating I_{g ON} during voltage steps to 0 mV from a −100-mV holding potential (Fig. 7 A). Similarly, I_{g OFF} was absent during steps down to −140 mV from 0 mV (Fig. 7 B). The inhibition of I_g at 0 mV indicates that GxTx inhibits movement of all Kv2.1 gating charge, stabilizing voltage sensors in their deepest resting state.

Figure 7.

GxTx inhibits outward gating-charge movement. (A) I_{g ON} elicited during voltage steps to the indicated potential from a holding potential of −100 mV. Black, vehicle; red, 1 µM GxTx; dotted lines, zero current level. (B) I_{g OFF} elicited during voltage steps to −140 mV following a 100-ms step to the potential indicated in A. (C) Integrals of control I_{g OFF} current following a 100-ms step to the indicated potential from individual cells (n = 3–4). (D) Integrals of 1 µM GxTx I_{g OFF} current following a 100-ms step to the indicated potential from individual cells (n = 3–4). Symbols mark same cells as in C. (E) Mean Q_OFF from C and D. Lines are fits of Eq. 5. Black, control; V_1/2 = −26 ± 1 mV, z = 1.6 ± 0.1 e₀; red, 1 µM GxTx V_1/2 = 47 ± 1 mV, z = 1.4 ± 0.1 e₀. (F) Integrals of I_{g ON} during the first 10 ms of a step normalized to the integral of I_{g OFF} to the indicated potential (n = 3–4). Lines are fits of Eq. 5. Black, control; V_1/2 = −12 ± 3 mV, z = 1.6 ± 0.1 e₀, A = 0.55 ± 0.02; red, 1 µM GxTx V_1/2 = 74 ± 6 mV, z = 1.1 ± 0.1 e₀, A = 0.39 ± 0.03.

Gating currents responding to voltage steps more positive than 0 mV overcame GxTx inhibition (Fig. 7, A and B), consistent with Kv2.1 ionic current activating at positive voltages. The total charge translocated (Q_OFF) was determined from the integration of gating current during a voltage step to −140 mV (Fig. 7, C and D). In GxTx, the maximal Q_OFF (following voltage steps of 100–120 mV) was slightly larger, 1.35 ± 0.13 times control. This could result from GxTx stabilizing resting voltage sensors at the −100 mV holding potential, and/or result from GxTx accelerating very slow phases of I_{g OFF} to be within the time window of Q_OFF integration. Altogether, these results indicate that GxTx selectively stabilizes Kv2.1 voltage sensors where no measurable gating charge has moved outward. The Q_OFF–voltage relation in individual cells was reasonably fit by a single Boltzmann function (Fig. 4 C). The mean charge movement from multiple patches was also reasonably well fit by a Boltzmann distribution, serving as a coarse quantification of the many charge movements underlying voltage gating (Fig. 7 E). The Q_OFF-voltage relation with GxTx had its V_1/2 shifted 73 mV more positive yet retained a similar slope (Fig. 7 E). The product of this 73-mV shift and an estimate of 3.125 e₀ gating charges per Kv2.1 subunit (Islas and Sigworth, 1999) indicates GxTx stabilizes gating charges in a resting conformation by 9.0 k_BT, or 8,100-fold. To calculate the impact of GxTx by a fitting-independent method, the shift of voltage sensor activation was estimated from the median voltage for activation, V_m (Chowdhury and Chanda, 2012). Integration of charge movement in Fig. 7 E revealed the test voltage closest to the Q_OFF V_m to be −25 mV in control, and 45 mV in 1 µM GxTx. Thus, GxTx shifted the Kv2.1 V_m by 70 mV, indicating stabilization of a resting conformation by 8.6 k_BT, or 5,400-fold, in reasonable agreement with the Boltzmann-fit method. The magnitude of this stabilization suggests GxTx’s interactions with its environment must be substantially more favorable when voltage sensors are at rest than when they are activated.

Kv2.1’s gating occurs in multiple, temporally distinct steps, and we examined the specific impact of GxTx on rapid, early gating charge movement. In response to positive voltage steps, the majority of Kv2.1 I_{g ON} amplitude decays to near baseline well before the activation of Kv2.1 ionic currents, indicating that this fast gating current does not represent the pore opening transition (Fig. 1 A; Fig. 2, A and C; and Fig. 7, A and B; Scholle et al., 2004). Furthermore, Q_OFF after 100 ms is substantially larger than the charge moved during the first 10 ms after activation (Q_ON-fast; Fig. 7). The comparison of Q_ON-fast to Q_OFF presents an opportunity to evaluate how GxTx affects these early transitions, as compared with slower gating current and pore opening. At all voltages tested, Q_ON-fast was less than the total Q_OFF charge movement (Fig. 7 F). The amplitude of the Q_ON-fast component indicated that about half of all gating charge moves in a fast, early component. To further evaluate the Q_ON-fast–voltage relation, a single Boltzmann function was fit for both conditions. The Q_ON-fast V_1/2 shift was 86 mV, larger than the 73-mV shift of Q_OFF (Fig. 7, E and F). Additionally, GxTx shallowed the Q_ON-fast slope, indicating that GxTx causes the fast component of gating currents to be less responsive to voltage, and suggesting that GxTx inhibits some early voltage sensor movements more than others. Overall, the greater impact of GxTx on Q_ON-fast than Q_OFF indicates that GxTx has a greater impact on the early, fast transitions in the Kv2.1 activation pathway than on the transitions that occur later, which include channel opening.

GxTx slows ON gating current and accelerates OFF gating current

To directly measure how GxTx alters the kinetics of voltage sensors, we extracted the time constant (τ_ON) from the decay phase of I_g by fitting the capacitive current that occurs before 10 ms with a double exponential function (Eq. 6). The double exponential function was fit to the observed rising and decaying currents under control and GxTx conditions (Fig. 8, A and B). The rising phases were impacted by the kinetics cell of cell charging and excluded from analysis. To characterize the modulation GxTx imposes on voltage sensor movement, τ_ON was compared over a range of voltages. Under control conditions, τ_ON became faster as the voltage increased (Fig. 8 C), with kinetics similar to previous reports of Kv2.1 gating currents in CHO cells (Scholle et al., 2004). The voltage dependence of τ_ON under control conditions appeared consistent with a single conformational change moving 0.5 e₀ before the transition state (Fig. 8 E, line). Remarkably, when GxTx was applied, τ_ON did not accelerate with voltage increments (Fig. 8 D). The mean τ_ON with GxTx remained between 1 and 3 ms at all voltages (Fig. 8 E). Unlike the analysis of G–V, ionic activation, sigmoidicity, deactivation, and Q–V, this finding is inconsistent with GxTx simply stabilizing voltage sensors in a resting conformation. The τ_ON–V relation indicates that modulation of early voltage sensor movement is more complex, and that multiple conformational changes determine the kinetics of early gating-charge movement within this voltage range.

Figure 8.

GxTx reduces voltage dependence of gating-current activation and accelerates deactivation. (A) Control I_{g ON-fast} response to the following voltage steps: −20 mV, purple; 20 mV, blue; 60 mV, green; 100 mV, red. Holding potential was −100 mV. Lines are fits of Eq. 6, falling phase τ_ON: 20 mV = 1.91 ± 0.02 ms; 60 mV = 0.867 ± 0.007 ms; 100 mV = 0.42 ± 0.01 ms. (B) I_{g ON-fast} in 1 µM GxTx, same cell and fitting as in A. τ_ON: 20 mV = 1.55 ± 0.06 ms; 60 mV = 1.98 ± 0.06 ms; 100 mV = 2.81 ± 0.04 ms. (C) Voltage response of τ_on from individual control cells (n = 6). (D) Voltage response of τ_on from individual cells after application of 1 µM GxTx. Symbols mark same cells as in C (n = 5). (E) Geometric means of τ_ON from C and D. Control, black; 1 µM GxTx, red. Line is the fit of Eq. 8; control, τ_{ON 0mV} = 3.1 ± 0.1 ms, z = 0.50 ± 0.01 e₀. (F) I_{g OFF} control response to voltage steps down from +100 mV to the following potentials: −20 mV, purple; −60 mV, blue; −100 mV, green; −140 mV, red. Lines are fits of Eq. 4, τ_OFF: −100 mV = 14.6 ± 0.2 ms; −140 mV = 6.06 ± 0.6 ms. (G) I_{g OFF} with 1 µM GxTx, same cell, voltages, and fitting as F. τ_OFF: −20 mV = 4.0 ± 0.2 ms; −60 mV = 4.3 ± 0.1 ms; −100 mV = 2.93 ± 0.03 ms; −140 mV = 1.82 ± 0.01 ms. (H) Voltage dependence of τ_OFF from individual cells in vehicle (n = 4). (I) Voltage response of τ_OFF from individual cells after application of 1 µM GxTx. Symbols mark same cells as in H (n = 4). (J) Geometric means of τ_OFF from H and I. Lines are fits of Eq. 4: control, z = −0.50 ± 0.03 e₀, τ_{OFF 0mV} = 120 ± 20 ms; 1 µM GxTx, z = −0.28 ± 0.04 e₀, τ_{OFF 0mV} = 11 ± 2 ms.

Gating currents associated with deactivation were elicited by stepping to negative voltages after 100-ms steps to +100 mV. The deactivation time constant (τ_OFF) was measured by fitting a single exponential to the falling phase of gating currents (Fig. 8, F–J). Under control conditions, τ_OFF had a consistent negative slope (Fig. 8, H and J). Gating current τ_OFF values were three to five times slower than τ_deact from ionic currents. This is likely due to a lack of permeant ions, which have been shown to alter the dynamics of Kv2.1’s pore opening/closing step (Jara-Oseguera et al., 2011). Additionally, we replaced the internal solution K⁺ with NMDG⁺, which has been shown to slow I_{g OFF} from Shaker channels (Melishchuk and Armstrong, 2001). The similar voltage dependence of τ_OFF and τ_deact in vehicle (z = −0.5 e₀) is consistent with I_{g OFF} kinetics limited by channel closing. The τ_OFF–V relation in GxTx was more complex than control conditions, indicating that transitions with different kinetics and voltage dependencies impact voltage sensor kinetics over the −140 to +20 mV range. Over the −140 to −70 mV range, where control τ_OFF was measured, the voltage dependence of τ_OFF was less steep with GxTX, z = −0.3 e₀, than under control conditions, z = −0.5 e₀ (Fig. 8 J).

Overall, the gating currents indicate that GxTx modulates the movement of all gating charge. With or without GxTx, gating-charge movement occurs with kinetics distinct from pore opening and closing. The profound effects of GxTx on voltage sensor movement, combined with the minimal effects on single-channel opening and closing kinetics, suggest that GxTx-induced changes in voltage sensor movement underlie the modulation of macroscopic currents.

GxTx modulates fast voltage sensor movements, not the slow pore-opening step

GxTx modulation of Kv2.1 activation presents a conundrum. In single-channel recordings, GxTx does not appear to modulate the opening transition that corresponds to the rate-limiting opening step. However, the Kv2.1 conductance increase in response to a positive voltage step is rate-limited by a slow, concerted pore-opening transition (Scholle et al., 2004). Under all conditions, we found the sigmoidicity of activation, σ, to be less than 4, indicating that independent transitions of the channel’s four voltage sensors cannot be the slowest step in the activation path, even when voltage sensors are detained by GxTx (Fig. 3). In pursuit of parsimony, we sought to determine the simplest gating model that could reconcile the action of GxTx on distinct steps in the activation path and activation kinetics.

Modeling GxTx modulation requires a model that represents Kv2.1 activation kinetics. Although rat Kv2.1 (originally called drk1) was one of the first K⁺ channels to be heterologously expressed, its activation pathway has not been nearly as well characterized as its fly cousin Shaker. Kv2.1 activation kinetics possess transitions with at least two distinct voltage dependencies (Fig. 2). This is consistent with I_g measurements, which reveal a fast movement of each voltage sensor (Fig. 8) and imply a slower component from the conservation of charge (Fig. 7). As macroscopic activation kinetics have sigmoidicity values of σ > 1 (Fig. 3), multiple conformational changes must contribute significantly to activation kinetics before pore opening.

Overall, our Kv2.1 gating data are consistent with the proposal of Scholle et al. (2004), in which each voltage sensor independently transitions to a voltage-activated state followed by a concerted transition to the open state that has little or no voltage dependence. This model is conceptually similar to that of the Shaker V369I/I372L/S376T (ILT) variant (Ledwell and Aldrich, 1999), with the activation kinetics of the concerted opening step much less voltage-dependent for Kv2.1. However, it appears that a Kv2.1 gating model that is sufficient to reproduce all the data in Figs. 1, 2, 3, 4, 5, 6, 7, and 8 will be more complex than a Scheme III or ILT model. Another unique feature of Kv2.1 gating is the multiple voltage dependencies apparent in the deactivation kinetics (Fig. 4 D). The multiphasic voltage dependence suggests that the coupling between voltage sensor movement and pore conformational changes may be weaker than in Shaker. Due to these complexities, we deemed a full treatment of the complexities of Kv2.1 gating beyond the scope of this paper. We instead focus on a simpler modeling strategy, involving only Kv2.1 activation kinetics, to assess plausible mechanisms by which GxTx could slow current rise in response to a voltage step without directly altering the rate of the slowest transition, the final pore-opening step.

GxTx slowing of K⁺-conductance activation is consistent with modulation of voltage sensor equilibria

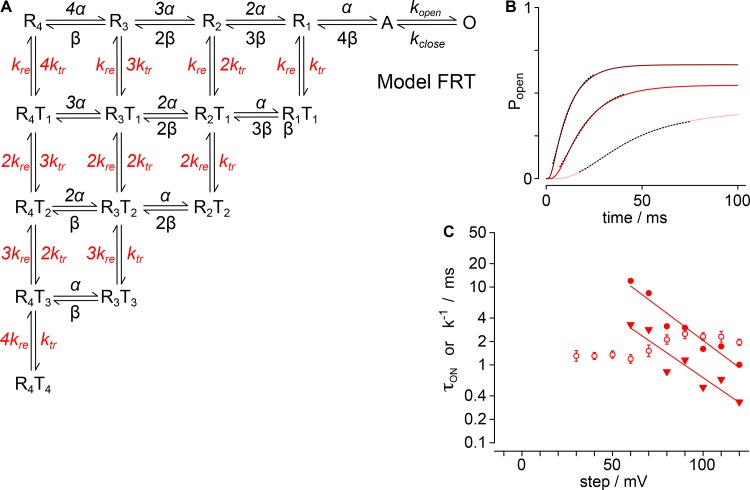
To develop a quantitative hypothesis for how GxTx modulates Kv2.1 activation gating, we constructed Markov chain models of a single independent voltage sensor conformational change in each of four subunits and a single cooperative step that opens the channel. Experimental data were used to constrain and evaluate each model. Our general approach was to generate gating models, whose parameters could be constrained to unique solutions with macroscopic K⁺-current kinetics, and then assess whether the models accurately predicted gating-current kinetics. As a test of each model’s predictive ability, we compared the predicted rates of voltage sensor transitions to gating-current kinetics. We present below the results of three gating model architectures (Models F, FR, and FRT), each of which recapitulates the kinetics of increasing K⁺-conductance in response to positive voltage steps under control conditions and with saturating GxTx. None of these relatively simple models predict all the complexities of Kv2.1 conformational changes, including gating-current kinetics with GxTx. However, the models do predict the kinetics of fast gating currents under control conditions. Importantly, Models FR and FRT reveal a mechanism that reconciles GxTx modulation of K⁺-conductance activation with the lack of a direct effect of GxTx on the rate-limiting pore opening step.

The simplest model that recapitulated the kinetics of activation of Kv2.1’s K⁺-conductance involves only forward activation transitions. This approach limits the voltage-dependent free parameters to two transitions: a single independent activation of each voltage sensor, formalized in Fig. 9 A as α, followed by k_open, the concerted pore-opening step. We refer to this as Model F as it contains forward rates only. The initial conditions of the model assume the channel begins with all four voltage sensors in a resting conformation and the pore is closed. At t = 0, the simulated channel is stepped to the indicated voltage for 100 ms, identical to our procedure to record macroscopic current activation. The rates of gating transitions in the models were adjusted to recapitulate the experimentally measured τ_act and σ values. The value of σ constrains the ratio α/k_open (Fig. 9 B). With this kinetic formalization, when the value of σ falls within the range 4 > σ > 1, σ determines a unique α/k_open ratio. All σ from Kv2.1 experiments fell within this range (Fig. 3 B), indicating that k_open is slower than α, and hence that concerted pore opening, not independent voltage sensor movement, is the rate-limiting step in Model F. The relations from Fig. 9, B and C, were used to assign values to α and k_open. The mean value of σ from experiments was used to determine the α/k_open ratio, by cubic spline interpolation between data points of the relation in Fig. 9 B. The mean value of τ_act from experiments was used as a scalar to assign explicit rates to α and k_open, by cubic spline interpolation between data points of the relation in Fig. 9 C. When simulations using these values were fit with Eq. 3, the resultant α and k_open from the fits to simulated data deviate by less than 1% from the mean of fits to experiments for both activation parameters (Fig. 9, D and E; and Fig. S1, A and B). The reciprocal of the rates α and k_open, α⁻¹ and k_open⁻¹, were compared with time constants τ_ON and τ_act, respectively (Fig. 9, F and G). k_open⁻¹ closely approximated τ_act, and remarkably, under control conditions, the value of α determined from ionic-current kinetics was predictive of fast gating-current kinetics. We fit α⁻¹ with Eq. 8 to assess voltage dependence, and the associated charge of α was determined to be 0.61 ± 0.03 e₀, slightly more than the empirically measured voltage dependence of τ_ON, 0.50 ± 0.01 e₀. The reciprocal rate at neutral voltage, α_0mV⁻¹, was within the experimental error of τ_{ON 0mV}. Notably, at the limit of our voltage range, when the step potential exceeds +100 mV, the model prediction of control α⁻¹ deviates from τ_ON. However, at these highly positive voltages, the macroscopic parameter σ asymptotically approaches its limiting value of 1, and consequently, the α/k_open values derived from σ have high associated errors and lose predictive value. We compared α from control conditions to the rate predicted when GxTx is bound and found the rate had an identical associated charge, but GxTx slowed α_0mV ninefold from 3.2 ± 1.1 to 29.2 ± 1.1 ms (Fig. 9 G). The predicted shift of α caused by GxTx only overlaps with the experimentally measured τ_ON with GxTx at voltages >90 mV and has markedly different voltage dependence, indicating that Model F does not predict the complexities of fast gating-current kinetics in GxTX at voltages <90 mV.

In the fitted Model F, k_open in control conditions is consistent with the ∼6 ms opening time constant seen in single-channel gating kinetics at +75 mV. However, the voltage dependence of k_open is clearly multiphasic with voltage, indicating that the k_open kinetics cannot be due to a single voltage-dependent conformational change. In fact, k_open appears nearly voltage-independent above +70 mV. Furthermore, in Model F, GxTx forces k_open to slow down several-fold, while the single-channel kinetics reveal that the ∼6 ms opening time constant persists with GxTx. Thus, in the Model F formulation with GxTx, k_open rates are compatible with neither the single-channel kinetics nor the multiphasic voltage dependence of k_open. This suggests that a gating model with a different architecture is needed.

One mechanism that can produce a graded change in pore-opening kinetics without altering the opening step itself is a model where pore opening kinetics are impacted by the probability that voltage sensors are in their activated state. This mechanism underlies the voltage-dependent kinetics of activation of large-conductance Ca²⁺-activated K⁺ channels (Horrigan and Aldrich, 1999). Such coupling in its most basic form requires forward and reverse transitions of voltage sensors, such that a distribution of resting and active voltage sensors can be rapidly established after a voltage step, followed by a slower pore-opening step. This model with forward and reverse rates is referred to as Model FR (Fig. 11 A). In Model FR, when the voltage sensor movements are much faster than pore opening and closing such that (α + β) >> (k_open + k_close), the R to A transition can be represented by an equilibrium K_eq = α/β as in Scheme IV in Fig. 10 A. If k_open and k_close possess no inherent voltage dependence, the system will relax to equilibrium at a rate described by Eq. 9 (see Methods). The fit of Eq. 9 to the τ_act–V relation was well constrained in the control condition (Fig. 10 B). This indicates that multiphasic voltage dependence of τ_act is characteristic of Scheme IV. The charge associated with the α/β equilibrium was 0.6 e₀ per subunit, too low to account for the estimate of 2.6 e₀ per subunit from the G–V relation (Fig. 1 C). This indicates that a more complicated model will be required to recapitulate both the activation kinetics and steady-state conductance levels. The value of (k_open + k_close)⁻¹ under control conditions was 5.1 ms (Fig. 10 B). With GxTx, (k_open + k_close)⁻¹ could not be adequately estimated by free fitting, and was constrained to the value determined without GxTx (black rates indicated in Fig. 10 B). With this constraint, fitting indicated a similarly low charge valence of 0.6 e₀ per subunit. The α/β equilibrium was fourfold more biased toward the resting state by GxTX. In Scheme IV, when the voltage sensors are fully activated, the ratio k_open/k_close will be equal to P_open/(1 − P_open). At +75 mV, the control Q–V relations indicate that the voltage sensors are fully active (Fig. 7, D and E). In the context of Scheme IV, the O and A states are occupied with probabilities of approximately P_open and (1 − P_open), respectively. As P_open after first opening is ∼0.8 (Fig. 6, E and G), the relations k_open = 4k_close and (k_open + k_close)⁻¹ = 5.1 ms were used to assign rates k_open⁻¹ = 6.4 ms and k_close⁻¹ = 26 ms. The k_open and k_close rates were constrained to these values in Model FR. The remaining free parameters in Model FR, α and β, (Fig. 11 A), were constrained by iteratively simulating ionic currents, fitting with Eq. 3 (Fig. 11, B and C), and then manually adjusting parameters until Model FR converged on an apparently unique solution that could reproduce τ_act and σ from fits to experiments (Fig. S1, C and D). The reciprocals of the resulting optimized rates are plotted with experimental τ_ON in Fig. 11, D and E, and the recapitulated activation parameters are shown in Fig. S1, C and D. We assessed the voltage dependence of α and β by fitting with Eq. 8 (lines, Fig. 11, D and E). Model FR suggests the rate-limiting voltage sensor activation rate α is approximately equal to 1/τ_ON of controls, similar to findings from Model F (Fig. 9 G). β_0mV was only twofold slower than α_0mV, and the independent voltage sensor transition had a net associated gating charge (z_α − z_β) of 0.48 ± 0.05 e₀, strikingly close to 0.50 ± 0.01 e₀ from τ_on. This fitting resulted in β being nearly voltage-independent, having a valence of 0.17 ± 0.04 e₀ and positive polarity. This indicates that Model FR, which is tightly constrained by the activation kinetics, is insufficient to recapitulate the G–V relation, as Boltzmann fitting of the G–V revealed that a minimum of 11 elementary charges are involved in the gating of each channel (from fit of Eq. 2; Fig. 1 C, left panel), and Model FR includes only 1.9 elementary charges (4z_α − 4z_β, Fig. 11 E). Similarly, the voltage dependence of β (z_β = 0.17 e₀) does not explain the voltage-dependent kinetics of deactivation (z = −0.60 e₀ from I_K, Fig. 4 D; −0.50 e₀ from I_g, Fig. 8 K). We interpreted this to indicate that β does not represent all the voltage sensor deactivation steps. This is not surprising, given that holistic models of Kv-channel gating require charge movements of each voltage sensor to be separated into multiple distinct steps (Zagotta et al., 1994a; Schoppa and Sigworth, 1998b; Ledwell and Aldrich, 1999).

Figure 11.

Forward–reverse activation model (Model FR). (A) Gating scheme for Model FR. Four identical resting voltage sensors independently activate with forward rate α and reverse rate β. Pore opening is modeled as a voltage-independent concerted event with rate k_open and reverse rate k_close. Rates susceptible to GxTx are red. (B) Simulated P_open from Model FR under control conditions. Light gray, 60 mV; dark gray, 90 mV; black, 120 mV. Dotted lines show fits of Eq. 3. τ_60mV = 6.68 ± 0.01 ms, σ_60mV = 1.602 ± 0.004; τ_90mV = 6.413 ± 0.008 ms, σ_90mV = 1.325 ± 0.002; τ_120mV = 5.729 ± 0.004 ms, σ_120mV = 1.141 ± 0.001. (C) Simulated P_open from Model FR with GxTx. Light pink, 60 mV; red, 90 mV; dark red, 120 mV. Dotted lines show fits of Eq. 3. τ_60mV = 18.147 ± 0.008 ms, σ_60mV =3.248 ± 0.003; τ_90mV = 11.23 ± 0.01 ms, σ_90mV = 2.508 ± 0.005; τ_120mV = 9.28 ± 0.01 ms, σ_120mV = 1.941 ± 0.004. (D) Comparison of the reciprocals of rates α and β to τ_ON from Kv2.1 control gating currents. Hollow circles, mean Kv2.1 τ_ON from Fig. 8 E; filled circles, α⁻¹ from model; filled triangles, β⁻¹ from model. Solid lines, fits of Eq. 8: z_α = 0.65 ± 0.05 e₀, α⁻¹_0mV = 4.2 ± 0.3 ms; z_β = 0.17 ± 0.04 e₀, β⁻¹_0mV = 9 ± 1 ms. (E) Comparison of the reciprocals of rates α and β to τ_ON from Kv2.1 gating currents in 1 µM GxTx. Hollow circles, mean Kv2.1 τ_ON with 1 µM GxTx from Fig. 8 E; filled circles, α⁻¹ from model; filled triangles, β⁻¹ from model. Solid lines, fits of Eq. 8: z_α = 0.73 ± 0.03 e₀, α_0mV⁻¹ = 60 ± 7 ms; z_β = 0.50 ± 0.04 e₀, β_0mV⁻¹ = 97 ± 15 ms.

Figure 10.

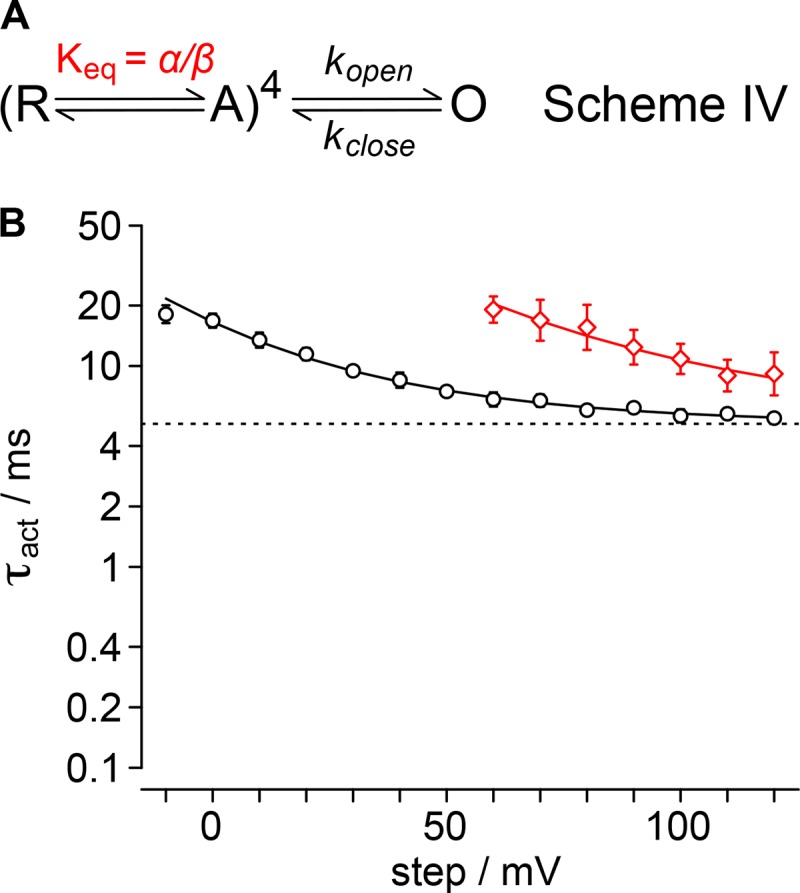
Voltage sensor equilibrium gating scheme. (A) Gating scheme in which τ_act is determined by the probability that voltages sensors are in their activated state. Activation of four identical resting voltage sensors is determined by the α/β equilibrium. Pore opening is a voltage-independent concerted event with rate k_open and reverse rate k_close. Equilibrium susceptible to GxTx is red. (B) Fit of Eq. 9 to τ_act from Fig. 2 C. Dashed line, (k_open + k_close)⁻¹ = 5.1 ± 0.1 ms; black solid line, vehicle; ${\beta }_{0mV}/{\alpha }_{0mV}$ = 0.33 ± 0.01, z = 0.61 ± 0.06 e₀; red solid line, 1 µM GxTx, ${\beta }_{0mV}/{\alpha }_{0mV}$ = 1.2 ± 0.2, z = 0.45 ± 0.04 e₀. Hollow black circles or diamonds, τ_act values.

Model FR did not predict voltage sensor kinetics in GxTx. The α⁻¹ values in GxTx overlapped with measured τ_ON only at voltages >90 mV. Similar to Model F, Model FR suggests that with GxTx at voltages <90 mV, gating charge movements are expected to be slower than the measured τ_ON. This suggests that recapitulating the voltage sensor dynamics in GxTx requires a model with additional activation transitions. A more complex model architecture is necessary to explain all the phenomenology of Kv2.1 gating, likely involving multiple independent voltage sensor movements and multiple pathways for closing.

Despite the above limitations, Model FR did reveal a general mechanism by which GxTx could slow macroscopic activation without directly altering the final rate-limiting opening transition: by reducing the probability of voltage sensors being activated, the final opening transition has less frequent opportunities to occur.

A voltage sensor trapping model can also account for the GxTx slowing of K⁺-conductance activation

While many complex models could potentially recapitulate all the features of Kv2.1 gating in GxTx, we chose to refrain from modeling that could not be well constrained by our dataset. We selected a final model architecture to test, with the same number of free parameters as Model FR. We speculated that the small component of gating charge that moves more quickly than Model FR predicts below 90 mV could be due to a transition that becomes rate limiting only when GxTx is bound to a voltage sensor. In this architecture, voltage sensors would be transiently trapped in a resting state that they need to be released from before continuing along the activation pathway. As this model requires forward and reverse rates and a trapping step, we refer to it as Model FRT (Fig. 12 A). This is conceptually similar to the voltage sensor trapping mechanism proposed for β scorpion toxins acting on sodium-channel voltage sensors (Cestèle et al., 1998; Campos et al., 2008). The mechanism of Model FRT is identical to Model FR, except that it introduces an additional conformational change in each independent voltage sensor that results in additional sigmoidicity. The trapping model uses the rates of α and β from Model FR under control conditions and allows GxTx to modulate gating by trapping the voltage sensor in a resting state at rate k_tr and releasing voltage sensors at rate k_re. Thus, optimization of Model FRT allows manipulation of only two rates, k_tr and k_re. Similar to the procedure used for Model FR, activation kinetics were simulated and fit with Eq. 8 in iterative rounds of simulation, parameter adjustment, and fitting until Model FRT converged on an apparently unique solution that could reproduce τ_act and σ from fits to experiments (Fig. S1, E and F). The rates of k_tr and k_re were again in the same range as τ_ON in GxTx, but both had positive voltage dependence (Fig. 12 C), indicating that they could not be responsible for the negative voltage dependence of gating-current kinetics below 90 mV. While the τ_ON–V relation indicates that early voltage sensor movement is split into multiple components, simply allowing GxTx to trap a component of early gating charge was insufficient to recapitulate the gating currents. Overall, allowing GxTx to create a new energetic barrier early in the voltage sensor activation pathway, Model FRT was equally effective at recapitulating K⁺-conductance activation kinetics as allowing GxTx to modulate the voltage sensor activation step that is rate-limiting under control conditions, Model FR.

Figure 12.

Forward-reverse-trapping activation model (Model FRT). (A) Gating scheme for GxTx-bound Kv2.1 trapping activation model. Four identical resting voltage sensors are independently trapped with trap rate k_tr and released with release rate k_re. Released voltage sensors activate with rate α and reverse rate β. Pore opening has forward rate k_open and reverse rate k_close. Rates susceptible to GxTx are red. (B) Simulated P_open from Model FRT with GxTx. Light pink, 60 mV; red, 90 mV; dark red, 120 mV. Dotted lines show fits of Eq. 3. τ_60mV = 21.296 ± 0.005 ms, σ_60mV = 3.851 ± 0.002; τ_90mV= 12.55 ± 0.01 ms, σ_90mV = 2.458 ± 0.005; τ_120mV = 8.07 ± 0.01 ms, σ_120mV = 1.941 ± 0.004. (C) Comparison of the reciprocals of rates k_re and k_tr to τ_ON from gating currents. Hollow circles, mean 1 µM GxTx Kv2.1 τ_ON from Fig. 8 E; filled circles, k_re⁻¹ from model; hollow triangles, k_tr⁻¹ from model. Solid lines show fits of Eq. 8, z_tr = 0.93 ± 0.17 e₀, k_{tr 0mV}⁻¹ = 26 ± 23 ms; z_rel = 1.0 ± 0.1 e₀, k_{re 0mV}⁻¹ = 115 ± 65 ms.

Discussion

GxTx stabilizes an early resting conformation of Kv2.1 voltage sensors, and does not modulate pore opening directly

This study revealed that all of Kv2.1’s conformational changes that occur in response to positive voltage steps are delayed by GxTx, and that the microscopic rates of conformational changes underlying pore opening are insensitive to GxTx. We propose a hypothesis for how GxTx alters gating: GxTx inhibits Kv2.1 channels by stabilizing a resting conformation with gating charges in their most intracellular configuration, but GxTx has little, if any, effect on pore opening itself.

Comparison of effects of GxTx on channel activation kinetics in both Models FR and FRT suggests GxTx slows voltage-sensitive conformational changes traversed during activation by about an order of magnitude (Table 1). However, this slowed component of gating charge was only observed in gating currents in response to activation to potentials of ∼90 mV and more positive. Our modeling based on ionic currents did not predict the kinetics of the fast component of Kv2.1 gating charge in GxTx that emerges at activation to potentials less than 90 mV. This small component of charge movement does not appear to limit the kinetics of channel activation and is not required to reproduce channel-opening kinetics. Overall, our modeling indicates that GxTx acts in a relatively simple manner: it selectively stabilizes voltage sensors in a resting state, and once sufficient voltage is provided to activate voltage sensors, the channel opens normally. The effect of GxTx on equilibrium open probability is due to the toxin biasing voltage sensor activation toward the resting state by 5,400-fold or 8.6 k_bT (by median-voltage analysis). Summing over four voltage sensors, the closed states of the channel are stabilized by 34 k_bT, or 20 kcal/mol. If Kv2.1 can only open with four voltage sensors activated, as indicated by limiting-slope analysis (Islas and Sigworth, 1999), four GxTx per channel could lower open probability by up to 5,400⁴- or 10¹⁴-fold. The outcome of this extremely efficacious allosteric inhibition is that the tarantula toxin pushes back against the sizeable energy the voltage sensors extract from the membrane electric field, preventing the channel from reaching high open probability in a physiological voltage range. We speculate that this degree of inhibition was sufficient to serve the venomous purpose of its tarantula.

Table 1. Rate constants for Models FR and FRT with and without GxTx.

Model	Condition	Rate constant	k0mV/s−1	z/e0
FR	Control	α	240	0.65
		β	110	0.17
	GxTx	α	17	0.73
		β	10	0.50
FRT	GxTx	ktr	38	0.93
		kre	8.7	1.0
FR, FRT	Control, GxTx	kopen	160	0
		kclose	38	0

Best fit of voltage-dependent rate constants to the simulations presented in Figs. 11 and 12. Values of α, β, k_trap, and k_release are from fits of Eq. 8 shown in Fig. 11, D and E; and Fig. 12 C. Values of k_open, and k_close were chosen as described in Results. The k_0mV column gives the rate at 0 mV for each rate constant, and the z column indicates the equivalent electronic charge assigned to the rate constant.

The GxTx inhibition of voltage sensor movement, but not the pore-opening step, suggests that Kv2.1 pore opening does not involve voltage sensor movement. The sufficiency of simulations with voltage-insensitive pore opening (Models FR and FRT) to reproduce the voltage dependence of activation kinetics (Figs. 11 and 12), and the minimal effects of GxTx on pore-opening and -closing time constants (Fig. 6, F and H) are consistent with Kv2.1 pore opening being rate limited by a voltage-independent concerted transition that GxTx does not impact directly. Moreover, a pore-opening step that receives all its voltage dependence from voltage sensor conformational changes that precede it can explain how GxTx could shift the kinetics of both τ_act and τ_deact, which require pore opening, by the same degree as voltage sensor movement, ~+80mV (Fig. 2 C, 4 D, and 7 E), while GxTx has little effect on the microscopic kinetics of pore opening and closing (Fig. 6, E–H). This suggests that voltage sensor movement may not be involved in pore-opening conformational changes, as it is difficult to imagine how a 36–amino acid peptide bound to the voltage sensor and partially embedded in membrane lipids (Milescu et al., 2009) could not impact conformational changes involving voltage sensor movement. In contrast, pore opening of Kv1 channels appears to involve voltage sensor movement. In the Shaker Kv1 channel, the concerted pore-opening step revealed by the ILT mutations is highly voltage-dependent (1.8 e₀) and involves a conformational change of the voltage sensor (Smith-Maxwell et al., 1998; Ledwell and Aldrich, 1999; Pathak et al., 2005). Consistent with a concerted voltage sensor/pore movement, when the HaTx binding site is grafted onto the Shaker-channel voltage sensor, the toxin alters pore opening (Milescu et al., 2013). These observations suggest that the pore-opening conformational change in the Shaker Kv1 channel is tied to voltage sensor movement, while in Kv2.1 it is not. Such differences in voltage dependence have been suggested before for Kv2 versus Kv1 channels (Scholle et al., 2004). In a carefully considered comparison of the dynamics of Kv2.1 channels, a compound was found to decouple pore opening from voltage sensor movement, such that the activation kinetics of Kv2.1 retained little, if any, voltage dependence; when the same compound was applied to Shaker channels, its activation kinetics retained voltage dependence (Jara-Oseguera et al., 2011). Further evidence for a voltage-independent step in Kv2.1’s activation path was seen here in the shallowing of voltage dependence of τ_act above 50 mV under control conditions (Fig. 2 C), and in the shallowing of τ_deact above −50 mV (Fig. 4 D). Thus, this study of the GxTx mechanism has unexpectedly revealed incomplete coupling between Kv2.1 voltage sensor movement and pore opening.

Limitations

While the hypothesis that pore opening in Kv2.1 is voltage independent is consistent with our analyses, more stringent testing and modeling are required to thoroughly test this hypothesis. The gating models proposed here are incomplete, as they are constrained only to reproduce ionic current activation kinetics, not deactivation, nor equilibrium gating. Importantly, the values of the voltage-sensitive deactivation rate constant β (Table 1) are unlikely to represent the kinetics of any single conformational change, but rather represent the impacts of multiple voltage-sensitive conformational changes. The positive voltage dependence of β is incompatible with several features of Kv2.1 gating, including the steepness of the G–V relation (Fig. 1 C), the negative voltage dependence below −60 mV of ionic current τ_deact (Fig. 4 D), and the negative voltage dependence of gating current τ_OFF (Fig. 8 J). Thus, a gating model with a different architecture is needed to reconcile channel activation kinetics with all the features of channel gating. The complexity of Kv2.1 gating dynamics led us to refrain from proposing a comprehensive gating model. Our observations suggest that Kv2.1’s activation path is distinct from the Shaker Kv1 channel and that the thermodynamics of coupling between Kv2.1’s voltage sensors and pore need to be understood before the gating with GxTx can be fully explained. The multiphasic voltage dependence of τ_deact under control conditions (Fig. 4 D) and the kinetics of gating current τ_OFF in GxTx (Fig. 8 J) suggest that Kv2.1 has multiple deactivation pathways. This could be due to Kv2.1 having weaker coupling than Shaker between channel voltage sensor movement and activation gating, as is seen in large-conductance Ca²⁺-activated K⁺ channels (Horrigan and Aldrich, 1999). Determining whether such coupling occurs will require further investigation.

We have suggested that the multiphasic voltage dependence of gating-charge kinetics with GxTx (Fig. 8 E) is due to GxTx fragmenting voltage sensor movement into multiple steps (Model FRT). However, other mechanisms could produce the capacitive transients that we interpret as early gating charge movement in GxTx. Possibilities include charge movement distinct from Kv2.1 voltage sensor movement, charge movement from voltage sensors that unexpectedly have no GxTx bound, or a movement of GxTx charges with the membrane. While we find these explanations to be less likely, we cannot currently eliminate them. Recapitulating these alternatives would require modeling that cannot be stringently constrained by our current data.

GxTx and HaTx modulate different voltage sensor transitions

The thermodynamic details of Kv2 channel modulation by a spider toxin are perhaps best understood for HaTx, while less was known about GxTx. The HaTx mechanism shares similarities yet is distinct from the GxTx mechanism. GxTx and HaTx share an overlapping S3b binding region on Kv2.1, despite the toxins having only 28% sequence identity (Swartz and MacKinnon, 1997b; Li-Smerin and Swartz, 2000; Milescu et al., 2009, 2013). HaTx markedly inhibits Kv2.1 ionic current when it binds to only one of four channel subunits; full efficacy is achieved when HaTx binds to all four subunits, and each subunit appears to bind HaTx independently (Swartz and MacKinnon, 1997a; Lee et al., 2003; Phillips et al., 2005). GxTx action is consistent with this mechanism. Both toxins bind to resting voltage sensors with higher-affinity; HaTx and GxTx both dissociate from Kv2.1 channels when stimulated by long positive voltage steps (Phillips et al., 2005; Tilley et al., 2014). The toxins dissociate from channels with time constants on the order of tens to hundreds of seconds, far slower than the milliseconds required for Kv2.1 activation with toxin bound. While the two toxins share these many similarities, their mechanisms are not identical. When the HaTx/GxTx binding determinants from the S3b of Kv2.1 are grafted onto the Shaker Kv channel, HaTx activates Shaker K⁺ currents, while GxTx inhibits them (Milescu et al., 2013). GxTx inhibits all Kv2.1 gating charge movement. In contrast, HaTx modulates only a fraction of Kv2.1’s gating current, indicating that HaTx impacts only the later voltage sensor movements (Lee et al., 2003). Together, the differences between GxTx and HaTx effects on gating currents and Shaker channels suggest that HaTx acts by stabilizing voltage sensors in conformations intermediate between resting and fully active, while GxTx stabilizes voltage sensors in a fully resting conformation.

Implications

GxTx is an effective inhibitor for physiological studies of Kv2 channels

In the physiological voltage range, approximately −100 to +40 mV, Kv2.1 voltage sensors do not voltage-activate when the toxin is bound. Thus any cellular functions, including K⁺ current conduction, that depend on Kv2.1 voltage activation are expected to be blocked by GxTx. A growing number of physiological studies have used GxTx as a Kv2-selective inhibitor (Li et al., 2013; Liu and Bean, 2014; Kimm et al., 2015; Pathak et al., 2016; Hönigsperger et al., 2017; Palacio et al., 2017). GxTx inhibits heterologously expressed versions of the two mammalian Kv2 channels, Kv2.1 and Kv2.2, with similar potency; GxTx inhibits Kv4.3, although less potently than Kv2 channels; GxTx has not been found to modulate any other class of channel (Herrington et al., 2006). Currently GxTx appears to be the most selective inhibitor known for Kv2 channels. Small molecule inhibitors with very good selectivity for Kv2 channels have also been found, but the mechanism of their state-dependent inhibition is unknown, and selectivity versus Kv4 channels was not determined (Herrington et al., 2011). A popular inhibitor of Kv2 channels, stromatoxin or ScTx, is a less efficacious partial inverse agonist than GxTx and also inhibits Kv4 channels more potently than Kv2 channels (Escoubas et al., 2002). Application of GxTx to dissociated brain neurons from mice inhibits a delayed rectifier Kv2-like K⁺ current. At a concentration of 100 nM, GxTx inhibited Kv2-like currents in rat superior cervical ganglion neurons and mouse hippocampal CA1 pyramidal neurons with only a slight reduction of a Kv4-like current (Liu and Bean, 2014). Our results suggest that 100 nM GxTx is sufficient to inhibit >97% of Kv2.1 current during short (100-ms) voltage steps to ≤40 mV. It is worth noting that the aforementioned studies use commercially available wild-type GxTx, whereas most figures in this paper use a variant where methionine residue 35 is replaced by the isostere norleucine. We have observed air oxidation of the methionine 35 coincident with a loss of potency of wild-type GxTx, and would urge users of wild-type GxTx to take precautions to minimize methionine oxidation.

GxTx application can reveal Kv2 gating currents

The gating current of Kv2.1 channels can be measured by subtracting the gating current that remains after GxTx application. Measurements of gating current from dihydropyridine-sensitive L-type voltage-gated Ca²⁺ channels have been instrumental in dissecting the function of these channels in muscle cells (e.g., Rios and Brum, 1987). Subtractive gating current measurements of this type would be expected to reveal the component of cellular gating currents that are due to endogenous Kv2 channels. While GxTx inhibits the movement of all Kv2.1 gating current, gating currents with altered kinetics do emerge from GxTx-bound channels with sufficient voltage stimulus. As the gating of Kv2 channels can be modulated by many factors, including the subunit types incorporated into functional channels, and post-translational modification, interpretation of gating currents should consider that endogenous Kv2 channels may not respond as Kv2.1 does when expressed in cells derived from a hamster’s ovary.

The Kv2.1 conformation with a high affinity for GxTx has all gating charge on the cytoplasmic side of the membrane

Median-voltage analysis of the GxTx-induced shift of gating currents indicated that GxTx stabilizes a resting conformation of the voltage sensor by 5,400-fold. Thus, the Kv2.1 complex with GxTx is 5,400-fold more stable when a voltage sensor is in this resting conformation. Therefore, free GxTx would be expected to have a 5,400-fold higher affinity for a resting conformation with gating charges all the way toward the cytoplasm than activated conformations. The mechanistic findings here imply that when cells are incubated with GxTx, GxTx binding is heavily biased toward channels with voltage sensors in their most intracellular resting conformation. This is consistent with findings that fluorophore-labeled GxTx derivatives have a higher affinity at negative voltages where the voltage sensor conformation is biased toward resting (Tilley et al., 2014). Our finding that GxTx acts by biasing all gating charge toward a resting state, and that other conformational changes are not directly affected by GxTx, indicates that the shift between high-affinity binding and low-affinity binding occurs when voltage sensors move their first gating charge outward. This suggests a simple model with which to interpret GxTx labeling: GxTx marks channels that have voltage sensors in their most intracellular resting conformation, and dynamic changes of GxTx labeling report changes in the occurrence of this conformation.

Conclusions

GxTx binds to and stabilizes the most intracellular resting conformation of the Kv2.1 channel’s voltage sensors, preventing voltage sensor movement and hence channel opening. The strong preference of GxTx for this resting conformation indicates that GxTx is a useful tool not just for inhibiting ionic currents, but also for trapping Kv2.1 gating charges in their most intracellular conformation, or labeling where the channel occurs in a resting conformation. GxTx stabilizes voltage sensors in this early resting conformation, and inhibits K⁺ currents by limiting opportunities for the channel pore to open, while Kv2.1’s unitary conductance and the microscopic kinetics of the pore-opening conformational change are little altered by GxTx. The impact of GxTx on channel gating suggests that Kv2.1’s pore opening step does not involve movement of its voltage sensors.