The Effect of Cortical Elasticity and Active Tension on Cell Adhesion Mechanics

Abstract

We consider a cell as an elastic, contractile shell surrounding a liquid incompressible cytoplasm and with nonspecific adhesion. We perform numerical simulations of this model to study the mechanics of cell-cell separation. By variation of parameters, we are able to recover well-known limits of the Johnson-Kendall-Roberts theory, the Derjaguin-Muller-Toporov model, adhesive vesicles with surface tension (Brochard-Wyart and de Gennes derivation), and thin elastic shells. We further locate biological cells on this parameter space by comparison to existing experiments on S180 cells. Using this model, we show that mechanical parameters can be obtained that are consistent with both dual pipette aspiration and micropipette aspiration, a problem not successfully tackled so far. We estimate a cortex elastic modulus of E_c ≈ 15 kPa, an effective cortex thickness of t_c ≈ 0.3 μm, and an active tension of γ ≈ 0.4 nN/μm. With these parameters, a Johnson-Kendall-Roberts-like scaling of the separation force is recovered. Finally, the change of contact radius with applied force in a pull-off experiment was investigated. For small forces, a scaling similar to both the Brochard-Wyart and de Gennes derivation and the Derjaguin-Muller-Toporov model is found.

Introduction

The mechanical response of a cell to deformation arises from the properties of the underlying cytoskeleton. The intricate dynamic structure and active nature of the actomyosin cortex produce complex time-dependent behavior, including a power-law-creep response (1) and nonlinear soft glassy rheology (2). This complicates mechanical measurements on cells because the parameterization of experimental results is often not invariant with respect to the conditions of the experiment. Still, simplified mechanical models may be adopted in the relevant spatiotemporal limits (3). For example, at long timescales, cells behave as Newtonian liquid drops under surface tension—“cortical shell-liquid core” model (4, 5)—whereas at short timescales and small deformations, the cell is elastic—“solid elastic sphere” model—with a characteristic Hertzian force upon indentation (6).

When applying these limits to micropipette aspiration (MA) experiments, the cell’s resistance to deformation is expressed either as a cortex tension or as a solid cell Young’s modulus E_cell. Extending from this, Chu et al. used dual pipette aspiration (DPA) experiments in controlled adhesion conditions to demonstrate how cell-cell pull-off forces compare to various limiting continuum theories, thereby indirectly probing the mechanical properties of suspension cells (7). For the cortical shell-liquid core model, the pull-off force required to separate two droplets with net adhesion energy w was derived by Brochard-Wyart and de Gennes (BWdG) as $F_s=\pi \hat{R}w$ (8), with $\hat{R}=R_1{R}_2/\left(R_1+R_2\right)$. For solid elastic spheres, Johnson-Kendall-Roberts (JKR) theory predicts the pull-off force in the limit of short range of adhesive interaction and soft spheres as $F_s=3/2\pi \hat{R}w$ (9). In the opposite limit of stiff spheres with a large adhesive range, the model of Derjaguin-Muller-Toporov (DMT) predicts a pull-off force $F_s=2\pi \hat{R}w$ (10, 11). For S180 cells, it was found that the pull-off force scales as $F_s\sim \frac{3}{2}\pi \hat{R}w$, consistent with the JKR model for adhesion between solid elastic asperities but not with the BWdG expression for adhesive droplets with surface tension (7). This suggests that a solid elastic model is an appropriate description of the cell in these conditions (suspension, short timescale). Yet, there is an apparent mismatch between the elastic modulus estimated from such a pull-off experiment using JKR theory and the Young’s modulus obtained from a simple single-cell aspiration experiment (12). For example, on S180 murine sarcoma cells, a Young’s modulus (only the composed modulus ${\hat{E}}_{\text{cell}}=E_{\text{cell}}/\left[2\left(1-{\nu }_{\text{cell}}^2\right)\right]$ can be estimated this way) E_cell > 1 kPa is obtained from applying JKR theory to a DPA experiment (7), whereas single-cell aspiration tests (MA) on the same cell line yield a much lower modulus of E_cell ≈ 100 Pa (12), even though both experiments are performed in similar conditions and at comparable timescales (seconds). (A value of E_cell ≈ 100 Pa is obtained when applying the analysis for elastic spheres (4) to the critical pressure that corresponds to the net tension of 0.9 nN/μm that was reported in (12). Note that only the order-of-magnitude of E_cell suffices for the argument provided.)

One obvious explanation is that the mechanical rigidity of a suspension cell is mostly concentrated in an elastic cortical shell rather than uniformly distributed throughout the cell. Thin elastic shell models have been frequently applied to cells, e.g., for analyzing the shape of blebbing (13), bulging (5), or dividing cells (14). For adhering curved elastic shells, an expression for the pull-off force as a function of Young’s modulus E_c, Poisson number v_c, and thickness t_c has been derived in (15):

$${\left(\frac{F_s}{P\ast }\right)}^3=\frac{w^4{\hat{R}}^4\left(1-{\nu }_c^2\right)}{E_c{t}_c^2}.$$ (1)

P^∗ is a dimensionless scaling factor that depends on the load conditions—for fixed load, P^∗ ≈ 13.2 (15). When applying this equation to cells, E_c refers to the Young’s modulus of the thin actin cortex that surrounds the cytosolic interior. A typical cell’s actomyosin cortex has a thickness of roughly 200 nm and a Young’s modulus on the order of 10 kPa (16). Within this range of properties and for a characteristic adhesion energy of w ≈ 1 nN/μm and a cell size of $\hat{R}\approx$ 5 μm, it can be verified using Eq. 1 that for a shell, the pull-off force $F_s\gg 2\pi \hat{R}w$, i.e., much greater than what was measured in (7). In other words, although the cell’s cytoskeletal structure resembles a thin shell, it behaves more like a solid elastic asperity during pull-off.

This discrepancy could be attributed to the highly nonlinear and anisotropic behavior of the cortical actomyosin and microtubule network (17, 18). As such, its “effective” mechanical thickness would be significantly higher than the thickness measured using optical methods (16, 19, 20). This explanation is in line with observations of cortical rheology at long timescales, at which a considerably elevated effective thickness is required to recover the rate of cell spreading using a simple Newtonian liquid model (21).

A second possible explanation lies in the active nature of the cortex: contractility induced by myosin II motors generates an active tension (γ), which counterbalances adhesion and thereby assists in the separation of two cells. For mature intercellular junctions, it has been shown that even the local regulation of contractility at the cell-cell interface rather than adhesion itself controls the extent of contact expansion. Then, the role of adhesion molecules is restricted to the mechanical anchoring of the cortex (5). Although this local regulation of cortical tension is unlikely to affect adhesive behavior in controlled adhesion experiments at very short timescales (seconds), the total (uniform) cortical tension is likely to play a major role in a pull-off experiment. It should be noted here that this active tension is not the same as the surface tension often reported from mechanical tests (4, 12, 16), in which a liquid model is used that assumes that no elastic stresses are present. This assumption can be valid at long timescales, when remodeling of the cortex effectively relaxes all elastic stresses. In the absence of this relaxation, these two quantities would only coincide in the limit of a soft/thin cortex (see further).

Here, we propose a numerical model that tries to reconcile the aforementioned observations, describing adhesive contact between cells as a function of the elastic properties of the cell’s acto-myosin cortex and its active contractility. Cells are represented as spherical elastic shells that maintain internal volume and for which adhesive/repulsive contact is described using a Dugdale approach (22). Active contractility is explicitly introduced through a contractile tension and acts similarly to an additional surface tension (see Fig. 1). Using this model, we show how different scaling laws for a pull-off experiment can be recovered by changing the stiffness E_c, effective thickness t_c, and the active tension γ of the cortex. Next, in a case study on S180 suspension cells, we demonstrate how JKR-like behavior can be recovered during pull-off while remaining consistent to single-cell MA experiments. Doing so allows us to estimate the (instantaneous) mechanical properties of the S180 cell cortex.

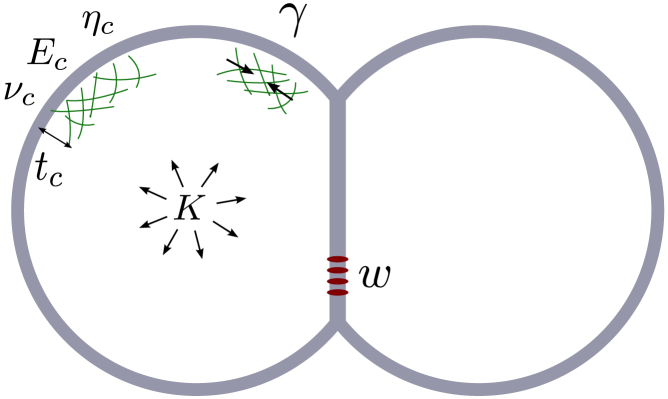
Figure 1.

Schematic representation of a doublet of adhering cells: the cell’s cortex with thickness t_c has passive elastic properties (Young’s modulus E_c, Poisson ratio v_c, and viscosity η_c) and an active contractile tension γ. Volume is maintained through a bulk modulus K, and adhesion energy w drives the formation of initial cell-cell contacts. To see this figure in color, go online.

Methods

Computational model

We introduce a dynamical model that represents the cells as a triangulated spherical shell. This shell represents the cortex-membrane complex, wherein the actin cortex accounts for the majority of its mechanical rigidity (13), see Fig. 1. Overdamped equations of motion Λ x = F are solved to obtain the positions x, representing the nodes from a triangulated shell. Viscous (velocity-dependent) forces are represented in the resistance matrix Λ, whereas all other forces are assembled on the right-hand side in F. A shell model for linear viscoelasticity (Young’s modulus E_c, Poisson number v_c, thickness t_c, and viscosity η_c) is implemented in a spring-damper network (see Supporting Materials and Methods, Section 1), in which for simplicity we have assumed that v_c = 1/3 (the Poisson’s ratio of a two-dimensional isotropic system is 1/3 if the constituents (nodes) interact with central forces that depend on distance alone (23)). To introduce active tension γ and conservation of volume with bulk modulus K, a local outward pressure is computed as

$$p\left(x\right)=2\gamma \left(\frac{1}{R}-\frac{1}{r_c\left(x\right)}\right)-K\frac{V-V^{\ast }}{V^{\ast }},$$ (2)

for a cell with radius R, volume V, and initial volume V^∗. r_c(x) is the local mean radius of curvature on the cell surface at position $\overrightarrow{x}$. We assume cell volume changes are negligible at the relevant timescale (13) and set K = 30 kPa, a value sufficiently high to prevent significant changes of cell volume during MA and DPA simulations—see Fig. S7. The cell’s surface is decorated with nonspecific stickers, which are assumed to be fixed and uniformly distributed on the cell and equal for both cells, leading to a work of interaction w = w₁ + w₂.

We aim to describe adhesive behavior in a wide range of cortical thickness. For larger t_c and low E_c, the normal (radial) elastic deformation of the cortex cannot be neglected anymore. Therefore, we use a modified Maugis-Dugdale contact model (22) that formulates a Hertzian repulsive pressure based on the contact stiffness, an adhesive traction based on the adhesion energy w, and an effective range of interaction h₀. For solid elastic spheres, the latter parameter captures the transition between the JKR (low h₀) and the (DMT) limit (high h₀)—for an in-depth review, see (11). For cells, the effective adhesive range is typically small and well in the JKR zone, and we set h₀ = 50 nm (24). Because the Hertzian repulsive model is valid for a “solid” elastic asperity, a requirement of this contact model is that the normal elastic compression of the cortex is small compared to its thickness. A discussion on the limitations of this model is provided in the Conclusions, and a detailed description of the full computational methodology is presented in the Supporting Materials and Methods, Sections 1 and 2.

Simulation setup

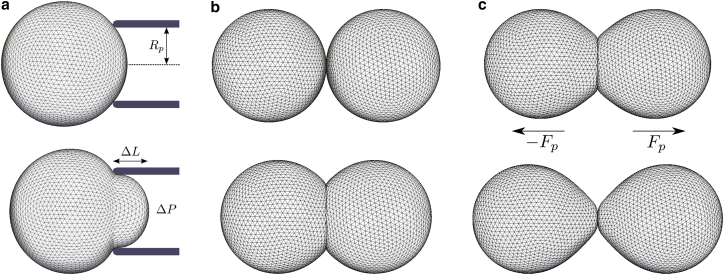
Setups are created for numerical simulation of two mechanical tests: MA and DPA. For MA, we include an idealized pipette with a tip of toroidal shape of inner radius R_p = 3.5 μm (12)—see Fig. 2 a and Supporting Materials and Methods. Within the pipette, an aspiration pressure P_a is applied normal to the cell surface. For DPA, we first let two cells freely adhere until their contact area reaches a steady value—Fig. 2 b. Next, a pulling force is distributed—see Supporting Materials and Methods—to the nodes of both cells (−F_p and F_p). We record the contact radius R_c while the pulling force is gradually increased until the cells suddenly lose contact—Fig. 2 c. The force at which this occurs is registered as the separation force F_s. Further details and numerical considerations of the simulation setup are provided in the Supporting Materials and Methods.

Figure 2.

Visualization of simulation setups for MA and DPA experiments. (a) Simulation of MA experiment. An underpressure ΔP is applied within a micropipette of radius R_p (top). The pressure is gradually increased (bottom) until the aspirated length ΔL = R_p. At this point, the pressure is registered as the critical pressure P_c. (b) Simulation of cell-cell adhesion. Two cells are brought in close proximity (top) and allowed to naturally adhere (bottom). (c) Simulation of DPA experiment, starting from a doublet of adhering cells. A pulling force F_p is applied on the cells (top) and gradually increased until rapid separation occurs (bottom). At this point, the pulling force is registered as the separation force F_s. To see this figure in color, go online.

Results

Pull-off force in cell model

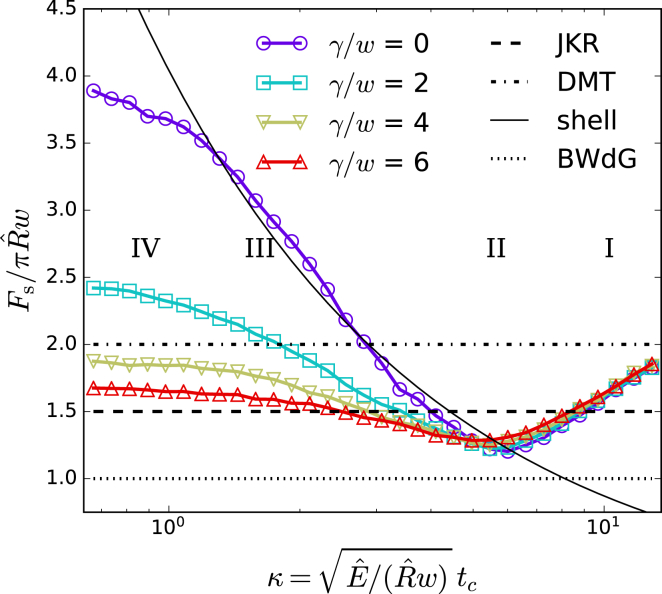
First, we show in general how the separation force depends on the mechanical properties of the cell’s cortex. For this, we define a dimensionless thickness as $\kappa :=\sqrt{\hat{E}/\left(\hat{R}w\right)}{t}_c$. This chosen normalization is a “rigidity” measure that ensures that a unique normalized separation force ${\overline{F}}_s:=F_s/\pi \hat{R}w$ is found for the limits of BWdG (${\overline{F}}_s=1$), JKR (${\overline{F}}_s=3/2$), DMT (${\overline{F}}_s=2$), and shells—Eq. 1—upon change of κ. Here, we are mainly interested in the role of the effective cortical thickness t_c and active tension γ.

Fig. 3 shows ${\overline{F}}_s$ as a function of κ by varying t_c for a simulated DPA experiment. Traversing from high κ (right) to low κ (left), four regions of distinct behavior can be recognized in these curves: 1) at high κ or for contact radius $R_c\ll t_c$, adhesion is dominated by localized elastic deformation normal to the contact plane. Here, solid-sphere Maugis-Dugdale adhesion is recovered, and ${\overline{F}}_s$ will range from the JKR to the DMT limit; 2) for lower κ, or $t_c\ll R_c\ll \hat{R}$, the contribution of bending resistance is dominant (bending rigidity $k_b\sim t_c^3$). This resistance to curvature change is similar to surface tension: the BWdG limit ${\overline{F}}_s=1$ is approached; 3) as κ decreases, a sharp increase in ${\overline{F}}_s$ is observed, similar to shell theory. The adhesion energy is balanced by in-plane elastic energy distributed over the complete cortex; 4) at very low κ, the complete cortex is under high strain, and shell theory breaks down. A maximal contact radius R_c on the order of $\hat{R}$ is reached, and volume conservation (bulk modulus K) limits further deformation. A plateau is observed at large values of ${\overline{F}}_s$. It should be noted that the proposed computational description becomes invalid at both extremes of κ. At very large κ, the thin-shell assumption of cortex elasticity breaks down. At low κ, indentations will become large compared to thickness, and the assumptions of our adhesion model break down. Although this can be safely mitigated by replacing the normal contact stiffness with a sufficiently stiff constraint, the system becomes prone to buckling instabilities in the absence of active tension. Unsurprisingly, the role of active tension γ is mainly significant at small values of κ, at which it reduces ${\overline{F}}_s$ toward the JKR-DMT zone. Given what we know about typical mammalian cells (see Introduction), we expect κ to be small, even if an “effective” thickness would be much greater than the optical thickness. In this case, a significant cortical tension is required for a pull-off force to be in the JKR-DMT zone, $3/2\le {\overline{F}}_s\le 2$.

Figure 3.

Normalized pull-off force $F_s/\pi \hat{R}w$ as a function of dimensionless thickness κ for varying active tension γ. The simulations were obtained by varying thickness t_c while $\hat{R}=$ 5 μm, E = 25 kPa, and $w=$ 0.25 n N/μm. For reference, the pull-off force from JKR, DMT, BWdG, and shell theory is shown for these parameters. To see this figure in color, go online.

Case study on S180 cells

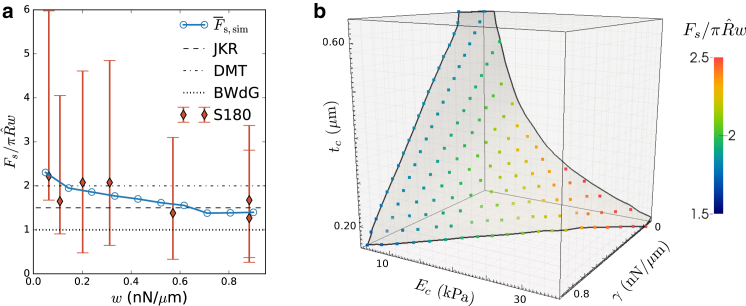
We try to locate cells in this general framework by considering S180 cells, a mechanically very well-investigated cell line. In Chu et al. (7), pull-off forces were measured using DPA in controlled adhesion experiments. We have replotted these results in Fig. 4 a. A scaling of ${\overline{F}}_s$ in the region of the JKR and DMT limits can be observed, with an average ${\overline{F}}_s\approx 1.75$ in the sampled region of w. In our model, such a scaling could be obtained for many possible combinations of E_c, t_c, and γ. To restrict the parameter space to realistic cell properties, we first compare our results to separate MA experiments on the same cell line. In Engl et al. (12), a (liquid model) mean cortical tension of 0.9 n N/μm was found (this value of 0.9 n N/μm already gives an upper limit for estimates of the active tension γ that should be approached in the limit of a soft and thin elastic shell) from MA on S180 cells, which corresponds to a critical pressure P_c ≈ 250 Pa. We sampled combinations of E_c, t_c, and γ in a full factorial 15 × 15 × 15 grid and performed MA simulations to compute the critical pressure (see Supporting Materials and Methods, Section 2). From this, an isosurface was extracted that represents all parameter combinations, yielding a critical pressure of 250 Pa—Fig. 4 b. Subsequently, we resampled points in a regular distribution on this isosurface. Each of these points represents a combination of E_c, t_c, and γ that resembles the mechanical behavior of an (average) S180 cell in an MA experiment.

Figure 4.

(a) Normalized DPA pull-off force $F_s/\pi \hat{R}w$ as a function of dextran-depletion-induced adhesion w between S180 cells, replotted from Fig. 2 in Chu et al. (7) (red diamonds), together with simulated DPA experiment at E_c = 15 kPa, t_c = 0.3 μm, and γ = 0.4 n N/μm, as consistent with MA data (blue circles). Error bars indicate the experimental SD. Guide-lines with BWdG, JKR, and DMT limits are provided as indication. We have assumed R = 6 μm. (b) Parameter space of E_c, t_c, and γ, with an isosurface obtained from simulations of MA on S180 cells, which delimits all parameter combinations for which the experimentally observed critical pressure P_c = 250 Pa (12) is attained. Colored dots represent new samples in this surface for which simulations of DPA were performed. The color scale indicates the value of ${\overline{F}}_s=F_s/\pi \hat{R}w$ obtained for an adhesion energy of w = 0.5 n N/μm. The overlaid rectangular lattice depicts the grid in which MA simulations were performed. To see this figure in color, go online.

Finally, we performed simulations of DPA on these new samples at an intermediate w = 0.5 n N/μm and registered ${\overline{F}}_s$. The result of this can be seen in Fig. 4 b. The lower values of $1.5\le {\overline{F}}_s\le 2$ observed in (7) occur only at lower E_c, when additional resistance to deformation is offered by either bending rigidity (at higher t_c) or active tension γ. This confirms our hypothesis that either the presence of active tension or a larger “effective thickness” is required to explain the adhesive behavior of cells. Moreover, it can be observed that a manyfold increase of t_c is required to have the same effect as a moderate active tension. Under the assumption that the apparent increase in t_c is moderate, t_c = 0.3 μm, we estimate for S180 cells that γ ≈ 0.4 n N/μm and E_c ≈ 15 kPa. The full parameter set of estimated properties is listed in Table 1. It should be stressed that the goal of this work is not to determine the mechanical properties of S180 cells but rather to demonstrate a quantitative relationship obtained between E_c, t_c, and γ and provide an estimate for the range of possible parameters.

Table 1.

Table of Numerically Estimated Mechanical Properties of S180 Cells That Is Consistent with MA and DPA Experiments

Parameter	Symbol	Value	Unit	Derived from
Cortex stiffness	Ec	15	kPa	MA + DPA (7, 12)
Poisson’s ratio cortex	vc	1/3	–	assumed
Thickness cortex	tc	0.3	μm	(16, 19, 20, 21), Fig. 4
Active tension	γ	0.4	nN/μm	MA + DPA (7, 12)
Bulk modulus cell	K	30	kPa	assumed, Fig. S7
Cell radius	R	6	μm	(7, 25, 36)
Adhesive range	h0	50	nm	(24)

We performed simulations of DPA with the parameters from Table 1 for varying adhesion energy and overlay the resulting ${\overline{F}}_s$ with experimental values from (7)—see Fig. 4 a. A reasonable agreement is found between simulation and experiment, and in both cases, a small decrease of ${\overline{F}}_s$ with w is observed, with ${\overline{F}}_s\approx 2$ for small w and ${\overline{F}}_s\approx 3/2$ for larger w. This trend is similar to the transition observed for solid elastic spheres: w affects the Tabor parameter $\mu ={\hat{R}}^{1/3}{w}^{2/3}{\hat{E}}^{-2/3}{z}_0^{-1}$ (with effective range of interaction h₀ ≈ 0.97z₀) (11) that describes the transition between JKR-like and DMT-like adhesion. Although we were not able to formulate a similar universal transition parameter for our more complex modeled system, the underlying mechanisms can be similar: at low w, h₀ is large compared to the contact radius, and the region of adhesive traction is affected little by elastic deformation (DMT assumption). At large w, the elastic deformation is much greater than h₀ and fully determines the adhesive region (JKR assumption).

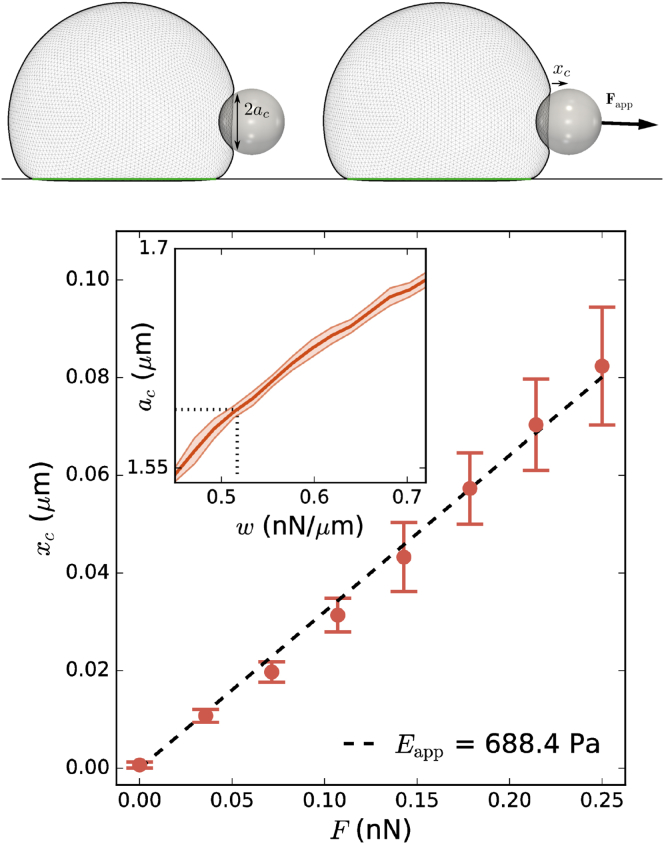
To further verify the obtained estimates of the mechanical properties of S180 cells, we compare them to a third, separate experimental method. Al-Kilani et al. (25) studied the stiffness of cell-bead contacts for spread S180 cells on adhesive patches of various size using an optical trap. For small patch sizes (<2R), the spread cell remains reasonably rounded, and the conditions are comparable to the suspension setting of the MA and DPA experiments. An adhesive bead of diameter 3.6 μm, maintained in an optical trap, was laterally attached to the spread cell. Next, a force F_app was applied to the bead by moving the stage in the optical trap. An apparent Young’s modulus of the cell was computed as

$$E_{\text{app}}=\frac{3}{4}\frac{F_{\text{app}}}{2a_c{x}_c},$$ (3)

with a_c the cell-bead contact radius and x_c the observed bead displacement. For mature adhesion between cell and bead (adhesion time more than 15 min), they obtained E_app ≈ 600 ± 140 Pa. Using the estimated mechanical properties of S180 cells (Table 1), we replicated this setup in our model for the smallest patch size L = 10 μm—Fig. 5 a. The cell-bead adhesion energy was tuned w_cb = 0.517 nN/μm to match the experimentally observed contact radius a_c ≈ 1.59 μm—see Fig. 5 b, inset. We then measured the ratio ΔF_app/Δx_c for small pulling forces and obtained E_app ≈ 688.4 Pa using Eq. 3—Fig. 5 b. This value is in line with the experimental value for mature adhesions. For immature adhesions, lower values of E_app were reported in (25). In their study, this was attributed to the lowered rigidity of the still-immature adhesion complexes themselves, which unravel upon application of tensile force. Because we considered the contacts nearly rigid ($E_c\gg E_{\text{app}}$), our estimated apparent stiffness could be considered an upper limit of the combined cytoskeleton-adhesion complex system.

Figure 5.

Simulation of optical tweezers experiment. Top: a visualization of simulation of optical trap experiment based on (25). A cell is allowed to adhere on a square adhesive pattern (green) to obtain a controlled spread size. Then, a spherical adhesive bead adheres to the cell until contact radius a_c is attained (left). Next, an external force F_app is applied to the bead, and its displacement x_c is recorded (right). Bottom: apparent Young’s modulus computed as E_app = 3F_app(8a_cx_c) in function of the cell radius for a cell with the estimated mechanical properties of an S180 cell (Table 1). Error bars indicate the SD across independent rotations of the cell. Inset: calibration of cell-bead adhesion energy w_cb = 0.517 nN/μm using the contact radius a_c. The dotted line indicates the experimentally observed contact radius. The shaded region indicates the SD across independent rotations of the cell. To see this figure in color, go online.

Contact radius

For the parameters in Table 1 and w = 0.6 nN/μm (hence, $\kappa \approx$ 0.87), we investigate in detail the change of contact radius R_c with increase of the applied pulling force F in a DPA experiment. For solid elastic spheres, the contact radius depends on the elastic modulus ${\hat{E}}_{\text{cell}}$. For DMT and JKR, the cube of the contact radius is given by

$$R_{c,\text{DMT}}^3=\frac{3\hat{R}}{4{\hat{E}}_{\text{cell}}}\left(2\pi \hat{R}w-F\right),$$ (4)

$$R_{c,\text{JKR}}^3=\frac{3\hat{R}}{4{\hat{E}}_{\text{cell}}}\left(3\pi \hat{R}w+\sqrt{-6\pi \hat{R}wF+{\left(3\pi \hat{R}w\right)}^2}-F\right).$$ (5)

Further, we will define the relative contact radius ψ: = R_c/R. For the BWdG model for adhesive vesicles with surface tension, the relationship between applied pull force and contact radius is nontrivial and is expressed in function of the deformed apex radius R_a (8) with ψ′: = R_c/R_a:

$$F=\frac{\pi R_a{\psi }^{\prime }}{1-{{\psi }^{\prime }}^2}\left(\sqrt{w\left(4\gamma -w\right)}-2\gamma {\psi }^{\prime }\right).$$ (6)

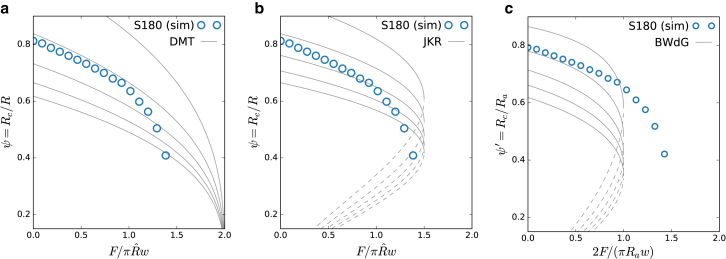
Fig. 6 shows ψ and ψ′ as a function of F for a simulated cell, compared to the theoretical predictions of DMT, JKR, and BWdG. For DMT and JKR, we expect the change of apical radius to be small, so approximate R_a ≈ R, hence ψ′ ≈ ψ. From this comparison, we list the following observations:

• 1)Pull-off force is close to the JKR limit. The maximal contact radius at R = 0 corresponds to an apparent elastic modulus—obtained from Eq. 5—${\hat{E}}_{\text{cell}}\approx$ 600 Pa. However, the change of contact radius with force does not follow JKR theory. The dependency of the effective ${\hat{E}}_{\text{cell}}$ on γ is further shown in Fig. S4.
• 2)Rupture occurs at much higher tensile loading than for ideal adhesive vesicles with surface tension (BWdG) because of the presence of bending resistance, which ensures the maintenance of low contact angles. The maximal contact radius at F = 0 corresponds to an adhesive vesicle with a surface tension of ∼0.8 nN/μm, which is in close agreement with the value of 0.9 nN/μm obtained from the analysis of the MA experiment, assuming that the cell is a liquid droplet with surface tension (12). This correspondence of cell contact radius to the BWdG model in (self- or externally) compressed conditions but not during tensile loading and pull-out has been observed experimentally on HeLa cells in (26).
• 3)At low F (large contacts), the change of ψ with F is DMT-like, i.e., ${\text{d}}_{\psi }F\approx -32{\hat{E}}_{\text{cell}}{\hat{R}}^2{\psi }^2$, with an apparent ${\hat{E}}_{\text{cell}}\approx$ 200 Pa when using Eq. 4. This indicates that the force-indentation F(δ) response of adherent cells with surface tension is remarkably Hertzian. This observation was confirmed in a simulated compression test on a spread-out cell: around F = 0, the contact force follows F ∼ δ^3/2 (see Fig. S5). This contrasts with the force-deformation response of a liquid-filled shell with no adhesion or active tension, which showcases cubic behavior F ∼ δ³ (27).

Figure 6.

Normalized contact radii ψ and ψ′ as a function of normalized applied force $F/\pi \hat{R}w$ of a simulated S180 DPA pull-off experiment (parameters in Table 1) and for w = 0.6 nN/μm, compared to (a) DMT, (b) JKR, and (c) BWdG limits. For solid elastic spheres (JKR and DMT), we assume that R_a ≈ R. Dashed lines indicate where contact is not stable and rupture of the cell doublet will occur. Different guide lines are shown (from top to bottom at F = 0) for DMT: ${\hat{E}}_{\text{cell}}$ (Pa) ∈ {100, 200, 300, 400, 500}; for JKR: ${\hat{E}}_{\text{cell}}$ (Pa) ∈ {400, 600, 800, 1000, 1200}; and for BWdG: γ (nN/μm) ∈ {0.6, 0.8, 1.0, 1.2, 1.4}. To see this figure in color, go online.

Discussion

In this work, we have quantified the adhesion behavior of filled elastic shells with active tension, which were used as a model for biological cells. Numerical simulations with this model were carried out to investigate the role of cortical stiffness, thickness, and active tension. These simulations showed that a combination of these properties can simultaneously explain the mechanics of cell deformation during aspiration and of cell-cell separation during a pull-off experiment. We estimate that cells exist in small to moderate ranges of a dimensionless thickness κ. In these conditions, the active tension plays a crucial role, and is required to explain the observed scaling of separation force.

Cortex mechanics

By comparison to existing experiments on S180 cells, we give tentative estimates of mechanical properties of their actin cortex that agree with characterizations in literature (7, 12, 16, 25). In contrast to a solid elastic model, a model of adhesive, tensed elastic shells can provide consistent estimates of mechanical properties across different mechanical experiments. We estimated an active tension of 0.4 nN/μm, in good agreement with other measurements of active tension, e.g., 0.41 nN/μm on L929 fibroblasts (13), 0.3 nN/μm on chick embryo fibroblasts (28), and 0.2 nN/μm on HeLa cells (29). Measurements of cortical stiffness in literature vary greatly, ranging from 1 kPa (5) to 40 kPa (16, 30), encompassing our estimate of 15 kPa. Of note is the over sixfold lower value of 2.4 kPa obtained on L929 cells, even though it was derived using a similar mechanical description of the cell (13). Aside from obvious differences in cell type, this discrepancy could be attributed to various explanations. First, they also include elastic deformation of the cytosol, whereas we have lumped any such effect in an “effective” increase of cortex thickness. Secondly, any loss of contractility near the bleb induced by laser ablation might have significantly reduced the apparent stiffness of the actin cortex that exhibits stress stiffening properties (31). An active tension of 0.4 nN/μm corresponds to a contractile stress of >1 kPa. For such a stress, the apparent stiffness of a cross-linked actin network is >1000 times higher than the stiffness in stress-free conditions (18). For simplicity, we have set Poisson’s ratio of the cortex to v_c = 1/3. In (13), a value of 1/2 was assumed. In biomimetic actin networks, Poisson’s ratio was estimated at v_c = 0.1 (32). Because its main contribution is through a factor of $\left(1-{\nu }_c^2\right)$ in the bending rigidity (see Supporting Materials and Methods), we expect v_c to be of relatively minor importance.

Force-deformation behavior

We show that JKR-like pull-off forces can exist for a wide range of adhesion energies. Furthermore, the scaling of contact radius with force at low loading force (or, conversely, large adhesive deformation) follows BWdG predictions but is also consistent with DMT theory, implying that force-deformation behavior is Hertz-like at sufficient deformation. This suggests that in an indentation experiment, for example, atomic force microscopy, this model would be almost indistinguishable from a solid elastic material. Because Hertz theory is ubiquitously used in atomic force microscopy experiments to parameterize cells with an apparent Young’s modulus, this begs the question of when its application is appropriate and when not. It can be argued that for strongly spread-out cells, where dense cytoskeletal material spans the full height of the cell, this parameterization is apt. Our results indicate that for cells that are more rounded in shape, e.g., suspension cells (7), weakly adhering cells (16, 25), or cells in dense packings (5), the description of a cell as a tensed shell is more consistent across experimental methods and conditions.

Limitations

We have presented a minimalistic mechanical model that disregards most of the complexities that accompany cell-cell adhesion in real biological settings. Some of these complications can well be expected to affect the results presented here in a nontrivial manner, and they will be briefly discussed.

Firstly, we considered the cell’s cytosol as liquid-like (i.e., bearing hydrostatic stresses, and this through an effective bulk modulus K). The physical properties of the cell’s internal structures are complex, and models that capture its mechanical behavior are often dependent on the timescale of interest. At fast timescales ($\ll$10 s), indented cells show a viscoelastic creep response, which might be attributed to Maxwell fluid behavior of the cell’s internal structures (33). The contribution of the cytosol’s elasticity was shown to be important for controlling the (fast) growth of blebs (13). The assumption in our analyses was that experiments were at least slow enough to relax any deviatoric stresses in the cytosol.

Secondly, our shell model consists of linearly elastic material, whereas the cell cortex has been shown to exhibit nonlinear behavior at large deformations, including both strain stiffening and strain softening (17). Typical strains in our simulated experiments are very low (<5%) but can locally reach up to 20%, e.g., near rupture at the contact site in a pull-off experiment. Here, nonlinearities in stretch response could have non-negligible effect on the separation force.

Finally, we model adhesion based on the assumption of fixed and nonspecific stickers (or with a mobility timescale that is much slower than the timescale of bond rupture). This assumption is valid for the experiment we compared our results against, in which depletion-induced adhesion was studied. In naturally adhering cells, adhesive ligands have been shown to diffuse in the plasma membrane and cluster at the site of cell-cell junctions (34). All these phenomena are expected to affect adhesion and debonding mechanics, both dynamically and at steady state (35). Although not the focus of this study, these properties need to be taken into account to model cell-cell adhesion in realistic biological settings.

Author Contributions

B.S. designed research. B.S. and J.P. performed research. B.S., J.P., M.C., and H.R. wrote the manuscript.

Editor: Jennifer Curtis.