A fiber coherence index for quality control of B-table orientation in diffusion MRI scans

Abstract

Purpose

The diffusion MRI “b-vector” table describing the diffusion sensitization direction can be flipped and permuted in dimension due to different orientation conventions used in scanners and incorrect or improperly utilized file formats. This can lead to incorrect fiber orientation estimates and subsequent tractography failure. Here, we present an automated quality control procedure to detect when the b-table is flipped and/or permuted incorrectly.

Methods

We define a “fiber coherence index” to describe how well fibers are connected to each other, and use it to automatically detect the correct configuration of b-vectors. We examined the performance on 3981 research subject scans (Baltimore Longitudinal Study of Aging), 1065 normal subject scans of high image quality (Human Connectome Project), and 202 patient scans (Vanderbilt University Medical Center), as well as 9 in-vivo and 9 ex-vivo animal data.

Results

The coherence index resulted in a 99.9% (3979/3981) and 100% (1065/1065) success rate in normal subject scans, 98% (198/202) in patient scans, and 100% (18/18) in both in-vivo and ex-vivo animal data in detecting the correct gradient table in datasets without severe image artifacts. The four failing cases (4/202) in patient scans, and two failures in healthy subject scans (2/3981), all showed prominent motion or signal dropout artifacts.

Conclusions

The fiber coherence measure can be used as an automatic quality assurance check in any diffusion analysis pipeline. Additionally, the success of this fiber coherence measure suggests potential broader applications, including evaluating data quality, or even providing diagnostic value as a biomarker of white matter integrity.

Introduction

Diffusion-weighted magnetic resonance imaging (dMRI) is increasingly used to investigate the structural geometry of the brain, with a range of applications in both clinical and basic neuroscience (1). For example, dMRI is currently the only technique able to infer the anatomical white matter connections of the in vivo brain, in a process known as fiber tractography (2, 3). Additionally, dMRI is sensitive to tissue microstructure, with the potential to provide physically and physiologically meaningful microstructural tissue parameters (4). In both cases, the process from data acquisition to final metric is a multi-step procedure with variables and parameters that act as input throughout; the validity and accuracy of these parameters are necessary for meaningful results.

A typical dMRI acquisition is described by three key pieces of information. First, the acquisition creates the visually displayed 4-dimensional set of images volumes. These include both non-diffusion weighted (i.e., the b0 image) and diffusion-weighted images (DWIs), each sensitized to diffusion along a spatial direction. Second, the set of volumes is associated with a set of “b-values” - a parameter that describes the amount of diffusion weighting in each image volume. A scan protocol consists of one or more volumes with b-values equal to 0 s/mm² (hence the name b0 image) and usually a larger number of DWIs, with typical b-values on the order of 1,000 s/mm². Third, each entry in the set of b-values is associated with a sensitization direction, known as a “b-vector”. The list of b-vectors is commonly written as a table and defined in the scan protocol. This table provides information about the direction that each image is sensitive to diffusion in, containing a unit vector (Xi+Yj+Zk) corresponding to each diffusion-weighted image. Together, the diffusion images, the b-values, and the b-vectors can be fit to a number of diffusion models in order to reconstruct voxel-wise estimates of tissue microstructure, fiber geometries, and axonal orientations, for example using the diffusion tensor (5, 6). The fiber orientation information is often visualized as diffusion encoded color (DEC) maps (where red, green, and blue represent diffusion primarily in right/left, anterior/posterior, and superior/inferior directions) (7) or as vector maps (where sticks point in the direction of greatest diffusivity) (8, 9) which allows qualitative representation of the local fiber orientation (Figure 1A). These orientations can then be followed in a step-wise manner in order to reconstruct entire pathways using fiber tractography (3, 10, 11). Note that the set of b-values and b-vectors specified in the acquisition design may not be precisely reflected in performed experiment (e.g., due to patient motion, software optimization, hardware considerations, etc.), thus it is important to interpret the dMRI acquisition from files generated during the scan process. Finally, the description of dMRI experiments in the literature uses a perhaps more rich vocabulary that is strictly necessary. For clarity, in the remainder of the manuscript we describe the set of gradient directions as “b-vectors”, the “b-table”, or the diffusion “scheme”.

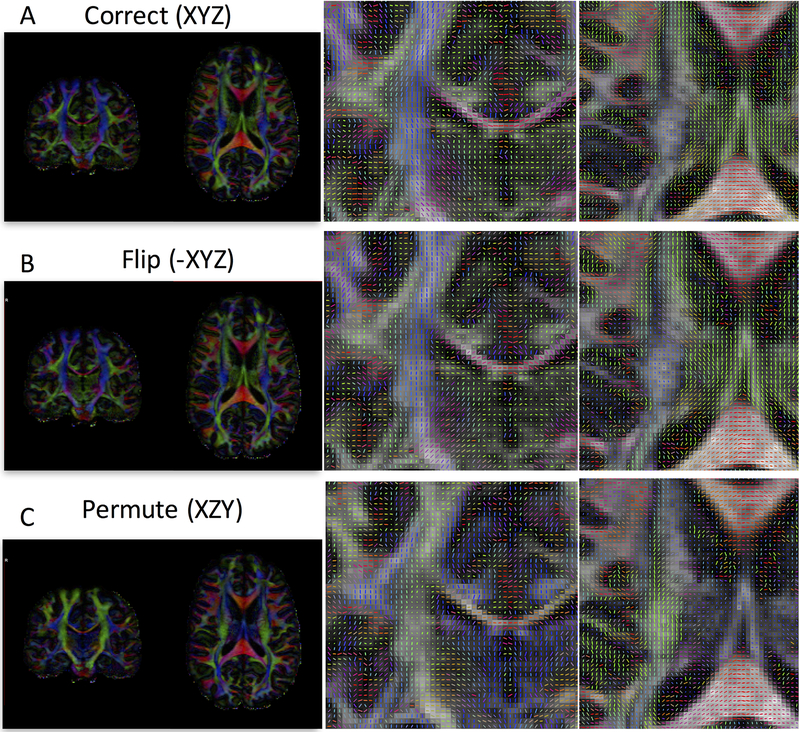
Figure 1.

Effects of incorrect b-vector tables. Diffusion encoded color (DEC) maps and vector maps are shown for a correct gradient table (A), a table with a flipped component (B), and one with permuted components (C). With a flipped component, the DEC map may appear correct, but unit vectors will be flipped in one plane (coronal plane in this example), and will appear correct in another (axial). For a permuted table, both the color maps and vectors will be erroneous. In both (B) and (C), directions are incorrect, and subsequent analysis and tractography will also be erroneous. DEC and vector maps are colored red, green, and blue for diffusion primarily in the right/left, anterior/posterior, and superior/inferior directions, respectively.

Despite the apparent simplicity in collecting and applying these sets of information, there are several ways that they can be corrupted, inaccurate, or incorrectly utilized. Specifically, the b-vectors can be a cause of orientation mismatch. For example, the X, Y, and Z directions of these vectors may not match the images first, second, and third dimensions, respectively. This could be due to an erroneous coordinate system (i.e., scanner bore versus patient coordinates), incorrect neuroimaging header information (in the creation of standardized medical image or neuroimaging file formats including NIFTI, PAR/REC, or DICOM files), incorrect slice collection order (e.g., bottom up or top down), or simple human error (e.g., assign a wrong b-table file for post-processing). In these cases, one error often encountered is a “flip” of a single diffusion direction. For example, the first (or any) dimension may be erroneously assigned to the patients left, when it is in fact a gradient to the patients right (Figure 1B). While the DEC map remains unchanged (in addition to various rotationally invariant scalar maps such as fractional anisotropy and mean diffusivity), and may actually pass a cursory visual inspection, the vector maps will point in the wrong direction, and accurate tractography cannot be adequately performed. Similarly, the b-vectors can also be incorrectly permuted (Figure 1C). In this case, both DEC and vector maps are clearly incorrect (although scalars remain the same), and again, tractography cannot be appropriately performed. A visual inspection of the data is highly recommended in any quality assurance assessment of diffusion MRI (12–14), where mistakes in the gradient table should be caught, and corrected for.

In our experience, practical failures in dMRI experiment interpretation occur most often when pulling data off the scanner and converting it to the desired neuroimaging format. For example, it is not uncommon to work with image data that has been converted to some radiological or neurological view, or standard coordinate system (LPS, RAS, etc.) at the same time forgetting to apply the same transformations to the gradient table. Alternatively, the wrong transformation can be applied when converting to standard formats, caused either by inaccurate image header attributes or copying headers from existing files (while replacing the image matrix) without checking that the header information is correct. In addition, the creator of the file may not know that the 1^st, 2^nd, and 3^rd dimension are uniquely defined based on anatomy in the header (or may not know how to define this). Some versions of commonly used third party tools were not designed with dMRI in mind and make manipulation of such data precarious with loose interpretation of absolute coordinate systems. Similarly, many imaging formats have one or more transform matrices defined in the header, indicating to the software reading it how it should be transformed and displayed, and many software packages handle these transforms in different ways. Any change in the coordinate system can cause this mismatch, for example moving to common atlas spaces, or registering across subjects or longitudinal time points. Another point of b-table error, particularly in our experience with animal scanners, is whether the diffusion magnetic gradients are defined based on the image matrix (readout, phase encode, and slice direction) or based on the bore of the scanner. Although this has largely been mitigated in human scanners (defined based on the image matrix by all major vendors), it has still caused frustration in the pre-clinical environment. Finally, human intervention can cause errors in the tables, for example entering the incorrect gradient table by hand, or using historical tables not defined on the scanner itself.

In this study, we present an automated check for whether the b-table is flipped and/or permuted incorrectly. This is realized by using a novel “fiber coherence index” which describes how well fibers are connected to each other by quantifying coherence of reconstructed orientations. With the assumption that brain white matter should result in coherent vector orientations, this function checks all combinations of b-vector permutations and/or flips in order to automatically detect, and correct, incorrect b-vectors. This quality assurance process is tested on both high-quality and clinical-quality human and animal datasets, including 3981 research subject scans, 1065 normal subject scans of high image quality, 202 patient scans, 9 animal in-vivo scans, and 9 animal ex-vivo scans, to examine the performance of this novel index. This index was implemented as part of a quality assurance and sanity check in one step of the diffusion pre-processing pipeline and is publically available in the DSI Studio diffusion software package (http://dsi-studio.labsolver.org).

Methods

Here, we begin by introducing the fiber coherence metric and how this was used to determine the correct b-vectors table. Experimental validation of this method was performed using four collections of datasets, two human and two non-human primates, that differ greatly in data quality, data size, and acquisition conditions.

Fiber Coherence

The fiber coherence index, quantifies the number of pairs of neighboring fiber orientations that are coherent, and weights them by their anisotropy values:

$$C=\sum _{\forall \{\widehat{u},\widehat{v}\}}\text{I}\left(|\langle \widehat{d},\widehat{u}\rangle |>\cos \left({30}^{°}\right)\right)\text{I}\left(|\langle \widehat{d},\widehat{v}\rangle |>\cos \left({30}^{°}\right)\right)(f(\widehat{u})+f(\widehat{v}))$$ 1

Here, $\widehat{u}$, $\widehat{v}$ are unit vectors of a pair of neighboring fiber orientations. The summation iterates through all possible pairs $\{\widehat{u},\widehat{v}\}$ in the image volume. In our implementation, we only iterated fiber orientations with a fractional anisotropy (FA) value greater than the Otsu’s threshold (15) (a clustering-based image thresholding method used to determine the optimum threshold separating two image classes in order to minimize intra-class variance) multiplied by 0.6 to ignore background noisy fibers and isolate white matter voxels, from which we expect coherency. In addition, in our implementation, we used only the 26 neighboring voxel configurations. $\widehat{d}$ is a unit vector providing the displacement orientation of the neighboring voxels. For example, if $\widehat{u}$, $\widehat{v}$ were resolved at voxel coordinates of $\stackrel{\rightharpoonup }{a}$, $\stackrel{\rightharpoonup }{b}$, then $\widehat{d}=(\stackrel{\rightharpoonup }{a}-\stackrel{\rightharpoonup }{b})/|\stackrel{\rightharpoonup }{a}-\stackrel{\rightharpoonup }{b}|$. The coherence was determined by $|\langle \widehat{d},\widehat{u}\rangle |>\cos \left({30}^{°}\right)$, which counted fiber orientations that form an inner-angle less than 30 degrees with the displacement vector. The function I() returns one if the condition is true, zero if false. $f(\widehat{u})$ provides a weighting using the anisotropy value of the resolved fiber $\widehat{u}$. This anisotropy value can be replaced by a fiber volume fraction, or other measure of interest from different reconstruction methods to achieve the same purpose. It is important to note that each voxel can have more than one resolved fiber orientations, for example if using a model that is able to resolve crossing fibers. This index was implemented as part of a quality assurance and sanity check in one step of the diffusion pre-processing pipeline and is publically available in the DSI Studio diffusion software package (http://dsi-studio.labsolver.org).

B-table corrections

There are a total of 24 possible combinations of b-vector permutation and flipping (Table 1), of which only one describes the correct gradient orientation with respect to the image volumes themselves. While a local coherence is calculated for each imaging voxel, the summation calculates a total coherence index across the white matter (Equation 1). For each individual dataset, we calculated the total coherence for all 24 possible configurations, selected the one resulting in the largest white matter coherence, and designated this as the “correct” b-vector configuration. For reference, the configurations of the example dataset of Figure 1 for case “B” (flip) and case “C” (permute) have a total coherence index (summed across all white matter) that is only 86% and 84% that of case “A” (the correct configuration), respectively. Thus, in this example, the maximum coherence value rightly determines the correct b-vector scheme.

Table 1.

24 possible b-vector permutations and direction-flipping combinations. X, Y, and Z correspond to the diffusion gradient vector orientations. Flipping corresponds to multiplying the unit vector in this direction by a −1.

(X,Y,Z)	(X,Z,Y)	(Y,X,Z)	(Y,Z,X)	(Z,X,Y)	(Z,Y,X)
(−X,Y,Z)	(−X,Z,Y)	(−Y,X,Z)	(−Y,Z,X)	(−Z,X,Y)	(−Z,Y,X)
(X,−Y,Z)	(X,−Z,Y)	(Y,−X,Z)	(Y,−Z,X)	(Z,−X,Y)	(Z,−Y,X)
(X,Y,−Z)	(X,Z,−Y)	(Y,X,−Z)	(Y,Z,−X)	(Z,X,−Y)	(Z,Y,−X)

Note that the raw value of the coherence index will be dependent on variables such as brain size (number of voxels in summation) and resolution, and is thus comparable only across the 24 combinations of b-vector schemes themselves, and not necessarily across subjects or datasets (see Discussion). The index is calculated and stored during voxel-wise reconstruction in DSI Studio.

The datasets

All human datasets were acquired after informed consent under supervision of the project Institutional Review Board. This study accessed only de-identified patient information.

The human datasets were composed of the 1200 subject (age range 22–35) data release of the human connectome project (HCP) acquired and provided by the Washington University– University of Minnesota HCP consortium (16, 17). Diffusion acquisition and processing are described in detail in (16, 18). Briefly, this includes very high-resolution acquisition (1.25 mm isotropic), multiple diffusion weightings (b=1000, 2000, and 3000 s/mm2), with 96 total volumes for each b-value (6 b0 + 90 DWIs), resulting in 288 total volumes per scan. Data were processed for eddy currents, susceptibility distortions, and motion (19, 20). In total, 1065 HCP datasets included diffusion data, and were incorporated in this study.

The “clinical-quality” datasets were composed of 202 patients scanned at Vanderbilt University Medical Center using a standard diffusion acquisition. This included a single b-value (b=1000 s/mm2), with 33 volumes (1 b0 + 32 DWIs), and acquired at 2.5 mm isotropic resolution. Diffusion data was processed for eddy currents, susceptibility distortions, and motion (19, 20).

An additional 3981 diffusion datasets from research subjects (age range 35–90) were acquired from the Baltimore Longitudinal Study of Aging (BLSA), with acquisitions typical of research and clinical studies (in contrast to the high-resolution, high-quality HCP dataset). For this study, we used data acquired from 2009 to present on the same scanner (a 3.0T Philips Achieva scanner, referred to as site number 10). Acquisition consists of a single b-value (b=700 s/mm2), with 33 volumes (1 b0 + 32 DWIs), acquired axially at 0.8×0.8mm resolution with a slice thickness of at 2.2 mm. This dataset includes a total of 934 individual subjects, each scanned anywhere from 1 to 16 times, acquired longitudinally over multiple imaging sessions – with typically 2 scans acquired per imaging session.

The animal model used in this study is the squirrel monkey, a commonly used primate in neuroscience (21–24), and specifically diffusion MRI research (25–27). The data were acquired as part of the creation of a digital atlas of the squirrel monkey brain (28–32). Here, we have chosen to use 9 ex vivo and 9 in vivo squirrel monkey datasets. Ex vivo acquisition permits extended scan times, allowing increased image resolution, increased signal to noise ratio, and increased diffusion volumes. The acquisition in this study included multiple b-values (3,000 and 9,000 s/mm2), with a total of 208 volumes (8 b0 + 200 DWIs), acquired at 0.300 mm isotropic resolution. The in vivo dataset can be considered of more clinically-feasible quality, containing a single b-value (1,000 s/mm2), 33 volumes (1 b0 + 32 DWIs), and acquired at 1 mm isotropic resolution.

Methodological Validation

For all datasets, the gradient table was first corrupted by randomly selecting and applying a combination of permutation and/or direction flipping (Table 1). This gradient table was input, along with the appropriate imaging data, into the DSI Studio diffusion tractography pipeline which consists of creating a “source file” (including the image volumes, b-values, and corrupted b-vectors) followed by voxel-wise reconstruction of the diffusion tensor. A “check b-table” flag was made available in both the GUI and command line DSI Studio interface, which was turned-on for all datasets. This flag runs the methodology described above, and automatically determines and corrects the b-vector table. This “corrected” table was extracted, and compared to the original gradient table. Of note, if a b-table correction is performed the user is informed both through the graphical interface and by naming conventions of the .fib (DSI Studio file format for fiber tracking) file.

Results

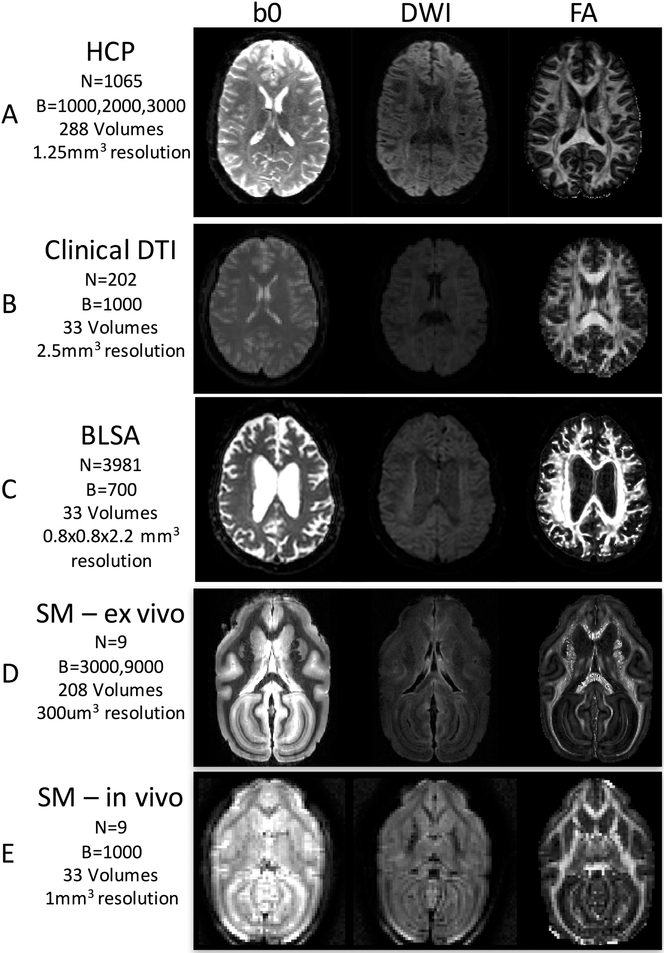
We validated the method on both human and animal models, and include both high-quality datasets as well as more clinically-feasible quality datasets for each model. Example b0 images, DWIs, and FA maps are shown in Figure 2. Figure 2A shows an example of the HCP subject data; Fig. 2B shows the patient scans acquired at Vanderbilt University Medical Center using a standard diffusion acquisition; Fig. 2C shows an example of the BLSA normal subject data, and Fig. 2D and 2E show the animal scans.

Figure 2.

Example images for each of the 4 tested datasets. We have chosen to validate the fiber coherence index as a quality assurance metric on high quality HCP data (A), clinical-quality patient DTI data (B), research subject BLSA data (C) high quality ex vivo squirrel monkey scans (E), and standard in vivo squirrel monkey acquisitions (E). For each, basic diffusion imaging parameters are given, and example b0, DWI, and FA images are shown to show large variability in image quality.

The coherence index was automatically calculated for all datasets, including 1065 HCP, 202 clinical DTI, 3981 BLSA, 9 ex vivo monkey, and 9 in vivo monkey, and the success rates are displayed in Table 2. The method was successful in 100% of all HCP trials, and all ex vivo and in vivo monkey datasets.

Table 2.

Success rates of automatically determining the correct b-vector scheme.

Dataset	# Datasets	# correct b-table detection	% Success
HCP	1065	1065	100
Clinical DTI	202	198	98.02
BLSA	3981	3979	99.93
SM - ex vivo	9	9	100
SM - in vivo	9	9	100

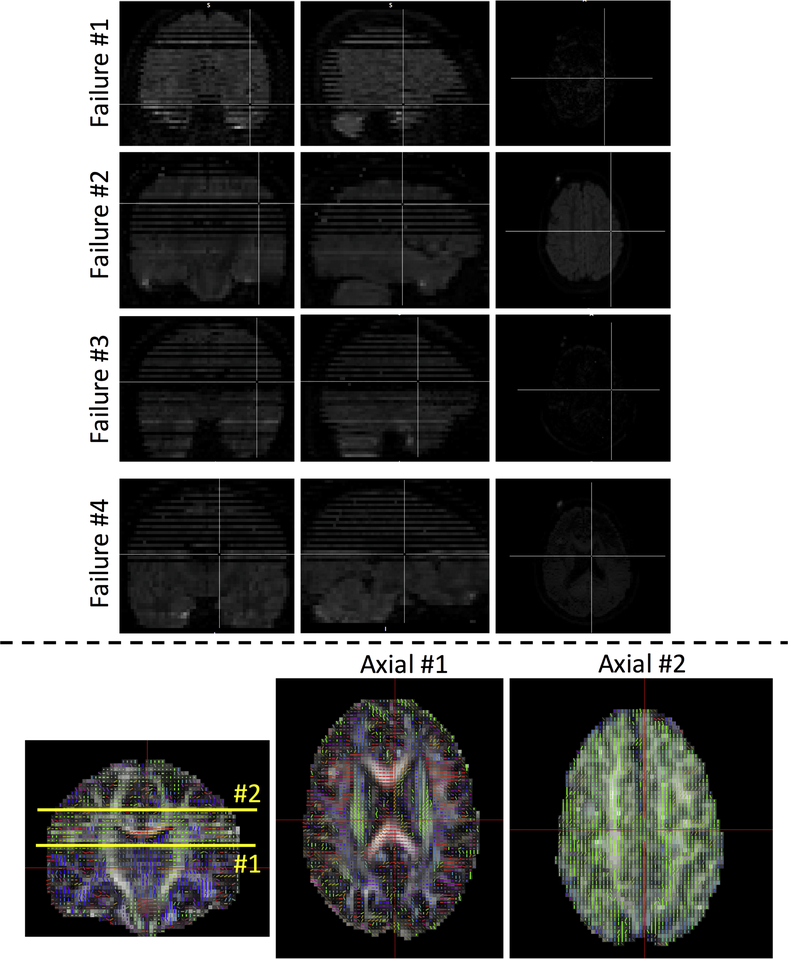
For the clinical DTI, 198 of 202 b-vector tables were successfully corrected. To explore the reasons for failure, we investigate the raw DWI data of the 4 failure datasets. In all four cases, severe image artifacts were present in the DWIs (Figure 3, top), all due to signal dropout, most likely caused by patient motion causing intensity loss throughout entire axial slices. Signal dropout for a given DWI, sensitive to diffusion in a given direction, typically result in orientation estimates in that same direction (Figure 3, bottom), causing artificially increased coherence. With such severe artifacts, the diffusion reconstruction becomes unusable, and more comprehensive image restoration and image processing are necessary if the scans are to be clinically useful (33, 34). If excluding the problematic dataset, the coherence index achieved a 100% accuracy.

Figure 3.

When the coherence index fails to correct gradient tables, image artifacts are always present. In this study, only 4 patient datasets had failures when correcting b-vectors, and all had slice dropout and subsequent reconstruction artifacts (top). In these cases, incorrect orientation estimates (bottom) were a result of signal dropout causing artificially increased coherence in a number of slices (see Axial slice #2).

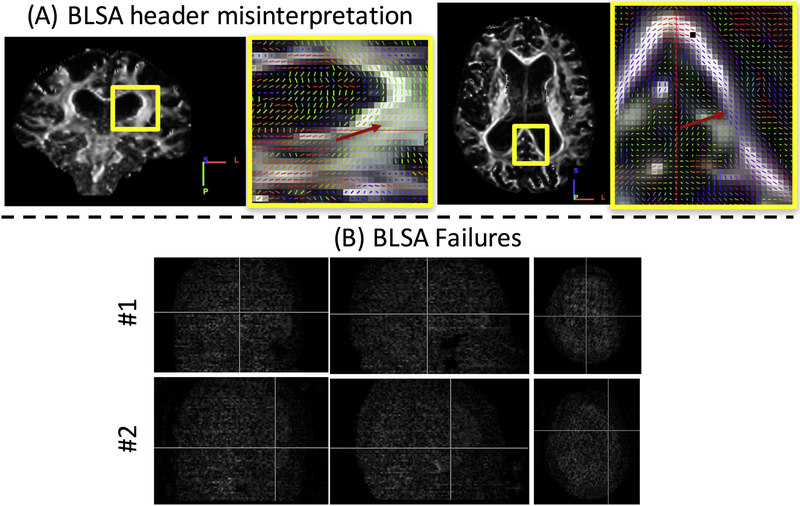
For the BLSA dataset, initial results showed that 259 instances of the entire 3981 had a different flipping or permutation from the correct b-tables, and only 3722 of 3981 b-vector tables were correctly detected. However, further inspection of the data showed that 257 out of 259 of these instances had a dimension swap in the y and z axis due to misinterpretation of the image header information by our code (identified as an incorrect application of the NIFTI s-form and q-form matrices, and corrected in DSI Studio builds September 2018 and later), and the coherence index correctly compensated for the dimension swapping (Figure 4A), resulting in vectors with correct orientation in the image matrix space. Importantly, even though the data was incorrectly read, the b-vectors now match the image matrix itself, and subsequent tractography would have been successful. The remaining two cases showed significant signal dropout in every DWI (Figure 4B), possibly caused by patient motion. In short, the coherence index also achieved perfect performance if the problematic or unusable datasets were excluded. Note that these datasets were accessed prior to the standard quality assurance procedures in a form directly following file format conversion from the scanner. These datasets would have been excluded with routine quality assurance (13).

Figure 4.

Image orientation misinterpretation and gradient correction failures. For the BLSA data, 259 scans had a misinterpreted header with our initial code (A, note the incorrect orientation labels), however the index was able to find the correct vectors to match the image, where vectors are oriented appropriately, but the wrong color (red arrows). Only 2 datasets had failures of correcting b-vectors, both containing severe signal dropout and motion artifacts (B).

Discussion

In this study, we have proposed a metric, the fiber coherence index, which allows detection and correction of b-vector tables. The coherence index is based on the assumption that white matter orientation is coherent on the scale of millimeters throughout the brain, and that the correct gradient table results in the highest recovered overall coherence. This method was effective across a range of diffusion data quality and acquisition strategies and was also successful on non-human animal models. Our result showed that this index successfully identified the correct configuration of b-vector table in 98% of all datasets tested, and in all 6 failure cases, severe image artifacts were present, most commonly entire axial slice dropout due to subject motion. Intuitively, because for an entire diffusion-weighted direction an entire slice (or many slices) has a low magnitude in the DWI, indicating higher diffusivity in that direction. Thus, an orientation-based coherence measure in those slices will always be erroneously magnified, and the correct gradient directions cannot be determined. In volumes without severe artifacts, our proposed algorithm was 100% successful. We don’t necessarily view these failures in a negative light. For example, if the data scientist or clinician is confident that the gradient table is correct, and the algorithm suggests otherwise, this could be an indication of artifacts again causing magnified and erroneous coherence. Hence, this methodology could be used to flag volumes that require further validation and inspection.

A number of software packages (19, 35–38) exist which perform excellent quality assurance/quality control in pre-processing and processing steps, including correcting b-tables based on motion (small rotations) and removing volumes with artifacts or outliers; however, few can identify major issues with the gradient schemes (i.e. flipping or permutations), and require the correct scheme in order to properly function. There are a nmber of reasons why the gradient table can be incorrectly flipped or permuted, including data conversion, space or view transformations, changes in coordinate systems, incorrect or incomplete image header information, transcription of accompanying text files, or simple human error. Additionally, as found in our results on the BLSA dataset, we found that various software can incorrectly read and apply transforms when loading image matrices. In this study, the coherence index was successfully able to correct the vector orientations in cases of both incorrect gradient table orientation and incorrect image matrix orientation. With all of these potential sources of error, we recommend calculation and implementation of this index as part of any standard diffusion quality assurance pipeline in order to detect possible inaccuracies in gradient tables. Specifically, this should be a first step in conjunction with other quality control and preprocessing approaches (or possibly immediately after a volume outlier detection in order to avoid errors such as that seen in a small percent of our datasets).

Similar quality assurance tools facilitate gradient table validation either through manual inspection (13) or automatic detection (39). Specifically, Jeurissen et al. (39) propose automated correction of gradient orientations by examining properties of resulting tractography, rather than properties of local reconstruction in the current study. Specifically, they reason that the optimal permuation of the table will be the one that results in the highest average whole-brain streamline length, and find successful correction of b-tables on par with the current study, across a range of datasets and SNR levels. Their method has the additional benefit of detecting small rotations of the gradient table (e.g., due to angulation of the imaging plane), at the expense of additional calculations (whole-brain tractography), time (27 minutes versus ~2 seconds), and potential sensitivity to tracking parameters, whereas ours does not rely on the additional steps of performing tractography. Future implementations of the current correction method should assess the ability to identify and correct for small rotational error of the gradient table in addition to simple flips and permuations. We note that no quality assurance tool will be able to detect human error of completely erroneous b-vectors (i.e. typos or simply the wrong direction sets).

We utilize the fiber coherence measure as a way to check the b-table prior to fiber reconstruction and tractography. However, there are other potential applications for this index. As previously described, this could be used as a data quality metric or artifact detection on the scale of voxels. Even more, this could be a potential measure of structural integrity. Currently, FA is often associated with “white matter integrity” (although this is certainly a misuse or misinterpretation of the actual measure (40)). The coherence, however, is a direct geometric measure of how well-aligned fiber populations are when stepping from voxel to voxel. Thus, this could conceivably be used as some index that indeed describes white matter order, or inversely, describes disorder. While we hypothesize a lower coherence index, it remains to be seen how this measure is impacted in patients with brain diseases, both locally and globally.

The coherence index seems to have the capability to probe into other quality issues such as slice signal dropout. For example, the abnormal flipping and permutation in 2 of our healthy controls and 4 of our patients all led to prominent signal quality issue. In practice, we can examine which scans have different flipping and permutation results to identify problematic dataset. Furthermore, we have briefly explored other potential uses of the coherence index that should inspire future work. Comparisons across datasets (for example HCP and patient data) was hindered by the large differences in voxel size, and number of overall voxels, making both whole-brain and voxel-wise comparisons of the coherence index challenging. Comparisons of pre-process data with those that had not been pre-processed (i.e., not corrected for susceptibility and eddy current), as well as comparisons against data with known acquisition instabilities (for example specific sets of HCP data had known coil instabilities - HCP data issue code C: https://wiki.humanconnectome.org/pages/viewpage.action?pageId=88901591) yielded no significant results. Comparisons of the six scans with artifacts against those without showed that coherence could be both decreased (due to more random orientations and lower FA) or dramatically increased (due to slice dropout causing all vectors in a given slice to point in the same direction), which suggests a potential way to filter or search for particular artifacts. It is possible that some other measure of orientation coherence, or conversely, orientation entropy, could solve these problems. It would be of interest to calculate a coherence over a given distance, which can be made consistent across differing acquisitions, rather than simply nearest neighborhoods. Alternative coherence measures, and weighting factors, could be an area of future exploration.

In conclusion, we recommend employing the fiber coherence measure as an automatic quality assurance check for b-table orientation in any diffusion analysis pipeline. The abnormal flipping or permutation may suggest further signal quality issues, and this fiber coherence measure may have broader applications in evaluating data quality, or even providing diagnostic value as a biomarker of white matter integrity.