A resting state fMRI analysis pipeline for pooling inference across diverse cohorts:An ENIGMA rs-fMRI Protocol

Abstract

Large-scale consortium efforts such as Enhancing Neuro Imaging Genetics through Meta Analysis (ENIGMA) and other collaborative efforts show that combining statistical data from multiple independent studies can boost statistical power and achieve more accurate estimates of effect sizes, contributing to more reliable and reproducible research. A meta-analysis would pool effects from studies conducted in a similar manner, yet to date, no such harmonized protocol exists for resting state fMRI (rsfMRI) data. Here, we propose an initial pipeline for multi-site rsfMRI analysis to allow research groups around the world to analyze scans in a harmonized way, and to perform coordinated statistical tests. The challenge lies in the fact that resting state fMRI measurements collected by researchers over the last decade vary widely, with variable quality and differing spatial or temporal signal-to-noise ratio (tSNR). An effective harmonization must provide optimal measures for all quality data. Here we used rsfMRI data from twenty-two independent studies with approximately fifty corresponding T1-weighted and rsfMRI datasets each, to (A) review and aggregate the state of existing rsfMRI data, (B) demonstrate utility of principal component analysis (PCA)-based de noising and (C) develop a deformable ENIGMA EPI template based on the representative anatomy that incorporates spatial distortion patterns from various protocols and populations.

Introduction

Changes in blood oxygenation level-dependent (BOLD) signal form the basis for most functional MRI studies (Bajaj et al. 2015a). In task and event related fMRI studies modest (25%) changes in BOLD signal during periods of mental activity are contrasted with baseline or control conditions. Likewise, fluctuations in BOLD signal during rest reflect neuronal baseline activity, representing the state of the brain in the absence of goal-directed neuronal action and external input (Gusnard and Raichle 2001; Peltier and Noll 2002). These slow fluctuations occur in synchrony for functionally relevant networks across different brain regions. Resting state fMRI (rsfMRI) studies investigate large-amplitude, spontaneous low frequency (<0.1 Hz) fluctuations in the fMRI signal that are temporally correlated across functionally related areas (Biswal et al. 1995; Fox and Raichle 2007; Margulies et al. 2007; Smith et al. 2009; Bajaj et al. 2015b). Concerns have been raised about some conclusions drawn from human neuroimaging studies in general (Bustin 2014; Button et al. 2013; Russell 2013), fMRI results in particular (Poldrack et al. 2017), and rsfMRI results (Bajaj et al. 2016) pointing to low reliability and unclear reproducibility of results. RsfMRI studies typically have less statistical power than task or event related approaches (Zhang et al. 2016) and may be more susceptible to this criticism. One way to address low statistical power in scientific research is through collection of larger samples. This may not be feasible for neuroimaging studies owing to recruitment constraints or financial limitations. An alternative approach is the meta- or mega-analytic pooling of data from multiple sites or studies. Enhancing Neuroimaging Genetics through Meta-Analysis (ENIGMA) and other big data consortia use this approach to boost statistical power and achieve more accurate estimates of effect sizes, contributing to more reliable and reproducible research (Thompson et al. 2014).

The growth of large-scale collaborative studies has led to more highly powered studies with more reproducible effects, also allowing “big data” analyses that draw on diverse datasets collected worldwide (Choudhury et al. 2014; Poldrack and Gorgolewski 2014; Zuo et al. 2014). One challenge in multi-site neuroimaging research – such as that led by ENIGMA – is to identify and homogenize phenotypes from images collected with a wide array of imaging protocols and from subjects of varying ages. One use of such data is for future genetic investigations, which have recently shown impressive results when aggregating datasets from tens of thousands of subjects (Major Depressive Disorder Working Group of the Psychiatric et al. 2013; Schizophrenia Working Group of the Psychiatric Genomics 2014). Prior work of ENIGMA in this direction led to development of imaging analyses pipelines to extract, homogenize, and quality control standardized phenotypes from structural T1-weighted (T1w) and diffusion tensor imaging (DTI) (Jahanshad et al. 2013). This led to large genome-wide association studies to uncover genetic loci associated with MRI-based phenotypes including hippocampal volumes (Bis et al. 2012; Stein et al. 2012; Hibar et al. 2017), intracranial volumes (Ikram et al. 2012; Stein et al. 2012; Adams et al. 2016), and others (Hibar et al. 2015). Related large scale data pooling of anatomical MRI scans led to the largest neuroimaging studies of major depression (Schmaal et al. 2016), bipolar disorder (Hibar et al. 2016), schizophrenia (van Erp et al. 2016), obsessive compulsive disorder (Boedhoe et al. 2016), attention deficit hyperactivity disorder (Hoogman et al. 2017), and brain asymmetry (Guadalupe et al. 2017) in thousands of subjects scanned worldwide.

Two major challenges in developing an analysis plan for multi-site rsfMRI data include the diversity in the data collection protocols and the lack of a generalized analysis approach. The first aim of this manuscript is to review available and representative rsfMRI datasets, across ENIGMA and elsewhere, and quantify their variability in terms of spatial resolution, duration and signal to noise ratio (SNR), including temporal-SNR (tSNR). The second aim of this manuscript is to show the utility of principal component analysis (PCA) based regression of Rician noise to improve the signal-to-noise characteristics of rsfMRI images. Some rsfMRI protocols such as that developed by the Human Connectome Project push the limits of spatial and temporal resolutions but are still limited by noise. SNR improvement using spatial smoothing reduces in spatial specificity, and thus complicates localization of effects in the rsfMRI/fMRI images. By exploiting the redundancy in the temporal domain, we can improve the SNR/tSNR without compromising the spatial resolution.

Presently, many fMRI analysis pipelines require input from multiple imaging modalities. For instance, a subject’s structural T1w scan may be required to regress out signal trends from the cerebrospinal fluid (CSF) and cerebral white matter. These signals are considered to have methodological or physiological rather than neural origins, so they are regressed out before analyzing cerebral connectivity. Likewise, T1w data is sometimes used for anatomical registration to an atlas space, such as the ICBM152 template space (FMRIB Software Library, FSL) (Jenkinson et al. 2012; Smith et al. 2004). RsfMRI are collected using gradient echo planar imaging (EPI) sequences, so they may suffer from geometrical distortions, especially in areas of high susceptibility such as bone-tissue interfaces. This limits the accuracy of spatial registration between functional and T1w data. Supplementary data such as the ‘field map’ or reversed-gradient scans are collected to correct for such distortions (Cusack et al. 2003; Hutton et al. 2002). However, even with field map-corrected EPI-to-T1 registration, residual misalignment between functional and T1w images may interfere with the analyses (Villain et al. 2010). The multi-modal approaches have further disadvantages for multi-site analyses since the variability in suplementary data such as the presence or absence of field mapping and the variance in the quality of T1w data may influence the results of the overall rsfMRI analysis. In the spirit of such multisite ENIGMA analyses, here we propose a single-modality pipeline that only uses a deformable template and tissue classification of rsfMRI data to achieve the same goal. This avoids the pitfalls of potential site-to-site variances in T1w data analyses and co registration biases that can influence the rsfMRI phenotypes. Here we use T1w data to make the ENIGMA EPI template below, but T1w data is not used or needed to do analyses with the template.

Detection of subtle fluctuations in neuronal activity-induced BOLD signal in the presence of various sources of noise is one of the central challenges in fMRI. It has led to an ongoing effort to increase the spatial SNR and tSNR by optimizing data collection and analysis parameters. The standard SNR metric does not capture the temporal noise characteristics of fMRI time courses. Therefore, a tSNR metric is used to estimate the temporal stability of the imaging signal. There are multiple ways to quantify tSNR. This paper uses two approaches: one quantifies tSNR by dividing the mean signal intensity by its variation over time; the second quantifies SNR by dividing the mean image intensity over the time trace by the noise in the image (Bodurka et al. 2007; Kruger and Glover 2001; Murphy et al. 2007; Triantafyllou et al. 2005). tSNR gives an indication of fMRI data quality and is a function of multiple protocol parameters including magnetic field strength, flip angle, image resolution, and echo time (Triantafyllou et al. 2006; Molloy et al. 2014; Triantafyllou et al. 2005). Several studies report that improved detection of stable functional networks was associated with higher tSNR (Gonzalez-Castillo et al. 2014; Molloy et al. 2014; Smith et al. 2013; Welvaert and Rosseel 2013).

A fundamental problem in big data neuroimaging research is achieving homogenization across diverse data collection protocols. Spatial normalization is used in brain mapping to reduce inter-individual anatomical variance by matching homologous spatial features of a source brain to those of a target brain (Kochunov et al. 2001). Spatial normalization of each subject’s brain to either an average or an individual target brain (Lancaster et al. 1999; Woods 1996) or to a single high-resolution MRI brain volume (Collins et al. 1995) inevitably leads to a bias in the quality of regional spatial normalization, with good matching for some brains and poor matching for others. One approach is to develop and evaluate a deformable brain template, created from a group of individual brain images, to minimize target-selection bias. This template based on deformation properties common to the group, yields a common representative brain template for multi-site statistical studies.

Here we develop a pipeline for multi-site rsfMRI analysis pipeline to support imaging research conducted by multisite efforts, such as participants in the ENIGMA consortium, although it could be equally beneficial in other related research efforts. In this study, we used twenty-two rsfMRI datasets that included up to fifty representative T1/rsfMRI datasets per study. We used this data to (i) demonstrate the utility of the PCA-based de noising and (ii) develop a deformable ENIGMA EPI atlas based on representative anatomy that incorporates spatial distortion patterns. This pipeline involves the basic preprocessing steps to de noise and harmonize a variety of resting state protocols; it serves as the basis for future analysis plans to calculate resting state metrics, which may include anything from independent components analysis (Calhoun and Adali 2012) to regional correlational analyses (Song et al. 2014) and beyond.

Methods

Study subjects and imaging protocols:

Twenty-two T1/rsfMRI datasets were analyzed (Table 1). Thirteen datasets were from ENIGMA sites; nine datasets were publicly available and downloaded (one dataset from Center of Biomedical Research Excellence (http://cobre.mrn.org/phase1/; http://schizconnect.org; (Çetin et al. 2014) and eight datasets from the Autism Brain Imaging Data Exchange II (ABIDE II) (http://fcon_1000.projects.nitrc.org/indi/abide/abide_II.html). There were differences in technical parameters such as spatial resolution, statistical data properties such as SNR and tSNR, and variability in the supplemental data that was available. Different types of scanners: ten Siemens, six GE, and six Philips were used to acquire the imaging data. The field strength of twenty-one of the scanners was 3 T and one scanner had the field strength of 1.5 T. Moreover, the rsfMRI datasets used in this study had substantial variability in their spatial (7.54 mm³-64.0 mm³) and temporal (720–3000 ms) resolution, the number of volumes per study (85–1200) and the total scan duration (3.8 min-14.8 min). The T1w data had also variability in spatial resolution (0.343 mm³-1.2 mm³) and image quality. Individual imaging protocols are described in the supplementary material.

Table 1:

Demographic and imaging information are listed, for the datasets used in this study.

Data sites	Age range (years)	Subjects	No. of volumes	Voxel size (mm3)	TR (ms)	Scanner	Field strength
MarbG	18–55	25M/25F	237	3.3×3.3×4.2	2000	Siemens	3 T
MuenG	19–62	25M/25F	237	3.3×3.3×4.2	2000	Siemens	3 T
MPRC1	19–67	25M/25F	150	3.44×3.44×4	2000	Siemens	3 T
MPRC2	16–66	25M/25F	140	3.44×3.44×3.99	2210	Siemens	3 T
MPRC3	19–61	25M/25F	444	1.72×1.72×4	2000	Siemens	3 T
VUMC1	22–70	25M/25F	200	3.3×3.3×3	1800	GE-Signa HDxt	3 T
VUMC2	23–54	26M/24F	200	3.3×3.3×3	1800	GE-Signa HDxt	3 T
COBRE	20–65	25M/25F	150	3.75×3.75×4.55	2000	Siemens	3 T
GOBS	20–85	25M/25F	150	1.72×1.72×3	3000	Siemens	3 T
ACP	16–77	26M/24F	420	2×2×2	780	Siemens	3 T
HCP	22–35	25M/25F	1200	2×2×2	720	Siemens	3 T
UCTSA	18–38	35M/15F	138	3.1×3.1×3.5	2500	Siemens	3 T
CAMH	20–55	23M/27F	212	3.125×3.125×4	2000	GE	3 T
ZHH	18–50	23M/22F	212	3.125×3.125×4	2000	GE	3 T
ETH	13.8–30.7	37M	210	3×3×3.3	2000	Philips Achieva	3 T
EUMC	6.2–10.7	40M/10F	160	3.594×3.594×4	2000	GE-MR750	3 T
IPRDH	6.1–46.4	25M/25F	85	3.594×3.594×4	2700	Philips Achieva	1.5 T
KKI	8–13	29M/21F	156	2.67×2.67×3	2500	Philips Achieva	3 T
SDSU	7.4–18	41M/9F	180	3.44×3.44×3.4	2000	GE-MR750	3 T
TCHS	10–20	42M	210	3×3×3.55	2000	Philips Achieva	3 T
KUL	18–35	28M	162	1.56×1.56×3.1	2500	Philips	3 T
BNI	18–64	50M	120	3.75×3.75×4	3000	Philips Ingenia	3 T

Here, MarbG=Marburg Germany, MuenG=Muenster Germany, MPRC=Maryland Psychiatric Research Center, VUMC=VU University Medical Center, GOBS=Genetics of Brain Structure and Function study, COBRE=Center Of Biomedical Research Excellence, ACP=Amish Connectome Project, HCP=Human Connectome Project, UCTSA=University of Cape Town, South Africa, CAMH=Centre for Addiction and Mental Health, ZHH=Zucker Hillside Hospital, ETH=Eidgenossische Technische Hochschule, EUMC=Erasmus University Medical Centre, IPRDH=Institut Pasteur and Robert Debre Hospital, KKI=Kennedy Krieger Institute, SDSU=San Diego State University, TCHS=Trinity Centre for Health Sciences, KUL=Katholieke Universiteit Leuven, BNI=Barrow Neurological Institute, M=Male, F=Female, TR=repetition time.

PCA de noising and t SNR calculation

PCA of a redundant M×N data matrix, X, shows that most of the signal-related variance is contained in a few components whereas the noise is spread over all components; in each measurement it is random, and will generally make all eigenvalues nonzero. The contribution of noise to the histogram of the covariance matrix eigenvalues becomes deterministic in the limit of large M and N (Veraart et al. 2016b). The nonzero eigenvalues are described by the Marchenko-Pastur (MP) distribution if the noise level is constant among all elements of X (Marchenko and Pastur 1967):

$$p\left(\lambda \right)=\frac{{\left(({\lambda }_{+}-\lambda )(\lambda -{\lambda }_{-})\right)}^{\frac{1}{2}}}{2\pi \gamma \lambda {\sigma }^2},{\lambda }_{-}\le \lambda \le {\lambda }_{+}$$

and $p\left(\lambda \right)\equiv 0$ otherwise, where ${\lambda }_{\pm }={\sigma }^2{\left(1\pm \sqrt{\gamma }\right)}^2$ with $\gamma =\frac{M}{N}$ and $N,M>>1$, and $\sigma$ the noise standard deviation.

The shape and range of the distribution depends on two parameters: γ and σ². The upper edge λ₊ of the MP distribution distinguishes between noise and significant signal-carrying principal components. In this Marchenko-Pastur Principal Components Analysis (MPPCA) de noising, recently applied to diffusion-weighted MR images (Veraart et al. 2016a; Veraart et al. 2016b), we estimate the noise level σ and the number of significant signal components simultaneously and regress out eigenvalues that are related to noise. The de noising algorithm does not alter the temporal domain trends. We first applied the MPPCA denoising algorithm to the rsfMRI data and obtained filtered data, then calculated tSNR (Method 1: “tSNR test”) values before and after applying the MPPCA de noising filter by dividing the data’s mean signal intensity by its variation over time. TSNR was then compared between the cleaned and uncleaned data. We evaluated how the MPPCA de noising effects vary as a function of the following image acquisition parameters: TR and voxel size (spatial resolution). In addition, we also computed the SNR (Method 2: “SNR test”) before applying the de noising filter as the ratio between the mean signal and the estimated noise level (σ), SNR_before= mean signal/σ. This σ was provided as an additional output parameter of the de noising algorithm. The residual map (de noised data minus the original data) singles out the noise that was removed during de noising, and allows for the computation of SNR after de noising. Here SNR_after=mean signal/σ_after with (σ_after)²=_σ²-variance (residuals).

Data preprocessing and template creation

Image preprocessing was carried out with FMRIB Software Library (FSL) software (Jenkinson et al. 2012; Smith et al. 2004) and image registration was carried out using Advanced Normalization Tools (ANTs) - an open source and freely available software that is built on the widely used Insight Tool Kit platform (Avants et al. 2015; Yoo et al. 2002; Ibanez et al. 2002). We used the ANTs Symmetric Normalization (SyN) algorithm (Avants et al. 2008) for nonlinear registration, as it has been shown to be robust (Klein et al. 2009). For each individual from a study, an average rsfMRI volume was calculated from all the available rsfMRI volumes from that individual, and brain extraction was carried out. The brain extracted average rsfMRI volume of each dataset was nonlinearly registered to the corresponding brain extracted T1w image using ANT’s ants Registration using the SyN transformation model according to the parameters in Table S1. Then, the skull-stripped T1w image from each individual subject was registered to a skull-stripped average 152 T1 (ICBM) brain template using FSL’s flirt. Brain extraction was performed to avoid field of view discrepancies between EPI and T1w images, which could result in severely misaligned images. The generated transformation matrix (from individual T1w to ICBM) was used for registering the resting state EPI image to the ICBM brain template. These normalized EPI images from all subjects for the given study were used as input images for using ANTs’ antsMultivariateTemplateConstruction2.sh using the SyN transformation and mutual information similarity metric, based on the joint histogram entropy according to the parameters in Table S2. This script averaged all the inputs to make an initial average target. Then, all brains were registered to the initial target. Then, those registered brains were averaged and this became the new target. This process, after many repetitions - here 7 times (default=4) - produced an image, the minimal deformation template, a representative EPI template for the dataset from each study. Repeating these steps for all 22 datasets, we obtained 22 representative EPI template images. Taking these images as input images for ANT’s antsMultivariateTemplateConstruction2.sh and following the same above-mentioned procedures, we computed the brain template, which we refer to from now on as the ENIGMA EPI template. ENIGMA quality control protocols were implemented to flag outliers via visual inspection. This two-step procedure is similar to the two-step procedure used in the development of the ENIGMA multi-site tensor based morphometry approach (Jahanshad et al. 2018). A flow chart provided in the Results section summarizes the main steps used for creating the ENIGMA EPI template.

Ventricle overlap analysis

To evaluate the quality of the registration to the ENIGMA EPI template, and compute the percentage (%) ventricular overlap, we chose the two data subsets from the ACP (Amish Connectome Project) site. Individual Free Surfer parcellated T1 images (aparc+aseg.nii.gz) were resampled into the 2×2×2 mm³ space of the EPI image. From these images, we derived ventricular segmentations. We registered the individual subjects’ rsfMRI data (average volume) to the ENIGMA EPI template and ICBM template using FSL’s (Jenkinson et al. 2012) (fsl.fmrib.ox.ac.uk/fsl) flirt and segmented them into tissue classes using FSL’s fast. Using the segmented EPI ventricular tissue masks, we found the number of voxels that overlapped with the subjects’ ventricular masks derived using the individual T1w Free Surfer parcellated images. Ventricle overlap was calculated using the Dice overlap metric. 34 subjects not included in the ACP study for representative EPI template creation and 50 subjects that were included to create representative EPI brain template in ACP study were used for this analysis.

Results

PCA-based de noising and tSNR maps

We calculated tSNR values at the voxel level, before and after applying the MPPCA denoising filter to the rsfMRI data. For a representative sample subject data from the Human Connectome Project (HCP) study, we show the tSNR maps for raw data (Fig. 1a) and filtered data (Fig. 1b). As a comparison, we applied Gaussian kernel smoothing to the raw data to enhance the tSNR; we found that Gaussian kernel smoothing, with σ=2mm, led to an average tSNR close to the tSNR after applying the MPPCA de noising filter (Fig. 1c), though it introduced a partial volume averaging effect along with compromised spatial resolution. The impact of the two de noising techniques is shown on the visual-sensory network extracted in the same sample subject using FSL-Melodic approach (Beckmann and Smith 2004). Following MPPCA filtering approach, the spatial structure of cortical network adherers to the cortical and subcortical gray matter. Gaussian smoothing and associated partial voxel averaging artifact lead to a smoother network pattern that encroaches in the cortical white matter and removal of the smaller nodes (Fig. 1d).

Fig. 1.

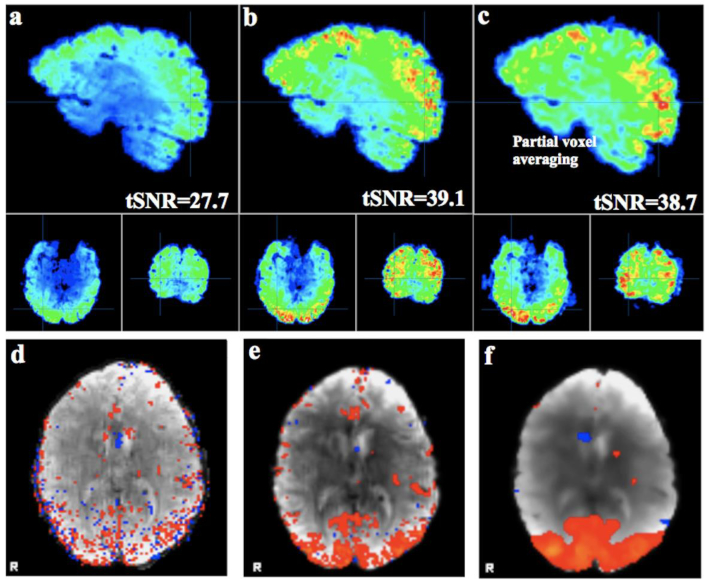
Temporal signal-to-noise ratio (tSNR) maps from a representative sample subject data from the HCP study. Maps shown are for raw data (a), filtered data using the MPPCA filter (b), and applying Gaussian kernel smoothing (σ=2mm) on the raw data yielding the average tSNR close to the tSNR of the filtered data using MPPCA filter (c). The impact of the denoising on the state visual network demonstrated by localization of the activity to the cortical gray matter in the MPPCA denoised data (e) versus raw data (d) and Gaussian smooth data (f) in bottom row.

The average tSNR values were calculated from the raw data before applying the MPPCA de noising filter and after applying the MPPCA de noising filter (filtered data) from the individual subjects for all datasets (shown in Fig. 2a). The tSNR values increased significantly due to MPPCA de noising filter, except for datasets from the CAMH (Centre for Addiction and Mental Health), ZHH (Zucker Hillside Hospital), and SDSU (San Diego State University) studies, which on average increased but were not statistically significant. The SNR values calculated as described in SNR test and as shown in Fig. 2b improved significantly for all datasets after applying the de noising filter. The higher tSNR and SNR values after applying MPPCA de noising showed the utility of this algorithm in enhancing the signal quality of the rsfMRI data. For HCP dataset, the tSNR and SNR values calculated from 9 min of scan time (labeled as ‘HCP_9min’) do not differ from those values calculated from the entire scan time (14 min 24 sec) (labeled as ‘HCP’) as shown in Fig. 2.

Fig. 2.

Average tSNR values for rsfMRI datasets before and after applying the MPPCA filter (raw and denoised data). Here, tSNR values were computed as tSNR=mean signal intensity/variation over time, as described in Method 1, Figure 2(a). The SNR values (Figure 2b) were computed using Method 2, described in text. The error bars represent the standard error of the mean.

Fig. 3 shows the variation of these tSNR values with the rsfMRI data acquisition parameters. The tSNR values from raw data showed a positive linear relation with TR (Fig. 3a), and voxel size (Fig. 3b). Here, the positive linear relationship between tSNR and TR is significant. The tSNR values from de noised data showed a positive linear relation with TR (Fig. 3c), and voxel size (Fig. 3d). Here, the positive linear relationship between tSNR and voxel size is significant. Fig. 4 shows the relationship between SNR values, calculated using Method 2, and rsfMRI acquisition parameters. The only significant effect found was a positive linear relationship between SNR values and voxel size for the de noised data.

Fig. 3.

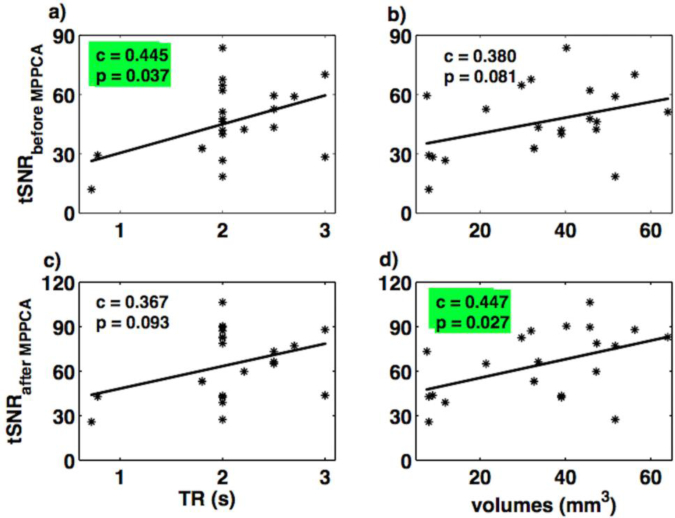
Relation of tSNR (using Method 1) with TR and spatial volumes for rsfMRI datasets, before (a-b) and after applying MPPCA denoising filter (c-d). The subplot marked with green color indicates the significant correlation between variables.

Fig. 4.

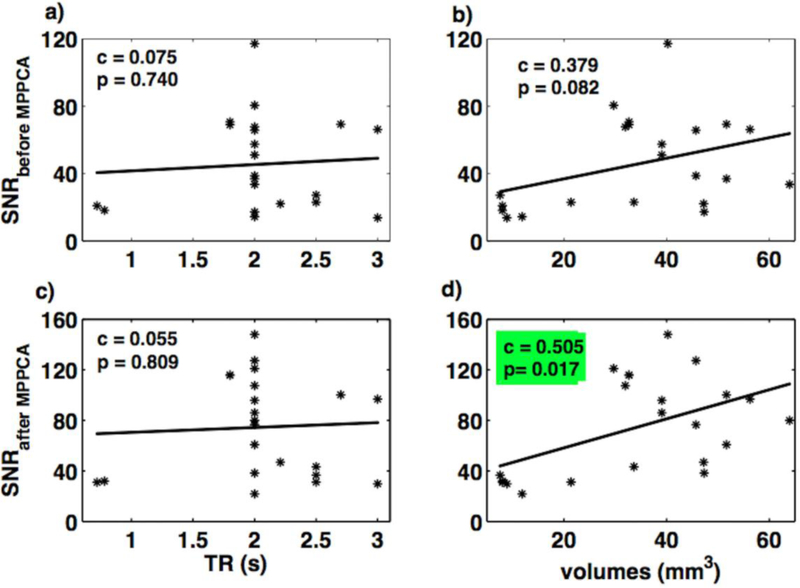
Relation of SNR (using Method 2) with TR and spatial volumes for rsfMRI datasets, before (a-b) and after applying MPPCA denoising filter (c-d). The subplot marked with green color indicates the significant correlation between variables.

ENIGMA EPI template creation

Fig. 5 shows the representative EPI template image for each of the 22 datasets used in our study. A flow chart that summarizes the description of used methods is shown in Fig. 6 These EPI template images were used to create the overall ENIGMA EPI template, shown in Fig. 7a. Tissue segmentation of this template into tissue classes shows the ventricular structure (Fig. 7(b-d)).

Fig. 5:

Representative brain template images for 22 datasets (~50 subjects are included in each dataset).

Fig. 6:

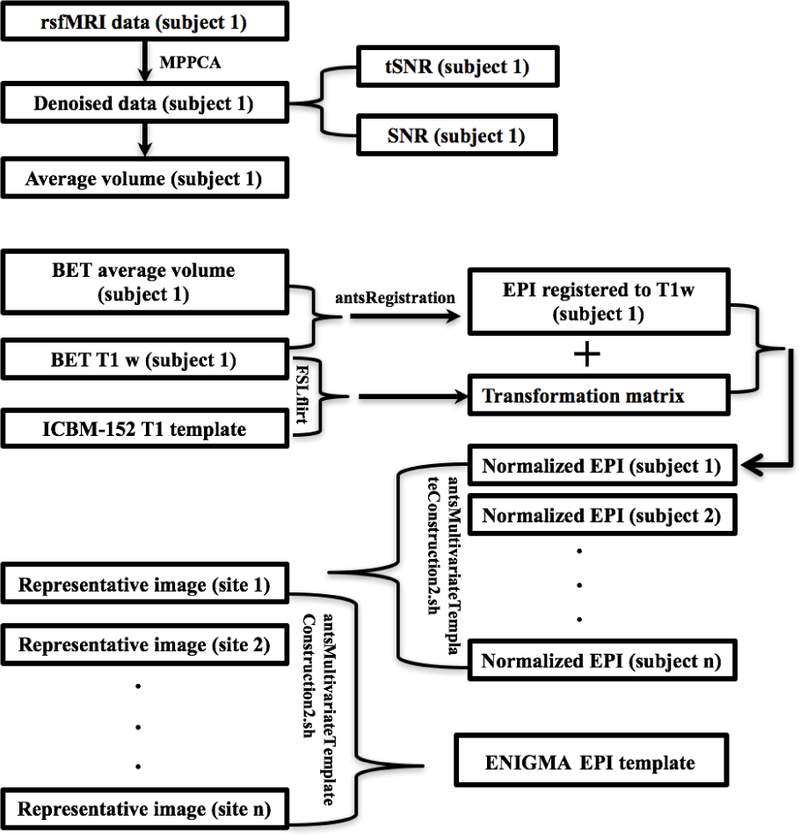
Flow chart that summarizes the description of used methods in ENIGMA rs-fMRI protocol.

Fig. 7.

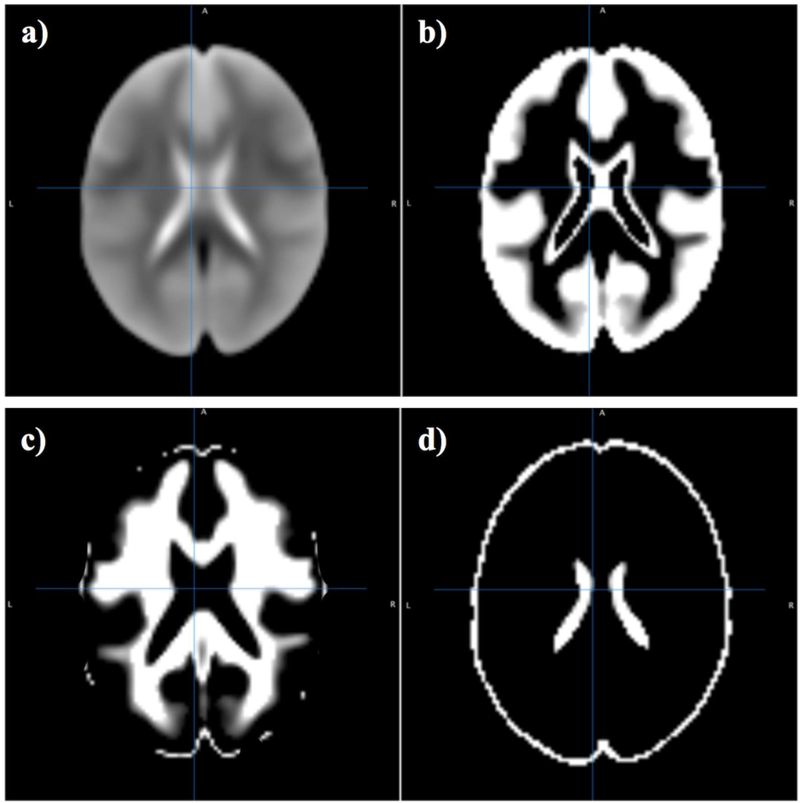
ENIGMA EPI brain template (a) and segmented tissue classes (b-d) for gray matter, white matter and cerebrospinal fluid respectively.

Ventricle overlap

We used individual subjects’ rsfMRI data, from a representative site – the ACP site - for the ventricle overlap calculation. Using 34 individuals who were not used to create the EPI representative template, the % ventricle overlap ranged from 16.6% – 45.2% when registering to the ICBM template and 27.5% – 73.8% when registering to the ENIGMA-EPI template, with mean (± standard error of the mean) % overlap: 28.8 (± 1.3) and 49.4 (± 3.6), respectively. When the brains were registered to ENIGMA EPI template, we found significantly enhanced ventricular overlap than when using the registration to ICBM template (p<10⁻⁹) (Fig. 8a). From the % ventricular overlap calculation, we found the brains that were used to create representative EPI brain template in ACP study were not different from the brains that were not used to create the representative ACP brain template when they were registered either to ICBM or to ENIGMA EPI template, as shown in Fig. 8b.

Fig. 8.

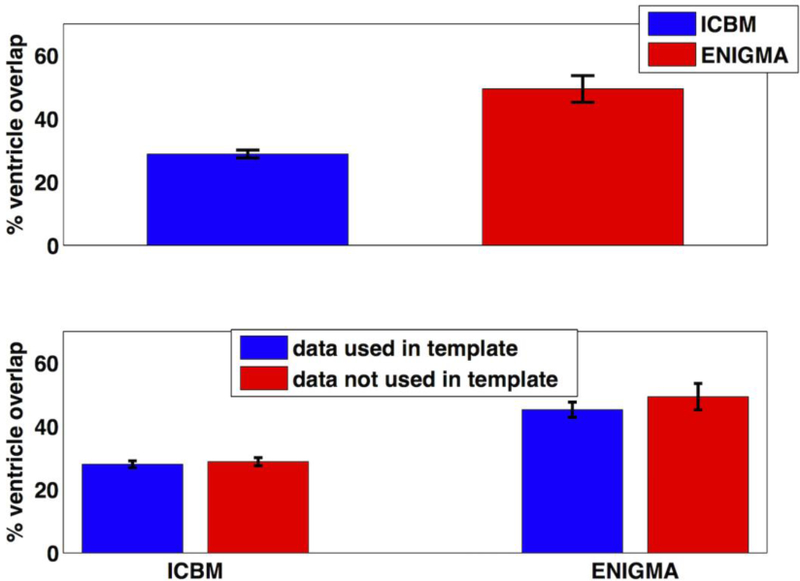
Percentage (%) ventricle overlap: (a) the overall average ventricular overlap was improved significantly (p<10⁻⁹) when the individual subjects’ rsfMRI data was registered to ENIGMA EPI template in comparison to ICBM template. These subjects were not used in ACP study to create a representative brain template. (b) The brains (N=50) that were used in creation of the template (blue in color) were not different from the brains (N=34) that were not used in template creation (red in color) in terms of the % ventricle overlap when computed using ICBM and ENIGMA EPI template. Here, the error bar represents the standard error of the mean.

Discussion

We used a diverse rsfMRI data from public repositories and/or provided by ENIGMA members to develop a harmonized preprocessing pipeline composed of two primary components. First, we propose the use of a novel de noising approach and second, we propose the registration to a deformable template, which we created here from twenty-two diverse datasets and refer to as the ENIGMA EPI template. These two preprocessing steps serve as the preliminary steps in developing a unimodality analytic pipeline to extract resting-state measurements across multiple independent sites with diverse acquisition protocols.

We analyzed twenty-two representative independent datasets to summarize the state of the existing rsfMRI data. There was a considerable variability in the rsfMRI protocols used across sites and studies. The datasets used had substantial variability in their spatial and temporal resolution, the number of volumes, and the total scan duration. The T1w data had also variability in spatial resolution and image quality. The signal to noise ratio (SNR) and temporal-SNR (tSNR) are two important quality parameters that describe a protocol’s ability to provide detection of changes in BOLD signal versus noise, especially in smaller brain structures. For instance, Murphy and colleagues (Murphy et al. 2007) derived an approximate relationship between tSNR, the size of the brain region and the duration of an fMRI experiment necessary to detect a given fMRI signal. This places an emphasis on choosing the correct protocol parameters as a compromise between duration, spatial resolution and sensitivity to neuronally induced BOLD changes (Brooks et al. 2013). The SNR and tSNR are dependent on the interaction between protocol parameters and the methodological and physiological noise in the fMRI signal. Sources of fMRI noise include physiological noise, such as cardio-respiratory effects (Kruger and Glover 2001) and head movement, physical noise, such as thermal noise from the subject and electronics (Weisskoff 1996; Greve et al. 2011) and external RF sources, and sequence-related artifacts such as aliasing, slice crosstalk, truncation artifacts (Gibbs ringing) and EPI ghosting (Heiland 2008). There is a complex interaction between protocol parameters and noise in the images. Aside from the thermal noise, the fMRI noise is generally heteroscedastic, nonstationary and temporally correlated (Turner and Twieg 2005), due to underlying physiological signal fluctuations (Biswal et al. 1995). Moreover, the SNR will vary with sampling rate and spatial resolution, so we should expect that the degree of correlation due to physiological signal fluctuations will vary accordingly (Purdon and Weisskoff 1998). For instance, reducing voxel size and repetition time will reduce the contribution from physiological signal fluctuations but will also reduce SNR and tSNR due to higher physical noise. In these aggregated data, we demonstrated that MPPCA denoising can improve SNR and tSNR properties of the diverse data while maintaining spatial resolution. In all datasets, we observed a positive correlation between SNR/tSNR and voxel sizes, and also between SNR/tSNR and the repetition time of the image acquisition. The smaller voxel sizes and shorter TR of the HCP dataset may help reducing the influence of physiological signal fluctuations, but it also led to lower tSNR than conventional protocols. Larger voxels tend to smooth the anatomy in larger volumes, so while the SNR may be higher, there is a clear tradeoff with level of detail and anatomical specificity.

There are multiple ways to improve both SNR and tSNR in fMRI. Spatial smoothing such as Gaussian kernel filtering are routinely used to improve both SNR and tSNR parameters but at the expense of reducing spatial specificity (Molloy et al. 2014; Triantafyllouet al. 2006). Advanced de noising techniques can improve SNR characteristics by taking advantage of the spatial and temporal dimensions of the fMRI data (Du et al. 2016). We tested a new PCA based de noising technique to reduce signal fluctuations rooted in thermal noise and hence increase the tSNR without altering the spatial resolution (Fig. 1). The thermal noise-selective nature is based on data redundancy in the PCA domain, using universal properties of the eigenspectrum of random covariance matrices (Veraart et al. 2016b). The bulks of PCA eigenvalues arise due to noise and can be approximated by the universal Marchenko-Pastur distribution (MPPCA). Marchenko-Pastur parameterization allows us to estimate the noise level in a local neighborhood based on the singular value decomposition of a matrix combining neighborhood voxels (Veraart et al. 2016a). After removing noise-only components, the resulting images show enhanced SNR due to suppression of thermal noise components of the signal. This de noising approach is free from the limitations of the loss of spatial resolution of the image and introduction of additional partial volume effects that lead to complications in further quantitative analyses or to biases in diffusion modeling (Veraart et al. 2016b). In addition, this approach does not alter the resting state network activation patterns as they are found from raw data. On the other hand, spatial smoothing using a Gaussian kernel leads to partial voxel averaging, spreading the activations across gray and white matter regions and removing smaller nodes (Fig. 1d). We observed a significant increase in SNR and tSNR characteristics across the datasets. Suppression of thermal noise reduced the linear relationship between tSNR and TR. The linear relation between SNR/tSNR and voxel size remained as expected.

We are developing a unimodal analysis workflow for rsfMRI analysis. Some rsfMRI analysis pipelines are multimodal and rely on spatial co-alignment of subject’s structural (T1w) and rsfMRI data for regressing of global connectivity signal and region-of-interest (ROI) analyses in a common anatomical frame. Tissue segmentation of T1w data provides spatial localization of the CSF-containing structures and cerebral white matter (WM) for regression of “global connectivity” signal that is believed to convey signal from physiological and/or methodological rather than neural origin (Hayasaka 2013). Likewise, T1w data is used to obtain anatomical ROIs from population-based atlases to derive regional connectivity metrics (Stanley et al. 2013). The disadvantage of this approach for retrospective ENIGMA-type projects, is the site-to-site variability in the quality of the T1w data and the variance in registration quality between T1w and rsfMRI images in the presence of EPI shape distortions (Jezzard 2012). Among the twenty-two datasets, only two, more modern connect omics oriented protocols collected supplementary data to correct EPI-related shape distortions. A recent study has shown the registration of rsfMRI images to an EPI template is better than the registration to T1w data for the same subject, unless the EPI distortion data is collected, in which case the two approaches are similar (Calhoun et al. 2017). There was also a substantial variability in the quality of the T1w datasets across studies. To minimize the potential for this variability to influence the extraction of rsfMRI phenotypes, we developed a deformable ENIGMA EPI template to serve the dual purpose of regression of the global signal and offering a common anatomical spatial reference frame. We show the use of deformable template greatly improves registration for individual EPI images, including ventricular overlap, when compared to the standard ICBM-152 template. The ENIGMA EPI template incorporates the common shape distortions observed across multisite EPI data as well as to serve as normalization target for transformation to ICBM152 standard space.

Registering the rsfMRI data with the brain template that has better ventricle overlap to regress out the noise ultimately improves the data quality. In our study, we found that the ventricle overlap with the ENIGMA EPI template (~50%) was greatly improved in comparison to the ventricle overlap with the ICBM 152 template (~29%). For an independent data subset from the ACP study, when EPI images were registered to the ENIGMA EPI template, ventricle overlap (~ 50%) was greatly improved in comparison to the ventricle overlap (~29%) when EPI images were registered to the ICBM template.

With the advances in image registration methods and techniques, they are widely used (Baloch and Davatzikos 2009; Chen et al. 2008; Cheung and Krishnan 2009; Fedorov et al. 2011; Murphy et al. 2011; Rueckert et al. 1999; van Dalen et al. 2004; Peyrat et al. 2010), leading to numerous new findings in studies of brain and behavior (Bearden et al. 2007), pathology, microscopy, surgical planning, and more (Chen et al. 2008; Cheung and Krishnan 2009; Kikinis and Pieper 2011; Miller et al. 2005; Murphy et al. 2011; Peyrat et al. 2010; Shelton et al. 2005). The symmetric normalization (SyN) algorithm used here was found to be one of the top-ranking methods when Klein et al. (2009) applied and tested 14 nonlinear deformation algorithms to human brain MRI registration. SyN also delivered the most consistently high accuracy across subjects and label sets (Klein et al. 2009). Symmetric approaches tend to outperform closely related asymmetric methods in quantitative evaluation studies (Avants et al. 2008; Beg and Khan 2007; Geng et al. 2009). SyN treats both template and target symmetrically and image features from the individual and template are used to drive the mapping throughout the optimization (Avants et al. 2010). Using 22 representative EPI brain template images as input, we obtained the overall ENIGMA EPI template (Fig. 2a), which, in turn, can be segmented into different tissue classes.

In summary, we are developing a pipeline for multi-site rsfMRI data analysis that offers the opportunity to analyze rsfMRI scans in a harmonized way, to extract comparable measures and perform coordinated statistical tests. Using rsfMRI data from twenty-two independent studies with approximately 50 corresponding T1w and rsfMRI datasets per study, we reviewed and aggregated the state of existing rsfMRI data. We first demonstrated the utility of the MPPCA de noising filter to improve (t)SNR. We then developed a deformable ENIGMA EPI atlas in ICBM152 space based on representative anatomy that incorporates the common shape distortions observed across multi-site EPI data. With this, we showed better ventricular overlap and registration of rsfMRI data, which may be beneficial for future seedbased and covariate analysis of the resulting data.