Optimal-transport analysis of single-cell gene expression identifies developmental trajectories in reprogramming

Summary

Understanding the molecular programs that guide differentiation during development is a major challenge. Here, we introduce Waddington-OT, an approach for studying developmental time courses to infer ancestor-descendant fates and model the regulatory programs that underlie them. We apply the method to reconstruct the landscape of reprogramming from 315,000 scRNA-seq profiles, collected at half-day intervals across 18 days. The results reveal a wider range of developmental programs than previously characterized. Cells gradually adopt either a terminal stromal state or a mesenchymal-to-epithelial transition state. The latter gives rise to populations related to pluripotent, extra-embryonic, and neural cells, with each harboring multiple finer subpopulations. The analysis predicts transcription factors and paracrine signals that affect fates, and experiments validate that the TF Obox6 and the cytokine GDF9 enhance reprogramming efficiency. Our approach sheds light on the process and outcome of reprogramming and provides a framework applicable to diverse temporal processes in biology.

Graphical Abstract

Introduction

Waddington introduced two metaphors that shaped biological thinking about cellular differentiation: first, trains moving along branching railroad tracks and, later, marbles rolling through a developmental landscape (Waddington, 1936, 1957). Studying the actual landscapes, fates and trajectories associated with cellular differentiation and de-differentiation — in development, physiological responses, and reprogramming — requires us to answer questions such as: What classes of cells are present at each stage? What was their origin at earlier stages? What are their likely fates at later stages? What regulatory programs control their dynamics?

Approaches based on bulk analysis of cell populations are not well suited to address these questions, because they do not provide general solutions to two challenges: discovering cell classes in a population and tracing the development of each class.

The first challenge has been largely solved by the advent of single-cell RNA-Seq (scRNA-seq) (Tanay and Regev, 2017). The second remains a work-in-progress. Because scRNA-seq destroys cells in the course of recording their profiles, one cannot follow expression the same cell and its direct descendants across time. While various approaches can record information about cell lineage, they currently provide only very limited information about a cell’s state at earlier time points (Kester and van Oudenaarden, 2018).

Comprehensive studies of cell trajectories thus rely heavily on computational approaches to connect discrete ‘snapshots’ into continuous ‘movies.’ Pioneering work to infer trajectories (Saelens et al., 2018) has shed light on various biological systems, including whole-organism development (Farrell et al., 2018; Wagner et al., 2018), but many important challenges remain. First, with few exceptions, most methods do not explicitly leverage temporal information (Table S6). Historically, most were designed to extract information about stationary processes, such as adult stem cell differentiation, in which all stages exist simultaneously. However, time-courses are becoming commonplace. Second, many methods model trajectories in terms of graph theory, which imposes strong constraints on the model, such as one-dimensional trajectories (“edges”) and zero-dimensional branch points (“nodes”). Thus, gradual divergence of fates is not captured well by these models. Third, few methods account for cellular growth and death during development (Table S6).

Here, we describe a conceptual framework, implemented in a method called Waddington-OT, that aims to capture the notion that cells at any time are drawn from a probability distribution in gene-expression space, and each cell has a distribution of both probable origins and probable fates (Figure 1). It uses scRNA-seq data collected across a time-course to infer how these probability distributions evolve over time, by using the mathematical approach of Optimal Transport (OT).

Figure 1. Modeling developmental processes with optimal transport.

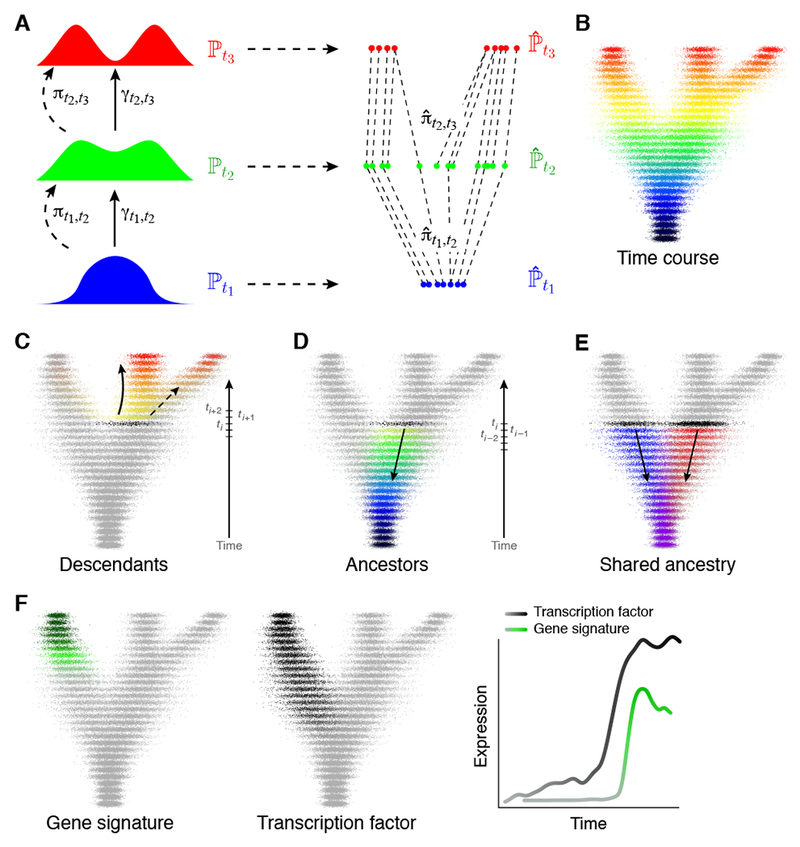
(A) A temporal progression of a time-varying distribution ℙ_t (left) can be sampled to obtain finite empirical distributions of cells ${\widehat{\mathbb{P}}}_{t_i}$. at various time points t₁, t₂, t₃ (right). Over short time scales, the unknown true coupling, γ_t1,t2, is assumed to be close to the optimal transport coupling, π_t1,t2, which can be approximated by ${\widehat{\pi }}_{t_1,t_2}$ computed from the empirical distributions ${\widehat{\mathbb{P}}}_{t_1}$ and ${\widehat{\mathbb{P}}}_{t_2}$. (B) Single-cell profiles (individual dots) are colored by the time of collection. (C) Descendants of a cell set (black) at later times. (D) Ancestors at earlier times. (E) Shared ancestry of two cell sets (black). Ancestors of each population shown in red and blue, shared ancestors in purple. (F) Expression of gene signatures (left; green, high expression; grey, low expression) can be predicted from earlier expression of transcription factors (middle; black, high expression; grey, low expression) in a gene regulatory model by analyzing trends along ancestor trajectories (right).

We apply this framework to the challenge of understanding cellular reprogramming, following transient overexpression of a set of transcription factors (TFs) (Takahashi and Yamanaka, 2016). We aim to address questions such as: What classes of cells arise in reprogramming? What are the developmental paths that lead to reprogramming and to any alternative fates? Which cell intrinsic factors and cell-cell interactions drive progress along these paths? Can the information gleaned be used to improve the efficiency of reprogramming toward a desired destination?

Reprogramming of fibroblasts to induced pluripotent stem cells (iPSCs) (Takahashi and Yamanaka, 2006) has been largely characterized to date by fate-tracing of cells based on a handful of markers, together with genomic profiling studies of bulk populations (O’Malley et al., 2013; Polo et al., 2012). Some studies (Mikkelsen et al., 2008; O’Malley et al., 2013; Parenti et al., 2016) have noted strong upregulation of several lineage-specific genes from unrelated lineages (e.g., neurons), but it has been unclear whether this reflects coherent differentiation of specific cell types or disorganized gene expression (Kim et al., 2015; Mikkelsen et al., 2008). A recent study (Zhao et al., 2018) profiled ~36,000 cells with scRNA-seq in chemical rather than TF-based reprogramming, but identified only a single bifurcation event.

Analyzing >315,000 cells sampled densely across 18 days of reprogramming mouse embryonic fibroblasts (MEFs) into iPSCs, we find that reprogramming unleashes a much wider range of developmental programs and subprograms than previously characterized. Using Waddington-OT to reconstruct the landscape of differentiation trajectories and intermediate states that give rise to these diverse fates, we describe a gradual transition to either stroma-like cells or a mesenchymal-to-epithelial transition (MET) state. Trajectories emerge from the MET state to iPSCs, extraembryonic cells and neural cells. Based on the trajectories, we infer TFs predictive of various fates and suggest paracrine interactions between the stromal cells and other cell types. We experimentally showed that two top predictions indeed enhance reprogramming efficiency.

Results

Reconstruction of probabilistic trajectories by Optimal Transport

Our goal is to learn the relationship between ancestor cells at one time point and descendant cells at another time point: given that a cell has a specific expression profile at one time point, where will its descendants likely be at a later time point and where are its likely ancestors at an earlier time point? We model a differentiating population of cells as a time-varying probability distribution (i.e., stochastic process) on a high-dimensional expression space. By sampling this probability distribution ℙ_t at various time points t, we wish to infer how the differentiation process evolves over time (Figure 1A). From a large number of cells at a given time point (Figure 1B), we can approximate the distribution at that time point, but, because different cells are sampled independently at different time points, we lose the joint distribution of expression between pairs of time points, called temporal coupling. Absent any constraint on cellular transitions, we cannot infer the temporal coupling, but if we assume that cells move short distances over short time periods, then we can infer the temporal coupling by using the mathematical technique of optimal transport (Figure 1A, Methods S1).

Optimal transport was originally developed to redistribute earth for the purpose of building fortifications with minimal work (Monge, 1781) and soon applied by Napoleon in Egypt. Kantorovich generalized it to identify an optimal coupling of probability distributions via linear programming (Kantorovich, 1942), minimizing the total squared distance that earth travels, subject to conservation of mass constraints.

However, the application to cells differs in one key respect: unlike earth, cells can proliferate. We therefore modify the classical conservation of mass constraints to accommodate cell growth and death (Methods S1). Leveraging techniques from unbalanced transport (Chizat et al., 2018), we estimate cellular growth and death rates based on prior estimates from signatures of cellular proliferation and apoptosis (Methods S1, STAR Methods).

Using optimal transport, we calculate couplings between consecutive time points and then infer couplings over longer time-intervals by composing the transport maps between every pair of consecutive intermediate time points. The optimal-transport calculation (i) implicitly assumes that a cell’s fate depends on its current position but not on its previous history (i.e., the stochastic process is Markov) and (ii) captures only the time-varying components of the distribution (see Discussion).

We define trajectories in terms of “descendant distributions” and “ancestor distributions”. For any set C of cells at time t_i, its “descendant distribution” at a later time t_i+1 is the mass distribution over all cells at time t_i+1 given by transporting C according to the temporal coupling (Figure 1C). Conversely, its “ancestor distribution” at an earlier time t_i−1 is the mass distribution over all cells at time t_i−1, obtained by “rewinding” time according to the temporal coupling (Figure 1D). Shared ancestry between two cell sets is revealed by convergence of the ancestor distributions (Figure 1E). The trajectory from C is the sequence of descendant distributions at each subsequent time point, and similarly the trajectory to C is the sequence of ancestor distributions (Figure 1C,D). Thus, we use the inferred coupling to calculate a distribution over representative ancestors and descendants at any other time. We can then determine the expression of any gene or gene signature along a trajectory by computing the mean expression level weighted by the distribution over cells at each time point.

To identify TFs that regulate the trajectory, we sample cells from the joint distribution given by the couplings to train regulatory models. One approach uses ‘local’ information, identifying TFs that are enriched in cells having many vs. few descendants in a target cell population. A second approach builds a global regulatory model, composed of modules of TFs and modules of target genes, to predict expression levels of gene signatures at later time points from expression levels of TFs at earlier ones (Figure 1F).

We implemented our approach in a method, Waddington-OT, for exploratory analysis of developmental landscapes and trajectories, including a public software package (Methods S1). The method: (1) Performs optimal-transport analyses on scRNA-seq data from a time course, by calculating temporal couplings and using them to find ancestors, descendants and trajectories; (2) Infers regulatory models that drive the temporal dynamics; (3) Uses Force-Directed Layout Embedding (FLE) to visualize the cells in 2D (Jacomy et al., 2014; Weinreb et al., 2016; Zunder et al., 2015), and (4) Annotates cells by types, ancestors, descendants, trajectories, expression, and more.

A dense scRNA-seq time course of iPS reprogramming

We generated iPSCs via a secondary reprogramming system (Figure 2A). We obtained MEFs from a single female embryo which constitutively expresses a Dox-inducible polycistronic cassette carrying Pou5f1 (Oct4), Klf4, Sox2, and Myc (OKSM), and an EGFP reporter incorporated into the endogenous Oct4 locus (Oct4-IRES-EGFP). We plated MEFs in serum, added Dox on day 0 to induce the OKSM cassette (Phase-1(Dox)), withdrew Dox at day 8, and transferred cells to either serum-free N2B27 2i medium (Phase-2(2i)) or maintained them in serum (Phase-2(serum)). Oct4-EGFP⁺ cells emerged on day 10 as a reporter for successful reprogramming to endogenous Oct4 expression (Figure 2A, S1A).

Figure 2. A single cell RNA-Seq time course of iPSC reprogramming.

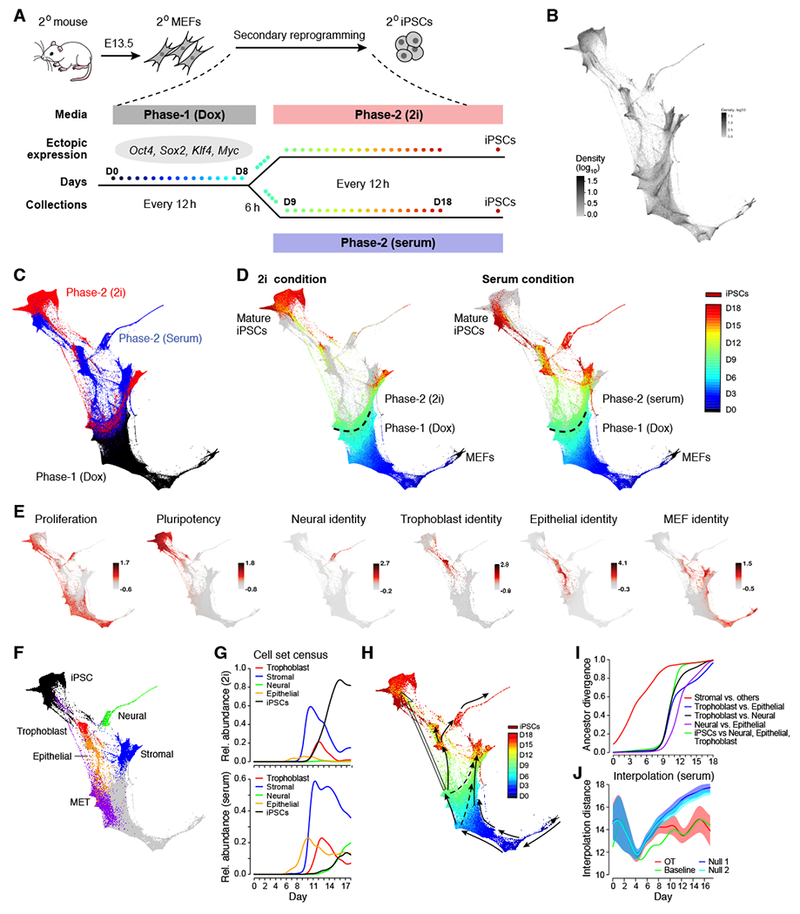
(A) Reprogramming of secondary (2°) MEFs from E13.5 embryos. Each dot represents a collection time-point. (B-F) FLE visualization of scRNA-seq profiles (individual dots). (B) Intensity indicates density of cells in the 2D FLE. (C) Cells colored by condition, with Phase-1 (dox) in black and Phase 2 in blue (serum) and red (2i). (D) Cells colored by time point, with Phase-2 points from only either 2i condition (left) or serum condition (right). Grey points represent Phase-2 cells from the other condition. (E) Patterns of gene signature scores on the FLE. (F) Cell set membership. (G) Relative abundance (y-axis) of each cell set (colored lines) plotted over time in 2i (top) and serum (bottom). (H) Schematic representation of trajectories. (I) Ancestor divergence for pairs of trajectories. Divergence (y-axis) is quantified as 0.5 times the total variation distance between ancestor distributions. (J) Quality of interpolation in serum for OT (red), null models with growth (blue) and without growth (teal). Shaded regions indicate 1 standard deviation. Note that OT is almost as accurate as the batch-to-batch baseline (green). See also Figure S1, S7, Table S1, S2, S6 and Movie S1.

We performed two time-course experiments. In the first, we collected 65,781 scRNA-seq profiles at 10 time points across 16 days, with samples taken every 48 hours. In the second, we profiled 259,155 cells collected at 39 time points across 18 days, with samples taken every 12 hours (every 6 hours between days 8 and 9) (Figure 2A, STAR Methods, Table S1). The two experiments were consistent (STAR Methods, Figure S1B, Figure S1C). We focused on the second experiment (Table S1), retaining 251,203 high quality cells, sequenced at a depth enabling robust analysis, as shown by downsampling (STAR Methods). Comparison to bulk RNA-seq indicated that, with few exceptions, there is minimal sampling bias among cell types (STAR Methods).

Overview of the developmental landscape

We visualized the 251,203 cells in a two-dimensional FLE (Figure 2B), annotated according to condition (Figure 2C) sampling time (Figure 2D, Movie S1), and expression scores of gene signatures (Figure 2E). We identified notable features, discussed below, including sets of cells classified as pluripotent-, epithelial-, trophoblast-, neural-, and stromal-like by expression of characteristic signatures (Figure 2E,F, Table S2). The proportions of these subsets differ between serum and 2i conditions (Figure 2G).

Using Waddington-OT, we identified trajectories to these cell sets (Figure 2H). The ancestors of stromal-like cells begin to diverge from the rest as early as day 1.5, and the distinction sharpens over the next several days (Figure 2I). By contrast, the ancestors of the pluripotent-, epithelial-, trophoblast-, and neural-like populations are indistinguishable until after day 8, when the cells appear to undergo a mesenchymal-to-epithelial transition (MET), as we detail below.

The model is predictive and robust

Because current experimental approaches for tracing cell lineage do not describe the transcriptional profile of a cell set’s ancestors, we developed a computational approach to validate the model. Given three time-points t₁ < t₂ < t₃, we used OT to predict the distribution of cells at time t₂, by interpolating the trajectory from t₁ to t₃ (STAR Methods). We compared our prediction to batches of observed cells at time t₂, they were are roughly as good as could be expected given batch-to-batch variation (Figure 2J and S1D-F). As expected, the quality of interpolation decreases over longer intervals (Figure S1D).

Our analysis is robust to data perturbations and parameter settings. We down-sampled the cells and reads at each time point, perturbed our initial estimates for cellular growth and death rates, and perturbed the parameters for entropic regularization and unbalanced transport (Figure S1G-I, STAR Methods). In all cases, the interpolation results are stable across wide range.

In initial stages of reprogramming, cells progress toward stromal or MET fates

Reprogramming begins with all cells exhibiting a rapid increase in cell-cycle signatures and a decrease in MEF identity (Figure 2E). Over time, cells assume either Stromal or MET identities (Figure 3A,B,C). Cells in the Stromal Region (SR) show distinctive signatures of extracellular matrix (ECM) rearrangement, senescence, cell cycle inhibitors, and a secretory phenotype (SASP) (Figure 3D,E). By contrast, the MET Region contains cells with increased proliferation and loss of fibroblast identity (Figure 3D,F).

Figure 3. In initial stages of reprogramming, cells progress toward stromal or MET fates.

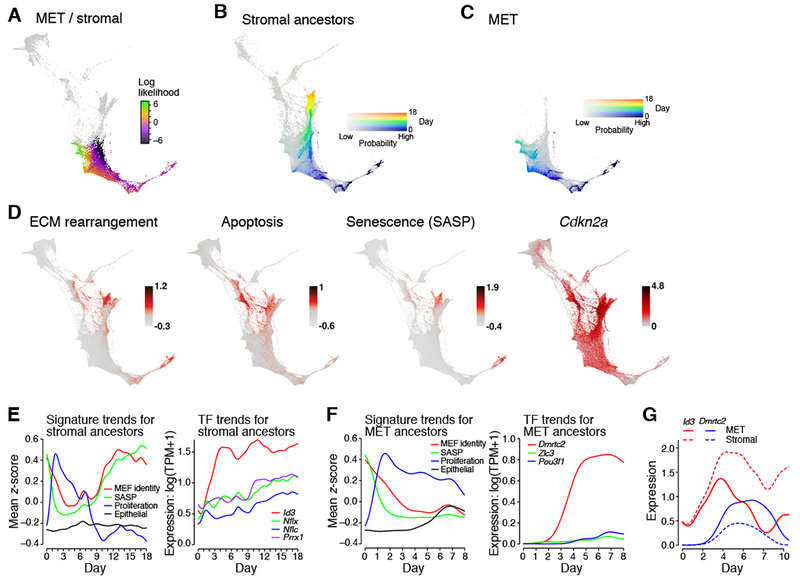
(A) The log-likelihood of obtaining stromal vs. MET fate shows a gradual emergence of fates from day 0 through 8. (B) Ancestors of day 18 stromal cells in serum. Color shows day, intensity shows probability. (C) Ancestors of day 8 MET cells have a distinct trajectory. (D) Activity of gene signatures and individual gene expression (log(TPM+1)) that are associated with stromal activity and senescence. (E) and (F) Gene signature trends along indicated trajectories. (G) TF expression trends along stromal and MET trajectories. See also Figure S2 and Table S2, S3.

While expressing signatures of embryonic mesenchyme and long-term cultured MEFs (Figure S2A), the SR does not simply reflect “MEF reversion” (Figure S2B). In particular, signatures of neonatal muscle and neonatal skin are enriched 20 to 30-fold in the SR.

The proportion of stromal cells peaks on days 10.5 to 11 and then declines through day 18 (Figure 2G). This is not due to cells exiting the SR (Figure S2C), but rather low proliferation and expression of an apoptosis signature.

Among the differentially expressed genes along the two trajectories were early markers of successful MET, including known markers such as Fut9 (which synthesizes the glycoantigen SSEA-1) and novel candidates such as Shisa8, the most differentially expressed gene at day 1.5. It is expressed in 50% of cells most likely to transition to MET (top quartile) but only 5% of cells in the bottom quartile (Table S3). At later time points, both Shisa8 and Fut9 are strongly expressed along the trajectory toward successful reprogramming, and lowly expressed in other lineages (Figure S2D). Shisa8 is a little-studied mammalian-specific member of the single-transmembrane, adapter-like Shisa family, that play developmental roles (Pei and Grishin, 2012).

Trajectory analysis allows us to trace how these fates are gradually established: the ancestor distributions of cells in the Stromal and MET Regions differ by 30% at day 3 and by 60% at day 6 (Figure 2I). A powerful predictor of a cell’s fate is its expression level of the OKSM transgene, whose expression level explains ~50% of the variance in the log fate ratio between MET vs. stromal fate by day 2 and 75% by day 5 (Figure S2E). The divergence is gradual rather than a sharp branch point.

Regulatory analysis identifies TFs associated with the two trajectories. Three TFs (Dmrtc2, Zic3, and Pou3f1) show higher expression along the trajectory to the MET Region (Figure 3C,F,G). Zic3 is required for maintenance of pluripotency (Lim et al., 2007), Pou3f1 for self-renewal of spermatogonial stem cells (Wu et al., 2010), and Dmrtc2 for germ cell development (Gegenschatz-Schmid et al., 2017). Four TFs (Id3, Nfix, Nfic, and Prrx1) show higher expression in cells with stromal fate (Figure 3B,E,G) which is maintained only in stromal cells following dox withdrawal. Nfix represses embryonic expression programs in early development, while Nfic and Prrx1 are associated with mesenchymal programs (Froidure et al., 2016; Messina et al., 2010). Higher expression of Id3 along the trajectory toward stromal cells may seem surprising, because its forced expression increases reprogramming efficiency (Liu et al., 2015). Id3 might cause increased efficiency by acting in stromal cells, which secrete factors that enhance iPSC reprogramming (below), or in non-stromal cells, in which it is expressed through day 8, albeit at lower levels.

iPSCs emerge through a tight bottleneck from cells in the MET Region

The iPSC trajectory encompasses ~40% of all cells at day 8.5, but only ~10% of cells at day 10 in 2i conditions and only ~1% at day 11 in serum conditions. This suggests that only a small and distinct subset of cells transitioning out of the MET Region has the potential to become iPSCs. These iPSC progenitors have not yet fully acquired the pluripotency signature but are changing rapidly toward this fate. They reside along certain thin ‘strings’ in the FLE representation (Figure 2H, white arrow and 4A, green). While the FLE shows what appears to be alternate paths (e.g., through trophoblasts), the vast majority of ancestors of iPSCs do not go through these routes by our model (especially in 2i), highlighting a key difference between the OT-model and visualization-based interpretation.

Figure 4. iPSCs emerge from cells in the MET Region.

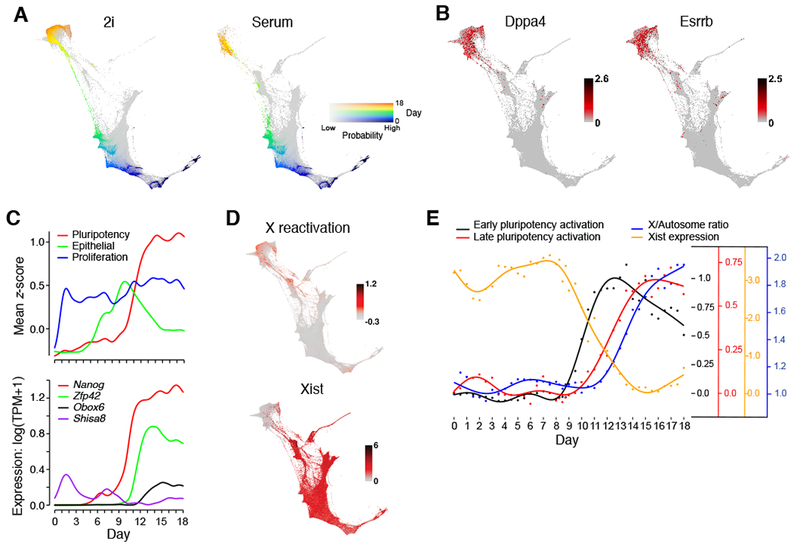
(A) Ancestor trajectory of day 18 iPSCs in 2i (left) and serum (right) (color shows day, intensity shows probability). (B) Expression (log(TPM+1)) of pluripotency marker genes. (C) Expression trends along ancestor trajectory in serum for gene signatures (top) and TFs (bottom). (D) X-reactivation signature (mean z-score) and Xist expression (log(TPM + 1)) on the FLE. (E) Trends in X-inactivation, X-reactivation and pluripotency (Table S4) along the iPSC trajectory in 2i. Each curve has a different y-axis, indicated by color. See also Figure S3 and Table S2, S4.

By day 11.5-12.5, some cells begin to show a clear signature of pluripotency, including canonical marker genes such as Nanog, Zfp42, Dppa4, Esrrb and an elevated cell-cycle signature (Figure 4B,C). In 2i conditions, these iPS-like cells account for 12% of cells by day 11.5 and 80-90% from days 15 through 18 (Figure 2G), reflecting rapid proliferation. In serum conditions, the trend is similar, but the process is delayed and less efficient: the pluripotency signature is found in 3.5% of cells by day 12.5 and peaks at just 10-15% from days 15.5 through 18.

Recent studies reported that a small subset of cells in 2i conditions show a signature characteristic of the embryonic 2-cell (2C) stage (Kolodziejczyk et al., 2015). In our data ~1% of iPSCs showed a 2C signature in both 2i and serum conditions (Table S2, Figure S3A).

Clustering genes by expression trend along the trajectory to iPSCs revealed groups of activated genes regulating pluripotency and repressed genes involved in metabolic changes and RNA processing (Figure S3B). We identified 24 candidate markers of fully reprogrammed cells (including Ooep, Fmr1nb, Lncenc1, and Tcl1) (Table S4).

Regulatory analysis identifies a sequence of TF activity along the trajectory to iPSCs (Figure 4C). The earliest predictive TFs are expressed on days 9-10 (Nanog, Sox2, Mybl2, Elf3, Tgif1, Klf2, Etv5, Cdc5l, Klf4, Esrrb, Spic, Zfp42, Hesx1, and Msc). A second wave is activated on days 12-14, including Obox6, Sohlh2, Ddit3, and Bhlhe40. Notably, Obox6 and Sohlh2 are not expressed in the trajectories to any other cell fate, and have roles in maintenance and survival of germ cells (Park et al., 2016; Rajkovic et al., 2002), but have not been previously implicated in pluripotency.

Finally, our trajectory analysis directly identifies the correct order of events in X-chromosome reactivation (Pasque et al., 2014): Xist is downregulated, then pluripotency-associated proteins are expressed, and finally the X-chromosome is reactivated (Figure 4D,E, STAR Methods).

Development of extra-embryonic-like cells during reprogramming

Another cell subset emerges from the MET Region, gains a strong epithelial signature by day 9, and expresses a trophoblast signature (Figure 5A-C) by day 10.5, peaking at day 12.5 (~20% of all cells) (Figure 2G and 5B).

Figure 5. Extra-embryonic and neural-like cells emerge during reprogramming.

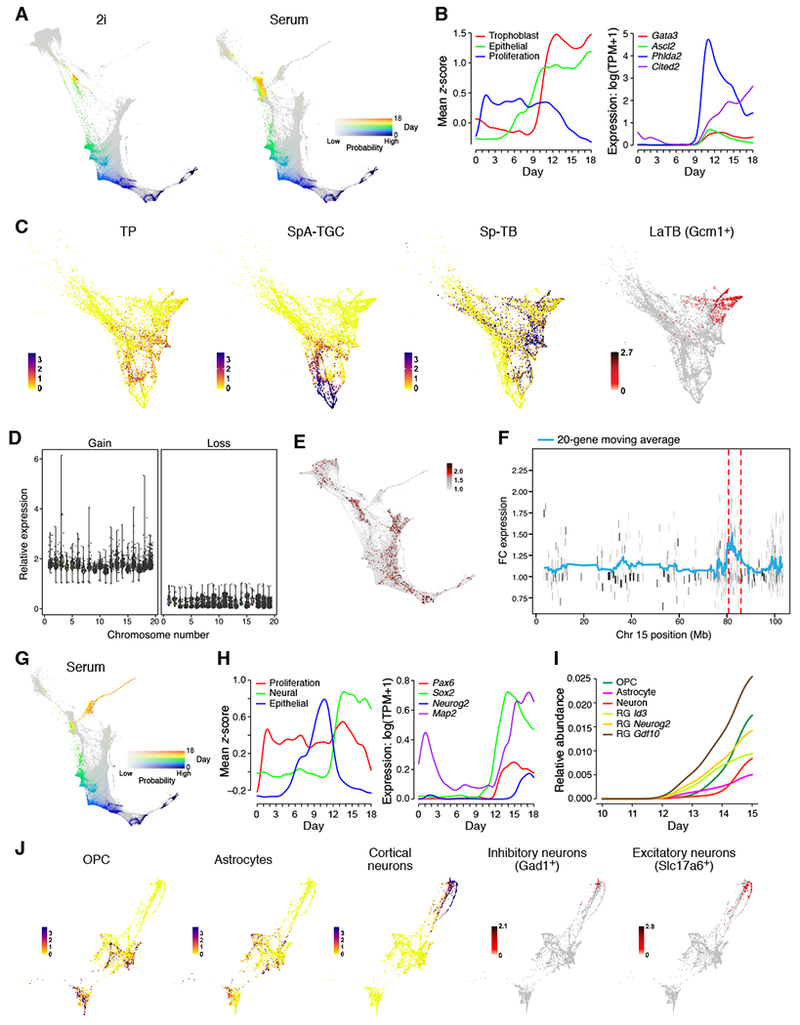
(A) Ancestor trajectory of day 18 trophoblasts in 2i (left) and serum (right) (color shows day, intensity shows probability). (B) Expression trends along trophoblast trajectory in serum for gene signatures (left) and individual TFs (right). (C) An embedding of trophoblasts, colored by signature scores (−log10( FDR q-value)) of TPs, SpA-TGCs, and SpTBs, or by expression of LaTB marker gene Gcm1 (log(TPM + 1)). (D) Average expression of housekeeping genes on chromosomes in single cells (dots) with evidence of genomic amplification (left) or loss (right), relative to all cells without evidence of aberrations (y-axis). (E) Cells are colored by statistical significance (−log10(q-value)) of sub-chromosomal aberrations. (F) Average expression of genes on chromosome 15 in trophoblast-like cells with evidence of a recurrent sub-chromosomal amplification (y-axis, fold change (FC) in expression relative to other cells). (G) Ancestors of day 18 cells in the neural region. (H) Expression trends along the neural trajectory for gene signatures (left) and individual TFs (right). (I) Abundance of neural subtypes. (J) A Neural FLE colored by significance of signature scores (−log10(FDR q-value)) and expression of markers (log(TPM + 1)). See also Figure S4 and Table S2.

Previous studies have noted the expression of some trophoblast-related genes (Cacchiarelli et al., 2015), but trophoblasts have not previously been characterized in reprogramming. We observe a remarkable diversity of subtypes. In normal development, the extraembryonic trophoblast progenitors (TPs) give rise to the chorion, which forms labyrinthine trophoblasts (LaTBs), and the ectoplacental cone, which forms spongiotrophoblasts (SpTBs) subtypes and trophoblast giant cells (TGCs), including spiral artery trophoblast giant cells (SpA-TGCs). Scoring our cells for signatures and markers of these cells (Figure S4A, Table S2, Figure 5C), we find TPs and SpTBs in 2i and serum and SpATGs in serum (Figure S4A), with cells that express LaTBs markers in a separate cluster (~200 cells in 2i but not serum) (Figure S4A). Another 181 cells from a single collection expressed a signature for primitive endoderm (XEN-like cells) (Figure S4B), as previously reported (Parenti et al., 2016).

Regulatory analysis identified TFs at day 10.5 that are predictive of subsequent trophoblast fate (Figure 5B). Several regulate trophoblast self-renewal (Gata3, Elf5, Mycn, Mybl2) (Kidder and Palmer, 2010) and early trophoblast differentiation (Ovol2, Ascl2, Phlda2, Cited2) (Latos and Hemberger, 2016; Tunster et al., 2016; Withington et al., 2006). Others are known to be expressed in trophoblasts, but have no known roles in trophoblast differentiation (Rhox6, Rhox9, Batf3 and Elf3).

Other TFs are predictive of specific subtype fates. Ancestors of TPs expressed Gata3, Pparg, Rhox9, Myt1l, Hnf1b, and Prdm11. These are all expressed in placenta, but only the first two have known roles in trophoblast differentiation (Ralston et al., 2010; Parast et al., 2009). Ancestors of SpTBs or LaTBs expressed Gata2, Gcm1, Msx2, Hoxd13, and Nr1h4. Gata2 is necessary for regulation of trophoblast programs (Ma et al., 1997). Gcm1 and Msx2 have roles in LaTB differentiation, EMT and trophoblast invasion (Liang et al., 2016; Simmons and Cross, 2005), respectively. Nr1h4 is expressed in placenta. Ancestors of SpA-TGCs expressed Hand1, Bbx, Rhox6, Rhox9, and Gata2. Hand1 is necessary for trophoblast giant cell differentiation and invasion (Scott et al., 2000). Bbx is a core trophoblast gene induced by Gata3 and Cdx2 (Ralston et al., 2010).

RNA expression reveals genomic aberrations in trophoblast-like and stromal cells

Trophoblasts are known to selectively amplify specific functional genomic regions by endocycles of replication (Hannibal and Baker, 2016), and we hypothesized that they might harbor detectable genomic aberrations. Similarly, because our stromal cells express stress and apoptosis genes that are often associated with DNA damage, we speculated they too may have aberrations.

We thus analyzed the scRNA-seq data to infer large copy number aberrations from coherent increases or decreases in gene expression (STAR Methods). We found evidence for whole-chromosome aneuploidy in 4.0% of trophoblast cells and 2.1% of stromal cells (vs. 1.1% of all other cells), mostly suggesting loss or gain of a single copy (Figure 5D).

We next searched for evidence of sub-chromosomal aberrations. We found evidence for events in 6.9% of trophoblasts and 3.2% of stromal cells (vs. 1.2% in most other cell types and 0.4% in neural cells) (Figure 5E). Our method has high specificity, but only 45% sensitivity (Figure S4C, STAR Methods).

In trophoblasts, one region, containing 74 genes appears to be highly enriched for sub-chromosomal aberrations (Figure 5F; 8.6% of trophoblasts); it includes Wnt7b, required for normal placental development (Parr et al., 2001); Prr5, which mediates Pdgfb signaling required for labyrinthine cell development (Woo et al., 2007); and several ‘core trophoblast genes’ (Cyb5r3, Cenpm, Srebf2, Pmm1). The top 15 recurrent events also included the amplification of the prolactin gene cluster on chromosome 13 in 1% of cells. Thus, the trophoblast-associated mechanisms of genomic alteration may occur in the trophoblast-like cells.

Stromal cells frequently amplified a region containing cell cycle inhibitors Cdkn2a, Cdkn2b, and Cdkn2c, and frequently lost a region contained Cdk13, which promotes cell cycling, and Mapk9, loss of which promotes apoptosis. These genomic alterations may reflect and contribute to stromal cell function.

Neural-like cells also emerge from the MET Region during reprogramming in serum

In serum (but not 2i) conditions, neural-like cells also emerge from the MET Region, forming a prominent spike in the FLE (Figure 5G). Their ancestors diverge from the ancestors of trophoblasts and iPSCs by day 9 (Figure 2I), and undergo a rapid transition at day 12.5, losing epithelial signatures, gaining neural signatures, and entering the “neural spike” (Figure 5G,H). Cells near the base of the spike express radial glial and neural stem-cell markers, and cells further out along the spike express markers of neuronal differentiation (Figure S4D,E).

In normal development, neuroepithelial cells lose their epithelial identity and turn into radial glial cells (RGCs), which then give rise to astrocytes, oligodendrocytes, and neurons. We used scRNA-seq from mouse brain to derive signatures for these three mature cell types (Table S2), as well as three types of RGCs expressing Id3, Gdf10, or Neurog2 (Figure S4D) (STAR Methods).

About 70% of neural-like cells express at least one of the six signatures. Cells with the three radial glial signatures appear first, concurrent with the loss of epithelial identity and gain of neural lineage identity on day 12.5 (Figure 5I). Cells expressing mature neurons and glia signatures emerge on day 14 and increase thereafter. Their ancestors are concentrated in the RGCs on day 13.5, especially Gdf10 RGCs. While the glial populations overlap substantially, the neurons form a distinct population with substantial substructure, including excitatory and inhibitory neurons (Figure 5J and S4C-E, STAR Methods).

Regulatory analysis identified TFs predictive of neural fate, many with known roles in early neurogenesis (Rarb, Foxp2, Emx1, Pou3f2, Nr2f1, Myt1l, Neurod4), late neurogenesis (Scrt2, Nhlh2, Pou2f2), survival of neural subtypes (Onecut1, Tal2, Barhl1, Pitx2), and neural tube formation (Msx1, Msx3).

The developmental landscape highlights potential paracrine signals

We next asked how these cell types might interact as they reprogram concurrently. For example, secretion of inflammatory cytokines is known to enhance reprogramming (Mosteiro et al., 2016).

Our data reveals rich potential for paracrine signaling (Figure 6A,B, Figure S5A, Table S5). We defined an interaction score based on concurrent expression of ligand-receptor pairs across cell sets (Figure 6A,B and S5A,B, STAR Methods). We observed high interaction scores for several SASP ligands in stromal cells with receptors expressed in iPSCs, such as Gdf9 with Tdgf1 and Cxcl12 with Dpp4 (Figure 6C,F, S5C).

Figure 6. Paracrine signaling.

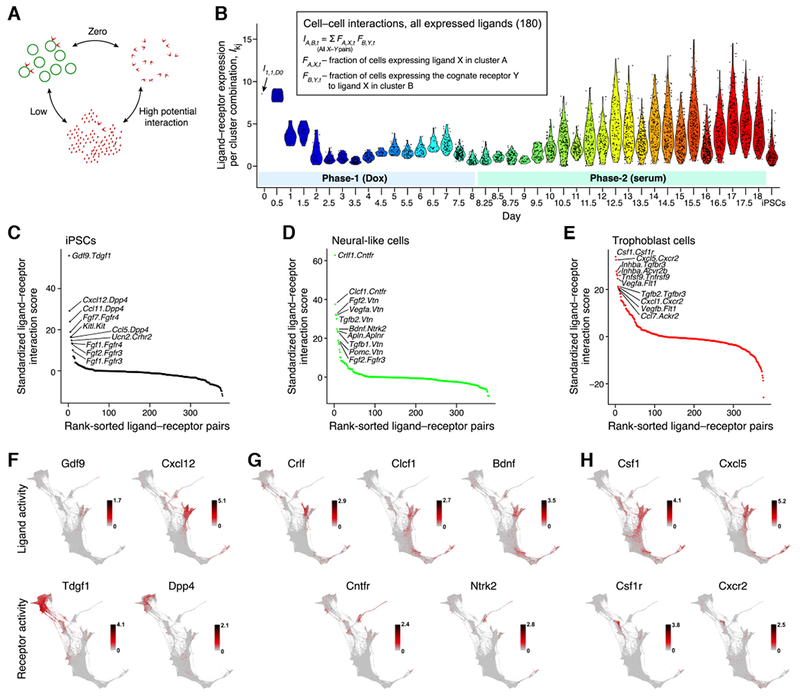
(A) High paracrine signaling interactions occur between groups of cells with high expression of ligand in one group and cognate receptor in the other group. (B) Net paracrine signaling interaction scores in serum. Each dot shows the net score for a pair of cell clusters (Figure S5A). (C-E) Potential ligand-receptor pairs between ancestors of stromal cells and iPSCs (C), neural-like cells (D), and trophoblasts (E). (F-H) Expression level (log(TPM+1)) of ligands (above) and receptors (below) for top interacting pairs between stromal cells and iPSCs (F), neural-like cells (G), and trophoblasts (H). See also Figure S5 and Table S5.

Neural-like cells exhibit potential interactions involving Cntfr (Figure 6D,G, S5D), an Il6-family co-receptor whose activation plays critical roles in neural differentiation and survival (Elson et al., 2000). On day 11.5, a day before neural-like cells appear, their ancestors upregulate expression of Cntfr; expression is 4.6-fold higher in epithelial cells that are neural ancestors versus those that are not. Stromal cells begin expressing three activating ligands for Cntfr (Crlf1, Lif, Clcf1) on day 10.5. These events may help trigger the program of neural differentiation in a subset of epithelial cells in serum. The same ligand-receptor interactions are seen in 2i conditions, but the MEK inhibitor in 2i medium would be expected to block Cntfr signaling and subsequent neural differentiation.

Trophoblast-like cells show potential interactions for Csf1 and Csf1r (Figure 6E,H, S5E). In early placental development, Csf1 is expressed in maternal columnar epithelial cells and Csf1r is expressed in fetal trophoblasts, suggesting a functional role of this interaction in trophoblast development. Many other top-ranked interactions for trophoblasts are between a single receptor (Cxcr2) and a multi-member ligand family (Cxcl5, Cxcl1, Cxcl2, Cxcl3, and Cxcl15) (Figure 6E,H, S5E). Cxcr2 is necessary for trophoblast invasion in human (Wu et al., 2016).

Experimental validation confirms that transcription factor Obox6 and cytokine GDF9 enhance reprogramming

We experimentally tested one of the TFs and one of the paracrine interactions that our analyses predicted might promote reprogramming.

We first tested the TF Obox6, which was the TF most strongly correlated with reprogramming success among those not previously implicated in the process (Figure 7A, S6A). Obox6 is a homeobox gene of unknown function that is preferentially expressed in the oocyte, zygote, early embryos and embryonic stem cells (Rajkovic et al., 2002). While it is expressed in a small fraction of cells (<1%) before day 12, almost all cells expressing it (94%) are biased toward the MET Region (Figure 7A, S6A).

Figure 7. Obox6 and GDF9 enhance reprogramming.

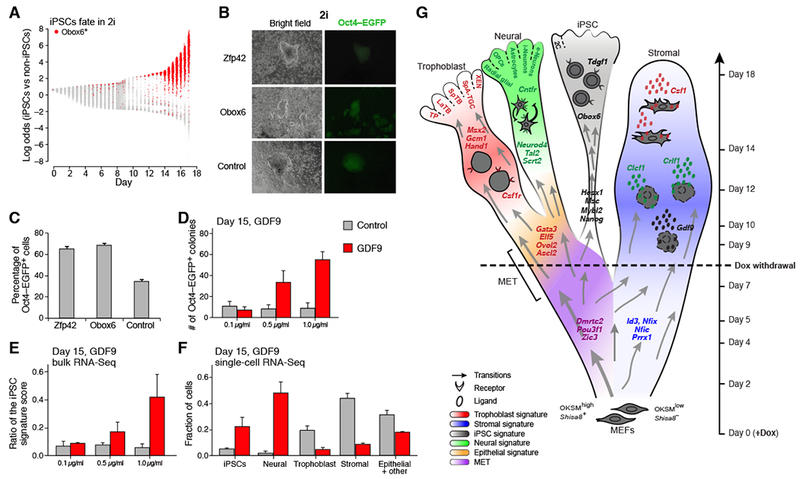
(A) Log-likelihood ratio of obtaining iPSC vs non-iPSC fate on each day (x-axis) in 2i. Obox6⁺ cells in red. (B) Bright field and fluorescence images of iPSC colonies generated in 2i by overexpression of OKSM with either Zfp42 or Obox6 (or negative control). (C) Percentage of Oct4-EGFP⁺ colonies in 2i on day 16, for one of five experiments (Figure S6D). Error bars show standard deviation of three biological replicates. (D-F) Effect of varying concentration of GDF9 (red) vs control (grey) on (D) Oct4-EGFP⁺ colonies (error bars show standard deviation); (E) the strength of iPSC signature score in bulk RNA-Seq; and (F) cellular composition assayed by scRNA-seq. (G) Schematic of the reprogramming landscape in serum. Color indicates cell-set membership. Color of TFs indicates which cell set they regulate. Color of cytokine indicates the cell class to which they signal. See also Figure S6.

To test whether Obox6 can boost reprogramming efficiency, we expressed it together with OKSM during days 0-8. We infected our secondary MEFs with a Dox-inducible lentivirus carrying either Obox6, the positive control Zfp42 (Rajkovic et al., 2002; Shi et al., 2006), or no insert as a negative control. Both Obox6 and Zpf42 increased reprogramming efficiency of secondary MEFs by ~2-fold in 2i and even more so in serum (Figure 7B,C, and Figure S6B-F). Assays in primary MEFs showed similar increases (Figure S6E,F). Our results support a potential role for Obox6 in reprogramming.

We next tested the cytokine GDF9, the ligand with the highest paracrine interaction score for the iPSC lineage, which is predicted to interact with the receptor Tdgf1 (Figure 6C,F). Tdgf1 is known to help maintain the pluripotent state (Klauzinska et al., 2014), but a role in the establishment of pluripotency has not been reported, and efforts to increase reprogramming efficiency through addition of GDF9 at the initial stages of reprogramming (days 0-2) were unsuccessful (Gonzalez-Munoz et al. 2014).

In our reprogramming landscape, Gdf9 and Tdgf1 are expressed in the ancestors of iPSCs and stromal cells, respectively, beginning at day 8. The strength of the predicted interaction increases until day 14 (Figure S5C). We tested whether addition of recombinant mouse GDF9 enhances reprogramming in serum by adding the cytokine daily, starting at day 8 (STAR Methods). We measured the abundance of cell types at day 15 (STAR Methods).

In multiple independent experiments, GDF9 substantially increased reprogramming efficiency in a dose-dependent manner, with the highest dosage producing an average increase of 4-to-5-fold as assayed by (i) counting number of Oct4-GFP positive colonies, (ii) bulk RNA-seq and (iii) scRNA-seq (Figure 7D-F and S6G-I). These results support a role for Gdf9 in reprogramming.

Interestingly, GDF9 also increased the fraction of cells with neural fates (Figure 7F, S6I), possibly in a competitive way with iPSCs. While Gdf9 has no reported function in neurogenesis, the Tgfβ superfamily has been reported to play important roles in various neural lineages specification and maintenance (Aigner and Bogdahn, 2008); this observation warrants further attention.

Discussion

Understanding the trajectories of cellular differentiation is essential for studying development and for regenerative medicine. Here, we describe an analytical approach to reconstructing trajectories, and its application to a dataset of 315,000 cells from dense time-courses of reprogramming fibroblasts into iPSCs, shedding light on this problem, and providing a template for studies in other systems.

An optimal transport framework to model cell differentiation

Waddington-OT describes transitions between time points in terms of stochastic couplings, derived from optimal transport. This yields a natural concept of trajectories in terms of ancestor and descendant distributions, without strict structural constraints on the nature of these processes. This allows us to recover shared vs. distinct ancestry between two cell sets, and to infer TFs involved in activating expression programs (Figure 1). Moreover, it can be applied to even a single pair of time points. We validated Waddington-OT by its ability to accurately infer cellular populations at held-out time points and its results are robust across wide variation in parameters.

To set Waddington-OT in context, we comprehensively reviewed 62 other approaches (Table S6), which fall into three classes: category 1 (33 tools) is not applicable to developmental time-courses with scRNA-seq; category 2 (25 tools) is applicable but does not incorporate time information; and category 3 (4 tools) leverages time information, but does not model cell growth rates over time. When we applied several of the most widely used methods from categories 2 and 3 on our data, the results revealed key limitations (STAR Methods, Figure S7). Category 2 methods produced trajectories that are completely inconsistent with the time course—making huge leaps across time points and, in some cases, going backward in time. For example, Monocle2 produced trajectories in which Day 0 cells give rise to Day 18 cells, which then give rise to Day 8 cells. Similar problems are evident in a Monocle2 analysis in a recent analysis of chemical reprogramming (Zhao et al., 2018), in which the program places late-stage cells at the beginning of the trajectory. Category 3 methods encounter a distinct challenge, as they do not account for the higher growth of iPSCs and consequently infer that many apoptotic stromal cells must transition to iPSCs. In addition, two of these Category 3 tools produced trajectories to incoherent final destinations, consisting of mixtures of very different cell types.

Waddington-OT is the only approach that incorporates temporal information and models cell growth over time (which we can consider a new Category 4). It is the only approach that produced reasonable trajectories on our data, suggesting that these features are critical for robust analysis of developmental processes. Moreover, it brings the powerful framework of optimal transport to biology and is the first application of OT to estimate the temporal coupling of a stochastic processes in any field.

Optimal-transport analysis is only intended to capture the time-varying components of a distribution ℙ_t. For systems in dynamic equilibrium, ℙ_t does not change over time and optimal transport would infer that each cell is stationary. (An example would be cells that are asynchronously undergoing cell division. Although each cell is changing, the overall distribution ℙ_t is constant across time.) Our focus is on out-of-equilibrium systems, where the distribution ℙ_t undergoes major changes over time.

Tracking cell differentiation trajectories and fates in a diverse reprogramming landscape

Although the reprogramming of fibroblasts to iPSCs has been intensively studied, our work provides insights that could only be obtained from large-scale profiling of single cells across dense time courses and appropriate analysis.

We uncovered remarkable diversity in the reprogramming landscape, with large classes of cells having distinct biological programs related to distinct states and tissues. Earlier studies based on bulk RNA analysis have detected expression of individual lineage-specific genes, but could not identify coherent cell types (Mikkelsen et al., 2008; O’Malley et al., 2013; Parenti et al., 2016). Further work will be need to characterize the cells’ full identity and relation to natural types.

This extensive diversity raises several key questions, including: (1) What are the differentiation and fate trajectories that span these cell subsets? What are their ancestors and when do they diverge? (2) What cell intrinsic regulatory mechanisms may drive each fate, especially TFs? (3) How do cells of different types affect each other’s development through paracrine signaling?

Our trajectory and regulatory analyses provide a systematic view of differentiation trajectories (Figure 7G). Cells gradually progress towards two initial fates: MET or Stromal (Figure 7G, blue and purple). There is an explosion of diversity following dox withdrawal at day 8: the MET state gives rise to iPSC-, trophoblast-, neural-, and epithelial-like cells. The ancestors of iPSCs pass through a narrow bottleneck before proliferating into iPSCs. Other cells in the MET region first assume an epithelial-like state which gives rise to trophoblasts and neural cells (in serum).

By characterizing events that occur along the trajectory toward any cell class, we identify TFs that regulate cell fates (Figure 7G). Along each trajectory, we rediscover known TFs known to play a role in the differentiation or reprogramming process, validating our approach, but also identify several TFs not previously implicated in the process. We demonstrate the role of Obox6 in increasing reprogramming efficiency.

Finally, we identify a rich potential for paracrine interactions with stromal cells which may play key roles in the initial differentiation and maintenance of iPS-, neural- and trophoblast-like cells.

Of these interactions, we experimentally validated that GDF9 increases reprogramming efficiency.

Future prospects for models and studies of differentiation and development

Our method can be extended to capture additional features of differentiation. First, the framework currently assumes that a cell’s trajectory depends only on its current gene-expression levels. One could incorporate other types of information like epigenomic state. Second, our framework for learning regulatory models assumes that trajectories are cell autonomous, but might be extended to incorporate intercellular interactions, such paracrine signaling, by using optimal transport for interacting particles (Ambrosio et al., 2008; Santambrogio, 2015) (Methods S1). Third, various methods exist for obtaining lineage information about cells, based on the introduction of barcodes at discrete time points or continuously (Kester and van Oudenaarden, 2018). Barcodes can be used to recognize cells that descend from a recent common ancestor cell, but do not currently directly reveal the full gene-expression state of the ancestral cell. However, they might be incorporated into our optimal-transport framework to better estimate temporal couplings. Finally, our method can be refined to analyze all time points simultaneously, rather than just consecutive pairs; this can be particularly useful for situations where the number of cells at different time points varies significantly.

In summary, our findings indicate that the process of reprogramming fibroblasts to iPSCs unleashes a much wider range of developmental programs and subprograms than previously characterized. In Waddington’s metaphor, the reprogrammed cells roll through a rich landscape of valleys. Ultimately, the analysis of natural and artificial trajectories has much to teach us about the genetic circuits that control organismal development and regulate cellular homeostasis.

STAR Methods

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to the Lead Contact Eric Lander at lander@broadinstitute.org.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Secondary MEFs

OKSM secondary Mouse embryonic fibroblasts (MEFs) were derived from E13.5 female embryos with a mixed B6;129 background. The cell line used in this study was homozygous for ROSA26-M2rtTA, homozygous for a polycistronic cassette carrying Oct4, Klf4, Sox2, and Myc at the Colla1 locus and homozygous for an EGFP reporter under the control of the Oct4 promoter (Stadtfeld et al., 2010). Briefly, MEFs were isolated from E13.5 embryos from timed- matings by removing the head, limbs, and internal organs under a dissecting microscope. The remaining tissue was finely minced using scalpels and dissociated by incubation at 37°C for 10 minutes in trypsin-EDTA (Thermo Fisher Scientific). Dissociated cells were then plated in MEF medium containing DMEM (Thermo Fisher Scientific), supplemented with 10% fetal bovine serum (GE Healthcare Life Sciences), non-essential amino acids (Thermo Fisher Scientific), and GlutaMAX (Thermo Fisher Scientific). MEFs were cultured at 37°C and 4% CO₂ and passaged until confluent. All procedures, including maintenance of animals, were performed according to a mouse protocol (2006N000104) approved by the MGH Subcommittee on Research Animal Care.

Primary MEFs

Primary MEFs were derived from E13.5 embryos with a B6.Cg-Gt(ROSA)26Sor^{tm1(rtTA*M2)Jae}/J × B6;129S4-Pou5f1^tm2Jae/J background. Both male and female embryos were used. Primary MEFs were homozygous for ROSA26-M2rtTA, and homozygous for an EGFP reporter under the control of the Oct4 promoter. MEFs were isolated as mentioned above.

METHOD DETAILS

Modeling developmental processes with optimal transport

We developed a probabilistic framework to analyze developmental time courses with single cell RNA seq data. We present here the basic elements of the method, and we refer the reader to Methods S1 for a complete and self-contained description written for a mathematical audience.

The framework is based on the notion of a developmental process, which is a special type of stochastic process (with a modified notion of temporal coupling to accommodate cellular growth and death). The temporal coupling specifies the mass transferred from one region of gene expression space to another over time. For example, a single cell is represented by a single unit of mass concentrated at one point in gene expression space. Over time—as this cell develops, divides, and differentiates—the mass is transported to different locations of gene expression space to form the descendant distribution of the cell.

In order to infer temporal couplings from data, we introduce a key modeling assumption which we refer to as the optimal transport principle. We assume that the true coupling is well approximated by optimal transport couplings over short time scales. Intuitively, this says that the developmental process is proceeding in a locally linear fashion in the space of probability distributions (when this space is equipped with the metric induced by optimal transport).

Given data in the form of samples at various time points along a developmental time-course, we can estimate the optimal transport couplings by solving a finite dimensional convex optimization problem. With enough data, this converges to a close approximation of the true coupling over short time scales. If we assume the process is Markov, then we can compose adjacent time points and estimate temporal couplings over longer intervals.

This mathematical model is described in Chapter I of Methods S1. Chapter I is organized as follows. Section 1 reviews the concept of gene expression space and introduces a probabilistic framework for time series of expression profiles. Section 2 introduces our key modeling assumption to infer temporal couplings of developmental processes. Over short time scales, the true coupling is well approximated by optimal transport couplings. Section 3 shows how we can estimate the optimal transport coupling from data by solving a convex optimization problem. Section 4 describes how to interpret transport maps and temporal couplings. Specifically, Section 4.1 shows how to compute ancestors and descendants of specific subpopulations of cells. Section 4.2 establishes a connection between entropic OT and Brownian motion of indistinguishable particles. Finally, Section 4.3 shows how OT generalizes Waddington’s classical picture of a developmental landscape. Flow through Waddington’s landscape is a gradient flow in gene expression space, which can only describe cell autonomous processes. On the other hand, OT can describe much more general gradient flows in the space of probability distributions on gene expression space, and therefore OT can model processes which involve cell-cell interactions.

We document the capabilities of the software package Waddington-OT in Chapter II of Methods S1. Chapter II is organized as follows. Section 2 shows how to compute transport maps. This takes as input a cost function, an entropy parameter, cell growth rates, and an unbalanced parameter. Section 3 shows how to compute trajectories. Section 4 shows how to fit local and global regulatory models. Section 5 shows how to interpolate the distribution of cells at held-out time points. This can be used to validate the transport maps.

Experimental methods

Reprogramming assay

For the reprogramming assay, 20,000 low passage MEFs (no greater than 3-4 passages from isolation) were seeded in a 6-well plate. These cells were cultured at 37°C and 5% CO₂ in reprogramming medium containing KnockOut DMEM (GIBCO), 10% knockout serum replacement (KSR, GIBCO), 10% fetal bovine serum (FBS, GIBCO), 1% GlutaMAX (Invitrogen), 1% nonessential amino acids (NEAA, Invitrogen), 0.055 mM 2-mercaptoethanol (Sigma), 1% penicillin-streptomycin (Invitrogen) and 1,000 U/ml leukemia inhibitory factor (LIF, Millipore). Day 0 medium was supplemented with 2 μg/mL doxycycline Phase-1(Dox) to induce the polycistronic OKSM expression cassette. Medium was refreshed every other day. At day 8, doxycycline was withdrawn, and cells were transferred to either serum-free 2i medium containing 3 μM CHIR99021, 1 μM PD0325901, and LIF (Phase-2(2i)) (Ying et al., 2008) or maintained in reprogramming medium (Phase-2(serum)). Fresh medium was added every other day until the final time point on day 18. Oct4-EGFP positive iPSC colonies should start to appear on day 10, indicative of successful reprogramming of the endogenous Oct4 locus.

Sample collection

We profiled a total of 315,000 cells from two time-course experiments across 18 days in two different culture conditions: in the first we profiled 65,781 cells collected over 10 time points separated by ~48 hours; in the second we profiled 259,155 cells collected over 39 time points separated by ~12 hours across an 18-day time course (and every 6 hours between days 8 and 9). In the larger experiment, duplicate samples were collected at each time point. Cells were also collected from established iPSCs cell lines reprogrammed from the same MEFs, maintained either in Phase-2(2i) conditions or in Phase-2(serum) medium. For all time points, selected wells were trypsinized for 5 mins followed by inactivation of trypsin by addition of MEF medium. Cells were subsequently spun down and washed with 1× PBS supplemented with 1% bovine serum albumin. The cells were then passed through a 40 micron filter to remove cell debris and large clumps. Cell count was determined using Neubauer chamber hemocytometer to a final concentration of 1000 cells/μl.

Single-cell RNA-seq

ScRNA-seq libraries were generated from each time point using the 10× Genomics Chromium Controller Instrument (10× Genomics, Pleasanton, CA) and Chromium^™ Single Cell 3’ Reagent Kits v1 (65,781 cells experiment) and v2 (259,155 cells experiment) according to manufacturer’s instructions. Reverse transcription and sample indexing were performed using the C1000 Touch Thermal cycler with 96-Deep Well Reaction Module. Briefly, the suspended cells were loaded on a Chromium controller Single-Cell Instrument to first generate single-cell Gel Bead-In-Emulsions (GEMs). After breaking the GEMs, the barcoded cDNA was then purified and amplified. The amplified barcoded cDNA was fragmented, A-tailed and ligated with adaptors. Finally, PCR amplification was performed to enable sample indexing and enrichment of the 3’ RNA-Seq libraries. The final libraries were quantified using Thermo Fisher Qubit dsDNA HS Assay kit (Q32851) and the fragment size distribution of the libraries were determined using the Agilent 2100 BioAnalyzer High Sensitivity DNA kit (5067-4626). Pooled libraries were then sequenced using Illumina Sequencing. All samples were sequenced to an average depth of 87 million paired-end reads per sample (see Experimental Methods), with 98 bp on the first read and 10 bp on the second read. In the larger experiment, we profiled 259,155 cells to an average depth of 46,523 reads per cell.

Lentivirus vector construction and particle production

To test whether transcription factors (TFs) improve late-stage reprogramming efficiency, we generated lentiviral constructs for the top candidates Zfp42, and Obox6. cDNAs for these factors were ordered from Origene (Zfp42-MG203929, and Obox6-MR215428) and cloned into the FUW Tet-On vector (Addgene, Plasmid #20323) using the Gibson Assembly (NEB, E2611S). Briefly, the cDNA for each TF was amplified and cloned into the backbone generated by removing Oct4 from the FUW-Teto-Oct4 vector. All vectors were verified by Sanger sequencing analysis. For lentivirus production, HEK293T cells were plated at a density of 2.6×10⁶ cells/well in a 10cm dish. The cells were transfected with the lentiviral packaging vector and a TF-expressing vector at 70-80% growth confluency using the Fugene HD reagent (Promega E2311), according to the manufacturer’s protocols. At 48 hours after transfection, the viral supernatant was collected, filtered and stored at −80°C for future use.

Determination of paracrine effects of GDF9 on reprogramming

To determine the effect of GDF9 on reprogramming, we plated secondary MEFs at a concentration of 5,000 cells per well of a 24-well plate and added either recombinant mouse GDF9 (R&D Systems, 739-G9-010, lot SOZ0516121) daily from day 8 onward, or control (0.1% Bovine Serum Albumin in 4 mM HCl, R&D Systems, RB04). We initially tested different doses (0, 0.1 μg/ml, 0.5 μg/ml, and 1 μg/ml) and then confirmed results seen at the highest dose in multiple independent experiments. We used three distinct approaches to determine the proportion of pluripotent cell at day 15: (i) counting the number of Oct4-EGFP⁺ colonies using a fluorescence microscope, (ii) bulk RNAseq (Quantseq, Lexogen) and (iii) scRNAseq (as above). For each assay, experiments were performed in biological triplicates (each assay using separate replicates).

Bulk RNAseq data were analyzed as follows: reads (83 bp) were aligned to the UCSC mm10 transcriptome, and a matrix of read counts was obtained using the QuantSeq processing pipeline with the reference genome sequence and gene annotations (GTF file) from the Cellranger 10× Genomics pipeline (v2.0.0). Bulk RNAseq data were used to compute the ratio of iPSC signature scores to the sum of signature scores of other major cell types (iPSC, trophoblast, neural, epithelial and stromal) in each sample (Figure 7E).

Single-cell RNAseq data were analyzed as follows: reads were aligned and processed as described in “Preparation of expression matrices” and cells in which fewer than 1,000 genes were detected were filtered out, yielding 47,540 cells for further analysis. We assigned cells to the major cell sets (iPSC, trophoblast, neural, epithelial and stromal) by clustering and annotation with gene signature scores. (To remove batch effects, we used tools in Seurat (Butler et al., 2018).) Cell-type proportions are shown in Figure 7F, S6H,I.

Reprogramming efficiency of secondary MEFs together with individual TFs

We sought to determine the ability of the candidate TFs to augment reprogramming efficiency in secondary MEFs; the use of secondary MEFs for reprogramming overcomes limitations associated with random lentiviral integration events at variable genomic locations. Briefly, secondary MEFs were plated at a concentration of 20,000 cells per well of a 6-well plate. Cells were infected with virus containing ZFP42, OBOX6, or an empty vector and maintained in reprogramming medium as described above. At day 8 after induction, cells were switched to either Phase-2(2i) or Phase-2(serum). On day 16, reprogramming efficiency was quantified by measuring the levels of the EGFP reporter driven by the endogenous Oct4 promoter. FACS analyses was performed using the Beckman Coulter CytoFLEX S, and the percentage of Oct4-EGFP⁺ cells was determined. Triplicates were used to determine average and standard deviation.

Reprogramming efficiency of primary MEFs with individual TFs and OKSM

We also independently tested the performance of TFs in primary MEFs. To this end, lentiviral particles were generated from four distinct FUW-Teto vectors, containing OCT4, SOX2, KLF4, and MYC, previously developed in the Jaenisch lab. MEFs from the background strain B6.Cg-Gt(ROSA)26Sor^{tm1(rtTA*M2)Jae}/J × B6;129S4-Pou5f1^tm2Jae/J were infected with these lentiviral particles, together with a lentivirus expressing tetracycline-inducible ZFP42, OBOX6 or no insert. Infected cells were then induced with 2 μg/mL doxycycline in ESC reprogramming medium (day 0). At day 8 after induction, cells were switched to either Phase-2(2i) or Phase-2(serum). On day 16, the number of Oct4-EGFP⁺ colonies were counted using a fluorescence microscope. Triplicates for each condition used to determine average values and standard deviation.

Preparation of expression matrices

To compute an expression matrix from scRNA-seq data, we aligned sequenced reads to obtain a matrix U of UMI counts, with a row for each gene and a column for each cell. To reduce variation due to fluctuations in the total number of transcripts per cell, we divide the UMI vector for each cell by the total number of transcripts in that cell. Thus, we define the expression matrix E in terms of the UMI matrix U via:

$$E=\frac{U_{ij}}{\sum {}_{i=1}^G{U}_{ij}}\times {10}^4.$$

In our subsequent analysis, we make use of two variance-stabilizing transforms of the expression matrix E. In particular, we define

1. $\tilde{E}$ to be the log-normalized expression matrix. The entries of $\tilde{E}$ are obtained via

   $$\tilde{E}=\mathit{log}(E_{ij}+1)$$

2. $\stackrel{‒}{E}$ to be the truncated expression matrix. The entries of $\stackrel{‒}{E}$ are obtained by capping the entries of $\stackrel{‒}{E}$ at the 99.5% quantile.

When we refer to an expression profile, by default we refer to a column of $\tilde{E}$ unless otherwise specified.

Read alignment

The 98 bp reads were aligned to the UCSC mm10 transcriptome, and a matrix of UMI counts was obtained using Cellranger from the 10× Genomics pipeline (v2.0.0) with default parameters. Quality control metrics about barcoding and sequencing such as the estimated number of cells per collection and the median number of genes detected across cells are summarized in Table S1. To estimate expression of exogenous OKSM factors from OKSM cassette, we extracted RBGpA sequence (839 bp) from the OKSM cassette FASTA file, and generated a reference using the mkref function from the Cellranger pipeline.

Downsampling and filtering expression matrix

The expression matrix was downsampled to 15,000 UMIs per cell. Cells with less than 2000 UMIs per cell in total and all genes that were expressed in less than 50 cells were discarded, leaving 251,203 cells and G= 19,089 genes for further analysis. The elements of expression matrix were normalized by dividing UMI count by the total UMI counts per cell and multiplied by 10,000 i.e. expression level is reported as transcripts per 10,000 counts.

Selecting variable genes

We used the function MeanVarPlot from the Seurat package (v2.1.0) (Satija et al., 2015) to select 1,479 variable genes. First, we divided genes into 20 bins based on their average expression levels across all cells. Second, we compute Fano factor of gene expression in each bin and then z-scored. The Fano factor, defined as the variance divided by the mean, is a measure of dispersion. Finally, by thresholding the z-scored dispersion at 1.0, we obtained a set of 1479 variable genes. After selecting variable genes, we created a variable gene expression matrix by renormalizing as described above.

Visualization: force-directed layout embedding

In this section we introduce our two dimensional visualization technique based on force-directed layout embedding (FLE) (Jacomy et al., 2014). FLE is large-scale graph visualization tool which simulates the evolution of a physical system in which connected nodes experience attractive forces, but unconnected nodes experience repulsive forces. It better captures global structures than tSNE. Initial FLE algorithms used simple electrostatic and spring forces, but modern FLE algorithms allow for more elaborate interactions that can depend on the degree of nodes or include gravity terms that attract all nodes to the center (this is especially important for disconnected graphs, which would otherwise fly apart). Starting from a random initial position of vertices, the network of nodes evolves in such a manner that at any iteration a new position of vertices is computed from the net forces acting on them.

We apply FLE to visualize the nearest neighbor graph generated from our data.

Implementation:

Our visualization takes as input the expression matrix of highly-variable genes, selected as described in Preparation of expression matrices. First, we reduce to 100 dimensions by computing a 100 dimensional diffusion component embedding of the dataset using SCANPY (v0.2.8) with default parameters. Second, for each cell we compute its 20 nearest neighbors in 100-dimensional diffusion component space to produce a nearest neighbor graph. For this step, we used the approximate k-NN algorithm Annoy from the R package RCPPANNOY (v0.0.10). Finally, we compute the force-directed layout on the k-NN graph using the ForceAtlas2 algorithm (Jacomy et al., 2014) from the Gephi Toolkit (v0.9.2).

Creating gene signatures and cell sets

Gene signatures

We then constructed curated gene signatures from various databases of gene signatures. Given a set of genes, we score cells based on their gene expression. In particular, for a given cell we compute the z-score for each gene in the set. We then truncate these z-scores at 5 or −5, and define the signature of the cell to be the mean z-score over all genes in the gene set.

The table below summarizes the sources from which we obtained signatures. In two cases (neural identity and epithelial identity) we constructed signatures manually using marker genes. A pluripotency gene signature was determined in this work using the pilot dataset. We performed differential gene expression analysis between two groups of cells: mature iPSCs and cells along the time course D0 to D16 and took the top 100 genes with increased expression in mature iPSCs. A proliferation gene signature was obtained by combining genes expressed at G1/S and G2/M phases.

In several places, we also compute gene signatures based on co-expression with a given gene of interest. For instance, in the stromal region we noticed several genes (Cxcl12, Ifitm1, and Matn4) with expression patterns that were distinct from a signature of long-term cultured MEFs (Figure S2B). For each gene, we computed a co-expression signature by finding the set of genes with expression levels in stromal cells that were >15% correlated with the gene of interest. We found that these gene signatures were significantly overlapping (p-value < 0.01, hypergeometric test) with signatures of stromal cells in neonatal muscle and neonatal skin in the Mouse Cell Atlas. Similarly, in the neural region we derived signatures of genes co-expressed with Gad1 and with Slc17a6 (Figure S4D). These signatures significantly overlapped signatures of inhibitory and excitatory neurons, respectively, derived from the Allen Brain Atlas.

Cell sets

Using the gene signatures described above, we created coarse cell sets defining the broad regions of the landscape (iPSC, Trophoblast, Neural, Stromal, Epithelial, and MET), and cell subtype sets defining different cell types within a region (stromal, trophoblast, and neural subtypes, along with 2-cell stage).

To define the coarse cell sets, we first computed a rough partitioning of the landscape by clustering cells using the Louvain method of spectral clustering to obtain 65 cell clusters using k=5 nearest neighbors (Figure S5B). By examining signature score activity levels over clusters, we grouped several clusters to form cell sets for the iPSC, Stromal and Neuronal regions. Because our densely sampled data does not always segregate into distinct clusters, we defined some additional coarse cell sets by signature scores. We define the trophoblast cell set to include all cells with Trophoblast signature greater than 0.7. We defined the epithelial cell set to include all cells with epithelial identity signature greater than 0.8, minus all cells included in other cell sets (mostly removing the trophoblasts with epithelial signature). Finally, we defined the MET Region as the ancestors of iPS, Trophoblast, Neural and Epithelial cells. In particular, we computed the top ancestors of each major cell set, then merged these cell sets and removed the cells in each major cell set.

Within the Stromal, Trophoblast, Neural and iPSC cell sets, we then conducted more sensitive statistical tests for cell subtype signatures. We did this by calculating empirical p-values for the subtype signature score for each (region-specific) subtype in each cell. In each of 100,000 permutation trials, we randomly and independently shuffled the expression levels of each gene across the cells within a region. In each cell, we then computed signature scores in the permuted data, and generated p-values by determining the frequency at which the permuted score was greater than the original score. While the results shown in figures and discussed in the main text are based on shuffling genes across cells, we similarly permuted the expression levels within each cell, and found consistent results. Finally, we controlled for multiple hypothesis testing by calculating FDR q-values, and used a threshold FDR of 10% to define cell subtype sets.

Estimating growth and death rates and computing transport maps

Initial estimate of growth rates

We form an initial estimate of the relative growth rate as the expectation of a birth-death process on gene expression space with birth-rate β(x) and death rate δ(x) defined in terms of expression levels of genes involved in cell proliferation and apoptosis. Multi-state birth-death processes have been used before to model growth, death, and transitions in iPS reprogramming (Liu et al., 2016). A birth-death process is a classical model for how the number of individuals in a population can vary over time. The model is specified in terms of a birth rate β and death rate δ: During a time interval Δt, the probability of a birth is βΔt and the probability of a death is δΔt.

The doubling time for a birth death process is defined as follows. Starting with N(0) = n, the time τ it would take to get to an expected population size of $𝔼N\left(t\right)=2n$ is

$$\tau =\frac{\ln 2}{\beta -\delta }$$

The half-life can be computed in a similar way. We apply a sigmoid function to transform the proliferation score into a birth rate. The sigmoid function smoothly interpolates between maximal and minimal birth rates. We specify the maximal birth rate to be β_MAX = 1.7. Therefore the fastest cell doubling time is

$$\frac{\ln 2}{1.7}\approx 0.41days\approx 9.6hours,$$

by the doubling time equation above. We define the minimal birth rate as β_MIN = 0.3. Therefore the slowest cell doubling time is

$$\frac{\ln 2}{0.3}=2.3days=55hours.$$

Similarly, we transform the apoptosis signature into an estimate of cellular death rates by applying a sigmoid function to smoothly interpolate between minimal and maximal allowed death rates. We define the minimal death rate parameter to be δ_MIN = 0.3, and the maximal death rate parameter as δ_MAX = 1.7. By the calculations above, these correspond to half-lives of 55 and 9.6 hours respectively.

Learning growth rates and computing transport maps

Using the growth rates defined in the previous section as an initial estimate, we compute transport maps and automatically improve these growth rates using the Waddington-OT software package (Methods S1). For the cost function, we use squared Euclidean distance in 30 dimensional local PCA space computed on the variable gene data from the relevant pair of time points. We use the following parameter settings:

ϵ = 0.05, λ₁ = 1, λ₂ = 50, growth_iters = 3.

The parameters λ₁ and λ₂ control the degree to which the row-sums and column-sums are unbalanced. A larger value of λ₁ induces a greater correlation between the input and output growth rates. The Waddington-OT package iterates the procedure of computing transport maps based on input growth rates, and then using the output growth rates as new input growth rates to recompute transport maps. We ran this for growth_iters = 3 total iterations.

This gives us a set of transport maps between each pair of time points, which can be used to estimate the temporal coupling. From this estimate of the temporal coupling, we compute ancestor and descendant distributions to each of the major cell sets defined in the previous section.

Regulatory analysis

We performed regulatory analysis to identify modules of transcription factors regulating modules of genes with our global regulatory model from the Waddington-OT software package (Methods S1). The optimization begins by specifying the number of gene modules, and establishing an initial estimate for each. We used spectral clustering to initialize the modules: genes were clustered into 50 sets, with one module corresponding to each set, and weights set to 0 for genes outside the set, and 1 for genes within the set.

We then specify a time lag between TF and gene module expression. In order to test for potential regulatory interactions on different time scales, we computed global regulatory models with three time lags: 6hrs, 48hrs, and 96hrs. This allowed us to identify factors that are predictive several days in advance -- for instance, Nanog is a very early predictor of pluripotency and was found to be associated with a pluripotency associated gene expression module in the 96 hour model -- as well as those predictive on shorter time scales -- for instance, we TFs that are predictive of neural-associated expression modules in the 6 and 48 hour models, but do not find such predictive TFs in the 96 hour model.

Finally, we set regularization and stochastic block size parameters. Default values available in the code online were used in this study. Briefly, regularization parameters were tuned on small training datasets to enforce sparsity (ℓ₁ penalties) and reduce model complexity (ℓ₂ penalty) while still achieving a good fit (>60% correlation between predicted and observed expression) in training data. These parameters may have to be specifically tuned in new datasets. The stochastic block size and number of epochs were set according to available hardware resources.

Validation by geodesic interpolation

We validate Waddington-OT by demonstrating that we can accurately interpolate the distribution of cells at held out time points. We applied geodesic interpolation (Methods S1) to our reprogramming data to predict the distribution of cells at each time point, using only the data from the previous and next time points. In other words, we sought to predict the distribution ℙ_t2 at time t₂ from the distributions at neighboring time points: ℙ_t1 and ℙ_t3 (Figure 2J, S1D-F). To determine a baseline for performance, we examined the distance between the two different batches of the held-out distribution.

To compute the optimal transport coupling from ℙ_t1 to ℙ_t3, we used the Waddington-OT package with default parameters. For the cost function we compute 30 dimensional local PCA coordinates using only the points from time t₁ and t₃. We then embedded the data from time t₂ into the 30 dimensional local PCA space which was computed using only the data from time t₁ and t₃. Finally, we use Wasserstein-2 distance to compute distance between point clouds.

We compare the performance of OT to four null models:

• Null 1 and Null 2: a point cloud is constructed by interpolating with the independent coupling. Null 1 uses growth in the interpolation. Null 2 does not use growth.

• Null 3 and Null 4: the observed distributions from earlier (Null 3) or later (Null 4) time points are used as the interpolating point cloud.

To estimate the standard deviation of the quality of interpolation, we interpolate using different batches of ℙ_t1 and ℙ_t3.

We investigated the time-scale over which optimal transport accurately recovers temporal couplings by interpolating over longer intervals. With 2-day intervals (Figure S1D) we see some performance degradation compared to 1-day intervals (Figure 2J).

Paracrine signaling analysis

Predicting ligand-receptor interaction pairs

To characterize potential cell-cell interactions between contemporaneous cells during reprogramming, we first collected a list of ligands and receptors found in the GO database. The set of ligands (415 genes) is a union of three gene sets from the following GO terms:

• 1)cytokine activity (GO:0005125),
• 2)growth factor activity (GO:0008083), and
• 3)hormone activity (GO:0005179).

The set of receptors (2335 genes) is defined by the GO term receptor activity (GO:0004872). Next, we used a curated database of mouse protein-protein interactions (Mertins et al., 2017) and identified 580 potential ligand-receptor pairs.

First, we defined an interaction score I_A;B;X;Y;t as the product of (1) the fraction of cells (F_A;X;t) in cell-set A expressing ligand X at time t and (2) the fraction of cells (F_B;Y;t) in cell-set B expressing the cognate receptor Y at time t. We define the aggregate interaction score I_A;B;t as a sum of the individual interaction scores across all pairs:

$$I_{A;B;t}=\sum _{\mathit{All}X-Ypairs}{I}_{A;B;X;Y;t}=\sum _{\mathit{All}X-Ypairs}{F}_{A;X;t}{F}_{B;Y;t}$$

We depicted the aggregate interaction scores for all combinations of cell clusters in Figure 6B, S5A.

Second, we sought to explore individual ligand-receptor pairs at a given day and condition between cell ancestors of interest. For this purpose we define the interaction score I_A;B;X;Y;t as the product of (1) the average expression of the ligand X in ancestors at time t of a cell set A and (2) the average expression of the cognate receptor Y in ancestors at time t of a cell set B. Values of the interaction scores I_A;B;X;Y;t are high for ubiquitously expressed ligands and receptors at a given day and may be nonspecific to a pair of cell ancestors of interest. Thus, we used permutations to generate an empirical null distribution of interaction scores. In each of the 10,000 permutations, we randomly shuffled the labels of cells and calculated the interaction score I^s_A;B;X;Y;t. We then standardized each ligand-receptor interaction score by taking the distance between the interaction score I_A;B;X;Y;t and the mean interaction score in units of standard deviations from the permuted data

$$((I_{\mathrm{A};\mathrm{B};\mathrm{X};\mathrm{Y};\mathrm{t}}-\mathrm{mean}(I^s{}_{\mathrm{A};\mathrm{B};\mathrm{X};\mathrm{Y};\mathrm{t}}))/\mathrm{sd}(I^s{}_{\mathrm{A};\mathrm{B};\mathrm{X};\mathrm{Y};\mathrm{t}})).$$

We depicted examples of standardized interaction scores ranked by their values in Figure 6C-E and S5C-E. Replacement of the average expression of the ligand with the total expression of the ligand in the calculation of the standardized interaction score does not affect the results.

Classification of differential genes along the trajectory to iPSCs

To identify differential genes along the successful trajectory to iPSCs we computed the average expression (TPM) of all 19,089 genes in ancestors of iPSCs. The average expression values were log2 transformed and we filtered out genes for which the difference between maximal and minimal expression value between day 0 and day 18 is less than 1, leaving 2311 genes for further analysis. The genes were classified into 15 groups by k-means clustering as implemented in the R package stats. To identify the number of clusters we applied a gap statistic using the function clusGap from R package cluster v2.0.6.

We performed functional enrichment analysis on the identified gene clusters using the findGO.pl program from the HOMER suite (Hypergeometric Optimization of Motif Enrichment, v4.9.1) (Heinz et al., 2010) with Benjamini and Hochberg FDR correction for multiple hypothesis testing (retaining terms at FDR < 0.05). All genes that passed quality-control filters were used as a background set.

Identifying large chromosomal aberrations

We have previously developed methods to identify copy number variations (CNVs) in scRNA- seq data from tumor samples (Tirosh et al., 2016). That analysis differed from our current study in two key aspects: (1) the data were based on full length scRNA-seq (SMART-Seq2), and sequenced to greater depth in each cell, and (2) there we could rely on the clonal expansion of CNVs to make it easier to identify recurring chromosomal aberrations.

We performed three types of analysis to detect aberrant expression in large chromosomal regions. First, we searched for cells with significant up- or down-regulation at the level of entire chromosomes. Second, we ran a coarse analysis to identify cells with significant net aberrant expression across windows spanning 25 broadly-expressed genes. Focusing on regions that were enriched for cells with significant aberrations found by this coarse filter, we then performed a more sensitive test to compute the significance of aberrations in each window in each cell.

Empirical p-values and false discovery rates (FDRs) were computed by randomly permuting the arrangement of genes in the genome, as described below. In each of 100,000 permutations we randomly shuffle the labels of genes in the entire dataset, while preserving the genomic coordinates of genes (with each position having a new label each time) and the expression levels in each cell (so that each cell has the same expression values, but with new labels). We then compute either whole chromosome or subchromosomal aberration scores for each cell.

To identify whole-chromosome aberrations scores in each cell, we begin by calculating the sum of expression levels in 25Mbp sliding windows along each chromosome, with each window sliding 1Mbp so that it overlaps the previous window by 24Mbp. For each window in each cell, we then calculate the Z-score of the net expression, relative to the same window in all other cells. We then count the fraction of windows on each chromosome with an absolute value Z-score > 2.

This fraction serves as the whole-chromosome aberration score for each chromosome in each cell. To assign a p-value to the whole-chromosome score for cell(i) chromosome(j), we calculate the empirical probability that the score for cell(i) chromosome(j) in the randomly permuted data was at least as large as the score in the original data.

Subchromosomal aberration scores were computed as follows. We begin by identifying the 20% of genes with the most uniform expression across the entire dataset. This is done by calculating the Shannon Diversity e^{−Σ_gE_gcln E_gc} for each gene g (where E_gc is the expression matrix as defined above in Preparation of expression matrices), and taking the 20% of genes with the largest values. Using these genes, we subset the expression matrix and renormalize by TPM, and then compute in each cell the sum of expression in sliding windows of 25 consecutive genes, with each window sliding by one gene and overlapping the previous window (on the same chromosome) by 24 genes. In each window, we calculate the Z-score relative to all cells at day 0. The net (coarse filter) subchromosomal aberration score for a cell is calculated as the l2-norm of the Z-scores across all windows. To assign a p-value to the subchromosomal aberration score for cell(i), we calculate the empirical probability that the score for cell(i) in the randomly permuted data was at least as large as the score in the original data.

Finally, to identify the specific region(s) of genomic aberrations in each cell, we conduct a more sensitive test using just the cells in the stromal and trophoblast regions. Again using 25 housekeeping gene windows, we compute the average z-score of gene expression for genes in each window in each cell. We then compare the scores in all windows in all cells to similar scores computed for each cell in 100,000 random permutation trials, and then assign p-values based on the frequency of extremely high (gain) or low (loss) expression values.

For each of the aberration scores and associated p-values described above, we controlled for mulstiple hypothesis testing by calculating FDR q-values, using a false discovery threshold of 10%.

We tested the sensitivity and specificity of our method using labeled data from Tirosh et al 2016 (Figure S4C).

QUANTIFICATION AND STATISTICAL ANALYSIS

Analyzing the stability of optimal transport

To test the stability of our optimal transport analysis to perturbations of the data and parameter settings, we downsampled the number of cells at each time point, downsampled the number of reads in each cell, perturbed our initial estimates for cellular growth and death rates, and perturbed the parameters for entropic regularization and unbalanced transport. We found that our geodesic interpolation results are stable to a wide range of perturbations, summarized in the following table:

Number of cells per batch	Number of UMIs Per cell	Max Growth βMAX	Min Growth βMIN	Max Death δMAX	Min Death δMIN	Entropy regularization ϵ	Unbalanced transport λ
Down to: 200	Down to: 1000	33 hrs to 5.5 hrs	None to 9.5 hrs	33 hrs to 5.5 hrs	None to 9.5hrs	5 × 10−5 to 0.5	0.1 to 32

To generate this table, we ran geodesic interpolation with all but one of these settings fixed to default values. The default parameter values that we used are:

ϵ = 0.05, λ₁ = 1, λ₂ = 50, β_MAX = 1.7, δ_MAX = 1.7, β_MIN = 0.3, δ_MIN = 0.3.

Moreover, by default we use all reads per cell and all cells per batch.

Benchmarking: comparing to other trajectory inference methods

We compared Waddington-OT to other trajectory inference methods. While many algorithms have been proposed to recover trajectories from single cell RNA-seq data, Waddington-OT is unique in its ability to model cellular growth, death and development over time. The benchmarking results below demonstrate that these features are crucial for accurate analysis: the other approaches considered fail in key respects because they do not leverage measured information about time, or because they do not model cellular growth and death rates.

Categorizing single cell trajectory inference methods

We comprehensively reviewed 62 methods — consisting of 59 methods noted in the recent review by Saelens et al 2018, plus three more recent methods: FateID (Herman et al., 2018), STITCH (Wagner et al., 2018), and URD (Farrell et al., 2018).

The methods fall into four categories:

• (1)methods that are not applicable to developmental time courses with scRNA seq—because they do not handle branching trajectories or apply only to systems at equilibrium;
• (2)methods that do not use information about the time of collection;
• (3)methods that use information about time of collection, but do not model cell growth rates over time;

From each category, we selected several of the best (most widely used) methods and applied them to our data.

Category	Defining feature	Number in category	Methods tested
Category 1	Not applicable to developmental time courses	33	None (because not applicable)
Category 2	Does not use information about time of sampling	25	FateID, URD, Approximate Graph Abstraction, Monocle2
Category 3	Uses information about sampling time, but does not model growth	4	STITCH, GPfates, scDiff

We describe the performance:

Category 1. (33 methods). These methods cannot be used to analyze developmental time courses.

Category 2. (25 methods). All the tested methods in category 2 produce trajectories that are inconsistent with the time course, make huge leaps across time points and in some cases go backward in time in the sense that late time point cells are inferred to be at early time point.

For example, Monocle2 produces trajectories with highly inconsistent temporal ordering — with Day 0 cells giving rise to Day 18 cells, which then give rise to Day 8 cells.

Category 3. (4 methods). All of the tested methods in category 3 are thrown off by the much higher growth rate of certain cell types (e.g., iPSCs) than others (e.g., apoptotic stromal cells). In order to account for the increase in iPSCs, the methods infer that a large fraction of apoptotic stromal cells must transition to iPSCs.

In addition, two of the methods (GPfates, scDiff) produced trajectories to incoherent final destinations (that is, sets composed of mixtures of radically different cell types).

Category 2 results

Monocle2.

This program (Qiu et al., 2017) computes a graph embedding of scRNA-seq data. Applied to our data, Monocle2 produces a graph consisting of 5 segments (Figure S7A). The trajectories are problematic in several respects. First, the trajectories disagree with known information about time. For example, they put day 18 Stromal cells together with Day 0 MEFs at the root of the tree (Branch 1). This gives rise to a branch (Branch 3) consisting of a group of cells spanning days 1.5 to 8 that give rise to a subsequent branch (Branch 4) consisting of a group of cells from day 4 – 9. So, the progression is out of order (with day 18 cells giving rise to day 8 cells which then give rise to day 4 cells). Second, Monocle2 fails to distinguish iPS, Neuronal, and Trophoblast fates as distinct destinations: these populations are all assigned to a common branch (Branch 5). These problems appear to be due to the fact that the method does not leverage known information about time, and because its fully unsupervised approach does not identify meaningful cell sets in the data.

URD.

This program (Farrell et al., 2018) computes a tree connecting a set of root cells to a set of terminal destinations by performing a large number of random walks. Applied to our data (40,000 serum cells, 1,000 per timepoint) with Day 18 iPSCs, Stromal, Neural, and Trophoblasts as terminal destinations, URD inferred a tree consisting of 7 segments (Figure S7B). The trajectories are problematic in several respects. First, fates are determined unreasonably early: the trophoblast lineage is specified by day 0.5 and all branches are specified by day 2. Second, URD predicts that the Neural and iPS lineages arise from Stromal cell set, which is unlikely because the Stromal population expresses signatures of senescence and apoptosis. Third, URD fails to assign over half of all cells to any trajectory. Over 85% of cells from days 4 through 8 are not assigned to any trajectory (96% of cells from day 6 and 94% from day 7). These problems appear to arise due to the failure to incorporate temporal information and to model rates of cellular growth and death. (It might be possible to modify the random walks of URD to account for this).

FateID.

This program (Herman et al., 2018) takes as input a set of terminal destinations and computes a “fate-bias probability” for each cell by iteratively classifying cells with a random- forest classifier. When we applied it to our data (2i conditions), FateID showed serious problems with the trajectories (Figure S7C). First, the fates of iPSCs, Trophoblast, and Stromal remain divergent through the beginning of the time-course (cells do not seem to share a common ancestor at day 0). Second, the trajectories are inconsistent with the temporal information in the sense that trajectories essentially skip over time points. For example, the Stromal trajectory effectively leaps over days 3 through 5, and the iPSC and Stromal trajectories do not contain any cells on day 0. These behaviors are likely due to the fact that FateID does not leverage time- course information in its present formulation. (It might be possible to modify FateID to connect individual pairs of time-points, as in our optimal transport approach).

Approximate graph abstraction.

This program (Wolf et al., 2017) connects clusters to identify a graphical representation of trajectories. We ran the method to connect 65 clusters in our data (2i conditions). The clusters are visualized in the left pane of Figure S7D and the connections inferred by AGA are in the right pane below. The program yielded trajectories that are clearly inconsistent with the temporal information – for example, with cells of day 0 (cluster 1) going directly to late-stage Stromal cells at days 14 through 18 (clusters 63 and 58). In addition, AGA infers extensive transitions from the Stromal region to the iPSC region; this is not biologically plausible because the Stromal cells express strong senesce programs. These problems appear to arise due to the failure to incorporate temporal information and to model rates of cellular growth and death.

Category 3 results

STITCH.

This method was developed by (Wagner et al., 2018), in an application to zebrafish embryonic development. The method constructs a k-NN graph within the cells at each time point and then stitches these together by connecting various cells from adjacent time points. Figure S7E shows the resulting graph when applied to our reprogramming data (2i conditions). The STITCH graph shows iPSCs are largely arising from the Stromal region (that is, the majority of edges connecting to the iPSC region come from the Stromal region). This inference is biologically implausible, as the Stromal cells express strong signatures of senescence and apoptosis. This method appears to fails on our data because it does not model the rapid proliferation of iPSCs — and thus concludes that iPSCs at later time points must come from other sources. (It might be possible to modify STITCH to incorporate cell growth by connecting each cell to a different number of neighbors, based on an estimate of growth).

scDiff.

This method (Rashid et al., 2017) produces a tree of clusters by clustering cells at each time point, moving cells between time points to account for asynchronicity, and assigning to each cluster a single parent cluster. Applied to our data (serum conditions), the method fails to identify iPS, Neural, Trophoblast and Stromal as coherent categories. It produces a tree with 54 leaves, only 4 of which consist of day 18 cells. Some of the leaves consist of day 2 cells. The method appears to fail on our data because its fully unsupervised approach fails to identify meaningful cell sets.

GPfates.

This method (Lönnberg et al., 2017) identifies trajectories by fitting a mixture of Gaussian processes to model a set of branching trajectories over time. Applied to our data (2i conditions), GPfates identifies trajectories to incoherent locations (Figure S7F). Multiple trajectories lead to cells sets containing both iPS and Stromal cells. This implies that iPSCs have significant ancestry in the Stromal region, where apoptotic and senescent programs are highly expressed. The method appears to fail on our data because its fully unsupervised approach does not identify meaningful cell sets and it does not model cell growth.

Sampling bias

In principle, sampling bias could be introduced in sample preparation (in which trypsinized cells are filtered to remove clumps prior to encapsulating the single cell suspension) or in single cell library preparation. To determine whether the proportion of cell types observed in our single-cell data accurately reflected the proportion of cell types in the biological sample, we performed two experiments.

First, we examined the effect of the filtering process by comparing bulk RNA-seq profiles of material collected before and after filtering. Samples were collected in triplicate at days 4, 8, 12, 14, and 16 in serum and 2i conditions. To test the effect of filtering, we compared the correlations between groups (prefiltered and post-filtered) to the variation within each group. We observed that the pre- and post-filtered samples were indistinguishable at all time-points, with the exception of day 16 in serum conditions (for which the pre- vs. post- correlation is lower than the pre- vs. pre- correlation and the post- vs. post- correlation.

Second, we examined the effect of the overall process, including both sample and library preparation. We collected bulk RNA-seq profiles directly from cells in the plate on days 12 and 16 in both 2i and serum (4 profiles). We compared these profiles to additional scRNA-seq data collected in singlicate at these days and conditions, as well as to the scRNA-seq data collected in duplicate in our main experiment (12 profiles, of which one was discarded as discordant with all of the time points in our main experiment). We examined whether the cell type proportions in the single-cell data were consistent with the bulk RNA-seq profile, based on gene signatures of each cell type. The results were consistent at all time-points, with the exception of day 16 in serum conditions (at which trophoblasts appear to be underrepresented by ~3-fold in the single-cell data).

To test whether such an underrepresentation of trophoblasts at day 16 in serum conditions would have an effect on our inferred trajectories, we reweighted the empirical distributions in our optimal transport framework and repeated our analyses. Because the reprogramming process was essentially complete by day 16, the reweighting had no impact on any of our biological conclusions (and had no significant on the optimal transport results apart from slightly increasing transitions to stromal cells from day 16 to day 18).

Pilot study

In our pilot study, we collected 65,000 expression profiles over 16 days at 10 distinct time points (and 9 in serum). We compare results from the larger study to the pilot study in Figure S1B,C, where we show trends in expression along trajectories to each major cell set: iPSCs, Neural-like, Trophoblast-like (placenta-like in pilot), and Stromal. We find that the expression trends are reasonably similar. Moreover, by comparing the ancestor divergence plots for the two studies, we find that in both studies the stromal population gradually diverges early in the time course and there is a sharp divergence of iPSC from Neural and Trophoblast just after removal of Dox at day 8.

DATA AND SOFTWARE AVAILABILITY

We have uploaded our data to NCBI Gene Expression Omnibus. The identification number is:

Single cell RNA-seq raw data

GSE122662

Our data is also available on the Broad Single Cell Portal:

https://portals.broadinstitute.org/single_cell/study/optimal-transport-analysis-of-ipsc-reprogramming

Our software package is available on GitHub:

https://github.com/broadinstitute/wot

ADDITIONAL RESOURCES

We have developed an interactive software package complete with simulated examples and tutorials:

https://broadinstitute.github.io/wot/

Supplementary Material

1

Figure S1. Related to Figure 2: Validation, stability, and comparison to pilot study.

(A) Bright field images of day 2 (Phase1-(Dox)), day 4 (Phase1-(dox)) and day 18 cells during reprogramming in (Phase-2(2i)) and (Phase-2(serum)) culture conditions. BF (bright field). GFP (Oct4-GFP). (B-C) Comparison to pilot dataset. (B) Trends in signature scores along ancestor trajectories to iPSC, Stromal, Neural, and Trophoblast cell sets. Trends for the pilot dataset are shown with open circles and trends for the large dataset are shown with solid lines. (C) Shared ancestry results for pilot dataset (solid lines) and for the larger dataset (dashed lines). (D,E,F) Validation by geodesic interpolation for serum conditions over 2-day intervals (D), for 2i over 1-day intervals (E). As in Figure 2J (which shows serum over 1-day intervals), the red curve shows the performance of interpolating held-out time points with optimal transport. The green curve shows the batch-to-batch Wasserstein distance for the held-out time points, which is a measure of the baseline noise level. The blue and teal curves show the performance of two null models: interpolating according to the independent coupling including growth (blue) or without growth (teal). (F) Validation by geodesic interpolation for serum conditions over 1-day intervals with alternate null models. The purple curve shows the distance between the third time point and the middle time point, and the orange curve shows the distance between the first time point and the middle time point. (G,H,I) Unbalanced transport can be used to tune growth rates. (G) When the unbalanced regularization parameter is large (λ =16), growth constraints are imposed strictly, and the input growth (x-axis; determined by gene signatures- see STAR Methods) is well-correlated to the output growth (y-axis; implicit growth rate determined from the transport map). (H) When the unbalanced parameter is small (λ =1), the growth constraints are only loosely imposed, allowing implicit growth rates to adjust and better fit the data. (I) The correlation of output vs input growth as a function of λ.

4

Figure S4. Related to Figure 5: Trophoblast and Neural subtypes.

(A) Expression of individual marker genes (red color bars, log(TPM +1); see also Table S2) for each subtype on the trophoblast FLE (as in Figure 5C). TP, trophoblast progenitors; SpA-TGC, spiral artery trophoblast giant cells; SpTB, spongiotrophoblasts; LaTB, labyrinthine trophoblasts. (B) Cells with a gene signature of extra-embryonic endoderm (XEN) arise in a single batch on day 15.5 (red color bar, average z-score). (C) Performance of CNV inference. Shown are precision and recall precision and recall at an FDR of 10% (intersecting red lines) for our CNV inference in published scRNA-Seq data that include annotated, clonal CNVs. (D-F) Cells in the neural region were re-embedded by tSNE and annotated with various features. (D) Marker gene expression (red color bar, log(TPM + 1)) of neural subtypes on the neural tSNE. OPC refers to oligodendrocyte precursor cells. (E) Cells with significant expression (black dots) of indicated signatures from the Allen Mouse Brain Atlas on the neural tSNE at an FDR of 10%. (F) Cells in the neural region present from days 12.5-14.5 (left) or days 17-18 (right).

5

Figure S5. Related to Figure 6: Temporal patterns of paracrine signaling.

(A) Temporal pattern of the net potential for paracrine signaling between contemporaneous cells in 2i condition. Each dot represents the aggregated interaction score across all ligand-receptor pairs for a given combination of clusters from (B) (see STAR Methods for details). (B) Cell clusters determined by Louvain-Jaccard community detection algorithm. (C-E) Changes in the standardized interaction scores for top ligand-receptor pairs between ancestors of stromal cells and ancestors of iPSCs (C), neural-like cells (D), and trophoblast cells (E).

6

Figure S6. Related to Figure 7: Impact of Obox6 + and GDP9 on reprogramming

(A-C) Log-likelihood ratio of obtaining iPSC vs non iPSC fate on each day (x-axis) in serum. Obox6⁺ cells in red. (D) Percentage of Oct4-EGFP⁺ cells at day 16 of reprogramming from secondary MEFs by lentiviral overexpression of Oct4, Klf4, Sox2, and Myc (OKSM) combined with either Zfp42, Obox6, or an empty control, in either 2i or serum conditions. Oct4-EGFP⁺ cells were measured by flow cytometry. Plot includes the percentage of Oct4-EGFP⁺ cells in three biological replicates (for Zfp42 and Obox6 overexpression, or an empty control) from five independent experiments (Exp). (E, F) Number of Oct4-EGFP⁺ colonies at day 16 of reprogramming from primary MEFs by lentiviral overexpression of individual Oct4, Klf4, Sox2, and Myc combined with either Zfp42, Obox6, or an empty control in (E) 2i and (F) serum conditions. Plot includes the number of Oct4-EGFP⁺ cells in three biological replicates (for Zfp42 and Obox6 overexpression, or an empty control) from two independent experiments (Exp). (G) The number of Oct4-EGFP⁺ cells at day 15 of reprogramming from four independent experiments (Exp) where mouse recombinant GDF9 were added at three different concentration. (H,I) Impact of GDF9 on cell proportions. (H) tSNE of day 15 cell profiles collected in serum condition supplemented with GDF9 (1 μg/ml) and controls from four independent experiments. Cells are colored by five cell sets by graph-clustering. (I) Proportion of cells from each cluster in (H) in each experiment.

7

Figure S7. Related to Figure 2: Benchmarking analysis

(A) Monocle2 computes a graph upon which each cell is embedded. The graph, which consists of 5 segments, is visualized in the upper-left pane. The 5 segments are visualized on our FLE in the 5 remaining panels of (A). Segment 1 (green) consists of day 0 cells together with day 18 Stromal cells. Segments 2 and 3 consist of cells from day 2 - 8 that supposedly arise from Segment 1 cells. Segment 3 gives rise to Segments 4 (purple) and 5 (red). Segment 4 contains the cells we identify as on the MET region and Segment 5 contains the iPSCs, Trophoblasts, and Neural populations, which Monocle2 infers come directly from the non-proliferative cells in segment 3. (B) The URD tree is displayed in the first panel, and the 7 segments are numbered and color coded. Each remaining panel displays the cells from a single segment on the FLE. Segment 1 (magenta) contains the day 0 MEF cells. The first bifurcation occurs on day 0.5, where segment 2 (consisting of day 0.5 cells) splits off from segment 3 (consisting of day 12-18 Stromal cells). Segment 2 splits to give rise to Segment 4 (consisting of day 2 cells) and Segment 5 consisting of day 12-18 Trophoblasts and Epithelial cells. Segment 4 splits on day 3 to give rise to Segment 6 (consisting of a diverse population including day 3 cells and day 14-18 iPSCs) and Segment 7 (consisting of a diverse population including day 3 cells and day 12-18 Neural-like cells). (C) The fate bias probabilities computed by FateID visualized on our FLE. Color: fate bias probability in barycentric coordinates. Pure green falls near the Trophoblast vertex in the triangular legend and represents 100% chance of Trophoblast fate, while teal, which falls on the edge of the triangle between Trophoblast and Stromal, represents 50% likelihood for each of these two fates and 0% for iPSC. Black points (at the center of the barycentric triangle) have an equal chance of obtaining any of the three fates. Note that bright green and red colors exist before day 8, indicating early fate specification, and note that Day 0 is essentially all blue but there are essentially no blue cells near day 3.5. (D) Our clusters are visualized on the left and the graph computed by Approximate Graph Abstraction is on the right. Note that cluster 1 connects to cluster 58. (E) The STITCH graph visualized on our FLE. Cells are colored by time of collection and edges of the STITCH graph are indicated with lines connecting cells. An abundance of edges connects the Stromal region to the iPSC region. (F) The 3 trajectories inferred by GPfates. Trajectories 2-3 all terminate in both the Stromal and iPSC region.

8

Methods S1. Related to STAR Methods. Mathematical background for optimal transport model of development.

9

Movie S1. Related to Figure 2. Visualizing the flow of cells through time in the FLE.

10

Table S1. Related to Figure 2. Summary of single cell sequencing statistics and sample information.

11

Table S2. Related to Figure 2,3,4,5. List of genes comprising gene signatures.

12

Table S3. Related to Figure 3. Differential genes between top ancestors of MET vs. top ancestors of stromal cells.

13

Table S4. Related to Figure 4. List of genes for 15 groups of genes along the successfully reprogrammed trajectory reported in Figure S3B

14

Table S5. Related to Figure 6. Potential ligand-receptor pairs between stromal cells and iPSCs, neural-like cells, and trophoblast cells ranked by standardized interaction scores.

15

Table S6. Related to STAR Methods. Categorization of single cell trajectory inference methods.

2

Figure S2. Related to Figure 3: Divergence of Stromal and MET fates during the initial stages of reprogramming.

(A) Cells from the stromal region were re-embedded by FLE, and scored for signatures of long-term cultured MEFs (left) or stromal cells in the embryonic mesenchyme (right) found in the Mouse Cell Atlas. (B) Day 0 MEFs (D0; black dots) we re-embedded together with cells from the stromal set (red dots) in a TSNE plot. (C) The Stromal region is a terminal destination as evidenced by (1) the large flow of cells into the region around day 9 (green spike, first and second panels) and (2) essentially zero flow out of the region (blue curves, first and second panels). By contrast, the MET region is a transient state as evidenced by the blue curves in the right two panels showing significant transitions out of MET. (D) Fut9⁺ and Shisa8⁺ expression patterns visualized in a fate-divergence layout. Each dot represents a single cell, colored by expression of either Fut9 (left) or Shisa8 (right). The x-axis shows time of collection and the y-axis shows the log-likelihood ratio of obtaining MET vs Stromal fate, as predicted by optimal transport. (E) Ectopic OKSM expression levels are predictive of MET fate. The y-axis shows correlation between OKSM expression and the log-likelihood of obtaining MET fate. Color (red vs blue) distinguishes the two batches at each time point (x-axis).

3

Figure S3. Related to Figure 4: iPSCs.

(A) False discovery rate q-values for expression of 2 cell signatures on iPSC-specific FLE. (B) Heatmap showing trends in expression of 1479 variable genes (STAR-Methods) along the ancestor trajectory to iPSCs. Color indicates fold-change in expression relative to day 0 (white). Each row shows the mean expression trend for a single gene, where the mean is computed with respect to the ancestor distribution. Genes are clustered into groups with similar trends. Terms on the right indicate significant gene set enrichment (GSEA, all adjusted p-values < 0.01) in one of several databases (M, MSigDB; BP, GO biological process; W, WikiPathways; C, chromosome; CC, GO cellular component).

• Optimal transport analysis recovers trajectories from 315,000 scRNA-seq profiles

• Induced pluripotent stem cell reprogramming produces diverse developmental programs

• Regulatory analysis identifies a series of TFs predictive of specific cell fates

• Transcription factor Obox6 and cytokine GDF9 increase reprogramming efficiency