Pervasive Linked Selection and Intermediate-Frequency Alleles Are Implicated in an Evolve-and-Resequencing Experiment of Drosophila simulans

Evolve-and-Resequence (E&R) experiments, where researchers allow populations to evolve within one or more controlled environments and then whole-genome sequence the resultant populations, are increasingly important in evolutionary genetics methodology. Here, Kelly...

Abstract

We develop analytical and simulation tools for evolve-and-resequencing experiments and apply them to a new study of rapid evolution in Drosophila simulans. Likelihood test statistics applied to pooled population sequencing data suggest parallel evolution of 138 SNPs across the genome. This number is reduced by orders of magnitude from previous studies (thousands or tens of thousands), owing to differences in both experimental design and statistical analysis. Whole genome simulations calibrated from Drosophila genetic data sets indicate that major features of the genome-wide response could be explained by as few as 30 loci under strong directional selection with a corresponding hitchhiking effect. Smaller effect loci are likely also responding, but are below the detection limit of the experiment. Finally, SNPs showing strong parallel evolution in the experiment are intermediate in frequency in the natural population (usually 30–70%) indicative of balancing selection in nature. These loci also exhibit elevated differentiation among natural populations of D. simulans, suggesting environmental heterogeneity as a potential balancing mechanism.

IN evolve-and-resequencing (E&R) experiments, populations evolve within one or more controlled environments and are then surveyed with genomic sequencing (Nuzhdin and Turner 2013; Long et al. 2015). A remarkable volume of data is produced; allele frequency changes at hundreds of thousands of loci within replicated populations. Researchers typically focus on the small fraction of sites exhibiting the largest or most consistent changes, but a wealth of information resides in the “background response,” the evolution of polymorphisms that are not direct targets of selection (the overwhelming majority of the genome). In this paper, we present an analytical framework for E&R studies, first to provide more detailed predictions regarding whole genome evolution, and second to robustly detect loci under parallel selection across replicate populations. We apply the method to a new E&R experiment on Drosophila simulans designed to answer two major questions: First, what is the genomic basis of rapid adaptation to a novel environment? And second, what do the features of the genetic response tell us about the maintenance of polymorphisms in nature?

The genetic basis of rapid adaptation

The traditional view is that adaptive evolution is slow relative to the ecological processes that influence contemporary populations (Slobodkin 1980; Gillespie 1991). In this paradigm, genetic change does not interact with ecological and demographic processes over the short term (few to several generations), encompassed by ecological processes (Thompson 1998; Hendry and Kinnison 1999; Palumbi 2001; Hairston et al. 2005). However, examples of rapid phenotypic evolution have been known since the mid-20th century (Kettlewell 1958; Ford 1964; Johnston and Selander 1964) and its prevalence has become increasingly appreciated in recent years. Rapid evolution has profound practical consequences for biological control of pathogens, pests and invasive species, fisheries management, and biodiversity conservation (Conover and Munch 2002; Darimont et al. 2009), especially in the context of accelerating climate change (Ward and Kelly 2004). Indeed, this growing appreciation for rapid evolution has spawned new subdisciplines such as eco-evolutionary dynamics (Ellner et al. 2011). Rapid evolution of ecologically important traits has been documented in invertebrates (Ellner et al. 1999; Daborn et al. 2002), vertebrates (Reznick et al. 1997; Grant 1999), plants (Franks and Weis 2008), yeast (Lang et al. 2013; Levy et al. 2015), and prokaryotes (Barrick et al. 2009). Biochemical (Ghalambor et al. 2015; Huang and Agrawal 2016), morphological (Losos et al. 1997; Grant 1999), life history (Rose 1984; Hairston and Walton 1986; Reznick et al. 1997), and behavioral (Turner and Miller 2012; Stuart et al. 2014) phenotypes can evolve substantially in just a handful of generations when populations experience new selective regimes. However, less is known about the genomic changes that occur during rapid adaptation to novel environments, especially in multicellular eukaryotes (Messer et al. 2016; Jain and Stephan 2017).

A key question is whether the standing genetic variation within populations is sufficient for adaptation to a novel environment, or if new mutations are required. In sexual eukaryotes, abundant standing variation is indicated by the observation that artificial selection can immediately, and often dramatically, change the mean of almost any variable trait (Lewontin 1974). Still, it is possible that natural selection may fail where artificial selection succeeds if the alleles that respond in artificial selection experiments are encumbered with deleterious side effects. E&R studies seem an ideal alternative to artificial selection experiments in this regard. While the researcher controls fitness with artificial selection, organisms “select themselves” in an E&R experiment. Pleiotropic effects on general vigor will be a major determinant of selection on alleles with favorable trait effects in an E&R experiment, but much less so in an artificial selection experiment. E&R experiments to date provide limited information on the evolutionary potential of natural populations, but only because most were initiated from laboratory-adapted populations or small numbers of founders. Here, we describe an E&R experiment using D. simulans, with replicate experimental populations initiated from large numbers of wild-caught individuals, to investigate the earliest stages of adaptive evolution.

Genome-wide evolution in E&R studies

E&R experiments using Drosophila have addressed questions about the number and kinds of loci under selection, the relative frequency of hard vs. soft selective sweeps, temporal dynamics, and the effect of selection on genome-wide patterns of diversity (Burke et al. 2010; Turner et al. 2011; Orozco-terWengel et al. 2012; Remolina et al. 2012; Turner and Miller 2012; Huang et al. 2014; Tobler et al. 2014; Kang et al. 2016; Barghi et al. 2017; Michalak et al. 2017; Schou et al. 2017). In a review of E&R studies, Nuzhdin and Turner (2013) noted a striking “excess of significance” in that thousands of polymorphisms respond to selection. The number of loci that selection can act on simultaneously is an important and long-standing controversy in evolutionary genetics (Haldane 1957; Sved et al. 1967; Barton 1995), but we generally expect that the more loci affecting fitness, the smaller the allele frequency change per locus. It is thus surprising that so many SNPs exhibit a large change in E&R experiments. There are numerous potential reasons for excessive significance, perhaps the simplest that testing procedures are anticonservative.

Hitchhiking (Maynard Smith and Haigh 1974) is the most likely driver of excessive significance in E&R experiments: most significant tests are neutral SNPs in linkage disequilibrium (LD) with selected loci (Huang et al. 2014). Hitchhiking requires an initial association between loci in the ancestral population(s) and also minimal subsequent recombination over the course of selection. Relevant to both, natural and laboratory-adapted D. melanogaster populations are polymorphic for large inversions and have dramatically suppressed recombination near centromeres (Corbett-Detig and Hartl 2012; Kapun et al. 2014; Tobler et al. 2014), potentially resulting in a large number of false-positive candidate SNPs (Tobler et al. 2014; Franssen et al. 2015; Barghi et al. 2017). We chose D. simulans for this study to evaluate rapid evolution in a population largely free of inversion polymorphism. LD declines rapidly with the physical distance between sites in D. simulans (Signor et al. 2018), but as emphasized by Nuzhdin and Turner (2013), sampling of haplotypes to form experimental populations can generate higher levels of LD (even at considerable physical distance) than are present in the natural population. The contribution of these sampling-generated associations to parallel evolution of replicate E&R populations can be mitigated by founding experimental replicates from distinct samples of the natural population.

Identifying selected loci

A variety of analytic techniques have been developed for E&R studies, applied both at the scale of individual SNPs [e.g., Burke et al. (2010)] and for windows of closely linked polymorphisms (Kelly et al. 2013; Beissinger et al. 2014, 2015). In some cases, tests have been designed to the specific features of the experiment (Turner et al. 2011; Turner and Miller 2012; Huang et al. 2014). Most frequently, the number of sequencing reads called to each alternative SNP base in each population are used as counts in a contingency table analysis; Fisher’s exact test for a single evolutionary replicate (Burke et al. 2010) or the Cochran–Mantel–Haenszel test (CMH) to aggregate signal across replicates (Orozco-terWengel et al. 2012; Huang et al. 2014; Kofler and Schlötterer 2014; Franssen et al. 2015; Barghi et al. 2017). As emphasized by Orozco-terWengel et al. (2012), contingency tables test only whether allele frequency differs between population, not whether differences imply selection. For this, researchers have employed simulations of neutral evolution to establish a threshold for the CMH statistic. Here, we implement a CMH testing pipeline, including neutral simulations, as a contrast to our likelihood/permutation method.

The genome-wide response in an E&R experiment (evolution at both selected and neutral loci) depends on the number/position of selected loci, how loci interact to determine fitness, the nature and extent of LD, the recombination map, and the experimental design. Given these myriad factors, we do not have a clear picture of how much hitchhiking is to be expected in a typical E&R experiment and thus a means to infer direct targets of selection. Here, we build a simulation framework to predict the full observed response of an E&R experiment (Kofler and Schlötterer 2014; Vlachos and Kofler 2018). The design of the experiment (how replicate populations are founded, how many individuals reproduce, and how many generations) is directly reiterated in this model to predict change of every polymorphism in the genome. The simulation is parameter rich, but prior work on D. simulans and its close relative D. melanogaster underpin essential assumptions (e.g., the recombination map, patterns of LD in nature) and observations from our specific experiment specify other features such as the number and genomic positions of polymorphisms and initial allele frequencies. Finally, we extract essential information not only from the extreme outliers (putative targets of selection), but from observations on the “typical SNP.” The amount and variability of change at neutral loci dispersed across the genome is an indicator of genetic draft and thus of selection (Gillespie 2001; Neher and Shraiman 2011). The simulation model provides important insights on the observed experimental results, not only in terms of the number of significant tests but also on the allele frequency spectrum (AFS) at fitness determining loci.

Methods

The experiment

Founding populations:

The ancestral populations of this experiment are from the offspring of wild-collected mated D. simulans females collected from compost piles at Orchard Pond Organic Farm in Tallahassee, Florida (Universal Transverse Mercator Grid coordinates 16N 761030 3386162) between October 28 and November 25, 2014. From each wild-collected female, we collected two male and two female offspring after verifying that male offspring were D. simulans. One male and one female offspring were flash-frozen immediately to represent the founding generation (kept at −80° until DNA extraction). The other male and female were used to found replicate laboratory populations. We initially established six replicate population cages, using one male and one female offspring of 250 wild-caught mated females per replicate and using the offspring of different wild female progenitors in each replicate. Approximately 3 weeks after founding these populations (December 2–3, 2014), the six cages were combined two at a time to form the A, B, and C population replicates. Equal numbers of flies were used from the pair of cages and mixed to create new cages. Thus, each of the A, B, and C populations was founded with ∼1000 individuals descended from non-overlapping sets of 500 wild-caught, mated female parents. The rapid progression from collecting wild flies to establishment of experimental populations minimized inbreeding of founders.

Laboratory rearing and maintenance:

Flies were housed in plexiglass containers, 6028 cm³ in volume, supplied with six 177-ml plastic bottles containing 50 ml of standard cornmeal-yeast-dextrose media. Every 2 weeks, we replaced three of the six bottles with bottles containing fresh media; each bottle remained in a cage for 4 weeks. We replaced plexiglass containers every 28 days, in sync with a media change. Only dead flies were removed when cages were cleaned, and as a consequence, populations had overlapping generations. We censused cages approximately every 5 weeks using digital images, obtaining population estimates: A (mean = 1277, range = 832–1635), B (mean = 849, range = 672–1147), and C (mean = 1187, range = 963–1620). Images were counted three times and the numbers of the three counts were averaged. Means might be underestimated if flies were obscured by other flies in the images.

We maintained populations under constant lighting and temperature conditions (12 hr light/dark cycle, 25°) for ∼195 days from initial collection (population A: founded from females collected October 8–November 1, 2014, descendants preserved May 12, 2015; B: founders collected November 4–11, descendants preserved May 22; C: founders collected November 19–25, descendants preserved June 5). That is, populations were sampled ∼7 months after collection of the wild founders. From the last generation of each population, we collected 500 males and 500 females by aspiration. We snap-froze flies on dry ice at −80° until DNA extraction. For DNA extraction and sequencing, we pooled the 1000 preserved offspring of the founding females to form ancestral samples A0, B0, and C0. Similarly, we pooled the 1000 flies collected at the end of the experiment to form descendant samples (A7, B7, and C7), with “7” designating months since population founding. We extracted and sequenced libraries simultaneously for all six populations.

Library preparation and level of sequencing:

We homogenized whole flies (500 males and 500 females from each ancestral and descendant population) and extracted DNA using DNAzol reagent (Thermo Fisher). We fragmented DNA using a Covaris E220 Ultrasonicator and size selected to produce insert lengths of 380–480 bp. We prepared one sequencing library for each population using the NEBNext Ultra DNA Library kit for Illumina (New England Biolabs, Beverly, MA) following manufacturers recommendations, a unique index for each [New England Biolabs (NEB) indices 13–15 for A0, B0, and C0; indices 16, 18, and 19 for A7, B7, and C7, respectively]. In the first sequencing run, we multiplexed ancestral population samples into one lane, and sequenced multiplexed descendant populations in three additional lanes. Because one library (C7) was overrepresented in the resulting data, we performed an additional sequencing run using the five remaining libraries (A0, B0, C0, A7, and B7), which were multiplexed and run on a single lane. All sequencing was conducted using an Illumina HiSeq 2500 instrument at the Translational Science Lab at Florida State University, using V3 chemistry. We sequenced 150 bp on each of the paired ends. In total, we sequenced DNA from 6000 flies.

Sequence analysis:

We edited read pairs (fastq format) from each population sample using Scythe (https://github.com/vsbuffalo/scythe/) to remove adaptor contamination and then with Sickle (https://github.com/najoshi/sickle/) to trim low-quality sequences. We used the mem function of BWA (Li 2013) to map read pairs to version r2.02 of the D. simulans reference genome, updated from the build published by Hu et al. (2013). We used picard-tools-1.102 to eliminate PCR duplicates from the mapping files; an important step given that PCR duplicates represent pseudoreplication in bulked population samples. Prior to variant calling, we applied the RealignerTargetCreator and IndelRealigner to each population bam file (McKenna et al. 2010). Bam files were input to Varscan v2.3.6 to call SNPs and indels. We piped the output from Samtools (Li et al. 2009) mpileup (version 1.2) to the varscan (Koboldt et al. 2009) functions mpileup2snp (for SNPs) and mpileup2indel (for indels). We obtained the read count (number of alleles) and reference allele frequency at each variant site for each sample. We suppressed indels in downstream analyses as well as all SNPs within 5 bp of an indel, and limited attention to the major chromosomes (X, 2R, 2L, 3R, and 3L).

We scored read depths within each population prior to filtering. The median depth at X-linked loci was very close to 3/4 the corresponding value for autosomal loci (ratio = 0.77 for ancestral populations and 0.75 for descendant populations). For subsequent analysis, we eliminated polymorphisms if the read depth across populations was too low for meaningful tests or atypically high across samples. For inclusion of a SNP, we required at least 60 reads per population for X-linked and 80 for autosomal loci. We excluded SNPs if the total read depth within ancestral and descendant populations (considered separately) was greater than the 95th percentile of the corresponding depth distribution, with separate filtering for autosomal and X-linked sites (the latter have lower coverage). After filtering, 291,272 SNPs remained (58,647, 49,940, 69,010, 71,289, and 42,386 on 2L, 2R, 3L, 3R, and X, respectively). The read depth and allele frequency at each SNP in each population is reported in Supplemental Material, Table S1.

Comparison to other data sets:

We attempted to ascertain SNPs investigated in this experiment within two other recent sequencing studies of D. simulans. Machado et al. (2016) and Signor et al. (2018) also mapped D. simulans reads to the genome assembly published by Hu et al. (2013). However, each study used different versions of this genome build with different coordinates for homologous sites: version r2.01a for Machado et al. (2016), version r2.01b for Signor et al. (2018), version r2.02 for this paper. To compare loci, we extracted the 100 bp sequence containing each of our 291,272 SNPs in the r2.02 reference genome and mapped these sequences to the two previous genome builds (using BWA and Samtools as described above). In most but not all cases, the r2.02 sequence mapped to a single unique location in the r2.01a and r2.01b genomes. Comparing homologous sites, we find that polymorphism observed in one study is often not reported in one or both of the others. This may be biological (if one of the alleles is fixed in the other populations) or bioinformatic (the polymorphism is present but not ascertained in the other populations), but the latter is clearly a major factor. Signor et al. (2018) report many more polymorphisms than Machado et al. (2016) or this study, despite sequencing a much smaller collection of flies (170 inbred lines), probably because variants are more confidently called in inbred lines, each sequenced to high depth, than in pooled population samples. Despite these issues, it is reassuring that when we do observe the same polymorphism across samples, the same bases are typically identified as alternatives in each population. This is demonstrated for a relevant set of loci in Table S2.

Machado et al. (2016) identified D. simulans SNPs exhibiting clinal variation, and this set was also enriched among clinal SNPs in D. melanogaster, suggesting that spatially varying selection operates on these loci. They surveyed eight natural populations of D. simulans over a geographic transect (Florida to Maine). We reanalyzed these data to test whether putatively selected loci from the present study are more or less geographically divergent than neutral loci. We determined the mean F_st (Wright 1943) within windows around our significant loci and compared this value to a null distribution established by randomly sampling windows from the genome as a whole (all ascertained loci). In this context, an ascertained locus is the sequence flanking each of our 291,272 SNPs (r2.02 build) that can be uniquely and perfectly matched to a sequence in the main chromosomes of the r2.01a build. Given a set of SNPs, we calculated F_st at each site based on the counts of reads for each allele in each population. We excluded SNPs not scored in all eight populations or with <125 reads in total. When windows overlapped, a SNP was only used once. Scoring individual reads as binary variables (0 if reference, 1 if alternate), the one-way ANOVA provides an unbiased estimate for the within and among group variance. F_st is the ratio of among group to total variance. We averaged F_st across all sites for each specific dataset. We conducted these calculations for a range of window sizes.

Analysis of evolutionary change at SNPs

Null divergence:

The raw data for each polymorphism is 12 numbers: the counts of reads for each alternative SNP base in each of the six populations (A0, B0, C0, A7, B7, and C7). The statistical treatment of data are based on transformed allele frequencies (Fisher and Ford 1947; Walsh and Lynch 2018). If $p_A$and$p_D$ are allele frequencies in ancestral and descendant populations, respectively, then $x_A=2{\sin }^{-1}\left(\sqrt{p_A}\right)$ and $x_D=2{\sin }^{-1}\left(\sqrt{p_D}\right)$, with x measured in radians (the A/D subscript denotes ancestral and descendant, respectively). This angular transformation is useful because, to a first approximation, the variance in change owing to genetic drift and sampling is independent of the true allele frequency (Fisher and Ford 1947). As a consequence, a common test can be applied across polymorphisms despite differing initial allele frequencies (Kelly et al. 2013). At a neutral autosomal SNP, divergence $\left(x_D-x_A\right)$ is normally distributed with mean 0 and variance $\frac{1}{2n_A}+\frac{1}{2n_D}+\frac{1}{m_A}+\frac{1}{m_D}+\frac{t}{2N_e}$, where m is read depth at the locus after sequencing, n is number of diploid individuals sampled for sequencing, N_e is the effective population size, and t is the number of generations. While five of these quantities are known, N_e is not. However, we can use the observed variance in divergence to estimate N_e. We focus on autosomal loci given that N_e differs between autosomes and the X chromosome (Charlesworth 2009), and 85% of our SNPs are on the autosomes. We estimate the “null variance,” $v$, on a population and chromosome specific basis using:

$$v=V^{\ast }-V_{rd} ,$$ (1)

where $V^{\ast }$ is a robust estimator for the variance in divergence between ancestral and descendant populations and $V_{rd}$ is the read depth variance. $V^{\ast }$ is calculated from the interquartile range of the distribution of changes in allele frequency (Kelly et al. 2013). $V_{rd}$ is estimated from the average of $\frac{1}{m_A}+\frac{1}{m_D}$ across all SNPs. $v$ aggregates the dispersive processes shared by all neutral SNPs; stochastic changes in allele frequency over the course of the experiment as well as the sampling of flies into bulks and any differential representation of the DNAs from each fly within the DNA pool. To estimate $v$ for each chromosome, we consider SNPs with 0.05 < $p_A$< 0.95 to avoid boundary effects. In the neutral case,

$$E\left[v\right]=\frac{t}{2N_e}+V_s,$$ (2)

where $V_s$ is the total variance associated with bulk formation. With selection, $v$ may be determined as much (or more) by genetic draft than by genetic drift.

Tests for selection:

Divergence between ancestral and descendant populations is statistically independent between replicates because each population was founded from distinct flies and there was no gene flow between replicates. With neutrality, $E\left[x_A-x_D\right]=0$ and the variance is given by ν, $m_A$, and $m_D$. The likelihood for this null model at each SNP (LL₀) is the product of three normal densities. We contrast the likelihood of the data under this model to an alternative allowing parallel evolution across replicates: $E\left[x_D-x_A\right]=\delta$, where δ is the (shared) change in allele frequency driven by parallel selection across replicate populations. For this alternative model, the maximum likelihood estimate (MLE) of $\mathrm{\Delta }$ is $\widehat{\delta }=\frac{w_{A}d{x}_A+w_{B}d{x}_B+w_{C}d{x}_C}{w_A+w_B+w_C}$, where the dx terms are the observed $\left(x_A-x_D\right)$ in each replicate and the w are replicate specific weights: $w=\frac{1}{v+\frac{1}{m_A}+\frac{1}{m_D}}$ [see Monnahan and Kelly (2017) for derivation]. The likelihood ratio test (LRT-1) for parallel evolution is 2(LL₁–LL₀). This is not a strict likelihood in the sense that ν are treated as constants and not free parameters, but the error is minimal given that ν are estimated from the aggregate of thousands of variant sites (Monnahan and Kelly 2017). Also, we use permutation (and not the parametric chi-squared distribution) to assess genome-wide significance LRT-1. To create a permutation replicate, we randomly scrambled observed standardized divergences across SNPs within each replicate population and then calculate LRT-1 at each SNP. The distribution of divergences (across SNPs within each population) is preserved by this procedure and so the test is based entirely on consistency of response of the same SNP across replicates (Table 1). We extracted the largest LRT-1 value from each permuted data set and repeated the procedure 1000 times. Importantly, LRT-1 is specific to each SNP and its value is not affected by the (correlated) responses of neighboring SNPs.

Table 1. A summary of the tests introduced in this study.

Test statistic	Signal to be measured	Null distribution
LRT-1	Parallel selection at individual SNPs	Permutation of SNPs or χ2 with 1 d.f.
LRT-2	Heterogeneous selection at individual SNPs	χ2 with 2 d.f.
Extreme windows	Loci with extreme response across replicates	Permutation of windows
Window rank correlation	Consistency of response across replicates	Permutation of windows

A second likelihood ratio, LRT-2, tests for heterogeneous divergence among populations. Here, we allow the expected change, $E\left[x_D-x_A\right]$, to be population specific. With three replicates, there are three free parameters. The MLE for the distinct $\delta$ of each population is simply the observed $x_D-x_A$. $\mathrm{LRT-2}=2\left(\mathrm{L}{\mathrm{L}}_2-\mathrm{L}{\mathrm{L}}_1\right)$. We compare LRT-2 to the chi-squared distribution with two degrees of freedom. Permutation cannot be used for LRT-2 because the null hypothesis, that selection is consistent across replicates, is not reiterated by randomizing SNP locations (Table 1).

We apply two additional tests at the scale of genomic windows. LRT-1 significance requires the same SNP to show a strong parallel response, which may not occur at a selected site because allele frequency estimates are encumbered with substantial error. Closely linked sites that all respond to selection owing to hitchhiking will exhibit differing signals across replicate populations, owing to differing estimation error. Linked SNPs might also exhibit different phase with the selected locus in different replicate populations. To capture the selection signal at such loci, we delineated nonoverlapping windows, each of 25 adjacent SNPs. Within each replicate, we identified the SNP with the maximum absolute value of (standardized) divergence between ancestor and descendant in each window (the maximum value for the window). We then used the sum of window-specific scores across replicates as a test statistic; loci exhibiting a strong response across replicates will have large sums (extreme windows test in Table 1). We established a significance threshold by permuting entire windows, preserving the linkage relationships among neighboring sites. The selection regimes that are distinctly measured by LRT-1 (parallel selection) and LRT-2 (heterogeneous selection) could both contribute positively to the extreme windows test.

Finally, we calculated the Spearman rank correlation (R) of window scores in pairwise contrasts between populations (A vs. B, A vs. C, and B vs. C). The average R measures the general tendency for magnitude of change per locus to vary consistently across independent replicate populations. Unlike the first three tests, it is not based on outliers. The permutation procedure for extreme windows is suitable here, except with the R values recalculated with each permuted data set and entire windows permuted. We first applied the window rank correlation test to the entire data set (∼11,500 windows) and then to a more restricted collection of windows (∼8500). The latter excluded regions near centromeres and telomeres (low recombination) and also excluded windows that were diagnosed as significant by the extreme windows test.

The simulator

The program tracks each chromosome of each individual in the population as a series of binary values (the allele present at each locus). The position of each of the 291,272 SNPs in the simulation matches positions in the experiment. To optimize use of computer memory, the program compresses genotypic information using the method of Sukumaran and Holder (2011). The population is defined as N_m male and N_f female diploid adults formed each generation (only one X haplotype in males). Each subsequent generation is formed by randomly selecting parents and synthesizing gametes from those parents to create a new set of N_m males and N_f females. In simulations with selection, individuals are chosen with probabilities proportional to their fitness (which is a function of the genotype at the subset of “selected” loci). We first consider neutral evolution and then two different models of selection. In the truncation selection model, individuals have fitness 1 if their genetic score (a sum of effects across loci) exceeds the threshold and 0 otherwise. In the multiplicative model, each site affecting fitness has a selection coefficient (s) of 1, 1+s, or 1+2s. Individual fitness is a product across loci. For both selection models, we assume that hemizygous male genotypes have the “homozygous” effect, e.g., 1 or 1+2s. A simulation replicate starts with creation of the founding population (described below) followed by sampling of three distinct experimental populations, each propagated for 15 generations (selection occurring in 14 of those generations if indicated).

We do not have a precise measure of generation time in the population cages, but our estimate for the simulations is based on the observation that D. simulans and D. melanogaster have very similar life history parameters under standard laboratory conditions (Sameoto and Miller 1966; Sevenster and Vanalphen 1993). We used the effective generation time in population cages of D. melanogaster of 13–15 days estimated by Frydenberg (1962), consistent with several experiments of this type (Crow and Chung 1967; Muir and Bell 1981). In each population, we simulate data collection to mimic the actual experiment with read depths at polymorphic sites equivalent to the observed values.

Two modeling challenges are how to synthesize the “founding haplotypes,” i.e., the genome sequences of generation 0 individuals, and how to impose recombination events in a realistic manner along chromosomes. Regarding the first challenge, the sequence data from our pooled generation 0 samples (A0, B0, and C0) provide strong information about allele frequencies, but not about haplotype structure in the ancestral population. Strong information about haplotype structure is provided by the inbred lines sequencing of Signor et al. (2018), but this is for a different population of D. simulans. LD between alleles is often idiosyncratic to population, and for this reason, we do not extract specific LD values from the Signor et al. (2018) lines. Instead, we use these sequences (downloaded from https://zenodo.org/record/154261#.W2hyqhhKhrk​) to estimate the overall strength of association between loci, or more precisely, the probability distribution of LD conditional on the frequencies of alleles at each locus and the distance between sites (Table S3; python scripts included in File S1). We established distinct probability tables for autosomes and the X chromosome [see Table 1 of Signor et al. (2018)] and also noted elevated LD in low recombination regions of the genome (near centromeres and telomeres; Figure S1 and Table S4). We separated these regions and calculated LD probability tables based on the “normal recombination” regions of the X and autosomes (Table S3). However, to simulate LD within reduced recombination areas, we adjusted the probabilities to produce average LD values similar to those observed in low recombination regions in the real data. We found that increasing the probability of the lowest value for D’ (Lewontin 1964) by 10% and reducing the probability of all intermediate values by 20% yielded a good match between simulated and observed values for average r² vs. genomic distance (Table S4).

Initial allele frequencies and SNP locations were copied directly from the ancestral populations (estimated from the A0, B0, and C0 data). The founding population of a simulation replicate is synthesized by stochastically sampling LD values conditional on allele frequencies and locations. The three experimental replicates within a simulation replicate are sampled from the same founding population, but different simulation replicates will have distinct founding populations owing to the stochastic determination of LD. Given a founding population, we sample the haplotypes of each animal in each replicate population as a vector of 0s and 1s (reference or alternative base at each SNP). We use a “target locus” approach for generating this vector, which is the length of the number of SNPs on each chromosome arm. A total of 238 of the 291,272 SNPs are denoted as target loci, located at ∼500 kb intervals across the genome. In simulations with selection, the fitness determining loci are a subset of the target loci. To simulate a haplotype, we first randomly sample alleles at target loci given site-specific allele frequencies. We assume no LD between target loci so these samples are independent. Given the allele at a target locus, we fill in SNPs sequentially by moving out from each target locus. The remaining 291,034 SNPs are “partners” to a specific target locus (the closest one), which is always within 250 kb. The probability of obtaining a particular allele (0 or 1) at a partner site is determined by the allele frequency at that site, the identity of the allele at its target locus, and the LD between these sites (determined previously when the founding population was simulated). We use the target locus approach because the full vector for a chromosome is not accurately described as a Markov chain. Table S4 indicates much greater LD is observed between distant SNPs than is obtained if one simulates a chromosome by progressing sequentially and conditioning only on the last SNP. Our simulations with selection specify the fitness determining loci as a subset of the targets. We thus reiterate the linkage between selected and neutral loci that is essential to hitchhiking. However, the target locus approach may fail to accurately describe (and likely underestimate) associations between closely linked neutral loci (when neither are target loci).

Gamete formation depends on the overall rate of crossover per chromosome and the locational distribution of these events. We assume no recombination in males. True et al. (1996) provide reasonable estimates for the map length (recombination probabilities) per chromosome arm in D. simulans females: 2L: 0.570, 2R: 0.655, 3L: 0.555, 3R: 0.830, and X: 0.590. The location of crossovers, when they occur, is probabilistic. Fine-scale recombination data are available from D. melanogaster (Comeron et al. 2012), but not yet for D. simulans. For the present study, we simulate recombination given the overall rates from True et al. (1996), but use the location distribution from D. melanogaster (Comeron et al. 2012), which exhibits reduced recombination rates near telomeres and centromeres. Recombination probabilities as a function of genomic location (500 kb intervals) are reported in Table S5. This component of the simulation will be improved when fine-scale recombination data from D. simulans becomes available.

For each parameter set (specified values for N_m and N_f, the number and location of selected sites, selection coefficients at each site, etc.), we simulate the entire experiment 1000 times. We then subject the simulated data from each replicate to the same analysis pipeline as applied to the real data. We first consider neutral evolution to confirm the validity of Equations 1 and 2 for estimating N_e, and also to provide the null distribution for the CMH tests that are subsequently applied to both real and simulated data. We next consider a range of cases with both truncation and multiplicative selection. We evaluate these outputs in relation to multiple aspects of the observed results including the magnitude of allele frequency change at selected loci, the mean and variability in the null variance (v) across chromosomes and replicate populations, and the distribution of test results obtained by different testing procedures. The simulation programs were written in C and are included in File S1.

Data availability

Table S1 summarizes responses at the full set of 291272 SNPs. Table S2 has the SNPs significant for LRT-1 where a polymorphism was also observed in the other D. simulans experiments. Table S3 contains the two locus haplotype frequencies conditional on allele frequencies and the distance between loci. Table S4 is a summary of LD estimates with varying distance. Table S5 shows the crossover location distribution used for simulation. Table S6 shows the 138 polymorphisms with an LRT-1 value (test for parallel selection) that exceed the permutation threshold of 47.0. Table S7 shows the maximum LRT-1 value (genome-wide) for each of 1000 permutations of the data. Table S8 shows all SNPs that were significant by either LRT-1 or CMH. Figure S1 reports LD measured as r² as a function of chromosomal location from Signor et al. (2018). Figure S2 is the average Spearman correlation obtained by permutation of windows (simulations with selection) after excluding windows in low-recombination regions and those containing LRT-1–significant SNPs. Figure S3 is the distribution of significant LRT-1 tests per experiment for 1000 simulations of the base parameter set. File S1 is the code developed for analysis and simulation. Sequence data are available from the NCBI trace archive (PRJNA 511980; BioSample accession numbers SAMN10654443, SAMN10654444, SAMN10654445, SAMN10654446, SAMN10654447, and SAMN10654448). Supplemental material available at Figshare: https://doi.org/10.25386/genetics.7124963.

Results

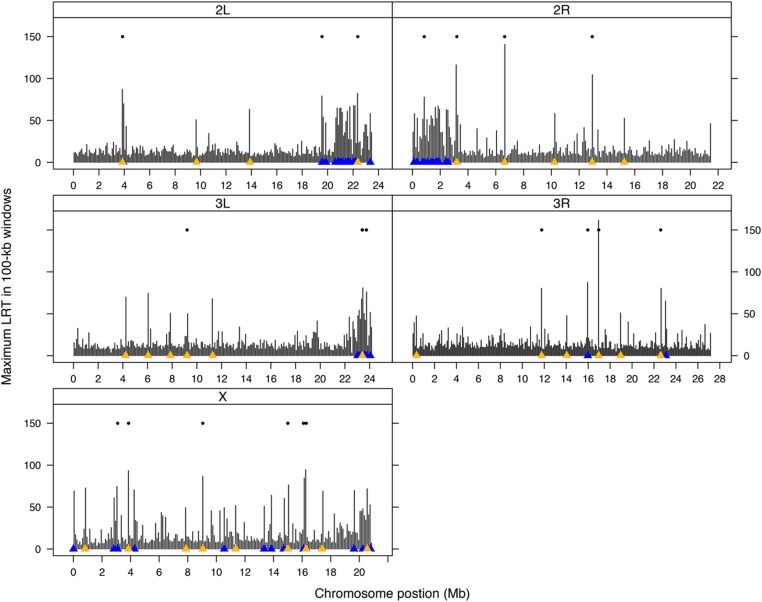
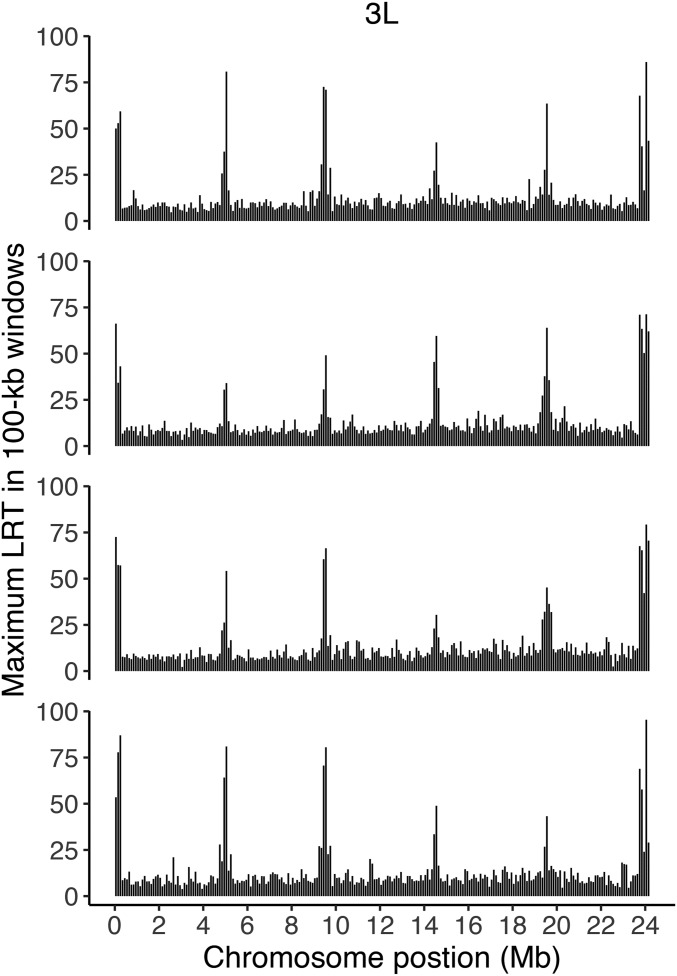
A total of 138 polymorphisms were genome-wide significant for LRT-1, indicating parallel adaptation (Figure 1, Figure 2, and Table S6). The LRT-1 value for these SNPs was larger than the most extreme single test in 95% of the permuted data sets (47.0 is the permutation threshold; Table S7). These sites do not all represent distinct selected loci; significant variants were often closely linked. Figure 1 illustrates the largest LRT-1 value per 100 kb window along each chromosome. There is clearly an aggregation of strong signal in regions of low recombination. The clumping of LRT in these regions nicely parallels the pattern of high LD among distant sites (Figure S1). If we bin significant tests that are closely linked (within 1 mb), then 30 distinct loci are evident as putative targets of selection across the genome (gold triangles in Figure 1).

Figure 1.

The maximum LRT-1 value (parallel selection) per 100 kb window along each chromosome is indicated by vertical bars. Triangles (x-axis) indicate genome-wide significant LRT-1 tests with gold denoting the most significant test per “locus.” The floating dots indicate windows significant for parallel change.

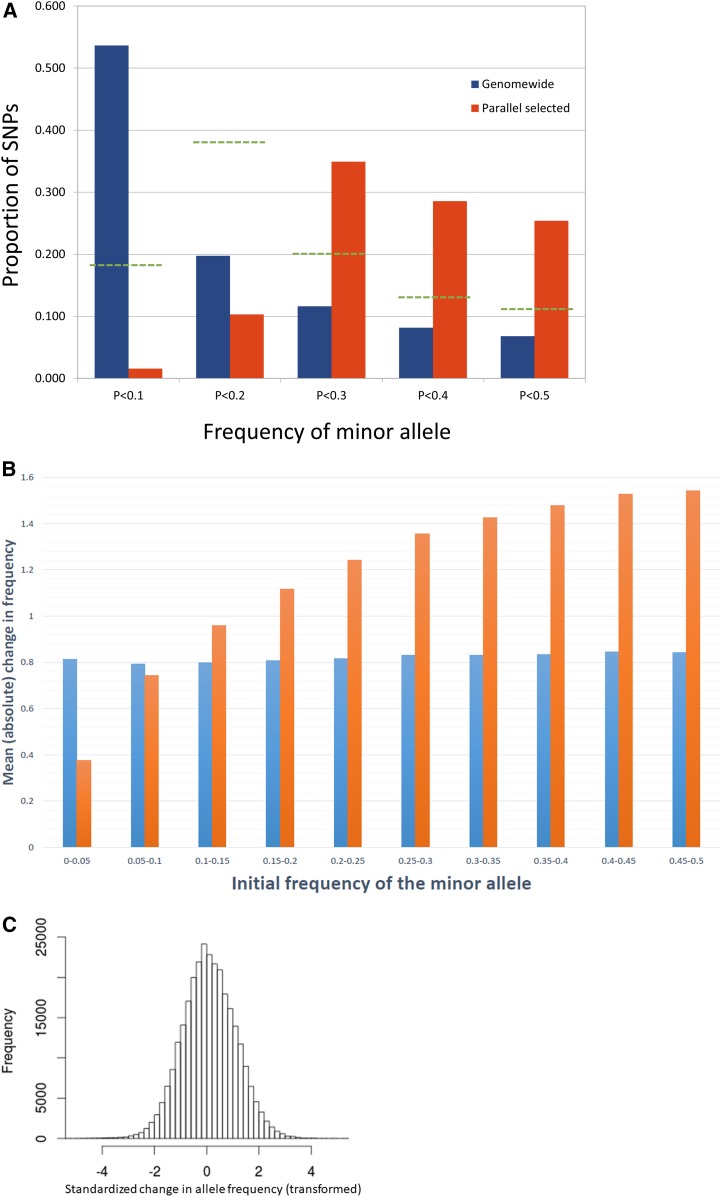
Figure 2.

(A) The allele frequency spectrum is given for all SNPs in the ancestral populations (blue bars) and for those that tested significant for parallel selection (orange bars). The green broken lines denote proportions observed in a simulation of parallel selection on 30 loci with initial allele frequencies sampled from genome-wide distribution (see text). (B) The average absolute change in z (blue bars) and of untransformed allele frequency (orange bars) as a function of initial allele frequency. The latter is multiplied by 20 to be on same scale as the former. (C) The distribution of changes in z between ancestral and descendant populations of replicate C (all SNPs). For B and C, z is the difference in transformed allele frequency (x_A – x_D) divided by the SD.

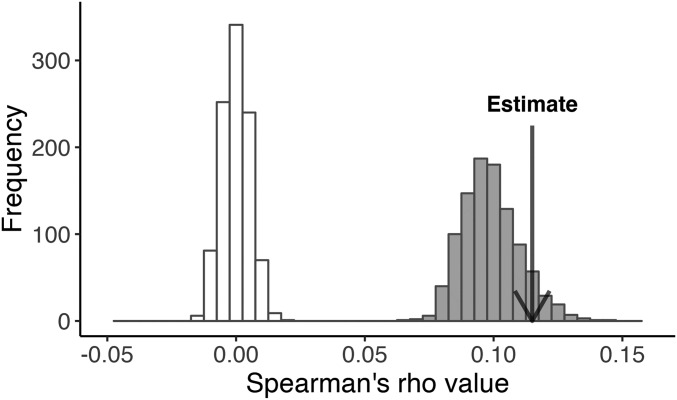
There was only one genome-wide significant test for heterogeneous selection (LRT-2) across replicate populations: X chromosome position 14,386,563 (P = 2.81 × 10⁻⁹) and the extreme window test yielded only 21 significant loci, all of which contained SNPs that were significant for LRT-1 (Figure 1 and Table S9). The window rank correlation, which tests for correlation in allele frequency change across each pair of populations, was significantly positive. With all windows included (Figure 3), the average R across pairwise contrasts of populations was 0.11; much greater than any value obtained by permutation. If we exclude highly divergent windows and those in low recombination regions, the average R is reduced to 0.061, which is still highly significant (P < 0.001; Figure S2).

Figure 3.

The average Spearman correlation is indicated relative to the distribution obtained by permutation of windows (open bars) and from simulations with selection on 30 loci (solid bars = base parameter set). These correlations were calculated with all windows included.

The striking feature of the SNPs that evolved in parallel (identified by LRT-1) was that nearly all have intermediate frequencies in the natural population (Figure 2A). The overall AFS in the ancestral population (blue bars) is typical of natural population samples of D. simulans (Signor et al. 2018). Less than half of SNPs have a minor allele frequency (MAF) >0.1; however, among SNPs testing positive for parallel evolution (orange bars), however, 98% of SNPs testing positive for parallel evolution had MAF>0.1 in the ancestral population and 88% had MAF > 0.2 (orange bars). This pattern is unchanged if we thin the data by taking only the most significant SNP within each of the 30 loci remaining after binning (see above). Among these SNPs, MAF < 0.1 for only one SNP and > 0.2 for 26 out of 30.

Large change at intermediate frequency polymorphisms is not a general feature of the data. Across all SNPs, divergence in transformed allele frequency was essentially homoscedastic, although this is not true of untransformed frequencies (Figure 2B). The overall distribution of changes in transformed frequencies was also highly normal (Figure 2C), justifying use of the angular transform (Fisher and Ford 1947). The null variance in divergence ($v$) varied substantially among chromosomes and replicate populations (Table 2) with an autosomal average of $v$= 0.0185. We estimated N_e using Equation 1: $\frac{15}{2N_e}=0.0185-\frac{3}{2000}$, yielding N_e = 440.9. Here, 15 is the estimated total number of generations (14 of selection plus the production of one progeny generation, assuming a 14-day generation time) and 3/2000 is $V_s$, the estimated variance owing to three sampling events, each involving 1000 diploid flies (from ancestrally sampled females to ancestral DNA pool, from ancestrally sampled females to generation 0 of the experimental population, and from the final generation of the descendant population into the descendant DNA pool). In this calculation, we are ignoring any differential representation of individual fly DNA within the pools and also the unknown relatedness of flies between ancestral pool and ancestral population 0 (which depends on number of sires per wild-caught pregnant female). Accommodation of these factors might slightly change the estimated N_e but would not affect the LRT tests for selection. Each of the tests in Table 1 depends only on $v$ and not on the underlying components (drift vs. bulk sampling variance). The numerical estimate for N_e is used only to establish a null distribution for the CMH test when we contrast it to LRT-1 (see Simulation results below).

Table 2. The estimated null variance for each chromosome in each replicate population.

Chromosome	Estimated null variance of divergence (ν)
	Population A	Population B	Population C
2L	0.0174	0.0170	0.0159
2R	0.0171	0.0189	0.0163
3L	0.0228	0.0227	0.0200
3R	0.0190	0.0173	0.0176
X	0.0152	0.0179	0.0191

Genomic regions containing LRT-1–significant SNPs exhibit elevated geographical variation (high F_st) in the Machado et al. (2016) natural population survey (Table 3). With our filters, the genome-wide mean F_st was 0.0150 across the eight populations (n = 2,340,197 SNPs) and nearly unchanged if we focus on windows around the 281,917 SNPs that could be ascertained in the r2.01a genome build (F_st = 0.0151, n = 330,597 SNPs). Among LRT-1–significant SNPs, we were able to ascertain 119 out of 138 loci for subsequent F_st calculation. Mean F_st around putatively selected sites declined with window size (Table 3), but was always much greater for selected loci than for the background genome (45–65% inflation). The F_st estimates for selected loci always exceeded even the highest values obtained by resampling (P < 0.001 for all window sizes).

Table 3. The F_st estimates for windows around selected sites are compared to the genome-wide distribution.

Window size (bp)	Number of SNPs	Fst	F0.025	F0.975	F0.999
200	332	0.0246	0.0107	0.0191	0.0218
500	718	0.0242	0.0116	0.0180	0.0200
1000	1246	0.0217	0.0123	0.0177	0.0192
2000	2446	0.0204	0.0126	0.0169	0.0189

F_0.025, F_0.975, and F_0.999 refer to distribution percentiles from sample number of loci (with matching window sizes) from all ascertained loci.

Simulation results

We first performed neutral simulations with N_m = N_f = 220 following the empirical estimate of N_e reported above. As predicted by Equations 1 and 2, the mean v across each autosome of each simulated population was very close to the average from Table 2 (0.0185). The LRT distributions were slightly inflated relative to the predicted chi-squared distributions (mean LRT-1 = 1.06 instead of 1.0, mean LRT-2 = 2.09 instead of 2.0), which suggests that chi-squared P-values might be marginally anticonservative. However, not a single LRT-1 value from any of the 1000 simulation experiments exceeded the permutation threshold (47.0) from the real data. These neutral simulations also established the null distribution for the CMH tests, which have been used to test for parallel evolution in E&R experiments. We extracted the largest CMH value from each simulation replicate and found the 95th percentile of these maxima: 71.5. Imposing this threshold on the SNP-specific CMH values in the real data, we found that 402 tests exceed 71.5 (Table S8), which is ≈3 times the number from LRT-1. All but one of the LRT-1–significant SNPs were within the CMH set.

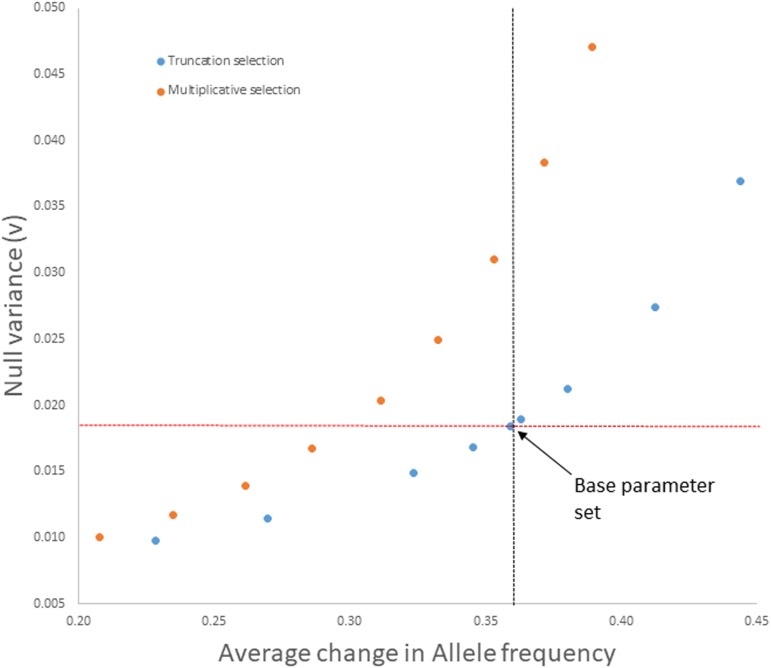
For simulations with selection, Figure 4 contrasts multiplicative and truncation selection models over a range of parameter sets in which 30 loci determine fitness (number based on observed results). In these simulations, the selected loci were uniformly positioned over each chromosome. The initial frequencies at selected sites were taken from the 30 selected loci in the real data with the specific allele frequency assigned to each SNP randomized with each simulation replicate. The direction of allelic effect was random except when the minor allele was <20%. In this situation, the minor allele increased fitness (as in the real data, Table S6). The average allele frequency change (x-axis) increased with the strength of selection by either model, but the magnitude of stochastic change generated by linked selection was much greater for multiplicative than truncation selection. Here, stochastic change at neutral loci (drift and draft combined) is measured by v on the y-axis. In the real experiment, the average estimated allele frequency change at the 30 selected loci was ∼0.36. At this point in Figure 4, v ≈ 0.0185 with truncation selection but is much greater with multiplicative selection (v ≈ 0.032).

Figure 4.

The null variance (mean v across simulation replicates) is reported for varying strengths of truncation selection (blue) and multiplicative selection (orange). The vertical and horizontal lines indicate the mean null variance (red) and mean allele frequency change (gray) from the real experiment. The fractions selected for truncation are 0.8, 0.75, 0.68, 0.65, 0.63, 0.625, 0.6, 0.55, and 0.5, respectively (left to right in graph). The selection coefficients for multiplicative fitness were 0.07, 0.08, 0.09, 0.1, 0.11, 0.12, 0.13, 0.14, and 0.15, respectively. Number of zygotes (preselection) was 1600 in all cases. The base parameter set is indicated by arrow.

From the Figure 4 simulations, we chose the truncation model with 63% selected as our base parameter set, given the match to observed allele frequency change and mean v. It also matched the real experiment with respect to the total number of significant LRT-1 tests per simulation replicate (Figure S3) as well as the genomic location of significant tests. Specifically, there was aggregation of strong signal in regions of low recombination, illustrated with four randomly chosen replicates in Figure 5 (compare with 3L in Figure 1). Unexpectedly, the 30-locus model generated a large genome-wide correlation of divergence within genomic windows between replicate populations using the window rank correlation test, which matches the association observed in the data (see shaded distribution in Figure 3). The simulations also reiterated the observed window correlation even if low recombination regions are suppressed (Figure S2). Finally, the parameter set with 1600 zygotes and 63% of individuals selected yields an adult population size close to our estimated values from the experiment (∼1000).

Figure 5.

The LRT test is applied to simulated data using the base parameter set (parameters reported in text). The maximum LRT test value for parallel selection per 100 kb window along chromosome 3L. Each row represents a different simulation.

To explore the difference in draft between truncation and multiplicative selection, we calculated the variances in allele frequency change (across all SNPs within each generation) and the covariance in change across generations. The total change in allele frequency is the sum of per-generation changes $\left({\displaystyle \sum _{i=1}^t\mathrm{\Delta }{p}_i}\right)$ and the variance is thus ${\displaystyle \sum _{i=1}^{t}Var\left[\mathrm{\Delta }{p}_i\right]}+{\displaystyle \sum _{i=1}^t{\displaystyle \sum _{j\ne i}^t\text{Cov}\left[\mathrm{\Delta }{p}_i,\mathrm{\Delta }{p}_j\right]}}$. As noted by Robertson (1961), selection can generate a positive correlation in $\Delta p_i$across generations even for neutral SNPs, which he called the “inbreeding effect” of selection. In our simulations, the stronger draft of multiplicative selection is caused by this across-generation covariance (Table S10). With parameter sets that yield the same average amount of change at selected SNPs, the per-generation $Var\left[\mathrm{\Delta }{p}_i\right]$ is similar between multiplicative and truncation models, and actually slightly higher for truncation. However, $\text{Cov}\left[\mathrm{\Delta }{p}_i,\mathrm{\Delta }{p}_j\right]$ is much greater with multiplicative selection. The ${\displaystyle \sum _{i=1}^t\text{Var}\left[\mathrm{\Delta }{p}_i\right]}$ term contributes only approximately one quarter of the variance in cumulative change with multiplicative selection, with the remainder due to positive intergenerational covariances. The two components are about equally important with truncation selection (Table S10).

The distribution of individual reproductive success is very different between truncation and multiplicative models (Figure S4). Truncation selection actually yields greater variance in individual fitness, although multiplicative selection is more likely to produce highly fecund individuals. However, the overall draft effect depends on the multigenerational genealogy of the population, on how likely highly fecund individuals are to beget highly fecund descendants. The multigenerational dependence is evident in the “covariance time lag” predicted by Robertson (1961). High values for $\text{Var}\left[\mathrm{\Delta }{p}_i\right]$ are evident in the first generation of selection, but the magnitude of $\text{Cov}\left[\mathrm{\Delta }{p}_i,\mathrm{\Delta }{p}_j\right]$ builds up incrementally over the first few generations (Table S10).

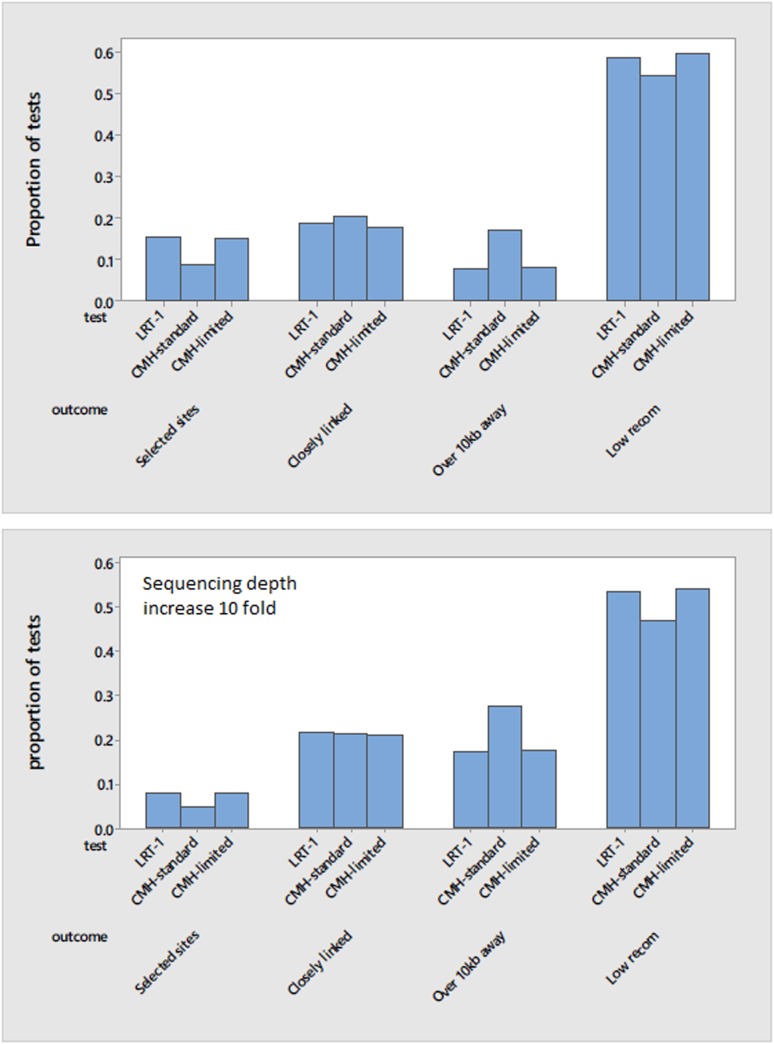
Figure 6 compares LRT-1 and CMH tests for simulations of the base parameter set using the thresholds from the real experiment (47.0 for LRT-1, 71.5 for CMH). There were over twice as many CMH as LRT-1 significant tests, mirroring the results from the real data (Table S8). We can classify each SNP as a causal site (leftmost group) or as a hitchhiker. The latter is subdivided into three outcomes: within 10 kb of selected SNP in a normally recombining region, over 10 kb distant from a selected SNP in such a region, or within a low recombination region that contains a selected locus. LRT-1 was considerably more precise in identifying causal SNPs (Figure 6, top): 15.2% of LRT-1 tests were at causal loci in the simulation vs. 8.6% for CHM. Both tests produced an abundance of significant results in low recombination regions under linked selection (rightmost grouping in Figure 6), but distant hitchhikers in normal recombination regions were more likely to appear as significant for CMH.

Figure 6.

The comparison between LRT-1 and CMH tests is given for the base parameter set using the observed read depths (top), and when we increase sequencing depth 10-fold at each SNP (bottom). Tests are classified as at a fitness determining locus, closely linked (within 10 kb) in a normal recombination region, distantly linked in a normal recombination region, or linked but within a low recombination region.

Much of the CMH/LRT-1 difference owes to the fact that CMH was more permissive under the conditions of this experiment (number of populations, read depths, etc.). The CMH-limited category reduced the number of CMH significant tests to the same number as for LRT-1 by inflating the CHM threshold above 71.5 on a replicate specific basis (Figure 6). This greatly reduced the difference between testing methods. Precision in identifying causal sites was only slightly higher for LRT-1 than CMH-limited (within 10%) and many of the CMH significant tests that were far from selected sites are erased. We also considered the effect of increasing read depths because our experiment had relatively low depths: 5–10% of the number of chromosomes sampled into each bulk, except for C7 (25%). We performed simulations of the base parameter set but with read depths increased 10-fold (Figure 6, bottom). To establish the appropriate significance threshold for CMH, we repeated the neutral simulations with elevated read depths (new threshold = 437.0). As expected, the number of significant tests increased for both methods (2.5× increase for LRT-1, 1.9× for CMH). However, the fraction of tests at selected sites declined. Nearly all selected sites were identified by both methods (average 29 out of 30) but the great majority of new significant tests with increased read depth were hitchhikers.

To evaluate the effects of LD on genome-wide patterns, we simulated the ancestral population with no LD and ran the base parameter set with all else unchanged (including limited recombination within centromeric/telomeric regions). The results were profoundly different. There was no effect on the mean (absolute) allele frequency change at selected sites, but the number of significant LRT-1 tests declined dramatically (from an average of 149 to 23.6). However, every single significant LRT-1 test across 1000 simulation replicates occurred at a causal site, illustrating the pronounced effect of hitchhiking even in a species with relatively low LD.

We next manipulated the initial distribution of allele frequencies at selected loci to address the question that emerges from Figure 2A: does the intermediate frequency of significant variants from the experiment imply that intermediate frequency variants were the primary targets of selection in the laboratory environment? We conducted simulations using the base parameter set except with initial allele frequencies of selected loci sampled from the genome-wide distribution (blue bars in Figure 2A). This change actually increased the average number of significant LRT-1 tests (from 149 to 182), but the number of significant tests at causal SNPs declined. The increase in significant hitchhikers suggests that linked selection has a more pronounced effect when the favored allele is initially uncommon. The broken lines (green) in Figure 2A illustrate the initial AFS of LRT-1 significant tests. There is a “pull to the middle,” that is, most selected sites had an MAF < 0.1, but those with higher initial frequencies were more likely to yield high LRT-1 (Figure 2A). Despite this ascertainment effect (among selected sites, those with intermediate frequency are more likely to be detected), the real data contain an excess of SNPs with MAF > 0.3 that yield significant tests (orange vs. green in Figure 3). The pull to the middle in simulations with selection from the background AFS reflects a biologically important feature: positively selected loci with higher MAF are generating greater variance in fitness when the population experiences the novel laboratory environment.

Finally, the fact that simulations with 30 fitness determining loci reiterated most of observed results (number and distribution of significant LRT-1 tests, mean v, correlations of genomic window divergence) does not imply that only 30 loci were under selection in the real experiment. We modified our base parameter set to consider a version of the “infinitesimal model” by distributing fitness effects equally across 238 loci (one every 500 kb across the genome). In the resulting simulations, the mean v was close to the base parameter set and the real data. However, very few loci emerged as genome-wide significant for LRT-1 (only 6 out of 1000 simulations yielded even one significant test). However, allowing effects to vary among loci greatly improved model fit. In simulations with every seventh locus (34 in total) having 10 times the effect of surrounding “minor loci,” significant LRT-1 tests were routinely observed at the major loci. The mean number of significant tests per replication (60.9) was lower than for the base parameter set, but some replicates exceeded 100 tests approaching the observed value. In these simulations, minor loci evolved, but allele frequency changes were never sufficient to reach genome-wide significance. Given that a distribution is more plausible than constant effects across loci, these simulations indicate that a longer experiment (30–50 generations instead of 14) is necessary to detect the portion of response due to smaller effect loci.

Discussion

In this E&R experiment, we observed parallel changes in allele frequency at >100 SNPs, clustered into ∼30 distinct loci across the genome. The AFS of these putatively selected sites is strongly biased toward intermediate allele frequencies. The source natural population clearly harbors abundant standing variation to allow rapid adaptation in a novel environment. A foundational principle of molecular population genetics is that genetic drift is the primary driver of allele frequency change at most polymorphisms. However, accumulating examples of rapid phenotypic and genomic evolution, as well as the observation that allele frequencies vary cyclically in natural Drosophila populations (Bergland et al. 2014), challenge this assumption (Gillespie 2001; Messer et al. 2016; Hermisson and Pennings 2017). In this experiment, several lines of evidence suggest that neutral SNPs were more affected by linked selection than by classical genetic drift. Below, we discuss these results in relation to the maintenance of polymorphisms in nature, the genome-wide response to strong selection, and the challenges to identifying targets of selection when thousands of loci exhibit excessive change.

The maintenance of polymorphism

We hypothesize that our putatively selected polymorphisms are enriched for loci under balancing selection in nature (Bergland et al. 2014; Charlesworth 2015) based on two features of the results. First, the AFS of SNPs that evolved in parallel across replicates (significant for LRT-1, Table 1) is strikingly different from the genomic background. The AFS for all SNPs (blue bars in Figure 2A) exhibits the expected preponderance of rare alleles (Moriyama and Powell 1996; Przeworski et al. 2001), consistent with the idea that most polymorphisms are neutral or nearly neutral (Wright 1931; Ohta 1976). However, the polymorphisms that responded to selection are intermediate in frequency (orange bars in Figure 2A). In molecular population genetics, the most common AFS-based test for selection is Tajima’s D (Tajima 1989), which has an expected value of zero under the equilibrium neutral model. At the gene level, values >2 are typically interpreted as evidence for balancing selection (assuming that large number of alleles are sequenced). For our selected SNPs, Tajima’s D = 4.88 (using the median ancestral read depth of 324 for n). This is hugely inflated relative to the neutral expectation, and also in comparison to the genomic AFS (Kolmogorov–Smirnov statistic = 0.626, P < 2.2 × 10⁻¹⁶).

Balancing selection can result in a stable MAF < 10% (in the lowest category of Figure 2A), but deleterious variants are unlikely to segregate at intermediate frequencies (higher categories in Figure 2A). Neutral variants may occasionally drift to intermediate frequencies, but the overall AFS of our significant SNPs is not consistent with neutrality. Ascertainment is an important consideration here: Does the excess of intermediate frequency polymorphisms result simply because change at these loci is easier to detect? For the great majority of polymorphisms, the answer is clearly no. The average magnitude of change is as large for rare alleles as for common (Figure 2B) because the angular transformation effectively normalizes the effects of genetic drift and experimental sampling on allele frequency change (Fisher and Ford 1947; Walsh and Lynch 2018). However, the transformation does not eliminate the dependency for selection-driven change because the variance in fitness is maximal at intermediate allele frequency. The difference between blue and green in Figure 2 illustrates that we are more likely to detect intermediate frequency alleles because they experience greater change with the same strength of selection. However, even after correcting for this effect, the real data still yield an excess of significant SNPs with MAF > 0.3 (orange vs. green in Figure 2A). Of course, all of these arguments are based on distributions. No conclusion can be made about individual SNPs simply from their allele frequency.

Another recent E&R experiment on D. simulans demonstrates that evolution based on rare alleles is detectable, if that is the basis of the response [see Figure 2 of Barghi et al. (2017)]. In that study, significant SNPs generally had MAF < 0.2 and became more intermediate in frequency during laboratory adaptation. There are a number of differences between the studies that could explain the differing outcomes. For example, the Barghi et al. (2017) founders were derived from isofemale lines, whereas the founders in our experiment were the offspring of wild-caught females. Regardless of the reason, however, the results of Barghi et al. (2017) indicate that rare, favorable alleles have detectable signal. If we run our simulator using the base parameter set, except replacing the observed AFS with an initial frequency of 0.02 for all favorable alleles, the number of significant LRT-1 tests actually increases. Mean allele frequency change at selected SNPs is reduced (from 0.36 to 0.23), as is the number of significant LRT-1 tests at those selected SNPs. However, the inflation of hitchhiking, particularly beyond 10 kb, more than compensates in producing significant tests.

Relevant to natural selection on our significant SNPs, the genomic regions harboring these SNPs exhibit elevated differentiation among natural populations of D. simulans in eastern North America [Table 3; Machado et al. (2016)]. This pattern suggests that alternative alleles at our significant SNPs are responsive to environmental heterogeneity (Lewontin and Krakauer 1973; Beaumont and Nichols 1996). We have emphasized that the laboratory environment is a novel selective challenge to wild D. simulans, but it is also relatively constant and homogeneous. With heterogeneity in the natural environment (e.g., seasonal variation in temperature or spatial structure in resource availability), a “multiniche polymorphism” (Levene 1953) can result if genotypes vary in their environmental optima. Such polymorphisms will not remain stable if environmental heterogeneity is eliminated. We cannot predict which allele would increase in captivity without detailed information about genotype-specific tolerances. However, it is likely that one genotype will, by chance, match the laboratory environment better than alternatives, resulting in the eventual loss of the latter. Frequency-dependent selection arising from competitive or social interactions (Antonovics and Kareiva 1988) can also maintain polymorphism in nature that the laboratory environment could remove or reduce.

Hitchhiking and excessive significance

Nuzhdin and Turner (2013) argue that the large number of significant tests in recent E&R experiments (Turner et al. 2011; Orozco-terWengel et al. 2012; Turner and Miller 2012), must be due to overestimating the number of loci under selection. Because a limited number of haplotypes are sampled to initiate E&R experiments, non-random associations between loci can occur between loci far apart in the genome. This sampling effect, combined with traditional hitchhiking, could produce large changes in allele frequency at many sites that are not the direct targets of selection. For the present experiment, we established each replicate population with a distinct sampling of genotypes from nature, which should reduce the scope for haplotype-sampled LD to generate false positives. The finite number of haplotypes that survive in each experimental population will yield idiosyncratic associations between distant SNPs, but these associations should be population specific, and thus less likely to generate consistent parallel changes across replicates.

While founding experimental populations with distinct samples from the natural population may reduce sampling LD, it will not eliminate genuine long-distance LD that is present in the natural population. Our treatment of LD in the simulations is based on the inbred line sequencing of Signor et al. (2018), which does reveal nontrivial levels of LD, particularly in low recombination regions (Figure S1, Tables S3 and S4). The simulations calibrated to this level of LD indicate a pervasive effect of hitchhiking (Figure 3, Figure 4, and Figure 5). Perhaps most surprising is that selection on only 30 loci generates a genome-wide positive association between locus-specific responses across independent replicated populations (Figure 3 and Figure S2). It is true that the Signor et al. (2018) data, on which we calibrate our simulations, is itself a finite sample of ∼170 alleles. It might thus have its own collection of sampling induced LD values. However, artificial LD is most likely to occur between rare variants that are accidentally captured in the same line or lines. The hitchhiking in our simulations is driven by associations between intermediate frequency alleles where the minor haplotype is sampled into many sequenced lines (and correspondingly into each of the replicated populations of our simulations). Estimates of LD between intermediate frequency alleles are far more robust. An important corollary is that, among our significant SNPs (Table S6), we cannot distinguish the actual targets of selection from hitchhikers. While this is a clear limitation of the experiment, the intermediate frequency result (Figure 2A) is not undermined by hitchhiking. Change at a hitchhiking locus will only match change at the selected locus if allelic association is maximal, it remains unbroken by recombination, and allele frequencies are similar at the two loci (r² near 1).

Significance testing

The number of significant tests (138 for LRT-1) is reduced by orders of magnitude from previous E&R studies. The independent founding of experimental populations (described above) is one factor, but minimum depth thresholds also caused many SNPs to drop out of the set tested for selection. The simulation results of Figure 6, bottom suggest that increased read depth would increase the number of significant tests, although the predicted inflation is caused overwhelmingly by the inclusion of additional hitchhikers rather than novel selected sites. Differing testing methods also contribute: we obtained two to three times as many significant tests for CMH than LRT-1 when applied to the same data set (either real or simulated). CMH and LRT-1 assimilate read counts in different ways. The contingency table method (CMH) should work well when each sequenced read is an independently sampled allele from the relevant population (ancestral or descendant in this case). This is not a requirement for LRT-1, but the independence assumption likely holds fairly well for this experiment given that read counts were far below the number of alleles in each population. Thus, the difference in outcomes is mostly caused by the different ways that significance thresholds are determined: neutral simulation for CMH vs. permutation for LRT-1, with the latter more conservative.

The four tests in Table 1 are intended to provide complementary information about the genome wide response to selection. In this experiment, the extreme windows test was redundant with LRT-1 and only one SNP was genome-wide significant for heterogeneous selection (LRT-2). This is surprising because even if environmental conditions were exactly the same across replicates, stochastic loss of alleles could generate significant LRT-2 tests. Rare alleles in the natural population might be randomly excluded from one or more of the experimental replicates. If the rare allele is favorable, it will increase where present but not where absent, yielding a heterogeneous response across replicates. Direct inspection of the full panel of SNPs (Table S1) indicates that this very rarely occurred. The minor allele was absent from at least one replicate population at 13,856 SNPs (∼5% of cases). At these SNPs, polymorphic populations showed very low average change. There were a small number of SNPs with substantial change, but at these, the response was limited to a single replicate and magnitude of allele frequency change (0.10–0.15) was much lower than at LRT-1 significant SNPs (average change 0.35). These observations further indicate that adaptive evolution mainly involved alleles at intermediate frequency in the ancestral wild population.

A biological reason for fewer significant SNPs here relative to E&R experiments on D. melanogaster (Burke et al. 2010; Turner et al. 2011; Orozco-terWengel et al. 2012) is that inversions are rare in D. simulans (Lemeunier and Aulard 1992) and the genome-wide recombination rate is 30% higher (True et al. 1996). Barghi et al. (2017) compared genomic change in D. melanogaster and D. simulans after ∼60 generations of hot laboratory conditions and found differing patterns between the two species. D. simulans had fewer candidate SNPs, and the regions of the genome implicated in response to selection were narrower and more distinct. Strikingly, almost all of chromosome arm 3R in D. melanogaster (which contains several overlapping segregating inversions) exhibited a pattern consistent with selection. In D. simulans, which lacks similar inversions on 3R, several narrow, distinct regions on this chromosome arm exhibited such a pattern. The authors attributed many of these differences in the frequency of segregating inversions and in centromeric recombination suppression.

Prospects

Predicting the evolutionary response to changing environments, and its genetic basis, are major goals of evolutionary genetics. We combine a genomic sequencing experiment with a simulation model tailored as closely as possible to the relevant features of that experiment. The simulation demonstrates that strong selection at a limited number of loci can generate a genome-wide response involving thousands of polymorphic sites through hitchhiking, consistent with the observations of the experiment. A more ambitious application would be to use the simulator for formal inference, to identify selected SNPs and the strength of selection on each. In principle, the simulator could be employed for approximate Bayesian computation (Beaumont et al. 2002) or as a trainer for supervised machine learning (Schrider and Kern 2018). However, Figure 4 indicates a question that should precede any such attempt: what should we estimate? Allele frequency change under multilocus selection depends on how locus-specific effects combine to determine survival and reproduction. We found a generally better fit to the data with truncation rather than multiplicative selection; the latter inducing an excessive amount of draft to achieve the same magnitude of allele frequency change at selected loci. While our base parameter set with truncation selection reiterates the major observations of the study, we do not think it fully accurate. The conundrum is that while both models (truncation and multiplicative selection) offer parameters to estimate, interpretation is problematic if neither model accurately describes the genotype-to-fitness mapping.

The contrast of truncation and multiplicative selection also illustrates how genetic draft depends on the genotype-to-fitness mapping. With the same strength of selection on 30 fitness determining loci, multiplicative selection causes a larger stochastic effect on neutral loci by generating a more positive covariance in allele frequency change across generations (Robertson 1961, Table S10). This observation is consistent with theoretical studies from over 50 years ago indicating a lower “substitution load” for truncation than multiplicative selection (Haldane 1957; Sved et al. 1967; Kimura and Maruyama 1969; Wallace 1970). The data from the experiment does not estimate generation to generation changes in allele frequency, but it is noteworthy that we could not find a neutral model sufficient to describe the start to end “background response.” Adjusting N_e allows a neutral model to predict the average change in frequency (mean v), but not the elevated variability of change (Table 2) or the covariance of change across independent replicated populations (genomic windows, Figure 3). Of course, a dominant role for draft in this experiment does not imply comparable importance in natural populations. However, the methods and simulation results described here suggest that genome-wide scoring of large population samples, sustained through time to estimate allele frequency trajectories, could shed considerable light on the relative importance of drift vs. draft in natural populations.

The most important biological conclusions from this experiment follow from the AFS of significant loci (Figure 2). The founding of our experimental populations may have been a critical determinant of the intermediate frequency result. Our ancestral populations were only one generation removed from nature, did not experience population bottlenecks, and did not undergo multiple generations of laboratory adaptation or inbreeding prior to the start of the experiment. Laboratory adaptation, inbreeding, or population contraction in the founders would likely have changed the starting frequencies. This aspect of experimental design not only affects patterns of evolution in an E&R experiment, but also inferences regarding the selective forces acting on these loci in nature.