Microfluidic-based observation of local bacterial density under antimicrobial concentration gradient for rapid antibiotic susceptibility testing

Abstract

The need for accurate and efficient antibiotic susceptibility testing (AST) has been emphasized with respect to the emerging antimicrobial resistance of pathogenic bacteria which has increased over the recent decades. In this study, we introduce a microfluidic system that enables rapid formation of the antibiotic concentration gradient with convenient bacterial growth measurement based on color scales. Furthermore, we expanded the developed system to analyze combinatory effects of antibiotics and measured the collective antibiotic susceptibility of bacteria compared to single microfluidic AST methods. By injecting a continuous flow precisely into the channel, the system enabled the concentration gradient to be established between two parallel channels of different antibiotic concentrations within 30 min, before bacteria enter the exponential growth phase. Moreover, the local bacterial growth levels under antibiotic gradient were quantitatively determined by calculating the position-specific grayscale values from the microscopic images and were compared with the conventional optical density measurement method. We tested five antibiotic types on our platform for the pathogenic Gram-negative bacteria strain Pseudomonas aeruginosa, and we were able to determine the minimum inhibitory concentration (MIC) at which 90% to 95% of bacterial growth was inhibited. Finally, we demonstrated the efficacy of our system by showing that most of the antibiotic MICs determined in our platform show good agreement with the MIC range suggested by the Clinical and Laboratory Standards Institutes.

INTRODUCTION

Antibiotic susceptibility testing (AST), which determines the type and doses of antibiotics that can effectively inhibit bacterial growth, has become more critical in recent years with the emergence of antibiotic-resistant pathogenic bacteria strains.^1,2 Also, the importance of AST is becoming more apparent as the damage caused by bacteria is prevalent in various environments such as hospital-acquired human infection, animal infection on farms, risks on water quality management, and food safety. For instance, Pseudomonas aeruginosa, a Gram-negative bacteria widely studied as a pathogenic strain, can infect humans through several routes and is identified as one of the causes of diseases such as pneumonia, urinary tract infections, and bloodstream infections in several surveillance studies.^3,4 Thus, antibiotic medications including combinatory therapy have been studied to overcome the risk of pathogenic bacteria.^5,6 The medications are known to effectively inhibit the antibiotic resistance of bacteria.⁷ However, depending on the types of the antibiotics, they may allow bacterial growth or increase antibiotic resistance.^8,9 Therefore, efficient and reliable in vitro AST is necessary for the appropriate medications.^10–16

The current AST technologies include broth dilution, disk diffusion, polymerase chain reaction (PCR)-based techniques, and commercially available automated systems.^17–19 Among the conventional systems, optical density (OD) measurements are widely used to find the bacterial density in the broth, which operates on the principle of estimating the bacterial growth level with the degree of refraction of light transmitted through the broth.²⁰ While these techniques have been advanced and standardized, there are still a number of limitations. For instances, in the broth dilution method commonly conducted on 96-well plates or in the disk diffusion test performed on Mueller-Hinton agar plates, preparing serial dilutions of the candidate antibiotics before testing is labor-intensive and inconvenient.²¹ It is also difficult to observe the bacterial growth in real time, and the time required to obtain the minimum detectable growth level may be up to 16 to 20 h.^22,23 In addition, PCR-based techniques enable rapid and sensitive genetic testing of antibiotic resistance through sequence-specific amplification; however, in many cases, the lack of knowledge on the genetic determinants of resistance and the complex procedures for sample processing limit their applicability.^17,24 Finally, although several automated systems facilitated more reliable and reproducible testing, they suffer from low sensitivity and limited range of dose.²⁵

Recently, a number of studies have been reported using newly developed microfluidic technologies to overcome the disadvantages of conventional AST methods.^26–30 Since most of the microfluidic AST platforms are microscale-systems, they not only reduce the excess cells and reagents required but also make it possible to analyze the morphology and number of single cells, which significantly improve the resolution.^23,31,32 In general, these platforms of single cell analysis test the efficacy of antibiotics based on phenotypic alteration of bacterial cells, rather than growth level.³³ In addition, some microfluidic AST platforms also test the antibiotic efficacy based on cell electrophysiology, because dielectrophoresis allows for more detailed approaches to cell wall synthesis or cytoplasmic functionality of bacteria and also enables to distinguish live cells from dead cells.^34–37 While the ASTs with single cell analysis or electrophysiology have reduced test time by requiring relatively low bacterial populations, these approaches cannot reflect the collective resistance of bacteria to the antibiotics, resulting in a possible discrepancy with the actual testing environments, such as high bacterial density in small volumes of space.^38,39 For high bacterial density microfluidic analysis, a method of measuring susceptibility based on grayscale value (GSV) has been suggested.^40,41 Although this method does not reveal the size or shape of individual bacteria induced by antibiotics as in single-cell analysis, it conveniently shows the collective bacterial susceptibility to antibiotics without the need for special imaging techniques such as fluorescence staining.

Several other microfluidic ASTs have increased the efficiency by automatically generating antibiotic concentrations. For example, multi-droplet and micro-array systems can prepare various concentrations of antibiotics automatically.^42–46 However, these approaches were limited in that the antibiotic concentrations are pre-fixed and discrete as well as instable.⁴⁷ In other types of microfluidic gradient generator, although continuous and linearized antibiotic concentrations were formed with an external power source, it took almost a third of the test time to linearize the antibiotic concentration gradient, so there may be a risk of adverse effects on the outcomes such as resistance emergence.^40,48,49

Here, we present a microfluidic-based AST system that enables the observation of bacterial susceptibility to continuous antibiotic concentrations in real time without labeling or staining and thereby allowing the test to be completed within 7 h. This model was based on the simple principle that the effective diffusion of antibiotic molecules occurs between the two parallel channels with different antibiotic concentrations. The computational fluid dynamics (CFD) simulation and the diffusion test of the fluorescence probes confirmed that the antibiotic concentration gradient was linearized within 30 min. It was also verified by comparison with OD measurements that it is reasonable to estimate the local bacterial density as the GSVs from the microscopy images. Consequently, AST was conducted against a Gram-negative wild-type strain, P. aeruginosa, using five types of antibiotics of four killing mechanisms, and the minimum inhibitory concentration (MIC) was determined and compared with the standard MIC range. Lastly, we showed the potent application of our system for combinatory AST by varying the configurations of antibiotics injected into the chip.

MATERIALS AND METHODS

Fabrication of the microfluidic chip

The detailed fabrication process of the chips is well introduced in previous research.⁵⁰ Briefly, we first fabricated 120 μm-deep-patterned PDMS chips (Dow Corning) by soft lithography using SU-8 silicon wafers (AMED Inc.). The medium and gel ports were pierced with biopsy punches of 4 mm and 1 mm diameter, respectively (KAI medical). After sterilization, an oxygen plasma treatment was applied to the cover glass and the pattern-engraved surface of PDMS, so that 120 μm-deep closed channels were made by bonding the PDMS to the cover glass. The resulting chips were stored in a drying oven at 80 °C for 24 h to recover their hydrophobicity and were used in the experiment.

Computational simulation and fluorescence experiment

Based on the chip geometry reconstructed by a commercialized program (SolidWorks, Dassault Systèmes), computational fluid dynamics (CFD) simulation of the agents in our system was conducted (COMSOL Multiphysics 5.2a). Since the z-height is 120 μm, which is less than one-tenth of the gel width of 1300 μm, it was assumed that there was no variation in the concentration of diffusing molecules along the z-axis.⁵¹ Therefore, the simulation could be performed in a 2D plane. It was also hypothesized that transport of the agents in the gel could be occurred by their diffusion. The diffusion coefficients were estimated based on the mathematical model such as the Ogston model, where a diffusing particle is assumed to be a spherical rigid molecule (see the supplemental material).⁵² The flow rate of the channels was set to 2 μl/min.

For the fluorescence experiment, Fluorescein (MW = 332.3 g/mol, Sigma-Aldrich) and Alexa 594 (MW = 819.9 g/mol, Thermofisher Scientific) were chosen, since they have a similar molecular weight as most of the antibiotics. The dyes were prepared as the stock solution according to the manufacturer's instructions and stored at −70 °C. If necessary, they were diluted with 1× phosphate buffered saline (PBS) (10 μg/ml for Fluorescein and 100 μg/ml for Alexa 594). The dye-supplemented PBS was injected in the channels, which were connected to the syringe pump (2 μl/min per channel). The acquired time-lapse fluorescence images were analyzed using a microscope software (AxioVision4, Carl Zeiss).

Bacteria and antibiotics preparation

Pseudomonas aeruginosa ATCC 27853 cryopreserved at −70 °C was inoculated in 10 ml Lennox broth (LB) (Invitrogen) medium and was incubated overnight at 37 °C. On the next day, a small amount of the bacteria were diluted in the LB medium and spread on an agar plate. Then, multiple colonies were obtained by overnight incubation in an incubator at 37 °C. A single colony was inoculated in 1.5 ml LB medium for 3 h at 37 °C prior to the experiment. The bacteria were then centrifuged at 4000 rpm for 8 min, and the supernatant was discarded. Then, bacterial samples of approximately 2E + 8 cells/ml were prepared by mixing 300 μl of cold 1× PBS with cell pellets.

All antibiotics were prepared as stock solutions according to the manufacturer's instructions. Then they were sterilized with a 0.22 μm syringe filter (Pall Life Sciences) and stored frozen at −70 °C. If necessary for the experiments, the solutions were diluted with Cation-adjusted Mueller-Hinton broth (CAMHB) (BD biosciences): 4 μg/ml for tobramycin (TOB) (Sigma-Aldrich), 2 μg/ml for gentamicin (GEN) (Thermofisher Scientific), 32 μg/ml for tetracycline (TET) (Sigma-Aldrich), 8 μg/ml for levofloxacin (LEV) (Sigma-Aldrich), and 4 μg/ml for meropenem (MER) (Sigma-Aldrich). Antibiotics diluted for over 2 days were not used in the experiments.

On-chip antibiotic treatments

After mixing 300 μl of 1% (w/v) agar gel melted above 80 °C and 100 μl of the prepared bacteria sample, 10 μl of the mixture was carefully injected into the gel region of the prepared chips. After gelation at room temperature for 5-8 min, both medium channels were filled with CAMHB. One ends of both channels were then connected to the syringe pump (PHD Ultra Syringe pump, Harvard Apparatus) with silicon tubing (ID = 0.8 mm, Masterflex). The other ends of the channels were filled with antibiotic-supplemented CAMHB for the antibiotic channel and antibiotic-free CAMHB for the antibiotic free channel (Fig. 1). Then, the media of the channels were withdrawn at a rate of 2 μl/min per channel with the pump. To maintain the required amount of media in the channel, we periodically replenished the respective media in the ends of the channels that were not connected to the pump. During the 6 h of testing, the concentration gradient was sustained with the pump and the phase contrast images were obtained every 10 min using a microscope (Objective 10×, NA 0.55, Observer Z1, Carl Zeiss).

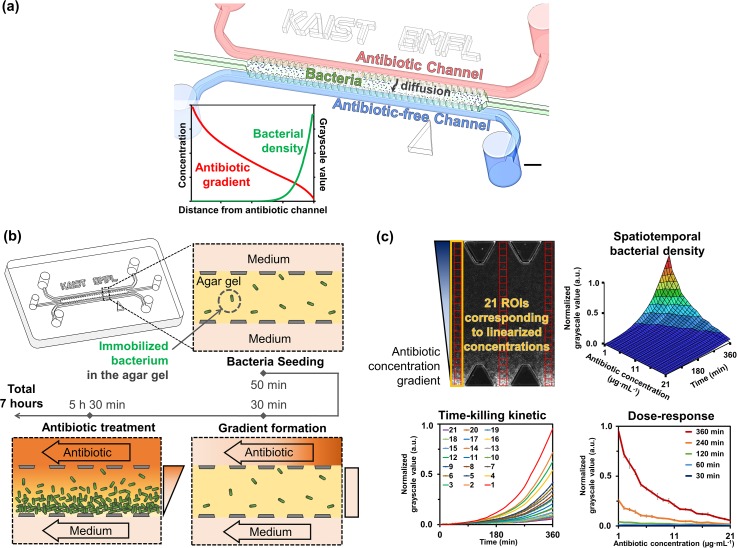
FIG. 1.

Schematic for the process of on-chip antibiotic treatments and image analysis. (a) The representative schematic for our AST chip. Scale bar is 1.2 mm. (b) Experimental process of the chip AST as shown where a mixture of bacterial sample and agar gel is introduced into the microfluidic channel. Then, the antibiotic concentration gradient is formed within 30 min and changes in local bacterial growth are observed due to treatment under antibiotic gradient. (c) Image analysis and quantification. GSVs are acquired from the ROIs corresponding to linearized concentrations, and the 3D diagram of normalized GSVs can be shown along linearized antibiotic concentrations over 6 h of treatment time. From the diagram, time-killing kinetic and the dose-response graphs can be reconstructed. The length of one side of the ROI is 60 μm.

Optical image acquisition and analysis

During the treatment, the microscope focus was fixed slightly below the bottom of the bacteria-trapped gel region (∼100 μm) to make all bacteria in the gel to be out-focused. In the obtained microscopic images, 21 regions of interest (ROI) boxes (60 by 60 μm for each ROI) were placed across the gel region, and the GSVs of each ROI box were imported using the Image J software (National Institutes of Health, http://imagej.nih.gov/ij). To ensure that the GSVs were within the 8-bit range of 0-255, different exposure time values were preliminarily tested and set to 20 ms.

For the normalization, based on the same ROI, we subtracted the initial mean GSV of growth control $(\mathrm{GS}{\mathrm{V}}_{\mathrm{\varnothing }})$ from the mean GSV of antibiotic X $(\mathrm{GS}{\mathrm{V}}_{\mathrm{X}})$ obtained at the specific time points. We then normalized it using the difference between initial mean GSV and final mean GSV of growth control. This calculation allowed the normalized GSV to have a value between 0 (no visible growth) and 1 (maximal growth):

$$\mathrm{Normalized}\mathrm{Grayscale}\mathrm{Value}=\frac{\mathrm{GS}{\mathrm{V}}_{\mathrm{X}}-{\mathrm{GS}{\mathrm{V}}_{\mathrm{\varnothing }}|}_{0\min }}{{\mathrm{GS}{\mathrm{V}}_{\mathrm{\varnothing }}|}_{360\min }-{\mathrm{GS}{\mathrm{V}}_{\mathrm{\varnothing }}|}_{0\min }}.$$ (1)

Off-chip bacterial growth measurements

OD₆₀₀ measurements were used to identify the off-chip bacterial growth. The bacterial samples were prepared in the same manner as the samples used in on-chip growth measurements. Every seven samples containing 300 μl 2E + 8 cells/ml bacteria in 1× PBS were prepared. Then, 900 μl of CAMHB medium was mixed to prepare seven diluted bacteria samples for OD₆₀₀ measurements so that the initial densities of samples were the same as those used in on-chip growth measurements. After 50 min, one sample was transferred to the 4 °C refrigerator, and other samples were sequentially transferred every hour for 6 h. At the end of the incubation of the last sample, all of the refrigerated samples were transferred to the 1 ml cuvette. Finally, the OD of each sample was measured on the 600 nm wavelength light and was compared with our estimation method (NanoPhotometer P-Class, Implen).

Assessments of synergy levels

To assess the synergy levels between the two antibiotics, parameters α and β that minimize the following two metrics were calculated, which correspond to Bliss independence and Gaddum's non-interaction models, respectively:⁵³

$${\sum }_{\mathrm{ROIs}}{(\mathrm{GS}{\mathrm{V}}_{\mathrm{MER},\mathrm{GEN}}-\alpha \times \mathrm{GS}{\mathrm{V}}_{\mathrm{MER}}\times \mathrm{GS}{\mathrm{V}}_{\mathrm{GEN}})}^2,$$ (2)

$${\sum }_{\mathrm{ROIs}}{(\mathrm{GS}{\mathrm{V}}_{\mathrm{MER},\mathrm{GEN}}-\beta \times \max \{\mathrm{GS}{\mathrm{V}}_{\mathrm{MER}},\mathrm{GS}{\mathrm{V}}_{\mathrm{GEN}}\})}^2,$$ (3)

where $\mathrm{GS}{\mathrm{V}}_{\mathrm{MER},\mathrm{GEN}}$ represents the final GSV calculated from the combinations of MER and GEN, and $\mathrm{GS}{\mathrm{V}}_{\mathrm{MER}}$ and $\mathrm{GS}{\mathrm{V}}_{\mathrm{GEN}}$ represent the final GSV calculated from a single gradient of MER and GEN, respectively. The dimensionless parameters, α and β, describe the deviation from null surfaces of models. The value of parameters being less than 1 or not determines whether the effect is synergistic or antagonistic.

RESULTS AND DISCUSSION

Engineered microfluidic-based chips for antibiotic susceptibility testing

The microfluidic chip aimed at generating an antibiotic concentration gradient on an agar gel in which the bacteria were fixed and calculated the difference in bacterial growth in the gel depending on the concentration [Fig. 1(a)]. The PDMS chip included two parallel 500 μm-wide side medium channels, a 1300 μm-wide middle gel region, and lined trapezoidal shaped posts that serve to trap the agar gel using surface tension. The agar gel immobilized the bacteria and prevented exposure of the bacteria to physical shear flow. Thus, we could observe the bacterial susceptibility to the antibiotics during the AST, which were time-dependent and concentration-dependent manners.

We conducted the AST experiments in several steps [Fig. 1(b)]. After mixing 300 μl of 1% (w/v) agar gel and 100 μl of the prepared bacteria sample (3:1 ratio), we injected 10 μl of the mixture into the gel region of the chip. The surface tension induced by trapezoidal posts prevented the liquefied agar gel from leaking into the medium channels on both sides. After gelation at room temperature for 5-8 min, both medium channels were filled with CAMHB. During incubation at room temperature for about 50 min, we connected the two medium channels to the syringe pump. After injecting antibiotic-supplemented CAMHB and antibiotic-free CAMHB into the medium channels, respectively, the media of both channels were withdrawn with the pump (at a rate of 2 μl/min per channel). Simultaneously, the microscope imaging was started and images were obtained every 10 min. Due to the pump, antibiotic molecules diffused from the source channel into the sink channel across the gel, and a linear concentration gradient of antibiotic was formed in 30 min. Afterward, the concentration gradient was maintained with the pump and the antibiotic treatment is continued for 5.5 h at room temperature.

For quantifying the bacterial growth of the microscope images, we placed 21 ROI boxes of 60 by 60 μm size across the gel region using the image J software [Fig. 1(c)]. The positions of each ROI box correspond to the linearized antibiotic concentration values. We imported GSVs of each ROI box for estimating bacterial density. After normalization of GSV with its maximum value, we plotted the GSVs in a 3D diagram according to the range of continuous antibiotic concentration over treatment time. The diagram contains temporal and spatial information about the bacterial density in the agar gel, and it provides a time-killing kinetic graph and a dose-response graph, independently.

Validation of on-chip bacterial growth measurements with the conventional method

Prior to performing on-chip AST, it was necessary to confirm the bacterial growth curve without antibiotics. The bacterial density inside the agar gel was estimated using the normalized GSVs calculated from the phase contrast images.⁴⁰ The obtained microscopic images showed that local bacterial density is related to the GSV range of 0 to 255, with the observation that the color is closer to black as the local bacterial density is low, whereas the color becomes whiter as the local bacterial density increases [Fig. 2(a)].

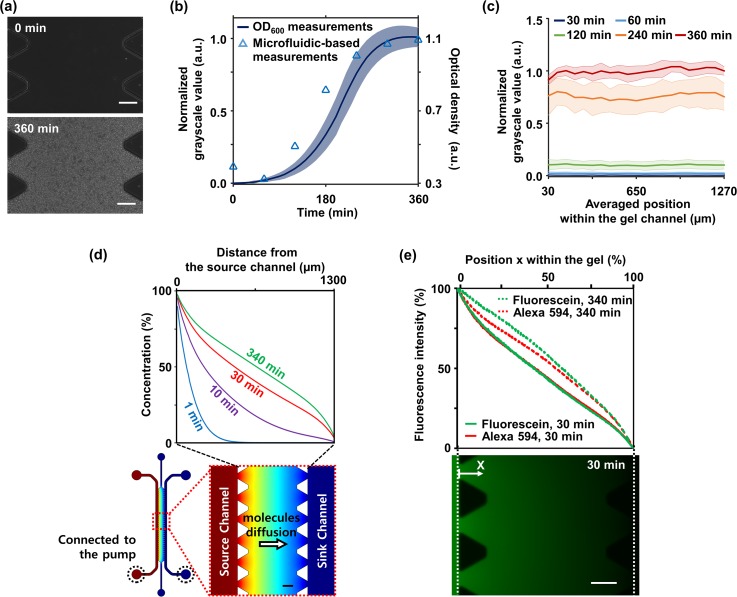
FIG. 2.

Validation of on-chip estimation of bacterial growth and formation of the linear antibiotic gradient. (a) Over culture of 360 min, changes of grayscale from black to white due to bacterial growth within the agar gel were captured under a microscope. (b) Comparison of on-chip bacterial growth estimation (solid line) and OD₆₀₀ measurement (triangular points) during 6 h of culture shows good agreement. (c) The GSVs in the gel had similar values regardless of positions. Measurements obtained from three rows of ROI sets were averaged, and the experiments were replicated four times. All shaded bands represent s.d. (n = 4 independent chips). (d) CFD simulation results identified the linearization time as 30 min. The configuration of the CFD result showed that antibiotic molecules of source channel effectively diffuse into the sink channel due to 2 μl/min flowing per channel by the externally connected syringe pump. Red indicates the maximum concentration of an antibiotic and blue indicates the minimum concentration of the antibiotic. (e) Fluorescent intensity measurements of diffusing Fluorescein (MW = 332.3 g/mol) and Alexa 594 (MW = 819.9 g/mol) showed the similar shape of plots and identified the linearization time as 30 min as well. Each quantity was normalized based on both end values in the gel channel. The fluorescence image below showed diffusing Fluorescein (green) into the agar gel from the source channel. All scale bars are 200 μm.

The GSVs measured on the microfluidic chip over 6 h were compared with OD₆₀₀ measurements, one of the conventional methods. As a result, we could confirm three distinct phases where the increase of the normalized GSV was insignificant (0 to 120 min), the increase rate was constant (120 to 270 min), and the increase was saturated (270 to 360 min) [Fig. 2(b)]. Such trends have also been confirmed in OD₆₀₀ measurements, commonly referred to as lag, exponential, and stationary phases [Fig. 2(b)].⁵⁴ Although the growth was slightly faster in the OD₆₀₀ measurements, comparing the two measurements, we were able to note the trend and three phase change match for both OD₆₀₀ and microfluidic GSV measurements. In addition, comparing the GSV within the gel, we found that there was no significant difference even after reaching 360 min [Fig. 2(c)].

Therefore, it is reasonable to estimate the local bacterial density with GSVs during antibiotic treatment within 6 h. In addition, since this method is performed on a microscale, there is no need for a long incubation time, no additional steps for density measurements such as fluorescence staining cells or attaching a bead.^55,56 It is also efficient and convenient because it can continuously measure in real time without discarding samples.

Validation of on-chip linear concentration gradients

With constant flow in the microchannel due to the pump, the medium channel of the chip acts as a source or sink for antibiotics. Thus, antibiotic molecules effectively diffuse across the agar gel from the source channel to the sink channel. This is important when trying to reduce the time for the antibiotic concentration to be linearized, and thereby minimizing the effect of a nonlinear gradient of the antibiotics on the bacteria.

In order to identify the linearization time, a CFD simulation was performed. Parameters such as the diffusion coefficients used in the simulation were estimated based on the Ogston model (see the supplemental material).⁵² The simulation results showed that the antibiotic concentration gradient was linearized in 30 min after applying a flow rate of 2 μl/min per channel within the 10% error to a steady-state profile of concentration gradient [Fig. 2(d)].

The simulation results were validated with the diffusion experiments using Fluorescein (MW = 332.3 g/mol, Sigma-Aldrich) and Alexa 594 (MW = 819.9 g/mol, Thermofisher Scientific). These fluorescent probes have a similar molecular weight as most of the antibiotics and consequently have similar diffusion coefficients (see the supplemental material). The medium with fluorescent molecules was injected into the source channel instead of antibiotics, and time-lapse of fluorescence images were captured. The fluorescence images showed that Fluorescein diffused from the source channel to the sink channel across the agar gel, and fluorescence intensity measurements showed that linearized profiles of Fluorescein and Alexa 594 were formed in 30 min with the flow [Fig. 2(e)]. These were also within the 10% error range of a steady-state profile of intensity gradients measured at 340 min. These results were consistent with the results of CFD simulation.

Through the CFD simulations and the fluorescence experiments, we confirmed the linearization time of 30 min. Rapid linearization is important to ensure complete linearization before the bacteria enter the exponential growth phase, considering the exponential growth rate of the bacteria. The initial incomplete and non-linear antibiotic gradient will adversely affect subsequent bacterial growth by the emergence of antibiotic resistance or tolerance and consequently may result in experimental errors in the AST.^48,49 For example, one of the fastest growing species, Escherichia coli, takes about 60 min to enter the exponential growth phase with 20 min doubling time since entering the growth phase.⁴⁰ This indicates that time for linearization should be at most 60 min in order to expect reliable results from the microfluidic-based AST. Our linearization time of 30 min suggests that the antibiotic concentration gradient is steadily formed before the exponential growth phase when compared to the curve of zero-drug growth. It also implies that our platform could be applied when testing a variety of bacteria strains including the stains with the fastest growth rate.

Monitoring on-chip bacterial growth under single antibiotic gradients and MIC determination

Bacterial susceptibility to five antibiotics that belong to four different antimicrobial mechanisms was monitored on our microfluidic platforms. The antibiotics tested were TOB and GEN of the aminoglycoside class, TET of the tetracycline class, LEV of the fluoroquinolone class, and MER of the β-lactam class (Table I in the supplementary material). The classes mentioned are typical antibiotic classes and are known to cause the death of Gram-negative bacteria through different mechanisms.⁵⁷

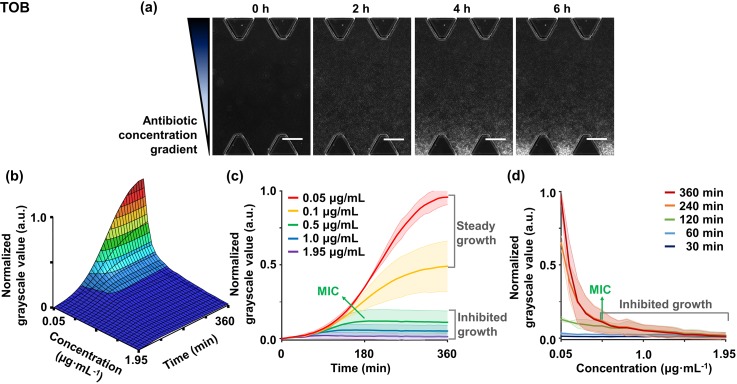
As a representative case, in the TOB gradient treatment, distinct grayscale levels indicating bacterial densities were clearly identified depending on the antibiotic concentrations [Fig. 3(a)]. As the treatment continued, sites that were close to the sink channel became whiter, which implies that the bacterial growth occurred. This tendency can be monitored in the susceptibility graphs [Fig. 3(b)]. According to the results, bacterial growth was inhibited at drug concentrations above 0.5 μg/ml of TOB in both time-killing and dose-response graphs [Figs. 3(c) and 3(d)].

FIG. 3.

Monitoring bacterial susceptibility to the linearized concentrations of TOB for 6 h. (a) Time-lapse microscopic images of on-chip bacterial growth under TOB gradient show distinct GSV levels depending on the locations corresponding to concentrations. Scale bars are 200 μm. (b) Different GSV changes depending on the concentrations are plotted into the spatiotemporal graph, and its (c) time-kill kinetic graph and (d) dose-response profile are represented. The graphs represent bacterial susceptibility to TOB gradient. (c) The time-kill graph shows five representative time-dependent responses of concentrations and (d) the dose-response graph shows concentration-dependent responses of specific time points. In the concentration range of inhibited growth of the graphs, we indicate a specific MIC value (green arrow), which belongs to the MIC range at which bacterial growth is suppressed from 90% to 95%. Measurements obtained from three rows of ROI sets were averaged, and the experiments were replicated two times. All shaded bands represent s.d. (n = 2 independent chips).

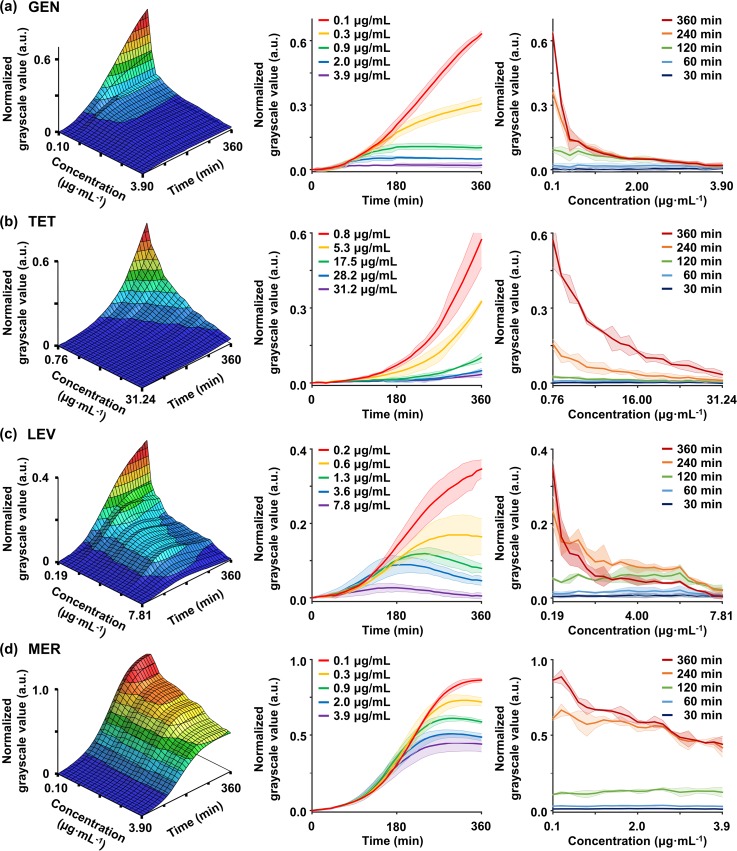
We also conducted AST for the remaining antibiotics. Comparing the results of GEN with those of TOB, the overall tendency was not significantly different in both temporal and spatial graphs [Fig. 4(a)]. We could also identify distinct bacterial growth rates depending on the linearized antibiotic concentrations. At a concentration of 0.1 and 0.3 μg/ml, GSV monotonically increased, but at a concentration of 0.7 μg/ml or higher, GSV finally became constant. In particular, at concentrations above 0.9 μg/ml, the GSVs were constant from 180 min, resulting in low GSVs of less than 0.1 at 360 min. TET also showed a significant difference in the bacterial growth levels depending on the antibiotic concentrations [Fig. 4(b)]. Notably, unlike other antibiotics, a gradually increasing bacterial growth was observed even at high concentrations of TET. These results may be due to the underlying mechanism of TET. TET is known to bind to the 30S ribosomal subunit of bacteria and interfere with the binding of aminoacyl tRNAs, but the binding to the 30S ribosomal subunit is reversible.⁵⁷ This characteristic may allow that bacteria population to continuously grow even at high concentrations as shown in the graph. In the case of LEV belonging to the fluoroquinolone class, killing effects could be confirmed in our experiments [Fig. 4(c)]. In addition to the difference in normalized GSVs depending on the concentration of LEV, GSVs began to decrease significantly from 240 min above 1.3 μg/ml. This decreasing tendency for GSVs was not found in the results of antibiotics with inhibiting protein translation. We estimated that these results are due to the excellent bactericidal effect of the fluoroquinolone class that is known to be fatal to P. aeruginosa.⁵⁸

FIG. 4.

Time-lapse monitoring bacterial susceptibility to the linearized concentration of (a) GEN, (b) TET, (c) LEV, and (d) MER. The spatiotemporal graphs of each antibiotic provide a complex understanding of the susceptibility of the bacteria to antibiotics. The left panels represent spatiotemporal diagrams of bacterial susceptibility. Either the middle panels or the right panels show five representative cases in the time-kill or the dose-response perspectives, respectively. Measurements obtained from three rows of ROI sets were averaged, and the experiments were replicated two times. All shaded bands represent s.d. (n = 2 independent chips).

Compared to other antibiotic types, MER showed a different trend [Fig. 4(d)]. Until 180 min of treatment, the normalized GSVs gradually increased regardless of the antibiotic concentrations. However, after 180 min, the increasing rates of GSV changed depending on each concentration, and the curves were sequentially separated. These results may be due to the bactericidal mechanism of the β-lactam class. The β-lactam antibiotics are known to bind to penicillin-binding proteins, which interfere with bacterial cell wall synthesis and cause morphological changes in a cell, resulting in lysis and eventual cell death.^59–61 Morphological changes such as filamentation or swelling cause changes of bacteria cell size, which may lead to distorting values of increased GSVs.⁴⁰ Therefore, even with the highest concentration of 3.9 μg/ml MER, the normalized GSV apparently seemed to increase at a rate similar to that of the low concentration before 180 min [Fig. 4(d)]. However, due to lysis of the bacterial cell wall, the sequential separation of growth curves occurred after 180 min. If bacteria cells are treated with β-lactam for a longer time, lysis would progress further, resulting in more cell death. Therefore, in a time frame similar to the duration of conventional tests, it is expected to record lower bacterial growth values than our GSVs in the presented graph.

The MIC, a universal indicator of bacterial inhibition of antibiotics, was determined from the dataset. We set the MIC range to be the concentrations of the antibiotic tested with a range of 0.05-0.1 normalized GSV at 360 min, which indicates 90% to 95% inhibition of bacterial growth at the end of AST.^7,22 With this criterion, the MICs for TOB, GEN, TET, and LEV were found to be 0.5–1 μg/ml, 0.9–2 μg/ml, 17.5–28.2 μg/ml, and 1.3–3.6 μg/ml, respectively (Table I). In the case of MER, however, the criterion could not be applied because the treatment had a distorted effect on GSVs at a high concentration due to the swelling effect. Therefore, we applied the criteria for MIC of MER to be the minimum concentration at which the normalized GSV started to decrease over time.^40,44 Thus, the MIC was determined to be 0.7 μg/ml with the expectation that lysis and death of bacteria would occur if bacteria are exposed to MER for several hours in the same manner of conventional AST methods.²³

TABLE I.

List of antibiotics that were tested and MICs determination.

Class	Primary target	Mechanism of action	Antibiotic	Abbreviation	CLSI MIC (μg/ml)	Chip MIC (μg/ml)
Aminoglycosides	30S ribosome	Inhibit protein translation	Tobramycin	TOB	0.25–1	0.5–1
			Gentamicin	GEN	0.5–2	0.9–2
Tetracyclines	30S ribosome	Inhibit protein translation	Tetracycline	TET	8–32	17.5–28.2
Fluoroquinolones	DNA gyrase	Inhibit DNA synthesis	Levofloxacin	LEV	0.5–4	1.3–3.6
β-lactams	Penicillin-binding proteins	Inhibit cell wall construction	Meropenem	MER	0.25–1	0.7

Finally, the MIC ranges of each antibiotic determined in our platforms were compared with the MICs presented by the Clinical and Laboratory Standards Institute (CLSI), referred to as a gold standard (Table I).²² The MIC ranges of all the antibiotics that were tested using the chip were included in the CLSI MIC range. The MIC ranges suggested by the CLSI were slightly broader than our chip-based MIC ranges, which could have originated from their conventional testing method, broth microdilution. In the method, antibiotic concentrations are diluted in two-fold for each well of a microtiter plate.⁶² Thus, the CLSI provides slightly broader MIC ranges compared to our chip-based MIC ranges determined in a continuous concentration gradient. Nevertheless, our MIC ranges showed good agreement with the standard results, demonstrating the efficacy of our device as a cell-based drug screening platform.

Monitoring on-chip bacterial growth under combinatory antibiotics

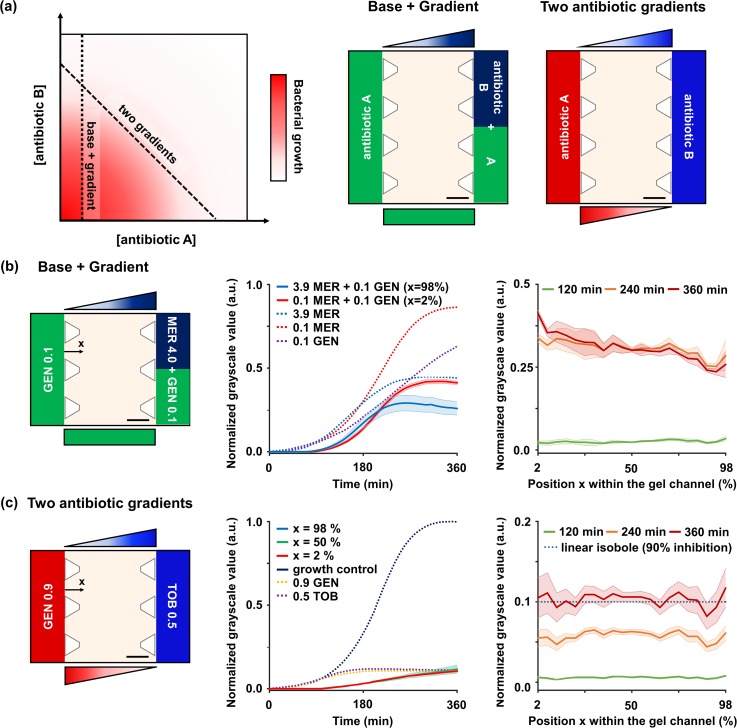
To test the combinatory antimicrobial effects of two drugs, we generally need a full dose-by-dose response matrix with a number of antibiotic combinations.⁶³ Although our platform cannot suggest the full response matrix, our systems are able to provide certain informative lines of the response matrix, by constructing the partial concentration combinations depending on the configurations of the antibiotics injected [Fig. 5(a)]. For acquiring bacterial growth along the two distinct lines shown in the matrix, we designed two ways of placing antibiotics, namely, “base + gradient” and “‘two antibiotic gradients.”

FIG. 5.

On-chip combinatory AST. (a) Schematic shows a general full response matrix. For constructing concentration combinations along the two distinct lines in the matrix, we note two configurations of antibiotics injected such as (b) “Base + Gradient” and (c) “Two antibiotic gradients.” They can be made by placing antibiotic A in one channel, and antibiotic B, or a mixture of A and B, in the other channel, respectively. (b) “Base + Gradient” indicates the formation of an antibiotic gradient on the base of another antibiotic. In order to create the GEN base and MER gradient, 0.1 μg/ml GEN was injected into a channel, and a mixture of 0.1 μg/ml GEN and 4.0 μg/ml MER was injected into the other channel. The time-killing kinetic and the dose-response profile show additional effects of 0.1 GEN base. (c) “Two antibiotic gradients” indicates the formation of two antibiotic concentration gradients that intersect in opposite directions. To create two concentration gradients in opposite directions, 0.9 μg/ml GEN was injected into a channel and 0.5 μg/ml TOB was injected into the other channel. The time-killing kinetic and the dose-response profile show an additive relationship between the two antibiotics. In all time-killing graphs, the results of the single AST are plotted together (dotted lines). All scale bars are 300 μm. Measurements obtained from three rows of ROI sets were averaged and the experiments were replicated two times. All shaded bands represent s.d. (n = 2 independent chips).

Firstly, for “base + gradient,” we injected the first antibiotic (antibiotic A) in a medium channel and the second antibiotic (antibiotic B) in both channels [Fig. 5(a)]. This placement results in a concentration gradient of antibiotic A with the constant concentration of antibiotic B, since antibiotic A forms a linearized gradient across the gel as in the previous case, and antibiotic B diffuses into the entire gel to form the base. The resulting antibiotic combinations correspond to horizontal or vertical lines in the full response matrix [Fig. 5(a)].

To create the antibiotic gradient on the base of another antibiotic, 4 μg/ml MER was selected as the source concentration for the gradient, and a subinhibitory concentration of 0.1 μg/ml GEN was selected as the base [Fig. 5(b)]. The 0.1 μg/ml GEN was injected into a channel, and a mixture of 0.1 μg/ml GEN and 4.0 μg/ml MER was injected into the other channel. After 30 min, the antibiotic combinations were formed with the desired compositions in the gel, and the combinatory AST was performed for a total of 360 min. We quantified the GSV of images as temporal and spatial graphs and identified the bacterial growth under the antibiotic combinations. Bacterial growth did not occur anywhere in the gel for the initial 90 min due to the effect of the 0.1 μg/ml GEN base, which showed 37% growth inhibition at 360 min in the single AST of GEN [Fig. 5(b)]. After 220 min, the growth rate of bacteria started to change as a function of position. Finally, at the end of the test after 360 min, different GSVs were recorded depending on the position within the gel [Fig. 5(b)]. Importantly, the addition of the GEN base led to lower GSVs of the MER gradient than the GSVs of the single MER gradient. However, the drop in GSVs was different for each position in the gel. Compared to the GSVs of the single MER gradient, the GSVs decreased by 45% in the ROI closest to the GEN-only channel (x = 2%), and 19% in the ROI closest to the MER + GEN channel (x = 98%). To assess the synergy levels between the two antibiotics, we computed parameters α and β, which were derived from Bliss independence and Gaddum's non-interaction models, respectively.⁵³ As a result, both parameters showed lower values than 1, so the two antibiotics were considered to be synergistic (α = 0.782 and β = 0.455)

Secondly, for “two antibiotic gradients,” we injected different antibiotics (antibiotic A and B) into each of the two medium channels [Fig. 5(a)]. This configuration creates two concentration gradients that intersect in opposite directions. If the potential efficacy of the antibiotic injected into each channel is the same, antibiotic combinations made along the two gradients can be expected to produce the same inhibition level of bacterial growth. From the perspective of Loewe additivity, if the same level of growth is obtained along the combination line, the line refers to a linear isobole.^9,63 The resulting antibiotic combinations correspond to a diagonal line in the full bacterial growth matrix [Fig. 5(a)].

To create antibiotic combinations that make potential linear isobole across the gel, two antibiotics of the same class, TOB and GEN, were selected. The concentrations of GEN and TOB were found in each single AST graph to be 0.9 μg/ml and 0.5 μg/ml, respectively, which lead to the potent 90% inhibition of growth [Fig. 5(c)]. The 0.9 μg/ml GEN was injected into a channel and the 0.5 μg/ml TOB was injected into the other channel to create two concentration gradients in opposite directions [Fig. 5(c)]. We quantified the GSV of images as temporal and spatial graphs and identified the bacterial growth under antibiotic combinations. Bacteria did not grow in the initial 90 min due to the effects of GEN and TOB [Fig. 5(c)]. They started to grow gradually after 90 min and reached about 0.1 GSV at the end of the test. We noted that at the end of the test, the GSV at all positions in the gel was close to 0.1 (mean ± s.d. = 0.103 ± 0.052) [Fig. 5(c)]. Therefore, it was confirmed that the antibiotic combination produced isobole of 0.1 growth level. We expect that the usage of the developed microfluidic platform enables identification of the interaction between two antibiotics of different classes as a response line of the measured bacterial growth would be concave or convex, depending on whether they are synergistic or antagonistic.

CONCLUSION

The microfluidic-based AST system proposed in this study showed comparable results to the CLSI standards, demonstrating its efficacy. It also suggested the potential to be used as an efficient platform in combinatory AST for determining whether certain combinatory antibiotics are synergistic, additive, or antagonistic. Compared to the previous AST systems, our system greatly reduced the linearization time for the concentration gradient and the antibiotic treatment time to 30 min and 6 h, respectively. The completion of AST in a short period of time is the most obvious advantage of our system, as the shortened test duration prevents the excessive use of antibiotics in addition to being economical. The time reduction can be also appreciated in that the risk of bacteria becoming resistance during the treatment of antibiotics may be lowered. Moreover, our system verified its efficiency by simultaneously establishing continuous antibiotic concentrations and confirming the bacteria susceptibility. These advantages result in the user-friendly impact of chip AST by eliminating the need to prepare multiple samples and antibiotic concentrations. Furthermore, our GSV-based estimation method for bacterial susceptibility observations allowed us to identify antimicrobial effects in real time without the loss of sample or any additional process of labeling.

SUPPLEMENTAL MATERIAL

See supplemental material for the estimation of diffusion coefficients of the antibiotics in an agar gel and the parameters for CFD simulation (Table I in the supplementary material).