Abstract
The resistive pulse method based on measuring the ion current trace as a biomolecule passing through a nanopore has become an important tool in biotechnology for characterizing molecules. A detailed physical understanding of the translocation process is essential if one is to extract the relevant molecular properties from the current signal. In this Perspective, we review some recent progress in our understanding of hydrodynamic flow and transport through nanometer sized pores. We assume that the problems of interest can be addressed through the use of the continuum version of the equations of hydrodynamic and ion transport. Thus, our discussion is restricted to pores of diameter greater than about ten nanometers: such pores are usually synthetic. We address the fundamental nanopore hydrodynamics and ion transport mechanisms and review the wealth of observed phenomena due to these mechanisms. We also suggest future ionic circuits that can be synthesized from different ionic modules based on these phenomena and their applications.
I. INTRODUCTION
Ionic conduction through nanometer-sized channels or pores is a common theme in biological systems.50 Cells as well as various internal organelles of cells are enclosed in lipid bilayer membranes that are impermeable to most molecules. In order to maintain the conditions necessary for life, these membranes must selectively allow the passage of certain molecules. Thus, biological membranes are decorated with a variety of protein channels with a wide range of functionality. Nerve cells, for example, contain channels that are permeable to sodium, potassium, or calcium ions and can switch between open and closed states in response to changes in electrical potential across the cell membrane. These voltage-gated ion channels make the propagation of nerve impulses possible. Another such protein nanochannel, aquaporin, helps regulate the water content of cells and plays an important role, for example, in the functioning of the kidney. In eukaryotic cells, the DNA is stored in a compacted form in the nucleus as chromosomes. When genes are expressed, the molecular machine RNA polymerase reads snippets of the DNA sequence to produce short strands of mRNA which are then translated to amino acid sequences by ribosomes in the cytosol. In order to reach the ribosomes, the mRNA must cross the nuclear membrane through a nanopore made of lipid bound proteins: the nuclear pore complex. Once a ribosome synthesised polypeptide chain folds into a protein, the problem of nanopore transport does not end! Some of these proteins are actually targeted to the mitochondria and must be unfolded and pulled across the mitochondrial membrane through protein pores.125 Thus, nanopores and nanopore transport are essential to the chemistry of life.
Natural and synthetic nanopores inspired by their biological counterparts have found many applications for in vitro systems. One example is the “resistive pulse” technique for biomolecular detection. Here, the current through a nanopore is transiently interrupted by the passage of a single molecule, and the information contained in the perturbation to the electric current is used to infer the properties of the transiting molecule. The technique is essentially a single molecule version of the Coulter counter39 for counting and sorting cells. The Coulter counter consists of a single cell sized pore in an impervious membrane that separates two chambers both filled with an electrolyte. When a voltage is applied, a small current flows due to ion movement through the pore. If one of the chambers contains objects such as cells, occasionally a cell will enter the pore. When this happens, the volume of electrolyte in the pore and, therefore, the conductance of the pore is reduced and this can be detected as a drop in the current. Thus, the device can be used to rapidly count cells and make estimates of their size. It was shown by Kasianowicz et al.53 that if the typically micron sized pore in the membrane is replaced by a much smaller nanochannel, the device is able to detect the passage of single molecules of DNA and RNA. Their nanopore was a reconstructed version of a natural ion channel from a bacterial cytotoxic agent released by Staphylococcus aureus. It is formed by a protein called alpha-hemolysin which can self-assemble on a lipid bilayer membrane to form a pore that remains open and stable for extended time periods.
Following the pioneering experiments of Kasianowicz et al., methods were developed for fabricating nanopores synthetically with no help from the molecules of life. One such technique,22 involving a combination of micro lithography followed by treatment using the beam from an electron microscope, yields artificial nanopores in the 1 to 10 nm range. These tend to be more stable and are easier to work with though not as reproducible as the alpha-hemolysin pores for which the shape is strictly determined by its molecular structure. Solid state nanopores include silicon nitride pores and graphene pores.
The closest approximation to a circular hole in a 2D membrane is a graphene nanopore made in a mounted section of graphene sheet by means of the electron beam in a transmission electron microscope. The use of graphene nanopores was demonstrated by Garaj et al.31,32 and Schneider et al.90 A low cost synthetic nanopore can be made by capillary pulling. A capillary (internal diameter 200–500 m) is heated at the middle by a focused laser beam and simultaneously pulled at either end by a capillary puller, until the capillary breaks in the middle. This produces a pair of capillaries with conical tapered tips. The tip diameter can be controlled by adjusting the parameters of the capillary puller. Capillaries with pores as small as nm may be produced in this way66 and used in a variety of single molecule experiments. A more recent development is the hybrid nanopore. Here, the nanopore is made by self-assembly of DNA using the technique of DNA origami.87,93 The DNA sheet with the nanopore is subsequently electrophoretically driven to the tip of a conical glass nanocapillary.8,9,48,49 These nanopores can be quite small nm and are suitable for translocation experiments involving single stranded DNA just like protein pores. The DNA origami technique is suitable for the fabrication of more complicated objects such as pores with sequence specific binding sites for selective detection.47
Yet another technique for fabricating solid-state nanopores is ion-track radiation26 on polymer membranes. The biggest difference between polymer ion-track nanopores and silicon nitride nanopores is the low permittivity of the polymer nanopores. The higher silicon nitride permittivity often leads to significant field leakage away from the pores, thus leading to lower field through the nanopore and hence lower throughput, as measured by the translocation frequency. There are currently two high-energy elementary particle facilities for single-ion irradiation. One is located in Germany and the other in China. Asymmetric etching of the single-ion irradiated membranes to produce ion-track nanopores was first reported by Apel et al.5 Currently, Siwy’s group at UC Irvine100 and Chang’s group at Notre Dame26 are the major users of such nanopores. Chang’s group has been using it for the quantification of microRNA in liquid biopsies. First at Peking University and then at Notre Dame, Wang has developed a modified asymmetric etching method to fabricate single asymmetric nanopores suitable for single biomolecule detection.84,121 He was the first to develop an Atomic Layer Deposition (ALD) method applicable for sub- nm asymmetric polymer nanopore surface modification, which significantly improved the biosensing capability of solid-state nanopores.122 The polymer substrate and the high-permittivity monolayer focus the field through the peripheral monolayer at the tip, such that molecules can be pinned by the leaking field at the tip edge to prolong their translocation time. Interestingly, single-stranded and double-stranded nucleic acids show different pinning and de-pinning mechanisms, with the former having a translocation time that is 100 times higher than its double-stranded duplex26 (see Fig. 1).
FIG. 1.
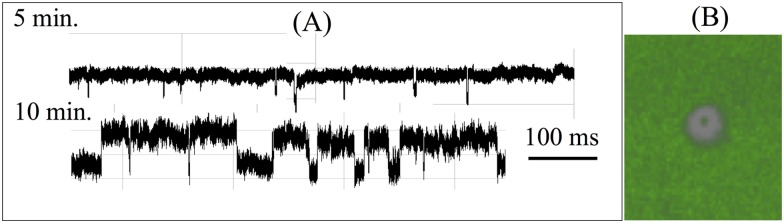
For solid-state nanopores on a membrane or silicon nitride substrates, an important unexplored issue is the adsorption of the translocating molecules onto the substrate before translocation. Such adsorption is enhanced by field leakage across the high-permittivity substrate. A critical barrier for translocation is then the transition from the adsorbed state on the substrate to a desorbed state in the nanopore. The molecule is pinned at the corner of the pore at this transition state and the barrier height is very different for ssDNA and dsDNA. (a) Translocation resistive pulse signals of a 50:50 mixture of 22b ssDNA and dsDNA after 5 min and 10 min. Average ssDNA translocation time is about 100 ms, compared to the average dsDNA translocation time of 1 ms. The distinctly different translocation times allow easy identification of the two events. The longer ssDNA translocation events initiate only after 10 min. (b) Stimulated Emission Depletion (STED) super-resolution microscopy image at 30 min shows that this delay of ssDNA translocation is due to an adsorption step onto the membrane surface before migration into the tip (see 100 nm depletion ring in the image). The nucleic acids within the depletion region have desorbed and translocated through the nanopore and the nucleic acids from the surrounding have yet to migrate into the region. Adapted with permission from Egatz-Gomez et al., Biomicrofluidics 10(3), 032902 (2016). Copyright 2016 AIP Publishing LLC.
Natural and synthetic nanopores have found many uses mainly relating to biomolecule detection and various single molecule experiments involving force11,55,62,77,113,117,118 and current measurements. These applications are discussed in depth in a number of excellent reviews.7,21,89 The work of Kasianowicz et al.53 was the first instance of single molecule detection using a nanopore. The current interruption signal can be calibrated quite easily to read out the length of the biopolymer. It was soon found that the technique could be used to do more. It can distinguish RNA homopolymers of identical length but with different bases and can even distinguish between block polymers consisting of long reads of a single base.12,78 This early work pointed to the possibility of a nanopore device that can detect nucleic acids at single base resolution. Such a device should be capable of reading off the sequence of bases in a long single strand of DNA or RNA in a manner analogous to the magnetic head of a tape recorder deciphering the signal encoded in a magnetic tape. Any such device would be a great improvement over existing techniques using wet chemistry and shot gun sequencing where a very large number of short reads need to be assembled like a jigsaw puzzle. The computational challenge involved in such a task is in itself quite formidable.61,99 The nanopore based approach has now been developed using protein pores or pore-enzyme complexes and single stranded DNA (ssDNA) into “third” and “fourth” generation gene sequencing technologies.27 Resistive pulse experiments to date in synthetic or “solid state” nanopores have mostly used double stranded DNA (dsDNA). This is because the persistence length of single stranded DNA (ssDNA) is much smaller and results in linear translocation in only subnanometer pores which are more difficult to produce. However, the bases in dsDNA are buried within the double helix structure and are not accessible for directly reading the sequence information. Nevertheless, resistive pulse experiments with dsDNA and synthetic pores have been used for a variety of applications such as mapping specific short sequence motifs on much longer DNA16 or multianalyte detection of protein targets using DNA bar codes.10
The charged surface of a nanopore attracts counterions in the fluid electrolyte and repels coions, creating a charge cloud of thickness (the Debye length), to be discussed later in Sec. III. Since nanochannels can be made with widths of the order of the Debye layer 1–10 nm,85,88 the diffuse charge cloud at the entrance of the nanochannel occupies a considerable fraction of the width of the pore. The charge cloud can be controlled using a “gate voltage,” as in a MOSFET transistor, to create an analog of semiconductor transistors3 in which the current is carried by ions rather than electrons. If controlling the ionic current with a gate voltage to create a transistor were the sole application of this technology, it would likely be of little interest. Semiconductor transistors achieve this far more efficiently and are a mature technology. Of much greater importance is the fact that the permeability to charged macromolecules can also be selectively controlled by changing the gate voltage.45 Thus, a pore that is selectively permeable to specific molecules can be created and the selectivity can be tuned at will. This is analogous to the gated pores in biological systems, though the gating is achieved in a different manner. Large scale practical use of the technology is likely but is still in the future.
Conical nanopores show a phenomenon known as “Ion Current Rectification” (ICR) and have a current voltage characteristic very similar to that of a semiconductor diode.5,51,100,102,124 The effect has many practical uses such as biosensing.120 Moreover, it has been shown that conical nanopores develop a strong hydrodynamic jet which also shows a rectification property for reasons not yet clearly understood.63 This jet can be used to apply pico-newton forces on objects. Conical pores have been used to perform a variety of single molecule experiments usually based on stalling DNA by applying forces to a bead attached to the end of the molecule furthest from the apex of the cone.54,55,62,118 Such “molecular tug of war” experiments have been used, for example, to measure forces generated by molecular motors as they pack DNA into viral capsids.106 Another interesting application of conical glass nanopores is “ion conductance microscopy” for non-destructively imaging soft objects, even living cells, in a fluid medium. Here, a conical glass nanopipette immersed in an electrolyte bath carries a small ionic current. As the glass slide with the sample approaches to within a distance of the order of the pore radius, there is a sharp decrease in the ionic current. If the sample is scanned in the - plane while adjusting the vertical position of the capillary tip so as to keep the current constant at a small fraction of the open pore current, a map of the sample shape may be generated.19,20,58
Nanopores have found many applications in biomolecular technologies in the last two decades and new applications are being found. In this Perspective, we attempt to provide an overview of the hydrodynamic and ionic transport properties of nanopores from the point of view of basic physics. For a broader perspective of other aspects of nanopores, we refer the reader to a number of excellent recent reviews of the subject.25,42,44,65,98,114 The review by Schoch92 is focused on transport properties in nanofluidic systems, including nanopores. Our paper is organized as follows. In Sec. II, we discuss how the most readily measurable property of a nanopore, its electrical conductance, can be related to its geometry. This is very useful as sizes of nanopores can often be estimated from resistance measurements. We also discuss the current rectification properties of conical pores. In Sec. III, we discuss the physics of the interactions of DNA or other biopolymers with nanopores. In Sec. IV, we discuss the problem of the transport of fluid through a nanopore in response to applied electric fields. Finally, conclusions are presented in Sec. V.
II. ELECTRICAL CONDUCTANCE OF NANOPORES
In resistive-pulse experiments, one tries to make inferences about the physical properties of the translocating DNA from the current trace. It follows therefore that a good understanding of the baseline case of the current voltage characteristic of the bare nanopore (in the absence of blockage) is important. In this area, the nanopore serves up some surprises as we shall see, but we begin this discussion by considering the electrical resistance of a pore which obeys Ohm’s law. In the laboratory context, this corresponds to a wide pore or to a high ionic concentration in the surrounding electrolyte so that the ratio of the Debye length to pore radius is vanishingly small. Furthermore, the surface charge on the substrate should be sufficiently small so that surface conductance effects can be neglected; formally, the Dukhin number,91 defined as the ratio of surface conductivity to bulk conductivity times pore radius, must be small compared to unity. In Sec. II A 3, we discuss work that relaxes the assumption that surface conduction can be neglected.
A. Theory
1. Ohmic resistance
The simplest electrical model of a nanopore is that of a cylindrical hole in an insulating membrane separating two reservoirs filled with an electrolyte regarded as a uniform conducting medium. We assume that the thickness of the membrane is , the radius of the pore is , and the electrical conductivity of the electrolyte is . The assumption of uniform electric conductivity can only be valid if (1) the Debye length is much smaller than the pore radius so that corrections due to nonuniform ionic concentrations within the Debye layer can be neglected and (2) the relative importance of surface conductance as measured by the Dukhin number is small. The pore resistance is then
| (1) |
Equation (1) indicates that as , which is evidently at variance with physical reality. In fact, Eq. (1) holds only if . As , the resistance of the pore approaches a constant value known as the “access resistance” of the pore.
Early calculations50 of the access resistance of a zero thickness membrane were based on the assumption that the field lines on either side of the membrane may be assumed to converge radially to the pore center. Thus, the radial electric field at a distance from the pore center is assumed to be
| (2) |
where is the current density on the radial direction and is the total current. We assume that as , the potentials approach on either side of the membrane and a current flows from the high to the low potential side through the hole in the membrane. The potential drop induced by the electric field in Eq. (2) is divergent unless the lower limit of the integration is truncated. If we choose to cut off the integration at , then
| (3) |
which implies an access resistance contribution of
| (4) |
from each side of the membrane. Imposing a lower limit of to arrive at Eq. (4) amounts to neglecting completely the resistance of the spherical region of radius centered on the origin, giving an error of the same order of magnitude as the estimate (4) for . Hall40 pointed out that the approximation leading to Eq. (4) is unnecessary as Laplace’s equation for the problem of a circular hole in a membrane (or equivalently, in the vicinity of a disk shaped charged conductor) can be solved exactly. The problem of access resistance of a hole can be mapped to the problem of determining the capacitance of a disk. The correct expression for the access resistance is then found to be
| (5) |
which exceeds the incorrect expression Eq. (4) by a factor of .
Returning once more to our basic model of the nanopore as a cylindrical conductor of uniform conductivity, one might ask how one should modify Eq. (1) for the resistance so that it approaches the correct limiting value of as ? Unfortunately, there is no analytical solution known for Laplace’s equation in the vicinity of a finite cylinder (or pore). It may be hoped that a reasonable approximation is obtained by regarding the finite pore as a set of three resistances in series; the resistance of a uniform cylindrical conductor (with end effects neglected) together with contributions from the inlet and outlet. Thus, Eq. (1) is replaced by the approximate expression
| (6) |
Equation (6) has the virtue of reproducing the correct asymptotic behavior in the two limits and , though it may be shown that it underestimates the true resistance by an amount that varies from 0 when to when .96
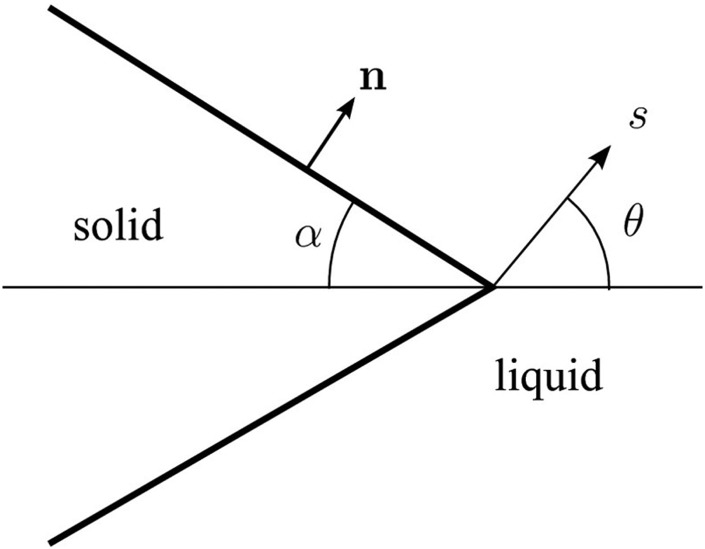
In many experimental situations, the nanopore actually has the geometry of a cone with exit radius and semi angle . In this case, an expression analogous to Eq. (6) may easily be obtained by replacing the expression for the Ohmic resistance of a cylinder by that of a cone:
| (7) |
Here, the access resistance at the wider end of the cone is neglected as it is usually much smaller than the contribution from the narrower end, and the access resistance of the narrow end of the cone will be an over-estimate, since current can flow to or from the aperture through a solid angle greater than . If denotes distance from the apex of the cone and corresponds to the pore entrance (Fig. 2), then the radius of the cross section at location “” is . The Ohmic resistance of a cone (of length ) may be obtained by adding in series the resistances of cylindrical slabs of material of conductivity :
| (8) |
where is the radius of the wide end of the cone. Thus, the Ohmic resistance of the truncated conical conductor is the same as that of a uniform cylinder of radius , a result noted by Maxwell (see Ref. 24). In many applications (such as nanocapillaries), so that the term and Eq. (7) reduces to
| (9) |
Equation (9) amounts to assuming that the cone is of fixed semi-angle but infinite in length. In nano capillaries,108 the taper angle is usually small, typically . In that case, the second term in the brackets in Eq. (9) is the correction due to access resistance and may be neglected.126
FIG. 2.
Sketch showing an idealized geometry for a conical nanopore.
2. Ion current rectification
The assumption that the electrolyte may be regarded as a uniform conducting medium of conductivity clearly does not hold in the vicinity of charged surfaces supporting a Debye layer. When the pore radius () is no longer large compared to the Debye length () or is small enough that the Dukhin number ( is the surface conductance) is no longer much less than unity, deviations from the Ohmic behavior discussed in Sec. II A 1 should be expected. Such non-Ohmic behavior was first observed in quartz nanocapillaries124 and subsequently in conical nanopores in track etched polyethylene terephythalate (PET) membranes.102 To a first approximation, the nonlinear current () voltage () characteristic may be represented as a piecewise linear function
| (10) |
similar to that of a semiconductor diode (Fig. 3). Here, and may be regarded as the resistances at forward and reverse bias, respectively, and we assume (by convention) that the voltage is positive when the current flows from the wide end to the narrow end of the pore. In most cases, the resistance at forward bias () is larger than that at reverse bias (). A rectification ratio may be defined as
| (11) |
Since the piecewise linear model (10) only approximately describes the measured characteristic, as defined above is in practice voltage dependent. This inconvenience may be avoided by taking the voltage in Eq. (11) as a standard voltage (e.g., V) to provide an operational definition of .100 The ratio is observed to depend on various aspects of pore geometry and substrate properties. In particular, it depends on the cone semiangle and approaches unity when , that is, for a cylindrical pore.
FIG. 3.
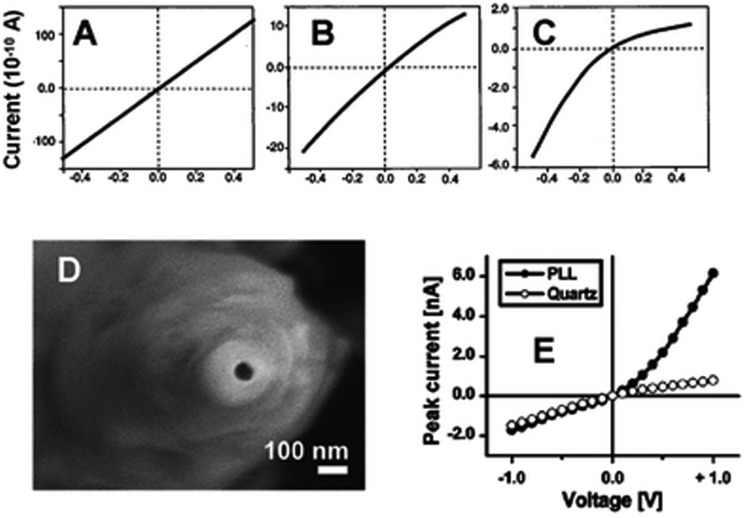
The rectification properties of single glass nano pipettes. (a)–(c) Current-voltage curves of a nano pipette recorded in (a) 1 M KCl, (b) 0.1 M KCl, and (c) 10 mM KCl. (d) Scanning electron microscopic image of a glass nano pipette whose transport properties are shown in (e). The narrow opening of this pipette was about 20 nm diameter. (e) The current-voltage curves recorded before and after modifying the nano pipette shown in (d) with poly-l-lysine (PLL) in 25 mM KCl, pH 5.0. Reproduced with permission from Z. S. Siwy and S. Howorka, Chem. Soc. Rev. 39(3), 1115–1132 (2010). Copyright 2010 The Royal Society of Chemistry.
Our understanding how relates to the pore properties has advanced significantly in the last 5 years. Wei et al.124 first presented convincing evidence that at least for quartz nanocapillaries, the current rectification is due to the Debye layer thickness being non-negligible compared to the pore radius. They observe (Fig. 3): (i) no rectification is found for micron sized pores. (ii) For a 10 nm radius pore, the rectification effect varies continuously from zero to a pronounced rectification as the electrolyte (KCl) concentration is progressively reduced from 1 M to 0.01 M. In this case, the fractional cross-sectional area occupied by the Debye layer increases from % to % as the salt concentration is reduced. (iii) If the substrate surface charge is varied by adding HCl to control the pH, then current rectification exhibits a sensitive dependence on pH. In particular, rectification disappears when the pH is close to the isoelectric point so that the substrate does not have a significant charge. At very low pH when the surface charge on the glass is reversed, an “inverted rectification” is observed with higher current at positive bias (). Wei et al. also presented a theoretical model based on ion transport in which it was assumed that the Debye layers conferred upon the pore a permselective property parametrized by an ion transferance ratio. The model is able to explain the current rectification phenomena, though the asymmetric ion transference ratio must be treated as an ad hoc parameter in this model.
A number of alternate ideas for explaining this “Ion Current Rectification” (ICR) phenomenon have been advanced. Proposed mechanisms include a voltage dependent pore size102 and Brownian ratcheting101,103 of ions due to an asymmetric electrostatic field in the pore. However, numerical solutions of the area averaged ion transport equations do seem to reproduce the nonlinear current-voltage curves15 suggesting that the continuum electrokinetic description may be adequate for a theoretical understanding of ICR along the lines originally proposed by Wei et al.124 A related rectification mechanism is induced polarization at the tip due to field leakage across the corner of the tip.134 This phenomenon is related to the induced charge electro-osmosis at a wedge corner, to be discussed in Sec. IV F. Here, however, it induces surface charge on the nanopore side of the tip and hence produces an induced surface conductance. The induced charge may be of the same or opposite sign to that of the native surface charge depending on the applied voltage bias, so that the ion current rectification may be increased or decreased. However, Zhang et al.134 found that polarization effects usually tend to diminish ion current rectification.
3. The effect of surface conduction
We have, so far, assumed that electrical conduction takes place solely within the fluid electrolyte, and that this has uniform conductivity . However, ionic number densities are perturbed adjacent to the charged surface of the pore, and this can lead to a change in the conductivity. We shall discuss the electrical charge cloud at the pore wall in Sec. IV. The change in electrical conductivity is confined to a region of width (the Debye length) adjacent to the wall and is therefore negligible unless is comparable to the dimensions of the pore and the change in ionic concentrations is sufficiently large compared to the concentrations in the bulk electrolyte. The Debye length (16) varies as the inverse square root of the ionic concentration, and as a result, surface conductivity usually increases more slowly than linearly with the ionic concentration. In addition, there may be conduction through adsorbed layers of ions (the Stern layer) or any other molecules that may have been adsorbed onto the pore walls during the manufacturing process.
The effect of a uniform surface conductivity on the total resistance of a uniform cylindrical pore in the absence of end effects can easily be modeled by considering two resistors in parallel, with combined resistance so that (1) becomes
| (12) |
where
| (13) |
is the Dukhin length. Lee et al.64 extended this analysis in order to include the effect of surface conductivity on the access resistance (5). By comparison with full numerical results, they concluded that the resistance of a cylindrical nanopore could be well represented by the expression
| (14) |
in which the radius of the nanopore in the expression (5) for the access resistance has been replaced by an effective radius .
B. Experiments
As discussed earlier, the current through a hole in a membrane of negligible thickness encounters a finite resistance given by Eq. (5). The best physical approximation to a zero-thickness membrane is perhaps a graphene sheet consisting of a single or several layers of carbon atoms. Graphene membranes are also charge neutral (unlike silica which normally has a strong negative charge) so that the idealization of a homogeneous conducting medium is more likely to be valid. Current voltage relations for single pores (radius 5–25 nm) in graphene sheets have recently been measured by Schneider et al.90 and Garaj et al..31,32 The measurements by Garaj et al. showed a resistance inversely proportional to the radius in excellent agreement with Eq. (5) for the access resistance. However, the measurements of Schneider et al. showed the rather unexpected result that the resistance of the pore scales as as might be expected for a thick membrane. This could be due6 to the 6-mercaptohexanoic acid coating applied to prevent DNA adsorption that presumably increases the effective thickness of the graphene layer.
In the case of glass nanocapillaries with small taper angles, Eqs. (7)–(9) may be used to efficiently estimate the diameter of a nanopore from conductance measurements when ionic concentrations are sufficiently large for the Debye length to be small compared to the pore radius. The diameters thus inferred for glass nano capillaries have been found to be in excellent accord with those determined by SEM imaging.109
At low ionic concentrations, surface conductivity may not be negligible, and as a result, the conductance of the pore is no longer proportional to the ionic concentration. This has been demonstrated in experiments by Smeets et al.105 and Lee et al.64 and has been used29,67 as a method to determine the geometry of pores more complicated than a uniform circular cylinder (e.g., cylinders with a conical entrance and exit).
Yan et al.126 were the first to show that the asymmetric Debye layer along the conic nanopore is a result of concentration polarization within the pore due to a conductivity gradient. At every cross section of the nanopore, electroneutrality must be obeyed due to the slender geometry. Hence, the net mobile space charge must be equal to the immobile surface charge at each cross section.
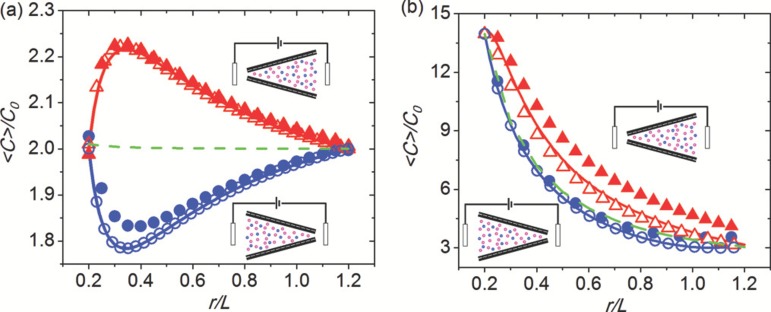
Since the surface charge density is constant, the amount of fixed charges on the wall is proportional to the circumference and therefore to the local radius. The equal and opposite mobile charge is, however, distributed almost uniformly over the cross section which varies as the square of the local radius. Thus, the local concentration of mobile charges is inversely proportional to the local radius and must vary along the axis of the conical pore. It is highest at the tip and lowest at the base. As the cations and anions are distributed according to the Boltzmann distribution governed by the surface field, the ionic strength also has a longitudinal gradient in the same direction. As such, depending on the electric field and the charge of the mobile counterion, the ion flux is either up or down the concentration gradient. Depletion or enrichment results, respectively, as seen in Fig. 4, where the leading-order depleted and enriched profiles, derived by Yan et al. using an area-averaged asymptotic expansion in the weakly selective limit, are shown against profiles simulated from the Nernst-Poisson-Boltzmann equation. Note that the sign convention adopted by Yan et al. is opposite to that used here, so that a potential applied at the tip of the cone by Yan et al. is equivalent (in our notation) to a potential applied at the base of the cone.
FIG. 4.
Comparison of the theoretical result from an asymptotic theory for the zero cone angle limit to computed results from the full Poisson-Boltzmann equation. The theoretical and computed cross-section averaged total ion concentration distribution , normalized by the bulk concentration , is plotted against the radial coordinate from the (imaginary) cone tip normalized by the pore length . The concentration distribution is observed to be very different for opposite polarization at and for weakly and strongly selective nanopores, as defined by a dimensionless parameter (see Ref. 126): the ratio of the surface charge concentration divided by the pore radius, to . The total concentration for Donnan equilibrium (green dashes), namely, when V = 0, is also given for comparison. The computation is done by solving both 1D (open symbol) and 2D (closed symbol) Poisson-Nernst-Planck equations. Enrichment occurs when applying a voltage from tip to base (positive V, red, lines, and up-triangles) and depletion with reverse bias (blue, lines, and circles). The tip radius, base radius, length, and surface charge density of nanopore are fixed at 5 nm, 30 nm, 1 m, and 0.05 C/m, respectively. The size of the reservoirs for 2D is 500 nm 500 nm. A symmetric electrolyte KCl with the diffusion coefficient of 2 m/s is used. (a) Weakly selective, the concentration is 1000 mM (X = 0.21). (b) Strongly selective, the concentration is 15 mM (X = 13.8). Adapted with permission from Yan et al., J. Chem. Phys. 138, 044706 (2013). Copyright 2013 AIP Publishing LLC.
Yan et al.’s weakly selective expansion yielded a simple closed-form estimate for their rectification ratio (11) in terms of the surface charge density , the gas constant , the bulk ion concentration , the pore tip radius , and the pore radius at the base, with
| (15) |
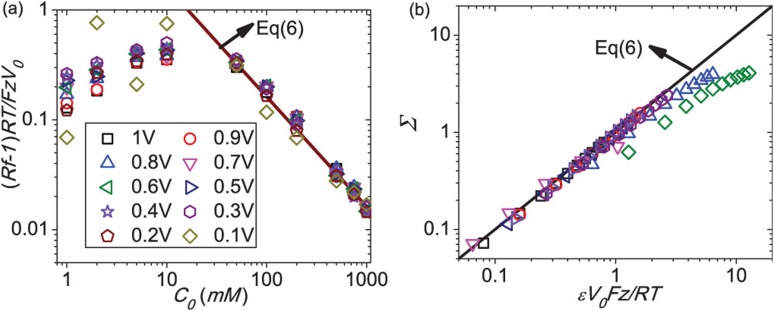
with (15) valid in the limit , where is a typical pore radius, is the Faraday constant, and is the ionic valency. Yan et al. were able to collapse the measured and simulated (from the Nernst-Poisson-Boltzmann equation) rectification factors with this simple prediction (15) in the high bulk concentration (), low applied voltage, and small surface charge density limit , as seen in the plots of and in Fig. 5.
FIG. 5.
(a) Collapse of measured rectification factor data for 12 m PET nanopore, with a tip radius of 19 nm and base 268 nm, surface charge 0.19 C/m (estimated from 1M data) by our small-X theory (line). (b) Collapse of 2D numerical rectification data for different geometries plus simulation data from the literature (magenta down triangle) with surface charge ranging from 0.00625 to 0.2 e/nm and bulk concentration from 0.25 M to 2.0 M. The simulation parameters (tip radius-base radius-length-surface charge-concentration) are 5 nm-30 nm-1 m-0.05 C/m-2000 mM (black square), 5 nm-30 nm-1 m-0.05 C/m-1000 mM (red circle), 5 nm-30 nm-1 m-0.05 C/m-250 mM (blue up-triangle), 5 nm-30 nm-1 m-0.1 C/m-250 mM (olive diamond), 5 nm-30 nm-1 m-0.01 C/m-250 mM (navy left triangle), 3 nm-30 nm-1 m-0.05 C/m-1000 mM (violet right triangle), and 15 nm-30 nm-1 m-0.05 C/m-1000 mM (purple hexagon), respectively. Reprinted with permission from Yan et al., J. Chem. Phys. 138, 044706 (2013). Copyright 2013 AIP Publishing LLC.
Curiously, Yan et al.126 predict a rectification inversion phenomenon at high voltages and low concentrations because of external concentration polarization at the tip, which has been extensively analyzed for ion-selective membranes and nanoslots (see review14). Such external concentration polarization does not require pore asymmetry and is mostly controlled by the tip side of a conic nanopore. Yan et al. were able to construct a phase diagram to determine the direction of rectification in the space.
The Ohmic conductor description fails when the diameter of the nano capillary is of the same order as the Debye length. As mentioned earlier, in this case, the capillary exhibits ion current rectification. In all cases investigated, an asymmetry in either pore shape, surface charge, or both these parameters simultaneously was found to be essential in order to achieve rectification. In fact, the rectification effect in a single conical pore can be greatly accentuated120 by modifying the charge locally near the tip of the pore (e.g., by adsorption of charged groups). Another approach to rectification has been demonstrated by Harrell et al.43 They used a gold coated conical pore in a polycarbonate substrate. A polymer brush of thiol terminated single stranded DNA was adsorbed to the gold surface. In this case, the electric field shifts the position of the DNA strands to block or unblock the pore. Here, the rectification function works at least partly by a steric mechanism as in many biological pores. The pore does not rectify in the absence of the adsorbed DNA. A similar tuning of the rectification using steric effects have been demonstrated by Yameen et al.,129 except that the electrolyte pH is used to control the rectifying characteristics. Logic gates using such pH modulated diodes have also been demonstrated.3 The ion current rectification property of nanopores has attracted much attention lately. A more detailed account may be found in several recent reviews.51,100,104
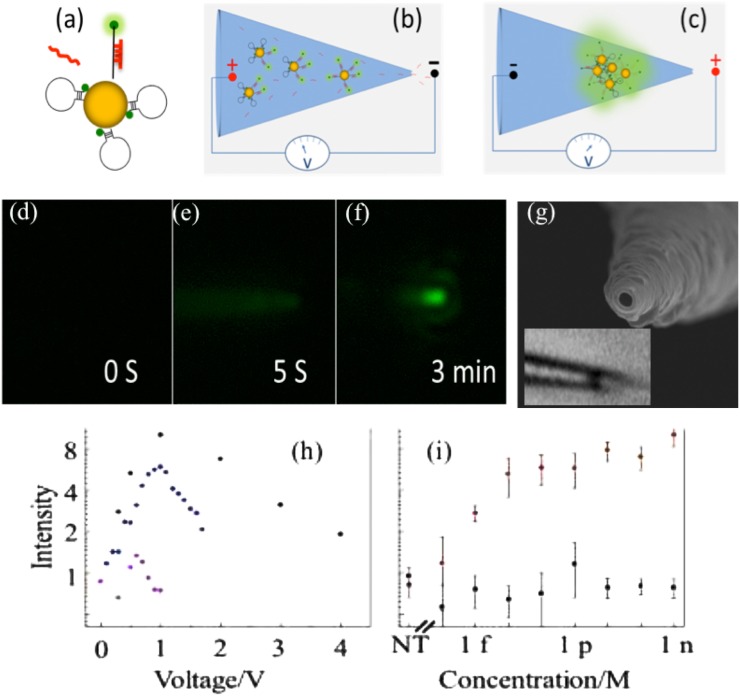
The intrapore ion concentration enrichment phenomenon described in Sec. II B can also be used to concentrate charged nanoparticles. Liu et al.68 used this phenomenon to concentrate and aggregate Au nanoparticles at the tip of a pulled nanopipette. By tuning the electric field, they were able to control the spacing between Au nanoparticles so that it reached an optimum value with large plasmonic intensity and without quenching the fluorophore on the labeled biomolecule (see Fig. 6). Pan et al.84 also used the large Ohmic heating at the tip of the conic nanopore to elevate the tip temperature to beyond boiling point such that nucleation of nanoscale bubbles occurs at the tip. Prior to nucleation, the viscosity of the fluid decreased rapidly with temperature and, hence, the current exhibited a distinctive quadratic increase with respect to voltage that camouflages the rectification phenomenon. One can, hence, use the current to estimate the tip temperature.
FIG. 6.
Hairpin Oligo Probe (HOP)-functionalized gold nanoparticles (AuNPs) nanopore-based detection. (a) Upon target hybridization, the fluorophore (green dot) is displaced beyond AuNP quenching distance. (b) Target miRNAs and HOP-AuNPs are driven into a conic nanocapillary by a negative voltage. (c) Voltage is reversed to aggregate AuNPs, promote hybridization, and plasmonically enhance fluorescence. (d)–(f) Microscopy sequence of HOP-AuNP packing and target miRNA hybridization in a silica conic nanocapillary; a negative voltage is applied at s and reversed at s; the plasmonically enhanced fluorescent signal is evident at min. (g) A nm nanocapillary tip SEM. Inset: light microscope image of a micron-sized nm-NP aggregate inside the silica nanocapillary. The inner nanocapillary diameter is about nm at the aggregate location; its distance from the tip ( ) corresponds to the ionic strength maximum in Fig. 9(a). (h) miRNA hybridization across a AuNP assembly in a conic glass nanocapillary: fluorescence intensity vs. voltage after target and non-target hybridization. (i) Fluorescent intensity for the target and for a -mismatch in the -nucleotide miRNA at different concentrations indicating little hybridization of the latter. Reproduced with permission from Egatz-Gomez et al., Biomicrofluidics 10(3), 032902 (2016). Copyright 2016 AIP Publishing LLC.
III. DNA NANOPORE INTERACTIONS
The most common molecular detection method for both protein and solid-state nanopore sensing is to monitor transient changes in ionic current through a nanopore. It is intuitive that the current should drop during the translocation, since the translocating molecule decreases the pore conductance by blocking the pore space that would otherwise be filled with electrolyte ions. Indeed, such resistive-pulse signals have been consistently observed at high salt concentration. However, for smaller nanopores and low ionic strengths, when the Debye length is comparable to or larger than the pore diameter, surface effects of the translocating molecule may reverse the resistive signal such that an increase in current is actually reported. This is most pronounced for highly charged molecules like DNA. Such negative resistive signals have been observed in a variety of nanopores and nanochannels at low ionic strength.59,105,119,133 The counterions that screen the negative charges on the DNA backbone can increase the pore conductance and produce an increase in the ionic current. In essence, surface conductance of the translocating DNA more than compensates the blocking effect.13 The ionic current signatures due to DNA translocation have been shown to be salt dependent and the two competing effects cancel at a KCl concentration of mM.105 In some cases, both positive and negative resistive signals have been observed during a single translocation event. These “biphasic” signals have been observed in both thin film nanopores and nanochannels. Dekker and Golovchenko independently observed composite events at low salt concentration, where within each single event, the current first decreases and then increases. The unexpected current decreases in the biphasic signal are caused by the docking of the DNA random coil onto the thin film solid-state nanopores.59,119 These biphasic current signals observed in nanopores with longer channels such as glass nanopores60 and track-etched nanopores80,94,122 are thought to be due to the change in ion concentration due to the translocation. In these nanopores with longer channels, the conductance is determined not only by the local conductance change at the pore tip but also by the ion distribution inside the nanopores. Both can be affected by the translocation of molecules or particles. Many of these complex translocating phenomena are still poorly understood, and we shall restrict ourselves to a review of the most fundamental issues concerning positive resistive signals, which have been exhaustively studied.
DNA is a strongly charged biopolymer with a linear charge density, , of two electrons per base pair (or C/m) under physiological conditions.2 The charge is due to ionization of the phosphate groups on the sugar phosphate backbone of the DNA double helix. The “effective” charge is actually lower due to counter-ion condensation effects discussed later. For many purposes, DNA can be modeled as a “wormlike chain” or a uniformly charged flexible cylinder of small radius.33 Depending on the material of the substrate and buffer conditions, the substrate supporting the nanopore often has a surface charge with charge density . A characteristic value of may be easily estimated from the following consideration. There is a characteristic length (the Bjerrum length) of closest approach between two like charges; closer separations being thermodynamically unlikely. This distance is obtained88 by equating the potential energy of interaction of the charges to the thermal energy: , where is the electronic charge, is the permittivity of the buffer, is the Boltzmann constant, and is the absolute temperature. In water at room temperature, nm. Thus, a rough upper bound for the substrate surface charge is mC/m. For silica, under typical buffer conditions, 4–60 mC/m. This charge is usually negative for all experiments involving DNA nanopore interactions, since a positive charge leads to strong non-specific binding to the substrate. In the case of protein pores (such as -hemolysin), the molecular channel may contain multiple charged groups which interact with the DNA through electrostatic forces.
The dominant effects in DNA nanopore experiments are the electrostatic interactions between the DNA charge, the pore surface charge, and the imposed electric field. These interactions are partially shielded by the very mobile counter-ions (cations) in the buffer. If a macro-ion is introduced into an ionic solution, the potential of the macro-ion is effectively “shielded” by the counter-ions on a length scale , where
| (16) |
Here, the summation runs over all the different ionic species (indexed by ) and are the valence and number density of ionic species far from the introduced charge. For typical experimental conditions, the Debye length, , ranges from nm at very high salt concentrations (1 M) to nm at low salt (1 mM).
A. DNA translocation is a stochastic process
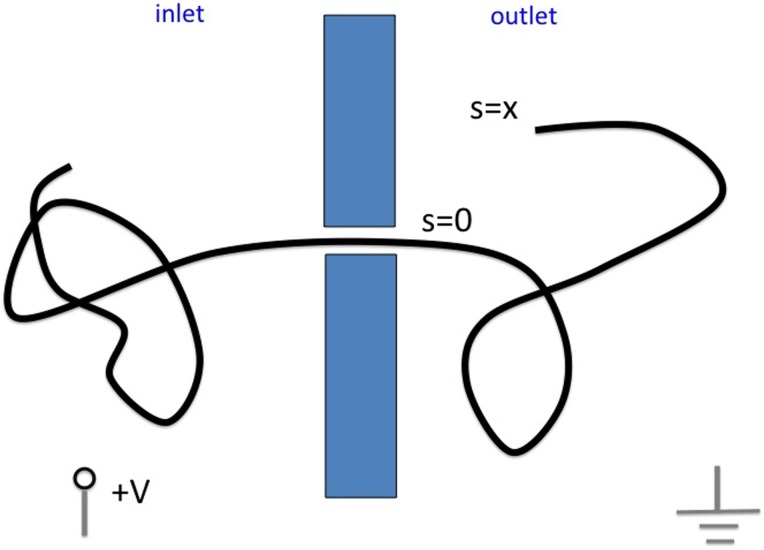
DNA translocations in resistive pulse experiments show a rather broad distribution of translocation times. Lubensky and Nelson73 proposed (see Fig. 7) that this is due to thermal fluctuations, which may be modeled as a one dimensional random walk in the following way: let represent the length of the polymer in the outlet reservoir. Then is a random variable with probability distribution at time , for which Lubensky and Nelson introduced a drift-diffusion model:
| (17) |
Here, is a one dimensional diffusivity corresponding to the back and forth sliding motions of the DNA along the pore axis and is a drift velocity describing the mean progression in the direction of the applied force and proportional to it. The problem of determining the translocation time may then be formulated in terms of the well known problem of first passage times of a particle crossing a barrier in one dimension under stochastic forces. Integration of the equation gives a distribution of translocation times in qualitative agreement with what is seen in free translocation experiments with DNA. Chern et al.18 simulated the idealized problem of a freely jointed chain crossing a hole in a membrane using a dynamic Monte Carlo (DMC) method and found their results to be in very good agreement with Lubensky and Nelson’s one dimensional model. To determine the drift velocity , and, therefore, the mean translocation time, we need to understand the forces driving the translocation and the forces resisting it. This is what we discuss next.
FIG. 7.
The Lubensky-Nelson73 model of DNA translocation: the length of DNA in the outlet reservoir is a stochastic variable under the simultaneous control of thermal fluctuations and a drift due to the applied potential .
B. Forces in DNA translocation
In a translocation experiment, an external voltage is applied across a membrane of thickness . Due to the very high electrical resistance of the pore, almost all of the potential drop occurs across the pore. Thus, the electric driving force on the DNA is , where is the charge per unit length along the DNA. If mV, we have pN. The electrical driving force is resisted primarily by the hydrodynamic force arising due to the fluid viscosity resisting the motion of the DNA.34 Since the viscous force is proportional to the gradient of the fluid velocity, the largest contributions arise in regions where fluid is pushed through narrow spaces. In the nanopore problem, this is the tight space between the DNA and the substrate as the DNA transits the pore. The action of the strong electric field in the pore on the Debye layer of counter-ions creates an unbalanced force which drives fluid flow through the pore in a direction opposite to that of the DNA movement. This effect, known as “electroosmosis,”85 has a strong influence in determining the hydrodynamic drag on the DNA and ignoring this results in a gross underestimate of the drag forces.36,37 Thus, the electrical problem is strongly coupled with the hydro-mechanical one, and these two influences must be considered together in determining the resistive force on the DNA. The hydrodynamic drag from the part of DNA outside the pore is expected to be small compared to the drag from the confined part.36 The latter contribution is discussed in detail in Sec. III C.
A different kind of force arises82 in the context of DNA nanopore interactions that seem to play a secondary role in the experiments we discuss but are important in other problems involving polymer translocation. This is the “entropic force” which has no analog in classical hydrodynamics but arises specifically due to the small scale nature of the system. Since DNA is a fluctuating polymer, a force is required to keep the two ends of the DNA separated by a distance , even if , where is the end-to-end distance in the fully stretched configuration. This force exists even if the DNA is regarded as having zero bending energy. In fact, it arises from the term in the expression relating the free energy of any thermodynamic system to the energy , the absolute temperature , and the entropy . Since the work done by an applied force in a quasistatic process of increasing the DNA end-to-end separation by an amount must increase its free energy by an amount , we have or . The free energy itself is
| (18) |
where is the partition function, is the energy associated with a specific configuration, and the summation is over all possible allowed configurations. In the case of a DNA strand with zero bending energy, the partition function is simply the number of configurations of the polymer. If one end of a DNA of length is anchored to a planar substrate, any configuration in which part of the polymer crosses this plane is disallowed. In this case, Sung and Park112 calculated the free energy by regarding the polymer as a restricted random walk in the three dimensional half space above a plane
| (19) |
the Kuhn length being the length of each segment in the freely jointed chain model. Thus, the force is . When a length of polymer of total length is translocated, the net entropic force is
| (20) |
Clearly, the force is the largest when is close to zero or . The maximum force can be estimated by putting or pN, which is many orders of magnitude less than the driving force, as noted by Lubensky and Nelson.73 The force is also an antisymmetric function of and vanishes at . Thus, the thermal fluctuations of the polymer determine the diffusion in Eq. (17) but do not result in net average drift. Such drift can arise only if there is an asymmetry between the two sides of the pore, for example, when the polymer is escaping from strong confinement within a viral capsid.81,82
As mentioned in Sec. I, Egatz-Gomez et al.26 have found that ssDNA and dsDNA of the same contour length have drastically different translocation velocities (a factor of 100) through a conic nanopore with a high permittivity monolayer. This suggests yet another physical mechanism that controls DNA translocation through solid nanopores. It is suspected that van der Waals interaction between the surface and the aromatic rings of the bases is responsible for such a discrepancy. At nanometer scales, van der Waals interaction often dominates the electrostatic interaction between the charged phosphate backbone and the charged alumina or titania surface. Experiments performed at different pH and ionic strength to change the electrostatic interaction did not significantly change the ratio of the translocation frequency. Instead, it is believed that the bases for single stranded DNAs are exposed and can adhere to the surface with a parallel dipole orientation that will maximize the dipole-induced dipole van der Waals interaction between the rings and the surface. In contrast, the bases of double stranded DNAs are within the helical phosphate backbone and are fixed at specific orientation due to base-stacking interaction within the helix. They are, hence, not free to orient and adhere to the high-permittivity surface.
C. Electrokinetic forces
If both the driving force and the resistive force are localized in the region within the pore, the translocation velocity should be independent of the polymer length. This is indeed seen in the experimental data for very small protein pores.53,79 For larger pores, such as solid state pores of diameter of the order of 10 nm, the data are not so clear. Storm et al.110 report a weak dependence of the mean translocation velocity () on polymer length (): . They attribute this effect to friction from the polymer coil outside the pore. Recent experiments with DNA in conical glass nanocapillaries show that is independent of when the DNA moves from the pore into the bath but with when the voltage polarity is reversed so that the DNA moves in the opposite direction.11 The asymmetry was explained as due to the difference in geometric configuration of the DNA. In the first case, the driving and resistive forces are directed so as to put the DNA in tension smoothing out the thermal fluctuations so that the DNA translocates the pore as a rigid rod. In the second case, these forces are compressive and, therefore, tend to buckle the DNA which then takes up a more random configuration. Here, we will adopt the view that, to a first approximation, the forces on the DNA arise from within the pore, with contributions from the fluctuating polymer outside the pore entering perhaps as a correction. This approach also has the advantage of simplicity, since in the pore region, the DNA can be regarded as a rigid cylinder along the axis rather than as a fluctuating polymer coil. The experimental data come from two kinds of experiments that we discuss in Sec. III D: (a) free translocations and (b) frustrated translocations. In the latter case, the DNA is attached to a coated polystyrene bead which is held in a laser optical trap. Thus, the translocation process initiated by the applied voltage is “stalled” with the DNA trapped within the pore. The experimental observables in this case are the stall force or tether force () and the conductance change of the pore on DNA capture, . The force replaces the mean translocation speed () measured in resistive pulse experiments.
In order to cover both kinds of experiments, we will consider a DNA molecule translocating at a speed while being held by a tether force . All our forces and velocities are algebraic quantities and we orient our axis so that is always positive. The applied voltage is regarded as the voltage applied to the inlet reservoir (the reservoir that the DNA moves into). The outlet reservoir is always grounded. Thus, for a negatively charged polymer such as DNA, is always positive. At any instant of time during the translocation,
| (21) |
where is the electric driving force and is the viscous resistive force. This is because the effect of inertia is utterly negligible for small scale systems such as the one we are considering and the mass of the DNA within the pore can be safely set to zero. Brownian fluctuations are neglected here as we are only interested in calculating the mean drift. There are two approaches available to us for determining the viscous force : (a) adopt the continuum view of a fluid and solve the macroscopic equations of fluid dynamics and (b) adopt the kinetic view of a fluid as a random collection of molecules and use molecular dynamic (MD) simulations. The first approach has the advantage that in simple cases, the fluid equations may be solved analytically, and even in the presence of complex boundaries, commercial software such as COMSOL permits rapid calculations. The principal limitation is that the relevant geometric sizes (DNA width, pore size) are approaching the average intermolecular separations ( nm), and, thus, we are approaching the boundary of the regime of validity of the continuum description. The second approach has the advantage that since the motion of individual molecules and their collisions are being tracked, there are no uncertainties arising from doubts as to the validity of the underlying physics. The principal limitation is one of practical feasibility. If one desires to follow a reasonably large collection of molecules over a reasonable time period to generate reliable statistics, the computational demands quickly outstrip all available resources. Typically, for the larger solid state nanopores (diameter greater than 5 nm), MD simulations tend to be very expensive, but the continuum approach appears to work quite well. Conversely, for protein nanopores, the MD simulations can be handled by large computing platforms, but the continuum approach would be unreasonable due to the extreme small size of the system.
Irrespective of the approach adopted to evaluate , as long as the translocation speed and applied voltage are not too large, we expect , where and are coefficients that depend on the system properties. Substitution in Eq. (21) yields a relation between the velocity and the applied force :
| (22) |
In the case of free translocation, so that
| (23) |
whereas in the case where the DNA is immobilized, so that
| (24) |
The parameters and are introduced in place of and as they are more easily measured experimentally. Thus, is the translocation velocity per unit voltage and is the tether force per unit voltage. According to the conventions we adopted, clearly, and . In order to interpret the experimental data, we need to know how to calculate and . We discuss this next following the approach of classical continuum hydrodynamics and we refer the reader elsewhere70 for MD approaches.
A detailed calculation of and in the continuum limit requires solving the coupled partial differential equations describing hydrodynamics, electrostatics, and ion transport with appropriate boundary conditions. This is difficult, and for general pore shapes must be done by numerical integration. However, analytical results can be provided if appropriate simplifying assumptions are made. The first such assumption we will make is that the distortion of the equilibrium Debye layers by the applied electric field can be neglected. A typical applied field may be about 100 mV over a 50 nm membrane or V/m. A typical zeta potential is about 30 mV and we may take 10 nm as a characteristic Debye length. This gives an internal field strength within the Debye layer of V/m which is quite comparable to the applied field. However, due to the geometry of the nanopore, the internal field is primarily directed perpendicular to the pore axis, whereas the applied field is predominantly along the pore axis. Thus, the component of the applied field that may cause distortion of the Debye layer is probably small except near the pore entrances. If the pore is assumed to be cylindrical and end effects are neglected, it may be shown35 that
| (25) |
| (26) |
where is the length of the pore and and are the zeta potentials of the DNA and the substrate, respectively. It follows that the ratio
| (27) |
is a quantity that depends only on pore geometry and should therefore, in particular, be independent of the ionic composition of the buffer or charge state of surfaces.
The potentials and may be obtained in several different ways.23 The zeta potential of a charged surface in the presence of a symmetric electrolyte (valence ) may be related to the surface charge density of the fixed charges by solving the equilibrium Poisson Boltzmann equation:
| (28) |
This equation may be used to infer the value of either or when the value of the other variable is known. In practice, often the zeta potential is more easily measured than the surface charge. At high salt concentrations (small ), the formula (28) can be linearized to
| (29) |
In the other limit of low salt concentrations (large ), replacing the hyperbolic sine by the corresponding exponential for large arguments gives
| (30) |
Since where is the salt concentration in the buffer, if the surface charge density remains constant, we would expect at high salt concentrations and to be a linear function of at low salt concentration. Kirby and Hasselbrink56,57 checked these deductions against extensive experimental data on silica substrates collated from the literature and concluded that the latter provides a much better representation of the available data. They proposed a formula of the type , where [pC] (in analogy to the pH) is the negative logarithm of the total counterion concentration. The coefficient is small, whereas is negative and its magnitude is approximately proportional to the buffer pH. When direct measurements of the zeta potential are not available, Kirby and Hasselbrink’s semi-empirical model appears to be the most prudent approach to estimating the substrate zeta potential. If one regards the DNA as a uniformly charged cylinder with a linear charge density and adopts the Debye-Hückel (DH) approximation,88
| (31) |
where denotes the modified Bessel function of order . Departure from the DH approximation close to the DNA may be approximately taken into account by replacing the DNA bare charge with the “effective” charge , where is the Manning factor.83
D. Experiments
Evidence for the hydrodynamic nature of the resistive forces comes from experiments with free as well as frustrated translocations. We discuss some of them in the context of the theory discussed above. A more detailed discussion may be found in several recent reviews.30
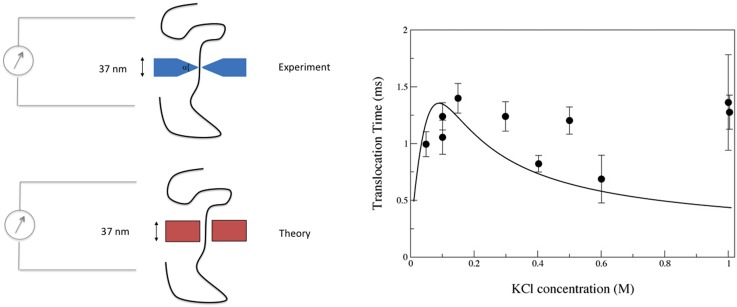
Figure 8 shows experimental data from free translocation experiments using 10.2 nm diameter nanopores in a silicon oxide/silicon nitride membrane. The solid line shows the result of a calculation35 using Eq. (23) with the coefficient evaluated using Eq. (25), where is calculated using Eq. (31) and the wall zeta-potential obtained from Kirby and Hasselbrink’s semi-empirical formula cited earlier. The DNA “bare” charge is reduced by the classical Manning factor of . The calculation yields a numerical value of the translocation time in reasonably good agreement with the data and is consistent with the experimental trend showing that the translocation time only has a weak dependence on the salt concentration. No fitting parameter is used in the theory. However, the pore shape is taken as that of a cylinder of radius such as to match the Ohmic conductance of the pore in the experiment. The pore in the experiment had an “hour glass” shape with a wedge angle of approximately 45 degrees. A generalization of the theory presented in Sec. III C that takes into account the precise pore geometry is possible as long as the Debye length is small compared to the pore dimensions and the pore is axisymmetric and slowly varying. Once again, good quantitative agreement with experimental data is observed.36 Such calculations can of course be done numerically so as to overcome the limitations imposed by these simplifying approximations.17,69 One interesting consequence of Eq. (25) is that the DNA translocation speed can be reduced (even reversed!) by altering the substrate zeta-potential through chemical modification. This has been demonstrated in computational studies of DNA translocation through solid state nanopores1,46,71,72,131 as well as in experiments.4,28 The effect is of interest as the high speed of DNA translocation in resistive pulse experiments is an impediment to the accuracy to which any information along the DNA can be read.54,123
FIG. 8.
Translocation times for a 48.5 kbp DNA through a 10.2 nm diameter nanopore. Solid line is calculated from theory assuming an “equivalent” cylindrical pore of radius such as to have an Ohmic conductance equal to the measured value (sketch on the left panel). The dependence on salt concentration is calculated based on the Debye-Hückel theory and effective DNA charge consistent with the Manning value. Symbols are measurements due to Smeets et al.105 in a solid state pore. Adapted with permission from S. Ghosal, Phys. Rev. Lett. 98, 238104 (2007). Copyright 2007 American Physical Society.
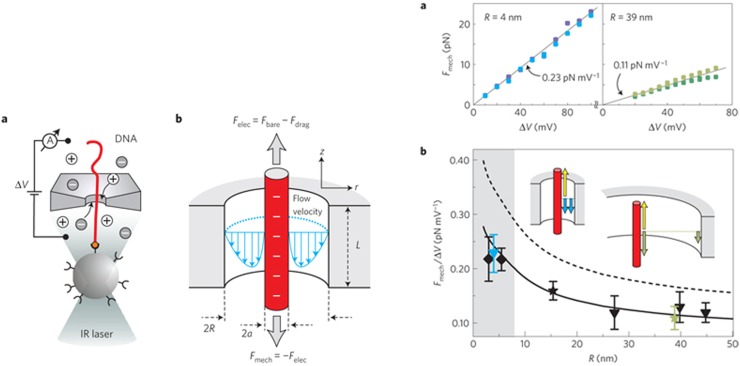
In frustrated translocation experiments,118 DNA is attached using biotin linkers to a streptavidin coated polystyrene bead that is held in a laser optical trap as shown in Fig. 9. When a voltage is applied across the pore, the DNA enters the pore, but translocation is frustrated by the opposing force applied through the laser optical trap which sets up a “molecular tug of war.” The force on the bead can be measured through its displacement in the trap simultaneously with the pore current. Panel (a) on the right-side of Fig. 9 shows measured values of the tether force (in pN) for two different pore radii. The force is seen to be proportional to the voltage in conformity with theory. Such proportionality can, however, be expected simply on the grounds that the electric driving force is proportional to the voltage . It does not say much about the physical nature of the resistive force. Evidence as to the nature of the resistive force is presented in Panel (b) of Fig. 9, which shows the measured tether force per unit voltage as a function of the pore radius. We see that the tether force has a clear dependence on pore radius, and moreover, the observed dependence closely follows the logarithmic dependence expected from Eq. (26). If the resistance to translocation arose from the movement of the DNA within the bulk fluid rather than from the pore, the tether force would be independent of pore radius: this is not what is seen in the experiment. The single adjustable parameter in the theory is the effective linear charge of the DNA . Since experimentally, neither nor is known very precisely, and the parameter has been left as an adjustable parameter. The dashed line shows the result that would be obtained if , and the wall charge were neglected. The fitted line is consistent with either (in the absence of wall charge) or the presence of a wall charge mC/m (with ). Thus, either a Manning factor or a wall charge or some combination of both effects is needed.
FIG. 9.
(Left panel) Schematic diagram of a “tethered DNA” experiment:118 DNA translocation is stalled by applying a pulling force on the DNA by attaching one end to a streptavidin coated polystyrene bead and holding the bead in a laser optical trap. Also shown is the flow field and balance of forces. (Right panel) Measured stall forces showing a linear dependence of the stall force on the voltage [Panel (a)] and the logarithmic dependence of the force per unit voltage on the pore radius [Panel (b)]. The symbols are measured values and the lines are theoretical results. Adapted with permission from van Dorp et al., Nat. Phys. 5(5), 347–351 (2009). Copyright 2009 Springer Nature.
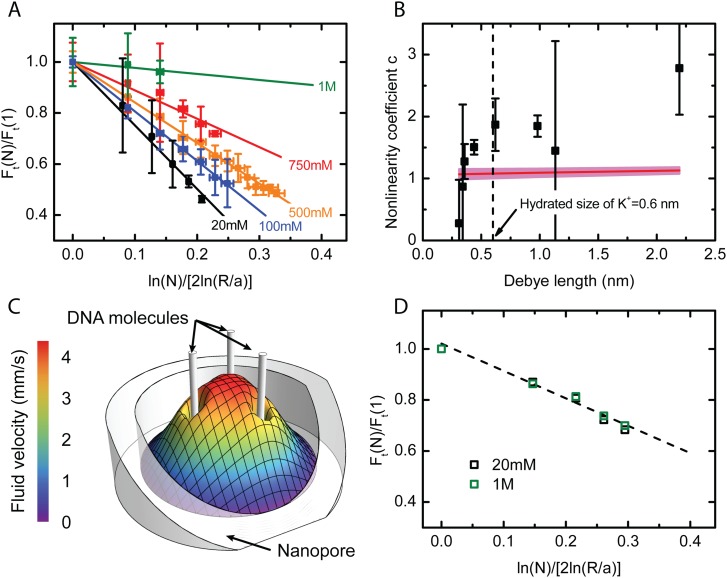
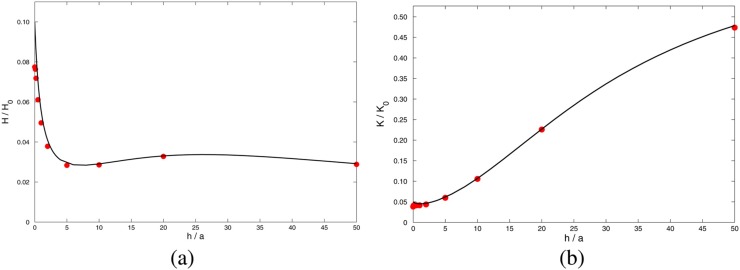
A consequence of the characteristic dependence of hydrodynamic interactions is seen in experiments where multiple DNA strands are confined within a pore.62 The result of such an experiment is shown in Fig. 10. The set up is as in Fig. 9, except here the bead is a “hair ball” of many DNA strands of which a number are trapped within the pore. It is found that the force on the bead does not increase linearly with , but the force per strand decreases with the number of molecules occupying the pore. It may be shown62 that if the individual DNA strands interact through hydrodynamic effects, the stall force per strand, , with strands in the pore should obey the simple scaling law
| (32) |
where is a dimensionless constant. This expectation is borne out both by continuum level simulation using COMSOL as well as by the experimental measurements shown in Fig. 10. In Panel (a), the experimentally measured values of are plotted as a function of for different salt concentrations. As expected, the relationship is linear, but the slope () is seen to depend on salt concentration. The coefficient at each salt concentration obtained from a linear fit is plotted in Panel (b) as a function of the Debye length. It is seen that is roughly constant for nm but sharply drops to zero for smaller Debye lengths. That is, at high salt concentrations, the non-linearity disappears, with a transition between the linear and non-linear regimes occurring at nm. The fact that the size of the hydrated K ion is roughly 0.6 nm suggests an explanation: for Debye lengths smaller than the size of the counterions, the continuum theory breaks down. Since the Poisson-Boltzmann theory assumes point-like particles, its failure to explain behavior at length scales smaller than the hydrated ion size is not surprising. In this limit, the counterions are confined to within a few ionic diameters of the DNA, quenching its charge as well as the associated hydrodynamic interactions. Numerical simulation using the continuum Nernst-Planck-Stokes equations on the other hand does not show this effect as such an approach effectively sets the ion radius to zero.
FIG. 10.
Experiments on multiple DNA strands within a pore. (a) The normalised force per strand plotted against gives straight lines with slope in accordance with the scaling law, Eq. (32). (b) The coefficient plotted as a function of the Debye length. The horizontal line represents the value of determined using the computed solution with the width of the band representing uncertainty in its value. (c) The computed axial hydrodynamic velocity profile inside a pore with three inserted DNA molecules. The electroosmotic pumping by each molecule enhances the flow strength around its neighbors thereby increasing the frictional drag. (d) The normalized force per strand plotted against as obtained from numerical simulation. Unlike in the case of the experiment, is found to be independent of salt concentration. Adapted with permission from Laohakunakorn et al., Nano Lett. 13(6), 2798–2802 (2013). Copyright 2013 American Chemical Society.
IV. NANOPORE HYDRODYNAMICS
A. The equilibrium Debye layer
The membranes supporting nanopores almost always bear a charge due to dissociation of surface groups and ion adsorption from the surrounding electrolyte. In an electrolytic medium, this surface charge is always shielded by the plentiful counter-ions in solution. The characteristic distance over which such electrostatic shielding takes place85,88 is the Debye length, , defined in Eq. (16), with typically in the range 1–10 nm for water under typical conditions of temperature and salt concentration. For pores of radius , electrostatic shielding ensures that the system effectively behaves as a round hole in an insulating membrane immersed in a uniformly conductive medium, except that the membrane may possess a surface conductance if the ionic concentrations within the Debye layer are sufficiently high. The radius of a biological pore is often such that : at this scale, usually the continuum description becomes wholly inappropriate and one must resort to a molecular level description. However, synthetic nanopores often have radius . For such nanopores, the structure of the Debye layer dominates the transport properties of the nanopore and its description must be the first step in any understanding of nanopore transport.
We first consider the structure of the Debye layer under conditions of thermodynamic equilibrium, i.e., in the absence of applied pressure or potential drops and in the absence of any hydrodynamic flow or current through the pore. When such external forcing is applied, thermodynamic equilibrium is disturbed. We shall see in Sec. IV B that under appropriate conditions, the resulting distortion of the Debye layer may be presumed small. Thermodynamic equilibrium is discussed in the context of a mean field description where an individual ion is regarded as being immersed in a smoothly varying potential field created by the presence of the surface charge and all the other ions. The electrostatic potential energy of the individual ion is then and its spatial concentration is therefore
| (33) |
The system of equations is completed by introducing the Poisson equation describing the electrostatic potential
| (34) |
where the right hand side represents the volume charge density of the ions. Equation (34) is the Gouy-Chapman model for the Debye layer.88
The simplest situation corresponds to a binary symmetric electrolyte, where , , and . Equation (34) then reduces to
| (35) |
Equation (35) is nonlinear and exact solutions are available only for charged planes. Numerical solutions may, however, be obtained quite readily under various boundary conditions and provide a good physical picture of the potential and ionic distributions around a nanopore. The computational effort in generating such results by solving Eq. (35) is miniscule compared to methods such as molecular dynamic simulations. However, when nm as in protein pores, the continuum description is no longer appropriate near the pore and techniques such as molecular dynamics must take over. Nevertheless, Eq. (35) should continue to be valid at distances greater than a Debye length, , from the pore.
Analytical progress can be made even with arbitrary electrolyte composition provided that surface charges are sufficiently low that the potential everywhere is much less than , where is the largest of the . This is known as the Debye-Hückel approximation and implies that the potential energy of an ion () is much less than its average kinetic energy due to thermal fluctuations. Since mV at room temperature and the surface potential of materials such as silica in common electrolytes is in the range – mV, the Debye-Hückel (DH) approximation is not always acceptable. However, there is a range of conditions of pH and salt for which the surface charge is sufficiently low that the DH approximation holds. Clearly, the DH approximation is more easily satisfied for monovalent ions than multivalent ones. Under such conditions of low potential, the nonlinear term on the right hand side of Eq. (34) may be expanded in a series with respect to the dimensionless small parameter
| (36) |
On neglecting all terms except the first two on the right hand side of Eq. (36) and substituting in Eq. (34), we have the linear equation
| (37) |
where is given by Eq. (16). Here, we have used the fact that the electrolyte is charge neutral very far from the interface
| (38) |
The Debye-Hückel equation, Eq. (37), is far more tractable mathematically than Eq. (35). Equation (35) has the advantage that it is applicable to high as well as low potentials; it is, however, restricted to a binary symmetric electrolyte.
Let us first consider a narrow cylindrical pore of radius in a membrane of thickness . Equation (37) can then be solved within the pore
| (39) |
where is the radial distance from the axis, is the zeroth order modified Bessel function, and is the zeta-potential at the surface. If a constant surface charge () is specified instead, then Eq. (39) is still valid, but must instead be regarded as an unknown parameter related to the specified surface charge density . This is quite straightforward if the Debye length is small compared to the pore radius (). In that case, the pore as a whole is electroneutral and this may be expressed as
| (40) |
which, on using Eq. (39), becomes
| (41) |
The asymptotic approximation on the right corresponds to . In fact, for very large values of , Eq. (41) reduces to the well known relation between the surface potential at a plane surface and the surface charge density .
When , some of the shielding counter-ions “overspill” from the pore96 and the electroneutrality condition Eq. (40) no longer holds. If , we may replace Eq. (40) by
| (42) |
where is the net overspill of charge from the nanopore. Thus,
| (43) |
where is the fraction of the shielding ions spilled from the pore. In the case of a nanopore in the form of a slit in a thick membrane, can be determined by asymptotic matching between the solution within the pore and in the reservoir.38
We now consider a circular pore (radius ) in an infinitely thin membrane. Thus, . If the surface charge () of the substrate is fixed, Eq. (37) may be solved96 in cylindrical co-ordinates using Hankel transforms
| (44) |
where the first (exponential) term on the right-hand side of (44) represents the potential adjacent to a uniformly charged plane and the second (integral) term represents the reduction in the potential when a charged disc of radius is removed from the plane. The integral can be evaluated by numerical quadrature. If the pore size is very small compared to the Debye length (), we simply recover the potential over a flat charged surface, .
Under conditions of high surface charge, the DH approximation may be invalid very close to the surface but may still be a reasonable approximation at distant points after the potential has decayed sufficiently due to the shielding by counterions. Thus, all of the results discussed here in the context of the DH approximation may be used in the limit of very high charge density with the simple artifice of replacing the surface charge by an effective surface charge, . A similar analysis in the context of a charged rod such as DNA leads to the concept of counter-ion condensation or “Manning condensation.”116
B. The weak field limit
When an external potential is applied across the membrane containing the pore, there will be fluxes of ions as well as bulk movement of water and the Debye layer is no longer in equilibrium. However, analytical progress can be made if one assumes that in addition to the potentials being small compared to the thermal scale, the applied electric field is also weak so that the equilibrium Debye layer is only slightly disturbed. Specifically, if is the applied potential drop, . Thus, we may define a small parameter which characterizes the strength of the applied field and seek an asymptotic solution to the transport problem in the form
| (46a) |
| (46b) |
| (46c) |
where the subscript 0 refers to the equilibrium solution and the superscript is a species label.
It may then be shown97 that the Stokes equations describing hydrodynamic flow with electric body forces may be written in the form
| (47) |
where is the dynamic pressure (normal stress, including electric contributions), is the equilibrium charge distribution, and
| (48) |
The function is actually the perturbation in the chemical potential which is made up of two terms: the electric potential perturbation and a term depending on perturbation to the charge density. It may be shown that the new “potential” satisfies
| (49a) |
| (49b) |
The latter follows from the condition that ion fluxes normal to the membrane must vanish. Thus, in any nanopore problem, the electroosmotic flow can be determined by the following sequence of steps:
-
1.
Determine the potential by solving the boundary value problem Eq. (49) for Laplace’s equation.
-
2.
Solve the Debye Hückel equation with appropriate boundary conditions to determine the equilibrium potential and, therefore, the equilibrium charge density .
-
3.
Solve the Stokes flow problem with the specified force density and appropriate hydrodynamic boundary conditions.
We illustrate this procedure in Sec. IV C by presenting an explicit analytical solution to the flow rate through a nanopore in the limit of low potentials and weak fields.
C. Flow through a circular hole in a uniformly charged thin membrane
The volumetric flow rate through the pore due to the applied potential can be determined without first determining the velocity field throughout the domain. This can be achieved by exploiting the reciprocal theorem for Stoke’s flow41
| (50) |
where and are two flow fields in a volume driven by force fields and and is the bounding surface with outward normal . Here, is the dynamic pressure, is the viscosity, is the strain rate tensor, and is the stress tensor. Variables with an overbar represent the corresponding quantities for the second flow. If we now identify as the electrokinetic velocity field caused by a potential difference applied across the pore and
| (51) |
as an auxiliary flow field due to a pressure difference imposed across the (uncharged) membrane, then on substituting in Eq. (50), one obtains75 an expression for the volume flux of fluid through the pore, i.e.,
| (52) |
from the side to of the membrane. Here, and are hemispheres centered on the pore on the two sides of the membrane.
Equation (52) can be used to determine provided , , and are known. Each of these functions are indeed known in the case of a circular hole in a uniformly charged infinite membrane of zero thickness. In the Debye-Hückel limit, , with given by Eq. (44), and and represent pressure driven Stokes flow and potential flow through a circular hole; the solutions to both these problems are well known. The flow rate is then determined analytically up to quadratures75
| (53) |
in terms of new scaled variables , , . Here, and are defined as
| (54) |
| (55) |
and are the sine and cosine integrals
| (56) |
In Eq. (53), is the uniform surface charge density on the membrane.
The analytical result Eq. (53) is compared with numerical solutions of the Debye Hückel equation in Fig. 11 for finite as well as zero thickness membranes, with the flow rate normalized by a characteristic rate . For a membrane of zero thickness, excellent agreement is found for all values of . When the membrane thickness is small but finite, Eq. (53) slightly underestimates the flow rate. For a Debye length large compared to the pore radius (), Eq. (53) reduces to .
FIG. 11.
The normalized flow rate through a circular pore of radius in a membrane of zero thickness as a function of determined from Eq. (53) (solid line), with asymptote (dashed line). The symbols are from the full finite volume simulations with 0 (triangle), 0.06 (circle), and 0.1 (square). Adapted with permission from Mao et al., J. Fluid Mech. 749, 167–183 (2014). Copyright 2014 Cambridge University Press.
D. Flow through a cylindrical channel in a membrane of arbitrary thickness
If the membrane is of finite thickness (), then, in addition to , we have a second dimensionless parameter of significance, the aspect ratio . In the limit , we should recover the zero thickness limit described above. In the opposite limit of , we simply have electroosmotic flow through a long cylindrical channel, in which case, the solution is well known. We are interested in the intermediate case where both and are of order unity.
An approximate solution to this problem is possible,96 provided that the perturbation of the equilibrium charge cloud by the applied electric field may be presumed small. In this approach, one assumes that the solution may be approximated by the known solution for a long cylindrical channel within the pore and the solution to the zero thickness membrane in each of the semi-infinite zones above and below the finite thickness membrane. The voltage drop and pressure drop across the pore are regarded as undetermined parameters. These quantities are in general different from the applied voltage and pressure drops. The unknowns are subsequently determined by requiring that the fluid volume flux and total current in the cylindrical pore are identical to those in the regions external to the pore. The final result is an expression for the electroosmotic conductance (flow rate per unit applied voltage) of the composite system of cylindrical pore and external entrance/exit regions
| (57) |
in terms of the electroosmotic conductances and of a thin membrane and long cylindrical pore, respectively.
E. Debye layer overlap and overspill
Figure 12 shows the approximation , scaled by , compared to numerical results derived from full Poisson-Nernst-Planck (PNP) computations.96 We see that Eq. (57) is always correct when . It is also reasonably accurate for any Debye length when or for any when the charge cloud is thin (). However, it is poor when . If , Eq. (57) is reasonably accurate as long as , but when , the fluid flux is greatly over-estimated by Eq. (57). The reason for this may be understood from the sketch in Fig. 13. When , the Debye layer at the walls overlaps and part of the counterion cloud “spills” out from the ends of the pore. The spilled charge is negligible compared to the total charge within the pore when , but this is no longer the case when . Since the applied potential drop occurs primarily across the pore, the spilled charge does not contribute to the electric driving force since the electric field outside the pore is negligible. Equation (57) fails to account for this charge “overspill” effect and, therefore, greatly over-estimates the electroosmotic flux when .
FIG. 12.
Normalized electroosmotic coefficient as a function of , for (a) , (b) , (c) , and (d) . Solid line is from Eq. (57); solid circles are the full PNP numerical computation. The surface charge density is uniform over the membrane surface. Adapted with permission from Sherwood et al., Langmuir 30(31), 9261–9272 (2014). Copyright 2014 American Chemical Society.
FIG. 13.
When the Debye length exceeds the pore radius , the cloud of counterions associated with the charged cylindrical wall of the pore spills out of the ends of the pore. Since the strongest electric field is localized primarily within the pore, the “spilled” charge is unavailable for driving the flow which results in a greatly decreased fluid flux as seen in Fig. 12.
The calculation leading up to Eq. (57) can be corrected96 to take into account this charge overspill effect when . In this limit, the Debye-Hückel equation within the pore is essentially one dimensional and hence is readily solved. Asymptotic matching with the solution outside the pore determines the constants and the flux may then be computed from Eq. (52). It is convenient to express the result in terms of the “lost-length” , which is the length of a pore segment (for an infinitely long pore) that would normally contain the same amount of counter-ion charges that is actually spilled from the two ends of the finite pore96
| (58) |
The pore also gains some counterions that we characterize by because some of the charge that would normally be associated with the planar membrane surface spills into the pore:
| (59) |
where
| (60) |
When these effects are taken into account, one gets modified expressions for and ,
| (61) |
| (62) |
which may now be used in Eq. (57). The resulting corrected electroosmotic coefficient is in much better agreement with the computed solution as shown in Fig. 14(a), which compares the corrected values of to results of the full PNP computation. The results may alternatively be presented in terms of a coefficient that relates the electroosmotic volume flux to the electrical current , with and being a natural scale for in terms of the fluid electrical conductivity . Figure 14(b) compares the same results as Fig. 14(a) but expressed in terms of an approximation , rather than .
FIG. 14.
(a) Same as Panel (d) of Fig. 12, but this time, the corrected coefficients Eq. (62) are used in Eq. (57). (b) shows the same results as (a) but expressed in terms of , where is the electrical current. Adapted with permission from Sherwood et al., Langmuir 30(31), 9261–9272 (2014). Copyright 2014 American Chemical Society.
F. Induced charge electroosmosis
In classical electroosmotic flow, the driving force results from the effect of an applied external electric field tangential to solid boundaries acting on the mobile charges in the Debye layer. Induced charge electroosmosis (ICEO) arises when the interface has no intrinsic charge, but a Debye layer develops due to dielectric polarization. Since the permittivity of water (about , where is the permittivity of free space) is large compared to that of most nonpolar solids such as silica, plastics, etc. (), the permittivity ratio between the substrate and electrolyte is usually much less than unity and is often neglected entirely and set to zero. When this ratio is not neglected, the jump conditions of the electric field at interfaces allow the existence of a normal electric field. In an electrolyte, such a normal field will drive free charges towards or away from the interface resulting in the establishment of a Debye layer, the strength of which is proportional to the applied field. The tangential component of the field acting on these induced Debye layer charges then creates a flow that depends quadratically on the electric field strength. The strength of the effect is proportional to the local curvature of the interface as well as the dielectric ratio. It is usually insignificant due to the dielectric ratio being very small for aqueous interfaces but can become noticeable at sharp corners where the curvature is very large. Another distinguishing feature of ICEO is that it operates for both AC and DC fields (unlike classical electroosmosis) since it depends quadratically on the applied field. Furthermore, ICEO effects can also arise at metal electrolyte interfaces.107
Electroosmotic flow at a dielectric corner was observed and explained by Thamida and Chang115 and Yossifon et al.132 We consider a plane two dimensional wedge of internal angle , the simplest geometry for demonstrating the effect (Fig. 15). The solution to Laplace’s equation for the electrochemical potential defined in Eq. (48) in polar co-ordinates (Fig. 15) takes the form
| (63) |
where is the radial distance from the corner, is a constant, and is an as yet undetermined parameter. Since ionic fluxes into the solid must vanish,
| (64) |
when , which determines :
| (65) |
Within the solid wedge,
| (66) |
which is antisymmetric about . Thus, there is an induced surface potential, ,
| (67) |
| (68) |
This induced potential becomes singular as and is responsible for the emergence of a corner jet. It should be noted that our analysis based on the Debye Hückel approximation breaks down if the potential at the corner becomes sufficiently large. In reality, any physical corner would have a large but nonetheless finite curvature. The usefulness of our approximations will then depend on the curvature being large enough to result in a noticeable corner jet but not so large that the underlying linearized Poisson-Boltzmann theory is invalidated. The treatment of large induced potentials is mathematically difficult as the full nonlinear Poisson-Boltzmann formulation must be employed. It has been discussed by Yariv and Davis130 in the case of binary symmetric electrolytes and spherical dielectric particles.
FIG. 15.
A dielectric wedge, of angle , with local cylindrical coordinates .
The tangential electric field at the wall in the immediate vicinity of the corner is
| (69a) |
| (69b) |
This large electric field would act upon the Debye layer charges associated with the induced zeta potential, in Eq. (68). When the distance to the apex is sufficiently large compared to the Debye length , so that variations of the tangential electric field with may be neglected, the Helmholtz-Smoluchowski slip velocity just outside the charge cloud is
| (70) |
In the case of a cylindrical pore in a uniform thickness membrane, the wedge solution discussed above applies provided the Debye length is small compared to the hole radius, . Here, , so that . The constant coefficient can be determined by comparing our local solution to the exact solution of Laplace’s equation in the vicinity of a semi-infinite rectangular domain that can be found using conformal mappings.95 The slip velocity is then
| (71) |
Figure 16 shows computed streamlines for a cylindrical pore. The parameters are , , and in the absence of any applied electric field, the surface charge density is zero. Since the problem is axially symmetric, the toroidal eddies are seen in cross section in the figure. When , two stagnation points merge to yield a geometry where eight eddies meet at a point as seen in Panel (c) of Fig. 16. A further increase in the value of leads to a bifurcation where two stagnation points move apart along the symmetry axis.
FIG. 16.
Numerically computed streamlines in the neighborhood of a circular hole (radius ) in a membrane of thickness . Here, , , and the membrane has no intrinsic charge. The four panels correspond to (a) ; (b) ; (c) ; (d) . Reproduced with permission from Sherwood et al., Phys. Fluids 26(11), 112004 (2014). Copyright 2014 AIP Publishing LLC.
In the presence of any asymmetry, such as a non-zero surface charge density or a difference in mobility between the two ionic species, there would, in general, be a net fluid flux across the membrane.76 However, if this asymmetry is weak, the eddy structure seen in Fig. 16 persists and the streamlines carrying the net flow have to snake their way between the toroidal eddies.52,115,132 These hydrodynamic eddies could potentially be used to apply pico-newton level forces and manipulate biopolymers at the molecular level to create synthetic molecular machines.
G. Hysteresis, inductance, and other ionic circuit elements
The myriad of hydrodynamic, concentration polarization, and charging phenomena that occur in nanopores smaller than the Debye length, particularly for conic nanopores or other asymmetric nanopores, can drive several anomalous ion current features in addition to rectification. Luo et al.74 showed that a conic pore can produce two stable flow states, due to the combination of pressure-driven and electroosmotic flow. The pressure driven flow is due to an intrapore pressure build up due to the potential gradient along the pore. The resulting hysteresis is reminiscent of memristors but here is all due to hydrodynamics and electrokinetics at the nanoscale. Hysteresis due to bistability of internal and external concentration polarization has also been reported for a wedge shaped funnel.86 Yan et al.127 showed that, under dynamic forcing, a conic nanopore behaves like an inductor at low frequencies because of the dynamics (ion electromigration waves) of the intrapore concentration polarization that will eventually lead to DC rectification126 once the dynamic forcing is removed. Using AC forcing, they were able to show impedance spectroscopy signatures of Debye layer capacitors, Warburg constant-phase elements, etc. In short, the full complement of ionic circuit elements now match the repertoire of electronic and semiconductor circuit elements: resistors, capacitors, constant-phase Warburg elements, inductors, diodes, memristors, etc.
V. CONCLUSION
In this article, we have summarized the important transport properties of nanopores with an emphasis on the basic transport processes that underlie their physical behavior.
Nanopores are ubiquitous in living systems, for example, in membranes of cells and organelles and are responsible for such basic functions as nerve impulse propagation and water management in cells. The microstructure of membranes that form the foundation of technologies such as energy storage, desalination, and separation science are determined at a fundamental level by the properties of nanopores. Individual nanopores are at the basis of numerous techniques in single molecule biophysics and biomedical technologies involving agent detection and sequencing.
Among transport properties, there are two aspects that are important. (i) The electrical conductance of the pore as determined by its geometry. (ii) The ability of the pore to pump fluid in response to an applied voltage. This pumping is due to the presence of surface charge and its associated electrical double layer. The behavior of the double layer dominates all of the transport properties of the nanopore. The electrical forces arising within the double layer and their effect on hydrodynamics (electroosmotic flow) are critical to understanding experimentally observed transport properties of macromolecules and polymers through the pore.
An important distinction between a nanopore and a larger hole in a membrane (e.g., of radius tens of microns) is that nanopores often lie in the regime . This implies an overlap of the Debye layers associated with diametrically opposite points on the wall. If the membrane is also thin, with , there may also be an “overspill” of the Debye layer so that some of the counterions that make the pore overall charge neutral could be lost to regions outside the pore entrance and exit. Both of these effects significantly alter the nature of the electroosmotic flow in the vicinity of the pore.
In this review, we have concentrated on effects that occur when the Debye layer thickness is comparable to the width of the pore. However, other effects can also be important, even when the Debye length is small compared to the pore size. For example, surface conductance effects arise when the surface charge is sufficiently large () so that the ionic composition of the electrolyte within the Debye layer differs significantly from that in the bulk. Surface conductance is always present, but in a nanopore, the relative importance of surface conduction compared to Ohmic conduction over the cross section could become significant. The role of such surface conductance effects on nanopore behavior remains an open question. A second effect, again not dependent upon Debye layer overlap, is induced charge electroosmosis. The induced charge effect is amplified at sharp corners and can produce a “corner jet” at the edge of the pore (Fig. 16). Induced charge electroosmosis can occur in pores of any size, but its effect on transport properties of nanopores may be significant.
The current application of nanopores is mostly for molecular translocation. However, with the full reservoir of nanopore ionic elements, integrated circuits can now be constructed for different applications. Yan et al.128 have constructed the first ionic oscillator using a nanoporous monolith. Consequently, all three types of cellular electrophysiological phenomena, excitability, bistability, and oscillation can now be mimicked by nanopore circuits. Sun et al.111 likewise constructed integrated ionic current transistors and amplifiers for analyte concentration on chip. We believe future culture chips will employ such circuits so that cell proliferation and evolution can be controlled by regulating their calcium wave signaling with nanopore circuit elements. The resulting hybrid circuit would then consist both of live cells and nanopore elements. This obviously requires some impedance matching of the linear RLC and nonlinear (hysteretic and diode) components for both the live and artificial elements. However, the fact that both sets of elements share the common current carrier, ions, suggests they would be very compatible hybrid partners. Cellular-nanopore circuits could then be followed by an even more intricate integration: nanopore interface with different ion channels or gap junctions of a single cell. This could then lead to control of molecular pathways within each cell.
ACKNOWLEDGMENTS
The nanopore work in HCC’s lab is supported by the National Institutes of Health (NIH) (No. 1R21CA206-904-01) and National Science Foundation (NSF)-CBET (No. 1065652). J.D.S. thanks the Department of Applied Mathematics and Theoretical Physics, University of Cambridge, for hospitality. S.G. acknowledges USIEF (Award No. 7428) and thanks Indian Institute of Technology, Kharagpur, India for hospitality.
REFERENCES
- 1.Ai Y. et al., “Field effect regulation of DNA translocation through a nanopore,” Anal. Chem. 82(19), 8217–8225 (2010). 10.1021/ac101628e [DOI] [PubMed] [Google Scholar]
- 2.Alberts B., Molecular Biology of the Cell, 6th ed. (Garland Science, New York, 2014). [Google Scholar]
- 3.Ali M. et al., “Modifying the surface charge of single track-etched conical nanopores in polyimide,” Nanotechnology 19(8), 085713 (2008). 10.1088/0957-4484/19/8/085713 [DOI] [PubMed] [Google Scholar]
- 4.Anderson B. N., Muthukumar M., and Meller A., “pH tuning of DNA translocation time through organically functionalized nanopores,” ACS Nano 7(2), 1408–1414 (2013). 10.1021/nn3051677 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Apel P. Y. et al., “Diode-like single-ion track membrane prepared by electro-stopping,” Nucl. Instrum. Methods Phys. Res. B 184(3), 337–346 (2001). 10.1016/S0168-583X(01)00722-4 [DOI] [Google Scholar]
- 6.Bayley H., “Nanotechnology: Holes with an edge,” Nature 467, 164–165 (2010). 10.1038/467164a [DOI] [PubMed] [Google Scholar]
- 7.Bayley H. and Martin C. R., “Resistive-pulse sensing from microbes to molecules,” Chem. Rev. 100(7), 2575–2594 (2000). 10.1021/cr980099g [DOI] [PubMed] [Google Scholar]
- 8.Bell N. A. W. et al., “DNA origami nanopores,” Nano Lett. 12(1), 512–517 (2011). 10.1021/nl204098n [DOI] [PubMed] [Google Scholar]
- 9.Bell N. A. W. et al., “Multiplexed ionic current sensing with glass nanopores,” Lab Chip 13(10), 1859–1862 (2013). 10.1039/c3lc50069a [DOI] [PubMed] [Google Scholar]
- 10.Bell N. A. W. and Keyser U. F., “Digitally encoded DNA nanostructures for multiplexed, single-molecule protein sensing with nanopores,” Nat. Nanotechnol. 11(7), 645 (2016). 10.1038/nnano.2016.50 [DOI] [PubMed] [Google Scholar]
- 11.Bell N. A. W. et al., “Asymmetric dynamics of DNA entering and exiting a strongly confining nanopore,” Nat. Commun. 8(1), 380 (2017). 10.1038/s41467-017-00423-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Branton D. et al., “The potential and challenges of nanopore sequencing,” Nat. Biotechnol. 26(10), 1146 (2008). 10.1038/nbt.1495 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Chang H.-C. and Yeo L., Electrokinetically Driven Microfluidics and Nanofluidics (Cambridge University Press, Cambridge, UK, 2009). [Google Scholar]
- 14.Chang H.-C., Yossifon G., and Demekhin E. A., “Nanoscale electrokinetics and microvortices: How hydrodynamics affects nanofluidic ionic flux,” Annu. Rev. Fluid Mech. 44, 401–426 (2012). 10.1146/annurev-fluid-120710-101046 [DOI] [Google Scholar]
- 15.Cervera J., Schiedt B., and Ramírez P., “A Poisson/Nernst-Planck model for ionic transport through synthetic conical nanopores,” Europhys. Lett. 71(1), 35 (2005). 10.1209/epl/i2005-10054-x [DOI] [Google Scholar]
- 16.Chen K. et al., “Ionic current-based mapping of short sequence motifs in single DNA molecules using solid-state nanopores,” Nano Lett. 17(9), 5199–5205 (2017). 10.1021/acs.nanolett.7b01009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Chen L. and Conlisk A. T., “DNA nanowire translocation phenomena in nanopores,” Biomed. Microdevices 12(2), 235–245 (2010). 10.1007/s10544-009-9378-5 [DOI] [PubMed] [Google Scholar]
- 18.Chern S.-S, Cárdenas A. E., and Coalson R. D., “Three-dimensional dynamic Monte Carlo simulations of driven polymer transport through a hole in a wall,” J. Chem. Phys. 115(16), 7772–7782 (2001). 10.1063/1.1392367 [DOI] [Google Scholar]
- 19.Clarke R. W. et al., “Surface conductivity of biological macromolecules measured by nanopipette dielectrophoresis,” Phys. Rev. Lett. 98(19), 198102 (2007). 10.1103/PhysRevLett.98.198102 [DOI] [PubMed] [Google Scholar]
- 20.Clarke R. W. et al., “Pipette-surface interaction: Current enhancement and intrinsic force,” J. Am. Chem. Soc. 135(1), 322–329 (2013). 10.1021/ja3094586 [DOI] [PubMed] [Google Scholar]
- 21.Deamer D. W. and Branton D., “Characterization of nucleic acids by nanopore analysis,” Acc. Chem. Res. 35(10), 817–825 (2002). 10.1021/ar000138m [DOI] [PubMed] [Google Scholar]
- 22.Dekker C., “Solid-state nanopores,” Nat. Nano 2(4), 209–215 (2007). 10.1038/nnano.2007.27 [DOI] [PubMed] [Google Scholar]
- 23.Delgado A. V. and Arroyo F. J., “Electrokinetic phenomena and their experimental determination: An overview,” in Interfacial Electrokinetics and Electrophoresis, Surfactant Science Series Vol. 106, edited by A. V. Delgado, (Marcel Dekker, Inc., New York, 2002).
- 24.DeSorbo W., “Ultraviolet effects and aging effects on etching characteristics of fission tracks in polycarbonate film,” Nucl. Tracks 3(1–2), 13–32 (1979). 10.1016/0191-278X(79)90026-X [DOI] [Google Scholar]
- 25.Nanofluidics, edited by J. Edel, A. Ivanov, and M. Kim (RSC Nanoscience and Nanotechnology, 2016), No. 41.
- 26.Egatz-Gomez A. et al., “Future microfluidic and nanofluidic modular platforms for nucleic acid liquid biopsy in precision medicine,” Biomicrofluidics 10(3), 032902 (2016). 10.1063/1.4948525 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Feng Y. et al., “Nanopore-based fourth-generation DNA sequencing technology,” Genomics Proteomics Bioinformatics 13(1), 4–16 (2015). 10.1016/j.gpb.2015.01.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Firnkes M. et al., “Electrically facilitated translocations of proteins through silicon nitride nanopores: Conjoint and competitive action of diffusion, electrophoresis, and electroosmosis,” Nano Lett. 10(6), 2162–2167 (2010). 10.1021/nl100861c [DOI] [PubMed] [Google Scholar]
- 29.Frament C. M., Bandara N., and Dwyer J. R., “Nanopore surface coating delivers nanopore size and shape through conductance-based sizing,” ACS Appl. Mater. Interfaces 5(19), 9330–9337 (2013). 10.1021/am4026455 [DOI] [PubMed] [Google Scholar]
- 30.Fyta M., Melchionna S., and Succi S., “Translocation of biomolecules through solid-state nanopores: Theory meets experiments,” J. Polym. Sci. B Polym. Phys. 49(14), 985–1011 (2011). 10.1002/polb.22284 [DOI] [Google Scholar]
- 31.Garaj S., “Graphene as a subnanometre trans-electrode membrane,” Nature 467, 190–193 (2010). 10.1038/nature09379 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Garaj S., “Molecule-hugging graphene nanopores,” Proc. Natl. Acad. Sci. U.S.A. 110(30), 12192–12196 (2013). 10.1073/pnas.1220012110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.deGennes P.-G., Scaling Concepts in Polymer Physics, 1st ed. (Cornell University Press, Ithaca, NY, 1979). [Google Scholar]
- 34.Ghosal S., “Electrophoresis of a polyelectrolyte through a nanopore,” Phys. Rev. E 74, 041901-1–041901-5 (2006). 10.1103/PhysRevE.74.041901 [DOI] [PubMed] [Google Scholar]
- 35.Ghosal S., “The effect of salt concentration on the electrophoretic speed of a polyelectrolyte through a nanopore,” Phys. Rev. Lett. 98, 238104 (2007). 10.1103/PhysRevLett.98.238104 [DOI] [PubMed] [Google Scholar]
- 36.Ghosal S., “Electrophoresis of a polyelectrolyte through a nanopore,” Phys. Rev. E 74(4), 041901 (2006). 10.1103/PhysRevE.74.041901 [DOI] [PubMed] [Google Scholar]
- 37.Ghosal S., “Effect of salt concentration on the electrophoretic speed of a polyelectrolyte through a nanopore,” Phys. Rev. Lett. 98(23), 238104 (2007). 10.1103/PhysRevLett.98.238104 [DOI] [PubMed] [Google Scholar]
- 38.Ghosal S. and Sherwood J. D., “Repulsion between finite charged plates with strongly overlapped electric double layers,” Langmuir 32, 9445–9450 (2016). 10.1021/acs.langmuir.6b02171 [DOI] [PubMed] [Google Scholar]
- 39.Graham M. D., “The Coulter principle: Foundation of an industry,” J. Assoc. Lab. Autom. 8(6), 72–81 (2003). 10.1016/S1535-5535-03-00023-6 [DOI] [Google Scholar]
- 40.Hall J. E., “Access resistance of a small circular pore,” J. Gen. Physiol. 66(4), 531–532 (1975). 10.1085/jgp.66.4.531 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Happel J. R. and Brenner H., Low Reynolds Number Hydrodynamics: With Special Applications to Particulate Media (Kluwer Academic, The Hague, The Netherlands, 1965). [Google Scholar]
- 42.Harms Z. D. et al., “Conductivity-based detection techniques in nanofluidic devices,” Analyst 140(14), 4779–4791 (2015). 10.1039/C5AN00075K [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Harrell C. C., Kohli P., Siwy Z. S., and Martin C. R., “DNA-nanotube artificial ion channels,” J. Am. Chem. Soc. 126(48), 15646–15647 (2004). 10.1021/ja044948v [DOI] [PubMed] [Google Scholar]
- 44.Haywood D. G. et al., “Fundamental studies of nanofluidics: Nanopores, nanochannels, and nanopipets,” Anal. Chem. 87(1), 172–187 (2015). 10.1021/ac504180h [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.He Y. et al., “Tuning transport properties of nanofluidic devices with local charge inversion,” J. Am. Chem. Soc. 131(14), 5194–5202 (2009). 10.1021/ja808717u [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.He Y. et al., “Controlling DNA translocation through gate modulation of nanopore wall surface charges,” ACS Nano 5(7), 5509–5518 (2011). 10.1021/nn201883b [DOI] [PubMed] [Google Scholar]
- 47.Hernández-Ainsa S. et al., “DNA origami nanopores for controlling DNA translocation,” ACS Nano 7(7), 6024–6030 (2013). 10.1021/nn401759r [DOI] [PubMed] [Google Scholar]
- 48.Hernández-Ainsa S. and Keyser U. F., “DNA origami nanopores: Developments, challenges and perspectives,” Nanoscale 6(23), 14121–14132 (2014). 10.1039/C4NR04094E [DOI] [PubMed] [Google Scholar]
- 49.Hernández-Ainsa S. et al., “Voltage-dependent properties of DNA origami nanopores,” Nano Lett. 14(3), 1270–1274 (2014). 10.1021/nl404183t [DOI] [PubMed] [Google Scholar]
- 50.Hille B., Ion Channels of Excitable Membranes, 3rd ed. (Sinauer Associates, Sunderland, MA, 2001). [Google Scholar]
- 51.Howorka S. and Siwy Z. S., “Nanopore analytics: Sensing of single molecules,” Chem. Soc. Rev. 38(8), 2360–2384 (2009). 10.1039/b813796j [DOI] [PubMed] [Google Scholar]
- 52.Jeffrey D. J. and Sherwood J. D., “Streamline patterns and eddies in low-Reynolds-number flow,” J. Fluid Mech. 96(2), 315–334 (1980). 10.1017/S0022112080002145 [DOI] [Google Scholar]
- 53.Kasianowicz J. J. et al., “Characterization of individual polynucleotide molecules using a membrane channel,” Proc. Natl. Acad. Sci. U.S.A. 93(24), 13770–13773 (1996). 10.1073/pnas.93.24.13770 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Keyser U. F., “Controlling molecular transport through nanopores,” J. R. Soc. Interface 8(63), 1369–1378 (2011). 10.1098/rsif.2011.0222 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Keyser U. F. et al., “Direct force measurements on DNA in a solid-state nanopore,” Nat. Phys. 2(7), 473–477 (2006). 10.1038/nphys344 [DOI] [Google Scholar]
- 56.Kirby B. J. and Hasselbrink E. F., “Zeta potential of microfluidic substrates: 1. Theory, experimental techniques, and effects on separations,” Electrophoresis 25, 187–202 (2004). 10.1002/(ISSN)1522-2683 [DOI] [PubMed] [Google Scholar]
- 57.Kirby B. J. and Hasselbrink E. F., “Zeta potential of microfluidic substrates: 2. Data for polymers,” Electrophoresis 25, 203–213 (2004). 10.1002/(ISSN)1522-2683 [DOI] [PubMed] [Google Scholar]
- 58.Klenerman D. et al., “Imaging the cell surface and its organization down to the level of single molecules,” Philos. Trans. R. Soc. Lond. B Biol. Sci. 368 1611), 20120027 (2013). 10.1098/rstb.2012.0027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Kowalczyk S. W. and Dekker C., “Measurement of the docking time of a DNA molecule onto a solid-state nanopore,” Nano Lett. 12, 4159–4163 (2012). 10.1021/nl301719a [DOI] [PubMed] [Google Scholar]
- 60.Lan W.-J. et al., “Effect of surface charge on the resistive pulse waveshape during particle translocation through glass nanopores,” J. Phys. Chem. C 118, 2726–2734 (2014). 10.1021/jp412148s [DOI] [Google Scholar]
- 61.Lander E. S. and Waterman M. S., “Genomic mapping by fingerprinting random clones: A mathematical analysis,” Genomics 2(3), 231–239 (1988). 10.1016/0888-7543(88)90007-9 [DOI] [PubMed] [Google Scholar]
- 62.Laohakunakorn N. et al., “DNA interactions in crowded nanopores,” Nano Lett. 13(6), 2798–2802 (2013). 10.1021/nl401050m [DOI] [PubMed] [Google Scholar]
- 63.Laohakunakorn N. et al., “A Landau-Squire nanojet,” Nano Lett. 13(11), 5141–5146 (2013). 10.1021/nl402350a [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Lee C. et al., “Large apparent electric size of solid-state nanopores due to spatially extended surface conduction,” Nano Lett. 12(8), 4037–4044 (2012). 10.1021/nl301412b [DOI] [PubMed] [Google Scholar]
- 65.Lepoitevin M. et al., “Functionalization of single solid state nanopores to mimic biological ion channels: A review,” Adv. Colloid Interface Sci. 250, 195–213 (2017). 10.1016/j.cis.2017.09.001 [DOI] [PubMed] [Google Scholar]
- 66.Li W. et al., “Single protein molecule detection by glass nanopores,” ACS Nano 7(5), 4129–4134 (2013). 10.1021/nn4004567 [DOI] [PubMed] [Google Scholar]
- 67.Liebes Y. et al., “Reconstructing solid state nanopore shape from electrical measurements,” Appl. Phys. Lett. 97(22), 223105 (2010). 10.1063/1.3521411 [DOI] [Google Scholar]
- 68.Liu S. et al., “Plasmonic hotspots of dynamically assembled nanoparticles in nanocapillaries: Towards a miRNA profiling platform,” Biomicrofluidics 7, 061102 (2013). 10.1063/1.4832095 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Lu B. et al., “Effective driving force applied on DNA inside a solid-state nanopore,” Phys. Rev. E 86(1), 011921 (2012). 10.1103/PhysRevE.86.011921 [DOI] [PubMed] [Google Scholar]
- 70.Luan B. and Aksimentiev A., “Electro-osmotic screening of the DNA charge in a nanopore,” Phys. Rev. E 78(2), 021912 (2008). 10.1103/PhysRevE.78.021912 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Luan B. and Aksimentiev A., “Control and reversal of the electrophoretic force on DNA in a charged nanopore,” J. Phys. Condens. Matter 22(45), 454123 (2010). 10.1088/0953-8984/22/45/454123 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Luan B., Stolovitzky G., and Martyna G., “Slowing and controlling the translocation of DNA in a solid-state nanopore,” Nanoscale 4(4), 1068 (2012). 10.1039/C1NR11201E [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Lubensky D. K. and Nelson D. R., “Driven polymer translocation through a narrow pore,” Biophys. J. 77(4), 1824–1838 (1999). 10.1016/S0006-3495(99)77027-X [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Luo L., Holden D. A., and White H., “Negative differential electrolyte resistance in a solid-state nanopore resulting from electroosmotic flow bistability,” ACS Nano 8, 3023–3030 (2014). 10.1021/nn500379j [DOI] [PubMed] [Google Scholar]
- 75.Mao M., Sherwood J. D., and Ghosal S., “Electro-osmotic flow through a nanopore,” J. Fluid Mech. 749, 167–183 (2014). 10.1017/jfm.2014.214 [DOI] [Google Scholar]
- 76.Mao M., Ghosal S., and Hu G., “Hydrodynamic flow in the vicinity of a nanopore induced by an applied voltage,” Nanotechnology 24(24), 245202 (2013). 10.1088/0957-4484/24/24/245202 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.McNally B., Wanunu M., and Meller A., “Electromechanical unzipping of individual DNA molecules using synthetic sub-2 nm pores,” Nano Lett. 8(10), 3418–3422 (2008). 10.1021/nl802218f [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Meller A. et al., “Rapid nanopore discrimination between single polynucleotide molecules,” Proc. Natl. Acad. Sci. U.S.A. 97(3), 1079–1084 (2000). 10.1073/pnas.97.3.1079 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Meller A., Nivon L., and Branton D., “Voltage-driven DNA translocations through a nanopore,” Phys. Rev. Lett. 86(15), 3435–3438 (2001). 10.1103/PhysRevLett.86.3435 [DOI] [PubMed] [Google Scholar]
- 80.Menestrina J. et al., “Charged particles modulate local ionic concentrations and cause formation of positive peaks in resistive-pulse-based detection,” J. Phys. Chem. C 118, 2391–2398 (2014). 10.1021/jp412135v [DOI] [Google Scholar]
- 81.Muthukumar M., “Translocation of a confined polymer through a hole,” Phys. Rev. Lett. 86(14), 3188–3191 (2001). 10.1103/PhysRevLett.86.3188 [DOI] [PubMed] [Google Scholar]
- 82.Muthukumar M., “Mechanism of DNA transport through pores,” Annu. Rev. Biophys. Biomol. Struct. 36(1), 435–450 (2007). 10.1146/annurev.biophys.36.040306.132622 [DOI] [PubMed] [Google Scholar]
- 83.Oosawa F., Polyelectrolytes (Marcel Dekker, New York, 1971). [Google Scholar]
- 84.Pan Z. et al., “Universal scaling of robust thermal hotspot and ionic current enhancement by focused Ohmic heating in a conic nanopore,” Phys. Rev. Lett. 117(13), 134301–134304 (2016). 10.1103/PhysRevLett.117.134301 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Probstein R. F., Physicochemical Hydrodynamics: An Introduction, 2nd ed. (Wiley-Interscience, 2003). [Google Scholar]
- 86.Rosentsvit L. et al., “Ion current rectification in funnel-shaped nanochannels: Hysteresis and inversion effects,” J. Chem. Phys. 143, 224706 (2015). 10.1063/1.4936915 [DOI] [PubMed] [Google Scholar]
- 87.Rothemund P. W. K., “Folding DNA to create nanoscale shapes and patterns,” Nature 440, 297–302 (2006). 10.1038/nature04586 [DOI] [PubMed] [Google Scholar]
- 88.Russel W. B., Saville D. A., and Schowalter W. R., Colloidal Dispersions (Cambridge University Press, Cambridge, UK, 1989). [Google Scholar]
- 89.Schatz M. C., “Nanopore sequencing meets epigenetics,” Nat. Methods 14(4), 347 (2017). 10.1038/nmeth.4240 [DOI] [PubMed] [Google Scholar]
- 90.Schneider G. F. et al., “DNA translocation through graphene nanopores,” Nano Lett. 10(8), 3163–3167 (2010). 10.1021/nl102069z [DOI] [PubMed] [Google Scholar]
- 91.Schnitzer O. and Yariv E., “Macroscale description of electrokinetic flows at large zeta potentials: Nonlinear surface conduction,” Phys. Rev. E 86(2), 021503 (2012). 10.1103/PhysRevE.86.021503 [DOI] [PubMed] [Google Scholar]
- 92.Schoch R. B., “Transport phenomena in nanofluidics,” Rev. Mod. Phys. 80(3), 839–883 (2008). 10.1103/RevModPhys.80.839 [DOI] [Google Scholar]
- 93.Seeman N. C., “Nucleic acid junctions and lattices,” J. Theor. Biol. 99(2), 237–247 (1982). 10.1016/0022-5193(82)90002-9 [DOI] [PubMed] [Google Scholar]
- 94.Sheng Q. et al., “A capacitive-pulse model for nanoparticle sensing by single conical nanochannels,” Nanoscale 8(3), 1565–1571 (2016). 10.1039/C5NR07596C [DOI] [PubMed] [Google Scholar]
- 95.Sherwood J. D., Mao M., and Ghosal S., “Electrically generated eddies at an eightfold stagnation point within a nanopore,” Phys. Fluids 26(11), 112004 (2014). 10.1063/1.4901984 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Sherwood J. D., Mao M., and Ghosal S., “Electroosmosis in a finite cylindrical pore: Simple models of end effects,” Langmuir 30(31), 9261–9272 (2014). 10.1021/la502349g [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Sherwood J. D. and Stone H. A., “Electrophoresis of a thin charged disk,” Phys. Fluids 7(4), 697–705 (1995). 10.1063/1.868595 [DOI] [Google Scholar]
- 98.Shi W., Friedman A. K., and Baker L. A., “Nanopore sensing,” Anal. Chem. 89(1), 157–188 (2017). 10.1021/acs.analchem.6b04260 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Sims D. et al., “Sequencing depth and coverage: Key considerations in genomic analyses,” Nat. Rev. Genet. 15(2), 121 (2014). 10.1038/nrg3642 [DOI] [PubMed] [Google Scholar]
- 100.Siwy Z. S., “Ion-current rectification in nanopores and nanotubes with broken symmetry,” Adv. Funct. Mater. 16(6), 735–746 (2006). 10.1002/(ISSN)1616-3028 [DOI] [Google Scholar]
- 101.Siwy Z. S. and Fulinacuteski A., “Fabrication of a synthetic nanopore ion pump,” Phys. Rev. Lett. 89(19), 198103 (2002). 10.1103/PhysRevLett.89.198103 [DOI] [PubMed] [Google Scholar]
- 102.Siwy Z. S. et al., “Rectification and voltage gating of ion currents in a nanofabricated pore,” Europhys Lett. 60(3), 349 (2002). 10.1209/epl/i2002-00271-3 [DOI] [Google Scholar]
- 103.Siwy Z. S. et al., “Asymmetric diffusion through synthetic nanopores,” Phys. Rev. Lett. 94(4), 048102 (2005). 10.1103/PhysRevLett.94.048102 [DOI] [PubMed] [Google Scholar]
- 104.Siwy Z. S. and Howorka S., “Engineered voltage-responsive nanopores,” Chem. Soc. Rev. 39(3), 1115–1132 (2010). 10.1039/B909105J [DOI] [PubMed] [Google Scholar]
- 105.Smeets R. M. M. et al., “Salt dependence of ion transport and DNA translocation through solid-state nanopores,” Nano Lett. 6(1), 89–95 (2006). 10.1021/nl052107w [DOI] [PubMed] [Google Scholar]
- 106.Smith D. E. et al., “The bacteriophage -29 portal motor can package DNA against a large internal force,” Nature 413, 748–752 (2001). 10.1038/35099581 [DOI] [PubMed] [Google Scholar]
- 107.Squires T. M. and Bazant M. Z., “Induced-charge electro-osmosis,” J. Fluid Mech. 509, 217–252 (2004). 10.1017/S0022112004009309 [DOI] [Google Scholar]
- 108.Steinbock L. J. et al., “Probing DNA with micro- and nanocapillaries and optical tweezers,” J. Phys. Condens. Matter 22(45), 454113 (2010). 10.1088/0953-8984/22/45/454113 [DOI] [PubMed] [Google Scholar]
- 109.Steinbock L. J. et al., “Detecting DNA folding with nanocapillaries,” Nano Lett. 10(7), 2493–2497 (2010). 10.1021/nl100997s [DOI] [PubMed] [Google Scholar]
- 110.Storm A. J. et al., “Fast DNA translocation through a solid-state nanopore,” Nano Lett. 5(7), 1193–1197 (2005). 10.1021/nl048030d [DOI] [PubMed] [Google Scholar]
- 111.Sun G., Senapati S., and Chang H.-C., “High-flux ionic diodes, ionic transistors and ionic amplifiers based on external ion polarization by an ion exchange membrane: A new scalable ionic circuit platform,” Lab Chip 16, 1171 (2016). 10.1039/C6LC00026F [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Sung W. and Park P. J., “Polymer translocation through a pore in a membrane,” Phys. Rev. Lett. 77(4), 783 (1996). 10.1103/PhysRevLett.77.783 [DOI] [PubMed] [Google Scholar]
- 113.Tabard-Cossa V. et al., “Single-molecule bonds characterized by solid-state nanopore force spectroscopy,” ACS Nano 3(10), 3009–3014 (2009). 10.1021/nn900713a [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Taniguchi M., “Selective multidetection using nanopores,” Anal. Chem. 87(1), 188–199 (2015). 10.1021/ac504186m [DOI] [PubMed] [Google Scholar]
- 115.Thamida S. K. and Chang H.-C., “Nonlinear electrokinetic ejection and entrainment due to polarization at nearly insulated wedges,” Phys. Fluids 14(12), 4315–4328 (2002). 10.1063/1.1519530 [DOI] [Google Scholar]
- 116.Trizac E. and Téllez G., “Onsager-Manning-Oosawa condensation phenomenon and the effect of salt,” Phys. Rev. Lett. 96(3), 038302 (2006). 10.1103/PhysRevLett.96.038302 [DOI] [PubMed] [Google Scholar]
- 117.Tropini C. and Marziali A., “Multi-nanopore force spectroscopy for DNA analysis,” Biophys. J. 92(5), 1632–1637 (2007). 10.1529/biophysj.106.094060 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.van Dorp S. et al., “Origin of the electrophoretic force on DNA in solid-state nanopores,” Nat. Phys. 5(5), 347–351 (2009). 10.1038/nphys1230 [DOI] [Google Scholar]
- 119.Vlassarev D. M. and Golovchenko J. A., “Trapping DNA near a solid-state nanopore,” Biophys. J. 103, 352–356 (2012). 10.1016/j.bpj.2012.06.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Vlassiouk I., Kozel T. R., and Siwy Z. S., “Biosensing with nanofluidic diodes,” J. Am. Chem. Soc. 131(23), 8211–8220 (2009). 10.1021/ja901120f [DOI] [PMC free article] [PubMed] [Google Scholar]
- 121.Wang C. et al., “Low-voltage electroosmotic pumps fabricated from track-etched polymer membranes,” Lab Chip 12, 1710–1716 (2012). 10.1039/c2lc40059f [DOI] [PubMed] [Google Scholar]
- 122.Wang C. et al., “Atomic layer deposition modified track-etched conical nanochannels for protein sensing,” Anal. Chem. 87(16), 8227–8233 (2015). 10.1021/acs.analchem.5b01501 [DOI] [PubMed] [Google Scholar]
- 123.Wanunu M., “Nanopores: A journey towards DNA sequencing,” Phys. Life Rev. 9(2), 125–158 (2012). 10.1016/j.plrev.2012.05.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 124.Wei C., Bard A. J., and Feldberg S. W., “Current rectification at quartz nanopipet electrodes,” Anal. Chem. 69(22), 4627–4633 (1997). 10.1021/ac970551g [DOI] [Google Scholar]
- 125.Wiedemann N., Frazier A. E., and Pfanner N., “The protein import machinery of mitochondria,” J. Biol. Chem. 279(15), 14473–14476 (2004). 10.1074/jbc.R400003200 [DOI] [PubMed] [Google Scholar]
- 126.Yan Y. et al., “Ion current rectification inversion in conic nanopores: Nonequilibrium ion transport biased by ion selectivity and spatial asymmetry,” J. Chem. Phys. 138, 044706 (2013). 10.1063/1.4776216 [DOI] [PubMed] [Google Scholar]
- 127.Yan Y. et al., “Universal low frequency asymptotes of dynamic nanopore rectification: An ionic nanofluidics inductor,” J. Chem. Phys. 143, 224705 (2015). 10.1063/1.4937360 [DOI] [PubMed] [Google Scholar]
- 128.Yan Y. et al., “Robust ion current oscillation under a steady electric field: An ion channel analog,” Phys. Rev. E 94, 022613 (2016). 10.1103/PhysRevE.94.022613 [DOI] [PubMed] [Google Scholar]
- 129.Yameen B. et al., “Single conical nanopores displaying pH-tunable rectifying characteristics. Manipulating ionic transport with zwitterionic polymer brushes,” J. Am. Chem. Soc. 131(6), 2070–2071 (2009). 10.1021/ja8086104 [DOI] [PubMed] [Google Scholar]
- 130.Yariv E. and Davis A. M. J., “Electro-osmotic flows over highly polarizable dielectric surfaces,” Phys. Fluids 22(5), 052006 (2010). 10.1063/1.3431695 [DOI] [Google Scholar]
- 131.Yeh L. et al., “Regulating DNA translocation through functionalized soft nanopores,” Nanoscale 4(8), 2685–2693 (2012). 10.1039/c2nr30102d [DOI] [PubMed] [Google Scholar]
- 132.Yossifon G., Frankel I., and Miloh T., “On electro-osmotic flows through microchannel junctions,” Phys. Fluids 18(11), 117108-1–117108-9 (2006). 10.1063/1.2391701 [DOI] [Google Scholar]
- 133.Zanjani M. B. et al., “Up and down translocation events and electric double-layer formation inside solid-state nanopores,” Phys. Rev. E 92, 022715 (2015). 10.1103/PhysRevE.92.022715 [DOI] [PubMed] [Google Scholar]
- 134.Zhang B. et al., “Polarization effect of a dielectric membrane on the ionic current rectification in a conical nanopore,” J. Phys. Chem. C 115, 24951–24959 (2011). 10.1021/jp2089388 [DOI] [Google Scholar]