Machine Learning Identifies Chemical Characteristics That Promote Enzyme Catalysis

Abstract

Despite tremendous progress in understanding and engineering enzymes, knowledge of how enzyme structures and their dynamics induce observed catalytic properties is incomplete, and capabilities to engineer enzymes fall far short of industrial needs. Here, we investigate the structural and dynamic drivers of enzyme catalysis for the rate-limiting step of the industrially important enzyme ketol-acid reductoisomerase (KARI) and identify a region of the conformational space of the bound enzyme–substrate complex that, when populated, leads to large increases in reactivity. We apply computational statistical mechanical methods that implement transition interface sampling to simulate the kinetics of the reaction and combine this with machine learning techniques from artificial intelligence to select features relevant to reactivity and to build predictive models for reactive trajectories. We find that conformational descriptors alone, without the need for dynamic ones, are sufficient to predict reactivity with greater than 85% accuracy (90% AUC). Key descriptors distinguishing reactive from almost-reactive trajectories quantify substrate conformation, substrate bond polarization, and metal coordination geometry and suggest their role in promoting substrate reactivity. Moreover, trajectories constrained to visit a region of the reactant well, separated from the rest by a simple hyperplane defined by ten conformational parameters, show increases in computed reactivity by many orders of magnitude. This study provides evidence for the existence of reactivity promoting regions within the conformational space of the enzyme–substrate complex and develops methodology for identifying and validating these particularly reactive regions of phase space. We suggest that identification of reactivity promoting regions and re-engineering enzymes to preferentially populate them may lead to significant rate enhancements.

Introduction

Enzymes are remarkable catalysts that produce substantial rate enhancements, often accompanied by high substrate and product selectivity. They are increasingly important for industrial-scale applications, because of the chemistry they can accomplish sustainably in mild, aqueous conditions. Despite substantial progress made, more is still required along two principal avenues in order to advance enzyme engineering to meet industrial needs. We need a better understanding of the drivers of reactivity promoted by enzymes, some of which have been hypothesized to be dynamic¹⁻³ rather than structural, along with a richer set of tools to probe and manipulate the active site catalytic environment.

Current approaches include directed evolution,⁴⁻⁶ catalytic antibodies,⁷⁻⁹ and computational enzyme design,^10,11 the latter two of which focus on tight-binding of transition states. While these approaches have produced tremendous successes, they have not yet become general-purpose tools. The need for directed evolution to improve designs obtained by other methods, and our inability to fully rationalize the improvements accumulated through evolution, suggests that our understanding may be incomplete, perhaps in some fundamental way, and may require us to incorporate other factors beyond transition-state binding and transition-state stabilization (relative to the bound or unbound ground state).

Here we investigate two fundamental questions of enzyme function motivated by the larger goal of enzyme engineering; note that our focus is on the enzyme–substrate complex without specific reference to the transition state. First, can we gain insight into the nature of the drivers of chemical reactivity, and to what extent are these drivers apparent in the behavior of the bound enzyme–substrate complex, well before the transition state? And second, based on previous work by ourselves and others¹²⁻¹⁶ can we identify regions of the conformational space of the enzyme–substrate complex that are inherently more reactive than others? These questions are addressed using a new approach that combines machine learning with path sampling, applied to the rate-limiting step for the industrially important enzyme ketol-acid reductoisomerase (KARI).

There are a number of approaches for studying enzyme reactivity that do not focus on the transition state per se, although it may enter implicitly. These include the literature investigating near-attack conformations, which has suggested that lowering the energetic barrier to facilitate selective formation of subsets of ground-state conformations that lie on the path to the transition state can be just as important as lowering the energetic barrier to the transition state itself^14,17−19 and the computational path sampling methods,^20,21 which are statistical mechanical techniques for directly computing the rate of a chemical reaction without reliance on transition-state theory or knowledge of either the transition state or a valid reaction coordinate connecting the reactant well with the product well on the free energy surface.

Here we use transition interface sampling²¹ (TIS), for its computational efficiency. TIS uses Monte Carlo sampling to construct an ensemble of trajectories that start in the reactant well and pass through an interface on the way toward the product well. Appropriate statistical methods exist to compute the progressive probability that a trajectory starting in the reactant well will reach each successive interface, a rapidly diminishing cumulative probability, and to convert the probability into a reaction rate, corresponding to the specific activity, k_cat, for enzymes. While a valid reaction coordinate is not a requirement, the method uses an order parameter that cleanly distinguishes reactant from product to track progress between the two wells.²¹ (The placement of interfaces is shown schematically in Figure 1A and their progression in Figure S1, with λ representing the order parameter.) Path sampling methods have been validated using experimental data in enzyme kinetic studies.¹²

Figure 1.

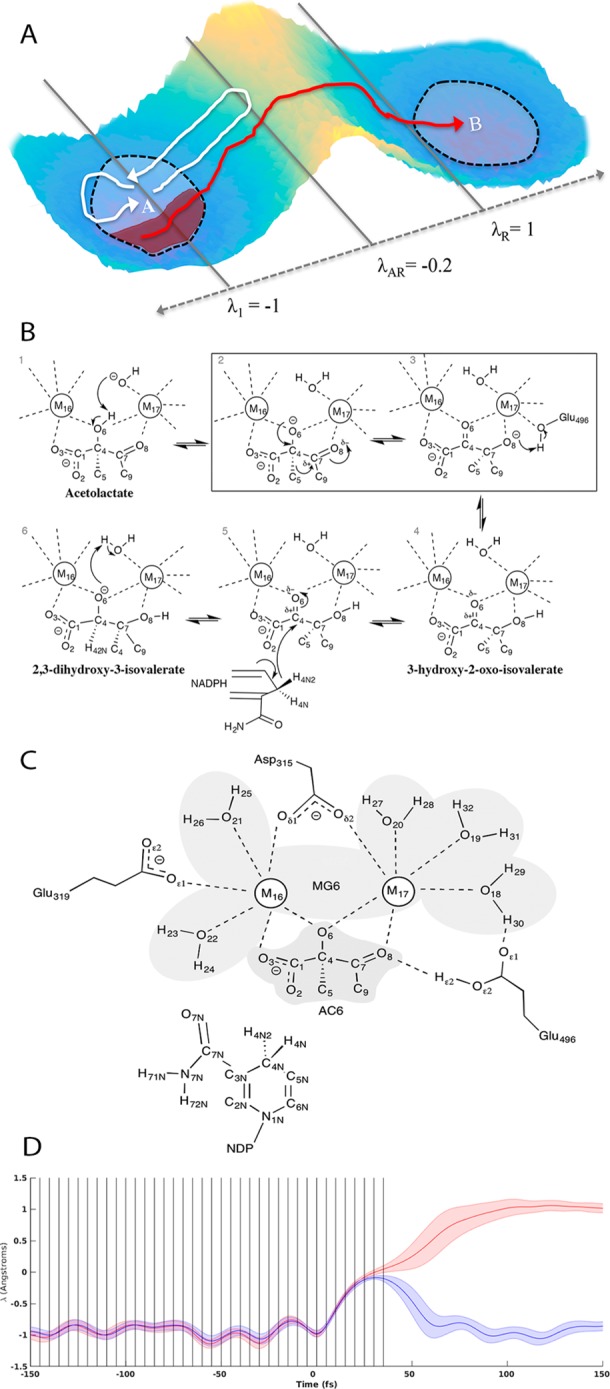
(A) Interface placements used to generate reactive and almost-reactive trajectories, where λ₁ denotes the reactant interface, λ_AR indicates the product interface used to generate the almost-reactive trajectory ensembles, and λ_R indicates the product interface used to generate the reactive trajectory ensembles. (B) Reaction catalyzed by KARI with states 2 and 3 indicating initial and final states used for the specific rate-limiting step of the isomerization studied. (C) Atoms and residues included in QM region (nonpolar hydrogens not shown). Note that the residue name AC6 is used in this study to refer to the reactant state of the substrate shown in Figure 1C. The residue name NDP refers to the NADPH cofactor, and the residue name MG6 refers to the five quantum mechanically treated waters and two magnesium ions in the active site. (D) Distribution of λ values for reactive (red) and almost-reactive (blue) trajectories time-shifted such that the last trough before the prospective catalytic event occurs at the 0 fs time point. Vertical lines indicate time points where features were computed.

The model system for this study, KARI, is a natural enzyme required for branched-chain amino acid synthesis, found broadly across plant and microbial species.²² It carries out two reactions in sequence, first an isomerization, which is generally rate limiting, consisting of an alkyl migration and then a faster reduction carried out by a nucleotide cofactor. It also has an important role in industrial processes for the production of isobutanol, and, due to its role as the rate-limiting step, improvements in its specific activity would improve processes for large-scale isobutanol production.²³ Our studies have focused on the homodimeric enzyme from Spinacia oleracea (spinach), due largely to the availability of appropriate crystal structures, and we have studied the industrially relevant, rate-limiting reaction step involving isomerization of (2S)-acetolactate (AL) to (2R)-2,3-dihyroxy-3-isovalerate through methyl migration²³⁻²⁵ (Figure 1B).

The natural spinach enzyme exhibits a strong preference for NADPH as a cofactor and has two divalent magnesium cations bound at the active site, in intimate contact with substrate,²⁶ which are each hexacoordinate with oxygen atoms from the substrate, active site water molecules, and residues Asp 315, Glu 319, and Glu 496 (Figure 1C). Note that the C5 represents the methyl group that migrates from C4 to C7.

The current study is based on previous work we carried out on KARI, which identified a “pump-and-push” mechanism for the rate-limiting isomerization reaction, whereby the local environment vibrationally excites the breaking C4–C5 bond and the side chain of Glu 319 helps direct and potentially stabilize the migrating methyl group toward its destination, bound to C7.¹² Moreover, the work suggested that some portions of the conformational and motional space of the bound enzyme–substrate complex (the reactant well) led to trajectories that have a greater probability of reacting than those that do not pass through or spend as much time in those same portions of the reactant well.

Here we carried out TIS simulations of wild-type spinach KARI and performed comparative analysis on two sets of ensembles of trajectories—one set that reacted and another set that approached the barrier but did not react (termed “almost-reactive”). We tabulated data on 68 different geometric measurements (Table S1 and Figure S2) in the active site that represent elements of the local conformation in the form of distances between pairs of atoms, planar angles across triplets of atoms, and dihedral angles across quadruplets of atoms. The set was selected based on mechanistic hypotheses of others and ourselves, and includes internal metrics within the substrate; measures of the position and orientation of substrate relative to the environment, particularly for groups that might stabilize the bound substrate or transition state; and measures of conformation of the environment.

Machine learning techniques were applied to identify subsets of this feature list and build predictive models that accurately distinguished reactive from almost-reactive trajectories, based only on data tabulated from before trajectories departed the reactant well. We reasoned that these reduced feature sets and models might indicate key features sufficient to drive reactivity. We analyzed these features in the context of the reactive and almost-reactive trajectories to understand in more detail these drivers and to gain insight into mechanism. We found that key descriptors capable of identifying reactive conformations included those that quantify substrate conformation, substrate bond polarization, and metal coordination geometry and suggest their role in promoting substrate reactivity. To test the notion that these descriptors are sufficient and that they define inherently reactive portions of the reactant well, we compared the computed specific activity of the wild-type enzyme when trajectories were constrained to visit these regions with those that were not. We found that ten features alone were sufficient to describe a portion of the reactant well that led to very large rate increases, demonstrating it to be a highly reactive portion of the well.

Methods

Note: Further details may be found in Supporting Methods.

Structure Preparation

The crystal structure of Spinacia oleracea KARI was obtained from the Protein Data Bank²⁷⁻²⁹ with the accession code 1YVE²⁶ and prepared as described previously by Silver.¹² Only the chain A monomer was used for all simulations in order to improve computational efficiency, justified by the significant separation between the active sites of the two monomers²⁶ (Figure S3).

A model of the substrate-bound enzyme was then constructed by running an in vacuo QM ground-state minimization of the substrate, two magnesium centers, five magnesium-coordinating water molecules, and the side chains of three surrounding active site residues, Asp 315, Glu 319, and Glu 496. Glu 496 was protonated, consistent with previous studies indicating its importance in stabilizing the transition and product state by forming a hydrogen bond with the substrate O8.³⁰ The GAUSSIAN03 computer program³¹ was used to perform in vacuo QM calculations at the rhf/3-21g* level of theory.^32,33

Simulation Methodology

CHARMM version 41^34,35 compiled with the SQUANTUM option was used to perform all molecular dynamics simulations. The QM portion of the energy function was calculated with the AM1 semiempirical quantum mechanical force field;³⁶ the MM portion of the energy function was computed using the CHARMM36 all-atom force field.³⁷ Additional AM1 parameters were used for the magnesium ions.³⁸ The following atoms made up the QM region: substrate (acetolactate), both magnesium centers, five magnesium-coordinating active site water molecules, the side chains of Asp 315, Glu 319, and Glu 496, and the nicotinamide group of NADPH (Figure 1C). The Generalized Hybrid Orbital method³⁹ was used to treat the QM/MM boundary atoms. The substrate O6 was deprotonated and the coordinating Glu 496 was protonated, paralleling previous QM/MM studies of KARI.³⁰

Seed Trajectory Generation

The initial reactive trajectories used to bootstrap the TIS simulations were found by computing a potential of mean force (PMF) along the order parameter λ, defined as the difference of the distance between the substrate breaking bond (C4–C5) and the forming bond (C5–C7), in units of angstroms. This PMF was computed using umbrella sampling and the weighted histogram analysis method.⁴⁰ The umbrella sampling was performed in CHARMM41 using the RXNCOR module with windows 0.05 Å in width and harmonic restraints of 300 kcal/(mol·Å²). Candidate seed trajectories were then generated by integrating forward and backward for 2000 fs without restraints starting from a randomly chosen frame from the umbrella sampling window ensembles centered at λ values of −0.05, 0.00, and +0.05. Trajectories were selected as successful seed trajectories if they connected the reactant basin (λ < −1) and product basin (λ > +1).

Training Data Set Generation and Time Point Selection

Three randomly selected connecting seed trajectories from the collection described above were used as starting trajectories for the generation of a larger ensemble of reactive and almost-reactive trajectories. Each seed was used to generate 9 reactive ensembles and 9 almost-reactive ensembles of 20,000 trajectories each. The combined data set contained 461,422 almost-reactive and 618,578 reactive trajectories. When the almost-reactive process produced a reactive trajectory, it was removed from that set and added to the reactive data set. To ensure a balanced number of reactive and almost-reactive trajectories in each training and testing data set, the reactive trajectories were randomly sampled without replacement to produce a set of 461,422 reactive trajectories.

For the reactive ensembles, the product interface was defined as λ_R = +1.00, and for the almost-reactive ensembles, the product interface was defined as λ_AR = −0.20 (Figure 1A). The TIS methodology was applied in parallel to produce statistical mechanical ensembles containing reactive and almost-reactive trajectories that could be compared to one another. In both ensembles, the reactant interface was defined as λ = −1.00. To collect time points early in the reactant basin for analysis, integration was not stopped once a trajectory reached the reactant and product interface (and had been accepted into the Markov chain), but continued forward and backward for a total of 200 fs in each direction.

To ensure that candidate features (see below) were computed at analogous time points between reactive and almost-reactive trajectory ensembles, in a postprocessing step, all almost-reactive and reactive trajectories from all 27 pairs of ensembles were time-shifted such that the 0 fs time point corresponded to the bottom of the last “trough” in λ (when plotted vs time) before the prospective alkyl migration event, a geometric feature that all the collected trajectories shared (Figure 1D). This trough was found by first finding the point in the trajectory closest to the transition region at λ = 0 and then scanning along the trajectory backward from this point until the first change in sign of the derivative of λ with respect to time was found with a value of λ less than 0 (i.e., was located in the reactant basin). All other time points were defined relative to this first trough at time 0. Cartesian coordinate frames of atomic positions were collected in 5 fs increments from the 0 fs time point, going backward to −150 fs and forward to +35 fs from the t = 0 fs point, for a total of 38 total time points. This collection of subsampled time points was used for all subsequent analysis.

Feature Computation

At each of the 38 time points between −150 and +35 fs, the set of 68 structural features in Table S1 were computed for each of the trajectories in each of the 27 reactive and 27 almost-reactive ensembles. The 68 features are illustrated structurally in Figure S2A (distances), Figure S2B (angles), and Figure S2C (dihedrals). These data were pooled across ensembles to produce one combined reactive and one combined almost-reactive data set at each of the 38 time points, which were used in machine learning and subsequent analysis described below and stored as a row in a data matrix. For model training, the data matrix at each time point was randomly sampled without replacement to produce five equal partitions containing 73,827 trajectories each, and for model testing, the remaining trajectories were randomly sampled to produce five equal partitions containing 18,456 trajectories each.

Machine Learning

For feature regularization and discovery, LASSO⁴¹ was used with the lassoglm implementation in MATLAB. In order to select a given number of features with LASSO, the regularization parameter λ was adjusted until a specific number m (1, 5, 10, 15, 20, 25, or 30) of nonzero coefficients β_j remained (using a tolerance of 1.0 × 10^–4). These m LASSO-selected predictor features with nonzero coefficients were then fit using the fitglm function in MATLAB to a logistic classifier. After fitting predictor coefficients, the area under the curve of the receiver operating characteristic (AUC) was computed for each logistic classifier using the perfcurve function in MATLAB.

Cluster Assignment

Reactive clusters were assigned by k-means clustering, with the kmeans function in MATLAB using k = 5 applied to the matrix of consensus feature Z-scores weighted by their corresponding logistic coefficient β_j for all correctly classified reactive trajectories. The number of clusters (5) was chosen based on a hierarchical clustering analysis also performed in MATLAB (data not shown). The Euclidian distance of the consensus feature set from each almost-reactive trajectory to each of the five k-means centers was computed, and each almost-reactive trajectory was then assigned to the cluster with the shortest Euclidian distance to its respective centroid.

Rate Constant Computations

For the TIS flux factor calculations, a total of 10 independent 1 ns molecular dynamics simulations were performed starting from reactant structures derived from each of 6 randomly selected seed trajectories generated as described above. The λ_A interface was set equal to the λ₁ interface at λ= −0.8. For the control flux factor computations (Figure S1A), the effective positive flux was computed as the number of times the trajectory crossed the λ_A = −0.8 interface, having come from the region below the λ_A interface, divided by the total amount of time spent below the λ_A interface. For the constrained test flux factor computations (Figure S1C), the top 10 LASSO-selected features at the t = 0 time point were written out during the dynamics run, and the effective positive flux was computed as the number of times the trajectory crossed the λ₁ = −0.8 interface, having come from the region A′, where region A′ refers to all points in phase space which lie at the last trough (i.e., the first point at which 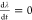and 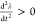) before crossing λ_A = −0.8, having first crossed λ₀ = −1, and for which the logistic classifier with coefficients and features listed in Table S2 evaluated to true.

For the probability factor calculations, a total of 29 P(λ_i+1 | λ_i) interface ensembles from each of the six seed trajectories were computed, with the λ_i interfaces spaced between λ = −0.8 and λ = 0. The placement of these interfaces relative to the PMF surface used to generate the initial seed is shown in Figure S4. For each interface ensemble, a total of 5000 shooting moves was attempted. In each λ_i ensemble, candidate trajectories were generated using full shooting moves and accepted if they both crossed the λ_A= −0.8 interface and crossed the λ = λ_i interface having first come from crossing interface λ_A. For the unconstrained control ensembles (Figure S1B), no further acceptance rules were applied.

Results

Machine Learning

Data sets consisting of 27 ensembles each of reactive and almost-reactive trajectories, generated using a combined QM/MM TIS approach, were analyzed with machine learning to identify features with the ability to distinguish reactive from almost-reactive trajectories. At each of 38 time points between −150 and +35 fs (5 fs spacing and shown in Figure 1D), the 68 features listed in Table S1 and illustrated structurally in Figure S2 were computed for both sets of reactive and almost-reactive ensembles. To assess individual feature performance, AUC (area under the curve of the receiver operating characteristic) was computed for all single features at the 0 fs time point (Figure 2A). The single feature with the maximum AUC performance was the distance between Glu 319 Oε1 and substrate C5 (AUC of 0.73). Only two features (distance Glu 319/Oε1–AC6/C5 and distance AC6/C4–AC6/C5) produced models with individual AUCs above 0.70, and 18 features produced models with AUCs above 0.60.

Figure 2.

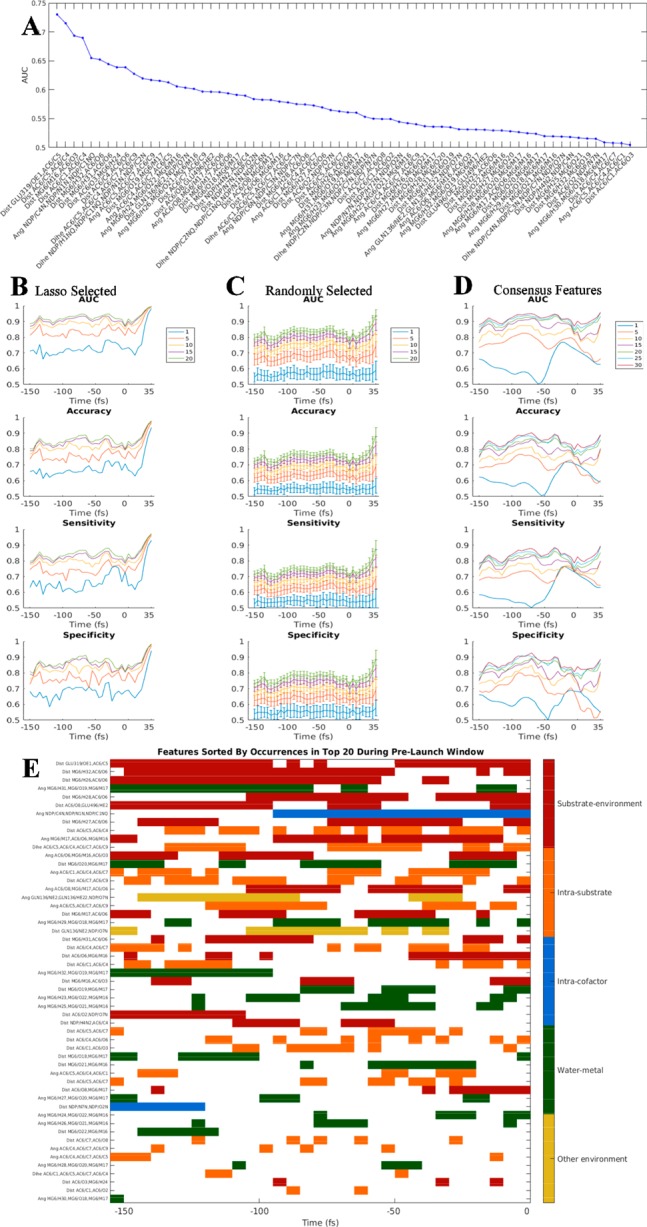
(A) AUC performance for all 68 individual features at the 0-fs time point. Values of AUC shown represent the mean computed across five equal cross-validation training and testing partitions. (B) AUC, accuracy, sensitivity, and specificity for models with LASSO-selected features. (C) AUC, accuracy, sensitivity, and specificity are plotted for models with randomly selected features. (D) AUC, accuracy, sensitivity, and specificity are plotted for models with 30 consensus features. Error bars in (C) correspond to standard error of the mean across 100 randomly selected feature sets. (E) Top 20 features selected by LASSO at each time point. Features are colored by feature type and sorted by the total number of occurrences in the top 20 between −150 and 0 fs.

To find highly predictive groups of features, LASSO⁴¹ was applied iteratively with different penalty strengths to identify an ordered set of features for each trajectory time point, optimized to distinguish reactive from almost-reactive conformations (see Methods). That is, for each time point a collection of separate classifiers was built, trained, and tested, enabling comparisons of the useful sets of features across time points as well as the performance benefits for increased numbers of features at each time point. Figure 2B shows the machine learning results for four classifier performance statistics (AUC, accuracy, sensitivity, and specificity) computed from each model constructed from data at each time point. Results for models constructed with optimized sets of 1, 5, 10, 15, and 20 features selected by LASSO are shown. The results show progressively improved performance as the number of features was increased, with not insignificant performance with just one feature (generally 0.65–0.75 AUC) that rose to excellent performance with 10, 15, and 20 features (generally 0.85–0.95 AUC). Note that the performance of the LASSO-selected 1-feature models, being the “best” feature for each time point, was significantly better than the average AUC of all possible 1-feature models shown in Figure 2A, which was 57.18%. The similarity in performance between 15- and 20-feature models suggests near convergence with this number of features. The models developed were well balanced between false positives and false negatives as judged by similar values for the sensitivity and specificity metrics of individual classifiers, as well as the AUC values. Models performed similarly (for the same number of features) for time points between −150 and +20 fs, and then became substantially better (approaching an AUC of 1.00) for time points after +20 fs, which corresponds to times when the reactive and almost-reactive trajectories began to separate based on the order parameter λ (Figure 1D).

To assess the effect of LASSO-optimized feature selection for use in machine learning models, a control was carried out in which a classifier was trained similarly but using feature sets randomly chosen from the original 68 features. That is, each control classifier was optimally trained for the best performance possible with the random (and not optimized) features it was assigned. Analogous performance statistics for these control classifiers are shown in Figure 2C. The results showed improved performance with additional features randomly selected from a chemically plausible set, together with large error bars, which is consistent with the notion that at any given time point some features or combinations of features were much better able than others to create predictive models, and the performance of models depended greatly on the features making up that model. Models with any given number of features performed much better on average when those features were selected by LASSO based on predictive ability than when selected randomly, demonstrating the value of the LASSO-selected features in distinguishing reactive from almost-reactive trajectories; for example, many of the one-feature models with LASSO-selected features had AUCs of about 0.70, whereas the random models had average AUCs of 0.57. The random models showed improved average performance after t = +20 fs, consistent with the notion that many features report on the fact that the reaction had largely begun by that time.

Analysis of Consensus Feature Set Predictive Throughout Prelaunch Time Window

The union of the complete 20-feature sets predictive at all 31 time points between −150 and 0 fs is depicted in Figure 2E. Features are listed in decreasing order of frequency of appearance, and the colored bars indicate the time points for which each feature appears as one of the 20 LASSO-selected features. (The time range −150 to 0 fs will be called the “prelaunch time window” for shorthand, as the 0 fs time point represents the last compression before the ultimate expansion of the putative breaking bond.) The results show that 17 of the features were used throughout at least half the window, 31 features were used at 10 or more time points, nearly all of the original features were used at least once (54 from the collection of 68), and 8 were used at five or fewer time points. The results suggest a commonality among the geometric descriptors that were broadly predictive across the prelaunch window. The names and feature types of the top 30 consistently predictive, consensus features are presented in Table S3 along with the number of occurrences in the top 20 LASSO-selected sets within the prelaunch window. Figure 2D shows the classification performance of models trained using the top 1, 5, 10, 15, 20, 25, and 30 consensus features across the 31 time points between −150 and 0 fs. With the 30 consensus features, classification performance was nearly equivalent to or better throughout the prelaunch window (approximately 0.90 AUC) than the performance obtained from 20 LASSO-selected features optimized for each of the individual time points. That is, 30 shared features performed as well as 20 custom features across the range, which is strong evidence that the fundamental determinants of reactivity are relatively consistent across the prelaunch window. Because the classifiers were each trained separately at each time point to produce models with different learned coefficients, these fundamental determinants of reactivity can (and do) play different roles at different times.

A structural representation of the set of 30 predictive consensus features is shown in Figure S5A (17 distances) and Figure S5B (12 planar angles and 1 dihedral angle). Half of the features (15) represent interactions between the substrate and its environment (nearby water molecules, the two magnesium ions, and the side chain of Glu 319), 7 represent intrasubstrate conformational metrics, 7 represent water–metal interactions, 1 represents an intra-cofactor orientation, and 2 represent other intraenvironment interactions. A full third of the features (10) represent distances or angles describing the relationship of a single atom, the substrate hydroxyl oxygen (O6), to its environment—the coordinating magnesium ions and water molecules interacting with the metal ions. The largest number of intermolecular features involving any other substrate atom is 2, for both a substrate carboxylate oxygen (O3) and the substrate carbonyl oxygen (O8), whose carbon receives the migrating methyl group. Only one intermolecular interaction involves the migrating methyl itself. We note two additional characteristics of the feature set: (1) the substrate intramolecular features involve the geometry local to the C4–C7 covalent bond, which is parallel to the path of the migrating methyl group, and (2) 8 of the 10 intermolecular angle features describe the orientation of groups coordinating the metal ions—either their ligated water molecules or oxygen atoms of the substrate. We acknowledge that the composition of the initial 68 features had some effect on the composition of the selected features; nevertheless, the resulting consensus feature set suggests important roles for substrate conformation, substrate bond polarization, and metal coordination in the reaction mechanism.

Average reactive and almost-reactive time traces for the consensus feature set are presented in Figure 3A. The closely overlapping distributions of most features in Figure 3A suggest the need for multiple features in combination to make usefully accurate predictions. 2D and 3D histograms of reactive and almost-reactive trajectories for feature pairs and triplets (data not shown) show somewhat greater separation than that seen in Figure 3A, but still considerable overlap between reactive and almost-reactive distributions at individual time points, consistent with the relatively poor classification performance of models with fewer than 10 features.

Figure 3.

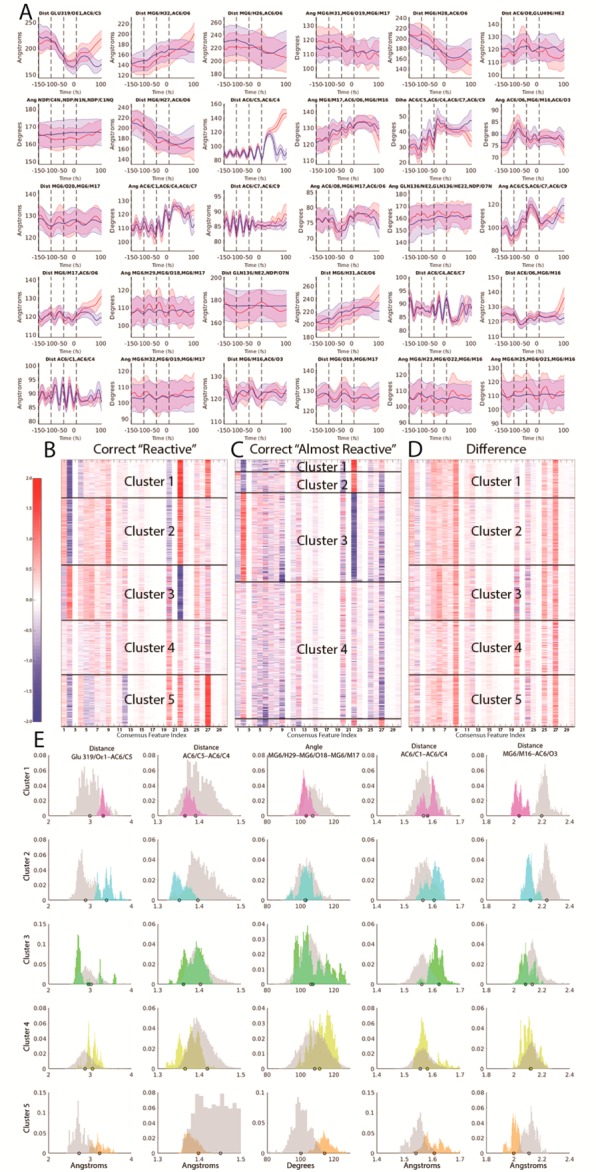
(A) Average time traces of consensus features across −150 to +100 fs time points with red indicating average reactive traces and blue indicating average almost-reactive traces. Error bars indicate 2 standard errors of the mean at each time point. Vertical black lines indicate time points at −150, −100, −50, and 0 fs where coefficients listed in Table S2 were fit. (B) Z-scores for consensus features (listed in Table S3 and illustrated structurally in Figure S5) evaluated at the 0 fs time point and weighted by their corresponding standardized logistic regression coefficient for all correctly classified reactive trajectories in data set. Dark lines indicate cluster boundaries assigned using k-means clustering with k = 5. Within each cluster, features are sorted by distance from the centroid of the respective cluster (closest to centroid at top). (C) Z-scores for the consensus features evaluated at the 0 fs time point and multiplied by their corresponding standardized logistic regression coefficient for all correctly classified almost-reactive trajectories in data set. Dark lines indicate cluster assignments, based on the closest centroid to the five centroids learned on the reactive features shown in (B). (D) Z-scores differences between reactive features in each cluster and the mean almost-reactive feature set of the corresponding almost-reactive cluster. (E) Histograms of weighted feature weight differences across each of the five reactive/almost-reactive cluster sets. The set of five features shown was determined by computing the top three weighted feature differences by absolute value for each cluster shown in Figure 3D, then taking the union of the resulting set. Magenta corresponds to cluster 1, cyan corresponds to cluster 2, green corresponds to cluster 3, yellow corresponds to cluster 4, orange corresponds to cluster 5, and gray corresponds to the corresponding almost-reactive cluster for the reactive cluster shown in each histogram. Dots indicate representative structures (the reactive or almost-reactive structures closest to the mean of the centroid for each respective cluster) which are shown in Figure S6.

Variations Distinguish Multiple Reactive Channels

We examined the question of whether the reaction proceeded along multiple channels. Clustering was used to organize the correctly predicted reactive and almost-reactive trajectories into related sets, and the magnitude of the differences between the sets was examined, allowing a more fine-grained analysis of the determinants of reactivity as identified by the machine learning. Specifically, all correctly predicted reactive trajectories were clustered based on the 0 fs time point using the 30 consensus features, each weighted by its β_j value (we refer to this as the feature weight, which is listed in Table S4 for the −150, −100, −50, and 0 fs time points (see Methods); results for five clusters are shown in Figure 3B). The results show at least five different modes of reacting, with each cluster distinguished by which features contribute most and least to the classifier outcome. In Figure 3B, the 30 columns represent the contribution from each of the 30 consensus features and the rows each represent one trajectory. Figure 3B shows that, at the 0 fs time point, roughly half of the 30 features contribute very little to the decision, as indicated by white bands in each cluster. Further confirmation is seen by the observation that features that appear as white bands usually do not occur in the top 20 LASSO selected set at this time point (see Figure 2E; distance AC6/O6–MG6/M16 and distance MG6/O19–MG6/M17 are exceptions and rank 15 and 18, respectively, in the top 20 LASSO selected set).

Grouping the weighted features into reactive clusters and corresponding almost-reactive clusters allows the subtle differences that define reactivity for each of these subgroups to be more closely examined. To this end, the mean feature contribution for each almost-reactive cluster in Figure 3C was subtracted from each of the weighted features from the corresponding cluster of reactive trajectories from Figure 3B to obtain a mapping of how each feature in each reactive trajectory differs from its mean in the corresponding almost-reactive cluster (Figure 3D); the results show several common features that distinguish correctly predicted reactive clusters from correctly predicted almost-reactive clusters. For example, across all five clusters shown in Figure 3D, the darkest red bands appear for distances AC6/C5–AC6/C4 and MG6/M16–AC6/O3 (features 10 and 27, respectively), indicating that these features are critical in driving the reactive/almost-reactive decision. However, there are other cluster-specific differences; for example, the distance AC6/O8–Glu 496/Hε2 (feature 6) is responsible for distinguishing reactive from nearly reactive more for cluster 3 than for any of the others, on average.

Distributions of feature values with the strongest contributions to differences in reactivity among the clusters (i.e., the darkest bands in Figure 3D) are shown, per cluster, in Figure 3E. Although there is often considerable overlap in the individual feature distributions between each reactive and almost-reactive cluster, the set of five features alone, when retrained on each cluster alone, achieved AUCs of 1.00, 1.00, 0.94, 0.91, and 1.00, in classifying trajectories from clusters 1 though 5, respectively, as reactive or almost-reactive. These very high scores suggest that the more general classifiers presented earlier somehow carry out the dual tasks of determining which reaction channel the trajectory is headed toward, as well as whether the trajectory will successfully react through that channel. The high AUCs for the second task above suggest that determining which channel is being approached may be the harder portion of the two, although this effect is convolved with the fact that these clusters are composed of trajectories that were correctly classified previously. When all (including incorrectly classified) data points are used, the intracluster AUCs using the same set of features are 0.92, 0.93, 0.80, 0.88, and 1.00 respectively, supporting the interpretation that predicting reactivity within a cluster is easier than in the absence of knowledge of the cluster for most of the clusters.

Figure 3E shows that across all five clusters, some general trends exist for the five features and their relative distribution between reactive and almost-reactive trajectories. The strongest observation is that, in almost every instance, each significant feature has a much narrower distribution in the reactive than the almost-reactive set of trajectories. This is consistent with the notion that there are many ways of not reacting, but fewer modalities for successfully traversing the reaction barrier. Across most of the five clusters, in general, reactivity is associated with a shorter AC6/C5–AC6/C4 bond length (column 2; feature 9; clusters 1, 2, 4, and 5), a longer AC6/C1–AC6/C4 bond length (column 4; feature 25; clusters 2, 3, and 5), a longer Glu 319/Oε1–AC6/C5 distance (column 1; feature 1; clusters 1, 2, 4, and 5), and a shorter MG6/M16–AC6/O3 distance (column 5; feature 27; clusters 1, 2, and 5). The value of the MG6/H29–MG6/O18–MG6/M17 angle (column 3; feature 20) is associated with reactivity for small values in cluster 1 but large values in cluster 5. Nevertheless, the absolute values associated with reactivity for some of the features varies greatly between clusters (column 3 for clusters 1 and 5, and column 5 for clusters 1 and 2, for example). Taken together, these results reinforce the notion that a common set of fundamental reaction-promoting mechanisms are deployed in somewhat different combinations in the different clusters.

An illustration and further discussion of representative structures corresponding to the feature histograms in Figure 3E can be found in Figure S6. In summary, a comparison of these histograms and representative structures shows that features distinguishing reactive from almost-reactive trajectories include internal conformational degrees of freedom of the substrate, which may provide distortion toward the transition state and ground-state destabilization; subtle changes to polar interactions of the two magnesium ions with the substrate and with their ligating water molecules and side chains, which could have important effects in polarizing the substrate toward reactivity; and interactions of the side chain of Glu 319 with the migrating methyl group, which could be important for steric, kinetic, and electronic reasons. It is anticipated that more detailed molecular orbital analyses will contribute to an understanding of how these structural differences are responsible for changes in relative reactivity.

Predictive Features Direct Reactivity

Machine learning was used to develop predictive models capable of distinguishing reactive from nearly reactive trajectories. Predictions of reactivity were successful, even when applied to trajectories not used in training the models, further supporting the notion that model features represent characteristics of reactivity. We reasoned that these characteristics could be useful not only to predict reactivity but also to direct it. That is, if the features identify characteristics that are largely sufficient for reactivity, rather than just indicative of it, then trajectories constrained to possess reactive characteristics should show markedly increased reactivity. We tested that notion, described below, and our findings confirm the directive power of the machine learning features and their associated models.

The LASSO-selected, ten-feature model at the 0 fs time point was used, with a testing performance AUC of 89.03% and an accuracy of 81.57%. Model features and the corresponding logistic-regression coefficients are listed in Table S2. Eight of the ten features occur in the 30-feature consensus set, with the exceptions being distance AC6/C4–AC6/O6 and distance AC6/O8–MG6/M17. Of the five features shown in Figure 3E, four appear in the ten-feature model, with the exception being angle MG6/H29–MG6/O18–MG6/M17 (feature 3). Thus, the ten-feature model achieves very good predictive performance and is composed of many of the consensus features found to be important at other time points.

The logistic regression models used here effectively create a dividing surface in the reactant well (the hyperplane defined by the β_j coefficients; see Methods) and make successful predictions of reactivity based on whether the trajectory is in the “reactive portion” of the well at the appropriate time. We modified the statistical mechanical TIS sampling procedure used here to compute reaction rates, so that we could require all trajectories to be on the reactive side of the hyperplane encoded in the ten-feature model (Table S2) during a rate calculation (see Methods). Calculations of the reaction rate were performed with (“test”) and without (“control”) this constraint applied only at the 0 fs time point from five different starting seeds (three were used previously to train the model, and two were new). The expectation was that the test simulations would show greater reactivity (larger computed k_cat) than the controls, as the test simulations satisfied the reactivity conditions in every trajectory (by constraint), whereas on average only 8.03% of control trajectories satisfied them through ordinary sampling.

The observed relative differences in rate constants in all five sets of simulations were consistent with this expectation and quite large, on the order of 10¹⁶ to 10¹⁹, depending on the initial seed trajectory (Table 1). The computed rate is a product of a factor representing the rate of reactant starting toward the barrier and a probability factor representing the cumulative likelihood of progress toward and over the barrier. Here the rate enhancement was driven by both factors, but with a significantly larger effect from the probability factor and with contributions across much of the approach to the barrier, which suggests that greater reactivity was due to increased productivity at multiple stages of the reaction, including those after leaving the reactant well.

Table 1. Computed Rate Constants, Probability Factors, and Flux Factors for Each Seed Studied.

Seed	Experiment	Mean P	Mean Flux (1/fs)	Mean Rate Constant (1/s)	Test/Control Fold Increase
1	Control	6.7 × 10–23	1.0 × 10–03	6.7 × 10–11	8.7 × 10+19
1	Test	1.4 × 10–08	4.2 × 1002	5.8 × 10+09
2	Control	1.2  × 10–22	9.0 × 10–04	1.1 × 10–10	1.3 × 10+17
2	Test	1.1 × 10–10	1.2 × 1002	1.4 × 10+07
3	Control	2.7 × 10–22	1.0 × 10–03	2.7 × 10–10	1.2 × 10+18
3	Test	3.5 × 10–09	9.6 × 10+01	3.4 × 10+08
4	Control	1.6 × 10–22	7.0 × 10–04	1.1 × 10–10	7.8 × 10+17
4	Test	1.0 × 10–09	8.7 × 10+01	8.7 × 10+07
5	Control	3.2 × 10–21	1.3 × 10–03	4.2 × 10–09	2.0 × 10+16
5	Test	3.0 × 10–10	2.7 × 10+02	8.2 × 10+07

Contributions to the probability factor were further examined. Figure S7A shows the cumulative logarithm of the probability factor as a function of reaction progress for test (red) and control (blue) simulations (essentially the probability that a trajectory that started toward the barrier will reach this value of λ). Figure S7B shows the individual multiplicative contribution to the probability factor at each progress window (essentially the probability that a trajectory that made it through the previous window will continue through this window). The test simulations show much smaller decreases in reaction probability (Figure S7A) and much larger contributions to reactivity (Figure S7B) than the control simulations earlier in the reaction (below λ = −0.4) but show similar behavior beyond that point (between λ = −0.4 and 0.0). These data indicate a strong reactivity advantage of the constrained simulations (which was applied at the 0 fs time point, corresponding to a λ value of approximately −0.9 and well before the barrier) across the whole region from λ = −0.9 to −0.4 but not past this point, noting that by λ = −0.2 the reaction has essentially already occurred. This is consistent with a picture in which the constraint achieved its large gains in reactivity not by giving those simulations a local, near-term boost in reaction progress, but by directing them into channels that retained a continuous reactivity advantage.

Discussion

In this work, we find that features evident in the enzyme–substrate complex before it departs the reactant well are highly predictive of reactivity through the identification of relatively subtle conformational effects. These structural characteristics include internal substrate conformation, interactions of substrate with its environment, and details of the electronic environment of the two magnesium ions that coordinate the substrate. A consensus set of 30 features are predictive across the prelaunch window, although the detailed roles of some descriptors change across the window.

Interestingly, velocities are not needed to reliably distinguish reactive from nonreactive trajectories. This does not mean that velocities cannot also be useful or important, but only that conformations alone are sufficient. In fact, velocities alone, without direct conformational measures, were also sufficient to distinguish reactive from almost-reactive trajectories. The top 20 velocity descriptors at the 0 fs time point are listed in Table S5, together with their individual predictive performance. Five of these velocities are for atoms involved in the consensus geometry feature set, and thus may be indicating the same or similar drivers of reactivity. Furthermore, Figure S8 compares the AUCs of the top 5, 10, 15, and 20 LASSO-selected features from (a) the set consisting of the 68 structural descriptors only, (b) the velocity magnitudes of the 341 atoms within 5 Å of the migrating methyl, and (c) the combined structural-velocity set of (a) and (b), showing that the combined set performs better than the structural or velocity set alone, but only by a very small margin. Together, Table S5 and Figure S8 suggest a largely effective overlap of information between geometric and velocity descriptors, in that different descriptors can be equally useful in understanding and predicting reactivity, perhaps through the same or similar explanations, with a small component of complementarity. The involvement of some of the same atoms, although possibly the result of there being a small reactive center, suggests that different classes of descriptors may be indicating the same fundamental chemical effects. Although the analysis in the current work appears static, relying on conformations evident at fixed points in time, this may implicitly contain dynamic information. For example, the 0 fs time point corresponds to the maximum compression of the breaking bond before the trajectory launches toward the activation barrier, and so a shorter bond distance, indicating greater potential energy stored in the bond, may signify greater kinetic energy available to surmount the barrier (and, indeed, the velocity of one atom in this bond, C4, was the second most predictive velocity feature). While this study has focused on geometry- and velocity-based features, they can also be interpreted in terms of local energetics. In many instances shorter distances seem to represent stronger local electrostatic interactions and higher velocities represent greater local kinetic energy contributions. Nevertheless, we have not found evidence of overall energetic differences between reactive and almost-reactive trajectories that we could discern.

We suggest that a more thorough description may be necessary to truly understand reactivity than to predict it. Whenever any fitting procedure is performed (as in this study), there is a danger of overfitting, but a number of lines of evidence suggest that overfitting is not responsible for the conclusions here. These include the vast overabundance of data points (order of a half million) relative to number of parameters included in the fitting procedure (order of up to a few dozen); the use of cross-validation, in which reported results are for testing data that is explicitly excluded from the fitting procedure (which used only training data); and the observation that the highly predictive features are also controlling (i.e., enforcing them enhances reactivity, even for ensembles seeded from trajectories not included in the training/testing data set). The use of multiple seeds provides opportunities to test for bias in the sampling simulations. In one such test, the Euclidean distance matrix of the 68-feature set for a random sampling of 20,000 trajectories was computed. Multidimensional scaling analysis of the samples showed significant overlap between both the reactive and nonreactive ensembles from each of the three seeds (data not shown). We also find a relatively narrow spread of results from simulations using multiple seeds (e.g., Table 1). Taken together, these results suggest adequate sampling of trajectory space.

This study presents evidence that there are multiple channels of reactivity, some of which are more productive than others. The existence of multiple reactive channels suggests that there are identifiably different reaction subpathways. Results further suggest that within each channel there could be more ways of not reacting than reacting, consistent with the notion that there are many conditions that must be met in order to produce a reactive trajectory, and failing to achieve any of multiple combinations of those features can be detrimental to reactivity. This study also highlights the important role that early active site conformational effects play in driving chemical catalysis, an idea that underlies existing theories of the importance of early conformational effects such as electrostatic preorganization^42,43 and enzyme-stabilized “near-attack conformations” in certain catalytic systems.^13,17 The fact that machine learning methods were able to identify early conformations predictive of reactivity lends additional support to the preorganization and near-attack conformation hypotheses of enzymatic activity, although further research is necessary to determine whether electrostatic preorganization or stabilization of near-attack conformations is a primary driver of catalysis in the KARI isomerization reaction studied.

Although this study was purely computational, the results are supported by data available from the literature. A number of KARI mutants have been made and characterized experimentally.⁴⁴ In the closest correspondence with the present work, mutations have been made in the E. coli KARI variant (which exhibits 100% conservation of the eight polar active site residues with the S. oleracea variant studied here), finding that mutations in positions corresponding to Asp 315, Glu 319, and Glu 496 all reduce specific activity against 2-acetolactate by more than 200-fold.⁴⁴ The relationship between these experimental results and our computational features is striking—two of the three instances of a debilitating mutation correspond to a residue involved in a feature in the top 30 consensus feature set. For example, Glu 319 is involved in the top ranked feature, the Glu 319/Oε1–AC6/C5 distance, and Glu 496 is involved in the sixth ranked feature, the Glu 496/Hε2–AC6/O8 distance. Asp 315 was not included in the features included for training and so could not appear in our consensus set.

In this work we also showed that that path-sampling techniques combined with QM/MM simulations can be used to generate valuable data sets that allow the question of reactivity to be phrased as a binary classification problem well suited for machine learning. We believe this represents not only an exciting and promising application but also a productive strategy for elucidating subtle yet meaningful drivers of catalysis in enzymatic systems. While this work utilized features selected through human intuition and a linear classification model (LASSO), the application of unsupervised learning techniques to identify perhaps better features combined with nonlinear classification models represents an opportunity to understand further the early events that lead to enzymatic catalysis. Although this work utilized TIS to generate only two types of data sets, reactive and almost-reactive, TIS can also be used to generate many more types of data (for example, to generate sets of trajectories that reach progressively higher points along the barrier). Applying machine learning to trajectory outcomes representing more than two states of reactivity can potentially yield new insights as to precisely when and how reactive and nonreactive trajectories diverge. Although this study identified features indicative of reactivity, an understanding of how those structural and potentially electronic effects cooperate to facilitate the reaction is not obvious from structures alone. It is possible that more detailed quantum chemical analysis, perhaps with a focus on orbital behaviors, will lend more insight.

A difference between this work and prior studies of near-attack conformations is that we have defined reactivity at time points relative to the temporal progress of the prospective catalytic event rather than purely configurational states.^13,14,17 Although the sampling constraints during the TIS simulations were enforced at specific time points relative to the progress of the prospective catalytic event, e.g. the “last trough” that we have defined as the 0 fs time point in the reaction, future work is needed to test how critical the time point is on the effectiveness of the constraint in leading to more reactive trajectories. Initial results (unpublished) for sets of constrained TIS simulations, in which a classifier was trained that was predictive of reactivity across the entire prelaunch window, suggests that reactive trajectories spend significantly more time in the reactive region of the reactant well than almost-reactive trajectories. This result implies that constraints broadly applied across a portion of the prelaunch window may be just as effective, if not more effective at enhancing reactivity than constraints applied at one specific time point.

The features identified are more than indicators that the reaction will likely occur; they are control levers that can guide and enhance reactivity. Our studies demonstrate that enforcing these indicators of reactivity leads to dramatic computed rate enhancements, largely by increasing the probability of trajectories reaching the product state. This enormous enhancement directly suggests an approach to re-engineering enzymes for enhanced specific activity. The results of this study suggest that the identification of mutants whose predominant effect is to selectively populate regimes identified as promoting reactivity for a set of geometric features could be a useful method for enhancing activity, by causing the enzyme–substrate complex to spend more time in highly reactive conformations. Such mutations could be especially useful if they have minimal effects elsewhere on the reactive energy surface. For example, Table S4 indicates (through positive regression coefficients at all four prereaction time points computed) that a somewhat larger angle between the atoms Gln136/Nε2, Gln136/Hε22 and the cofactor NDP/O7N (the 17th feature listed in Tables S3 and S4) consistently leads to enhanced reactivity, and so identifying mutations that favorably alter this side chain/cofactor polar contact orientation could be useful. Likewise, Table S4 indicates that increasing the angle between magnesium M16 and one of its coordinating water molecules (the fourth feature listed in Tables S3 and S4) leads to enhanced reactivity. This water also coordinates the side chains of Glu 319 and Glu 496, and thus, identifying mutations that alter the packing of these side chains to affect the water orientation might also be useful. Although many of the reactivity-predicting features involve substrate conformation and metal chelating water geometry, we note that design changes to protein side chains making contact with substrate and water molecules can alter these geometries, making them accessible to alteration through protein design. Indeed, in other ways, several recent studies have attempted to leverage insights from path-sampling simulations in order to design enzyme variants,^46,47 which represents a promising and novel framework for biocatalyst design. This study advances the field by defining a specific approach for identifying the goals such mutations should achieve.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.8b13879.

• Illustration of constrained and unconstrained TIS computations (Figure S1). List of features computed at each time point (Table S1). Structural representation of features computed at each time point (Figure S2). Illustration of KARI homodimer subunits (Figure S3). Top 10 LASSO selected features at 0 fs time point used to constrain TIS computations (Table S2). Placement of interfaces used in TIS probability factor calculations superimposed onto the PMF surface used to generate initial seed trajectories (Figure S4). Listing of 30 feature consensus set (Table S3). Structural representation of 30 consensus feature set (Figure S5). Standardized regression coefficients for 30 consensus feature set at various time points (Table S4). Representative structures for the reactive cluster and corresponding almost-reactive clusters described in Figure 3B–E (Figure S6). Analysis of probability factor calculations (Figure S7). Top 20 atomic velocity magnitudes at the 0 fs time point ranked by individual AUC (Table S5). Comparison of AUC versus reaction progress for top LASSO-selected features from structural-only, velocity-only, or combined set (Figure S8) (PDF)

The authors declare no competing financial interest.