Genome-wide Significance Thresholds for Admixture Mapping Studies

Abstract

Admixture mapping studies have become more common in recent years, due in part to technological advances and growing international efforts to increase the diversity of genetic studies. However, many open questions remain about appropriate implementation of admixture mapping studies, including how best to control for multiple testing, particularly in the presence of population structure. In this study, we develop a theoretical framework to characterize the correlation of local ancestry and admixture mapping test statistics in admixed populations with contributions from any number of ancestral populations and arbitrary population structure. Based on this framework, we develop an analytical approach for obtaining genome-wide significance thresholds for admixture mapping studies. We validate our approach via analysis of simulated traits with real genotype data for 8,064 unrelated African American and 3,425 Hispanic/Latina women from the Women’s Health Initiative SNP Health Association Resource (WHI SHARe). In an application to these WHI SHARe data, our approach yields genome-wide significant p value thresholds of 2.1 × 10⁻⁵ and 4.5 × 10⁻⁶ for admixture mapping studies in the African American and Hispanic/Latina cohorts, respectively. Compared to other commonly used multiple testing correction procedures, our method is fast, easy to implement (using our publicly available R package), and controls the family-wise error rate even in structured populations. Importantly, we note that the appropriate admixture mapping significance threshold depends on the number of ancestral populations, generations since admixture, and population structure of the sample; as a result, significance thresholds are not, in general, transferable across studies.

Introduction

Understanding the genetic causes of human diseases and traits has long been of interest in the scientific community. However, the large majority of the research in this area has been conducted in populations of European descent.^{1, 2, 3} Admixed populations, such as African Americans and Hispanics/Latinos, are historically underrepresented in genetic studies, yet their mixed and diverse ancestry presents unique opportunities for detecting genetic variants associated with complex traits and diseases.

Due to the processes involved in the inheritance of genetic material, the genomes of admixed individuals are a mosaic of segments with different ancestral origins (Figure 1). This mosaic pattern of locus-specific ancestry, or local ancestry, varies considerably across individuals within an admixed population and proves useful for identifying causal genetic variants via admixture mapping. Admixture mapping studies scan the genomes of admixed individuals for associations between local ancestry and a trait of interest.^{4, 5, 6} Disease prevalence and trait values often differ across ancestral groups (e.g., asthma,⁷ prostate cancer,⁸ blood pressure⁹), due to a combination of genetic and environmental causes. By looking for associations between a trait and local ancestry, admixture mapping seeks to identify the genetic variants that differ in frequency across these ancestral groups and drive the observed phenotypic differences. In recent years, admixture mapping has become more widely used and has proven to be a powerful approach for localizing causal genetic variants.^{8, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30}

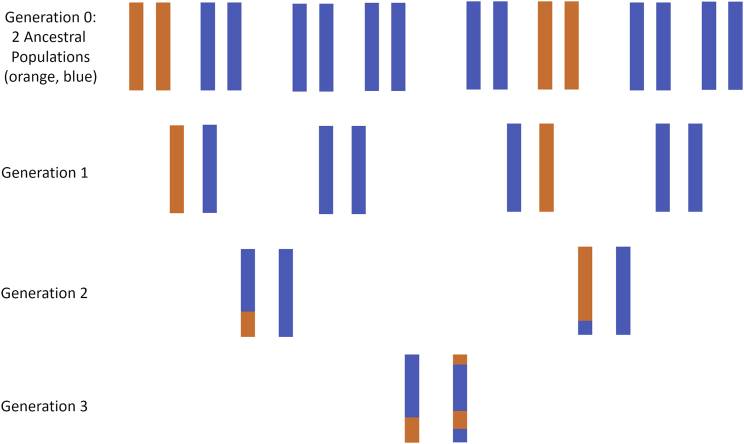
Figure 1.

Inheritance of Genetic Material in an Admixed Population with Two Ancestral Populations

Colors indicate the ancestral origin of genetic material across a single chromosome, with two ancestral populations (orange, blue). In each generation, genetic material is passed from parents to offspring, with crossover events leading to chromosomes with a mixture of genetic material from the parent’s maternal and paternal chromosomes. Over time, blocks of ancestry are broken up by additional crossover events, resulting in a mosaic of segments of different ancestral origins. We refer to the locus-specific ancestral origin of genetic material as local ancestry, while admixture proportion or global ancestry refers to the overall (genome-wide) proportion of genetic material inherited from each ancestral population.

A single genome-wide admixture mapping study will typically involve hundreds of thousands or millions of hypothesis tests, and multiple testing correction procedures are needed to control the overall type I error rate. Perhaps the best-known multiple testing correction procedure involves a Bonferroni correction on the total number of hypothesis tests. Although easy to implement, this approach is widely criticized for yielding conservative significance thresholds in the presence of correlated tests. A related approach involves a Bonferroni correction on the estimated effective number of independent tests;^{13, 19, 31, 32} however, a number of authors^{33, 34, 35} have suggested that this approach does not always guarantee family-wise error rate control in genome-wide association studies. Permutation-based^{22, 24, 36, 37} and simulation-based^{20, 38, 39} multiple testing correction procedures are often considered to be the gold standard for genetic association studies but can be very computationally intensive. Alternatives to these procedures, based on the multivariate normal distribution, have been suggested to speed up computation time.^{35, 40, 41}

A promising alternative to the above-mentioned approaches involves an analytic multiple testing correction.^{36, 42, 43} In particular, Siegmund and Yakir⁴³ derived the correlation of admixture mapping test statistics and used that theoretical result to provide an analytic approximation to the appropriate significance threshold for admixture mapping studies in admixed populations with two ancestral populations and equal admixture proportions across individuals. However, many admixed populations have more than two ancestral populations (e.g., Hispanics/Latinos) and/or unequal admixture proportions across individuals in the population,^{44, 45, 46, 47, 48} the latter being a consequence of population structure.⁴⁹

In this paper, we develop a theoretical framework which applies to admixed populations with any number of ancestral populations or distribution of admixture proportions, and then use that theoretical framework to develop multiple testing correction procedures for admixture mapping studies in admixed populations with population structure. We apply our proposed procedures to genotype data for samples of African American and Hispanic/Latina ancestry from the Women’s Health Initiative SNP Health Association Resource (WHI SHARe). We also perform a simulation study using these WHI SHARe genotype data and simulated traits to validate our theoretical work and evaluate the performance of our approach relative to other commonly used multiple testing correction procedures.

Material and Methods

Admixture Mapping Model

Following previous studies,^{6, 39, 50} we use marginal regression to perform admixture mapping in samples with unrelated individuals, regressing the trait of interest on inferred local ancestry at each observed locus across the genome. At each locus, we quantify local ancestry as the number of alleles (0, 1, or 2) inherited from each ancestral population at that locus. In an admixed population with K ancestral populations, we characterize the local ancestry for admixed individual i at locus j via the vector ${\mathit{a}}_{ij}={\left(\begin{array}{ccc}{a}_{ij1}& \dots & a_{ijK}\end{array}\right)}^T$, where ${\sum }_{k=1}^K{a}_{ijk}=2$ and the k^th component of this vector, a_ijk, denotes the number of alleles inherited by individual i from ancestral population k at locus j. Similarly, we represent the admixture proportions for each individual via the vector ${\mathit{\pi }}_i={\left(\begin{array}{ccc}{\pi }_{i1}& \dots & {\pi }_{iK}\end{array}\right)}^T$, where ${\sum }_{k=1}^K{\pi }_{ik}=1$ and the components of this vector represent the overall (genome-wide) proportion of genetic material inherited by individual i from each ancestral population. To perform admixture mapping, we regress the trait of interest, $\mathit{y}$, on each component of the local ancestry vector $\left(k=1,\dots ,K\right)$ at each locus $\left(j=1,\dots ,m\right)$ using the marginal regression model

$$E\left[y_i|a_{ijk},{\mathit{\pi }}_i\right]=\alpha +{\beta }_{jk}{a}_{ijk}+\mathit{\gamma }{\mathit{\pi }}_{i,-K},$$ (Equation 1)

where ${\mathit{\pi }}_{i,-K}={\left(\begin{array}{ccc}{\pi }_{i,1}& \dots & {\pi }_{i,K-1}\end{array}\right)}^T$ includes the first $K-1$ components of the vector of admixture proportions. We fit separate regression models for each ancestral group in order to investigate which ancestral population(s) drive the association between the trait and local ancestry at each locus, and we adjust for estimated admixture proportions in all models to account for potential population structure.^{5, 50} We test for association between the trait and local ancestry using a Wald test, where the test statistic is the ratio of the estimated regression coefficient for the local ancestry term and its standard error $\left(Z_{jk}={\hat{\beta }}_{jk}/\widehat{se}\left({\hat{\beta }}_{jk}\right)\right)$, with one test statistic per locus and ancestral component.

Theoretical Framework: Joint Distribution of Admixture Mapping Test Statistics

Our goal is to derive a significance threshold that controls the family-wise error rate, or the probability of making at least one type I error, for a genome-wide admixture mapping study. In other words, we wish to find the genome-wide test statistic threshold $Z^{\ast }$ such that

$$\mathrm{Pr}\left(\underset{1\le j\le m,1\le k\le K}{\max }\left|Z_{jk}\right|>Z^{\ast }|{\beta }_{jk}=0\forall j,k\right)={\alpha }^{\ast },$$

for some pre-specified level ${\alpha }^{\ast }$ (e.g., 0.05). To derive this threshold, we must understand the asymptotic joint distribution of our admixture mapping test statistics $Z_{11},\dots ,Z_{mK}$.

The first step is to characterize the correlation of local ancestry vectors at pairs of loci across the genome. For an admixed population with any number of ancestral populations, generations since admixture, or distribution of admixture proportions across the population, we can show that the correlation of local ancestry vectors $\left({\mathit{a}}_j,{\mathit{a}}_{j^{\text{'}}}\right)$ at two loci $\left(j,j^{\text{'}}\right)$ depends on the recombination fraction between the loci $\left(\theta \right)$, the number of generations since admixture (g), and the population mean (E), variance (V), and covariance (Cov) of the admixture proportions:

$$Corr\left(a_{jk},a_{j^{\text{'}}{k}^{\text{'}}}\right)=\{\begin{array}{c}{\left(1-\theta \right)}^g+\left[1-{\left(1-\theta \right)}^g\right]\frac{2V\left({\pi }_k\right)}{E\left({\pi }_k\right)-E^2\left({\pi }_k\right)+V\left({\pi }_k\right)}ifk=k^{\text{'}}\\ \frac{2Cov\left({\pi }_k,{\pi }_{k^{\text{'}}}\right)-{\left(1-\theta \right)}^g\left[Cov\left({\pi }_k,{\pi }_{k^{\text{'}}}\right)+E\left({\pi }_k\right)E\left({\pi }_{k^{\text{'}}}\right)\right]}{\sqrt{\left[E\left({\pi }_k\right)-E^2\left({\pi }_k\right)+V\left({\pi }_k\right)\right]\left[E\left({\pi }_{k^{\text{'}}}\right)-E^2\left({\pi }_{k^{\text{'}}}\right)+V\left({\pi }_{k^{\text{'}}}\right)\right]}}ifk\ne k^{\text{'}}.\end{array}$$

We refer to this result as Lemma 1, and a proof is available in Appendix A. Note that if all individuals in the population have the same admixture proportions (i.e., ${\mathit{\pi }}_i=\mathit{\pi }\forall i$), then the local ancestry correlation is simply ${\left(1-\theta \right)}^g$ when $k=k^{\text{'}}$, as had been shown previously in the context of admixed populations with two ancestral populations.⁴³

Using Lemma 1, it is straightforward to derive the asymptotic joint distribution of our collection of admixture mapping test statistics $\mathit{Z}={\left(\begin{array}{ccc}{Z}_{11}& \dots & Z_{mK}\end{array}\right)}^T$. For an admixed population with any number of ancestral populations, generations since admixture, or distribution of admixture proportions across the population, we can show that the asymptotic joint distribution of the test statistics $\mathit{Z}$ can be approximated by a mean zero Gaussian process with covariance (and correlation) given by

$$Cov\left(Z_{jk},Z_{j^{\text{'}}{k}^{\text{'}}}\right)=\{\begin{array}{c}{\left(1-\theta \right)}^{g}ifk=k^{\text{'}}\\ -{\left(1-\theta \right)}^g\frac{E\left({\pi }_k\right)E\left({\pi }_{k^{\text{'}}}\right)}{\sqrt{E\left({\pi }_k\right)\left[1-E\left({\pi }_k\right)\right]E\left({\pi }_{k^{\text{'}}}\right)\left[1-E\left({\pi }_{k^{\text{'}}}\right)\right]}}ifk\ne k^{\text{'}},\end{array}$$

where the recombination fraction $\left(\theta \right)$, generations since admixture (g), and population mean admixture proportions $\left(E\left({\pi }_k\right)\right)$ are defined as above. We refer to this result as Theorem 1, and a proof is available in Appendix A. Note that the covariance of test statistics simplifies conveniently when the admixed population has only two ancestral populations $\left(K=2\right)$:

$$Cov\left(Z_{jk},Z_{j^{\text{'}}{k}^{\text{'}}}\right)=\{\begin{array}{c}{\left(1-\theta \right)}^g\approx e^{-0.01g\delta }ifk=k^{\text{'}}\\ -{\left(1-\theta \right)}^g\approx -e^{-0.01g\delta }ifk\ne k^{\text{'}},\end{array}$$

where $\delta$ is the genetic distance, in centimorgans (cM), between loci $j,j^{\text{'}}$; it follows that the distribution of admixture mapping test statistics can then be approximated by an Ornstein-Uhlenbeck process.

Multiple Testing Correction Procedures

We propose two multiple testing correction procedures which use the asymptotic joint distribution of admixture mapping test statistics provided by Theorem 1 to derive a genome-wide significance threshold that will control the family-wise error rate in admixture mapping studies. Both approaches are implemented in our R package STEAM (Significance Threshold Estimation for Admixture Mapping).

Simulation-Based Approach

To estimate the appropriate genome-wide test statistic threshold for an admixture mapping study, we simulate test statistics from their asymptotic joint distribution (Theorem 1) and choose the threshold that controls the empirical family-wise error rate at the desired level. This approach differs from traditional simulation-based multiple testing approaches in that we simulate test statistics directly, rather than simulating traits and re-calculating test statistics at each locus for each simulation replicate. By simulating test statistics directly, computation time for our multiple testing correction procedure is considerably reduced and, importantly, is independent of sample size. To simulate admixture mapping test statistics from this distribution, we have developed a fast algorithm that requires only the genetic distances between loci, the estimated admixture proportions for individuals in the sample, and an estimate of the parameter g (see Appendix B for details).

Analytic Approximation Approach

An alternative approach for deriving genome-wide significance thresholds in the special case of admixed populations with two ancestral populations $\left(K=2\right)$ was developed previously.⁴³ Siegmund and Yakir⁴³ showed that, under some assumptions, the asymptotic joint distribution of admixture mapping test statistics can be approximated by an Ornstein-Uhlenbeck process, and then used that result to provide an analytic approximation to the family-wise error rate:⁴³

$$\mathrm{Pr}\left(\underset{1\le j\le m,k}{\max }\left|Z_{jk}\right|>z\right)\approx 1-\exp \left\{-2C\left[1-\text{Φ}\left(z\right)\right]-2\beta Lz\varphi \left(z\right)\nu \left(z\sqrt{2\beta \text{Δ}}\right)\right\},$$ (Equation 2)

where C is the number of chromosomes analyzed, having total genetic length L cM; $\text{Δ}$ is the marker density; $\text{Φ}$ and $\varphi$ are the cumulative distribution and density functions, respectively, of the standard normal distribution; $\beta =0.01g$; and the function $\nu$ is an infinite sum which can be approximated by $\nu \left(y\right)\approx \left(2/y\right)\left[\text{Φ}\left(y/2\right)-0.5\right]/[\left(y/2\right)\text{Φ}\left(y/2\right)+\varphi \left(y/2\right)]$. Although this analytic approximation was initially proposed for admixture mapping studies in populations with equal admixture proportions across individuals,⁴³ our work (i.e., Theorem 1) shows that it is also applicable to populations with heterogeneous admixture proportions, provided that the admixture proportions are included as covariates in the regression analysis. As a result, we can use this analytic approximation to find the admixture mapping test statistic threshold that will control the family-wise error rate at the desired level $\left({\alpha }^{\ast }\right)$ in an admixed population with two ancestral populations and any distribution of admixture proportions: we simply find the value z that sets the right hand side of Equation 2 equal to ${\alpha }^{\ast }$. This involves an optimization step that can be quickly solved using existing tools (e.g., uniroot in R⁵¹). Simulation is not required for this approach, so the significance threshold can be derived in a matter of seconds.

Estimating the Number of Generations since Admixture

Both the analytic approximation and simulation-based multiple testing correction approaches rely on the number of generations since admixture. We can estimate the number of generations since admixture (g) using the observed pattern of local ancestry correlation in our sample, since g determines the rate of decay of this correlation (see Lemma 1). We propose an approach similar to that of Hellenthal et al.,⁵² where we use non-linear least-squares to find the value of g that provides the best fit to the observed local ancestry correlation curves. We implement this approach in our R package STEAM, along with our multiple testing correction procedures.

Analysis of WHI SHARe Data

We applied our multiple testing correction procedures to two cohorts of admixed individuals with African American and Hispanic/Latina ancestry from the Women’s Health Initiative SNP Health Association Resource (WHI SHARe), and also used these data to perform simulation studies comparing the performance of our proposed multiple testing correction procedures to competing approaches.

The Data

The WHI is a long-term health study of postmenopausal women in the United States. A total of 161,808 postmenopausal women aged 50–79 years old were recruited, including 12,151 self-identified African Americans (AA) and 5,469 self-identified Hispanic Americans (HA) who had consented to genetic research. Study design details and cohort characteristics are described elsewhere.⁵³ A subsample of these women were selected for genotyping, using the Affymetrix Genome-Wide Human SNP Array 6.0 that contains 906,000 single-nucleotide polymorphisms (SNPs) and more than 946,000 probes for the detection of copy-number variants. In these analyses, we focus only on the SNPs. The genotype data were processed for quality control, including call rate, concordance rates for blinded and unblinded duplicates, and sex discrepancy, leaving 871,309 unflagged SNPs with a genotyping rate of 99.8% and 12,008 (8,421 AA and 3,587 HA) women used in the current analysis.¹⁴

Local Ancestry Inference

To implement and evaluate our proposed multiple testing correction procedures in the WHI SHARe data, we first needed to infer local ancestry. First, we formed reference panels for local ancestry inference using individuals of European, African, and Native American descent from the International HapMap Project⁵⁴ (HapMap) and the Human Genome Diversity Project⁵⁵ (HGDP). In particular, the reference panels for both the AA and HA cohorts included 165 individuals of European descent (HapMap CEU, Utah residents with Northern and Western European ancestry) and 203 individuals of African descent (HapMap YRI, Yoruba in Nigeria), and the HA reference panel additionally included 63 individuals of Native American descent from HGDP. We identified a set of 551,025 and 536,374 SNPs common to the reference panels and the WHI AA and HA samples, respectively. Second, we used an iterative procedure suggested by Conomos et al.⁵⁶ to identify sets of 8,064 and 3,425 mutually unrelated AA and HA individuals, respectively. Third, we performed phasing and imputation of sporadic missing genotypes using Beagle⁵⁷ version 3. Genetic distances were estimated using the publicly available HapMap genetic map.⁵⁸ After these pre-processing steps, we performed local ancestry inference using RFMix⁵⁹ to estimate the number of alleles inherited from each ancestral population at each locus across the genome.

Application of Multiple Testing Correction Procedures

We implemented the analytic approximation approach in the AA cohort and our test statistic simulation-based approach (with 10,000 replications) in both the AA and HA cohorts. Both approaches require the number of generations since admixture, which we estimated from the observed pattern of local ancestry correlation in these samples using our non-linear least-squares approach described above. Our simulation-based approach additionally requires admixture proportions, which we estimated for each individual using the genome-wide average inferred local ancestry.

Simulation Study Using WHI SHARe Genotypes

To evaluate the performance of our proposed methods, we simulated 10,000 sets of traits for each individual according to the model $y_i{\sim }_{iid}N\left(\mathrm{0,1}\right)$. We used PLINK v.1.9⁶⁰ to perform admixture mapping in each cohort, adjusting for estimated admixture proportions. We calculated the observed correlation of these tests across simulation replicates to compare to our theoretical result (Theorem 1) and evaluated the empirical family-wise error rate of our methods across the 10,000 simulation replicates. Finally, we compared our approaches to two competing methods: a Bonferroni correction on the total number of hypothesis tests and the trait simulation approach (with 10,000 replicates).

Results

Population Structure and Validation of Theoretical Results in WHI SHARe

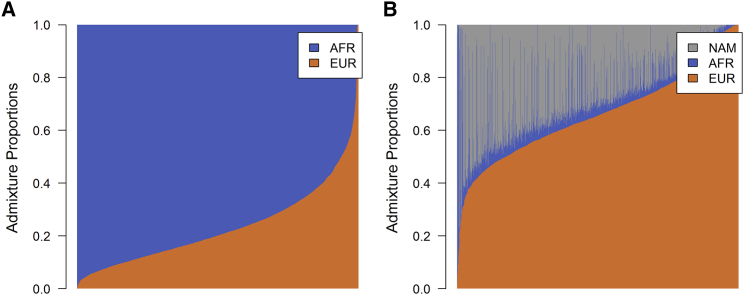
The WHI SHARe African American (AA) and Hispanic American (HA) cohorts exhibit considerable heterogeneity in estimated admixture proportions (Figure 2), indicating that the theoretical work of previous authors⁴³ would not be applicable to these samples, even in the case of the AA cohort with just two ancestral populations. However, we do observe that the patterns of local ancestry and test statistic correlation in the WHI SHARe samples are consistent with our new theoretical results (Figure 3). Furthermore, a non-linear least-squares regression on the observed local ancestry curves yields estimates of the generations since admixture for each cohort $\left({\hat{g}}_{AA}=5.9,{\hat{g}}_{HA}=9.6\right)$ that are consistent with previously published studies.^{49, 61, 62, 63, 64}

Figure 2.

Estimated Admixture Proportions in WHI SHARe

(A) Estimated proportions of genetic material inherited from European (EUR) and African (AFR) ancestral populations for the African American samples.

(B) Proportions of European (EUR), African (AFR), and Native American (NAM) ancestry for the Hispanic/Latina samples.

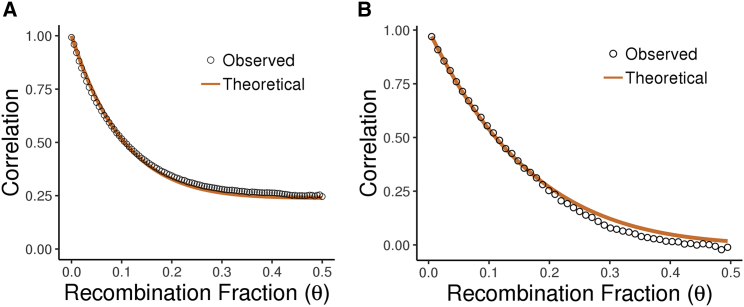
Figure 3.

Correlation of Local Ancestry and Test Statistics in WHI SHARe

(A) Comparison of the observed and expected (theoretical) correlation of the European component of local ancestry vectors in the Hispanic/Latina cohort, averaging across pairs of markers falling into bins defined by their distance apart. The expected correlation comes from Lemma 1, with $g=9.6$.

(B) Comparison of the observed and expected (theoretical) correlation of admixture mapping test statistics in the African American cohort, with expected correlation corresponding to Theorem 1, using $g=5.9$.

Comparison of Multiple Testing Correction Procedures in WHI SHARe

In the African American cohort, our multiple testing correction procedures yield genome-wide p value thresholds of 2.1 × 10⁻⁵ and 2.0 × 10⁻⁵ for the test statistic simulation and analytic approximation approaches, respectively. Both thresholds are consistent with the threshold given by the trait simulation approach (see Table 1) and are three orders of magnitude less stringent than the Bonferroni threshold. The empirical family-wise error rate for each approach from a simulation study using simulated traits is reported in Table 2. As expected, the trait simulation approach controls the empirical family-wise error rate exactly at the nominal level 0.05. Our proposed correction procedures also control family-wise error rate at the nominal level, while the Bonferroni correction, as expected, is very conservative.

Table 1.

Comparison of p Value Thresholds from Four Multiple Testing Correction Procedures in WHI SHARe African American (AA) and Hispanic American (HA) Samples

	Bonferroni (# Tests)	Simulation (10,000 reps)		Analytic Approximation
		Traits	Test Statistics
AA	$9.1\times {10}^{-8}$	$2.1\times {10}^{-5}$	$2.1\times {10}^{-5}$	$2.0\times {10}^{-5}$
(95% CI)		$\left(1.9,2.3\right)\times {10}^{-5}$	$\left(1.9,2.2\right)\times {10}^{-5}$
HA	$3.1\times {10}^{-8}$	$4.3\times {10}^{-6}$	$4.5\times {10}^{-6}$	n/a
(95% CI)		$\left(4.0,4.6\right)\times {10}^{-6}$	$\left(3.9,4.9\right)\times {10}^{-6}$

For simulation-based approaches, we also provide a 95% bootstrap confidence interval. Both simulation-based approaches used 10,000 replications. The nominal genome-wide type I error rate (${\alpha }^{\ast }$) is 0.05.

Table 2.

Empirical Family-wise Error Rate of Four Multiple Testing Correction Procedures in Simulation Studies using WHI SHARe African American (AA) and Hispanic American (HA) Genotype Data

	Bonferroni (# Tests)	Simulation (10,000 reps)		Analytic Approximation
		Traits	Test Statistics
AA	$5\times {10}^{-4}$	$0.050$	$0.050$	$0.048$
HA	$8\times {10}^{-4}$	$0.050$	$0.052$	n/a

Empirical family-wise error rate was calculated across 10,000 replications of a simulated null trait. The nominal genome-wide type I error rate (${\alpha }^{\ast }$) is 0.05.

The derived significance thresholds for the Hispanic American cohort are more stringent than those in the African American cohort, reflecting the differences between the two cohorts in terms of the number of ancestral populations, number of generations since admixture, and distribution of admixture proportions. Our test statistic simulation procedure yields a p value threshold of 4.5 × 10⁻⁶, which is again consistent with the trait simulation threshold and controls the empirical family-wise error rate at the nominal level (see Tables 1 and 2). As in the African American cohort, the Bonferroni correction yields a significance threshold that is orders of magnitude too conservative.

Computation Time

Computation time differs considerably across the four approaches. The Bonferroni correction can be used to compute the significance threshold nearly instantaneously. The analytic approximation approach is also very quick, taking under half a second on a 12-core 2.4 GHz computer with Intel Xeon E5-2630Lv2 processors and 128 GB of memory. The slowest is the trait simulation approach: for our WHI SHARe analyses, each replicate (which involved running a genome-wide admixture mapping study) took approximately 5 min on the same computer, for a total of more than 800 h of computation time to run all 10,000 replicates. In comparison, our test statistic simulation approach took only a fraction of a second per replicate, amounting to less than 10 min to run all 10,000 replicates in the African American and Hispanic American cohorts.

Discussion

We have developed a theoretical framework to characterize the correlation of local ancestry vectors and admixture mapping test statistics in admixed populations with any number of ancestral populations and distribution of admixture proportions. Our application to data from the Women’s Health Initiative SNP Health Association Resource highlights the importance of this extension, as both the African American and Hispanic American samples display considerable heterogeneity in admixture proportions (Figure 2). Based on these new theoretical results, we show that an existing analytic approximation⁴³ can be used to derive significance thresholds for admixture mapping studies in admixed populations with two ancestral populations, even in the presence of population structure, as long as the admixture mapping model adjusts for admixture proportions. For admixed populations with any number of ancestral populations, we propose an approach that simulates test statistics directly from their asymptotic joint distribution, saving considerable computation time relative to the trait simulation approach, while still yielding an appropriate significance threshold that controls the family-wise error rate.

Our multiple testing correction procedures are based on theoretical work that explicitly models the correlation of admixture mapping test statistics, so are not conservative like the commonly used Bonferroni correction; this will translate to gains in power in genome-wide admixture mapping studies. Compared to the trait simulation approach, our correction procedures yield comparably appropriate significance thresholds but are far less computationally intensive, and we provide an R package for easy implementation. Furthermore, by simulating test statistics directly from their asymptotic distribution, the computation time of our simulation-based multiple testing does not increase with sample size, which will prove useful as future studies are able to recruit larger and larger numbers of individuals. We believe that our approaches provide an attractive alternative for researchers looking to control for multiple testing in genome-wide admixture mapping studies, particularly in admixed populations with population structure.

In this paper, our theoretical work and data analyses have focused on genome-wide admixture mapping studies with quantitative traits and unrelated individuals. However, preliminary analyses indicate that our theoretical work extends easily to binary traits (see Figure S1). In the case of quantitative traits that are heavily skewed (or otherwise depart considerably from normality) larger sample sizes may be needed for asymptotic normality of the test statistics to be achieved; to address this problem, transformations such as rank normalization^{65, 66} could be considered. The presence of relatedness, accounted for by use of a mixed model,⁶⁷ should not change the marginal distribution of admixture mapping test statistics, but would likely change their correlation structure. We expect that this will not have a large impact on the appropriate significance threshold, but further investigation is needed to confirm this hypothesis.

Our multiple testing correction procedures require estimates of the admixture proportions for each admixed individual, the number of generations since admixture, and the genetic distance between consecutive loci. To assess sensitivity to the choice of genetic map used to produce these pairwise genetic distances, we implemented STEAM in the WHI African American cohort using both the HapMap genetic map and an African American-specific genetic map.⁶⁸ Although these maps are quite different in some regions of the genome, we found that they still produce similar estimates of the number of generations since admixture (HapMap: 5.9, African American map: 5.7) and the genome-wide p value threshold (HapMap: 2.1 × 10⁻⁵ [95% CI: 1.9 × 10⁻⁵, 2.2 × 10⁻⁵]; African American map: 2.0 × 10⁻⁵ [1.8 × 10⁻⁵, 2.3 × 10⁻⁵]). Our estimates of the number of generations since admixture (g) may be sensitive to assortative mating or departures from the assumption of a single instantaneous admixture event. Assortative mating can lead to increased variability in admixture proportions across a population,^{49, 69} which our approach accounts for by allowing these proportions to vary, and may additionally change the pattern of local ancestry correlation in the sample,⁶⁹ which will impact our estimate of the number of generations since admixture. However, in application to real admixed populations (e.g., WHI SHARe) where departures from the assumption of a single instantaneous admixture event and/or random mating (e.g., due to geographic constraints) are likely, we find that our approach still works well. In estimating the parameter g from observed data using our proposed method, we are able to appropriately capture the correlation structure of admixture mapping test statistics in the sample, which is what is important for estimating an appropriate genome-wide significance threshold.

The p value threshold 5 × 10⁻⁸ has become quite widely adopted as a control for multiple testing in genome-wide association studies,^{38, 70, 71, 72} but there is no such “established” threshold for admixture mapping studies. Even in the specific context of the WHI SHARe genotype data, at least four different genome-wide p value thresholds have been used in published admixture mapping analyses in the African American cohort (including 7 × 10⁻⁶,^{14, 17} 1 × 10⁻⁵,¹⁵ 1.5 × 10⁻⁵,¹⁶ and 1.82 × 10⁻⁵²²), demonstrating the lack of consensus up to this point (even across analyses of the same dataset) on how best to derive significance thresholds for genome-wide admixture mapping studies. In practice, many admixture mapping studies cite the work of other studies (e.g., Tang et al.³⁶) as the basis for their chosen significance threshold. However, our theoretical work and analysis of the African American and Hispanic WHI SHARe cohorts demonstrate that admixture mapping significance thresholds are not necessarily transferable across studies. In particular, the appropriate significance threshold depends on the number of ancestral populations, generations since admixture (to which it is particularly sensitive), population structure (through the distribution of admixture proportions), and density of markers tested, all of which often differ from one study to another. We encourage investigators to take this important point into consideration when choosing a significance threshold for their own genome-wide admixture mapping study.

Declaration of Interests

The authors declare no competing interests.

Published: February 14, 2019

Appendix A: Proofs of Theoretical Results

Lemma 1: Local Ancestry Correlation

Consider an admixed population with K ancestral populations, g generations since admixture, and admixture proportions distributed according to $\mathit{\pi }\sim F$, where F has finite first and second moments. Then, the correlation of local ancestry vectors at two loci $j,j^{\text{'}}$ separated by recombination fraction $\theta$ is given by:

$$Corr\left(a_{jk},a_{j^{\text{'}}{k}^{\text{'}}}\right)=\{\begin{array}{c}{\left(1-\theta \right)}^g+\left[1-{\left(1-\theta \right)}^g\right]\frac{2V_F\left({\pi }_k\right)}{E_F\left({\pi }_k\right)-E_F^2\left({\pi }_k\right)+V_F\left({\pi }_k\right)}ifk=k^{\text{'}}\\ \frac{2Co{v}_F\left({\pi }_k,{\pi }_{k^{\text{'}}}\right)-{\left(1-\theta \right)}^g\left[Co{v}_F\left({\pi }_k,{\pi }_{k^{\text{'}}}\right)+E_F\left({\pi }_k\right)E_F\left({\pi }_{k^{\text{'}}}\right)\right]}{\sqrt{\left[E_F\left({\pi }_k\right)-E_F^2\left({\pi }_k\right)+V_F\left({\pi }_k\right)\right]\left[E_F\left({\pi }_{k^{\text{'}}}\right)-E_F^2\left({\pi }_{k^{\text{'}}}\right)+V_F\left({\pi }_{k^{\text{'}}}\right)\right]}}ifk\ne k^{\text{'}}.\end{array}$$

Proof

Consider an admixed population with K ancestral populations and g generations since admixture. Denote the admixture proportions by the vector $\mathit{\pi }={\left({\pi }_1\dots {\pi }_K\right)}^T,{\sum }_{k=1}^K{\pi }_k=1,$ and let that vector be drawn from a distribution F with finite first and second moments. Let ${\mathit{a}}_j={\left(a_{j1}\dots a_{jK}\right)}^T$ be the local ancestry vector, where ${\sum }_{k=1}^K{a}_{jk}=2$ and a_jk denotes the number of alleles inherited from ancestral population k at locus j. Similarly, let ${\mathit{a}}_j^P={\left(a_{j1}^P\dots a_{jK}^P\right)}^T$ be the parental local ancestry vector, where now ${\sum }_{k=1}^K{a}_{jk}^P=1$ and $a_{jk}^P$ denotes the number of alleles inherited from parent $P$ ($P=M,F$ for mother and father, respectively) that are derived from ancestral population k at locus j. Consider two loci $j,j^{\text{'}}$ separated by recombination fraction $\theta$ or, equivalently, genetic distance $\delta$ cM. We wish to derive the correlation of local ancestry vectors ${\mathit{a}}_j,{\mathit{a}}_{j^{\text{'}}}$ at these loci, but first we will consider the correlation of the parental local ancestry vectors ${\mathit{a}}_j^P,{\mathit{a}}_{j^{\text{'}}}^P$.

Note that for the parental local ancestry vector ${\mathit{a}}_j^P$, exactly one of the components takes the value 1 and the other K −1 components must take the value 0. Then, conditional on the admixture proportions $\mathit{\pi }$, the correlation of components $k,k^{\text{'}}$ of the parental local ancestry vectors at loci $j,j^{\text{'}}$ is:

$$Corr\left(a_{jk}^P,a_{j^{\text{'}}{k}^{\text{'}}}^P|\mathit{\pi }\right)=\frac{Cov\left(a_{jk}^P,a_{jk}^P|\mathit{\pi }\right)}{\sqrt{V\left(a_{jk}^P|\mathit{\pi }\right)V\left(a_{j^{\text{'}}{k}^{\text{'}}}^P|\mathit{\pi }\right)}}=\frac{\mathrm{Pr}\left(a_{jk}^P=1,a_{j^{\text{'}}{k}^{\text{'}}}^P=1|\mathit{\pi }\right)-{\pi }_k{\pi }_{k^{\text{'}}}}{\sqrt{{\pi }_k\left(1-{\pi }_k\right){\pi }_{k^{\text{'}}}\left(1-{\pi }_{k^{\text{'}}}\right)}}$$

To reduce this further, we must consider two cases: $k=k^{\text{'}}$ and $k\ne k^{\text{'}}$. First, suppose that $k=k^{\text{'}}$. Then, $\mathrm{Pr}\left(a_{jk}^P=1,a_{j^{\text{'}}{k}^{\text{'}}}^P=1|\mathit{\pi }\right)={\left(1-\theta \right)}^g{\pi }_k+\left[1-{\left(1-\theta \right)}^g\right]{\pi }_k^2$. Second, suppose that $k\ne k^{\text{'}}$. Now, $\mathrm{Pr}\left(a_{jk}^P=1,a_{j^{\text{'}}{k}^{\text{'}}}^P=1|\mathit{\pi }\right)={\left(1-\theta \right)}^g\times 0+\left[1-{\left(1-\theta \right)}^g\right]{\pi }_k{\pi }_{k^{\text{'}}}$. After simplifying, it follows that

$$Corr\left(a_{jk}^P,a_{j^{\text{'}}{k}^{\text{'}}}^P|\mathit{\pi }\right)=\{\begin{array}{c}{\left(1-\theta \right)}^{g}ifk=k^{\text{'}}\\ {\left(1-\theta \right)}^g\frac{-{\pi }_k{\pi }_{k^{\text{'}}}}{\sqrt{{\pi }_k\left(1-{\pi }_k\right){\pi }_{k^{\text{'}}}\left(1-{\pi }_{k^{\text{'}}}\right)}}ifk\ne k^{\text{'}}.\end{array}$$

At each locus, we can separate the local ancestry vector ${\mathit{a}}_j$ into the sum of the parental local ancestry vectors ${\mathit{a}}_j^P$, such that ${\mathit{a}}_j={\mathit{a}}_j^M+{\mathit{a}}_j^F$. The parental local ancestry vectors are conditionally independent (conditional on $\mathit{\pi }$). Thus, $Cov\left(a_{jk},a_{j^{\text{'}}{k}^{\text{'}}}|\mathit{\pi }\right)=Cov\left(a_{jk}^M,a_{j^{\text{'}}{k}^{\text{'}}}^M|\mathit{\pi }\right)+Cov\left(a_{jk}^F,a_{j^{\text{'}}{k}^{\text{'}}}^F|\mathit{\pi }\right)=2Cov\left(a_{jk}^P,a_{j^{\text{'}}{k}^{\text{'}}}^P|\mathit{\pi }\right)$, and the conditional correlation of components of the local ancestry vectors ${\mathit{a}}_j$ is the same as that of the parental vectors ${\mathit{a}}_j^P$:

$$Corr\left(a_{jk},a_{j^{\text{'}}{k}^{\text{'}}}|\mathit{\pi }\right)=\frac{2Cov\left(a_{jk}^P,a_{jk}^P|\mathit{\pi }\right)}{\sqrt{2V\left(a_{jk}^P|\mathit{\pi }\right)2V\left(a_{j^{\text{'}}{k}^{\text{'}}}^P|\mathit{\pi }\right)}}=Corr\left(a_{jk}^P,a_{j^{\text{'}}{k}^{\text{'}}}^P|\mathit{\pi }\right).$$

We use the laws of total expectation, variance, and covariance to find the marginal correlation of local ancestry vectors:

$$Corr\left(a_{jk},a_{j^{\text{'}}{k}^{\text{'}}}\right)=\frac{Cov\left(a_{jk},a_{j^{\text{'}}{k}^{\text{'}}}\right)}{\sqrt{V\left(a_{jk}\right)V\left(a_{j^{\text{'}}{k}^{\text{'}}}\right)}}=\frac{E\left[Cov\left(a_{jk},a_{j^{\text{'}}{k}^{\text{'}}}|\mathit{\pi }\right)\right]+Cov\left[E\left(a_{jk}|\mathit{\pi }\right),E\left(a_{j^{\text{'}}{k}^{\text{'}}}|\mathit{\pi }\right)\right]}{\sqrt{\left\{E\left[V\left(a_{jk}|\mathit{\pi }\right)\right]+V\left[E\left(a_{jk}|\mathit{\pi }\right)\right]\right\}\left\{E\left[V\left(a_{j^{\text{'}}{k}^{\text{'}}}|\mathit{\pi }\right)\right]+V\left[E\left(a_{j^{\text{'}}{k}^{\text{'}}}|\mathit{\pi }\right)\right]\right\}}}=\frac{E\left[2Cov\left(a_{jk}^P,a_{j^{\text{'}}{k}^{\text{'}}}^P|\mathit{\pi }\right)\right]+Cov\left[2{\pi }_k,2{\pi }_{k^{\text{'}}}\right]}{\sqrt{\left\{E\left[2{\pi }_k\left(1-{\pi }_k\right)\right]+V\left[2{\pi }_k\right]\right\}\left\{E\left[2{\pi }_{k^{\text{'}}}\left(1-2{\pi }_{k^{\text{'}}}\right)\right]+V\left[2{\pi }_{k^{\text{'}}}\right]\right\}}}$$

With a bit of algebra (excluded from this proof for the sake of brevity), it follows that the marginal correlation of components $k,k^{\text{'}}$ of the local ancestry vectors at loci $j,j^{\text{'}}$ is

$$Corr\left(a_{jk},a_{j^{\text{'}}{k}^{\text{'}}}\right)=\{\begin{array}{c}{\left(1-\theta \right)}^g+\left[1-{\left(1-\theta \right)}^g\right]\frac{2V_F\left({\pi }_k\right)}{E_F\left({\pi }_k\right)-E_F^2\left({\pi }_k\right)+V_F\left({\pi }_k\right)}ifk=k^{\text{'}}\\ \frac{2Co{v}_F\left({\pi }_k,{\pi }_{k^{\text{'}}}\right)-{\left(1-\theta \right)}^g\left[Co{v}_F\left({\pi }_k,{\pi }_{k^{\text{'}}}\right)+E_F\left({\pi }_k\right)E_F\left({\pi }_{k^{\text{'}}}\right)\right]}{\sqrt{\left[E_F\left({\pi }_k\right)-E_F^2\left({\pi }_k\right)+V_F\left({\pi }_k\right)\right]\left[E_F\left({\pi }_{k^{\text{'}}}\right)-E_F^2\left({\pi }_{k^{\text{'}}}\right)+V_F\left({\pi }_{k^{\text{'}}}\right)\right]}}ifk\ne k^{\text{'}},\end{array}$$

as desired.

Theorem 1: Test Statistic Correlation

Consider an admixed population with K ancestral populations, g generations since admixture, and admixture proportions distributed according to $\pi \sim F$, where F has finite first and second moments. For loci $j\in \left\{1,\dots ,m\right\}$ and ancestry components $k\in \left\{1,\dots ,K\right\}$, define test statistics $Z_{jk}={\hat{\beta }}_{jk}/\widehat{se}\left({\hat{\beta }}_{jk}\right)$ based on the regression model in Equation 1. Then, under the universal null hypothesis $\left({\beta }_{jk}=0\forall j,k\right)$, the collection of test statistics $\mathit{Z}={\left(Z_{11}\dots Z_{mK}\right)}^T$ has an asymptotic multivariate normal distribution with mean $\mathbf{0}$ and covariance (and correlation) given by

$$Cov\left(Z_{jk},Z_{j^{\text{'}}{k}^{\text{'}}}\right)=\{\begin{array}{c}{\left(1-\theta \right)}^g\approx e^{-0.01g\delta }ifk=k^{\text{'}}\\ -{\left(1-\theta \right)}^{g}h\left(E_F\left({\pi }_k\right),E_F\left({\pi }_{k^{\text{'}}}\right)\right)\approx -e^{-0.01g\delta }h\left(E_F\left({\pi }_k\right),E_F\left({\pi }_{k^{\text{'}}}\right)\right)ifk\ne k^{\text{'}},\end{array}$$

where $h\left(x,y\right)=\raisebox{1ex}{$xy$}\!\left/ \!\raisebox{-1ex}{$\sqrt{x\left(1-x\right)y\left(1-y\right)}$}\right.$, $\theta$ is the recombination fraction between loci $j,j^{\text{'}}$, and $\delta$ is the genetic distance (cM) between those loci.

Proof

Consider an admixed population with K ancestral populations and g generations since admixture. Denote the admixture proportions by the vector $\mathit{\pi }={\left({\pi }_1\dots {\pi }_K\right)}^T,{\sum }_{k=1}^K{\pi }_k=1,$ and let that vector be drawn from a distribution $F$ with finite first and second moments. Let ${\mathit{a}}_j={\left(a_{j1}\dots a_{jK}\right)}^T$ be the local ancestry vector, where ${\sum }_{k=1}^K{a}_{jk}=2$ and $a_{jk}$ denotes the number of alleles inherited from ancestral population $k$ at locus $j$. Define Wald test statistics $Z_{jk}={\hat{\beta }}_{jk}/\widehat{se}\left({\hat{\beta }}_{jk}\right)$ based on the marginal linear regression model $E\left[\mathit{y}|a_{jk},{\mathit{\pi }}_{-K}\right]=\alpha +{\beta }_{jk}{a}_{jk}+\mathit{\gamma }{\mathit{\pi }}_{-K}$ (Model 1). Suppose that the universal null hypothesis holds, such that ${\beta }_{jk}=0\forall j\in \left\{1,\dots ,m\right\},k\in \left\{1,\mathrm{..},K\right\}$. We must show that the collection of test statistics $\mathit{Z}$ is asymptotically multivariate normal with mean $\mathbf{0}$ and covariance as defined above.

It is straightforward to show (e.g., by using the asymptotic equivalence between Wald tests and score tests, combined with existing results about the asymptotic distribution of score tests from such a model³⁵, ⁴⁰) that the test statistics $\mathit{Z}$ are asymptotically multivariate normal with mean $\mathbf{0}$ and covariance matrix $\mathbf{\Sigma }$ with elements ${\mathbf{\Sigma }}_{\mathrm{jk},{\mathrm{j}}^{\text{'}}{k}^{\text{'}}}=Cov\left(Z_{jk},Z_{j^{\text{'}}{k}^{\text{'}}}\right)$. Furthermore, we can show (e.g., as in Joo et al.⁷³) that test statistics $\mathit{Z}$ from the unadjusted admixture mapping model (Model 1 without ${\mathit{\pi }}_{-K}$) have covariance $Cov\left(Z_{jk}^{UNADJ},Z_{j^{\text{'}}{k}^{\text{'}}}^{UNADJ}\right)=Corr\left(a_{jk},a_{j^{\text{'}}{k}^{\text{'}}}\right)$. From the adjusted model (Model 1 with ${\mathit{\pi }}_{-K}$), the covariance of test statistics is simply the correlation of local ancestry conditioned on the covariates ${\mathit{\pi }}_{-K}$:³⁵ $Cov\left(Z_{jk},Z_{j^{\text{'}}{k}^{\text{'}}}\right)=Corr\left(a_{jk},a_{j^{\text{'}}{k}^{\text{'}}}|\mathit{\pi }\right)$. Combining these results with Lemma 1 and the approximation ${\left(1-\theta \right)}^g\approx \exp \left(-0.01g\delta \right)$ from Siegmund and Yakir,⁴³ we see that asymptotically the test statistics $\mathit{Z}$ will have covariance defined by$Cov\left(Z_{jk},Z_{j^{\text{'}}{k}^{\text{'}}}\right)=Corr\left(a_{jk},a_{j^{\text{'}}{k}^{\text{'}}}|\mathit{\pi }=E\left[\mathit{\pi }\right]\right)$, where

$$Corr\left(a_{jk},a_{j^{\text{'}}{k}^{\text{'}}}|\mathit{\pi }=E\left[\mathit{\pi }\right]\right)={\left(1-\theta \right)}^g\approx e^{-0.01g\delta }ifk=k^{\text{'}},$$

$$Corr\left(a_{jk},a_{j^{\text{'}}{k}^{\text{'}}}|\mathit{\pi }=E\left[\mathit{\pi }\right]\right)={\left(1-\theta \right)}^g\frac{-E\left[{\pi }_k\right]E\left[{\pi }_{k^{\text{'}}}\right]}{\sqrt{E\left[{\pi }_k\right]\left(1-E\left[{\pi }_k\right]\right)E\left[{\pi }_{k^{\text{'}}}\right]\left(1-E\left[{\pi }_{k^{\text{'}}}\right]\right)}}\approx e^{-0.01g\delta }\frac{-E\left[{\pi }_k\right]E\left[{\pi }_{k^{\text{'}}}\right]}{\sqrt{E\left[{\pi }_k\right]\left(1-E\left[{\pi }_k\right]\right)E\left[{\pi }_{k^{\text{'}}}\right]\left(1-E\left[{\pi }_{k^{\text{'}}}\right]\right)}}ifk\ne k^{\text{'}},$$

as desired.

Corollary

When $K=2$, $h\left(E_F\left({\pi }_k\right),E_F\left({\pi }_{k^{\text{'}}}\right)\right)=1$ since ${\sum }_{k=1}^K{E}_F\left({\pi }_k\right)=1$, so the covariance of test statistics simplifies nicely:

$$Cov\left(Z_{jk},Z_{j^{\text{'}}{k}^{\text{'}}}\right)=\{\begin{array}{c}{\left(1-\theta \right)}^g\approx e^{-0.01g\delta }ifk=k^{\text{'}}\\ -{\left(1-\theta \right)}^g\approx -e^{-0.01g\delta }ifk\ne k^{\text{'}},\end{array}$$

and the distribution of test statistics can then be approximated by an Ornstein-Uhlenbeck process, as shown by Siegmund and Yakir.⁴³

Appendix B: Recursive Simulation Algorithm

We propose a simulation-based multiple testing correction approach that simulates admixture mapping test statistics $\mathit{Z}={\left(Z_{11}{Z}_{12}\dots Z_{mK}\right)}^T$ from their asymptotic joint distribution (Theorem 1). To do so, we use the following recursive algorithm:

$$\mathrm{1}\mathrm{.}\mathrm{Set}{\mathit{Z}}_1={\left(Z_{11}\dots Z_{1K}\right)}^T=\mathit{L}{\mathit{X}}_1,where{\mathit{X}}_{\mathbf{1}}~N_{K-1}\left(0,{\mathit{I}}_{K-1}\right).$$

$$\mathrm{2}\mathrm{.}\mathrm{Set}{\mathit{Z}}_2=a_{12}{\mathit{Z}}_1+b_{12}\mathit{L}{\mathit{X}}_2,where{\mathit{X}}_2~N_{K-1}\left(0,{\mathit{I}}_{K-1}\right).$$

$$\mathrm{3}\mathrm{.}\mathrm{Set}{\mathit{Z}}_3=a_{23}{\mathit{Z}}_2+b_{23}\mathit{L}{\mathit{X}}_3,\mathrm{where}{\mathit{X}}_3~N_{K-1}\left(0,{\mathit{I}}_{K-1}\right).$$

$$\cdots$$

$$\mathrm{m}\mathrm{.}\mathrm{Set}{\mathit{Z}}_m=a_{m-1,m}{\mathit{Z}}_{m-1}+b_{m-1,m}\mathit{L}{\mathit{X}}_m,\mathrm{where}{\mathit{X}}_m~N_{K-1}\left(0,{\mathit{I}}_{K-1}\right).$$

Here,$K$ is the number of ancestral populations, $m$ is the number of loci, $\mathit{L}$ is a $K\times \left(K-1\right)$ matrix which depends on the first and second moments (which we can estimate using their sample equivalents) of the distribution of admixture proportions in the population, and $a_{ij},b_{ij}$ are scalars which depend on the number of generations since admixture ($g$) and the genetic distance (in cM) between consecutive loci $i\text{and}j$.

Others³⁵, ⁷³ have proposed multiple-testing correction procedures that similarly utilize knowledge of the asymptotic distribution of test statistics; however, our approach takes advantage of the specific, convenient form of this distribution for admixture mapping studies to speed up computation time. Note that this algorithm scales linearly with the number of loci $m$, but run time does not depend on the number of samples $n$ (except through calculation of the first and second moments of the sample admixture proportions). Computation time can be drastically reduced by considering just a single locus per unique ancestry block (if applicable; not all local ancestry inference programs perform calling within windows). Run time does increase slightly, but not drastically, with increasing number of ancestral populations $K$. Running 10,000 replicates on the WHI SHARe data took approximately 8 and 9 min for the African American ($K=2$) and Hispanic American ($K=3$) samples, respectively. We have implemented this algorithm in our R package STEAM (Significance Threshold Estimation for Admixture Mapping), which is available on GitHub.

Web Resources

STEAM, https://github.com/kegrinde/STEAM