Solving matrix equations in one step with cross-point resistive arrays

Significance

Linear algebra is involved in virtually all scientific and engineering disciplines, e.g., physics, statistics, machine learning, and signal processing. Solving matrix equations such as a linear system or an eigenvector equation is accomplished by matrix factorizations or iterative matrix multiplications in conventional computers, which is computationally expensive. In-memory computing with analog resistive memories has shown high efficiencies of time and energy, through realizing matrix-vector multiplication in one step with Ohm’s law and Kirchhoff’s law. However, solving matrix equations in a single operation remains an open challenge. Here, we show that a feedback circuit with cross-point resistive memories can solve algebraic problems such as systems of linear equations, matrix eigenvectors, and differential equations in just one step.

Abstract

Conventional digital computers can execute advanced operations by a sequence of elementary Boolean functions of 2 or more bits. As a result, complicated tasks such as solving a linear system or solving a differential equation require a large number of computing steps and an extensive use of memory units to store individual bits. To accelerate the execution of such advanced tasks, in-memory computing with resistive memories provides a promising avenue, thanks to analog data storage and physical computation in the memory. Here, we show that a cross-point array of resistive memory devices can directly solve a system of linear equations, or find the matrix eigenvectors. These operations are completed in just one single step, thanks to the physical computing with Ohm’s and Kirchhoff’s laws, and thanks to the negative feedback connection in the cross-point circuit. Algebraic problems are demonstrated in hardware and applied to classical computing tasks, such as ranking webpages and solving the Schrödinger equation in one step.

Linear algebra problems, such as solving systems of linear equations and computing matrix eigenvectors, lie at the heart of modern scientific computing and data-intensive tasks. Traditionally, these problems in forms of matrix equations are solved by matrix factorizations or iterative matrix multiplications (1, 2), which are computationally expensive with polynomial time complexity, e.g., O(N³) where N is the size of the problem. As conventional computers are increasingly challenged by the scaling limits of the complementary metal-oxide-semiconductor (CMOS) technology (3), and by the energy and latency burdens of moving data between the memory and the computing units (4), improving the computing performance with increasing hardware resources becomes difficult and noneconomic. To get around these fundamental limits, in-memory computing has recently emerged as a promising technique to conduct computing in situ, i.e., within the memory unit (5). One example is computing within cross-point arrays, which can accelerate matrix-vector multiplication (MVM) by Ohm’s law and Kirchhoff’s law with analog and reconfigurable resistive memories (5–8). In-memory MVM has been adopted for several tasks, including image compression (5), sparse coding (6), and the training of deep neural networks (7, 8). However, solving matrix equations, such as a linear system Ax = b, in a single operation remains an open challenge. Here, we show that a feedback circuit including a reconfigurable cross-point resistive array can provide the solution to algebraic problems such as systems of linear equations, matrix eigenvectors, and differential equations in just one step.

Resistive memories are two-terminal elements that can change their conductance in response to applied voltage stimuli (9, 10). Owing to their nonvolatile and reconfigurable behavior, resistive memories have been widely investigated and developed for storage-class memory (11, 12), stateful logic (13–15), in-memory computing (5, 6, 16, 17), and neuromorphic computing applications (7, 8, 18, 19). Resistive memories include various device concepts, such as resistive switching memory (RRAM, refs. 9–12), phase-change memory (PCM, ref. 20), and spin-transfer torque magnetic memory (21). Implemented in the cross-point array architecture, resistive memories can naturally accelerate data-intensive operations with enhanced time/energy efficiencies compared with classical digital computing (5, 6, 17). It has also been shown recently that iterated MVM operations with resistive cross-point arrays can solve systems of linear equations, in combination with digital floating-point computers (22). The higher the desired accuracy of the solution, the more iterations are needed to complete the operation. However, iteration raises a fundamental limit toward achieving high computing performance in terms of energy and latency.

Results

Cross-Point Circuits for Solving a System of Linear Equations.

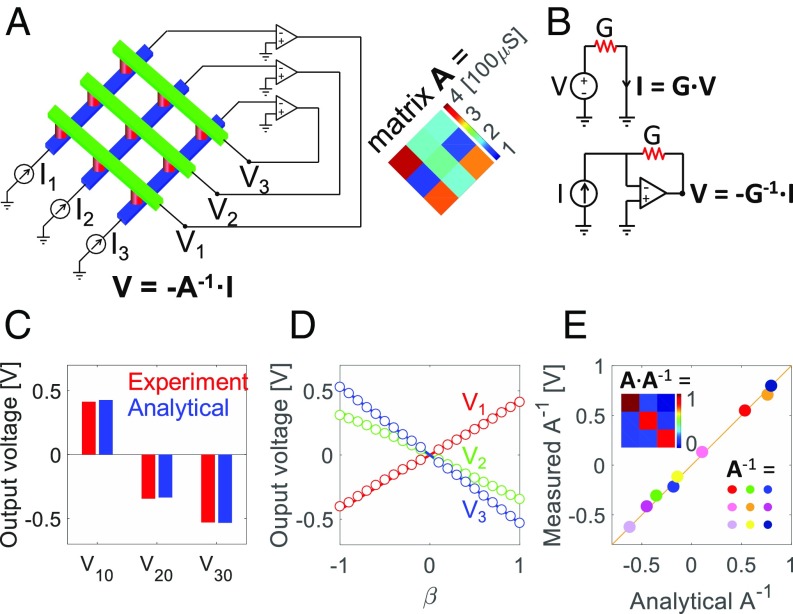
Fig. 1A shows the proposed feedback circuit for solving a system of linear equations in one step, and the hardware circuit on a printed circuit board is shown in SI Appendix, Fig. S1. The circuit is a cross-point array of RRAM devices, each consisting of a metal-insulator–metal stack with a HfO₂ layer between a Ti top electrode and a C bottom electrode (15). The devices show a set transition from high resistance to low resistance when a positive voltage above the threshold V_set is applied to the Ti electrode, and a reset transition from low resistance to high resistance when a negative voltage above the threshold V_reset is applied to the Ti electrode. Multilevel operation is also possible by executing the set transition at variable maximum (compliance) current I_C, or executing the reset transition at variable maximum voltage V_stop (23), as shown in SI Appendix, Fig. S2. The 3 × 3 cross-point array in the figure can perform MVM with open loop, i.e., by applying a voltage vector V to the columns and measuring the current vector I at the rows without the row-column connections enabled by the operational amplifiers (OAs), which is shown in SI Appendix, Fig. S3. The measured currents yields the dot product I = A·V between the applied analog voltages and the matrix A of the RRAM conductance values in the cross-point array. The results evidence a small error generally below 8%, mostly arising from the nonlinearity of conductance in cross-point resistive devices. This is in line with previous results, where the MVM accuracy appeared satisfactory (5), although not aligned with single- and double-precision full digital operation.

Fig. 1.

Solving systems of linear equations with a cross-point array of resistive devices. (A) Cross-point circuit for solving a linear system or inverting a positive matrix. RRAM elements (red cylinders) are located at the cross-point positions between rows (blue bars) and columns (green bars). (Inset, Right) Experimental conductance values mapping the elements of matrix A. The transformation units between the real-valued matrices/vectors and the physical implementations were G₀ = 100 μS, V₀ = 1 V, and I₀ = 100 μA for RRAM conductance, input/output voltage, and output/input current, respectively. The other cases also follow this convention if not specified. (B) Circuits to calculate a scalar product I = G·V by Ohm’s law, and to calculate a scalar division V = −I/G by a TIA. (C) Measured solution to a linear system with an input current vector I = [0.2; 1; 1]I₀. The experimental output voltages give a solution very close to the analytical one. (D) Measured solution to the linear systems, namely output voltages, as functions of parameter β controlling the input current given by I = β·[0.2; 1; 1]I₀ with −1 ≤ β ≤ 1. The experimental solutions (color circles) are compared with analytical solutions (color lines) of the system, supporting the accuracy of the physical calculation. (E) Experimental matrix inverse A⁻¹, namely measured output voltages in three subsequent experiments with input current I = [1; 0; 0]I₀, [0; 1; 0]I₀, and [0; 0; 1]I₀, respectively. The analytical solution is also shown. (Inset) Matrix product AA⁻¹ is very close to the unit matrix U, thus supporting the experimental inversion.

The MVM operation is a consequence of physical Ohm’s law I = G·V, where G is the device conductance, V is the applied voltage, and I is the measured current (Fig. 1B, Top). On the other hand, the inverse operation V = −I/G can be obtained for a given I and G, simply by forcing the current I at a grounded node of the resistive device and measuring the potential V at the second node. This physical division is accomplished by the transimpedance amplifier (TIA) in Fig. 1B (Bottom), where the current is injected at the inverting-input node of an OA, and the feedback conductance G connects input and output nodes of the OA. The differential input voltage V⁺ − V⁻ at the OA is minimized by the high gain of the OA, thus establishing a virtual ground (V⁻ = 0) at the inverting-input node (24, 25) and enabling the physical division. This provides the basis for the circuit in Fig. 1A, which solves a system of linear equations expressed by the matrix formula:

$$Ax=b,$$ [1]

where A is a nonsingular square matrix mapped with conductance values of cross-point RRAM devices, b is a known vector, and x is the unknown vector. In this circuit, the input currents I = −b are applied to cross-point rows connected to the virtual-ground nodes of the OAs. As a result, currents are forced to automatically distribute among the resistive elements in the cross-point array, to establish an output potential V satisfying

$$\mathit{A}·\mathit{V}+\mathit{I}=0,$$ [2]

which implies V = −A⁻¹·I = x. A circuit similar to the one in Fig. 1A was previously presented in the report of the International Roadmap for Devices and Systems (25) and suggested by ref. 26, although no demonstration was shown regarding the ability to solve a linear system by either experiments or simulations.

To demonstrate the concept of Fig. 1A, we measured the output voltages in the 3 × 3 RRAM cross-point array of Fig. 1A, where the conductance matrix is also shown. All of the matrices adopted in the experiments of this work are reported in SI Appendix, Table S1. A current vector [I₁₀; I₂₀; I₃₀] with I₁₀ = 20 μA, I₂₀ = 100 μA, and I₃₀ = 100 μA, was applied to the array rows, and the resulting potential at the array columns, i.e., [V₁₀; V₂₀; V₃₀], was measured, as shown in Fig. 1C. The good agreement (with relative errors within 3%) with the analytical solution supports the functionality of the feedback circuit of Fig. 1A for solving the matrix equation in Eq. 1. The circuit was further demonstrated by linearly changing the input currents according to I_i = β I_i0, where i = 1, 2, or 3, and β was changed uniformly in the range from −1 to 1. Results are reported in Fig. 1D, showing the measured output voltages compared with the analytical solutions x = A⁻¹b. The error remains below 10% for |β| > 0.5 (SI Appendix, Fig. S4). Notably, Eq. 1 is physically solved in just one step thanks to the physical MVM in the cross-point array and to the feedback connection forcing the virtual ground at cross-point rows.

The same concept can be extended to compute the inversion of a matrix A satisfying AA⁻¹ = U, where U is the unit matrix. The ith column of A⁻¹ can be measured as the output voltage when the ith column of U is applied as an input, thus realizing matrix inversion in N steps. Fig. 1E shows the measured elements of A⁻¹ compared with the analytically solved inverse-matrix elements, and the relative errors are calculated in SI Appendix, Fig. S5. Fig. 1E (Inset) shows that the experimental product AA⁻¹ well approximates U, which further supports the computed matrix inversion.

The circuit of Fig. 1A is essentially a matrix-inversion operator, which can be utilized to solve linear systems and matrix inversions, while a cross-point array without feedback is a matrix operator, which can be naturally used to perform MVM. Since the matrix-inversion circuit is a negative feedback system, the stability of the output voltage requires that the loop gain (G_loop) of every feedback loop is negative (27). The analysis reveals that the condition G_loop < 0 is satisfied when the signs of the diagonal elements of A⁻¹ are all positive (SI Appendix, Fig. S6). Following this guideline, a system of linear equations and the inversion of a 5 × 5 matrix have been solved, with the matrix implemented in a cross-point array of discrete resistors. The small relative error around few percent in this ideal case with discrete resistors evidences that a high accuracy might be achieved with accurate and linear resistive memory devices (SI Appendix, Fig. S7).

Solving a Linear System with Positive and Negative Coefficients.

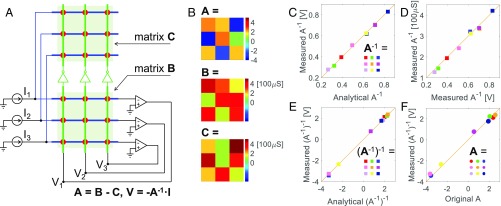
Since conductance can only be positive in a resistive element, the scheme of Fig. 1 can only solve linear systems with a positive matrix of coefficients. To solve linear systems with nonpositive coefficients, the mixed-matrix circuit in Fig. 2 shall be adopted. Here, the matrix A is split into two cross-point arrays according to A = B − C, where B and C are both positive. Fig. 2A shows the two cross-point-array implementation, where the input current I is split by the circuit into two components I_B and I_C = I − I_B, being submitted to virtual-ground rows of B and C, respectively. Analog inverters enable voltage inversion between the columns of B and C. Based on Ohm’s law and Kirchhoff’s current law, the output voltage V of the OAs is given by

$$\mathit{B}·\mathit{V}+\mathit{C}\left(-\mathit{V}\right)+\mathit{I}=0,$$ [3]

or A·V + I = 0, which solves the linear system of Eq. 1 with I = −b.

Fig. 2.

Inversion of a mixed matrix. (A) Schematic of two cross-point-array circuit for matrix inversion, where two cross-point arrays contain the elements of matrices B (Bottom) and C (Top) with A = B − C. The voltage in matrix C is inverted in the other by analog inverters, while the input current is injected in virtual-ground lines and split in the two matrices. (B) Measured values of the matrices A, B, and C, with A = B − C. In the experiment, matrix B was implemented by a cross-point array of RRAM, while matrix C was implemented by a cross-point array of discrete resistors. (C) Measured values of the inverse matrix A⁻¹ as a function of the analytically calculated elements of A⁻¹. As A⁻¹ is a positive matrix, it can be inverted by a single cross-point array as in Fig. 1. (D) Conductance values for matrix A⁻¹ implemented in RRAM elements, as a function of the experimental values of A⁻¹ in C. To make the devices work in the high-conductance region, the matrix A^-1 was implemented with G₀ = 500 μS for RRAM conductance. (E) Measured elements of matrix (A⁻¹)⁻¹ as a function of analytical calculations. I₀ = 500 μA and V₀ = 1 V were used for input current and output voltage, respectively. (F) Measured elements of matrix (A⁻¹)⁻¹ as a function with the original matrix A, showing a remarkable accuracy despite the accumulated errors over the two sequential inversion processes and the device-programming process.

We experimentally demonstrated the inversion of a 3 × 3 mixed matrix A with the two matrices B and C implemented in an RRAM array and a resistor array, respectively. The values of A, B, and C are shown in Fig. 2B, while Fig. 2C shows the measured elements of A⁻¹ as a function of the analytical results, demonstrating good accuracy. To further support physical matrix inversion, we inverted A⁻¹, which is a positive matrix, with a single cross-point array. For that purpose, the elements of A⁻¹ were first mapped as conductance values in an RRAM array by employing a program-and-verify algorithm with error below 5% (SI Appendix, Fig. S8). Although the program-and-verify algorithm was applied to an individual RRAM device at a time, a cross-point array is suitable for parallel programming to significantly reduce the array initialization time (28, 29). Fig. 2D shows the measured RRAM conductance values as a function of the target values obtained from the experimental A⁻¹ in Fig. 2C. The inversion of A⁻¹, i.e., (A⁻¹)⁻¹, was computed by the matrix-inversion circuit of Fig. 1A, yielding the results in Fig. 2E. The computed (A⁻¹)⁻¹ is compared with the original matrix A in Fig. 2F, which supports the good accuracy of the double inversions (A⁻¹)⁻¹ = A. The relative errors of the above operations are reported in SI Appendix, Fig. S9.

Similar to the single cross-point-array circuit of Fig. 1A, the condition for negative feedback applies to the mixed matrix A. Besides, since cross-point array B is directly involved in the closed-loop feedback with the OAs, matrix B also has to satisfy the condition G_loop < 0. As a proposal for practical applications, a reference matrix B satisfying the G_loop condition can be adopted in the mixed-matrix circuit, while matrix C can be freely arranged with an RRAM cross-point array with the condition C = B − A. To demonstrate the generality of this concept, the one-dimensional steady-state Fourier equation for heat diffusion was solved with a cross-point-array circuit (SI Appendix, Figs. S10 and S11). By using the finite difference method, the differential equation is first converted into a system of linear equations, where the characteristic matrix A is a mixed tridiagonal matrix. Input currents correspond to the known term, namely the dissipated power in the one-dimensional structure. The solution yields the temperature profile along the reference structure, which solves the numerical Fourier equation.

A key parameter to describe the stability of the solution of a linear system is the condition number κ of matrix (30). The condition number reflects the stability of the solution x upon small variations of the known term b in Eq. 1, where the sensitivity to perturbations increases with the condition number. To study the impact of the condition number on the solution of linear systems in resistive memory arrays, we simulated the circuit-based inversion of three 10 × 10 matrices with increasing condition number. To test the stability of the solution, a random variation of 0.1 or −0.1 was added to each element in the term b of the equation Ax = b, where b is the ith column of the unit matrix U, x is the ith column of A⁻¹, and i was swept from 1 to 10 to calculate the whole inverse matrix. The results are reported in SI Appendix, Fig. S12, indicating that the computing error increases with the condition number of the matrix.

The impact of the condition number was also tested in experiments, by performing a double inversion of a matrix with a larger condition number (κ = 16.9), compared with the one with κ = 9.5 in Fig. 2. Condition numbers for all of the matrices in experiment are summarized in SI Appendix, Table S1. As shown in SI Appendix, Fig. S13, the matrix with a larger κ is successfully inverted twice, although the computing errors are larger than the case in Fig. 2 (SI Appendix, Fig. S14). It should be noted that the matrices addressed in this work are well conditioned. For an ill-conditioned matrix with extremely high condition number, additional schemes should be required, possibly including iterative refinement algorithms that can be either supported by a conventional digital computer (22) or implemented in a resistive memory array (26). The error caused by the thermal noise and shot noise of the components in the cross-point circuit also increases with the condition number, although representing a much less significant concern (SI Appendix, Fig. S15).

Cross-Point Circuits for Computing Eigenvectors.

The solution of a linear system in Eq. 1 can be further extended to the calculation of eigenvectors via physical computing in a cross-point array. The eigenvector equation reads

$$\mathit{Ax}=\lambda \mathit{x},$$ [4]

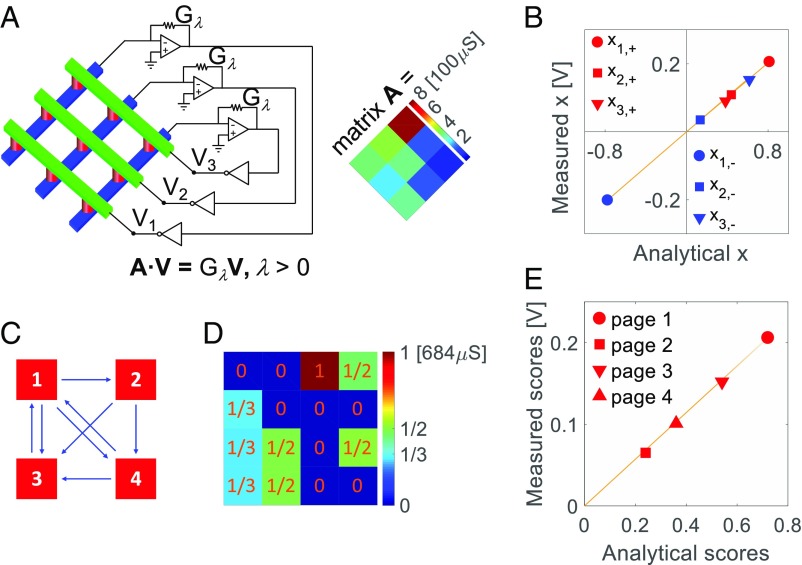
where A is a real square matrix, λ is its eigenvalue, and x is the corresponding eigenvector. Fig. 3A shows the eigenvector circuit, consisting of a self-operated feedback circuit where the voltage vector V developed at the cross-point columns develops a current vector I = A·V, with the conductance of a cross-point array mapping the matrix A. The output currents are converted into voltages by TIAs with the feedback resistors G_λ mapping the known eigenvalue λ. The outputs of the TIAs are then inverted and fed back to cross-point columns. Combining Ohm’s law and Kirchhoff’s law, one gets −A·V/G_λ = −V, hence A·V = G_λV, which satisfies Eq. 4. As physical voltages and currents can only have real values, the eigenvector circuit only applies to real eigenvalues and eigenvectors. For a positive matrix, according to the Perron–Frobenius theorem (31), the highest eigenvalue must be a positive real number, and its eigenvector also consists of positive real numbers. As a result, the eigenvector of the highest eigenvalue of a positive matrix can always be solved with a cross-point circuit. If the eigenvector of the lowest negative eigenvalue is real, it can also be measured by removing the analog inverters in the feedback circuit (SI Appendix, Fig. S16A). Note that the eigenvector circuit in Fig. 3A works in a self-sustained manner, similar to a positive-feedback oscillator, thanks to the active TIAs establishing the voltage vector V.

Fig. 3.

Eigenvector and PageRank calculations. (A) Cross-point circuit for the solution of the eigenvector equation Ax = λx, where x is the eigenvector and λ is the highest positive eigenvalue of a positive matrix A reported in the inset. To prevent set/reset disturb to the RRAM conductance, the output voltages of the OAs were limited to ±0.2 V. (B) Measured eigenvectors corresponding to the highest positive eigenvalue and the lowest negative eigenvalue, as a function of the normalized eigenvectors obtained by analytical solutions. The highest positive eigenvalue and the lowest negative eigenvalue were stored as the feedback conductance G_λ of the TIAs with conductance of 940 and 331 μS, respectively. (C) A system of four webpages with their respective links. An arrow pointing from page i to page j indicates a citation of j in page i, thus the importance of a webpage can be stated from the number of arrows pointing at that page. (D) The link matrix for the system in C. The elements in each column sum to 1, while diagonal elements are all null as pages do not cite themselves. The transformation unit was G₀ = 684 μS for RRAM conductance, to minimize RRAM nonlinearity. The highest positive eigenvalue is 1, corresponding to feedback resistors with conductance G₀. (E) Measured eigenvector, representing the importance scores of four pages, as a function of the analytically solved normalized eigenvector.

The eigenvector circuit in Fig. 3A was experimentally demonstrated for an RRAM cross-point array with conductance values G mapping the matrix A (Fig. 3A, Inset), by computing the eigenvectors for the highest positive eigenvalue (λ₊ = 9.41) and the lowest negative eigenvalue (λ₋ = −3.31). Fig. 3B shows the measured values of the eigenvectors as functions of the normalized eigenvectors obtained by the analytical solutions. The proportionalities between experimental and calculated eigenvectors in the figure indicate the correct physical computation of the eigenvectors.

While the restriction of the solution to the highest/lowest eigenvalues might seem inconvenient, it turns out that for many applications only the highest positive or the lowest negative eigenvalues are concerned. For instance, in the PageRank algorithm (32, 33), which yields the importance scores of webpages for their ranking, the eigenvector of a link matrix is calculated for the highest positive eigenvalue. The latter is always equal to 1, since the link matrix is a stochastic matrix (33). Fig. 3C shows an example of four pages with their respective links while Fig. 3D shows the corresponding link matrix which was implemented as the conductance values of a 4 × 4 RRAM cross-point array. Using the eigenvector circuit of Fig. 3A, the eigenvector of the link matrix was solved to compute the importance scores of the pages. Fig. 3E shows the experimental scores compared with the analytical scores, demonstrating good accuracy of physically computing the eigenvector. A real-world case of PageRank is reported in SI Appendix, Fig. S17.

The analysis of the eigenvector circuit of Fig. 3A shows that G_loop should be ideally equal to 1 (SI Appendix, Fig. S18), which however can never be exactly satisfied in practical circuits. In practice, G_λ can be experimentally chosen such that G_loop is slightly larger than 1, which enables the correct solution of the eigenvector with an acceptable error. In fact, although the output initially increases due to G_loop > 1, the circuit nonlinearity arising from the saturation of the TIA output reduces the G_loop to 1. On the other hand, setting G_loop smaller than 1 results in vanishing output voltages, which should thus be avoided. Similar to Fig. 2A, the eigenvector solution can be extended to a mixed matrix A by the splitting technique with two cross-point arrays connected by analog inverters (SI Appendix, Fig. S16B).

We validated the physical computation of eigenvectors for the solution of the one-dimensional time-independent Schrödinger equation:

$$\mathit{H}\text{Ψ}=\mathit{E}\text{Ψ},$$ [5]

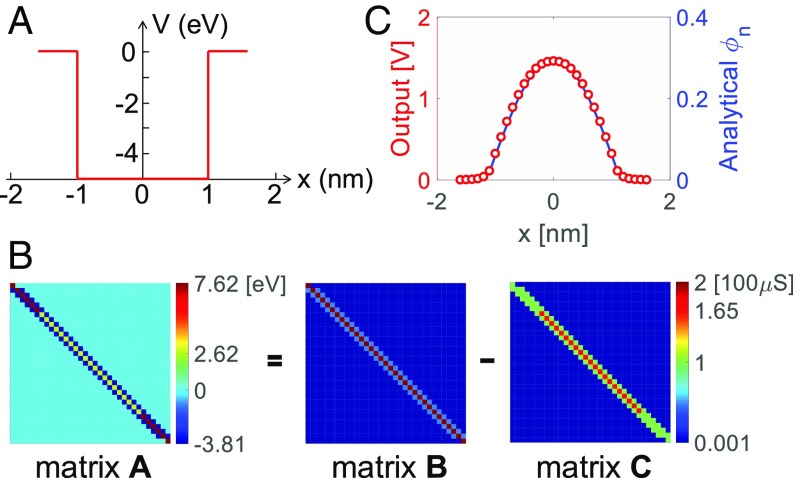
where H is the Hamiltonian operator, E is an energy eigenvalue, and Ψ is the corresponding eigenfunction. Eq. 5 can be numerically solved by the finite difference method, yielding an eigenvector problem given by Eq. 4, where A is a tridiagonal matrix of coefficients, x is the vector of Ψ values at discrete positions, and λ is the highest/lowest eigenvalue. The Schrödinger equation was solved for a square potential well shown in Fig. 4A, which was divided equally into 32 segments (SI Appendix, Figs. S19 and S20). Fig. 4B shows the 33 × 33 tridiagonal mixed matrix A describing the eigenvector equations. The matrix A is split into two positive tridiagonal matrices B and C, which are mapped into the conductance values of two cross-point arrays, respectively. The eigenvector was calculated for the ground state with energy E = −4.929 eV, corresponding to the lowest negative eigenvalue of the problem. The eigenvalues and eigenvectors obtained by numerical solution in a digital computer are also reported in SI Appendix, Fig. S19. Fig. 4C shows the eigenvector obtained by a simulated eigenvector circuit, compared with the analytically computed eigenvector. The physically computed wave function agrees well with the numerical solution, which further supports physical computing in cross-point circuits for real-world applications.

Fig. 4.

Solution of the Schrödinger equation in a cross-point circuit. (A) Rectangular well of potential V(x) adopted in the Schrödinger equation. The potential well has a depth of −5 eV and a width of 2 nm, while the solution is conducted on an overall width of 3.2 nm, discretized in 32 equal intervals. (B) Matrix A with size 33 × 33 obtained from the space discretization of the Schrödinger equation, and the two positive matrices B and C implemented in the cross-point arrays, with A = B − C. A conversion unit of 100 μS for 7.6195 eV was adopted in matrices B and C. The two conductance matrices share the same color bar. The ground-state eigenvalue is −4.929 eV, which was mapped into the conductance (65 μS) of the TIA feedback resistors. (C) Discrete ground-state eigenfunction obtained as the simulated output voltage in the cross-point circuit compared with the analytical solutions. Note that the peak voltage is around the supply voltage 1.5 V of the OA due to saturation.

Discussion

Cross-point arrays allow solutions of a broad set of algebra problems, from linear systems to eigenvector problems, thus enabling the physical solution of differential equations describing real-world problems in industry, economy, and health. The solution relies on extremely simple circuit elements, such as commercially available OAs and state-of-the-art resistive memories such as RRAM and PCM. In comparison, previous solutions of linear systems by using a quantum-computing approach (34, 35) are less attractive, since quantum circuits generally operate at cryogenic temperature and require dedicated instrumentation and noncommercial technology. Other proposed solutions with neural network architectures (36) or CMOS-based analog accelerators (37) rely on iterative operations, resulting in polynomial computation time and cost. In contrast, the cross-point array allows for fast solution in just one step without iteration. The computing time is limited by the settling time of the OA, which can reach the few-nanosecond range in advanced CMOS technology (38).

To fulfill the expectations of practical applications, the cross-point circuit should be scaled up to demonstrate the circuit feasibility. To demonstrate the scalability of the cross-point circuit, solving a system of linear equations for a 100 × 100 model coefficient matrix in simulation is shown in SI Appendix, Fig. S21. The results show that the linear system is precisely solved by the circuit, which supports the suitability of the cross-point circuit to address real-world problems. Since the matrix coefficients are stored in real nanoscale devices with inherent stochastic variations, the cross-point circuit only provides an approximate solution to the linear problem. To evaluate the impact of device variations, we included a random deviation to the conductance of each cross-point device for the 100 × 100 matrix and calculated the relative errors of the output voltages (SI Appendix, Fig. S22). The simulation results show relatively low errors (around 10%), even with a variation of 10%. High-precision storage of conductance values by program-and-verify techniques is thus essential to improving the accuracy of the solution, depending on the specific applications. Nonlinear conduction in the resistive element, physically arising from hopping conduction and local Joule heating, also affects the accuracy of the solution. Conduction linearity can be maximized by increasing the device conductance (5), which however leads to a higher energy demand for reconfiguring and operating the cross-point circuit. Advancing the technology of resistive memories, aiming at a higher accuracy of multilevel placement and better linearity of conduction, can boost the cross-point circuit for in-memory computing of linear algebra.

As the cross-point circuit scales up, the parasitic resistance due to the dense interconnect wiring in the memory array can become an additional concern. To assess the impact of the parasitic resistance, we simulated the same 100 × 100 linear system of SI Appendix, Fig. S21 with an additional parasitic wire resistance (SI Appendix, Fig. S23). As a reference, the interconnect parameters were taken from the International Technology Roadmap for Semiconductors at the 65- and the 22-nm technology nodes (39). The relative errors are found to be within ∼10 and 30% for 65- and 22-nm nodes, respectively. These results suggest that there is a tradeoff between scaling and accuracy of circuit-based solutions of algebra problems. It should also be noted that the computing errors are essentially dictated by the resistance ratio between the device resistance and the parasitic resistance. As a result, the computing accuracy might be improved by increasing the resistances of memory devices, which in turn might raise an issue about the conduction nonlinearity that also affects the computing accuracy. We conclude that there is a complex tradeoff between scaling, parasitic resistance, and device nonlinearity, to optimize the operations (40, 41). In this scenario, 3D integration of the cross-point memory, where density does not necessarily cause an increase of interconnect resistance, may improve the immunity of computing accuracy to the parasitic resistance (42).

While the lack of iteration is a highly attractive feature for fast computation, the time needed to program individual matrix coefficients in the memory should also be considered for a comprehensive assessment of the technology. Although the write time in our devices was relatively long for the purpose of a tight tuning of conductance values (see, e.g., SI Appendix, Fig. S8), the programming time in a real application might be strongly accelerated thanks to the parallel programming (28, 29), analog programming schemes (43), in addition to the subnanosecond switching of RRAM devices (44) and PCM devices (45). Also, according to the concept of in-memory computing, the same data can be frequently reused for computation (42), thus the programming time can play a negligible role in the overall computing time.

Although the accuracy of our scheme cannot be compared with that of a floating-point solution in a high-precision digital computer, it is important to note that the required accuracy might not be high for all applications. There are in fact many cases where a linear algebra problem must be solved in a short time, with a low energy budget, and with sufficient tolerance to errors. For instance, in machine-learning algorithms, the coefficients for classification/recognition can settle with a certain amount of inaccuracy. The network coefficients can be obtained by a pseudoinverse matrix (46), the calculation of which can be accelerated by our approach. Another example is webpage ranking, where the computed website scores should appear in the correct order, although some amount of inaccuracy might still be tolerated for the individual scores. For similar types of application, our circuits can provide a solution with an excellent tradeoff between accuracy, speed, and energy consumption.

In conclusion, solutions of linear algebra problems in cross-point resistive arrays have been presented. Problems such as systems of linear equations, matrix eigenvectors, and differential equations are solved (i) in one step (and matrix inversion in N steps), (ii) in situ within the cross-point memory array, and (iii) via physical laws such as Ohm’s law, Kirchhoff’s law, and feedback mechanisms in closed-loop circuits. The proposed in-memory computing paves the way for future in-memory approximate computing systems to solve practical big-data problems with huge savings of time and energy for a wide range of real-world applications.

Methods

Details of device fabrication and characterization, circuit design and measurement techniques are reported in SI Appendix.