Covariance-Insured Screening

Abstract

Modern bio-technologies have produced a vast amount of high-throughput data with the number of predictors far greater than the sample size. In order to identify more novel biomarkers and understand biological mechanisms, it is vital to detect signals weakly associated with outcomes among ultrahigh-dimensional predictors. However, existing screening methods, which typically ignore correlation information, are likely to miss weak signals. By incorporating the inter-feature dependence, a covariance-insured screening approach is proposed to identify predictors that are jointly informative but marginally weakly associated with outcomes. The validity of the method is examined via extensive simulations and a real data study for selecting potential genetic factors related to the onset of multiple myeloma.

1. Introduction

Rapid biological advances have generated a vast amount of ultrahigh-dimensional genetic data. Extracting information from these data have become a major driving force for the development of modern statistics in the last decade.

A seminal paper by [1] proposed sure independence screening (SIS) for selecting variables from ultrahigh-dimensional data. The essence of this approach is to select variables with strong marginal correlations with the response. Much research has been inspired thereafter. [2] expanded SIS to accommodate generalized linear models, [3] studied variable screening under the Cox proportional hazards models, and further proposed a score test-based screening method [4]. Additional researches have ensured on semiparametric and nonparametric screening: semiparametric marginal screening methods have been proposed for linear transformation models [5] and general single-index models [6], whereas nonparametric marginal screening methods have been proposed for linear additive models [7] and quantile regressions [8].

Though varied in many contexts, these methods are based on marginal associations of individual predictors with the outcome; i.e. they assume that the true association between the individual predictors and outcomes can be inferred from their marginal associations. The condition, however, is often violated in practice. As marginal screening methods ignore inter-feature correlations, they tend to select irrelevant variables that are highly correlated with important variables (false positive) and fail to select relevant variables that are marginally unimportant but jointly informative (false negative).

Because of these limitations, there has been a surge of interest in conducting multivariate screenings that account for inter-feature dependence: [9] developed a partial correlation based algorithm (PC-simple); [10] proposed a sequential approach (Tilting) that measures the contribution of each variable after controlling for the other correlated variables; [11] introduced high-dimensional ordinary least squares projection (HOLP) that projects response to the row vectors of the design matrix, which may preserve the ranks of regression coefficients; and [12] proposed Graphlet Screening (GS) by using the sample covariance matrix to construct a regularized graph and sequentially screening connected subgraphs.

Conceptually, multivariate screenings have been appealing. However, the computational burden increases substantially with the number of covariates. Although simplifications, such as PC-simple and Titling, have been applied to improve computational efficiency in ultrahigh-dimensional cases, they may not adequately assess the true contribution of each covariate.

For adequately assessing the association of each covariate with the response, while maintaining computational feasibility, this paper presents a covariance-insured screening (CIS). Leveraging the inter-feature dependence, the proposed approach is able to identify marginally unimportant but jointly informative features that are likely to be missed by conventional screening procedures. In our methodological development, we have relaxed marginal correlation conditions that have often been assumed in the literature. Without such restrictive assumptions, we can still produce the consistency results for variable selection in ultrahigh-dimensional situations. Moreover, the proposed method is computationally efficient and suitable for the analysis of ultrahigh-dimensional data.

The remaining article is organized as follows. In Section 2, we provide some requisite preliminaries and describe our proposed method in Section 3. We then compare it with existing methods in Section 4. In Section 5, we study the theoretical properties and propose a procedure for selecting tuning parameters. Finite-sample properties are examined in Section 6. We apply the proposed method to analyze multiple myeloma data in Section 7. We conclude with a discussion in Section 8. All technical proofs have been deferred to Appendix.

2. Notation and Model

Consider a multiple linear regression model with n independent samples, y = Xβ + ϵ, where y = (Y₁, …, Y_n)^T is the response vector, ϵ = (ϵ₁, …, ϵ_n)^T is a vector of independently and identically distributed random errors, X is an n × p design matrix, and β = (β₁, …, β_p)^T is the coefficient vector. We write X = [X₁, …, X_n]^T = [x₁, …, x_p], where X_i is a p-dimension covariate vector for the i-th subject and x_j is the j-th column of the design matrix, 1 ≤ i ≤ n, 1 ≤ j ≤ p. Without loss of generality, we assume that each covariate x_j is standardized to have sample mean 0 and sample standard deviation 1. For any set $\mathcal{D}\subset \{1,\dots ,p\}$, we define sub-vectors, $X_{i,\mathcal{D}}=\{X_{i,j}:j\in \mathcal{D}\}$ and $x_{\mathcal{D}}=\{x_j:j\in \mathcal{D}\}$. Let X_i,−j = {X_i,1, …, X_i,p} \ {X_i,j} and denote by Σ = Cov(X_i).

When p ≫ n, β is difficult to estimate without the common sparsity condition that assumes only a small number of variables related with the response. For improved model interpretability and accuracy of estimation, our overarching goal is to identify the active set

$${\mathcal{M}}_0=\{j:{\beta }_j\ne 0,j=1,\dots ,p\}.$$ (1)

2.1. Partial Correlation and PC-simple Algorithm

The direct linkage between β and the partial correlations has been well established in the literature; see [13] and [14], among many others. Recently there has been much interest [9, 10] in conducting variable screening via partial correlations, which are defined below.

Definition 1 The partial correlation, ρ*(Y_i,X_i,j|X_i,−j), is the correlation between the residuals resulting from the linear regression of X_i,j on X_i,−j and Y_i on X_i,−j

$${\rho }^{*}(Y_i,X_{i,j}|X_{i,-j})=\frac{\text{Cov}[Y_i-E(Y_i|X_{i,-j}),X_{i,j}-E(X_{i,j}|X_{i,-j})]}{{\left\{\text{Var}(Y_i-E(Y_i|X_{i,-j}))\text{Var}(X_{i,j}-E(X_{i,j}|X_{i,-j}))\right\}}^{1/2}}.$$ (2)

When p is large, estimating partial correlations is computationally cumbersome. [9] proposed a PC-simple algorithm to compute lower-order partial correlations ${\rho }^{*}(Y_i,X_{i,j}|X_{i,\mathcal{C}})$ sequentially for some $\mathcal{C}\subseteq \{1,\dots ,p\}\backslash \left\{j\right\}$ with the cardinality $\Vert \mathcal{C}{\Vert }_0=0,\dots ,m$, where m is a pre-specified integer. When m = 0 or $\mathcal{C}$ is empty, the PC-simple algorithm is a special case of the SIS procedure.

The PC-simple algorithm reduces the computational burden in multivariate screening and provides a new approach for variable screening. The validity of this algorithm hinges upon the condition that ${\rho }^{*}(Y_i,X_{i,j}|X_{i,\mathcal{C}})=0$ implies ρ*(Y_i,X_i,j|X_i,−j) = 0. To further examine this condition, [10] considered a sample version of (2)

$${\widehat{\rho }}^{*}(Y_i,X_{i,j}|X_{i,\mathcal{C}})=\frac{x_j^T(I_n-{\mathrm{\Pi }}_{\mathcal{C}})y}{\sqrt{x_j^T(I_n-{\mathrm{\Pi }}_{\mathcal{C}})x_j}\sqrt{y^T(I_n-{\mathrm{\Pi }}_{\mathcal{C}})y}},$$

where I_n is the identity matrix and ${\mathrm{\Pi }}_{\mathcal{C}}=x_{\mathcal{C}}{\left(x_{\mathcal{C}}^T{x}_{\mathcal{C}}\right)}^{-1}{x}_{\mathcal{C}}^T$ is the projection matrix onto the space spanned by $x_{\mathcal{C}}$. The numerator of ${\widehat{\rho }}^{*}(Y_i,X_{i,j}|X_{i,\mathcal{C}})$ can be decomposed as

$$x_j^T(I_n-{\mathrm{\Pi }}_{\mathcal{C}})y={\beta }_j{x}_j^T(I_n-{\mathrm{\Pi }}_{\mathcal{C}})x_j+\sum _{k\in {\mathcal{M}}_0\backslash (C\cup \{j\})}{\beta }_k{x}_j^T(I_n-{\mathrm{\Pi }}_{\mathcal{C}})x_k+x_j^T(I_n-{\mathrm{\Pi }}_{\mathcal{C}})\mathit{ϵ}.$$ (3)

Equation (3) indicates that, only when the last two terms on the right hand side of (3) are negligible compared to the first one, the PC-algorithm is valid and ${\widehat{\rho }}^{*}(Y_i,X_{i,j}|X_{i,\mathcal{C}})$ can be used to identify ${\mathcal{M}}_0$ in lieu of ${\widehat{\rho }}^{*}(Y_i,X_{i,j}|X_{i,-j})$. However, there is no guarantee this condition would hold for an arbitrary set $\mathcal{C}$.

3. Proposed Method

As discussed previously, to adequately assess the true contribution of each covariate, the conditional set $\mathcal{C}$ is critical. We propose compartmentalizing covariates into blocks so that variables from distinct blocks are less correlated. This solution may bypass the difficulty encountered in existing multivariate screening procedures and render improved computational feasibility, better screening efficiency and weaker theoretical conditions.

3.1. Preamble

First, in order to identify the active set ${\mathcal{M}}_0$, we consider the semi-partial correlation [15], a modified version of partial correlation that is defined below.

Definition 2 The semi-partial correlation, ρ(Y_i,X_i,j|X_i,−j), is the correlation between Y_i. and the residuals resulting from the linear regression of X_i,j on X_i,−j, i.e.

$$\rho \left(Y_i,X_{i,j}|X_{i,-j}\right)=\frac{\text{Cov}[Y_i,X_{i,j}-E(X_{i,j}|X_{i,-j})]}{{\left\{\text{Var}(Y_i)\text{Var}(X_{i,j}-E(X_{i,j}|X_{i,-j}))\right\}}^{1/2}}.$$ (4)

Indeed, the following lemma reveals that ρ(Y_i,X_i,j|X_i,−j) infers the effect of X_i,j on Y_i conditional on X_i,−j and hence identifying (1) is equivalent to finding

$${\mathcal{M}}_0=\{j:\rho (Y_i,X_{i,j}|X_{i,-j})\ne 0,j=1,\dots ,p\}.$$ (5)

Lemma 1 Suppose that Σ is positive definite. Then

$${\beta }_j=0ifandonlyif\rho (Y_i,X_{i,j}|X_{i,-j})=0$$

The intuitions of the proposed CIS method are further provided by the following lemma.

Lemma 2 Suppose that the predictors can be partitioned into independent blocks, ${\mathcal{S}}_1,\dots ,{\mathcal{S}}_G$. For any j = 1, …, p and some g such that $j\in {\mathcal{S}}_g$,

$$\rho (Y_i,X_{i,j}|X_{i,-j})=\rho (Y_i,X_{i,j}|X_{i,{\mathcal{S}}_g\backslash \left\{j\right\}}).$$

We first note that the equality in Lemma 2 does not hold for partial correlations, which motivates the use of semi-partial correlations instead. Second, Lemma 2 provides the intuition behind the proposed method. However, the independent block assumption is not required for the proposed method, which is valid for more general settings by thresholding the sample covariance matrix [16] and compartmentalizing covariates into blocks. Constructing covariance-based blocks is well understood in genetics literature and is often of interest per se [17]. For example, in a cutaneous melanoma study [18], 2,339 single-nucleotide polymorphisms (SNPs) could be grouped into 15 blocks; see Figure 1.

Figure 1:

(a) Graphical representation of 2,339 SNPs shown in He et al. (2016). The covariance plot clearly shows that SNPs form 15 distinct pathways. Specifically, SNPs are placed in the same pathway when their absolute sample correlation ≥ 0.2. (b) Fifteen pathways presented in (a) can be presented by a block-diagonal covariance matrix.

3.2. Thresholding Sample Covariance Matrix

To formalize the idea of thresholding, consider $\widehat{\Sigma }$ the sample estimate of Σ. For a constant δ > 0, let ${\widehat{\Sigma }}^{\delta }$ be the thresholded matrix of $\widehat{\Sigma }$ such that

$${\widehat{\Sigma }}_{jk}^{\delta }={\widehat{\Sigma }}_{jk}1\{\left|{\widehat{\Sigma }}_{jk}\right|\ge \delta \}.$$

We then partition the vector β into blocks, ${\widehat{\mathcal{S}}}_1,\dots ,{\widehat{\mathcal{S}}}_G$, in a way such that all off-diagonal blocks of ${\widehat{\Sigma }}^{\delta }$ are zero; e.g.

$${\widehat{\Sigma }}_{jk}^{\delta }=0forallj\in {\widehat{\mathcal{S}}}_g,k\in {\widehat{\mathcal{S}}}_{g^{\prime }},g\ne g^{\prime }.$$

Here G is the number of blocks and ${\widehat{\mathcal{S}}}_1,\dots ,{\widehat{\mathcal{S}}}_G$ forms a partition of the p predictors:

$${\widehat{\mathcal{S}}}_g\cap {\widehat{\mathcal{S}}}_{g^{\prime }}=\varnothing forg\ne g^{\prime },and{\widehat{\mathcal{S}}}_1\cup {\widehat{\mathcal{S}}}_2\cdots \cup {\widehat{\mathcal{S}}}_G=\{1,\dots ,p\}.$$

To identify the partition, we use a simple correlation based partition procedure, which is along the lines of the breadth-first search algorithm for finding connected components in graph theory [19]. To illustrate the idea, we consider a toy example. Suppose we have five variables (X_l, X₂, X₃, X₄, X₅) with a sample correlation matrix,

$$\widehat{\Sigma }=\left[\begin{array}{ccccc}1& 0.1& 0.7& 0.3& 0\\ 0.1& 1& 0.3& 0.5& 0\\ 0.7& 0.3& 1& 0.1& 0.8\\ 0.3& 0.5& 0.1& 1& 0.2\\ 0& 0& 0.8& 0.2& 1\end{array}\right],$$

and the thresholding parameter δ = 0:4. The corresponding adjacency matrix is

$$1(\left|\widehat{\Sigma }\right|>\delta )=\left[\begin{array}{ccccc}1& 0& 1& 0& 0\\ 0& 1& 0& 1& 0\\ 1& 0& 1& 0& 1\\ 0& 1& 0& 1& 0\\ 0& 0& 1& 0& 1\end{array}\right].$$

Further details for the partition are provided below:

• Step 1: We begin by treating each of the variables as its own block: {1}, {2}, {3}, {4}, {5}.

• Step 2: Two variable X_j and X_j′ are connected if and only of the jj′-th element in the adjacency matrix is non-zero. Note that X₃ is the only variable connected with X₁ and, hence, these two variables are merged to form the block {1, 3}. Thus, there are four blocks left: {1, 3}, {2}, {4}, {5}.

• Step 3: Next, X₁ and X₅ are the only variable connected with X₃. Therefore, X₅ is merged with the block {1, 3} to form a new block of {1, 3, 5}. That is, we have three blocks: {1, 3, 5}, {2}, {4}.

• Step 4: Because X₁ and X₃ are the only variable connected with X₅, there is no other variable that can be fused into the block {1, 3, 5}. Moreover, because X₂ and X₄ are connected, they are merged to form a new block of {2, 4}. The blocking process terminates as there are no unvisited variables. We have two blocks with respect to δ = 0.4: {1, 3, 5}, {2, 4}.

To implement the above algorithm, we utilize the R package igraph [20], which is computationally efficient for large p (e.g. from 10, 000 to 100, 000). Further discussion on thresholding the sample covariance matrix and detecting the block-diagonal structure can be found in [21].

3.3. Covariance-Insured Screening

With the block diagonal ${\widehat{\Sigma }}^{\delta }$, the disconnected blocks are approximately orthogonal, which motivates us to apply block-wise procedures to compute the semi-partial correlation within each identified block. The proposed approach can be summarized as follows.

• Step 1: Identify the disconnected blocks by thresholding the sample covariance matrix.

• Step 2: Compute the block-wise sample semi-partial correlations $\widehat{\rho }(Y_i,X_{i,j}|X_{i,{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}})$ For each $j\in {\widehat{\mathcal{S}}}_g$, 1 ≤ g ≤ G denote by ${\prod }_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}}$ the projection matrix onto the space spanned by $x_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}}$. That is,

  $${\mathrm{\Pi }}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}}=x_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}}{\left(x_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}}^T{x}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}}\right)}^{-1}{x}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}}^T.$$

  Then the block-wise sample semi-partial correlation can be calculated as

  $$\widehat{\rho }(Y_i,X_{i,j}|X_{i,{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}})=\frac{x_j^T(I_n-{\mathrm{\Pi }}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}})y}{\sqrt{x_j^T(I_n-{\mathrm{\Pi }}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}})x_j}\sqrt{y^{T}y}}.$$
• Step 3: Compute

  $${\widehat{\mathcal{M}}}_{CIS}=\{j\in {\widehat{\mathcal{S}}}_g,1\le g\le G:|\widehat{\rho }(Y_i,X_{i,j}|X_{i,{\widehat{S}}_g\backslash \left\{j\right\}})|>\nu \},$$

  where ν is a pre-defined threshold.

As suggested by a referee, one may also implement the ordinary least square (OLS) regression within each block and screen variables based on the OLS regression estimates. Empirically, we find that, when the within-block correlations are high, the proposed approach slightly outperforms the OLS-based approach. However, the OLS-based approach is relatively easier to be extended with the penalized methods to allow a large number of predictors within blocks.

4. Related Works

4.1. Sure Independence Screening (SIS)

The sure independence screening (SIS) [1] is the simplest approach for ultrahigh-dimensional variable screening, which selects all variables having sufficiently large absolute values of marginal sample correlation with the response. For a threshold parameter ν > 0, and let $\widehat{\text{Corr}}(Y_i,X_{ij})$ be the sample correlation between Y_i and X_ij, the selection index set by SIS is

$${\widehat{\mathcal{M}}}_{\text{SIS}}=\{j:|\widehat{\text{Corr}}(Y_i,X_{ij})|>\nu \}.$$

4.2. Tilting Procedure

The marginal screening methods ignore the correlation between the predictors. As a remedy, the Tilting procedure [10] considers partial correlation. For a threshold parameter ν > 0, the selection index set by Tilting is

$${\widehat{\mathcal{M}}}_{\text{Tilting}}=\{j:|{\rho }^{*}(Y_i,X_{i,j}|X_{i,\mathcal{C}})|>\nu \}.$$

Specifically, for each variable under consideration, the corresponding $\mathcal{C}$ contains all variables that are highly correlated with it. While successful in some applications, this way of selecting $\mathcal{C}$ may not adequately assess the true contribution of each covariate. As a result, important predictors that have weak marginal effects but strong joint effects can be missed (a simple example is provided in the Supplementary Materials). Moreover, the computational cost grows drastically with the number of predictors.

4.3. Proposed Procedure

These concerns motivate the proposed method, which leverages the group information including covariance by compartmentalizing covariates into disconnected blocks. This approach may bypass the difficulty encountered in the Tilting procedure, assess the true contribution of each covariate, and render improved computational feasibility. However, the computation burden of the proposed method increases when the maximal number of variables in the disconnected blocks is large. Further investigations are needed to extend the proposed method to more general settings.

5. Asymptotic Property for CIS

5.1. Conditions and Assumptions

To make our results general, we allow the dimension of covariates and the active set to grow as functions of sample size, i.e., p = p_n, G = G_n, and ${\mathcal{M}}_0={\mathcal{M}}_{0,n}$. Under some commonly assumed conditions below, we show that the CIS procedure identifies the true active set ${\mathcal{M}}_{0,n}$ with probability tending to 1.

• (A1) ${\Vert {\mathcal{M}}_{0,n}\Vert }_0=O(n^a)$ for some $a\in [0,\frac{1}{2})$, where ‖ · ‖₀ denotes the cardinality.

• (A2) The dimension of the covariates is log(p_n) = O(n^c) for some c ∈ [0,1 – 2b), where $b\in (a,\frac{1}{2})$.

• (A3) Assume that the predictors can be partitioned into disconnected blocks, ${\mathcal{S}}_1,\dots ,{\mathcal{S}}_{G_n}$, in a way such that all off-diagonal blocks of Σ are zero; e.g.

  $${\Sigma }_{jk}=0forallj\in {\mathcal{S}}_g,k\in {\mathcal{S}}_{g^{\prime }},g\ne g^{\prime },$$

  where G_n is the number of blocks (depending on n). Moreover, assume that the maximal number of variables in the disconnected blocks is bounded

  $$\underset{1\le g\le G_n}{\text{max}}{\Vert {\mathcal{S}}_g\Vert }_0\le C_1{n}^d$$

  for some constant C₁ > 0 and d ∈ [0, b − a).
• (A4) For a threshold ${\delta }_n=K(\sqrt{\text{log}(p_n)/n})=o(1)$ with K a positive constant, assume that all nonzero elements of Σ satisfy

  $$\text{inf}\{\left|{\Sigma }_{jk}\right|:{\Sigma }_{jk}\ne 0;j,k=1,\dots ,p_n\}\ge {\tau }_n,$$

  where

  $$\sqrt{n^{1-c}}({\tau }_n-{\delta }_n)\to \infty .$$
• (A5) For 1 ≤ j ≤ p_n, let F_j be the cumulative distribution function of $X_{i,j}^2$. Assume

  $${\int }_0^{\infty }\text{exp}(\lambda t)d{F}_j(t)<\infty$$

  for 0 < |λ| < λ₀ with some λ₀ > 0.
• (A6) Let λ_max(A) and λ_min(A) represent the largest and smallest eigenvalues of a positive definite matrix A. There exist positive constants γ, τ_min and τ_max such that

  $$P\left(\underset{\mathcal{D}}{\text{min}}\{{\lambda }_{min}(\frac{1}{n}{x}_{\mathcal{D}}^T{x}_{\mathcal{D}})\}\le {\tau }_{min}\text{or}\underset{\mathcal{D}}{\text{max}}\{{\lambda }_{max}(\frac{1}{n}{x}_{\mathcal{D}}^T{x}_{\mathcal{D}})\}\ge {\tau }_{max}\right)\le \text{exp}(-\gamma n)$$

  for any $\mathcal{D}\subset \{1,\dots ,p\}$ with cardinality ${\Vert \mathcal{D}\Vert }_0\le n^{\text{max}\{a,d\}}$.

• (A7) Assume that, with probability 1, max_1≤j≤p ‖x_j‖_∞ ≤ K_x for a constant K_x > 0, where ‖x_j‖_∞ = max_1≤i≤n |X_i,j|.

• (A8) Assume non-zero coefficients β_j satisfying ${\text{max}}_{j\in {\mathcal{M}}_{0,n}}\left|{\beta }_j\right|<M$ for some M ∈ (0, ∞) and n^κ ${\text{min}}_{j\in {\mathcal{M}}_{0,n}}\left|{\beta }_j\right|\to \infty$ for κ ∈ [0, b − a − d).

• (A9) The random errors follow a sub-exponential distribution; i.e. ϵ₁, …, ϵ_n are independent random variables with mean 0 and satisfy

  $$\frac{1}{n}\sum _{i=1}^{n}E{\left|{ϵ}_i\right|}^m\le \frac{m!}{2}{K}_{ϵ}^{m-2},m=2,3,\dots ,$$

  where K_ϵ is a constant depending on the distribution.

Condition (A1) allows the number of non-zero coefficients ${\Vert {\mathcal{M}}_{0,n}\Vert }_0$ to grow with the sample size n. Condition (A2) allows for ultrahigh-dimensionality. Conditions (A3)-(A5) guarantee the existence of the projection matrix ${\mathrm{\Pi }}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}}$ and hence the corresponding sample semi-partial correlations. In particular, Condition (A3) assumes a block diagonal structure of the population covariance matrix. Conditions (A4) and (A5) are also assumed in [21], which imply the consistency of the covariance matrix partitioning procedure. Condition (A6) rules out the strong collinearity between variables, which is similar to Assumption 1 in [11] and Assumption 5 in [10]. Moreover, as shown in Lemma 1 of [22], there is a connection between Condition (A6) and the condition requiring strict positive definiteness of the population covariance matrix, which is commonly assumed in the variable selection literature [23, 24, 9]. For instance, when both X and ϵ follow the normal distribution, the former is implied by the latter. Condition (A7) is usually satisfied in practice. Condition (A8) controls the magnitude of the non-zero coefficients, which was also assumed in [1] and [11]. We note that, when the magnitude of the non-zero coefficients is small, to correctly identify the true signals, a smaller bound is needed for the maximum number of predictors within each correlated blocks. The sub-exponential distribution in Condition (A9) is general and includes many commonly assumed distributions.

5.2. Main Theorem

We start from a lemma summarizing some results for the consistency property of thresholding covariance matrix, meaning that the partitioning algorithm identifies the true diagonal blocks with probability tending to 1.

Lemma 3 Let ${\widehat{\Sigma }}^{{\delta }_n}$ be the thresholded covariance matrix:

$${\widehat{\Sigma }}_{jk}^{{\delta }_n}={\widehat{\Sigma }}_{jk}1\{\left|{\widehat{\Sigma }}_{jk}\right|\ge {\delta }_n\},1\le j,k\le p_n.$$

Assume conditions (A2)-(A5), with positive constants C₂ and C₃,

$$P\left(\sum _{j,k}1({\widehat{\Sigma }}_{jk}^{{\delta }_n}\ne 0,{\Sigma }_{jk}=0)>0\right)\le C_2{p}_n^2\text{exp}(-n{C}_3{\delta }_n^2)\to 0,$$

where we choose ${\delta }_n=K\sqrt{\text{log}(p_n)/n}=o(1)$, with the constant K large enough such that C₃K² > 2. Applying the additional condition $\sqrt{n^{1-c}}({\tau }_n-{\delta }_n)\to \infty$,

$$P\left(\sum _{j,k}1({\widehat{\Sigma }}_{jk}^{{\delta }_n}=0,{\Sigma }_{jk}\ne 0)>0\right)\le C_2{p}_n^2\text{exp}(-n{C}_3{\left({\tau }_n-{\delta }_n\right)}^2)\to 0.$$

Therefore,

$$P({\widehat{\mathcal{S}}}_g^{{\delta }_n}={\mathcal{S}}_g,1\le g\le G_n)\ge 1-C_2{p}_n^2\text{exp}(-n{C}_3{\delta }_n^2)-C_2{p}_n^2\text{exp}(-n{C}_3{\left({\tau }_n-{\delta }_n\right)}^2)\to 1.$$

We establish the important properties of CIS by presenting the following theorem.

Theorem 1 (screening consistency) Assume that (A1)-(A9) hold. Denote by ${\widehat{\mathcal{M}}}_{CIS}({\nu }_n,{\delta }_n)$ the set of selected variables from the CIS procedure with the tuning parameters ν_n = O(n^−κ) and ${\delta }_n=K(\sqrt{\text{log}(p_n)/n})$. Then the following two statements are true:

$$\begin{gathered} P\left(\underset{j\in {\widehat{\mathcal{S}}}_g\cap {\mathcal{M}}_{0,n},g=1,\dots ,G_n}{\text{min}}{\nu }_n^{-1}|\widehat{\rho }(Y_i,X_{i,j}|X_{i,{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}})|\ge O(n^{\kappa }\underset{j\in {\mathcal{M}}_0}{\text{min}}\left|{\beta }_j\right|)\right) \\ \ge 1-O(\text{exp}(-(C_3{K}^2-2)n^c)), \end{gathered}$$

$$\begin{gathered} P\left(\underset{j\in {\widehat{\mathcal{S}}}_g\backslash {\mathcal{M}}_{0,n},g=1,\dots ,G_n}{\text{max}}{\nu }_n^{-1}|\widehat{\rho }(Y_i,X_{i,j}|X_{i,{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}})|\le O(n^{-(b-a-d/2-\kappa )})\right) \\ \ge 1-O(\text{exp}(-(C_3{K}^2-2)n^c)), \end{gathered}$$

for a poistive constant η. These results imply the screening consistency property

$$P({\widehat{\mathcal{M}}}_{CIS}({\nu }_n,{\delta }_n)={\mathcal{M}}_{0,n})\ge 1-O(\text{exp}(-(C_3{K}^2-2)n^c)).$$

5.3. Iterative CIS

Even though theoretical thresholds have been derived in various variable screening procedures, it remains a challenge to implement them. Moreover, strong correlations among predictors may deteriorate the performance of screening procedures in finite samples. To address these challenges, iterative SIS (ISIS) [1] was proposed as a remedy for marginal screening procedures. Along the same lines, we design an iterative CIS algorithm (termed ICIS) and further build a thresholding procedure to control false discoveries.

• Step 1: Resample the original data with replacement multiple (say B) times.

• Step 2: For each resampled data, first identify the variables by the proposed CIS procedure, followed by applying adaptive Lasso for variable selection and computing the associated residuals in the regression.

• Step 3: Treating those residuals as new responses, we apply CIS to the remaining variables.

• Step 4: We repeat the procedure until a pre-specified number of iterations is achieved or the selected variables do not change.

• Step 5: Denote the selected variable index set from the r-th resampled data as ${\widehat{\mathcal{M}}}^{(r)}$ for r = 1, …, B. Let ${\widehat{\Psi }}_j$ be the empirical probability that the j-th variable is selected:

  $${\widehat{\Psi }}_j=\frac{1}{B}\sum _{r=1}^{B}I(j\in {\widehat{\mathcal{M}}}^{(r)}).$$

  For a threshold ψ ∈ (0, 1), the procedure selects variables with

  $${\widehat{\mathcal{M}}}_{ICIS}=\{j:{\widehat{\Psi }}_j\ge \psi ,j=1,\dots ,p\}.$$ (6)

To determine data-driven thresholds for the selection frequency ψ, we further adopt a random permutation-based approach [18] to control the empirical Bayes false discovery rate [25]. For a pre-specified value q ∈ (0, 1), ψ will be chosen to ensure that at most q proportion of the selected variables would be false positives. Further technical details are provided in the Supplementary Materials.

6. Simulation Study

6.1. Performance of the CIS

We assess the performance of the proposed CIS method by comparing it with SIS, non-iterative versions of HOLP and the Tilting under various simulation configurations. Block-wise semi-partial correlation are estimated by applying R package corpcor. For each configuration a total of 100 independent data are generated.

• (Model A) Data are generated with n = 1, 000 and p = 10, 000, from a multivariate normal distribution with a block-diagonal covariance structure (m = 100 independent blocks, each with 100 predictors). Within each block the variables follow an AR1 model with the auto-correlation (ρ) varying from 0.5 to 0.9. The variables with non-zero effects are

  $$X_1,X_2,X_{m+1},X_{m+2},X_{2m+1},X_{3m+1},X_{4m+1},X_{5m+1},X_{6m+1},X_{7m+1}$$

  with the corresponding coefficients 1, −1,1, −1, −1,1, −1,1, −1,1.
• (Model B) This model is similar to Model A, but the variables with non-zero effects are

  $$X_1,X_{m+1},X_{2m+1},X_{3m+1},X_{4m+1},X_{5m+1},X_{6m+1},X_{7m+1},X_{8m+1},X_{9m+1}$$

  with the corresponding coefficients 1, 1, −1, 1, −1, 1, −1, 1, −1, 1.
• (Model C) This model is similar to Model A, but the covariance matrix is not block-diagonal (e.g. the variables follow an AR1 model with the auto-correlation (ρ) varying from 0.5 to 0.9). The variables with non-zero effects are

  $$X_{j_1},X_{j_1+1},X_{j_2},X_{j_2+1},X_{j_3},X_{j_4},X_{j_5},X_{j_6},X_{j_7},X_{j_8}$$

  with the corresponding coefficients 1, −1, 1, −1, −1, 1, −1, 1, −1, 1, where the indices j₁, …, j₈ are randomly drawn from {1, …, p}.

Table 1 compares the minimum model size (MMS) to include the true model. For Model A and B, the threshold $\delta =5\sqrt{\text{log}(p)/n}$ is used to determine blocks in the CIS procedure. The purpose of simulation Model C is to provide a sensitivity analysis so that we can assess the proposed method when its assumed conditions are violated. Instead of applying δ, we partition variables into blocks with 10 variables within each block (stop merging new variables if the number of variables achieves the limit). When the correlations are low, all methods perform well and the MMS is close to 10, the true model size. When the correlation is greater than 0.6, CIS outperforms SIS and Tilting in the presence of signal cancellation (Models A and C). The poor performance of SIS and Tilting can be explained in part because the strong marginal correlation condition is not satisfied. Interestingly, HOLP is competitive and performs well for Model B and C, but does not work well for Model A. This might be caused by the violation of the diagonal dominance of X^T(XX^T)⁻¹X required by HOLP.

Table 1:

The minimum model size (MMS) to include the true model (standard deviation in parentheses) for Models A-C.

Models	ρ	SIS	HOLP	Tilting	CIS
A	0.9	7103.2 (1937.4)	3458.4 (2932.2)	1041.1 (648.7)	73.7 (141.7)
	0.8	2835.0 (2334.0)	660.7 (877.2)	168.3 (131.2)	11.4 (5.1)
	0.7	505.9 (594.9)	102.9 (253.2)	31.0 (8.7)	10.0 (0.0)
	0.6	60.4 (75.3)	21.9 (20.9)	21 (2.9)	10.0 (0.0)
	0.5	18.1 (7.7)	13.2 (2.2)	19.5 (21.7)	10.0 (0.0)
B	0.9	21.2 (5.4)	12.2 (1.9)	154.2 (515.1)	68.6 (80.4)
	0.8	13.2 (2.5)	10.7 (1.1)	13.9 (4.4)	10.9 (2.2)
	0.7	10.7 (1.1)	10.2 (0.5)	10.7 (1.1)	10.0 (0.0)
	0.6	10.2 (0.5)	10.0 (0.0)	10.2 (0.5)	10.0 (0.0)
	0.5	10.0 (0.0)	10.0 (0.0)	10.0 (0.0)	10.0 (0.0)
C	0.9	3729.2 (944.3)	220.7 (555.1)	910.4 (1215.3)	270.3 (453.4)
	0.8	1570.4 (1343.2)	47.2 (946.1)	147.8 (86.2)	14.8 (8.6)
	0.7	350.6 (523.2)	27.0 (11.6)	47.4 (16.5)	10.8 (0.8)
	0.6	58.1 (54.5)	17.8 (3.3)	26.5 (5.7)	10.2 (0.4)
	0.5	21.9 (5.0)	11.5 (1.7)	18.3 (3.9)	10.0 (0.1)

6.2. Performance of the iterative CIS (ICIS)

We compare ICIS with Lasso, adaptive Lasso, ISIS, iterative HOLP and Tilting.

• (Model D) This model is similar to Model A. Within each block, the variables follow a AR1 model with parameter 0.9. The effect size of β is chosen as 0.5, 0.75 and 1 to generate a wide range of signal strength.

Data are generated with p = 1, 000 or 10, 000. No results are reported for Tilting with p = 10, 000 due to its intensive computation. As indicated in Table 2, iterative CIS outperforms most methods, yielding the smallest false negative (FN) and false positive (FP) combined.

Table 2:

Numbers of false positives (FP) and numbers of false negatives (FN) for Model D.

P	|β|	Measures	Lasso	Adaptive Lasso	ISIS	HOLP	Tilting	ICIS
10,000	0.5	FP	45.47	0.01	0.02	0.13	NA	0.20
		FN	3.47	4.00	4.00	4.00	NA	0.33
	0.75	FP	145.57	0.10	26.88	0.19	NA	0.22
		FN	1.31	2.31	2.85	4.00	NA	0.00
	1	FP	220.87	0.06	23.62	0.21	NA	0.08
		FN	0.00	0.00	0.14	4.00	NA	0.00
1,000	0.5	FP	85.35	7.64	0.80	0.27	0.21	0.73
		FN	0.28	0.52	3.80	3.09	3.08	0.06
	0.75	FP	90.85	3.83	10.15	0.75	0.95	0.80
		FN	0.00	0.00	0.12	0.32	0.90	0.00
	1	FP	92.49	2.28	2.15	0.13	0.78	0.22
		FN	0.00	0.00	0.00	0.00	0.00	0.00

We next compare the proposed method with iterative Graphlet Screening (GS). We consider Experiment 2b reported in [12], which is described as follows:

• (Model E) Data are generated with p = 5,000 and n = p^κ with κ = 0.975. We consider the following Asymptotic Rare and Weak (ARW) model [12]. The signal vector β is modeled by β = b ○ μ, where ○ denotes the Hadamard product (i.e. entrywise product). The vector of μ consists of z_j|μ_j|, j = 1, …, p, where z_j = ±1 with equal probability and $\left|{\mu }_j\right|~0.8{\nu }_{{\tau }_p}+0.2h$, where ${\nu }_{{\tau }_p}$ is the point mass at τ_p with ${\tau }_p=\sqrt{6\text{log}(p)}$. The h(x) is the density of τ_p(1 + V/6), $V~{\chi }_1^2$. We choose the correlation matrix to be a diagonal block matrix where each block is a 4 by 4 matrix satisfying Corr(X_i,j, X_i,j′) = I(j = j′) + 0.4I(|j − j′| = 1) × sign(6 − j − j′) + 0.05I(|j − j′| > 2) × sign(5.5 − j − j′), 1 ≤ j, j′ ≤ 4. The vector b consists of b_j, j = 1, …, p, where b_j = 0 or 1. Let k be the number of variables with b_j ≠ 0 within each block. With π = 0.2 and ϑ = 0.35, we randomly choose (1 − 4p^−ϑ) fraction of the blocks for k = 0 (e.g. b_j = 0 for all j belongs to these block), 4(1 − π)p^−ϑ fraction of the blocks for k = 1, and 4πp^−ϑ fraction of the block for k ∈ {2, 3,4}.

Table 3 compares Lasso, adaptive Lasso, ISIS, ICIS and GS. No results are reported for HOLP (intensive computation for large n) or Tilting (intensive computation for large p). Web Figure A1 in the Supplementary Materials compares ICIS and GS with various choices of tuning parameters. The results suggest that the perturbation of tuning parameters has relatively small effects on the proposed ICIS, which outperforms GS.

Table 3:

Numbers of false positives (FP) and false negatives (FN) for ModelE.

Measures	Lasso	Adaptive Lasso	ISIS	GS	ICIS
FP	959.84	0.16	137.90	48.78	20.13
FN	2.99	21.66	10.90	26.04	2.55

7. Real Data Study

7.1. Multiple Myeloma Data

Multiple myeloma (MM) represents more than 10 percent of all hematologic cancers in the U.S. [26], resulting in more than 10,000 deaths each year. Developments in gene-expression profiling and sequencing of MM patients have offered effective ways of understanding the cancer genome [27]. Despite this promising outlook, analytic methods remain insufficient for achieving truly personalized medicine. The standard procedure is to evaluate one gene at a time, which results in low statistical power to identify the disease-associated genes [28]. Thus, more accurate models that leverage the large amounts of genomic data now available are in great demand.

Our goal is to identify genes that are relevant to the Beta-2-microglobulin (Beta-2-M), which is a continuous prognostic factor for multiple myeloma. We use gene expression and Beta-2-M from 340 multiple myeloma patients who were recruited into clinical trial UARK 98–026, which studied total therapy II (TT2). These data are described in [29], and can be obtained through the MicroArray Quality Control Consortium II study [30], available on GEO (GSE24080). Gene expression profiling was performed using Affymetrix U133Plus2.0 microarrays. Following the strategy in [4], we averaged the expression levels of probesets corresponding to the same gene, resulting in 20,502 covariates.

7.2. Analysis Methods

The genetic variants often possess block covariance structures. In our motivating MM study, the estimated covariance matrix of gene expressions is nearly block diagonal under a suitable permutation of the variables. The predictors are strongly correlated within blocks and are less correlated between blocks (a sample covariance plot is shown in Figure 2a). Hence, many elements of the covariance matrix are small. A major challenge, arising from such a covariance structure, is that some genes can be jointly relevant but not marginally relevant to the disease outcome. In such a difficult setting, popular methods such as marginal screening and multivariate screening are overwhelmed, because marginal screening largely neglects correlations across predictors. Exhaustive multivariate screening is computationally infeasible.

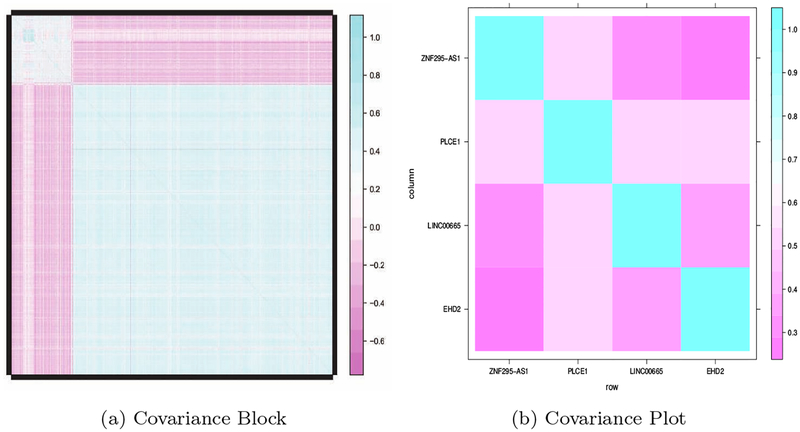
Figure 2:

(a) The covariance block containing PLCE1, EHD2, LINC00665 and ZNF295-AS1. (b) Covariance plot

To select the informative genes, the proposed ICIS is implemented on the MM data set with 340 subjects. The thresholding parameter for δ_n is fixed at $5\sqrt{\text{log}(p)/n}$ such that the maximal number of variables in the disconnected blocks satisfies q_n ≤ n. The importance of predictors is evaluated by the selection frequencies among the 50 resampled data. The estimated false discovery rate is calculated to determine a data-driven threshold ψ (defined in Section 5.3) for the selection frequency such that at most q proportion of the selected variables would be false positives. We compare the ICIS with Lasso, adaptive Lasso, ISIS and iterative HOLP.

7.3. Results

Using our method, a total of 24 genes pass the threshold for q = 0.1. In comparison, the Lasso, adaptive Lasso, ISIS and HOLP procedures select 74, 0, 0 and 54 genes, respectively. All these results are consistent with those from the Simulation section. The Lasso tends to select many irrelevant variables, while the adaptive Lasso and ISIS suffer from a reduced power to identify informative predictors. The proposed method selects substantially fewer variables than the HOLP and provides a control for false discoveries. Some of the genes selected by the proposed method confirm those identified by Lasso and HOLP. One of the top common genes, MMSET (multiple myeloma SET domain containing protein), is known as the key molecular target in MM [31] and has been involved in the chromosomal translocation in MM. Another selected gene, FAM72A (Family With Sequence Similarity 72 Member A), has been reported to be associated with poor prognosis in multiple myeloma [32]. Moreover, expression level of gene ATF6 (Activating Transcription Factor 6) has been reported to predict the response of multiple myeloma to the proteasome inhibitor Bortezomib [33].

In addition, among the genes in our finding but not in other methods, Phospholipase C epsilon 1 (PLCE1), EH-domain containing 2 (EHD2), long inter-genic non-protein coding RNA 665 (LINC00665) and ZNF295 Antisense RNA 1 (ZNF295-AS1) are correlated with each other (see Figure 2b) and have reversed covariate effects (−0.51, 1.02, −0.23 and −0.43). These results suggest the existence of signal cancelations. The failure of identifying such genes by other screening methods may be explained in part because the strong marginal correlation condition is not satisfied. In fact, these genes are likely to be associated with the prognostic of the MM, as reported by previous literature. For instance, PLCE1, located on chromosome 10q23, encodes a phospholipase that has been reported to be associated with intracellular signaling through the regulation of a variety of proteins such as the protein kinase C (PKC) isozymes and the proto-oncogene ras [34, 35]. On the other hand, EDH2 is a plasma membrane-associated member of the EHD family, which regulates internalization and is related to actin cytoskeleton. Abnormal expression of EHD2 has been linked to metastasis of carcinoma [36]. In addition, [37] suggested linc00665 might play a role as sponge to indirectly de-repress a series of mRNAs in nasopharyngeal nonkeratinizing carcinoma. It appears that the proposed approach is able to identify jointly-informative variables that only have marginally weak associations with outcomes.

8. Discussion

We have developed a covariance-insured screening method for ultrahigh-dimensional variables. The innovation lies in that, as opposed to conventional variable screening methods, the proposed approach leverages the dependence structure among covariates and is able to identify jointly informative variables that only have weak marginal associations with outcomes. Moreover, the proposed method is computationally efficient, and thus suitable for the analysis of ultrahigh-dimensional data.

Appendix

Proof of Lemma 3

By the construction of ${\widehat{\Sigma }}^{{\delta }_n}$, the set

$$\{(j,k):{\widehat{\Sigma }}_{jk}^{{\delta }_n}\ne 0,{\Sigma }_{jk}=0\}=\{(j,k):\left|{\widehat{\Sigma }}_{jk}^{{\delta }_n}\right|>{\delta }_n,{\Sigma }_{jk}=0\}\subseteq \{(j,k):\left|{\widehat{\Sigma }}_{jk}^{{\delta }_n}-{\Sigma }_{jk}\right|>{\delta }_n\}.$$

Thus,

$$P\left(\sum _{j,k}1({\widehat{\Sigma }}_{jk}^{{\delta }_n}\ne 0,{\Sigma }_{jk}=0)>0\right)\le P\left(\underset{j,k}{\text{max}}|{\widehat{\Sigma }}_{jk}^{{\delta }_n}-{\Sigma }_{jk}|>{\delta }_n\right).$$

Assuming condition (A5) and applying Lemma 1 of [21], we have

$$P\left(\underset{j,k}{\text{max}}|{\widehat{\Sigma }}_{jk}^{{\delta }_n}-{\Sigma }_{jk}|>{\delta }_n\right)\le C_2{p}_n^2\text{exp}(-n{C}_3{\delta }_n^2).$$

Assuming condition (A2),

$$C_2{p}_n^2\text{exp}(-n{C}_3{\delta }_n^2)=O(\text{exp}(-(C_3{K}^2-2)n^c))\to 0,$$

with C₃K² > 2. Similarly,

$$\{(j,k):{\widehat{\Sigma }}_{jk}^{{\delta }_n}=0,{\Sigma }_{jk}\ne 0\}\subseteq \{(j,k):|{\widehat{\Sigma }}_{jk}^{{\delta }_n}-{\Sigma }_{jk}|>{\tau }_n-{\delta }_n\}.$$

Thus,

$$\begin{gathered} P\left(\sum _{j,k}1({\widehat{\Sigma }}_{jk}^{{\delta }_n}=0,{\Sigma }_{jk}\ne 0)>0\right)\le P\left(\underset{j,k}{\text{max}}|{\widehat{\Sigma }}_{jk}^{{\delta }_n}-{\Sigma }_{jk}|>{\tau }_n-{\delta }_n\right) \\ \le C_2{p}_n^2\text{exp}(-n{C}_3{\left({\tau }_n-{\delta }_n\right)}^2)=O(\text{exp}(-(C_3{n}^{1-c}{\left({\tau }_n-{\delta }_n\right)}^2-2)n^c))\to 0, \end{gathered}$$

with n^1−c(τ_n − δ_n)² → ∞. Therefore,

$$P({\cup }_{g=1}^{G_n}\{{\widehat{\mathcal{S}}}_g^{{\delta }_n}\ne {\mathcal{S}}_g\})\le O(\text{exp}(-(C_3{K}^2-2)n^c))+O(\text{exp}(-(C_3{n}^{1-c}{\left({\tau }_n-{\delta }_n\right)}^2-2)n^c)).$$

In fact, the first term dominates the second one. In summary,

$$P({\widehat{\mathcal{S}}}_g^{{\delta }_n}={\mathcal{S}}_g,1\le g\le G_n)\ge 1-O(\text{exp}(-(C_3{K}^2-2)n^c))\to 1.$$

Proof of Theorem 1

The block-wise sample semi-partial correlation can be calculated as

$$\widehat{\rho }(Y_i,X_{i,j}|X_{i,{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}})=\frac{\frac{1}{n}{x}_j^T(I_n-{\mathrm{\Pi }}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}})y}{\frac{1}{n}\sqrt{x_j^T(I_n-{\mathrm{\Pi }}_{{\mathcal{S}}_g\backslash \left\{j\right\}})x_j}\sqrt{y^{T}y}},$$

where $j\in {\widehat{\mathcal{S}}}_g$ for some g, a factor 1/n is applied to both numerator and denominator to facilitate asymptotic derivations, and ${\mathrm{\Pi }}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}}$ is the projection matrix onto the space spanned by $x_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}}$

$${\mathrm{\Pi }}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}}=x_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}}{\left(x_{{\mathcal{S}}_g\backslash \left\{j\right\}}^T{x}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}}\right)}^{-1}{x}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}}^T.$$

Because ${\beta }_k{x}_j^T(I_n-{\mathrm{\Pi }}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}})x_k=0$ for $k\in {\mathcal{M}}_{0,n}\cap ({\widehat{\mathcal{S}}}_g\backslash \{j\})$, the numerator can be decomposed as

$$\frac{1}{n}{x}_j^T(I_n-{\mathrm{\Pi }}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}})y=\frac{1}{n}{\beta }_j{x}_j^T(I_n-{\mathrm{\Pi }}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}})x_j+\frac{1}{n}\sum _{k\in {\mathcal{M}}_{0,n}\backslash {\widehat{\mathcal{S}}}_g}{\beta }_k{x}_j^T(I_n-{\mathrm{\Pi }}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}})x_k+\frac{1}{n}{x}_j^T(I_n-{\mathrm{\Pi }}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}})\mathit{ϵ}.$$ (7)

To show the first and the second statements in Theorem 1, we consider the following two scenarios respectively: (1) $j\in {\mathcal{M}}_{0,n}$ and (2) $j\in \{1,\dots ,p_n\}\backslash {\mathcal{M}}_{0,n}$.

Step 1: $j\in {\mathcal{M}}_{0,n}$

Step 1.1 We first aim to show that for $j\in {\mathcal{M}}_{0,n}$ the absolute value of the first term on the right hand side of (7) can be bounded from below and the last two terms on the right hand side of (7) are negligible compared to the first term.

Specifically, for the first term we can show that for some g such that $j\in {\widehat{\mathcal{S}}}_g$,

$$P\left(\underset{j\in {\widehat{\mathcal{S}}}_g\cap {\mathcal{M}}_{0,n,g=1,\dots ,G_n}}{\text{min}}\left|\frac{1}{n}{\beta }_j{x}_j^T(I_n-{\mathrm{\Pi }}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}})x_j\right|\ge \alpha \underset{j\in {\mathcal{M}}_{0,n}}{\text{min}}\left|{\beta }_j\right|\right)\ge 1-O(\text{exp}(-(C_3{K}^2-2)n^c)),$$

where α > 0 is a given constant. By the property of the determinant of a partitioned matrix, when A is non-singular,

$$\text{det}\left(\begin{array}{cc}A& B\\ C& D\end{array}\right)=\text{det}(A)\text{det}(D-C{A}^{-1}B).$$

Then we have

$$\begin{gathered} \text{det}\left(\frac{1}{n}{x}_{{\widehat{\mathcal{S}}}_g}^T{x}_{{\widehat{\mathcal{S}}}_g}\right)=\text{det}\left(\frac{1}{n}{x}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}}^T{x}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}}\right)\text{det}\left(\frac{1}{n}{x}_j^T{x}_j-\frac{1}{n}{x}_j^T{\mathrm{\Pi }}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}}{x}_j\right) \\ =\text{det}\left(\frac{1}{n}{x}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}}^T{x}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}}\right)\frac{1}{n}{x}_j^T(I_n-{\mathrm{\Pi }}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}})x_j. \end{gathered}$$

By Condition (A6), there exists a constant α > 0 such that

$$P\left(\frac{1}{n}{x}_j^T(I_n-{\mathrm{\Pi }}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}})x_j\le \alpha |{\widehat{\mathcal{S}}}_g={\mathcal{S}}_g\right)\le \text{exp}(-\gamma n).$$

Therefore,

$$\begin{gathered} P\left(\underset{j\in {\widehat{\mathcal{S}}}_g\cap {\mathcal{M}}_{0,n},g=1,\dots ,G_n}{\text{min}}\left|\frac{1}{n}{\beta }_j{x}_j^T(I_n-{\mathrm{\Pi }}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}})x_j\right|\le \alpha \underset{j\in {\mathcal{M}}_{0,n}}{\text{min}}\left|{\beta }_j\right|\right) \\ \le P\left(\underset{j\in {\widehat{\mathcal{S}}}_g\cap {\mathcal{M}}_{0,n},g=1,\dots ,G_n}{\text{min}}\left|\frac{1}{n}{\beta }_j{x}_j^T(I_n-{\mathrm{\Pi }}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}})x_j\right|\le \alpha \underset{j\in {\mathcal{M}}_{0,n}}{\text{min}}\left|{\beta }_j\right||{\widehat{\mathcal{S}}}_g={\widehat{\mathcal{S}}}_g,g=1,\dots ,G_n\right) \\ +P({\cup }_{g=1}^{G_n}\{{\widehat{\mathcal{S}}}_g^{{\delta }_n}\ne {\widehat{\mathcal{S}}}_g\}) \\ \le \text{exp}(-\gamma n)+O(\text{exp}(-(C_3{K}^{-2}-2)n^c)), \end{gathered}$$

where the second term dominates the first one. Thus,

$$P\left(\underset{j\in {\widehat{\mathcal{S}}}_g\cap {\mathcal{M}}_{0,n},g=1,\dots ,G_n}{\text{min}}\left|\frac{1}{n}{\beta }_j{\text{x}}_j^T(I_n-{\mathrm{\Pi }}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}})x_j\right|\ge \alpha \underset{j\in {\mathcal{M}}_{0,n}}{\text{min}}\left|{\beta }_j\right|\right)\ge 1-O(\text{exp}(-(C_3{K}^2-2)n^c)).$$

Step 1.2 We next consider the second term in (7) and show that for j = 1, …, p_n and some g such that $j\in {\widehat{\mathcal{S}}}_g$,

$$P\left(\left|\sum _{k\in {\mathcal{M}}_{0,n}\backslash {\widehat{\mathcal{S}}}_g}\frac{{\beta }_k}{n}{x}_j^T(I_n-{\mathrm{\Pi }}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}})x_k\right|\le O(n^{-(b-a-d/2)})\right)\ge 1-O(\text{exp}(-(C_3{K}^2-2)n^c)).$$

Indeed, by the triangular inequality, given ${\widehat{\mathcal{S}}}_g$,

$$\left|\sum _{k\in {\mathcal{M}}_{0,n}\backslash {\widehat{\mathcal{S}}}_g}\frac{{\beta }_k}{n}{x}_j^T(I_n-{\mathrm{\Pi }}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}})x_k\right|\le \left|\sum _{k\in {\mathcal{M}}_{0,n}\backslash {\widehat{\mathcal{S}}}_g}\frac{{\beta }_k}{n}{x}_j^T{x}_k\right|+\left|\sum _{k\in {\mathcal{M}}_{0,n}\backslash {\widehat{\mathcal{S}}}_g}\frac{{\beta }_k}{n}{x}_j^T{\mathrm{\Pi }}_{{\widehat{\mathcal{S}}}_g\backslash {\left\{j\right\}}^{{\text{X}}_k}}\right|.$$

By Condition (A1), ${\Vert {\mathcal{M}}_{0,n}\Vert }_0=O(n^a)$. By the construction of ${\widehat{\mathcal{S}}}_g$,

$$\left|n^{-1}{x}_j^T{x}_k\right|\le {\delta }_n$$

for $j\in {\widehat{\mathcal{S}}}_g$ and $k\in {\mathcal{M}}_{0,n}\backslash {\widehat{\mathcal{S}}}_g$, where ${\delta }_n=O(\sqrt{\text{log}(p_n)/n})\le O(n^{-b})$. By Condition (A7), ${\text{max}}_{j\in {\mathcal{M}}_{0,n}}\left|{\beta }_j\right|<M$. Therefore, given ${\widehat{\mathcal{S}}}_g$,

$$\left|\sum _{k\in {\mathcal{M}}_{0,n}\backslash {\widehat{\mathcal{S}}}_g}\frac{{\beta }_k}{n}{x}_j^T{x}_k\right|\le O(n^{-(b-a)}).$$ (8)

Moreover, given ${\widehat{\mathcal{S}}}_g$,

$$\left|\sum _{k\in {\mathcal{M}}_{0,n}\backslash {\widehat{\mathcal{S}}}_g}\frac{{\beta }_k}{n}{x}_j^T{\mathrm{\Pi }}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}}{x}_k\right|\le \frac{M{n}^a}{n}{\Vert {\mathrm{\Pi }}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}}{x}_j\Vert }_2\underset{k\in {\mathcal{M}}_{0,n}\backslash {\widehat{\mathcal{S}}}_g}{\text{max}}{\Vert {\mathrm{\Pi }}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}}{x}_k\Vert }_2,$$

where ‖u‖₂ is the ℓ₂–norm for $u\in {ℝ}^n$. By Condition (A6),

$$P\left({\lambda }_{max}\left({\left(\frac{1}{n}{x}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}}^T{x}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}}\right)}^{-1}\right)\le 1/{\tau }_{min}|{\widehat{\mathcal{S}}}_g={\mathcal{S}}_g\right)\ge 1-\text{exp}(-\gamma n)$$

and applying Lemma 3

$$P\left(\underset{k\in {\mathcal{M}}_{0,n}\backslash {\widehat{\mathcal{S}}}_g}{\text{max}}\frac{1}{\sqrt{n}}{\Vert {\mathrm{\Pi }}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}}{\text{x}}_k\Vert }_2\le O\left(n^{-(b-d/2)}\right)\right)\ge 1-\text{exp}(-\gamma n)-O(\text{exp}(-(C_3{K}^2-2)n^c)).$$

Moreover, given ${\widehat{\mathcal{S}}}_g$,

$$\frac{1}{\sqrt{n}}{\Vert {\mathrm{\Pi }}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}}{x}_j\Vert }_2\le \frac{1}{\sqrt{n}}{\Vert x_j\Vert }_2=1.$$

We have

$$P\left(\left|\sum _{k\in {\mathcal{M}}_{0,n}\backslash {\widehat{\mathcal{S}}}_g}\frac{{\beta }_k}{n}{x}_j^T{\mathrm{\Pi }}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}}{x}_k\right|\le O(n^{-(b-a-d/2)})\right)\ge 1-\text{exp}(-\gamma n)-O(\text{exp}(-(C_3{K}^2-2)n^c)).$$ (9)

Combining (8) and (9),

$$P\left(\left|\sum _{k\in {\mathcal{M}}_{0,n}\backslash {\widehat{\mathcal{S}}}_g}\frac{{\beta }_k}{n}{x}_j^T(I_n-{\mathrm{\Pi }}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}})x_k\right|\le O(n^{-(b-a-d/2)})\right)\ge 1-O(\text{exp}(-(C_3{K}^2-2)n^c))$$

Step 1.3 We move on to study the third term in (7) and show that, under Condition (A7) and (A9), the third term is negligible compared to the first term. To proceed, we first reproduce a result from Lemma 14.9 of [38] for the sake of readability.

Lemma 4 (Bernstein’s inequality) Assume Condition (A9). Let t > 0 be an arbitrary constant. Then

$$P\left(\frac{1}{n}\sum _{i=1}^n{ϵ}_i\ge K_{ϵ}t+\sqrt{2t}\right)\le \text{exp}(-tn).$$

The following Lemma provides the ground for the proof of Step 1.3.

Lemma 5 Assume Condition (A7) and (A9). For t > 0

$$P\left(\underset{1\le j\le p_n}{\text{max}}\frac{1}{n}\left|x_j^Tϵ\right|\ge K_0\left(t+\frac{\text{log}\left(2p_n\right)}{n}\right)+{\sigma }_0\sqrt{2\left(t+\frac{\text{log}\left(2p_n\right)}{n}\right)}\right)\le \text{exp}(-tn),$$

where K₀ = K_xK_ϵ and σ₀ = K_xσ.

Proof of Lemma 5

We have

$$\frac{1}{n}\sum _{i=1}^{n}E{\left|{ϵ}_i{X}_{i,j}\right|}^m\le K_x^m\frac{1}{n}\sum _{i=1}^{n}E({\left|{ϵ}_i\right|}^m)\le \frac{m!}{2}{\left(K_x{K}_{ϵ}\right)}^{m-2}{\left(K_x\sigma \right)}^2=\frac{m!}{2}{\left(K_0\right)}^{m-2}{\left({\sigma }_0\right)}^2,m=2,3,\dots .$$

Therefore, ϵ_iX_i,j follows a sub-exponential distribution as well. Lemma 4 (Bernstein’s inequality) implies that

$$P\left(\frac{1}{n}\left|{\text{x}}_j^Tϵ\right|\ge K_0\left(t+\frac{\text{log}\left(2p_n\right)}{n}\right)+{\sigma }_0\sqrt{2\left(t+\frac{\text{log}\left(2p_n\right)}{n}\right)}\right)\le 2\text{exp}\left(-n\left(t+\frac{\text{log}\left(2p_n\right)}{n}\right)\right).$$

Therefore,

$$\begin{gathered} P\left(\underset{1\le j\le p_n}{\text{max}}\frac{1}{n}\left|x_j^Tϵ\right|\ge K_0\left(t+\frac{\text{log}\left(2p_n\right)}{n}\right)+{\sigma }_0\sqrt{2\left(t+\frac{\text{log}\left(2p_n\right)}{n}\right)}\right) \\ \le \sum _{j=1}^{p_n}P\left(\frac{1}{n}\left|x_j^Tϵ\right|\ge K_0\left(t+\frac{\text{log}\left(2p_n\right)}{n}\right)+{\sigma }_0\sqrt{2\left(t+\frac{\text{log}\left(2p_n\right)}{n}\right)}\right) \\ \le 2p_n\text{exp}\left(-n\left(t+\frac{\text{log}\left(2p_n\right)}{n}\right)\right)=\text{exp}(-tn). \end{gathered}$$

Proof of Step 1.3

We move on to study the third term in (7) and show that the third term is negligible compared to the first term. We have

$$K_0\left(n^{-2b}+\frac{\text{log}\left(2p_n\right)}{n}\right)\le K_0\left(\frac{n^{1-2b}+\text{log}\left(2p_n\right)}{n}\right)\le 3K_0{n}^{-2b},$$

$${\sigma }_0\sqrt{2\left(n^{-2b}+\frac{\text{log}\left(2p_n\right)}{n}\right)}\le \sqrt{6}{\sigma }_0{n}^{-b}.$$

Therefore,

$$\begin{gathered} P\left(\underset{1\le j\le p_n}{\text{max}}\frac{1}{n}\left|{\text{x}}_j^Tϵ\right|\ge 3K_0{n}^{-2b}+\sqrt{6}{\sigma }_0{n}^{-b}\right) \\ \le P\left(\underset{1\le j\le p_n}{\text{max}}\frac{1}{n}\left|x_j^Tϵ\right|\ge K_0\left(n^{-2b}+\frac{\text{log}\left(2p_n\right)}{n}\right)+{\sigma }_0\sqrt{2\left(n^{-2b}+\frac{\text{log}\left(2p_n\right)}{n}\right)}\right)\le \text{exp}(-n^{1-2b}), \end{gathered}$$

where the last inequality holds by Lemma 5. Similarly

$$P\left(\underset{1\le j\le p_n}{\text{max}}\frac{1}{n}\left|x_j^T(I_n-{\mathrm{\Pi }}_{{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}})ϵ\right|\le 3K_0{n}^{-2b}+\sqrt{6}{\sigma }_0{n}^{-b}\right)\ge 1-O(\text{exp}(-(C_3{K}^2-2)n^c)).$$

Step 1.4 We are now in a position to show the first statement in Theorem 1. Indeed, we have so far shown that for $j\in {\mathcal{M}}_{0,n}$, the last two terms in (7) are negligible compared to the first term. Similarly, the two terms in the denominator of $\widehat{\rho }(Y_i,X_{i,j}|X_{i,{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}})$ can be shown to be bounded from above. Combining these results and applying the Bonferroni inequality, we have

$$P\left(\underset{j\in {\widehat{\mathcal{S}}}_g\cap {\mathcal{M}}_{0,n},g=1,\dots ,G_n}{\text{min}}{\nu }_n^{-1}\left|\widehat{\rho }(Y_i,X_{i,j}|X_{{\widehat{\mathcal{S}}}_g\left|\right\{j\}})\right|\ge O(n^{\kappa }\underset{j\in {\mathcal{M}}_{0,n}}{\text{min}}\left|{\beta }_j\right|)\right)$$ (10)

$$\ge 1-O(\text{exp}(-(C_3{K}^2-2)n^c)).$$ (11)

That is, the CIS procedure satisfies the sure screening property

$$P({\mathcal{M}}_{0,n}\subseteq \widehat{\mathcal{M}}({\nu }_n,{\delta }_n))\ge 1-O(\text{exp}(-(C_3{K}^2-2)n^c)).$$

Step 2: $j\in \{1,\dots ,p_n\}\backslash {\mathcal{M}}_{0,n}$

We then move on to prove the second statement in Theorem 1 by considering the scenario when $j\in \{1,\dots ,p_n\}\backslash {\mathcal{M}}_{0,n}$. Since β_j = 0 for $j\in \{1,\dots ,p_n\}\backslash {\mathcal{M}}_{0,n}$, the first term in (7) vanishes. Also, we showed that the absolute values of the second and the third terms can be bounded from above. Coupled with the fact that the denominator of $\widehat{\rho }(Y_i,X_{i,j}|X_{i,{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}})$ is bounded from below, an application of the Bonferroni inequality yields

$$P\left(\underset{j\in {\widehat{\mathcal{S}}}_g\backslash {\mathcal{M}}_{0,n},g=1,\dots ,G_n}{\text{max}}{\nu }_n^{-1}\left|\widehat{\rho }(Y_i,X_{i,j}|X_{i,{\widehat{\mathcal{S}}}_g\backslash \left\{j\right\}})\right|\le O(n^{-(b-a-d/2-\kappa )})\right)$$ (12)

$$\ge 1-O(\text{exp}(-(C_3{K}^2-2)n^c)).$$ (13)

Finally, the first and the second statements in Theorem 1 immediately imply the screening consistency property:

$$P({\widehat{\mathcal{M}}}_{CIS}({\nu }_n,{\delta }_n)={\mathcal{M}}_{0,n})\ge 1-O(\text{exp}(-(C_3{K}^2-2)n^c)).$$