Leveraging summary statistics to make inferences about complex phenotypes in large biobanks

Abstract

As genetic sequencing becomes less expensive and data sets linking genetic data and medical records (e.g., Biobanks) become larger and more common, issues of data privacy and computational challenges become more necessary to address in order to realize the benefits of these datasets. One possibility for alleviating these issues is through the use of already-computed summary statistics (e.g., slopes and standard errors from a regression model of a phenotype on a genotype). If groups share summary statistics from their analyses of biobanks, many of the privacy issues and computational challenges concerning the access of these data could be bypassed. In this paper we explore the possibility of using summary statistics from simple linear models of phenotype on genotype in order to make inferences about more complex phenotypes (those that are derived from two or more simple phenotypes). We provide exact formulas for the slope, intercept, and standard error of the slope for linear regressions when combining phenotypes. Derived equations are validated via simulation and tested on a real data set exploring the genetics of fatty acids.

1. Introduction

The continued move to digitize medical records raises a plethora of opportunities and challenges in the search to elucidate the genetic and environmental contributions to human disease. The amount of genetic, environmental, and disease-related data continues to grow rapidly, offering new opportunities to discover relationships between genetic variants and expressed physical characteristics. Of particular interest are the genetic contributions to diseases that can have dramatic impacts on societal well-being (e.g., cardiovascular diseases, mental health, and cancer). The advent of large, publicly available biobanks (e.g., UK Biobank¹) offers exciting possibilities for leveraging these datasets to have a dramatic impact on human health and disease.

However, this unprecedented opportunity also comes with roadblocks and challenges.² The size of datasets in biobanks makes it challenging to transfer, store, and analyze them locally. And even though cloud computing minimizes some of these issues, they bring their own challenges with regard to cost (storage and computation), transfer, and access to cloud computing systems. Furthermore, data security and privacy issues are of paramount importance throughout all aspects of the data access, storage, and analysis pipeline.^3–4 Thus, there is a great demand for simplified data transfer, exploration, visualization, and analysis strategies which simultaneously address privacy, security, storage, and computational challenges, while still allowing researchers to make the best possible use of biobank repositories.

An interesting recent development related to these issues are efforts to provide summary statistics in publicly available formats. For example, GeneAtlas provides basic summary statistics for simple linear regression models of each available single nucleotide variants with each available phenotypic variable for 452 thousand individuals in the UK Biobank.⁵ Likewise, Pheweb provides access to the UK Biobank data via a series of easy-to-navigate visualization and summary tools based on publicly available data produced by the Neale lab.^5–6 GeneAtlas and Pheweb mitigate many of the privacy and security concerns mentioned above since no individual information is shared. There is no way to use summary statistics alone to gather information about any one individual. In addition, the size of these repositories are only fractions of the size of the individual level datasets, making transfer and storage of the data much more efficient. Finally, these services have already computed some of the most common summary statistics, which alleviates much of the computational burden on researchers.

However, while these approaches are promising and provide valuable insight, major questions abound about how to best leverage this summary-level information in more complex downstream analyses. While basic exploratory data analysis and data visualization are straightforward and commonplace, using pre-computed genotype-phenotype associations (summary statistics) to explore ‘complex’ phenotypes, which are functions of existing phenotypes present in a biobank, hasn’t been previously investigated. For example, if a researcher is interested in phenotype Y, where Y = f(y₁, y₂, y₃, … y_m) and y₁, y₂, y₃, …, y_m are existing phenotypes present in the biobank (with m being the number of phenotypes), is there a way to utilize the precomputed summary statistics from each linear model fit for each y₁, y₂, y₃, …, y_m in order to make conclusions about the relationship between Y and genetic variation? This is the primary question of interest for this manuscript.

In particular, we begin by providing a framework for how to think about using summary statistics from individual phenotypes to investigate general classes of ‘complex’ phenotypes. We then illustrate how to utilize summary statistics for inferences about a complex phenotype which is a linear combination of an arbitrarily large set of individual phenotypes. Despite extensive literature review we have found little in the way of similar approaches thus most of our work has been built from the ground up. We validate our approach using both simulated data and real data from the Framingham Heart Study.

2. Methods

2.1. Notation

Throughout this paper we use y_ij to represent the phenotypes, where i ∈ {1, 2, . . ., m} with m being the number of phenotypes and j ∈ {1, 2, . . ., n} with n being the number of subjects. Similarly, x_j is used to represent the genotype. We use bolded letters (such as y_i and x) to refer to a vector of values across all subjects. The term y_c is used to represent the linear combination of the y_i’s (y_c = c₁y₁ + c₂y₂+. . . +c_my_m) with the $c_i^{\prime }s$ being constants. For each linear regression model fit for y_i ~ x, we use the notation y_i = β_ix + α_i, where β_i is the slope and α_i is the intercept. The standard error for β_i is represented by SE(β_i). We use β_i to represent all betas for phenotype i across all genotypes.

In addition, the following formulas are used frequently in this paper and should be kept in mind.

$${\beta }_i=\frac{cov\left(x,y_i\right)}{var(x)}=\frac{{\sum }_{j=1}^n\left(x_j-\overline{x}\right)\left(y_{ij}-\overline{y}\right)}{{{\sum }_{j=1}^n\left(x_j-\overline{x}\right)}^2}$$ (1)

$$\text{SE}\left({\beta }_i\right)=\frac{\sqrt{\frac{{{\sum }_{j=1}^n\left(y_{ij}-{\widehat{y}}_{ij}\right)}^2}{n-2}}}{\sqrt{{{\sum }_{j=1}^n\left(x_j-\overline{x}\right)}^2}}$$ (2)

2.2. Linear combination of two phenotypes using only summary statistics

We will first show the formulas for the slope, intercept, and standard error of the slope in the case of a linear combination of two phenotypes (y_c = c₁y₁ + c₂y₂), where c₁ and c₂ are any constants. We will then show how these formulas generalize to an arbitrary number of phenotypes. In this portion of the paper we will only state the formulas – detailed derivations for each of the formulas can be found in the supplemental materials.

2.2.1. Slope

To determine the slope, ${\widehat{\beta }}_c$, for the combined linear model of a linear combination of two phenotypes (y_c = c₁y₁ + c₂y₂), formula 1 was manipulated. We begin by inserting y_c = c₁y₁ +c₂y₂, into the least squares estimate of the slope:

$${\widehat{\beta }}_c=\frac{{\sum }_{j=1}^n\left(x_j-\overline{x}\right)\left(\left(c_1{y}_{1j}+c_2{y}_{2j}\right)-\left(\overline{c_1{y}_1+c_2{y}_2}\right)\right)}{{{\sum }_{i=1}^n\left(x_i-\overline{x}\right)}^2}$$ (3)

After algebraic simplifications, ${\widehat{\beta }}_c$ equals the same linear combination of the two phenotypes except with the slope instead of the phenotype:

$${\widehat{\beta }}_c=c_1{\widehat{\beta }}_1+c_2{\widehat{\beta }}_2$$ (4)

2.2.2. Intercept

To determine the y-intercept, $\widehat{\alpha }$, for the combined linear model of a linear combination of two phenotypes, the mathematical formula for the least-squares estimate of the intercept was manipulated. As before, we begin by inserting y_c = c₁y₁ + c₂y₂, into the formula for the intercept in a standard least squares linear regression:

$${\widehat{\alpha }}_c=\overline{c_1{y}_1+c_2{y}_2}-{\widehat{\beta }}_c\overline{x}.$$ (5)

Simplifying this equation shows that ${\widehat{\alpha }}_c$ equals the same linear combination of the two phenotypes except with the intercepts instead of the phenotypes:

$${\widehat{\alpha }}_c=c_1{\widehat{\alpha }}_1+c_2{\widehat{\alpha }}_2$$ (6)

2.2.3. Standard error of slope

To determine the standard error of ${\widehat{\beta }}_c$, SE(${\widehat{\beta }}_c$), formula 2 was manipulated. c_1y1j + c_2y2j was substituted for y_i and $\left(c_1{\widehat{\beta }}_1+c_2{\widehat{\beta }}_2\right)x_j+\left(c_1{\widehat{\alpha }}_1+c_2{\widehat{\alpha }}_2\right)$ for ${\widehat{y}}_{ij}$. After some algebraic manipulation of the formula for SE(${\widehat{\beta }}_c$), the formula was determined to be (see supplement 3 for details):

$$SE\left({\widehat{\beta }}_c\right)=\sqrt{c_1^{2}SE{\left({\widehat{\beta }}_1\right)}^2+c_2^{2}SE{\left({\widehat{\beta }}_2\right)}^2+\frac{2c_1{c}_2}{n-2}\left(\frac{cov\left(y_1,y_2\right)}{var(x)}-{\widehat{\beta }}_1{\widehat{\beta }}_2\right)}$$ (7)

2.3. Linear combination of an arbitrary number of phenotypes using summary statistics

Having provided the formulas for the linear combination of two phenotypes, we now explore the more general case of a linear combination of m phenotypes.

2.3.1. Slope

Following from the demonstration of the resulting ${\widehat{\beta }}_c$ formula for the linear model for a linear combination of two phenotypes, it can be shown that the ${\widehat{\beta }}_c$ from the linear regression of the linear combination of an arbitrary number of phenotypes is simply the same linear combination of the phenotypes except with ${\widehat{\beta }}_i$’s from the simple linear regressions instead of the phenotype (complete demonstration in supplement 1). Thus if there is a linear combination of m phenotypes the slope of the combined linear model is

$${\widehat{\beta }}_c=c_1{\widehat{\beta }}_1+c_2{\widehat{\beta }}_2+\cdots +c_m{\widehat{\beta }}_m.$$ (8)

2.3.2. Intercept

Following from the demonstration of the resulting ${\widehat{\alpha }}_c$ formula for the linear model in which there is a linear combination of two phenotypes, it can easily be seen that the ${\widehat{\alpha }}_c$ from the linear regression of the linear combination of an arbitrary number of phenotypes is simply the same linear combination of the phenotypes except with the ${\widehat{\alpha }}_i$’s from the simple linear regressions instead of the phenotypes (complete demonstration in the supplement 2). Thus if there is a linear combination of m phenotypes the intercept of the combined linear model is

$$\widehat{\alpha }=c_2{\widehat{\alpha }}_1+c_2{\widehat{\alpha }}_2+\cdots +c_m{\widehat{\alpha }}_m.$$ (9)

2.3.3. Standard error of beta

Following from the demonstration of the resulting SE(${\widehat{\beta }}_c$) formula for the linear model for a linear combination of two phenotypes, it can be demonstrated through induction that the SE(${\widehat{\beta }}_c$) from the linear regression of the linear combination of an arbitrary number of phenotypes is the following (complete demonstration in the supplement 4):

$$\begin{gathered} SE\left({\widehat{\beta }}_c\right)= \\ \sqrt{\left(\sum _{i=1}^m{c}_i^{2}SE{\left({\widehat{\beta }}_i\right)}^2\right)+\frac{2}{n-2}\left(\frac{{\sum }_{q=1}^{m-1}{\sum }_{r=q+1}^m{c}_q{c}_{r}cov\left(y_q,y_r\right)}{var(x)}-\left(\sum _{q=1}^{m-1}\sum _{r=q+1}^m{c}_q{c}_r{\widehat{\beta }}_q{\widehat{\beta }}_r\right)\right)} \end{gathered}$$ (10)

2.3.3.1. Estimating terms in the equation for the standard error of beta

All of the terms in formula 10 for the standard error of the combined $\widehat{\beta }$ are summary level statistics. While this eliminates the need for individual level data and thus alleviates many of the previously-discussed privacy issues, there are two summary statistics within that formula that aren’t often publicly available. In particular, the covariances between each unique pair of phenotypes and the variance of x are not frequently provided. As such, it would be helpful if there were methods for estimating these terms from the information that is readily available.

We first explore a method for estimating the covariance between a given pair of phenotypes. Since linear models have already been run on the entire data set, slopes are given for each genotype-phenotype combination. Thus, we hypothesized that the correlation between two of the response variables could be estimated by finding the correlation between the betas for the first phenotype and the betas for the second phenotype. However, the quantity needed for the standard error formula is covariance. Therefore, to find the covariance, we propose the following approximation:

$$cov\left(y_1,y_2\right)=cor\left(y_1,y_2\right)*\sqrt{var\left(y_1\right)var\left(y_2\right)}\approx cor\left({\beta }_{{}_1},{\beta }_2\right)*\sqrt{var\left(y_1\right)var\left(y_2\right)}$$ (11)

Note that this, in turn, requires that we have the variance of y₁ and y₂.

Next, we explore a method for estimating the variance of x. Because we can model x by the binomial distribution, the variance of x can be estimated using the minor allele frequency (MAF). Thus, by using the formula for the variance of a binomial distribution we can accurately estimate the variance of x using the known minor allele frequency.

$$\text{2}MAF\text{(1}-MAF\text{)}.$$ (12)

While this approximation is close to the true value, the accuracy of the estimate changes with the Hardy-Weinberg equilibrium (HWE) p-value. In the next section we explore this using simulations.

2.4. Simulations

2.4.1. Estimation of covariance of y’s simulations

To test the hypothesis for our covariance estimate, simulations were conducted in R.⁷ We wrote a function for performing these simulations, which generated two phenotypes and a large number of genotypes. The parameters altered from trial to trial were the number of observations, the number of genotypes, the covariance between the two phenotypes, and the variance of each of the two phenotypes.

2.4.2. Estimation of variance of x simulations

To check the accuracy of the variance of x, simulations were run in R. Ten thousand genotypes from 1,000, 10,000, 100,000, and 500,000 subjects were generated using a binomial distribution. The genotypes were of varying minor allele frequencies and varying Hardy-Weinberg equilibrium p-values. For each genotype the following statistics were calculated: MAF, HWE p-value, the observed variance, estimated variance, and the difference between the observed variance and the estimated variance. At HWE p-value thresholds of 0.05, 0.5, 0.75, 0.90, and 0.99, the mean difference between the observed variance and the estimated variance of genotypes, and the standard deviations of those differences of the genotypes that met or exceeded the thresholds were also calculated.

2.5. Real data analysis

Previous genome wide association studies, investigated the association between 425,380 SNP’s and red blood cell fatty acid (RBC FA) levels indicative of cardiovascular health using data from the offspring cohort (n=2384) of The Framingham Heart Study as we’ve done in other recent publications. ^8–11 Two of the RBC FA included were Docosahexaenoic acid (DHA) and Eicosapentaenoic acid (EPA). The sum of DHA and EPA is reported as the omega3 index (O3I). In the studies, genome wide association analyses were conducted for DHA, EPA, and O3I using residual models adjusting for age, sex, and familial relationships. We will use this data to demonstrate our method. We will show the accuracy of the slope and standard error of the slope calculated using the summary statistics from the individual EPA and DHA models and the method presented in this paper as compared to the slope and standard error that is obtained from running the entire linear model specifically on the O3I. Please refer to the studies cited for more information about the significance of their findings, the collection of red blood cell fatty acids and the Framingham cohort.^8–11

3. Results

3.1. Estimating the covariance of phenotypes

We begin by investigating the performance of our proposed estimation (formula 11) for the covariance of phenotypes (y_i’s). As seen in Table 1, our results suggest that the error in our approximation is highest when the correlation between y₁ and y₂ is close to 0. As the correlation between a pair or y_i’s increases, the standard deviation of the error in the estimated correlation decreases.

Table 1.

This table shows the results from the simulations. The “Correlation” column lists the correlation at which the data was generated. The other two columns display the mean and standard deviation of the error of the estimate.

Correlation	Mean error of estimated correlation	Standard deviation of error of estimated correlation
0	−0.000486	0.050
0.3	0.000400	0.045
0.75	6.23E-05	0.022
0.9	0.000282	0.0096

The other two parameters (number of genotypes and number of observations) had little to no impact on the standard deviation of the errors (detailed results not shown).

3.2. Estimating variance of genotype

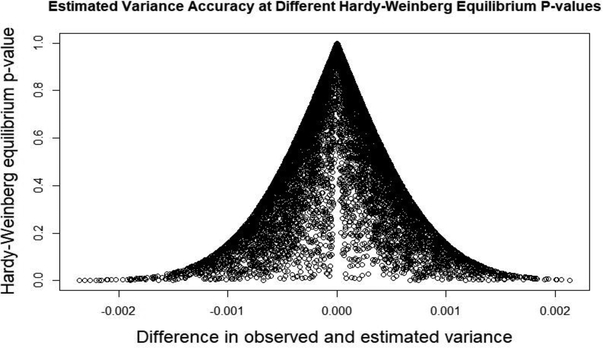
The detailed results of the variance of x simulations can be found in Table 2. Overall, the difference between the observed variance of x and the estimated variance of x across all simulated genotypes was small with a mean of 0.000043 and standard deviation of 0.0064. Thus as the length of the genotype gets larger, the difference between the observed and estimated variances seems to go to zero. While the mean differences are quite small, they are nearly all positive indicating that we are underestimating the variance. Because the standard error formula (formula 7) divides by the variance our standard error will be inflated and thus this method will be slightly conservative. Additionally, as can be seen in Table 2 and Figure 1, genotypes with larger HWE p-values have differences between the observed and estimated variances that are closer to zero.

Table 2.

Results for variance of x simulations, with 10,000 genotypes simulated for 500,000, 100,000, 10,000 and 1,000 individuals.

Number of individuals	P-value	Number of genotypes that fall at or above p-value threshold	Mean of the difference between observed and estimated variance	Lower bound of Wald confidence interval for mean	Upper bound of Wald confidence interval for mean
500,000	≥ 0.99	104	1.4E-06	−7.1E-06	1.0E-05
	≥ 0.90	1042	2.6E-06	−7.8E-05	8.3E-05
	≥ 0.75	2510	7.5E-07	−2.0E-04	2.0E-04
	≥ 0.50	5002	4.5E-06	−4.1E-04	4.2E-04
	≥ 0.05	9494	9.6E-06	−9.3E-04	9.5E-04
	All	10000	4.1E-06	−1.1E-03	1.1E-03
100,000	≥ 0.99	98	4.3E-06	−1.3E-05	2.2E-05
	≥ 0.90	1025	1.1E-06	−1.7E-04	1.8E-04
	≥ 0.75	2551	6.8E-06	−4.4E-04	4.5E-04
	≥ 0.50	5015	2.3E-06	−9.2E-04	9.3E-04
	≥ 0.05	9497	6.9E-06	−2.1E-03	2.1E-03
	All	10000	1.2E-05	−2.4E-03	2.4E-03
10,000	≥ 0.99	94	3.7E-05	−2.6E-05	1.0E-04
	≥ 0.90	999	4.5E-05	−5.2E-04	6.2E-04
	≥ 0.75	2481	5.1E-05	−1.4E-03	1.5E-03
	≥ 0.50	4938	5.0E-05	−2.8E-03	2.9E-03
	≥ 0.05	9501	5.5E-05	−6.8E-03	6.7E-03
	All	10000	−8.4E-05	−7.7E-03	7.5E-03
1,000	≥ 0.99	114	3.8E-04	1.2E-04	6.4E-04
	≥ 0.90	962	3.9E-04	−1.4E-03	2.2E-03
	≥ 0.75	2439	3.4E-04	−4.2E-03	4.8E-03
	≥ 0.50	4963	4.1E-04	−8.8E-03	9.6E-03
	≥ 0.05	9452	1.8E-04	−2.1E-02	2.1E-02
	All	10000	2.4E-04	−2.4E-02	2.4E-02

Fig. 1.

This plot shows the results of the simulation of 10,000 genotypes from 500,000 subjects. The Hardy-Weinberg equilibrium p-value is on the y-axis and the difference in the variance is on the x-axis.

3.3. Real data results

3.3.1. Using exact formulas

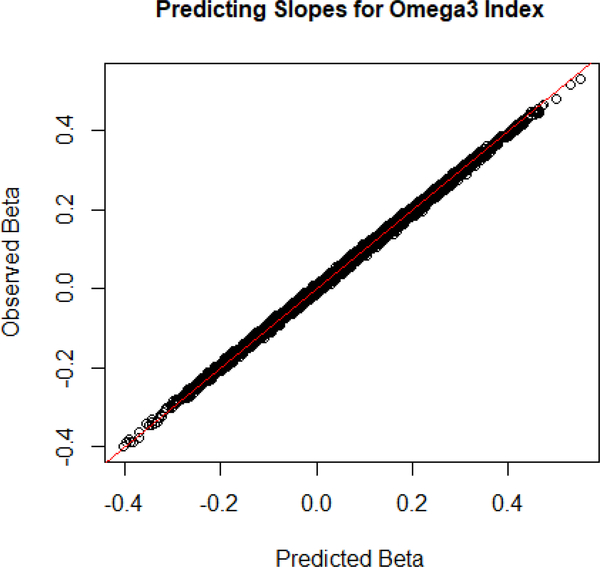
We first consider the accuracy of adding the two residual models after adjusting for covariates. It appears that the predictions for the slope of the combined linear model made using prediction ${\widehat{\beta }}_{EPA}+{\widehat{\beta }}_{DHA}={\widehat{\beta }}_{RO3I}$ were accurate. The predictions of the model adjusting for covariates after addition $\left({\widehat{\beta }}_{O3I}\right)$ had a mean difference of 0.0000469 and a standard deviation of 0.00204. Figure 2 shows the observed values of ${\widehat{\beta }}_{O3I}$ plotted against the estimate values, and appears to show that the estimate is relatively accurate on the entire range of true slopes.

Fig. 2.

The observed beta values are on the y-axis and the predicted beta values are on the x-axis. This shows the accuracy of the combined beta formula.

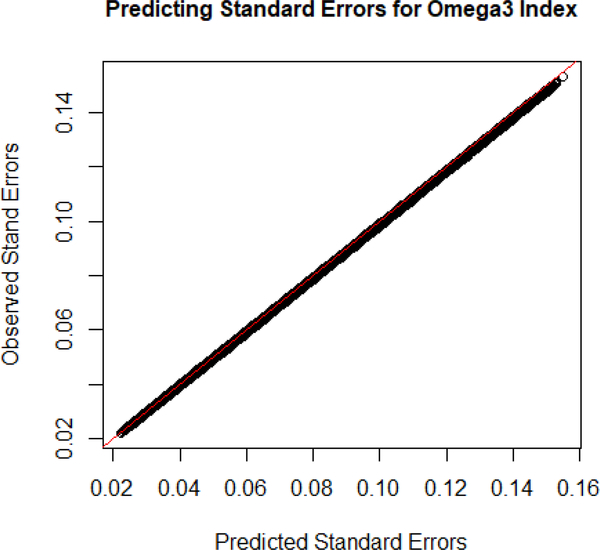
Using formula 7 for predicting the standard error for the β_RO3I, there was a mean error of −0.00000177 with a standard deviation of 0.00004717. When comparing the estimate for standard error to the actual O3I standard error, the mean error was 0.00058 with a standard deviation of 0.000276. Figure 3 demonstrates that when applying the covariates separately to the models DHA and EPA we see a slight over prediction of the standard errors.

Fig. 3.

The observed standard errors for the beta is on the y-axis and the predicted standard errors of the beta is on the x-axis. This shows the accuracy of our standard error estimate.

3.3.2. Estimating covariance of the y’s

Using the method described in 2.4 the estimated correlation between EPA and DHA was 0.707 while the actual correlation between the two variables is 0.682. The error between the true value and the predicted value will in turn lead to a slightly inflated standard error estimate.

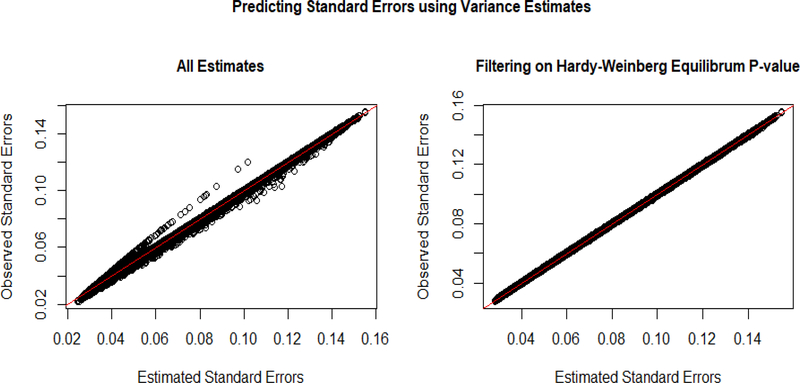
3.3.3. Estimating the variance of x

When using our estimate of the variances of the genotype in the standard error equation, we see some increased variation in the estimations, as seen in Figure 4. However, filtering by Hardy Weinberg equilibrium p-value (eliminate genotypes with HWE p-values less than 0.000001 as per GWAS standard)¹² removes all of the extreme variation between estimated and predicted estimates of the variation of the genotypes.

Fig 4.

The graph on the left demonstrates the accuracy of the standard error estimates for the beta values using all SNP’s in the data set. The graph on the right filters by Hardy-Weinberg equilibrium p-value of 0.000001, which removes most of the less accurate predictions.

3.3.4. Analysis of p-value

We examine –log₁₀ p-value plots to see the overarching effect the method presented in this paper has on the significance of the study. In this analysis we compare the p-values obtained from using our summary statistic model with the true p-values from the linear model before adjusting for covariates. When estimating the variance of the genotype we filtered by a Hardy-Weinberg equilibrium p-value of 0.000001.

3.3.5. Careful analysis of top hits

One of the important aspects of using summary level statistics is that it will not greatly affect the most significant genotype phenotype associations. As seen in supplemental tables 5, 6, and 7 the differences in β, SE(β) and overall p-values between the summary statistic model and the traditional model is minimal.

4. Discussion

We have demonstrated how to accurately estimate the strength of association for a linear combination of an arbitrary number of individual phenotypes with a single genotype of interest using only commonly available summary statistics from large biobanks. In addition, we have provided a mathematical overview of why these relationships hold, demonstrated how to estimate these values from summary statistics and distributions of summary statistics, and then evaluated their performance on both simulated and real data.

Practically, we have now provided a tool for researchers to perform genome-wide and related analyses on linear combinations of phenotypes using only summary statistics, which has the potential to dramatically reduce computational time and storage, simplify data transfer, and grossly mitigate privacy and security concerns, especially for large biobank-style datasets. For example, in our data analysis of The Framingham Heart Study the Rdata file size needed to run the analysis was reduced from 1.2 GB to 0.04 GBs. Notably, the reduction in file size and processing time should increase significantly with an increased sample size. While linear combinations of phenotypes are a powerful tool (e.g., averaging multiple measurements of a trait of interest), future work is needed to explore more general ways of combining phenotypes which will have broader applicability. For example, multiplicative combinations of phenotypes (y₁ * y₂ or y₁⁄y₂) and exponentiated phenotypes are also a powerful and common class of complex phenotypes (e.g., BMI = Weight/Height^2). ). If future work is able to establish a similar class of methods for multiplicative phenotypes as has been shown in this manuscript for linear combinations, we would then be in position to also derive general methods for ‘logical’ combinations of dichotomous phenotypes. Logical combinations can be expressed as arithmetic operations. The ‘and’ operation can be expressed as y1* y2 and the ‘or’ operation can be expressed as (y1+ y2) − (y1* y2). Future work also includes consideration of multi-allelic models, the impact of different assumptions in models/software creating summary statistics on downstream inference using our proposed method, and direct comparison and evaluation of changes in computation time.

Some limitations of our method are worth noting. First, we have been able to accurately estimate the variance of x (x in other words, the genotype) using the variance formula for a binomial distribution and the minor allele frequency. This estimate has been verified through simulations and we have shown that as the genotypes reach perfect Hardy-Weinberg equilibrium the difference between the observed and estimated variances of x approaches 0. While in practice, variants out of HWE are removed from the data, variants that are ‘nearly’ out of HWE using standard GWAS quality thresholds¹¹ (e.g., HWE p-value < 1×10⁻⁶) may experience more noise in downstream estimates. Secondly, while our simulations and real data application are reasonably comprehensive, application to additional datasets and consideration of additional simulated datasets (e.g., with different sample sizes; different proportions of and distributions of missing data; different levels of correlation between phenotypes) is recommended.

The use of summary statistics from large biobanks in downstream statistical analyses offers great promise to address numerous hurdles in the use of biobank data and dramatically increase the opportunity to leverage biobanks to understand the etiology of complex human diseases. We have provided precise equations to leverage summary statistics for linear combinations of phenotypes. The method presented in this paper sets the essential foundation and provides a necessary building block for being able to investigate the genetic associations of millions of complex phenotypes with summary statistics alone. Future work is needed to explore multiplicative and other more complex ways to combine phenotypes to provide a complete approach to phenotype combinations.

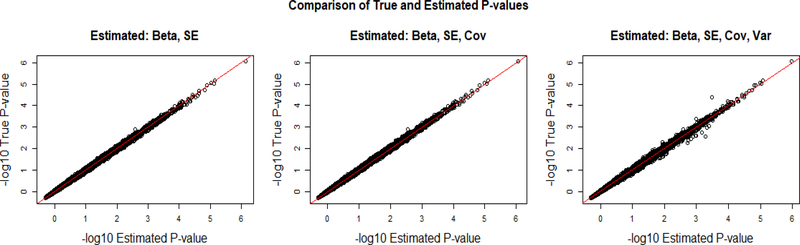
Fig 5.

The graph on the left demonstrates the accuracy of the negative log of the p-value when our formulas for the slopes and standard errors are used with the true variance of x and covariances between phenotypes. The middle graph shows the accuracy when covariance of the y’s is estimated using our estimation. The graph on the right depicts the accuracy of the p-values when the covariance of the y’s and the variance of x are estimated using our given estimates.