Within-host dynamics shape antibiotic resistance in commensal bacteria

Abstract

The spread of antibiotic resistance, a major threat to human health, is poorly understood. Simple population-level models of disease transmission predict that above a certain rate of antibiotic consumption in a population, resistant bacteria should completely eliminate non-resistant strains, while below this threshold they should be unable to persist at all. This prediction stands at odds with empirical evidence showing that resistant and non-resistant strains coexist stably over a wide range of antibiotic consumption rates. Not knowing what drives this long-term coexistence is a barrier to developing evidence-based strategies for managing the spread of resistance. Here, we argue that competition between resistant and sensitive pathogens within individual hosts gives resistant pathogens a relative fitness benefit when they are rare, promoting coexistence between strains at the population level. To test this hypothesis, we embed mechanistically-explicit within-host dynamics in a structurally-neutral disease transmission model. Doing so allows us to reproduce patterns of resistance observed in the opportunistic pathogens Escherichia coli and Streptococcus pneumoniae across European countries, and to identify factors that may shape resistance evolution in bacteria by modulating the intensity and outcomes of within-host competition.

Antibiotic-resistant infections tend to be more common in populations that consume more antibiotics^1–3. The explanation seems obvious: greater antibiotic use selects for more resistance. But capturing this pattern in an explicit model of disease transmission has been notoriously difficult⁴. The problem is that empirical observation suggests a gently rising, roughly linear relationship between consumption and resistance, with both resistant and sensitive (i.e., non-resistant) strains coexisting over a 4- to 20- fold range of antibiotic treatment rates^1–3 (Fig. 1a). In contrast, simple models of disease transmission predict competitive exclusion⁵—that is, they predict that resistant strains will either disappear completely or spread to fixation, depending upon the rate of antibiotic consumption in a population (Fig. 1b–d). Although potential explanations for this discord between theory and observation have been proposed^4,6–8, a generalisable, biologically-explicit mechanism that accounts for widespread coexistence has yet to be identified. In short, despite the global public health threat of antibiotic resistance^9,10, we do not fully understand how resistance spreads in human populations.

Fig. 1. The problem of coexistence.

(a) Resistant and sensitive strains of E. coli and S. pneumoniae coexist, and resistance increases moderately with antibiotic consumption¹–³. The proportion of invasive isolates testing positive for drug resistance (with 95% confidence intervals) is plotted against community-level antibiotic consumption for 30 European countries (linear regressions with 95% confidence intervals overlaid). In contrast with observed coexistence, a simple model of resistant disease transmission (b) predicts competitive exclusion (c). The model is defined by the system of ordinary differential equations $\frac{dS}{dt}=\beta SX-(u+\tau )S,\frac{dR}{dt}=\beta (1-c)RX-uR,X=1-S-R,$ with X non-carriers, S sensitive-strain carriers, and R resistant-strain carriers. Here, β is the transmission rate (solid arrows), u is the natural clearance rate (dotted arrows), τ is the antibiotic treatment rate (dashed arrow), and c is the cost of resistance. When β > u + τ and β(1–c) > u, either strain can persist in isolation, but only one strain persists when both are present, with the sensitive strain prevailing when τ/u > c/(1−c). (d) The average resistance prevalence in Europe has hardly changed in recent years, suggesting that observed coexistence is stable rather than a transient state on the way to competitive exclusion.

We propose that within-host competition shapes resistance evolution and can promote widespread coexistence in commensal bacteria (i.e., species that are normally part of the host microbiota, but which occasionally cause disease when they invade sterile sites). Mathematical models of resistant disease transmission routinely overlook within-host interactions between different bacterial strains, but commensal bacteria regularly cohabit with genetically- and phenotypically-distinct strains of the same^11–15 or different^16–18 species. Laboratory experiments have shown that resistant and sensitive microbes inhibit each other’s growth when co-colonising the same host^19–22, suggesting that these distinct strains engage in exploitative competition²³ for host resources. Meanwhile, theory developed for malarial parasites²⁴ has proposed that within-host competition between co-colonising resistant and sensitive strains may interact with antimicrobial treatment to generate frequency-dependent selection^25,26 for resistance at the population level, promoting coexistence. We develop this theory, arguing that population-level coexistence can be promoted by any phenotypic diversity that mediates competition between co-colonising strains. Accordingly, we expect co-colonisation to promote coexistence not only between resistant and sensitive bacteria, but also among other diverse microbes exploiting the same host niche, such as pneumococcal serotypes²⁷.

We develop a “mixed-carriage” model that mechanistically captures within-host competition in an explicit model of bacterial transmission. This stochastic individual-based model—which can be approximated using deterministic ordinary differential equations (ODEs) for analytical simplicity—observes the key requirement of structural neutrality²⁸, i.e., it avoids systemic biases that non-mechanistically promote (or inhibit) coexistence. When fit to data across 30 European countries, the model provides a parsimonious and generalizable explanation for empirical patterns of resistance across four pathogen-drug combinations. We also show how within-host competition can help to explain observed patterns of resistance⁷ and antigenic diversity²⁷ among competing serotypes of the commensal bacterium Streptococcus pneumoniae.

Results

Co-colonisation creates frequency-dependent selection for resistance

Frequency-dependent selection^25,26 is known to promote diversity among competitors in animals^25,29, plants³⁰, and microbes³¹. In the classic scenario, a rare mutant invades a population by exploiting some weakness of wild-type individuals, but gradually becomes a victim of its own success by displacing the competitors it relies upon to exploit. Stable coexistence between types can result if mutants tend to increase in frequency when they are rare (because there are ample wild-type individuals to exploit) but decrease in frequency when they are common (because there are too few wild-type individuals to exploit). Extending a hypothesis suggested by Hastings for malarial parasites²⁴, we suggest that frequency-dependent selection for resistant bacteria is created by within-host competition among co-colonising strains.

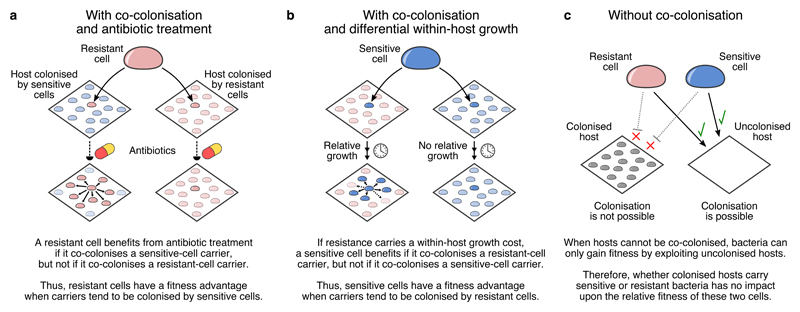
The mechanism works as follows. Suppose that a small group of resistant cells could colonise one of two hosts. One host already carries sensitive bacteria, while the other carries resistant bacteria. All else equal, the resistant cells would benefit more by colonising the sensitive-cell carrier, because if that host were to subsequently take antibiotics—eliminating the resident sensitive cells—the newly-arrived resistant cells could multiply to fully exploit the host niche, increasing their potential to be transmitted to new hosts. Indeed, in vivo studies have shown that in co-colonised hosts harboring both sensitive and resistant cells, the resistant pathogens increase in abundance when their sensitive competitors are killed by antibiotic treatment^19,20,32,33—that is, treatment results in competitive release²⁰ for the resistant cells. On the other hand, co-colonising the resistant-cell carrier offers no such benefit to resistant cells, because later antibiotic use gives no advantage to the invading bacteria over the resident bacteria. This disparity creates frequency-dependent selection for resistance (Fig. 2a) because—on average—a resistant cell is more likely to find itself co-colonising a sensitive-strain carrier when resistance is rare.

Fig. 2. Co-colonisation creates frequency dependent selection for resistance.

With co-colonisation, (a) antibiotic treatment causes resistant cells to have higher fitness when sensitive-strain hosts are more common and (b) differential within-host growth causes sensitive cells to have higher fitness when resistant-strain hosts are more common. Either mechanism can promote coexistence between resistant and sensitive strains. (c) Without co-colonisation, the relative frequency of sensitive-strain and resistant-strain carriers has no differential impact upon the fitness of resistant versus sensitive cells, so there is no frequency-dependent selection acting on resistance phenotypes.

Although originally phrased in terms of competition between malarial parasites mediated by antibiotic treatment and resistance²⁴, this mechanism has broader applicability. First, other forms of within-host competition—not just treatment-mediated competitive release—can promote coexistence. For example, in vitro²¹ and in vivo^22,32 studies have shown that, in the absence of antibiotics, sensitive cells often exhibit greater within-host growth relative to resistant cells—consistent with resistance carrying a fitness cost^34,35 manifesting as a reduced growth rate. Sensitive cells would then benefit more from co-colonising a resistant-strain carrier than a sensitive-strain carrier (Fig. 2b). This relative advantage may also promote frequency-dependent selection acting on resistance phenotypes, because a sensitive cell is more likely to co-colonise a resistant-strain carrier when resistance is common. Second, there is no requirement that competing strains are closely related—only that they competitively suppress each other when colonising the same niche—although we focus here on competition between strains of the same species.

Implicit versus explicit models of within-host dynamics

Models that do not account for within-host competition will fail to capture this source of frequency-dependent selection for resistance (Fig. 2c). Nonetheless, existing models that do incorporate co-colonisation have not convincingly reproduced empirically-observed coexistence^4,6. We suggest that these models have fallen short not because within-host competition is a poor driver of coexistence, but because they feature unrealistic assumptions concerning within-host dynamics. To illustrate this point, we compare two models of resistant disease transmission: an existing model⁴ which we refer to as the “knockout model”, and a new “mixed-carriage model”. These models share the same population-level dynamics, but differ in how they capture within-host dynamics, resulting in a substantial disparity in population-level patterns of resistance.

The shared assumptions of both models are as follows. There are two co-circulating bacterial strains, one resistant and one sensitive. Hosts mix randomly, with each colonised host infecting other hosts at rate β, transmitting a “germ” to a randomly-selected host. A germ contains cells of one strain, chosen randomly in proportion to the number of cells of each strain carried by the transmitting host; all colonised hosts, including those carrying multiple strains, are assumed to be equally infectious. Resistant germs fail to transmit with probability c, where c is the transmission cost of resistance^34,35; additionally, transmission only succeeds with probability k if the recipient is already a carrier, where k is the efficiency of co-colonisation relative to primary colonisation. Finally, each host is naturally cleared of all strains at rate u, and cleared of sensitive cells by antibiotic treatment at an additional rate τ.

Starting from this common framework, the two models make divergent assumptions about within-host dynamics. First, the existing “knockout” model^4,28 assumes that hosts can be treated as though they contain two subcompartments of equal size (Fig. 3a). When a germ is transmitted to an uncolonised host, the invading strain fills the entire host niche, occupying both subcompartments. If instead, germs are successfully transmitted to an already-colonised host, the invading strain “knocks out” and replaces the contents of one of the two subcompartments at random. These assumptions allow the knockout model to be implemented using only four host states—namely, X hosts are uncolonised, S hosts carry the sensitive strain only, R hosts carry the resistant strain only, and SR hosts carry both strains, one in each subcompartment (Fig. 3b). In the Methods, we describe how these model dynamics may be analysed either using stochastic individual-based methods or by integrating systems of ordinary differential equations (ODEs).

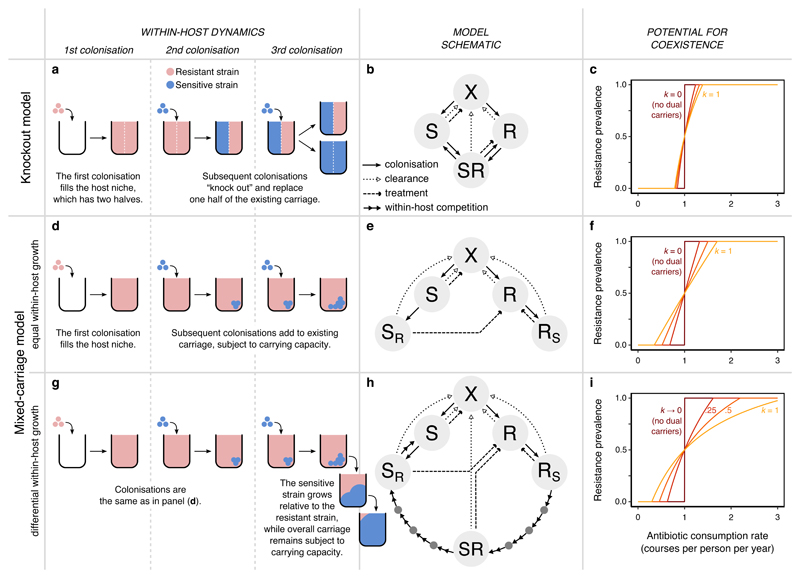
Fig. 3. Two models of within-host dynamics.

(a) In the knockout model²⁸, hosts contain two subcompartments. A resident strain must be “knocked out” from its subcompartment for a new strain to invade. (b) The knockout model requires four host states, adding the “SR” dual carriage state to the model of Fig. 1b. (c) We plot the equilibrium resistance prevalence (the probability that a randomly-selected pathogen from a randomly-selected host is resistant) as a function of the treatment rate τ and the relative efficiency of co-colonisation k (with k = 0, 0.25, 0.5, 1.0 shown, from dark to light). Coexistence increases with k but remains limited. Setting k = 0 recovers the single-strain model of Fig. 1b and competitive exclusion. (d) The mixed-carriage model explicitly tracks within-host strain frequencies and treats cells of either strain equally, relaxing the assumption of host subcompartments that contain only one strain at a time. When new cells enter the host, they mix freely with existing strains. (e) The mixed-carriage model can be approximated using five host states, where S_R and R_S represent hosts colonised primarily by one strain, with a small complement of the other. (f) Explicitly tracking within-host dynamics promotes coexistence. (g) We extend the mixed-carriage model to incorporate differential within-host growth of strains, adding (h) “intermediate” host states representing different relative frequencies of the two strains. Treatment and clearance events for intermediate states (dark grey circles) are omitted for clarity. (i) Within-host growth further promotes coexistence. In panels c, f, and i, β = 5 mo^-1 and u = 1 mo^-1, while specific values of c ≈ 0.07–0.12 (panels c, f) and w_s ≈ 14–34 (panel i) are chosen such that resistance prevalence passes through 0.5 when τ = 1 y^-1 (Supplementary Note 1).

As shown by Lipsitch et al.²⁸, the knockout model is the simplest mathematical model that allows co-colonisation without exhibiting systemic biases that artificially promote coexistence (i.e., it is structurally neutral²⁸). Nonetheless, a mechanistic interpretation of a host’s two equally-sized subcompartments, as posited by this model, is challenging. For example, they could represent two physically-distinct but ecologically-equivalent niches, but the identity of these two niches would be unclear, and it is known that bacteria of different strains can readily occupy the same host niche^11–14. Alternatively, the two subcompartments may be a way of representing a single host niche—e.g. the nasopharynx or the gut—but it is unclear why a group of invading cells should replace either all resistant cells or all sensitive cells from an SR carrier rather than replacing cells from either strain at random. In addition to these conceptual difficulties, the knockout model predicts coexistence only across a narrow range of treatment rates that does not reflect the wide range over which coexistence is observed empirically (Fig. 3c).

To overcome these issues, we propose a new “mixed-carriage” model that explicitly tracks within-host strain frequencies without splitting the host niche into two subcompartments. As in the knockout model, when a host is newly colonised, the invading strain is assumed to immediately occupy the entire host niche, reaching the host’s carrying capacity (Fig. 3d). But when new cells enter, they are simply added to the cells that are already being carried. Carrying capacity is then immediately reimposed by eliminating excess cells at random, rather than by eliminating all cells from a given subcompartment containing only one strain. That is, following co-colonisation, the host niche contains a fraction $\frac{1}{1+\iota }$ of the “old” cells—an unbiased sample of the host’s carriage prior to co-colonisation—and a fraction $\frac{\mathrm{\iota }}{1+\iota }$ of the “new” cells, where ι is the “germ size”, the relative size of an invading group of cells compared to the host’s carrying capacity. Because this model allows hosts to carry an arbitrary mix of cells of different strains, it requires keeping track of a large number of host states, which our stochastic individual-based implementation achieves. However, under the simplifying assumption that germ sizes are small (ι ≪ 1), the model is well approximated using a system of ODEs with only five host states (Fig. 3e), for a similar mathematical tractability to the knockout model (see Supplementary Note 1 for details). Strikingly, the mixed-carriage model supports much more coexistence than the knockout model, suggesting that a more explicit model of within-host dynamics may more readily explain observed patterns of resistance (Fig. 3f).

Because it specifically tracks within-host strain frequencies, the mixed-carriage model can serve as a starting point for more complex models. To illustrate this, we add differential within-host growth to the model, such that sensitive cells gradually grow in frequency relative to resistant cells sharing the same host (Fig. 3g). Accordingly, we assume that the sensitive strain grows exponentially relative to the resistant strain at rate w_s—eliminating the resistant strain completely if its relative within-host frequency drops below a critical threshold f_min—while overall carriage remains fixed at the host’s carrying capacity. Again, this differential growth requires tracking a large number of host states, which can either be accounted for directly with an individual-based model implementation or be approximated using a finite number of mixed-carriage states in a system of ODEs, with the number of states depending upon the desired degree of concordance with the idealised dynamics of within-host growth (Fig. 3h; Supplementary Note 1). Differential within-host growth tends to gradually eliminate resistant cells from co-colonised carriers, partially reducing the frequency-dependent benefit associated with resistant cells co-colonising sensitive-strain carriers. However, it also introduces an additional frequency-dependent advantage for sensitive cells co-colonising resistant-strain carriers, which, overall, can further expand the potential for coexistence (Fig. 3i).

In each model, the potential for coexistence depends upon the prevalence of co-colonisation, which is partly governed by the parameter k: while setting k = 0 eliminates co-colonisation and recovers competitive exclusion, allowing co-colonisation (k > 0) promotes coexistence. In Supplementary Note 2, we identify the key processes that inhibit coexistence in the knockout model and promote coexistence in the mixed-carriage model, showing how the extent of coexistence depends crucially upon the prevalence of hosts carrying both sensitive and resistant strains.

Structural neutrality of the knockout and mixed-carriage models

A structurally-neutral model is one in which, when the biological differences between two strains are stripped away, pathogens of either strain are not treated differently from one another²⁸. The aim of structural neutrality is to ensure that the predicted outcome of competition between strains—whether it is coexistence or competitive exclusion—is attributable to identifiable, biological differences between the strains, rather than to hidden assumptions embedded in the model structure. The knockout model meets the mathematical criteria for structural neutrality proposed by Lipsitch et al.²⁸, but we argue that it violates the spirit of neutrality nonetheless. Specifically, the knockout model assumes that when a host carrying pathogens of two different strains is invaded by a new strain, the invading strain completely replaces one of the two resident strains while leaving the other untouched—even if the two resident strains differ only by a neutral, biologically-meaningless label. This property artificially depletes within-host strain diversity, inhibiting coexistence by reducing the scope for within-host competition. By contrast, the mixed-carriage model avoids this artificial loss of diversity, while adhering to both the spirit and the letter of structural neutrality. In Supplementary Note 3, we demonstrate the structural neutrality of the mixed-carriage model, and discuss how a model’s adherence to within-host neutrality depends upon the interpretation of within-host states.

Explicitly capturing within-host dynamics reproduces widespread coexistence

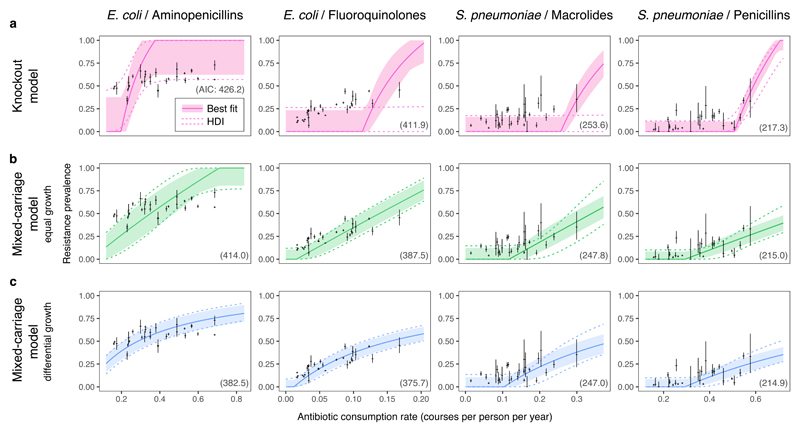
We used Bayesian inference via Markov chain Monte Carlo (MCMC) to fit both the knockout and mixed-carriage models to consumption and resistance data reported by 30 European countries across two common drug classes for the commensal pathogens E. coli and S. pneumoniae^2,3. We assumed that countries differ only in antibiotic consumption, while other epidemiological parameters are shared across countries and are constrained to be consistent with empirically-observed ranges for carriage prevalence and average duration of carriage. Due to the limited range of coexistence predicted by the knockout model, we find that it cannot capture observed patterns of resistance^4,6 (Fig. 4a). However, the empirical data are better captured by the mixed-carriage model (Fig. 4b), particularly when differential within-host growth is introduced (Fig. 4c). Using the Akaike Information Criterion to select the most parsimonious model, we find that the mixed-carriage model with differential within-host growth has the most statistical support across all bacteria-drug combinations (Fig. 3). Frequent co-colonisation by sensitive and resistant cells—irrespective of the overall prevalence of the species of interest—is needed to maintain widespread coexistence via within-host competition (Supplementary Note 4).

Fig. 4. Within-host dynamics explain patterns of resistance in commensal bacteria.

The knockout model (a) does not capture widespread coexistence, while the mixed-carriage model without (b) or with (c) differential within-host growth does. Solid lines and ribbons show the single best-fit run for each model (solid lines) and the 67% highest density interval (HDI) incorporating between-country random effects (shaded ribbon). Regions bounded by dashed lines show the 67% HDI across the estimated posterior, again incorporating between-country random effects. The Akaike Information Criterion associated with each model fit is given in parentheses on each panel; note that AICs are not strictly comparable across pathogen-drug data sets (columns) as the number of countries and sample sizes differ.

Patterns of coexistence among pneumococcal serotypes

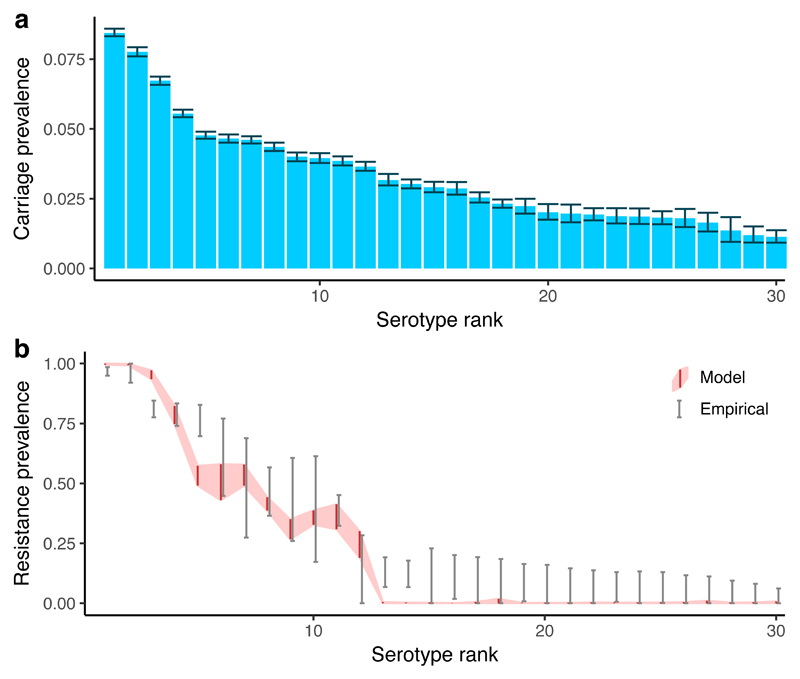
So far, we have focused on a simplified scenario in which bacterial diversity is limited to sensitive versus resistant strains, but the mixed-carriage model can be extended in this respect. The nasopharyngeal coloniser S. pneumoniae exhibits extensive diversity in the expression of capsular proteins exposed to the host immune system, subdividing the species into nearly 100 distinct “serotypes” that—like resistant versus sensitive strains—are known to stably coexist in host populations^27,36. Understanding both the coexistence of these serotypes and the evolution of resistance within each is vital for building a comprehensive picture of resistance evolution in pneumococci. We thus extended the two-strain mixed-carriage model (Supplementary Note 5) by parameterising it with the serotype-specific duration of carriage for 30 of the most common S. pneumoniae serotypes⁷, assuming a 10% transmission cost and a 20% growth cost of resistance, and introduced serotype- specific adaptive immunity to the model (i.e. host immunity to colonisation by previously-cleared serotypes). The extended model captures much of the observed serotype diversity and patterns of resistance among serotypes (Fig. 5).

Fig. 5. Resistance in coexisting pneumococcal serotypes.

We use the mixed-carriage model to simulate 30 co-circulating pneumococcal serotypes, using a previously-published data set⁷,⁵⁰ to assign measured durations of carriage to each serotype, while incorporating a simple model of host adaptive immunity. We assume that serotypes with a longer duration of carriage also have a within-host growth rate advantage²⁷, and that resistance carries a 10% transmission cost and a 20% within-host growth cost. We recover extensive diversity in (a) pneumococcal carriage (error bars show 95% interquantile range for the prevalence of each serotype among carriers in the final 100 years of the 400-year simulation) and (b) resistance prevalence (grey error bars show 95% confidence intervals for empirical resistance prevalence; red ribbon shows 95% interquantile range for model resistance prevalence). Note that model serotypes are ranked from high to low duration of carriage (a, b) while empirical serotypes are ranked from high to low resistance prevalence (b), to facilitate comparing general trends of within-serotype coexistence. Results from one model run are shown.

General predictions of the mixed-carriage model

Our extended serotype model illustrates that within-host competition can promote pathogen diversity more broadly than for resistance-associated phenotypes per se. For example, consider a host carrying cells of two different serotypes. If one serotype is cleared by the host immune system, the other serotype may benefit from competitive release. So long as clearance of one serotype does not result in clearance of all serotypes within a host, clearance will tend to promote rare serotypes, since the hosts they co-colonise are more likely to be carrying a different serotype, and hence they are more likely than common serotypes to be the beneficiaries of competitive release mediated by natural clearance. This effect can promote serotype diversity (Fig. 6a) even in the absence of any host acquired immunity^27,36.

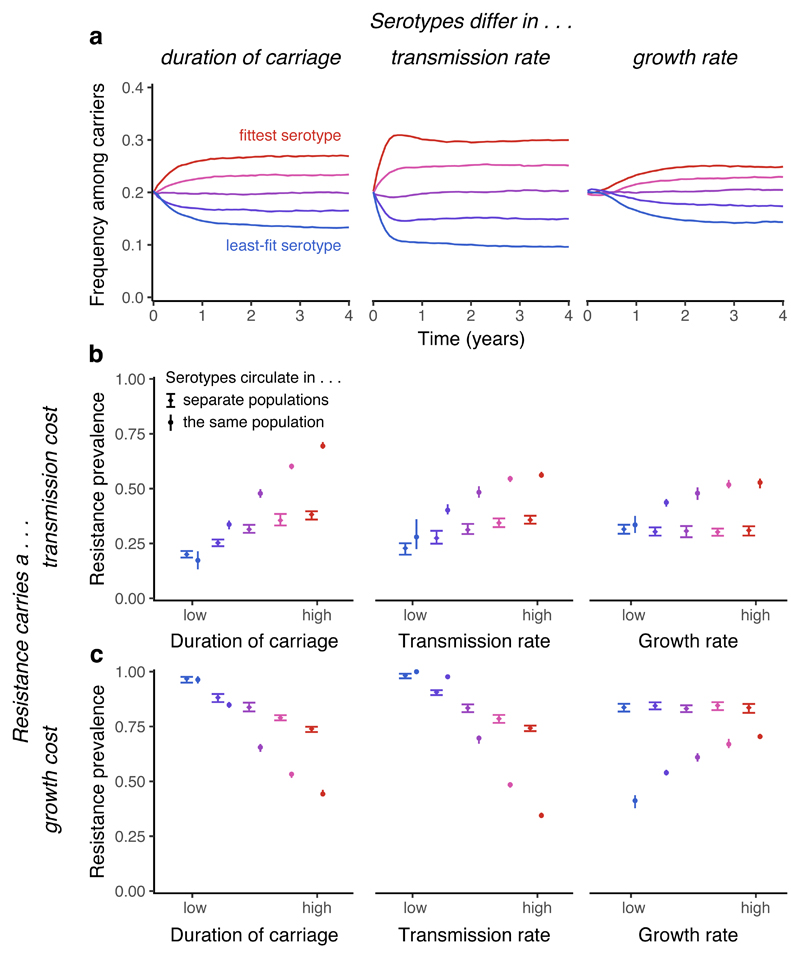
Fig. 6. General effects of within-host competition.

Serotype-specific clearance promotes coexistence between serotypes, and intrinsic fitness differences between serotypes are correlated with resistance prevalence within serotypes. Serotypes are assumed to differ in duration of carriage (u = 1.04, 1.02, 1, 0.98, 0.96), transmission rate (β = 1.84, 1.92, 2, 2.08, 2.16), or within-host growth rates (w = 1, 2, 4, 8, 16). In each plot, the fittest serotype is shown in red. (a) In a model with five serotypes (all antibiotic-sensitive) differing in various measures of intrinsic fitness, serotype-specific clearance maintains coexistence between serotypes in the absence of any acquired immune response. (b) When resistance carries a 10% transmission-rate cost, fitter serotypes are more strongly selected for resistance. We contrast trends in resistance when serotypes circulate in separate populations or together in the same population; circulating together tends to magnify differences in resistance between serotypes. The mean and 95% interquantile range for the last 50 years of each 100-year simulation is shown. (c) When resistance carries a growth-rate cost (with sensitive strains growing at 10 times the rate of resistant strains), fitter serotypes are less strongly selected for resistance, except when serotypes differ in growth rate, where the trend is reversed. While serotypes circulating in the same population tends to increase average resistance prevalence when resistance carries a transmission cost, it tends to decrease resistance when resistance carries a growth cost. For each plot, results from a single model run are shown.

We conclude by considering the impact of carriage duration, transmission rate and growth rate upon resistance evolution. In agreement with previous theoretical work⁷, we find that a longer duration of carriage promotes greater resistance when resistance carries a transmission cost (Fig. 6b). However, this association can be reversed when resistance instead carries a within-host growth rate cost (Fig. 6c), because a longer duration of carriage affords sensitive cells a greater opportunity to outcompete resistant cells within hosts. Accordingly, the overall relationship between duration of carriage and resistance likely depends upon the balance of these two costs of resistance for a given species. Our model also predicts that a higher transmission rate promotes co-colonisation. In co-colonised hosts, sensitive strains may be eliminated by treatment, while resistant strains may be eliminated by faster-growing sensitive strains. The relative importance of these two forms of competition determines whether increased transmission promotes or inhibits resistance (Fig. 6b & c). This mechanism may elucidate an observed positive relationship between resistance prevalence and population density³⁷. Finally, we find that resistance is promoted in serotypes with greater within-host growth, as they are less likely to be excluded by other serotypes before antibiotic treatment results in their competitive release. Each of these three trends appears stronger when serotypes circulate in the same population than in different populations (Fig. 6b&c). Why various species exhibit different levels of resistance when faced with similar rates of antibiotic treatment is an outstanding problem in resistance evolution, which further analysis may help to resolve.

Discussion

Our model provides two advances over previous work: it harmonises pathogen dynamics by mechanistically capturing both between-host and within-host processes, and it better captures empirical patterns of antibiotic resistance. We argue that frequency-dependent selection drives these patterns of resistance, and that explicitly tracking within-host dynamics helps to reproduce them.

In order for within-host competition to maintain substantial coexistence, a high proportion of hosts must be colonised by both resistant and sensitive bacteria. Co-colonised strains must also compete for transmission; models with co-colonisation but no competitive release do not produce extensive coexistence⁶. Empirical estimates suggest that dual carriage may be widespread. A study of Staphylococcus aureus carriage in children found 21% of carriers were colonised by both resistant and sensitive S. aureus strains¹⁴. Relatively few studies have measured simultaneous carriage of both sensitive and resistant strains of the same species, but carriage of multiple strains more generally appears to be common: genotyping studies have found up to 48% multiple carriage of genetically-distinct S. pneumoniae strains^11,12 and up to 86% multiple carriage of E. coli strains^13,15. Although we have focused on competition between conspecific strains, competition between different species could also promote coexistence, reducing the need for widespread carriage of multiple strains of the same species. There is ample opportunity for between-species competition: the nasopharynx typically hosts tens or hundreds of species^16,17, while the gut typically hosts thousands¹⁸. The extent to which this extensive diversity may contribute to resistance evolution remains to be evaluated.

Alternative mechanisms that could explain coexistence between drug-sensitive and resistant pathogens have been proposed^{4,6–8,38–40}. Some support only modest amounts of coexistence^4,6, while others may be less empirically generalisable, such as strongly age-assortative mixing^6,7, independent mappings of balancing selection⁷, or specific immune responses to resistance-associated phenotypes^4,38–40. We have focused on how within-host competition can promote substantial coexistence on its own. A more complex model incorporating additional drivers of coexistence would support similar amounts of coexistence while diminishing the relative importance of within-host competition.

The models we have contrasted here make a number of simplifying assumptions. We have assumed that observed resistance patterns represent the equilibrium state, following from the lack of conclusive evidence for significant time lags in resistance prevalence⁴¹ (Supplementary Note 6). We have assumed that antibiotics kill all sensitive cells instantaneously rather than adopting a more mechanistically-explicit model of treatment⁴², and that host immunity completely prevents colonisation by previously-cleared serotypes rather than providing partial protection²⁷. We have ignored effects of population structure, such as age-assortative mixing^6,7 and heterogeneity in antibiotic consumption^4,6, which may promote additional coexistence. We have assumed that co-colonisation occurs through sequential transmission, ignoring the alternative routes of de novo mutation (which may be especially important for long-lived chronic infections^43,44), acquisition or loss of resistance through horizontal gene transfer, and simultaneous transmission of multiple strains from co-colonised carriers. Finally, we have focused on modelling resistance to a single drug at a time rather than exploring multi-drug resistance⁴⁵. Elaborations of our simple mixed-carriage model incorporating these additional complexities may provide a means with which to explore the importance of these mechanisms.

Antibiotic resistance is one of the foremost threats to human health, and combating this threat will require the global deployment of coordinated interventions^9,10. Mathematical models of disease transmission will play a crucial role in this endeavour, because they can explicitly integrate the mechanisms that drive resistance evolution in a population-level framework and allow us to quantify long-term trends as well as the likely impact and cost-effectiveness of any large-scale interventions for reducing resistance⁴⁶. Providing a framework in which to answer public health questions demands a balance between mathematical tractability and necessary complexity; building on the simple model proposed here will help to establish that balance. If mathematical models incorporate a truly mechanistic understanding of resistance evolution, they will be better able to explain empirical patterns of resistance and accurately predict the impact of interventions at a national and global level⁴⁶.

Methods

The problem of coexistence

Data and sources

We use data from the European Centre for Disease Prevention and Control (ECDC) on primary-care consumption of penicillins, fluoroquinolones, and macrolides² versus aminopenicillin resistance and fluoroquinolone resistance in E. coli, and macrolide non-susceptibility and penicillin non-susceptibility in S. pneumoniae³, across up to 30 European countries. All data are from 2015, except for S. pneumoniae penicillin non-susceptibility versus penicillin consumption, which are from 2007 as breakpoints for S. pneumoniae penicillin non-susceptibility were changed in some countries after this year, yielding inconsistencies in resistance data between countries^4,47. Antibiotic use is classified into primary-care and hospital consumption, with the majority of consumption in primary care². We use primary-care data only, as we are focusing on community-acquired bacterial carriage. Resistance is measured from invasive isolates extracted from blood and cerebrospinal fluid³. We assume that each isolate is an unbiased sample of commensally-carried strains⁷. See Supplementary Note 7 for full details.

Trends in resistance prevalence

In Fig. 1a, linear regressions are least-squares fits to maximum-likelihood estimates of the resistance prevalence in each country. In Fig. 1d, the average resistance prevalence in Europe is calculated as the population-weighted mean of resistance prevalence across countries that reported data for all years in 2007–2015. See Supplementary Note 6 for more details.

Two models of within-host dynamics

In the Results section, we contrast two models of within-host dynamics: the existing knockout model^4,28, and the novel mixed-carriage model. Here, we describe how the knockout and mixed-carriage models can be implemented for two strains in a stochastic individual-based framework, then show how they can be approximated using systems of ODEs. The individual-based and ODE implementations are equivalent under certain limiting assumptions and produce similar results (Supplementary Note 1). We use the ODE implementations to illustrate coexistence between resistant and sensitive strains and for model fitting (Figs. 1, 3, & 4). The individual-based implementation of the mixed-carriage model can be extended to simulate an arbitrary number of strains (Supplementary Note 5) and is used to analyse serotype dynamics (Figs. 5 & 6).

Knockout model^4,28

In a population of N hosts indexed by i ∈ [1..N], there are N_X non-carriers, N_S sensitive-strain carriers, N_R resistant-strain carriers, and N_SR dual carriers; we notate host i’s state as h_i ∈ {X, S, R, SR}. The following host-state transitions occur as inhomogeneous Poisson point processes at the specified per-host rates:

$$\begin{array}{l}X\stackrel{{\lambda }_{\text{s}}}{\to }S(sensitivestraincolonisation)\\ X\stackrel{{\lambda }_{\text{r}}}{\to }R(resistantstraincolonisation)\\ S\stackrel{k{\lambda }_{\text{r}}}{\to }SR(sensitivestrainco-colonisation)\\ R\stackrel{k{\lambda }_{\text{s}}}{\to }SR(resistantstrainco-colonisation)\\ SR\stackrel{\frac{1}{2}k{\lambda }_{\text{s}}}{\to }S(knockoutofresistantstrain)\\ SR\stackrel{\frac{1}{2}k{\lambda }_{\text{r}}}{\to }R(knockoutofsensitivestrain)\\ S\stackrel{u+\tau }{\to }X(sensitive-straincarrierclearanceortreatment)\\ R\stackrel{u}{\to }X(resistant-straincarrierclearance)\\ SR\stackrel{u}{\to }X(dualcarrierclearance)\\ SR\stackrel{\tau }{\to }R(dualcarriertreatment).\end{array}$$

For example, non-carriers (X) become sensitive-strain carriers (S) at rate λ_s, and so on. Above, ${\lambda }_{\text{S}}=\beta \frac{N_{\text{S}}+\frac{1}{2}{N}_{\text{SR}}}{N}$ is the sensitive strain’s force of infection, ${\lambda }_{\text{r}}=\beta (1-c)\frac{N_{\text{R}}+\frac{1}{2}{N}_{\text{SR}}}{N}$ is the resistant strain’s force of infection, β is the transmission rate, c is the transmission cost of resistance, k is the relative efficiency of co-colonisation, u is the natural clearance rate, and τ is the treatment rate. In this model, the resistance prevalence is $\rho =(N_{\text{R}}+\frac{1}{2}{N}_{\text{SR}})/(N_{\text{S}}+N_{\text{R}}+N_{\text{SR}}).$

Mixed-carriage model

In a population of N hosts indexed by i ∈ [1..N] as above, host i’s state is (s_i,r_i), where s_i ≥ 0 is host i’s carriage of the sensitive strain and r_i ≥ 0 is host i’s carriage of the resistant strain. In a non-carrier, s_i = r_i = 0, while in a carrier, s_i + r_i = 1. We model transmission, clearance, and treatment events as inhomogeneous Poisson point processes, while within-host strain growth is updated in each host at regular discrete time steps. The following host-state transitions occur at the specified per-host rates:

$$\begin{array}{l}\left(s_i,r_i\right)\stackrel{{\kappa }_i{\lambda }_{\text{S}}}{\to }\left(\frac{s_i+\iota }{s_i+r_i+\iota },\frac{r_i}{s_i+r_i+\iota }\right)(sensitivestraintransmission)\\ \left(s_i,r_i\right)\stackrel{{\kappa }_i{\lambda }_{\text{r}}}{\to }\left(\frac{s_i}{s_i+r_i+\iota },\frac{r_i+\iota }{s_i+r_i+\iota }\right)(resistantstraintransmission)\\ \left(s_i,r_i\right)\stackrel{u}{\to }(0,0)(clearance)\\ \left(s_i,r_i\right)\stackrel{\tau }{\to }\{\begin{array}{cc}(0,0)& \text{if}{r}_i=0\\ (0,1)& \text{if}{r}_i>0\end{array}(treatment).\end{array}$$

For example, a host with state (s_i, r_i) = (0,1) changes state to $\left(s_i,r_i\right)=\left(\frac{\iota }{1+\iota },\frac{1}{1+\iota }\right)$ at rate κ_i λ_s, and so on. Above, κ_i = 1 if (s_i, r_i) = (0,0) and κ_i = k otherwise; ι is the germ size; and force-of-infection terms are ${\lambda }_{\text{S}}=\beta \max \left(Y_{\min },{\sum }_i{S}_i\right)/N$ and ${\lambda }_{\text{r}}=\beta (1-c)\max \left(Y_{\min },{\sum }_i{r}_i\right)/N,$ where we can set Y_min = 1 to effectively assume there is always at least one carrier of each strain to avoid stochastic elimination of strains²⁷, or set Y_min = 0 to not do this. The resistance prevalence is $\rho ={\sum }_i{r}_i/{\sum }_i(s_i+r_i).$

Updates to within-host strain growth happen to all hosts simultaneously at intervals of Δt (unless otherwise specified, Δt = 0.001 mo^–1), as follows. For each host, any strains for which carriage is less than f_min are set to zero (we primarily use f_min = 3×10^-5 to keep strains from persisting when they reach low frequencies, but can set f_min = 0 to allow them to remain at any frequency until treatment and/or natural clearance occurs). Then the sensitive strain in each carrier grows by a factor ${\omega }_{\text{s}}=w_{\text{s}}^{\Delta t}$, where w_s is the sensitive strain’s relative growth rate (such that w_s = 1 translates to no differential within-host growth). Finally, each colonised host’s total carriage is normalised so that s_i + r_i = 1. That is, every Δt units of time, each colonised host undergoes the transition

$$(s_i,r_i)\to \left(\frac{{\omega }_{\text{s}}q(s_i)}{{\omega }_{\text{s}}q(s_i)+q(r_i)},\frac{q(r_i)}{{\omega }_{\text{s}}q(s_i)+q(r_i)}\right),$$

where

$$q(a)=\{\begin{array}{cc}a& \text{if}a\ge f_{\text{min}}\\ 0& \text{if}a<f_{\text{min}}\end{array}.$$

In our implementation, we calculate the force-of-infection terms and the number of events of each type between time t and t + Δt during the “updating” step, then execute each event in a random order.

Systems of ODEs

The knockout and mixed-carriage models can be approximated using ODEs (Supplementary Note 1). Following previous work^4,28, the knockout model is implemented as

$$\begin{array}{l}\frac{dS}{dt}=\beta S_{\text{tot}}X-(u+\tau )S-k\beta (1-c)R_{\text{tot}}S+\frac{k\beta S_{\text{tot}}D}{2}\\ \frac{dR}{dt}=\beta (1-c)R_{\text{tot}}X-uR-k\beta S_{\text{tot}}R+\frac{k\beta (1-c)R_{\text{tot}}D}{2}+\tau D\\ \frac{dD}{dt}=k\beta (1-c)R_{\text{tot}}S+k\beta S_{\text{tot}}R-(u+\tau )D-\frac{k\beta S_{\text{tot}}D}{2}-\frac{k\beta (1-c)R_{\text{tot}}D}{2}\\ X=1-S-R-D.\end{array}$$ (1)

Here, S is the fraction of sensitive-strain carriers in the population; R is the fraction of resistant-strain carriers; D is the fraction of dual carriers (i.e., SR hosts); and X is the fraction of non-carriers. Here, S_tot = S + D/2 and R_tot = R + D/2 give the effective population burden of sensitive- and resistant-strain colonisation, respectively, and the resistance prevalence is ρ = R_tot/(1–X). The parameters β,c,u,τ, and k correspond to those used in the individual-based implementation of the knockout model, described above.

Similarly, the mixed-carriage model (in the absence of differential within-host growth) can be approximated using the following system of ODEs:

$$\begin{array}{l}\frac{dS}{dt}=\beta S_{\text{tot}}X-(u+\tau )S-k\beta (1-c)R_{\text{tot}}S\\ \frac{dR}{dt}=\beta (1-c)R_{\text{tot}}X-uR-k\beta S_{\text{tot}}R+\tau (S_R+R_S)\\ \frac{d{S}_R}{dt}=k\beta (1-c)R_{\text{tot}}S-(u+\tau )S_R\\ \frac{d{R}_S}{dt}=k\beta S_{tot}R-(u+\tau )R_S\\ X=1-S-R-S_R-R_S.\end{array}$$ (2)

Here, the compartment S_R captures the fraction of the population predominantly colonised with sensitive bacteria, but also carrying a small amount of resistant bacteria that are carried in insufficient quantity to transmit, and S_tot = S + S_R gives the effective population burden of sensitive-strain colonisation. Similarly, the compartment R_S captures the fraction of the population predominantly colonised with resistant bacteria, but also carrying a small amount of sensitive bacteria that are carried in insufficient quantity to transmit, and R_tot = R + R_S gives the effective population burden of resistant-strain colonisation. The overall resistance prevalence is ρ = R_tot/(1–X). The parameters β,c,u,τ, and k correspond to those used in the individual-based implementation of the mixed-carriage model, described above.

Finally, the mixed-carriage model with differential within-host growth can be approximated with ODEs by adding “intermediate” compartments between R_S and S_R:

$$\begin{array}{l}\frac{dS}{dt}=\beta S_{\text{tot}}X-(u+\tau )S-k\beta (1-c)R_{\text{tot}}S+b_0{S}_R\\ \frac{dR}{dt}=\beta (1-c)R_{\text{tot}}X-uR+\tau \left(S_R+{\displaystyle \sum _{v=1}^Z{D}_v}+R_S\right)-k\beta S_{\text{tot}}R\\ \frac{d{S}_R}{dt}=k\beta (1-c)R_{\text{tot}}S-(u+\tau )S_R-b_0{S}_R+b{D}_1\\ \frac{d{D}_v}{dt}=-(u+\tau )D_v-b{D}_v+b{D}_{v+1}\text{for}\text{all}v\in [\mathrm{1..}Z]\\ D_{Z+1}\equiv R_S\\ \frac{d{R}_S}{dt}=k\beta S_{\text{tot}}R-(u+\tau )R_S-b{R}_S\\ X=1-S-R-S_R-{\displaystyle \sum _{v=1}^Z{D}_v}-R_S.\end{array}$$ (3)

Here, there are Z “intermediate” compartments between R_S and S_R, labelled D₁ through D_Z (we use Z = 7; see Supplementary Note 1 for a graphical illustration of the dynamics of these intermediate compartments). Here, b determines the within-host growth rate of the sensitive strain relative to the resistant strain, setting the rate at which individuals move from the R_S compartment through intermediate compartments and finally through to S as the resistant strain is gradually outcompeted by the sensitive strain. A separate parameter b₀ sets the rate of the final transition from S_R to S. In practice, we set $b_0=\frac{1}{2}b,$ which for Z = 7 and ι = 0.001 corresponds to the resistant strain effectively becoming lost once its within-host frequency drops below f_min = 3×10^-5 (Supplementary Note 1). The parameters b and b₀ replace the parameters w_s and f_min from the individual-based implementation of the mixed-carriage model, above; all other parameters (i.e. β,c,u,τ, and k) correspond to those used in the individual-based implementation.

Notating the fraction of a host’s bacterial carriage that is resistant as r_Y for a host with state Y, we assume that $r_{{\text{R}}_{\text{S}}}=\frac{1}{1+\iota },r_{{\text{S}}_{\text{R}}}=\frac{\iota }{1+\iota },$ and that intermediate compartments are evenly spaced between these points on a logistic curve, i.e. that $r_{D_v}=\frac{1}{1+\exp (y(v){)}^{\prime }}\text{where}y(v)=\log (\iota )\left(\frac{2v}{Z+1}-1\right).$ We assume that individuals in compartment D_v transmit the resistant strain a fraction r_Dv of the time and transmit the sensitive strain a fraction 1 − r_Dv of the time, but that R_S individuals only transmit the resistant strain and S_R individuals only transmit the sensitive strain. Ignoring transmission of the minor strain for these two host types maintains consistency with equations (2) and maintains structural neutrality for equivalent strains in equations (3). Accordingly, in the model above, S_tot = S + S_R + ∑_vD_v(1 − r_Dv) and R_tot = R + R_S + ∑_vD_vr_Dv. Note that the mixed-carriage model without differential within-host growth can be recovered from the above model by setting b = b₀ = 0; in model fitting, when we allow differential growth (i.e. b > 0) we assume that this accounts for the cost of resistance, and accordingly set c = 0. In this model, the overall resistance prevalence is ρ = R_tot/(1–X).

Initial conditions and solutions

For all individual-based model simulations, we assume that 5% of hosts are colonised at the beginning of the simulation by a single randomly-selected strain, and run the simulation for 100–400 years, taking the average state over the last 50–100 years as the equilibrium state. Individual-based models are simulated in C++. All ODE models are solved by setting single-carriage compartments (S and R) equal to 0.001 and all dual-carriage compartments to 0, then integrating the systems of ordinary differential equations numerically in C++ using the Runge–Kutta Dormand–Prince method until they reach equilibrium.

Model fitting to resistance prevalence in commensal bacteria

In the source data², antibiotic consumption rates are given in defined daily doses (DDD) per thousand people per day; we convert these to overall treatment rates by assuming that 10 DDD comprise one treatment course for penicillin⁷ and fluoroquinolones, while 7 DDD comprise one treatment course for macrolides.

We use Bayesian inference to fit the model to empirical data, using differential evolution Markov chain Monte Carlo (DE-MCMC⁴⁸) to estimate the posterior distribution of model parameters. We assume that the number of resistant isolates observed in a given country is binomially distributed; the probability of observing a resistant isolate is equal to the resistance prevalence ρ predicted by the model, plus some additional dispersion modelled using a [0,1]–truncated normal distribution. Modelling the “true” resistance prevalence as a random variable allows us to account for between-country variation in resistance prevalence not captured by our dynamic model. As we assume that the only parameter that varies between European countries is the rate of antibiotic consumption, this additional variation is intended to account for other factors that may vary between countries, whether they are explicitly part of the model structure (e.g. transmission rates varying from country to country) or not (e.g. differences in laboratory procedures, population structure, or prescription patterns from country to country).

For a given model fit with parameters θ, suppose that country m (where countries are numbered 1 to M) has antibiotic treatment rate τ_m and reports that r_m out of n_m isolates are resistant. Over all M countries, these data are denoted τ = (τ₁, τ₂, …, τ_M), r = (r₁, r₂, …, r_M), and n = (n₁, n₂, …, n_M), respectively. We also have Y⁽⁰⁾ and Y⁽¹⁾, which are the lower and upper bounds for carriage prevalence in any country (see below). Together, τ,r,n,Y⁽⁰⁾ and Y⁽¹⁾ are the data to which the model is being fit, and model parameters are θ = (β,c,b,u,k,σ). (Note that, for certain data sets, not all of the parameters in θ are permitted to vary; specifically, we assume u = 1 when fitting S. pneumoniae for consistency with previous studies, and we only allow one of c and b to vary at a time in order to contrast these two alternative costs of resistance.) Suppose that, for a given treatment rate τ_m, the model predicts a resistance prevalence of ρ(τ_m|θ) and a prevalence of carriage Y(τ_m|θ). Then, the likelihood of the model fit is

$$ℒ\left(\mathit{\tau },\mathit{\text{r}},\mathit{\text{n}},Y^{\left(0\right)},Y^{\left(1\right)}|\theta \right)={\displaystyle \prod _m𝒞\left({\tau }_m,Y^{\left(0\right)},Y^{\left(1\right)}|\theta \right)ℛ\left({\tau }_m,r_m,n_m|\theta \right)},$$

which is constructed of two components that are evaluated for each country. The first component,

$$𝒞\left({\tau }_m,Y^{\left(0\right)},Y^{\left(1\right)}|\theta \right)=\{\begin{array}{cc}1& \text{if}{Y}^{\left(0\right)}\le Y\left({\tau }_m|\theta \right)\le Y^{\left(1\right)}\\ \text{exp}\left(-1000\right)& \text{otherwise}\end{array},$$

heavily penalises any model fit which predicts that any country has a prevalence of carriage not within the bounds [Y⁽⁰⁾,Y⁽¹⁾] and is used to prevent the model-fitting process from predicting an unrealistic carriage prevalence for any country. The second component,

$$ℛ({\tau }_m,r_m,n_m|\theta )={\displaystyle \underset{0}{\overset{1}{\int }}𝒯(x|\mu =\rho ({\tau }_m|\theta ),\sigma =\sigma (\theta ))}ℬ(r_m|n=n_m,p=x)\text{d}x,$$

assigns a likelihood to the model-predicted resistance prevalence ρ(τ_m|θ) given that country m has reported that r_m of n_m bacterial isolates are resistant. Above: $𝒯(x|\mu ,\sigma )=\phi (x|\mu ,\sigma )/\left(\Phi (1|\mu ,\sigma )-\Phi (0|\mu ,\sigma )\right)$ is the probability density function (PDF) of a truncated normal distribution with bounds 0 and 1, where $\phi (x|\mu ,\sigma )=\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left(-\frac{{(x-\mu )}^2}{2{\sigma }^2}\right)$ is the untruncated normal PDF and $\Phi (x|\mu ,\sigma )=\frac{1}{2}(1+\text{erf}\left(\frac{x-\mu }{\sigma \sqrt{2}}\right))$ is the untruncated normal cumulative distribution function (CDF); and $ℬ(r|n,p)=\left(\begin{array}{c}n\\ r\end{array}\right)p^r{(1-p)}^{n-r}$ is the binomial distribution probability mass function (PMF), such that the integral calculates a weighted likelihood over all possible “true” resistance prevalences x. The parameter σ(θ) of the truncated normal distribution is fit as one of the parameters of the model so that between-country variation is estimated separately for each alternative model.

Priors used for model fitting, posterior distributions from model fitting, and further details of MCMC can be found in Supplementary Note 4. Note that since we are only fitting to the measured resistance prevalence in each European country and to a fixed range of carriage prevalence, the values of certain parameters are difficult to identify, particularly for the knockout model.

Model comparison

For each model fit, we calculate the Akaike Information Criterion $AIC=2K-2\log (\widehat{ℒ}),$ where K is the number of free parameters and $\widehat{ℒ}$ is the maximum likelihood for a given model fit.

Patterns of resistance and coexistence among bacterial subtypes

For Figs. 5 & 6, we extend the individual-based mixed-carriage model to accommodate an arbitrary number of strains (Supplementary Note 5). For Fig. 5 only, we also introduce serotype-specific adaptive immunity. Hosts develop immunity to a serotype when they naturally clear that serotype, and immunity provides complete protection against future colonisations by that serotype. We assume that hosts are replaced by new, immunologically-naïve, uncolonised hosts at rate α = 1/60 mo^-1, reflecting the relative importance of hosts aged 5 years and under for pneumococcal transmission^4,49. Other parameters for Fig. 5 are β = 3.2 mo^-1 for sensitive strains and β = 2.88 mo^-1 for resistant strains (i.e. a 10% transmission cost of resistance), w ranging from 1 to 30 for sensitive strains, where the serotype with the highest growth rate also has the longest duration of carriage, w ranging from 0.8 to 24 for resistant strains (i.e. a 20% growth cost of resistance), k = 1, τ = 0.025, and N = 1×10⁶. For Fig. 6, other parameters are β = 2 mo^-1, u = 1 mo^-1, w = 1, and k = 1 unless otherwise specified in the caption. The treatment rate is τ = 0 for Fig. 6a and τ = 0.075 for Fig. 6b for serotypes circulating both separately and in the same population. For Fig. 6c, the treatment rate is τ = 0.075 when serotypes circulate together, but τ = 0.05 when serotypes circulate individually. The reduced treatment rate when serotypes circulate individually is necessary to observe the trend in resistance prevalence among serotypes (with τ = 0.075, all serotypes show 100% resistance prevalence, so trends are not apparent). We use a population size of N = 1×10⁶ for runs with serotypes circulating together, and N = 2×10⁵ for runs with serotypes circulating individually.

Supplementary Material

Supplementary Notes 1–7 (with figures, tables, references, and appendices inline)