Non-invasive monitoring of single-cell mechanics by acoustic scattering

Abstract

Monitoring mechanics of the same cell throughout the cell cycle has been hampered by the invasiveness of mechanical measurements. Here, we quantify mechanical properties via acoustic scattering of waves from a cell inside a fluid-filled vibrating cantilever with a temporal resolution of <1 min. Through simulations, experiments with hydrogels and chemically perturbed cells, we show that our readout, the size-normalized acoustic scattering (SNACS), measures stiffness. We demonstrate the noninvasiveness of SNACS over successive cell cycles using measurements that result in < 15 nm deformations. Cells maintain constant SNACS throughout interphase but exhibit dynamic changes during mitosis. Our work provides a basis for understanding how growing cells maintain mechanical integrity and demonstrates that acoustic scattering can non-invasively probe subtle and transient dynamics.

Introduction

Although spatiotemporal changes in cytoskeletal components have been widely characterized by optical microscopy^1,2, mechanical measurements are necessary for fully understanding the functional consequences of cytoskeletal remodeling³. Mechanical properties of living cells such as stiffness often play a fundamental role in various intra- and intercellular processes such as migration⁴, metastasis^5,6 and development⁷. From atomic force microscopy (AFM)^8,9, to optical stretching^10–12, fluid shear stress^13,14 and particle tracking methods^15–17 numerous strategies have been introduced for measuring mechanical properties of single cells, yet they are typically invasive and used as end-point assays. Microindentation and AFM techniques are capable of continuous monitoring by probing stiffness changes through a series of indentations across the top surface of a cell^18,19. However, these measurements are influenced by the location and geometry where the tip physically makes contact, which makes long-term monitoring of whole-cell stiffness with high temporal resolution challenging. Recently, acoustic fields have been used to non-invasively probe cellular stiffness^20–22. This is typically achieved by applying acoustic radiation forces in microchannels and tracking the stiffness-dependent trajectories of cells in order to obtain end-point measurements.

Here we introduce an acoustic method for continuously and non-invasively monitoring single-cell mechanics over multiple cell generations. This enables us to precisely follow the mechanical dynamics of single cells in the time scales less than a minute and observe mechanical changes that are too subtle to be observed at the population level due to cellular heterogeneity.

Results

Acoustic scattering shifts resonant frequency at the node of a suspended microchannel resonator

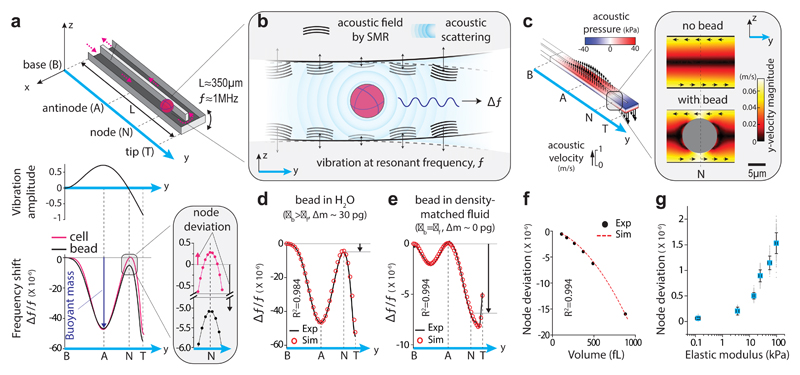
We utilized the vibration of a suspended microchannel resonator (SMR, Fig. 1a, top) as an acoustic energy source and investigated if the scattered acoustic fields from the cell could provide a signal to monitor its mechanical properties (Fig. 1b). The SMR is a cantilever-based microfluidic mass sensor that has previously been used to measure cell buoyant mass²³. Vibrating the SMR at its second mode (resonant frequency f) causes the vibration amplitude to vary along the length of the cantilever, with one local maximum (antinode) near the center and a zero-minimum (node) near the tip (Fig. 1a, middle). When a cell is at the antinode, the net change in mass (i.e. the buoyant mass of the cell) corresponds to a change in the kinetic energy of the system²⁴, and thus causes a shift in the resonant frequency of the SMR (Δf/f|_antinode) (Fig. 1a, bottom and Supplementary Note 1). When the cell is at the node, the net change in mass is not expected to shift the resonant frequency (Δf/f|_node = 0) because the vibration amplitude is zero and there is no change in kinetic energy. Surprisingly, we observed a consistent resonant frequency shift at the node (Δf/f|_node ≠ 0) when we flowed a single cell or polystyrene bead in the SMR (Fig. 1a, bottom). This resonant frequency shift, which we termed “node deviation” (Δf/f|_node), was different for cells and beads of similar buoyant mass. We therefore hypothesized that the node deviation corresponds to an energy change due to acoustic scattering from the cell’s surface, and that the node deviation depends on cellular mechanical properties.

Figure 1. Acoustic scattering causes a resonant frequency shift at the node of a suspended microchannel resonator (SMR).

a, Top, schematic of SMR with a particle flowing through the embedded fluidic channel. Pink arrows mark the particle trajectory. Middle, normalized vibration amplitude at the 2^nd mode. Bottom, resonant frequency shift (Δf/f) from experiments with a single cell (pink) and a polystyrene bead (black). Vertical dotted lines mark the particle positions along the cantilever, as in top panel. Buoyant mass (size) is measured at the antinode (Δf/f|_antinode, blue arrow). Inset, Δf/f at the node where node deviation is measured (Δf/f|_antinode, black and pink arrows). b, Conceptual illustration of frequency shift due to acoustic scattering. A particle interacts with acoustic fields (black waves) generated by the SMR vibration (black arrows) at resonant frequency f. The particle-fluid interaction causes acoustic scattering (blue waves), which shifts the resonant frequency (Δf). The wavelength (λ) of the acoustic fields is depicted qualitatively (λ ~ 1 mm, which is ~ 100 times the channel height). c, Acoustic pressure (colors) and acoustic velocities (arrows) within SMR from Finite Element Method simulations. Inset, magnitudes of y-acoustic velocities with and without a polystyrene bead at the node. Black arrows show directions of y-acoustic velocities. d, e, Δf/f from simulations (red circles) and experiments (black lines) with polystyrene beads flowing through SMR filled with H₂O (d) or density-matched fluid (ρ_bead = ρ_fluid) (e). Black arrows show node deviation. f, Node deviation vs particle volume from simulations (red dashed line) and experiments (black dots) with polystyrene beads. g, Node deviation vs mean elastic modulus, as measured using AFM indentation (Methods), for synthetic hydrogels of same volume (n=92, 115, 243, 146, 134 and 186 hydrogels for node deviation measurements, n=4 hydrogels for each AFM measurements). Data depicts mean (blue squares) ± s.d. (error bars).

First, to determine if the node deviation corresponds to acoustic scattering, we utilized Finite Element Method (FEM) simulations for fluid-structure acoustic interactions (Supplementary Note 2). This revealed that the acoustic pressures and velocities vary along the SMR similarly to the vibration amplitude (Fig. 1c, Supplementary Fig. 1 and Supplementary Video 1). Positioning a particle at the node changes the acoustic velocities (Fig. 1c, inset and Supplementary Video 2). When we calculated the resonant frequency shift by integrating the acoustic energy terms obtained from the simulation (Supplementary Tables 1, 2 and Supplementary Note 2), we obtained excellent agreement (R²=0.984) with our measurements (Fig. 1d). We confirmed that the particle-fluid density difference has negligible effect on node deviation (Supplementary Fig. 2). To validate that acoustic effects can be measured independently of buoyant mass, we measured a bead in a density-matched fluid (ρ_fluid = ρ_bead). This resulted in zero resonant frequency shift at the antinode (Δf/f|_antinode = 0), but a noticeable resonant frequency shift at the node in both the experiment and simulation, which showed excellent agreement with each other (R²=0.994, Fig. 1e). Additional measurements revealed that node deviation is independent of fluid velocity or vibration amplitude (Supplementary Fig. 3a,b). Therefore, by measuring the resonant frequency shift at the node and antinode as cells flow through the SMR, it is possible to simultaneously and independently quantify the acoustic scattering and buoyant mass of the cell (Fig. 1a, bottom).

We compared polystyrene particles with different volumes and observed that node deviation changes with particle volume (Fig. 1f). The volume dependence can be accounted for by utilizing the buoyant mass measurement. To establish the correlation between node deviation and stiffness, we fabricated hydrogels with varying elastic modulus by changing their chemical composition and characterized the elastic modulus of the hydrogels using AFM. When measuring the mechanical properties with the SMR, we observed that the node deviation of the hydrogels increases monotonically with their elastic modulus over the range 0.1-100kPa (Fig. 1g). We also observed that node deviation is not sensitive to particle shape for hydrogels of the same elastic modulus and aspect ratios in the range of 1-2.5 (Supplementary Fig. 3c).

Size-normalized acoustic scattering (SNACS) depends on cell cortex mechanical properties

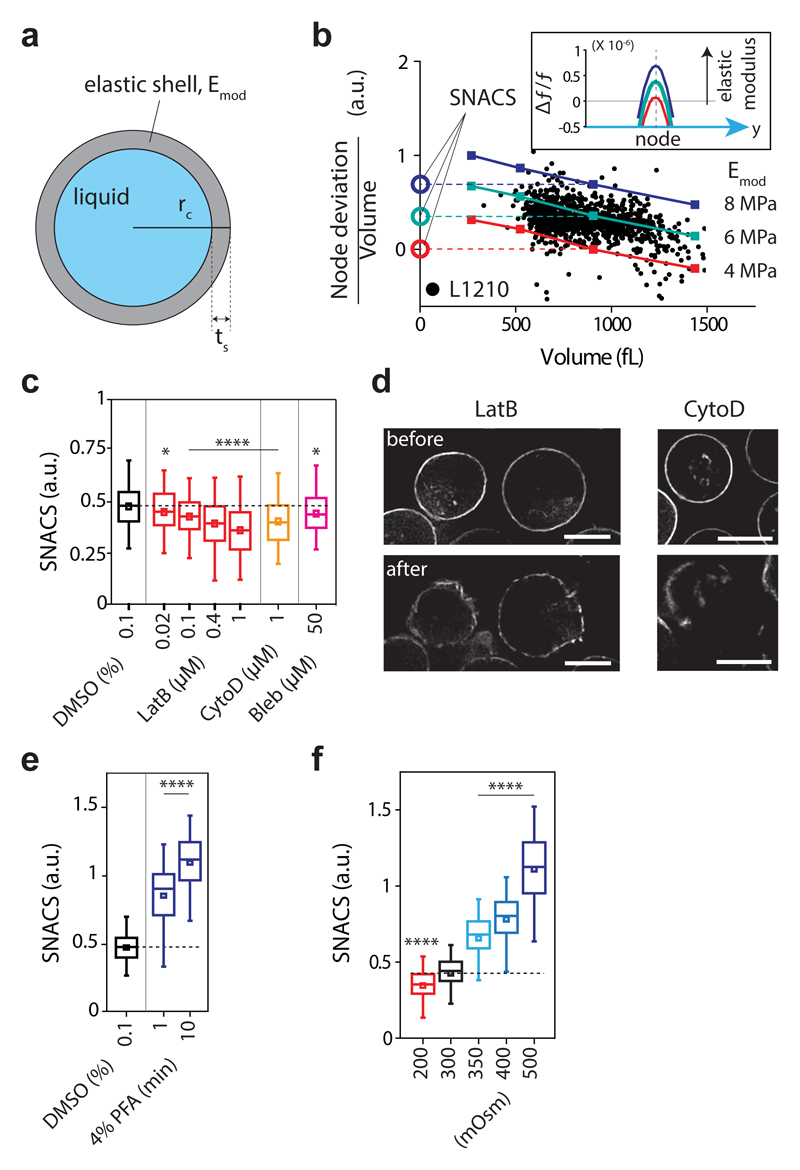
Next, we asked if mechanical properties of live cells could be probed by measuring node deviation. We implemented the ‘Cortical Shell – Liquid Core’ model²⁵ in our FEM simulation (Fig. 2a), which highlights the role of actomyosin cortex in cell mechanics^26,27. We calculated that the acoustic interactions caused relatively small deformations (<15 nm) on the cell surface (Supplementary Note 2), suggesting that node deviation may be primarily governed by the actomyosin cortex²⁸. We then compared our FEM simulations with the node deviation of mouse lymphoblast (L1210) cells (Fig. 2b). FEM simulations yielded similar range signals to the experiments when we used an elastic modulus of 4-8 MPa for the cortex (Fig. 2b), which is 1-2 orders of magnitude higher than the previously reported value using AFM^27,28. This is likely due to the high frequency of our mechanical measurement (~1 MHz) compared to the conventional frequency range of AFM operation (1-100 Hz) and a power-law relationship between apparent elastic modulus (E) and the frequency (f): E ∝ f^{0.2-0.3 29}. Consistent with our results, a similar value was reported with other high-frequency stiffness measurements of red blood cells³⁰. Next, to correct for cell size dependence of the node deviation measurement (Fig. 1f), we derived a size-independent acoustic scattering parameter from the iso-elasticity lines obtained from the FEM simulations (Fig. 2b, Supplementary Fig. 4). We called this the size-normalized acoustic scattering, SNACS (Fig. 2b). The iso-elasticity lines fit well with the measurements from hundreds of live cells. The FEM simulations indicated that SNACS increases with elastic modulus of the cortex (E_mod, Fig. 2b, inset) as well as with cortical thickness (t_s), but is insensitive to both intracellular pressure and cortical tension (Supplementary Fig. 5). We also tested three other mechanical models but none of them matched well with our observations (Supplementary Table 3). These results are consistent with previous observations showing small deformation primarily probes mechanical properties of the cell cortex^28,31.

Figure 2. Size-normalized acoustic scattering (SNACS) measures changes in mechanical properties of cells.

a, Schematic of ‘Cortical Shell – Liquid Core’ model, where E_mod is the elastic modulus of a shell. Cortical thickness (t_s) was set to 2% of the cell radius (r_c)⁴⁵. b, Node deviation (volume-normalized) vs volume V from experiments with L1210 cells (black dots) and simulations using the model for three values of cortical elastic modulus (E_mod, 4, 6 and 8 MPa, color lines). Vertical offsets of iso-elasticity lines define SNACS (Methods). Inset, Δf/f from simulations with different cortical elastic modulus (4, 6 and 8 MPa, V = 900 fL). c, SNACS obtained from L1210 cells treated with inhibitors of actomyosin cortex: Latrunculin B (LatB, 0.02, 0.1, 0.4 and 1 μM, n = 381, 385, 346 and 383 cells, respectively, P = 0.036, 3.8 × 10^-5, 1.03 × 10^-8 and 4.5 × 10^-18, respectively), Cytochalsin D (CytoD, 1 μM, n = 332 cells, P = 1.2 × 10^-8), and Blebbistatin (Bleb, 50 μM, n = 349 cells, P = 0.023). Statistical comparisons (two-sided Welch’s t-test) were made to DMSO control (0.1 %, n = 337 cells). d, Representative single z-layer images of F-actin (LifeAct) from live L1210 cells before and after 1 μM LatB (n = 9 fields of views) and 1 μM CytoD (n = 12 fields of views) treatment. Scale bars, 10 μm. e, SNACS of L1210 cells after crosslinking with 4% Paraformaldehyde (PFA, 1 and 10 min exposure, n=247 and 367 cells, respectively, P = 2.0 × 10^-56 and 6.7 × 10^-175, respectively). Statistical comparisons (two-sided Welch’s t-test) were made to DMSO control (0.1 %, n = 1047 cells). f, Effect of osmotic stress on SNACS. Cells were resuspended in hypo- (200 mOsm, n = 611 cells, P = 2.9 × 10^-10) or hyperosmotic (350, 400 and 500 mOsm, n = 544, 571 and 574 cells, respectively, P = 8.1 × 10^-65, 2.6 × 10^-144 and < 10^-200, respectively) media. Statistical comparisons (one-way ANOVA, Fisher’s LSD) were made to iso-osmotic (300 mOsm, n = 539 cells) media. In c,e,f, boxes: interquartile range, squares: mean, whiskers: 5-95%, horizontal dashed lines: mean SNACS of control (DMSO or 300 mOsm); *P < 0.05, ****P < 0.0001.

To experimentally validate whether SNACS correlates with mechanical properties of live cells, we examined SNACS upon chemical perturbations. All actomyosin inhibitors tested decreased SNACS (Fig. 2c). We also generated a L1210 cell line that stably expresses the LifeAct-RFP F-actin probe³². We imaged these cells and observed that the chemical inhibitors of actin polymerization caused either a punctured cortex (Latrunculin B) or polarized cortex (Cytochalsin D) (Fig. 2d). Both of these cortex phenotypes yielded a reduction in SNACS (Fig. 2c), substantially more than our system noise (Supplementary Fig. 6). We also observed a reduced SNACS after microtubule perturbing Nocodazole treatment, but this treatment also affected the actin cortex morphology (Supplementary Fig. 7). The opposite change in SNACS was observed when we cross-linked cellular structures using a 1-10 min exposure to 4% Paraformaldehyde (Fig. 2e). Moreover, when we osmotically perturbed cells, SNACS changed with the applied osmotic pressure (Fig. 2f). Importantly, these perturbations resulted in SNACS changes (Figs. 2c-f) that are consistent with previous experiments where stiffness was measured by a wide range of methods^{9,10,13,14,33,34}. Thus, taken together with the hydrogel results (Fig. 1g) and our FEM simulation results, SNACS measures stiffness.

SNACS remains stable during interphase but is dynamic during mitosis

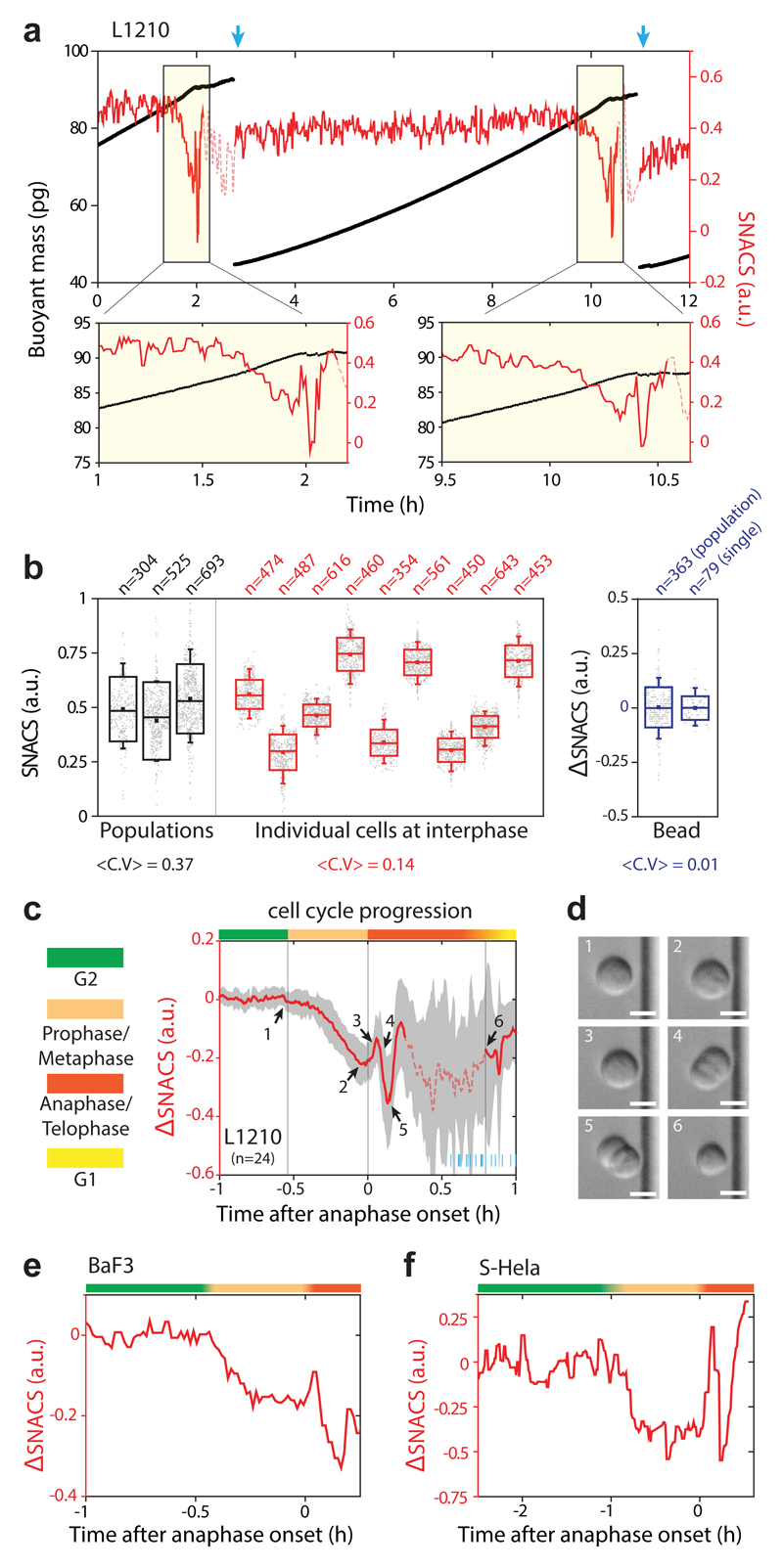
Next, we asked if both SNACS and buoyant mass of the same cell could be repeatedly measured throughout the cell cycle. To do this, we implemented a previously reported fluidic control strategy that enables continuous, non-invasive SMR measurements of the same cell³⁵. We simultaneously measured SNACS and buoyant mass of the same cell over multiple generations (Fig. 3a). Interdivision times measured in the SMR during the SNACS measurements were unchanged from bulk culture (Supplementary Fig. 8), suggesting that our measurement is not invasive. We observed that individual cells display stable SNACS throughout the interphase, exhibiting significantly lower variability than what is seen across different cells in interphase (Fig. 3b). This suggests that cell-to-cell variability in cell mechanical properties during interphase does not arise from cell cycle dependent variability, but rather from mechanical differences that accumulate over generations.

Figure 3. Continuous monitoring of single-cell SNACS throughout the cell cycle.

a, Top, buoyant mass (black) and SNACS (red) of a L1210 cell was measured over two cell divisions with < 1 min temporal resolution by flowing the cell back-and-forth through the SMR. Blue arrows mark cell division. Bottom, SNACS near mitosis. SNACS is shown in dashed lines when measurement error becomes statistically significant (Methods). b, SNACS variability during interphase at a cell population level (black), in individual cells (red), and for 12 µm polystyrene beads (blue). Bead SNACS is relative to its mean value. Large (mitotic) cells were removed from the population data. <C.V> is the average coefficient of variation. n is the number of cells (black) or beads (blue) measured from each population and the number of repeated measurements during interphase of each individual cell (red) or bead (blue). Boxes: ± s.d., squares: mean, whiskers: 5-95%. c, mean SNACS (red) and ± s.d. (gray) of L1210 cells during mitosis (n = 24 cells from 13 independent experiments). Vertical lines and color bars indicate the phase of the cell cycle. Short blue lines at the bottom right mark the end of cell division for each cell. Dashed line same as in a. d, Representative morphology of a L1210 cell (n = 24 cells from 13 independent experiments) captured by DIC imaging on the SMR chip. Numbering corresponds to arrows in c. Scale bars, 10 μm. e,f, SNACS in mamalian cells BaF3 (e) and S-Hela (f). Color bars same as in c.

In contrast to interphase, mitotic cells displayed large changes in SNACS (Fig. 3c). Employing on-chip microscopy to acquire Differential Interference Contrast (DIC) images, we imaged the morphology of the cell to pinpoint the onset of anaphase (Fig. 3d), and correct for mass elongation effects on the SNACS measurement during anaphase and telophase (Supplementary Fig. 9, Supplementary Table 4 and Supplementary Notes 3, 4). SNACS decreased gradually during early mitosis, but not in G2, and abruptly increased at the onset of anaphase followed by a rapid decrease and recovery (Fig. 3c and Supplementary Fig. 10a,b). The error in the SNACS measurement increased after cells became full doublets (~15 min after the onset of anaphase), making subsequent SNACS changes until division not statistically significant (P > 0.05; two-sided Welch’s t-test, Fig. 3c). Although the duration and magnitude of the SNACS dynamics varied in other mammalian cells (Fig. 3e,f), we observed similar trends.

Mitotic swelling is responsible for SNACS decrease in early mitosis

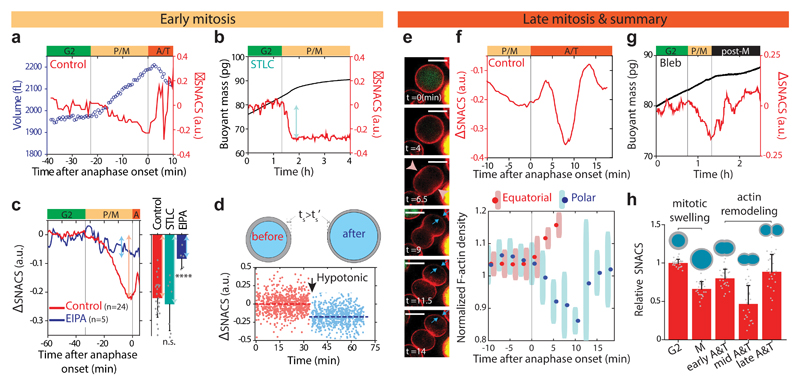
Given that SNACS scales inversely with swelling (Fig. 2f), we hypothesized that mitotic swelling occurring in prophase and metaphase^36,37 might be responsible for the gradual decrease in SNACS. To test this hypothesis, we first correlated the timing of the mitotic swelling and SNACS change by simultaneously measuring SNACS and cell volume. Briefly, we consecutively weighed cells in two fluids of different densities during each cycle in order to derive single-cell volume, density and mass using a previous technique³⁷. By combining this technique with the SNACS measurement, we observed that the SNACS decreases concomitantly with mitotic swelling (Fig. 4a). We further validated this by arresting cells in metaphase, where mitotic swelling is at a maximum³⁷, using the kinesin inhibitor S-trityl-l-cysteine (STLC). Upon mitotic entry, STLC treated cells displayed similar change in SNACS to that seen during mitotic swelling of untreated cells (Fig. 4b, c). However, with STLC treatment, SNACS remained low for several hours (Fig. 4b). These results suggest that SNACS decreases concomitantly with mitotic swelling during prophase and metaphase, and further confirm that the subsequent increase in SNACS happens after metaphase.

Figure 4. Mitotic swelling and actin remodeling are responsible for SNACS dynamics in mitosis.

a, L1210 cell volume (blue circles) and SNACS (red) in mitosis. b, Buoyant mass (black) and SNACS (red) of a L1210 cell arrested in metaphase by treating with S-trityl-cysteine (STLC, 5 μM). c, Left, mean SNACS change of control (red) and ethylisopropylamiloride (EIPA, 10 μM, blue) treated L1210 cells in early mitosis. Right, quantification of SNACS change with STLC (5 μM, n = 7 cells from 7 independent experiments, P = 0.58) and EIPA (10 μM, n = 5 cells from 5 independent experiments. P = 3.0 × 10^-5) treatments. Data depicts mean ± s.d. of the maximal SNACS change in prophase and metaphase. Statistical comparisons (two-sided Welch’s t-test) were made to the control (n = 24 cells from 13 independent experiments). ****P < 0.0001, n.s., not significant. d, Top, illustration of hypothetical cortical thinning scenario by shell expansion during swelling (Supplementary Note 5). Bottom, SNACS of L1210 cells vs time before (red, n = 728 cells) and after (-Δ50 mOsm, blue, n = 733 cells) exposure to hypotonic stress. Dashed lines represent the mean SNACS of each condition. Arrow marks the time of osmotic shock. e, Representative single z-layer images of F-actin (red, LifeAct) and FUCCI (green, mAG-hGem) from a live L1210 cell (n = 7 cells). Time zero marks the onset of anphase. Furrow initiation in the equatorial region (pink arrowheads) and cortical relaxation at the poles (blue arrows) are highlighted. Scale bars, 10 μm. f, Top, zoom-in view of mean SNACS in late mitotic L1210 cells (n = 24 cells). Bottom, L1210 cortical LifeAct signal density in equatorial (red) and polar (blue) regions (Methods), as shown in e. Data depicts mean ± s.d. (n = 7 cells). g, Buoyant mass (black) and SNACS (red) of a L1210 cell treated with Blebbistatin (Bleb, 25 μM). h, Summary of SNACS dynamics in mitosis. Data depicts mean ± s.d. of the SNACS normalized to G2 (n = 24 cells). Actin (gray shell) and morphology of a cell in each time points of mitosis are illustrated. In a,b,c,f,g, vertical lines separate the cell cycle positions marked by color bars shown in Fig. 3c. Black bar marks post-metaphase. P: prophase, M: metaphase, A: anaphase, T: telophase, post-M: post-metaphase.

We next acquired causative evidence that mitotic swelling causes the reduction in SNACS during prophase and metaphase. Previously we showed that inhibiting the Na+/H+ antiporter with ethylisopropylamioride (EIPA) reduces mitotic swelling without inhibiting mitosis³⁷. Here, we found that upon EIPA treatment, SNACS in early mitosis was no longer reduced to the same extent as in the control cells and cells arrested in metaphase (Fig. 4c and Supplementary Fig. 10c). ΔSNACS of EIPA treated cells in early mitosis was -0.08 ± 0.02 (n = 5 cells, all values are mean ± s.e.m. unless stated otherwise) whereas ΔSNACS of control cells and cells arrested in metaphase were -0.22 ± 0.01 (n = 24 cells) and 0.24 ± 0.03 (n = 7 cells), respectively. These findings suggest that mitotic swelling is largely responsible for the reduction in SNACS. To determine if swelling without a mitotic event can decrease SNACS, we induced swelling with a hypotonic shock (-Δ50 mOsm) in non-mitotic (interphase) cells. Immediately after the osmotic shock, cells swelled by ~15% in volume, as normally observed in mitotic swelling³⁷, and SNACS was reduced by a similar magnitude (ΔSNACS = -0.18 ± 0.01, n = 733 cells) to that seen during mitotic swelling (Fig. 4d). To mimic the gradual swelling during mitosis and potentially prevent membrane detachment from the cortex³³, we compared fast and slow swelling (-Δ50 mOsm instantaneously or over 20 minutes) and the swelling rate did not affect the SNACS decrease (Supplementary Fig. 11). We hypothesized that swelling reduces cortical thickness by hydrostatic pressure, thereby expanding actin to cover a larger surface area (Supplementary Note 5). We estimated that swelling of ~15% would lead to ~10% cortex thickness decrease assuming that the amount of cortical actin does not change during swelling (Supplementary Table 5). We used live cell fluorescent microscopy and showed that the cortex thickness gradually decreased during mitotic swelling by an amount similar to our calculation (~10%) after nuclear envelope breakdown but before the onset of anaphase (Supplementary Figs. 12 and 13), consistent with previous studies^1,38. Altogether, these data suggest that mitotic swelling is responsible for cortical thinning and consequent decrease in SNACS.

SNACS reveals mechanical changes during actin remodeling in late mitosis

We investigated the rapid SNACS change during anaphase and telophase (Fig. 3c). First, we observed that the SNACS increase in early anaphase (Fig. 4a, c, red) was not present in EIPA treated samples (Fig. 4c, blue and Supplementary Fig. 10c), suggesting that the SNACS increase represents recovery from mitotic swelling. To link mechanical dynamics to actin remodeling, we imaged changes in actin cortex distribution during anaphase and telophase (Fig. 4e and Supplementary Fig. 14). In early anaphase (~5 min after onset of anaphase) where SNACS initially increases, cells started to elongate and the cleavage furrow was initiated. At approximately 10 min into anaphase, where SNACS decreased, cells redistributed their cortical actin out of the polar regions. This polar relaxation² caused a 10-15% depletion in F-actin at the poles and lasted approximately 5 min (Fig. 4f and Supplementary Fig. 12). Both SNACS and polar relaxation were recovered approximately 15 min after the onset of anaphase (Fig. 4f). When we inhibited cytokinesis and actin remodeling using the myosin II motor inhibitor Blebbistatin, cells still displayed a gradual SNACS decrease in early mitosis caused by mitotic swelling, but the mechanical dynamics in anaphase and telophase observed in untreated cells disappeared (Fig. 4g). These observations reveal how cortical thinning induced by mitotic swelling in early mitosis and actin remodeling, especially polar relaxation, in late mitosis result in dynamic changes in cellular mechanical properties (Fig. 4h).

Discussion

During early mitosis where SNACS decreases, it is known that cells exhibit swelling, the actin cortex thickness is reduced and cortical tension is increased^1,38, yet prior work on how stiffness changes has not been consistent. Previously it has been thought that mitotic cells become stiffer due to increased tension³⁹ from contractility in the membrane during mitotic round up. Early AFM⁴⁰ and optical tweezer⁴¹ results on cells in mitosis supported this notion. The observed SNACS decrease we observe could result from the reduction in both cortex thickness and modulus. However, a separate report using AFM found no change in mitotic stiffness⁴², whereas others using hydrodynamic forces have observed mitotic cells being more deformable⁴³. All of these studies^40–43 were conducted as end-point assays on different cell types with strains that were 10 to 100-fold larger than those used during our SNACS measurement. Future work will be necessary to determine how the cortex tension, modulus and thickness govern cell stiffness dynamics during mitosis. Aside from the cortex, it remains plausible that SNACS reflects other attributes of the cell such as the plasma membrane and the way in which it is attached to the underlying cortex.

We also found that at the onset of anaphase, SNACS first recovers from cell swelling and then reduces again during anaphase and telophase. Early work on mechanical properties of sea urchin eggs suggested similar dynamic changes in anaphase⁴⁴. This second reduction in SNACS was dependent on actomyosin remodeling and coincided with the polar relaxation of actin cortex².

Finally, our SNACS measurement is influenced by the cell’s mass distribution along the cantilever. During anaphase and telophase, the cell’s mass distribution changes substantially, which causes the SNACS measurement to depend on the cell’s orientation within the channel (Supplementary Fig. 15, Supplementary Note 4 and Supplementary Table 4). Therefore, obtaining mechanical measurements by acoustic scattering requires mass distribution information through bright-field images unless cell shape is known a priori. In round interphase cells, such as the ones we have studied here, this correction is not required.

We show that measuring single-cell mechanical properties continuously, with high temporal resolution over extended periods is critical for observing small changes which are both transient and asynchronous between cells. We demonstrate this by measuring mitotic-specific mechanical changes that are smaller than the population variance and occur within minute timescales. Importantly, our SNACS measurement quantifies the overall mechanical properties of a cell, complementing spatially resolved measurements such as time-lapse microscopy, traction force microscopy and atomic force microscopy.

Online methods

System Setup

SMR devices were fabricated using a previously described process^23,46 and carried out at CEA-LETI, Grenoble, France. The geometry and dimensions of SMR devices used in the experiments described in this work are shown in Supplementary Fig. 1 and Supplementary Table 2. The measurement system for trapping a cell throughout its cell cycle has been previously described in³⁵. The SMRs were vibrated with a piezo-ceramic plate bonded underneath the chip, providing actuation to resonate the cantilever beam in the second mode. To track the changes in the resonant frequency of the cantilever as a function of time, we used a closed feedback loop to drive the cantilever to always oscillate at its resonant frequency. The motion of the cantilever was measured using piezoresistors that are implanted at the base of the silicon cantilever⁴⁷. A digital control platform that was previously reported⁴⁸ was utilized to oscillate the SMR in direct feedback mode, where the motion signal acquired from the piezoresistor is delayed, amplified and utilized as the drive signal used to actuate the cantilever. We set the measurement bandwidth of this control system at ~1,500 Hz, which is wide enough to capture frequency modulation signals created by cell transit events and narrow enough to minimize noise.

For on-chip optical measurements, a modular microscope (Nikon) was mounted on top of the SMR device. A 20X objective lens (Nikon-CFI, LU Plan ELWD N.A 0.4 WD 13 mm) or 50X objective lens (Nikon-CFI, LU Plan ELWD N.A. 0.55, W.D 10.1 mm) was used to collect light into a CMOS camera (FLIR, BFS-U3-13Y3M-C) or PMT (Hamamatsu, H10722-20), respectively, in order to obtain DIC images or measure fluorescent intensity. The field of view and area of light exposure was typically reduced to 100 µm x 100 µm (DIC imaging) or 40 x 60 µm (fluorescent measurements) to minimize the background noise as well as phototoxicity. To further improve the signal-to-noise ratio, a rectangular slit (Thorlab) was adjusted to fit the channel width and placed at the image plane. An illumination light source (Lumencor, Spectra X Light Engine) was shuttered by the measurement software (Labview 2012) to excite each fluorescent measurement for less than 550 ms. The optical path and components for imaging and fluorescent measurements are similar to what has been previously described³⁵.

System Operation

As previously reported³⁷, a chip was placed on top of a hollow copper plate that is connected to a water bath by tubing to maintain constant temperature on the chip. For all single-cell, long-term monitoring experiments, temperature of the copper plate was kept at 37°C. The sample was loaded to the SMR from vials pressurized with air containing 5% CO₂ to maintain the pH of the culture. A 0.007” inner diameter fluorinated ethylene propylene (FEP) tubing (IDEX Health & Science) is utilized to push the sample into the chip. The fluid flow was controlled using two electronic pressure regulators (Proportion Air QPV1) and three solenoid valves (SMC-S070), which are controlled by National Instruments control cards and a custom measurement software (Labview 2012). Typically, differential pressure of ~0.5 psi was applied across the SMR, yielding a flow rate of ~ 2 nL/s (calculated based on the frequency modulation signal due a cell transit; typically 200-300 ms) to maintain constant shear and data rate. Under these conditions, the L1210 cell growth rate was similar to that in culture³⁵. Beads, hydrogels and drug-response end-point assays were measured at room temperature. All end-point assays were conducted within 30 min after samples were loaded. New samples were flushed every several minutes into the input bypass to minimize potential size bias due to particle or cell settling in the tubing and sample vials.

Frequency peak analysis

To measure buoyant mass (antinode) and node deviation (node) from the acquired resonant frequency waveforms, we filtered the frequency data with a third order Savitzky-Golay low-pass filter and find the local minima (antinode) that is below a user-defined threshold. Next, local maxima (node) around the peaks were determined. Then to correct for the possible slope during the particle or cell transition through the cantilever, a baseline was calculated and subtracted from the measured peaks by fitting a first order polynomial at frequency data points prior and posterior of the cell signal. Typically, we acquire frequency data for ~1 s before and after the transit of each cell in order to estimate the baseline frequency. As a result, the measurement time is typically 2-3 s per cell which leads to a throughput of about 1,200 cells per hour (accounting for occasional doublets and delays between cell measurements). For single-cell volume measurements (Fig. 4a), baselines were fitted with 2^nd order polynomial to account for the baseline fluctuation due to fluid exchange. Both local maxima and minima in the cell signal were subtracted from the linear baseline to obtain the buoyant mass (local minima, antinode) and node deviation (local maxima, node). For single-cell end-point assays (population measurements), frequency peaks were rejected when local minima (two antinodes) differed from each other more than 10% of the average value and/or local maxima (two nodes) differed from each other more than 15% of the average value of local minima, which occur when multiple cells or cell with debris enter the SMR simultaneously. Peaks were rejected if their shape was atypical (e.g. particle or cell stuck in the cantilever). For single-cell long-term monitoring, all frequency peaks were accepted and presented except extremely rare events such as when a doublet separated into two daughter cells during the transit through the cantilever or entered apoptosis due to persistent drug pressure. Frequency peaks were calibrated (Hz per pg) using monodisperse 10 µm diameter polystyrene beads with a known density of 1.05 g/cm³ (Thermofisher, Duke Standards).

Hydrogel particle synthesis

Hydrogel microparticles were fabricated via stop-flow lithography (SFL)^49,50. Microfluidic synthesis devices were fabricated by previously reported procedures.² Briefly, PDMS (10:1 monomer to curing agent, Sylgard 184, Dow Corning) was cured on silicon wafers patterned with SU-8 features, and devices were bonded to PDMS-coated glass slides. Prepolymer solutions were prepared by mixing 20% (v/v) poly (ethylene glycol) diacrylate (PEGDA; Mn = 700, Sigma-Aldrich), 5% 2-hydroxy-2-methyl-propiophenone (photoinitiator, Sigma-Aldrich), 25% DI water, and 50% polyethylene glycol (PEG; Mn = 200, Sigma-Aldrich).

Using the previously reported SFL setup^49,50, prepolymer solution was loaded into the synthesis device by pressure-controlled flow. After stopping the flow, particles were polymerized by ultraviolet light (Thorlabs, 365 nm LED, 2200 mW cm^-2) in mask-defined shapes (transparency masks designed in AutoCAD, printed by Fineline Imaging). The three steps (flow, stop, exposure) were repeated to achieve semi-continuous particle synthesis. Polymerized particles were collected from the channel outlet and purified with PBST (phosphate buffered saline with 0.05% Tween-20) by centrifugation.

Hydrogel microparticles with varying elastic modulus (Fig. 1g) were synthesized using the SFL setup. Prepolymer solutions were prepared with varying concentrations of PEGDA (Mn = 700) in the range 10-35% (v/v), plus 5% photoinitiator, 25% DI water, and PEG (Mn = 200) in the range 35-60% to make up the remaining volume. For all prepolymer compositions, particles were polymerized using an 11 µm circle mask in microfluidic channels with heights of 10 µm, resulting in a particle heights of 7-8 µm.

Hydrogels of three aspect ratios 1.0, 1.5 and 2.5 (Supplementary Fig. 3) were fabricated by using three masks with same cross-sectional area for exposure, but three different shapes, respectively: a 11μm-diameter circle, an ellipse with aspect ratio 1.5 (major axis: minor axis), and an ellipse with aspect ratio of 2.5. The volumes of hydrogels were measured using the Dynamic Light Scattering (DLS) with means 655, 658 and 602 µm³ for aspect ratios 1, 1.5 and 2.5, respectively. Particle dimensions (height and major/minor axes) were measured from brightfield microscopy images using ImageJ software, taking an average from at least ten particles.

Measurement of particle elastic modulus by atomic force microscopy (AFM)

To determine the elastic modulus of the hydrogel microparticles, force spectroscopy measurements were performed using a MFP-3D-BIO atomic force microscope with an integrated optical microscope (Asylum Research). A 50 µl drop of particle solution (~10 particles in PBST) was placed on a glass slide. Silicon nitride cantilevers with silica spherical indenters of 10 µm diameter (Novascan) were used to indent the particles in PBST after they settled to the surface of the slide. For particles with composition 10-25% PEGDA, a cantilever with nominal spring constant of 0.12 N m^-1 was used. For stiffer particles with higher composition 30-35% PEGDA, a cantilever with nominal spring constant 0.35 N m^-1 was used. The inverse optical lever sensitivity (InvOLS) for each cantilever was calibrated from deflection-displacement curves on a rigid glass slide (23.21 and 17.46 nm V^-1, respectively) and the actual spring constant of each cantilever was measured using the thermal noise method⁵¹ to be 0.114 and 0.475 N m^-1 respectively. For each sample, we indented four particles with four indents per particle. Elastic modulus was calculated by fitting the force-indentation curves to a maximum indentation depth of 400 nm using the Hertz model for spherical elastic contact with IGOR data processing software (Wavemetrics). The indentation velocity was 1 µm s^-1. The PEGDA hydrogels were assumed to be incompressible elastic materials, with a Poisson’s ratio of 0.5^52,53.

Cell culture, chemical perturbations and transfections

L1210 and BaF3 cells were cultured in RPMI containing L-glutamine, Phenol Red, 11 mM D-glucose, and the RPMI was supplemented with 10% heat inactivated fetal bovine serum (FBS), 10mM HEPES, 100 units/mL of penicillin, 100 µg/mL of streptomycin, and 0.25 µg/mL of Amphotericin B. S-HeLa cells were cultured in DMEM containing L-glutamine, Phenol Red, 25 mM D-glucose, and the DMEM was supplemented as RPMI. All cell culture reagents were obtained from Thermo Fisher Scientific, except FBS which was obtained from Sigma-Aldrich. The L1210 cells were obtained from ATCC (CCL-219). BaF3 cells expressing BCR-ABL were obtained from RIKEN BioResource center. S-HeLa cells were a gracious gift from Dr. Kevin Elias (Brigham and Women’s Hospital). All experiments were started from cell cultures that had not reached more than 40% confluence.

For chemical perturbations, cells were pretreated with chemicals for 20-30 min under normal cell culture conditions and loaded into the SMR along with the chemical containing media. Chemical concentrations used were 0.1% DMSO (controls, Sigma-Aldrich), 0.02 – 1 µM Latrunculin B (Sigma-Aldrich), 1 µM Cytochalsin D (Sigma-Aldrich), 25 µM (inhibiting Cytokinesis, long-term traces) or 50 µM (Actomyosin cortex disruption, end-point assay) Blebbistatin (Sigma-Aldrich), 10 µM EIPA (Sigma-Aldrich), 5 µM STLC (Sigma-Aldrich) and 2 µM RO3306 (R&D Systems). For surface crosslinking experiment, cells were treated with 4% PFA (Electron Microscopy Sciences) in PBS for 1 or 10 min. Cells were then washed with PBS and resuspended in normal culture media. For all wash and re-suspension steps, cells were centrifuged at 500 g for 2 min. For the osmotic challenge, desired osmolarity of the external solutions were achieved by mixing cell culture media with deionized water or D-mannitol (Sigma-Aldrich) for hypotonic or hypertonic conditions, respectively. Cell culture media was set to be isotonic (300 mOsm). Cells in the culture media were mixed 1:1 with the prepared external solution (e.g. mixed 1:1 with 500 mOsm solution to achieve final osmolarity of 400 mOsm) to obtain desired osmolarity. We kept the cells in the prepared media solution at room temperature for 20 min before loading them into the SMR containing media of the desired osmolarity. For hypotonic experiment shown in Fig. 4d, cells were loaded immediately after the osmotic shock. For the slow hypotonic shock condition shown in Supplementary Fig. 11, cells were treated with DI water every 2 minutes for a total of 20 minutes. The desired osmolarity of 250 mOsm was achieved by adding 10uL of water every 2 min (total of 10 times) into 500 µL of cell solution.

L1210 FUCCI cells, which express the fluorescence cell cycle marker construct mAG-hGem, were generated in a previous study³⁵. These cells were transfected with LifeAct, a F-actin labelling red fluorescent protein construct³², using rLVUbi-LifeAct-TagRFP lentiviral vector obtained from ibidi GmbH. Several rounds of transfections were carried out using spinoculation. In short, 1.5 x 10⁵ L1210 FUCCI cells were mixed with 10 µg/ml Polybrene (EMD Millipore) and 1 x 10⁶ TU of lentivirus, and the mixture was centrifuged at 800 g for 60 min at 25°C. After centrifugation, the cells were moved to normal cell culture media, grown overnight and the spinoculation procedure was repeated. After 3 rounds of transfections cells were moved to normal culture media and 24 h later selection was started by adding 10 µg/ml Puromycin (Sigma-Aldrich). After a week of selection, the transfected population was enriched for cells expressing high levels of LifeAct by FACS sorting using BD FACS Aria.

Size normalizing node deviation to obtain SNACS values

Since node deviation decreases with particle volume (Fig. 1f, Fig. 2b), size-normalization is required to compare node deviation of different size particles or cells. To obtain the size-normalized acoustic scattering (SNACS), we first obtained the volume following a previously described method⁵. In short, we converted buoyant mass obtained from individual peaks (Supplementary Fig. 4a) to volume using a median density of the population. Median density of the population relative to the fluid $\left(\overline{\Delta \rho }=\overline{{\rho }_{\text{c}}-{\rho }_{\text{f}}}\right)$ was obtained by fitting the buoyant mass distribution with a log-normal distribution to estimate the mean buoyant mass ($\overline{BM},$ > 300 cells). Mean volume $(\overline{V})$ was obtained by fitting the log-normal distribution to the volume distribution obtained from the Coulter Counter measurements (Beckman Coulter, >5000 counts). Single-cell volume was then obtained using the following equation:

$$V=BM/\overline{\Delta \rho },\text{where}\overline{\Delta \rho }=\frac{\overline{BM}}{\overline{V}}$$

The mean density $\left(\overline{\Delta \rho }\right)$ of the population was calculated for each condition. Then, the node deviation for each cell (Supplementary Fig. 4a) was divided by its volume (V) to obtain node deviation/volume (NV). Representing each cell as a data point in the scatter plot (NV vs V, Supplementary Fig. 4b), an iso-elasticity line of slope m is passed through each point (Supplementary Fig. 4c). All data points along a given iso-elasticity line have the same mechanical property based on the FEM simulation (Fig. 2b). Finally, the SNACS for each cell was obtained by taking the linear interpolation of NV at V_ref along the iso-elasticity line (Supplementary Fig. 4d):

$$\text{SNACS}=NV-m\left(V_{ref}-V\right)$$

The slope (m) was obtained by performing a linear regression on the population data (typically >300 cells) in the NV versus V scatter plot (Fig. 2b). The reference volume (V_ref) was set to the median volume of the population, which for L1210 cells was 900 fL.

Cell cycle transition points

To pinpoint the G2/M transition, we utilized a previously reported finding that mitotic swelling starts in early prophase and prometaphase³⁷. As the SNACS decrease was simultaneous with swelling (Fig. 4a), and SNACS decrease was not observed in G2 arrested cells (Supplementary Fig. 10a), we marked the G2/prophase transition to take place right before the SNACS decrease starts. The FUCCI signal (mAG-hGem) decrease (when fluorescence first reaches 85% of the maximum value) was used to mark the metaphase to anaphase transition. Based on fluorescence imaging, we obtained the average time lag between the time when FUCCI signal (mAG-hGem) begins to drop (below 85% maximum) and the first time point for when a cell deviates from spherical to be approximately 3.8 min. Then, to assign the cell cycle transition points in figures, we subtracted the 3.8 min time lag from the first time point when cell shape deviates from sphere to mark the start of anaphase. SNACS traces of the metaphase arrested cells (treated with STLC), where SNACS remained low for several hours, supported our timing of the metaphase-anaphase transition (Fig. 4b).

Microscopy

L1210 cells expressing the FUCCI (mAG-hGem) and LifeAct-RFP F-actin probe (rLVUbi-LifeAct-TagRFP) constructs were imaged on poly-lysine coated glass bottom CellView cell culture dishes (Greiner Bio-One). Media, CO₂ and temperature conditions during the imaging were the same as within the SMR. Imaging was carried out using DeltaVision widefield deconvolution microscope with standard FITC and TRICT filters, 100X oil immersion objective and immersion oil with refractive index of 1.522. No binning was used and the image resolution was 9.245 pixels/µm in xy-planes. When examining the effects of actin perturbing chemicals on the F-actin structure, a 3 µm thick section from the middle of the cells was imaged in 0.2 µm thick z-layers. After the first round of imaging, the cells were treated with the indicated chemical for 30 min and the same cells were imaged again. When examining the F-actin distribution in early mitosis, a 1 µm thick section from the middle of the cells was imaged in 0.2 µm thick z-layers every 5 min. Only the middle z-layer was used for final analysis and presentation. When examining the F-actin distribution during cytokinesis, three 0.2 µm thick z-layers were imaged with 1 µm height intervals to capture both the mother and the daughter cells at the central height of the cell, and this imaging was repeated every 2.5 min. The total duration of all imaging experiments was limited to 5 h, as prolonged light exposure induced photo-toxicity and started to interfere with mitotic progression.

Image analysis – actin cortex thickness in early mitosis

All images were deconvolved using standard settings in the softWoRX software. To normalize the effect of photo-bleaching, first we calculated the total LifeAct signal in the entire images (2048 x 2048 pixels) that contained multiple cells. Then, we fitted a second order polynomial to the total LifeAct signal in the image as a function of frame index. During the subsequent image analyses, we corrected the LifeAct intensity with the corresponding decay coefficient calculated from the polynomial fit for each frame. To analyze individual cells, we first determined the representative cells that went through the nuclear envelope breakdown and/or cytokinesis during the experiment. These cells were cut out of the larger images and analyzed individually (Supplementary Fig. 12a).

For analyzing each cell, we utilized MATLAB’s circular Hough transform algorithm to detect circles on images (imfindcircles). We applied this algorithm to binary images that were processed by a 2-dimensional median filter with 3-by-3 neighborhood (Supplementary Fig. 12b) and a threshold filter (Supplementary Fig. 12c). After determining an initial position for the cell center and radius (Supplementary Fig. 12d) we obtained the actin signal at the raw, unfiltered image across 100 radial paths around the detected circle ranging from the estimated cell center to 125% of the estimated cell radius (Supplementary Fig. 12e). Then, we recorded the prominent peak location of the actin signal that was closest to the estimated radius as the cortex position for that particular radial path. We took the median of LifeAct signals recorded from each radial path after aligning them at their calculated cortex locations (Supplementary Fig. 12f). Using this median LifeAct profile of the cell cross-section, we calculated the full width at half maximum (FWHM) of the LifeAct signal at the cortex (Supplementary Fig. 12f, red circles) in reference to the LifeAct signal that is recorded at the cytoplasm. We defined the baseline signal at the cytoplasm of L1210 cells as approximately 85 to 90% of the radial measurement path (Supplementary Fig. 12f, red line). This FWHM value of LifeAct at the cortex functioned as a proxy for the cortex thickness.

To analyze F-actin distribution dynamics through mitosis, we repeated our analysis for each time point we collected throughout the experiment. At each time point we also analyzed the distribution of the FUCCI signal (mAG-hGem) in the cell (Supplementary Fig. 12g). We aligned the data from different cells to the time of nuclear envelope breakdown using the FUCCI signal (mAG-hGem) spread from nucleus to across the entire cell area as marker for the nuclear envelope breakdown (Supplementary Fig. 12h). Finally, for comparing different cells, we normalized the FWHM signals of each cell with respect to the median FWHM signal that was recorded from the frames of that cell prior to the nuclear envelope breakdown.

Image analysis – equatorial and polar actin cortex density during mitosis

To study how the distribution of F-actin changes through mitosis, we considered four regions of the cell. Each region covers a 90-degree area extending from 65% of the estimated radius of the cell to its full radius. We utilized the same cell detection algorithm that was described in the previous section, with the additional capability of detecting two adjacent cells (Supplementary Fig. 12i,j). To determine the division axis and the regions of interest we started the analysis from the frames after cytokinesis with two cells clearly visible, and worked back in time until the onset of anaphase. At each time point, if we detected two cells, even if the cell was in mid-anaphase, we determined the division axis and the equatorial and polar regions of interest. We set the polar region as the 90-degree segments that are at two opposite sides of the detected cells (Supplementary Fig. 12k). We set the equatorial region as the regions that are in the middle of the two cells and have an angular span that is perpendicular to the polar regions (Supplementary Fig. 12l). To compensate for the observed non-circular shapes, we utilized an edge detection algorithm to determine the true extent of the cells overlapping with the region of interest. If we detected a single cell, we defined the four equal area regions using the same angular span that was determined in the previous frames (during cytokinesis) of the same cell. Finally, we calculated the relative F-actin density in each region by normalizing the total LifeAct signal to the area in each region. In the cases, where an adjacent, brighter cell was interfering with the cell of interest, we disregarded the signal in the affected region. Finally, we aligned the timing of different cells using the first frame, where two separate cells are apparent (mid-anaphase).

Data presentation

To characterize the system noise, we repeatedly measured node deviation of the same 12 μm diameter polystyrene bead, size-normalized to SNACS and calculated their standard deviation (Supplementary Fig. 6a). SNACS of L1210 cells (n = 24 cells) were aligned to the latest time point where the cells maintained round morphology (3.8 min after anaphase onset, Fig. 3c,d). Then, we interpolated each data points for 0.01 h and calculated the mean value and standard deviation out of the interpolated data for each time point. All SNACS plots were filtered with median filter of length 3, except in late mitosis (data points after anaphase onset) where we show raw data. From the onset of anaphase, we calculated P values between the maximum and minimum within moving 5 minute time block to characterize how much of the temporal change has statistical significance. We observed that temporal SNACS changes were not significant (P > 0.05, two-sided Welch’s t-test) from 15.2 min after the onset of anaphase to cell division (Fig. 3, red dashed lines).

After defining the size-normalized acoustic scattering parameter SNACS at the end of Fig. 2, we illustrated all node deviation changes, which reflect the mechanical property of a cell, using SNACS or ΔSNACS. ΔSNACS represents the change in SNACS relative to the median value of first 10-15 minutes of data presented (except in Fig. 4d, where mean value of the whole cells before hypotonic shock is used), and is only used for better visualization of data.

Statistics and Reproducibility

To quantify the agreement between the data from the experiments and the simulations (Fig. 1d-f), we calculated the coefficient of determination R-squared (R²). We assumed that the observed data are the experiments and the fitted are the simulations. Thus, for number N of data points where y_i,experiment and y_i,simulation are the observed and the fitted values (i=1,2,…N), we calculated:

$$R^2=1-\frac{\sum {\left(y_{i,experiment}-y_{i,simulation}\right)}^2}{\sum {\left(y_{i,experiment}-\overline{y}\right)}^2},\text{where}\overline{y}=\frac{1}{N}\sum y_{i,experiment}$$

Statistical analysis were performed by Origin and MATLAB. We performed two-sided Welch’s t-test for comparisons between two groups and one-way ANOVA for comparisons between multiple groups. Post hoc analysis (Fisher’s LSD) was performed only when ANOVA yielded a statistical difference (P < 0.05). Null hypothesis was always that mean values are the same. The detailed statistics performed for each experiment are shown in figure legends.

All single-cell SNACS traces were obtained on separate days. All single-cell SNACS traces were repeated at least five times in independent experiments. The population SNACS measurements were repeated at least in three independent experiments, yielding comparable results.

FEM simulation

See Supplementary Note 2 for details.

Mass distribution correction

See Supplementary Note 3 and Supplementary Fig. 9 for details.

Orientation-dependent noise

See Supplementary Note 4 and Supplementary Fig. 15 for details.

Cortical thickness reduction during swelling

See Supplementary Note 5 for details.

Reporting Summary

Further information on research design is available in the Life Sciences Reporting Summary.