The Distance Precision Matrix: computing networks from non-linear relationships

Abstract

Motivation

Full-order partial correlation, a fundamental approach for network reconstruction, e.g. in the context of gene regulation, relies on the precision matrix (the inverse of the covariance matrix) as an indicator of which variables are directly associated. The precision matrix assumes Gaussian linear data and its entries are zero for pairs of variables that are independent given all other variables. However, there is still very little theory on network reconstruction under the assumption of non-linear interactions among variables.

Results

We propose Distance Precision Matrix, a network reconstruction method aimed at both linear and non-linear data. Like partial distance correlation, it builds on distance covariance, a measure of possibly non-linear association, and on the idea of full-order partial correlation, which allows to discard indirect associations. We provide evidence that the Distance Precision Matrix method can successfully compute networks from linear and non-linear data, and consistently so across different datasets, even if sample size is low. The method is fast enough to compute networks on hundreds of nodes.

Availability and implementation

An R package DPM is available at https://github.molgen.mpg.de/ghanbari/DPM.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Gene network reconstruction is an instance of a generic problem which has become ubiquitous in many fields of science: Network reconstruction generally refers to representing associations between variables in the form of a graph, where nodes correspond to variables and edges to associations postulated by the chosen network reconstruction method. Besides the biological Gene Regulatory Networks (GRNs) (Markowetz and Spang, 2007), other examples comprise co-authorship networks among researchers (Newman, 2004), connectivity networks between brain regions Smith et al. (2011), or social networks among people (Carrington et al., 2005). In machine learning, graphical models have been introduced for this purpose (Bishop, 2006; Koller and Friedman, 2009).

Typical input data for network reconstruction would be either a similarity matrix or a set of vectors, one per variable. The latter is the standard input for GRNs, where each gene is described by a vector containing its expression values (centered to mean 0) under many conditions (D'Haeseleer et al., 2000). Let us call W the matrix containing these vectors as columns. ${\mathbf{W}}^T\times \mathbf{W}$ is the sample covariance matrix for those variables and can be seen as a measure of similarity among them. This is the basis for many network reconstruction applications, though not for all.

To better understand the problem it is helpful to focus not on the edges, but rather on the lack thereof. For example, in Relevance Networks, no edge is drawn between two variables if their correlation is close to 0. The rationale behind this is that, for Gaussian data, a correlation coefficient of 0 is equivalent to stochastic independence of the variables. Therefore reconstructing a network becomes determining the pairs of variables that are independent and leaving out those edges.

Using correlation to determine the presence or absence of edges highlights another important aspect of network reconstruction. When a variable X is correlated with another one Y, which is in turn correlated with a third variable Z, a correlation will likely also be observed between X and Z. For the purpose of simplicity and interpretability however, we would much prefer to display direct associations only and discard such transitive ones. This issue was already identified by Fisher, Pearson and Yule [see Aldrich (1995)] who introduced the concept of partial correlation to weed out correlations that can better be explained by a third variable. de la Fuente et al. (2004) used first- and second-order partial correlation (i.e. correlation conditioned on 1 and 2 variables respectively) for gene networks.

In machine learning, this has become the basis for Gaussian Graphical Models (GGMs) (Bishop, 2006; Lauritzen, 1996). Those rest on the mathematical observation that the entries of the inverse of the covariance matrix (the precision matrix) are related to the corresponding full-order partial correlation coefficients. The term full-order refers to partial correlation between two variables given all other variables. In practice, based on the assumption that data is Gaussian, the absence of an edge in a GGM corresponds to a very small entry in the precision matrix, i.e. to conditional independence given the other variables. Conditional independence can be seen as an extension of independence that is able to model knowledge context. Two variables X and Y might only appear to be linked where in reality the association is explained by a set of variables Z. Formally, X and Y are conditionally independent given Z if $p\left(X,Y|Z\right)=p\left(X|Z\right)p\left(Y|Z\right)$. For Gaussian variables, a partial correlation of 0 between two variables is equivalent to their conditional independence. In the context of epigenetics, Lasserre et al. (2013) use GGMs to determine direct interactions among chromatin modifications, and Perner et al. (2014) to extend the chromatin network to chromatin-associated proteins.

GGMs and the precision matrix are at the core of many network reconstruction methods, even sometimes of those that appear to approach the problem differently. Indeed Feizi et al. (2013) recently proposed a network deconvolution method to estimate direct interactions based on an inversion formula in analogy to the summation of a geometric series. A comment on the original paper by Alipanahi and Frey (2013) notes the similarity to the precision matrix. Likewise, the Maximum Entropy approach to network reconstruction (Weigt et al., 2009; Zhou and Troyanskaya, 2014) has been shown under certain conditions to correspond closely to the use of the precision matrix [see Appendix in Morcos et al. (2011)].

How can we now detect independence when data is non-linear? So far we have discussed the concept of independence in the context of Gaussian linear data, but if this assumption is false, standard correlation based methods are no longer suitable. Supplementary Figure S3 shows examples of possible relationships among variables, many of which are non-linear. In practical applications such as gene regulation, this is a realistic scenario (Atkins and de Paula, 2002; Marbach et al., 2009), and low sample size can make it even more difficult as shown in Supplementary Figure S1. In principle, mutual information can detect non-linear relationships (Dykstra, 2014) since it is 0 for two independent distributions, regardless of their form. However, sample mutual information requires density estimation and is therefore notoriously difficult to compute accurately Steuer et al. (2002). In recent years, some progress has been made (Kinney and Atwal, 2014), for example Reshef et al. (2011) try to solve the binning problem associated with density estimation through optimization, but it remains unpractical.

A promising alternative to mutual information is distance covariance introduced by Székely et al. (2007). For two random variables X and Y, the distance covariance is 0 if and only if X and Y are statistically independent. The original data is mapped onto an induced high-dimensional space where the square sample distance covariance can be computed as a standard inner product of vectors. The induced space has dimensionality n² where n is the number of samples.

How can we now detect conditional independence when data is non-linear? There have been attempts to introduce the concept of conditional mutual information such as Wyner (1978), which however do not alleviate the density estimation problem posed by mutual information. In fact, the problem takes much larger proportions for conditional independence as the size of the conditional set increases and with it the number of possible conditions, since the variables of interest get less and less populated for each condition, making full-order conditional information measures mostly intractable with standard sample sizes. Recently, Zhao et al. (2016) introduced Part Mutual Information (pmi), a measure which is 0 if and only if two variables are independent. This is clearly a big step forward, and yet inherits the problems of estimation of all information based measures. In the realm of biological networks, Margolin et al. (2006) used information inequality for this purpose.

In the search for a non-linear conditional independence measure, distance covariance is a good starting point because it maps the original data into a new, higher-dimensional space where linear correlations can be computed. It thus appears natural to proceed in the high-dimensional space as in the linear case and compute partial correlations among the high-dimensional vectors. Not only can one compute partial correlations, one can also stack the high-dimensional vectors into a matrix D, the high-dimensional analog of the matrix W. We can then compute the covariance matrix ${\mathbf{D}}^T\times \mathbf{D}$ and invert it. We thereby handle non-linear associations via distance correlation and compute full-order partial correlations via what we call the ‘Distance Precision Matrix’ (DPM).

Székely and Rizzo (2014) also discuss this approach in their consideration of how to partialize distance correlation. They propose a modified, more sophisticated definition of partial distance correlation (pdcor) based on the consideration that the projection of one vector onto another one need not fall into the inner-product (Hilbert-)space which harbors the high-dimensional images of the data, and that the naïve estimator introduces a statistical bias. In this work, we will develop the DPM approach for network constructions and compare it, among others, with pdcor, which we will discuss in more detail in Section 2.

While Guo et al. (2014) use distance correlation for gene network reconstruction, pdcor is considered as a network construction method in (Zhao et al., 2016). We are not aware of other work that would have applied a partial version of distance correlation to biological data. Here, we will present extensive simulations to show that it is the merge of the two elements, distance correlation as a non-linear association measure and the partial correlation to eliminate transitive effects, which together form a practical method for gene network reconstruction, not requiring any parameter tuning and totally parsimonious in its underlying logic. So far, such an analysis has been missing in the literature.

In biological applications, one frequently encounters a situation where one has many more genes (nodes) than samples available for constructing a network. This lack of information results formally in the inversion of a singular matrix. This is a known problem in statistics and it is generally advantageous to compute the inverse of the covariance matrix using a regularization method like, e.g. Schäfer and Strimmer (2005). By reducing our problem to the inversion of a (distance) covariance matrix, we also open the path to adding regularization on top of our non-linear network reconstruction method.

Section 2 will provide definitions of the notions mentioned and introduce the Distance Precision Matrix together with partial distance correlation. Section 3 will summarize data and methods used for validation and testing. Section 4 will provide evaluation results for our method as well as for a number of competing methods on both simulated data and real data from DREAM challenges.

2 Approach

2.1 Distance correlation

Distance correlation was introduced as a measure of association between random variables, and denoted $\text{dcor}\left(X,Y\right)$(Székely et al., 2007).

For distributions with finite first moments, $\text{dcor}\left(X,Y\right)\in [0,1]$ and is 0 if and only if X and Y are independent. Note that this holds true in general and not only for Gaussian data, which makes the method applicable to the detection of non-linear associations. Furthermore, it is defined for X and Y in arbitrary and not necessarily equal dimensions, rather than for univariate quantities. Here we recapitulate the definition for univariate variables that we will need.

The sample distance correlation for two random variables X and Y with n given samples $X_i,Y_i,i=1,\dots ,n$ is calculated as follows. First, the entries of the distance matrices ${\mathbf{A}}^0$ and ${\mathbf{B}}^0$ are obtained using $a_{ij}^0={\Vert X_i-X_j\Vert }_2$ and $b_{ij}^0={\Vert Y_i-Y_j\Vert }_2$. Then the double centered (D-centered) distance matrices A and B are obtained from ${\mathbf{A}}^0$ and ${\mathbf{B}}^0$ by subtracting the row- and column-means and adding the grand mean using

$$a_{ij}=a_{ij}^0-\frac{1}{n}\sum _{k=1}^n{a}_{ik}^0-\frac{1}{n}\sum _{k=1}^n{a}_{kj}^0+\frac{1}{n^2}\sum _{k,l=1}^n{a}_{kl}^0$$ (1)

An analogous definition is used for B. The sample distance covariance is then defined as the square root of

$${\text{dcov}}^2\left(X,Y\right)=\frac{1}{n^2}\sum _{i,j=1}^n{a}_{ij}{b}_{ij}$$ (2)

and the sample distance correlation as the square root of

$${\text{dcor}}^2\left(X,Y\right)=\frac{{\text{dcov}}^2(X,Y)}{\sqrt{{\text{dcov}}^2(X,X){\text{dcov}}^2(Y,Y)}}$$ (3)

2.2 Partial distance correlation based on D-centered vectors

Partial distance correlation, in analogy to partial correlation, should be a version of distance correlation which controls the associations between two variables for the effect of other variables in the system. Let A, B and C be the D-centered distance matrices corresponding to the variables X, Y and Z obtained above from n samples. Let ${\mathbf{v}}_{\mathbf{A}},\hspace{0.17em}{\mathbf{v}}_{\mathbf{B}}$ and ${\mathbf{v}}_{\mathbf{C}}$ be the vector versions of the respective matrices (obtained by concatenating their columns into a vector), and referred to as double centered (D-centered) vectors. Since the matrices are n × n, the vectors contain n² elements. It is easy to show that ${\text{dcov}}^2\left(X,Y\right)=\text{cov}\left({\mathbf{v}}_{\mathbf{A}},{\mathbf{v}}_{\mathbf{B}}\right)$, which leads to

$${\text{dcor}}^2\left(X,Y\right)=\text{cor}\left({\mathbf{v}}_{\mathbf{A}},{\mathbf{v}}_{\mathbf{B}}\right)$$ (4)

This form of sample distance correlation offers a possible definition of sample partial distance correlation, by applying standard partial correlation to the D-centered vectors of the correspondent variables. ${\mathbf{v}}_{\mathbf{A}}$ and ${\mathbf{v}}_{\mathbf{B}}$ can be regressed on ${\mathbf{v}}_{\mathbf{C}}$ to obtain the residuals ${\mathbf{r}}_{\mathbf{A},\mathbf{C}}$ and ${\mathbf{r}}_{\mathbf{B},\mathbf{C}}$ respectively. Partial distance correlation between X and Y given Z can then be defined as

$$\text{partial}‐\text{dcor}\left(X,Y|Z\right)=\text{cor}\left({\mathbf{r}}_{\mathbf{A},\mathbf{C}},{\mathbf{r}}_{\mathbf{B},\mathbf{C}}\right)$$ (5)

Székely and Rizzo (2014) argue that this definition introduced a bias, which, however, our simulations below and in Supplementary Material show to be small.

2.3 Distance Precision Matrix

Let us assume we are given a n × p matrix W, which contains as columns n samples from p random variables, and where columns have been centered to mean 0. ${\mathbf{W}}^T\times \mathbf{W}$ is the sample covariance matrix and the precision matrix $\mathbf{\Lambda }$ is defined as its inverse (Bishop, 2006). The entries of $\mathbf{\Lambda }$ are related to the full-order partial correlation coefficients by $\text{pcor}(i,j)=-\frac{{\lambda }_{ij}}{\sqrt{{\lambda }_{ii}{\lambda }_{jj}}}$.

Our Distance Precision Matrix method (DPM) is based on applying the same mechanism in the n²-dimensional space of D-centered vectors. For each X_i, a D-centered vector is computed. Let D be the matrix with the D-centered vectors as columns. The Distance Precision Matrix is then the inverse of ${\mathbf{D}}^T\times \mathbf{D}$.

2.4 Partial distance correlation as introduced in Székely and Rizzo (2014)

For the purpose of introducing partial distance correlation, Székely and Rizzo (2014) defined an unbiased version of distance matrix called unbiased double centered (U-centered) matrix $\tilde{\mathbf{A}}$, where ${\tilde{a}}_{ij}=a_{ij}^0-\frac{1}{n-2}\sum _{k=1}^n{a}_{ik}^0-\frac{1}{n-2}\sum _{k=1}^n{a}_{kj}^0+\frac{1}{(n-1)(n-2)}\sum _{i,j=1}^n{a}_{ij}^0$. Note that the diagonal of this matrix is not integrated in the sum of the estimator. Based on this unbiased version that we will refer to as udcor, they put forward and defined partial distance correlation (pdcor) that, similarly to DPM, uses the high-dimensional space induced by the distance matrices to perform linear operations (Székely and Rizzo, 2014).

In the definition of DPM however, we keep all variables separate, and as a result only consider univariate variables (for example the expression of one gene), and apply full-order partial correlation. In the definition of pdcor, all control variables are merged into one single high-dimension variable, i.e. they define a multivariate control variable that includes the expressions of all control genes). Pdcor is then defined as the first-order partial correlation. In Supplementary Material Section S15, we deconstruct DPM and compare each stage with pdcor using Spearman correlation between the respective scores. For example, when sample size is large, merging variables makes the most difference. We also compare DPM using D-centered vectors and U-centered vectors (referred to as uDPM). D-centered vectors yield better or equal results.

Pdcor is designed for multivariate variables, which makes U-centering the method of choice. However, gene expression vectors are univariate variables, raising the question whether the U-centering is actually a necessity. Besides studying the results of both approaches in simulations and on real data, we provide in Supplementary Material Section S16 a numerical analysis of the bias discussed in Section 4.

2.5 Network reconstruction and regularization of the Distance Precision Matrix

For network reconstruction purposes, following the principle of Gaussian Graphical Models, only edges with a ‘large’ absolute value in the precision matrix are considered, ‘large’ being defined here as above a certain threshold. Below we will discuss how to choose such a threshold. For comparison purposes however, we use precision-recall and ROC curves based on edge rankings and no threshold is needed.

Inverting the matrices ${\mathbf{W}}^T\times \mathbf{W}$ or ${\mathbf{D}}^T\times \mathbf{D}$ can be challenging. In many applications one has to deal with the case when $p\gg n$, i.e. when the number of variables is much larger than the number of samples. This results in a singular or ill-conditioned matrix ${\mathbf{W}}^T\times \mathbf{W}$ or ${\mathbf{D}}^T\times \mathbf{D}$. The increased size of the row-space of D from n to n² does not necessary alleviate those problems for ${\mathbf{D}}^T\times \mathbf{D}$. Significant efforts in many parts of science, including biology, economics and finance, have in recent years produced regularization based inversion routines for the covariance matrix [see Pollak (2012) for a review]. In this study we use the method of Schäfer and Strimmer (2005) to estimate and invert the covariance matrices ${\mathbf{W}}^T\times \mathbf{W}$ or ${\mathbf{D}}^T\times \mathbf{D}$, leading to regularized partial correlation and regularized DPM (reg-DPM) respectively.

3 Materials and methods

3.1 Data simulation

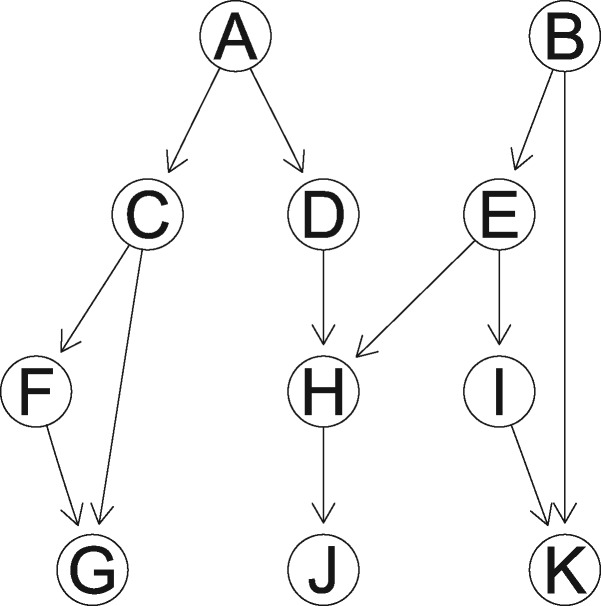
In order to study the behavior of methods in a controlled setting, we use simulated data. For Gaussian data, a random graph is easily obtained in R using various packages as described in Supplementary Material Section S3. Our results are averaged over data sampled from 100 different simulated graphs. To test the methods on non-linear data, we designed an 11 node directed graph shown in Figure 1. The graph contains all possible connections: a chain $(x\to y\to z),$ a fork $(x\leftarrow y\to z)$, a collider $(x\to y\leftarrow z)$ and a feed-forward loop ($(x\to y\to z)$ together with $(x\to z)$). The value of each node is obtained from its parents using arbitrarily defined non-linear functions given in Supplementary Material Section S2, and Gaussian noise is added. Supplementary Figure S3 shows the scatter plots of one realization of the simulated data with direct interactions highlighted in blue.

Fig. 1.

Directed graph H used to generate non-linear data

3.2 Data from DREAM challenge

DREAM (Dialogue for Reverse Engineering Assessments and Methods) challenge (Marbach et al., 2009, 2012; Prill et al., 2010) provides gene expression data with various numbers and types of variables together with a gold standard network for each dataset to benchmark methods. We use data from editions DREAM3, DREAM4 and DREAM5. Note that simulated data in DREAM challenges does display non-linear interactions due to the physico-chemical laws that were taken into account for data-generation (Marbach et al., 2009; Schaffter et al., 2011), an example of which is shown in Supplementary Figure S2.

Note that DREAM5 also contains real data from E.coli and S. cerevisiae. The networks are very large with thousands of nodes and come with relatively very few samples. The full networks are computed, however, following the rules of the challenge, performance is reported on edges between regulators and transcription factors only (transcription factors are also regulators). DREAM5 time series data was not used.

3.3 Competitor methods

In this study, we compare the performance of DPM and reg-DPM with nine other methods (implementation details are given in Supplementary Material Section S5):

• Pearson correlation (cor), partial correlation (pcor) and regularized partial correlation following Schäfer and Strimmer (2005) (reg-pcor).

• Network deconvolution (Feizi et al., 2013) with the absolute value of the correlation matrix as input (nd).

• Mutual information (mi), part mutual information (Zhao et al., 2016) (pmi) and ARACNE (Margolin et al., 2006) (arac). Note that pmi had to be used using the Gaussian assumption since it has no non-linear version available for multivariate conditioning.

• distance correlation (Székely et al., 2007) (dcor) and partial distance correlation (Székely and Rizzo, 2014) (pdcor).

3.4 Evaluation methodology

In this study, we only consider undirected edges, i.e. $A\to B$ and $B\to A$ are treated equally. We compare our method to others using the area under the precision-recall curve (AUPRC). The corresponding figure for the area under the receiver-operating characteristic curve (AUROCC) will be shown in Supplementary Material. More details about these curves can be found in Supplementary Material Section S4. All methods are assessed equivalently, no parameters are tuned, and if parameters are required (for example in arac), they are set to their default value. The precision-recall (PR) and receiver-operating characteristic (ROC) curves are computed based on the ranking of edges, not by changing the parameters.

4 Results and discussion

4.1 Performance comparison on Gaussian data

DPM should perform comparably to partial correlation. We generate 100 random 10-nodes networks and, for each of them, simulate 100 samples of Gaussian data and univariate Gaussian noise. False positive rate (FPR), recall and precision are averaged over all networks.

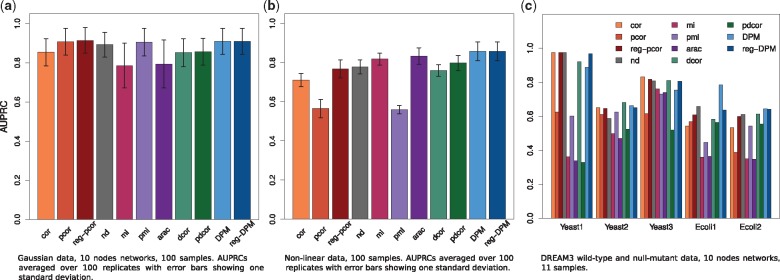
Figure 2a shows the average AUPRCs of all selected methods on a 10-node/100 samples example. The corresponding PR curves can be found in Supplementary Figure S4.

Fig. 2.

Performance on simulated data. The plots show the average AUPRCs of all selected methods. Error bars show one standard deviation. (a) Gaussian data. The expected AUPRC on this task is 0.27. (b) Non-linear data. The expected AUPRC on this task is 0.2

Mutual information based methods (mi and arac) perform worst on this task, probably because of the discretization step. pmi is solved analytically and does not suffer. pcor, reg-pcor, pmi, nd, DPM and reg-DPM (overlapping) perform best. Regarding ROC curves and AUROCCs (see Supplementary Fig. S6), all methods are roughly comparable except those based on mutual information which never perform as well. The same experiments were run on 50 nodes networks (Supplementary Fig. S5), and on 10/50 nodes networks using 200 samples (Supplementary Fig. S7); results are shown and discussed in Supplementary Material Section S6.

Overall, DPM performs well and does not lose out over partial correlation (pcor), which was developed for Gaussian data. DPM even performs better when the number of samples is limited compared with the number of nodes. Network deconvolution (nd) also performs well especially on the larger networks. We note that partial distance correlation (pdcor) yields edge-rankings inferior to the ones produced by DPM.

4.2 Performance comparison on non-linear data

DPM should be able to detect non-linear associations. We generate 100 samples from the network H in Figure 1 and add univariate standard Gaussian noise to each variable. FPR, recall and precision are averaged over 100 replicates.

Figure 2b shows the average AUPRCs of all selected methods. The corresponding PR curves can be found in Supplementary Figure S8. pcor and pmi, which are geared towards Gaussian data and require a larger number of samples, perform worst on this task. DPM, reg-DPM (overlapping) perform best. While regularization dramatically improves the performance of pcor, there is no visible difference between DPM and reg-DPM with 100 samples. Regarding ROC curves and AUROCCs (see Supplementary Fig. S9), mi, dcor, pdcor, DPM and reg-DPM perform best. The same experiments were run using 200 samples; results are shown and discussed in Supplementary Material Section S7.

In conclusion, distance correlation-based and mutual information-based methods perform best, with a slight advantage for DPM and reg-DPM. Partial distance correlation (pdcor) performance follows after mi, aracne and (reg-)DPM.

4.3 Application to gene regulatory networks (DREAM data)

We show results on null-mutant (and wild-type) data for DREAM3, knockout (and wild-type) data for DREAM4 and all three official DREAM5 networks, but results on all other subsets of DREAM3 and DREAM4 data are shown in Supplementary Material Sections S8 and S9 for completeness.

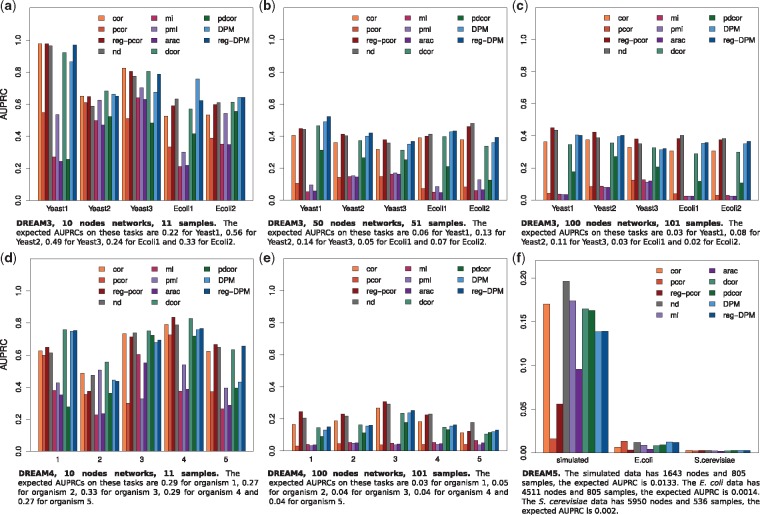
Figure 3a, b and c show the AUPRCs obtained on DREAM3, for a total of (number of nodes + 1) samples for each network, which is rather low. In 10 nodes and 50 nodes networks, DPM and reg-DPM are in some cases the best, in all cases competitive. In 100 nodes networks, DPM and reg-DPM are slightly outperformed by reg-pcor and nd, suggesting that DPM might suffer on larger networks. pcor and pdcor consistently underperform. The performance of pcor is not surprising since, as discussed above, it generally does poorly with small sample sizes. pmi requires even more data and could not run properly on 100-nodes networks with 101 or 201 samples (it was assigned random performance).

Fig. 3.

Performance on DREAM data. The plots show the AUPRCs of all selected methods on various DREAM datasets. (a, b, c) DREAM3 wild-type and null-mutant data. (d, e) DREAM4 wild-type and knockout data. (f) DREAM5

Figure 3d and e show the AUPRCs obtained on DREAM4, for a total of (number of nodes + 1) samples for each network. In 10 nodes networks, DPM and reg-DPM are almost never the best but are always competitive. Here again, pcor, mi, arac and pdcor consistently underperform, and pmi could not handle the 100-nodes networks with 101 or 201 samples. In 100 nodes networks, DPM and reg-DPM are slightly outperformed by reg-pcor, nd and even cor.

Figure 3f shows the AUPRCs obtained on data from DREAM5. We have zoomed into the AUPRC plot and added the AUROCC plot in Supplementary Figure S15. On simulated data, nd performs best, with an AUPRC around 0.18. DPM and reg-DPM are below but still competitive with the other methods. For E.coli data, pcor, nd, DPM and reg-DPM perform better. For S.cerevisiae data, the AUPRCs are all comparable but too low to be of any use.

In conclusion, DPM and reg-DPM are competitive on the the DREAM datasets with the exception of simulated DREAM5 data, and perform really well on DREAM3 data. As seen before on our own simulated data, DPM and reg-DPM perform better than their direct competitor pdcor, which may outweigh the theoretical advantages of pdcor when it comes to practical application.

4.4 Detection of direct edges only

To verify that direct edges are favored, we repeat the experiments described above, however performance is computed using as negatives the indirect edges only. More details can be found in Supplementary Material Section S12.

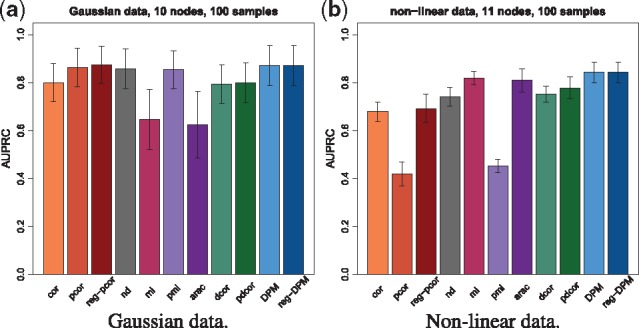
Figure 4 shows the AUPRCs of all selected methods on linear and non-linear data, and on DREAM3 null-mutant (and wild-type) data. For linear data (Fig. 4a), all methods based on partial methods (pcor, reg-pcor, pmi, nd, DPM and reg-DPM) perform best except pdcor, which stays at the level of cor and dcor. For non-linear data (Fig. 4b), arac, DPM and reg-DPM perform best. pdcor performs only slightly better than dcor. On DREAM data (Fig. 4c), DPM and reg-DPM are always competitive.

Fig. 4.

Performance on direct vs indirect edges. The plots show the average AUPRCs of all selected methods for distinguishing direct edges from indirect ones. Error bars show one standard deviation. DPM and reg-DPM are among the top-performers. (a) Gaussian data. The expected AUPRC on this task is 0.26. (b) Non-linear data. The expected AUPRC on this task is 0.2

In conclusion, DPM and reg-DPM are able to discard indirect edges on all the datasets used in this study at least as well as other methods. Similar results using larger networks can be found in Supplementary Figure S12.

4.5 Effect of sample size

We repeat the simulations for Gaussian and non-linear data described in their respective subsections, and vary the number of samples drawn from the networks. This important analysis tests the consistency of a method, i.e. its ability to reconstruct the correct network if given enough data. Figure 5 shows the evolution of the average AUPRCs for all selected methods as sample size increases. The ROC counterpart is shown in Supplementary Figure S21.

Fig. 5.

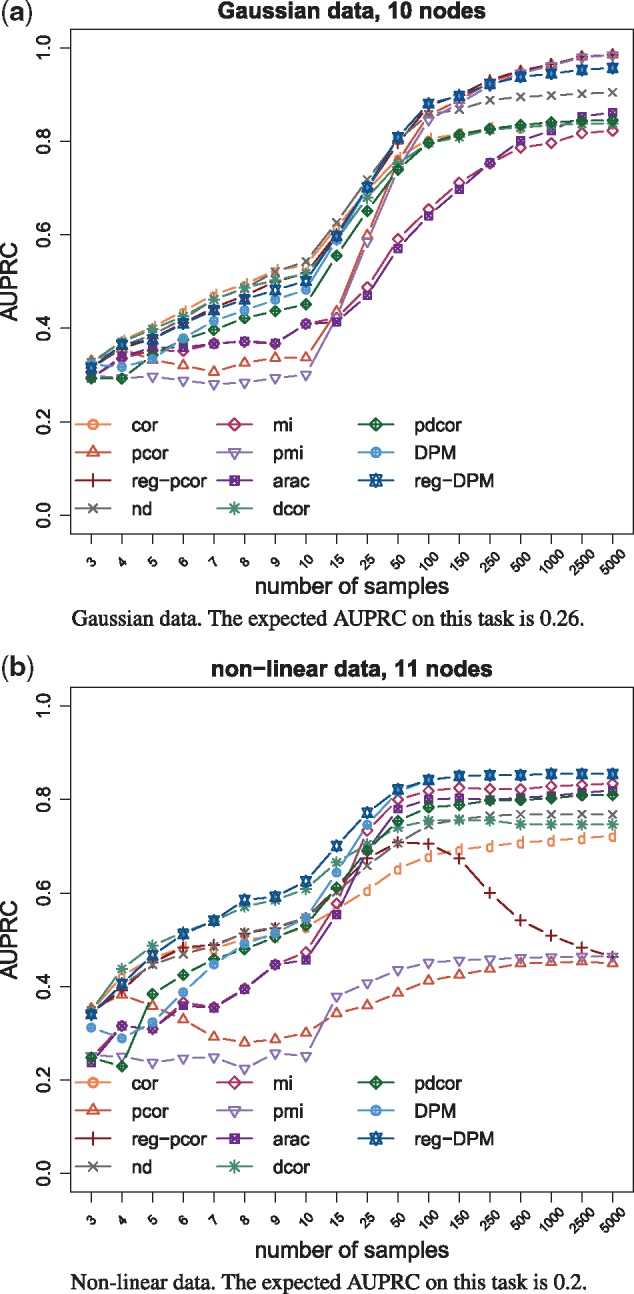
Effect of sample size on performance on simulated data. The plots show the evolution of the average AUPRCs as sample size increases. reg-DPM is the most consistent method on this task

For Gaussian data (Fig. 5a), cor and dcor overlap at the top for very small amounts of samples (here up to 8), nd takes slightly over for small amounts of samples (here up to 25), DPM and reg-DPM catch up for large amounts of samples (here up to 250) while pcor, reg-pcor and pmi take over for very large amount of samples. DPM and reg-DPM are always just below the top performers, if not the top performers themselves. Note that pdcor, even under large sample sizes, remains below these methods and appears to level out at around 0.8. All methods improve as the number of samples increases, but reg-DPM and reg-pcor are the most consistent across various numbers of samples.

For non-linear data (Fig. 5b), none of the methods approaches the perfect score of 1, but the best ones level out slightly above 0.8. reg-DPM is clearly the best method, improving over DPM for small sample sizes and the two versions being equally good for large sample sizes. The next best methods in terms of consistency are mi and pdcor, followed by nd.

In conclusion, reg-DPM improves with more samples like all other methods but is consistently among the top performers for both types of data. The methods requiring the most samples are pcor, mi, pmi and arac.

4.6 Effect of noise

We repeat the simulations for Gaussian and non-linear data described in their respective subsections, and vary the variance of the univariate Gaussian noise that is added to the data drawn from the networks. Supplementary Figures S22 and S23 show the evolution of performance for all selected methods as noise increases, using respectively 150 and 500 samples. Insights are discussed in Supplementary Material Section S14. DPM and reg-DPM are methods of choice for small amounts of noise, but do not perform as well as mi or arac for large amounts of noise on non-linear data. However mi and arac do not perform well on Gaussian data, while DPM and reg-DPM are reliable on both types of data.

4.7 Bias in DPM and pdcor

The use of dcor as opposed to udcor to build the double centered vectors raises the question of a potential bias in the values of the edge scores given by DPM. We argue that using dcor for DPM in our context does not pose a problem since we are only interested in the ranking of the edges and not in the actual values of the edge scores. In Supplementary Material Section S16, we present a bias analysis for Gaussian networks and for our non-linear network. On a 3-nodes network, DPM shows a small bias but this decreases as sample size increases, and is negligible in comparison with the bias in dcor. Moreover DPM seems to deal better with transitive associations than pdcor, and to separate edges from non-edges more which is consistent with results from Figures 2b and 4.

4.8 DPM in practice

PR and ROC curves are useful to compare methods in the presence of a gold standard, but provide little guidance as to which edges to include in the network when the method is applied to a novel dataset. In the absence of an analytic theory on threshold selection for our method, Supplementary Material Section S11 compares possible heuristics for setting a threshold. In particular, a simple k-means clustering of edges into two classes—included and discarded edges—works well and this has been implemented in our R-package. We are not pursuing simulating the p-values of edge-scores since it would be too computationally demanding.

Supplementary Material Section 17 also shows runtimes for various algorithms. DPM is not the fastest but it is fast enough to be applicable to most situations. In particular, on one CPU, DPM and reg-DPM are much faster than pdcor. Experiments on DREAM5 data took several hours for DPM (using 1 CPU) but several weeks for pdcor.

5 Conclusion

Since relationships among interacting genes need not be linear, there has always been a sense of frustration about the lack of network reconstruction methods for non-linear data. On the side of the information based methods, part mutual information constitutes substantial progress, although the estimation problem for information measures remains hard. Distance correlation has offered both an analytical measure and an estimator, and has been extended to a partial version both in pdcor and in our DPM. We think that with these developments the theory bottleneck in gene network reconstruction has largely disappeared.

In this work we have tried to show that DPM can detect both linear and non-linear associations among variables. Our results on simulated non-linear data confirm that the distance correlation based methods are well suited to such general relationships because they build on the concept of full-order partial correlation used in GGMs (Bishop, 2006). In GGMs, i.e. in the context of Gaussian linear data, full-order partial correlations are computed via linear regression or via inversion of the covariance matrix. Distance correlation maps non-linear data into a high dimensional space where linear operations make sense again, and DPM simply uses full-order partial correlation in that space. We have shown in our simulations that DPM can indeed discard non-direct associations.

In spite of the theoretical advances concerning the non-linear relationships, it remains a truism that for gene networks one frequently studies networks on many more nodes than we have data samples. This is generally known as the $p\gg n$ problem, where n corresponds to the number of samples. The established remedy of regularization can be easily emulated using the DPM. We have introduced reg-DPM as one option how DPM can handle small sample numbers. Our simulations show that reg-DPM is robust to small sample sizes.

A fair comparison of methods relies on the presence of a gold standard. For simulated data this is easy and this is why we have presented extensive tests of the properties of the methods on simulation scenarios testing Gaussian data, non-linear data and in terms of consistency and stability with respect to random noise. After all, one would preferably apply a method to real data which has already performed well on controlled scenarios.

No method performs best on all the datasets presented in this study. However, in contrast to many other methods, the distance correlation based approaches, in particular DPM and reg-DPM, yield good results across all datasets. Notably, (reg-)DPM, like pdcor, has no parameters to tune and DPM was not optimized in any way for particular test data. At the same time, we have observed that DPM runs faster than pdcor and makes computation of even large networks feasible. Taken together, our performance comparison has not only quantified the success of the various methods on simulated and real test data, but we also studied in great detail the behavior of many approaches and methods upon changing sample sizes, under the influence of noise, etc. We think that an analysis like this has been long overdue and we hope that it will aid in laying a rational basis for the further development of the field.

We have observed mutual information to work well on non-linear data but not on Gaussian data. We speculate that this is due to the difficulty of binning-based estimation in the Gaussian domain. Regularized partial correlation works well on Gaussian data but not so much on non-linear data. Methods such as conditional mutual information or part mutual information require estimation by binning making them more vulnerable to small sample numbers. Having to discretize also makes the conditioning on many variables computationally extremely demanding, which is why, e.g. pmi then resorts to a Gaussian assumption again.

We observed partial distance correlation often to perform below DPM on our controlled simulation settings. We speculate that this is due to the merging of control variables into a single variable done by pdcor, rather than the full-order partial correlation implicitly computed by DPM. Why this makes a difference may be a subject for further investigation.