Validating Molecular Dynamics Simulations Against Experimental Observables in Light of Underlying Conformational Ensembles

Abstract

Far from the static, idealized conformations deposited into structural databases, proteins are highly dynamic molecules that undergo conformational changes on temporal and spatial scales that may span several orders of magnitude. These conformational changes, often intimately connected to the functional roles that proteins play, may be obscured by traditional biophysical techniques. Over the past forty years, molecular dynamics (MD) simulations have complemented these techniques by providing the ‘hidden’ atomistic details that underlie protein dynamics. However, there are limitations of the degree to which molecular simulations accurately and quantitatively describe protein motions. Here we show that although four molecular dynamics simulation packages (AMBER, GROMACS, NAMD and ilmm) reproduced a variety of experimental observables for two different proteins (engrailed homeodomain and RNase H) equally well overall at room temperature, there were subtle differences in the underlying conformational distributions and the extent of conformational sampling obtained. This leads to ambiguity about which results are correct, as experiment cannot always provide the necessary detailed information to distinguish between the underlying conformational ensembles. However, the results with different packages diverged more when considering larger amplitude motion, for example the thermal unfolding process and conformational states sampled, with some packages failing to allow the protein to unfold at high temperature or providing results at odds with experiment. While most differences between MD simulations performed with different packages are attributed to the force fields themselves, there are many other factors that influence the outcome, including the water model, algorithms that constrain motion, how atomic interactions are handled, and the simulation ensemble employed. Here four different MD packages were tested each using best practices as established by the developers, utilizing three different protein force fields and three different water models. Differences between the simulated protein behavior using two different packages but the same force field, as well as two different packages with different force fields but the same water models and approaches to restraining motion, show how other factors can influence the behavior, and it is incorrect to place all the blame for deviations and errors on force fields or to expect improvements in force fields alone to solve such problems.

Graphical Abstract

Introduction

Molecular dynamics (MD) simulations, “virtual molecular microscopes”, employ computational methods to probe the dynamical properties of atomistic systems and proffer insights into molecular behavior. Beginning with the report of a 9.2 picosecond simulation of bovine pancreatic trypsin inhibitor (BPTI) in 1977,¹ MD simulations have provided the means to visualize proteins in action and to investigate that paradigmatic relationship between form and function.^2,3 When taken in context with experimental results, MD simulations can drive discoveries in protein design,^4,5 protein folding,^6–9 and other spheres of protein science.¹⁰ However, two factors limit the predictive capabilities of MD: first, lengthy simulations may be required to correctly describe certain dynamical properties (i.e. the sampling problem¹¹) second, insufficient mathematical descriptions of the physical and chemical forces that govern protein dynamics may yield biologically meaningless results (i.e. the accuracy problem¹²).¹³ To increase our confidence in the ability of MD simulations to provide meaningful results for arbitrary proteins and peptide systems, it is necessary to benchmark computational results against experimental data.

Improved computational infrastructure,¹⁴ software,^15,16 and parallelization schemes^17,18 allow contemporary simulations to probe increasingly larger systems at timescales approaching those of experiment.^19–22 However, the requisite simulation times to accurately measure dynamical properties are rarely known a priori; instead, simulations are deemed ‘sufficiently long’ when some observable quantity has ‘converged’. In the context of molecular simulation, Sawle and Ghosh argue that convergence is a misnomer and show that the timescales required to satisfy the most stringent tests of ‘convergence’ or ‘self-consistency’ vary from system to system and are dependent on the method used to assess convergence.²³ This behavior is mirrored in the analysis of MD simulations: we have shown that the overall level of insight into the dynamics of a system can be modulated by the type of analysis performed and the level of detail described.²⁴ Thus, how long is ‘sufficiently long’ remains unanswered. A wealth of information can be obtained from simulations that probe native state dynamics as well as conformational changes that result in excursions from the native state. However, for slow dynamical processes like the folding of typical globular proteins and the non-folding of intrinsically disordered proteins,^25,26 the requisite timescales remain out of reach for the time being, at least for conventional MD simulations.

Approximations built into the mathematical forms of MD force fields and their associated parameterizations give rise to the accuracy problem. These force fields are empirical and begin with parameters obtained from high-resolution experimental data and quantum mechanical calculations for small molecules, and then they are modified to reproduce different experimental properties or desired behaviors.^27–36 Over time, modification of these parameters has yielded improved force fields with similar functional forms.³⁷ In addition, it is important to note that while usually the focus, or blame, is on the force field, it is not just the potential energy function and associated parameters that determine the results of MD simulations. Protein dynamics are often more sensitive to the protocols used for integration of the equations of motion, treatment of nonbonded interactions and various unphysical approximations.

The most compelling measure of the accuracy of a force field is its ability to recapitulate and predict experimental observables. However, there are challenges associated with this method of validation.¹³ Namely, the experimental data used for validation are averages over space and time; the underlying distributions and timescales associated with these averages are often obscured. Consequently, correspondence between simulation and experiment does not necessarily constitute a validation of the conformational ensemble(s) produced by MD, i.e. multiple, and possibly diverse, ensembles may produce averages consistent with experiment. This is underscored by simulations that demonstrate how force fields can produce distinct pathways of the lid-opening mechanism of adenylate kinase that nevertheless sample the crystallographically identified ‘open’ and ‘closed’ conformers.³⁸ Furthermore, extensive simulations of the villin headpiece demonstrated that while MD-derived folding rates and native state structures had good agreement with experiment, the folding pathways and denatured state properties were force-field dependent.³⁹ In addition, experimental observables may be derived using relationships that are functions of molecular conformation and are themselves associated with some degree of error. For example, most chemical shift predictors produce chemical shifts from molecular structures via training against high-resolution structural databases, not solely via calculations from first principles.

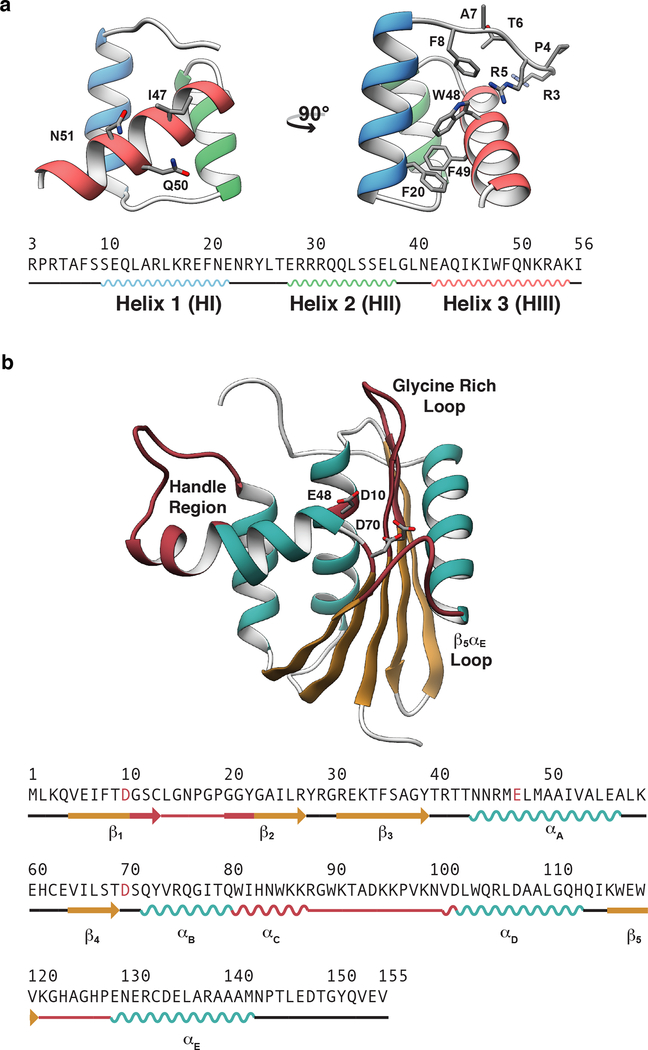
Here, we address the extent to which multiple simulations performed for 200 ns each agree with experimental data. Multiple short simulations yield better sampling of protein conformational space than a single simulation with total sampling time equal to the aggregate sampling time of multiple small simulations.^40,41 As simulations see increased usage, particularly by those not trained in the method, it is important to place quantitative bounds on the extent to which these simulations agree with experimental data and to understand the limits of their ability to explain experimental findings. Consequently, we have compared how three force fields (AMBER ff99SB-ILDN,⁴² Levitt et al.,⁴³ and CHARMM36⁴⁴) used within four MD packages (AMBER,^45–47 in lucem molecular mechanics (ilmm),⁴⁸ GROMACS,⁴⁹ and NAMD⁵⁰) agree with a diverse set of experimental data for two globular proteins with distinct topologies: the Engrailed homeodomain (EnHD) and Ribonuclease H (RNase H) (Figure 1). The Drosophila engrailed homeodomain has 54 residues arranged into three α-helices (denoted HI-HIII) and constitutes the DNA-binding domain of the larger transcription factor in which it is found. RNase H is an endonuclease α/β protein composed of 155 residues organized into five α-helices (denoted α_A – α_E) and a single, five-stranded β-sheet (denoted β₁ – β₅) that hydrolyzes the RNA strand in double stranded RNA-DNA hybrid.⁵⁸

Figure 1. X-ray crystal structures of the engrailed homeodomain and ribonuclease H.

(a) The simple tertiary structure, small size, and ability to fold autonomously without either disulfide bonds or ligands have made homeodomains the subject of numerous investigations into the mechanisms of protein folding. Here, the crystal structure and sequence of the engrailed homeodomain are shown. On the front view (left), the DNA binding residues in HIII are represented as balls and sticks; on the side view (right), the DNA binding residues on the N-terminus as well as four aromatic residues within the hydrophobic core are shown as balls and sticks. (b) RNase H functions in numerous biological processes including inhibition of replication by removal of R-loops,⁵¹ removal of Okazaki fragments,⁵² synthesis of multicopy single-stranded DNA,⁵³ and removal of misincorporated ribonucleotides.⁵⁴ Here the crystal structure and sequence of ribonuclease H are shown with the β-sheet colored tan, α-helices cyan, and functional regions burgundy. Four functional regions of RNase H have been identified that are critical for RNase H to bind and hydrolyze RNA-DNA hybrids.^55–57 These regions include α_C and the loop between α_C and α_D (residues 81 to 101, referred to as the handle region), the loop between β₁ and β₂ (residues 11 – 22, referred to as the glycine rich loop), the loop between β₅ and α_E α/β (residues 121–127 referred to as the β₅/α_E loop), and the active site, which contains three conserved carboxylate residues (Asp10, Glu48, and Asp70) that coordinate divalent cations that are required for catalysis.

Methods

Molecular Dynamics Simulations

The initial coordinates for simulations of EnHD were obtained from the 2.1 Å resolution X-ray crystal structure solved by Clarke et al. (PDB ID: 1ENH).⁵⁹ The initial coordinates for simulations of RNase H were obtained from the 1.48 Å resolution crystal structure solved by Katayanagi et al. (PDB ID: 2RN2).⁵⁸ Crystallographic solvent atoms were removed from these structures and then conventional molecular dynamics simulations were performed using four software package-force field combinations: in lucem molecular mechanics (ilmm)⁴⁸ with the Levitt et al. force field,⁴³ AMBER with the Amber ff99SB-ILDN force field,⁴² GROMACS⁴⁹ with the Amber ff99SB-ILDN force field,⁴² and NAMD⁵⁰ with the CHARMM36 force field.^44,60,61 The simulations were performed under conditions consistent with those under which the experimental data were obtained. Simulations of EnHD were performed at neutral pH (7.0) at 298 K, and simulations of Rnase H were performed at acidic pH (5.5, histidine residues protonated) at 298 K. All simulations were performed in triplicate for 200 nanoseconds using periodic boundary conditions, explicit water molecules and ‘best practice parameters’, as determined by recent papers in the literature by authors of the software packages [AMBER,^62–64 ilmm,⁶⁵ GROMACS,⁶⁶ and NAMD⁶⁷] and their associated force fields typically contain many adjustable parameters. Here, we aimed to strike a balance between keeping these parameters consistent and adjusting them only when necessary for specific force fields/ MD package combinations. Within each package/force field combination, simulation methods were kept constant for the two proteins. Simulations of the native state were performed at 298 K and thermal unfolding was simulated at 498 K. Details for the initial preparation of the systems and the 298 K simulations for each force field follows. To promote the inclusion of simulation software parameterizations in ongoing and future force field evaluations, we have included the input files for each of our simulations in the supplementary information. We maintain that the algorithms used and associated input control parameters are as important as the force field per se in determining simulated behavior. This information may also be of use in meta analyses that evaluate force field/ MD software. Also, as there is some overlap in the protein (AMBER and GROMACS) and water (GROMACS and NAMD) force fields used by different programs, the simulations will be referred to throughout by the name of the simulation package used.

AMBER

Simulations were performed with the AMBER14 package and ff99SB-ILDN force field.⁴² Explicit hydrogen atoms were modeled onto the X-ray structure using the leap module and each protein was solvated with explicit TIP4P-EW⁶⁸ waters in a periodic, truncated octahedral box that extended 10 Å beyond any protein atom. Each system was then minimized in three stages. First, solvent atoms were minimized for 500 steps of steepest descent minimization followed by 500 steps of conjugate gradient minimization in the presence of 100 kcal mol⁻¹ restraints on protein atoms. Second, solvent atoms and protein hydrogens were minimized for 500 steps of steepest descent minimization followed by 500 steps of conjugate gradient minimization in the presence of 100 kcal mol⁻¹ restraints on protein heavy atoms. Third, all atoms were minimized for 500 steps of steepest descent minimization followed by 500 steps of conjugate gradient minimization in the presence of 25 kcal mol⁻¹ restraints on protein C_α atoms. After minimization, systems were heated to 298 K during 6 successive stages. In each stage, the system temperature was increased by 50 K over 200 ps (25,000 steps) using the canonical NVT (constant number of particles, volume, and temperature) ensemble. (25 kcal mol⁻¹ restraints on protein C_α atoms were present during each stage). After the system temperature reached 298 K, the systems were equilibrated over 7 successive stages. During the first 5 stages, the systems were minimized for 1000 steps (500 steps of steepest descent followed by 500 steps of conjugate gradient minimization) and restraints on protein C_α atoms were decreased from 5 kcal mol⁻¹ to 1 kcal mol^-1. Next, the systems were equilibrated using the NVT ensemble for 500,000 steps (1 ns) and then the NPT ensemble for an additional 500,000 steps (1 ns) in the presence of 0.5 kcal mol⁻¹ restraints were present on protein C_α atoms. Production dynamics were then performed using the isobaric-isothermal NPT (constant Number of particles, Pressure, and Temperature) ensemble using a 2 fs time step and coordinates were saved every picosecond for analysis. The SHAKE algorithm was used to constrain the motion of hydrogen-containing bonds.^69,70 Long-range electrostatic interactions were calculated using the particle mesh Ewald (PME) method.

GROMACS

Simulations were performed with GROMACS version 5.0.6⁴⁹ and the AMBER ff99SB-ILDN⁴² force field. Hydrogen atoms were modeled onto the X-ray structure using pdb2gmx prior to solvation with TIP3P⁷¹ waters in periodic, cubic boxes that extended 10 Å beyond any protein atom. Solvent molecules were replaced with counter ions until the system was neutralized. Throughout the following stages, a Verlet cutoff scheme⁷² was employed with a 10 Å cutoff for both electrostatic and van der Waals interactions and LINCS was employed to constrain bonds.⁷³ Electrostatic interactions were calculated using PME. The solvated systems were minimized for 50,000 steps using steepest descent minimization. Systems were then equilibrated over two stages in the presence of positional restraints on protein atoms. First, systems were equilibrated in the NVT ensemble for 50,000 steps followed by equilibration in the NPT ensemble for an additional 50,000 steps. Finally, production dynamics were performed in the NPT ensemble with a 2fs time step and coordinates were saved every picosecond for analysis.

ilmm

Simulations were performed with the in lucem molecular mechanics (ilmm) package and Levitt et al. force field⁴³ using our standard protocols. Explicit hydrogen atoms were modeled onto the X-ray crystal structures prior to steepest descent minimization for 1000 steps. Each protein was solvated with explicit flexible 3-center (F3C)⁷⁴ water molecules in a periodic, cubic box that extended 10 Å beyond any protein atom, with the solvent density set to the experimental value at 298 K (0.997 g mL⁻¹).⁷⁵ Solvent atoms were then minimized for 1000 steps and equilibrated for 500 steps (1 ps) prior to additional, separate minimization of the solvent (500 steps) and protein (500 steps) atoms. Conventional molecular dynamics simulations were then performed using the microcanonical NVE (constant Number of particles, Volume, and Energy) with a target temperature of 298 K. The equations of motion were propagated using a 2 fs time step with a 10 Å force-shifted nonbonded cutoff,^43,76 and coordinates were saved every picosecond for analysis. In contrast to the other software packages described here, ilmm with the Levitt et al. force field⁴³ subscribes to a molecular-level representation and natural Boltzmann sampling through use of the NVE ensemble rather than trying to control macroscopic variables, such as temperature and pressure, in these microscopic systems. Such temperature and pressure coupling lead to very frequent scaling of the velocities, which in turn provides discontinuous trajectories. This may not be an issue if conformational sampling is desired as opposed to pathways for those conformational changes, but ilmm was developed with the objective of characterizing both ‘kinetic’ pathways and ‘equilibrium’ states. In addition, ilmm does not restrain atomic motion via algorithms such as LINCS and SHAKE nor introduce artificial periodicity into the molecular system via algorithms such as PME. ⁷⁶

NAMD

Simulations were performed with NAMD version 2.10⁵⁰ and the CHARMM36 force field⁴⁴. Hydrogen atoms were modeled onto the X-ray crystal structures using psfgen prior to solvation with TIP3P waters⁷¹ in a periodic box that extended 10 Å beyond any protein atom. Next, minimization was performed in two phases. In the first stage, minimization was performed for 20,000 steps with all hydrogen-containing bonds constrained and protein atoms fixed. In the second stage, minimization was performed for 1000 steps with all protein backbone atoms fixed and an additional 1000 steps with no fixed atoms. After minimization, systems were heated to 298 K over 10,000 steps with harmonic restraints on backbone atoms that were gradually decreased from 5.0 to 0 kcal mol^-1. After heating, systems were equilibrated for 100,000 steps (200 ps) in the NPT ensemble. Finally, production dynamics were performed in the NVT ensemble using a 2 fs time step. Van der Waals interactions were truncated with a switching potential and coordinates were saved every picosecond for analysis. Electrostatic interactions were calculated via PME summation and SHAKE was used to constrain bonds.

High Temperature Unfolding Simulations

In addition to the native state simulations described above, we also performed high temperature unfolding simulations of EnHD with the same force fields as for the native simulations. The high temperature unfolding protocols were similar to those for the native state simulations, with the following changes. The simulations were performed at 498 K in triplicate for 10 ns, non-bonded cutoffs were reduced by 2 Å, and structures were saved every 0.2 ps for analysis. To keep solvent molecules in the liquid state, the pressure was set to ~26 atm⁷⁷ for simulations with GROMACS, AMBER, and NAMD; for ilmm, the solvent density was set to the experimental value at 498 K and ~26 atm (0.829 g ml⁻¹).^75,77 For AMBER, the two final equilibration phases were reversed, with NPT equilibration (500,000 steps) followed by NVT equilibration (500,000 steps), and the NVT ensemble was employed for production dynamics. For NAMD, the NPT ensemble was employed for production dynamics.

Analysis of MD Data

After production dynamics were completed, all trajectories were converted into an ilmm-compatible format and analyses were performed identically for all trajectories. Unless otherwise specified, 298 K analyses were performed on an ensemble created by pooling all three replicate simulations and the first 20 ns of each simulation were excluded from analysis, yielding 5.4 × 10⁵ structures in each ensemble.

Calculation of Gross Structural Changes and Dynamic Fluctuations

The root mean squared deviations (RMSDs) were calculated by aligning each frame to the crystal structure and fluctuations (RMSFs) were calculated by aligning each frame to the average structure calculated after the 20 ns equilibration period. The C_α atoms for all ‘core’ residues were included in the alignment and subsequent calculations. ‘Core’ residues refer to all residues except for flexible N- and C-terminal residues (EnHD: residues 8–53, RNase H: residues 5–142). Experimental Β-factors were compared with RMSFs via Equation 1, where B = experimental B-factors.⁷⁸

$$\mathrm{RMSF}={(3\mathrm{B}/8{\mathrm{\pi }}^2)}^{1/2}$$ Equation 1

Calculation of NMR chemical shifts.

Simulated chemical shifts were calculated with the SHIFTX2 program.⁷⁹ Experimental data for EnHD and RNase H were obtained from the Biological Magnetic Resonance Bank (BMRB)⁸⁰ entries 15536⁸¹ and 1657,⁸² respectively. Chemical shifts were calculated for 1% of the ensemble (one frame every 100 ps). For RNase H, the re-referenced chemical shifts provided by the RefDB were used.⁸³

Calculation of NMR scalar coupling constants

We calculated ³J_Hα,HN scalar coupling constants from MD simulations using the Karplus relation⁸⁴ (Equation 2) by taking the average of the coupling constants calculated for each frame in the simulation. The coefficients for the Karplus equation (C₀, C₁, and C₂) were obtained from the literature, and we used 7 different parameterizations.^85–91 Experimental data for EnHD and RNase H were obtained from the BMRB entries 15536⁸¹ and 1657,⁸² respectively.

$${}^3\mathrm{J}(\mathrm{\theta })={\mathrm{C}}_0+{\mathrm{C}}_1\cos \mathrm{\theta }+{\mathrm{C}}_2{\cos }^2\mathrm{\theta }$$ Equation 2

Calculation of NOE satisfaction

Experimental nuclear Overhauser effect (NOE) values for EnHD and RNase H were obtained from the BMRB, entries 15536⁸¹ and 1657,⁸² with 654 and 1428 NOEs, respectively. NOEs were classified as satisfied in simulations based on the inequality in Equation 3, where r is the distance between a pair of protons, N is the number of frames, and r_UB is either the experimental upper bound restraint distance or 5 Å, whichever is greater.

$$<{\mathrm{r}}^{-6}>\le {\mathrm{r}}_{\mathrm{UB}}$$ Equation 3

Calculation of generalized amide S² order parameters

Experimental order parameters for EnHD were obtained from BMRB entry 15336.⁸¹ Experimental order parameters for RNase H were obtained from the supplemental information of Stafford et al.⁹² MD-derived NH bond order parameters were calculated using the method described by Wong and Daggett using a 250 ps window for EnHD and a 10,000 ps window for RNase H given its ~9.7 ns tumbling time.⁹³ Final order parameters are reported by averaging the results from the three replicate simulations.

Dihedral Angle Principal Component Analysis

Principal component analysis (PCA) is frequently employed to investigate protein dynamics by systematically reducing the dimensionality of complex motions into simpler components.⁹⁴ Here, we used PCA to investigate the dynamics of the Gly-rich loop in RNase H. Although Cartesian coordinates are normally employed in PCA calculations, we chose to use dihedral angle PCA of selected residues to investigate dynamics in the Gly-rich loop region of RNase H using the sine and cosine components of the ϕ and ψ dihedral angles of residues 11–22 as input.

Transition State Identification

The protein folding/unfolding transition states were identified from the high temperature unfolding simulations by using a previously established conformational clustering method.^95–97 Using this method, a pairwise C_α RMSD matrix describes the conformational similarity of all structures in n x n-dimensional space (where n = the number of frames in each simulation). This matrix is then projected into three dimensions such that frames with similar conformations are clustered in the reduced dimensional space. We then choose an ensemble of conformers prior to the onset of a significant conformational change to model the transition state structure.

Transition State Evaluation

To assess how well the putative transition state ensemble chosen from MD simulations agrees with experimental observations, we performed a comparative analysis between MD-derived S values and ϕ-values.⁶ S values, or structure index values, are semi-quantitative equivalents of experimental ϕ-values^98,99 and incorporate secondary and tertiary structure components. S values are defined as S = (S_2°)(S_3°), where S_2° describes the secondary structure component and S_3° describes the tertiary structure component, and provide the fraction of native structure present in the transition state on a per-residue basis. The fraction of native secondary structure, S_2°, for residue i is defined as the fraction of time that the dihedral angles of residues i - 1, i, and i + 1 spend within ± 35° of the values in the X-ray structure. The fraction of native tertiary structure, S_3°, for residue i is defined as the number of tertiary contacts present in the transition state divided by the number of tertiary contacts present in the native state. Tertiary contacts were defined for interactions that heavy atoms in the residue of interest form with others separated by two or more residues. (≤ 5.4 Å for C-C contacts and ≤ 4.6 Å for all others).

Results & Discussion

Native State Sampling

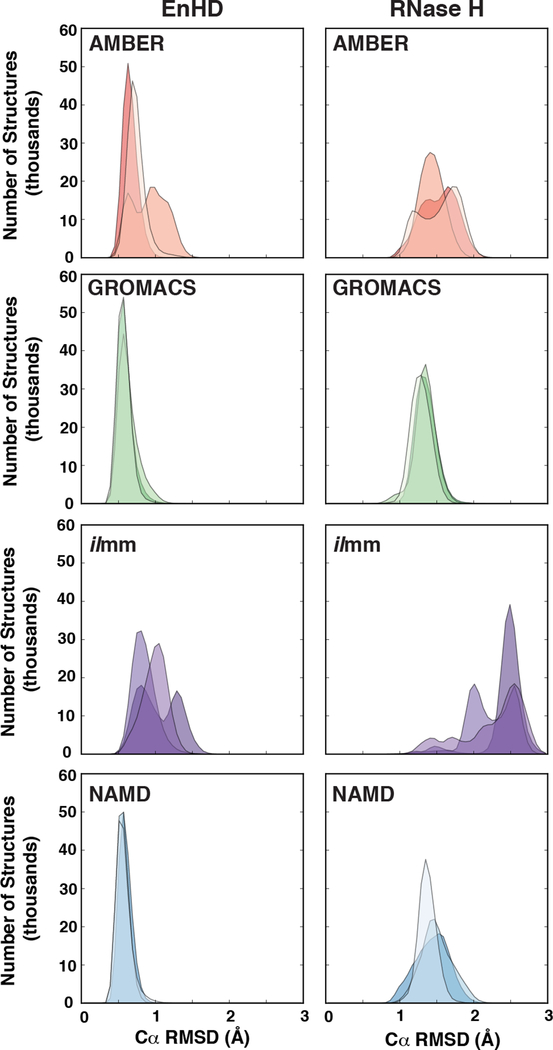
The X-ray and NMR-derived structures deposited in the Protein Data Bank (PDB, www.rcsb.org)¹⁰⁰ are averages over space and time, washing over the subtle and varied excursions from the native state frequently taken by globular proteins in solution.¹⁰¹ One of the chief goals of MD simulations is to explore such excursions beyond the native state. Before comparing the simulations against NMR observables, we first examined their conformational sampling relative to the starting native structures. We calculated the C_α RMSDs and RMSFs for EnHD and RNase H by aligning the core residues to either the starting structure (RMSD) or the average MD-ensemble structure (RMSF). For EnHD, the core residues were 8–53 and for RNase H, the core residues were 5–142 (Figure 1). For both proteins in all force fields, the C_α RMSDs reached stable values by 100 ns (Figure S1). Averaging over all three replicate simulations per MD package, we found that EnHD had average C_α RMSDs ranging from 0.6 Å (GROMACS and NAMD) to 0.8 Å (AMBER) to 1.0 Å (ilmm) and that RNase H had average Cα RMSDs ranging from 1.3 Å (GROMACS) to 1.4 Å (NAMD) to 1.5 Å (AMBER) to 2.4 Å (ilmm) (Figure 2, Table 3). Independent of the protein system, GROMACS and NAMD produced narrow C_α RMSD distributions with little variation between replicate simulations, whereas AMBER and ilmm produced broader distributions with more variation between simulation replicates (Figure 2, Table 3).

Figure 2. The distribution of Cα root mean squared deviations for EnHD and RNase H.

Overlaid histograms of Cα RMSDs were constructed for each of the three replicate simulations of EnHD (left) and RNase H (right) for simulations performed with AMBER (orange), GROMACS (green), ilmm (purple), and NAMD (blue) at 298 K.

Table 3.

Average (± standard deviation) C_α RMSDs for EnHD and RNase H native state simulations. The first 20 ns of each simulation was excluded in this calculation.

	AMBER		GROMACS		ilmm		NAMD
EnHD	Avg. (Å)	St. Dev. (Å)	Avg. (Å)	St. Dev. (Å)	Avg. (Å)	St. Dev. (Å)	Avg. (Å)	St. Dev. (Å)
Run 1	0.67	0.10	0.59	0.11	1.07	0.26	0.60	0.09
Run 2	0.95	0.22	0.64	0.14	0.85	0.16	0.56	0.08
Run 3	0.75	0.13	0.58	0.09	1.01	0.16	0.57	0.10
Ensemble	0.79	0.20	0.61	0.12	0.98	0.22	0.57	0.09
RNase H	Avg. (Å)	St. Dev. (Å)	Avg. (Å)	St. Dev. (Å)	Avg. (Å)	St. Dev. (Å)	Avg. (Å)	St. Dev. (Å)
Run 1	1.57	0.22	1.35	0.14	2.50	0.12	1.44	0.23
Run 2	1.45	0.16	1.37	0.12	2.28	0.26	1.50	0.21
Run 3	1.58	0.24	1.30	0.13	2.35	0.33	1.38	0.12
Ensemble	1.53	0.22	1.34	0.14	2.38	0.27	1.44	0.20

We analyzed the per-residue contributions to the C_α RMSDs and found that for EnHD, all force fields consistently produced some deviation from the native conformation in two regions. The first region was HIII, the C-terminal helix that contains many DNA binding residues. In ilmm and AMBER, HIII frayed at the C-terminus; however, the nature of this local unfolding was force field dependent. In one ilmm simulation, HIII rotated away from the hydrophobic core, exposing W48 to solvent. After sampling this near-native conformation, HIII began to refold (Figure S2). In one AMBER simulation, the C-terminal residues lost helical structure (Figure S2). Partial loss of helical structure was also present for GROMACS and NAMD, but to a lesser extent (Figure S2). The second region with significant deviation from the native conformation was the loop connecting HI and HII. In ilmm, residues 24 and 25 underwent a dihedral transition, reducing the chain length of the HI-HII loop and producing a 1.9 Å C_α RMSD for residue 29. A similar event was observed with AMBER, however, instead of a single flip, multiple residues in the HI-HII loop experienced small dihedral angle shifts, resulting in a 2.7 Å C_α RMSD for residue 29 (Figure S3). The heightened degree of motion is supported by experiment. Stollar et al. found that the HI-HII loop undergoes conformational fluctuations on the μs-ms timescale.¹⁰² These initial displacements seen in MD may be precursors to more significant conformational changes.¹⁰² For RNase H, the major contributions to the RMSD came from 5 different regions of the protein: the Gly-rich loop (residues 11–22), the β₂-β₃ loop (residues 28–30), the α_A-β₄ loop (residue 59–63), the handle region (residues 81–101), and the β₅-α_E loop (residue 121–127) (Figure 1).

We then compared the simulated C_α RMSFs to crystallographic B-factors and found that AMBER and ilmm had substantially lower root-mean-squared error (RMSE) between the simulated and experimental values than GROMACS or NAMD (Table 1). The correlation coefficients were high for all force fields, ranging between 0.82 and 0.87. The lower RMSEs for AMBER and ilmm can be traced to the HII-HIII loop, N-terminal residues, and C-terminal residues (Figure S4). The dynamics in the AMBER and ilmm simulations lead to the lower errors relative to GROMACS and NAMD. Lower correspondence between the B-factors and simulation was observed for RNase H for all MD packages (correlation coefficients all below 0.7), but the associated RMSEs were low (less than 0.3 Å) (Table 2).

Table 1.

Correspondence between simulation and experiment for EnHD

	AMBER		GROMACS		ilmm		NAMD
	Rb	RMSEc	Rb	RMSEc	Rb	RMSEc	Rb	RMSEc
B-factor	0.82	0.65	0.87	1.24	0.83	0.4	0.83	1.1
Cα CSa	0.98	0.83	0.98	0.83	0.96	0.95	0.98	0.75
Cβ CS	0.99	0.66	0.99	0.7	0.99	0.82	0.99	0.71
C CS	0.90	1.69	0.88	1.63	0.91	1.84	0.92	1.57
N CS	0.84	1.02	0.85	1.1	0.82	0.92	0.86	0.86
Hα CS	0.92	0.13	0.92	0.13	0.87	0.17	0.92	0.14
H CS	0.75	0.38	0.77	0.37	0.79	0.35	0.82	0.34
3JHN,Hα	0.68	1.10	0.82	0.70	0.70	0.94	0.83	0.87
S2	0.71	0.13	0.90	0.08	0.78	0.11	0.94	0.07

^a.CS = Chemical shift

^b.R = Pearson’s correlation coefficient

^c.RMSE = root mean squared error

Table 2.

Correspondence between simulation and experiment for RNase H

	AMBER		GROMACS		ilmm		NAMD
	Rb	RMSEc	Rb	RMSEc	Rb	RMSEc	Rb	RMSEc
B-factor	0.67	0.32	0.62	0.38	0.49	0.37	0.68	0.33
Cα CSa	0.98	0.82	0.98	0.78	0.97	1.19	0.99	0.73
N CS	0.92	2.48	0.94	2.32	0.86	3.16	0.93	2.34
Hα CS	0.93	0.26	0.94	0.23	0.86	0.36	0.93	0.25
H CS	0.83	0.42	0.85	0.39	0.77	0.47	0.86	0.37
S2	0.85	0.10	0.90	0.09	0.83	0.11	0.88	0.09

^a.CS = chemical shift

^b.R = Pearson’s correlation coefficient

^c.RMSE = root mean squared error

Comparison with NMR Observables

Next, we assessed the ability of MD simulations to reproduce four types of NMR observables: chemical shifts, nuclear Overhauser effect crosspeaks (NOEs), backbone NH order parameters, and scalar coupling constants.

Chemical Shifts

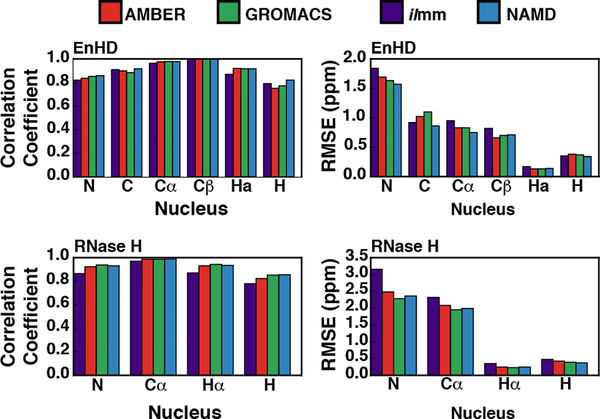
Chemical shifts report on the local electronic environments of distinct nuclei within proteins. We calculated the chemical shifts from our simulations using SHIFTX2.⁷⁹ For the calculation, the first 20 ns of each trajectory was excluded and all three replicate simulations were combined into a single ensemble. To determine the level of sampling required to accurately report chemical shifts, we calculated the chemical shifts for run 1 of RNase H performed with AMBER using 1 ps, 10 ps, and 100 ps granularity and confirmed that subsampling the simulation at 100 ps resulted in predicted shifts that were nearly identical for the same calculation run at full granularity (Figure S5). All the MD packages in this study reproduced chemical shifts with errors comparable to those associated with SHIFTX2 (Figure 3, Figures S6–7, Tables 1–2). For comparison, we also calculated the agreement for the X-ray crystal structures for EnHD and RNase H. Prior to chemical shift calculations, hydrogens were modeled onto the crystal structure using ilmm and the hydrogen atoms were minimized for 1000 steps of steepest descent minimization. For some nuclei, the MD-generated ensembles produced better agreement than the X-ray conformations. For example, the X-ray conformation of K17 in EnHD did not agree well with the experimental data, especially for the N, C_α, H_α, and H_N nuclei (Figure S8). In general, MD ensembles produced chemical shifts more consistent with the experimental data than the X-ray structure alone, particularly for the N and H_N chemical shifts; however, little improvement was observed for C_α shifts (Figure S8). We investigated the origins of this discrepancy and found that K17 had distinct hydrogen bonding patterns within different force fields (Table S1). The rate of formation of a main chain hydrogen bond between K17 (donor) and A14 (acceptor) may modulate the predicted chemical shift for the amide hydrogen of K17 (Table S1). Wagner et al. and others have demonstrated that hydrogen bond geometry can influence the chemical shifts for H_N nuclei and a subtle difference in hydrogen bonding patterns can contribute to enhanced correspondence between MD and experiment.¹⁰³ Additionally, there were a few instances where MD simulations produced worse agreement with the experimental data than the reference X-ray structure. Overall however, all the MD packages produced strong agreement with experimental chemical shifts, exhibited by the high correlation coefficients and low RMSEs (Figure 3, Tables 1–2, Figure S6, S7).

Figure 3. Comparison of the correspondence between MD-derived and experimental chemical shifts.

The correlation coefficients (left column) and RMSEs (right column) for the chemical shift correspondence for EnHD (top row) and RNase H (bottom row) are shown, stratified by nucleus type.

Nuclear Overhauser Effect Crosspeaks

Nuclear Overhauser effect crosspeaks (NOEs) relate to interproton distances and provide significant conformational information. We calculated NOEs from our simulations and stratified the results in two ways. First, we analyzed the percentage satisfaction for NOEs as a function of sequence separation: short-range NOEs refer to NOEs arising from residues i → i + 1, i + 2; medium-range NOEs: i → i + 3, i + 4, i + 5; and long-range NOEs: i → i >i+5. Second, we analyzed the number of NOE violations, stratified by violation distance. For comparison, we also calculated the NOE satisfaction for the EnHD and RNase H crystal structures. For crystal structure analyses, we used the crystal structures containing hydrogens, as described above. For comparison, we also calculated the NOE satisfaction for the EnHD NMR ensemble (PDB ID: 2JWT). For EnHD (654 total NOEs), GROMACS, ilmm, and NAMD ensembles had marginally better agreement with the NOE data (96%, 97%, and 96%, respectively) than the crystal structure alone (95%), while AMBER had marginally worse agreement (94%) (Table S2). Deviations from the level of agreement with the crystal structure were small (< 2%) and there was little variation among replicate simulations. In addition, the total number of NOE violations was small. Across all force fields, the mean number of violations was 28 with an average violation distance of 0.625 Å. The number of severe NOE violations (i.e. those with a violation distance > 2 Å) was also small (AMBER: 2, mean distance = 2.6 Å; GROMACS: 2, mean distance = 2.6 Å; ilmm: 1, mean distance = 2.7 Å; NAMD: 4, mean distance = 3.0 Å); however, there were 12 severe violations in the first NAMD replicate (Table S2). For RNase H (1428 total NOEs), the X-ray structure had marginally better agreement with the experimental NOE data than any MD-generated ensemble (X-ray: 98%, AMBER: 97%, GROMACS: 97%, ilmm; 95%, NAMD: 97%) (Table S3). Again, deviations from the level of agreement with the crystal structure were small (< 3.5%) and there was little variation in the agreement among replicate simulations. Across all force fields, the mean number of violations was 47 with an average violation distance of 0.775 Å. There were a number of severe NOE violations (i.e. those with a violation distance > 2 Å): AMBER: 3, mean distance = 3.5 Å; GROMACS: 2, mean distance = 3.5 Å; ilmm: 5, mean distance = 2.9 Å; NAMD: 4, mean distance = 4.3 Å) (Table S3).

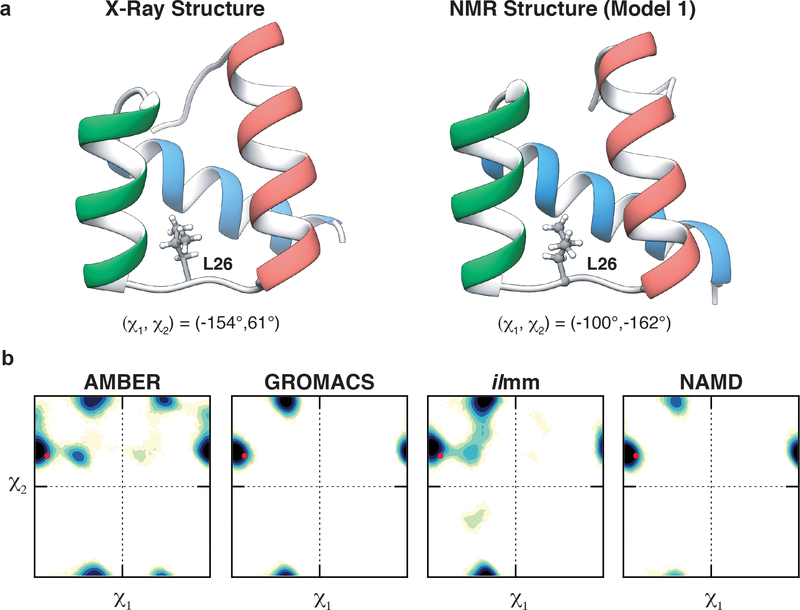
Next, we grouped NOEs by the residues with which they were associated and found that several residues had force field-dependent NOE satisfaction. For example, Leu 26 of EnHD, located in the HI-HII loop, is associated with 50 NOEs: 34 were satisfied by all MD simulations, the X-ray structure, and the NMR ensemble; 1 was never satisfied; and 15 had model-dependent satisfaction (Table S4). Of the 15 NOEs with model-dependent satisfaction, there were 4 NOEs satisfied by the X-ray structure and not the NMR ensemble and 10 satisfied by the NMR ensemble and not the X-ray structure (Table S4). The satisfaction of these NOEs was dependent on the rotameric state of Leu 26, which was in the t, g+ conformation in the X-ray structure and the g-, t conformation in the NMR ensemble (Figure 4). In AMBER, GROMACS, and ilmm, Leu 26 alternated between these two conformations; however, simulations performed with NAMD largely retained the X-ray conformation for Leu 26, populating the t, g+ conformation for 97% of the simulation (Figure 4, Table S5). While no one model satisfied all the NOEs associated with Leu 26, AMBER, GROMACS, and ilmm had better agreement with the NOEs (and on par with the NMR ensemble) than the crystal structure or NAMD. In this instance, rotameric exchange was necessary to satisfy the NOEs that were not present in the crystal structure. The χ₁ torsional potentials for Ile, Leu, Asn, and Asp were modified in the ff99SB-ILDN force field, which we used in the AMBER and GROMACS simulations. The improvements made in this force field likely contributed to the modelling of L26 in the AMBER and GROMACS simulations; however, control simulations employing the ff99SB force field were not performed, so the degree of improvement cannot be quantified here. Although we found that 3 of the 4 MD packages had better agreement than the crystal structure with respect to the solution behavior of L26, we cannot say which MD-generated ensemble best agreed with the ‘true’ behavior of L26 in solution. We found that the force fields/packages had variable populations and lifetimes of the two primary rotamer conformations (Tables S5, S6). Furthermore, the HI-HII loop undergoes conformational exchange on the μs-ms timescale, indicating that the MD simulations may not have captured the full extent of dynamics associated with the side chain of this residue.¹⁰²

Figure 4. Conformational heterogeneity in Leu 26.

(a) Leu 26 occupies distinct rotameric conformations in the X-ray structure and NMR ensemble of EnHD. In the X-ray crystal structure (left), L26 occupies the t, g+ conformation while it occupies the g-, t conformation in the NMR ensemble (right). (b) Side chain χ₁ / χ₂ dihedral angle maps for the different MD packages. The red point denotes the conformation of L26 in the X-ray structure.

Scalar Coupling Constants

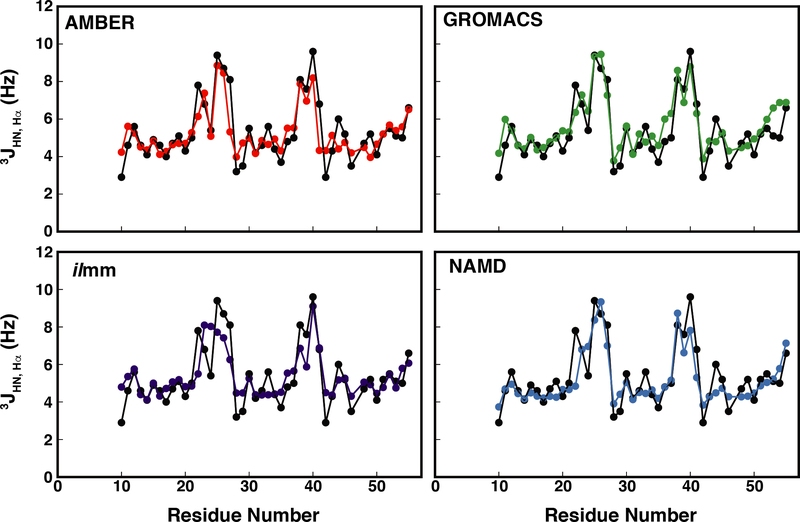
Scalar coupling constants can be related to various dihedral angles via the Karplus relation (Equation 2). Here we calculated the ³J_HN,Hα coupling constants, which are related to the ϕ dihedral angle, using seven different parameter sets obtained from the literature for the Karplus equation.^85–91 Table S7 shows that the choice of Karplus parameters affects the level of agreement between simulation and experiment, with the Schmidt et al. and Smith et al. parameter sets consistently producing higher RMSEs. Overall, the Habeck parameter set, which was derived by applying Bayesian regression models to high-resolution data from ubiquitin, produced the best agreement, with correlation coefficients ranging from 0.80 to 0.89 and RMSDs ranging from 0.8 Hz to 0.98 Hz (Table S7, Figure 5). While most residues had excellent agreement with the experimental data, some residues, such as E22, had poor agreement independent of force field or parameter set, and some residues, such as N41, had force-field dependent agreement (Figure S9). The N41 coupling constant was not described well in the X-ray structure, the AMBER ensemble, or the NAMD ensemble; however, both ilmm and GROMACS-derived ensembles had excellent agreement (ilmm error: 0.04 Hz, GROMACS error: 0.5 Hz). In all MD-generated ensembles, N41 sampled two regions of Ramachandran space: one located in the P_IIL basin and one located on the boundary between the β and P_IIL basins (Figure S9). The ratio of sampling in these two regions dictated the ensemble-averaged value for ϕ and, in turn, the coupling constant. Upon further analysis, we found that, structurally, N41 functions as a dynamic helix cap, with both the backbone carbonyl and side chain carboxamide group forming multiple hydrogen bonds with the N-terminal residues of HIII (Figure S9, Table S8). These data suggest that force-field specific hydrogen bonding patterns for N41 may have contributed to the level of agreement with experimental data; however, it is also possible that intrinsic ϕ/ψ preferences for individual amino acids, which are known to be force-field dependent,¹⁰⁴ may have also influenced the agreement for N41. Ultimately, however, it is not possible to assess which MD-generated ensemble produced the best prediction for in-solution behavior, as numerous ϕ/ψ distributions can yield ensembles that satisfy the experimental data. The difficulties in evaluating simulated and experimental coupling constants are exacerbated by the fact that 2–4 ϕ values map to a single coupling constant and use of the Karplus relation itself can introduce error in the form of the three coefficients.

Figure 5. MD simulations reproduce experimentally determined ³J_HN,Hα coupling constants for EnHD.

Simulated vs experimental coupling constants are plotted as a function of residue number. Here, the Habeck et al. parameters have been used.

S² Generalized Order Parameters

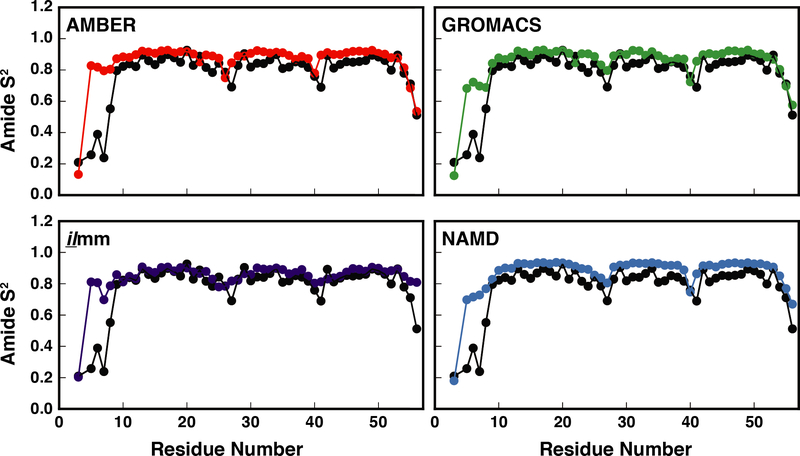
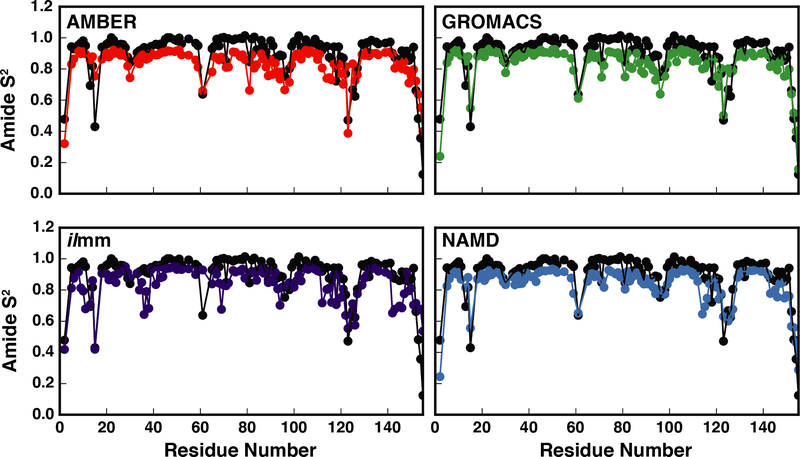
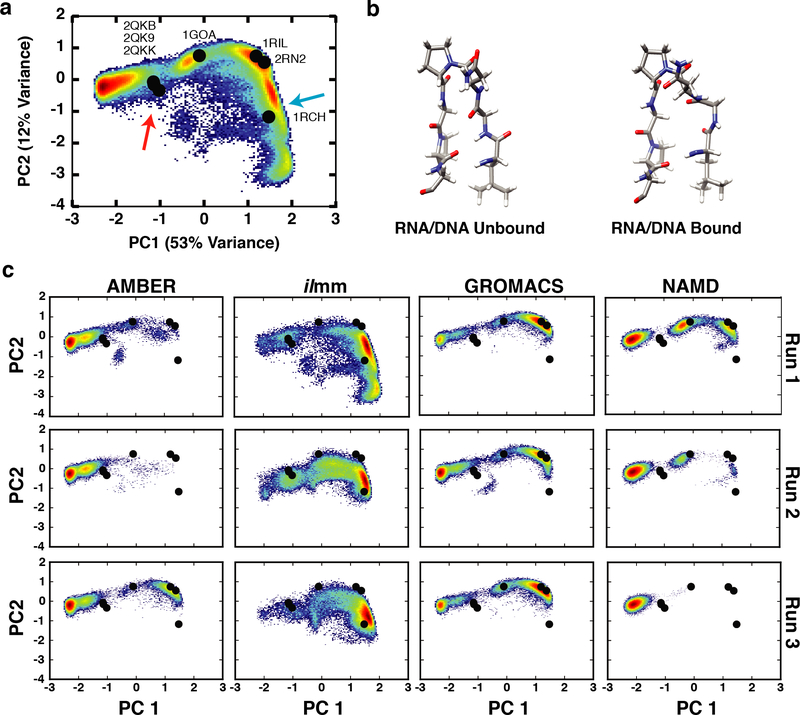
NMR-derived generalized S² order parameters of NH groups report on the local extent of motion of the polypeptide chains. We calculated the backbone order parameters for EnHD and RNase H separately for each simulation and the reported values were averaged over the three replicates. For EnHD, there was good correspondence between the simulated and experimental values, with correlation coefficients ranging from 0.71 – 0.94 and RMSEs ranging from 0.7 – 1.3 (Figure 6, Table 1). Across all force fields, the N-terminal residues and turns had the greatest error. Furthermore, although ilmm had above-average errors for N-terminal residues, it produced better agreement for helical residues, particularly residues 10–14 and 48–51. (Figure 6, Figure S10) There was also good correspondence between simulation and experiment for RNase H (Table 2, Figure 7). The level of agreement for Gly 15 was force field dependent, with ilmm producing the best agreement (Figure 7, Figure S11). Gly 15 is within the Gly-rich loop, which, along with the β₅α_E loop, coordinates the DNA/RNA hybrid prior to catalysis. We performed dPCA to explore the conformational distributions of the Gly-rich loop. Our analysis was aided by multiple X-ray and NMR structures of RNase H and several homologues. The following structures were included in our analysis: RNase H from E. coli (X-ray, PDB ID: 2RN2), RNase H from E. coli (NMR, PDB ID: 1RCH), RNase H from Thermus thermophilus (X-ray, PDB ID: 1RIL), a stabilized RNase H variant from E. coli (X-ray, PDB ID: 1GOA), and two structures of RNase H D210N from Homo sapiens in complex with DNA/RNA hybrids (X-ray, PDB ID: 2QKB, in complex with a 20-mer DNA/RNA hybrid; X-ray, PDB ID: 2QKK, in complex with a 14-mer DNA/RNA hybrid). The first two principal components described 53% and 12% of the variance within the dataset and Gly15 had strong weights. There were several highly populated regions in PC space (Figure 8). Of these, one corresponded to the unbound conformation of the Gly-rich loop observed in solution (denoted by a blue arrow in Figure 8) and another corresponded to the bound conformation of the loop observed in solution (denoted by the red arrow in Figure 8). Figure 8c breaks down the sampling of PC space by force field and simulation number. Visualization of the PC maps shows that ilmm was the only force field / MD package that sampled both the bound and unbound conformations; furthermore, the unbound solution conformations were the dominant conformers sampled by ilmm. In contrast, the remaining force fields primarily sampled the X-ray conformation and another region that was not observed in the experimental data (far left of Figure 8). Moreover, even with 600 ns of aggregate simulation time, AMBER, GROMACS, and NAMD were unable to achieve the level of sampling seen in ilmm with 300 ns of aggregate simulation time (i.e. ilmm reached this degree of sampling in < 100 ns). While there are dramatic differences in the sampling, there is a limit to the extent to which we can determine the level of agreement between simulation and experiment, as the number, distribution, and interconversion rates of Gly-rich loop conformations cannot be derived from static structures alone.

Figure 6. Correspondence between experimental and MD-derived order parameters for EnHD.

The experimental (black points) and MD-derived order parameters (red points – AMBER, purple points – ilmm, green points – GROMACS, and blue points – NAMD) are plotted as a function of residue number for EnHD. Excellent correspondence was observed for all force fields except at the N-terminus. A larger number of simulations or significantly longer simulations are required for MD to reproduce the order parameters for highly flexible terminal residues that may become trapped in local minima.

Figure 7. Correspondence between experimental and MD-derived order parameters for RNase H.

The experimental (black points) and MD-derived order parameters (red points – AMBER, purple points – ilmm, green points – GROMACS, and blue points – NAMD) are plotted as a function of residue number for RNase H.

Figure 8. Conformational heterogeneity in the Gly-rich loop.

(a) The dPCA landscape for the residues in the Gly-rich loop, constructed using conformations aggregated from the experimental reference structures and MD simulations, maps the conformational heterogeneity in the Gly-rich loop. Black points denote the location of RNase H reference structures (2RN2, 1RIL, 1RCH, 1GOA, 2QKB, 2QK9, and 2QKK) within the dPCA landscape. The blue arrow denotes the region corresponding to the unbound conformation of the Gly-rich loop in solution (b, left). The red arrow denotes the region corresponding to the DNA/RNA bound conformation of the Gly-rich loop in solution (b, right). (c) Conformations sampled by the Gly-rich loop in MD simulations.

Global Comparison with NMR Observables

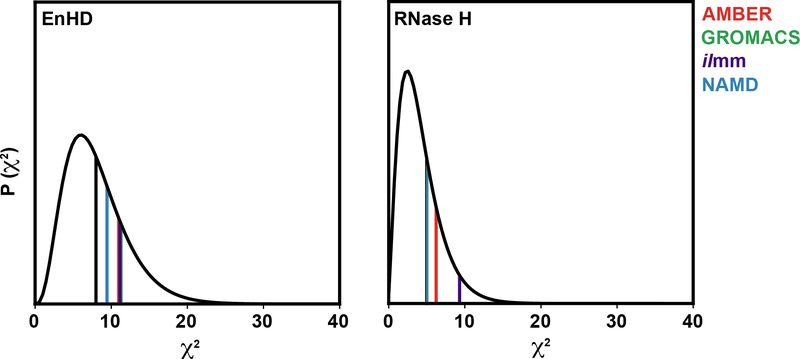
To assess the overall agreement of the modeled dynamics with experimental observables, we calculated the χ² statistic using the method of Panelopulos et al.¹⁰⁵ χ² was calculated using Equation 4, where N is the total number of types experimental observables, rmsd^{MD, Experiment} is the RMSD between MD and experiment for a set of observables, and σ is the error associated with each individual measurement. Prior to calculation of the χ² statistic, we excluded data for residues that were poorly modeled in at least 3 of the 4 force field/software package sets. Data were excluded on a per-protein, per-data-type basis. Residues were considered poorly modeled if the absolute value of the difference between the experimental and MD derived values was greater than a data-type specific cutoff. The cutoffs were set as twice the mean of the absolute value of the difference between the experimental and MD derived values for all data points. (Figure S12) The data associated with EnHD were organized into 8 types of observables: N chemical shifts, C_α chemical shifts, C_β chemical shifts, C’ chemical shifts, H_α chemical shifts, H_N chemical shifts, ³J_HN,Hα coupling constants, and backbone NH order parameters. The data associated with RNase H were organized into 5 types of observables: N chemical shifts, C_α chemical shifts, H_α chemical shifts, H_N chemical shifts, and backbone NH order parameters. A value of 0.78 was used for the error associated with the coupling constants, as determined by Beauchamp et al.¹⁰⁶ A value of 0.1 was used for the error associated with the backbone NH order parameters. Nucleus-specific errors were used for the chemical shift data, based on the rms errors calculated for SHIFTX2: 0.44 ppm (C_α), 0.52 ppm (C_β), 0.53 ppm (C), 0.12 ppm (H_α), 0.17 ppm (H_N), and 1.12 ppm (N). In the case of RNase H, the expected rms error for SHIFTX2 versus the chemical shifts in the RefDB⁸³ entry for 2RN2 were used for N, C_α, H_α, and H_N chemical shifts (1.48, 0.79, 0.14, and 0.30 ppm respectively). For EnHD and RNase H, the χ² values fell within the expected distribution (Figure 9, Table S9).

Figure 9. Global correspondence between simulation and experiment as assessed by the χ² statistic.

Each plot shows the χ² distribution (black curves) for the degrees of freedom associated with each comparison (8 degrees of freedom for EnHD, left; 5 degrees of freedom for RNase H, right). The vertical lines denote the χ² value calculated for each force-field/software package combination (AMBER, red; GROMACS, green; ilmm, purple; NAMD, blue) as well as the expectation value for that distribution (black).

$${\chi }^2={\sum }_{i=1}^N\frac{{\left(rms{d}_i^{MD,Experiment}\right)}^2}{{\sigma }_i^2}$$ Equation 4

High Temperature Unfolding

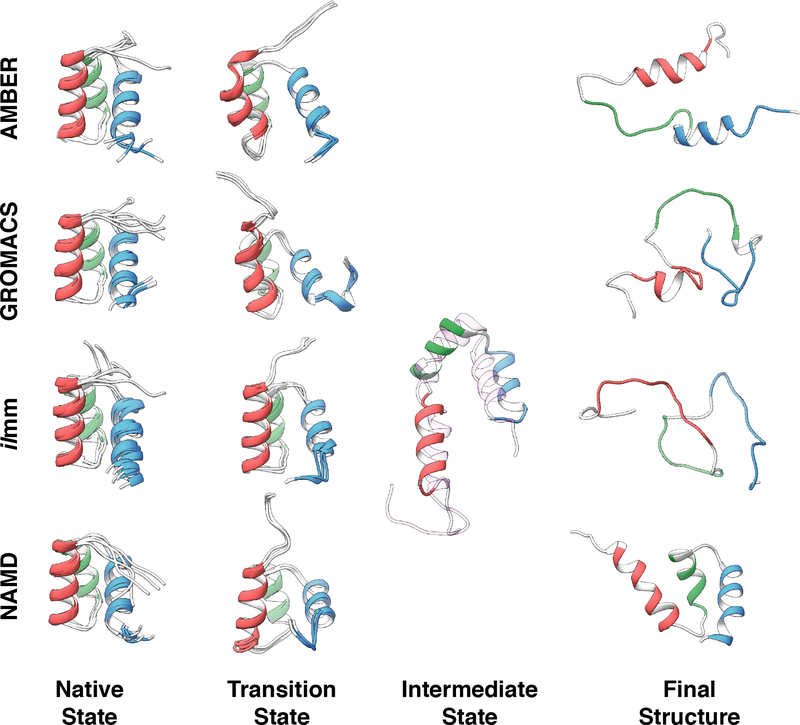
High temperature simulations have been used to probe protein folding/unfolding pathways^6,7 and to aid in the design of thermostable protein variants.⁴ In prior studies, putative protein (un)folding transition states have been identified from high temperature simulations for multiple proteins including EnHD,¹⁰⁷ c-Myb,¹⁰⁷ chymotrypsin inhibitor 2,⁶ and barnase^7,97 and others. We evaluated the ability of the different MD packages and force fields to model known components of the (un)folding pathway of EnHD. First, we evaluated the sampling of the transition state of protein (un)folding by comparing MD-derived S-values to experimentally derived ϕ-values.¹⁰⁷ The ϕ- and S-values reflect the degree of structure present in the transition state along the sequence. The S-values were calculated for the putative transition state ensembles identified via conformational clustering (Figure S13), and the averages over the 3 replicates showed decent agreement with the experimentally derived ϕ-values for ilmm (R = 0.70) and moderate correspondence for AMBER (R = 0.48), GROMACS (R = 0.50) and NAMD (R = 0.35) (Table S10). Next, we examined whether any of the unfolding simulations sampled the known EnHD folding intermediate, the structure of which was first predicted computationally in 2000^108,109 and later confirmed by NMR in 2005.¹¹⁰ This intermediate structure was observed in simulations performed with ilmm, but not AMBER, GROMACS or NAMD. Finally, we examined whether the unfolding simulations sampled the denatured state after 10 ns at high temperature. Simulations performed with GROMACS and ilmm sampled highly denatured states, followed by AMBER, whereas simulations performed with NAMD retained significant native-like structure over the course of the simulation (Figure 10). The unfolding pathway of EnHD was strongly dependent on the choice of force field and simulation software. Only one force field/software combination, ilmm with the Levitt et al. force field, sampled transition state, intermediate state, denatured state structures, and kinetics of unfolding consistent with the experimental results for this system.^108–110 While GROMACS sampled somewhat appropriate transition state-like conformations, significant helical structure was lost after passing through the transition state, resulting in increased sampling of denatured state conformers but without sampling the obligatory intermediate structures.^109,110 NAMD also sampled transition-state like conformations, but in contrast to GROMACS, the protein never unfolded, preventing sampling of the intermediate and denatured states over the course of the simulations (Figure 10).

Figure 10. Survey of conformations populated during high temperature unfolding of EnHD.

Native state: Five snapshots, extracted from simulation one of the 298 K simulations at 0 ns, 50 ns, 100 ns, 150 ns, and 200 ns, serve as a visual reference of native state sampling. Transition state: For each of the four MD packages, the transition state is represented by three overlaid structures extracted from the simulation that best modeled the experimentally determined transition state. Intermediate state: One intermediate state structure was extracted from the ilmm simulation that best modeled the experimentally determined intermediate state. Model 1 of the experimentally determined intermediate state structure is shown as a transparent ribbon and aligned against the MD-derived intermediate structure. Final structure: To represent the extent of unfolding that occurred during high temperature MD, the most-disrupted final structures from the 498 K replicates are shown.

Summary and Outlook

The ultimate objective of MD simulations is to visualize dynamic behaviors and structural conformations that cannot be described by experimentally derived structures alone. Usually, the inability of MD simulations to produce conformational ensembles that are consistent with experiment is blamed on the force field. However, the force field is not the sole determinant of MD-simulated behavior or accuracy; if it were, the results from the simulations performed with GROMACS and AMBER would be more similar, as the same force field was used with both packages. To this end, we encourage authors of MD studies to include the standard input files used to model and perform any published simulations. This will facilitate meta-analyses and discussions of the impact of MD software-specific parameters on modeled behavior. Given the differences that we observed, ongoing and future validation efforts must account for both the force field parameterizations as well as the methods and approximations used to propagate systems in time without conflating the two. This includes approximations that may introduce artificial periodicity, such as PME (ref. 76 and references therein), or overly constrain the simulated systems, such as LINCS and SHAKE. In addition, the choice of simulation ensemble can play a role in the dynamics, as suggested by the inability of AMBER, GROMACS and NAMD to reproduce the known unfolding behavior of EnHD. We believe that the improved ability of ilmm to sample conformational intermediates lies in the flexibility and conformational changes that are made possible when such approximations are not allowed to constrain or impede molecular motions. In addition, the force fields use different force constants on the dihedral angles; the Levitt et al., force field uses a value of 0 for the barrier to readily allow conformational transitions subject to steric and electrostatic interactions. AMBER and CHARMM force fields use values of 1.13/1.88 kcal/mole and 1.36/1.46 kcal/mole for Φ/Ψ, respectively. These barriers, while relatively small, may also aid in retention of the starting structure such that native states are well maintained, and unfolding, even at high temperature is discouraged. Another possibility lies in the use of microcanonical ensemble in ilmm, which allows for Boltzmann sampling of an isoenergetic surface of the conformational landscape over continuous reaction pathways without frequent scaling of the velocities, which dampen motion.

In cases where dynamic behavior is required, restricted sampling results in worse agreement with experimental data that reflect protein dynamics in solution. We observed several instances of this in our simulations, particularly with NAMD. For example, simulations of EnHD performed with NAMD had the lowest C_α RMSDs relative to the crystal structure, but they were unable to recover NOEs associated with Leu 26 that were satisfied by the other MD packages. In addition, the coupling constant for N41 as predicted by NAMD was nearly identical to the value present in the X-ray structure. However, the X-ray structure is not in agreement with the solution behavior of N41, and ilmm, GROMACS and AMBER (both using the same protein force field but different TIP4P-EW and TIP3P water models, respectively) showed improved agreement with experiment. Finally, after 10 ns of simulation at 498 K, NAMD (using the CHARMM36 force field and TIP3P water model) was unable to produce significantly denatured structures comparable to those produced by the other MD packages and instead all three helices remained intact and packed. This highlights a more general issue. Many force field/MD packages have been developed to maintain the conformation of the starting crystal structure by attenuating or impeding dynamics in a variety of ways, and this is generally viewed as desirable. However, this becomes problematic if one is interested in characterizing larger scale native protein dynamics or protein unfolding.

Another crucial component to improving MD software is to establish more complex means of comparing experimental and computational results in a systematic and quantitative fashion. As we have shown here, when observables were evaluated at a coarse level of detail, these MD packages showed similar agreement with experiment with respect to the native state. However, when individual residues were examined in detail, significant differences were observed in native dynamics. A prominent difference was the behavior of L26 in EnHD. While three of the four MD packages recovered many NOEs missing from the crystal structure, the underlying dynamics of L26 (i.e. the populations and lifetimes of different rotameric states) varied significantly. This observation highlights not the shortcomings of MD, but the limitations of the data used to assess the computational results. That is, the available experimental data for L26, for example, are unable to identify which MD package best models the L26 dynamics. Recent studies examining different force fields (AMBER, CHARMM, and OPLS) and their ability to correctly model the strength of salt bridges¹¹¹ and main chain propensities¹¹² in simple model systems highlight how consideration of detailed interactions and behavior reveals dramatic differences between these force fields / MD packages. More broadly, however, the experimental data presented here are unable to distinguish, with high confidence, which MD-generated ensemble best approximates native protein behavior in solution. Starker differences were seen for protein unfolding, in which case only one of the four MD packages produced unfolding trajectories consistent with experiment. Moving forward, access to the underlying distributions that give rise to the experimental observables will be necessary to improve the quality of MD and to better detect when a simulation does or does not appropriately model protein dynamics.

The results presented here, along with other recent force field validation efforts, show that contemporary force fields produce models that are in similar agreement with experimental results. Additionally, these results show that certain force fields agree better with certain observables than others. Considering these results, it is not possible to prescribe a ‘best’ model; instead, models should be selected based on the information sought. For example, simulations of intrinsically disordered proteins typically require significant alterations to model parameters to obtain accurate results, here is a case where it is undesirable to constrain conformational sampling. Along those lines, additional conformational sampling, obtained through longer or more numerous conventional MD simulations, may aid in the identification of an ‘optimal’ model, but it is not guaranteed to do so. Pantelopulos et al. found that longer simulation times yielded better agreement with experiment, independent of the force field chosen.¹⁰⁷ In an evaluation of order parameter agreement, Bowman found that a larger aggregate sampling time yielded better agreement for side chain methyl group order parameters, but essentially no change in the level of agreement for backbone order parameters.¹¹³ That study also concluded that the aggregate simulation time and method used to calculate observables affected the level of agreement more than the force field.¹¹³ However, these comparison were all between MD packages that constrain motion, and here we found that flexible molecular representations and simulation protocols that do not artificially restrain motion provide greater sampling of conformational space in shorter periods of time. Nonetheless, increased conformational sampling, whether obtained through longer or more numerous simulations or choice of MD/FF package, should facilitate model selection in cases where the data clearly indicate that observation of the dynamics across longer timescales is necessary.

Conclusions

Our results show that the MD programs and force fields studied here show comparable agreement overall with experimental data for the native state. However, we observed instances where the MD packages generated distinct conformational ensembles that agreed equally well with the experimental data. This underscores the fact that agreement with experimental data is necessary, but not sufficient, to validate atomistic simulations. The four MD package/force field combinations unquestionably produced distinct ensembles. For example, hydrogen bond networks, including both the residues engaged in the networks as well as the frequency of different interactions, were variable across the MD packages. While these differences in dynamics may be small in magnitude, such dynamic modes form the background over which more extensive conformational changes occur. Ultimately, quantitative comparisons between such rapid, small amplitude motions and experimental data should enhance our ability to isolate the ‘True’ ensembles present in solution.