Load-dependent detachment kinetics play a key role in bidirectional cargo transport by kinesin and dynein

Abstract

Bidirectional cargo transport along microtubules is carried out by opposing teams of kinesin and dynein motors. Despite considerable study, the factors that determine whether these competing teams achieve net anterograde or retrograde transport in cells remain unclear. The goal of this work is to use stochastic simulations of bidirectional transport to determine the motor properties that most strongly determine overall cargo velocity and directionality. Simulations were carried out based on published optical tweezer characterization of kinesin-1 and kinesin-2, and for available data for cytoplasmic dynein and the dynein-dynactin-BicD2 (DDB) complex. By varying dynein parameters and analyzing cargo trajectories, we find that net cargo transport is predicted to depend minimally on the dynein stall force, but strongly on dynein load-dependent detachment kinetics. In simulations, dynein is dominated by kinesin-1, but DDB and kinesin-1 are evenly matched, recapitulating recent experimental work. Kinesin-2 competes less well against dynein and DDB, and overall, load-dependent motor detachment is the property that most determines a motor’s ability to compete in bidirectional transport. It follows that the most effective intracellular regulators of bidirectional transport are predicted to be those that alter motor detachment kinetics rather than motor velocity or stall force.

Introduction:

In neurons, vesicles and organelles are transported by teams of opposed kinesin and dynein motors that direct cargo out toward the cell periphery and back toward the cell center ^1–3. At the molecular level, in vitro single-molecule investigations and transient kinetics assays have generated a solid framework for understanding the fundamental principles underlying kinesin and dynein mechanochemistry ^4,5. And at the cell and organismal level, studies of intracellular transport in cultured cells and in vivo live imaging studies have characterized vesicle and organelle transport dynamics in both wild-type and mutant backgrounds, identifying many proteins responsible for carrying out and regulating these processes ³. However, there exists a gap between our mechanistic understanding of motors, adapters, and regulatory proteins at the molecular level and our ability to predict how specific perturbations at the cellular level alter bidirectional transport dynamics in disease states such as neurodegenerative diseases and ciliopathies. A fuller understanding of bidirectional transport requires bridging the gap between molecules and cells by understanding how teams of motors coordinate and compete to achieve net anterograde or retrograde transport.

A number of mean-field and stochastic models of bidirectional transport have been developed and used to investigate the influence of motor numbers, parameters, and coupling geometries on the resulting transport dynamics ^6–11. The dominant model in the field is the tug-of-war model, in which the direction of net transport is determined by one population of motors overpowering the opposing population. The present work is motivated by recent high resolution optical tweezer experiments on kinesin-2 and activated dynein that have uncovered new mechanochemical properties of these motors. Recent work on the kinesin-2 motor KIF3A/B showed that, even though the stall force matches that of kinesin-1, the motor detachment rate is strongly sensitive on applied load, which predicts its bidirectional transport abilities will be diminished ^12–14. Recent work on mammalian dynein showed that when complexed with dynactin and the activator BicD2 (termed a DDB complex), both the unloaded run length and the stall force are increased substantially ^15–18. These results suggest that activated dynein will compete much more effectively against kinesins than dynein alone and that previous modeling efforts that incorporated the ~1 pN stall force of isolated dynein may not represent the properties of activated dynein found in cells ^6,7,9.

The goal of the present work is to quantitatively examine how changes in kinesin and dynein stall forces and load-dependent detachment kinetics alter the predicted velocity and directionality of cargo transported by teams of kinesin and dynein motors. We take the approach of using a relatively simple modeling framework and incorporate the nearly complete single-molecule characterization of kinesin-1 and kinesin-2 to investigate the predicted net speed and directionality of cargo driven by kinesin and dynein motors. We find that net cargo transport depends only minimally on the dynein stall force, but is strongly dependent on the dynein load-dependent detachment kinetics. As predicted from single-molecule experiments, kinesin-1 dominates dynein during bidirectional transport, whereas kinesin-2 competes poorly with dynein. We simulated activated dynein using experimental DDB parameters and found that DDB competes on equal footing with kinesin-1, matching experimental results, and DDB dominates kinesin-2. This work highlights specific directions for future experimental work, and provides quantitative predictions that can be tested using in vitro and in vivo model systems.

Results:

Single motor simulations recapitulate experimental optical tweezer experiments

To investigate cargo transport by kinesin-1, kinesin-2, and cytoplasmic dynein, we first developed stochastic stepping models for each motor based on published single-motor optical tweezer experiments (Table 1) ^9,12,19–26. Motor behavior was defined by load-dependent rate constants for forward stepping, backward stepping, and detachment, and a load-independent motor reattachment rate (Fig. 1). The Gillespie Stochastic Simulation Algorithm (see Methods) was used to simulate single-motor stepping, such that at each time point, each motor can step forward, step backward, or detach, with the probability of each being proportional to their respective first-order rate constants (Table 2). Simulated single-molecule behaviors for kinesin-1 and kinesin-2, shown in Fig. 2 A and B, match experimental results from Andreasson et al that showed that kinesin-2 has a similar stall force, more gradual force-velocity curve, and greater sensitivity of detachment to load than kinesin-1 ^12,19.

Table 1:

Published in vitro motor properties

Dynein or Dynein/Dynactin
Reference	Vel (nm/s)	RL (nm)	koff (1/s)	Fs (pN)
Kunwar et al., 2011 9	-	431		1.25
Belyy et al., 2016a17	76/(49–257)	-	-	2.0
Schlager et al., 2014 16	399	1300	0.31	-
Ross et al., 2006 33	1200	880	1.4	-
King et al., 2000b34	700/700	700/1500	1.0/0.47
Ori-McKenney et al., 2010 35	750	339	2.2	1.4
Mallik et al., 2005c36	213/312	738/450	0.29/0.69	1.0
McKenney et al., 2014 15	89
Consensus dynein (Fig. 2–4)	212	212	1	1.25
Dynein sensitivity analysis (Fig. 5)	500	1000	0.5	1
Dynein-Dynactin-BicD2 (DDB)
Reference	Vel (nm/s)	RL (nm)	koff (1/s)	Fs (pN)
Schlager et al., 2014 16	499	5000	0.1	-
Belyy et al., 2016 17	513	-		4.3
McKenney et al., 2014 15	379	8840	0.04
Gutierrez et al., 2017 18	479/933
Olenic et al., 2016 37	637	1531	0.42
Urnavicius et al., 2018 38	860	5200	0.16	3.6
Consensus DDB (Fig. 6)	500	5000	0.1	4
Kinesin-1
Andreasson et al., 2015 12	764	1203	0.66	8
Kinesin-2
Andreasson et al., 2015 12	511	380	1.41	8

Notes:

^aSingle motors/(range with different bead sizes)

^bDynein/Dynein-dynactin

^cRun/Minus-end-segment

Figure 1: Stochastic model of bidirectional cargo transport.

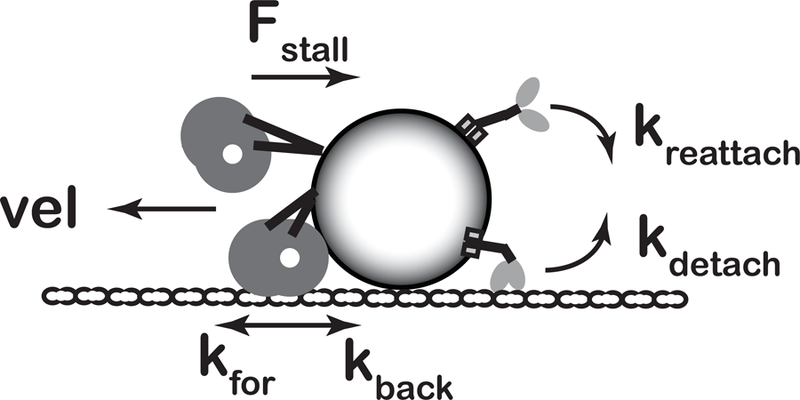
Kinesin and dynein motors are attached to a shared cargo and motor stepping and detachment/reattachment modeled using published parameters. Single-molecule forward and backward stepping rates, k_for and k_back, depend on load, and motor velocity is equal to the net stepping rate multiplied by the 8 nm step size. The stall force, F_stall, is defined as the force at which k_for = k_back and thus velocity is zero. Motor detachment is modeled as a slip-bond with an exponential dependence on load, $k_{det}\left(F\right)=k_{det}^0{e}^{\frac{F}{F_{det}}}$, where k⁰_det is the unloaded off-rate and F_det is the detachment force parameter. Motors that detach from the microtubule reattach with first-order on-rate, k_reattach. At every time step, each motor can step forward or backward, or detach or reattach from the microtubule. See Methods for model details and parameters.

Table 2:

List of parameters used in simulations.

Parameter	Kinesin-1	Kinesin-2	Dynein	DDB	Reference
k2 (s−1)	2753	1469			12
k3 (s−1)	99	66.8			12
δ (nm)	3.6	2.25			12
Fs (pN)	8	8	1.25	4.3	9,12,17
kfor0 (s−1)			35.3	83.3	9,17,36
kback (s−1)a	0.34*F	0.71*F	8.8	20.8	12,24,26
L0 hindering (nm)	1203	380/182b			12,52
δL hindering (nm)	2.3	4.7/1.7 b			12,52
L0 assisting (nm)	87				32,52
δL assisting (nm)	0.27				32,52
kdet0 (s−1)	0.66c	1.41c/15d	1	0.1	9,12,15–17,32
Fdet (pN)		2.0d	0.87	2 pNe	9,12,17,32
kattach (s−1)	5	5	5	5	6,53
ks (pN/nm)	0.3	0.3	0.065	0.065	54,55

Notes:

^aKinesin backstepping rates vary linearly with hindering load; dynein backstepping rates are independent of load. For all motors, backstepping rates are set to zero for assisting loads. Dynein backstepping rates are chosen to achieve a 25% zero-load backstepping frequency ^24,26

^bFirst value is up to 1 pN hindering, second value is above 1 pN assisting load.

^cCalculated by dividing unloaded velocity by unloaded run length.

^dk_det⁰ and F_det in assisting load direction for kinesin-2.

^eF_det for DDB was chosen empirically to optimize net kinesin-1-DDB cargo velocity

Figure 2: Single-motor characteristics of kinesin and dynein.

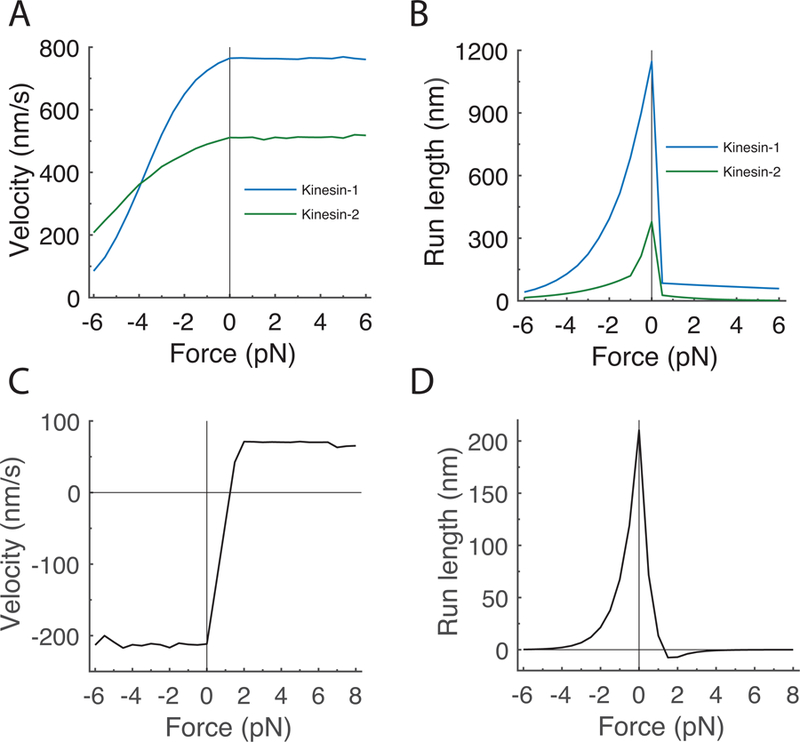
A and B: Simulated force-velocity (A) and force-run length (B) curves for kinesin-1 and kinesin-2, with motor parameters taken from published work ^12,19. C and D: Corresponding curves for dynein using stall force of 1.25 pN of dynein ^22,28–30. Experimental constraints and specific motor parameters are given in Table 1 and 2, respectively.

In contrast to kinesin, a consensus set of parameters describing mammalian dynein stepping do not yet exist in the literature. Although a body of single-molecule data exist for yeast dynein ^24–27, mammalian dynein moves faster and has a smaller stall force ^{9,22,23,28,29}. Mammalian dynein stall forces are in the range of 1 pN ^22,28–30, whereas activated dynein-dynactin-BicD2 (DDB) complexes have stall forces of 4.3 pN and long processive run lengths ¹⁷. Table 1 presents a list of reported run lengths for isolated dynein or dynein/dynactin, and for the activated dynein-dynactin-BicD2 (DDB) complex. Our initial simulations focused on dynein alone, and modeled dynein with a linear force-velocity curve and exponential dependence of detachment on load, as follows:

$$k_{off}\left(F\right)=k_{off}^0{e}^{\frac{F}{F_{det}}}$$

Here k_off(F) is the first-order motor detachment rate under load F, k_off⁰ is the detachment rate in the absence of load, and F_det is the detachment force parameter, defined as the force at which the off-rate is increased by e-fold. This form is exactly equivalent to the Bell model, with $F_{det}=\frac{k_{B}T}{\delta }$, where δ is a distance parameter and k_BT is Boltzman’s constant times absolute temperature ^31,32. We chose a consensus set of parameters for dynein alone (Table 2), based around an unloaded velocity of 212 nm/s and an unloaded off-rate of 1 s⁻¹ (parameter sensitivity is considered below). Dynein stepping dynamics under load were simulated, and the dynein force-velocity and force-run length relationships are shown in Fig. 2C and D.

Kinesin-1 and kinesin-2 compete differently with dynein in a stochastic tug of war

To predict intracellular cargo movement driven by teams of kinesin and dynein motors, simulations were carried out with varying numbers of kinesin and dynein motors attached to a common cargo. All motors were initially bound to the microtubule track, and motors stochastically stepped along the microtubule, detaching and reattaching, with the kinetics governed by load-dependent rate constants. Each motor was linked to the cargo through a Hookean spring, and at each reaction time the cargo position was adjusted to achieve zero net force on the cargo. The resulting cargo position traces showed bidirectional behavior with episodes of unidirectional plus-end-movement driven by kinesin only, minus-end movement driven by dynein only, and mixed movements driven by simultaneous engagement of both motors (Fig. 3A-D). Because of the unique properties of each motor type, different pairings of motor type had different characteristics. Cargo carried by one kinesin-1 and one dynein moved persistently toward the microtubule plus-end, with a velocity near the unloaded kinesin-1 velocity (Fig. 3A). Upon closer inspection, it can be seen that periods when only kinesin-1 was attached dominate, meaning that dynein modeled using these parameters readily detaches during tug-of-war episodes. In contrast, simulations with one kinesin-2 and one dynein showed more bidirectional behavior with both plus- and minus-end runs but still with a consistent plus-end net directionality (Fig. 3C). To achieve net transport rates near zero, 11 dyneins were necessary to balance one kinesin-1 (Fig. 3B) and 5 dyneins were necessary to counteract one kinesin-2 (Fig. 3D). By varying the number of dyneins on the cargo and calculating the mean velocity (Fig. 3E), it can be seen that multiple dyneins are required to counteract one kinesin, and that kinesin-2 is less able to overpower dynein than kinesin-1.

Figure 3: Simulated bidirectional transport behavior.

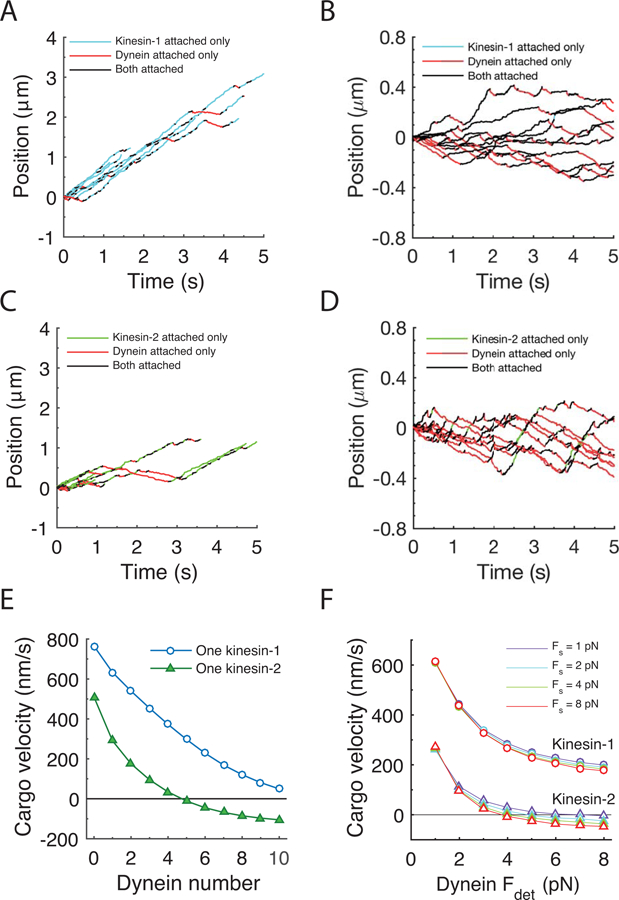
A: Traces of cargo position over time for cargo with one kinesin-1 and one dynein. B: Traces of one kinesin-1 and 11 dynein motors, which gives mean velocity near zero. C: Traces for one kinesin-2 and one dynein, illustrating that kinesin-2 competes less effectively with dynein than does kinesin-1. D: Traces for one kinesin-2 and five dynein. E: Mean cargo velocity as a function of dynein motor number for cargo having one of kinesin-1 or one kinesin-2. Note: for panels A-E, dynein stall force was F_s = 1.25 pN and detachment force parameter was F_det = 0.87 pN (Table 2). F: Mean cargo velocity for kinesin-dynein motor pairs as a function of the dynein detachment force parameter, F_det for different dynein stall forces, F_s. Open circles denote kinesin-1-dynein pairs and open triangles denote kinesin-2-dynein pairs. Thus, changes in the detachment force parameter have a strong effect on the net cargo velocity, whereas differences in the stall force, F_s, from 1–8 pN have little effect on net transport behavior. For panels E and F, a total of 5000 samples were obtained for each point; simulations were terminated when all motors detached from the microtubule tracks or after a maximum simulation time of 5 seconds.

Because the kinesin-1 and −2 stall forces are 8 pN ^12,19, whereas the dynein stall force is set to 1.25 pN ^22,28–30, it is perhaps unsurprising that multiple dynein are required to balance one kinesin. However, in addition to the stall force, F_s, the load-dependence of detachment, defined by the detachment force metric, F_det, also plays a role in motor behavior during bidirectional transport. To investigate the relative importance of the stall force and detachment force parameters on transport dynamics, we systematically varied F_s and F_det and determined the average velocity for cargo with one kinesin and one dynein (Fig. 3F). Interestingly, the dynein stall force had almost no effect on the mean cargo velocity, whereas the detachment force had a strong effect on the resulting cargo velocity. Thus, the first conclusion from these simulations is that when dynein detachment is modeled as a slip-bond, bidirectional transport behavior is predicted to be strongly affected by the load-dependent detachment rate of dynein and is only minimally affected by the dynein stall force.

The force dependence of dynein detachment influences cargo behavior more than the dynein stall force

One way to demonstrate the role that motor detachment plays in bidirectional transport is to examine how fast each motor class detaches from the microtubule when dynein and kinesin are competing to pull the cargo in opposite directions. To quantify this behavior, we evaluated an Estimated Effective Detachment Rate, ${\widehat{k}}_{det}^{eff}$, for each motor by calculating the mean motor attachment duration during bidirectional runs and inverting it to generate an effective first-order rate constant. For comparison, the unloaded detachment rate, $k_{det}^0$, calculated by dividing the unloaded velocity by the unloaded run length in Fig. 2, was 0.66 s⁻¹, 1.41 s⁻¹, and 1.0 s⁻¹ for kinesin-1, kinesin-2, and dynein, respectively (see also Table 2). For kinesin-1 the observed detachment rate approximately doubled when challenged by a dynein having a minimal load-sensitivity of detachment (high F_det) (Fig. 4A). As expected, the observed detachment rate of dynein was highly dependent on the detachment force parameter. At low dynein F_det, plus-end directed forces from the kinesin partner resulted in a 10-fold increase in the detachment rate above the unloaded value (Fig. 4A), whereas at higher F_det (meaning dynein detachment is less sensitive to load), the observed off-rates were similar at ~2 s⁻¹. Because kinesin-2 inherently is more sensitive to load, its detachment rate when paired with a dynein increased substantially, especially for dynein whose detachment kinetics were relatively insensitive to load (large F_det) (Fig. 4B). Accordingly, the observed dynein off-rates were slower when paired with a kinesin-2. These motor detachment kinetics provide an explanation for the strong dependence of cargo velocity on the dynein detachment force parameter shown Fig. 3F, and they emphasize the important role that load-dependent motor detachment plays in bidirectional transport.

Figure 4: Estimated effective motor detachment rates during bidirectional transport.

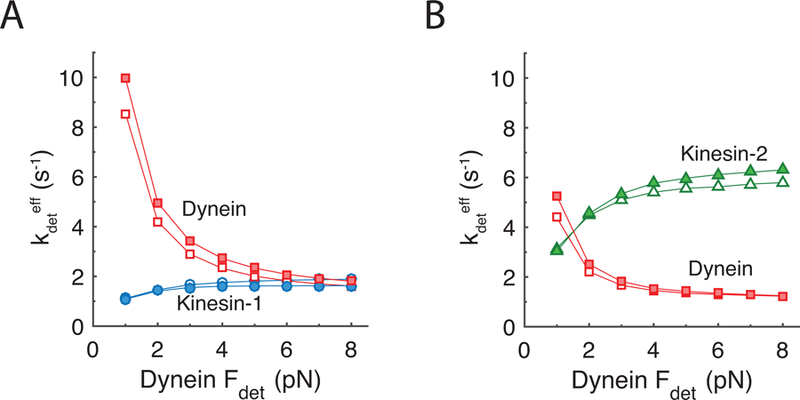
Simulations used one dynein motor and one kinesin-1 (A) or one kinesin-2 (B) motor. The estimated effective motor detachment rate, ${\widehat{k}}_{det}^{eff}$, was calculated as the inverse of the mean run time for each motor, and plotted as a function of dynein detachment force parameter (F_det) with dynein stall force (F_s) equal to 1 pN (open symbols) or 8 pN (filled symbols). The steep fall in the dynein off-rate with increasing F_det demonstrates the strong influence of the dynein detachment force parameter on the effective motor detachment rate. The similarity of open and filled symbols demonstrates the weak dependence of detachment on the dynein stall force.

Influence of different dynein mechanochemical parameters on bidirectional transport velocity

The above simulations predict that dynein alone competes poorly against kinesin. However, the recent discovery that BicD2 and other dynein adapter proteins substantially enhance dynein motility activity ^15–17,37 has caused a rethinking of how in vitro motility of isolated dynein relates to the true in vivo activity of the motor. More broadly, there are thought to be a number of regulatory proteins that alter dynein mechanochemistry ³⁹, but how these modulations alter the bidirectional dynamics of kinesin-dynein complexes is difficult to predict. Thus, using the framework developed above, we carried out a systematic exploration of the dynein motor parameters that most strongly determine bidirectional transport characteristics of kinesin-dynein complexes. The activated dynein-dynactin-BicD2 (DDB) complex has been shown to move faster, generate higher stall forces, and have much longer run-lengths than isolated dynein alone ^15–17,37. Hence, dynein activators alter multiple chemomechanical parameters, but precisely which parameters are modulated by this activation and the impact on the overall bidirectional transport characteristics are not clear. For these parameter sensitivity studies, we chose a new default parameter set that is in the range of both dynein and DDB, and we systematically varied each parameter, keeping all others constant. The “default” dynein moved at 500 nm/s with a run length of 1000 nm (giving k_off⁰ of 0.5 s⁻¹), had a 1 pN stall force and 1 pN detachment force parameter; other dynein characteristics were identical to above. The strategy was to systematically vary one parameter at a time and simulate the net transport velocity when one dynein was paired with either one kinesin-1 or one kinesin-2 motor.

The first result, which recapitulates the simulations above, is that the dynein stall force has no effect on the overall net transport velocity, whereas the sensitivity of detachment to load, as determined by varying the detachment force parameter, F_det, had a strong effect (Fig. 5 A and B). As seen in Fig. 5C, the unloaded off-rate is another strong determinant of the net cargo velocity. Thus, when motor detachment kinetics are modeled as an unloaded off-rate having an exponential dependence on force (Bell-type model ³¹), both parameters are important determinants of the bidirectional transport behavior. This strong effect of the dynein processive run duration is particularly relevant for DDB because the extended run durations are the most notable hallmark of activated dynein ^15,16. Experimentally, processivity is normally quantified by the motor run length, which in our modeling framework is an emergent parameter equal to the motor velocity divided by the motor off-rate (RL = vel/k_off). As shown in Fig. 5D, increasing the dynein run length either by slowing the off-rate or by increasing the motor velocity resulted in a strong minus-end shift in the net velocity.

Figure 5: Influence of dynein mechanochemical parameters on simulated transport velocity of kinesin-dynein complexes.

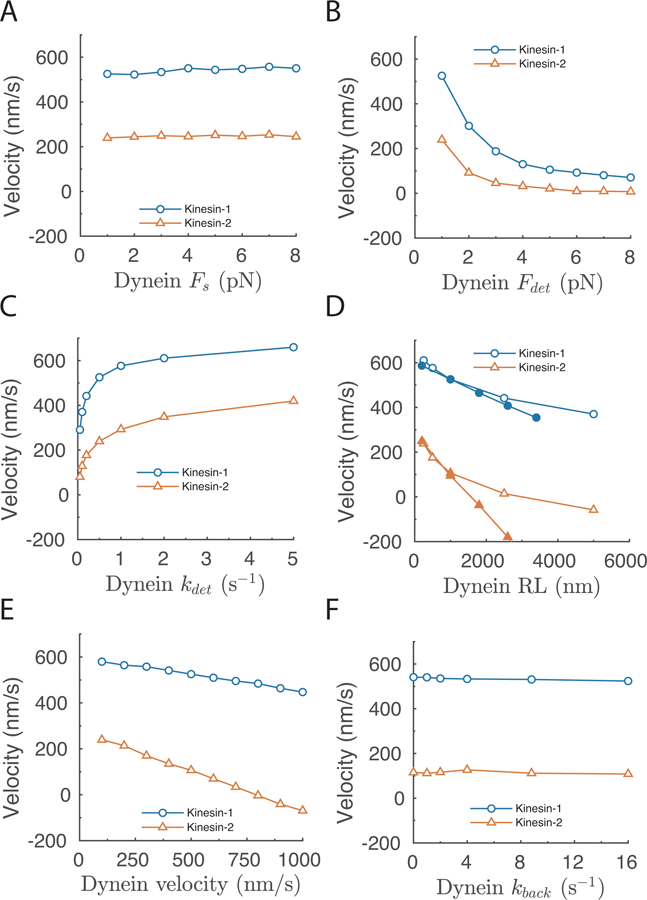
A-C: Net cargo velocity as a function of (A:) dynein stall force; (B:) dynein detachment force parameter, F_det; (C:) dynein unloaded off-rate, k_off⁰. D: Net cargo velocity as a function dynein run length, where run length (RL = vel/k_off⁰) is varied by either changing the unloaded velocity (closed symbols) or the unloaded off-rate (open symbols). E-F: Net cargo velocity as a function of (E:) dynein unloaded velocity, and (F:) dynein backstepping rate. Default dynein parameters were vel = 500 nm/s, RL = 1000 nm, k_off⁰ = 0.5 s⁻¹, F_s = 1 pN, and F_det = 1 pN, k_back = 20.8 s⁻¹ (Tables 1 and 2). In each case, one parameter was varied while all other parameters were kept constant, and net cargo velocity plotted. Each point is average from 5000 runs, each run was terminated when both motors detached or after 5 sec.

The next parameters we examined were the dynein unloaded velocity and backstepping frequency. The naïve expectation is that a faster dynein unloaded velocity should strongly bias minus-end net transport; first, because during antagonistic stepping against kinesin the dynein will be stepping faster, but also because during transient episodes when kinesin detaches the cargo will be moving toward the minus end at the unloaded dynein velocity. As seen in Fig. 5D, when competing against kinesin-2 the net cargo velocity varied strongly with the dynein motor velocity, but when competing against kinesin-1 the influence of the dynein velocity was quite small – a 10-fold change in the dynein velocity only reduced the net plus-end cargo transport rate by roughly 20%. Finally, one might predict that dynein’s propensity to backstep would play an important role when working against kinesin, but as seen in Fig. 5E, varying the dynein backstepping rate had no effect on the overall net transport velocity. Thus, to summarize the parameter sensitivity analysis in Fig. 5, the net transport velocity of kinesin-dynein complexes is most strongly determined by features that cause dynein to remain attached to the microtubule, namely the unloaded off-rate (or run length) and the load dependence of the off-rate.

Simulated kinesin-DDB bidirectional transport dynamics

We next explored the predicted behavior of kinesin-DDB complexes, using best estimates from the literature for the properties of activated dynein. From published single-molecule investigations of DDB (Table 1), we settled on a “consensus” DDB having a 500 nm/s velocity, 5000 nm run length, 0.1 s⁻¹ off-rate, 4.3 pN stall force, and 2 pN force detachment parameter (Table 2). It has been shown that, although BicD2 forms a complex containing only one dynein, the adapters BicDR and Hook3 are able to make complexes containing two dynein molecules. Furthermore, these complexes can generate larger stall forces than DDB ^38,40. We simulated the effects of two dyneins being attached to a given adapter complex by simulating two DDB. We carried out simulations for one DDB or two DDB versus one kinesin-1 or one kinesin-2 motor, and plotted raw trajectories and mean velocities over a 5 second window (Fig. 6).

Figure 6: Simulation of kinesin-DDB bidirectional transport.

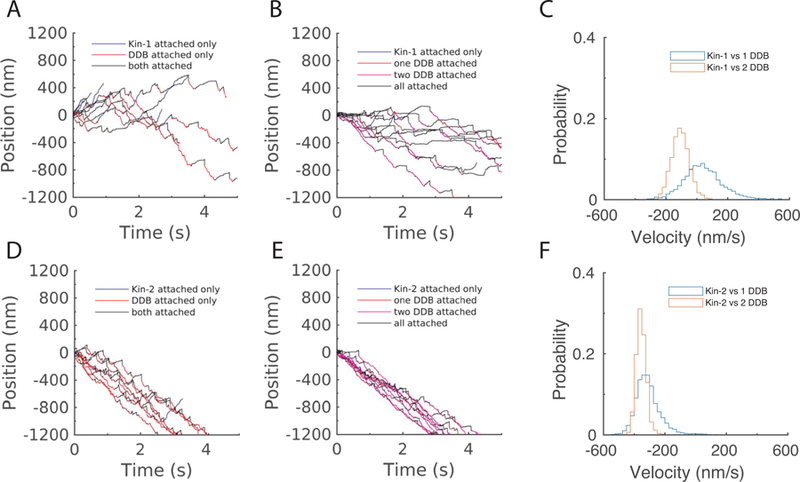
DDB connotes activated complex containing one activated dynein. To model activated complexes like DDH and DDR that contain two dyneins, we carried out simulations with two DDB as a simplified model. A-B: Simulated traces for kinesin-1 versus (A:) one or (B:) two DDB complexes. Colors denote periods when only kinesin, only dynein, or both motors are attached. C: Velocity distributions over 5 second windows for kinesin-1 against one or two DDB complexes; distributions contain 5000 simulations. D-F: Identical panels for kinesin-2.

Importantly, in our kinesin-DDB simulations, a single kinesin-1 balanced a single DDB quite closely, with complexes having a mean velocity of 41 ± 135 nm/s (mean ± SD over 5 second interval, N = 5000; Fig. 6A and C). Belyy and coworkers used DNA linkers to experimentally connect one kinesin-1 to one DDB, and measured a median velocity of +26 nm/s for this complex ¹⁷. Thus, our simulations are able to recapitulate published in vitro experiments. The wide distribution of simulated velocities (Fig. 6C) was also similar to the wide distribution of observed experimental velocities. One difference was that in the simulations, individual complexes are clearly seen switching direction over the 5 s observation window (Fig. 6A), whereas in the published experimental traces, different complexes moved in different directions, but directional switching of individual complexes was not clearly observed. It should be noted that the choice of F_det = 2 pN for DDB was not constrained by any experimental data, and for larger F_det values, the net velocity shifted increasingly minus-end directed (data not shown). Overall, however, this similarity between modeled and experimental values is striking.

For a complex of kinesin-1 with two activated dyneins, the net directionality was minus-end directed with a mean velocity of −106 ± 59 nm/s (Fig. 6B and C). This simulation thus makes a quantitative prediction for an experiment linking one kinesin-1 to DDR or DDH. Against kinesin-2 motors, DDB competed very successfully, with minus end velocities of −307 ± 88 nm/s and −344 ± 33 nm/s for kinesin-2 against one and two DDB, respectively (Fig. 6D-F). Again, these simulations make predictions for experiments that have not yet been reported in the literature. To summarize, activated dynein in DDB complexes is almost equally balanced with one kinesin-1, but it dominates kinesin-2.

Discussion:

Understanding the bidirectional cargo transport dynamics observed in cells requires both understanding the properties of the underlying motors as well as the motor coordination and competition mechanisms that give rise to the emergent cargo velocity and directionality. By developing a stochastic cargo transport model and integrating the best available motor parameters in the literature, we find that kinesin-1 is predicted to overpower dynein and that kinesin-2 competes on more equal footing with dynein. Activated dynein in a DDB complex competes nearly equally with kinesin-1, whereas activated dynein dominates kinesin-2 due to that motor’s load-dependent detachment properties. Interestingly, the net speed and direction of cargo transport depended only minimally on motor stall forces, and instead was strongly affected by the force-dependent detachment properties of the underlying motors. It follows that in cells, the most effective regulatory proteins would be those that alter motor detachment kinetics rather than the motor velocity or stall force.

A number of studies have found that vesicles purified from neurons contain both kinesin and dynein motors attached, and in some cases two classes of kinesins are simultaneously attached ^41–44. For instance, Hendricks and colleagues found that 90 nm neuronal vesicles co-purified with kinesin-1, kinesin-2 and dynein motors at a ratio of 1:4:6 ⁴⁴. These vesicles moved bidirectionally both in cells and in vitro on isolated microtubules and spent similar times moving in plus- and minus-end directions. The finding that more kinesin-2 than kinesin-1 are bound to the cargo parallels results from the present simulations that found that, compared to kinesin-1, more kinesin-2 motors are required to balance the forces generated by dynein.

Other studies found different results for kinesin-dynein competitions. For instance, Derr et al investigated kinesin-dynein competition using a DNA origami scaffold to create cargo with defined numbers of attached kinesin and dynein motors ²⁷. Interestingly, directional switching was not observed in that work; instead, motile events were unidirectional with the proportions of plus- and minus-end runs determined by the kinesin:dynein ratio. There was also a fraction of cargo that were immobile but could be induced to move by photocleaving one motor population, meaning that stalls resulted from the antagonistic motors both pulling and reaching a draw. Notably, for DNA origami with similar numbers of kinesin and dynein motors, minus-end transport events dominated, the opposite of the kinesin-dominated runs resulting from the present simulations. However, an important difference is that the DNA origami work of Derr used yeast dynein, which is more processive and has a larger stall force than the mammalian cytoplasmic dynein modeled here ^23–25,45. Thus, there are expected to be quantitative differences between the present simulations and the Derr study.

The experimental study most relevant for the present work is from Belyy and colleagues who tracked the motility of pairs of human kinesin-1 and human dynein or dynein-dynactin-BicD (DDB) connected through a DNA linker ¹⁷. Against dynein alone, which was shown to have a 2 pN stall force, the complexes moved very near the kinesin-1 speed, consistent with our present simulations that found that kinesin-1 dominated dynein. Complexing dynein with dynactin and BicD resulted in the stall force increasing to 4.3 pN, and long run lengths ^15,16. In contrast to dynein alone, DDB-kinesin-1 complexes moved at a median velocity of +26 nm/s, roughly 30-fold slower than kinesin alone. When we simulated this experiment using the available experimental parameters for DDB and setting F_det = 2 pN, we found that a kinesin-1-DDB complex moved at a mean speed of 41 nm/s; thus, our simulations were able to recapitulate the experimental velocities. Other characteristics, such as the directional switching differed between experiment and simulation, and many of the simulated kinesin-1-DDB complexes dissociated by 4 seconds (Fig. 6A), whereas in the experimental kymographs the complexes moved slowly and steadily for tens of seconds ¹⁷. Based on our explorations of the different dynein mechanochemical parameters (Fig. 5), the most likely explanation of why DDB and kinesin-1 pull to nearly a draw is not because of the greater stall force of DDB, but rather the load-dependent off-rate parameters. We stress that the current mechanochemical description of DDB should be considered a starting point that must be refined and verified through single-molecule experiments and further simulations. In particular, the long duration of the experimental runs suggests that DDB may have catch-bond behavior, as has been observed for dynein alone ^9,28,46.

One question from the present simulations is how kinesin-3 motors like KIF1A compete with dynein on the same cargo. There are many examples, such as synaptotagmin and amyloid-precursor-protein positive vesicles in axons, where the anterograde movement is driven by kinesin-3 motors and the retrograde movement by dynein ^43,47. However, in vitro experiments showed that when kinesin-3 is grouped with kinesin-1, either as a team in mixed motor gliding assays or as a pair with an artificial scaffold, the transport speed is very similar to kinesin-1 alone, suggesting that kinesin-3 motors readily detach under load ^32,48,49. Thus, to an even greater degree than kinesin-2, kinesin-3 motors are predicted to compete poorly against dynein, and the prediction is that in cases where anterograde movement of dynein-kinesin-3 cargo dominate, the number of kinesin-3 attached to the cargo far outnumber the dynein.

The goal of the present work was to use a relatively simple modeling paradigm and incorporate the most recent high-precision single-molecule results for kinesin-1 and kinesin-2 to make predictions about how these motors compete with dynein during bidirectional transport. Our current approach that models the stepping of multiple motors attached through elastic linkers to a common cargo is similar to the approach of Kunwar et al ⁹, with the difference here being the specific kinesin and dynein motor parameters that we explored, as well as extending the approach to simulating DDB-kinesin complexes. We find when working at a 1:1 ratio, kinesin-1 is predicted to overwhelm dynein and to evenly match DDB; kinesin-2 is predicted to dominate dynein but be dominated by DDB. Importantly, we find that the results depend strongly on the load-dependent detachment kinetics of dynein and DDB, which are not fully characterized and need to be better understood, especially in the context of these multi-motor tug-of-war scenarios. In contrast, the results depended only minimally on motor stall forces. In cells, tubulin post-translational modifications and microtubule associated proteins may alter motor interactions both positively and negatively, and there may be other levels of motor regulation. So, considerably more effort will be needed to quantitatively understand bidirectional transport in cells. These simulations show that even in the most reductionist systems, subtle changes in motor numbers and motor characteristics can have strong effects on the net speed and directionality of bidirectional transport.

Methods:

Kinesin and dynein modeling

Kinesin and dynein motor behavior was simulated using a stochastic stepping algorithm, where at each time point an attached motor can step forward, step backward, or detach from the microtubule. Detached motors rebind with a defined reattachment rate, and for simplicity, motors were assumed to take 8 nm steps along a single protofilament.

To describe the time evolution of the system, the Gillespie Stochastic Simulation Algorithm ⁵⁰ was used, as follows. For a reaction with a first-order transition rate constant, k, an exponential distribution of transition times was generated by taking:

$$t=\frac{1}{k}\ln \left(\frac{1}{R}\right)$$

where R is a uniformly distributed random number from 0 to 1 ⁵⁰. In a system with N possible transitions, the rate that some event will happen equals the sum of the rates of all possible transitions ⁵¹. Hence, the time before any event can be computed as:

$$t=\frac{1}{{\sum }_{i=1}^N{k}_i}\ln \left(\frac{1}{R}\right)$$

For reactions controlled by the first-order rate constant ${\text{k}}_{\text{i}}$, the probability of event $i$ occurring is:

$$P_i=\frac{k_i}{\Sigma k_i}$$

where $\Sigma P_i=1$. At each time point, the chosen event $i$ (stepping, detachment or reattachment) is determined by taking a new random number from a uniform distribution in the unit interval, and finding where it lies within the domain of the computed probabilities (i.e.$\left(0,k_1/\mathrm{\Sigma }{k}_i], (k_1/\mathrm{\Sigma }{k}_i,(k_1+ k_2)/\mathrm{\Sigma }{k}_i], \dots \left(\mathrm{\Sigma }{k}_{i-1}/\mathrm{\Sigma }{k}_i, 1\right]\right)$. The corresponding transition is then selected as the next event with transition time, $t$. This method is then repeated until all motors detach from the microtubule or a maximum run duration or length is reached.

Kinesin-1 and kinesin-2 stepping parameters

Because kinesins step toward the microtubule plus-end, hindering loads (oriented toward the minus-end) were defined as negative forces and assisting loads (oriented toward the plus-end) were defined as positive forces. Kinesin-1 and kinesin-2 stepping were modeled using a load-dependent forward and backward stepping rates, k_for and k_back, where the effective stepping rate, $k_{step}$ is:

$$k_{step}=k_{for}-k_{back}$$

Following Andreasson ¹², the forward step was divided into three transitions: an ATP binding step, a load dependent transition that includes a forward displacement, and a load-independent transition to complete the cycle, as follows:

$$\left[\mathrm{A}\right]\stackrel{k_1\left[ATP\right]{/k}_{-1}}{\leftrightarrow }\left[\mathrm{B}\right]\stackrel{k_{2}exp\left(-\frac{F\delta }{k_{B}T}\right)}{\to }\left[\mathrm{C}\right]\stackrel{k_3}{\to }\left[\mathrm{A}\right]$$

Here, δ is the size of the forward displacement and k_BT is Boltzmann’s constant times the absolute temperature, equal to 4.1 pN-nm at 25 °C. Because all simulations were carried out at saturating ATP, the ATP binding step was assumed to be infinitely fast. Therefore, under hindering loads, the forward stepping rate is:

$$k_{for}={\left(\frac{1}{k_2*e^{-\frac{\left|F\right|\delta }{k_{B}T}}}+\frac{1}{k_3}\right)}^{-1},\hspace{0.17em}\text{F} \le 0$$

It has been shown that assisting loads do not substantially speed up kinesin stepping ¹⁹. Therefore, for assisting loads:

$$k_{for}={\left(\frac{1}{k_2}+\frac{1}{k_3}\right)}^{-1},\hspace{0.17em}\text{F} > 0$$

The kinetic parameters for kinesin-1 and kinesin-2 were obtained from Andreasson ¹²; for simplicity, the kinesin-2 parameters were taken as the average of KIF3A and KIF3B parameters in that work. Parameters are summarized in Table 2.

Andreasson et al found that at a $4 pN$ hindering load, kinesin-1 and kinesin-2 backsteps occurred at a frequency of 3% and 6% respectively ¹². Plugging in the forward stepping kinetic values in Table 2 and these backstepping frequencies, the backstepping rates at 4 pN are 1.35 s⁻¹ for kinesin-1 and 2.84 s⁻¹ for kinesin-2. Backstepping rates were assumed to be zero for assisting loads and to scale linearly with force under hindering loads:

$$k_{back}=0, F>0$$

$$k_{back}=k_{back@4pN}*\frac{\left|F\right|}{4pN}, F\le 0$$

Kinesin load-dependent off-rates

Load-dependent kinesin off-rates were estimated from force-clamp optical trapping experiments that measured the dependence of run length, RL, on applied load, F ^12,52:

$$RL=L_0\exp \left(-\frac{\left|F\right|{\delta }_L}{k_{B}T}\right)$$

where $L_0$ is the run length at zero load, and ${\delta }_L$ is the distance parameter. The first-order dissociation rate, k_det, equals the velocity divided by the run length, hence:

$$k_{det}=\frac{8nm*\left(k_{for}-k_{back}\right)}{L_0\exp \left(-\frac{\left|F\right|{\delta }_L}{k_{B}T}\right)}, F\le 0$$

Run length parameters for kinesin-1 are shown in Table 2. Kinesin-2 run lengths were experimentally measured for hindering forces above 1 pN ¹². For hindering loads between 0 and 1 pN, an exponential dependence was chosen to connect the 380 nm unloaded run length to the 121 nm run length at 1 pN. For kinesin-2 detachment in the assisting direction, parameters were taken from previous work ³² that used iterative fitting of a computational model to mixed motor gliding experiments to give:

$$k_{det}=15\exp \left(\frac{\left|F\right|}{2.0}\right)$$

For all motors, the reattachment rate to the microtubule after dissociating was $k_{attach}=5 s^{-1}$ ^6,53.

Dynein and DDB parameters

To generate a kinetic model for dynein, we combined experimental results from the literature, and made appropriate approximations where data were not available. We set the unloaded velocity to $212 nm/s$ based on Mallik et al. ³⁶ and defined the load-independent backstepping rate to be 25% of the unloaded forward stepping rate ^24,26. Therefore, at zero load, k_for⁰ = 35.3 s⁻¹ and k_back = 8.8 s⁻¹. Under hindering loads, the motor was assumed to exhibit a linear force-velocity curve up to 1.33 times the stall force, F_s. Thus:

$$k_{for}=k_{for}^0\left(1-\frac{3}{4}\frac{F}{F_s}\right), F\le \frac{4}{3}{F}_s$$

$$k_{for}=0, F>\frac{4}{3}{F}_s$$

Velocity under assisting loads was set equal to the unloaded velocity, similar to kinesin.

The dynein detachment rate, k_det, was modeled with an exponential load dependence:

$$k_{det}=k_{det}^{0}exp\left(\frac{\left|F\right|}{F_d}\right), \forall F$$

where k_det⁰ is the detachment rate at zero load and F_det is the detachment force parameter, defined as k_BT/δ. Default values were F_s = 1.25 pN and F_det = 0.87 pN ⁹.

For dynein simulations where F_s was varied, this scaling of F_det = (0.87/1.25) * F_s was maintained for detachment up to stall, and at superstall loads:

$$k_{det}=\frac{1}{0.254\left(1-\exp \left(-\frac{1.25}{1.97}\frac{F}{F_s}\right)\right)}, F\ge F_s$$

For simulations where dynein velocity was varied, k_for and k_back were both varied to achieve the desired velocity while maintaining a 25% unloaded backstepping frequency ^24,26.

The tug of war model

Kinesin and dynein were linked to the cargo through a linear springs with k_s^kin = $0.3 pN/nm$ for kinesin ⁵⁴, and k_s^dyn = $0.065 pN/nm$ for dynein ⁵⁵. A force balance between the N_kin and N_dyn opposed kinesin and dynein motors was maintained at all times, and cargo position, x_c, was obtained by:

$$x_c= \frac{k_s^{kin}\Sigma x_i^{kin}+k_s^{dyn}\Sigma x_i^{dyn}}{k_s^{kin}{N}_{kin}+k_s^{dyn}{N}_{dyn}}$$

where x_i^kin is the position of each kinesin and x_i^dyn is the position of each dynein motor.

Mean cargo velocities were calculated by dividing the total distance travelled by the duration of the simulation for each path for multiple paths. Estimated effective detachment rates during multi-motor transport were calculated by taking inverse of the mean run duration for each motor.

Synopsis:

To better understand the molecular mechanisms underlying bidirectional cargo transport, we incorporated experimental single-molecule parameters for kinesin-1, kinesin-2, and dynein into a computational model of multi-motor bidirectional transport. We find that kinesin-1 is predicted to compete much more effectively against dynein than is kinesin-2, and that activated dynein-dynactin-BicD2 (DDB) competes on equal footing with kinesin-1 and dominates kinesin-2. The load-dependent detachment rate of each motor is the key determinant of their effectiveness in bidirectional transport.