Recoil-induced ultrafast molecular rotation probed by dynamical rotational Doppler effect

Significance

Ionization of molecules by hard X-ray photons induces ultrafast rotation up to an effective rotational temperature of about 10,000 K due to the recoil caused by emission of a fast photoelectron. The goal to monitor the recoil-induced rotational motion and finally control its dynamics is achieved by recording high-resolution Auger spectra of the C1s core-ionized carbon monoxide molecule. The time-delayed Auger electron emission offers a unique opportunity to probe the dynamics of ultrafast molecular rotation, since we show that a significant change of the molecular orientation occurs during Auger decay. We exploit the fact that the rotational period is comparable with the core-hole lifetime. We manipulate this dynamics by changing the rotational speed using X-ray photons of different energies.

Abstract

Observing and controlling molecular motion and in particular rotation are fundamental topics in physics and chemistry. To initiate ultrafast rotation, one needs a way to transfer a large angular momentum to the molecule. As a showcase, this was performed by hard X-ray C1s ionization of carbon monoxide accompanied by spinning up the molecule via the recoil “kick” of the emitted fast photoelectron. To visualize this molecular motion, we use the dynamical rotational Doppler effect and an X-ray “pump-probe” device offered by nature itself: the recoil-induced ultrafast rotation is probed by subsequent Auger electron emission. The time information in our experiment originates from the natural delay between the C1s photoionization initiating the rotation and the ejection of the Auger electron. From a more general point of view, time-resolved measurements can be performed in two ways: either to vary the “delay” time as in conventional time-resolved pump-probe spectroscopy and use the dynamics given by the system, or to keep constant delay time and manipulate the dynamics. Since in our experiment we cannot change the delay time given by the core-hole lifetime $\tau$, we use the second option and control the rotational speed by changing the kinetic energy of the photoelectron. The recoil-induced rotational dynamics controlled in such a way is observed as a photon energy-dependent asymmetry of the Auger line shape, in full agreement with theory. This asymmetry is explained by a significant change of the molecular orientation during the core-hole lifetime, which is comparable with the rotational period.

It is a widespread textbook statement that Auger spectra are independent of the photon energy used for the preceding ionization process. However, in recent years, it has been shown by detailed studies that this statement is violated at least near the photoionization threshold due to shape resonances (1), postcollisional interaction (2, 3), and Cohen–Fano interference (4, 5). These effects vanish with an increase of the X-ray photon energy. Still, it was common belief that the Auger spectra cease to depend on the photon energy far away from the core-ionization threshold.

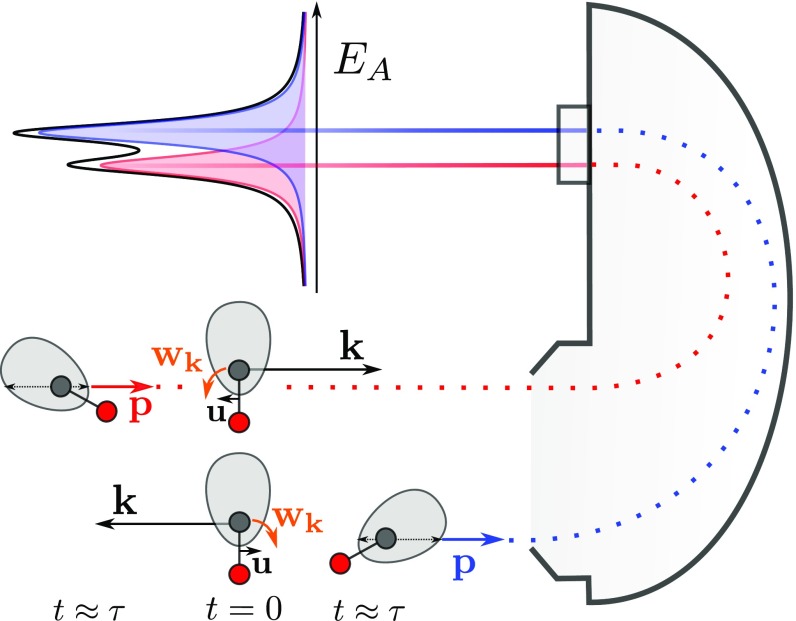
In this work, we present an effect that influences molecular Auger spectra and that increases by increasing the photon energy. This is the rotational Doppler splitting caused by ultrafast rotation induced by the ejection of a fast photoelectron. As a consequence of the ultrafast rotation, the molecule has the time to change its orientation during the lifetime of the core-hole state (Fig. 1), which brings dynamics into the rotational Doppler effect (6).

Fig. 1.

Classical picture of the dynamical rotational Doppler effect. In Bottom, a photoelectron with momentum $\mathbf{k}$ is at $t=0$ ejected from the carbon atom (long black arrow) in the direction away from the detector. Induced by the recoil momentum, the molecule translates with a velocity $\mathbf{u}=\mathbf{k}/M$ and rotates with an angular velocity ${\mathbf{w}}_k$ toward the detector. Therefore, an Auger electron with momentum $\mathbf{p}$ emitted at $t=\tau$ toward the detector is blue shifted as indicated in the schematic spectrum displayed in Top. In Middle, the photoelectron is emitted in the opposite direction so that velocity $\mathbf{u}$ and angular velocity ${\mathbf{w}}_k$ are inverted, resulting in a red-shifted Auger electron in the detector. The shaded gray areas around the carbon atoms represent an Auger emission with anisotropic angular distribution in the molecular frame. In Bottom, the preferred direction of the Auger emission is rotated from the top toward the detector so that the blue-shifted Auger peak gains intensity as indicated by the long thin black arrow in the gray area. The opposite rotation in Middle lowers the intensity for the red-shifted Auger peak (short thin black arrow).

In a “classical” picture, the Auger electron energy is “blue shifted” or “red shifted” according to the direction of emission of the photoelectron and the subsequent sense of rotation. The shift is not symmetric due to the shape of the Auger angular distribution. The semiclassical picture used in this publication makes the Auger profile asymmetric due to an interference between the “instantaneous” and “time-delayed” parts of the rotational wave packet. This corresponds in a pure quantum approach to the interference between rotational states (SI Appendix). We wish to stress the point that these descriptions coincide in the limit of high quantum rotational numbers, as consistent with the fundamental correspondence principle (7), which is at the heart of the connection between classical and quantum physics.

With its increase with photon energy (Fig. 2 B and C), this effect qualitatively differs from all above-mentioned photon energy-dependent effects. In this context, one should mention the Doppler splitting caused by the translational recoil effect (8). This very general effect results in a symmetric doublet and also grows with the photon energy, as it was observed in the Auger spectra of Ne (9) after core ionization by hard X-ray photons.

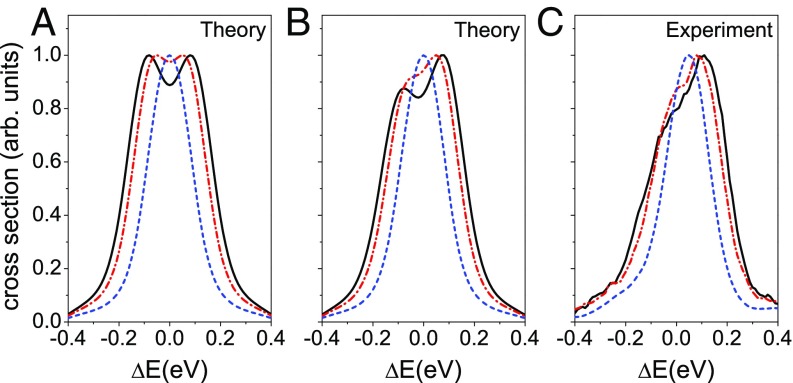
Fig. 2.

Theoretical and experimental C1s⁻¹→d¹Σ⁺ Auger spectra of CO given for the X-ray photon energies $\omega =2.5$ keV (blue dashed line), 8 keV (red dashed–dotted line), and 12 keV (black solid line). (A) The symmetrical part ${\sigma }_0$ of the calculated partial cross section (Eq. 8), where the dynamical contribution to the rotational Doppler shift is neglected. (B) The total theoretical cross section $\sigma$ of the Auger process displaying the asymmetry of the Auger profile caused by the dynamical rotational Doppler effect. The simulations are convoluted with a Gaussian instrumental function of 0.1-eV width. (C) Experimental data in agreement with the simulations (Fig. 2B) showing that the dynamical asymmetry is growing with increasing photon energy.

In general, the observation of phenomena linked to recoil effects induced by the emission of high-energy photoelectrons has recently become possible due to the advent of sources delivering hard X-ray photons. Already existing sources of X-ray radiation, such as SOLEIL (France) (10) and SPring-8 (Japan) (11), deliver high-brilliance synchrotron radiation up to 10 keV. X-ray photons with energy of 50–100 keV are available at the ESRF (European Synchrotron Radiation Facility) (12, 13) and PETRA III (Positron Electron Tandem Ring Anlage III) (14) synchrotrons. One should also mention the X-ray free electron laser (XFEL) facility SACLA (SPring-8 Ångstrom Compact free electron LAser) (Japan) (15), with photons up to 20 keV and intensity $10^{20}W/{\mathrm{c}\mathrm{m}}^2$, as well as the European XFEL (Hamburg, Germany), with photons up to 25 keV (16); these facilities make it possible to overcome low-ionization cross section in the high-energy region.

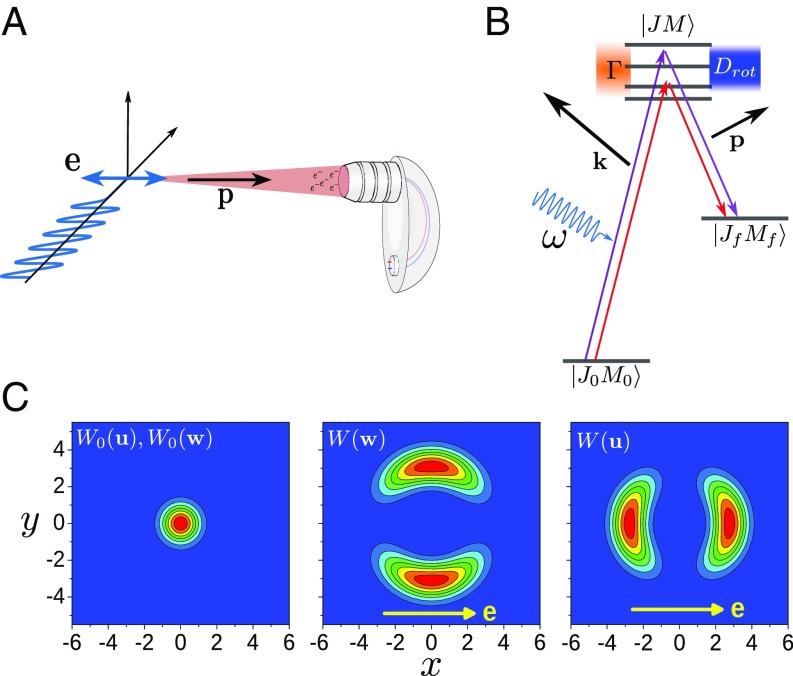
The experimental procedure (Figs. 1 and 3) consists of the first step of C1s photoionization of the showcase molecule CO with X-rays of energies high above the ionization energy of 296.24(3) eV (17), namely $\omega =2.5$, 8, and 12 keV. The large momentum of the photoelectron of $k\approx 30$ a.u. at a photon energy of $\approx 12$ keV gives a recoil “kick” that creates a nonequilibrium distribution over translational and rotational degrees of freedom (6, 8, 9) [$W\left(\mathbf{u}\right)$ and $W\left(\mathbf{w}\right)$ in Fig. 3C, respectively] and makes it possible to reach rotational quantum numbers of $J\approx 40$ for the core-ionized molecule. In comparison, to force molecules to rotate with the corresponding speed (${\nu }_{\mathbf{k}}=w_{\mathbf{k}}/2\pi \approx 4$ THz) in thermal equilibrium, a gas temperature above 4,000 K has to be assumed. These results suggest that highly excited rotational states with $J$ in the order of 100 can be created in the future by using X-ray photons in the energy range of several tens of thousands of electronvolts.

Fig. 3.

Experimental setup and physical picture of the molecular Auger process initiated by photoionization with high-energy X-ray photons. (A) Diagram of the experimental setup with the polarization direction of the synchrotron radiation $\mathbf{e}$ and the momentum of the detected Auger electron $\mathbf{p}$. (B) Quantum picture of the Auger process accompanied by rotational excitations. The Auger process is strongly affected by the interference of the Auger channels going through different rotational levels of the core-ionized state (more details are in the text and SI Appendix). (C) Velocity distributions $W\left(\mathbf{u}\right)$ and angular velocity distributions $W\left(\mathbf{w}\right)$. Left shows the thermal velocity distribution $W_0\left(\mathbf{u}\right)=\exp \left(-{\mathbf{u}}^2/{ū}^2/{\left(\sqrt{\pi }ū\right)}^{3/2}\right)$ and the thermal angular velocity distribution $W_0\left(\mathbf{w}\right)=\exp \left(-{\mathbf{w}}^2/{\overline{w}}^2/{\left(\sqrt{\pi }\overline{w}\right)}^{3/2}\right)$ with $ū=\sqrt{2k_{BT}/2M}$, $x=u_x/ū$, and $y=u_y/ū$ for the translational degrees of freedom as well as $\overline{w}=\sqrt{2k_{BT}/2I}$, $x=w_x/\overline{w}$, and $y=w_y/\overline{w}$ for the rotational degrees of freedom. Center and Right display the angular velocity distribution $W\left(\mathbf{w}\right)$ and the velocity distribution $W\left(\mathbf{u}\right)$, respectively, caused by the emission of a high-energy photoelectron. The distributions $W\left(\mathbf{w}\right)$ and $W\left(\mathbf{u}\right)$ are planar cuts through the torus- and dumbbell-like 3D distributions, respectively, that include the axis along $\mathbf{e}$.

The recoil-induced molecular rotation can be detected in principle by a probe light pulse. In that case, it would be difficult to synchronize the probe photon with the molecule as well as with the ejected photoelectron. This is in principle possible by using a coincidence technique but not with fast-rotating molecules. However, this problem can be overcome by what we would like to define as a natural X-ray “pump-probe” single-molecule device based on the Auger process (Figs. 1 and 3). The Auger electron emitted from the same molecule during the core-hole lifetime $\tau$ after fast photoelectron ejection can be used as a probe of the recoil-induced ultrafast rotation, since the rotational Doppler shift is time-dependent on the same “internal” timescale, as we will show below.

Contrary to a conventional pump-probe experiment where the real time delay between the pump and the probe pulse is changed, the “time delay” is constant in this experiment. Instead, we change the speed of the process, namely the rotational velocity, by varying the kinetic energy of the photoelectron. In simple words, by increasing the photoelectron energy, we control the recoil-induced rotation of the molecular axis; effectively, we make our core-hole clock “tick” slower by speeding up the recoil-induced rotation. In this context, we should clarify this usage of the term time delay. The actual time delay between the instant of photoelectron ejection and the Auger electron emission is given by a statistical distribution fully governed by the natural lifetime $\tau =1/2\mathrm{\Gamma }\cong 7.5$ fs.

In this Auger experiment, the recoil-induced ultrafast rotation (Fig. 1) is probed using a time-dependent rotational Doppler shift

$$D_{\mathrm{r}\mathrm{o}\mathrm{t}}\left(t\right)={\mathbf{w}}_k\cdot {\mathbf{j}}_p\left(t\right),{\mathbf{j}}_p\left(t\right)=\alpha \left[\mathbf{R}\left(t\right)\times \mathbf{p}\right]$$ [1]

of the energy $E_A$ of Auger electron. Here, $t$ is the time delay between the photoionization process and the emission of the Auger electron. As we shall demonstrate, this time delay $t$, which is in the order of $\tau$, leads to crucial differences of the rotational Doppler shift in photoionization (6, 18–20) and in Auger decay. Apparently, after ejection of the fast photoelectron at the instant $t=0$, the molecule rotates with the constant angular velocity ${\mathbf{w}}_k=\alpha \left[\mathbf{k}\times \mathbf{R}\left(0\right)\right]/I$; note that we assume the angular velocity $\mathbf{w}=0$ before photoionization (i.e., we neglect thermal rotation). Here, $\mathbf{k}$ and $\mathbf{p}$ are the momentums of the photoelectron and Auger electron, respectively, while $\mathbf{R}\left(0\right)$ and $\mathbf{R}\left(t\right)$ describe the internuclear radius vector at the time of the photoemission and the Auger decay, respectively. The quantity ${\mathbf{j}}_p\left(t\right)$ is the recoil angular momentum that the molecule acquires at the instant $t$ by ejection of the Auger electron, $I$ is the momentum of inertia, $\alpha =m_O/\left(m_O+m_C\right)$, and $m_O$ and $m_C$ are the masses of oxygen and carbon atoms, respectively.

We would like to point out that there is a qualitative difference of the time-dependent rotational Doppler shift for the Auger electron described in Eq. 1 in comparison with the angular Doppler shift $D_{\mathrm{r}\mathrm{o}\mathrm{t}}^{\mathrm{p}\mathrm{h}}={\mathbf{w}}_{\mathbf{k}}\cdot {\mathbf{j}}_{\mathrm{p}\mathrm{h}}$ for photon emission, since a photon possesses a well-defined angular momentum of $\left|{\mathbf{j}}_{\mathrm{p}\mathrm{h}}\right|=1$ (21–23).

The rotational Doppler shift allows observing directly the rotational dynamics $\dot{\widehat{\mathbf{R}}}\left(t\right)={\mathbf{w}}_k\times \widehat{\mathbf{R}}\left(t\right)$ induced by the photoelectron; note that, throughout this work, the hat indicates unit vectors (i.e., $\widehat{\mathbf{R}}\equiv \mathbf{R}/R$ is the unit vector along the vector $\mathbf{R}$). The observation of the rotation is possible, since the duration of the Auger process is short, with a natural delay time $\tau =1/2\mathrm{\Gamma }\approx 7.5$ fs between the “pump” ionization and the “probe” Auger decay (Fig. 1). This implies a femtosecond Auger spectroscopy clock with sufficient “time resolution” to probe the ultrafast rotational dynamics and offers a possibility for monitoring the recoil-induced molecular dynamics.

To illustrate our scheme, we study the Auger process in the carbon monoxide molecule

$$\begin{array}{ccc}\hfill & \hfill & \omega +CO\left(X^1{\mathrm{\Sigma }}^{+}\right)\to C{O}^{+}\left(C1s^{-1}\right)+e_{\mathbf{k}}^{-}\hfill \\ \hfill & \hfill & \to C{O}^{++}\left(d^1{\mathrm{\Sigma }}^{+}\right)+e_{\mathbf{k}}^{-}+e_{\mathbf{p}}^{-},\hfill \end{array}$$ [2]

where the high-energy X-ray photon (2.5 $\le \omega \le$ 12 keV) ionizes a 1s core electron of the carbon atom. The created core hole is filled in the course of the electronic decay accompanied by the ejection of the Auger electron. The spectrum of the studied C1s⁻¹→d¹Σ⁺ Auger transition consists of only one peak, which is formed mainly by three almost perfectly overlapping vibrational components ($v\prime \prime =0\to v\prime =0$, $v\prime \prime =1\to v\prime =1$, and $v\prime \prime =2\to v\prime =2$), since in this particular case, the equilibrium distances of the core-ionized and dicationic final states are almost identical (24, 25). One should notice that the vibrational recoil effect (26) causes mainly a redistribution of the intensities of these overlapping components (SI Appendix). Because of this simple vibrational structure, the spectrum is well suited to illustrate how the dynamics of a fast rotating molecule affects the Auger spectral shape. In the quantum picture of the process shown in Fig. 3B, the molecule is excited to an intermediate rotational state $\left|JM\right.⟩$, which then decays to the final rotational state $\left|J_f{M}_f\right.⟩$. Despite the fact that the quantum approach quantitatively explains the experiment (SI Appendix), the quantum language is too cumbersome to be used for a clear physical picture of the studied effect to emerge. Instead, we describe the process using a semiclassical picture of rotational motion. This is possible, since in the course of the process, the fast photoelectron ejected from the C1s orbital transfers a large angular momentum ${\mathbf{j}}_k\left(0\right)=\alpha \left[\mathbf{k}\times \mathbf{R}\left(0\right)\right]$ to the molecule, which is about $1\ll j_k\le \alpha kR\approx 36$ for $\omega =12$ keV. These high values for the angular momentum also make it possible to neglect thermal rotation. The semiclassical approach used in this work gives a deeper insight into the studied problem in comparison with the full quantum picture outlined in SI Appendix. One should notice that the dynamical picture used here in the time domain is equivalent to the interference between quantum rotational states in the energy domain (27, 28) (SI Appendix). This interference and hence, the rotational dynamics imply the use of a formalism that goes beyond the frequently used two-step model, which has been applied to the same system in previous works (29, 30).

To understand how the rotational dynamics affects the Auger profile, let us start from a semiclassical equation for the cross section $\sigma$ of the studied Auger process:

$$\begin{array}{ccc}\hfill \sigma & =\hfill & ⟨P_{\mathbf{k}}{Q}_{\mathbf{p}}{\left|F\right|}^2⟩,\hfill \\ \hfill F& =\hfill & -ı\underset{0}{\overset{\infty }{\int }}{e}^{ı\underset{0}{\overset{t}{\int }}{D}_{\mathrm{r}\mathrm{o}\mathrm{t}}\left(t_1\right)d{t}_1}{e}^{ı\left(\mathrm{\Delta }E+D_{\text{tr}}+ı\mathrm{\Gamma }\right)t}dt,\hfill \end{array}$$ [3]

where the brackets denote an integration over $\widehat{\mathbf{k}}$ and $\widehat{\mathbf{R}}\left(0\right)$. The scattering amplitude $F=1/\left(\mathrm{\Delta }E+D_{\text{tr}}+D_{\mathrm{r}\mathrm{o}\mathrm{t}}+ı\mathrm{\Gamma }\right)$ is written in the time-dependent representation, similar to ref. 6, to take into account the time dependence of $D_{\mathrm{r}\mathrm{o}\mathrm{t}}\left(t\right)$ (SI Appendix). Contrary to the translational Doppler shift $D_{\text{tr}}=\mathbf{k}\cdot \mathbf{p}/M$, the rotational counterpart $D_{\mathrm{r}\mathrm{o}\mathrm{t}}\left(t\right)$ depends on the time, the ionization site (6), and the final electronic state (20). Moreover, $\mathrm{\Delta }E=E_A-E_{res}$ is the difference between the Auger energy $E_A$ and the resonance energy $E_{res}$ of the C1s⁻¹→d¹Σ⁺ transition.

The quantity $P_{\mathbf{k}}={\left(\mathbf{e}\cdot \widehat{\mathbf{k}}\right)}^2$ describes the angular distribution of the photoelectron. Here, $\mathbf{e}$ is the polarization direction of the synchrotron light so that the angular distribution is identical to the well-known form $P_{\mathbf{k}}=1+\beta {\mathrm{P}}_2\left(cos\mathrm{\Theta }\right)$. Here, ${\mathrm{P}}_2$ is a Legendre Polynomial, $\mathrm{\Theta }$ is the angle between $\mathbf{e}$ and $\mathbf{k}$, and $\beta =2$ is the angular distribution parameter expected for s ionization.

As we shall show in the following, the observed line shape depends significantly on the geometrical setup of the experiment shown in Fig. 3A. In detail, the axis of the electron analyzer is mounted parallel to the polarization direction $\mathbf{e}$ and can detect Auger electrons with a momentum $\mathbf{p}$ in a cone of $\chi =22.5°$ around the direction of $\mathbf{e}$. Using the given experimental setup, $P_{\mathbf{k}}$ can be rewritten as a function of the angle between the momentum of the photoelectron ($\mathbf{k}$) and the Auger electron ($\mathbf{p}$), resulting in $P_{\mathbf{k}}=1+\zeta P_2\left(\widehat{\mathbf{k}}\cdot \widehat{\mathbf{p}}\right)$. Here, $\zeta =\cos \chi \left(1+\cos \chi \right)$ is a parameter that depends on the opening angle $2\cdot \chi$ of the detector, and we shall see further below that it is important for the size of the asymmetry in the Auger line shape (SI Appendix has more details). One should notice that the ionization probability $P_{\mathbf{k}}$ can be affected by polar anisotropy caused by the forward scattering effect. However, the forward scattering of a fast photoelectron by the oxygen atom does not bring asymmetry to the Doppler profile; therefore, it is excluded from this analysis (SI Appendix).

The probability of the Auger decay $Q_{\mathbf{p}}={\left|A_{\mathbf{p}}\right|}^2$ depends on the angle between the molecular axis $\widehat{\mathbf{R}}\left(t\right)$ and the direction of the Auger electron $\widehat{\mathbf{p}}$. In the simulations, we take into account the first antisymmetric contribution to $A_{\mathbf{p}}$ [i.e., $A_{\mathbf{p}}\approx 1+\eta \left(\widehat{\mathbf{p}}\cdot \widehat{\mathbf{R}}\left(t\right)\right)/2$], where the effective parameter $\eta$ describes the strength of this antisymmetrical term (SI Appendix). The term proportional to $\eta$ is neglected in conventional analyses of Auger spectra, because the orientational averaging of the related contribution in $\sigma$ is equal to zero as soon as the rotational motion is disregarded. However, we show in the following that the dynamical rotational Doppler shift given by Eq. 1 renders this contribution important, since it explains the observed asymmetry of the Auger profile shown in Fig. 2C.

We shall now look into the evolution of the time-dependent rotational Doppler shift $D_{rot}\left(t\right)$. After the ejection of the photoelectron, the initial molecular orientation $\widehat{\mathbf{R}}\left(0\right)$ starts to rotate with constant angular velocity ${\mathbf{w}}_k$ until the instant $t$ according to the Newton law $\dot{\widehat{\mathbf{R}}}\left(t\right)={\mathbf{w}}_k\times \widehat{\mathbf{R}}\left(t\right)$. As a result, the time-dependent molecular orientation becomes

$$\widehat{\mathbf{R}}\left(t\right)=\widehat{\mathbf{R}}\left(0\right)\cos \left(w_{k}t\right)+{\widehat{\mathbf{R}}}_{\perp }\sin \left(w_{k}t\right)\approx \widehat{\mathbf{R}}\left(0\right)+{\widehat{\mathbf{R}}}_{\perp }\theta \left(t\right),$$ [4]

where $\theta \left(t\right)=w_{k}t$ is the angle of rotation of the molecular axis and ${\widehat{\mathbf{R}}}_{\perp }=\left({\widehat{\mathbf{w}}}_k\times \widehat{\mathbf{R}}\left(0\right)\right)$ is a vector orthogonal to $\widehat{\mathbf{R}}\left(0\right)$. Throughout this study, we use for $\widehat{\mathbf{R}}\left(t\right)$ an approximation linear in time, because the molecule has no time to perform a full rotation during $\tau =1/2\mathrm{\Gamma }$, since $w_k\tau \approx 0.2\widehat{=}11°$, even for a photon energy of $\omega =12$ keV. The rotation of the molecular axis described with Eq. 4 brings dynamics into the rotational Doppler effect and produces in particular a rotational Doppler shift that depends on the instant $t$ of the Auger electron ejection, namely

$$D_{\mathrm{r}\mathrm{o}\mathrm{t}}\left(t\right)={\mathbf{w}}_k\cdot {\mathbf{j}}_p\left(t\right)\approx D_{\mathrm{r}\mathrm{o}\mathrm{t},\mathrm{0}}-\rho {\left(\widehat{\mathbf{R}}\left(0\right)\times \widehat{\mathbf{k}}\right)}^2\left(\widehat{\mathbf{p}}\cdot \widehat{\mathbf{R}}\left(0\right)\right)t.$$ [5]

Here, $D_{\mathrm{r}\mathrm{o}\mathrm{t},\mathrm{0}}$ is the rotational Doppler shift at the instant $t=0$. The parameter $\rho ={\alpha }^3{R}^3{k}^{2}p/I^2$ defines the magnitude of the asymmetric contribution to the line shape, since it is—because of $k^2$—proportional to the kinetic energy of the photoelectron.

With $\rho t^2\lesssim \alpha j_p{\left(w_k/D_{\mathrm{r}\mathrm{o}\mathrm{t},\mathrm{0}}\right)}^2\ll 1$, we can approximate the scattering amplitude $F$ defined in Eq. 3 to

$$\begin{array}{ccc}\hfill & \hfill & F\approx F_0+F_d=-ı{\int }_0^{\infty }dt{e}^{ı\left[\mathrm{\Delta }E+D_{\text{tr}}+D_{\mathrm{r}\mathrm{o}\mathrm{t},\mathrm{0}}+ı\mathrm{\Gamma }\right]t}\hfill \\ \hfill & \hfill & \times \left(1-ı\frac{\rho }{2}{\left(\widehat{\mathbf{R}}\left(0\right)\times \widehat{\mathbf{k}}\right)}^2\left(\widehat{\mathbf{p}}\cdot \widehat{\mathbf{R}}\left(0\right)\right)t^2\right)\hfill \end{array}$$ [6]

by two qualitatively different contributions, namely

$$\begin{array}{ccc}\hfill F_0& =\hfill & -ı{\int }_0^{\infty }dt\exp \left(ı\varphi \left(0\right)t\right)=\frac{1}{\mathrm{\Delta }E+D_{\text{tr}}+D_{\mathrm{r}\mathrm{o}\mathrm{t},\mathrm{0}}+ı\mathrm{\Gamma }},\hfill \\ \hfill F_d& =\hfill & -\rho {\left(\widehat{\mathbf{R}}\left(0\right)\times \widehat{\mathbf{k}}\right)}^2\left(\widehat{\mathbf{R}}\left(0\right)\cdot \widehat{\mathbf{p}}\right){\int }_0^{\infty }dt\exp \left(ı\varphi \left(0\right)t\right)t^2/2\hfill \\ \hfill & =\hfill & \frac{ı\rho {\left(\widehat{\mathbf{R}}\left(0\right)\times \widehat{\mathbf{k}}\right)}^2\left(\widehat{\mathbf{p}}\cdot \widehat{\mathbf{R}}\left(0\right)\right)}{{\left[\mathrm{\Delta }E+D_{\text{tr}}+D_{\mathrm{r}\mathrm{o}\mathrm{t},\mathrm{0}}+ı\mathrm{\Gamma }\right]}^3},\hfill \end{array}$$ [7]

where $\varphi \left(0\right)=\mathrm{\Delta }E+D_{\text{tr}}+D_{\mathrm{r}\mathrm{o}\mathrm{t},\mathrm{0}}+ı\mathrm{\Gamma }$. The instantaneous term $F_0$ describes the Auger process where the molecule has no time to change the orientation. The recoil-induced rotation of the molecular axis is taken into account by the smaller dynamical time-delayed term $F_d$

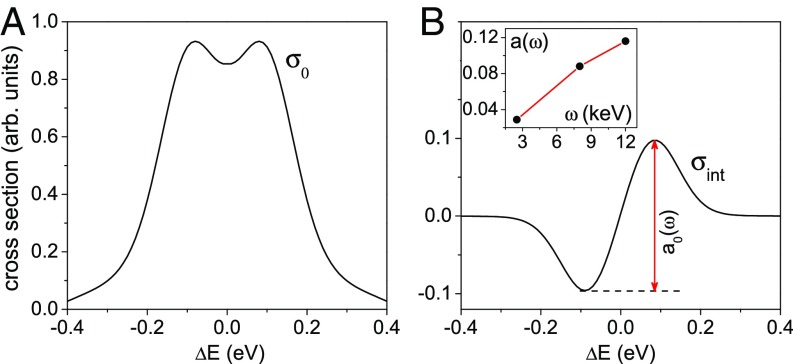
Using Eq. 3 as well as the approximations given for $F$ and $Q_p$, the total cross section becomes $\sigma \left(\mathrm{\Delta }E\right)={\sigma }_0\left(\mathrm{\Delta }E\right)+\eta {\sigma }_{\mathrm{i}\mathrm{n}\mathrm{t}}\left(\mathrm{\Delta }E\right)$, where ${\sigma }_0\left(\mathrm{\Delta }E\right)$ and ${\sigma }_{\mathrm{i}\mathrm{n}\mathrm{t}}\left(\mathrm{\Delta }E\right)$ are the two first nonvanishing terms. As can be seen in Fig. 4A, the first term due to the instantaneous scattering channel described by ${\left|F_0\right|}^2$ results in a Doppler broadening and splitting of the symmetric Auger profile (6, 8, 9):

$${\sigma }_0\left(\mathrm{\Delta }E\right)=\frac{1+\zeta P_2\left(\widehat{\mathbf{k}}\cdot \widehat{\mathbf{p}}\right)}{{\left(\mathrm{\Delta }E+D_{\text{tr}}+D_{\mathrm{r}\mathrm{o}\mathrm{t},\mathrm{0}}\right)}^2+{\mathrm{\Gamma }}^2}.$$ [8]

As defined above, the brackets denote an integration over $\widehat{\mathbf{k}}$ and $\widehat{\mathbf{R}}\left(0\right)$; note the implicit presence of $\widehat{\mathbf{R}}\left(0\right)$ due to $D_{\mathrm{r}\mathrm{o}\mathrm{t},\mathrm{0}}={\mathbf{w}}_k\cdot {\mathbf{j}}_p\left(0\right)={\mathbf{w}}_k\cdot \alpha \left[\widehat{\mathbf{R}}\left(0\right)\times \widehat{\mathbf{p}}\right]$. The splitting refers to the opposite translation and rotational Doppler shifts of two islands in the velocity distribution $W\left(\mathbf{u}\right)$ and angular velocity distribution $W\left(\mathbf{w}\right)$ shown in Fig. 3C. The physical picture of this effect is rather similar to what was discussed in refs. 8 and 9. Despite the fact that the rotational motions are treated classically, there is indeed a pure quantum effect to consider: owing to the well-defined phase between the instantaneous and time-delayed parts of the rotational wave packet in the core-ionized state, there are interferences between these waves. The interference $\mathrm{R}\mathrm{e}\left(F_0{F}_d^{*}\right)$ of instantaneous ($F_0$) and time-delayed ($F_d$) scattering amplitudes leads to the second antisymmetric contribution

$$\begin{array}{ccc}\hfill & \hfill & {\sigma }_{\mathrm{i}\mathrm{n}\mathrm{t}}\left(\mathrm{\Delta }E\right)=-{\sigma }_{\mathrm{i}\mathrm{n}\mathrm{t}}\left(-\mathrm{\Delta }E\right)\hfill \\ \hfill & \hfill & =4\rho \mathrm{\Gamma }\frac{\left(\mathrm{\Delta }E+D_{\text{tr}}+D_{\mathrm{r}\mathrm{o}\mathrm{t},\mathrm{0}}\right)f}{{\left[{\left(\mathrm{\Delta }E+D_{\text{tr}}+D_{\mathrm{r}\mathrm{o}\mathrm{t},\mathrm{0}}\right)}^2+{\mathrm{\Gamma }}^2\right]}^3},\hfill \end{array}$$ [9]

where $f=\left[1+\zeta P_2\left(\widehat{\mathbf{k}}\cdot \widehat{\mathbf{p}}\right)\right]{\left(\widehat{\mathbf{R}}\left(0\right)\times \widehat{\mathbf{k}}\right)}^2{\left(\widehat{\mathbf{R}}\left(0\right)\cdot \widehat{\mathbf{p}}\right)}^2$ (Fig. 4B; details are SI Appendix, Eq. S15). The quadratic term ${\left(\widehat{\mathbf{R}}\left(0\right)\cdot \widehat{\mathbf{p}}\right)}^2$in $f$ is important, since it does not vanish after averaging over $\widehat{\mathbf{R}}\left(0\right)$. It originates from the product $\mathrm{R}\mathrm{e}\left(F_0{F}_d^{*}\right)\cdot Q_{\mathbf{p}}$, where both $F_d^{*}$ and $Q_{\mathbf{p}}\approx 1+\eta \left(\widehat{\mathbf{R}}\left(0\right)\cdot \widehat{\mathbf{p}}\right)+{\eta }^2{\left(\widehat{\mathbf{R}}\left(0\right)\cdot \widehat{\mathbf{p}}\right)}^2/4$ contribute linearly to $\left(\widehat{\mathbf{R}}\left(0\right)\cdot \widehat{\mathbf{p}}\right)$; note that we approximated $\eta \left(\widehat{\mathbf{R}}\left(t\right)\cdot \widehat{\mathbf{p}}\right)$ by $\eta \left(\widehat{\mathbf{R}}\left(0\right)\cdot \widehat{\mathbf{p}}\right)$, since the molecule typically rotates less then $10°$ before the Auger decay. This shows that the term $\eta \left(\widehat{\mathbf{R}}\left(0\right)\cdot \widehat{\mathbf{p}}\right)$ in $Q_{\mathbf{p}}$, which describes the polar anisotropy of the Auger electron emission with respect to the molecular axis, is important for the observation of the dynamical rotational Doppler shift; note that $\eta \left(\widehat{\mathbf{R}}\left(0\right)\cdot \widehat{\mathbf{p}}\right)$ changes sign when $\mathbf{R}\left(0\right)\to -\mathbf{R}\left(0\right)$ (i.e., when the positions of the C and O atoms are exchanged).

Fig. 4.

The dynamical rotational Doppler effect together with the anisotropy of the Auger decay makes the Auger profile asymmetric. (A) The symmetric partial cross section ${\sigma }_0$ is responsible for the translational and rotational Doppler broadening and the Doppler splitting caused by the anisotropy of core ionization. (B) During the Auger process, the molecule has time to change the orientation. The interference of the instantaneous and time-delayed Auger channels results in an antisymmetric contribution ${\sigma }_{\mathrm{i}\mathrm{n}\mathrm{t}}$. The results are convoluted with a Gaussian instrumental function of 0.1-eV width. Inset shows the increase of the asymmetry parameter $a\left(\omega \right)=\eta a_0\left(\omega \right)$ with the photon energy, where $a_0\left(\omega \right)$ is the asymmetry of ${\sigma }_{\mathrm{i}\mathrm{n}\mathrm{t}}$ at given photon energy as indicated in B for $\omega =12$ keV.

For comparison with theory, the experimental spectra of the C1s⁻¹→ d¹Σ⁺ Auger transition measured subsequent to photoionization with photon energies of $\omega =$ 2.5, 8, and 12 keV are displayed in Fig. 2C. This figure clearly shows that the width and the asymmetry increase with the photon energy. We calculated the Auger line shapes based on the above given model for the same photon energies as in the experiment. Moreover, we used the parameters $\zeta =1.78$ and $\eta =0.6$ as well as $\mathrm{\Gamma }=0.043$ eV and convoluted the results with a Gaussian function of 0.1 eV to simulate the experimental resolution. Figs. 2A and 4A show the instantaneous contribution, which is described by ${\sigma }_0$. It leads to a symmetric double-peak structure, which becomes more pronounced with the increase of the photon energy. This Doppler splitting (8, 9) refers to the “two-island” distributions for the velocities and angular velocities that have opposite Doppler shifts [$W\left(\mathbf{u}\right)$ and $W\left(\mathbf{w}\right)$ in Fig. 3C]. To reproduce the experimentally observed peak asymmetry, it is, however, also necessary to take the dynamical term ${\sigma }_{\mathrm{i}\mathrm{n}\mathrm{t}}$ defined by Eq. 9 into account. As can be seen in Fig. 4B, this term is antisymmetric so that it leads, together with ${\sigma }_0$, to asymmetric Auger profiles, as shown in Fig. 2B. These theoretical results agree well with the experimental ones shown in Fig. 2C. To quantify the spectral asymmetry, we introduce a parameter $a\left(\omega \right)$, which is the amplitude of the antisymmetric contribution ${\sigma }_{\mathrm{i}\mathrm{n}\mathrm{t}}$ (Fig. 4B). This asymmetry parameter increases with $\omega$ in the studied energy range $\omega \le 12$ keV. However, we expect its decrease at much higher photon energies when the molecule has the time to perform full rotation during the core-hole lifetime $\tau$.

Conclusions

Recording high-resolution Auger spectra of core-ionized carbon monoxide over a wide excitation energy range offers a unique opportunity to study recoil-induced molecular rotation. This rotational dynamics is probed by time-delayed Auger electron emission. Distinctive Auger spectral features are the rotational Doppler broadening and splitting as well as a line asymmetry: the dynamical contribution has an intrinsic antisymmetry, which makes the whole Auger profile asymmetric. The heart of this asymmetry is the significant change of the molecular orientation during core-hole lifetime. Carbon monoxide is an ideal showcase to illustrate this very general molecular phenomenon of recoil-induced rotation with a period comparable with the core-hole lifetime.

The recent availability of new sources of intense hard X-ray radiation (10–15) will make it possible to study polyatomic molecules with higher moment of inertia and to reach a regime in which the molecule has the time to perform full rotations during the core-hole lifetime. We wish to point out that the main requirement to observe rotational recoil in pure form is the presence of isolated vibrational states in the Auger transitions, which are already known to exist in several triatomic molecules [e.g., ${\mathrm{C}\mathrm{O}}_2$ (31), ${\mathrm{H}}_2$S (32), and OCS (33)]. In addition, such vibrationally resolved Auger spectra can also be expected for other polyatomic molecules (e.g., ${\mathrm{C}\mathrm{S}}_2$, ${\mathrm{N}}_2$O, ${\mathrm{S}\mathrm{O}}_2$, ${\mathrm{C}}_2{\mathrm{H}}_2$, ${\mathrm{C}}_2{\mathrm{N}}_2$, and ${\mathrm{C}}_6{\mathrm{H}}_6$) (34–37). Although this effect was singled out in this work for a specific transition in CO, due to its simple vibrational structure, it will influence any Auger spectra after the emission of fast photoelectrons, even in complex systems. High-energy photons also allow for reaching ro-vibrational states with the effective temperature $10^5-10^6$ K and for creating highly coherent ro-vibrational nuclear wave packets, which can be probed by analyzing X-ray fluorescence or Auger spectra of core-ionized molecules. Furthermore, in gas-phase studies, the orientation of dissociating molecules is frequently determined by detecting the direction of the dissociation fragments. This approach is based on the axial recoil approximation (29, 30) (i.e., the assumption that the molecule does not rotate before dissociation). In this context, this study clearly shows that this widespread approximation is not valid in the hard X-ray region.

This experiment illustrates that hard X-ray electron spectroscopy at high resolution, which recently became available, offers unprecedented possibilities to monitor ultrafast molecular dynamics. Moreover, full control over all of the degrees of freedom of highly excited molecular cations with very high quantum numbers is a prerequisite for exploring the transitions between quantum and classical worlds.

Materials and Methods

Experiment.

The experiment was performed at the Synchrotron SOLEIL using the HAXPES (Hard X-ray PhotoElectron Spectroscopy) end station (38) of the GALAXIES beamline (10), which covers the 2.3- to 12-keV photon energy range and provides horizontal polarization. The energy of the incoming X-rays is selected by a liquid nitrogen-cooled fixed exit Si(111) double-crystal monochromator, and electrons are analyzed by an EW4000 Scienta hemispherical analyzer with a lens axis that is set parallel to the $\mathbf{e}$ vector as shown in Fig. 3A and ref. 38. The spectrometer lens mode used for the measurements corresponds to an acceptance angle of $\mathrm{45}°$. Pure carbon monoxide (99.997%) from Air Liquide was used, and the pressure in the vacuum chamber was kept constant around $1\times 10^{-5}$ mbar. The electron spectrometer was operated at a pass energy of 100 eV, providing a kinetic energy resolution of about 100 meV. The calculations were performed using both semiclassical and strict quantum approaches and are based on the theoretical method outlined in SI Appendix.

Data Availability.

The datasets generated and/or analyzed during this study are available from the Laboratory of Physical Chemistry-Matter and Radiation (CNRS) repository, https://lcpmr.cnrs.fr/content/relaxation-de-molecules-excitees-en-couche-interne/downloads.