Guiding the first biopsy in glioma patients using estimated Ki-67 maps derived from MRI: conventional versus advanced imaging

Abstract

Background

Undersampling of gliomas at first biopsy is a major clinical problem, as accurate grading determines all subsequent treatment. We submit a technological solution to reduce the problem of undersampling by estimating a marker of tumor proliferation (Ki-67) using MR imaging data as inputs, against a stereotactic histopathology gold standard.

Methods

MR imaging was performed with anatomic, diffusion, permeability, and perfusion sequences, in untreated glioma patients in a prospective clinical trial. Stereotactic biopsies were harvested from each patient immediately prior to surgical resection. For each biopsy, an imaging description (23 parameters) was developed, and the Ki-67 index was recorded. Machine learning models were built to estimate Ki-67 from imaging inputs, and cross validation was undertaken to determine the error in estimates. The best model was used to generate graphical maps of Ki-67 estimates across the whole brain.

Results

Fifty-two image-guided biopsies were collected from 23 evaluable patients. The random forest algorithm best modeled Ki-67 with 4 imaging inputs (T2-weighted, fractional anisotropy, cerebral blood flow, K^trans). It predicted the Ki-67 expression levels with a root mean square (RMS) error of 3.5% (R² = 0.75). A less accurate predictive result (RMS error 5.4%, R² = 0.50) was found using conventional imaging only.

Conclusion

Ki-67 can be predicted to clinically useful accuracies using clinical imaging data. Advanced imaging (diffusion, perfusion, and permeability) improves predictive accuracy over conventional imaging alone. Ki-67 predictions, displayed as graphical maps, could be used to guide biopsy, resection, and/or radiation in the care of glioma patients.

Key Points.

1. Proliferative activity in gliomas can be predicted with MRI to guide biopsy and therapy.

2. Machine learning of clinical imaging data can be used to predict quantitative pathological markers.

Importance of the Study.

At the time this study was conceived there were very few brain tumor imaging studies that attempted to make quantitative correlations to a hard histopathologic gold standard, and it was considered unlikely that such correlations could be successfully made. Most practitioners still do no more than qualitative imaging interpretation, believing that the level of prognostic information that histopathology yields is out of reach for imaging. The published evidence to the contrary is still sparse and incomplete. Our study shows proof-of-concept that modern imaging and machine learning techniques can make clinically useful quantitative predictions of important histopathologic findings such as proliferation index. These methods can dramatically increase the (already high) value of imaging in the care of brain tumor patients, and point the way for similar advances to be made in multiple other tumors and conditions also.

Ki-67 is a nuclear antigen expressed only by cells that have left the resting (G0) state and are in the mid G1, S, G2, or the M phase of the cell cycle.¹ The background levels of Ki-67 expression in the normal brain are very low.^2,3 Ki-67 levels correlate with higher tumor grade and poor prognosis,⁴ although molecular alterations such as isocitrate dehydrogenase (IDH) mutation, 1p/19q codeletion, and telomerase reverse transcriptase promoter mutation are thought to be more fundamental predictors of prognosis, as illustrated by their emphasis in the 2016 revision of the World Health Organization (WHO) CNS tumor classification.^5,6 The accuracy of tumor grade, the final synthesis of prognostic information, depends critically on accurate biopsy sampling of the highest grade disease present, and is vulnerable to undersampling.⁷ Targeting highly proliferative areas should increase the likelihood of sampling highly malignant tumor areas, which will improve the accuracy of prognosis.

Conventional MRI, the mainstay of imaging care for brain tumor patients, has been augmented by multiple advanced sequences: diffusion, perfusion, and permeability imaging. These functional imaging methods provide additional information about tissue pathology.⁸

There is a gap in knowledge regarding the quantitative strength of radiologic-pathologic correlations for Ki-67 expression. We show how, and with what degree of confidence, predictive hypotheses about Ki-67 might be made from imaging data inputs. Specifically, in this study we use: (i) tight correlation between imaging and pathological data at the resolution of modern stereotactic biopsy technology, (ii) an extensive set of modern imaging techniques (including anatomic, diffusion weighted, permeability/dynamic contrast enhanced [DCE], and perfusion/dynamic susceptibility contrast [DSC] imaging techniques) matched to (iii) quantitative histopathology for proliferation/Ki-67, in (iv) a reasonable number of glioma patients/biopsies comprising most relevant tumors and grades encountered in adult practice. We also made use of the latest machine learning techniques to analyze our data into clinically applicable models.

We hypothesized that MR contains sufficient information to quantitatively estimate the Ki-67 expression levels of biopsies. We demonstrate that Ki-67 levels can be estimated to clinically useful levels of certainty using a relatively small set of non-redundant imaging inputs, displayed as clinically informative graphical maps, and can indicate which imaging sequences are best suited for such predictions.

Materials and Methods

Patients

This was a prospective, institutional review board–approved clinical trial compliant with the Health Insurance Portability and Accountability Act and requiring signed consent. Adult patients with treatment-naïve glioma were consecutively recruited based on specific criteria for inclusion/exclusion (see Supplementary Table 1 for full list of criteria).

Biopsy Sites—Selection and Pathology Analysis

Biopsy samples were collected using either a Nashold-type needle prior to the opening of the dura or surgical forceps after dural opening but before any resection or debulking. The surgical technique specifically focused on minimizing brain shift, which was negligible for needle biopsies and minimal for open forceps biopsies. In all cases, cranial neuronavigation software (Brainlab) was used to guide the biopsy and record the spatial coordinates as the sample was collected.

Up to 5 biopsy targets were specified per patient, based on neuroradiological and surgical assessments of either the anatomic imaging findings or areas of relatively high cerebral blood volume (CBV), high K^trans, and/or low apparent diffusion coefficient (ADC). The specific procedure is as follows: biopsy sites were first targeted using conventional imaging findings followed by the addition of advanced imaging data from diffusion, perfusion, and DCE sequences. The neurosurgeon/radiologist first selected a biopsy target using standard clinical procedures while blinded to advanced imaging data. These “conventional” targets were placed in areas of contrast enhancement or T2 hyperintensity closest to the surface of the tumor in the planned operative bed. After being unblinded to the imaging data, “advanced” targets were placed in areas of high CBV, high K^trans, or low ADC (restricted diffusion) (in order of importance). The conventional and advanced targets were considered the same if they were less than 3 mm apart. Additionally, samples were collected along the needle tract as it traversed other tissue fated for resection, with tumor border and normal brain samples obtained where possible. These selection procedures are close to regular clinical practice at our institution, and ensure a realistic range of values for Ki-67 in our samples.

A board-certified neuropathologist performed pathological assessment on a per-sample basis while blinded to imaging data. Biopsies were immunostained for cell proliferation (Ki-67; MIB-1 antibody, Dako Denmark) and reported as the Ki-67 index (% positive nuclei).

For each biopsy, a control volume of interest (VOI) was placed in normal-appearing white matter contralateral to the lesion by an oncologic neuroradiologist. These “virtual biopsies” balanced the high number of tumor biopsies with data from normal tissues. For virtual biopsy sites, Ki-67 expression was assumed to be absent (0%).^3,9–12

Imaging Sequences and Maps

Four categories of imaging were obtained for each patient: anatomic/conventional, diffusion, perfusion, and permeability.^13–15 We chose these categories of imaging because metrics such as decreased diffusivity and increased blood flow have been linked to tumor presence and malignancy.^16,17 As malignant tumors are generally more actively proliferating, we suspected these metrics will also be associated with Ki-67 expression. In order to identify the strongest specific predictors, we acquired a wide range of imaging sequences and parametric maps and removed redundant and non-informative variables with aggressive variable selection.

Patients were imaged for surgical planning on clinical GE 3.0T MR systems as detailed in the the Supplementary Material (section S1.1, Supplementary Tables 2 and 3). Specific imaging parameters are detailed in Supplementary Table 4 and Supplementary Table 5). Conventional images included T1, T1 post-gadolinium (T1C), T2, T2*/susceptibility, fluid attenuation inversion recovery (FLAIR), and susceptibility-weighted angiography (SWAN) sequences.¹⁸ These sequences are routinely used in the clinic and provide structural anatomic information and localize the tumor. Advanced imaging included: diffusion, perfusion, and permeability imaging. Diffusion images were processed to maps of ADC, exponential ADC, and fractional anisotropy (FA).^19–21 Permeability (DCE) images were processed using NordicICE (Nordic Neuro Lab) to parameter maps using the extended Tofts pharmacokinetic model: K^trans, k_ep, v_p, and v_e.^22–24 Also calculated were the parameters of: wash-in (upslope of the time-signal curve), wash-out (downslope), time to peak, area under the time-signal curve, and peak enhancement value. The DCE sequence serves as a preload for the perfusion (DSC) sequence, which was processed to yield maps of leakage-corrected relative CBV, relative cerebral blood flow (CBF), mean transit time, delay, and K2 (leakage parameter, cutoff of 0.1).^25–27

Image Registration, Normalization, and VOI Extraction of Imaging Values

Brain-extracted images were registered to the T2 reference image.²⁸ Image registration was performed using the open-source program Advanced Normalization Tools (ANTs²¹), which first used a rigid, 6 degrees-of-freedom (DOF), mutual-information (MI) based registration for each image volume, followed by an affine, 12 DOF, MI-based registration. Note that the registration performance of the ANTs package has been previously evaluated for brain applications.²² Anatomic image intensities were independently normalized by a linear transformation so that the average intensity of internal reference tissues (gray matter, white matter, cerebrospinal fluid [CSF]) was consistent between patients. To do this, regions of interest (ROIs) were placed in the ventricles (for CSF), the putamen in the lentiform nucleus (for gray matter), and normal-appearing white matter to construct internal intensity reference standards for quantitative analysis. Each image was independently linearly transformed such that the average CSF, gray matter, and/or white matter voxel intensities inside the ROI had mean 0 or 1, respectively, with the specific pair of tissues used depending on the sequence being normalized. This process enforces a consistent intensity normalization across the study population (Supplementary Fig. 1) and reduced interpatient and interscanner variability.²⁹ The Supplementary Material (section S1.2, Supplementary Fig. 1) provides details.

Five-millimeter diameter spherical VOIs were centered on the biopsy coordinates, and mean imaging values from both real and virtual biopsy locations were recorded (Supplementary Fig. 2), meaning that each biopsy site had 23 imaging parameters associated with it (Supplementary Tables 4 and 5). The 5 mm diameter was chosen based on the physical size of the tissue sample. Needle biopsies produce a tissue sample approximately 10 mm long, of which half is used for pathological analysis. So, a 5 mm diameter VOI contains the whole sample. For consistency, the same size 5 mm VOI was used for forceps biopsies as well. The level of spatial uncertainty due to registration is small, less than about 1.5 mm.²⁸

Variable Reduction and Modeling of Image Features to Estimate Ki-67

We evaluated our modeling performance using 5-fold cross validation by randomly dividing our data pool into 5 roughly equal parts (folds). We divided the set of real biopsy samples equally into 5 random folds. Then, the virtual biopsies were assigned to the same folds as their corresponding real biopsies, so each fold was composed of half real and half (matched) virtual biopsies. We performed variable selection and trained a random forest model on the combined data from 4 of the 5 folds. This model was then used to estimate the Ki-67 expression in the remaining, fifth, fold. We repeated this process 5 times: once for each combination of 4 training folds. Cross validation allowed us to estimate the generalization error and the sensitivity of the model to data partitioning. We implemented variable selection and modeling using R.³⁰

Variable reduction serves to (i) identify the most informative predictive variables and (ii) simplify the resulting models by reducing collinearity, making them more generalizable. Based on clinical knowledge, we suspected that images or maps from the same imaging family (anatomic, diffusion, perfusion, and permeability) contained substantial redundant information. We used only the dominant predictor, as defined by the random forest algorithm (see Supplementary section S1.3), from each imaging family in order to minimize and reduce this overlap in information to a total of 4 predictors. Finally, to assess the added benefit of advanced imaging, we repeated the variable selection process, but using only conventional imaging sequences (T1, T1C, T2, FLAIR, T2*, SWAN), and selected the most important 4 inputs from this set.

We chose to use the random forest algorithm based on past success in medical imaging applications.³¹ The random forest is an ensemble classifier that uses many voting decision trees to categorize new data. Each decision tree is trained on a subset of the input variables and training data to learn different relationships between the training data. We measured the model performance using the coefficient of determination (R²) between observed and estimated values in the testing fold³² (see Supplementary Fig. 3 for a schematic of this process and Supplementary section S1.3 for a description of R²), the root mean square error (RMSE), and the maximum error. Additionally, we tested other popular machine learning algorithms, including single decision trees, support vector machines, neural networks, and elastic net linear regression,^33,34 but did not find any that outperformed the random forest.

After evaluating our best models based on all available imaging (conventional plus advanced) or just conventional sequences, we combined the results of the 5 separate variable selections into a single variable set based on the consensus of the 5 selections. This allows us to define a final model with patient-independent variable selections. We repeated the cross validation with these fixed variable sets to estimate final accuracy.

Mapping of Ki-67 Predictions

Based on the fixed variable selections for our best performing approach (Supplementary Table 6), we chose a single 4-variable set (T2, FA, CBF, K^trans) to generate quantitative maps of estimated Ki-67. We estimated the Ki-67 for each voxel in a patient’s brain using a leave-one-patient-out scheme. This represents the closest approximation to a clinical implementation of the algorithm and uses all the available data while maintaining independence in the resulting maps. Each map was smoothed using a 2 mm Gaussian filter.

Results

Patients

Thirty-one patients were recruited from January 2013 to May 2016 (demographics and clinical data are given in Tables 1 and 2). Exclusions were due to various technical and surgical difficulties (Fig. 1), leaving 23 evaluable patients with 2–4 biopsies each, for a total of 52 real biopsies (average of 2.3 per patient) and 52 virtual biopsies. Thirty-four biopsies were collected with the Nashold-type needle and 18 were collected with forceps. Summary statistics of the 23 evaluable patients are provided in Table 1.

Table 1.

Patient demographic information

N = 23 Patients
Age, mean	43.9 ± 16.9 y; range 21–80
Sex	14 Females (42.3 ± 16.0 y; range 21–75) 9 Males (46.4 ± 18.8 y; range 28–80)
Ethnicity (white/black/Hispanic/Asian)	17/2/4/0
WHO grade (I/II/III/IV)	0/7/9/7
Biopsy samples/patient	2.26 ± 0.54
No. of biopsy samples in final analysis	52

Patients were prospectively recruited between January 2013 and May 2016. A summary of the 23 evaluable patients is listed here and a summary of exclusions is given in Fig. 1.

Table 2.

Pathology description

Patient WHO Grade	# Patients	# Real Samples	Ki-67 (% Pos. Nuclei)
II	7	13	2.36 ± 1.07
III	9	21	6.04 ± 3.93
IV	7	18	12.59 ± 13.17
Total	23	52	7.39 ± 9.00

Number of real biopsy samples in each WHO grade, along with quantitative pathology values (mean ± SD) for both real and virtual biopsies.

Fig. 1.

Patient recruitment. Among the 26 patients with successful tissue harvest of a total of 64 biopsies, additional patient exclusion occurred due to missing DCE imaging (1 patient, 3 biopsies) and missing histological values due to lack of analyzable tissue (2 patients, 4 total biopsies). Further exclusion of biopsies occurred due to poor VOI placement (n = 3 biopsies), insufficient quality of tissue for pathology analysis (n = 1), and missing grade (n = 1). When a biopsy site was excluded, its corresponding imputed virtual biopsy site was also excluded. Note that 5 biopsies had SWAN data imputed as median values. In the final analysis, the 52 evaluable samples were repeatedly split into 80% training and 20% validation datasets for cross validation of variable selection and model building.

Biopsy Sites—Selection and Pathology Analysis

Patients were fairly evenly distributed between low-, mid-, and high-grade tumors. We had 13 biopsies from 7 grade II gliomas, 21 biopsies from 9 grade III gliomas, and 18 biopsies from 7 grade IV gliomas. The lack of grade I disease is expected in a non-pediatric population. The average Ki-67 measured was 7.39% and correlated with tumor grade (Table 2).

Image Sequences, Processing, Registration, Normalization, and VOI Extraction of Imaging Values

SWAN image coverage was lacking for 5 biopsies in 2 patients and was imputed as median values. The composite spatial distribution of real and virtual biopsies is shown in Supplementary Fig. 2.

Variable Reduction and Modeling Results

There were strong correlations between images and derivatives from the same family (Supplementary Fig. 4A). Variable reduction using the random forest variable importance ranking reduced the variability in R² values across folds compared with using all variables, which suggests increased generalizability (Table 3). The variable selections were also highly consistent between folds of cross validation (Supplementary Table 6). Principal component analysis (Supplementary section S2.0 and Supplementary Table 7) was attempted but did not improve model performance.

Table 3.

Predictive modeling performance

Metric	Variables (#)	Conventional	Conventional Plus Advanced
R2	All variables	0.508 ± 0.093 (6)	0.660 ± 0.201 (23)
	RF rank	0.504 ± 0.065 (4)	0.749 ± 0.137 (4)
	RF (fixed variables)	0.496 ± 0.083 (T2, T1C, FLAIR, T1)	0.747 ± 0.168 (T2, FA, CBF, Ktrans)
RMSE (%)	All variables	5.34 ± 2.25	4.19 ± 1.78
	RF rank	5.47 ± 2.33	3.85 ± 1.82
	RF (fixed variables)	5.40 ± 2.34	3.46 ± 1.39
Max error across all folds (%)	All variables	30.50	27.03
	RF rank	28.94	24.93
	RF (fixed variables)	28.75	20.49

RF = random forest. Summary of the performance of the random forest model using variables selected by random forest rankings. Accuracy was estimated using 5-fold cross validation. Conventional = conventional MR only (T1, T2, T1 contrast enhanced, FLAIR, SWAN, T2*). Conventional plus advanced = conventional imaging plus diffusion, permeability and perfusion imaging. Numbers in parentheses indicate the number of variables included to obtain the predictive performance stated (see text).

As a baseline we used all 23 imaging inputs and found an average predictive performance of R² = 0.660 ± 0.201, RMSE = 4.19% ± 1.78%. In order to reduce the number of input variables, we started with all of the conventional plus advanced imaging and selected the dominant predictor from each family of sequences. For conventional, diffusion imaging, and perfusion imaging T2, FA, and CBF were selected in all 5 folds of cross validation. For permeability (DCE) imaging, K^trans was selected in 3 of 5 folds, making it the dominant predictor. The predicted and observed values using a random forest trained on these single dominant predictors from each family within each fold were significantly correlated (P < 0.0001) with R² = 0.749 ± 0.137. The RMSE was 3.85% ± 1.82% and the maximum error in any fold was 24.93%, summarized in Table 3.

To assess the benefit of the advanced imaging in predicting Ki-67, we repeated the cross validation using conventional imaging data only. The top 4 predictors were T2, T1C, FLAIR, and T1 in 3 folds, 1 fold selected T2* instead of T1C, and 1 fold selected T2* and SWAN instead of T1 and T1C. This model performed slightly worse than the model based on conventional plus advanced imaging with R² = 0.504 ± 0.065 and a slightly higher RMSE of 5.47% ± 2.33%. The correlation between predicted and observed values was still significant (P < 0.001).

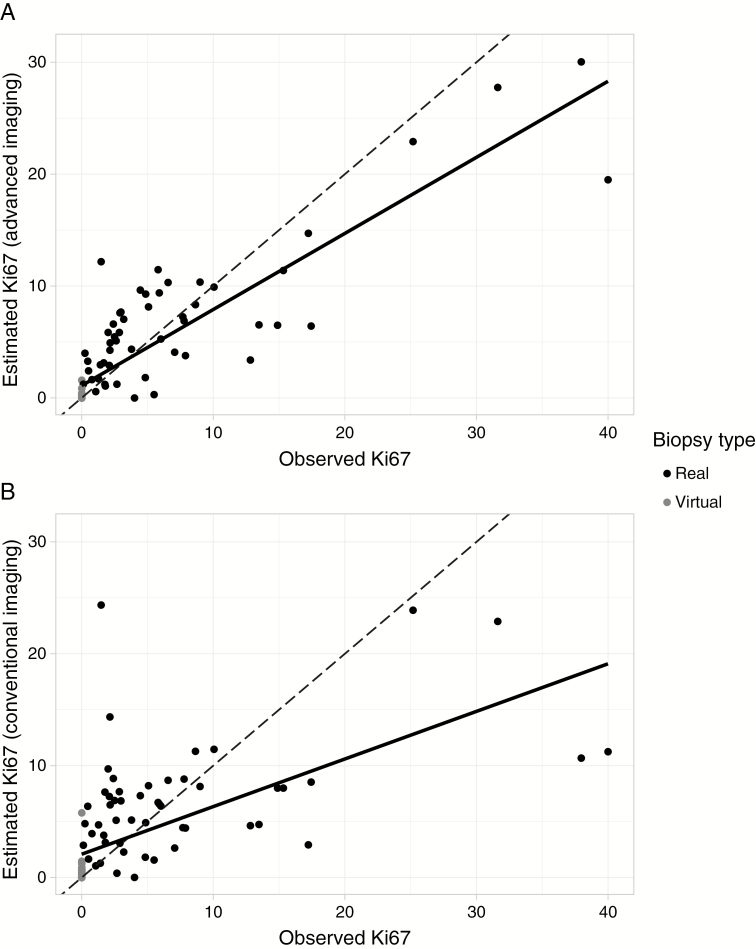
Finally, we aggregated the results of the repeated variable selection from each of the 5 folds of cross validation to create a single set of input parameters for clinical use. From conventional, diffusion, and perfusion imaging, T2-weighted, FA, and CBF, respectively, were obvious choices. For permeability imaging we chose K^trans because it was selected in 60% of folds. We repeated the cross validation using these 4 variables (T2, FA, CBF, K^trans; Supplementary Fig. 4B) on every fold. With these fixed variable selections, the model performance increased to R² = 0.747 and RMSE of 3.46%. Similarly, when we considered conventional sequences only, the variable selections were highly consistent and we selected T2, T1C, FLAIR, and T1 as the conventional fixed variable set (Supplementary Fig. 4C). However, using only these variables left the model performance unchanged at R² = 0.496 and RMSE of 5.4%. The predicted and observed Ki-67 for the final models are shown in Fig. 2, demonstrating the superiority of conventional plus advanced over conventional imaging only, using these fixed variable sets.

Fig. 2.

Model predictions. Plots show the observed Ki-67 at each biopsy location compared with predicted Ki-67 from a random forest using 5-fold cross validation. Each point represents a prediction made on a member of a fold not used for training during cross validation. The dashed lines indicate perfect agreement (predicted equals observed) and the solid line is a best-fit. In both plots the correlation between predicted and observed values is significant (P < 0.0001). (A) The final model using 4 imaging inputs (T2, FA, CBF, K^trans) based on conventional plus advanced imaging gives good estimates of Ki-67 compared with the ground truth immunohistochemistry (best fit line: predicted = 0.680 * observed + 1.10, R² = 0.771). (B) Using conventional imaging data, only the model performance decreases, as shown by the weakened correlation between predicted and observed values (best fit line: predicted = 0.426 * observed + 2.09, R² = 0.397). There are also considerably more outliers using conventional imaging only. The R² values for these plots are comparable to the average R² values from cross validation listed in Table 3, which calculates the correlations between predicted and observed values for each fold separately and averages.

Maps of Predicted Ki-67 Expression

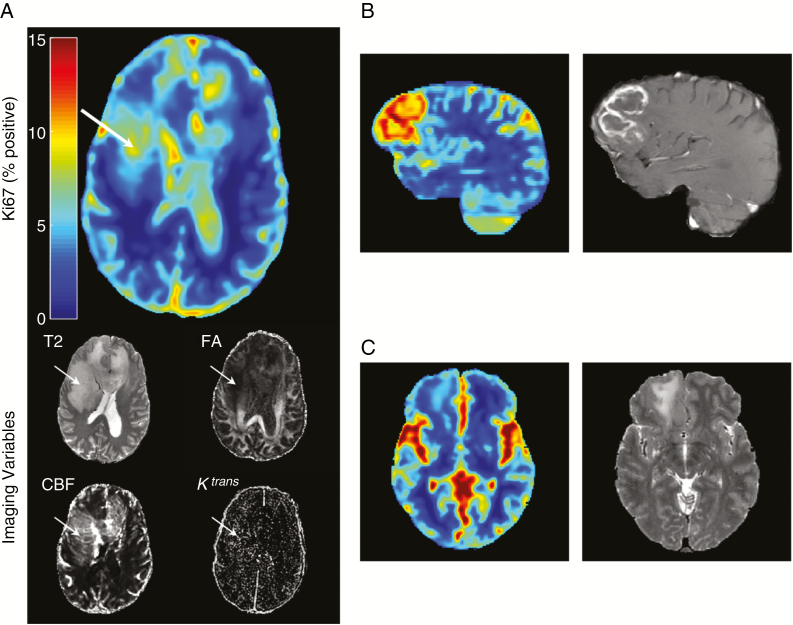
Ki-67 estimate maps were generated for all patients (representative examples are shown in Fig. 3) with observations: first, the highest estimated Ki-67 was almost always inside the contrast enhancing volume for enhancing tumors (panel B). This is consistent with clinically known proliferation-leakage associations. Second, for some non-enhancing tumors, areas of high estimated Ki-67 provided a clear biopsy target, often different from the closest-to-brain-surface rule usually employed (panel A). Finally, for some low-grade (II) tumors, estimated Ki-67 was homogeneous and low with no local maximum, reflective of their low actual Ki-67 values and quiescent biology (panel C).

Fig. 3.

Quantitative maps. Ki-67 map generated using the random forest trained on the 4 imaging inputs shown in axial view: T2-weighted image, FA, K^trans transfer constant, and CBF. Areas of increased estimated Ki-67 (white arrow) likely contain more actively dividing tumor cells and provide a better target for biopsy. In tumors like (A), a grade III anaplastic astrocytoma, sampling the most malignant area of the tumor is important for correctly grading the tumor. This tumor did not demonstrate contrast enhancement, which is clinically used for biopsy target selection, when present. (B) for enhancing tumors (glioblastoma multiforme shown), the highest estimated Ki-67 generally corresponds to enhancement (the currently used clinical target for biopsy selection). (C) For low-grade tumors (shown grade II diffuse glioma) the estimated (and measured) Ki-67 is generally low. Seemingly raised Ki-67 values in the sulci and cisterns are artefactual, but are unlikely to confuse an experienced clinician.

Discussion

Predictive models using conventional plus advanced imaging and a random forest model can estimate the Ki-67 expression of biopsies across all grades with an R² of 0.75 and an average error of about 3.5%. This error is much smaller than the range of Ki-67 values found in our samples (0.13% to 39.9%). Therefore, it is reasonable to expect that extrapolated maps like Fig. 3 should accurately localize regions of high and low Ki-67 expression prospectively in new patients using only the dominant 4 input variables (T2, FA, K^trans, and CBF). When only conventional imaging data are used for predictions, R² is 0.50 and the error is 5.4%. These results indicate: (i) imaging data can be used to make clinically useful predictions of a quantitative pathological parameter, Ki-67, (ii) advanced imaging (diffusion, perfusion, and permeability) adds considerable value to the predictive accuracies obtained over conventional imaging alone, and (iii) graphical maps of Ki-67 expression can be generated to aid image-guided therapies.

Our results generally agree with other studies comparing Ki-67 measurements with imaging. Studies by Price and Barajas found that perfusion imaging (CBV) was significantly correlated with Ki-67 in stereotactic biopsies of glioblastoma patients.^35,36 We also found this correlation, but in our final model we selected CBF, a near relation of CBV, since it appeared more often in our variable selection procedure. Barajas also found T1 contrast enhancement to be associated with proliferation, similar to our findings (Fig. 3B). However, in our study we found T2-weighted image intensity to be a better predictor of Ki-67. This might be because we combined values from a variety of grades and normal brain, as opposed to sampling from the enhancing volumes of glioblastomas.

Ki-67 estimation accuracy improved when advanced imaging data were added to conventional imaging data. The informative nature of advanced imaging agrees with clinical practice. However, the quantification of this improvement (R² improved from 0.496 to 0.747 and error from 5.4% to 3.5%) has to our knowledge never been published previously. This provides quantitative evidence for the usefulness of advanced imaging in addition to routine conventional imaging.

Ki-67 predictions, presented as graphical maps, are clinically useful to plan image-guided therapies, and can help overcome the pitfall of undersampling.³⁷ For this purpose, it stands independent of other prognostic factors like IDH1,^6,38 and correlates well with tumor grade.³⁹ We are not aware of previous work presenting Ki-67 predictive models in a graphical format, although nuclear density maps and tumor infiltration maps have been presented in work by Durst,⁴⁰ Akbari,⁴¹ and Chang.⁴² However, Akbari and colleagues had no histopathologic ground truth in their modeling and the study by Chang et al included only T1 post-contrast, FLAIR, and ADC measurements. Both Durst and Chang report correlations between predicted and observed values around R² ~ 0.55, considerably lower than our result of R² = 0.75. In the same way that clinical imaging is used to inform and guide treatment, we propose maps like the ones presented currently as a tool to improve the ability for clinicians to deliver effective therapy.

Limitations

Our study has a relatively small dataset (n = 23 patients, 52 biopsy sites) but still did yield statistically significant results and correlations. Stereotactic biopsy collection is expensive and time-consuming. The use of contralateral normal VOIs could be challenged due to the fact they are not real biopsies. However, this practice is justified based on well-documented pathology values for normal tissue and the ethical constraints of removing of tissue from normal brain.

We had fewer high Ki-67 expressing biopsies than preferred, even though the clinical tumor grades were well distributed. This deficit reflects the clinical problem of sampling error and false undergrading in the face of tumor heterogeneity, as clinical tumor behavior follows the highest grade present. This reduces our predictive power for predicting very high Ki-67 and indicates the need for larger datasets.

Future Work

While we are able to achieve accurate estimation of Ki-67, there are still many challenges to overcome before a “virtual” biopsy from a mathematical model can compete with gold standard tissue biopsy. Perhaps one of the greatest is overcoming the substantial variability in MR image data across vendor platforms, sequence parameters, and institutions. Dynamic contrast imaging is further complicated by sensitivity to post-processing techniques. Training data for our models were carefully collected and curated to minimize these sources of uncertainty, which allows better results but limits the immediate generalizability. The next logical step is a validation trial where prospective predictions are compared with the results of tissue biopsy for patients outside the training cohort.

We foresee that much better predictive models could be constructed in future with more data of similar quality. Further future goals will link our imaging information to genomic information, 1p/19q codeletion status, and methylation status of O⁶-methylguanine-DNA methyltransferase, as well as clinical information, such as survival⁴³ and recurrence.⁴¹ Another common target for imaging-genomic correlation is IDH1 mutation status. However, IDH mutations are known to be very homogeneous within tumors and thus predictions of IDH status are likely better suited to whole-tumor analysis rather than to spatially precise tissue samples.⁴⁴

In conclusion, a few well-chosen clinical MR sequences with machine learning modeling can be used to quantitatively estimate the histopathologic proliferation marker, Ki-67, to clinically useful accuracies in glioma patients. Ki-67 predictions can be presented as graphical maps for image-guided therapies such as biopsy, surgery, and radiation, and have great potential to improve the care of glioma patients. Further clinical trials are justified to verify and build on these findings.

Funding

This work was partially supported by the National Institutes of Health and National Cancer Institute grants R01-CA194391, R01-CA160736 and Cancer Center Support grant P30 CA016672 (Biostatistics Shared Resource) to V.B. The Baylor College of Medicine Medical Scientist Training Program and the Cullen Trust for Higher Education Physician/Scientist Fellowship Programs supported J.S.L. during the duration of this research. The John S. Dunn Sr. Distinguished Chair in Diagnostic Imaging (to Dr William A Murphy) and M D Anderson Cancer Center Internal Research Grant and Clinical Research Support mechanisms contributed funding to support data collection.

Conflict of interest statement.

The authors disclose no conflicts of interest related to this work.

Authorship statement.

Study design: EDHG, JSL, JW, SP, JH, DS. Figures: EDHG, JSL, GNF, DF, DS. Data collection, analysis, interpretation: EDHG, JSL, JW, SP, JDH, JH, GNF, VB, DF, DS. Manuscript writing: EDHG, JSL, JDH, JH, GNF, DF, DS.