Advanced methods for accessing protein shape-shifting present new therapeutic opportunities

Abstract

A protein is a dynamic shape-shifter whose function is determined by the set of structures it adopts. Unfortunately, atomically-detailed structures are only available for a few conformations of any given protein, and these structures have limited explanatory and predictive power. Here, we provide a brief historical perspective on protein dynamics and introduce recent advances in computational and experimental methods that are providing unprecedented access to protein shape-shifting. Next, we focus on how these tools are revealing the mechanism of allosteric communication and features like cryptic pockets, both of which present new therapeutic opportunities. A major theme is the importance of considering the relative probabilities of different structures and the control one can exert over protein function by modulating this balance.

A brief history

A protein has the potential to adopt an enormous number of different structures. For example, a small protein with 100 amino acid residues has ~200 rotatable bonds along its backbone. Assuming that each of these rotatable bonds can adopt one of two dominant rotameric states, then such a protein can adopt approximately 10⁶⁰ different backbone structures, not to mention the additional possible structures if one considers the rotatable bonds in side-chains. Only a small fraction of these structures is capable of performing a given function. The process by which a newly synthesized or unfolded protein transitions to one of these functional structures is called protein folding and represents a particularly dramatic example of protein shape-shifting (see Glossary). If a protein sampled 1000 different backbone structures each second, it would take about 10⁴⁰ times the age of the universe to enumerate every possibility. The impossibility of enumerating all possible structures is often called Levinthal’s Paradox [1]. The number of potential structures is dramatically reduced by the fact that many of the configurations considered above are infeasible because no pair of atoms can occupy the same volume in space, called the excluded volume principle. However, there are still an enormous number of different structures that do not violate the excluded volume principle.

The set of possible structures a protein can adopt is often conceptualized as a vast, multidimensional landscape, called an energy landscape (Fig. 1). This term derives its name from the fact that each structure a protein could adopt has an associated energy that results from the interactions between different atoms in the protein and its surroundings. The probability of a protein adopting a given structure on this energy landscape is proportional to the exponential of the structure’s energy. Therefore, a protein spends exponentially more time in valleys than it does crossing the higher energy peaks separating different minima. The lowest energy structure is often referred to as the ground state and will have the highest probability of all the different structures a protein could adopt. Other higher-energy states are often referred to as excited states and will have lower probabilities than the ground state. Many of these excited states have negligible probabilities because their energies are so much higher than the ground state. This train of thought leaves an open question: how many different structures can a typical protein effectively adopt?

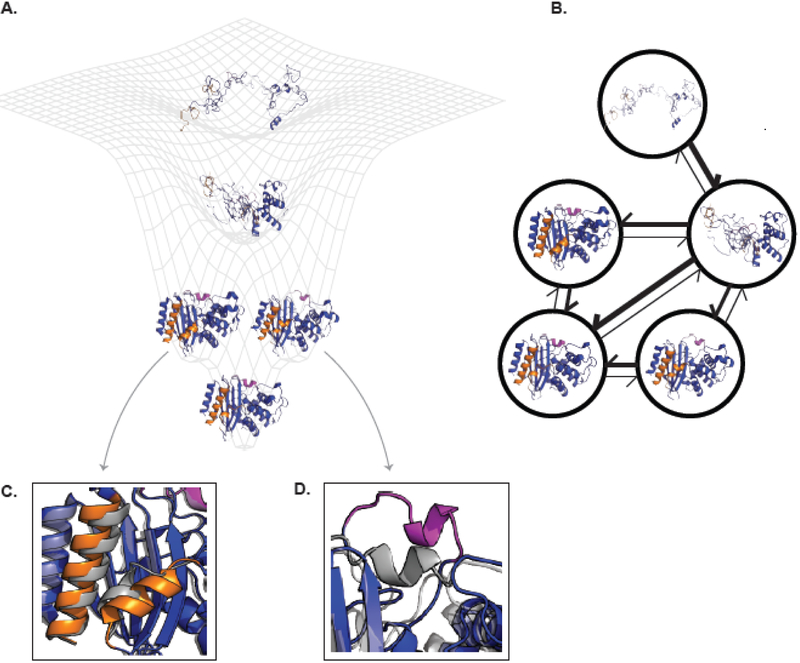
Figure 1. The connection between energy landscapes, MSMs, and protein shape-shifting.

(A) A simplified energy landscape for TEM β-lactamase. The ground state (lowest energy, highest probability state) is represented by an apo crystal structure (PDB ID 1JWP) and is shown in the bottom minima. The next two highest energy excited states each have a different cryptic pocket. The conformation on the left comes from a ligand-bound crystal structure where helices 10 and 11 (orange) have separated (PDB ID 1PZO). The structure on the right comes from computer simulations that uncovered the opening of the omega-loop (pink). The next highest energy state is a folding intermediate where the alpha-helical domain is folded while the alpha-beta domain is unfolded. The highest energy (and lowest probability) structure shown is the unfolded state. (B) The corresponding MSM for TEM β-lactamase. Each node corresponds to one of the structural states from A. The weight of the arrows is related to the probability of transitioning between the two states connected by the arrow. The same coloring is used as in (A). (C) and (D) show enlarged views of the orange and pink cryptic pockets, respectively. Each is overlaid on the apo crystal structure (gray) to highlight how the protein’s conformation has changed. Abbreviation: MSM, Markov state model.

Early experiments suggested that a protein can adopt a large number of different conformations. For example, the hydrogen exchange technique (also called hydrogen-deuterium exchange, or HDX) was originally developed to test the hypothesis that amino acid residues can form helices [2]. This method leverages the fact that the bond between the nitrogen and hydrogen in the amide of the backbone of every amino acid is relatively weak. Therefore, if a protein is immersed in D₂O, then the hydrogens of amides that are exposed to solvent will exchange with deuterium. However, amides that form hydrogen bonds will be protected from exchange. The complex kinetics of early hydrogen exchange experiments suggested a diversity of structures were present at equilibrium.

Nuclear magnetic resonance (NMR) has also been a rich source of information on proteins’ conformational heterogeneity. NMR provides a means to assess the chemical environment of particular nuclei, often the same amide groups monitored by hydrogen exchange experiments. NMR, however, can provide information on more than just solvent exposure of the backbone amides. For example, early work showed that the phenyl groups of phenylamine residues buried in a protein’s core are capable of rotating despite the tight packing of atoms in this environment [3]. NMR can also be used for structure determination, and to study other conformational changes. However, performing these experiments is often time consuming and expensive. NMR also faces a number of technical limitations, such as the difficulty of studying large proteins.

Despite early evidence for dynamics, much of what we know about any given protein often comes from a single structure. While NMR can be used for structure determination, the first structure of a folded, globular protein was solved by x-ray crystallography [4]. In crystallography, protein is prepared under conditions that promote the formation of a regular crystal lattice. X-ray beams are then directed at the crystal, and the resulting diffraction pattern is used to infer the protein’s structure. Typically, practitioners focus on solving a single structure that best explains the diffraction data. Crystallography yields atomic resolution structures with a greater throughput then NMR, so it has come to dominate structural biology. Tens of thousands of different structures have been deposited into an online repository, called the protein data bank (PDB). These structures are often thought to represent the ground state structure in solution, but it is more accurate to think of them as the average of many low energy structures under the conditions used for crystallization. It is typically hard to capture important excited states without stabilizing the higher energy state, such as having a binding partner (i.e., small molecule or another protein). Despite this limitation, crystal structures have proved extremely valuable for gaining insight into how proteins function, as well as designing drugs and new proteins. The wealth of information a crystal structure provides sometimes even leads people to conclude that it encodes all the information one could need, rendering the role for protein dynamics negligible. For example, many methods for predicting protein stability assume that a single crystal structure is sufficient to predict the relative populations of the folded and unfolded states. Computational drug design software also tends to make the simplifying assumption that a single protein structure is a sufficient characterization of the protein.

Structures from techniques like crystallography and NMR are tremendously valuable, but their explanatory and predictive power is limited. The first crystal structure ever solved is a powerful illustration [4]. In this structure of myoglobin, the heme group used to bind and hold the protein’s substrate, oxygen, is buried within the protein’s core. Oxygen clearly has to get into the protein’s core to interact with heme, but it’s not obvious how it does so from this structure. Therefore, this first structure was both a demonstration of structural biology’s power, and the unmet need to capture protein dynamics to achieve a complete understanding of how a protein functions. Given a single structure, it is also extremely challenging to predict essential properties for understanding a protein’s function, such as its stability [5], its affinity for different binding partners [6], or the effect of mutations on its function [7]. Often times, the crystal structures of protein variants with dramatically different activities or stabilities are essentially identical, making it difficult to explain how mutations exert their effect [8]. It is possible that this lack of explanatory and predictive power results from an inability to extract information appropriately from available structural data. However, there is mounting evidence that protein dynamics, and the conformational diversity these fluctuations give rise to, is a crucial missing factor.

Progress towards capturing proteins’ shape-shifting

There is increasing consensus that trying to understand proteins without accounting for their shape-shifting is like trying to infer the rules of football from a single photo taken during a game. However, it has proven easier to acknowledge the importance of protein dynamics than to account for the role it plays in protein function. A growing community has been working to remedy this situation by developing methods to access proteins’ excited states.

Solution NMR has been particularly valuable, providing insight into both thermodynamics and kinetics. For example, relaxation dispersion NMR spectroscopy can detect the presence of an excited state with a population of less than 1%. Application of this methodology to an enzyme arrested in one step of its catalytic cycle has demonstrated that the next step of the cycle is present as an excited state [9]. Such experiments have also revealed a correlation between the effects of mutations on dynamics and catalysis [9,10]. For example, a combination of NMR, crystallography, and computer simulations have been used to map out the energy landscapes of kinases. Based on these models, it has been possible to rationalize autophosphorylation and the effects of cofactors and mutations on the activities of these enzymes [11,12]. Initially, it was often unclear what the excited states uncovered by such experiments looked like. However, it is now possible to solve the structures of excited states [13]. Looking beyond solving the structures of particular excited states, NMR is also being used to measure a protein’s conformational entropy as a means to quantify the number of accessible excited states [14].

Many other experimental techniques have also provided valuable insight into protein dynamics. Enumerating them all is beyond the scope of this review. To give a couple of examples, developments in room-temperature crystallography [15] and cryo-electron microscopy (CryoEM) [16] are providing new opportunities for obtaining high-resolution structures of excited states. Typically, crystal structures are solved based on the diffraction from a crystal at cryogenic temperatures that favor low energy structures more heavily than the temperatures where most proteins operate in vivo. Room-temperature crystallography and CryoEM both attempt to capture the distribution of structures that exists at more physiologically-relevant temperatures. Multiple structures are often required to fit the electron density detected by these methods. The relative contributions of these structures to the total density may report on their relative populations in solution. Leveraging this insight into the structures of excited states and their populations has led to improved methods for drug design [17].

Molecular dynamics simulations provide a foundation for building atomically-detailed, quantitatively predictive models of proteins’ shape-shifting that complement experiments. Such simulations are often referred to as computational microscopes because they provide a means to watch how the position of every atom in a protein evolves over time [18,19]. The perfect simulation would provide a complete description of a protein’s thermodynamics and kinetics. However, these simulations face three key limitations: 1) the accuracy of the force fields used to model interatomic interactions, 2) the computational challenge of gathering enough data to sample slow processes, and 3) the scientific challenge of extracting useful information from large datasets embedded in high-dimensional spaces. Significant effort has been dedicated to all of these issues and is reviewed elsewhere [20,21]. As discussed below, simulations are now in quantitative agreement with many experiments and agree qualitatively with many others. As a result, they are a powerful means to explain the physical origins of experimental observations, as well as to guide the design of new experiments.

One noteworthy development that will be referenced throughout this review is the emergence of Markov state models (MSMs) [22]. An MSM is a network model that represents a protein’s energy landscape as a set of structural states it tends to adopt and the probabilities of hopping between adjacent states (Fig. 1). These models facilitate analysis by providing a convenient, coarse-grained representation of enormous datasets. One could learn an MSM from a single long simulation that eventually gathers statistics on the probabilities of every state and the transitions between them. However, the main advantage of the MSM approach is that it provides a framework for integrating information from many independent simulations (each of which may explore different subsets of states) into a model that captures slow events that are far beyond the reach of any individual simulation. By analogy, one could determine the best route for driving from San Francisco to New York City by driving back and forth between them, trying different routes many times to gather statistics on how long they typically take. However, one could reach the same conclusion far more quickly by aggregating data from many drivers, each of whom only explores the region where they live/work. One can exploit this property to great effect using a technique called adaptive sampling. In adaptive sampling, one iteratively runs a batch of simulations, builds an MSM, and then uses the MSM to decide which of the structures that have been discovered so far it would be most valuable to start a new batch of simulations from. A number of metrics for deciding where to start new simulations have been developed that consider factors like minimizing statistical uncertainty, choosing a structurally diverse set of starting conformations, and favoring states with desirable structural properties [23-28].

Work from our lab, among others, has established quantitative agreement between MSMs and a variety of experiments [29,30]. These results demonstrate that existing force fields are accurate enough for many applications, given that sufficiently large datasets are collected. For example, we have shown that the agreement between different 10 nanosecond simulations and NMR experiments is highly variable, but that 10 microsecond simulations reliably yield quantitative agreement with these experiments [31]. In agreement with NMR and room-temperature crystallography, MSMs also reveal substantial dynamics in proteins’ cores despite the tight packing that one could imagine would prevent conformational changes [32].

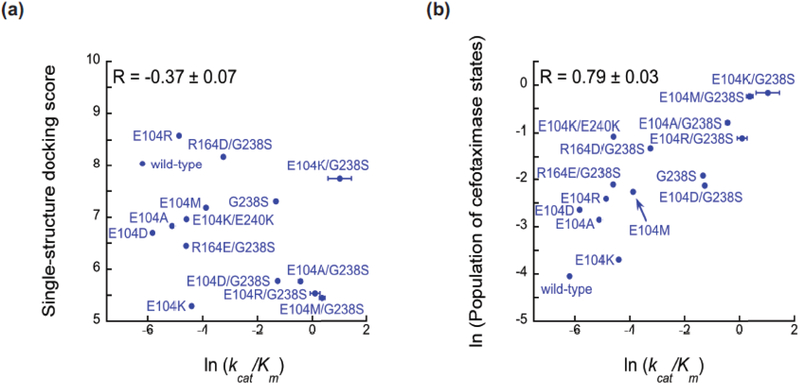
Encouraged by the agreement between simulations and existing experimental data, we have placed increasing emphasis on making bona fide predictions and then testing these predictions in subsequent experiments. For example, we recently established the importance of accounting for excited states to understand how mutations alter the activity of an enzyme called TEM β-lactamase [7], which is a major source of antibiotic resistance in bacterial infections. To set a baseline, we showed that docking the antibiotic cefotaxime against the active sites of different enzyme variants is a poor predictor of their activity against this substrate (Fig. 2A). Comparing an MSM for a variant with a high activity against cefotaxime to an MSM for a variant with a low activity against this substrate suggested that the populations of particular protein conformations are key determinants of the enzyme’s catalytic efficiency. To test this insight, we designed new β-lactamase variants to modulate the populations of these states, and experimentally verified that the total equilibrium probability of these states is a strong predictor of cefotaxime activity (Fig. 2B). We have also used a similar approach to understand and predict how mutations alter a protein’s stability [33], as well as the pH-dependence of a protein-protein binding affinity [34]. Other successes using MSMs to make true predictions are discussed below.

Figure 2. Accounting for protein shape-shifting leads to improved predictions of an enzyme’s catalytic efficiency.

(A) Docking the antibiotic cefotaxime against the active site of a single structure of different TEM variants is a poor predictor (R = −0.37±0.07) of their activity against cefotaxime. (B) The total population of a set of states from an MSM, called cefotaximase states because they are believed to be active against cefotaxime, is a strong predictor of cefotaxime activity (R = 0.79±0.03). Figure adapted from [7]. Abbreviation: MSM, Markov state model.

Shape-shifting gives rise to allosteric communication between distant structural elements

A protein’s ability to shift between an ensemble of different structures can give rise to communication between distant regions of a protein, called allostery [35]. Allostery was first recognized in hemoglobin, where the binding of oxygen to one subunit increases the affinity of other subunits for oxygen. For many years, hemoglobin and allostery were almost synonymous. As time has progressed, it has become increasingly clear that allostery plays an important role in a broad range of processes, especially in signaling. For example, G protein-coupled receptors (GPCRs) are famous for their ability to transmit information across membranes by binding stimuli on their extracellular surfaces and then changing the geometry of their intracellular surfaces to trigger signaling cascades [36]. Exerting allosteric control over such signaling processes is of great interest, both for understanding basic biology and for therapeutic applications. Despite the broadening scope of allostery, it is still common to assume that allostery is only relevant for a subset of proteins where it has been selected for.

Given that all proteins are capable of adopting an ensemble of different shapes, it is interesting to speculate that allostery may be extremely prevalent, possibly even universal [37]. The pervasiveness of allostery is supported by studies of both natural and directed evolution [8,38]. Both have revealed that mutations far from enzyme active sites (and other key functional sites) frequently have a profound effect on function. We propose that these mutations exert their influence by tapping into allosteric networks to modulate the distribution of structures at distant functional sites. Given the potential prevalence of allostery, systematically capturing this coupling could open many new opportunities for controlling biological processes. Work is ongoing to develop methods capable of detecting allostery, assessing how pervasive it is, and harnessing this insight to improve the design of new proteins and drugs.

Widespread allostery would present a number of attractive therapeutic opportunities, such as enhancing (rather than inhibiting) protein function and targeting ‘undruggable’ proteins. These objectives are currently difficult to achieve because drug design is generally limited to sterically occluding key functional sites to inhibit undesirable activities. However, diseases where a mutation causes a loss of function—such as cystic fibrosis—are prime examples of cases where one would prefer to enhance desirable activities. An allosteric drug could be designed to reverse the effects of such deleterious mutations. There are also many cases where key functional sites are apparently undruggable. For example, protein-protein interactions are notoriously difficult to target because the relevant binding sites are often too flat for a small molecule to bind tightly [39]. Kinases and GPCRs can also be difficult to target because their active/functional sites are highly conserved across large families, so targeting them is likely to result in undesirable off-target effects. Targeting allosteric sites that are less broadly conserved could provide a means to achieve specificity [40]. Combined with the fundamental importance of allostery for basic biological processes, the therapeutic opportunities this communication presents have helped spur research into allosteric mechanisms and approaches for identifying allosteric coupling.

Historically, allosteric communication has typically been conceptualized in terms of concerted structural changes. For example, Fig. 3A shows an example of a system with two binding sites that each jump between two alternative structures in tandem. Binding of a ligand to one structure of the first binding site then locks the other binding site in a specific conformation. An extreme version of the conformational selection mechanism like the one just described could be identified by comparing crystal structures of the apo protein to structures with one or both ligands bound. Alternatively, a number of algorithms have been developed for identifying allosteric coupling by detecting concerted structural changes in computer simulations [41,42]. For example, the MutInf method identifies correlations by utilizing a mutual information metric to quantify how much better one can predict the structure of one part of a protein (specifically, the rotameric state of one dihedral angle) given the structure of a second region of the protein [43]. Application of such methods to proteins that are not classically considered allosteric has revealed substantial coupling, supporting the notion that allostery is pervasive [44].

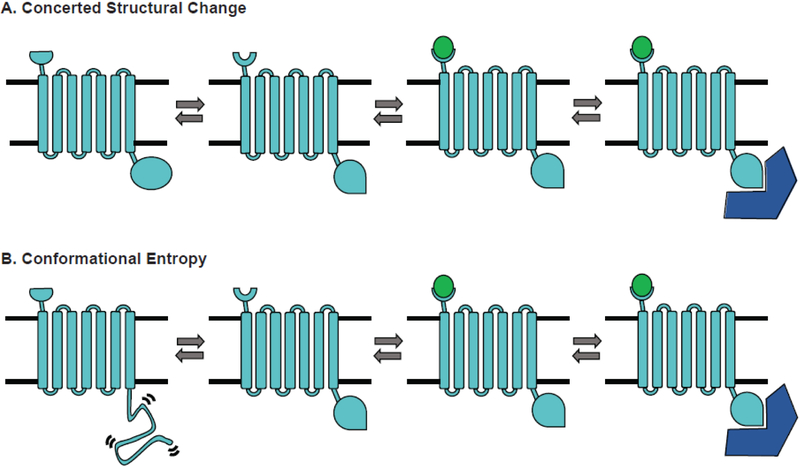
Figure 3. Mechanisms of allosteric communication.

A signaling protein (light blue) binds a ligand (green) that allosterically impacts binding of an effector protein (dark blue) by two different mechanisms. (A) A classic concerted structural change. The ligand-binding site and effector-binding site each hop between two alternative structures in a correlated fashion. Ligand-binding stabilizes one structure of the ligand-binding site, thereby stabilizing a particular structure of the effector-binding site. (B) A model where conformational entropy plays an important role. Now the structure of the ligand-binding site is correlated to whether the effector-binding site is in a disordered state, consisting of many different structures, or in an ordered state that can bind the effector. Ligand binding stabilizes the ordered state.

In recent years, there has also been a growing recognition that conformational entropy has an important role to play in allosteric communication. The potential importance of conformational entropy was first proposed in a theoretical paper that demonstrated allostery could be achieved by coupling the breadth of two probability distributions without any change in the locations of their maxima [45]. Experimental evidence for allosteric communication of this form wasn’t obtained until decades later, when NMR successfully identified allosteric coupling in the absence of a concerted structural change [46]. Intrinsically disordered regions can also play an important role in allostery. Fig. 3B shows an example where the structure of one binding site is correlated to whether a second site adopts a well-defined structural state or is in a disordered state. The fact that the disordered state consists of many different structures distinguishes this scenario from a concerted structural change, where there are essentially two distinct structures.

Increased appreciation for the importance of conformational disorder for allostery has led to the development of new algorithms for detecting this form of communication in computer simulations. The first method focused entirely on allostery without conformational change [47]. The author developed the conditional activity metric for measuring correlations between the timing of motions. Specifically, the conditional activity quantifies how much the motion of one dihedral changes the barrier to the motion of a second dihedral. Importantly, the author demonstrated that timing correlations can convey signals over longer distances than concerted structural changes. Subsequently, our lab developed an approach called correlation of all rotameric and dynamical states (CARDS) that captures both concerted structural changes and the role of conformational disorder [48]. Like MutInf, CARDS uses the mutual information between every pair of dihedral angles to identify allosteric coupling. However, CARDS calculates the mutual information between both the structural and dynamical state of each dihedral. Here, dynamical state refers to the fact that CARDS borrows ideas from condensed matter physics to classify each dihedral from every snapshot of a simulation as being ordered or disordered. The method has proved extremely valuable for making sense of allosteric coupling in a number of systems. For example, using CARDS to account for the role of conformational disorder has helped uncover the mechanism of allosteric communication in a common family of signaling proteins, called G proteins [49].

Cryptic pockets present novel therapeutic targets

Taking advantage of allostery requires a site for therapeutics, such as small molecules, to bind. The crystal structures of some proteins clearly present multiple pockets where small molecules could potentially bind and influence allosteric networks. However, this is not always the case, and some proteins do not have any obvious druggable pockets.

Fortunately, proteins’ shape-shifting can also populate excited states with pockets that are absent in available crystal structures, called cryptic pockets (Fig. 1). These sites are called cryptic allosteric sites when they coincide with allosteric networks. Cryptic allosteric sites with coupling to key functional sites have great potential value [50]. Small molecules that bind such sites can exert allosteric control over functional sites by modulating the relative probabilities of different protein structures. They can either enhance or inhibit activity, depending on whether they increase or decrease the probability of functional conformations, respectively [51,52].

Cryptic pockets can also have therapeutic value apart from allostery. For example, a cryptic pocket that forms in the middle of a key protein-protein interaction surface could be targeted to sterically block that protein-protein interaction. Cryptic pockets that extend known functional sites also provide opportunities for developing novel competitive inhibitors. For example, one could take an enzyme inhibitor that is known to bind the active site and add additional functional groups to leverage a cryptic extension to the active site.

The value of cryptic sites has not been fully realized because it is difficult to intentionally identify and target them. Most examples of cryptic pockets have been discovered serendipitously through screens that are agnostic to whether a hit binds a known functional site or a cryptic pocket. For example, a small molecule that binds in a cryptic pocket between the orange helices in Fig. 1 was discovered through a screening campaign [53]. In this particular study, the authors sought to identify novel active site inhibitors by computationally docking a large library of chemical compounds against TEM β-lactamase’s active site and then experimentally testing the chemicals with the highest docking scores. Experimental tests of some of the top ranked compounds confirmed that they inhibited the enzyme. However, solving the co-crystal structures of these compounds with the enzyme revealed that they did not function as intended. Instead of binding the active site, they turned out to bind a cryptic pocket between the orange helices in Fig. 1.

A screening method called tethering has been developed to target a specific site on a protein, such as a cryptic site [54]. To achieve this specificity, the method requires the protein to contain a single cysteine residue near the site of interest. Satisfying this requirement often requires one or more mutations to the protein sequence. The protein is incubated with a library of chemical fragments that are capable of forming a disulfide bond with the cysteine. This disulfide tether localizes the compounds to the site of interest. Importantly, a reducing agent is also introduced along with the fragment library. This reducing agent ensures that fragments bind reversibly. Fragments that have strong non-covalent interactions with the target site will tend to stay bound even when the disulfide tether is broken by the reducing agent, while compounds that only form weak interactions with the protein will tend to dissociate. As a result, one can identify tight binding fragments by mass spectrometry. Tethering has successfully identified a number of novel compounds and pockets [55,56]. However, a cryptic pocket could go unnoticed if the fragment library does not happen to contain any sufficiently tight binders. Moreover, it is expensive to apply tethering to multiple locations on a protein in search of a cryptic pocket. A general method for identifying cryptic sites without requiring the simultaneous discovery of compounds that bind them would be valuable for guiding the application of tethering.

Computer simulations provide an alternative approach to discover cryptic sites [57]. One of the earliest examples is the discovery of a cryptic binding trench in HIV integrase [58]. Efforts to target this pocket eventually led to the development of raltegravir, a first-line treatment for HIV [59]. However, this success has not been replicated in a wide variety of other systems because of the challenges that molecular dynamics simulations face, as described above. A variety of techniques have been developed to overcome these limitations. Many of these methods use enhanced sampling algorithms to improve the performance of molecular dynamics simulations [60,61]. Other approaches attempt to infer cryptic pockets from available crystal structures [62] or use alternate simulation strategies, such as the Rosetta software, to identify excited states with cryptic pockets [63].

Our lab is actively developing a pipeline that combines MSMs and experiments to identify and target cryptic pockets, with an emphasis on separating the discovery of cryptic pockets from the identification of ligands that bind them. As a first step, we demonstrated that building an MSM for TEM β-lactamase and applying a simple pocket detection algorithm to a representative structure for each state in the model readily identified the known cryptic pocket between the orange helices in Fig. 1 [44]. The MSM also captured correlations between the structure of the cryptic pocket and that of the active site, consistent with the allosteric coupling between these sites. Moreover, the model predicted a multitude of new pockets with allosteric coupling to the active site. While many of these pockets are probably poor candidates for a drug design campaign [57], we proposed that a subset are potentially viable targets.

Thiol labeling experiments are a valuable means to initially test computationally predicted cryptic sites [64]. These experiments require a cysteine at a position that is buried in the apo crystal structure but that gets exposed by the opening of a cryptic pocket. Satisfying this requirement often requires the introduction of a cysteine. However, in one case, we identified a native cysteine that satisfies these criteria, alleviating any concern that introducing a cysteine might create a cryptic pocket where none existed before [65]. Then a labeling reagent is introduced that is capable of forming a covalent bond with the cysteine if it gets exposed. An observed labeling rate that is considerably faster than that expected due to unfolding supports the existence of a cryptic pocket. For cryptic allosteric sites, one can also measure the activity of labeled protein as a first test for allosteric communication. However, the effect of labeling on activity does not necessarily determine the extent or direction of allosteric modulation that other compounds may achieve given that compounds that bind the same site can be activating, inhibiting, or have no effect on activity [51,52].

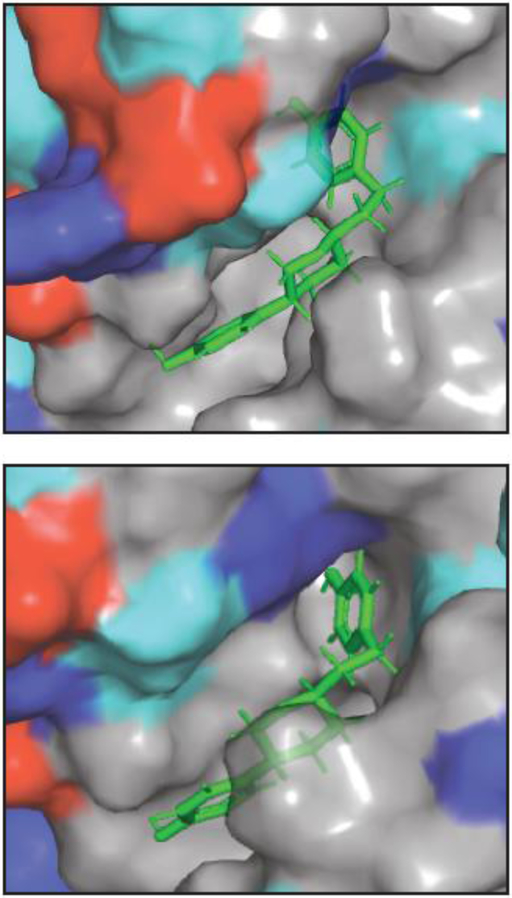
To target experimentally verified cryptic pockets, we developed a method called Boltzmann docking that uses MSMs to account for the target protein’s conformational heterogeneity [7]. In Boltzmann docking, a library of compounds is docked against a representative structure from every state of an MSM where a pocket of interest is open. Then compounds are ranked based on their population-weighted average docking score. This approach balances the desire for high-affinity interactions against the cost of stabilizing higher energy excited states. It is also capable of identifying compounds that bind tightly to a single structure or that bind somewhat less tightly to a set of different structures. In the first application of Boltzmann docking to cryptic pockets in TEM β-lactamase, we expected to find inhibitors given the intuition that disrupting a particular active site structure should be easier than stabilizing one. Surprisingly, we discovered two activators and one inhibitor [52]. This result suggests that it may be easier to enhance the activity of other proteins than one may have expected. Fig. 4 shows an example of one of the compounds we discovered. It also highlights that this particular pocket is largely hydrophobic. The lack of different interaction types may make it difficult to find potent inhibitors that bind this particular site, motivating our continued search for other cryptic pockets, some of which are discussed below. Further research is also needed to accurately predict whether a compound will be an activator or inhibitor. Apart from allostery, accounting for conformational heterogeneity in key functional sites could also be valuable [17].

Figure 4. Two views of an allosteric activator bound to a cryptic pocket.

The protein surface is colored according to whether an amino acid is acidic (red), basic (blue), polar (cyan), or non-polar (gray). The compound is shown as sticks. A cartoon representation of the pocket can be found in Fig. 1C.

These findings have inspired new methods to expedite the hunt for cryptic sites. For example, we developed a goal-oriented adaptive sampling method, called fluctuation amplification of specific traits (FAST) [24], to identify excited states with specific geometric features more efficiently. While FAST is entirely general, one of the applications that motivated the development of the method was finding cryptic sites by searching for excited states with large pocket volumes. While our original work on cryptic pockets in TEM β-lactamase used 100 microseconds of simulation, FAST reproduces these results with just a few microseconds of simulation. We have also developed a new algorithm for quickly extracting interesting excited states, such as those with cryptic pockets and cryptic allosteric sites, from large ensembles of structures generated with molecular dynamics simulations [65]. These methods have revealed yet more pockets in TEM, as well as other β-lactamases, that may be more attractive drug targets (Fig. 1D). In the future, we expect that incorporating quantitative measures of the druggability of cryptic sites will also be useful [57].

Assessing the conservation of cryptic sites may also be valuable. One attractive feature of sterically blocking enzyme active sites is that selective pressure to maintain function reduces the probability of mutations that are likely to disrupt inhibitor binding. If the residues lining a cryptic pocket are not constrained, then it may be easier to evolve resistance to compounds that target these sites. However, it is possible that many cryptic pockets are not so susceptible to mutation. For example, enzyme activity could be just as sensitive to mutations in cryptic allosteric sites with strong coupling to the active site as it is to mutations in the active site itself. Therefore, the conservation of residues lining different cryptic sites may also be worth considering when trying to prioritize different potential targets.

Disrupting constrained conformational equilibria as a powerful therapeutic strategy

The discussion above essentially divides the different structures a protein adopts into two classes, functional and non-functional. Modulating the relative probabilities of these two classes opens a number of new therapeutic opportunities, as described above. However, this binary classification may not be adequate for many proteins, such as those with multiple functions.

Proteins that must maintain a delicate balance between populating multiple functional structures may be particularly attractive therapeutic targets because having more constraints makes them more sensitive to perturbations. For example, conformational switches involved in signaling are likely to populate at least two distinct functional states—on and off—with reasonably low energies, as well as non-functional states with higher energies. Stabilizing or destabilizing any of these states may disrupt such proteins’ ability to function appropriately. Furthermore, having more constraints to satisfy may make evolving resistance to therapeutics more challenging.

The nucleoprotein from negative sense RNA viruses presents a concrete example. For instance, Ebola virus nucleoprotein, like other negative sense RNA viral nucleoproteins, is responsible for coating the viral genome to protect it from being recognized and destroyed by a host cell. But nucleoprotein must also release RNA to allow the transcription machinery to access the viral genome. Recent work suggests that nucleoprotein can accomplish these tasks by switching between different conformations to control its affinity for RNA, and that isolated nucleoprotein has a reasonable probability of adopting both of these alternative structures in solution [66]. This balance enables nucleoprotein to serve as a context-dependent regulatory module, binding tightly to RNA until interactions with the transcription complex trigger a conformational change that favors dissociation from RNA. Furthermore, a peptide has been isolated from the transcription machinery that prevents viral replication by potently inhibiting the interaction between nucleoprotein and RNA [67]. It has been proposed that this peptide works by stabilizing nucleoprotein conformations that have a lower affinity for RNA [66]. Together, these results suggest that the relative populations of these alternative structures are constrained by the need to switch between RNA-bound and RNA-free states and that modulating this equilibrium is a powerful therapeutic strategy. We expect many other proteins have similarly constrained equilibria and, therefore, can be targeted in a similar fashion.

Concluding remarks

The study of protein dynamics has a rich history and the importance of this shape-shifting is broadly acknowledged. However, limited ability to characterize excited states has made it challenging to understand or exploit the connection between proteins’ conformational heterogeneity and function. New methodological advances are providing unprecedented insight into the full spectrum of conformational changes that proteins undergo and how these dynamic processes give rise to phenomena like allostery and cryptic sites. This understanding, in turn, is uncovering new therapeutic opportunities.

Progress on understanding protein shape-shifting also raises new questions that must be addressed to fully realize the value of insight into protein dynamics for the design of new drugs and proteins (see Outstanding Questions). For example, more basic research is required to understand why some compounds are allosteric activators while others are inhibitors. The druggability and conservation of cryptic pockets are also important determinants of the value of these sites for drug discovery. Interestingly, the conservation of cryptic pockets may determine how they are used, not if they are useful. Highly conserved pockets may be useful for applications like antibiotic development where one wishes to hit multiple related targets. In contrast, limited conservation may be desirable for targets like kinases, where one wants to achieve great specificity for a particular kinase without eliciting off-target effects by binding other kinases. How to incorporate protein shape-shifting into protein design is even more open ended as the field is still just beginning to understand the connection between dynamics and function.

Outstanding Questions.

• How can one predict whether a drug/mutation will be a positive, negative, or neutral allosteric modulator?

• Are cryptic pockets viable drug targets? If so, what fraction of the cryptic pockets are viable targets?

• How conserved are cryptic pockets and allostery?

• Can access to excited states be incorporated into protein design algorithms to increase the likelihood of creating highly functional proteins?

Highlights.

• Proteins are highly dynamic shape-shifters. However, it has proven easier to acknowledge the prevalence of protein dynamics than to account for the role it plays in protein function.

• Advanced methods for capturing protein dynamics are providing fundamental insights into the mechanism of allosteric communication.

• Cryptic pockets provide novel targets where therapeutics can bind and manipulate allosteric networks.

• Many proteins maintain a delicate equilibrium between multiple functional structures. Disrupting this sensitive balance provides new therapeutic opportunities.

Box 1: Technology Corner: Molecular Dynamics and Monte Carlo.

Molecular dynamics and Monte Carlo are two of the dominant algorithms for sampling the distribution of structures that a protein adopts. In molecular dynamics, one starts with the positions and velocities of every atom in a system and then iteratively calculates where each atom will be some small time in the future and how the velocities will change. One of the major strengths of this approach is that it provides both thermodynamic and kinetic information. However, a major weakness is that each timestep is on the order of a femtosecond, while many of the biological processes of interest take a millisecond or longer. Performing over 10¹² iterations is extremely computationally expensive, and greatly limits the applicability of molecular dynamics. In Monte Carlo simulations, one samples the distribution by proposing random perturbations to an initial structure and then accepting or rejecting this move based on the energy difference between the initial and proposed structure. The main advantage of this type of algorithm is that it can capture very slow processes if the move set used to propose perturbations to the initial structure is designed appropriately. However, designing an appropriate move set can be extremely difficult and a poor move set will be extremely computationally inefficient as every proposed move will be rejected. Furthermore, Monte Carlo simulations only provide thermodynamic (not kinetic) information. Rosetta is one of the most successful software packages for sampling the ensemble of structures that a protein adopts with the Monte Carlo algorithm.

Glossary

Adaptive sampling

a class of algorithms for constructing MSMs

Allostery

communication between distant parts of a protein

Cryptic pocket

a pocket that is absent in available structures

Energy landscape

a conceptual framework for protein dynamics where each point represents a protein conformation and a protein spends exponentially more time in lower energy structures than higher energy ones (Fig.1)

Excited state

any minima on an energy landscape besides the ground state

Ground state

the lowest energy (i.e. highest probability) minima in an energy landscape

Markov state model (MSM)

a computational model of an energy landscape

Mutual information

a metric for measuring pairwise correlations

Shape-shifting

proteins fluctuate between different conformations