The positive effects of population-based preferential sampling in environmental epidemiology

Summary

In environmental epidemiology, exposures are not always available at subject locations and must be predicted using monitoring data. The monitor locations are often outside the control of researchers, and previous studies have shown that “preferential sampling” of monitoring locations can adversely affect exposure prediction and subsequent health effect estimation. We adopt a slightly different definition of preferential sampling than is typically seen in the literature, which we call population-based preferential sampling. Population-based preferential sampling occurs when the location of the monitors is dependent on the subject locations. We show the impact that population-based preferential sampling has on exposure prediction and health effect estimation using analytic results and a simulation study. A simple, one-parameter model is proposed to measure the degree to which monitors are preferentially sampled with respect to population density. We then discuss these concepts in the context of PM_2.5 and the EPA Air Quality System monitoring sites, which are generally placed in areas of higher population density to capture the population's exposure.

1. Introduction

In the past few decades, numerous epidemiological studies have investigated the health effects of air pollution. Many studies have found statistically significant associations between ambient levels of air pollution and a variety of adverse health outcomes. Examples of such studies can be found in Dockery and others (1993), Samet and others (2000), and Dominici and others (2006), and a review of the literature can be seen in Dominici and others (2003), Pope III (2007), and Breysse and others (2013). Difficulty in these studies arises due to spatial misalignment of the data, as the locations of the subjects do not coincide with the locations at which air pollution levels are measured.

One technique for addressing this issue is to jointly model the exposure and outcome (Nikolov and others, 2008, 2011), though the most common approach to overcome spatial misalignment is a two-stage analysis. The first stage consists of estimating parameters of an exposure model using data from a fixed air pollution monitoring network, such as the IMPROVE network or the EPA's Air Quality System. Investigators predict air pollution levels at subject locations using nearest neighbor, kriging, or land use regression approaches (Oliver and Webster, 1990; Kloog and others, 2012). The monitor locations from these networks are chosen for specific reasons, such as measuring areas of high pollution levels or areas of high pollution density. Examples of monitors being chosen for these reasons can be found in Chow and others (2002) and Matte and others (2013).

The second stage uses the estimated exposure from the first stage to investigate the association between exposure and an outcome. This leads to a complex form of measurement error, which does not fall specifically into the category of either classical or Berkson measurement error, and a variety of methods have been proposed to correct for this measurement error. Kim and others (2009) looked at the impact of various predicted exposures on health effect estimation in air pollution studies. Gryparis and others (2009) examined the effectiveness of a variety of standard correction methods via simulation and gave intuition for when these measurement error corrections will work. More recently, Szpiro and others (2011) showed that the measurement error can be decomposed into two components: a classical-like component and a Berkson-like component. They further came up with a computationally efficient form of the parametric bootstrap to correct for measurement error in two-stage analyses. Szpiro and Paciorek (2013) derived asymptotic results about the impact of these two components of measurement error on health effect estimates.

In this article, we examine the impact of population-based preferential sampling of monitors in two-stage analyses of air pollution and health. Preferential sampling, as defined by Diggle and others (2010), is the scenario where the location of the monitors is dependent on the values of the spatial process they are measuring. We consider a slightly different definition of preferential sampling in which the location of the monitors is dependent on the subject locations. We refer to our definition as population-based preferential sampling to differentiate it from the definition of Diggle and others (2010). Preferential sampling occurs in an air pollution monitoring network when the monitors are placed based on the levels of the pollution (e.g., monitors are located in highly polluted areas). Population-based preferential sampling occurs in a study when the monitors are located in areas with the highest population density.

Diggle and others (2010) showed that variogram estimates are biased under preferential sampling and developed a method to control for preferential sampling in geostatistical inference. Gelfand and others (2012) showed that preferential sampling can perform drastically worse with respect to estimating a spatial surface than sampling under complete spatial randomness (CSR). Lee and others (2015) examined the impacts of preferential sampling on health effect estimation in environmental epidemiology and found that the locations of monitors can drastically impact inference in second-stage analyses. They also illustrated in a simulation study how inference in the second stage is improved under CSR compared with preferential sampling.

In this article, we show that population-based preferential sampling can improve the estimation of a health effects model in a two-stage analysis. The key difference between this work and previous studies on preferential sampling is that we will be emphasizing the role that population density plays when considering the locations of monitors. Our results will illustrate the claim made in Szpiro and Paciorek (2013) that the densities governing the location of the subjects and the monitors should be the same. We will show that population-based preferential sampling can lead to drastically improved inference in air pollution studies.

The outline of our article is as follows: Section 2 introduces the motivating example of ${\text{PM}}_{2.5}$ in New England, Section 3 introduces notation and the modeling framework, Section 4 provides mathematical results regarding the bias and variance of a health effect estimate from a two-stage design, Section 5 presents a simulation study, Section 6 highlights these results in the context of ${\text{PM}}_{2.5}$ monitoring locations in New England, and Section 7 concludes with a discussion.

2. Motivating example

The majority of the preceding discussion and previous work on measurement error in environmental two-stage analyses has been motivated by studying the adverse health effects of ${\text{PM}}_{2.5}$. ${\text{PM}}_{2.5}$ is a pollutant defined as the combination of all fine particles less than 2.5 μm in diameter. Nearly all research to date on the associations between ${\text{PM}}_{2.5}$ and health outcomes have been contingent on monitors to estimate exposure. Even recent studies that have used aerosol optical depth (AOD) to estimate ${\text{PM}}_{2.5}$ on a finer grid incorporate information from monitors in their models (Kloog and others, 2012). Generally exposure is estimated conditional on monitoring data, and little attention is paid to the location of the monitors. The left panel in Figure 1 shows a map of the EPA AQS monitor locations over New England as well as a map of estimated ${\text{PM}}_{2.5}$ across New England. The estimated ${\text{PM}}_{2.5}$ for New England is taken from the aforementioned models that use AOD to estimate exposure on a fine grid (1 km by 1 km). Figure 1 helps to show the motivation for this work, as it appears that there are more monitors in areas of higher pollution. It should be noted that these areas of higher pollution correspond to higher population densities, illustrated by the right panel of Figure 1. We take the number of census tracts within 0.3° of a location to be a measure of population density. We calculate this value on a 1 km by 1 km grid across New England and at each of the EPA AQS monitoring sites and find that monitor locations are generally in more populated areas than New England as a whole.

Fig. 1.

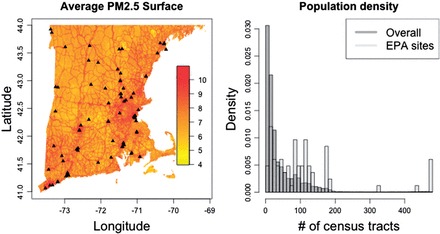
The left-hand panel shows the average predicted PM_2.5 surface in New England for the year 2003, with the black points representing the location of the EPA AQS monitoring system. The right-hand panel shows a histogram of the number of census tracts within 0.3° of each grid point in New England, along with the histogram of the number of census tracts within 0.3° degrees of the EPA monitoring sites.

Although not definitive, it seems plausible that the location of monitors in New England follows a nonrandom sampling scheme, which meets our criteria for population-based preferential sampling. If we are able to gain intuition about the impact of population-based preferential sampling, we should also gain knowledge on how inference is impacted in studies of ${\text{PM}}_{2.5}$ that use the EPA AQS monitoring system.

3. General setup

3.1 Notation and model

For convenience, we adopt similar notation to Gryparis and others (2009), Szpiro and others (2011), and Lee and others (2015). Throughout we will have $n$ subjects in the study (second stage of analysis) and $n^{\ast }$ monitors at which we observe exposure (first-stage of analysis). We define $X$ to be the true exposure at the $n$ subject locations and $X^{\ast }$ to be the exposure at the $n^{\ast }$ monitor locations. In general we will allow the exposure to follow a Gaussian process such that

$$\left(\begin{array}{c}X\\ X^{\ast }\end{array}\right)\sim N\{\left(\begin{array}{c}{\mu }_X(\alpha )\\ {\mu }_{X^{\ast }}(\alpha )\end{array}\right),\left(\begin{array}{cc}{\mathrm{\Sigma }}_{X,X}(\varphi )& {\mathrm{\Sigma }}_{X,X^{\ast }}(\varphi )\\ {\mathrm{\Sigma }}_{X^{\ast },X}(\varphi )& {\mathrm{\Sigma }}_{X^{\ast },X^{\ast }}(\varphi )\end{array}\right)\},$$ (3.1)

where ${\mu }_X(\alpha )$ represents the mean of the exposure surface and is a linear function of a set of covariates dictated by a parameter vector, $\alpha$. The covariance matrix of this distribution is dictated by a parameter vector, $\varphi$, which represents the Gaussian process covariance function parameters such as the range. This framework is general and allows for a broad class of exposure models for predicting exposure at new locations such as kriging and land use regression. We now define our outcome model as

$$Y={\beta }_0+{\beta }_{1}X+ϵ,$$ (3.2)

where $ϵ$ is a vector of i.i.d random noise. In general this model can include a vector of covariates, though we keep it simple here to simplify results about the parameter of interest, ${\beta }_1$. In any realistic scenario, we will not observe $X$ and therefore must estimate $X$ with $W$ defined as

$$W=E(X|X^{\ast },\hat{\alpha },\hat{\varphi }).$$ (3.3)

Assuming (3.1) holds, this expectation is easily written out using properties of Normal distributions as

$$W={\mu }_X(\hat{\alpha })+{\mathrm{\Sigma }}_{X,X^{\ast }}(\hat{\varphi }){\mathrm{\Sigma }}_{X^{\ast },X^{\ast }}(\hat{\varphi }{)}^{-1}(X^{\ast }-{\mu }_{X^{\ast }}(\hat{\alpha })).$$ (3.4)

For the remainder of this article, we will examine the impact of using $W$ in place of $X$ in the outcome model, more specifically the impact of that measurement error under different sampling schemes for monitoring locations.

3.2 Definition of population-based preferential sampling

In Diggle and others (2010), preferential sampling is defined as any dependence between the values of the underlying spatial process ($X^{\ast }$ in our setting) and the locations at which we observe the process (the monitors in our setting). Mathematically this can be written as

$$p(X^{\ast },S^{\ast })\ne p(X^{\ast })p(S^{\ast }),$$ (3.5)

where $S^{\ast }$ is a random variable to denote the locations at which we observe $X^{\ast }$. An example of this would be a network of monitors that are placed to measure high levels of a given process. Most geostatistical procedures assume independence between these two quantities and therefore likelihood-based inference in the presence of preferential sampling can lead to bias as the likelihood is misspecified and estimates are no longer assured to be consistent. Diggle and others (2010) introduce preferential sampling by allowing their locations to be drawn from an inhomogeneous Poisson process of the following form

$$\lambda (S^{\ast })=\text{exp}({\gamma }_0+{\gamma }_1{X}^{\ast }),$$ (3.6)

where preferential sampling is the scenario when ${\gamma }_1\ne 0$. Lee and others (2015) also introduce preferential sampling of monitors in their simulations by drawing locations from an inhomogeneous Poisson process whose intensity function depends on observed covariates and unobserved spatial features of the process. We will define population-based preferential sampling in a related, though slightly different way, which we feel is illuminating for studies involving predicted air pollution from monitors. We will investigate scenarios in which sampling depends on the population density with which subjects in the second-stage model are drawn from. This can be written as

$$P(S,S^{\ast })\ne P(S)P(S^{\ast }),$$ (3.7)

where $S$ now denotes the locations at which we observe subjects from the second-stage analysis. This does not strictly imply preferential sampling as defined in (3.5), though it will meet that criteria for preferential sampling if the population density is associated with the exposure surface. We will refer to our definition as population-based preferential sampling to distinguish it from that of Diggle and others (2010). We noted in Section 2 that the location of monitors appeared nonrandom, and it seemed that there were more monitors in areas that have both a higher population density and higher pollution levels. This implies that the motivating example meets the criteria for preferential sampling and population-based preferential sampling.

The reason for considering population-based preferential sampling is that it commonly occurs in air pollution epidemiology, where monitors are generally placed in more populated areas and the extent to which this population-based preferential sampling affects inference is unclear. Previous studies have shown the negative impact that preferential sampling can have on estimation of a spatial process; however, the main interest in air pollution epidemiology is the second stage outcome model that uses predictions of this process from the first-stage modeling.

4. Understanding bias and variance of${\hat{\beta }}_1$

We now provide mathematical justification that population-based preferential sampling can improve estimation in two-stage analyses. We will focus on results regarding ${\beta }_1$ from (3.2), as this is the parameter of interest in most environmental epidemiology studies examining the effect of ${\text{PM}}_{2.5}$ on a health outcome. We will use the same notation as before and define $C_i$ to be the vector of covariates for subject i, and $C_j^{\ast }$ to be the vector of covariates for monitor j. As a simplifying assumption we assume that the joint distribution of all the necessary quantities ($Y$, $X$, $X^{\ast }$, $C$, $C^{\ast }$) follows a multivariate normal distribution, as this will simplify some of the algebraic operations. We further impose the following models:

$$X=C\alpha +{ϵ}_x$$ (4.1)

$$X^{*}=C^{*}\alpha +{ϵ}_x^{*},$$ (4.2)

where ${ϵ}_x$ and ${ϵ}_{x^{\ast }}$ are mean zero vectors of noise. Notice that we do not impose any independence assumptions about ${ϵ}_x$ and ${ϵ}_{x^{\ast }}$ allowing for spatial structure in the residuals. Conditional on the estimates $\hat{\alpha }$ and $\hat{\varphi }$ from the first-stage analysis, we estimate exposure via (3.4). Our interest lies in the distribution of ${\hat{\beta }}_1$, the estimate of ${\beta }_1$ we get in the second stage of the model when we use $W$ instead of $X$.

4.1 Bias of ${\hat{\beta }}_1$

To examine the bias we can look at the conditional distribution of $Y$ given $W$. Since we defined everything to be jointly normal, the joint distribution of $Y$ and $W$ can we written as

$$\left(\begin{array}{c}Y\\ W\end{array}\right)\sim N\{\left(\begin{array}{c}{\mu }_y\\ {\mu }_w\end{array}\right),\left(\begin{array}{cc}{\sigma }_y^2& {\sigma }_{yw}\\ {\sigma }_{yw}& {\sigma }_w^2\end{array}\right)\},$$ (4.3)

which leads to

$$Y|W\sim N({\mu }_y+\frac{{\sigma }_{yw}}{{\sigma }_w^2}(W-{\mu }_w),{\sigma }_y^2-\frac{{\sigma }_{yw}^2}{{\sigma }_w^2}).$$ (4.4)

The coefficient of interest is the one that lies in front of $W$ in the mean component of the above conditional distribution. Using this fact and defining $\theta =[\alpha ,\varphi ]$ we can say that

$$\begin{array}{ccc}E\left({\widehat{\beta }}_1\right)& =& \frac{{\sigma }_{yw}}{{\sigma }_w^2}\\ & =& {\beta }_1\frac{cov(X,W)}{Var(W)}\\ & =& f(\widehat{\theta })\end{array}$$ (4.5)

and details of this derivation as well as the exact expression for $f(\hat{\theta })$ can be found in Appendix A of supplementary material available at Biostatistics online. One important thing to note is that when $\hat{\theta }=\theta$ then $f(\hat{\theta })={\beta }_1$ and there exists no bias. This shows that the small sample bias in estimating ${\beta }_1$ is a function of $\hat{\alpha }$ and $\hat{\varphi }$, so if we knew the true parameters from the exposure model then we would get an unbiased estimate of ${\beta }_1$ in the outcome model. To gain more intuition into this bias we can perform a taylor series expansion of $f(\hat{\theta })$ around $f(\theta )$.

$$f(\hat{\theta })-f(\theta )\approx \frac{\mathrm{\partial }f(\theta )}{\mathrm{\partial }\theta }(\hat{\theta }-\theta )+\frac{1}{2}(\hat{\theta }-\theta {)}^T\frac{{\mathrm{\partial }}^{2}f(\theta )}{\mathrm{\partial }\theta \mathrm{\partial }{\theta }^T}(\hat{\theta }-\theta )$$ (4.6)

and now we can take the expectation on both sides with respect to the distribution governing the monitoring locations. Denoting these expectations by $E_{S^{\ast }}()$ we see that

$$\begin{array}{ll}{E}_{S^{\ast }}(f(\hat{\theta })-f(\theta ))& \hspace{0.17em}=E_{S^{\ast }}({\hat{\beta }}_1-{\beta }_1)\\ & \hspace{0.17em}\approx \frac{\mathrm{\partial }f(\theta )}{\mathrm{\partial }\theta }{E}_{S^{\ast }}(\hat{\theta }-\theta )+\frac{1}{2}Tr(\frac{{\mathrm{\partial }}^{2}f(\theta )}{\mathrm{\partial }\theta \mathrm{\partial }{\theta }^T}Va{r}_{S^{\ast }}(\hat{\theta }-\theta ))\\ & \hspace{0.17em}+\frac{1}{2}{E}_{S^{\ast }}(\hat{\theta }-\theta {)}^T\frac{{\mathrm{\partial }}^{2}f(\theta )}{\mathrm{\partial }\theta \mathrm{\partial }{\theta }^T}{E}_{S^{\ast }}(\hat{\theta }-\theta )\end{array}$$ (4.7)

The first and third terms are functions of the bias of the exposure model parameters, while the second term is a function of the variance of the exposure model parameters. This shows that the bias of ${\hat{\beta }}_1$ (the health effect estimate) is a function of the bias and variance of $\hat{\theta }$ (the exposure model parameters).

4.2 Variance of ${\hat{\beta }}_1$

To gain intuition into the variance of ${\hat{\beta }}_1$ we can look at $\text{var}(X-W)$ , the variance of the measurement error. While this does not translate directly into the variance of ${\hat{\beta }}_1$ , it is well understood that increasing the amount of measurement error in an exposure will lead to increased variance in the effect of that exposure on the outcome, regardless of the form of the measurement error. To better understand this quantity we can assume that we know the true model parameters and without loss of generality that the mean of the exposure is zero. We also write our estimated exposure in a somewhat more general way as $W=\sum _{i=1}^{n^{\ast }}{w}_i{X}_i^{\ast }$ , where the weights $w_i$ are a function of the distance between the $i$ th monitor and the location at which we are trying to estimate $X$ . Noting these weights sum to one we can write the variance as

$$\begin{array}{ll}\text{var}(X-W)& \hspace{0.17em}=\text{var}(X-\sum _{i=1}^{n^{\ast }}{w}_i{X}_i^{\ast })\\ & \hspace{0.17em}=\text{var}(X)+\sum _{i=1}^{n^{\ast }}\sum _{j=1}^{n^{\ast }}{w}_i{w}_{j}cov(X_i^{\ast },X_j^{\ast })-2\sum _{i=1}^{n^{\ast }}{w}_{i}cov(X,X_i^{\ast })\\ & \hspace{0.17em}=\text{var}(X)+\sum _{i=1}^{n^{\ast }}\sum _{j=1}^{n^{\ast }}{w}_i{w}_{j}cov(X_i^{\ast },X_j^{\ast })-2\sum _{i=1}^{n^{\ast }}\sum _{j=1}^{n^{\ast }}{w}_i{w}_{j}cov(X,X_i^{\ast })\\ & \hspace{0.17em}=\text{var}(X)+\sum _{i=1}^{n^{\ast }}\sum _{j=1}^{n^{\ast }}{w}_i{w}_j(cov(X_i^{\ast },X_j^{\ast })-2cov(X,X_i^{\ast }))\end{array}$$ (4.8)

and it is of interest for us to examine how this quantity changes across different sampling schemes. The first term on the right-hand side of (4.8) does not change across monitoring schemes so it is not of interest to us when comparing uniform and population-based preferential sampling. The other terms are where we see changes under population-based preferential sampling. The term involving $w_i{w}_{j}cov(X,X_i^{\ast })$ goes up on average under population-based preferential sampling since we place monitors closer on average to the location where we are trying to estimate $X$ (i.e., the subject locations). This term going up leads the overall measurement error variance to go down. However, the term $w_i{w}_{j}cov(X_i^{\ast },X_j^{\ast })$ also goes up on average under population-based preferential sampling, since monitors are now closer together on average and this leads the overall measurement error variance to rise. This illustrates the trade-off that comes with population-based preferential sampling. On one hand we should preferentially sample monitors so that their exposure value is more correlated with the subject-specific exposure values, while on the other hand we cannot preferentially sample too much as the monitors will be too close to each other. We show how this trade-off also manifests for $var({\hat{\beta }}_1)$ under some simplifying assumptions in Appendix B of supplementary material available at Biostatistics online.

5. Simulation study

We will now illustrate the impact of population-based preferential sampling with a simulation study. To simplify visualizations and interpretation of results, we restrict attention to the 1D setting. A 2D simulation study is included in Appendix C of supplementary material available at Biostatistics online and we found that our results are not sensitive to the dimension. Let $s$ represent location, which goes from 0 to 1, and treat values of $s$ between 0.6 and 0.9 as being “urban” by defining population density to be higher in these locations, with the highest population between 0.7 and 0.8. We simulate exposure using (3.1) where the mean component of the model is a linear function of covariates and the covariance is defined by an exponential covariance function. The exponential covariance takes the form, $C(d)=\text{exp}(-d/\varphi )$ , and we set $\varphi =0.05$ . The mean component of the model is defined by $C\alpha$ , where $C$ consists of an intercept, $1(0.7<s<0.8)$ , $(s-0.6)\ast 1(0.6<s\le 0.7)$ , and $(s-0.9)\ast 1(0.8\le s<0.9)$ . The first covariate is simply an indicator of being in the high-density area, while the other two are linear functions of s that allow exposure to linearly decrease away from the high-density area. We set $\alpha =[5,3,3,-3]$ . An illustration of the population density and a subsequent realization of the exposure surface can be found in Figure 2. We simulate our outcome from (3.2) with ${\beta }_0=100$ , ${\beta }_1=5$ , and ${ϵ}_i\stackrel{iid}{\sim }N(0,9)$ . We explored situations where our outcome model included a vector of potential confounders in Appendix D of supplementary material available at Biostatistics online, but found no differences, so we present here simplified results to ease intuition.

Fig. 2.

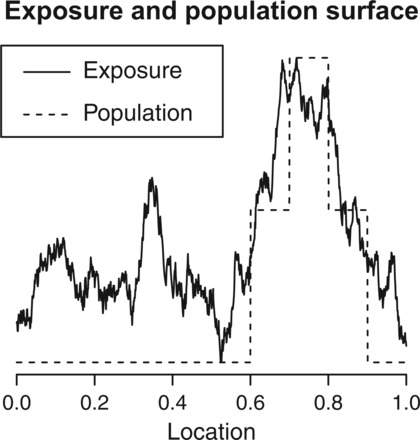
Illustration of population and exposure across area of interest.

Monitoring locations are drawn from a simple, interpretable scheme where we sample monitors with probabilities proportional to the population density. Specifically, we sample monitoring sites proportional to $D^p$ , where $D$ is the population density at a location and $p$ is a parameter that governs the magnitude of population-based preferential sampling. $p=0$ represents sampling under CSR, while $p>0$ represents sampling areas of higher population densities. We sample $n^{\ast }=30,40,50$ monitors for values of $p\in [0,2]$ to see the impact that the number of monitors plays in the performance of various sampling schemes. In all situations, we simulate 10 000 data sets. Empirical standard errors are taken as the standard deviation of the estimated parameters across the 10 000 simulated datasets. We exclude simulations where monitors are not placed in each of the three elevated areas of population density to ensure identifiability of the exposure model parameters. The lack of identifiability occurs since the exposure model includes a main effect for each of the three elevated areas of population density. If there is no data in one of the regions, then we have no information to estimate the exposure level in that region.

5.1 Impact on exposure estimation

In light of our analytic results that show bias in the health effect estimate is a function of the bias and variance of the exposure model parameter estimates, we can look at the impact that varying $p$ has on estimating $\theta =(\varphi ,\alpha )$ (the exposure model parameters). Table 1 lists the estimates of the exposure model parameters for a variety of preferential sampling parameters and number of monitors. Both $\alpha$ and $\varphi$ are estimated with little to no bias under any sampling scheme. The biggest differences seen between values of $p$ is in the standard errors of the parameter estimates. The intercept standard errors grow slightly as we increase $p$ , though the differences are fairly small. The values of the parameters representing differences between high- and low-population areas have drastically lower standard errors under population-based preferential sampling. For instance, under $n^{\ast }=30$ , the standard error of $\widehat{{\alpha }_2}$ drops from 0.85 under CSR to 0.69 under $p=1$ . Similar results are seen for $\widehat{{\alpha }_3}$ as the standard error ranges from 0.89 to 0.67.

Table 1.

Mean of estimated exposure model parameters across 10 000 simulations. Empirical standard errors are in parentheses

	p	$\widehat{{\alpha }_0}$	$\widehat{{\alpha }_1}$	$\widehat{{\alpha }_2}$	$\widehat{{\alpha }_3}$	$\hat{\varphi }$
n* = 30	0.0	5.00 (0.19)	3.00 (0.47)	3.00 (0.85)	−3.01 (0.89)	0.05 (0.06)
	0.5	5.00 (0.19)	3.00 (0.44)	2.98 (0.76)	−3.00 (0.75)	0.05 (0.06)
	1.0	5.00 (0.20)	3.00 (0.42)	3.01 (0.69)	−3.02 (0.71)	0.05 (0.06)
	1.5	5.00 (0.22)	3.00 (0.44)	3.00 (0.69)	−3.00 (0.67)	0.05 (0.06)
	2.0	5.00 (0.25)	3.01 (0.44)	3.00 (0.68)	−3.00 (0.67)	0.04 (0.07)
n* = 40	0.0	5.00 (0.18)	3.00 (0.45)	2.99 (0.74)	−3.00 (0.75)	0.05 (0.05)
	0.5	5.00 (0.18)	3.00 (0.42)	3.00 (0.65)	−3.00 (0.66)	0.05 (0.05)
	1.0	5.00 (0.19)	3.00 (0.41)	3.00 (0.60)	−3.00 (0.60)	0.04 (0.04)
	1.5	5.00 (0.20)	3.01 (0.42)	3.01 (0.59)	−3.02 (0.57)	0.04 (0.05)
	2.0	5.00 (0.23)	3.00 (0.43)	3.00 (0.59)	−2.99 (0.60)	0.04 (0.05)
n* = 50	0.0	5.00 (0.18)	2.99 (0.43)	2.99 (0.66)	−2.99 (0.68)	0.04 (0.03)
	0.5	5.00 (0.18)	3.00 (0.41)	2.99 (0.60)	−2.99 (0.60)	0.04 (0.03)
	1.0	5.00 (0.19)	3.00 (0.42)	3.00 (0.55)	−2.99 (0.56)	0.04 (0.04)
	1.5	5.00 (0.20)	3.00 (0.41)	3.00 (0.54)	−3.00 (0.54)	0.04 (0.03)
	2.0	5.00 (0.21)	3.01 (0.42)	3.01 (0.54)	−3.01 (0.54)	0.04 (0.04)

We can also look at the variance of the estimated exposure itself. The top row of Figure 3 shows the variance of (X – W) for a variety of preferential sampling parameters, p, and number of monitors, n^*. This represents the magnitude of the measurement error induced by using monitors to estimate exposure. In Section 4, we discussed the trade-off between placing monitors too close together and placing them near the locations of the subjects. We see that the overall variance is lowest under population-based preferential sampling, around p = 1, indicating that the gain from placing monitors near the subjects is outweighing the loss induced by putting monitors close together when monitors are preferentially sampled. To gain further intuition into this trade-off we separate the measurement error variance into a rural and urban component. The urban components enjoys significantly smaller variation under population-based preferential sampling, since we are placing more monitors in these locations when p > 0. The rural component on the other hand suffers from more variation, because we placed less monitors in those areas. More subjects live in the urban areas, therefore the overall variance is driven by the urban variance, and the ideal trade-off between reducing variance for urban locations and increasing it for rural locations seems to occur around p = 1, when monitor and population densities align.

Fig. 3.

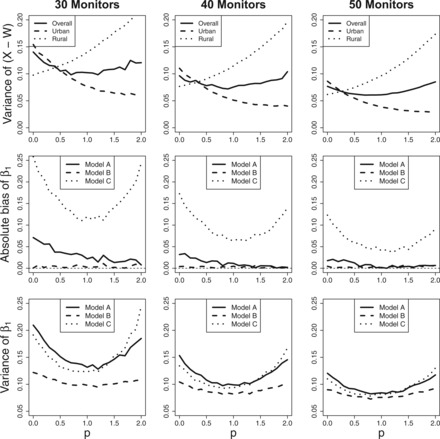
The top row displays the measurement error variance, the middle row shows the absolute bias in estimating β₁, and the lower row is the variance of β₁. All quantities are calculated across 10 000 simulations for a variety of values of p and n^*.

5.2 Impact on outcome model estimation

To fully understand the impact that population-based preferential sampling plays on the estimates of the second stage outcome model we fit three different outcome models: (i) a model that regresses $Y$ on $W$ (Model A); (ii) a model that regresses $Y$ on the estimated exposure we would get if we knew the true values of $\theta$ (Model B); and (iii) A model that regresses $Y$ on the exposure we would get if we misspecify the exposure model and do not include population into the set of covariates, $C$ (Model C). Model A is what is fit in practice, Model B will show us if and how population-based preferential sampling improves estimation beyond any improvements in exposure model estimation, and Model C is a realistic scenario in which we misspecify how population enters into the exposure model. This is arguably the worst type of misspecification as we are leaving population out completely, but it should lend intuition into what happens when the exposure model is incorrect. We will restrict attention to the estimation of ${\beta }_1$ .

The middle row of Figure 3 shows the absolute bias of ${\beta }_1$ under the three models and a variety of values of $p$ . We see that under any of the three models, population-based preferential sampling performs as well or better than CSR with respect to bias, although it should be noted that the magnitude of the bias relative to the true effect size is not substantial under any of the models, with the exception of Model C. The solid line (Model A) shows that the small bias under $p=0$ decreases as we increase $p$ . The dashed line (Model B) shows no bias for any value of $p$ , which highlights our result from Section 4 that says the bias is a function of the bias and variance of the exposure model parameters. The most interesting of the lines is the dotted line (Model C), which shows that when we misspecify the model, $p=1$ leads to the smallest amount of bias.

Figure 3 also shows the empirical variance across 10 000 simulations of ${\hat{\beta }}_1$ , and we see a similar U-shape trend in all three models. The greatest gains from population-based preferential sampling occur in Models A and C. Under Model A and $N^{\ast }=30$ the variance drops from 0.21 at $p=0$ to 0.13 at $p=1$ , and it drops from 0.19 to 0.12 for Model C. The gains are smaller for model B, but the variance still drops from 0.12 to 0.10 when we go from $p=0$ to $p=1$ . The variance tends back upward after $p=1$ as we approach $p=2$ illustrating the trade-off that occurs under population-based preferential sampling. Similar results are found for $n^{\ast }=40,50$ as the variance drops near $p=1$ but increases as we preferentially sample too far. These results suggest that the ideal value of $p$ is 1, when monitor and population densities align.

6. AQS monitoring system

Now that we have gained insight into the effects of population-based preferential sampling, it is of interest to relate these results to the motivating example. Figure 1 shows the locations of the EPA's AQS monitoring system in New England. Data from these monitors is publicly available and has been used in several environmental studies (Air Quality System (AQS)—US EPA, 2016,Dominici and others, 2003).

6.1 One-parameter population-based preferential sampling model

To relate the locations of the EPA monitors back to the results we have seen, we can impose a simple model for the locations of the monitors. We can split New England into a very fine grid that consists of K grid cells. For each grid cell define $D_k$ to be a measure of population density in grid cell k. We will define $D_k$ to be the number of census tracts within 0.3 ${\hspace{0.17em}}^{\circ }$ of the center of grid k. Now further define

$$Z_k=\{\begin{array}{ll}1& \text{grid}\hspace{0.17em}\text{cell}\hspace{0.17em}\text{k}\hspace{0.17em}\text{has}\hspace{0.17em}\text{a}\hspace{0.17em}\text{monitor}\\ 0& \text{grid}\hspace{0.17em}\text{cell}\hspace{0.17em}\text{k}\hspace{0.17em}\text{does}\hspace{0.17em}\text{not}\hspace{0.17em}\text{have}\hspace{0.17em}\text{a}\hspace{0.17em}\text{monitor},\end{array}\hspace{0.17em}$$ (6.1)

where $\sum _k{Z}_k=n^{\ast }$ , so the number of monitors is fixed. Then the joint distribution of $z=[z_1...z_K]$ can be decomposed into successive conditionals and written out as

$$\begin{array}{ll}P(Z=z)& \hspace{0.17em}=P(Z_1)\hspace{0.17em}P(Z_2|Z_1=z_1)\hspace{0.17em}...\hspace{0.17em}P(Z_K|Z_1=z_1...Z_{K-1}=z_{K-1})\\ & \hspace{0.17em}=\prod _{i=1}^{n^{\ast }}\text{categorical}(w_1,...,w_K)\end{array}$$ (6.2)

and we define the vector w as follows:

$$w_k=\{\begin{array}{ll}0& \text{grid}\hspace{0.17em}\text{cell}\hspace{0.17em}\text{k}\hspace{0.17em}\text{already}\hspace{0.17em}\text{has}\hspace{0.17em}\text{a}\hspace{0.17em}\text{monitor}\\ D_k^p& \text{grid}\hspace{0.17em}\text{cell}\hspace{0.17em}\text{k}\hspace{0.17em}\text{does}\hspace{0.17em}\text{not}\hspace{0.17em}\text{have}\hspace{0.17em}\text{a}\hspace{0.17em}\text{monitor}.\end{array}\hspace{0.17em}$$ (6.3)

We have now defined a joint probability model for the location of the monitors that depends on a single parameter, $p$ . We can use this model and the location of the EPA monitors to estimate $\hat{p}$ via maximum likelihood. We obtain $\hat{p}=0.64$ for the AQS monitoring system, which tells us that monitors are preferentially sampled with respect to population density. In light of our previous results this suggests that this has led to improved estimation for health effect analyses that rely on an estimated exposure. Obviously the mechanism by which monitor locations are chosen is more complex than the one-parameter model we have introduced here, but the results do provide some intuition as to the accuracy of estimates based on this monitoring system. This also provides guidance both for future researchers using monitors to estimate exposure and for guidance on where to place new monitors. If in a different study researchers were to estimate $\hat{p}$ for their monitoring system and find that it were near 0 or even negative, then additional work would have to be done to correct for bias in the health effect estimate. It is possible that an algorithm could be devised which would take a set of monitors and select which ones to use to achieve a given level of population-based preferential sampling that would be beneficial for inference.

6.2 Sampling new monitors in New England

The left side of Figure 1 gives us a realistic view of the true ${\text{PM}}_{2.5}$ surface across New England, and we can use this to examine the impact that different monitoring schemes would have on health effect estimates in epidemiological studies. We again discretize New England into a fine grid and select locations to place monitors under CSR and a variety of values of $p$ . Using the values, $D_k$ , for a grid cell k, we can sample locations proportionally to $D_k^p$ and vary $p$ as we did in our simulation study. The difference here is that our exposure will be taken from the predicted satellite surface seen in Figure 1 and will be more realistic to what is actually seen in these studies. Once we have a set of monitors we simulate outcomes from (3.2) with ${\beta }_0=100$ , ${\beta }_1=5$ , and ${ϵ}_i\stackrel{iid}{\sim }N(0,9)$ . Then we can sample $n^{\ast }=83$ monitoring sites without replacement, as this is the number of monitors that exist in the EPA AQS monitoring system. Figure 4 shows the corresponding results across 1000 simulations. We see that the 95% confidence bands for ${\hat{\beta }}_1$ decrease in width as $p$ grows larger indicating that the variability in our estimates decreases as we preferentially sample. The confidence interval for CSR goes from 1.4 to 12.1, while the interval under $p=1$ goes from 3.1 to 7.9. The interval gets even smaller as $p$ grows, although it comes with some bias. The right panel shows the means of ${\hat{\beta }}_1$ and the estimates are roughly unbiased near $p=1$ , while there is bias under CSR or extreme population-based preferential sampling.

Fig. 4.

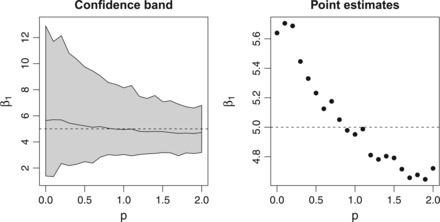
Estimates of β₁ after sampling monitors within New England. Left panel shows the confidence band representing the 2.5th and 97.5th quantiles of the 1000 simulations. The right panel shows the mean across 1000 simulations.

7. Discussion

In this article, we have illustrated the impact that population-based preferential sampling can have on exposure prediction and outcome model estimation in two-stage analyses. The fact that our results differ from previous literature on preferential sampling is not surprising, as we take a different approach to defining preferential sampling. We defined population-based preferential sampling of monitors as the scenario when the location of monitors is associated with population density. Defining preferential sampling with respect to population density is a more specific scenario and is in fact a subset of the scenarios proposed in Diggle and others (2010) and Lee and others (2015). However, we believe that population-based preferential sampling is a very important scenario to consider, as it is very likely to occur in practice. We showed that the EPA's AQS monitoring system is preferentially sampled with respect to the population density in New England.

The main intuition behind the idea that population-based preferential sampling can improve estimation has to do with the fact that while estimation of the exposure surface might be biased under preferential sampling (Diggle and others, 2010), it is more accurately estimated in areas where the majority of the population of interest resides. Possibly more importantly, the standard errors of our exposure estimates are smaller in areas of high population density, which effectively reduces the amount of measurement error induced by using estimates of the exposure. This reduction in measurement error leads to substantial reductions in the variance of estimates from second stage outcome models, which are usually of interest in air pollution epidemiology.

Our results can be used to help interpret past and future studies that use monitors to predict exposure in environmental studies. Studies where exposure estimation uses monitoring sites that align spatially with the population being studied will be more reliable than those based on monitors in different areas. One example of worsened inference due to the distribution of monitor locations not aligning with the distribution of subjects is a study that estimates exposure using the IMPROVE network. The IMPROVE network is placed in rural areas to measure natural pollution levels. As such, the monitor locations do not align with population density, and our results indicate that there is a potential for worsened inference on the health effects of air pollution. Our results agree with the claim made by Szpiro and Paciorek (2013) that the density of the monitor locations should agree with the density of the subject locations in a two-stage analysis. While it is difficult to say whether this holds exactly in any study, we have proposed a simple method to check for population-based preferential sampling that can be used to gain intuition to whether the two densities are close enough to lead to valid inference. This, along with our analytic and simulation results, should help to guide further research on the health impacts of air pollutants.

Supplementary material

Supplementary material is available at http://biostatistics.oxfordjournals.org.

Funding

(DARPA FA8750-14-2-0117, ARO W911NF-15-1-0172, NSF 1461435, and NSERC) to L.B. National Institutes of Health (ES007142, ES024332, ES022585-01); U.S Environmental Protection Agency grant (RD-83479801) to J.A.