Abstract
Many Bayes factors have been proposed for comparing population means in two-sample (independent samples) studies. Recently, Wang and Liu (2015) presented an “objective” Bayes factor (BF) as an alternative to a “subjective” one presented by Gönen et al. (2005). Their report was evidently intended to show the superiority of their BF based on “undesirable behavior” of the latter. A wonderful aspect of Bayesian models is that they provide an opportunity to “lay all cards on the table.” What distinguishes the various BFs in the two-sample problem is the choice of priors (cards) for the model parameters. This article discusses desiderata of BFs that have been proposed, and proposes a new criterion to compare BFs, no matter whether subjectively or objectively determined: A BF may be preferred if it correctly classifies the data as coming from the correct model most often. The criterion is based on a famous result in classification theory to minimize the total probability of misclassification. This criterion is objective, easily verified by simulation, shows clearly the effects (positive or negative) of assuming particular priors, provides new insights into the appropriateness of BFs in general, and provides a new answer to the question, “Which BF is best?”
Keywords: effect size, prior probability, decision theory, optimal classification
1. Introduction
The recent statement by the American Statistical Association on the use of p-values (Wasserstein and Lazar, 2016) notes, “By itself, a p-value does not provide a good measure of evidence regarding a model or hypothesis” (p. 132), and notes that alternative measures of evidence, including Bayes factors (BFs), can and should be used. This article applies to BFs for any scenario; however, to maintain focus, we consider the important special case of the two-sample comparison, perhaps the most common type of study where either p-values or Bayes factors may be used to summarize the evidence comparing the groups. For this type of study we call model M1:
| (1) |
And we call the (null) model M0:
| (2) |
Standard, textbook testing of M0 against M1 is based on the t-statistic
| (3) |
where is the effective sample size, is the estimated effect size, and sp is the usual pooled standard deviation. The corresponding p-value is given by p = 2Pr( Tν > |t| ), where Tν has the T-distribution with ν = n1 + n2 – 2 degrees of freedom. By classical frequentist thinking, one rejects M0 in favor of M1 when p < 0.05.
Related to the recent statement of the ASA on p-values, there is a long line of research that is critical of common uses of p-values that will not be repeated here. Bayes factors (BFs) have been touted as a viable alternative to frequentist testing going back at least to Jeffreys (1961). The Bayes factor is a statistic that measures the relative plausibility of the data under M1 versus M0:
| (4) |
Thus, BF >1 (<1) suggests that the data favor M1 (M0). Calculating the BF in (4) requires prior distributions for the parameters under M0 and M1 in models (1) and (2), and integrating these out:
| (5) |
Here, ∏i(θi|Mi) is the prior distribution of the parameter vector under model Mi, i = 0, 1.
The null model for the two-sample comparison states that δ = 0, where δ = (μ1 − μ2)/σ is the well-known effect size parameter. Defining γ = (μ1 + μ2)/2, the primary focus will be on δ throughout and thus we regard γ and σ2 as nuisance parameters. The Bayesian model requires a joint prior distribution on (δ, γ, σ2), which we write as p(δ, γ, σ2) = p(δ | σ2)p( γ)p(σ2); we are thus assuming independence of δ and γ. Depending on the BF considered, we may assume δ is independent of σ2 as well. Many approaches that we discuss involve placing a standard diffuse (improper) prior on (γ, σ2):
| (6) |
In this setting, we categorize BFs as either “objective” or “subjective” depending on the assumed prior for δ. A subjective prior might involve a web search, a literature search, or identification of relevant data from similar studies for information about the effect sizes from similar studies that can be converted into a prior distribution for δ. An objective prior for δ does not refer to scientific knowledge, but instead is selected so that properties of the posterior are “nice” in various ways; see the desiderata given below. Comparing these two approaches begs the often-debated question, “Should priors be chosen for convenience or to reflect prior knowledge?” which we address in this article.
In addition to Jeffreys (1961), Bayes factors are discussed by Kass and Raftery (1995). General “objective” Bayesian methods are discussed by Berger and Pericchi (1996, 2001); failings of BFs due to use of “local priors” under the alternative hypothesis are discussed by Johnson and Rossell (2010), and a development of BFs based on the criterion of uniformly most powerful Bayesian tests is given by Johnson (2013A, 2013B).
While general BFs have been around for decades and apply to a variety of problems, specific BFs for the two-sample comparison have appeared more recently, including Gönen et al. (2005), Johnson and Rossell (2010), Rouder et al. (2009), Johnson (2013A), and Wang and Liu (2016). Of these, the only explicitly subjective method is by Gönen et al. Nevertheless, objective methods choose priors as well, and our goal is to lay bare the scientific consequences of these choices. Specifically, we use methods related to the standard “Classification Theorem” for minimizing the total probability of misclassification (TPM), and apply it to compare BFs. A main contribution of our article is that this theorem provides a new, scientifically relevant answer to “which BF is best.”
Although Classification Theorem-related methods can be used to evaluate any BF in any setting, we evaluate only a sampling of recently proposed two-sample BFs. We do not consider Bayesian analyses for the two-sample comparison that are found in gene expression analysis (see e.g. Do, Müller and Vannucci, 2012), where there are thousands of two-sample tests, and typical methods for flagging genes as “significant” involve borrowing strength from the entire set of all tests (Fox and Dimmic, 2006; Guindani, Müller and Zhang, 2009; Shahbaba and Johnson, 2013). Nor do we consider Bayes/frequentist hybrid statistics espoused by Brad Efron (2010) and others involving BF-like quantities that similarly utilize all the information in a large collection of concurrent tests.
In Section 2, we give desiderata for BFs, both “objective” and “subjective.” In Section 3, we discuss particular BFs from recent literature that apply to the two-sample comparison. In Section 4, we show how to compare BFs using methodology inspired by the Classification Theorem; the application of the theorem to the present study is that the BF that uses the “correct prior” most often classifies the data as coming from the correct model. By “correct prior” we simply mean that the analysis is performed using the same prior distribution that is assumed (implicitly or explicitly) to give rise to the current study data. In Section 5, we provide a Bayesian simulation study to compare particular, recently proposed BFs, as a function of the “correct prior,” as well as the ordinary frequentist t-test; however, the study we describe can be easily applied to other BFs that we did not include. Meta-analytic effect size data reviewed in Section 6 suggest that scientists have prior information when they design their studies that they can use for prior selection. Section 7 provides additional comments and extensions.
2. Properties BFs “Should Have”
Objective BFs typically involve priors chosen to give the resulting BFs “nice” properties, often frequentist. They generally do not incorporate subjective, scientific information. Objective priors are often termed as “diffuse,” “reference,” “flat,” or “non-informative” among others. As a cautionary note, we mention that so-called “non-informative” priors may be “dis-informative”: A uniform (“non-informative”) prior on the unknown prevalence of HIV infection among blood donors would stipulate a 50% chance that the prevalence is above 0.5 and a 95% chance that it is above 0.05.
On the other hand, subjective Bayesian methods incorporate scientific information in the form of a prior distribution, which is combined with a likelihood function via Bayes theorem to obtain the posterior distribution, which gives the subjective Bayesian inference. Like objectivists, subjective Bayesians are also concerned about the sensitivity of inferences to the choice of prior distribution, and will generally report the effects of alternative priors.
Several desiderata of BFs have been discussed in the literature, including Bayarri et al. (2012), Johnson and Rossell (2010), and Johnson (2013A, 2013B). Those in the following list are essentially objective properties, not necessarily good ones, which is why “should have” in the title of this section is in quotes. Our main contribution is to offer a new desideratum, one that is inherently subjective in nature, and which we argue may be scientifically more relevant.
D1: Consistency:
As the sample sizes grow (for both samples), the BF should grow without bound if the alternative hypothesis is true, and it should converge to zero if the null is true.
D2: Finite Sample Consistency (FSC):
FSC means that for fixed sample sizes, as |t| tends to infinity, the BF should also tend to infinity.
D3: Robustness to Prior:
A standard motivation for using BFs rather than posterior probabilities P(Mi |data) is that BF does not depend on the priors P(Mi). But in addition, the BFs should be reasonably insensitive to the within-model priors Πi(θi | Mi).
D4: Compatibility with Frequentist Testing:
In cases where |t| is large, leading to frequentist rejection of M0, the BF should not favor M0. In other words, the BF should not exhibit the behavior of the Bartlett “paradox” (Bartlett, 1957).
D5: Ability to Accumulate Evidence Favoring M0 or M1:
As the sample size grows, the evidence favoring either M0 or M1 should be able to grow at the same rate.
D6: High Power:
The (frequentist) probability that the BF exceeds a given threshold should be large relative to BFs computed using other priors.
Researchers typically propose prior distributions to get BFs that satisfy these desiderata, rather than to incorporate scientific prior knowledge. An additional criterion that a BF should satisfy, which has not been given much attention in this literature, puts the scientifically chosen prior inputs foremost:
D7: Correct Classification:
The rule “BF >1 (<1) suggests that the data favor M1 (M0)” should classify the data as having come from the correct model most often. Here, “most often” refers to the frequency with which the different models might reasonably occur.
A standard result in classification theory, which we call the “Classification Theorem,” discussed in Section 4, makes this desideratum easy to apply using simulation and/or analytic calculations. This theorem is currently popular in data science circles, being the basis for the “naïve Bayes classifier” (e.g., Kuhn and Johnson, 2013, p. 353). There is no right answer to the question, “how often might the different models occur?” for the current experiment; however, because the answer to this question affects classification rates so substantially, researchers should carefully consider this question when choosing a BF. We analyze historical data to provide partial answers.
A natural extension of desideratum D7 is the following, which we discuss briefly in Section 7.
D8: Optimal Decisions:
Decisions “conclude M0,” “conclude M1,” and “conclude nothing” based on the BF should have minimum loss (or maximum benefit). For example, it may be considered worse to incorrectly classify as M1 when M0 is true; this desideratum can be modeled using loss functions.
3. Objective and Subjective Bayes Factors
In this section, we discuss several BFs for the two-sample comparison. The BF (GBF) developed by Gönen et al. (2005) is the only subjective one; many other BFs are obtained as hierarchical extensions of it. Motivation of the current work stems partly from criticism of GBF by Wang and Liu (2015, hereafter WL); their main points of contention were that GBF is finite-sample inconsistent and may suffer from Bartlett’s “paradox” (i.e., GBF lacks desiderata D2 and D4). While our main goal is to promote desideratum D7 (optimal classification) for comparing all BFs, we wish to set the record straight on these issues raised by Wang and Liu. Because these papers appeared in The American Statistician, we consider GBF and WBF more extensively than other BFs.
3.1. GBF
The GBF prior on δ is independent of σ2 and the prior on nuisance parameters is given in (6):
| (7) |
where λ and are (subjectively) selected by the analyst. The resulting BF is (from Equation (2) of Gönen et al (2005), but inverted to correspond to the present paper),
| (8) |
where Tv(t|l,d) is the Student density with df ν, location l and dispersion d. Objective Bayesians often set λ = 0, since they would prefer to allow for an unbiased belief about whether the effect could be negative or positive, if it is not zero (an exception is Johnson, 2013A, who provides an objectively determined BF for which λ ≠ 0). On the other hand, researchers very often have specific prior knowledge that λ ≠ 0, which they use in power analysis; data from multiple historical studies that we analyze in Section 7 support this assertion. Nonetheless, setting λ = 0 results in
| (9) |
Gönen et al. argue that λ and should be selected subjectively; here we elaborate. Consider a generic situation where the scientist involved in the current study is aware of published literature about effect sizes in studies related to his or her study, where it has been ascertained that the effects are truly non-null. In these cases, suppose there are studies with estimates of effect sizes between 0.1 and 0.5 with a median of 0.3. Then absent of additional information, a natural choice for λ would be 0.3 and a natural choice for σδ would be 0.1, since the range (0.1, 0.5) covers 95% of the normal distribution. However, in the words of Dennis Lindley, “always leave a little room for doubt” (Jones and Johnson, 2014); such doubt reflects uncertainty about differences between current study and historical ones, as well as concerns about selection biases in the literature. How much additional “room for doubt” of course depends on the scientist-statistician collaboration in analyzing the data, but as in Gönen et al (2005), one might imagine a 10% chance of a negative effect, implying Φ(−0.3/σδ) = 0.1, and hence σδ = 0.234.
A main criticism of GBF by WL is that it may suffer from Bartlett’s paradox, i.e., does not satisfy desideratum D4, which we now counter. Suppose that a critic were to argue that we should not be so restrictive in our specification of possible values for δ, instead demanding that δ could plausibly lie in the range (−20, 20). This would correspond to the choice of σδ ≈10, a terrible choice of prior in light of the available scientific information, since this prior anticipates that 92% of possible (non-null) values of |δ | that may apply to the current study are greater than 1.0. In addition, since this prior is anticipating large effect sizes, and since, in all likelihood, the data will provide evidence that the effect size is relatively small, relative to this prior, the model will tend to favor the null hypothesis, even for “significant” values of |t|. This is the Bartlett (1957) phenomenon, which occurs when using a large σδ. For instance, with P(Mi) ≡ 0.5 and with t = 2, σδ = 10, n1 = n2 = 10 (500), P(M1|data) = GBF0 /(1+ GBF0) = 0.23(0.044), giving a clear preference for the null, especially in the large sample case, despite the “significant” t. With t = 2.5, we get 0.43(0.13), with t = 4 we obtain 0.949(0.947), and finally with t = 5, we have 0.9942(0.9993). This is all reasonable: With an alternative prior that anticipates much larger effect sizes, it will take a larger t to conclude M1. As such, GBF0 does not always favor the null hypothesis as criticized by WL, unless t is relatively small. We view this as perfectly reasonable behavior of the GBF, an argument in favor of the Bartlett effect being a good effect, and an argument for carefully choosing one’s prior.
Now, we consider finite sample consistency, desideratum D2, discussed in, e.g., Liang et al. (2008). Wang and Liu (2015) note that the GBF0 is not finite sample consistent: With fixed sample sizes that as |t| →∞, . Does this mathematical fact have any practical/scientific meaning? To investigate, suppose = 1 (Masson, 2011; Wagenmakers, 2007; Kass and Raftery, 1995), P(Mi) ≡ 0.5, and ni ≡ 10. Using GBF0, P(M1| data) = GBF0 /(1+ GBF0) → 0.9999999 as t → ∞. If the observed t is 3, 5 or 7, the corresponding posterior probabilities are 0.90, 0.995, and 0.9997 respectively, so the limiting bound plays no important role under these circumstances, and even less of a role with larger sample sizes. In other words, as |t| →∞, GBF0 and finite-sample-consistent BFs all reach the same practical conclusion: M1 should be highly favored. It is only the extremely small sample size case where it matters: In the scenario above with n1 = n2 =2, the limiting value is 0.667. Thus, with extremely small sample sizes finite sample inconsistency may be a concern with GBF, but for typical studies, it has no practical importance.
3.2. WBF
Wang and Liu (2015) developed a novel BF by starting with the model that leads to GBF0, and then placing a Pearson Type VI prior on , instead of a Cauchy distribution as was done by other authors. Their particular selection is , with b = (ν + 1)/2 – a – 5/2 and any a ∈ (−1, −1/2], which guarantees that WBF, given below, will be finite sample consistent for all positive ν. Based on empirical robustness arguments they select a = −0.75 in their illustrations. This specific Pearson Type VI distribution places much probability mass on very large values; see for example Figure 1 in WL, p. 12. There is even considerable mass to the right of their truncation point, 20.
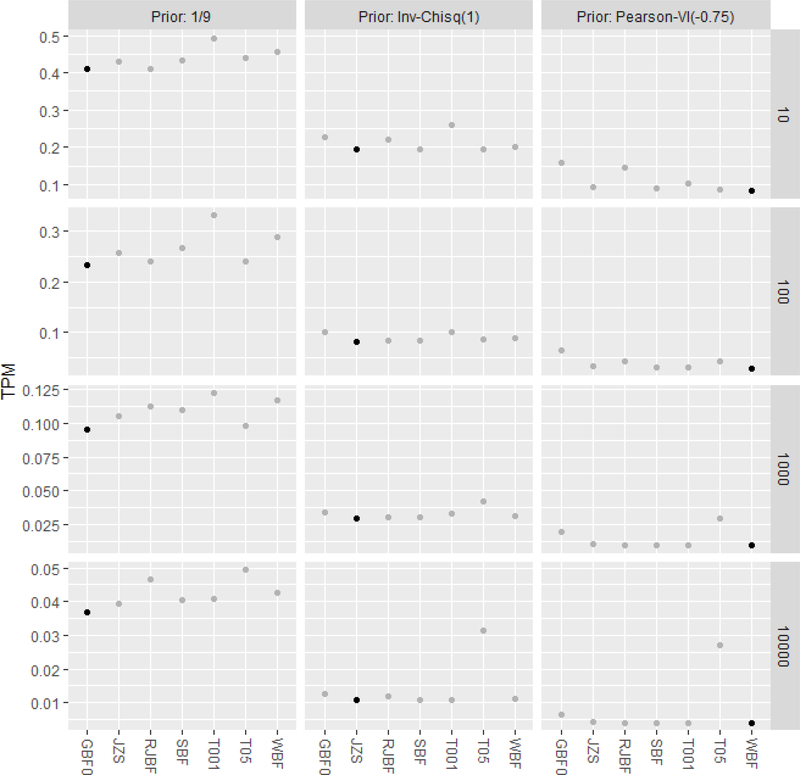
Figure 1.
Total probability of misclassification as function of nδ (rows 10, 100, 1,000, 10,000) under the three different prior settings for (columns = 1/9, ∼ Inv-, ∼ Pearson-VI (−0.75)). The points indicating minimum TPM are highlighted in black, all others are grey. The BF that uses the prior corresponding to the true model has minimum TPM. The ordinary t test using α = (0.001, 0.05) is shown as (T001, T05).
The WBF is obtained by marginalizing over in (9). Wang and Liu obtain
| (10) |
This is equivalent to computing the BF based on the prior p(δ | λ) = ∫ p(δ | λ,)p()d, with λ=0; WL also use the prior (6) for the nuisance parameters. WL note that, unlike GBF, WBF is finite sample consistent (satisfies Desideratum D2) provided a ∈ (−1, v/2 −1).
To understand the WL prior, we characterize the Pearson VI distribution as a function of a Beta distribution. Let q ~ Beta(a*,b*) with a* = (ν +1)/2 – a – 3/2 and b* = a+1. Then let O = q/(1-q). Then O ~ Betaprime(a*,b*), where Betaprime is also known as the inverted Beta distribution or Beta distribution of the second kind. It follows that ~ O/nδ . The mean of O and thus the mean of doesn’t exist unless a > 0. Thus for the WL choice of a, no prior moments exist. On the other hand, prior quantiles of are easily obtained from the quantiles of q. With n₁=n₂=10, the WL prior has median and 90th percentiles for σδ of 6.2 and 158 respectively, while the prior mode is only 1.11. With n₁=n₂=50, their median σδ value is 6.7 and a mode of 1.24 and ninetieth percentile 169.3. While these priors might be relevant in some applications, they provide unrealistically large values of σδ for typical applications. Data analyzed below support this assertion.
WL justify large σδ by stating “a large value of is often chosen to minimize prior information” (p. 5), and further claim insensitivity of the WBF to the parameter a is a desirable feature. They treat a as a tuning parameter and are concerned about robustness, and make comparisons with the GBF0, treating as a tuning parameter. In addition, Wang and Liu remind the reader that the GBF is quite sensitive to this choice. But the GBF was not developed for its objective desiderata; further, as we show below, the properties of any BF depend strongly on the choice of prior. WL’s statement is also troubling because a large value in fact represents a strong prior belief that extremely large effect sizes are probable.
3.3. Other Objective BFs
We now briefly discuss several other objective BFs in chronological order.
JBF:
Jeffreys’ JBF is based on a scaled Cauchy(0, σ) prior for σδ , which results in a marginal distribution that is standard Cauchy for δ, namely p(δ) ∝ 1/(1 + δ2 ). This prior is symmetric about zero with tails that are so fat that no moments exist, and the probabilities that the absolute value of δ exceeds 2, 3, 5, 10 and 20 are about 0.3, 0.2, 0.12, 0.06 and 0.03 respectively. So fairly large effect sizes are anticipated under this prior and huge effects are accommodated with moderate prior probability.
ZSBF:
Zellner and Siow (1980) developed a BF in the linear model context based on a (marginal) prior for δ that reduces to a non-standard Cauchy(0,). Thus with equal sample sizes, the ZSBF is identical to the JBF. This marginal Cauchy prior on δ is induced by the N(0, ) prior for δ | λ=0, , in conjunction with the inverse distribution for . The prior for nuisance parameters was given in (6). ZS developed the following approximation:
| (11) |
Rouder et al. (2009) compare the JBF, SBF (discussed below) and GBF0 with .
JZS:
The JBF is not analytically tractable. However, Rouder et al. (2009) took advantage of the fact that placing an inverse χ2 with 1 degree of freedom hyperprior on results in an induced standard Cauchy prior on δ as discussed above. The JBF for comparing the null to the alternative is just the integral of 1/GBF0 in (9) against this prior, which is then inverted to give the JBF for comparing the alternative to the null. Rouder et al. call this the JZS Bayes factor to credit Jeffries, Zellner and Siow.
| (12) |
The one-dimensional integral is easy to approximate numerically; Rouder et al. have a web-based program that gives the JZS and the GBF0 with = 1. See Held and Ott (2016) for asymptotic approximations to these and other BFs.
SBF:
The Schwarz (1978) criterion is based on the Bayesian Information Criterion (BIC) and has been discussed by many, including Kass and Raftery (1995), Berger and Pericchi (2001) and Rouder et al. (2011). The BIC is just minus twice the log of the maximized likelihood under a particular model plus a penalty that is the number of parameters in the model times the log of the total sample size, v + 2. Then
| (13) |
IPBF:
Berger and Pericchi (1996) develop intrinsic Bayes factors, which involve the use of the data for construction of the “prior.” The goal is to obtain a BF that is free of subjective input, free of arbitrary choices of proper priors, is “fully automatic” and which “seems to correspond to very reasonable actual Bayes factors.” They term their prior a “reference prior.” A motivation is that many users of statistical methods may not be capable of developing informative priors, and thus would benefit from a “fully automatic” approach. An approximation of the intrinsic Bayes factor is given in Rivera (2011).
Rivera (2011) studies finite sample consistency of various objective Bayes factors for Student’s t test including JBF, ZSBF and IPBF mentioned above, and argues that desiderata D2 (finite sample consistency) and D3 (robustness) are two important properties shared by those BFs.
Johnson and Rossell:
Johnson and Rossell (2010) also argued against traditional objective BFs involving local priors having mode at 0 under the alternative. Instead, they propose using symmetric non-local priors, which require low probability mass near the null. They argue that with local alternative priors, “it is often impossible for such tests to provide strong evidence in favor of a true null hypothesis, even when moderately large sample sizes have been obtained” (p. 143). They propose two classes of non-local priors and study their properties. Software to evaluate their BF for regression models is freely available in the “mombf” package of R; use of a dummy variable gives the two-sample test, and we evaluate this BF (called RJBF), along with others below, by assuming a moment normal prior with prior modes of effect size at ±0.2.
All of the BFs we have discussed so far, except for GBF, have a prior distribution for δ necessarily having median at 0 under the alternative model. This choice is questionable from the subjective viewpoint, because in many cases researchers have theory and prior studies to suggest that, if there is an effect, it is more likely to be on one direction than another; this information is typically used in power analysis. The following BF (Johnson) also supposes λ > 0, except the BF is objective, not requiring elicitation of prior distributions.
Johnson:
Johnson (2013A, 2013B) proposes a BF based on a uniformly most powerful Bayesian test (UMPBT) Bayes factor that maximizes the probability of exceeding a given evidence threshold for all possible alternative prior distributions. This prior is objective, and the resulting analysis has a close correspondence with frequentist fixed-α test procedures. Interestingly, the UMPBT results in a BF based on testing a fixed alternative that is O(n−1/2) from the point null, an alternative prior that is closely related to one suggested by Gönen et al (2005) on subjective grounds. While the method allows for Bayesian interpretation of classical testing, Johnson notes that it does not satisfy desiderata D5 noted above because it cannot increasingly accumulate evidence in favor of M0 as the sample size grows. This is a property shared by a version of GBF studied below as well. Hence, there remains the need for additional comparative criteria.
Next, we compare different BFs based on a single objective criterion, desideratum D7.
4. The Classification Theorem and Its Applications
Let p1 = P(M1) and p0 = P(M0), the prior probabilities that models M1 and M0 are the true ones. A natural (and optimal, as we will see) approach to deciding between these two models is to calculate their posterior probabilities. Bayes factors have an intimate connection with these posterior probabilities:
Thus, model M0 (M1) has the highest posterior probability if BF < p0/p1 (BF > p0/p1). WL suggest that BF > 1 favors model M1; implicitly this assumes p0 = p1 = 0.5, a common default.
Use of the posterior probability (or BF, as shown immediately above) to classify the model as M0 or M1 is justified by a standard result in classification theory that is used to assign observed data as having come from one of several possible populations (models). The result appears in many sources; the following theorem uses notation from Johnson and Wichern (2007, p. 582–584).
The Classification Theorem:
Suppose a continuous random vector X is distributed as X ∼ M0 with probability (wp) p0 and X ∼ M1 with probability (wp) p1 = 1 – p0. Consider the decision rule, “classify the model as M1 (M0) if P(M1| X=x) > 0.5 (<0.5).” Then this decision minimizes the total probability of misclassification, TPM = p0P(Classify as M1 | M0) + p1P(Classify as M0 | M1).
Corollary:
If P(M0) = P(M1) = 0.5, then the rule “classify the model as M1 (M0) if BF > 1 (<1)” minimizes the TPM.
An immediate application of the corollary is a method for objective comparison of BFs based on calculation of their TPMs in a stream of hypothetical studies. This type of analysis is suggested by Berger and Sellke (1987), who, in a stream of hypothetical studies where the frequentist p-value is 0.05 (their Example 1), show that in approximately 30% of such studies, the true model is actually M0. Using a similar construction, one can evaluate the “best” BF objectively by calculating (either analytically or via simulation) the true TPM for various BFs in a stream of hypothetical studies, assuming particular priors; see Section 4. The Classification Theorem and its Corollary imply that, if the distributions used to produce the parameters in this stream correspond to the priors used to calculate a particular BF, then that BF will have minimum TPM.
We note that in most cases we do not precisely believe the null model M0 is even plausible, let alone having 50% probability, because true effect sizes are rarely 0 to the infinite decimal. Rather, we view the rule “classify as M0” as instead a classification to the “perinull” case, a term coined by John Tukey (see Benjamini and Braun, 2002), where the true effect is very near zero. The model M0 is a good approximation to the perinull case, as proven by Berger and Delampady (1987).
We note further that the TPM method of comparing BFs, especially as implemented via simulation, clarifies the researcher’s implicit assumption that half of the possible models relevant to the current experiment will come from the (peri) null case, and half from the alternative. While BFs have been touted as a way to avoid making such (0.5,0.5) prior specifications, this assumption is in fact necessary for optimal TPM since the BF >1 (<1) rule requires p0 = p1. A benefit of considering simulation-based TPM, is that it allows researchers to easily visualize the collection of possible models that they are assuming when they use a particular BF. In the simulation, the researcher generates thousands of models, half of which will be null, and the other half which use parameters sampled from the researcher’s assumed alternative model. If, after viewing these simulated models, the researcher feels that either the 50% null, 50% alternative assumption or the collection of possible models assumed under the alternative is not at all relevant to the current experimental setting, then he or she should assume a different prior for δ, different p0 and p1, or perhaps not use BFs at all. But, it is worth noting that if a BF is a simple function of the t-statistic, the TPM may be calculated analytically (see the Appendix).
5. Objective Comparison Based on The Classification Theorem
The Classification Theorem shows that, when the prior is “correct,” the resulting BF has minimum TPM. This suggests a fair and objective comparison of BFs based on different assumed priors. TPM can often be computed analytically, but simulation may be preferred for scientific understanding, as mentioned above.
Simulation Study to Compare Two-Sample Comparisons BFs Objectively:
Step 1: Randomly generate a from an assumed prior distribution or assign a pre-specified positive constant value.
Step 2: Randomly generate a δ from N(λ,) conditional on the from Step 1 or set δ =0, each with 50% chance. The parameter λ is fixed according to the method chosen.
Step 3: Randomly generate the t-statistic as a function of δ : , where Z ∼ N(0,1) is independent of U ∼ . (All BFs we consider here are functions of the t-statistic.)
Step 4: Calculate BFs using the simulated t value from Step 3.
Step 5: A misclassification error occurs if BF>1 and δ =0 or BF<1 and δ is from N(λ,).
Step 6: Repeat Steps 1–5 NSIM times to estimate the TPM.
Figure 1 shows TPM rates (estimated using NSIM=1,000,000) associated with the GBF0, WBF, JZS, RJBF, as well as the frequentist t-test usingα = 0.05 and 0.001, as a function of nδ , assuming n1 = n2, under the three different prior settings for : (a) = 1/9, (b) ∼ Inv-, and (c) ∼ Pearson-VI (−0.75), and λ =0. As per the Classification Theorem, when δ is generated from an assumed prior distribution, the BF corresponding to that prior always has the minimum TPM, and is objectively the “best” BF.
One of the BFs considered in Gönen et al. (2005) used the prior , which was not meant to be a “default” or “objective” prior, but simply one that is consistent with subjective prior information that is commonly used in power analysis: Researchers often choose a large sample size to accommodate a priori information that the effect size is small. Gönen et al. (2005) note that this prior makes predictions that are reasonably consistent with published oncology studies. Our purpose here is not to recommend this prior for general use, but rather to highlight the fact that researchers do have prior information that can be used to construct their prior distribution; data shown in the next section support this assertion.
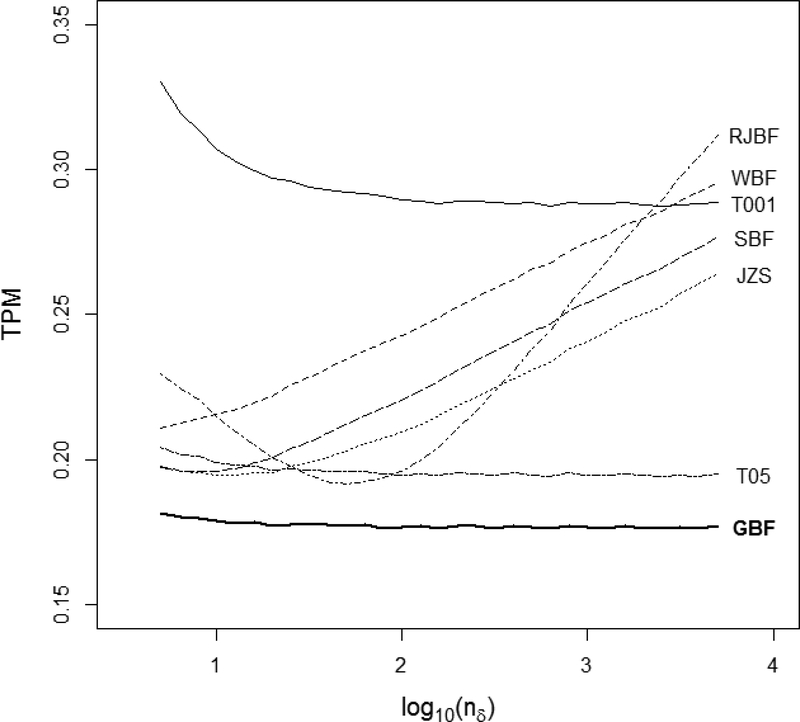
We estimated TPM for the various methods when ; Figure 2 summarizes the results. GBF considerably out-performs the others in this case. Thus subjective information matters.
Figure 2.
Total probability of misclassification as function of nδ . GBF is calculated using λ = 2.80 and σδ = 2.19 , these settings also define the model-generating process. WBF is calculated using a = −0.75. The ordinary t test using α = (0.001, 0.05) is shown as (T001, T05).
6. Real Data Effect Sizes and Implications for Practice
What kinds of priors for effect sizes are reasonable in practice? We first briefly discuss a particular case study involving prior elicitation for effect sizes, and the subsequent use of BFs to compare relative evidence in the data for no effect versus any effect. Then we analyze two recently published meta-analytic data sets on effect sizes to suggest priors.
6.1. Effect sizes in PSI testing
A study was performed to ascertain whether a particular type of psychic phenomenon (PSI) exists or not based on the frequentist analysis of nine experiments (Bem, 2011). Wagenmakers et al. (2011) argued that the analysis should have been done using BFs based on Cauchy priors for effect sizes, and consequently JBFs instead of p-values, which resulted in an analysis that contradicted Bem’s analysis.
In their rejoinder, Bem et al. (2011) analyzed the data using GBF0s. They then pointed out that estimated effect sizes in psi studies typically range from 0.2 to 0.3, and they referred to a previous meta-analysis of 56 psi experiments with estimated median effect size across studies of 0.18 (Utts et al., 2010), and a meta-analysis of 38 studies, with an average estimated effect size of 0.28 (Mossbridge, Tressoldi, and Utts, 2011). Based on this information, they asserted that “no reasonable observer would ever expect effect sizes in laboratory psi experiments to be greater than 0.8.”
If a standard Cauchy distribution is used as a prior on the effect size, the prior probability that it will equal or exceed 0.8 is 0.57! It even places a probability of .06 on effect sizes exceeding 10. If effect sizes were really that large, there would be no debate about the reality of PSI. Thus we would consider this to be a wildly unrealistic prior for the particular PSI problem under study.
6.2. Effect sizes in Psychology studies: Wetzels at al. (2011)
We consider two more recent meta-analytic studies in psychology that further support the notion that researchers have prior knowledge of effect sizes. The data show that they tend to design studies with larger sample sizes when the effect size is expected to be smaller, and that the actual effect sizes are similar to their expectations. These facts support the use of specific, rather than generic priors.
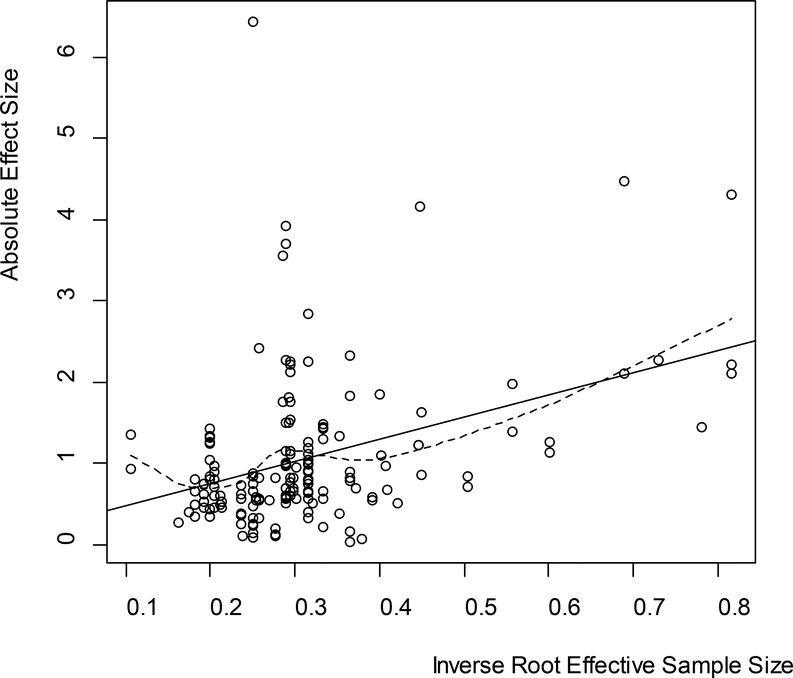
Wetzels et al. (2011) report results on 855 t tests from publications in psychology journals. Of the 855 t tests, 166 were for two-sample comparisons discussed in this paper, and the remaining 689 involved paired comparison and one-sample tests. Figure 3 plots the pairs (, ) (absolute values are used because it is not clear from Wetzels et al. whether the negative test statistics were in the anticipated directions) for the 166 two-sample comparisons along with least squares and LOESS fits. The empirical data give a least squares fit 0.20 + 2.75 , comfortably agreeing with the Gönen et al. mild suggestion of 0.00 + 2.80 for a prior mean function. (Use of raw rather than absolute effect sizes gives 0.23 + 2.25 , also in reasonable agreement.) Similar results were obtained for the one-sample and paired-sample effect sizes reported in Wetzels et al., further supporting the claim that researchers use prior information about effect sizes when choosing sample sizes.
Figure 3.
Plot of (,) for 166 two-sample comparisons reported in the psychology literature. The solid line is the least squares fit 0.20 + 2.75 ; the dotted line is a LOESS fit using a Gaussian kernel.
6.3. Effect sizes in replicated studies: The Open Science Collaboration
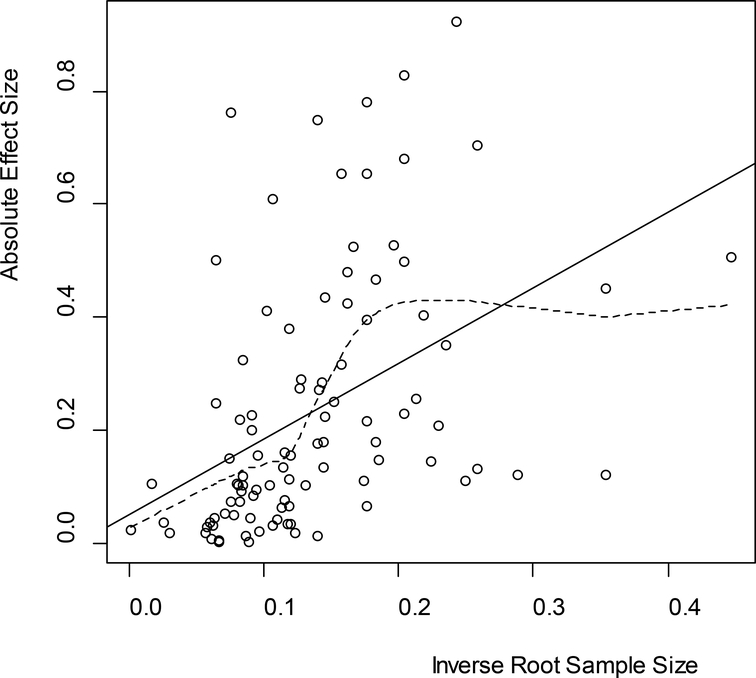
The Open Science Collaboration (2015, hereafter OSC), completely replicated actual studies published in psychology journals, obtaining fresh effect size estimates. There are few two-sample comparisons in the OSC study – most of the effect sizes are based on chi-square tests, F tests, paired comparisons, etc. As such, all reported effect sizes were converted to a correlation (−1 to 1) scale. Figure 4 shows similar information as Figure 3, except with all effect sizes in the absolute correlation metric, and with the horizontal axis n−1/2 using the sample size reported by OSC.
Figure 4.
Plot of (, ) for OSC’s 97 replicated effect sizes of studies performed in the psychology literature. The solid line is the least squares fit, while the dotted line is a LOESS fit using a Gaussian kernel.
A more sophisticated analysis could be performed, say fitting a mixture model with unknown prior on zero effect as well as scale, location, and regression parameters. Indeed, OSC reports “Ninety-seven percent of original studies had significant results (p < .05). Thirty-six percent of replications had significant results.” Hence it appears that a mixture model where many of the effects are truly null would fit nicely. However, due to differing types of tests, the data are too limited to tease out these effects. And in any event, our goal here is simply to show that true effect size is indeed associated with sample size chosen by the researcher, indicating that researchers can and do use prior information in the study design. Such prior information can, and, we argue, should be used in prior distributions.
7. Concluding Remarks
The main conclusion of our study is that regardless of whether objective or subjective, a desired property of a Bayes factor is that it should classify the data as coming from the correct model most often. A corollary is that one needs to carefully specify prior models based on realistic scientific information. We have argued for specific priors for BFs, rather than generic ones, and we have also argued that empirical data suggests that researchers do indeed have prior information (used in the design of the study), about effect sizes.
Some claim that objective priors are better than the subjective ones for teaching; for one reason, because students do not have to think about prior assessment. This claim is debatable. The recent ASA stance on p-values makes it clear that more thinking, not less, is needed when teaching hypothesis testing. Ben-Zvi and Makar (2016, p. 7) concur, reporting that members of the study group on teaching and learning statistics at the Twelfth International Congress on Mathematics Education in Seoul “all shared a common desire to improve statistics education … by focusing … on students’ … conceptual understanding rather than rote learning…”
Also, from a subjective standpoint, there is no “paradoxical” behavior of BFs: If the prior is “correct,” then the resulting BF provides the right results. In addition, supposed “paradoxes” are wonderful devices to catch students’ attention and to help them learn complex material: Kleiner and Movshovitz-Hadar (1994, p. 963) write, “Paradoxes … serve a useful role in the classroom ... [they are] useful pedagogical devices (provided, of course, that they are dealt with).” Good teaching involves explaining how and why such “paradoxes” occur.
We have also argued that the Classification Theorem provides a useful and natural objective criterion to compare BFs, to understand differences between them, and even to decide whether BFs should be used at all. This theorem is a special case of more general Bayesian decision theory, and leads naturally to the more general comparison of BFs based on expected losses of decisions, such as decision A: conclude M0, decision B: conclude M1, or decision C: make no decision (reserve judgment). Such an approach allows researchers to differentially weight ‘Type I’ and ‘Type II’ errors if desired; examples of loss functions are given in Shaffer (1999). Published BF thresholds for claiming M0, M1, or nothing at all, also follow from appropriate loss functions. Indeed, many of the desiderata of BFs listed above actually correspond to losses (or benefits) perceived. Thus, rather than force prior distributions to make BFs achieve these desiderata, it makes more sense (to us) to first specify priors scientifically, then to specify appropriate loss functions, and then to apply decision theory, choosing the action with minimum expected loss. And, of course, to “lay all the cards on the table,” showing chosen priors and loss functions.
Supplementary Material
Acknowledgments
Dr. Gönen’s work was supported by grant NCI P30 CA008748.
Appendix: Analytical Calculation of TPMs of GBF0 and WBF
Simple algebra shows, when GBF0=1 and WBF=1,
and
If M0 is true, t2 follows an F-distribution with degrees of freedom (1, v) (the pdf is denoted as f1, v). Otherwise, t2 follows a non-central F-distribution with degrees of freedom (1, v) and noncentral parameter λ =nδδ 2 (the pdf is denoted as f1, v, λ).Then TPMs for GBF0 and WBF given δ 2 and are expressed as
and
respectively. Then, by numerically integrating out δ 2 and using their “true” prior distributions, we calculate marginal TPMs of GBF0 and WBF. Table A.1 below summarizes these calculations under different prior settings of as used for creating Figure 1.
Table A.1:
Analytical estimates of total misclassification rates of GBF0 and WBF
| nδ | GBF0 |
WBF |
||||
|---|---|---|---|---|---|---|
| 1/9 | Inv-Chisq(1) | Pearson-VI(−0.75) | 1/9 | Inv-Chisq(1) | Pearson-VI(−0.75) | |
| 10 | 0.411 | 0.227 | 0.157 | 0.455 | 0.205 | 0.082 |
| 100 | 0.232 | 0.101 | 0.066 | 0.288 | 0.088 | 0.029 |
| 1000 | 0.096 | 0.036 | 0.021 | 0.117 | 0.032 | 0.010 |
It is seen that the results in Table A.1 match the simulated TPMs shown in Figure 1 well.
Footnotes
The R code and data used in this study are available as supplementary materials.
Contributor Information
Mithat Gönen, Memorial Sloan-Kettering Cancer Center.
Wesley O. Johnson, Department of Statistics, UC Irvine.
Yonggang Lu, Department of Information Systems and Decision Sciences, University of Alaska, Anchorage, AK 99508.
Peter H. Westfall, Area of Information Systems and Quantitative Sciences, Texas Tech University.
References
- Bartlett MS (1957), “A Comment on D. V. Lindley’s Statistical Paradox,” Biometrika, 44, 533–534. [Google Scholar]
- Bayarri MJ, Berger JO, Forte A, and García-Donato G (2012), “Criteria for Model Choice with Application to Variable Selection,” The Annals of Statistics 40, 1550–1577. [Google Scholar]
- Bem DJ (2011), “Feeling the Future: Experimental Evidence for Anomalous Retroactive Influences on Cognition and Affect,” Journal of Personality and Social Psychology, 100, 407–425. [DOI] [PubMed] [Google Scholar]
- Bem DJ, Utts JM, and Johnson WO (2011), “Must Psychologists Change the Way They Analyze Their Data?” A Response to Wagenmakers, Wetzels, Borsboom and Van der Mass, Journal of Personality and Social Psychology, 101, 716–19. [DOI] [PubMed] [Google Scholar]
- Benjamini Y, and Braun H (2002), “John W. Tukey’s Contributions to Multiple Comparisons,” The Annals of Statistics 30, 1576–1594. [Google Scholar]
- Berger JO, and Delampady M (1987), “Testing Precise Hypotheses,” Statistical Science 2, 317–335. [Google Scholar]
- Berger JO and Pericchi LR (1996), “The Intrinsic Bayes Factor for Model Selection and Prediction,” Journal of the American Statistical Association 91, 109–122 [Google Scholar]
- Berger JO and Pericchi LR (2001), “Objective Bayesian Methods for Model Selection: Introduction and Comparison,” in Model Selection, 135–207, Institute of Mathematical Statistics, Beachwood, OH. [Google Scholar]
- Berger JO, and Sellke T (1987), “Testing a Point Null Hypothesis: The Irreconcilability of p values and Evidence,” Journal of the American Statistical Association 82, 112–139. [Google Scholar]
- Ben-Zvi D, and Makar K (2016), The Teaching and Learning of Statistics: International Perspectives, Springer, New York. [Google Scholar]
- Do KA, Müller P, and Vannucci M (2012), Bayesian Inference for Gene Expression and Proteomics, Cambridge University Press. [Google Scholar]
- Efron B (2010), Large-Scale Inference: Empirical Bayes Methods for Estimation, Testing, and Prediction, Cambridge University Press. [Google Scholar]
- Fox RJ, and Dimmic MW (2006), “A Two-Sample Bayesian t-test for Microarray Data,” BMC Bioinformatics 7:126, doi: 10.1186/1471-2105-7-126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gönen M, Johnson WO, Lu Y, and Westfall PH (2005), “The Bayesian Two-Sample t Test,” The American Statistician 59, 252–257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guindani M, Müller P, and Zhang S (2009), “A Bayesian Discovery Procedure,” Journal of the Royal Statistical Society: Series B 71, 905–925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Held L and Ott M (2016), “How the Maximal Evidence of p-values Against Point Null Hypotheses Depends on Sample Size,” The American Statistician 70, 335–341. [Google Scholar]
- Jeffreys H (1961), Theory of Probability, Oxford: Oxford University Press. [Google Scholar]
- Johnson VE (2013A), “Uniformly Most Powerful Bayesian Tests,” Annals of Statistics 41, 1715–1741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson VE (2013B), “Revised Standards for Statistical Evidence,” Proc. Natl. Acad. Sci. U S A. 110(48), 19313–19317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson VE, and Rossell D (2010), “On the Use of Non-Local Prior Densities in Bayesian Hypothesis Tests,” Journal of the Royal Statistical Society, Series B 72, 143–170. [Google Scholar]
- Jones G, and Johnson WO (2014), “Prior Elicitation: Interactive Spreadsheet Graphics with Sliders Can be Fun, and Informative,” The American Statistician 68, 42–51. [Google Scholar]
- Kass RE, and Raftery AE (1995), “Bayes Factors,” Journal of the American Statistical Association 90(430), 773–795. [Google Scholar]
- Kleiner I and Movshovitz-Hadar N (1994), “The Role of Paradoxes in the Evolution of Mathematics,” The American Mathematical Monthly 101, 963–974. [Google Scholar]
- Kuhn M, and Johnson K (2013), Applied Predictive Modeling, Springer, New York. [Google Scholar]
- Liang F, Paulo R, Molina G, Clyde MA, and Berger JO (2008), “Mixtures of g Priors for Bayesian Variable Selection,” Journal of the American Statistical Association 103(481), 410–423. [Google Scholar]
- Masson ME (2011), “A Tutorial on a Practical Bayesian Alternative to Null-Hypothesis Significance Testing,” Behavior Research Methods, 43(3), 679–690. [DOI] [PubMed] [Google Scholar]
- Mossbridge J, Tressoldi P, and Utts J (2011), “Physiological Anticipation of Unpredictable Stimuli: A Meta-Analysis,” Unpublished manuscript. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Open Science Collaboration (2015), “Estimating the Reproducibility of Psychological Science,” Science 349, aac4716 (2015). DOI: 10.1126/science.aac4716. [DOI] [PubMed] [Google Scholar]
- Rivera IA (2011), “The Objective and Robust Student’s t Test,” Unpublished presentation, Department of Mathematics, University of Puerto Rico, http://www.pericchi.info/content.html?content=D0A089CD92FAF37DC1E6B3CB951AE92D. [Google Scholar]
- Rouder JN, Speckman PL, Sun D, Morey RD, and Iverson G (2009), “Bayesian t Tests for Accepting and Rejecting the Null Hypothesis,” Psychonomic Bulletin & Review 16, 225–237. [DOI] [PubMed] [Google Scholar]
- Shaffer JP (1999), “A Semi-Bayesian Study of Duncan’s Bayesian Multiple Comparison Procedure,” Journal of Statistical Planning and Inference 82, 197–213. [Google Scholar]
- Shahbaba B, and Johnson WO. (2013), “Bayesian Nonparametric Variable Selection as an Exploratory Tool for Discovering Differentially Expressed Genes,” Statistics in Medicine, 32, 2114–2126. [DOI] [PubMed] [Google Scholar]
- Utts J, Norris M, Suess E, and Johnson WO (2010), “The Strength of Evidence Versus the Power of Belief: Are We All Bayesians?,” in Reading C (Ed.), Data and context in statistics education: Towards an evidence-based society. Proceedings of the Eighth International Conference on Teaching Statistics (ICOTS8, July, 2010), Ljubljana, Slovenia. Voorburg, The Netherlands: International Statistical Institute. [Google Scholar]
- Wagenmakers EJ (2007), “A Practical Solution to the Pervasive Problems of p Values,” Psychonomic Bulletin & Review, 14(5), 779–804. [DOI] [PubMed] [Google Scholar]
- Wagenmakers EJ., Wetzels R, Borsboom D, and van der Maas H (2011), “Why Psychologists Must Change the Way They Analyze Their Data: The Case of Psi,” Journal of Personality and Social Psychology, 100, 426–432. [DOI] [PubMed] [Google Scholar]
- Wang M, and Liu G (2015), “A Simple Two-Sample Bayesian t-Test for Hypothesis Testing,” The American Statistician 70, 195–201. [Google Scholar]
- Wasserstein RL, and Lazar NA. (2016), “The ASA’s Statement on p-Values: Context, Process, and Purpose,” The American Statistician 70, 129–133. [Google Scholar]
- Wetzels R, Matzke D, Lee MD, Rouder JN, Iverson GJ, and Wagenmakers E-J (2011), “Statistical Evidence in Experimental Psychology: An Empirical Comparison Using 855 t Tests,” Perspectives on Psychological Science 6, 291–298. [DOI] [PubMed] [Google Scholar]
- Zellner A and Siow A (1980), “Posterior Odds Ratio for Selected Regression Hypotheses,” In Bayesian Statistics 1, 585–603, Valencia University Press. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.