Verticalization of bacterial biofilms

Abstract

Biofilms are communities of bacteria adhered to surfaces. Recently, biofilms of rod-shaped bacteria were observed at single-cell resolution and shown to develop from a disordered, two-dimensional layer of founder cells into a three-dimensional structure with a vertically-aligned core. Here, we elucidate the physical mechanism underpinning this transition using a combination of agent-based and continuum modeling. We find that verticalization proceeds through a series of localized mechanical instabilities on the cellular scale. For short cells, these instabilities are primarily triggered by cell division, whereas long cells are more likely to be peeled off the surface by nearby vertical cells, creating an “inverse domino effect”. The interplay between cell growth and cell verticalization gives rise to an exotic mechanical state in which the effective surface pressure becomes constant throughout the growing core of the biofilm surface layer. This dynamical isobaricity determines the expansion speed of a biofilm cluster and thereby governs how cells access the third dimension. In particular, theory predicts that a longer average cell length yields more rapidly expanding, flatter biofilms. We experimentally show that such changes in biofilm development occur by exploiting chemicals that modulate cell length.

Biofilms are groups of bacteria adhered to surfaces^1–3. These bacterial communities are common in nature, and foster the survival and growth of their constituent cells. A deep understanding of biofilm structure and development promises important health and industrial applications^4,5. Unfortunately, little is known about the microstructural features of biofilms due to difficulties encountered in imaging individual cells inside large assemblies of densely-packed cells. Recently, however, advances in imaging technology have made it possible to observe growing, three-dimensional biofilms at single-cell resolution^6–8.

In the case of Vibrio cholerae, the rod-shaped bacterium responsible for the pandemic disease cholera^9,10, high-resolution imaging revealed a surprisingly complex biofilm developmental program^7,8. Over the course of 12-24 hours of growth, an individual founder cell gives rise to a dome-shaped biofilm cluster, containing thousands of cells that are strongly vertically ordered, especially at the cluster core. Notably, this ordering is an intrinsically non-equilibrium phenomenon, as it is driven by growth, not by thermal fluctuations^7,11.

An important clue to understanding the emergence of vertical order in V. cholerae biofilms comes from genetic analyses that established the biological components relevant for biofilm development^7,8,12. To facilitate their growth as biofilms, V. cholerae cells secrete adhesive matrix components: Vibrio polysaccharide (VPS), a polymer that expands to fill gaps between cells, and cell-to-cell and cell-to-surface adhesion proteins. Cell-to-surface interactions enable vertical ordering by breaking overall rotational symmetry. However, despite previous work on the orientational dynamics of bacterial cells and related types of driven active matter^13–25, the nature of this physical process remains unclear.

In this work, we establish the biophysical mechanisms controlling V. cholerae biofilm development. We show that the observed structural and dynamical features of growing biofilms can be reproduced by a simple, agent-based model. Our model treats individual cells as growing and dividing rods with cell-to-cell and cell-to-surface interactions, and thus serves as a minimal model for a wide range of biofilm-forming bacterial species. By examining individual cell verticalization events, we show that reorientation is driven by localized mechanical instabilities occurring in regions of surface cells subject to high in-plane compression. These threshold instabilities explain the tendency of surface-adhered cells to reorient rapidly following cell division. We incorporate these verticalization instabilities into a continuum theory, which allows us to predict the expansion speed of biofilms as well as overall biofilm morphology as a function of cell-scale properties. We verify these predictions in experiments in which we use chemicals that alter cell length. Our model thus elucidates how the mechanical and geometrical features of individual cells control the emergent features of the biofilm, which are relevant to the survival of the collective.

Biofilm radius and vertical ordering spread linearly over time

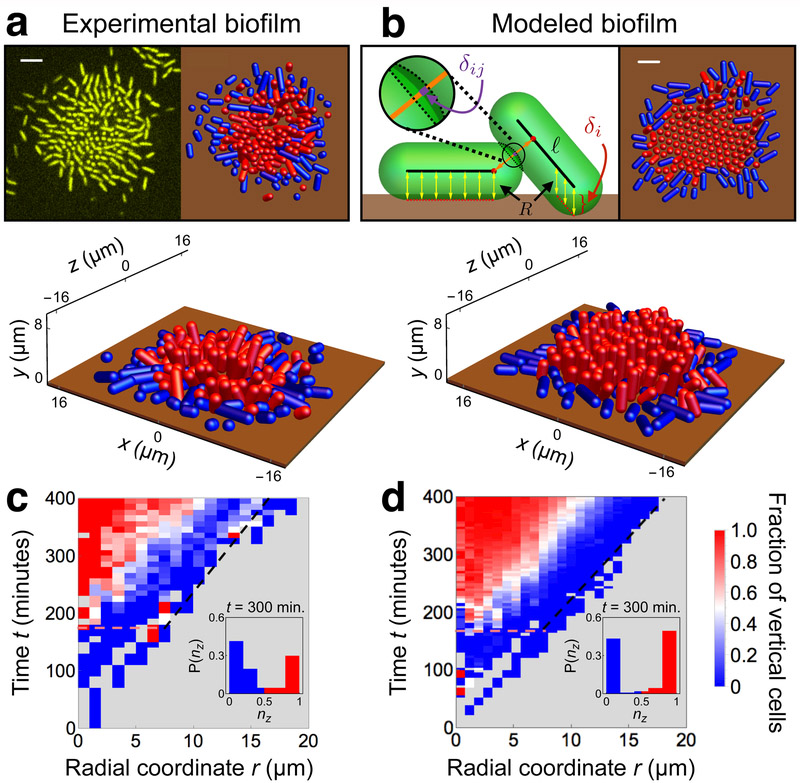
How do cells in V. cholerae biofilms become vertical? Biofilms grown from a single, surface-adhered founder cell initially expand along the surface (Fig. 1a, Supplementary Video 1). This horizontal expansion occurs because cells grow and divide along their long axes, which remain parallel to the surface due to cell-to-surface adhesion⁷. After about three hours, progeny near the biofilm center begin to reorient away from the surface (Fig. 1c). Reorientation events typically involve a sharp change in a cell’s verticality n_z, defined as the component of the cell-orientation vector n̂ normal to the surface (inset Fig. 1c). At later times, the locations of the reorientation events spread outward, and eventually the biofilm develops a roughly circular region of vertical cells surrounded by an annular region of horizontal cells. Both of these regions subsequently expand outward with approximately equal, fixed velocities. The radial profile of verticality versus time shows that the local transition of cells from horizontal to vertical occurs rapidly, taking 10-30 minutes for cell-sized regions to develop a vertical majority.

Figure 1.

Development of experimental and modeled biofilms. (a, b) Top-down and perspective visualizations of the surface layer of (a) experimental and (b) modeled biofilms, showing positions and orientations of horizontal (blue) and vertical (red) surface-adhered cells as spherocylinders of radius R = 0.8 μm, with the surface shown at height z = 0 μm (brown). Cells with n_z < 0.5 (> 0.5) are considered horizontal (vertical), where n̂ is the orientation vector. The upper-left panel of (a) shows a confocal fluorescence microscopy image, and the upper-right panel shows the corresponding reconstructed central cluster using the positions and orientations of surface cells. The upper-left panel of (b) shows a schematic representation of modeled cell-cell (orange) and cell-surface (yellow) interactions, which depend, respectively, on the cell-cell overlap δ_ij (purple) and cell-surface overlap δ_i (red) (see Methods for details). Scale bars: 5 μm. (c, d) 2D growth of biofilm surface layer for (c) experimental biofilm (same as shown in (a)) and (d) modeled biofilms. The color of each spatiotemporal bin indicates the fraction of vertical cells at a given radius from the biofilm center, averaged over the angular coordinates of the biofilm (gray regions contain no cells). In (d), each spatiotemporal bin is averaged over ten simulated biofilms. In (c,d), the horizontal dashed pink lines show the onset of verticalization. The black dashed lines show the edge of the biofilm. Insets show the distribution of cell orientations at time t = 300 minutes, with color highlighting horizontal and vertical orientations.

Agent-based model captures spreading of biofilm and vertical ordering

To understand how the behavior of living biofilms arises from local interactions, we developed an agent-based model for biofilm growth (left inset Fig. 1b, Methods, Supplementary Fig. 1). The model extends existing agent-based models^18,26–28 by incorporating the viscoelastic cell-to-surface adhesion^29,30 that is crucial for V. cholerae biofilm formation^9,12. Specifically, we treat the cells as soft spherocylinders that grow, divide, and adhere to the surface. We simulated biofilms by numerically integrating the equations of motion starting from a single, surface-adhered founder cell (Supplementary Video 2, Methods). To make the computations more tractable for systematic studies, we simulated only the surface layer of cells by removing from the simulation cells that become detached from the surface. This quasi-3D model is a reasonable approximation of the full 3D model at early times (Supplementary Fig. 2), and closely matches the dynamics and orientational order observed over the full duration of the experiment (Fig. 1b,d). The emergence of this distinctive orientational-temporal pattern demonstrates that our simple agent-based model is sufficient to capture the physical interactions that underpin the observed “verticalization” transition of experimental biofilms.

Mechanical instabilities cause cell verticalization

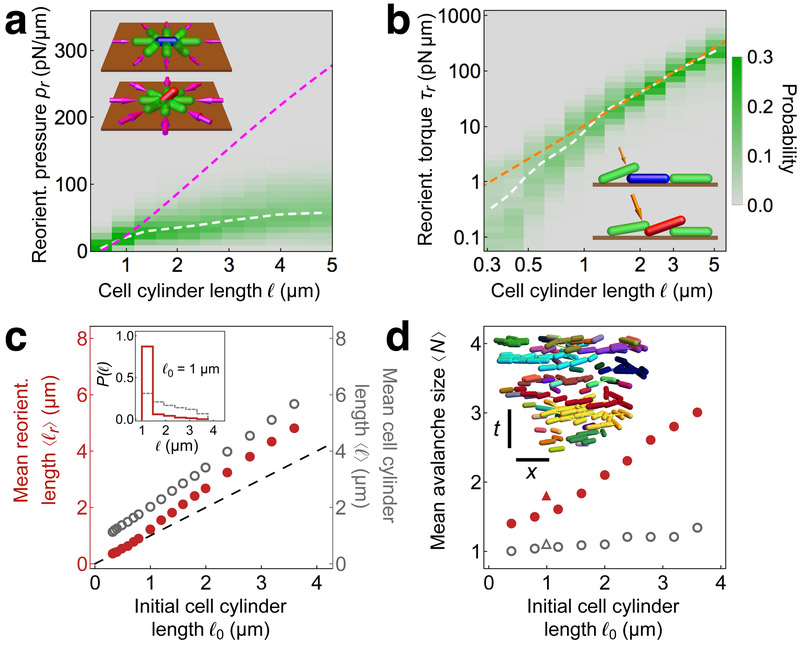
Why do the experimental and modeled cells segregate into horizontal and vertical orientations, with transitions from horizontal to vertical proceeding rapidly? To investigate the local mechanics that drive verticalization, we considered the dynamics of a single model cell of cylinder length ℓ adhered to the surface. The surface provides a combination of attractive and repulsive forces that, in the absence of external forces, maintain the cell at a stable fixed point with elevation angle θ = 0 (i.e. horizontal) and penetration into the surface δ₀. However, when additional forces are applied to the cell, the cell may become unstable to vertical reorientation.

We determined the onset of this instability by performing a linear stability analysis for a cell under constant external forces (inset Fig. 2a). For simplicity, we took the external forces to be applied by a continuum of rigid, spherical pistons that are distributed uniformly around the cell perimeter. The pistons compress the cell in the xy plane with an applied surface pressure p. For values of p larger than a threshold surface pressure p_t, the cell becomes linearly unstable to spontaneous reorientation (Supplementary Figs. 3-4). Our model yields a value of p_t that increases with ℓ. In particular, over a broad range of ℓ, we find a linear increase of p_t with ℓ (Fig. 2a). Intuitively, this increase occurs because the surface adhesion of the model cell scales with its contact area, creating an energy barrier to reorientation that increases with cell length.

Figure 2.

Mechanics of cell reorientation in modeled biofilms, (a-b) Properties of individual cells at the time t_r of reorientation, defined as the time of the peak of total force on the cell prior to it becoming vertical. Analyses are shown for all reorientation events among different biofilms simulated for a range of initial cell lengths ℓ₀ (a) Distributions of reorientation “surface pressure” p_r, defined as the total contact force in the xy plane acting on a cell at time t_r, normalized by the cell’s perimeter, versus cell cylinder length ℓ. The white dashed curve shows the average reorientation surface pressure ⟨p_r⟩ as a function of ℓ. The magenta dashed curve shows the threshold surface pressure p_t from linear stability analysis for a modeled cell under uniform pressure, depicted schematically in the inset, (b) Distributions of the logarithm of reorientation torque τ_r, defined as the magnitude of the torque on a cell due to cell-cell contact forces in the z direction at time t_r, for different cell cylinder lengths ℓ. The white dashed curve shows the average values ⟨log τ_r⟩ as a function of ℓ. The orange dashed curve shows the scaling τ_t ~ ℓ² of the threshold torque for peeling from linear stability analysis for a modeled cell, depicted schematically in the inset, (c) Mean reorientation length ⟨ℓ_r⟩ (red), defined as the average value of cell length at t_r, and mean cell cylinder length ⟨ℓ⟩ (gray), defined as the average length of all horizontal cells over all times of biofilm growth, averaged over ten simulated biofilms, each with initial cell cylinder length ℓ₀, plotted versus ℓ₀. The inset shows the distribution of reorientation lengths (red) and horizontal surface-cell lengths (gray) for ℓ₀ = 1 μm. (d) Mean avalanche size ⟨N⟩, defined as the average size of a cluster of reorienting cells that are proximal in space and time (Supplementary Figs. 8-10), versus initial cell length ℓ₀ for the experimental biofilm (red triangle) and the modeled biofilm (red circles). Open gray triangle and circles indicate the corresponding mean avalanche sizes for a null model. Inset shows a side view of cell configurations in the xy plane at times t_r for all reorientation events in a simulated biofilm with ℓ₀ = 2.5 μm. Reorientation events are colored alike if they belong to the same avalanche. Scale bars: 10 μm and 1 hour.

To determine whether this simple model can predict verticalization events in the biofilm surface-layer simulations, we examined the forces acting on individual modeled cells throughout the development of a biofilm. Specifically, we computed the reorientation “surface pressure” p_r, defined as the sum of the magnitudes of the in-plane cell-cell contact forces on a cell, normalized by the perimeter of its footprint, at the instant it begins to reorient (Supplementary Fig. 5). We found that the average reorientation surface pressure ⟨p_r⟩ increases with ℓ, as expected from the compressive instability model (Fig. 2a). Furthermore, the predicted value p_t is in good agreement with the observed ⟨p_r⟩ for short cells. However, for long cells, ⟨p_r⟩ saturates more rapidly than p_t.

The dominant mechanism of verticalization depends on cell length

How can longer cells become vertical at surface pressures much lower than the threshold values predicted by the compressive instability model? The large extent of the discrepancy suggests that for long cells, the in-plane forces alone are insufficient to cause the instabilities (Fig. 2a). Indeed, incorporating the numerically-observed distribution of in-plane forces acting on cells into the compressive instability model does not significantly improve the prediction for ⟨p_r⟩ (Supplementary Fig. 6). Thus, we hypothesized that in the case of long cells, forces acting in the z direction might play an important role in triggering verticalization.

To explore this idea, we returned to the single-cell model and considered the effect of forces in the z direction (inset Fig. 2b). Applying small forces in the z direction to a cell with fixed center-of-mass height shifts the equilibrium elevation angle of the cell to a small finite value of θ, proportional to the net torque. Under large enough torque, a single end of the cell becomes free of the surface, at which point the cell becomes unstable to further rotation and effectively “peels” off the surface. This nonlinearity, inherent in the geometry of contact, competes with the compressive instability, and under specific conditions can initiate reorientation at much smaller values of surface pressure. Specifically, for a fixed center-of-mass penetration depth δ₀ ≪ ℓ, the threshold torque for peeling a cell off the surface due to forces in the z direction scales as τ_t ~ ℓ² (Supplementary Fig. 4). For the whole-biofilm surface-layer simulation, the average reorientation torque, defined as the total torque due to forces in the z direction at the instant of reorientation, closely obeys the predicted ℓ² scaling for long cells (Fig. 2b). Taken together, our predictions from the compressive and peeling instabilities explain the verticalization of modeled cells over the entire range of cell lengths studied.

Cell division can trigger verticalization

For both compressive and peeling instabilities, the presence of an energy barrier to reorientation explains the sharp distinction we observed between horizontal and vertical cell orientations. Furthermore, both mechanisms predict larger reorientation thresholds for longer cell lengths. Hence, the model suggests that shorter cells should reorient more readily. To confirm this effect in our simulated biofilms, we compared the distribution of reorientation lengths ℓ_r, defined as the cell cylinder length at the instant of reorientation, to the full distribution of horizontal cell lengths for a series of simulations with different values of the initial cell cylinder length ℓ₀, defined as the cell cylinder length immediately following division (Fig. 2c). For all values of ℓ₀, we found that the mean reorientation cell length ⟨ℓ_r⟩ is substantially smaller than the mean horizontal cell length. In addition, for simulations with average cell lengths comparable to those in our experiments, most reorientation events occur immediately after cell division. The limited time resolution of the experiments precludes a quantitative analysis of division-induced verticalization; nevertheless, the propensity for cell division to trigger reorientation is clearly observed in the experimental biofilm (Supplementary Video 1, Supplementary Fig. 7).

Verticalization is localized

We next investigated how the surface compression and peeling instabilities influence the propagation of reorientation through a biofilm. First, we generalized our model for the surface compression instability to the multicellular level. A linear stability analysis of the model suggests that reorientation events should be independent and spatially localized for short cell lengths (Supplementary Fig. 3). By contrast, for long cell lengths, the tendency of neighboring vertical cells to trigger reorientation suggests an (inverse) domino-like effect in which one cell standing up can induce its neighbors to stand up.

To quantify the extent of cooperative verticalization, we computed the size N of reorientation “avalanches”, defined as groups of verticalization events that are proximal in space and time³¹ (inset Fig. 2d, Supplementary Fig. 8). We found that for long cell lengths, the mean avalanche size ⟨N⟩ is significantly larger than the value predicted by a null model that consists of randomizing the angular position of cells within the biofilm (Fig. 2d, Supplementary Fig. 8). Thus, the dependence of ⟨N⟩ on cell length is consistent with the prediction of the inverse domino effect. Interestingly, however, the distribution of avalanche sizes decays roughly exponentially for all values of cell length we studied (Supplementary Fig. 9), with only a modest number of cells (N ~ 2 — 3) involved in typical avalanches (Fig. 2d).

A natural explanation for the small mean avalanche size comes from the reduction in cell footprint that occurs upon reorientation, which rapidly alleviates the local surface pressure responsible for verticalization (Supplementary Fig. 5). This effect combines with the disorder of the contact geometries and forces throughout the biofilm, which separates horizontal cells near the verticalization threshold into disconnected groups (Supplementary Video 3, Supplementary Fig. 10). Thus, although the inverse domino effect transiently increases verticalization cooperativity, avalanches quickly exhaust the local supply of horizontal cells that are susceptible to becoming vertical. Consequently, verticalization occurs throughout the biofilm in scattered, localized regions.

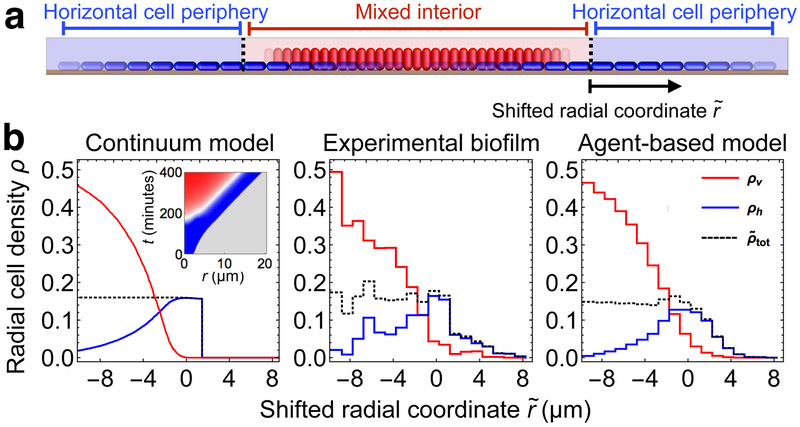
Two-fluid model describes propagation of verticalization

To understand how localized cell verticalization gives rise to the global patterning dynamics of the biofilm, we developed a two-dimensional continuum model that treats horizontal and vertical cell densities as two coupled fluids (Fig. 3a, Methods). The local horizontal cell density ρ_h grows in the plane at α rate a and converts to vertical cell density ρ_v in regions of high surface pressure at a rate β. The total 2D cell density is ${\tilde{\rho }}_{\text{tot}}\equiv {\rho }_h+\xi {\rho }_v$, where ξ is the ratio of vertical to horizontal cell footprints, and we approximate the surface pressure as linearly proportional to the areal deformation ${\tilde{\rho }}_{\text{tot}}-{\tilde{\rho }}_0$, where ${\tilde{\rho }}_0$ is the close-packed, but uncompressed, cell density. These interactions yield the following equation for the change in ${\tilde{\rho }}_{\text{tot}}$ in regions of nonzero surface pressure:

$${\dot{\tilde{\rho }}}_{\text{tot}}=\gamma {\nabla }^2{\tilde{\rho }}_{\text{tot}}+\alpha {\rho }_h-(1-\xi )\beta \Theta ({\tilde{\rho }}_{\text{tot}}-{\tilde{\rho }}_t){\rho }_h,$$ (1)

where γ is the ratio of the Young’s modulus of the biofilm to the surface drag coefficient, Θ is the Heaviside step function, and ${\tilde{\rho }}_t$ is the threshold surface density for verticalization. We simulated this continuum model, and found that for α < β, the biofilm generically develops into a circular region containing both horizontal and vertical cells (“Mixed interior”) surrounded by an annular region containing horizontal cells (“Horizontal cell periphery”), closely matching both the experimental biofilm and the agent-based model biofilms (Fig. 3b, Supplementary Video 4, Supplementary Note). In this regime, the biofilm front spreads linearly in time at a fixed expansion speed c*. Furthermore, the total cell density and the surface pressure are constant in the mixed interior. This constancy is stabilized by the competing effects of cell growth and cell verticalization, and occurs provided that α < β(1 – ξ) (Supplementary Fig. 11). When this condition is satisfied, verticalization can reduce cell density faster than cell density can be replenished by cell growth and cell transport due to gradients in surface pressure. Physically, this results in the cell density rapidly fluctuating around the verticalization threshold. This rapid alternation effectively tunes the verticalization rate down to α = β(1 – ξ), and thereby ensures a constant total cell density and surface pressure in the mixed interior. The resulting “dynamical isobaricity” (constancy of pressure) provides the boundary condition for the horizontal cell periphery that determines the horizontal expansion speed c*, independent of β and ξ. In the limit of slow expansion $c^{\ast }\ll \sqrt{\alpha \text{γ}}$, c* is given by:

$$c^{\ast }\simeq c_0^{\ast }\sqrt{1-\frac{{\tilde{\rho }}_0}{{\tilde{\rho }}_t}},$$ (2)

where $c_0^{\ast }=\sqrt{2\alpha \text{γ}}$. This expansion speed increases with ${\tilde{\rho }}_t$ until it saturates at $c^{\ast }=2\sqrt{\alpha \text{γ}}$ for ${\tilde{\rho }}_t\gg {\tilde{\rho }}_0$ (Supplementary Note). Intuitively, higher values of the verticalization threshold density ${\tilde{\rho }}_t$ sustain a wider periphery of horizontal cells, which results in a higher rate of increase in the total number of surface cells. Thus, our continuum model reveals how the geometrical and mechanical properties of individual cells influence the global morphology of the growing biofilm.

Figure 3.

Two-component fluid model for verticalizing cells in biofilms. (a) Schematic illustration of the two-component continuum model. Horizontal cells (blue) and vertical cells (red) are modeled, respectively, by densities ρ_h and ρ_v in two spatial dimensions. The total cell density ${\tilde{\rho }}_{\text{tot}}$ is defined as ρ_h + ξρ_ν, where ξ is the ratio of vertical to horizontal cell footprints. (b) Radial densities ρ of vertical cells (ρ_v, red), horizontal cells (ρ_h, blue), and total density (${\tilde{\rho }}_{\text{tot}}$, black), versus shifted radial coordinate $\tilde{r}$, defined as the radial position relative to the boundary between the mixed interior and the horizontal cell periphery. Results are shown for the continuum model (left; radial cell density in units of μm⁻²), the experimental biofilm (middle; radial cell density in each μm-sized bin averaged over an observation window of 50 minutes), and the agent-based model biofilm (right; radial cell density in each μm-sized bin averaged for ten biofilms over an observation window of 6 minutes). For the continuum model and the agent-based model biofilms the parameters were chosen to match those obtained from the experiment (Supplementary Figs. 12-13). Inset in the left-most panel shows the fraction of vertical cells in the continuum model at a given radius from the biofilm center (gray regions contain no cells, color scale is the same as in Fig. 1).

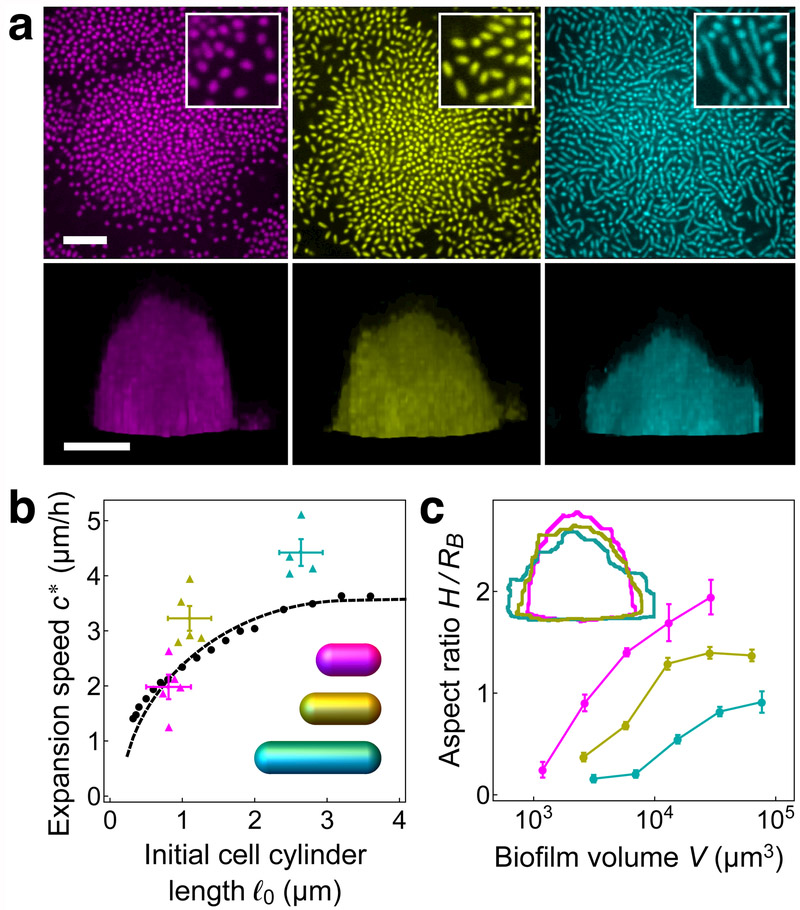
Increasing cell length yields more rapidly expanding, flatter biofilms

Because the threshold surface density for verticalization ${\tilde{\rho }}_t$ increases with cell length, we expect biofilms composed of longer cells to maintain a wider periphery of horizontal cells and to thereby expand faster along the surface than biofilms composed of shorter cells. To test this notion in our agent-based model, we computed the expansion speed of the modeled biofilms for a range of initial cell cylinder lengths ℓ₀ (Fig. 4b). Upon fitting the continuum model parameters to those of the agent-based model (Supplementary Figs. 12-13), we found that the expansion velocities of the two models were equal to within a few percent. In living, experimental biofilms, we can increase or decrease the average cell length using chemical treatments^10,32 (Fig. 4a, top row). Similar to the agent-based model biofilms, in experimental biofilms, the surface expansion speed increases with increasing cell length (Fig. 4b, Supplementary Video 5). Furthermore, when the model biofilm parameters are fitted to experiment (Supplementary Fig. 1), the experimental and model biofilm speeds agree to within twenty percent or better. Taken together, these observations support the conclusion that self-organized dynamical isobaricity governs the expansion of V. cholerae biofilms along surfaces.

Figure 4.

Global morphological properties of experimental and modeled biofilms, (a) Top-down (upper row) and side views (lower row) of experimental biofilms grown with 0.4 μg/mL A22 (magenta), without treatment (yellow), and with 4 μg/mL Cefalexin (cyan), following overnight growth (upper row) and 7 hours after inoculation (lower row). Scale bar: 10 μm. Insets show magnifications of 10 μm²-sized regions of top-down views taken from the peripheries of biofilms. (b) Expansion speed c*, defined as the speed of the biofilm edge along the surface, versus the initial cell cylinder length ℓ₀ for experimental biofilms (A22, magenta; no treatment, yellow; Cefalexin, cyan), agent-based model biofilms (black circles), and continuum model (dashed black curve). Expansion velocities were determined from a linear fit of the basal radius R_B of the biofilm versus time, where R_B is defined at each time point as the radius of a circle with area equal to that of the biofilm base. For experimental biofilms, the boundary was extracted from the normalized fluorescence data (see Methods for details). For each treatment, the vertical error bars show the standard error of the mean of the expansion speed and the horizontal error bars bound the measured initial cell cylinder length (Supplementary Fig. 1). Inset: model cells with lengths and radii corresponding to the averages for different treatments, (c) Biofilm aspect ratio H/R_B for experimental biofilms grown under different treatments, where the biofilm height is defined as $H=3V∕2R_B^2$, the height of a semi-ellipsoid with a circular base of radius R_B and volume V equal to that of the biofilm. Error bars show the standard error of the mean. Inset: overlay of biofilm outlines from bottom row of panel (a). Color designations and treatments same as in panel (a).

How do different surface expansion speeds influence the ensuing biofilm development into the z direction? After a few hours, living biofilms grow into roughly semi-ellipsoidal shapes with volume $V=(2∕3)R_B^{2}H$, where R_B is the basal radius and H is the height. For equal rates of total volume growth, we expect a biofilm that expands more rapidly along the surface to develop a lower aspect ratio H/R_B than a biofilm that expands less rapidly along the surface. We verified that the chemical treatment does not affect the total volume growth rates of the experimental biofilms (Supplementary Fig. 14), and found that the measured aspect ratio H/R_B does indeed decrease with cell length over a wide range of volumes (Fig. 4a, bottom row; Fig. 4c). Thus, our results show how the elongated geometries of individual cells govern the global morphology of the collective, an important determinant of biofilm survival in nature.

Discussion

Our results suggest that bacteria have harnessed the physics of mechanical instabilities to enable the generation of spatially and orientationally patterned architectures. Here, we showed that cell verticalization begins to occur when the local effective surface pressures that arise from cell growth become large enough to overcome the cell-to-surface adhesion that otherwise favors a horizontal orientation. Subsequently, the reduction in cell footprint that occurs upon cell verticalization, which acts to reduce the effective surface pressure, provides a mechanical feedback that controls the rate of biofilm expansion. We expect that individual cell parameters have evolved in response to selective pressures on global biofilm morphology, e.g. during resource competition^6,35–38. Since optimal morphology may be condition dependent, cells may also have evolved adaptive strategies that alter biofilm architecture, which could be investigated experimentally by screening for environmental influences on cell size, shape, and surface adhesion³⁹.

For simplicity, we focused on flat surfaces, nutrient-rich conditions, and V. cholerae strains that have been engineered to have simpler interactions than those in wild type biofilms (Methods). Moreover, our agent-based model does not explicitly incorporate the VPS matrix secreted by cells^2,27,40. Understanding the modifying effects of the VPS matrix, cell and surface curvature (Supplementary Fig. 15), cell-to-cell adhesion (Supplementary Fig. 16), and chemical feedback⁴¹ will be important directions for future studies. More broadly, we must develop a systematic method to account for the diversity of architectures that can be produced by local mechanical interactions (Supplementary Discussion).

Our study of a two-fluid model for verticalizing biofilms led us to discover a novel type of front propagation. Interestingly, in the biofilm surface layer, the front profile of cell density is precisely uniform starting at some finite distance from the edge, whereas previous models of front propagation saturate asymptotically toward uniformity^42–45. The self-organized nature of this process yields a universal dependence of the expansion speed on the cell geometrical and mechanical parameters that is robust to details of the mechanical feedback. We have focused on the mean-field behavior of biofilms, but an open question is to understand the role of fluctuations in the “pressure” acting on cells, e.g. either from a jamming perspective⁴⁶, a fluctuating hydrodynamical perspective^47,48, or a combination of approaches.

In summary, we have elucidated the physical mechanism underlying a complex developmental program observed at the cellular scale in bacterial biofilms. The relative biochemical and biophysical simplicity of this prokaryotic system allowed us to quantitatively understand the developmental pathway from the scale of a single cell to the scale of a large community assembly. Going forward, we expect bacterial biofilms will take on increasingly important roles as tractable models that can be used to understand how living systems generate and maintain their structures.

Methods

Growing and imaging experimental biofilms

Strains and media.

The V. cholerae strain used in this study is a derivative of wild-type Vibrio cholerae O1 biovar El Tor strain C6706, harboring a missense mutation in the vpvC gene (VpvC W240R) that elevates c-di-GMP levels and confers a rugose biofilm phenotype¹. Additional mutations were engineered into this strain using Escherichia coli S17-λpir carrying pKAS32. Specifically, the biofilm gene responsible for cell-cell adhesion, rbmA, was deleted. To avoid the effects of cell curvature, we deleted crvA encoding the periplasmic protein CrvA responsible for the curvature of V. cholerae cells. Biofilm experiments were performed in M9 minimal medium, supplemented with 2 mM MgSO₄, 100 μM CaCl₂, and 0.5% glucose. When indicated, Cefalexin (Sigma Aldrich) was added at 4μg/mL and A22 (a gift from the Gitai group) was used at 0.4 μg/mL. These concentrations were experimentally determined to modulate cell morphology without affecting overall mass accumulation.

Biofilm growth.

V. cholerae strains were grown overnight at 37 °C in liquid LB medium with shaking, back-diluted 30-fold, and grown for an additional two hours with shaking in M9 medium until early exponential phase (OD₆₀₀ = 0.1 — 0.2). These re-grown cultures were diluted to OD₆₀₀ = 0.001 and 100 μL of the diluted cultures were added to wells of 96-well plates with #1.5 coverslip bottoms (MatTek). The cells were allowed to attach for ten minutes, after which the wells were washed twice with fresh M9 medium, and, subsequently, 100 μL of fresh M9 medium was added, with or without drugs. The low initial inoculation density enabled isolated biofilm clusters to form. The locations of the founder cells were identified, and one hour after inoculation, imaging was begun on the microscope stage at 25 °C.

Microscopy.

Details of the imaging system have been described elsewhere⁸. Briefly, images were acquired with a spinning disk confocal microscope (Yokogawa) a 543 nm laser (OEM DPSS), and an Andor iXon 897 EMCCD camera. For single-cell resolution imaging, a 60× water objective with a numerical aperture of 1.2 plus a 1.5× post-magnification lens was used. To avoid evaporation, immersion oil with a refractive index of 1.3300 ± 0.0002 (Cargille) was used instead of water. The time difference between each image acquisition was 10 minutes, and the total imaging time was 8 hours. Only the bottom 5 μm of the biofilm was imaged (with a z step size of 0.2 μm) to avoid excessive photobleaching and phototoxicity. For coarse-grained imaging, a 20× multi-immersion objective was used without post-magnification. In this case, the time difference between each image acquisition was 30 minutes, and entire biofilms were imaged (with a z step size of 1 μm). At the end of the coarse-grained time course, the biofilm clusters were imaged again with high magnification to determine cell lengths. All image acquisitions were automated using Nikon Element software. All cells harbored mKO fluorescent proteins expressed from the chromosome. Experimental images in Fig. 4 were false-colored to differentiate between different growth conditions.

Image processing.

The cell segmentation protocol and Matlab codes have been described elsewhere in detail⁸. Cell position, cell length, and cell orientation were used as input for 3D rendering in Fig. 1a and for further analysis. For biofilm clusters grown in the presence of A22 or Cefalexin, cell lengths were manually measured in the bottom cell layers of the biofilms using the Nikon Element software. To define the biofilm shape parameters in the coarse-grained images, the bottom cell layers of the biofilms were first identified by finding the brightest z-cross section, according to the total fluorescence intensity. The contour of the individual biofilm cluster was next identified using the three-dimensional Canny edge detection method implemented in Mathematica. To correct for the inevitable optical stretching in the z-direction, we compared the heights obtained from the same cluster in the coarse-grained and the fine resolution images. By imaging a series of biofilm clusters of different sizes, we obtained a curve of a biofilm cluster’s actual height versus its apparent height in the coarse-grained images, which we used to calibrate the heights measured in the coarse-grained images.

Modeling biofilms

Agent-based model.

We model the volume occupied by a cell as a cylinder of length ℓ with two hemispherical end caps each of radius R. We treat cell growth as elongation that increases cell volume at a fixed rate α (chosen randomly at birth from a narrow Gaussian distribution to desynchronize cell divisions). Cells are born with an initial cell cylinder length ℓ₀ and grow to twice their total length. When a cell reaches the division length, the cell is instantaneously replaced by two identical daughter cells. In our model, cell-to-cell and cell-to-surface overlaps exert repulsive forces according to Hertzian contact mechanics for elastic materials². In the case of the cell-to-surface overlap, we also include an attractive interaction with an energy proportional to the cell-to-surface contact area, i.e., the Derjaguin approximation^29,30. To account for symmetry-breaking microscopic irregularities, we add a small amount of random noise to each component of the generalized force at every time step (10⁻⁸ E₀R² to the force acting on the center-of-mass r and 10⁻⁸ E₀R³ to the generalized force acting on the orientation vector n̂). Finally, we include two sources of viscous drag: a modest damping of three-dimensional motion through the surrounding fluid and biopolymer matrix, and a much larger damping of sliding motion along the adhesive surface²⁹. We determine the parameters in our model by fitting to the experimental data (Supplementary Fig. 1).

Simulation of agent-based model.

To simulate the agent-based model, we numerically integrate the equations of motion using an explicit embedded Runge-Kutta-Fehlberg method. Our implementation of this method in C++ is adapted from the GNU Scientific Library³, and available freely online at GitHub⁴. The initial conditions consist of a single cell of length ℓ₀ at elevation angle θ = 0 and penetration depth δ₀.

Continuum model.

To describe the radial expansion and orientational dynamics of the biofilm, we treated the horizontal cells and vertical cells as continuous fields ρ_h and p_v, with the total density ${\tilde{\rho }}_{\text{tot}}$ defined as the sum p_h + ξρ_ν, where ξ is the ratio of vertical to horizontal cell footprints. In regions where ${\tilde{\rho }}_{\text{tot}}$ exceeds the close-packing density ${\tilde{\rho }}_0$, the rate of change of the horizontal cell density is proportional to the divergence of the flux of cells due to cell transport plus terms due to cell growth and cell verticalization. We assume that cell transport is given by the gradient of surface pressure divided by a surface viscosity coefficient η₁, where surface pressure is approximated as linearly proportional to the areal deformation ${\tilde{\rho }}_{\text{tot}}-{\tilde{\rho }}_0$, i.e. following “Hooke’s law”. Cell growth in the plane is proportional to the local horizontal cell density and occurs at a fixed rate α. We assume that cell verticalization locally converts horizontal cell density to vertical cell density at a fixed rate β in regions where ${\tilde{\rho }}_{\text{tot}}>{\tilde{\rho }}_t$, where ${\tilde{\rho }}_t$ is the threshold surface density for verticalization.

Simulation of continuum model.

We simulated the dynamics of the radial cell densities in Python using FiPy, a finite volume PDE solver⁵. We performed our simulation on a cylindrical grid containing 30000 radial points with a spacing of Δx = 1 nm and a temporal step size of Δt = 1 ms.

Data availability

The simulation used for the agent-based model is available on GitHub⁴. The code used for the analysis in the current study is available from the corresponding author following request.