Electronic structure at coarse-grained resolutions from supervised machine learning

Machine learning–enhanced molecular simulation opens a pathway to multiscale prediction for organic electronics.

Abstract

Computational studies aimed at understanding conformationally dependent electronic structure in soft materials require a combination of classical and quantum-mechanical simulations, for which the sampling of conformational space can be particularly demanding. Coarse-grained (CG) models provide a means of accessing relevant time scales, but CG configurations must be back-mapped into atomistic representations to perform quantum-chemical calculations, which is computationally intensive and inconsistent with the spatial resolution of the CG models. A machine learning approach, denoted as artificial neural network electronic coarse graining (ANN-ECG), is presented here in which the conformationally dependent electronic structure of a molecule is mapped directly to CG pseudo-atom configurations. By averaging over decimated degrees of freedom, ANN-ECG accelerates simulations by eliminating backmapping and repeated quantum-chemical calculations. The approach is accurate, consistent with the CG spatial resolution, and can be used to identify computationally optimal CG resolutions.

INTRODUCTION

Modeling organic semiconductors offers promise for high-performance optoelectronic devices (1, 2). The functionality of these devices is inherently dependent on the underlying morphology of these semiconductors, which influences the corresponding electronic structure and transport. A central challenge for the design of new molecules with enhanced transport characteristics is to understand how molecular structure, morphology, and electronic structure are interrelated. Past computational studies of organic semiconductors have provided mechanistic insights into the nature of electron transport in gas-phase, solution-phase, and crystalline systems (3, 4). However, because of the high computational cost of analyzing the conformationally dependent electronic structure of noncrystalline morphologies, the number of computational studies of electron transport in disordered materials has been comparatively limited (5, 6), preventing the high-throughput modeling of a technologically relevant class of organic semiconductors.

To capture the relationship between bulk electronic functionality and morphology, one must adopt a multiscale approach, in which classical simulations are used to explore conformational space and quantum mechanical calculations are used to predict electronic structure (7). More specifically, classical molecular dynamics (MD) or Monte Carlo (MC) trajectories provide representative molecular configurations of the bulk material, and quantum-chemical calculations provide the corresponding energies and couplings of valence or conduction band orbitals. These energies and couplings can then be used to parameterize semiclassical rate theories or model Hamiltonians with which to analyze carrier transport within the material (5, 8, 9). For organic semiconductors, the relaxation time scales of the bulk material are frequently not accessible via atomistic simulations. Coarse-grained models can access the relevant length and time scales, but these models must then be mapped onto atomistic coordinates to perform electronic structure calculations. Software suites that aid in implementing this workflow (6, 10) have been developed.

Every aspect of a multiscale simulation presents its own challenges. One of the most computationally demanding aspects of the protocol outlined above, however, is the quantum-mechanical calculation of electronic structure in systems of thousands, or tens of thousands, of molecules. To put these demands into perspective, it is instructive to consider a model Hamiltonian or master equation that is parameterized using a nearest-neighbor interaction assumption; a simulated system comprising 10,000 molecules, each with N nearest neighbors, involves 10,000 single-molecule electronic structure calculations to obtain the required site energies and approximately 5000 × N electronic structure calculations to obtain the dimer electronic couplings. Note that these tens of thousands of electronic structure calculations would parameterize a model Hamiltonian (or master equation) for only a single morphology configuration. Thus, the prospect of exploring the morphological dependence (using thousands of configurations) of bulk electronic properties, notably charge carrier mobilities, is virtually infeasible with current computers and simulation protocols.

The recent surge of machine learning and data science in the chemical and material sciences has led to the widespread application of powerful regression and classification algorithms conceived to enhance materials discovery and accelerate simulations. Multiple research groups have developed high-accuracy force fields via the fitting of ab initio energies and forces to artificial neural networks (ANNs) and Gaussian approximate potentials (11–17). The application of machine learning for the prediction of static geometry electronic properties has reached a relatively mature point, with impressive predictive performance obtained across a diverse chemical space (18–21). Other implementations of machine learning have led to the direct assessment of molecular electron density (22) and the circumvention of conventional approaches to density functional theory (DFT) calculations (23). A benefit of machine learning methods is that they can be trained on computationally expensive models and then used to predict quantitatively similar results at a fraction of the computational cost. These techniques could be particularly advantageous in the context of organic semiconductors, where electronic structure is strongly coupled to subtle changes in molecular configuration and must be calculated repeatedly to estimate macroscopic observables.

While explicit quantum-chemical calculations provide the “exact” answer to the conformationally dependent electronic structure problem, there is a precedent for using phenomenological, often tight-binding (TB) Hamiltonians to understand the conformational dependence of molecular electronic structure at a coarser length scale (24–26). For example, the second hyperpolarizabilities (24) and hole mobilities (25) of linear conjugated polymers can be described by incorporating only the dihedral degrees of freedom in a TB Hamiltonian. In the context of deriving the electronic structure from only the CG configurational degrees of freedom (CDOF), these phenomenological Hamiltonians provide an intriguing route toward the assessment of conformation-dependent electronic structure at a coarser resolution. In the past, however, CG electronic Hamiltonians have been largely limited to systems in which the degrees of freedom that modulate the phenomenological Hamiltonian are well known. Hence, these CG electronic Hamiltonians do not represent a general strategy due to the lack of availability of simple functional forms for describing molecular orbital (MO) couplings and energetics in systems with degrees of freedom beyond simple intermonomer dihedral angles. More specifically, quantitatively encoding the conformationally dependent electronic structure of complex organic molecules at a CG resolution is an unsolved problem for which new theoretical and computational methods are required.

In what follows, supervised machine learning is proposed as a means to quantitatively compute conformationally dependent electronic structure at CG spatial resolutions, allowing for the determination of electronic properties from only the system’s CG representation. For an explicit mapping from an atomistic system to a CG representation, regressing the configurationally dependent electronic structure to the CG degrees of freedom can be accomplished via the training of machine learning algorithms, in this case, ANN. Here, we apply this philosophy to a set of conjugated materials, focusing on an oligomer of poly(3-methylthiophene) to create CG electronic structure models that act on reduced CDOF. By doing so, we circumvent the need to back map the atomistic structure and perform quantum-chemical calculations for every generated CG configuration. We outline the scope, advantages, and limitations of this method, denoted as ANN electronic coarse graining (ANN-ECG), and discuss future directions for the proposed methodology.

MATERIALS AND METHODS

The ANN-ECG method is described schematically in Fig. 1 and consists of the following elements. First, using a set of atomistic configurations, one computes the electronic structure of each molecular conformation and extracts the desired electronic structure properties. Second, using a defined CG mapping, one maps the atomistic coordinates of each molecular conformation onto a reduced set of CG coordinates. Last, one uses a simple distance matrix between CG bead positions to construct a feature vector for each configuration. This feature vector was used as the input to the machine learning algorithm, with the output vector being the electronic structure property of interest that corresponds to the atomistic configuration. The machine learning algorithm was then trained to predict the atomistic electronic structure from only the CG degrees of freedom.

Fig. 1. Schematic of the ANN-ECG method used in this work.

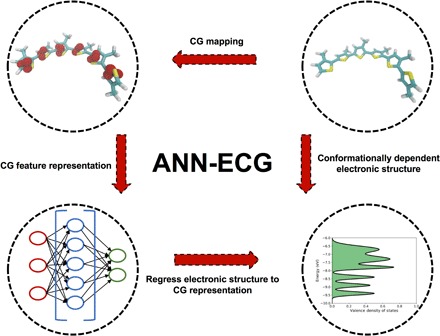
Schematic example shows a three-bead/monomer CG mapping for S3MT.

To test the ANN-ECG method, we focused on a hexamer of poly(3-hexyl)thiophene (27), with the alkylic side chains cleaved to methyls, denoted as sexi(3-methyl)thiophene (S3MT). S3MT was chosen as representative of organic semiconductor chemistries commonly found in both molecular and polymeric semiconductors. S3MT has many soft degrees of freedom, leading to a strong conformation dependence of the electronic structure; in principle, if all intermonomer dihedrals are 90°, the six highest occupied MO (HOMO) energies will be nearly degenerate. Otherwise, the intermonomer electronic couplings will strongly split the six HOMO energies by as much as 3 eV (see fig. S2). Applications to a chemically complex donor-acceptor conjugated copolymer, PTB7 (28), and a nonfullerene acceptor, TPB (29), are also provided in fig. S6.

To evaluate the sensitivity of ANN-ECG to different CG mapping schemes, a variety of CG resolutions of S3MT were generated using different CG mapping protocols. First, we used a CG mapping for each 3MT monomer, such that the orientation of each 3MT monomer was mapped to three CG beads, each corresponding to the end of a unit vector of an orthonormal coordinate system centered at each 3MT monomer’s center of mass (COM) (Fig. 1). The orthonormal coordinate system of each 3MT monomer was constructed using a vector between the COM and the 2-carbon, the COM and the 4-carbon, and their associated cross products. In the case of atomistic simulations in which the intramolecular degrees of freedom of each 3MT monomer are frozen with rigid-body constraints, the CG distance matrix between any pair of three-bead 3MT representations is isomorphic with their relative atomistic degrees of freedom because of the fact that the absolute relative orientation of any two rigid bodies can be defined using five rays (30). Under these constraints, ANN-ECG should exhibit high predictive performance as the reduced CG description is equivalent to the full atomistic representation.

A more conventional CG mapping scheme was also used for the case of fully flexible S3MT, in which specific atomic identities were grouped into single CG beads, positioned at the grouping’s COM. We obtained these specific mappings by relying on a systematic graph-based CG algorithm recently developed in our group (31). These specific mappings are provided in the Supplementary Materials.

Four distinct datasets of conformationally dependent electronic structure for S3MT were obtained by running MD simulations under the following four conditions: 300 K/rigid, 500 K/rigid, 300 K/flexible, and 500 K/flexible. In this notation, “rigid” refers to the use of rigid-body constraints on all intramonomer CDOF for each 3MT monomer of S3MT, “flexible” refers to the MD simulations with no rigid-body constraints imposed, and the temperature denotes the simulation temperature in the NVT ensemble maintained with a Langevin thermostat with a damping parameter of 100 fs⁻¹. MD simulations of a single S3MT molecule were first equilibrated at 600 K for 2 ns, annealed to the desired temperature over the course of 2 ns, and then run at the desired temperature for a total of 100 ns, with molecular configurations extracted every 10 ps, resulting in 10,000 independent configurations per dataset. Scripts used to generate the configurations are provided in the Supplementary Materials. Note that in the rigid simulations, while all internal CDOFs of each 3MT monomer are frozen, two-body stretches, three-body angle bends, and four-body dihedrals are still permitted between all bonded 3MT rigid bodies. The atomistic force field of P3MT uses an optimized potentials for liquid simulations (OPLS)–style (32) force field with a partial charge distribution and intermonomer dihedral potential parameterized following the procedures defined in previous work (33). All MD simulations were performed using LAMMPS (34). The six HOMO energy levels for each S3MT configuration were computed using Zerner method of intermediate neglect of differential overlap for spectroscopy (ZINDO/S) and BP86/def2-SVP (see fig. S7) in ORCA (35).

For the regression of electronic structure to a CG representation, a fully connected, feed-forward ANN with three hidden layers, each containing 50 neurons, was applied to each of the four S3MT MD datasets to simultaneously predict the six HOMO energy levels. A delta–machine learning approach (36) was also implemented (see the Supplementary Materials) to predict the difference between the ZINDO/S and the TB model described below. ANN weights were initialized according to an He normal distribution (37), batch normalization (38) was used on all layers except the output layer, and an exponential linear unit activation function (39) was used on each neuron. The L2 norm of each layer’s weight matrix was constrained to be less than 3.0. The mean of each input and output feature was shifted to zero, and the rest of the feature data were scaled by the SD of that feature. Training of the ANN used the Nesterov-accelerated adaptive moment estimation (ADAM) algorithm (40) with a batch size of 1000 to minimize the mean squared error of the training set predictions. Hyperparameter optimizations were performed and are provided in tables S1 and S2. The root mean squared error (RMSE) and coefficient of determination (r²) (41) were used as performance metrics for ANN-ECG and evaluated using a fivefold cross-validation for each dataset. Models trained on specific datasets were also applied to datasets generated from other temperatures and rigidity constraints as validation sets to assess overfitting. Keras (42) and scikit-learn (41) were used for the implementation of all machine learning methods, with scripts provided in the Supplementary Materials.

ANN results for S3MT were also compared to a TB Hamiltonian using the intermonomer dihedral angles of S3MT. This valence band Hamiltonian is defined by

$$\mathit{H}={\displaystyle \sum _{\mathit{i}}}{\mathrm{\epsilon }}_{\mathit{i}}{\mathit{c}}_{\mathit{i}}^{†}{\mathit{c}}_{\mathit{i}}-{\mathit{t}}_{\mathit{i},\mathit{i}+1}({\mathit{c}}_{\mathit{i}}^{†}{\mathit{c}}_{\mathit{i}+1}+{\mathit{c}}_{\mathit{i}+1}^{†}{\mathit{c}}_{\mathit{i}})$$ (1)

where i indexes the monomers of S3MT, ${\mathit{c}}_{\mathit{i}}^{†}$ and c_i are the fermionic creation and annihilation operators for a hole on monomer i, respectively, t_i,i+1 is the electronic coupling between neighboring HOMO orbitals, and ε_i is the HOMO energy of the ith 3MT monomer site. In our analysis, t_i,i+1 is defined as a cosine of the intermonomer dihedral angles, θ_i,i+1.

$${\mathit{t}}_{\mathit{i},\mathit{i}+1}={\mathit{H}}_{\mathit{i},\mathit{i}+1}\text{cos}({\mathrm{\theta }}_{\mathit{i},\mathit{i}+1})$$ (2)

where H_i,i+1 is the maximum value of the intermonomer coupling obtained when two neighboring 3MT monomers are coplanar. Dihedral angles, θ_i,i+1, are defined between neighboring 3MT monomers i and i + 1 using the vector perpendicular to each 3MT’s conjugated ring, which was constructed using the same vectors as described previously for the three-bead CG mapping scheme. The six HOMO energy levels were obtained by calculating the eigenvalues of the matrix representation of Eq. 1. Fitting of the datasets to the TB model parameters was obtained using the Sbplx nonlinear optimization routine (43), and for fitting, we assumed that ε_i and H_i,i+1 are independent of site position, leading to two fitting parameters per dataset. Fitting parameters are provided in the Supplementary Materials. A two-band (HOMO/HOMO-1) Hamiltonian with distinct end sites using seven fitting parameters was also applied in the Supplementary Materials but yielded quantitatively similar results.

In a step toward the application of ANN-ECG to multimolecule, condensed-phase electronic structure prediction, we also tested ANN-ECG in the prediction of the electronic structure of intermolecular dimers in two contexts: (i) the prediction of the valence band structure of a S3MT dimer and (ii) the prediction of hole self-exchange couplings between thiophene dimers in a bulk thiophene liquid. To learn the electronic structure of S3MT dimers, configurations were generated via MD at 300 K using the rigid constraints on 3MT monomers and a weak harmonic constraining potential between the COM of two S3MT molecules. Configurations were sampled every 10 ps for a total of 30,000 dimer configurations. The six HOMO energy levels of these dimers were then computed at the ZINDO/S level of theory. The CG distance matrix between all beads was used as the input feature. Standard scaling was performed to the input and output features, and a hyperparameter grid search was performed leading to a best-performing ANN structure of [100,80,60,40,20,6].

Last, we applied ANN-ECG to learn the complex nodal structure of the intermolecular coupling between two rigid thiophene dimers at a coarse-grained resolution. To learn the hole self-exchange couplings, configurations were generated via a rigid-body NPT MD simulation with configuration snapshots taken every 10 ps. We limited ourselves to a total of 100,000 unique dimer configurations. These snapshots were then decomposed into all unique dimer pairs using a cutoff radius of 1 nm between thiophene COM. These dimer pairs were then used to compute the absolute value of the electronic coupling associated with hole self-exchange at the HF/6-31G* level of theory (44). A distance matrix between CG (five-bead—united atom) representations of thiophene dimers was then computed as the input feature. ANN-ECG was then applied to learn the log of the thiophene dimer couplings at the five-bead CG resolution. Standard scaling transformation was applied to the input and output features. A hyperparameter search was performed, and an ANN structure of five hidden layers, each containing 200 neurons and using a batch size of 256, were selected.

RESULTS

We begin by comparing the predictive performance of ANN-ECG to that of the TB model (Eq. 1) for the 300 and 500 K/rigid datasets. Figure 2 demonstrates that ANN-ECG substantially outperforms the TB model (Eq. 1) in both RMSE and r² using a fivefold cross-validation for each dataset (Table 1). For both 300 and 500 K/rigid datasets, RMSE of less than 20 meV can be obtained over the entire 3-eV interval using ANN-ECG, whereas the TB model produces a RMSE greater than 50 meV for both datasets. Larger prediction errors are observed at 500 K relative to 300 K, which is anticipated because of the greater amount of configuration space explored by the 500-K MD simulation and consequently the possibility for more diversity in the configuration-dependent HOMO energies. The observed difference in performance between ANN-ECG and the TB model is due to the fact that TB only uses intermonomer dihedral angles with a predefined functional form (Eq. 2), whereas ANN-ECG uses a learned function of all degrees of freedom available at a given CG resolution. It is critical to emphasize that existing phenomenological CG electronic Hamiltonians require that specific degrees of freedom be defined a priori, along with the corresponding functional forms for the dependence of energies and couplings on those degrees of freedom. In this sense, ANN-ECG is a method that learns a nonlinear transformation of the distance matrix at the CG resolution to map an optimal coarse-grained electronic “Hamiltonian” that can predict valence band electronic structure. Notably, in principle, the predicted error associated with ANN-ECG can be trivially decreased by sampling additional configurations and using more powerful machine learning approaches, whereas the physics-based approach is strictly limited by the posited functional form.

Fig. 2. Predictive accuracy of ANN-ECG versus TB Hamiltonian.

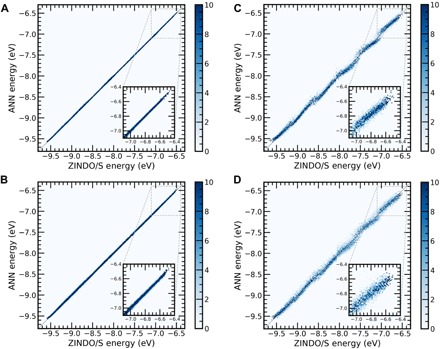
Two-dimensional (2D) histogram plots of ANN-ECG performance applied to the (A) 300 and (B) 500 K/rigid datasets and the TB model (Eq. 1) applied to the (C) 300 and (D) 500 K/rigid datasets. Color bar denotes the probability distribution of predicted HOMO energy levels, and the inset shows the prediction in the interval of the highest-energy HOMO.

Table 1. RMSE and r² results for all models and datasets in this study.

Method	Train/test	Validation	RMSE (meV)	r2
TB	300 K/rigid		54.7 ± 1.0	0.780 ± 0.001
TB	500 K/rigid		66.7 ± 1.3	0.790 ± 0.001
ANN	300 K/rigid		13.5 ± 0.5	0.989 ± 0.001
ANN	500 K/rigid		19.7 ± 0.6	0.984 ± 0.001
ANN	300 K/flexible		90.7 ± 0.6	0.573 ± 0.008
ANN	500 K/flexible		121.7 ± 0.9	0.466 ± 0.009
ANN	300 K/rigid	500 K/rigid	29.3 ± 1.2	0.964 ± 0.003
ANN	500 K/rigid	300 K/rigid	12.4 ± 0.5	0.990 ± 0.007
ANN	300 K/flexible	300 K/rigid	61.4 ± 2.0	0.752 ± 0.016
ANN	500 K/flexible	500 K/rigid	82.7 ± 1.7	0.704 ± 0.010

The results of Fig. 2 used datasets of 10,000 independent configurations to train an ANN-ECG model that significantly outperformed the TB Hamiltonian predictions. However, for situations with limited data availability, it is important to gauge how much data are required for ANN-ECG to learn a model of sufficient predictive accuracy. To quantify the influence of training data size on ANN-ECG performance, we plot the RMSE and r² of ANN-ECG across a fivefold split training dataset of variable size in fig. S2. Performance is measured by applying the averaged model from the fivefold cross-validation to a held-out 1000 configuration validation set. The 500 K/rigid dataset is used for fig. S2, but analogous results can be obtained for the 300 K/rigid dataset. An RMSE of less than 40 meV across all six HOMO energy levels can be obtained with less than 2500 independent, single-molecule configurations, which we believe is eminently obtainable in most organic semiconductor contexts, as this is simply a single configurational snapshot of many bulk MD simulations. The high r² value (~0.93) supports the accuracy of the prediction using 2500 data points, and the performance on the held-out validation set ensures that the results are not biased by overfitting. In the context of the TB model results, ANN-ECG begins to outperform the TB r² after ~1500 data points, while the low value of both RMSE and r² at data sizes less than 1000 suggests overfitting. For dataset sizes smaller than 1000 data points, as with many ANN applications, extra precautions (e.g., dropout regularization) should be taken to fit a reliable ANN-ECG model, and more likely, an alternative machine learning algorithm would be required.

To determine the generalizability of ANN-ECG, we examined its performance when trained and validated on configurations from MD simulations performed at different temperatures. In principle, the temperature should only dictate the amount of configuration space that is explored by the MD trajectories, but the ANN-ECG algorithm could still lack generalizability because of overfitting of the configurations at a specific training temperature. In fig. S1, 2D histograms of the prediction error for ANN-ECG trained on the 300 K/rigid dataset, applied to the 500 K/rigid dataset (fig. S1A), and vice versa (fig. S1B) are shown. These results support the generalizability of ANN-ECG as the configurations of 300 and 500 K/rigid datasets are generated from MD trajectories at different temperatures. The RMSE and r² of ANN-ECG in these contexts are quantified in Table 1. We observe that ANN-ECG trained at 500 K/rigid applied to the 300 K/rigid dataset (RMSE = 12.4 meV/r² = 0.990) outperforms ANN-ECG trained at 300 K/rigid applied to the 500 K/rigid dataset (RMSE = 29.3 meV/r² = 0.964). This result is supported by the physical intuition that temperature is a metric for the amount of configuration space explored—the underlying quantum-mechanical function can be better learned if more configurational space is explored in the training data. However, it is important to emphasize that both ANN-ECG models display high accuracy, especially when compared to the performance of the TB model, for the prediction of the HOMO energy levels. Moreover, in Table 1, the 500 K/rigid trained model applied to the 300 K/rigid dataset actually marginally outperforms the cross-validated predictions of the 300 K/rigid dataset. We interpret this result not only as an assurance that we are not overfitting our data but also that ANN-ECG trained on higher-temperature configurations might exhibit higher accuracy and more generalizability relative to calculations trained at lower temperatures.

All previous results have relied on the use of S3MT configurations derived from the MD simulations where the internal degrees of freedom of all 3MT monomers were frozen. To test the utility of ANN-ECG for flexible atomistic systems, we release the rigid monomer constraints of S3MT and gauge the predictive ability of ANN-ECG when trained on configurations derived from fully flexible MD simulations (300 and 500 K/flexible). The same mapping of the three CG beads is used as that for the rigid simulations. As shown in Fig. 3 and Table 1, the RMSE is larger than that in the case of the rigid simulations by a factor of ~6 to 7. This increase in RMSE is due to the additional intramolecular degrees of freedom of each 3MT monomer contributing to a broadening of the HOMO energies, as multiple atomistic configurations can be equivalently mapped to the same CG configuration. For flexible simulations, the predictive accuracy of ANN-ECG will be contingent on the CG resolution, and consequently, the three-bead CG mapping is limited in this regard, although it still exhibits reasonable performance (r² = ~0.5) at both temperatures. CG mappings that span the range of CG resolution using a more conventional COM-based mapping scheme will be explored later in the article.

Fig. 3. ANN-ECG performance on rigid and flexible configurations.

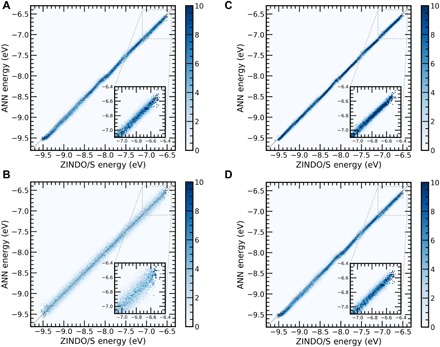
2D histograms of ANN-ECG performance with a (A) 300 K/flexible trained model applied to 300 K/flexible test set, (B) 500 K/flexible trained model applied to 500 K/flexible test set, (C) 300 K/flexible model applied to 300 K/rigid test set, and (D) 500 K/flexible model applied to 500 K/rigid test set. Color bar denotes the probability distribution of predicted values, and the inset shows the prediction in the interval of the highest-energy HOMO.

For flexible configurations, a useful insight is derived when the ANN-ECG model trained on the flexible configurations (300 and 500 K/flexible) is used to predict the electronic structure of the rigid configurations (300 and 500 K/rigid). If the ANN trained on the flexible model learns the underlying quantum-mechanical function and is not overfitting, then when applied to the rigid datasets, ANN-ECG should still exhibit high accuracy, as the rigid configurations occur at 3MT energy minimums, which should be interpolatable from the ANN-ECG model trained on flexible configurations. Figure 3 and Table 1 show that 300 and 500 K/flexible predictions exhibit an r² of ~0.5. When the ANN-ECG models trained on those datasets are applied to 300 and 500 K/rigid datasets, the r² increases to ~0.7 to 0.75. This result suggests that ANN-ECG correctly learns the quantum-mechanical function required to predict the HOMO valence band regardless of molecular constraints. Furthermore, this supports the idea that ANN-ECG can be used to map configurationally dependent electronic structure from fully flexible simulations onto CG representations and that it does not require configurations drawn from constrained MD simulations. In this context, the only constraint on the accuracy of the ANN-ECG prediction is the number of CDOF maintained by the CG model, which is consistent with the general philosophy that a CG model can only predict features consistent with its assumed length and time scale resolutions.

The choice of CG representation is often dictated by physical intuition or convenience; in that sense, it can be viewed as somewhat arbitrary. In the case of ANN-ECG, the selected CG resolution will necessarily affect its ability to resolve the conformationally dependent electronic structure, and it is therefore of interest to examine whether an optimal level of description exists for which computational efficiency (and exploration of phase space) are maximized, without loss of the quantum-mechanical predictive power. There are two extremes of resolution for the representation of S3MT: the inclusion of all atomistic degrees of freedom and the treatment of the entire molecule as a single CG bead. In the detailed resolution, one expects the highest predictive accuracy, as these degrees of freedom are the same as those used as input to the original electronic structure calculation. At the coarsest resolution, one expects to predict only the mean value of the electronic structure of the molecule, without the ability to capture any conformational dependence. To demonstrate the impact of resolution choice on the accuracy of ANN-ECG, in Fig. 4A, we show the fivefold cross-validated RMSE and r² in the prediction of the S3MT valence band energies for the 300 K/flexible dataset as a function of the CG resolution used. The CG mappings used at each resolution are presented for a representative configuration in Fig. 4B, with the exact mapping provided in the Supplementary Materials. Note that a hyperparameter optimization is performed for ANN-ECG at each resolution.

Fig. 4. ANN-ECG performance applied to a systematically reduced set of coarse-grained representations.

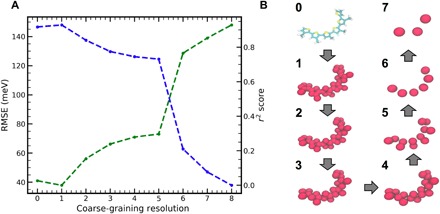
(A) ANN-ECG fivefold cross-validated RMSE (green) and r² (blue) of 300 K/flexible S3MT configurations as a function of CG resolution. (B) Visualizations of the CG mappings for S3MT occurring at all resolutions shown in (A). Resolution 8 in (A) corresponds to one CG bead per S3MT molecule and is not explicitly shown.

Figure 4 demonstrates the ability of ANN-ECG to reproduce the conformation-dependent electronic structure of S3MT for different levels of CG resolution. It is important to note that the atomistic representation (representation 0) performs marginally worse than representation 1 (equivalent to a united atom model) because of overfitting from the large size of the distance matrix input and its associated large number of ANN weights. As the representation coarseness increases from 1 to 5, ANN-ECG’s RMSE increases from 40 to 75 meV because of the decimation of relevant conformational information. However, the slow rate of this decline between resolutions 1 and 5 suggests that CG models with relatively coarse resolutions (e.g., resolution 5 involves only two beads/3MT monomer) can still capture much of the conformationally dependent electronic structure. When the coarse-graining progresses to representation 6, a drastic increase in the RMSE (130 meV) is observed. Resolution 6 represents the point at which one CG bead per monomer is obtained—at this resolution, intermonomer dihedrals cannot be described by the CG representation. As intermonomer dihedrals are a critical parameter in describing the conformationally dependent electronic structure of conjugated molecules (24–26), this result supports physical intuition. It is also useful to point out that the RMSE of representation 5 for the 300 K/flexible dataset (75 meV) is comparable to even the TB model for the rigid configurations. As the resolution is further coarsened to 7 (three beads per S3MT molecule) and 8 (one bead per S3MT molecule), the accuracy corresponding to the prediction of the mean of the valence band positions is reached.

The results of Fig. 4 suggest a means of obtaining computationally optimal CG resolutions for studies of molecules having conformationally dependent electronic structure. The sudden drop in predictive performance observed in going from CG resolution 5 to 6 confirms our physical intuition regarding the critical influence of intermonomer dihedrals—if these CDOFs are not captured, the ANN-ECG performance deteriorates strongly. In systems where the important CDOF are not well known, it might be useful to feed various CG mapping schemes into the ANN-ECG algorithm to derive an optimal CG resolution—one where a relatively high accuracy of conformationally dependent electronic structure prediction can be maintained with a minimal number of beads while accelerating the conformational sampling procedure via MD or MC.

With the goal of predicting condensed-phase electronic structure, we next apply ANN-ECG to the problem of predicting the conformationally dependent electronic structure of intermolecular dimers at a coarse-grained resolution. We focus on ANN-ECG in two specific contexts: (i) the prediction of the conformationally dependent HOMO band structure of the S3MT dimer (Fig. 5A) and (ii) the prediction of the conformationally dependent hole self-exchange coupling between thiophene dimers extracted from the liquid state (Fig. 5C).

Fig. 5. ANN-ECG applied to the prediction of configurationally dependent dimer electronic structure.

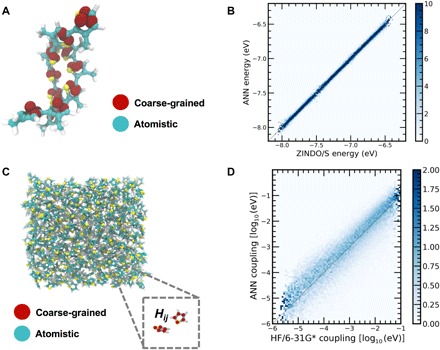
(A) Schematic of atomistic and coarse-grained representations of a S3MT dimer. (B) 2D histogram of ANN-ECG performance applied to the S3MT dimer six highest HOMO energy levels. (C) Schematic of dimer configurations taken from a classical MD simulation of the thiophene fluid, with both atomistic and CG representations shown. (D) 2D histogram of ANN-ECG performance applied to predict the hole self-exchange coupling between thiophene dimers at the CG resolution.

Figure 5B shows the predictive accuracy of ANN-ECG applied to the HOMO energies of the CG S3MT dimer computed at the ZINDO/S level of theory. A hyperparameter search of the ANN structure yielded a fivefold cross-validated RMSE of 25.6 ± 0.9 and an r² of 0.921 ± 0.002. As the configuration space of the dimer is exponentially larger than that of a single S3MT molecule, the marginal decrease in predictive accuracy relative to the monomer is anticipated for our dataset size (30,000 configurations). This result is of particular interest because of the fact that, to our knowledge, there are no existing methods (e.g., phenomenological Hamiltonians) capable of predicting the conformationally dependent electronic structure of intermolecular dimers at a coarse-grained resolution, making ANN-ECG a unique tool for the coarse-graining of electronic structure at increased spatial resolutions.

Next, we apply ANN-ECG to learn the logarithm of the electronic coupling associated with hole self-exchange between thiophene dimers using a five-bead coarse-grained representation. This particular application presents specific challenges due to the complex and rapidly varying nodal structure of the intermolecular coupling (45). A hyperparameter search achieves a fivefold cross-validated RMSE of the base 10 logarithm of the electronic coupling of 0.506 ± 0.002 and an r² of 0.753 ± 0.003, which corresponds to a predictive accuracy of a factor of ~3.0 for the magnitude of the electronic couplings. Provided the relatively large size of the dataset of thiophene dimer conformations (100,000), an analysis of this limited accuracy is warranted. The ANN, on average, overpredicts the magnitude of the coupling, although a long and diffuse tail of underpredictions exists below the diagonal. Upon examination of the error distribution in Fig. 5D, it is evident that predicting the complex nodal structure of the overlap of thiophene orbitals is a challenge for the ANN. Specifically, the distribution of predicted errors broadens significantly at smaller values of the couplings, which we attribute to poor fits of the nodal planes at larger intermolecular distances; the visual examination of validation sets using planar coupling surfaces often shows that these fine nodal planes where the couplings rapidly go to zero are missed by the ANN.

Despite this limited accuracy, ANN-ECG applied to electronic couplings still has meaningful practical applications. Specifically, for a loss of a factor of 2 to 3 in predictive accuracy, the computation of electronic couplings between molecular dimers can be accelerated by a factor of ~10⁵ for thiophene dimers, an acceleration that should scale as a function of system size with the scaling of the competing electronic structure method. This accuracy is comparable with variations in computed electronic couplings as a function of quantum chemistry, basis set, or method for computing couplings (46). Also note that the configurations were drawn from a liquid state where the peak of the first shell of the radial distribution function is located ~5.5 Å—this distance is substantially larger than the typical π-stacking distance of 3 to 4 Å, and consequently, many of the rapid changes in coupling values attributable to the nodal planes may simply be seen as noise by the ANN. In this regard, alternative configurational sampling schemes, better descriptors, a larger dataset, and more advanced machine learning protocols could help improve the predictive accuracy in the future.

DISCUSSION

It is useful to provide context for where ANN-ECG sits in the current landscape of simulation protocols for soft materials. First, ANN-ECG accomplishes a distinct goal that we believe is unachievable by any existing methodology: The determination of conformationally dependent electronic structure at a spatial resolution consistent with the coarse-grained model used to generate configurations. This makes ANN-ECG an important advance in the use of machine learning methods to develop quantitatively accurate coarse-grained electronic “Hamiltonians” capable of being endowed with chemical specificity. Second, ANN-ECG has the potential to be faster than even cheap semiempirical methodologies [e.g., ZINDO/S or semiempirical TB (47)], as a single forward pass of a trained neural network takes on the order of 10 to 100 μs, whereas a similar electronic structure evaluation typically takes on the order of 1 to 1000 s depending on the molecule’s size and the scaling of the quantum chemistry. Even accounting for the ANN hyperparameter optimization, the computational savings of ANN-ECG, especially for large systems and molecules, are substantial. Third, fast semiempirical and TB methodologies are dependent on their underlying parameterization, whereas ANN-ECG can be applied in conjunction with any quality of quantum chemistry [even CCSD(T)] if the training data exist. This is a critical difference as many TB methods are parameterized at the hybrid DFT level to reproduce geometries and vibrational frequencies and not ionization potentials, electron affinities, or band structures. Moreover, we view ANN-ECG as synergistic with existing semiempirical methods—future work could conceivably use TB to obtain the conformationally dependent electronic structure of large molecular aggregates at the limit of the size scaling of TB, and ANN-ECG could be applied on top to screen the morphological dependences of electronic structure at even larger (hundreds of nanometer) length scales. ANN-ECG is not limited to the prediction of purely energetic quantities, and future applications to the predictions of polarizabilities, excited state electronic structure, wave functions, and length-transferable polymeric electronic structure at coarse-grained resolutions are under way.

In summary, we have presented a machine learning–based strategy—ANN-ECG—for mapping conformationally dependent electronic structure, averaged over decimated degrees of freedom, onto CG models at arbitrary levels of resolution. ANN-ECG performs well when trained on configurations derived from different temperature and molecular constraint simulations and serves as a general means of deriving coarse-grained electronic structure. We explicitly note that ANNs were chosen as the machine learning approach for the simplicity and rapidity of their training using the backpropagation algorithm; however, many other machine learning algorithms, such as Gaussian approximation potentials, could find accurate and effective use in the mapping of electronic structure to CG representations. We anticipate the ANN-ECG methodology to have a suite of potential applications in coarse-grained simulations of materials that have traditionally required computationally laborious back-mapping (48) and multiscale simulation schemes to derive fine-grained detail from coarse-grained simulations.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/3/eaav1190/DC1

Fig. S1. Temperature transferability of the ANN-ECG model.

Fig. S2. ANN-ECG performance versus training data aize for 500 K/rigid dataset.

Fig. S3. Distribution of HOMO energy levels for 300 K/flexible and 300 K/rigid datasets.

Fig. S4. Atomic numbering scheme used for each 3MT monomer.

Fig. S5. Delta–machine learning fitting results for ANN-ECG using 300 K/rigid dataset.

Fig. S6. Application of ANN-ECG to conjugated copolymer PTB7 and non-fullerene acceptor TPB.

Fig. S7. ANN-ECG results for the HOMO-5→HOMO energy levels of S3MT using 300 K/rigid dataset computed at the BP86/6-31G* level of theory.

Table S1. Hyperparameter optimization for ANN layers and neurons.

Table S2. Hyperparameter optimization for number of training epochs.

Table S3. Results using ANN-ECG and a systematic coarse-graining strategy.