Identifying spinon excitations from dynamic structure factor of spin-1/2 Heisenberg antiferromagnet on the Kagome lattice

Significance

In frustrated quantum magnets, the interplay between quantum fluctuation and geometric frustration may prevent magnetic ordering and result in exotic quantum spin liquids, where the spin degrees of freedom form disordered liquid-like states with novel fractionalized excitations. Here, we study the dynamical response of spin liquids on a Kagome lattice Heisenberg antiferromagnet. Our results reproduce the main observations in the inelastic neutron scattering measurements of herbertsmithite and unveil the spin liquid nature of the ground state with fractionalized spinon excitations. By crossing the quantum-phase transition between the spin liquid and magnetically ordered phase, we identify the condensation of two-spinon bound state as the driving force.

Abstract

A spin-$1/2$ lattice Heisenberg Kagome antiferromagnet (KAFM) is a prototypical frustrated quantum magnet, which exhibits exotic quantum spin liquids that evade long-range magnetic order due to the interplay between quantum fluctuation and geometric frustration. So far, the main focus has remained on the ground-state properties; however, the theoretical consensus regarding the magnetic excitations is limited. Here, we study the dynamic spin structure factor (DSSF) of the KAFM by means of the density matrix renormalization group. By comparison with the well-defined magnetically ordered state and the chiral spin liquid sitting nearby in the phase diagram, the KAFM with nearest neighbor interactions shows distinct dynamical responses. The DSSF displays important spectral intensity predominantly in the low-frequency region around the $\mathbf{Q}=M$ point in momentum space and shows a broad spectral distribution in the high-frequency region for momenta along the boundary of the extended Brillouin zone. The excitation continuum identified from momentum- and energy-resolved DSSF signals emergent spinons carrying fractional quantum numbers. These results capture the main observations in the inelastic neutron scattering measurements of herbertsmithite and indicate the spin liquid nature of the ground state. By tracking the DSSF across quantum-phase transition between the chiral spin liquid and the magnetically ordered phase, we identify the condensation of two-spinon bound state driving the quantum-phase transition.

Quantum spin liquid (QSL) is a novel quantum phase, which behaves differently from conventional magnetic states (1–3). It does not show any magnetic order or lattice symmetry breaking even on approaching the zero-temperature limit. Theoretical studies have shown the intrinsic nature of a QSL, including massive entanglement and fractionalized excitations (4–7), although these quantities are challenging to measure directly in experiments. Experimentally, QSL candidates have been identified in frustrated magnetic materials, such as Kagome and triangular lattice compounds (8–15). Among them, the Kagome antiferromagnet (KAFM) herbertsmithite (8–11) is one of the most promising spin liquid candidates. A possible magnetic order of this material has been excluded down to temperatures a few orders of magnitude below the coupling energy scale (9, 10). Furthermore, the inelastic neutron scattering (INS) measurement characterizes the dynamic spin structure factor (DSSF) as a broad continuum spectrum in frequency domain (10), which is distinct from the spectrum of conventional magnon excitations. So far, it remains an open issue as to what information regarding the topological order and the fractionalization of spin excitations can be extracted from such measurements. Moreover, additional factors in real materials, such as disorder, may also lead to a similar continuum of the DSSF (16), making theoretical understanding of the INS essential for distinguishing different physics. Furthermore, whether such a spin liquid candidate has a finite spin gap remains unresolved in experimental probes, including INS (10) and NMR (11). To clarify these questions, theoretical studies on dynamic responses related to experimental probes are highly desired.

Theoretically, the ground state of the spin-$1/2$ KAFM with nearest neighbor Heisenberg interactions, which captures the dominant interactions for herbertsmithite, has been investigated intensively (17–35). Although a QSL ground state has been established in the KAFM, its full nature, including fractionalized quasiparticles and the existence of a spin gap, is still under debate. While earlier density matrix renormalization group (DMRG) simulations suggested a gapped spin liquid (25–28), parton construction and variational Monte Carlo studies found a gapless $U\left(1\right)$ Dirac spin liquid as the energy-optimized ground state (20–23). Such a gapless spin liquid scenario is also indirectly supported by recent DMRG and tensor network results (34, 35). However, more direct evidence from low-energy excitations is still absent. The open question regarding the nature of this QSL phase demands new theoretical approaches to explore excited-state properties, such as the DSSF. To date, other than the studies based on a mean field analysis or approximate methods (36–40), the unbiased evidence from microscopic calculations is rare or limited to small systems (41).

In this paper, we aim to understand the DSSF for the KAFM and extended models with either small farther neighbor Heisenberg interactions or Dzyaloshinskii–Moriya (DM) interaction, and both are relevant to the experimental material. With these perturbative couplings, we identify characteristic features of the DSSF for different quantum phases, including a $\mathbf{q}=\left(\mathrm{0,0}\right)$ magnetically ordered phase, a gapped chiral spin liquid (CSL), and a QSL connecting to the phase of the KAFM with nearest neighbor interactions [we denote it as Kagome spin liquid (KSL)]. In the $\mathbf{q}=\left(\mathrm{0,0}\right)$ phase, the key signature of long-range magnetic order is a single-magnon excitation mode with the largest intensity at the corresponding magnetic wave vector. In the CSL phase, the energy scans of the DSSF show a peak in intensity at finite frequency, which illustrates the emergent gapped spinon pair excitations. In the KSL, the momentum-resolved DSSF concentrates along the boundary of the extended Brillouin zone (BZ) and shows a broad maximum at the $M$ point. In the energy scans for the KSL, the intensity of the DSSF forms a continuum, which extends over a wide frequency range, concomitant with a pronounced intensity in the low-energy region. These findings are consistent with the INS results on herbertsmithite (10). The evidence from the DSSF, including the excitation continuum in energy scans and the sensitivity of the excitation gap by imposing different boundary conditions (BCs) and by tuning the DM interaction, is in support of a QSL with gapless fractionalized spin excitations.

Results

Model.

We study the spin-$1/2$ KAFM with farther neighbor antiferromagnetic interactions

$$H=J_1\sum _{⟨i,j⟩}{\mathbf{S}}_i\cdot {\mathbf{S}}_j+J_2\sum _{⟨⟨i,j⟩⟩}{\mathbf{S}}_i\cdot {\mathbf{S}}_j+J_3\sum _{⟨⟨⟨i,j⟩⟩⟩}{\mathbf{S}}_i\cdot {\mathbf{S}}_j,$$ [1]

where $J_1,J_2,J_3$ are the first-, second-, and third-neighbor couplings [$J_3$ is the coupling inside the hexagon (Fig. 1A, Inset), and we take $J_1=1$ as the energy scale]. The previously obtained ground-state phase diagram is shown in Fig. 1A (42). Different phases surround the KSL, including a $\mathbf{q}=\left(\mathrm{0,0}\right)$ magnetically ordered phase, a gapped CSL phase, and a valence bond crystal (VBC) phase. Motivated by the experimental observation (43, 44), we also consider a DM interaction ${\mathbf{D}}_{ij}\hspace{0.17em}\cdot \left({\mathbf{S}}_i\times {\mathbf{S}}_j\right)$ (45, 46) in addition to the KAFM. The phase diagram is shown in Fig. 5A, and the related discussion will be shown below.

Fig. 1.

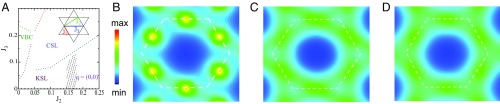
Static spin structure factor of different quantum phases on the KAFM. (A) Quantum-phase diagram of the Kagome model in the $J_2-J_3$ plane obtained in ref. 42. (B–D) Static spin structure factor in momentum space for (B) the $\mathbf{q}=\left(\mathrm{0,0}\right)$ phase at $J_2=0.25,J_3=0.0$; (C) the CSL at $J_2=0.25,J_3=0.25$; and (D) the KSL at $J_2=J_3=0$. The extended BZ is marked by the white dashed line.

Fig. 5.

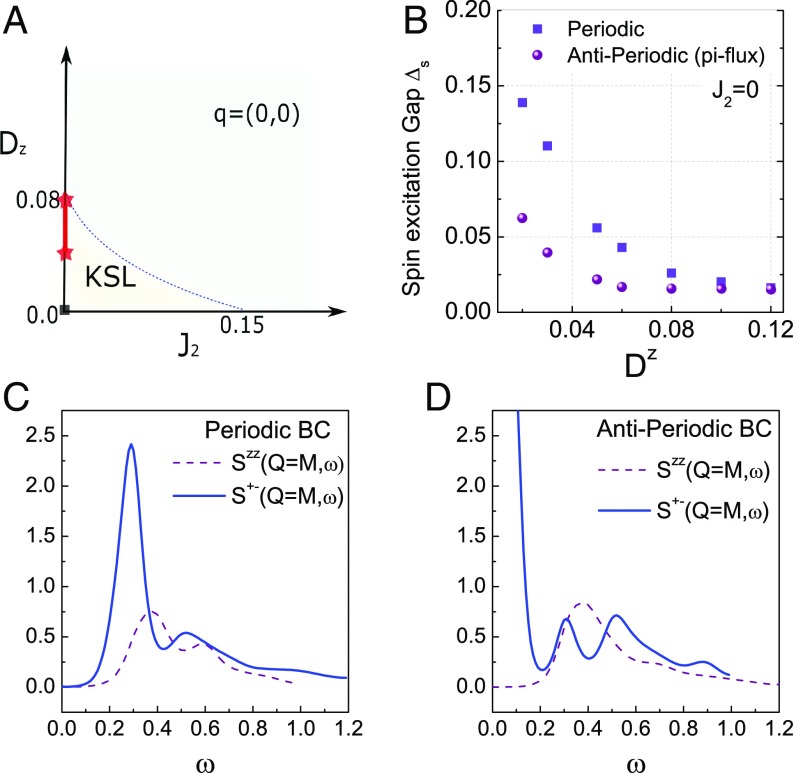
DSSF of the KSL when including the DM interactions. (A) Phase diagram of the KAFM when including second nearest neighbor coupling $J_2$ and out-of-plane DM interaction $D^z$. The black square represents the KAFM with nearest neighbor couplings. The red star line shows the possible parameter regime for herbertsmithite (43, 44). (B) Spin gap for various $D^z$ under periodic (blue squares) and antiperiodic (purple circles) BC. The DSSF of the KSL phase at $J_2=0,D^z=0.06$ under (C) periodic BC and (D) antiperiodic BC for the longitudinal mode (purple dashed line) and the transverse mode (blue line).

Static Spin Structure Factor.

We first present the static spin structure factor that is defined as (SI Appendix, section II)

$$\mathcal{S}\left(\mathbf{Q}\right)=⟨\mathbf{S}\left(-\mathbf{Q}\right)\cdot \mathbf{S}\left(\mathbf{Q}\right)⟩=\frac{1}{N}\sum _{i,j}{e}^{i\mathbf{Q}\cdot \left({\mathbf{r}}_i-{\mathbf{r}}_j\right)}⟨{\mathbf{S}}_i\cdot {\mathbf{S}}_j⟩,$$ [2]

where the wave vector $\mathbf{Q}=\left(q_1,q_2\right)=q_1{\overrightarrow{b}}_1+q_2{\overrightarrow{b}}_2$ in the BZ is defined by the reciprocal vectors ${\overrightarrow{b}}_{\mathrm{1,2}}$ (Fig. 2D). In Fig. 1B, $\mathcal{S}\left(\mathbf{Q}\right)$ shows sharp peaks at the $M$ points, revealing a $\mathbf{q}=\left(\mathrm{0,0}\right)$ magnetic order (47). In the nonmagnetic phases, $\mathcal{S}\left(\mathbf{Q}\right)$ is featureless as shown in Fig. 1 C and D. In the KSL phase, $\mathcal{S}\left(\mathbf{Q}\right)$ concentrates along the boundary of the extended BZ and shows a broad maximum near the $M$ point, which agrees with the features of the INS data of herbertsmithite (10).

Fig. 2.

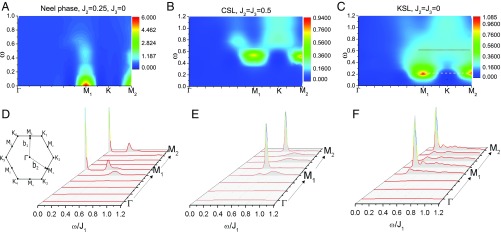
DSSF of different quantum phases on the KAFM. (A–C) Contour plots of the DSSF as a function of energy and momentum for (A) $q=\left(\mathrm{0,0}\right)$ phase at $J_2=0.25,J_3=0.0$; (B) CSL at $J_2=0.5,J_3=0.5$; and (C) KSL at $J_2=J_3=0$. The white (black) dashed line in C shows the constant-energy values at the low-frequency (high-frequency) region, which are compared with the INS observations in herbertsmithite (Fig. 4 has details). (D–F) The energy scans of the DSSF with the momentum along the path $\mathrm{\Gamma }\to M_1\to K_1\to M_2$ in the extended BZ. The intensity scales differ among the different panels. D, Inset shows the extended BZ with denoted high-symmetry momentum points and reciprocal vectors (${\overrightarrow{b}}_{\mathrm{1,2}}$).

DSSF.

The DSSF is defined as

$${\mathcal{S}}^{\alpha \beta }\left(\mathbf{Q},\omega \right)=-\frac{1}{\pi }\mathrm{I}\mathrm{m}⟨S^{\alpha }\left(-\mathbf{Q}\right)\frac{1}{\omega -\left(H-E_0\right)+i\eta }{S}^{\beta }\left(\mathbf{Q}\right)⟩,$$ [3]

where $E_0$ is the ground-state energy, $\eta$ is a small smearing energy (SI Appendix, section I), and $\alpha ,\beta$ denote spin components. We first discuss the salient features of the DSSF in different phases as shown in Fig. 2. For the $\mathbf{q}=\left(\mathrm{0,0}\right)$ phase (Fig. 2 A and D), we observe a sharp elastic peak at the $M$ point resulting from the contribution of static correlations of Néel order. Obscured by the finite-size effect, a small excitation gap is observed in the DSSF (as the second peak at nonzero $\omega$ at $\mathbf{Q}=M$ in Fig. 2D). Despite this, magnetic excitations form a single mode-like peak structure at each momentum, which is related to the magnon excitations. The magnetic excitation peak at $M$ point shows a tail with reduced weight in the higher-energy region, which we speculate is related to magnon–magnon interactions. For all other momenta, the spectral intensity is significantly reduced, consistent with the expectation that the largest weight should be at the magnetic ordering wave vector for Néel order.

For the CSL, the DSSF along high-symmetry lines is presented in Fig. 2 B and E. Importantly, the DSSF shows a fully gapped excitation branch. The extracted spin gap $\sim 0.4J_1$ is consistent with a direct measurement of the gap in static simulations. For momentum points along the boundary of the extended BZ, the DSSF has a broad distribution with suppressed intensity. Since theoretically, the CSL is well described as the Laughlin state with spinons satisfying semionic statistics (48), the peak at the $M$ point is composed of spinon pair excitations (SI Appendix, section III).

Next, we turn to the KSL shown in Fig. 2 C and F. The dominant intensity of the DSSF is carried by the momenta near the $M$ point, and the spectrum at each momentum (along the boundary of the extended BZ) shows a broad distribution that spans a wide energy regime. For example, $\mathcal{S}\left(\mathbf{Q}=M,\omega \right)$ shows a dominant intensity at low energies and a long tail up to $\omega \approx 1.2$ (in units of $J_1$); the overall feature is quite different from the spectrum of the $\mathbf{q}=\left(\mathrm{0,0}\right)$ phase, where the overwhelming part of the spectral weight is carried by a single excitation mode. Compared with the CSL phase, here the spectral weight moves down in energy, consistent with a reduction of the spin excitation gap. Interestingly, $\mathcal{S}\left(\mathbf{Q}=M,\omega \right)$ shows a dominant narrow peak structure, which supports deconfined stable (long-lifetime) spinon excitations. The appearance of an excitation continuum in the high-frequency region is similar to the case of the one-dimensional Heisenberg model, where a critical spin liquid phase has been identified as the ground state with gapless spinon excitations (49). We remark that the DSSF results of the KSL phase capture the main features of the INS results on herbertsmithite, including the low-energy spectral peak at the $M$ point and the nearly flat spin excitations between the $M$ and $K$ points at higher energy, which will be discussed below in detail.

Condensation of Two-Spinon Bound State and Quantum-Phase Transition.

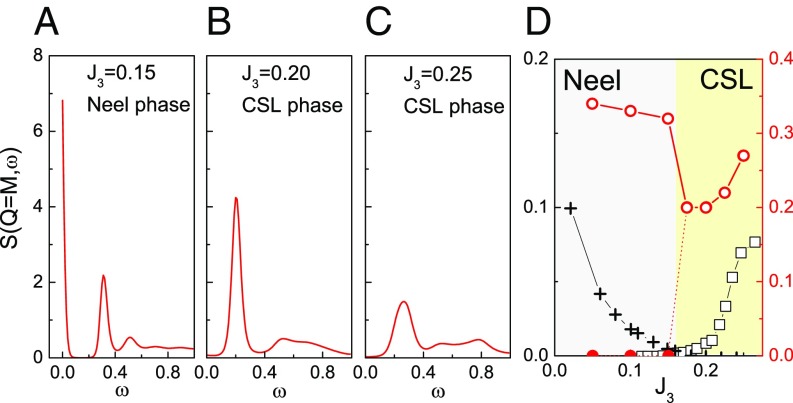
It is also interesting to study the quantum-phase transition from the perspective of the DSSF, which reveals the dynamic driving mechanism of the transition. Here, we study the transition from the CSL to the $\mathbf{q}=\left(\mathrm{0,0}\right)$ phase (SI Appendix, section III). As shown in Fig. 3 A–C, from the evolution of the DSSF at the $M$ point by tuning $J_3$, we observe the following key features. Starting inside the CSL phase ($J_3>0.15$) and approaching the transition point, the predominant peak moves toward lower frequency, and the peak intensity gradually increases. Around the phase boundary ($J_3\sim 0.15$), the lowest excitation peak experiences a discontinue jump together with the appearance of an elastic peak (Fig. 3D). In this context, a natural interpretation of the peak structure in the CSL phase is a two-spinon resonance state, while the magnetic excitation in the Néel phase corresponds to a two-spinon bound state, which is equivalent to the magnon state. The above observations indicate that the quantum-phase transition between the CSL and the Néel phase can be understood as being driven by the condensation of the spinon pairs to form spin-1 magnon excitations. That the lowest peaks in DSSF of the CSL and the Néel phase occur at the same momentum point $\mathbf{Q}=M$ makes the above picture possible. Here, the evolution of the DSSF across the critical point not only elucidates the nature of the low-energy peak structure in the DSSF but also, provides a microscopic understanding for the continuous-phase transition between a spin liquid and a magnetically ordered phase that is less understood in a previous study using static probes (42).

Fig. 3.

Evolution of the DSSF across the phase boundary. (A–C) We show the evolution of $\mathcal{S}\left(Q=M,\omega \right)$ by varying $J_3$ and setting $J_2=0.2$. (D) The positions of excitation peaks (red circles) at different $J_3$ around the phase boundary. Black crosses (squares) show the long-distance spin correlations $\sqrt{\left|⟨{\mathbf{S}}_0{\mathbf{S}}_d⟩\right|}$ [chiral correlation $\sqrt{\left|⟨{\chi }_0{\chi }_d⟩\right|}$; $d=L_x/2$ is the longest available distance, $\chi ={\mathbf{S}}_i\cdot \left({\mathbf{S}}_j\times {\mathbf{S}}_k\right)$, and $i,j,k$ belong to the same triangle]. Red circles are peak positions of the two-spinon state (solid circles mark elastic peak in Néel phase).

Connection with Experiment.

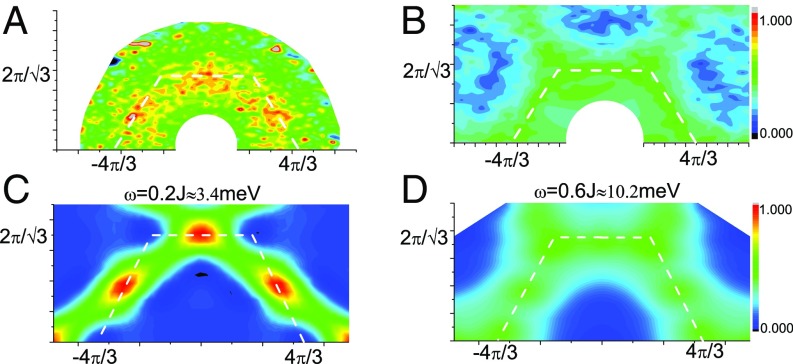
In Fig. 4, we show the plots of the constant-energy scan of the DSSF and compare our results qualitatively with the experimental data (figure 1 in ref. 10). The main observation from the INS experiment is that (10), in the low-frequency region, the measured DSSF shows a peak structure around the $M$ points; while at higher frequencies, the peak structure is smeared out, and the DSSF is almost evenly distributed along the boundary of the extended BZ. In Fig. 4 A and B, we replot two constant-energy plots of the DSSF from the experimental measurements at low and high frequencies, respectively. Accordingly, we show two calculated DSSF plots at two constant energies in Fig. 4 C and D. Our numerical DSSF develops peak structures around the $M$ points at low frequencies and a flat distribution along the boundary of the extended BZ at high frequencies, respectively. Through this comparison, we conclude that the calculated DSSF can capture the main INS experimental observations in both the low-frequency regime and the high-frequency regime.

Fig. 4.

Comparison between experimental measurements and numerical results for the DSSF. Rescaled experimental data at fixed frequency are shown for (A) $\omega =0.75$ meV and (B) $\omega =6$ meV [data from ref. 10]. Theoretical results for the DSSF of KAFM with nearest neighbor couplings ($J_2=J_3=0$) at fixed frequency are plotted for (C) $\omega =0.2J_1$ and (D) $\omega =0.6J_1$ (related to the dashed line cut in Fig. 2C). The extended BZ is indicated by the white dashed lines.

While the KAFM is generally believed to be a good starting point to understand the spin liquid-like behaviors of herbertsmithite, due to the absence of inversion symmetry, the spin–orbit coupling between two adjacent Cu²⁺ ions in herbertsmithite yields a DM interaction ${\mathbf{D}}_{ij}\cdot \left({\mathbf{S}}_i\times {\mathbf{S}}_j\right)$ (45, 46). Electron spin resonance (43) and magnetic susceptibility measurements (44) suggest an out-of-plane DM interaction $D_{ij}^z\approx 0.04\sim 0.08$ (in units of $J_1$). To make a closer comparison between experiments and numerical simulations, we study the DSSF of the KAFM with an out-of-plane DM interaction $D^z$ for nearest neighbor spins.

We show the phase diagram of the extended KAFM as a function of $D^z$ and $J_2$ in Fig. 5A (we set $J_3=0$), which includes the KSL and the $\mathbf{q}=\left(\mathrm{0,0}\right)$ phase. We obtain the phase diagram by studying the magnetic order parameter and spin excitation gap (SI Appendix, section IV). In the absence of $J_2$, we find a transition at $D_c^z\approx 0.08$, slightly smaller than previous results (36, 50, 51) but larger than the estimation in ref. 52. With increasing $D^z$, the spin excitation gap (defined by the energy difference between lowest-energy state with $S_{\mathrm{t}\mathrm{o}\mathrm{t}}^z=1$ and that with $S_{\mathrm{t}\mathrm{o}\mathrm{t}}^z=0$) decreases monotonically as shown in Fig. 5B. For $D^z\hspace{0.17em}<\hspace{0.17em}0.08$, the spin excitation gap depends on the BCs. Since the DM interaction breaks spin rotational symmetry, we calculate the DSSF in both the longitudinal and transverse modes as shown in Fig. 5 C and D under different BCs. It is found that the intensity distribution of the DSSF remains similar to the results of the KAFM (SI Appendix, section IV), showing a broad distribution with a long tail to higher energies. Importantly, the low-energy excitations are governed by the transverse mode, which also shows substantial difference by tuning the BC. The dominant spectral peak in the antiperiodic BC shifts toward the low-frequency regime, showing the signal of gapless spin excitations. These results indicate the KSL as a critical phase.

Summary and Discussion

We have investigated the DSSF of the spin-$1/2$ Heisenberg model on a Kagome lattice with either farther neighbor or additional DM interactions using DMRG. The DSSF of the KSL shows different features from those in the gapped CSL or in the $\mathbf{q}=\left(\mathrm{0,0}\right)$ magnetic phase. For the KSL, the weight of the DSSF mainly concentrates along the boundary of the extended BZ, with a broad maximum near the $\mathbf{Q}=M$ point. In the energy scans, the dominant intensity shifts to the low-energy region, and a wide spectral distribution spans the high-energy region, showing a continuum expected for a spin liquid state. In particular, the calculated DSSF fairly reproduces the key features of the INS measurements of herbertsmithite. We also unveil the properties of the DSSF around the quantum critical point between the spin liquid and the magnetically ordered phase, which could be used to characterize topological quantum-phase transitions.

In closing, we would like to make some remarks about the nature of the KSL. The DSSF and spin gap for the KSL are sensitive to the BCs, pointing to the gapless nature of the KSL. In this respect, one plausible scenario is that the KSL is a $U\left(1\right)$ Dirac QSL (19–21, 23, 34, 53). The comparison of the low-energy behaviors of the DSSF in the CSL and KSL phases (SI Appendix, section I.D) also supports that the KSL is not consistent with a gapped spin liquid, although the finite-size calculations are not optimal to distinguish a gapless ground state. However, the Dirac QSL can be considered as the “parent state” for the CSL. That is, the CSL arises if a finite topological mass term (induced by flux piercing the hexagons and triangles) is spontaneously generated in the Dirac QSL by the correlation effect. Therefore, when the energy scale exceeds the gap value of the CSL, higher-energy excitations of the CSL and the Dirac QSL will likely be similar in terms of spectral weight distribution of the DSSF. In this context, the similarity of the dynamic spectra (above the gap scale) of the CSL and the KSL in our calculations (Fig. 2) is another indication of the nature of the KSL as a $U\left(1\right)$ Dirac QSL.

Methods

In this study, we develop a DMRG program to calculate dynamic structure factor, which can apply to general strongly correlated systems. We consider cylinder geometry with closed boundary in the $y$ direction and open boundary in the $x$ direction, with $L_x$ ($L_y$) as the numbers of unit cells along the $x$ ($y$) direction. Most of calculations are performed on the $L_y=4$ cylinder. [For the $\mathbf{q}=\left(\mathrm{0,0}\right)$ phase, we also obtain results for $L_y=6$.] The length of the cylinder is set to be $L_x=24$. Generally, we first obtain the ground state on the cylinder using finite DMRG (54). We ensure that the discard error of ground state is of the order or smaller than $10^{-6}$ by keeping up to 3,200 states. The static spin structure factor (Eq. 2) is calculated using static correlations in the middle $L_y\times L_y$ unit cells. After obtaining the ground state, we calculate the dynamical properties in the middle $L_y\times L_y$ unit cells by finite sweeping (55, 56). The advantage of this method is avoidance of edge excitations, which is similar to the setup to calculate the spin excitation gap as proposed in ref. 57. More details of this numerical scheme and related benchmarks on the square antiferromagnet Heisenberg model are presented in SI Appendix, section I.