Fast pressure-jump all-atom simulations and experiments reveal site-specific protein dehydration-folding dynamics

Significance

When proteins fold, water is squeezed out of the hydrophobic core, leaving small desolvated pockets. Such voids are critical for protein flexibility and function, but not much is known about how and when they form during protein folding. We combine long atomic-level simulations with rapid pressure-drop experiments to see how water gets out of a protein as it folds. For one small protein, we find that dry pockets can form repeatedly between various pairs of protein α-helices before a successful folding event finally occurs. For another small protein, drying and folding are much more concerted. Thus, the formation of void pockets that enhance protein flexibility can occur in a concerted fashion or by coincidence of several local events.

Abstract

As theory and experiment have shown, protein dehydration is a major contributor to protein folding. Dehydration upon folding can be characterized directly by all-atom simulations of fast pressure drops, which create desolvated pockets inside the nascent hydrophobic core. Here, we study pressure-drop refolding of three λ-repressor fragment (λ_6–85) mutants computationally and experimentally. The three mutants report on tertiary structure formation via different fluorescent helix–helix contact pairs. All-atom simulations of pressure drops capture refolding and unfolding of all three mutants by a similar mechanism, thus validating the nonperturbative nature of the fluorescent contact probes. Analysis of simulated interprobe distances shows that the α-helix 1–3 pair distance displays a slower characteristic time scale than the 1–2 or 3–2 pair distance. To see whether slow packing of α-helices 1 and 3 is reflected in the rate-limiting folding step, fast pressure-drop relaxation experiments captured refolding on a millisecond time scale. These experiments reveal that refolding monitored by 1–3 contact formation indeed is much slower than when monitored by 1–2 or 3–2 contact formation. Unlike the case of the two-state folder [three–α-helix bundle (α₃D)], whose drying and core formation proceed in concert, λ_6–85 repeatedly dries and rewets different local tertiary contacts before finally forming a solvent-excluded core, explaining the non–two-state behavior observed during refolding in molecular dynamics simulations. This work demonstrates that proteins can explore desolvated pockets and dry globular states numerous times before reaching the native conformation.

Water is a critical participant in protein folding (1). Roughly half of the folding free energy of proteins is related to reorganization of water molecules (2), and the hydrophobic effect plays an important role (3, 4). Understanding folding mechanisms in the context of a protein’s hydration is one of the outstanding challenges in molecular biophysics (5, 6). To this end, previous studies using hydrogen exchange combined with mass spectrometry have shown a concerted desolvation of secondary structural units during the process of folding (7). Both dry and wet globules have been observed on the path to the native state using fluorescence and circular dichroism (8, 9) and NMR (10). In addition, molecular dynamics (MD) simulations have captured the process of protein folding at atomic resolution, including explicit simulation of water (11, 12). However, the validation of MD with experimental data that monitor desolvation has been challenging (13).

Pressure denaturation can be used to study protein–water interactions during folding (14). Hydrostatic pressure causes penetration of water molecules into the hydrophobic but imperfectly packed protein core, thereby reducing the protein’s partial molar volume (15). Recently, large pressure jumps with microsecond time resolution have been demonstrated experimentally (16, 17) and simulated using MD (18). Desolvated cavities in the protein core (15) are restored by downward pressure jumps, which facilitate refolding without a change in solvent or thermal motion. In addition, pressure perturbation reduces the effects of protein aggregation, common in temperature-jump (T-jump) experiments performed near the denaturation temperature (16, 17). Finally, pressure-jump (P-jump) experiments can utilize intrinsic fluorophores and fluorescence contact quenchers, such as tryptophan and tyrosine (17).

Desolvation and contact formation can occur in many parts of a protein, yet fluorescence experiments that measure protein dynamics usually rely on a single probe or donor–acceptor pair that reports on a single-order parameter. Thus, deviations from two-state behavior are difficult to capture (19). Previous work has used multiprobe tryptophan fluorescence (20, 21), NMR spectroscopy (22, 23), and IR spectroscopy (24, 25), as well as a combination of multiple approaches (26–28), to address this challenge. To probe three sites, we previously engineered the λ_6–85 mutants λ₁₂, λ₃₂, and λ₁₃, which contained tryptophan–tyrosine pairs as contact probes between α-helices 1–2, 3–2, and 1–3 (29, 30) (sequences are shown in SI Appendix, Fig. S1). Tyrosine quenches tryptophan via Dexter energy transfer when the two α-helices containing these residues contact each other, such that the side chains are less than ∼5 Å apart. Thus, we can monitor the formation of specific tertiary contacts between secondary structure elements.

As shown in this work, the enhanced computational capacity of MD now can simulate each multiprobe protein mutant individually. We performed all-atom, explicit-solvent MD on a long time scale (110 μs of total simulation time) to simulate P-jump refolding of λ₁₂, λ₃₂, and λ₁₃. A transient refolding event is captured for each mutant to validate that the fluorescent contact probes used in our experiments do not perturb the folding mechanism. In addition, we performed fast pressure-jump relaxation experiments on the mutants λ₁₂, λ₃₂, and λ₁₃, and compared these experimental results with P-jump MD simulations. The computed time scales of local helix–helix contact formation correlate with the much slower experimental global folding time scales monitored by local helix–helix contacts. Experimental and computational analysis suggests that the rate-limiting step in λ_6–85 folding is the formation of interhelical contacts between noncontiguous α-helices 1 and 3. In addition, MD simulations reveal that multiple local dehydration and rehydration events of the local core contacts precede the critical folding step. The kinetic barrier that limits the rate of hydrophobic core formation must be even greater in experiments than in the simulations, as evidenced by the 60- to 70-fold slower observed experimental refolding time scales.

Results

The three multiprobe λ_6–85 constructs have been studied previously using 100-ns-long MD simulations, protein expression level analysis, tryptophan fluorescence spectroscopy, T-jump, and circular dichroism spectroscopy (29). The previous MD trajectories were too short to test whether the dynamics of λ_6–85 are significantly altered from mutant to mutant. Instead, an MD trajectory of a single mutant (11) was used by us for the analysis of λ_6–85 folding. Thus, Prigozhin et al. (29) assumed that the folding mechanism of one mutant was representative of all.

Here, an independent MD simulation was performed for each of the three Trp/Tyr contact-pair mutants on the Anton 2 supercomputer (31) (Methods and SI Appendix, section 2). The initial state of each mutant was prepared by mutating the protein conformation of the last frame of a 1.45-μs high-pressure simulation from a previous study (18) (summarized in SI Appendix, section 2). Next, the mutants were subjected to an additional 100 ns of simulation at high pressure (5,000 bar), which was flanked by a 10-ns pressure jump and a 10-ns pressure drop, for total of 120 ns (Fig. 1B). Finally, λ₁₂ was simulated at 1 bar and 350 K for 25 μs, λ₃₂ at 1 bar and 340 K for 25 μs, and λ₁₃ at 1 bar and 340 K for 60 μs. The simulation temperatures were chosen to be ∼40 K higher than the experimental melting temperatures of each mutant because the thermal stability of λ_6–85 is significantly higher with the Charmm22* simulation force field (32).

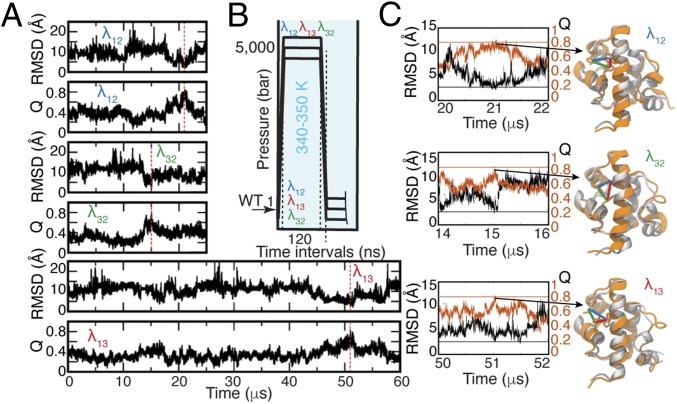
Fig. 1.

MD simulations of the three λ_6–85 multiprobe mutants. (A) Time trajectories of Q and rmsd based on α-carbon atoms of the λ_6–85 crystallographic state [PDB ID code 3KZ3 (33)]. Red dashed vertical lines indicate the time points when the proteins visited the folded state. (B) Simulation protocol (details are provided in SI Appendix, section 2 and Table S1). The unfolded WT from our previous study (18) was mutated and simulated at 5,000 bar and 340 or 350 K before jumping the pressure down to 1 bar. (C) Close-up view of time dynamics of Q (orange) and rmsd (black) near the folded states. Horizontal lines correspond to Q_max = 0.8 (orange) and rmsd = 2.5 Å (black). The crystallographic state (gray) overlapped with the simulated structures of each mutant at the time when these mutants visited the folded state with Q_max = ∼0.8 (21.0 μs for λ₁₂, 15.0 μs for λ₃₂, and 51.5 μs for λ₁₃). Distances between residues used in fluorescence measurements are shown with colored lines (contact 1–2 in blue, contact 3–2 in green, and contact 1–3 in red).

In each simulation, the corresponding mutant transiently visited a conformation close to the crystallographic folded state (33). The folded state was observed at 21.0 μs (λ₁₂), 15.0 μs (λ₃₂), and 51.5 μs (λ₁₃) of simulation time, as highlighted with red vertical lines in Fig. 1A. The similarity of the simulated proteins to the folded state was characterized by the fraction of native contacts (Q; the equation for the calculation of Q is provided in SI Appendix, section 12) and the root-mean-square deviation (rmsd) of α-carbon atoms calculated with respect to the crystallographic folded state of the three mutants [Protein Data Bank (PDB) ID code 3KZ3 (33)], as shown in Fig. 1A. Fig. 1C zooms in on the trajectories when the folded state (Q_max ≥ 0.8) was reached by each mutant. In addition, Fig. 1C shows overlays of the crystallographic state with the near-folded MD-simulated states for each λ_6–85 mutant to verify that the folded state was achieved.

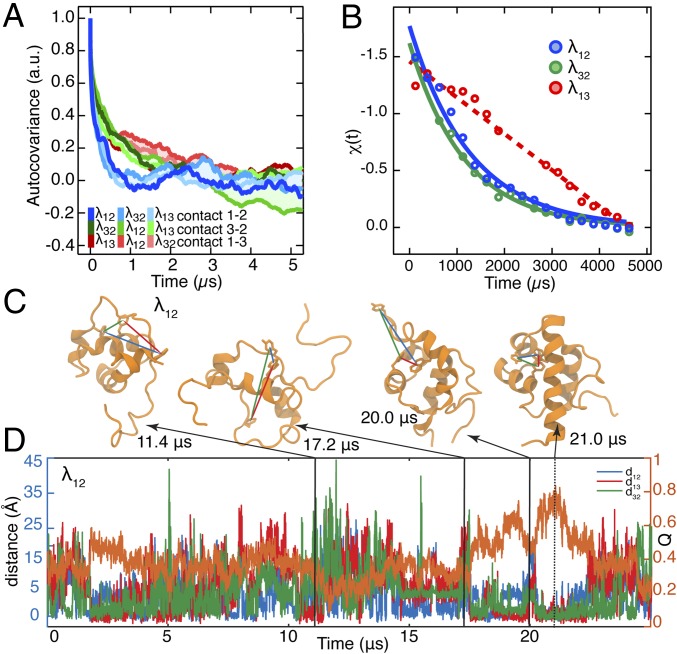
MD simulations were analyzed to extract the dynamics captured by the fluorescent probes (Fig. 2). For each mutant, all three distances between the side chains of residues located at the positions used for fluorescent probes and quenchers were calculated, measuring contacts between helix pairs 1–2, 3–2, and 1–3. Thus, a total of nine time trajectories were generated: three for each of the three mutants (SI Appendix, Figs. S2–S4). In the MD simulations, each of the three helix–helix distances was able to reach folded-like values multiple times, while the whole protein was not in the folded conformation. Fig. 2C shows structural examples for λ₁₂, with arrows pointing to the corresponding time points on the trajectory (blue = 1–2, green = 3–2, and red = 1–3, while orange is Q, the fraction of total native contacts).

Fig. 2.

Dynamics of λ_6–85 captured by three fluorescent contact pairs. (A) Autocovariance analysis of the MD time trajectories of distances between residues used as contact probes in ${\text{λ}}_{6-85}$. In each simulation, the three residue–residue distances were extracted regardless of whether the mutants had the fluorescent probes in those positions or not. Autocovariance analysis was performed on the resulting time trajectories and shows fast exploration of contacts before folding. (B) Experimental fluorescence lifetime relaxation traces collected following a P-jump of ${\text{λ}}_{12}\left(\tau =1.4\pm 0.5\right)$ ms, ${\text{λ}}_{32}\left(\tau =1.2\pm 0.3\right)$ ms, and λ₁₃. The time constant could not be extracted for the slow λ₁₃ decay [linear fit (dashed line) is shown instead]. All P-jump time traces are normalized from 0 to 1. (C) Representative protein structures with at least one folded-like distance for λ₁₂. Interresidue distances are shown with lines color-coded by the contact pair (λ₁₂, blue; λ₃₂, green; λ₁₃, red). The simulation time points when these structures were observed are indicated. (D) Time trajectories of the λ₁₂ fraction of native contacts (Right axis; orange trace) and distances between the side chains of residues located at the positions used for fluorescent probes (Left axis; blue, green, and red traces).

Autocovariance functions of these distances report on the characteristic time scale for the local contact formation/dissolution dynamics between the specified residues, which ultimately lead to helix–helix contacts that result in folding of λ_6–85 mutants. The nine autocovariance functions shown in Fig. 2A suggest that the α-helix 1–2 contact (blue) forms and dissolve fastest and the α-helix contact 1–3 (red) forms and dissolves slowest. All three mutants feature a very similar time scale for each contact pair. Thus, the contact pair time scale is not affected by the mutations. Dynamic fingerprint analysis of the autocovariances (Methods and SI Appendix, Fig. S5), which uses an inverse Laplace transform to numerically predict time scales that contribute to a given autocovariance function, reveals the following slowest characteristic time scales: 0.35 ± 0.05 μs (contact 1–2), 0.9 ± 0.1 μs (contact 3–2), and 2.5 ± 0.5 μs (contact 1–3). Exponential fits of the autocovariances in Fig. 2A produce the same ranking as fingerprinting (0.24–1.6 μs; SI Appendix, Fig. S6 and Table S2), with 1–2 being fastest and 1–3 being slowest. Simulated P-jump refolding of λ₁₃ is also slowest (Fig. 1 A and C), hinting that helix contact time scales and overall folding time may be correlated, although a single simulated refolding event is insufficient to draw that conclusion.

Thus, we performed P-jump experiments at 22 °C on the three λ_6–85 mutants to see if the simulated ordering of helix contact time scales correlates with actual folding times (Fig. 2B). The proteins were expressed as described previously (18), pressurized to 1,200 bar (λ₁₂) or 1,500 bar (λ₃₂, λ₁₃), and dropped down to atmospheric pressure within 3 μs (Methods) to monitor refolding. The longer dead time than in the study by Dumont et al. (16) precluded resolving the fast “downhill phase.” During the P-jump, tryptophan fluorescence lifetime decays were collected with a photomultiplier tube every 12.5 ns and analyzed as described in Methods: χ(t) measures normalized average lifetime (χ = 0 is shortest, χ = 1 is longest).

P-jump data for λ₁₃ in Fig. 2B appeared linear and did not fully decay to equilibrium within the 5-ms measurement window because the relaxation time of this mutant is longer than 3 ms. The other two mutants, λ₁₂ and λ₃₂, showed P-jump relaxation decays of ${\tau }_{12}=1.4\pm 0.5\hspace{0.17em}\text{ms}$ and ${\tau }_{32}=1.2\pm 0.3\hspace{0.17em}\text{ms}$, respectively (Fig. 2B and SI Appendix, section 6). Thus, the 1–3 contact yields the slowest experimental folding time, the slowest folding time by MD (single event), and the slowest time scale for local helix contact formation as determined by MD. The 1–2 and 3–2 contacts are always faster than the 1–3 contact, but their time scales are too close to be ranked.

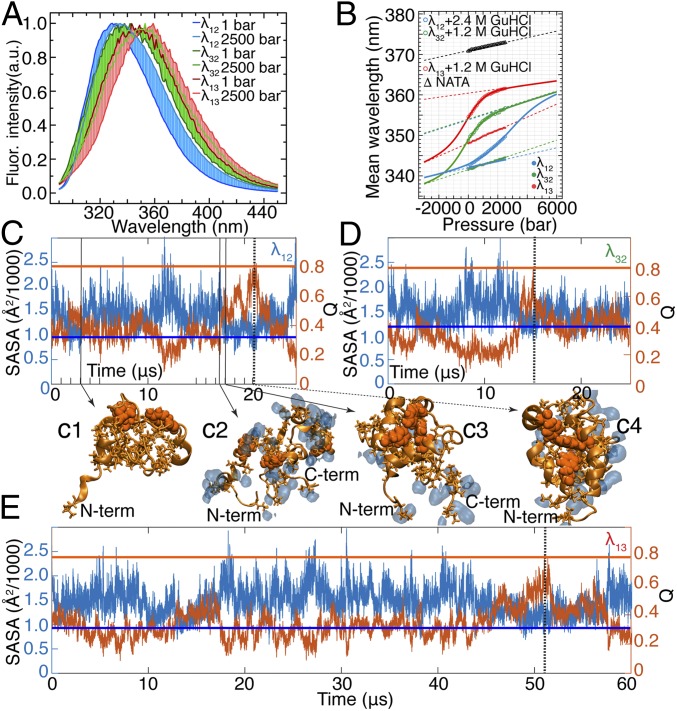
The experimental fluorescence spectrum of tryptophan is sensitive to solvent exposure of the side chain upon pressure denaturation when the dry core is solvated (34) (Fig. 3A). The mean fluorescence wavelength of a tryptophan derivative, N-acetyl-l-tryptophanamide (NATA), is 371 nm at 1 bar (Fig. 3B), but this value is 342 nm for the tryptophan in position 22 of λ₁₂ at 1 bar and in the absence of the denaturant guanidine hydrochloride (GuHCl) (Fig. 3B). Pressure-induced unfolding of all three λ_6–85 mutants in the presence of GuHCl increases their mean fluorescence wavelength (Fig. 3 A and B). (An analysis of pressure-induced equilibrium unfolding of λ_6–85 mutants is provided in SI Appendix, section 7, with SI Appendix, Figs. S18–S21 and Table S3 A and B).

Fig. 3.

Water-coupled dynamics in the hydrophobic core of λ_6–85. (A) Fluorescence (Fluor.) spectra of λ_6–85 mutants at 1 bar and 2,500 bar (the full datasets are provided in SI Appendix, Fig. S21). The point of maximal intensity is normalized to unity to highlight the pressure-induced spectral shift. λ₁₂ is in 2.4 M GuHCl; λ₁₃ and λ₃₂ are in 1.2 M GuHCl. (B) Change of mean wavelength of the spectra in A as a function of pressure. Connected solid circles are the data collected for each mutant in the absence of GuHCl. Connected open circles represent the data collected at 2.4 M GuHCl for λ₁₂ and 1.2 M GuHCl for λ₁₃ and λ₃₂. The data for NATA are also shown (△). Solid lines are two-state thermodynamic fits, and dashed lines are the corresponding baselines of folded and unfolded states (the detailed fitting procedure is described in SI Appendix, section 7). (C–E) SASA of hydrophobic side chains of λ_6–85 mutants is anticorrelated with Q. Horizontal lines mark SASA (blue) and Q (orange) values in the folded state of each protein mutant. SASA values are 984 Ų for λ₁₂, 1,180 Ų for λ₃₂, and 908 Ų for λ₁₃. Vertical dashed lines (black) mark time points when each protein visited the folded-like conformation (21.0 μs for λ₁₂, 15.0 μs for λ₃₂, and 51.5 μs for λ₁₃). Representative structures of λ₁₂ (tryptophan/tyrosine contact pairs are shown as orange van der Waals spheres, hydrophobic side chains are shown as orange sticks) demonstrate that expulsion of water (shown as blue shapes within 2.5 Å from hydrophobic side chains) from the protein core can form a nonnative overpacked (low Q and SASA below folded value) conformation (C1), while the protein core can be hydrated (C2) en route to the native conformation (C3 and C4). C-term, C terminus; N-term, N terminus.

The interdependence of the protein conformational dynamics and the solvation of its hydrophobic residues by water can be visualized in the MD simulations using the solvent-accessible surface area (SASA) of hydrophobic side chains and Q (fraction of total native contacts) calculated for each protein mutant. In Fig. 3 C–E, the horizontal blue lines indicate the SASA values of the folded state of each mutant and the horizontal orange lines indicate the Q values of the folded state of each mutant. Although SASA and Q are roughly anticorrelated, it is evident that solvent exclusion of hydrophobic side chains does not necessarily lead to a native-like state. For example, λ₁₂ expelled water at the beginning of the simulation (∼3 μs; Fig. 3 C, 1), but then failed to fold. In this particular case, a transient “dry” globule (8, 35) did not directly lead to the formation of the native state (Fig. 3 C, 4). Instead, the hydrophobic core of λ₁₂ was first unpacked again and hydrated several more times (Fig. 3 C, 2) before water was eventually removed and the protein core folded in a concerted fashion (Fig. 3 C, 3 and C, 4). Thus, local drying is a necessary, but not sufficient, condition for forming a folded structure.

Figs. 1A and 3 C–E show that the dynamics of λ_6–85 have low cooperativity, as evidenced by the gradual conformational transitions characterized by such conventional order parameters as Q or rmsd (5) (Fig. 1). This lack of cooperativity has been attributed to downhill folding or short-lived intermediates (36, 37). In Figs. 1 and 3, no clear evidence for a small number of intermediates was observed. Although multiple intermediates with small barriers cannot be ruled out, downhill folding on a rough free energy landscape is the most parsimonious explanation of that limiting case (35).

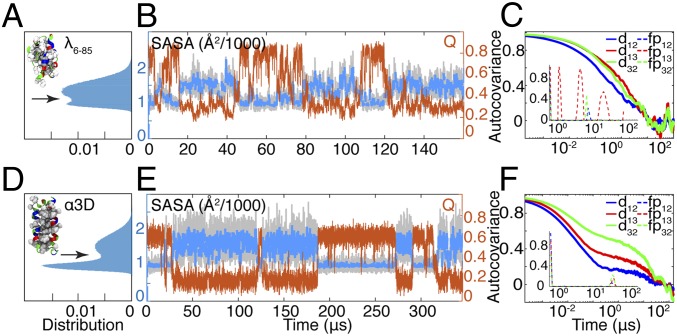
A seemingly similar model protein, the three–α-helix bundle (α₃D), experiences much more cooperative behavior by the same metrics (11) (Fig. 4). α₃D contains 73 amino acids compared with 80 in λ_6–85, and both proteins are α-helical proteins. MD simulations (11) suggest that these proteins have similar folding times of 27 μs and 49 μs, respectively. SASA of only hydrophobic side chains (Fig. 4B) calculated using the MD simulations of Shaw and coworkers (11) revealed two-state–like dynamics in the case of α₃D (Fig. 4 D and E), but less so for λ_6–85 (Fig. 4 A and B; details are provided in SI Appendix, Fig. S22 and Table S4). Notably, when all side chains are included in the SASA calculation, the folded and unfolded ensembles are indistinguishable for either protein.

Fig. 4.

Comparison of solvation dynamics of λ_6–85 (A–C) and α₃D (D–F). Native structures in A and D are color-coded by residue type (hydrophobic, white; polar, green; basic, blue; acidic, red). Hydrophobic residues used in SASA calculations are shown using the van der Waals representation. (A and D) SASA serves as a more effective reaction coordinate for the two-state folder, α₃D, compared with λ_6–85. α₃D SASA shows a clear saddle point (arrow) separating native and unfolded ensembles. (B and E) Smoothed (2-μs Gaussian filter) time traces of SASA of the hydrophobic side chains (blue; raw time traces shown in gray) follow the folding dynamics of both the two-state system, α₃D, and the less cooperative λ_6–85. Q (orange) is anticorrelated with SASA in the case of α₃D, while there are instances of low SASA and low Q for λ_6–85. (C and F) Autocovariance of distances between side chains of the residues that can be used as probes for interhelical distances (solid lines). Fingerprints (Inset, dashed lines) calculated using software developed by Noé et al. (38) report on the characteristic time scales contributing to each autocorrelation function (SI Appendix, Fig. S24 and Table S5).

We also compared pairwise helix distances for both proteins, using the side chains of Leu10, Ile35, and Ala60 (located roughly in the middle of helices 1, 2, and 3) for α₃D. Autocovariance functions show very different folding dynamics for α₃D and λ_6–85 (Fig. 4 C and F): α₃D shows dynamics that are similar between the contact probes, while the interresidue distances of λ_6–85 show varying time scales. Again, the dynamic fingerprinting technique (38) (Methods) revealed that while both proteins have fast relaxations, on the longer time scale, the proteins display radically different behavior. All of the fingerprints of α₃D are clustered near 20 μs. A similar cluster is also observed for λ_6–85 dynamics at shorter time scales (∼4 μs), but contact 1–3 of λ_6–85 explores the structural space on multiple time scales (red dashed lines, Fig. 4C, Inset).

Discussion

MD Simulations Validate Nonperturbative Contact Pairs.

The MD simulations presented here suggest that the folding mechanism of λ_6–85 is not influenced by the mutations that introduced the fluorescent probes for two reasons. First, all of the simulated proteins visited the near-native crystallographic-like state (within 2.0 Å, 2.2 Å, and 2.2 Å rmsd from the crystal structure for λ₁₂, λ₃₂, and λ₁₃, respectively) within their simulation times. The fact that each mutant folded into the same crystallographic-like state during the simulation suggests that the native state is unchanged regardless of the mutations. Second, the autocovariance analysis reported in Fig. 2A shows that the characteristic time scales for 1–2, 3–2, and 1–3 contact formation are conserved across the mutants, with 1–2 forming/dissolving most frequently and 1–3 forming/dissolving least frequently. Thus, the collective effect of residues other than the ones in the probe sites dominates the dynamics of the λ_6–85 conformational search. These results, in combination with the previously reported experimental analysis (29, 30), suggest that the fluorescent contact probe mutations are conservative, thus validating λ₁₂, λ₃₂, and λ₁₃ as experimental proxies to study λ_6–85 folding at the level of the tertiary contact formation.

Such minimal perturbation is by no means universal. Even within λ_6–85, we have previously shown that α-helix 4 was not amenable to the incorporation of fluorescent contact probes at the positions that were tested (29). In such a case, it may be necessary to make size-complementary mutations to conserve packing volume, as has been accomplished already for a λ-repressor fragment (39). Validation by MD will enable the use of short-range donor–quencher contact pairs; IR and NMR experiments are, of course, essentially label-free, although they require larger sample concentrations where aggregation may become an issue.

Water Tracks Motions of the Helices in λ_6–85.

Dynamic fingerprint analysis of the SASA autocovariance for the hydrophobic side chains of α₃D folding simulations (SI Appendix, Fig. S23) reveals a time scale comparable to the folding time of the protein, ∼27 μs, indicating that water is expelled as global folding proceeds in a two-state manner. In addition, all α₃D distances have similar dynamic content in Fig. 4F. In contrast, the fingerprints of λ_6–85 SASA contain a wide range of fast time-scale components, consistent with the time scale of repeated interhelical contact formation that precedes overall folding. Water can track λ_6–85 helix packing, both drying and hydrating λ_6–85 core residues multiple times, before the core is finally dewetted and compacted into the correct local topology characteristic of the native conformation (Fig. 3 C, 3). Thus, a local drying transition alone does not necessarily guarantee folding. A number of studies have pointed out the importance of drying the protein core during folding (5, 6, 13).

Similar dynamic patterns are observed in SASA and in the number of water molecules located near the fluorescent probes. In particular, hydration of Trp-51 in our folding simulations of λ_6–85 mutants reveals this pattern (SI Appendix, Figs. S2–S4). Mechanistically, our short-lived folded conformations (Fig. 1C) are followed by rapid influx of the water as hinted by the SASA of hydrophobic residues (Fig. 3 C–E). Future fast P-jumps with spectral resolution could shed more light on dewetting of at least Trp residues via Stokes shift.

Local and Global Dynamics of λ_6–85 Are Correlated over Different Time Scales.

In the absence of multiple folding/unfolding events, the autocovariance decay curves in Fig. 2A are dominated by fast dynamics of the nonnative ensemble. It is this high frequency of local attempts that ultimately leads to global folding, making it critical for the folding mechanism of λ_6–85. Local contact formation occurs on a much faster time scale (0.35–2.5 μs from fingerprinting analysis, 0.24–1.6 μs from exponential fits in SI Appendix, Table S2) than global folding. As expected, local contact formation occurs near the “folding speed limit” of ca. 1 μs (40), which is much faster than activation barrier-limited global refolding.

Nonetheless, the computed speed of local transient contact formation in the nonnative ensemble is correlated with the computed and experimental rates of overall folding. The computed (Fig. 1A) and experimental (Fig. 2B) overall refolding time scale of λ₁₃ relative to λ₁₂ and λ₃₂ is in agreement with the slower formation/dissolution of the 1–3 contact pair relative to the 1–2 and 3–2 contact pairs (SI Appendix, Fig. S5). Trapped state analysis of our folding MD simulations demonstrates the presence of a low-energy trap: a high-Q ensemble with a large 1–3 distance (SI Appendix, Fig. S25) in all mutants. Thus, the observed trends suggest that a highly dynamic sampling of the 1–2 helix contact in the nonnative ensemble precedes folding, while the slower contact formation between noncontiguous helices 1 and 3 is part of the rate-limiting step during which at least both of these pieces must fall into place simultaneously.

Comparison with Previous T-Jump Experiments.

The refolding dynamics from the pressure-denatured state at 22 °C occur in ≈1 ms for λ₁₂ and λ₃₂, and even more slowly for λ₁₃. This observation is in contrast to the ≈50-μs relaxation times observed for these mutants at elevated temperature (40–50 °C higher) by T-jump experiments (29). Using k(T₁)/k(T₂) = η(T₂)/η(T₁) exp[ΔG^†(T₂⁻¹ − T₁⁻¹)/R] to relate rate coefficients k, viscosities η, and activation barriers ΔG^† at two different temperatures, the folding barrier would have to be ≈40 kJ/mol or ≈16 k_BT to account for the reduced rate [η(T₂)/η(T₁) ≈ 0.45 for 65 °C vs. 20 °C]. However, natural logarithm of the folding rate [ln(k_f)] of λ_6–85 is known to have a nonlinear temperature dependence (41), and the pressure- and temperature-denatured states may be structurally different (42), accounting for some of the difference.

Discrepancy Between Experimental and Computational Folding Times.

The simulated refolding times of λ_6–85 after the pressure jump (15–51.5 μs) were 60- to 80-fold faster than the experimental refolding times (1.2 to >3 ms). Some of the possible reasons for this discrepancy are discussed below.

Temperature.

The higher simulation temperature (e.g., 340 K in MD of ${\text{λ}}_{13}$ vs. ∼295 K used in experiments) could contribute to faster activated dynamics observed in simulations. Faster activation at a 45 K higher simulation temperature could contribute a factor of ∼10 for a folding barrier of ∼40 kJ/mol. This is also consistent with faster T-jump results at higher temperature, as noted above.

Viscosity.

Reduced viscosity of the simulated water is a known artifact of MD simulations that could be partially responsible for fast diffusion and a large prefactor for contact formation and global folding (43). The present simulations were run well above room temperature, and the low viscosity of the TIP3P water model (43) and higher temperature could account for the up to ∼10-fold faster helix contact formation (as low as 0.24 μs for λ₁₂) compared with the “speed limit” set by the P-jump burst phase (2.1 μs in ref. 16).

Sampling.

Since only a single transient folding event was observed in each simulation run, the observed folding times are subject to a significant uncertainty caused by insufficient sampling. However, the simulations of the three mutants are consistent (15–50.5 μs), so it is highly unlikely that undersampling can account for the full factor of 60- to 80-fold. Bayesian two-state analysis suggests that it could plausibly account for a factor of 2.

Force field.

Some of the difference in computed vs. observed rates may be due to the force field allowing parts of the protein to stick to each other too easily. Such sticking could effectively lower the activation barrier in the simulations relative to experiments. There is evidence for such sticking, forced filed corrections have been implemented to reduce it (44). If sticking is a significant contributor, we predict a somewhat paradoxical outcome: While folding of a single protein in a water box can be sped up in simulations, simulated folding in the presence of other proteins (e.g., a simulated cytoplasm) can be slowed down.

In conclusion, our simulations of three mutants of λ_6–85 show consistent trends in the interhelix contact formation time scales regardless of mutant identity, validating the minimally perturbative nature of mutants used here to study the mechanism of folding by local contact formation. MD simulations, in agreement with experiments, revealed that fast-folding proteins, such as λ_6–85, may show local drying dynamics that are asynchronous with hydrophobic core formation, while bona fide two-state folders, such as α₃D, are highly cooperative and demonstrate close anticorrelation between the hydrophobic core solvation and protein folding. Such asynchronicity does not necessarily imply slower folding and is not related to protein size, as λ_6–85 and α₃D have very similar size and folding time scales.

Methods

Protein Mutagenesis, Expression, and Purification.

Proteins were expressed in Escherichia coli, strain BL21 (Stratagene) as described previously (29). The gene of interest was cloned into a pET-15b vector, which contained an N-terminal sequence for six consecutive histidine residues for purification. The cells were transformed with the plasmid containing the gene of interest, and induction was done with 1 mM isopropyl β-d-1-thiogalactopyranoside overnight. The cells were lysed using sonication in the presence of DNase and 1 mM PMSF to reduce protease activity. The protein was then purified using a nickel-nitrilotriacetic acid column (Qiagen), followed by dialysis in 50 mM K₃PO₄ buffer. Mutagenesis was done using a Stratagene site-directed mutagenesis protocol.

Equilibrium Experiments.

A Varian Eclipse spectrophotometer was used to acquire fluorescence spectra. A pressurization cell from ISS and a hydrostatic pump (HiP) were used for pressure thermodynamic experiments. A Jasco spectrometer was used to acquire circular dichroism spectra. GuHCl was purchased from Sigma–Aldrich.

Kinetic Experiments.

P-jump experiments were performed using a custom-built system, which was described in detail previously (16, 17). Briefly, the sample (∼8 μL at 200 μM concentration) was placed in a dimple machined in a sapphire cube. Pressurization was achieved using an HiP. The pressure was released by rupturing a stainless-steel burst membrane using ∼10-kA current that was generated using a custom capacitor bank. The sample was probed using a mode-locked, frequency-tripled titanium-sapphire laser (center wavelength of ∼285 nm) at an 80-MHz repetition rate. Fluorescence decays were recorded in real time with an oscilloscope using a sampling period of 100 ps. With the 1.2- to 1.5-kbar P-jumps used here, the dead time of the instrument was 3 μs as determined by NATA jumps, about sixfold longer than for 2.5-kbar jumps in a study by Dumont et al. (16).

Data Analysis.

Data were analyzed using Igor Pro (Wavemetrics) and MATLAB (MathWorks). Two-state thermodynamic fits were done as described by Prigozhin et al. (29). Fluorescence lifetime data from the P-jump experiments were recorded in real time using a sampling period of 100 ps. Fluorescence decays, f(t_i) at t_i = 0, 12.5, 25, ^… ns were then parametrized by decomposition into a before-jump profile f₁ and a postjump (5 ms) profile f₂ as f(t_i) = a₁(t_i) f₁ + a₂(t_i) f₂. Signal was reported as χ(t) = a₁(t_i)/[a₁(t_i) + a₂(t_i)], where χ(t) is a dimensionless parameter that reports on the change of fluorescence lifetime as a function of time. This two-state assumption was sufficient to fit the data, although it does not imply true two-state folding. The parameter χ(t) was fitted to a single-exponential function of the form $A\ast \text{exp}\left[-t/\tau \right]$.

Atomic Models.

To make direct comparisons with experiments, three λ-repressor (λ_6–85) mutants were constructed at the same pressure-denatured state with the exact amino acid sequences as in the experiments (SI Appendix, Fig. S1). The initial structures of the λ_6–85 mutants were taken from a previous computational model (18) [PDB ID code 3KZ3 (33)], and the following mutations were made to match the exact sequence as shown in SI Appendix, Fig. S1A: F22W, Q33Y for λ₁₂, F22W, F51Y for λ₁₃, and Q33Y, F51W for λ₃₂. The mutated structures were then solvated using the TIP3P water model (45) and 55 mM of NaCl. Each prepared system contained ∼69,000 atoms.

MD Simulations.

MD simulations were performed with the CHARMM22* force field (46) for protein and ions in a 9 × 9 × 9-nm³ water box with appropriate ionization and periodic boundary conditions in the isothermal-isobaric ensemble at the temperature chosen for each λ_6–85 mutant. To mimic the P-jump experiments, the steps summarized in Fig. 1B and SI Appendix, section 2 were then taken in the simulations.

MD Simulations on NAMD2.

Step 2 in the above protocol and the equilibration was performed with NAMD2 (47). The systems to be simulated were minimized for 6,000 steps, followed by 12 ns of equilibration with harmonic constraints on heavy atoms [force constant = 1 kcal/(mol Ų)]. The constant temperature was controlled by Langevin dynamics, and the constant pressure was regulated by the Nosé–Hoover–Langevin piston method (48). The particle mesh-Ewald method was employed to calculate long-range electrostatic forces (49). The time step was set to 2 fs. Data analysis and figure rendering were done using the VMD computer program (50).

MD Simulations on Anton 2.

Refolding simulations for all three λ-repressor mutants were carried out on the Anton 2 platform (31) for a total time of 110 μs (λ₁₂ = λ₃₂ = 25 μs, λ₁₃ = 60 μs). The multigrator integration method was applied (51). Short-range forces were evaluated at every time step, and long-range electrostatics were calculated every three time steps using the Gaussian split Ewald method (52). The time step was set to 2.5 fs.

Dynamics Fingerprint Analysis.

Dynamic fingerprint analysis of autocovariance of MD distance and SASA were performed using software developed by Noé et al. (38). In brief, the method performs a multiexponential fit, which reports on characteristic time scales present in the autocovariance time traces. Noise was assumed to be constant with intensity (SD) of $0.5/\sqrt{time}$. The profiles were optimized (38) for 2 × 10⁷ steps (default) or 5 × 10⁷ steps for d₁₃. Time scales of the fingerprint peaks were estimated using single-Gaussian fits (SI Appendix, Table S5). Convergence was checked with likelihood, which is constant after a relatively small number of iterations (SI Appendix, Fig. S24).